Автоматика и телемеханика, № 12, 2021

Линейные системы

Н.М. НОВОЖИЛКИН (nikitanovozhilkin261@outlook.com),

Е.Ю. ПОРЦЕВА (katyhka2007@yandex.ru)

(Московский авиационный институт

(национальный исследовательский университет))

О ДОСТАТОЧНЫХ УСЛОВИЯХ ОПТИМАЛЬНОСТИ

ГАРАНТИРУЮЩЕГО УПРАВЛЕНИЯ В ЗАДАЧЕ БЫСТРОДЕЙСТВИЯ

ДЛЯ ЛИНЕЙНОЙ НЕСТАЦИОНАРНОЙ ДИСКРЕТНОЙ СИСТЕМЫ

С ОГРАНИЧЕННЫМ УПРАВЛЕНИЕМ¹

Рассматривается решение задачи быстродействия для линейных неста-

ционарных дискретных систем с выпуклыми ограничениями на управле-

ние. Предложен метод сведения общего случая задачи быстродействия к

случаю линейных ограничений на управление при помощи алгоритмов по-

лиэдральной аппроксимации. Сформулированы и доказаны достаточные

условия оптимальности гарантирующего решения. Приведены примеры.

На основе полученных методов решена задача наискорейшего демпфи-

рования высотного сооружения, расположенного в зоне сейсмической ак-

тивности.

Ключевые слова: дискретная система управления, задача быстродей-

ствия, оптимальное позиционное управление, задача линейного програм-

мирования, множество управляемости, выпуклый многогранник, полиэд-

ральная аппроксимация.

DOI: 10.31857/S0005231021120047

1. Введение

Задача быстродействия известна достаточно давно как задача оптималь-

ного управления с естественным функционалом качества — времени, за-

трачиваемого системой на достижение некоторого заданного терминального

состояния [1-3]. При рассмотрении систем с непрерывным временем данная

задача не обладает какими-либо существенными особенностями, выделяю-

щими ее из общей проблематики теории оптимального управления. Решение,

полученное на основе принципа максимума Понтрягина [1], гарантирует ре-

лейный характер управления для линейных систем.

В то же время системы с дискретным временем имеют ряд фундаменталь-

ных отличий от непрерывных систем при построении оптимального управле-

ния [4-6]. Тогда как в непрерывном случае оптимизационная задача является

¹ Работа выполнена при финансовой поддержке Российского фонда фундаментальных

исследований (проект № 18-08-00128-а).

задачей вариационного исчисления, в дискретном времени она представляет

собой задачу выпуклого программирования. Данный факт определяет прин-

ципиально иной набор средств для построения оптимальных процессов в дис-

кретном случае. Но несмотря на то что посредством дискретного принципа

максимума [6, 7] и метода динамического программирования [8] удается ре-

шить большую часть задач теории оптимального управления дискретными

системами, для решения задачи быстродействия эти принцип и метод оказы-

ваются неприменимыми в силу нерегулярности экстремума почти для всех

начальных состояний, неединственности оптимальной траектории и дискрет-

ного характера критерия качества управления - числа шагов, необходимого

для достижения фиксированного терминального состояния из заданного на-

чального [9, 10].

В связи с этим оказывается актуальным поиск альтернативных подхо-

дов для решения поставленной задачи. На данный момент продемонстриро-

вал свою эффективность метод, базирующийся на использовании множеств

0-управляемости [11] — множеств тех начальных состояний, из которых за

конечное число шагов можно перевести систему в начало координат посред-

ством выбора допустимого управления. При этом доказано, что метод реше-

ния во многом зависит от ограничений, накладываемых на управление. В слу-

чае строго выпуклых ограничений для построения оптимального по быстро-

действию управления удается модифицировать известный принцип максиму-

ма [9, 10]. Если множество допустимых значений управлений представляет

собой многогранник, на основе метода динамического программирования ре-

шение исходной задачи может быть сведено к решению ряда задач линейного

программирования [12, 13]. Однако в случае произвольных выпуклых огра-

ничений на управление аналогичные подходы оказываются неприменимыми.

Одним из методов сведения общего случая исходной задачи к случаю ли-

нейных ограничений на управление является проведение предварительной

полиэдральной аппроксимации множества допустимых значений управлений

системы. Данный подход аппроксимации одного множества другим, более

удобным в описании, широко используется не только в теории оптимального

управления [14, 15], но также, например, в задачах стохастической оптими-

зации [16, 17] и дискретной оптимизации [18]. На данный момент известно

большое количество алгоритмов полиэдральной аппроксимации [19-22], раз-

личающихся по сложности, эффективности и свойствам сходимости.

В публикациях [23, 24] рассмотрены методы построения субоптимально-

го решения в задаче быстродействия для линейной дискретной системы и

алгоритм оценки его точности на основе алгоритмов полиэдральной аппрок-

симации. Однако существенным недостатком этих работ является то, что в

них не проводится исследование сходимости критерия качества управления,

отсутствуют условия, при которых субоптимальное решение может оказаться

оптимальным.

Данная статья посвящена исследованию точности субоптимального реше-

ния, полученного на основе методов полиэдральной аппроксимации, в зада-

че быстродействия для линейной дискретной системы. Доказано, что если

алгоритмы внешней и внутренней аппроксимации гарантируют сходимость

к исходному выпуклому компакту в смысле расстояния Хаусдорфа [25], то

почти для всех начальных состояний за конечное число итерационного ал-

горитма удается добиться оптимальности гарантирующего решения. Данный

факт позволяет в полной мере свести задачу быстродействия для дискретной

линейной системы общего вида к случаю линейных ограничений.

Структура статьи следующая. В разделе 2 приведены постановка задачи

быстродействия и описание семейства множеств 0-управляемости, описан ме-

тод решения задачи быстродействия в случае линейных ограничений, произ-

ведена постановка задачи об аппроксимации. В разделе 3 рассмотрены неко-

торые свойства пространства компактных множеств, наделенного метрикой

Хаусдорфа. В разделе 4 сформулирован и доказан критерий оптимальности

гарантирующего решения в задаче быстродействия для произвольных вы-

пуклых ограничений. В разделе 5 опробована эффективность полученных

результатов на примере различных систем управления. В разделе 6 приве-

дено решение задачи наискорейшего демпфирования высотного сооружения,

расположенного в зоне сейсмической активности.

2. Постановка задачи

Рассматривается нестационарная линейная система управления с дискрет-

ным временем и ограниченными множествами допуcтимых значений управ-

лений (A, U):

x(k + 1) = A(k)x(k) + u(k),

(1)

x(0) = x₀, u(k) ∈ U(k), k ∈ N ∪ {0},

где x(k) ∈ Rⁿ - вектор состояния системы, U = {U(k)}∞k=0 - последователь-

ность множеств допустимых значений управлений системы, u(k) ∈ U(k) -

управление, A = {A(k)}∞k=0 - последовательность матриц системы. Пред-

полагается, что для каждого k ∈ N ∪ {0} множество допустимых значений

управлений U(k) ⊂ Rⁿ является выпуклым и компактным, 0 является отно-

сительно внутренней точкой U(k), A(k) ∈ R^n×n, det A(k) = 0. Для системы

(A, U) решается задача быстродействия, т.e. требуется вычислить минималь-

ное число шагов N_min, за которое можно перевести систему из заданного на-

чального состояния x₀ ∈ Rⁿ в начало координат, а также построить процесс

, удовлетворяющий условию x^∗(N_min) = 0, который

будем называть оптимальным. Предполагается, что N_min < ∞.

Множество состояний, из которых систему (A, U) можно перевести в 0

за N шагов посредством выбора допустимого управления начиная с шага k,

называется множеством 0-управляемости за N шагов:

⎧{

⎪

x(k) ∈ Rⁿ : ∃ u(k + i) ∈ U(k + i), i = 0, N - 1:

⎨

}

(2)

X (N, k) =

x(N + k) = 0 , N ∈ N,

⎪

⎩

{0}, N = 0.

Тогда N_min можно вычислить с помощью класса множеств 0-управляемости:

(3)

N_min = min {N ∈ N ∪ {0}: x₀

∈ X(N,0)}.

Для двух произвольных X₁, X₂ ⊂ Rⁿ через X₁ + X₂ обозначим сумму мно-

жеств по Минковскому. Для произвольной матрицы A ∈ R^n×n и множества

X ⊂ Rⁿ через AX обозначим образ X в результате действия линейного опе-

ратора, порожденного матрицей A:

AX = {Ax: x ∈ X }.

Построим аналитическое описание класса множеств 0-управляемости (2).

Лемма 1. Пусть класс множеств {X(N,k)}∞N,k=0 определяется соотно-

шениями (2). Тогда для всех N ∈ N и k ∈ N ∪ {0} справедливо представление

∑

(

)

X (N, k) =

-A-1(k) · ... · A-1(i + k)

U (k + i).

i=0

Доказательства леммы 1 и всех последующих утверждений приведены в

Приложении.

Следствие 1. Пусть для всех k ∈ N ∪ {0}

(4)

A(k) = A ∈ R^n×n, U(k) = U₀ ⊂ Rⁿ,

т.е. система

(1)

является стационарной, семейство множеств

{X (N, k)}∞N,k=0 определяется соотношениями (2).

Тогда для всех N ∈ N и k ∈ N ∪ {0} справедливы следующие соотношения:

∑

1) X (N, k) = - A^-iU₀,

i=1

2) X (N + 1, k) = A-1X (N, k) + (-A-1U₀).

В публикациях [12, 13] подробно рассмотрен подход к решению задачи

быстродействия для системы (1) в случае, когда на управление на каждом

шаге наложены только линейные ограничения

I(k)⋂

(5)

U (k) =

{u ∈ Rⁿ : (u, nⁱ(k)) ≤ a_i

(k)}, k ∈ N ∪ {0},

i=1

т.е. множество допустимых значений управлений на k-м шаге U(k) ⊂ Rⁿ пред-

ставляет собой полиэдр, ограниченный I(k) ∈ N числом гиперплоскостей с

векторами нормалей nⁱ(k) ∈ Rⁿ, ориентированными вовне множества U(k).

Известно, что в случае (5) задача быстродействия может быть сведена к за-

даче линейного программирования.

Обозначим через μ(x, X ) функционал Минковского [25]:

μ(x, X ) = inf{r ∈ R: r > 0, x ∈ rX },

где X ⊂ Rⁿ - выпуклое тело, x ∈ Rⁿ.

Для произвольных N ∈ N и k = 0, N - 1 определим отображение S_N,k :

Rⁿ → Rⁿ следующим образом:

S_N,k(x) = arg min μ(A(k)x + u,X(N - k - 1,k + 1)).

u∈U(k)

Как продемонстрировано в [13], если известно представление

{

}

X (N - k - 1, k + 1) = conv

x¹(N - k - 1,k + 1),... ,x^M (N - k - 1,k + 1)

то вычисление отображения S_N,k в случае (5) в каждой точке x ∈ Rⁿ сводится

к решению задачи линейного программирования:

min r,

r,λ₁,...,λ_M ,u

∑

A(k)x + u = xⁱ(N - k - 1, k + 1)λ_i,

i=1

(6)

∑

λ_i ≤ r,

i=1

0 ≤ λ_i ≤ r, i = 1,M,

(u, n^j(k)) ≤ a_j(k), j = 1, I(k).

Также в [13] сформулирована и доказана теорема, определяющая вид оп-

тимального позиционного управления в задаче быстродействия для систе-

мы (1) в случае (5).

Теорема 1

[13, теорема 5.1]. Пусть система (1) удовлетворяет усло-

определяется соотношениями

x^∗(k + 1) = A(k)x^∗(k) + S_N

min,k(x∗(k)), k = 0,Nmin - 1,

x^∗(0) = x₀.

Тогда

1) x^∗(N_min) = 0;

2) оптимальное по быстродействию позиционное управление на k-м шаге

имеет вид

u^∗(k,x^∗(k)) = S_N

min,k(x∗(k)).

На основе теоремы 1 удается полностью решить задачу быстродействия

для системы (1) в случае (5), используя только средства линейного програм-

мирования. Тем не менее аналогичный подход в общем случае, когда последо-

вательность множеств допустимых значений управлений U состоит из произ-

вольных выпуклых компактов, оказывается неприменимым, так как приво-

дит к необходимости решения задачи выпуклого программирования общего

вида. В результате оказывается актуальной следующая аппроксимационная

задача.

Обозначим для каждого k ∈ N ∪ {0} через {U_m(k)}m∈N, {U_m(k)}m∈N после-

довательности нижних и верхних оценок соответственно множества допусти-

мых значений управлений U(k) системы (1) на k-м шаге, т.е. для каждого

m ∈ N верно включение

U_m(k) ⊂ U(k) ⊂ U_m(k).

Везде далее будем предполагать, что для всех m ∈ N и k ∈ N ∪ {0} каждое из

множеств U_m(k), U_m(k) ⊂ Rⁿ является выпуклым компактом, содержащим 0.

Тогда в общем случае справедливы оценки

(7)

N_min(m) ≥ N_min ≥ N_min

(m),

где N_min(m), N_min(m) - оптимальные значения критерия качества управле-

(

)

(

)

ния в задаче быстродействия для систем

A,{U_m(k)}∞k=0

A,{U_m(k)}^∞

k=0

соответственно.

Предполагая, что последовательности {U_m(k)}m∈N, {U_m(k)}m∈N построены

на основе методов полиэдральной аппроксимации, требуется сформулировать

достаточные условия, при которых для произвольной системы (1) найдется

m₀ ∈ N, удовлетворяющее равенству

(8)

N_min(m₀) = N_min = N_min(m₀

(

)

Таким образом, оптимальное управление для системы A, {Um0 (k)}^∞

, вы-

k=0

численное на основе теоремы 1, окажется не только гарантирующим, т.е. удо-

влетворяющим оценкам (7), но и оптимальным для исходной системы (A, U).

Для рассмотрения вопросов сходимости исследуемые множества будем

предполагать элементами метрического пространства компактов (K_n, ρ_H ),

наделенного метрикой Хаусдорфа:

K_n = {X ⊂ Rⁿ : X - компакт} ,

{

}

ρ_H(X,Y) = max sup

inf ∥x - y∥; sup

inf ∥x - y∥

y∈Y

x∈X

y∈Y

Известно, что (K_n, ρ_H ) является полным метрическим пространством [25].

3. Дополнительные построения

Для решения поставленной задачи сформулируем и докажем некоторые

свойства пространства (K_n, ρ_H ).

Лемма 2

[23, лемма 4.3]. Пусть отображение A: Rⁿ → Rⁿ непрерыв-

но. Тогда A: K_n →K_n непрерывно, где для произвольного X ∈ K_n в каче-

стве A(X) рассматривается образ множества X.

Лемма 3. Пусть X₁,X₂,Y₁,Y₂ ∈ K_n такие, что

ρ_H(X₁,X₂) < ε₁, ρ_H(Y₁,Y₂) < ε₂.

Тогда

ρ_H(X₁ + Y₁,X₂ + Y₂) < ε₁ + ε₂.

Лемма 4. Пусть для каждого i = 1,N последовательность {X^im}m∈N ⊂

⊂K_n сходится к Xⁱ ∈ K_n:

−→ 0.

Тогда

(

)

∑ N∑

ρ_H

X^im,

−→ 0.

i=1

На основе лемм 2 и 4 можно сформулировать асимптотические свой-

ства класса множеств 0-управляемости (2) системы (1). Обозначим через

{X_m(N, k)}∞N,k=0 класс множеств 0-управляемости вспомогательной системы

(A, {U_m(k)}∞k=0) . Тогда справедливо следующее утверждение.

Следствие 2. Пусть для каждого k ∈ N ∪ {0} последовательность

{U_m(k)}m∈N ⊂ K_n сходится к множеству допустимых значений управлений

U (k) системы (1):

−→ 0.

Тогда для любых N, k ∈ N ∪ {0} справедливо соотношение

−→ 0.

Обозначим через B_R(x₀) ⊂ Rⁿ замкнутый шар радиуса R > 0 с центром в

точке x₀ ∈ Rⁿ.

Лемма 5. Пусть X,Y ∈ K_n - выпуклые компакты, Y ⊂ X, ρ_H(X,Y) < ε,

B_ε(x₀) ⊂ X.

Тогда x₀ ∈ Y.

Следствие 3. Пусть {X_m}m∈N ⊂ K_n - последовательность выпуклых

компактов, X ⊂ Rⁿ - выпуклый компакт такой, что для каждого m ∈ N

верно включение X_m ⊂ X ,

−→ 0.

Тогда для всех x₀ ∈ int X найдется N ∈ N такое, что x₀ ∈ X_N .

Лемма 6. Пусть X,Y ∈ K_n - выпуклые компакты, X ⊂ Y, ρ_H(X,Y) < ε,

x₀ ∈ Rⁿ такой, что B_ε(x₀) ∩ X = ∅.

Тогда x₀ ∈ Y.

Следствие 4. Пусть {X_m}m∈N ⊂ K_n - последовательность выпуклых

компактов, X ⊂ Rⁿ - выпуклый компакт такой, что для каждого m ∈ N

верно включение X ⊂ X_m,

−→ 0.

Тогда для всех x₀ ∈ X существует N ∈ N такое, что x₀ ∈ X_N .

4. Достаточные условия оптимальности гарантирующего решения

Утверждения, доказанные в разделе 3, позволяют сформулировать доста-

точные условия, которым должен удовлетворять метод полиэдральной ап-

проксимации, чтобы на некоторой итерации m₀ ∈ N аппроксимационного ал-

горитма выполнилось равенство (8).

Согласно (3) величина N_min однозначно определяется посредством элемен-

тов семейства множеств 0-управляемости (2). В силу следствия 2 последова-

тельность множеств 0-управляемости за N ∈ N ∪ {0} шагов вспомогательных

систем (A, {U_m(k)}∞k=0) сходится к X (N, k), если для каждого k ∈ N последо-

вательность {U_m(k)}m∈N сходится к исходному множеству U(k). С другой

стороны, следствия 3 и 4 гарантируют, что за конечное число итераций как

внешней, так и внутренней аппроксимации удастся выполнить для каждого

x₀ ∈ int X(N_min,0) \ X(N_min - 1,0) включение

x₀ ∈ X_m(N_min,0) \ X_m(N_min - 1,0),

откуда для заданного начального состояния следует равенство (8).

Сформулируем данный факт в виде следующих теорем.

Теорема 2. Пусть для каждого k ∈ N ∪ {0} верно, что {U_m(k)}m∈N ⊂

⊂K_n - последовательность выпуклых компактов такая, что для каждого

−→ 0.

Тогда почти для всех x₀ ∈ Rⁿ, для которых N_min < ∞, существует

m₁ ∈ N такое, что

N_min = N_min(m₁),

где N_min(m₁) - оптимальное значение критерия в задаче быстродействия₍

)

для системы A, {Um1 (k)}^∞

k=0

Теорема 3. Пусть для каждого k ∈ N ∪ {0} верно, что {U_m(k)}m∈N ⊂

⊂K_n - последовательность выпуклых компактов такая, что для каждого

−→ 0.

Тогда почти для всех x₀ ∈ Rⁿ, для которых N_min < ∞, существует

m₂ ∈ N такое, что

N_min = N_min(m₂),

где N_min(m₂) - оптимальное значение критерия в задаче быстродействия

для системы (A, {Um2 (k)}∞k=0).

Следствие 5. Пусть выполняются условия теорем 2 и 3 одновременно.

Тогда существует m₀ ∈ N такое, что

N_min(m₀) = N_min = N_min(m₀).

Основным результатом раздела 4 являются сформулированные и дока-

занные в виде теорем 2 и 3 достаточные условия того, что применение ме-

тодов полиэдральной аппроксимации позволит свести общий случай зада-

чи быстродействия для исходной системы (1) к случаю (5), для которого

оптимальный процесс может быть вычислен исключительно средствами ли-

нейного программирования на основе теоремы 1. Если метод полиэдральной

аппроксимации гарантирует сходимость в смысле расстояния Хаусдорфа к

аппроксимируемому множеству, то почти для всех начальных состояний га-

рантирующее решение окажется также и оптимальным по быстродействию

за конечное число итераций аппроксимационного алгоритма.

5. Численные расчеты величины N_min

Проведем ряд численных экспериментов для демонстрации прикладного

значения результатов раздела 4. Для наглядности все рассматриваемые си-

стемы вида (1) будут предполагаться стационарными, т.е. удовлетворяющими

условиям (4). В качестве алгоритма полиэдральной аппроксимации для по-

строения последовательностей {U_m}∞m=1 и {U_m}∞m=1 используется алгоритм

сближающихся многогранников. Такой выбор обусловлен тем, что, как про-

демонстрировано в [20], он обеспечивает сходимость в смысле расстояния Ха-

усдорфа (в пространстве K_n) к исходному множеству допустимых значений

управлений U₀. С другой стороны, данный алгоритм позволяет строить по-

следовательности внутренних и внешних аппроксимаций одновременно. Бо-

лее подробно описание алгоритма сближающихся многогранников и иссле-

дование его свойств приведено в [20], сопоставление сложности с другими

методами полиэдральной аппроксимации подробно исследуется в [19].

Пример 1. Продемонстрируем поэтапное вычисление величины N_min

для линейной дискретной системы, удовлетворяющей условию (4), на основе

теорем 2, 3 и следствия 5. Пусть размерность фазового пространства n = 2,

(

)

{

}

0,7

-0,2

u²

U₀ = (u₁,u₂)^T ∈ R² : u²¹ +

≤1

0,6

0,8

В качестве начального состояния рассмотрим вектор

(

)

x₀ =

Многогранники U₃ и U₃, представляющие собой внутреннюю и внешнюю

оценки множества U₀ соответственно, имеют следующий вид:

{(

) (

)}

0,8407

- 0,8893

0,0486

U₃ = conv

1,0830

0,9146

-1,9976

{(

) (

)}

- 0,0972

- 1,6814

1,7786

U₃ = conv

3,9953

-2,1660

-1,8292

x₂

x₀

x₁

x₀

x₃(6, 0)

x₄(6, 0)\ x₃(6, 0)

x₅(6, 0)\ x₄(6, 0)

x₆(6, 0)\ x₅(6, 0)

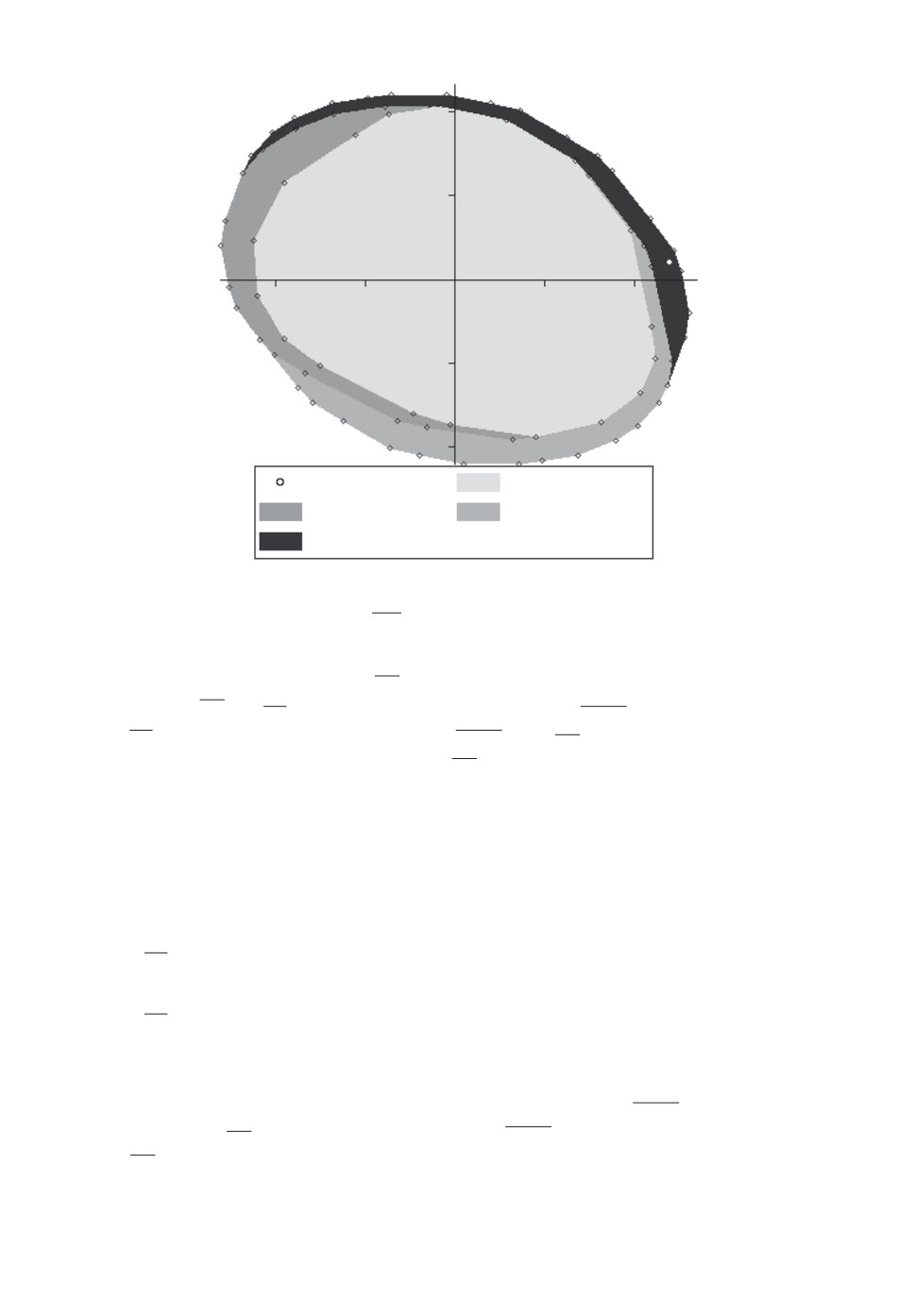
Рис. 1. Множества {X_m(6, 0)}6m=3 и начальное состояние x₀.

Тогда на основе следствия 1 можно построить классы множеств 0-управ-

ляемости

{X₃(N, k)}∞N,k=0,

{X₃(N, k)}∞N,k=0 для вспомогательных систем

(

)

(

)

A,{U₃}∞k=0

. Величины N_min(3) = 7, N_min(3) = 5 вычислены на

основе соотношения (3). Множества X₃(7, 0) и X₃(5, 0) представляют собой

многогранники с 21-й и 15-ю вершинами соответственно, иллюстрации кото-

рых представлены на рис. 1.

Поскольку при m = 3 равенство (8) не достигнуто, уточним внутреннюю

и внешнюю аппроксимации U₀ при помощи алгоритма сближающихся много-

гранников:

{(

) (

)}

0,8407

- 0,8893

0,0486

- 0,0486

U₄ = conv

1,0830

0,9146

-1,9976

1,9976

{(

) (

)}

0,5281

- 0,6253

- 1,6814

1,7786

U₄ = conv

2,0538

1,9415

-2,1660

-1,8292

Аналогичным образом вычислим оптимальные значения критерия качества

управления для вспомогательных систем: N_min(4) = 7, N_min(4) = 5. Множе-

ства X₄(7, 0) и X₄(5, 0) представляют собой многогранники с 28-ю и 20-ю вер-

шинами соответственно.

Продолжим процесс уточнения множества U₀ при помощи алгоритма сбли-

жающихся многогранников до тех пор, пока неравенство (7) не перейдет в

равенство (8). Приводим далее результаты расчетов.

{(

) (

)}

0,8407

- 0,8893

0,0486

- 0,0486

- 0,8407

U₅ = conv

1,0830

0,9146

-1,9976

1,9976

-1,0830

{(

) (

)}

0,5281

- 0,6253

- 1,1533

- 0,5281

1,7786

U₅ = conv

2,0538

1,9415

-0,1123

-2,0537

-1,8292

N_min(5) = 7, N_min(5) = 5.

Множества X₅(7, 0) и X₅(5, 0) представляют собой многогранники с 28-ю и

20-ю вершинами соответственно.

{(

) (

)

0,8407

- 0,8893

0,0486

U₆ = conv

1,0830

0,9146

-1,9976

(

) (

)}

- 0,0486

- 0,8407

0,8893

1, 9976

-1,0830

-0,9146

{(

) (

)

0,5281

- 0,6253

- 1,1533

U₆ = conv

2,0538

1,9415

-0,1123

(

) (

)}

- 0,5281

0,6253

1,1533

-2,0537

-1,9415

0,1123

N_min(6) = 6, N_min(6) = 6.

Множества X₆(6, 0) и X₆(6, 0) представляют собой многогранники с 36-ю вер-

шинами каждый.

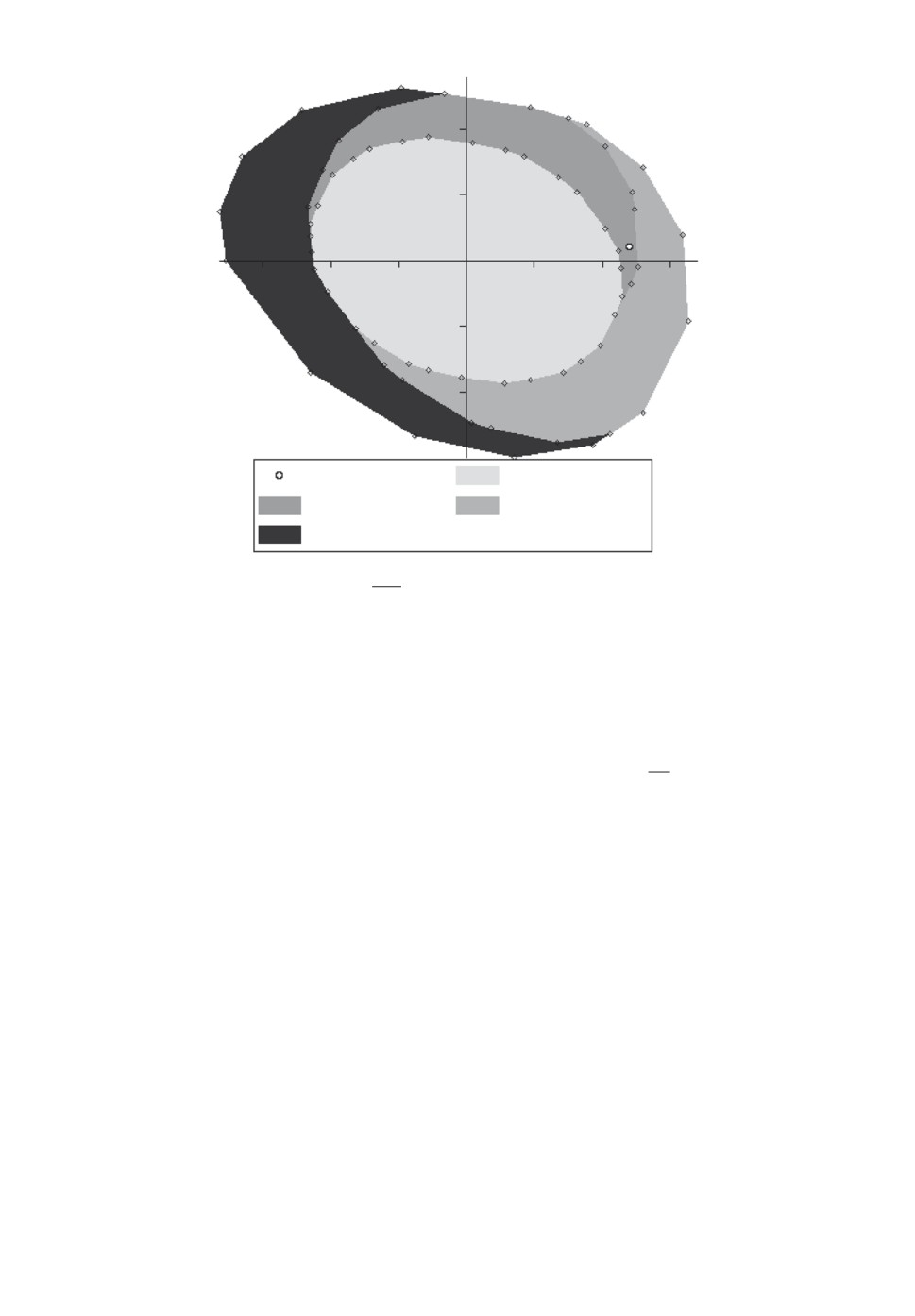
Таким образом, удается вычислить для выбранного x₀ величину N_min = 6

для исходной системы (A, U) в соответствии со следствием 5. При этом также

справедливо равенство

m₁ = m₂ = m₀ = 5.

Процесс сходимости величин N_min(m) и N_min(m) к N_min продемонстри-

рован на рис. 1 и 2 соответственно. На рис. 1 различными цветами изоб-

ражен набор возрастающих по включению множеств {X_m(6, 0)}6m=3. Множе-

ство X₆(6, 0) при этом является первым множеством, содержащим началь-

ное состояние x₀. Данное включение гарантирует выполнение неравенства

N_min ≥ 6. На рис. 2 различными цветами изображен набор убывающих по

включению множеств {X_m(5, 0)}6m=3. Множество X₆(5, 0) при этом является

первым множеством, не содержащим начального состояния x₀, что гаранти-

рует выполнение неравенства N_min > 5.

x₂

x₀

x₁

x₀

x₆(5, 0)

x₅(5, 0)\x₆(5, 0)

x₄(5, 0)\x₅(5, 0)

x₃(5, 0)\x₄(5, 0)

Рис. 2. Множества {X_m(5, 0)}6m=3 и начальное состояние x₀.

Пример 2. Рассмотрим линейную дискретную систему (1), удовлетво-

ряющую условию стационарности (4). Пусть размерность фазового простран-

ства n = 2,

(

)

{

}

0,1

-0,1

u²

U₀ = (u₁,u₂)^T ∈ R² : u²¹ +

≤1

0,1

В качестве начальных состояний рассмотрим следующие три вектора:

(

)

(

)

(

)

9,5

9,9

x0,1 =

x0,2 =

x0,3 =

9,5

9,9

Выбор данных начальных состояний обусловлен их расположением относи-

тельно границы множества 0-управляемости X (1, 0). Согласно лемме 1 и свой-

ствам эллиптических множеств [26] верно следующее представление:

(

)

{

}

0,0125

-0,0075

X (1, 0) = -A-1U₀ = u ∈ R² : u^THu ≤ 1 , H =

-0,0075

0,0125

Тогда верны включения x0,1, x0,2 ∈ int X (1, 0), x0,3 ∈ ∂X (1, 0). В силу (3)

N_min = 1 для всех трех предложенных начальных состояний. Тем не менее

каждое из них находится на различном расстоянии от границы множества

X (1, 0), что влияет на сложность вычисления величины N_min при помощи

Таблица 1

x₀

x0,1

x0,2

x0,3

m₁

m₂

следствия 5 и равенства (8). В качестве начального приближения в алгорит-

ме сближающихся многогранников выбраны

{(

) (

)}

- 0,985726

0,168356

0,985726

- 0,168356

U₄ = conv

-0,336713

-1,971452

0,336713

1,971452

{(

) (

)}

- 0,817370

1,154083

0,817370

- 1,154083

U₄ = conv

-2,308164

-1,634740

2,308164

1,634740

Результаты расчетов величин m₁, m₂ из теорем 2, 3 приведены в табл. 1.

При этом величину m₁ для начального состояния x0,3 вычислить не уда-

ется вплоть до аппроксимации U₂₀₃, т.е. N_min(203) = 2. Данный факт связан

с тем, что теоремы 2 и 3 не гарантируют достижимость равенства (8) для на-

чальных состояний, расположенных на границах множеств 0-управляемости

{X (N, 0)}∞N=0, в том числе и для x0,3. Однако при этом можно построить

субоптимальное решение задачи быстродействия при помощи теоремы 1, ис-

пользуя U_m вместо множества U₀, оценка точности критерия качества управ-

ления может быть вычислена в соответствии с неравенством (7) как величина

N_min(m) - N_min(m). В частности, для x0,3 при m = 203 точность составляет

N_min(203) - N_min(203) = 1.

6. Задача демпфирования высотного сооружения

Продемонстрируем эффективность разработанных методов на примере ре-

шения задачи оптимального по быстродействию демпфирования высотного

сооружения.

Сейсмические возмущения вызывают колебания сооружения, которые

влияют на устойчивость и в конечном счете приводят к его разрушению.

В этой связи возникает задача гашения колебаний сооружения посредством

дополнительно прикладываемых сил, рассчитанных на основе приобретенных

изменений, т.е. задача управления системой по принципу обратной связи. На

сегодняшний день наиболее активно применяются два принципиально раз-

личных способа организации такого управления: динамическое гашение коле-

баний с использованием дополнительных материальных тел и виброзащита,

предполагающая изоляцию сооружения от подвижного основания. Один из

возможных вариантов технической реализации динамического гашения ко-

лебаний заключается в создании дополнительных технических этажей с раз-

мещением некоторой достаточно малой массы (по сравнению с общей массой

сооружения), которая будет перемещаться в соответствии с заданным зако-

ном управления в форме обратной связи по текущим показаниям датчиков,

которая позволит оказывать управляющее воздействие на смежные этажи.

В качестве механической системы, моделирующей колебания высотного

сооружения, предполагается одномерная последовательность упругосвязан-

ных материальных точек (этажей или секций сооружения), одна из кото-

рых (основание) совершает поступательное движение, порождаемое сейсми-

ческим воздействием. Предполагается, что масса основания намного превы-

шает массы остальных материальных точек, поэтому влиянием движения

секций сооружения на движение основания можно пренебречь. В дальнейшем

будем считать, что массы всех материальных точек одинаковы, а упругие и

демпфирующие связи моделируются линейными элементами с одинаковыми

коэффициентами упругости и демпфирования.

Уравнения движения рассматриваемой системы согласно модели, предло-

женной в [27], имеют вид

⎧

⎪

ξ₁(t) = - 2

ξ₁(t) - 2cξ₁(t) +

ξ₂(t) + cξ₂(t) + U₁(t),

⎪

⎨

ξ_i(t) = - 2

ξ_i(t) - 2cξ_i(t) +

b˙ξi-1(t)+

(9)

⎪

+ cξi-1(t) +

ξi+1(t) + cξi+1(t) + U_i(t),

⎪

^⎩

ξ_n(t)= - 2

ξ_n(t) - 2cξ_n(t) +

ξn-1(t) + cξn-1(t) + U_n(t),

где ξ_i - координата i-й материальной точки относительно основания, U_i -

управляющая сила, приложенная к i-й материальной точке, m - масса мате-

риальной точки, b и c - коэффициенты демпфирования и упругости межсек-

ционных связей соответственно.

Введем обозначения:

⎛

⎞

⎛

⎞

⎛

⎞

ξ₁(t)

⎜

⎟

⎜

⎟

⎜

⎟

⎜

⎟

⎜

⎟

⎜1

0⎟

⎜

⎟

⎜

⎟

⎜

⎟

⎜

⎟

⎜ξn(t)⎟

⎜

⎟

⎜0

0⎟

⎜

⎟

⎜

⎟

y(t) =

⎜

⎟,

v(t) =

K =

⎜

⎟

⎜

⎟

⎜ξ1(t)⎟

U₁(t)

⎜

⎟

⎜

⎟

⎜

⎟

⎜

⎟

⎜

⎟

⎜

⎟

⎝

⎠

⎝0 0 0 ...

1⎠

⎝

⎠

U_n(t)

n(t)

β =

ω² =

Тогда уравнения (9) можно привести к каноническому виду

y(t) =

Ay(t) + v(t),

(

)

-ω²K -βK

Пусть высота здания составляет 6 этажей, т.е. n = 6. Также пусть β = 1,

ω² = 100. Значение параметров выбраны на основе модели, описанной в [27].

Полагая, что управление v(t) является кусочно-постоянной функцией, ме-

няющей свои значения через промежутки времени Δt, можно перейти к дис-

кретному аналогу системы (9), обозначив

x(k) = y(kΔt), k ∈ N ∪ {0}.

Пусть Φ(t) - матрица фундаментальной системы решений (9). Тогда, по-

лагая v(kΔt) = v_k, справедливо представление

(

)

x(k + 1) = Φ(Δt)Φ-1(0)x(k) + Φ(Δt)Φ-1(0

A-1

v_k.

Введем обозначения:

A = Φ(Δt)Φ-1(0),

B=Φ(Δt)Φ-1(0

A-1

A-1,

u(k) = Bv_k, k ∈ N ∪ {0}.

Окончательно получим систему управления, эквивалентную виду (1):

x(k + 1) = Ax(k) + u(k),

(10)

x(0) = y₀, u(k) ∈ BU₀,

где A ∈ R12×12 - матрица дискретизированной системы, BU₀ ⊂ R¹² - множе-

ство допустимых значений управлений, x(k) ∈ R¹² - состояние системы на

k-м шаге. Данная система является стационарной, что можно рассматривать

как частный случай нестационарной системы (1).

Предполагается, что демпфирующие устройства расположены на 2-м, 4-м

и 5-м этажах. В качестве множества допустимых значений управлений рас-

сматривается трехмерный эллипсоид в R¹²:

{

}

U₀ = u ∈ R¹² : u²⁸ +

u²¹⁰ +

u²¹¹ ≤ 1, u_i = 0, i ∈ {8,10,11}

Для аппроксимации U₀ используется алгоритм сближающихся многогран-

ников

[20], который позволяет построить последовательности

{U_m}∞m=1,

{U_m}∞m=1 верхних и нижних оценок BU₀, сходящиеся к исходному множе-

ству BU₀ в смысле расстояния Хаусдорфа. Тогда в силу теорем 2, 3 и след-

ствия 5 почти для всех начальных состояний также должны быть верны

сходимости

−→ N_min,

−→ N_min.

.⁴

x*(0)

x*(1)

x*(2)

x*(3)

x*(4)

x*(5)

Рис. 3. Оптимальная траектория системы (10).

Результаты расчетов приведены в табл. 2.

Здесь через m ∈ N обозначены число вершин многогранника U_m и число

гиперграней многогранника U_m. На шаге m₀ = 8 аппроксимационного алго-

ритма неравенство (7) переходит в равенство (8), откуда следует оптималь-

ность уп

(

)

системы A, {BUm0 }^∞

, в задаче быстродействия для исходной системы

k=0

управления (10),

N_min = 5.

Также на основе теоремы

построен оптимальный процесс системы

. Результаты расчетов представлены в табл. 3 и 4.

На рис. 3 схематично изображена оптимальная траектория системы (10).

Переход от непрерывной системы (9) к дискретной системе (10) выполнен

без погрешностей и основан на возможности аналитически построить реше-

ние системы линейных дифференциальных уравнений (9) в предположении,

что управление является кусочно-постоянным. В связи с этим фактом траек-

тория, представленная на рис. 3, также визуализирует траекторию исходной

непрерывной системы (9).

Таблица 2

N_min(m)

Таблица 3. Оптимальная траектория системы

x∗1(k)

0,0001

-0,0031

-0,0135

-0,0111

-0,0012e-03

x∗2(k)

-0,0038

-0,0162

-0,0109

0,0038

0,024e-03

x∗3(k)

-0,0156

-0,0013

0,0035

-0,0151

0,021e-03

x∗4(k)

-0,0037

-0,0169

-0,0198

-0,0168

0,015e-03

x∗5(k)

-0,0011

-0,0147

-0,0352

-0,0315

0,0345e-03

x∗6(k)

-0,0158

-0,0212

-0,0215

-0,0335

0,032e-03

x∗7(k)

0,0026

0,0747

0,0915

-0,1694

-0,015e-03

x∗8(k)

0,1099

0,0866

-0,1702

-0,0279

-0,052e-03

x∗9(k)

-0,2835

-0,4534

-0,1461

-0,1240

-0,065e-03

x∗10(k)

0,1024

0,1161

-0,0423

0,0302

0,01e-03

x∗11(k)

0,0568

0,2169

0,1296

-0,1887

-0,014e-03

x∗12(k)

0,1112

0,2312

0,0975

0,0426

0,026e-03

Таблица 4. Оптимальное управление

u∗1(k)

0,0003

0,0032

0,0104

-0,0024

-0,0245

u∗2(k)

0,0032

0,0123

-0,0053

-0,0148

0,0127

u∗3(k)

0,0222

-0,0144

-0,0047

0,0186

-0,0006

u∗4(k)

0,0037

0,0131

0,0030

-0,0031

0,0079

u∗5(k)

0,0037

0,0137

0,0205

-0,0037

-0,0187

u∗6(k)

0,0132

0,0054

0,0003

0,0120

0,0129

u∗7(k)

0,0117

-0,0721

-0,0168

0,2609

0,0484

u∗8(k)

0,0943

0,0232

0,2568

-0,1423

-0,2448

u∗9(k)

-0,1508

0,1698

-0,3072

-0,0221

0,2824

u∗10(k)

0,1069

-0,0136

0,1583

-0,0724

-0,0385

u∗11(k)

0,0898

-0,1601

0,0873

0,3183

-0,1186

u∗12(k)

0,1261

-0,1201

0,1337

0,0549

-0,2133

7. Заключение

В статье рассмотрена задача быстродействия для линейной дискретной

нестационарной системы. Множества допустимых значений управлений на

каждом шаге предполагаются выпуклыми компактами. Предложен метод

сведения общего случая задачи быстродействия к случаю линейных ограни-

чений на управление посредством полиэдральной аппроксимации множеств

допустимых значений управлений. Сформулировано и доказано, что полу-

ченное таким образом гарантирующее решение сходится к оптимальному, ес-

ли последовательность аппроксимирующих многогранников на каждом шаге

сходится в смысле расстояния Хаусдорфа к истинному множеству допусти-

мых значений управлений.

Отдельно рассмотрена задача наискорейшего демпфирования высотного

сооружения, расположенного в зоне сейсмической активности. Произведе-

на дискретизация непрерывной системы. Для заданного множества допусти-

мых значений управлений в виде эллипсоида проведена аппроксимация по

предложенным алгоритмам и приведены иллюстрации. Найдены оптималь-

ное управление и траектория системы.

ПРИЛОЖЕНИЕ

Доказательство леммы 1. Включение x ∈ X(N,k) в силу определе-

ния класса множеств 0-управляемости эквивалентно существованию векто-

ров

u(k) ∈ U(k), . . . , u(N + k - 1) ∈ U(N + k - 1)

таких, что

0 = x(N + k) = A(N + k - 1)x(N + k - 1) + u(N + k - 1) =

= A(N + k - 1)A(N + k - 2)x(N + k - 2) +

+ A(N + k - 1)u(N + k - 2) + u(N + k - 1) = . . . =

= A(N + k - 1) · . . . · A(k)x + A(N + k - 1) · . . . · A(k + 1)u(k) +

+A(N + k - 1) · . . . · A(k + 2)u(k + 1) + . . . + u(N + k - 1).

Тогда в силу невырожденности матриц из последовательности A

x = -A-1(k) · ... · A-1(N + k - 1)u(N + k - 1) - ... - A-1(k)u(k),

что равносильно утверждению леммы 1.

Доказательство следствия 1. Доказательство следует непосред-

ственно из леммы 1.

Доказательство леммы 3. В силу определения алгебраической сум-

мы множеств верна следующая цепочка неравенств:

ρ_H(X₁ + Y₁,X₂ + Y₂) =

{

}

= max sup

inf

∥x - y∥; sup

inf

∥x - y∥

x∈X₁+Y₁

y∈X₂+Y₂

x∈X₁+Y₁

⎧

⎨

= max sup

inf

∥(x₁ - x₂) + (y₁ - y₂)∥;

x₂∈X₂

⎩x1∈X₁

y₁∈Y₁

y₂∈Y₂

⎫

⎬

sup

inf

∥(x₁ - x₂) + (y₁ - y₂)∥

≤

x₂∈X₂

x₁∈X₁

⎭

y₂∈Y₂

y₁∈Y₁

{

≤ max sup

inf

∥x₁ - x₂∥ + sup

inf

∥y₁ - y₂||;

x₁∈X₁

x₂∈X₂

y₁∈Y₁

y₂∈Y₂

}

sup

inf

∥x₁ - x₂∥ + sup

inf

∥y₁ - y₂∥

≤

x₂∈X₂

x₁∈X₁

y₂∈Y₂

y₁∈Y₁

{

}

≤ max

sup

inf

∥x₁ - x₂∥; sup

inf

∥x₁ - x₂∥

x₁∈X₁

x₂∈X₂

x₁∈X₁

{

}

+ max sup

inf

∥y₁ - y₂∥; sup

inf

∥y₁ - y₂∥

y₁∈Y₁

y₂∈Y₂

y₁∈Y₁

= ρ_H(X₁,X₂) + ρ_H(Y₁,Y₂) < ε₁ + ε₂.

Лемма 3 доказана.

Доказательство леммы 4. По определению сходимости для любого

ε > 0 существует m ∈ N такое, что для всех i = 1,N справедливо неравенство

ρ_H(X^im,Xⁱ) <^εN .

Тогда в силу леммы 3

(

)

∑ N∑

∑

ρ_H

X^im,

Xⁱ

= ε,

i=1

откуда согласно определению предела следует утверждение леммы 4.

Доказательство следствия 2. В силу леммы 2 для каждого i =

= 0, N - 1 верно, что

(

ρ_H

(-A-1(k) · . . . · A-1(i + k))U_m(k + i),

)_m→∞

(-A-1(k) · . . . · A-1(i + k))U(k + i)

-→

Тогда в силу лемм 1 и 4 верны соотношения

∑

X_m(N,k) =

−→

i=0

∑

→

(-A-1(k) · . . . · A-1(i + k))U(k + i) = X (N, k).

i=0

Доказательство леммы 5. Предположим, что x₀ ∈ Y. Пусть

y₁ = arg min∥x0 - y∥.

y∈Y

Определим x^∗ ∈ X из условий

^{x^∗ = x₀ + β(x₀ - y₁),

(Π.1)

x^∗ ∈ ∂X,

т.е. x^∗ - точка пересечения границы множества X и луча, выходящего из

точки y₁ и проходящего через x₀. Поскольку B_ε(x₀) ⊂ X , то ∥x₀ - x^∗∥ ≥ ε.

Так как ρ_H (X , Y) < ε, существует y₂ ∈ B_ε(x^∗) ∩ Y, т.е. ∥x^∗ - y₂∥ ≤ ε.

Рассмотрим следующую величину:

(y₂ - x₀, x^∗ - x₀) = (y₂ - x^∗ + x^∗ - x₀, x^∗ - x₀) =

= (x^∗ - x₀, x^∗ - x₀) + (y₂ - x^∗, x^∗ - x₀).

В силу неравенства Коши-Буняковского

√

(x^∗ - x₀, x^∗ - x₀)(y₂ - x^∗, y₂ - x^∗) ≤ (y₂ - x^∗, x^∗ - x₀),

√

(x^∗ - x₀, x^∗ - x₀) -

(x^∗ - x₀, x^∗ - x₀)(y₂ - x^∗, y₂ - x^∗) ≤ (y₂ - x₀, x^∗ - x₀),

(√

)

√

(x^∗ - x₀, x^∗ - x₀)

(x^∗ - x₀, x^∗ - x₀) -

(y₂ - x^∗, y₂ - x^∗)

> 0.

Отсюда

(Π.2)

(y₂ - x₀, x^∗ - x₀

) > 0.

Представим y₁ как линейную комбинацию: y₁ = x₀ + α(x₀ - x^∗). В силу

(Π.1) α > 0. Тогда справедливы соотношения

(y₁ - x₀, y₂ - x₀) = (x₀ + α(x₀ - x^∗) - x₀, y₂ - x₀) =

= (α(x₀ - x^∗), y₂ - x₀) = -α(x^∗ - x₀, y₂ - x₀).

С учетом (Π.2)

(y₁ - x₀, y₂ - x₀) < 0.

Обозначим через y^∗ проекцию x₀ на аффинную оболочку y₁ и y₂:

(x₀ - y₁, y₂ - y₁)

y^∗ =

(y₂ - y₁) + y₁.

(y₂ - y₁, y₂ - y₁)

Обозначим

(x₀ - y₁, y₂ - y₁)

λ=1-

(y₂ - y₁, y₂ - y₁)

Тогда верно представление

y^∗ = λy₁ + (1 - λ)y₂.

Докажем, что λ ∈ [0; 1].

0 > (y₁ - x₀,y₂ - x₀) = (y₁ - x₀,y₂ - y₁ + y₁ - x₀) =

+ (y₁ - x₀, y₂ - y₁) + (y₁ - x₀, y₁ - x₀),

0 ≤ (y₁ - x₀,y₁ - x₀) < (x₀ - y₁,y₂ - y₁) ≤

√

≤

(x₀ - y₁, x₀ - y₁)(y₂ - y₁, y₂ - y₁).

Отсюда

(x₀ - y₁, y₂ - y₁) > 0,

(x₀ - y₁, x₀ - y₁) < (y₂ - y₁, y₂ - y₁),

что эквивалентно λ ∈ [0; 1]. Поскольку Y выпуклое, y₁, y₂ ∈ Y, то y^∗ ∈ Y. При

этом ∥x₀ - y^∗∥ < ∥x₀ - y₁∥. С учетом определения y₁ получаем противоречие.

Следовательно, x₀ ∈ Y. Лемма 5 доказана.

Доказательство следствия 3. Поскольку x₀ ∈ int X, то существует

−→ 0 существует

N ∈ N, удовлетворяющее неравенству

ρ_H(X_N ,X) < ε.

Тогда в силу леммы 5 верно включение x₀ ∈ X_N .

Доказательство леммы 6. Предположим, что x₀ ∈ Y. Пусть

y₁ = arg min∥y - x0∥.

y∈X

Определим x^∗ ∈ Y из условий

^{x^∗ = x₀ + β(x₀ - y₁),

(Π.3)

x^∗ ∈ ∂Y,

т.е. x^∗ - точка пересечения границы множества Y и луча, выходящего из точ-

ки y₁ и проходящего через x₀. Так как ρ_H (X , Y) < ε, то существует y₂ ∈ X

такой, что ∥x^∗ - y₂∥ ≤ ε. В силу того что B_ε(x₀) ∩ X = ∅, справедливы нера-

венства ∥x₀ - y₁∥ ≥ ε, ∥x₀ - y₂∥ ≥ ε.

Рассмотрим следующую величину:

(y₂ - x₀, x^∗ - x₀) = (y₂ - x₀, x^∗ - x₀ + y₂ - y₂) =

= (y₂ - x₀, y₂ - x₀) + (y₂ - x₀, x^∗ - y₂).

В силу неравенства Коши-Буняковского

√

(y₂ - x₀, y₂ - x₀)(x^∗ - y₂, x^∗ - y₂) ≤ (y₂ - x₀, x^∗ - y₂),

√

(√

√

)

0≤

(y₂ - x₀, y₂ - x₀)

(y₂ - x₀, y₂ - x₀) -

(x^∗ - y₂, x^∗ - y₂)

√

= (y₂ - x₀, y₂ - x₀) -

(y₂ - x₀, y₂ - x₀)(x^∗ - y₂, x^∗ - y₂) ≤ (y₂ - x₀, x^∗ - x₀).

Отсюда

(Π.4)

(y₂ - x₀, x^∗ - x₀

) ≥ 0.

Представим y₁ как линейную комбинацию: y₁ = x₀ + α(x₀ - x^∗). В силу

(Π.3) α > 0. Тогда справедливы соотношения

(y₁ - x₀, y₂ - x₀) = (x₀ + α(x₀ - x^∗) - x₀, y₂ - x₀) =

= (α(x₀ - x^∗), y₂ - x₀) = -α(x^∗ - x₀, y₂ - x₀) < 0.

С учетом (Π.4)

(y₁ - x₀, y₂ - x₀) < 0.

Обозначим через y^∗ проекцию x₀ на аффинную оболочку y₂ и y₁:

(x₀ - y₁, y₂ - y₁)

y^∗ =

(y₂ - y₁) + y₁.

(y₂ - y₁, y₂ - y₁)

Обозначим

(x₀ - y₁, y₂ - y₁)

λ=1-

(y₂ - y₁, y₂ - y₁)

Тогда

y^∗ = λy₁ + (1 - λ)y₂.

Докажем, что λ ∈ [0; 1].

0 > (y₁ - x₀,y₂ - x₀) = (y₁ - x₀,y₂ - y₁ + y₁ - x₀) =

= (y₁ - x₀, y₂ - y₁) + (y₁ - x₀, y₁ - x₀),

0 ≤ (y₁ - x₀,y₁ - x₀) < (x₀ - y₁,y₂ - y₁) ≤

√

≤

(x₀ - y₁, x₀ - y₁)(y₂ - y₁, y₂ - y₁).

Отсюда

(x₀ - y₁, y₂ - y₁) > 0,

(x₀ - y₁, x₀ - y₁) < (y₂ - y₁, y₂ - y₁),

что эквивалентно условию λ ∈ [0; 1]. Поскольку X выпуклое, y₁, y₂ ∈ X , то

y^∗ ∈ X. При этом ∥x₀ - y^∗∥ < ∥x₀ - y₁∥. Получаем противоречие. Следова-

тельно, x₀ ∈ Y. Лемма 6 доказана.

Доказательство следствия 4. Поскольку x0 ∈ X , X ∈ Kn, то со-

гласно аксиоме отделимости существует ε > 0 такое, что B_ε(x₀) ∩ X = ∅. В

−→ 0 найдется N ∈ N, удовлетворяющее неравен-

ству

ρ_H(X_N ,X) < ε.

Тогда в силу леммы 6 верно, что x₀ ∈ X_N .

Доказательство теоремы 2. Условие Nmin = Nmin(m1) в силу (3)

и (7) эквивалентно включению x₀ ∈ X (N_min, 0) ∩ X_m(N_min, 0).

В силу следствия 2

(

)_m→∞

ρ_H

X_m(N_min,0),X(N_min,0)

-→ 0.

Тогда согласно следствию

для любого x₀ ∈ int X (N_min, 0) существует

m₁ ∈ N такое, что x₀ ∈ Xm1 (N_min,k). Теорема 2 доказана.

Доказательство теоремы 3. Рассмотрим точку

x₀ ∈ X(N_min,0) \ X(N_min - 1,0).

Тогда X (N_min - 1, 0) ⊂ X_m(N_min - 1, 0) и согласно следствию 2

(

)_m→∞

ρ_H

X (N_min - 1, 0), X_m(N_min - 1, 0)

-→ 0.

Тогда в силу следствия 4 существует m₂ ∈ N такое, что x₀ ∈ Xm2 (N_min - 1, 0),

откуда с учетом (3) и (7) следует утверждение теоремы 3.

Доказательство следствия 5. В силу теорем 2 и 3 для выполнения

следствия 5 достаточно выбрать m₀ = max{m₁; m₂}.

СПИСОК ЛИТЕРАТУРЫ

Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Б.Ф. Матема-

тическая теория оптимальных процессов. М.: Наука, 1969.

Болтянский В.Г. Математические методы оптимального управления. М.: Наука,

1969.

Моисеев Н.Н. Элементы теории оптимальных систем. М.: Наука, 1975.

Евтушенко Ю.Г. Методы решения экстремальных задач и их приложения в

системах оптимизации. М.: Наука, 1982.

Болтянский В.Г. Оптимальное управление дискретными системами. М.: Наука,

1973.

Пропой А.И. Элементы теории оптимальных дискретных процессов. М.: Наука,

1973.

Holtzman J.M., Halkin H. Directional Convexity and the Maximum Principle for

Discrete Systems // J. SIAM Control. 1966. V. 4. No. 2. P. 263-275.

Беллман Р. Динамическое программирование. М.: ИИЛ, 1960.

Ибрагимов Д.Н., Сиротин А.Н. О задаче быстродействия для класса линейных

автономных бесконечномерных систем с дискретным временем и ограниченным

управлением // АиТ. 2017. № 10. C. 3-32.

Ibragimov D.N., Sirotin A.N. On the Problem of Operation Speed for the Class of

Linear Infinite-Dimensional Discrete-Time Systems with Bounded Control // Autom.

Remote Control. 2017. V. 78. No. 10. P. 1731-1756.

10.

Ибрагимов Д.Н. О задаче быстродействия для класса линейных автономных

бесконечномерных систем с дискретным временем, ограниченным управлением

и вырожденным оператором // АиТ. 2019. № 3. C. 3-25.

Ibragimov D.N. On the Optimal Speed Problem for the Class of Linear Autonomous

Infinite-Dimensional Discrete-Time Systems with Bounded Control and Degenerate

Operator // Autom. Remote Control. 2019. V. 80. No. 3. P. 393-412.

11.

Сиротин А.Н., Формальский А.М. Достижимость и управляемость дискретных

систем при ограниченных по величине и импульсу управляющих воздействи-

ях // АиТ. 2003. № 12. С. 17-32.

Sirotin A.N., Formal’skii A.M. Reachability and Controllability of Discrete-Time

Systems under Control Actions Bounded in Magnitude and Norm // Autom. Remote

Control. 2003. V. 64. No. 12. P. 1844-1857.

12.

Ибрагимов Д.Н., Сиротин А.Н. О задаче оптимального быстродействия для ли-

нейной дискретной системы с ограниченным скалярным управлением на основе

множеств 0-управляемости // АиТ. 2015. № 9. С. 3-30.

Ibragimov D.N., Sirotin A.N. On the Problem of Optimal Speed for the Discrete

Linear System with Bounded Scalar Control on the Basis of 0-controllability Sets //

Autom. Remote Control. 2015. V. 76. No. 9. P. 1517-1540.

13.

Ибрагимов Д.Н. Оптимальное по быстродействию управление движением аэро-

стата // Электрон. журн. Тр. МАИ. 2015. № 83. Доступ в журн.

http://trudymai.ru/published.php

14.

Костоусова Е.К. О внешнем полиэдральном оценивании множеств достижимо-

сти в «расширенном» пространстве для линейных многошаговых систем с инте-

гральными ограничениями на управление // Вычислительные технологии. 2004.

Т. 9. № 4. С. 54-72.

15.

Kurzhanskiy A.F., Varaiya P. Theory and computational techniques for analysis of

discrete-time control systems with disturbancens // Optim. Method Software. 2011.

V. 26. No. 4-5. P. 719-746.

16.

Кибзун А.И., Иванов С.В., Степанова А.С. Построение доверительного множе-

ства поглощения в задачах анализа статистических стохастических систем //

АиТ. 2020. № 4. С. 21-36.

Kibzun A.I., Ivanov S.V., Stepanova A.S. Construction of Confidence Absorbing Set

for Analysis of Static Stochastic Systems // Autom. Remote Control. 2020. V. 81.

No. 5. P. 589-601.

17.

Васильева С.Н., Кан Ю.С. Аппроксимация вероятностных ограничений в зада-

чах стохастического программирования с использованием ядра вероятностной

меры // АиТ. 2019. № 11. С. 93-107.

Vasil’eva S.N., Kan Yu.S. Approximation of Probabilistic Constraints in Stochastic

Programming Problems with a Probability Measure Kernel // Autom. Remote

Control. 2019. V. 80. No. 11. P. 2005-2016.

18.

Гайнанов Д.Н., Кибзун А.И., Рассказова В.А. Задача о декомпозиции мно-

жества путей ориентированного графа и ее приложение // АиТ. 2018. № 12.

С. 142-166.

Gainanov D.N., Kibzun A.I., Rasskazova V.A. The Decomposition Problem for the

Set of Paths in a Directed Graph and Its Application // Autom. Remote Control.

2018. V. 79. No. 12. P. 2217-2236.

19.

Каменев Г.К. Численное исследование эффективности методов полиэдральной

аппроксимации выпуклых тел. М.: Вычислительный центр РАН, 2010.

20.

Каменев Г. К. Алгоритм сближающихся многогранников // Журн. вычисл. ма-

тем. и матем. физ. 1996. Т. 36. № 4. С. 134-147.

21.

Sonnevend G. Asymptotically Optimal, Sequential Methods for the Approximation

of Convex, Compact Sets in R-n in the Hausdorff Metrics // Colloquia Math. Soc.

Janos Bolyai. 1980. V. 35. No. 2. P. 1075-1089.

22.

Ludwig M. Asymptotic Approximation of Smooth Convex Bodies by General

Polytopes // Mathematika. 1999. V. 46. P. 103-125.

23.

Ибрагимов Д.Н. Аппроксимация множества допустимых управлений в задаче

быстродействия линейной дискретной системой // Электрон. журн. Тр. МАИ.

2016. № 87. Доступ в журн. http://trudymai.ru/published.php