Автоматика и телемеханика, № 12, 2021

К.А. ЦАРЬКОВ, канд. физ.-мат. наук (k6472@mail.ru)

(Институт проблем управления им. В.А. Трапезникова РАН, Москва)

НЕКОТОРЫЕ АЛГОРИТМЫ УЛУЧШЕНИЯ НЕСТАЦИОНАРНЫХ

РЕГУЛЯТОРОВ НА БЕСКОНЕЧНОМ ИНТЕРВАЛЕ ВРЕМЕНИ¹

Исследуется задача оптимизации линейной по состоянию и нелиней-

ной по управлению динамической стохастической системы, функциони-

рующей на бесконечном интервале времени, относительно квадратичного

функционала качества. Предлагается несколько алгоритмов последова-

тельного улучшения заданного нестационарного программного управле-

ния. Они могут быть использованы, в частности, для построения каче-

ственных динамических регуляторов неполной обратной связи в детер-

минированных линейных стационарных системах. Для обоснования алго-

ритмов улучшения сформулирован и доказан ряд строгих утверждений

относительно исходной оптимизационной проблемы.

Ключевые слова: динамическая обратная связь, бесконечный интервал

времени, нелинейная стохастическая система, структурные ограничения.

DOI: 10.31857/S0005231021120059

1. Введение

Предположим, что исследуется задача управления линейной динамиче-

ской системой

(1)

x(t) = Ax(t) + Bu(t)

с заданными начальным условием x(0) = x₀ ∈ Rⁿ и матрицами системы

A ∈ R^n×n, B ∈ R^n×m, в которой качество управления оценивается значени-

ем функционала

+^∞

(

)

(2)

J (u) =

x(t)^TQx(t) + u(t)^TEu(t)

всюду, где он определен. Здесь Q ∈ R^n×n и E ∈ R^m×m - положительно опре-

деленные матрицы.

Будем считать, что функцию управления u(t) необходимо построить в виде

линейного регулятора

u(t) = P (t)x(t),

¹ Работа выполнена при частичной финансовой поддержке Российского фонда фунда-

ментальных исследований (проект № 20-08-00400).

так что (1)-(2) преобразуются к виду

(3)

x(t) = (A + BP (t))x(t), x(0) = x₀,

+∞

(4)

J (P ) = x(t)^T(Q + P (t)^T

EP(t))x(t)dt.

Пусть, для начала, на матричную функцию P (t) не наложено никаких

ограничений, кроме естественного требования сходимости несобственного ин-

теграла в правой части (4). Множество всех таких функций P (t) обозначим

через S. В этом случае задача J(P ) → min_P∈S совпадает с классической

линейно-квадратичной задачей оптимального регулирования на бесконечном

временном интервале, ее решение хорошо известно из теории аналитического

конструирования оптимальных регуляторов (АКОР) и является постоянной

по времени матричной функцией P (t) ≡ P^∗, одной и той же для любого x₀.

Предположим теперь, что дополнительно требуется удовлетворить неко-

торый набор структурных ограничений на функцию P (t) (например, P_ij (t) ≡

≡ 0 для каких-то i,j и т.п.). Оказывается, что в этом случае решение задачи

J (P ) → min_P∈S на соответствующем множестве S может не быть постоянной

матрицей. Это обстоятельство несколько удивительно ввиду того, что все па-

раметры A, B, Q и E в задаче остаются стационарными, но стационарный

регулятор уже не является оптимальным среди всех возможных. Возникает

естественная потребность в алгоритме построения оптимального нестацио-

нарного регулятора в подобной задаче (или, по крайней мере, в алгоритме

улучшения имеющегося оптимального регулятора среди всех стационарных),

чему и посвящена данная работа. Соответствующие результаты формули-

руются для существенно более общей стохастической задачи оптимального

управления, а затем обсуждаются, в том числе и для указанной выше ситуа-

ции, на примерах.

В контексте изучаемой проблемы и предлагаемых ниже путей ее реше-

ния нелишним будет указать ссылку на монографию [1], где в числе прочего

обсуждается вопрос минимизации функционала (4) с условием (3) на мно-

жестве постоянных стабилизирующих матриц P (t) ≡ P^∗, удовлетворяющих

заданным структурным ограничениям. В частности, для задачи линейного

регулирования по выходу выписан градиент функционала J на указанном

множестве [1, с. 253]. Там же отмечается, что использование затем гради-

ентной процедуры минимизации не гарантирует отыскание решения (ввиду

невыпуклости как самого функционала, так и его области определения) и по-

тому такую задачу следует отнести к разряду нерешенных проблем. То же

самое, безусловно, можно сказать и об изучаемой в настоящей работе более

общей задаче, однако в качестве ее «решения» здесь тем не менее предла-

гается улучшающая процедура градиентного типа. Это связано с тем, что

для задач нестационарного регулирования в условиях структурных ограни-

чений глобальный минимум значений J может, вообще говоря, не достигаться

(см. [2], где построен простой пример расходящейся минимизирующей после-

довательности в линейно-квадратичной задаче на конечном временном ин-

тервале). Последнее означает, что даже наличие каких бы то ни было необхо-

димых и достаточных условий оптимальности данного нестационарного регу-

лятора также не гарантирует окончательного решения задачи, в то время как

градиентная процедура одинаково успешно (или неуспешно) может отыскать

и минимизирующую последовательность, и некоторое приближение к стацио-

нарной точке.

2. Формальная постановка задачи и предварительные результаты

Рассмотрим стохастическое дифференциальное уравнение Ито [3]

(5)

dx(t) = A(u(t))x(t)dt + G(u(t))x(t)dw(t), x(0) = x₀,

где x₀ — n-мерный случайный вектор с известной конечной матрицей вторых

начальных моментов E[x₀x^T0] = N₀ ≽ 0, матричные функции A, G : R^m →

→ R^n×n непрерывно дифференцируемы на всей области определения. Для

заданных отображений A и G определено открытое множество S (стабили-

зирующих) векторов v ∈ R^m таких, что вещественные части всех собствен-

ных значений матрицы A(v) ⊕ A(v) + G(v) ⊗ G(v) строго меньше нуля (сим-

волы ⊕ и ⊗ означают сумму и произведение Кронекера). Последнее условие

гарантирует асимптотическую устойчивость (стабилизируемость) динамиче-

ской системы (5) при u(t) ≡ v ∈ R^m в среднем квадратичном (это вытекает

из векторного представления матричного уравнения для второго начально-

го момента случайного процесса x(t) [4]). Если G = 0, то оно эквивалентно

классическому условию гурвицевости матрицы A(v).

Будем исследовать задачу на минимум

⎡

⎤

∫

(6)

J (u) = E⎣ x(t)^TQ(u(t))x(t)dt⎦ → inf ,

u∈U

где для удобства записи опущена неявная зависимость в смысле уравне-

ния (5) вектора состояния x от функции управления u, матричная функция

Q : R^m → R^n×n непрерывно дифференцируема, Q(u) ≽ 0 ∀u ∈ R^m,

⋃

U = U_T,

T≥0

а U_T - множество измеримых на [0;+∞) функций u таких, что выполнены

условия:

1) u|[0;T] ∈ Lm2([0; T ]), если T > 0;

2) u(t) = u_T ∈ S для всех t ≥ T .

Ясно, что U_T можно рассматривать как открытое множество в

Lm2([0;T]) × R^m при T > 0 и как открытое множество в R^m при T = 0.

Предполагается, что функционал J на множестве U определен корректно, то

есть при любом u ∈ U существует единственное сильное решение [3] уравне-

ния (5), а несобственный интеграл в правой части (6) сходится к случайной

величине с конечным вторым моментом.

Отметим, что постановку задачи (5)-(6) и нижеследующие результаты

можно элементарно обобщить на случай многомерного случайного возмуще-

ния, но здесь для удобства изложения ограничимся одномерным стандартным

винеровским процессом w(t). Если же положить G(u) ≡ 0, A(u) = A^c + B^cP_u,

Q(u) = Q^c + PTuE^cP_u, x₀ = E[x₀], то получается детерминированная зада-

ча (3)-(4) оптимизации линейного регулятора со структурными ограничения-

ми (здесь P_u - матрица регулятора, а вектор u составляется из максимального

набора линейно независимых компонент матрицы P_u).

Рассмотрим также три вспомогательные задачи: при фиксированном зна-

чении T > 0

⎡

⎤

∫

(7)

J_∗(u) = E⎣ x(t)^TQ(u(t))x(t)dt⎦ → inf ;

u∈U_T

на конечном интервале времени

⎡

⎤

∫

(8)

J_α(u) = E⎣

x(t)^TQ(u(t))x(t)dt + x(T )^TαIx(T )⎦ →

inf

T > 0,

([0;T ])

u∈Lm2

где α ≥ 0 - скалярный коэффициент, а I - единичная матрица размеров n × n;

и на множестве допустимых управлений в виде постоянных векторов

⎡

⎤

∫

(9)

J_c(u) = E⎣ x(t)^TQ(u)x(t)dt⎦ → min.

u∈S

Задачи (8) и (9) ранее исследовались в [5, 6]. Воспользуемся некоторыми ре-

зультатами из этих работ для построения различных алгоритмов улучше-

ния в задаче (6). Начнем с формулировки необходимых утверждений каса-

тельно задач (7)-(9). Здесь и далее под градиентом ∇F (v₀) функционала

F : Lm2 ([0;T]) → R в точке v₀ ∈ Lm2 ([0;T]) понимается, как обычно, элемент f

пространства Lm2[(0; T )] такой, что 〈f, v〉 = F^′(v₀)v ∀v ∈ Lm2([0; T ]), где 〈·, ·〉

означает скалярное произведение в Lm2([0; T ]), а F^′(v₀) : Lm2([0; T ]) → R - ли-

нейный функционал производной Фреше отображения F в точке v₀. Кратко

будем писать ∇F (v₀) = t → f(t).

Утверждение 1. Компоненты градиента функционала J_α в произволь-

ной точке u ∈ Lm2([0; T ]) имеют вид

)

]

∂J_α(u)

^[(∂Q(u(t))

∂A(u(t))

∂G(u(t))

= t→tr

- 2M(t)

- 2G(u(t))^TM(t)

N (t) ,

∂u_j(·)

∂u_j

j = 1,m, где матричная функция N : [0;T] → R^n×n является единственным

решением задачи Коши

^N (t) = A(u(t))N(t) + N(t)A(u(t))^T + G(u(t))N(t)G(u(t))^T , N(0) = N₀,

а матричная функция M : [0;T] → R^n×n — единственным решением задачи

Коши

^M (t) = -M(t)A(u(t)) - A(u(t))^TM(t) - G(u(t))^TM(t)G(u(t)) + Q(u(t)),

M (T ) = -αI,

причем

J_α(u) = -tr [M(0)N₀].

Утверждение 2. Компоненты градиента функционала J_c в произволь-

ной точке u ∈ S имеют вид

)

]

∂J_c(u)

^[(∂Q(u)

∂A(u)

∂G(u)

= tr

- 2M_T

- 2G(u)^TMT

N_T

j = 1,m,

∂u_j

где матрица N_T ∈ R^n×n является единственным решением уравнения

A(u)N_T + N_T A(u)^T + G(u)N_T G(u)^T + N₀ = 0,

а матрица M_T ∈ R^n×n — единственным решением уравнения

Q(u) - M_T A(u) - A(u)^TM_T - G(u)^TM_T G(u) = 0,

причем

J_c(u) = -tr [M_T N₀].

Утверждение 3. Градиент функционала J_∗ в произвольной точке

u ∈ U_T имеет вид

⎛

⎞

∂J_∗(u)

⎜

∂u(·)

⎟

⎜

⎟

∇_uJ_∗(u) =

Lm2([0;T]) × R^m,

⎠^∈

⎝ ∂J_∗(u)

∂u_T

)

]

∂J_∗(u)

^[(∂Q(u(t))

∂A(u(t))

∂G(u(t))

= t→tr

- 2M(t)

- 2G(u(t))^TM(t)

N (t) ,

∂u_j(·)

∂u_j

)

]

∂J_∗(u)

^[(∂Q(u_T )

∂A(u_T )

∂G(u_T )

= tr

- 2M_T

- 2G(u_T )^TMT

N_T , j = 1,m,

∂uTj

∂u_j

где матричная функция N : [0; T ] → R^n×n и матрица N_T ∈ R^n×N являются

единственным решением системы уравнений

^N (t) = A(u(t))N(t) + N(t)A(u(t))^T + G(u(t))N(t)G(u(t))^T , N(0) = N₀,

A(u_T )N_T + N_T A(u_T )^T + G(u_T )N_T G(u_T )^T + N(T ) = 0,

а матричная функция M : [0;T] → R^n×n и матрица M_T ∈ R^n×n - единствен-

ным решением системы уравнений

^M (t) = -M(t)A(u(t)) - A(u(t))^TM(t) - G(u(t))^TM(t)G(u(t)) + Q(u(t)),

M (T ) = M_T ,

Q(u_T ) - M_T A(u_T ) - A(u_T )^TM_T - G(u_T )^TM_T G(u_T ) = 0,

причем

J_∗(u) = -tr [M(0)N₀].

Утверждение 1 для задачи (8) было впервые сформулировано и доказано

в [5], а утверждение 2 для задачи (9) - в [6]. Утверждение 3 для задачи (7)

формулируется впервые и комбинацией утверждений 1-2 не выводится. В це-

лях соблюсти целостность текста статьи, а также подчеркнуть единый подход

к задачам, полное доказательство всех этих утверждений приведено в Прило-

жении. Альтернативные формулы для вычисления значений функционалов в

каждом из сформулированных утверждений могут быть эффективно исполь-

зованы для контроля значений этих функционалов в процессе применения

улучшающих процедур. Это подразумевается в дальнейшем при формулиров-

ке алгоритмов. Важно отметить, что значение функционала J_α в отличие от

значений J_c и J_∗ никак в общем случае не соотносится со значением исходного

функционала J, так как речь идет о модифицированном функционале (8).

3. Алгоритмы улучшения нестационарных регуляторов

В [7] был предложен достаточно простой алгоритм улучшения имеющего-

ся оптимального стационарного регулятора в задаче (9) за счет построения

кусочно-постоянного управления, где при переходе к новому интервалу по-

стоянства фиксируется текущее начальное условие и строится оптимальный

для него стационарный регулятор на бесконечном времени. Уже такой подход

в ряде случаев позволяет серьезно повысить качество управления. Проблема

развития идей улучшения на «полностью нестационарный» случай состоит

в том, что для нестационарного регулятора в подавляющем большинстве си-

туаций невозможно аналитически определить оптимальное решение, а уда-

ется лишь построить улучшающую последовательность, быть может являю-

щуюся (а быть может, и нет [2]) некоторым приближением к одной из множе-

ства стационарных точек. Исследование примеров также позволяет устано-

вить существенную неединственность таких улучшающих последовательно-

стей, поэтому получение конкретного результата сильно зависит как от выбо-

ра начального приближения, так и от изменения величины шага улучшающей

процедуры. Наконец, в изучаемой здесь оптимизационной проблеме (6) речь

уже идет о совокупности задач, каждая из которых обладает указанными

особенностями. Как итог, предлагаемые ниже алгоритмы улучшения не мо-

гут гарантировать отыскание близкого к оптимальному нестационарного ре-

гулятора и потому являются скорее полезным инструментом исследования

проблемы, нежели сколь-нибудь полного ее решения. Тем не менее они могут

быть эффективно применены в конкретных прикладных задачах, где поря-

док улучшения значительно важнее близости к неизвестному оптимальному

решению.

Итак, пусть имеется какой-либо регулятор u ∈ U_T при некотором T ≥ 0.

В частности, при T = 0 имеется стационарный регулятор. Будем считать его

начальным приближением и рассмотрим возможные варианты его улучшения

в смысле функционала качества (6).

Алгоритм 1. А) Случай T > 0. Построить улучшающую последователь-

ность в задаче (7), не изменяя T . Для этого осуществить градиентный спуск

исходя из формулы для ∇_uJ_∗(u) в утверждении 3. На каждом шаге при этом

необходимо проверять принадлежность нового приближения множеству U_T , в

частности, должно быть выполнено включение u_T ∈ S (проверяется по опре-

делению). Завершить расчеты при выполнении условия достаточной малости

совокупного градиента ∇_uJ_∗(u) по какой-либо норме.

Б) Случай T = 0. Построить улучшающую последовательность в зада-

че (9). Для этого осуществить градиентный спуск исходя из формулы для

∇_uJ_c(u) в утверждении 2. На каждом шаге проверять принадлежность ново-

го приближения множеству S. Завершить расчеты при выполнении условия

достаточной малости градиента ∇_uJ_c(u) по какой-либо норме.

Особенность алгоритма 1 состоит в том, что улучшающая последователь-

ность относительно проблемы (6) будет построена только в заданном классе

управлений U_T . Если задан стационарный регулятор, то он останется стацио-

нарным.

Алгоритм 2. Построить улучшающие последовательности в задаче (7)

с увеличением значения T относительно данного вплоть до некоторого T_max.

Для этого осуществлять градиентный спуск исходя из формулы для ∇_uJ_∗(u)

в утверждении 3. На каждом шаге проверять принадлежность нового при-

ближения множеству U_T . При каждом T завершать расчеты при выполне-

нии условия достаточной малости совокупного градиента ∇_uJ_∗(u) по какой-

либо норме. При достижении стационарности получающегося решения u(t)

на некотором интервале заданной длины [T^∗ - ε; T^∗] проверить условие

u(T^∗) ∈ S и в случае его выполнения закончить расчеты в целом, положив

u(t) = u(T^∗), t > T^∗; иначе произвольно выбрать u^∗ ∈ S и положить u(t) = u^∗,

t>T^∗.

Алгоритм 2 предполагает многократный градиентный спуск на растущем

конечном интервале времени и все так же требует проверки условий u_T ∈ S

и нахождения стабилизирующего регулятора при T = T^∗. Вместе с тем по-

иск осуществляется в том числе и за пределами заданного исходного мно-

жества U_T , однако и здесь могут быть потеряны некоторые потенциально

качественные в смысле функционала (6) решения. Оказывается, существует

способ существенно уменьшить вычислительную сложность алгоритма 2 и

одновременно несколько изменить область поиска решений задачи (6) путем

перехода к исследованию задачи (8).

Алгоритм 3. Задать некоторым образом весовой коэффициент α ≥ 0 и

построить улучшающие последовательности в задаче (8), варьируя значе-

ния T в некотором диапазоне (0; T_max]. Для этого осуществлять градиент-

ный спуск исходя из формулы для компонент градиента в утверждении 1.

В качестве начального приближения брать u|_[0;T]. При каждом T завершать

расчеты при выполнении условия достаточной малости градиента ∇_uJ_α(u)

по какой-либо норме. При достижении стационарности получающегося ре-

шения u(t) на некотором интервале заданной длины [T^∗ - ε; T^∗] проверить

условие u(T^∗) ∈ S и в случае его выполнения закончить расчеты в целом,

положив u(t) = u(T^∗), t > T^∗; иначе произвольно выбрать u^∗ ∈ S и положить

u(t) = u^∗, t > T^∗. В случае отсутствия стационарности использовать значение

T^∗ = T_max. Проверить улучшение начального приближения в смысле функ-

ционала качества J_∗ и в случае отсутствия улучшений считать применение

алгоритма безуспешным.

За счет задания достаточно большого значения α можно добиться отыска-

ния алгоритмом 3 таких решений, которые соответствуют «быстрому обнуле-

нию» ковариационной матрицы случайного процесса x(t), после чего любой

стабилизирующий регулятор достаточно быстро «гасит» оставшийся «хвост».

Более того, подходящий регулятор может быть найден автоматически. Есте-

ственно ожидать от таких решений высокого качества в смысле (6). Однако

особенности рассматриваемой задачи не предполагают, что такое решение

будет найдено именно в момент остановки алгоритма 3. Последний, учиты-

вающий это обстоятельство алгоритм имеет следующий вид.

Алгоритм 4. Задать некоторым образом весовой коэффициент α ≥ 0 и

построить улучшающие последовательности в задаче (8), варьируя значе-

ния T в некотором диапазоне (0; T_max]. Для этого осуществлять градиент-

ный спуск исходя из формулы для компонент градиента в утверждении 1.

В качестве начального приближения также брать u|[0;T]. При каждом T за-

вершать расчеты при выполнении условия достаточной малости градиента

∇_uJ_α(u), по какой-либо норме. При достижении стационарности получающе-

гося решения u(t) на некотором интервале заданной длины [T^∗ - ε; T^∗] (или

при T^∗ = T_max) сравнить между собой все найденные до этого решения и вы-

брать наилучшее из них (в смысле используемого здесь функционала J_α),

соответствующее какому-то

T. Проверить условие u

T) ∈ S и в случае его

выполнения закончить расчеты в целом, положив u(t) = u

T), t

T; иначе

произвольно выбрать u^∗ ∈ S и положить u(t) = u^∗, t

T. Проверить улучше-

ние начального приближения в смысле функционала J_∗ и в случае отсутствия

улучшений считать применение алгоритма безуспешным.

Финальное условие остановки в алгоритмах 2-4 и произвольный выбор

u^∗ ∈ S обусловлены тем, что для любого стабилизирующего (тем более оп-

тимального) вектора выполнено limt→+∞ N(t) = 0, из чего следует, что при

достаточно большом T^∗ выбранное произвольно u^∗ ∈ S, для которого было

бы положено u(t) = u^∗, t > T^∗, отличается достаточно мало по значению J_∗ от

любого другого ũ ∈ S. Это, в свою очередь, означает малость компонент гра-

диента J_∗ по u_T относительно задачи (7). Отметим также, что формально все

алгоритмы являются только неухудшающими в том смысле, что не улучша-

ют стационарные точки соответствующих функционалов. Более того, струк-

тура алгоритмов 3 и 4 до последнего шага даже не может гарантировать, что

значение функционала качества J не ухудшится, и потому эти алгоритмы со-

держат дополнительную проверку найденного приближения по критерию J_∗.

4. Примеры

Для начала рассмотрим детерминированный вариант модельного примера

из [4]:

{

x₁(t) = 2x₂(t), x₁(0) = 1,

x₂(t) = -x₁(t) - u(t)x₂(t), x₂(0) = 1,

+∞

((

)

J =

u(t)² + 1

x₁(t)² + x₂(t)²

dt → min .

Воспользуемся утверждением 2, чтобы найти аналитическое решение за-

дачи в классе S стабилизирующих постоянных значений u ∈ R. Сперва опре-

делим множество S. Имеем

(

)

−1 -u

откуда получаем собственные значения матрицы A

√

-u ±

u² - 8

λ1,2 =

так что S = (0; +∞). Из утверждения 2 получаем следующие соотношения:

∂J_c(u)

= 2un₁₁ + 2m₁₂n₁₂ + 2m₂₂n₂₂,

∂u

⎧

⎪

4n₁₂ + 1 = 0,

⎪

2n₂₂ - n₁₁ - un₁₂ + 1 = 0,

⎪

⎨

-2n₁₂ - 2un₂₂ + 1 = 0,

⎪

u² + 1 + 2m₁₂ = 0,

⎪

m₂₂ - 2m₁₁ + um₁₂ = 0,

⎪

⎩

1 - 4m₁₂ + 2um₂₂ = 0.

Последовательно находим (с учетом 0 ∈ S)

n₁₂ = -

n₂₂ =

n₁₁ =

+ 1,

u² + 1

u³ + 3u

m₁₂ = -

m₂₂ = -u -

m₁₁ = -

u(t)

1,2

0,8

0,4

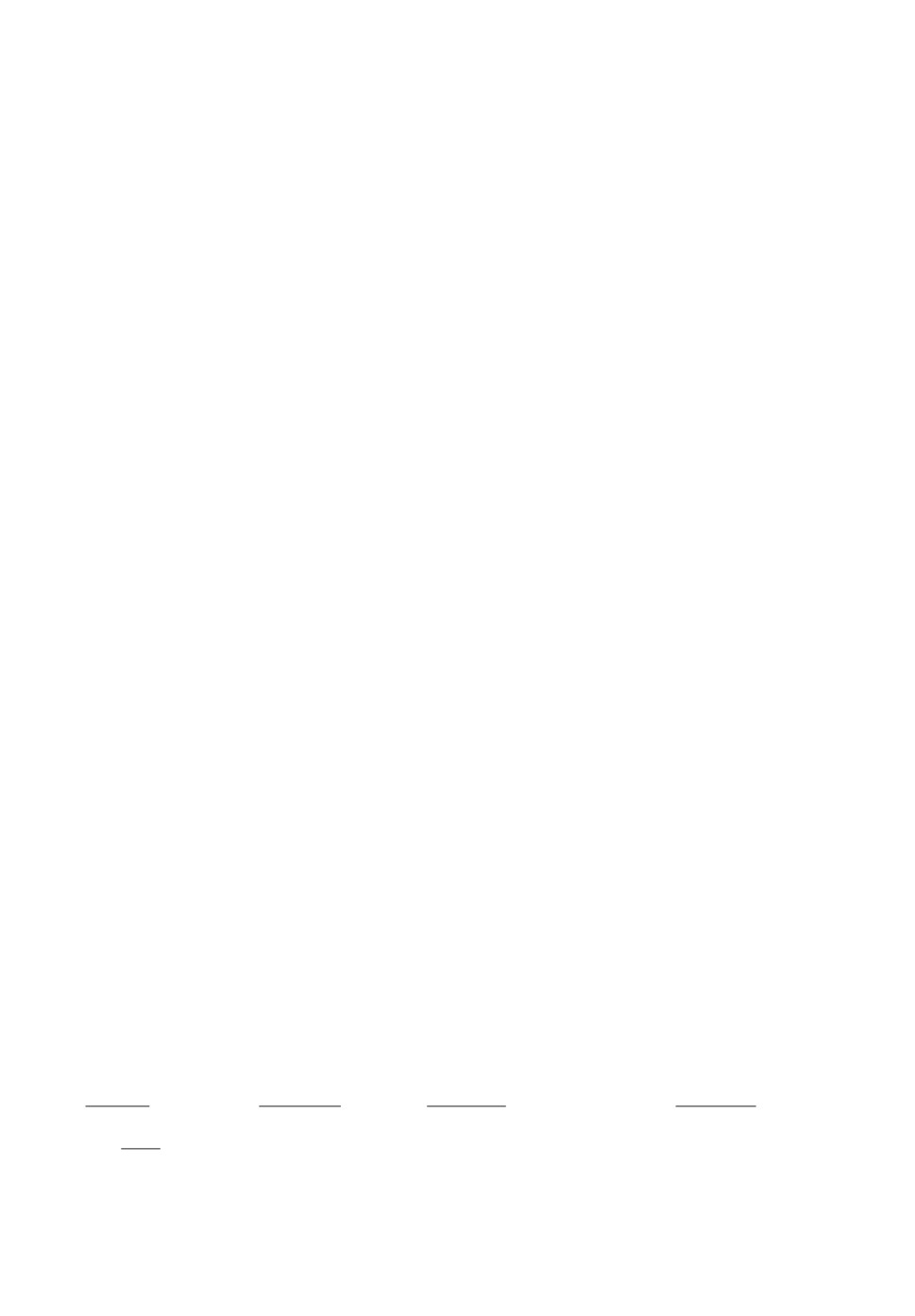
Рис. 1. Нестационарный регулятор ũ (алгоритм 2).

u(t)

1,2

0,8

0,4

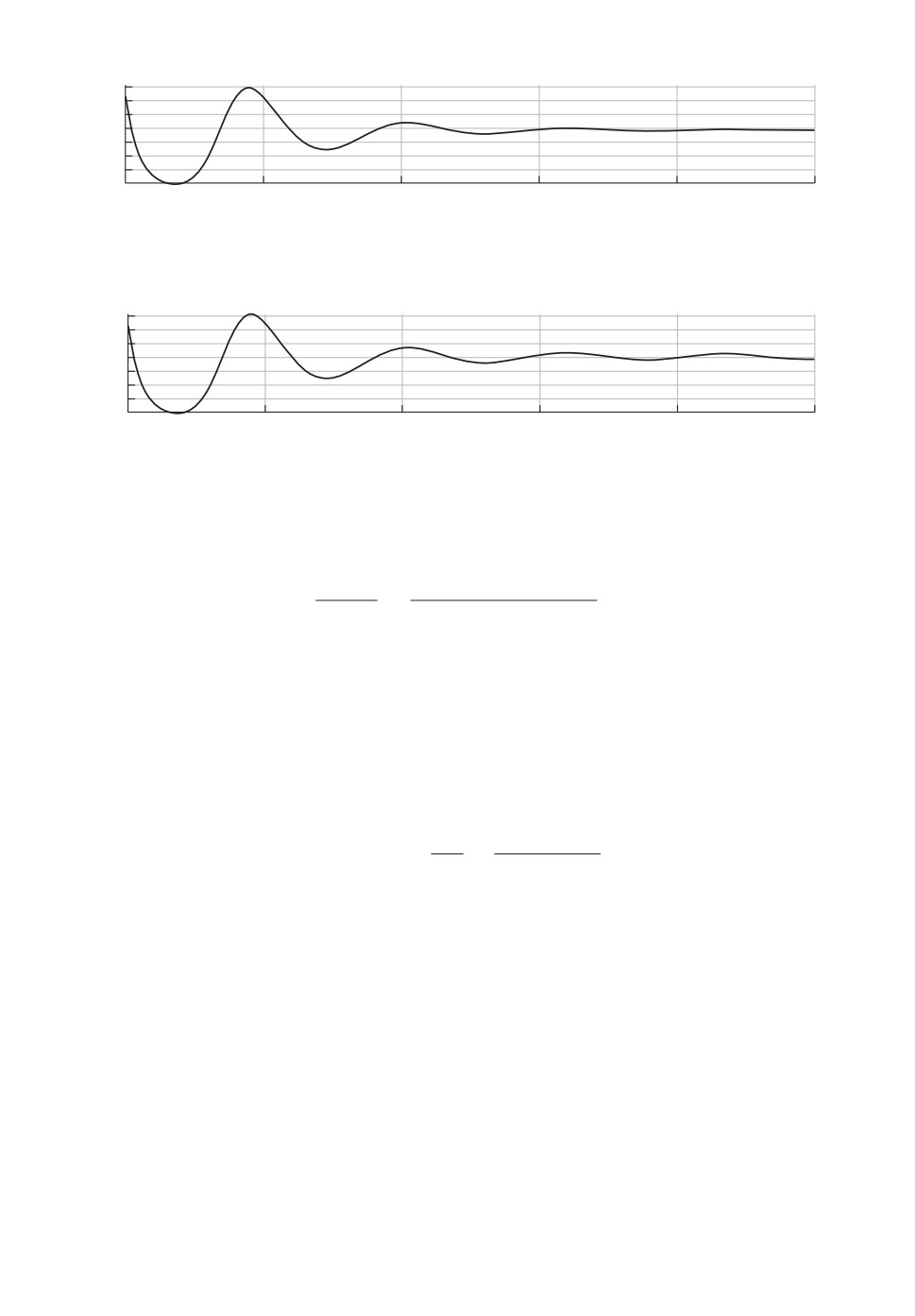
Рис. 2. Нестационарный регулятор û (алгоритм 3).

откуда

∂J_c(u)

3u⁴ + 8u³ + 7u² - 9

∂u

4u²

В области S имеется единственное решение уравнения ∂J_c(u)/∂u = 0, а имен-

но, u^∗ ≈ 0, 775.

Итак, решение задачи в классе стабилизирующих постоянных управлений

существует и определяется аналитически как единственный положительный

действительный корень уравнения 3u⁴ + 8u³ + 7u² - 9 = 0. При помощи аль-

тернативной формулы для J_c(u) из утверждения 2 также можно заключить,

что значение функционала качества на этом решении равно

∗

(u^∗)³ + 7u

J_c(u^∗) = -m∗11 - 2m∗12 - m∗22 =

+ (u^∗)² + 1 ≈ 5,976.

4u^∗

Теперь интересен следующий вопрос: «Возможно ли улучшить качество

найденного оптимального стационарного управления при помощи алгорит-

мов 1-4, и если да, то насколько сильно?»

Ясно, что алгоритм 1 не может улучшить найденное u^∗, но с его помощью

можно приблизиться к u^∗ сколь угодно точно, стартуя из произвольного ста-

билизирующего значения.

Реализуем численно алгоритм 2 (технические подробности относительно

используемой в работе реализации алгоритмов 1-4 приведены в следующем

разделе), взяв в качестве начального приближения u(t) ≡ u^∗. В результате

окажется найдено приближение ũ, представленное на рис. 1. Значение функ-

ционала качества также вычисляется численно по альтернативной формуле

из утверждения 1:

J(ũ) = J_∗(ũ) ≈ 4,385.

u(t)

0 t

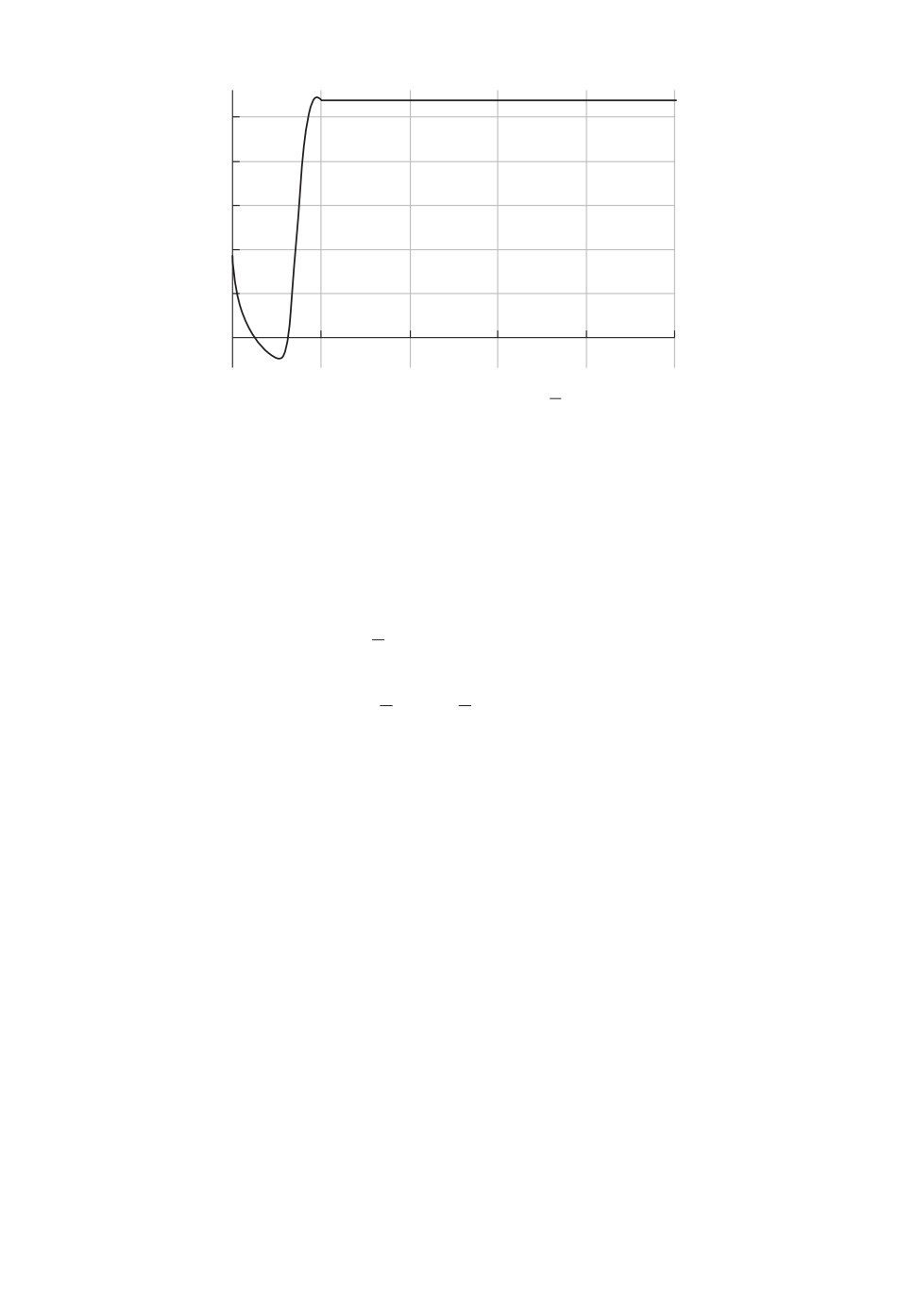
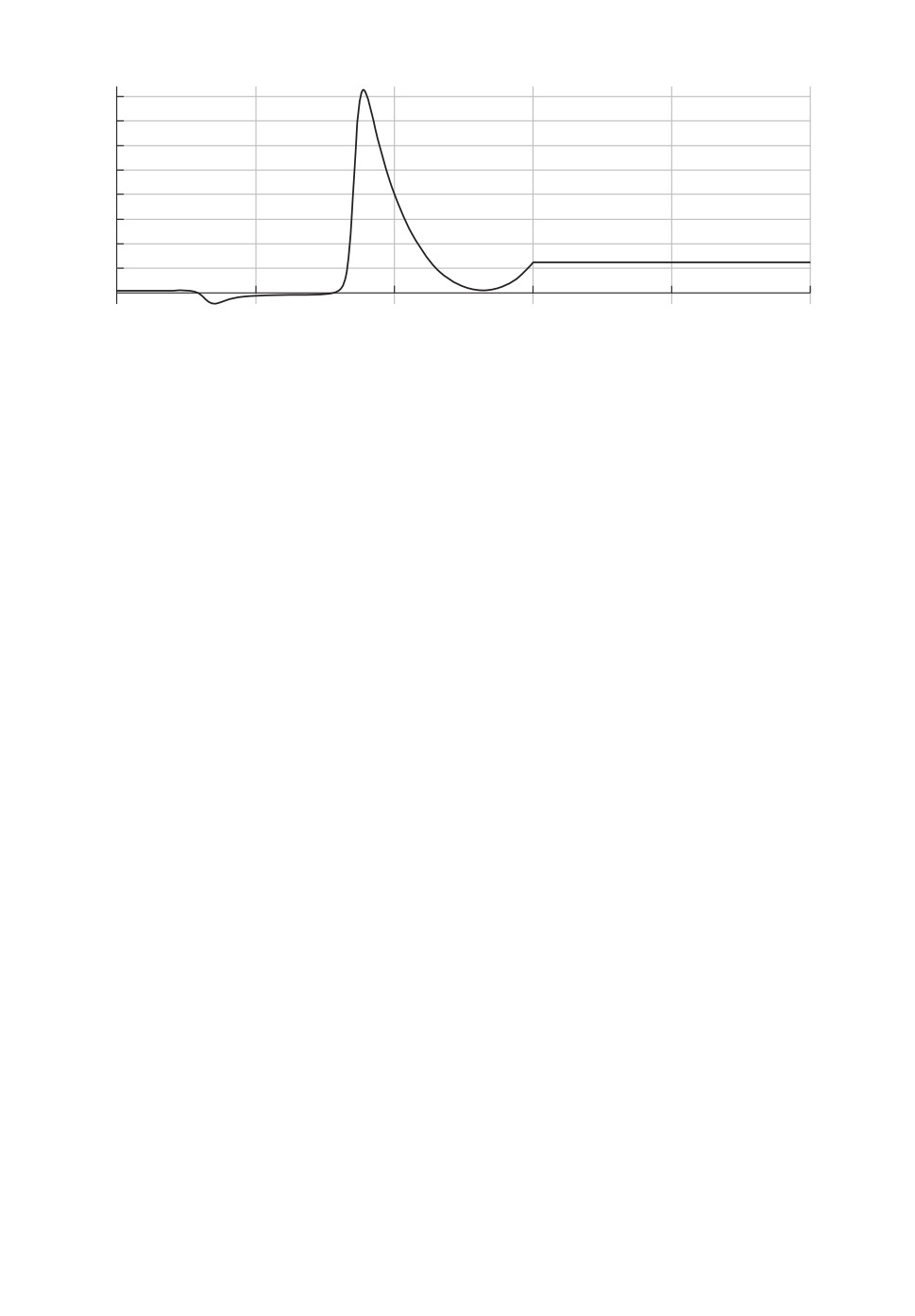
Рис. 3. Нестационарный регулятор u (алгоритм 4).

Используя то же начальное приближение u(t) ≡ u^∗, применим алгоритм 3.

В результате окажется найдено û, отличающееся (хоть и незначительно) от ũ.

Приближение û представлено на рис. 2. Значение функционала качества на

нем

J(û) = J_∗(û) ≈ 4,332.

Наконец, алгоритм 4 позволяет получить из начального приближения

u(t) ≡ u^∗ совершенно другое u (см. рис. 3). При этом значение функциона-

ла качества

J (u) = J_∗(u) ≈ 3,572.

Как итог, получена возможность построить нестационарный регулятор,

почти вдвое превышающий по качеству оптимальное стационарное решение.

Ясно, что варьирование начального приближения и параметров алгоритмов

может привести к дальнейшему улучшению.

Этот результат можно интерпретировать следующим образом. В стацио-

нарной линейно-квадратичной задаче оптимального управления

x(t) = Ax(t) + Bu(t), x(0) = (1, 1)^T,

(

)

(

)

−1 0

-1

+∞

(

)

J (u) =

x(t)^TQx(t) + u(t)Eu(t)

dt → min,

(

)

E=1

наилучший стационарный линейный регулятор вида

u(t) = u^∗x₂(t)

u(t)

1,2

1,0

0,8

0,6

0,4

0,2

0,5

1,0

1,5

2,0

2,5

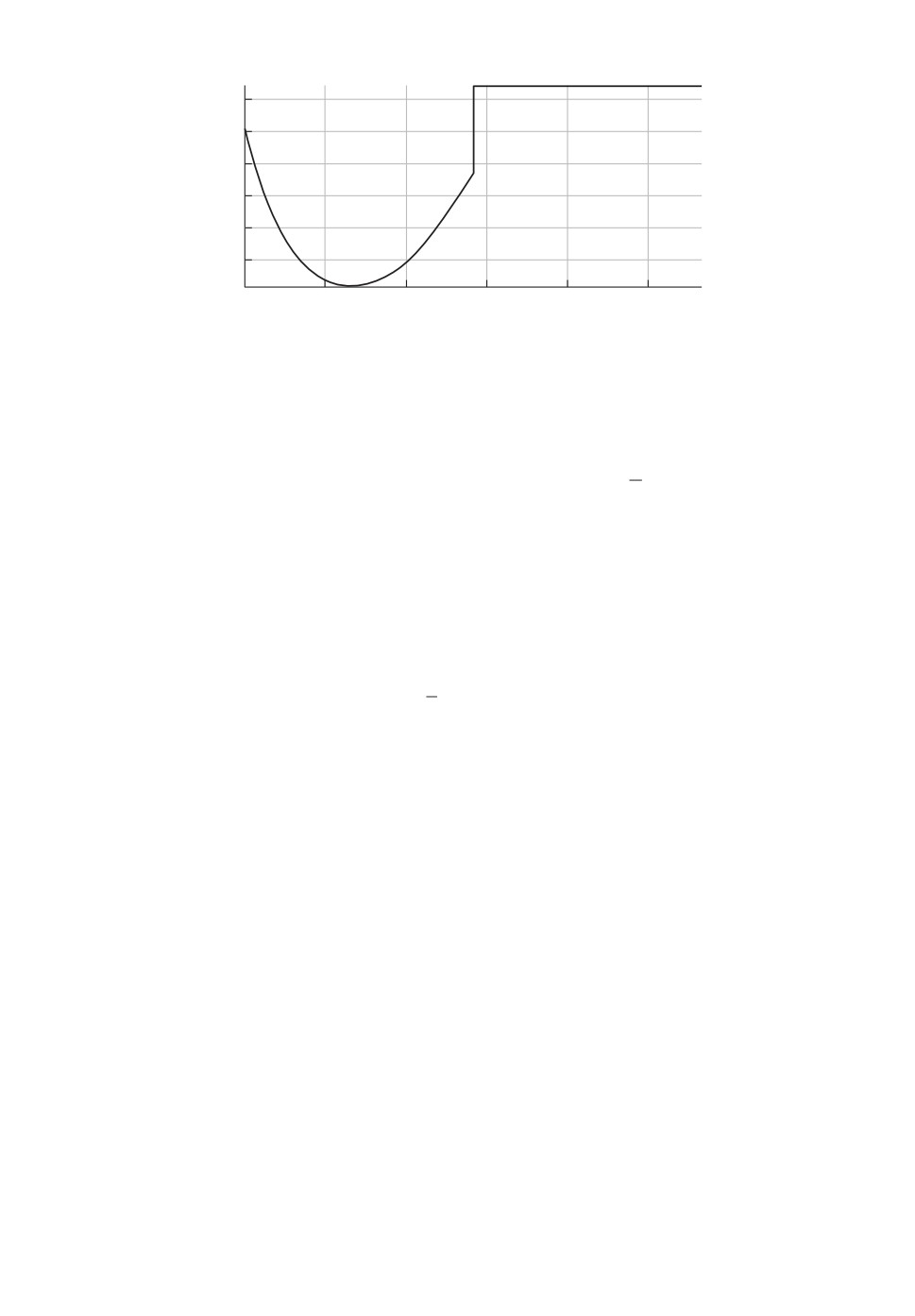
Рис. 4. Нестационарный регулятор û (алгоритм 1; стохастический случай).

не является оптимальным среди всех регуляторов, линейных по второй коор-

динате вектора состояния; в частности, регуляторы

u(t) = ũ(t)x₂(t), u(t) = û(t)x₂(t), u(t) = u(t)x₂(t)

обеспечивают лучшее качество управления в смысле заданного функциона-

ла J.

Сопоставим теперь результаты настоящей работы с исследованиями ста-

тьи [4]. В [4] обсуждается стохастический вариант предыдущего примера, а

именно

⎧

⎨

dx₁(t) = 2x₂(t)dt +

u(t)x₁(t)dw(t), x₁(0) = 1,

⎩

dx₂(t) = -(x₁(t) + u(t)x₂(t))dt, x₂(0) = 1,

⎡

⎤

∫

((

)

J =E⎣

u(t)² + 1

x₁(t)² + x₂(t)²

dt^⎦ → min .

Там же найдено оптимальное решение в классе стабилизирующих постоян-

ных управлений. Аналогично предыдущему можно показать, что это решение

является единственным в области устойчивости S действительным корнем u^∗

уравнения 6-й степени ∂J_c(u)/∂u = 0 и u^∗ ≈ 0,678, J_c(u^∗) ≈ 6,777. В [4] также

предлагается улучшающий алгоритм построения кусочно-постоянного управ-

ления, с помощью которого найдено новое приближение

^{ 0,678, 0 ≤ t < 1,42,

ũ(t) =

J(ũ) ≈ 6,185.

1,239,

1,42 ≤ t < +∞,

Ясно, что ũ ∈ U_T при T = 1,42, поэтому можно использовать для его улуч-

шения алгоритм 1. Результат û представлен на рис. 4,

J(û) = J_∗(û) ≈ 5,165.

u(t)

Рис. 5. Нестационарный регулятор (алгоритм 4; стохастический случай).

Алгоритмы 2-4 позволяют в дальнейшем улучшить качество управления

до значений функционала

J₂ ≈ 4,734, J₃ ≈ 4,639, J₄ ≈ 3,562.

Приближения, построенные по алгоритмам 2 и 3, практически не отличаются

от представленных на рис. 1 и 2. Приближение по алгоритму 4 приведено на

рис. 5.

5. Комментарии по реализации алгоритмов улучшения

Все алгоритмы реализованы в СКМ Maple в виде двух блоков программ

(блок 1 - алгоритмы 1 и 2; блок 2 - алгоритмы 3 и 4). Численное решение за-

дач Коши для линейных матричных дифференциальных уравнений в утвер-

ждениях 1 и 3 реализовано простейшим методом Эйлера с шагом h = 0,001,

численное решение алгебраических уравнений в утверждениях 2 и 3 - встро-

енным решателем solve. При реализации градиентного спуска использованы

динамически изменяющиеся величины шагов раздельно для «функциональ-

ной» и «хвостовой» части градиента. Значения параметров выбраны равными

T_max = 10, α = 100. Изменение параметра T в алгоритмах 3 и 4 осуществля-

ется на множестве {0, 1, . . . , T_max}. В соответствии с шагом численного инте-

грирования функциональная составляющая градиента считается принадле-

жащей пространству R^N , N = T/h, а норма совокупного градиента вычис-

ляется по формуле ||x||_∞ = max0≤i≤N+1 |x_i|. Условие остановки градиентного

спуска: норма совокупного градиента не превышает значение ε = 1.

ПРИЛОЖЕНИЕ

Справедливость всех сформулированных в работе утверждений непосред-

ственно вытекает из следующего общего результата.

Лемма 1. Пусть заданы банахово пространство X, открытое мно-

жество O в гильбертовом пространстве U, непрерывное отображение

F : O → X и произвольная функция J : X × O → R. Если существуют

множество Λ, отображение F^∗ : O → Λ и функции L : X × O × Λ → R,

J^∗ : O × Λ → R такие, что

1) L(F (u), u, λ) = J(F (u), u)

∀(u, λ) ∈ O × Λ;

2) L(x, u, F^∗(u)) = J^∗(u, F^∗(u))

∀(x, u) ∈ X × O;

3) ∀(u, λ) ∈ O×Λ существует непрерывное отображение x → L_u(x, u, λ) :

X → U,

то в любой точке u ∈ O функция u → J(F(u),u) дифференцируема и выпол-

нены соотношения

J (F (u), u) = J^∗(u, F^∗(u)),

∇_uJ(F(u),u) = L_u(F(u),u,F^∗(u)).

Доказательство леммы 1. Первое соотношение очевидно следует из

условий 1) и 2). Кроме этого, с учетом 3) для любых u ∈ O и ũ из окрестно-

сти u внутри O справедливо

J (F (ũ), ũ) - J(F (u), u) = L(F (ũ), ũ, F^∗(ũ)) - L(F (u), u, F^∗(u)) =

= L(F(ũ), ũ,F^∗(u)) - L(F(ũ),u,F^∗(u)) =

= 〈L_u(F (ũ), u, F^∗(u)), ũ - u〉 + o(||ũ - u||).

Отсюда ввиду непрерывности F и x → L_u(x, u, F^∗(u))

J (F (ũ), ũ) - J(F (u), u)

lim

= 〈L_u(F (u), u, F^∗(u)), e〉 , e ∈ S_U ,

ũ→u

||ũ - u||

где S_U := {e ∈ U : ||e|| = 1}, что завершает доказательство дифференцируе-

мости и второго соотношения.

В дальнейшем будет удобно использовать следующее вспомогательное

утверждение (AC^n×n([0; T ]) - пространство абсолютно непрерывных на от-

резке [0; T ] матричных функций размеров n × n).

Лемма 2. Для любого допустимого управления u на множестве

AC^n×n([0;T]) × R^n×n существует единственное непрерывно зависящее от

изменений u ∈ U решение (N, N_T ) уравнений

(Π.1)

(t) = A(u(t))N(t) + N(t)A(u(t))^T + G(u(t))N(t)G(u(t))^T, N(0) = N₀,

(Π.2)

A(u_T )N_T + N_T A(u_T )^T + G(u_T )N_T G(u_T )^T

+ N(T) = 0,

причем значение функционала (6) удовлетворяет равенству

∫T

J (u) = tr [Q(u(t))N(t)] dt + tr [Q(u_T )N_T ] .

Доказательство леммы 2. Уравнения (Π.1) и (Π.2) представляют

собой линейную матричную задачу Коши и линейное матричное алгебраи-

ческое уравнение (обобщенное уравнение Ляпунова), разрешимые раздельно.

Существование и единственность решения в условиях задачи (5)-(6), а также

его непрерывная зависимость от параметров хорошо известны [8, 9]. Исполь-

зуя формулу Ито [3], нетрудно проверить следующие равенства:

⎡

⎤

∫

N (t) = E[x(t)x(t)^T], N_T = E ⎣ x(t)x(t)^Tdt⎦ ,

где x(t) - сильное решение уравнения (5). Остается записать исходя из (6),

что

⎡+∞

⎤

∫

J (u) = E⎣ x(t)^TQ(u(t))x(t)dt⎦ = tr [Q(u(t))N(t)] dt + tr [Q(u_T )N_T ] .

Доказательство утверждения 1. Дано число T > 0. Положим в

условиях леммы 1 X = AC^n×n([0; T ]), O = U = Lm2([0; T ]), отображение F

определим как решение уравнения (Π.1), функцию J будем считать задан-

ной на X × O формулой (8). Далее, определим Λ = X, отображение F^∗ - как

единственное решение задачи Коши

^M (t) = -M(t)A(u(t)) - A(u(t))^TM(t) - G(u(t))^TM(t)G(u(t)) + Q(u(t)),

M (T ) = -αI,

а функции L и J^∗ - формулами

L(N, u, M) = J_α(u) + tr [M(T )N(T )] - tr [M(0)N(0)] -

∫T

[

- tr

^M (t)N(t) +

(

)]

+ M(t)

A(u(t))N(t) + N(t)A(u(t))^T + G(u(t))N(t)G(u(t))^T

dt,

J^∗(u,M) = -tr [M(0)N₀] .

Справедливость условий 1)-2) леммы 1 очевидна (в самом деле, условие 1)

следует из (Π.1) и конструкции L, а отображение F^∗ построено непосред-

ственно исходя из 2)), условие 3) следует из исходных требований на отобра-

жения A, G, Q. Применяя лемму 1, а затем лемму 2, завершаем доказатель-

ство.

Доказательство утверждения 2. Положим в условиях леммы 1

X = R^n×n, U = R^m, O = S, отображение F определим как решение урав-

нения (Π.2) при N(T ) = N₀, функцию J будем считать заданной на X × O

формулой (9). Далее, определим Λ = X, отображение F^∗ - как единственное

решение обобщенного уравнения Ляпунова

Q(u_T ) - M_T A(u_T ) - A(u_T )^TM_T - G(u_T )^TM_T G(u_T ) = 0,

а функции L и J^∗ - формулами

L(N_T , u, M_T ) =

[

(

)]

= J_c(u) - tr

M_T

A(u_T )N_T + N_T A(u_T )^T + G(u_T )N_T G(u_T )^T + N₀

J^∗(u,M_T ) = -tr [M_T N₀] .

Справедливость условий 1)-3) леммы 1 вновь очевидна. Остается применить

ее, а затем лемму 2.

Доказательство утверждения 3. Дано число T > 0. Положим в

условиях леммы 1 X = AC^n×n([0; T ]) × R^n×n, U = Lm2([0; T ]) × R^m, O = U_T ,

отображение F определим как решение уравнений (Π.1), (Π.2), функцию J

будем считать заданной на X × O формулой (7). Далее, определим Λ = X,

отображение F^∗ - как единственное решение системы уравнений

^M (t) = -M(t)A(u(t)) - A(u(t))^TM(t) - G(u(t))^TM(t)G(u(t)) + Q(u(t)),

M (T ) = M_T ,

Q(u_T ) - M_T A(u_T ) - A(u_T )^TM_T - G(u_T )^TM_T G(u_T ) = 0,

а функции L и J^∗ - формулами

L(N, N_T , u, M, M_T ) = J_∗(u) + tr [M(T )N(T )] - tr [M(0)N(0)] -

∫T

[

- tr

^M (t)N(t) +

(

)]

+ M(t)

A(u(t))N(t) + N(t)A(u(t))^T + G(u(t))N(t)G(u(t))^T

dt -

[

(

)]

−tr

M_T

A(u_T )N_T + N_T A(u_T )^T + G(u_T )N_T G(u_T )^T + N(T )

J^∗(u,M,M_T ) = -tr[M(0)N₀] .

Для завершения доказательства вновь последовательно применяем леммы 1

и 2.

В заключение отметим, что утверждения 1-3 вовсе не обязательно дока-

зывать, опираясь на весьма общую лемму 1. В частности, в [5, 6] утвержде-

ния 1 и 2 были доказаны непосредственным анализом приведенных выше

конструкций L с использованием аналогов леммы 2. Лемма 1, в свою оче-

редь, выделяет и обобщает до абстрактного уровня ключевую концепцию,

присущую каждому из трех доказанных утверждений.

СПИСОК ЛИТЕРАТУРЫ

1. Поляк Б.Т., Щербаков П.С. Робастная устойчивость и управление. М.: Наука,

2002.

2. Rumyantsev D., Tsarkov K. On Certainty Equivalence Property in Deterministic LQ-

problems with Random Initial Data and Information Constraints // Proceedings of

the 15th International Conference “Stability and Oscillations of Nonlinear Control

Systems” (Pyatnitskiy’s Conference) (STAB-2020, Moscow). М.: IEEE, 2020.

3. Королюк В.С., Портенко Н.И., Скороход А.В., Турбин А.Ф. Справочник по тео-

рии вероятностей и математической статистике. М.: Наука, 1985.

4. Онегин Е.Е. Оптимальная стабилизация квазилинейной стохастической систе-

мы с управляемыми параметрами // Мехатроника, автоматизация, управление.

2019. Т. 20. № 10. С. 589-599.

5. Хрусталев М.М., Румянцев Д.С., Царьков К.А. Оптимизация квазилинейных

стохастических систем диффузионного типа, нелинейных по управлению //

АиТ. 2017. № 6. С. 84-105.

Khrustalev M.M., Rumyantsev D.S., Tsarkov K.A. Optimization of Quasilinear

Stochastic Control-nonlinear Diffusion Systems // Autom. Remote Control. 2017.

V. 78. No. 6. P. 1028-1045.

6. Onegin E., Khrustalev M. Optimal Stabilisation of a Quasilinear Stochastic System

with Controllable Parameters // Proceedings of the 14th International Conference

“Stability and Oscillations of Nonlinear Control Systems” (Pyatnitskiy’s Conference)

(STAB-2018, Moscow). М.: IEEE, 2018.

7. Онегин Е.Е., Хрусталев М.М. Субоптимальная стабилизирующая стратегия

управления линейной стохастической системой с управляемыми параметрами //

Труды 13-го Всероссийского совещания по проблемам управления (ВСПУ XIII,

Москва, 2019). М.: ИПУ РАН, 2019. С. 870-874.

8. Hartman P. Ordinary Differential Equations. John Wiley & Sons, 1964.

9. Damm T. Rational Matrix Equations in Stochastic Control. Springer-Verlag Berlin

Heidelberg, 2003.

Статья представлена к публикации членом редколлегии А.И. Маликовым.

Поступила в редакцию 07.03.2021

После доработки 27.04.2021

Принята к публикации 30.06.2021