Автоматика и телемеханика, № 12, 2021

Стохастические системы

Е.А. БАРАБАНОВА, д-р техн. наук (elizavetaalexb@yandex.ru)

(Институт проблем управления им. В.А. Трапезникова РАН, Москва)

АНАЛИТИЧЕСКИЙ МЕТОД АНАЛИЗА НЕОДНОРОДНЫХ

НЕПРЕРЫВНЫХ МАРКОВСКИХ ПРОЦЕССОВ С

КУСОЧНО-ПОСТОЯННЫМИ ИНТЕНСИВНОСТЯМИ ПЕРЕХОДА

В статье рассматривается неоднородный марковский процесс с конеч-

ным числом дискретных состояний, непрерывным временем и кусочно-по-

стоянными интенсивностями перехода. Впервые приведены аналитиче-

ские выражения, описывающие и переходной, и стационарный режимы

случайного процесса. Для решения этой задачи фундаментальная матри-

ца системы дифференциальных уравнений Колмогорова найдена в анали-

тическом виде в элементарных функциях. Кроме того, рассматривается

неоднородный процесс с периодически изменяющимися интенсивностя-

ми переходов. Для этого случая представлены условия существования

стационарного режима. Приведены численные расчеты для процесса без

скачков, со скачками и с периодическими скачками интенсивностей пере-

ходов.

Ключевые слова: неоднородный марковский процесс, кусочно-постоянные

интенсивности переходов, уравнения Колмогорова.

DOI: 10.31857/S0005231021120060

1. Введение

Марковские случайные процессы используются для решения целого ря-

да задач в системах управления, теории надежности, системах массового

обслуживания, поддержки принятия решений и т.д. [1-5]. Как правило, в

литературе рассматриваются стационарные марковские процессы, однако во

многих случаях реальные системы необходимо описывать с использованием

нестационарных марковских процессов, в которых интенсивности переходов

из состояния в состояние зависят от времени, а в ряде случаев их изменения

носят скачкообразный характер [4]. Причинами таких изменений интенсив-

ностей перехода, например в системах связи и управления, являются помехи,

в том числе периодические.

Изучение марковских процессов с зависимыми от времени интенсивностя-

ми переходов началось с работ Кларка [6, 7] и продолжилось Лемуаном [8]

и Харисоном [9]. В дальнейшем данная тема получила развитие в работах

Когана Я.А., Литвина В.Г., Дудина А.Н., Миллера Б.М., Бондровой О.В.

и Головко Н.И. [4, 10-14,] и др. Так, в [10] рассмотрено функционирование

узлов информационных сетей Интернет, описываемых системами массового

обслуживания с параметрами, изменяющимися в случайные моменты време-

ни. В [12] рассматриваются системы массового обслуживания с основным и

резервным приборами и скачкообразной интенсивностью входного потока и

для данного случая получена система интегро-дифференциальных уравнений

типа Колмогорова-Чепмена. В [13] также изучались марковские процессы

со скачкообразным изменением интенсивностей входного потока. Предложен

так называемый функционально-аналитический метод. В этой работе также

приводится доказательство существования и единственности нестационарно-

го и стационарного режимов. В [14] выведены интегро-дифференциальные

уравнения относительно нестационарных и стационарных характеристик чис-

ла заявок на основе метода Колмогорова-Чепмена.

При рассмотрении систем массового обслуживания часто исследуется во-

прос о возможности установления в системе стационарного режима [4, 5]. Од-

нако стационарный режим во многих случаях не раскрывает реальной кар-

тины поведения многих систем, поскольку он не учитывает переходные про-

цессы как в момент запуска системы, так и в момент внешних воздействий.

В большинстве практических приложений как интенсивности переходов, так

и вероятности состояний претерпевают изменения, которые можно проана-

лизировать только в переходном режиме. Кроме этого, если, например, в

начальный момент времени в системе массового обслуживания отсутствуют

заявки, то время пребывания запросов в системе, их число и другие парамет-

ры будут отличаться от значений в установившемся режиме, и, следователь-

но, использование результатов расчета параметров системы в стационарном

состоянии для анализа переходного режима не является корректным.

Одно из первых исследований переходного режима было представлено в

работе Харрисона [9] в 1981 г. Но затем эта проблема долгое время не рас-

сматривалась. Увеличение сетевого трафика и возникновение так называ-

емых катастроф [15] привело к актуальности изучения переходного режи-

ма [16, 17]. В [16] представлены выражения для вероятностей состояний в

переходном режиме для гетерогенной многосерверной марковской системы

массового обслуживания, подверженной катастрофам. В [17] рассматривает-

ся система массового обслуживания M/M/2 с катастрофами, для которой

получены зависящие от времени вероятности нахождения различного числа

заявок в системе.

Таким образом, целый ряд случайных процессов описывается системой

уравнений Колмогорова с зависящими от времени коэффициентами. Одна-

ко на данный момент отсутствует аналитическое решение для вероятностей

состояний случайного марковского процесса с дискретным числом состоя-

ний и интенсивностями переходов, изменяющимися скачками в произвольные

неслучайные моменты времени, выражающееся через интенсивности перехо-

дов в явном виде.

В данной работе впервые представлен аналитический подход для иссле-

дования как переходного, так и стационарного режимов случайного марков-

ского процесса с дискретным числом состояний и изменяющимися скачками

интенсивностями переходов. В разделе 3.1 представлена фундаментальная

матрица системы уравнений Колмогорова для случая постоянных интенсив-

ностей переходов. Здесь следует отметить, что определитель матрицы коэф-

фициентов исходной системы дифференциальных уравнений равен нулю, а

фундаментальная матрица не является унимодулярной, как в большинстве

случаев [18-20]. Фундаментальная матрица для скачкообразных интенсивно-

стей переходов получена в разделе 3.2. Несмотря на то что на сегодняшний

день данный случай широко исследуется, аналитического выражения фун-

даментальной матрицы, выраженной в интенсивностях переходов в явном

виде, в литературе представлено не было. Важным является также тот факт,

что функция, описывающая интенсивности переходов, является произволь-

ной детерминированной кусочно-постоянной, т.е. имеет произвольное число

скачков. Случай периодически изменяющихся интенсивностей переходов ис-

следован в разделе 3.3. Исследование условий существования переходного и

стационарного режимов здесь основывается на аппарате теории устойчиво-

сти Ляпунова [18]. Численные расчеты для процесса с тремя состояниями

представлены в разделе 4.

2. Постановка задачи

В данной работе рассматривается неоднородный марковский процесс с M

дискретными состояниями и непрерывным временем (рис. 1). Пространство

состояний процесса есть множество неотрицательных целых чисел. Вре-

мя пребывания процесса в состоянии j имеет показательное распределе-

ние. Здесь предполагается, что все интенсивности переходов описывают-

ся кусочно-постоянными функциями (например, рис. 2). Cистема уравнений

Колмогорова для этого случая, составленная с помощью Δt-метода [4-6, 8],

имеет вид

∑

dP_j (t)

(1)

= -P_j(t)

λ_ji(t) +

λ_ij(t)P_i

(t),

i=1,i=j

где λ_ij(t) - кусочно-постоянные функции, P_j (t) - вероятности состояний про-

цесса, M - число состояний процесса. Основной целью статьи является разра-

ботка аналитического метода исследования неоднородного марковского про-

цесса со скачкообразным изменением интенсивностей переходов, описывае-

мого системой (1) с кусочно-постоянными коэффициентами.

Для решения (1) традиционно используется преобразование Лапласа [4, 5].

Однако такой подход не позволяет записать общее выражение для случая

S₁

S₂

S₃

S_M

Рис. 1. Граф переходов рассматриваемого случайного процесса.

p(t)

1,0

1,2

1,0

0,8

p₁(t)

0,8

0,6

p₃(t)

0,6

0,4

p₂(t)

0,4

p₃(t)

0,2

p₂(t)₂₂

0,2

Рис. 2. Зависимость вероятностей состояний от времени для случая постоян-

ных интенсивностей переходов.

произвольного числа состояний и произвольных интенсивностей переходов.

Поэтому здесь предлагается принципиально иной подход, основанный на ме-

тоде фундаментальной матрицы системы линейных однородных дифферен-

циальных уравнений с кусочно-постоянными коэффициентами.

3. Фундаментальная матрица

В данном разделе представлен аналитический метод решения системы

уравнений Колмогорова, описывающей марковский случайный процесс с ко-

нечным числом M состояний в произвольный момент времени как с постоян-

ными, так и с кусочно-постоянными интенсивностями переходов. Для этого

использована концепция фундаментальной матрицы системы линейных од-

нородных дифференциальных уравнений.

Известно, что фундаментальной матрицей L(t) является матрица [18-20],

столбцы которой образуют фундаментальную систему решений. С практиче-

ской точки зрения она связывает вероятности состояний процесса в некото-

рый момент времени t с теми же вероятностями в начальный момент време-

ни t₀. Таким образом, для случая M состояний процесса можно написать

(2)

U(t) = L_M×M (t)U(t₀

Здесь L_M×M (t) - искомая фундаментальная матрица размерностью M × M,

U(t) = (P_j )^T - вектор состояний случайного процесса, где j = 1, M, T - опе-

ратор транспонирования.

3.1. Фундаментальная матрица системы уравнений Колмогорова,

описывающей процесс с постоянными интенсивностями переходов

В этом подразделе фундаментальная матрица L(t), описывающая переход-

ный режим случайного однородного марковского процесса с M дискретными

состояниями и постоянными интенсивностями переходов, получена в анали-

тической форме, удобной для дальнейшего исследования кусочно-постоянных

интенсивностей переходов. В рассматриваемом случае L(t) — это матрица

(M × M), имеющая вид

∑

(3)

L(t) =

A_j exp(γ_j

t).

i=1

Элементы (M × M) — матрицы A_j записываются как

(-1)k+lΔ_ij

(4)

(A_j)_kl =

ξ_kj,

⎛

⎞

ξ₁₁

ξ₁₂

... ξ1M

⎜

⎟

ξ₂₁

ξ₂₂

... ξ2M

⎜

⎟

(5)

Δ=

⎝

⎠^,

ξM1

ξM2

... ξ_MM

Δ_lj - определитель алгебраического дополнения к элементу ξ_lj матрицы Δ,

Δ - собственный базис матрицы коэффициентов системы (1) в M-мерном

пространстве [18], γj - j-й корень характеристического уравнения систе-

мы (1). Отметим, что выражение (3) справедливо, если все корни характе-

ристического уравнения простые. Причем в рассматриваемой задаче один из

корней всегда равен нулю, поскольку определитель матрицы коэффициентов

равен нулю при любых положительных λ_ij(t).

Одной из важнейших задач при рассмотрении переходного режима являет-

ся нахождение постоянной времени процесса в переходном режиме и времени

установления стационарного режима [9]. В данном случае процесс в переход-

ном режиме представляет собой линейную комбинацию экспоненциальных

процессов с постоянными времени τ_j = 1/ | γ_j |. Постоянная времени общего

процесса определяется как величина, обратная модулю наименьшего ненуле-

вого γ_j, т.е. τ = 1/ | γ_min |, где ∀γ_j ∈ Γ (γ_j ≥ γ_min ⇒ γ_j = γ_min) [9]. Тогда время

переходного режима можно определить как τ_tr = (3 ÷ 5)τ = (3 ÷ 5)/ | γjmin |.

3.2. Фундаментальная матрица системы уравнений Колмогорова,

описывающей процесс с кусочно-постоянными

интенсивностями переходов

Фундаментальная матрица системы уравнений Колмогорова с кусочно-

постоянными интенсивностями переходов, описывающей процесс на N-м ин-

тервале, может быть найдена как произведение матриц с постоянными ин-

тенсивностями переходов [18-21]

[

]

∏

(6)

L_Σ(t) = L_N(t - tN-1)

L_i(Δt_i)

i=N-1

где L_i(Δt_i) - фундаментальная матрица системы уравнений Колмогорова,

описывающая процесс на i-м интервале с постоянными интенсивностями пе-

реходов, Δt_i = t_i - ti-1 - длительность i-го интервала, N - число интервалов,

L_N(t) - фундаментальная матрица системы уравнений Колмогорова, опи-

сывающая процесс на N-м интервале, L_Σ(t) - результирующая фундамен-

тальная матрица. Действительно, пусть на первом интервале с постоянными

интенсивностями переходов процесс описывается системой уравнений Кол-

могорова, фундаментальная матрица которой равна L₁(t - t₀). Тогда на этом

интервале состояния системы в произвольный момент времени находятся как

(7)

U(t) = L₁(t - t₀)U(t₀

а при t = t₁ имеем

(8)

U(t₁) = L₁(Δt₁)U(t₀

Аналогично для второго интервала запишем

(9)

U(t) = L₂(t - t₁)U(t₁

где L₂(t - t₁) - фундаментальная матрица системы уравнений Колмогорова,

описывающей процесс на втором интервале с постоянными интенсивностя-

ми переходов. Учитывая условие непрерывности вероятностей состояний на

границе между интервалами [18-20], можно подставить (8) в (9)

(10)

U(t) = L₂(t - t₁)L₁(Δt₁)U(t₀

Из (10) следует, что фундаментальная матрица, описывающая поведение про-

цесса на интервале t₁ ≤ t ≤ t₂, имеет вид

(11)

L_Σ(t) = L₂(t - t₁)L₁(Δt₁

Проделав эту процедуру для произвольного конечного числа интервалов N,

получим выражение (6).

В результате доказано, что матрица (6) описывает поведение случайно-

го процесса и предполагает отсутствие скачков вероятностей состояний на

границах интервалов. Однако скачки первой производной не исключаются.

Действительно, в соответствии с методом [18-20] фундаментальная матри-

ца системы (1) составляется при условии непрерывности функций, но не их

производных. С точки зрения практических приложений это означает, что

каждый из скачков интенсивностей перехода приводит к новому переход-

ному режиму с начальными значениями, равными вероятностям состояний

непосредственно перед скачком.

Подставляя (3) в (6), проводя алгебраические преобразования, применяя

операцию логарифмирования, а затем потенцирования, найдем выражение

фундаментальной матрицы для N интервалов с постоянными интенсивно-

стями переходов и M состояниями системы:

[

]

∑

(

)

(12) L =

exp

Ln(Aiji ) + γiji Δt_i

+Ln(ANjN)+γNjN (t-tN-1) ,

j_i=1

i=N-1

1≤j≤N

где i - номер интервала с постоянными интенсивностями переходов, j_i - но-

мер состояния процесса на интервале i, Aiji - матрицы с элементами (3) на

i-м интервале, γiji - j_i-й корень характеристического уравнения системы (1)

на интервале i.

Таким образом, найдена фундаментальная матрица системы уравнений

Колмогорова для неоднородного марковского процесса с произвольным ко-

нечным числом состояний и произвольными кусочно-постоянными интен-

сивностями переходов. Отметим, что преобразование произведения фунда-

ментальных матриц в конечную сумму экспонент без нарушения граничных

условий в моменты скачков интенсивностей переходов является важным мо-

ментом для данного результата. Действительно, каждая из экспонент в (12)

описывает некоторый непрерывный экспоненциальный процесс. Такой под-

ход позволяет анализировать влияние каждого интервала с постоянными па-

раметрами на результирующее состояние процесса. Кроме того, очевидно,

что результирующее состояние процесса определяется параметрами каждого

из интервалов с постоянными интенсивностями переходов. Поэтому нельзя

считать, что общее решение является результатом простого совмещения ре-

шений на интервалах с постоянными параметрами. Более того, отметим, что

предложенный подход не требует использования численных методов, которые

обычно применялись для решения дифференциальных уравнений с кусочно-

постоянными коэффициентами.

3.3. Процесс с периодическими кусочно-постоянными

интенсивностями переходов

Приведенные выше результаты очень важны для самых разнообразных

приложений. Например, изучение процессов с периодическими интенсивно-

стями переходов является очень интересной, но не изученной практической

задачей. Допустим, что интенсивности переходов являются периодическими

функциями времени λ_ij (kT + t) = λ_ij (t), k ∈ Z, T - период изменения интен-

сивностей переходов. Причем λ_ij(t) на периоде является кусочно-постоянной

функцией. Очевидно, что фундаментальная матрица для K периодов T из-

менения интенсивностей переходов может быть найдена как K-я степень мат-

рицы (12) [18]:

⎧

⎫

⎪

[

]⎪

⎨

∑

⎬

(13)

L_K =

exp

(Ln (Aiji ) + γiji Δt_i)

⎪

⎩ ji=1

i=1

⎭

1≤i≤N

Вычисление выражения (13) является достаточно сложной задачей, осо-

бенно если число состояний M очень велико. Однако для описания рассмат-

риваемого периодического процесса достаточно исследовать фундаменталь-

ную матрицу процесса за период T в виде (13). Действительно, собственные

числа и собственные векторы матрицы (13) полностью характеризуют рас-

сматриваемый случайный процесс [18]. Отметим также, что при периодиче-

ской зависимости коэффициентов (1) от времени нет необходимости рассмат-

ривать динамику процесса внутри каждого периода, но необходимо исследо-

вать изменение вероятностей состояний за один период. Этот вопрос является

одной из важнейших задач теории устойчивости дифференциальных уравне-

ний [18, 21, 22]. При этом наиболее часто используется понятие устойчивости

решений по Ляпунову, поскольку оно является наиболее строгим. Согласно

теории устойчивости, процесс будет устойчивым по Ляпунову и достигнет

стационарного состояния с течением времени только в том случае, если все

мультипликаторы q_m системы (1) (собственные числа q_m фундаментальной

матрицы (12)) по модулю меньше единицы (q_m ≤| 1 |, m = 1, M) или, други-

ми словами, характеристические показатели Ляпунова α_m = (1/T ) Lnq_m ≤ 0

должны быть отрицательными либо равными нулю.

Более того, процесс является экспоненциальным, если все мультипликато-

ры q_m системы (1) с периодическими коэффициентами действительны. Про-

цесс является незатухающим гармоническим, если мультипликаторы q_m мни-

мые. Процесс должен быть затухающим волнообразным, если хотя бы один

мультипликатор q_m является комплексным и его действительная часть по

модулю меньше единицы.

Отметим также, что мультипликаторы системы (1) могут быть мнимы-

ми или комплексными, даже если ее собственные числа на интервалах с по-

стоянными коэффициентами действительны и отрицательны [18, 21, 22]. При

этом данный факт не означает, что комплексными или мнимыми являются

вероятности состояний, а означает лишь волнообразный характер процесса.

Действительная часть мультипликатора определяет скорость затухания пере-

ходного режима, а мнимая часть определяет частоту переколебаний вероят-

ностей состояний в этом режиме. Таким образом, если все мультипликаторы

по модулю меньше единицы, то время переходного режима процесса опре-

деляется как τ_tr = 1/ | Re (q_min) |, где q_min - минимальный мультипликатор

системы.

4. Численный расчет

В этом разделе приводится тестовый расчет на примере частного случая

марковского случайного процесса с тремя дискретными состояниями, непре-

рывным временем и зависящими от времени кусочно-постоянными интенсив-

ностями переходов. В данном случае система уравнений Колмогорова приво-

дится к следующему виду:

⎧

dP₁(t)

⎪

= -(λ₁₂(t) + λ₁₃(t))P₁(t) + λ₂₁(t)P₂(t) + λ₃₁(t)P₃(t),

⎪

⎨

dP₂(t)

(14)

= λ₁₂(t)P₁(t) - (λ₂₁(t) + λ₂₃(t)) P₂(t) + λ₃₂(t)P₃(t),

⎪

P₃(t)

⎩ d

= λ₁₃(t)P₁(t) + λ₂₃(t)P₂(t) - (λ₃₁(t) + λ₃₂(t)) P₃(t),

для постоянных коэффициентов (λ_ij = const) ее характеристические числа

являются решением линейного алгебраического уравнения третьего порядка,

один из которых всегда равен нулю.

Из вида матрицы коэффициентов уравнения (1) следует, что корни γ2,3

всегда будут отрицательными [18]. Общие решения для вероятностей P₁(t),

P₂(t) и P₃(t) при λ_ij = const можно записать в виде

P₁(t) = ξ₁₁A + ξ₁₂B exp(γ₂t) + ξ₁₃C exp(γ₃t),

(15)

P₂(t) = ξ₂₁A + ξ₂₂B exp(γ₂t) + ξ₂₃C exp(γ₃t),

P₃(t) = ξ₃₁A + ξ₃₂B exp(γ₂t) + ξ₃₃C exp(γ₃t).

Здесь A, B, C - постоянные интегрирования, определяемые начальными усло-

виями, γ_j - корни характеристического уравнения системы (14), ξ_kj - коэф-

фициенты, соотносящие P₁(t), P₂(t), P₃(t), образующие собственный базис

матрицы коэффициентов системы (14).

Далее также обычно учитывается известное соотношение

(16)

P₁ + P₂ + P₃

= 1.

С учетом (16) находится постоянная интегрирования A как функция от λ_ij,

а константы B и C определяются начальными условиями процесса.

Отметим, что из (15) очевидно следует, что при t → ∞, γ1,2 ≤ 0 и любых

начальных условиях процесс стремится к стационарному режиму с вероят-

ностями состояний

⎛

⎞

⎛

⎞

(i)

⎛

⎞

P₁

ξ(i)11

ξ(i)12

ξ(i)13

⎜

⎟

⎜

⎟

⎜

⎟

⎜

⎟

⎜

⎟

⎜

⎟

⎜

⎟

(17)

P(i)2

ξ(i)21

ξ(i)22

ξ(i)23

⎝B⎠

⎜

⎟

⎜

⎟

⎝

⎠

⎝

⎠

(i)

P(i)

ξ₃

ξ(i)32

ξ(i)

и результаты совпадают с ранее полученными [4, 5].

Однако в данной работе рассматривается классический подход [18-20] к

решению системы линейных однородных дифференциальных уравнений (14),

не использующий напрямую тождество (16). Ниже будет показано, что при

использовании фундаментальной матрицы условие (16) выполняется авто-

матически и, следовательно, нет необходимости дополнительно вычислять

константу A. Для рассматриваемого случая матрица (3) для i-го интервала

с постоянными интенсивностями переходов принимает вид

∑

(18)

L_i =

A(i)j exp(γ(i)jΔt_i

j=1

где

⎛

⎞

⎜

ξ(i)1jΔ(i)j1 ξ(i)1jΔ(i)j2 ξ(i)1jΔ(i)j3

⎟

⎜

⎟

⎜

⎟

(19)

A(i)j =

⎜

ξ(i)2jΔ(i)j1 ξ(i)2jΔ(i)j2 ξ(i)2jΔ(i)j3

⎟

⎜

⎟^,

⎜

⎟

⎝

⎠

ξ(i)3jΔ(i)j1 ξ(i)3jΔ(i)j2 ξ(i)3jΔ(i)

(

)

(

)

(

)

Δ(i) = ξ(i)21 ξ(i)32 - ξ(i)

+ξ(i)

ξ(i)33 - ξ(i)

+ξ(i)

ξ(i)31 - ξ(i)

;

Δ(i)11 = ξ(i)22ξ(i)33 - ξ(i)23ξ(i)32; Δ(i)21 = ξ(i)23ξ(i)31 - ξ(i)21ξ(i)33; Δ(i)31 = ξ(i)21ξ(i)32 - ξ(i)22ξ(i)31;

Δ(i)12 = ξ(i)32 - ξ(i)33; Δ(i)22 = ξ(i)33 - ξ(i)31; Δ(i)32 = ξ(i)31 - ξ(i)32; Δ(i)13 = ξ(i)23 - ξ(i)22;

Δ(i)33 = ξ(i)22 - ξ(i)21; ξ(i)1j = 1.

Далее для скачкообразного изменения интенсивностей переходов необхо-

димо использовать матрицу (12).

Теперь рассмотрим случайный процесс с постоянными интенсивностя-

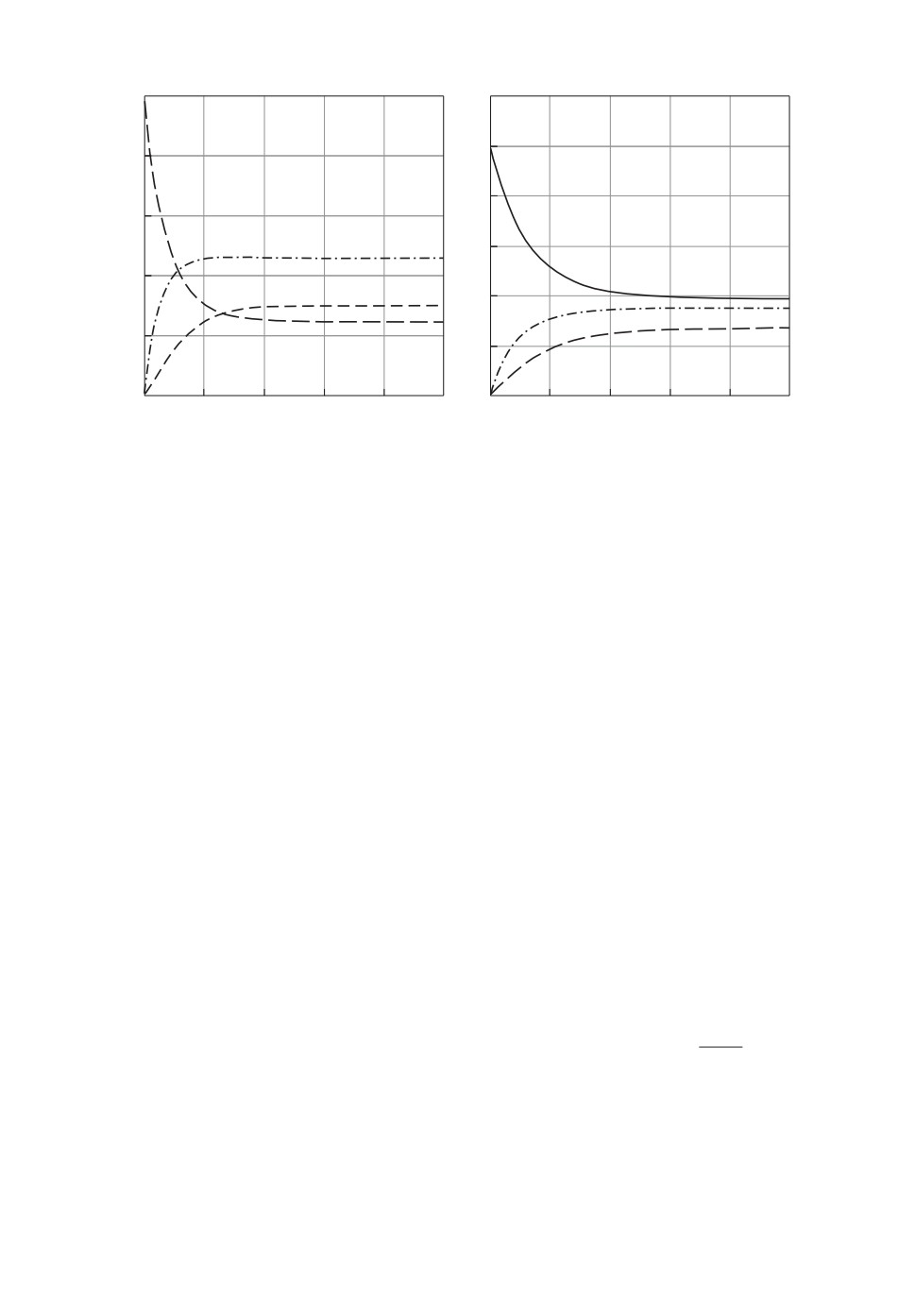
ми переходов. На рис. 2,a представлены зависимости вероятностей состоя-

ний от времени для интенсивностей переходов λ₁₂ = 0,1, λ₁₃ = 0,9, λ₂₁ = 0,2,

λ₂₃ = 0,8, λ₃₁ = 0,4, λ₃₂ = 0,6, λ₁₁ = λ₂₂ = λ₃₃ = 0 при начальных условиях

(P₁(0), P₂(0), P₃(0))^T = (1, 0, 0)^T .

Расчеты показывают, что сумма вероятностей состояний в любой мо-

мент времени равна единице. Таким образом, условие (16) выполняется ав-

томатически и никаких дополнительных расчетов при использовании пред-

ставленного подхода не требуется. Также видно (рис. 2,a), что для этих

параметров переходный режим имеет экспоненциальный характер, а ста-

ционарный режим устанавливается приблизительно при t = 4,3. Действи-

тельно, время переходного режима определяется характеристическими чис-

лами системы уравнений

(1), которые в данном случае равны γ₁ = 0,

γ₂ = -1,168, γ₃ = -1,832. Таким образом, переходной режим представля-

ет собой суперпозицию двух переходных режимов с постоянными време-

ни τ₂ = 1/ | γ₂ | и τ₃ = 1/ | γ₃ |. Тогда время каждого переходного режима

t_tr2 = (3 ÷ 5)τ₂ = 2,57 ÷ 4,28, t_tr3 = (3 ÷ 5)τ₃ = 1,64 ÷ 2,73, большее из кото-

рых 4,28 соответствует началу стационарного режима (рис. 2,a).

На рис. 2,б представлен результат расчетов для случая, когда есть вероят-

ность того, что процесс не выйдет из какого-либо состояния. Здесь λ₁₁ = 0,5,

λ₁₂ = 0,1, λ₁₃ = 0,4, λ₂₁ = 0,2, λ₂₂ = 0,2, λ₂₃ = 0,6, λ₃₁ = 0,4, λ₃₂ = 0,5,

λ₃₃ = 0,1, начальные условия (P₁(0),P₂(0),P₃(0))^T = (1,0,0)^T. Из расчетов

видно, что сумма вероятностей состояний в каждый момент времени в дан-

ном случае также равна единице, а стационарный режим устанавливается

при t = 8,5.

p(t)

1,0

p₁(t)

0,8

p₁(t)

0,6

p₂(t)

0,4

p₂(t)₂₂

0,2

p₃(t)₃₃

0,2

p₃(t)₃₃

Рис. 3. Зависимость вероятностей состояний от времени при одном скачке.

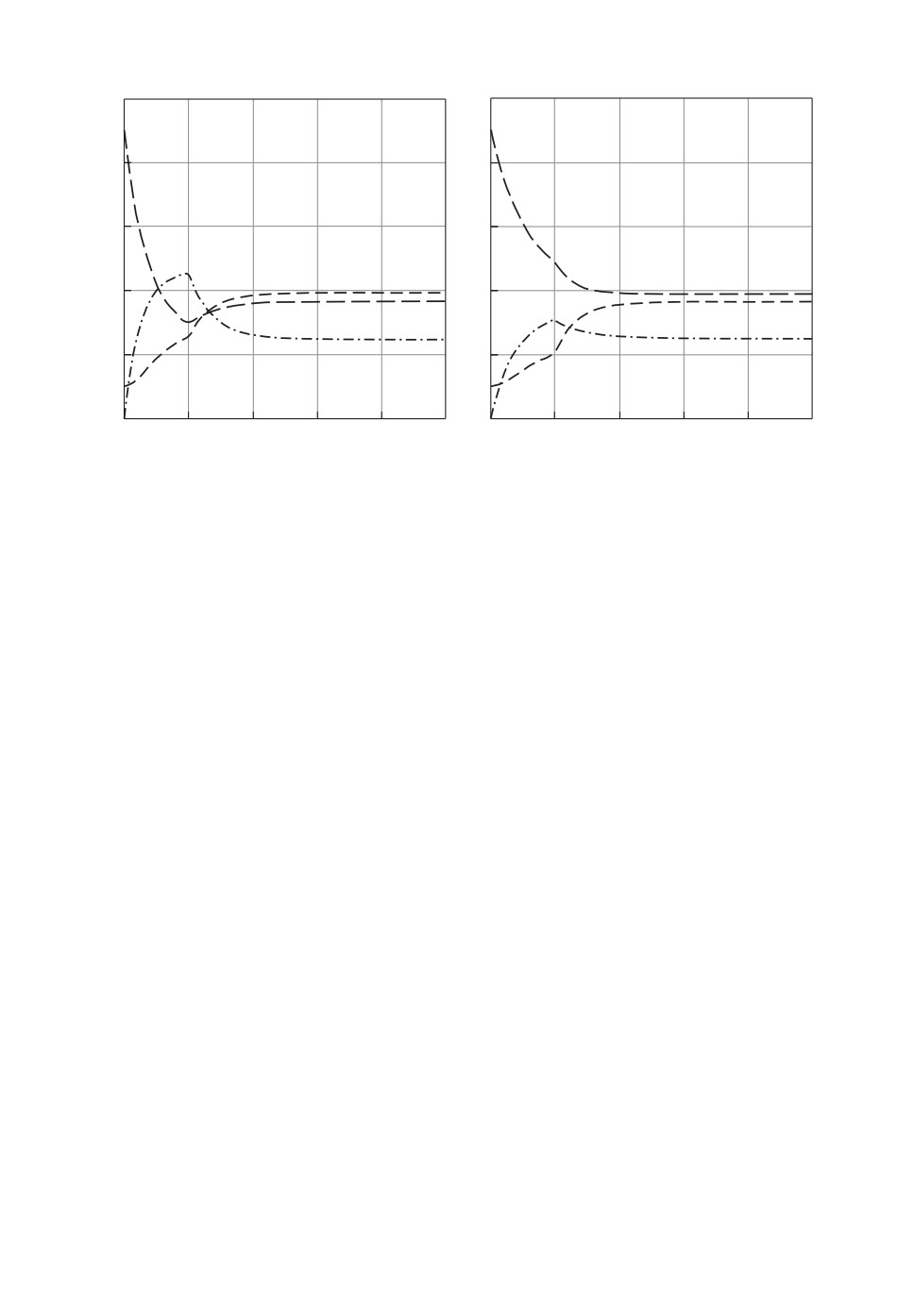
Результаты численных расчетов для одного скачка интенсивностей пере-

ходов представлены на рис. 3,а. Скачок происходит в момент времени t = 2.

Здесь на первом интервале с постоянными интенсивностями λ₁₂ = 0,1, λ₁₃ =

= 0,9, λ₂₁ = 0,2, λ₂₃ = 0,8, λ₃₁ = 0,4, λ₃₂ = 0,6, λ₁₁ = λ₂₂ = λ₃₃ = 0; на втором

интервале λ₁₂ = 0,7, λ₁₃ = 0,3, λ₂₁ = 0,65, λ₂₃ = 0,35, λ₃₁ = 0,45, λ₃₂ = 0,55,

λ₁₁ = λ₂₂ = λ₃₃ = 0, начальные условия (P₁(0),P₂(0),P₃(0))^T = (1,0,0)^T.

Из рис. 3,a видно, что вероятности состояний не испытывают скачков при

скачках интенсивностей переходов (t = 2), тем не менее для их первых произ-

водных наблюдаются скачки. Время переходного режима после скачка опре-

деляется параметрами процесса на втором интервале и составляет t = 6.

Результаты численных расчетов вероятностей состояний для одного скач-

ка при наличии вероятностей того, что процесс не покинет определенные

фиксированные состояния, показаны на рис. 3,б . Скачок происходит в мо-

мент времени t = 2. Здесь на первом интервале с постоянными интенсивно-

стями λ₁₁ = 0,5, λ₁₂ = 0,1, λ₁₃ = 0,4, λ₂₁ = 0,2, λ₂₂ = 0,2, λ₂₃ = 0,6, λ₃₁ = 0,4,

λ₃₂ = 0,5, λ₃₃ = 0,1; на втором интервале λ₁₁ = 0,1, λ₁₂ = 0,7, λ₁₃ = 0,2, λ₂₁ =

= 0,65, λ₂₂ = 0,05, λ₂₃ = 0,3, λ₃₁ = 0,45, λ₃₂ = 0,3, λ₃₃ = 0,25, начальные усло-

вия (P₁(0), P₂(0)P₃(0))^T = (1, 0, 0)^T. В этом случае сумма вероятностей P₁(t),

P₂(t), P₃(t) в любой момент времени также равна единице. Стационарный

режим устанавливается при t = 7, т.е. время переходного режима увеличи-

лось в сравнении с этим временем для предыдущего случая. Это обусловлено

уменьшением значений характеристических показателей системы Колмого-

рова в рассматриваемом случае.

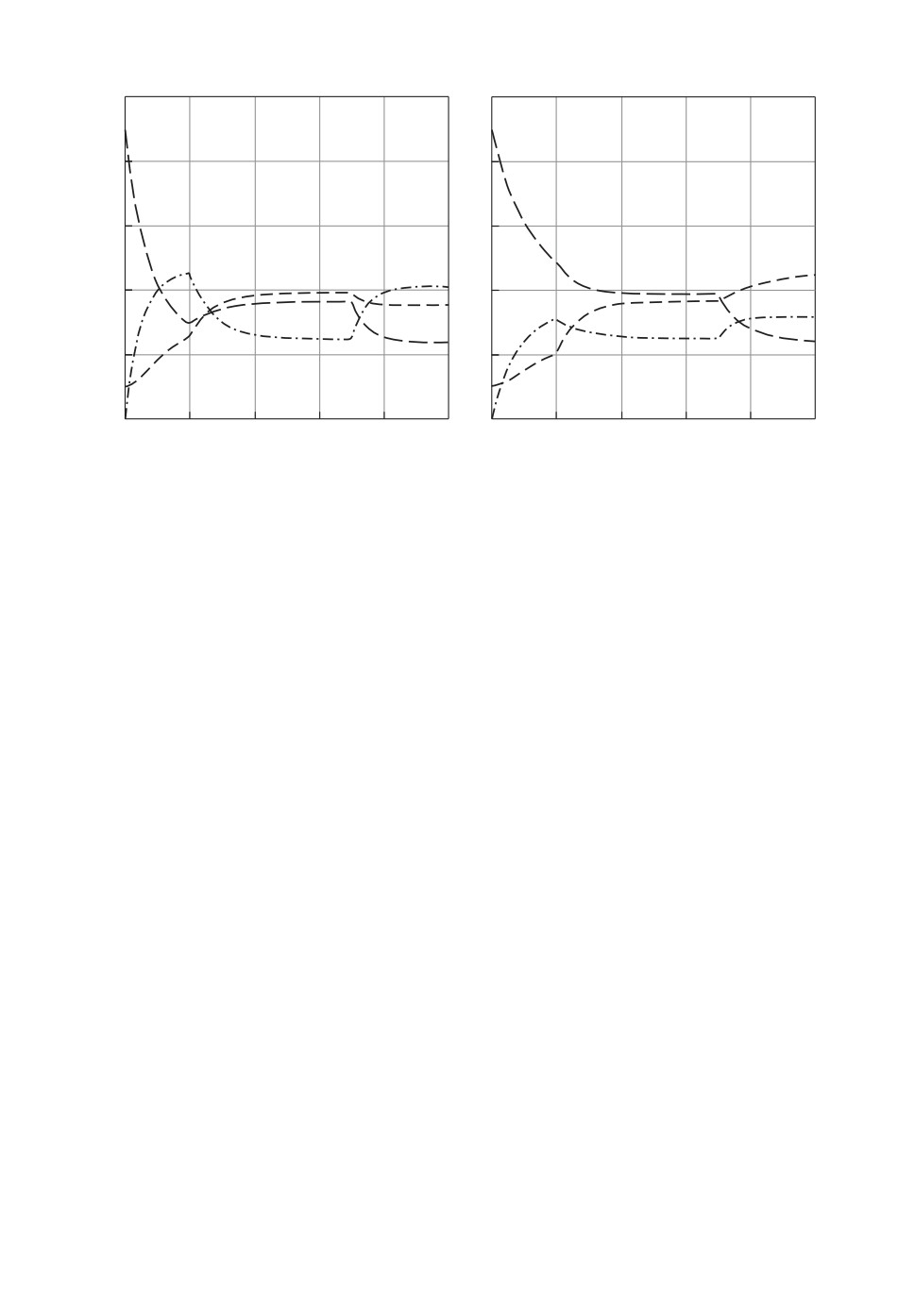
Также рассчитан процесс с тремя состояниями и двумя скачками интен-

сивностей переходов, результаты представлены на рис. 4,а,б . На рис. 4,a по-

казаны зависимости вероятностей состояний от времени для случая, когда

100

p(t)

1,0

0,8

p₁(t)

0,6

p₂(t)₂₂

0,4

0,2

p3(t)

0,2

(t)

p₂(t)

Рис. 4. Зависимость вероятностей состояний от времени.

λ₁₁ = λ₂₂ = λ₃₃ = 0. Остальные параметры процесса следующие: на первом

интервале с постоянными интенсивностями λ₁₂ = 0,1, λ₁₃ = 0,9, λ₂₁ = 0,2,

λ₂₃ = 0,8, λ₃₁ = 0,4, λ₃₂ = 0,6; на втором интервале λ₁₂ = 0,7, λ₁₃ = 0,3,

λ₂₁ = 0,65, λ₂₃ = 0,35, λ₃₁ = 0,45, λ₃₂ = 0,55, λ₁₁ = λ₂₂ = λ₃₃ = 0; на третьем

интервале λ₁₂ = 0,3, λ₁₃ = 0,7, λ₂₁ = 0,1, λ₂₃ = 0,9, λ₃₁ = 0,6, λ₃₂ = 0,4. Скач-

ки происходят в моменты времени t = 2 и t = 7. Также для рассматриваемо-

го случая сумма вероятностей состояний равна единице для любого момента

времени, а стационарный режим устанавливается при t = 9,5.

Также анализируется случай марковского процесса с тремя состояния-

ми и двумя скачками интенсивностей переходов для ненулевых λ₁₁, λ₂₂, λ₃₃

(рис. 4,б ). Параметры процесса следующие: на первом интервале с посто-

янными интенсивностями λ₁₁ = 0,5, λ₁₂ = 0,1, λ₁₃ = 0,4, λ₂₁ = 0,2, λ₂₂ = 0,2,

λ₂₃ = 0,6, λ₃₁ = 0,4, λ₃₂ = 0,5, λ₃₃ = 0,1; на втором интервале λ₁₁ = 0,1, λ₁₂ =

= 0,7, λ₁₃ = 0,2, λ₂₁ = 0,65, λ₂₂ = 0,05, λ₂₃ = 0,3, λ₃₁ = 0,45, λ₃₂ = 0,3, λ₃₃ =

= 0,25; на третьем интервале λ₁₁ = 0,2, λ₁₂ = 0,3, λ₁₃ = 0,6, λ₂₁ = 0,1 λ₂₂ =

= 0,4, λ₂₃ = 0,5, λ₃₁ = 0,6, λ₃₂ = 0,3, λ₃₃ = 0,1. Скачки также происходят при

t = 2 и t = 7. Как и для случая с двумя скачками и ненулевыми λ₁₁,λ₂₂,λ₃₃,

время переходного режима увеличилось в сравнении со случаем нулевых

λ₁₁,λ₂₂,λ₃₃.

Теперь рассмотрим неоднородный процесс с периодическими кусочно-по-

стоянными интенсивностями переходов. Здесь предполагается, что период со-

держит три интервала с постоянными параметрами. Интенсивности перехо-

дов соответствуют значениям случая, представленного на рис. 4,а, длитель-

ности первого и второго интервалов Δt₁ = 1 и Δt₂ = 2 соответственно. На

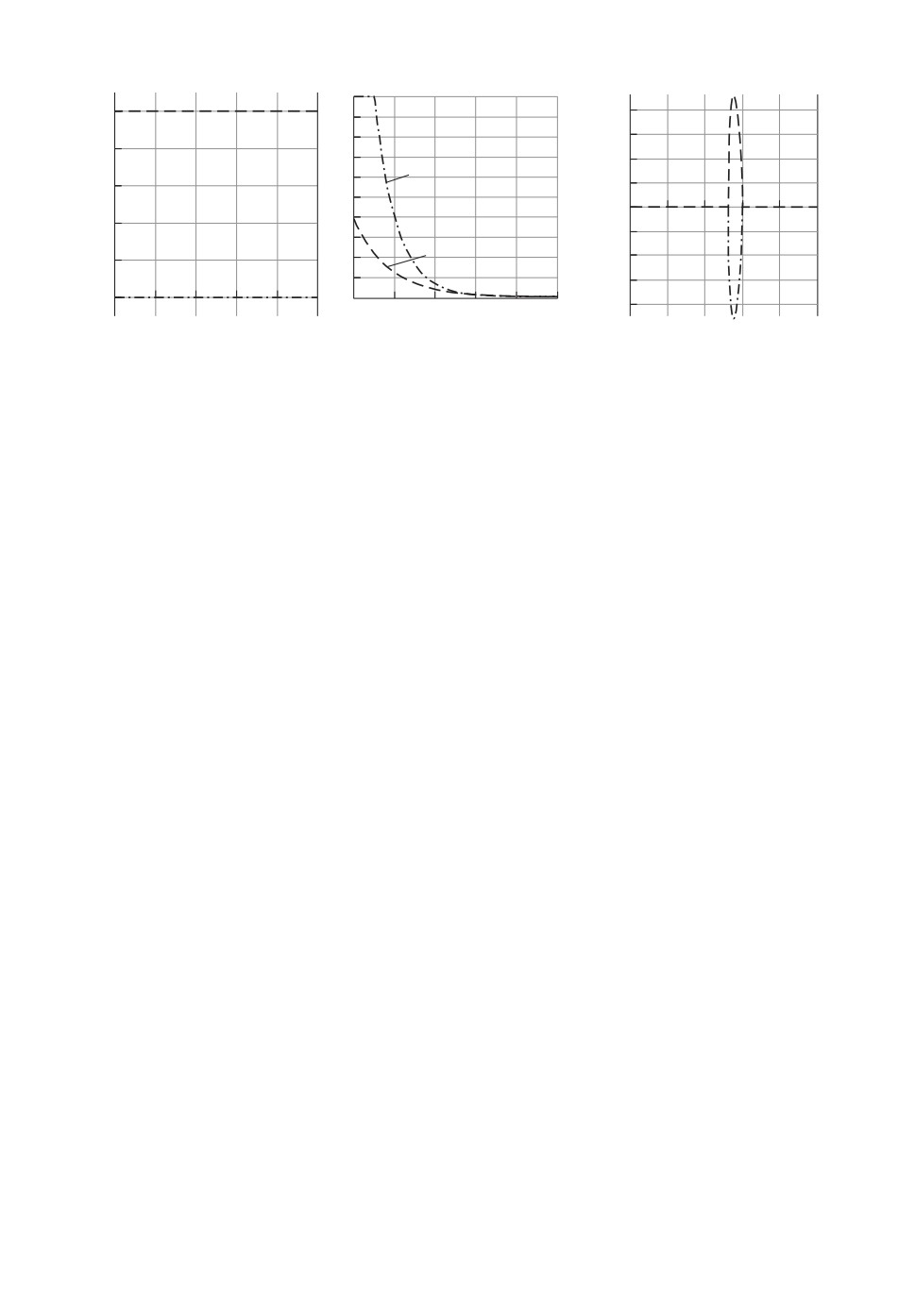
рис. 5 представлена зависимость мультипликаторов матрицы (19) от длитель-

ности третьего интервала Δt₃. Из результатов расчета видно, что два мульти-

пликатора по модулю меньше единицы, а третий равен единице, т.е. в соответ-

101

Re[q

t₃)]

1,0

0,0008

0,9

0,8

0,0006

0,8

Im[q

2( t3

)]

0,7

0,0004

Re[q₃( t₃)]

0,6

0,0002

0,5

0,4

0,3

0,0002

t₃

Re[q2(

t₂)]

0,2

0,0004

Im[q1(

t₃)]

0,1

0,0006

Im[q

3( t3

)]

0,0008

t₃

Рис. 5. Зависимость мультипликаторов системы (1) от длительности третьего

интервала периода: а) действительная и мнимая части первого мультиплика-

тора, б) действительные части второго и третьего мультипликаторов, в) мни-

мые части второго и третьего мультипликаторов.

ствии с теоремой Ляпунова [18] процесс имеет стационарное состояние. Кроме

того, два из трех мультипликаторов являются комплексно-сопряженными, ес-

ли 2,63 ≤ Δt₃ ≤ 3,0 (рис. 5,б ,в). Следовательно, при большом числе периодов

процесс имеет стационарное состояние, а переходной режим имеет затухаю-

щий гармонический характер.

5. Заключение

В этой статье рассматривается неоднородный марковский процесс с конеч-

ным числом дискретных состояний M, непрерывным временем и кусочно-по-

стоянными интенсивностями переходов λ_ij (t). Выражения, описывающие од-

новременно как переходные, так и стационарные режимы случайного процес-

са, представлены впервые. В работе предложено аналитическое решение си-

стемы уравнений Колмогорова (1) с кусочно-постоянными коэффициентами.

Для решения этой задачи фундаментальная матрица (6) или (12) системы (1)

находится в аналитическом виде в элементарных функциях. Предлагаемый

метод позволяет исследовать рассматриваемый марковский процесс без ис-

пользования численных методов. Изучение фундаментальной матрицы дает

возможность описать характер процесса даже без начальных условий. Дей-

ствительно, собственные значения и собственные векторы этой матрицы да-

ют полную картину поведения решений системы дифференциальных уравне-

ний Колмогорова. Более того, решение представлено в виде конечной суммы

членов, описывающих некоторые случайные процессы. Дополнительно рас-

сматривается неоднородный процесс с периодически изменяющимися интен-

сивностями переходов. Представлены условия существования стационарного

режима при периодически изменяющихся интенсивностях переходов. Также

приведены численные расчеты, доказывающие правильность разработанного

метода.

102

СПИСОК ЛИТЕРАТУРЫ

Abubakar U.Y., Hakimi D., Mohammed A., Lawal A.A. A Non-stationary Transition

Probabilities for a Reservoir Elevation of Hydro Electric Power Dam // IOSR J.

Math. 2014. V. 10. No. 3. С. 39-44.

Shirdel G.H., Abdolhosseinzadeh M. The shortest path problem in the stochastic

networks with unstable topology // SpringerPlus. 2016. No. 5:1529.

https://doi.org/10.1186/s40064-016-3180-7

Jaime González-Domınguez, Gonzalo Sánchez-Barroso and Justo Garc´ıa-Sanz-

Calcedo. Scheduling of Preventive Maintenance in Healthcare Buildings Using

Markov Chain // Appl. Sci. 2020. V.10. No. 15. 5263.

https://doi.org/10.3390/app10155263

Миллер А.Б., Миллер Б.М., Степанян К.В. Одновременное импульсное и непре-

рывное управление марковской цепью в непрерывном времени // АиТ. 2020. № 3.

С. 114-131.

Miller A.B., Miller B.M., Stepanyan K.V. Simultaneous Impulse and Continuous

Control of a Markov Chain in Continuous Time // Autom. Remote Control. 2020.

V. 81. No. 3. P. 469-482.

Вишневский В.М., Дудин А.Н., Клименюк, В.И. Cтохастические системы с кор-

релированными потоками. Теория и применение в телекоммуникационных се-

тях. М.: Техносфера, 2018.

Clarke A.B. The time-dependent waiting line problem. Umv Michigan Rept M720-

1RS9. 1953.

Clarke A.B. On time-dependent waiting line processes // Ann. Math. Statist. 1953.

V. 24. P. 491-492.

Lemoine A.J. On queues with periodic Poisson input // J. Appl. Prob. 1981. V. 18.

P. 889-900.

Harrison P.G. Transient Behaviour of Queueing Networks // J. Appl. Prob. 1981.

V. 18. No. 2. P. 482-490.

10.

Коган Я.А., Литвин В.Г. К вычислению характеристик систем массового об-

служивания с конечным буфером, работающей в случайной среде // АиТ. 1976.

№ 12. С. 49-57.

11.

Дудин А.Н. Об обслуживающей системе с переменным режимом работы // Ав-

томатика и вычислительная техника. 1985. № 2. С. 27-29.

12.

Бондрова О.В., Крылова Д.С., Головко Н.И., Жук Т.А. Вывод уравнений для

систем массового обслуживания с бесконечным накопителем и скачкообразной

интенсивностью входного потока // Вестник ВГУ: Серия: физика. математика.

2015. № 4. С. 89-100.

13.

Головко Н.И., Каретник В.О., Пелешок О.В. СМО с бесконечным накопителем

и скачкообразной интенсивностью входного потока // Автоматика и вычисли-

тельная техника. 2009. № 10. С. 75-96.

14.

Бондрова О.В., Головко Н.И., Жук Т.А. Вывод уравнений типа Колмогорова-

Чепмена с интегральным оператором // Дальневосточный мат. журн. 2017.

Т. 17. № 2. С. 135-146.

15.

Dudin A.N., Karolik A.V. BMAP/SM/1 Queue with Markovian Input of Disasters

and Non-instantaneous Recovery // Performance Evaluat. 2001. V. 45. No. 1.

P. 19-32.

103

16. Dharmaraja S., Rakesh Kumar. Transient solution of a Markovian queuing

model with heterogeneous servers and catastrophes // OPSEARCH. 2015. 52(4).

P. 810-826.

17. Kumar B. Krishna, Madheshwari S. Pavai, Venkatakrishanan K.S. Transient

solution of an M/M/2 queue with heterogeneous servers subject to catastrophes //

Int. J. Inform. Management Sci. 2017. V. 18. No. 1. P. 63-80.

18. Гантмахер Ф.Р. Теория матриц. М.: Наука, 1966.

19. Vytovtov K., Barabanova E., Vishnevskiy V. Accurate mathematical model of two-

dimensional parametric systems based on 2 × 2 Matrix // Commun. Comput. Inform.

Sci. 2019. V. 1141. P. 199-211.

20. Vytovtov K., Barabanova E. Mathematical model of four-dimensional parametric

systems based on block diagonal matrix with 2 × 2 blocks // Commun. Comput.

Inform. Sci. 2019. P. 139-155.

21. Барбашин Е.А. Введение в теорию устойчивости. М.: Наука, 1967.

22. Розо М. Нелинейные колебания и теория устойчивости. М.: Наука, 1971.

Статья представлена к публикации членом редколлегии Б.М. Миллером.

Поступила в редакцию 29.01.2021

После доработки 03.05.2021

Принята к публикации 30.06.2021

104