Автоматика и телемеханика, № 12, 2021

Интеллектуальные системы управления,

анализ данных

А.А. ЗАМЫШЛЯЕВА, д-р физ.-мат. наук (zamyshliaevaaa@susu.ru),

Н.А. МАНАКОВА, д-р физ.-мат. наук (manakovana@susu.ru),

Г.А. СВИРИДЮК, д-р физ.-мат. наук (sviridyuk@susu.ru)

(Южно-Уральский государственный университет, Челябинск),

А.В. КЕЛЛЕР, д-р физ.-мат. наук (alevtinak@inbox.ru)

(Воронежский государственный технический университет)

ВОССТАНОВЛЕНИЕ ДИНАМИЧЕСКИ ИСКАЖЕННОГО СИГНАЛА НА

ОСНОВЕ ТЕОРИИ ОПТИМАЛЬНЫХ ДИНАМИЧЕСКИХ ИЗМЕРЕНИЙ¹

Представлен новый алгоритм обработки результатов динамических

измерений, при которых по известному выходному или наблюдаемому

сигналу и известной передаточной функции измерительного устройства

необходимо найти входной сигнал. Ранее авторами была построена теория

оптимальных динамических измерений, в рамках которой для восстанов-

ления динамически искаженных сигналов успешно использовались мето-

ды теории оптимальных управлений. Первые численные алгоритмы тео-

рии оптимальных динамических измерений на модельных примерах по-

казали эффективность результата по достигаемой погрешности при зна-

чительном времени счета. Предлагаемый численный алгоритм решения

исследуемой задачи позволяет снизить время счета более чем в 5 раз.

Приводятся необходимые теоретические сведения, общая схема алгорит-

ма, данные эксперимента, результаты обработки экспериментальных дан-

ных по предлагаемому алгоритму.

Ключевые слова: динамические измерения, обработка результатов экспе-

римента, численные методы, оптимальные динамические измерения, дат-

чики давления, статистические методы.

DOI: 10.31857/S0005231021120084

1. Введение

В теории динамических измерений задачу восстановления входящего сиг-

нала по известным характеристикам измерительного устройства (ИУ) и вы-

ходного сигнала принято считать одной из сложных [1]. Ранее для ее решения

принято было использовать в качестве основных математических методов

теорию обратных задач [2].

¹ Исследование выполнено при финансовой поддержке Министерства науки и высшего

образования РФ (государственное задание FENU-2020-0022).

125

На современном этапе развития теории динамических измерений активно

ведутся исследования в двух направлениях. Первое связано с оцениванием

неопределенности в динамических измерениях [3, 4], второе развивает мето-

дологию применения теории автоматического управления для решения за-

дач динамических измерений [5]. В рамках развития второго направления

разрабатывались не только различные технические решения, но и развива-

лись математические методы решения задач динамических измерений. Так,

для решения задачи по восстановлению динамически искаженного сигнала

А.Л. Шестаковым и Г.А. Свиридюком была сформулирована задача опти-

мальных динамических измерений, в которой восстанавливаемый входной

сигнал определялся как решение задачи оптимального управления [6-8] для

системы леонтьевского типа. Отметим, что использование начального усло-

вия Коши вызывает значительные трудности и накладывает ограничения при

численном решении задач оптимального динамического измерения. В связи

с этим было предложено использовать условие Шоуолтера-Сидорова, кото-

рое не требует согласования начальных данных при численном исследова-

нии прикладных задач [9]. Подчеркнем, что математическая модель слож-

ной измерительной системы, например, состоящей из нескольких измеритель-

ных устройств, строится как система леонтьевского типа [10], которая, с од-

ной стороны, является частным случаем дескрипторной системы [11], с дру-

гой - конечномерным случаем уравнения соболевского типа. Именно поэто-

му все математические результаты стали возможны благодаря развиваемой

Г.А. Свиридюком и его учениками теории оптимального управления реше-

ниями уравнений соболевского и леонтьевского типов (см. обзор результатов

в [12]).

Формирование теории оптимальных динамических измерений включало в

себя построение математических моделей и разработку численных методов.

Первый алгоритм численного решения задачи оптимального динамического

измерения был предложен А.В. Келлер и Е.И. Назаровой, при этом предпо-

лагалось, что динамическое искажение являлось следствием только инерци-

онности ИУ [13]. В следующем алгоритме, разработанном Ю.В. Худяковым,

численное решение задачи восстановления динамически искаженного сигнала

проводилось с учетом инерционности ИУ и наличия резонансов [14]. Важным

в развитии численных методов решения задач теории оптимальных динами-

ческих измерений стал алгоритм с использованием сплайнов, предложенный

А.В. Келлер [15].

Необходимо отметить, что все обсуждаемые алгоритмы были апробиро-

ваны на модельных примерах, в рамках которых рассматривались сигналы

простой формы, например u = a sin ωt. Когда измеряемые сигналы имеют бо-

лее сложную форму, разработанные ранее алгоритмы требовали либо значи-

тельного объема машинного времени, либо большей мощности персональных

компьютеров, что в конечном итоге привело к пониманию необходимости раз-

работки нового численного метода для решения задачи восстановления ди-

намически искаженного сигнала.

126

В данной статье представлен новый численный метод, базирующийся на

идеях теории оптимальных динамических измерений, позволяющий более эф-

фективно обрабатывать эмпирические данные и восстанавливать динамиче-

ски искаженный сигнал по результатам натурного вычислительного экспери-

мента.

2. Основные понятия и методы теории оптимальных

динамических измерений

В теории оптимальных динамических измерений важной математической

моделью является модель ИУ. Динамические свойства ИУ определяются си-

стемой леонтьевского типа

^{L˙x = Ax + Bu + Gζ,

(2.1)

y=Cx+Dη,

а его состояние в начале работы - начальным условием Шоуолтера-Сидорова

[

(2.2)

(αL - A)-1 L]p+1 (x(0) - x0

)=0

при некоторых x₀ ∈ Rⁿ, α ∈ ρ^L(A). Здесь ρ^L(A) = {α ∈ C : det(αL - A) = 0}

[13]. Математическая модель ИУ (2.1), (2.2) связывает x(t) и x(t) - вектор-

функции состояния и скорости изменения состояния ИУ соответственно;

y(t) - вектор-функция наблюдений (или выходного сигнала); A и L - квадрат-

ные матрицы состояний и взаимовлияния скоростей состояния ИУ соответ-

ственно; C и D - матрицы, характеризующие связи между состоянием ИУ

и наблюдением; u(t) - вектор-функция измерения (или входного сигнала);

η(t) и ζ(t) - вектор-функции помех на выходе и в цепях ИУ соответственно.

Отметим, что при моделировании может быть получен случай, когда

det L = 0 [10]. Кроме того, при решении задачи (2.1) и (2.2) важным усло-

вием является (L, p)-регулярность матрицы A.

В [3, 5] для решения задачи восстановлении входного сигнала u = u(t)

по наблюдаемому выходному сигналу y = y₀(t) конструируется модель ИУ,

при этом качество модели оценивается величиной расхождений значений вы-

ходных сигналов ИУ и его модели при соответствующих t. Если различия

незначительны, то значения входных сигналов ИУ и его модели будут также

незначимо различаться. Это положение легло в основу математической мо-

дели оптимальных динамических измерений как задачи оптимального дина-

мического измерения: необходимым условием для построения функционала

штрафа является отражение в нем разности между выходными сигналами

реального ИУ и его математической моделью, а минимизация функционала

обеспечивает нахождение такого входного сигнала, который является мате-

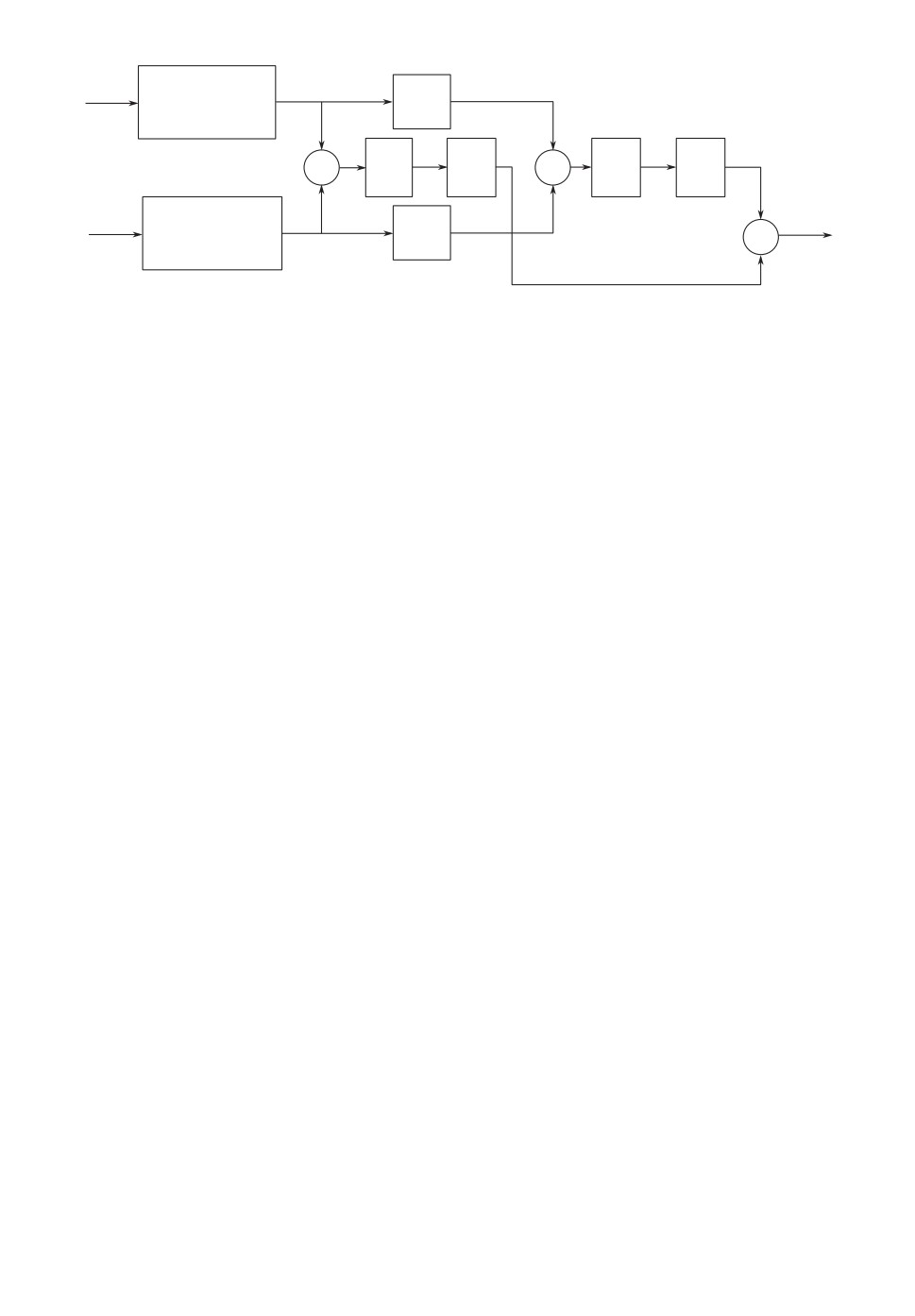
матической моделью искомого измерения (рис. 1).

Для построения математической модели оптимальных динамических из-

мерений будем использовать пространство состояний

{

}

χ = x ∈ L2 ((0,τ),Rⁿ) : x ∈ L2 ((0,τ),Rⁿ)

127

Измерительное

y₀

устройство

(ИУ)

f ²

g²

Модель

J(u)

измерительного

устройства

Рис. 1. Структурная схема математической модели динамических измерений.

пространство измерений

{

}

U = u ∈ L2 ((0,τ),Rⁿ) : u(p+1) ∈ L2 ((0,τ),Rⁿ)

и пространство наблюдений Y = C[χ], причем Y изоморфно некоторому под-

пространству в χ, хотя не всегда Y = χ.

Функционал штрафа имеет вид

∫



∑



(2.3)

J (u) =

y(q)(u,t) - y⁽

(t)

dt,

q=0 0

где y₀(t) - выходной сигнал, получаемый в ходе натурного эксперимента,

y(t) - моделируемый выходной сигнал (получаемый при работе с математи-

ческой моделью восстановления динамически искаженного сигнала), ||·|| -

евклидова норма в Rⁿ. Заметим, что вид функционала штрафа обусловлен

также и постановкой задачи, например при наличии резонансов в цепях ИУ

функционал имеет другой вид [14].

Будем искать решение задачи на множестве допустимых моделируемых

измерений U_∂. В качестве U_∂ возьмем компактное выпуклое подмножество U:

⎧

⎫

∫

⎨



⎬

∑



(2.4)

U_∂ =

u∈U:

u(q)(t)

dt ≤ d

⎩

⎭

q=0 0

где d = const.

Таким образом, задача оптимального динамического измерения заключа-

ется в нахождении такой вектор-функции моделируемого измерения v ∈ U_∂,

при которой функционал штрафа (2.3) достигает минимального значения,

т.е.

(2.5)

J (v) = min

J (u),

u∈U_∂

при этом x(v) ∈ χ удовлетворяет системе (2.1) почти всюду на (0, τ) и при

некоторых x₀ ∈ Rⁿ, α ∈ ρ^L(A) - условию Шоуолтера-Сидорова (2.2).

128

Вектор-функцию v ∈ U_∂, начиная с первых работ по теории оптимальных

динамических измерений, называют оптимальным динамическим измерени-

ем [6]. Подчеркнем, что требование близости не только значений наблюдае-

мого сигнала и моделируемого наблюдения, но и скоростей их изменения,

обосновано результатами качественных исследований и присутствует во всех

математических моделях оптимальных динамических измерений [6, 8, 14, 15].

3. Алгоритм восстановления динамически искаженного сигнала

В качестве исходной информации известны элементы матриц системы

(2.1), начальные условия (2.2) и функционал качества (2.3), множество до-

пустимых измерений (2.4), массив значений Y0i наблюдаемого сигнала в мо-

менты времени t_i с интервалом δ, i = 1, 2, . . . , N.

1. Из множества значений Y0i формируется подмножество, элементы кото-

рого выбираются через равный интервал, который назовем интервалом дис-

кретизации алгоритма Δ по времени. Отметим, что тогда Δ = K · δ, K ∈ Z.

Выбор интервала дискретизации является важной самостоятельной задачей,

поэтому ей будет посвящен раздел 5 статьи. Выбор Δ при известном δ опреде-

ляет значение K, которое в свою очередь задает количество основных циклов

алгоритма. Обозначим порядковый номер цикла буквой ℓ, таким образом, ℓ =

= 1, 2, . . . , K.

2. Выполняются базовые расчеты для каждого из основных циклов на-

хождения приближенного динамического измерения входного сигнала v^ℓ(t),

ℓ = 1,2,...,K:

2.1. Определяются начальные точка расчета tℓ0 и состояние системы xℓ0:

tℓ0 : t¹⁰ = 0, tℓ0 = t¹⁰ + (ℓ - 1)δ, ℓ = 2,... ,K,

xℓ0 : x¹⁰ = 0, xℓ0 = C-1Y (t¹⁰ + (ℓ - 1)δ), ℓ = 2,... ,K;

2.2. Выбираются точки для базового расчета T^ℓk = tℓ0 + (k - 1)Δ, k = 1,

2, . . . , R, где R = [NK]. Эти точки группируются по четыре (Tℓ1,Tℓ2,Tℓ3,Tℓ4),

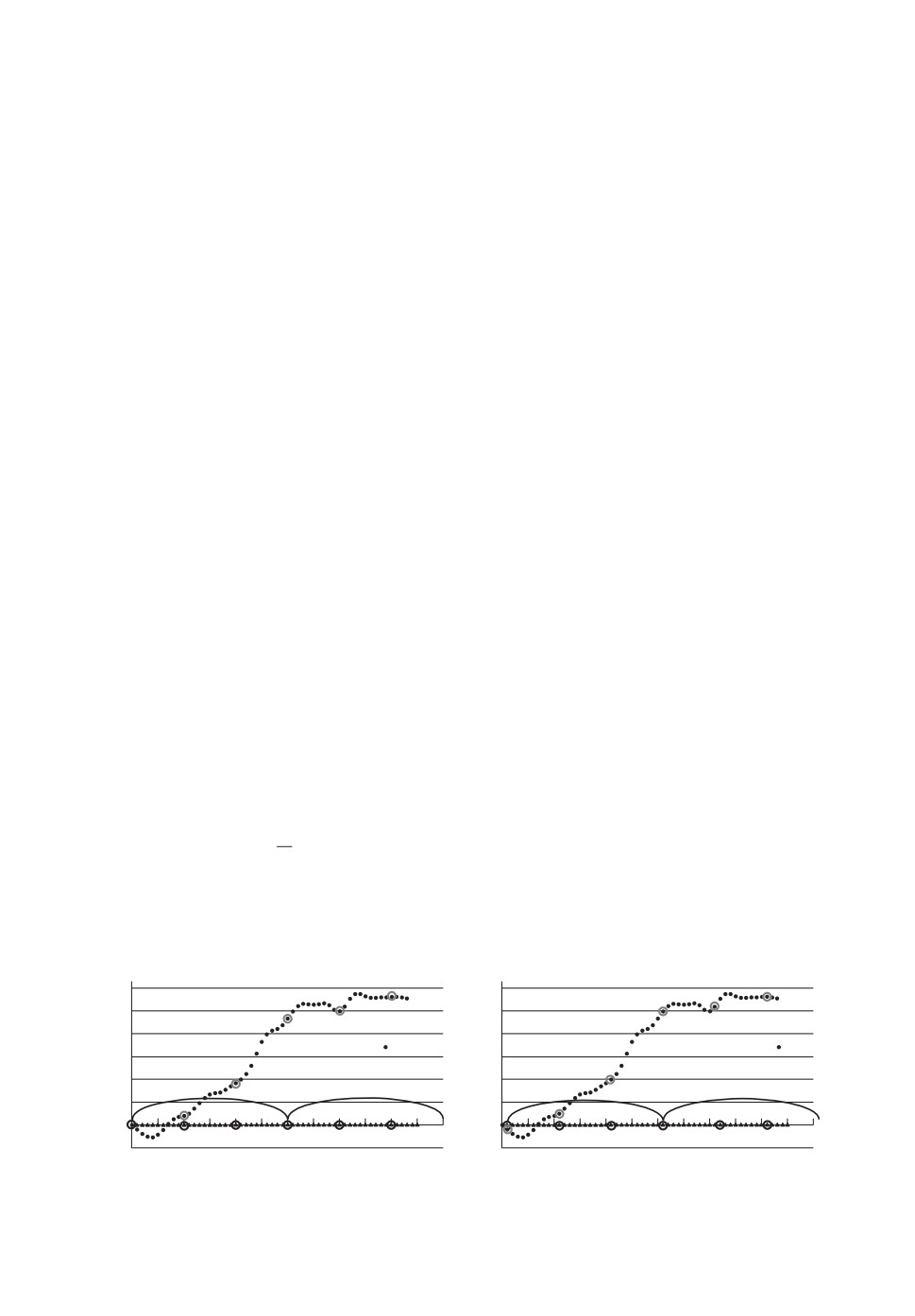
(Tℓ4, Tℓ5, Tℓ6, Tℓ7) и т.д. Эти группы будем называть “наборами по T ”. На рис. 2,а

точки первого основного цикла T1k обведены черными кругами, “наборы по T ”

показаны дугами;

0,06

0,05

0,04

0,03

0,02

0,01

0,002

0,004

0,006

0,008

0,010

0,012

0,002

0,004

0,006

0,008

0,010

0,012

0,01

Рис. 2. а - Точки для базового расчета в первом основном цикле ℓ = 1; б -

точки для базового расчета во втором основном цикле ℓ = 2.

129

0,3

0,2

0,1

0,002

0,004

0,006

0,008

0,010

0,012

0,014

0,016

0,1

0,2

Y UR1 UR2 UR4 UR8

0,3

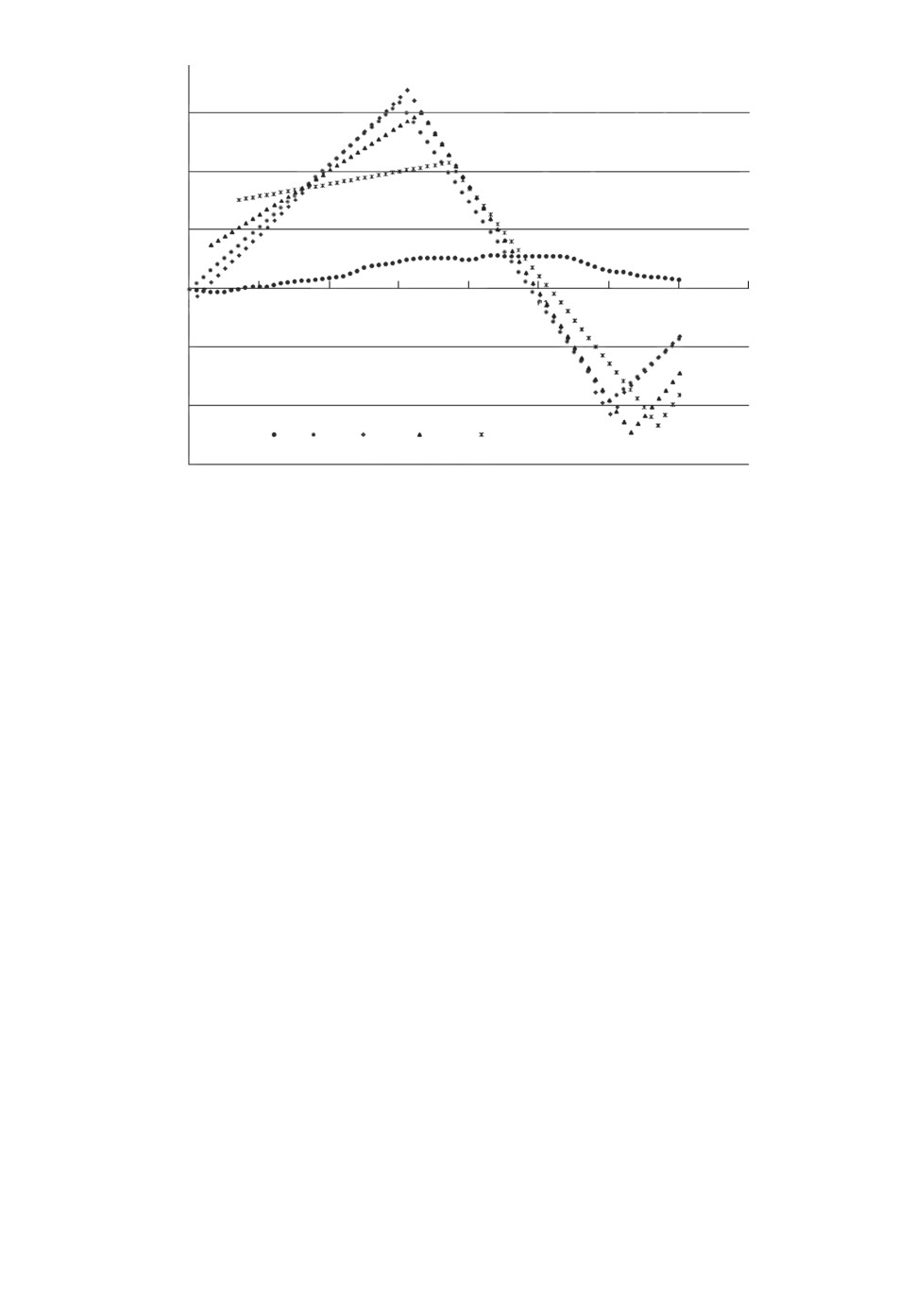
Рис. 3. Значения v^ℓi = v^ℓj(t_i) (этап 2.5).

2.3. По каждому “набору по T ” формируем “наборы по Y ”: (Yℓ1, Yℓ2, Yℓ3, Yℓ4),

(Yℓ4, Yℓ5, Yℓ6, Yℓ7) и т.д. На рис. 2,a для первого основного цикла точки

Y¹¹,Y¹²,Y¹³,Y¹⁴,Y¹⁴,Y¹⁵,Y¹⁶ обведены серыми кругами. На рис. 2,б показаны

точки для базового расчета во втором основном цикле T2k и Y2k, “наборы по T ”;

2.4. Для каждого j-го набора ℓ-го основного цикла на временном проме-

жутке [Tℓ3j+1, Tℓ3j+4], j = 0, . . . , [(R - 1)/3]: 1) по Y^ℓk интерполяцией опреде-

ляется функция наблюдения y^ℓj(t); 2) по построенной функции наблюдения

решается задача оптимального динамического измерения.

Приближенное измерение ищется на основе метода Ритца в виде триго-

нометрического полинома или многочлена заданной степени. Так как в ал-

горитме применяется сплайн метод, то решено использовать представление

приближенного измерения в виде многочлена. Его степень, как правило, не

превосходит степени интерполяционного многочлена y^ℓj(t) (в данном алго-

ритме равной трем) и выбирается с учетом вычислительной мощности и за-

данного шага дискретизации. Основная процедура сводится к поиску тако-

го массива коэффициентов искомого многочлена, при котором достигается

минимум функционала. В алгоритме для этого реализуется многошаговый

итеративный метод, предложенный в [16]. В нем использованы идеи покоор-

динатного многошагового спуска с памятью, при подборе шага используют-

ся результаты предшествующей итерации с выполнением проверки условий

ограничений на принадлежность множеству допустимых измерений. Завер-

шается процедура нахождения минимума функционала штрафа по дости-

жению абсолютной величины разности значений функционала последней и

предпоследней итерации цикла меньшего значения, чем заданная погреш-

ность. Основные этапы алгоритма решения задачи оптимального динамиче-

ского измерения изложены в [15]. Особенностью предлагаемого здесь алго-

130

ритма является условие равенства значений u^ℓj (t) в граничных точках на-

боров [u^ℓj(T3j+4) = uℓj+1(T3(j+1)+1)], j = 0, . . . , [(R - 1)/3]. В результате полу-

чим приближенное оптимальное динамическое измерение v^ℓj(t) для каждого

j-го набора ℓ-го основного цикла на временном промежутке [Tℓ3j+1, Tℓ3j+4], j =

= 0, . . . , [(R - 1)/3];

2.5. Вычисляются значения v^ℓi = v^ℓj(t_i), ℓ = 1, 2, . . . , K, i = 1, 2, . . . , N, j =

= 1, . . . , [(R - 1)/3] (см. рис. 3).

3. Используя полученные K значений v^ℓi, ℓ = 1, . . . , K, в каждой точке t_i,

вычисляются средние значения v_i в каждой точке t_i.

4. Моделируемое оптимальное динамическое измерение v(t) получается ин-

терполяцией средних значений v_i.

4. Описание эксперимента

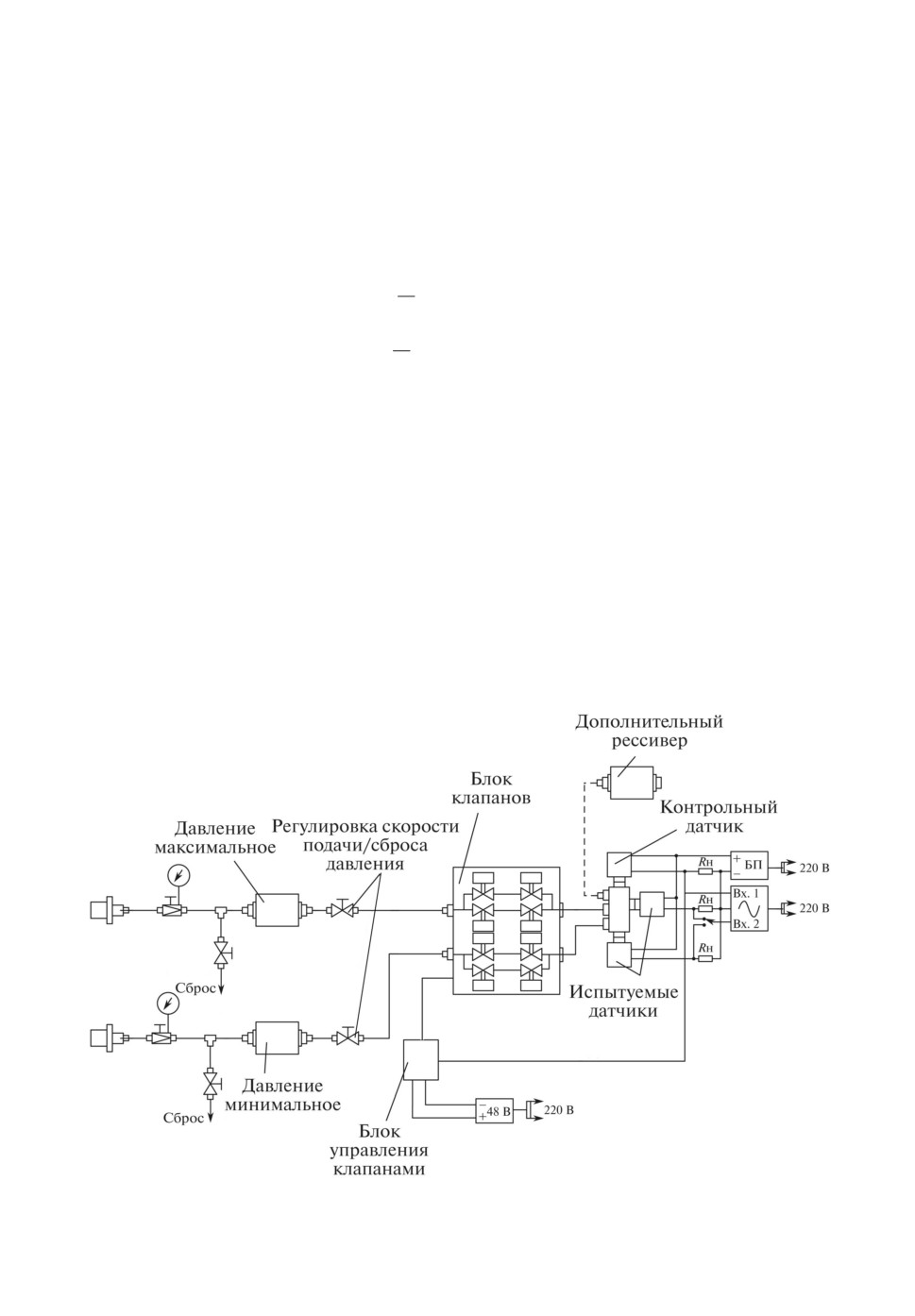
Экспериментальные данные были получены на стенде, схема которого

представлена на рис. 4. Основными параметрами стенда являются:

— минимальное входное давление - 800 кПа;

— форма пульсации давления на выходе - синус, меандр, произвольная;

— частота пульсации - от 0 до 100 Гц;

— максимальное давление на выходе - 600-800 кПа;

— амплитуда пульсации - от 0 до 100%;

— погрешность формирования формы пульсации - не более 10%.

Рис. 4. Схема стенда.

131

0,8

0,6

0,4

0,2

0,02

0,04

0,06

0,08

0,10

0,12 t, c

Рис. 5. Результаты испытания датчика.

На стенде испытывается датчик давления Метран-43 с аналоговым элек-

тронным преобразователем. Передаточная функция датчика имеет вид

0,72

(4.1)

W (p) =

0,0119p + 1

Преобразуя ее к виду дескрипторной системы, получим

^{ ˙x = -84x + u,

(4.2)

y = 60,5x.

Зададим начальное состояние системы

(4.3)

x(0) = 0.

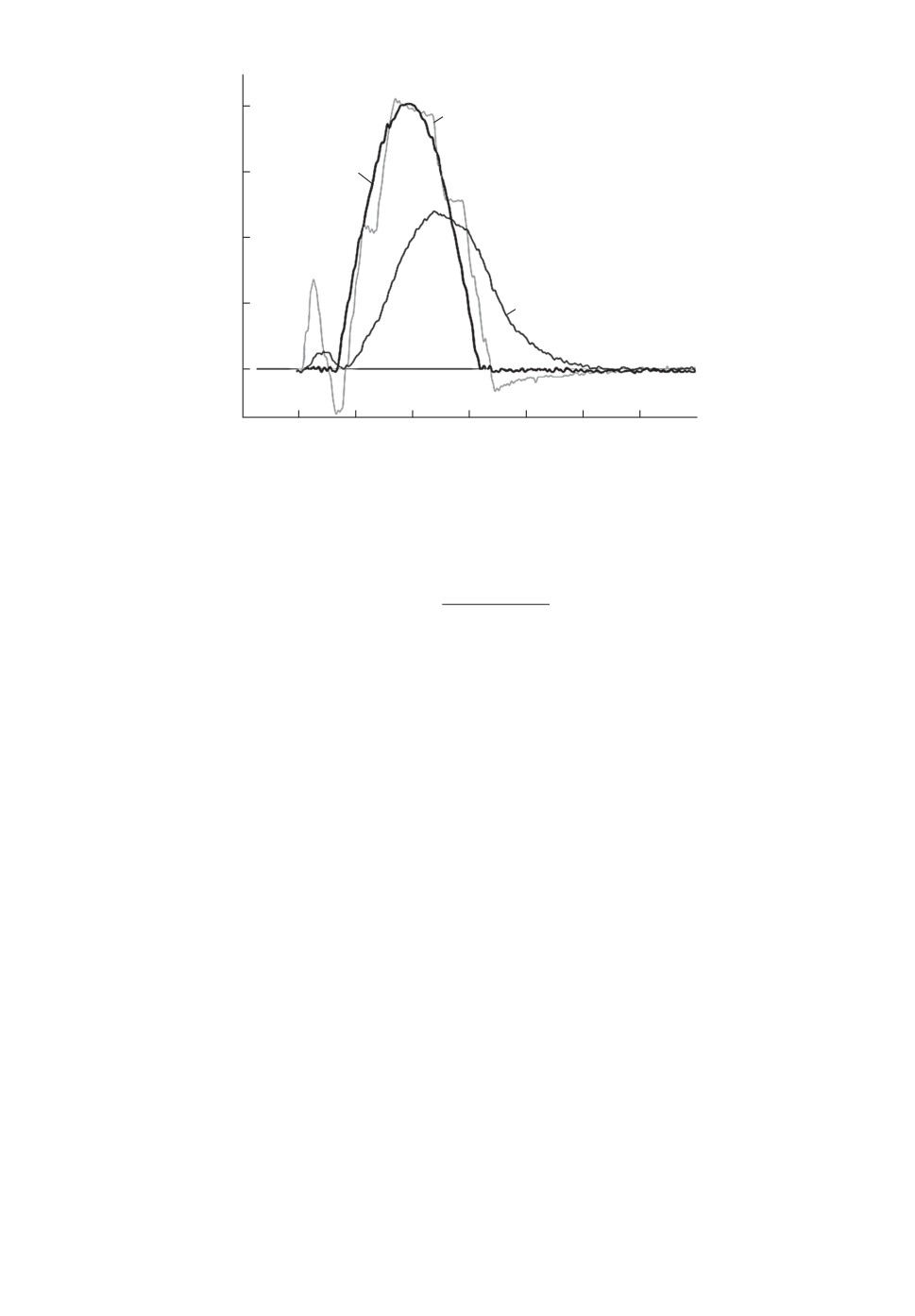
На рис. 5 представлены результаты испытания датчика на стенде. Чер-

ным цветом обозначен задающий сигнал w(t), подаваемый на блок управ-

ления клапанами. Светло-серым цветом обозначен входящий сигнал u(t) ис-

пытуемого датчика, фиксируемый контрольным датчиком. Характеристики

контрольного датчика на порядок превышают такие характеристики испы-

туемого датчика, как точность и быстродействие, что позволяет считать этот

сигнал истинным. Темно-серым цветом обозначен наблюдаемый (или выхо-

дящий) сигнал y(t) испытуемого датчика.

Заметим, что ступенчатый вид истинного сигнала обусловлен особенно-

стью системы управления стенда, связанной с работой по открытию и закры-

тию клапанов. Проверка математической модели датчика (4.2), (4.3) показала

соответствие полученного наблюдаемого сигнала входящему.

Получив экспериментальные данные наблюдаемого сигнала и математи-

ческую модель датчика, ставится вторая обратная задача динамических из-

мерений - восстановить методами теории оптимальных динамических изме-

рений входящий сигнал, а затем сравнить его с истинным сигналом.

132

5. Шаг дискретизации и его определение в алгоритме

Определение интервала дискретизации на первом шаге предлагаемого ал-

горитма является основополагающим для адекватного решения задачи опти-

мального динамического измерения. При проведении вычислительных экс-

периментов было рассмотрено несколько случаев с различным интервалом

дискретизации. Качественное сравнение результатов стало возможно в свя-

зи с известным истинным сигналом, фиксируемым контрольным датчиком

испытательного стенда.

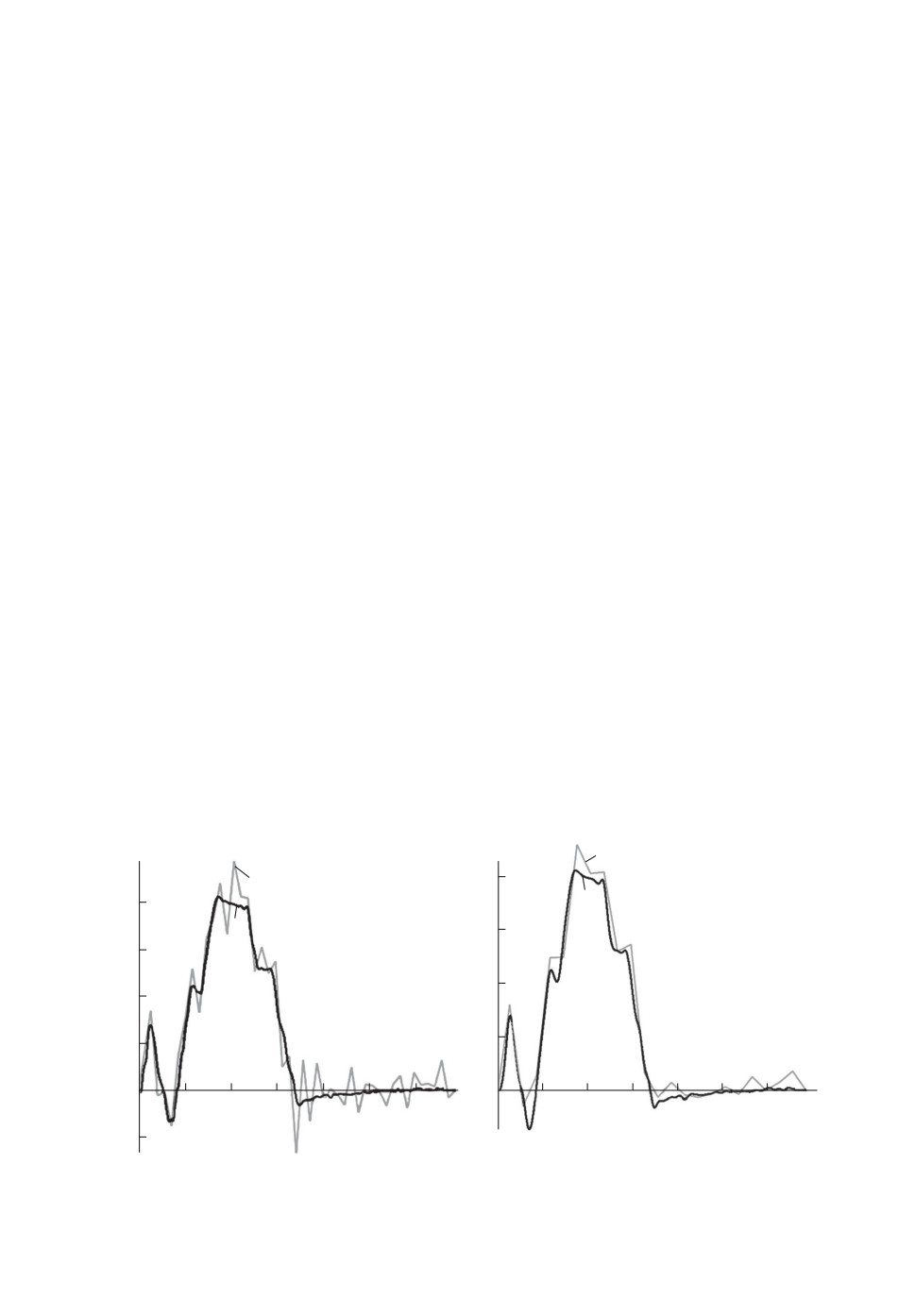
На рис. 6,а представлены результаты реализации алгоритма при интер-

вале дискретизации Δ_i = 0,002, при котором подмножество множества зна-

чений Y0i для базового расчета содержит 70 точек. Этот интервал дискрети-

зации позволил провести реализацию алгоритма нахождения приближенного

оптимального динамического измерения в виде полинома первой степени. От-

метим, что ограничения прежде всего связаны с реализацией большого числа

вычислений для малых величин как независимых, так и зависимых при необ-

ходимости приемлемых временных затрат на вычисления. На рис. 6,а показан

результат расчета по одному циклу: серым цветом отражен график модели-

руемого оптимального динамического измерения, черным цветом — отражено

истинное измерение.

На рис. 6,б представлены результаты реализации алгоритма при интерва-

ле дискретизации Δ_i = 0,001, при котором подмножество множества значе-

ний Y0i для базового расчета содержит 140 точек. Этот интервал дискрети-

зации позволил провести реализацию алгоритма нахождения приближенного

оптимального динамического измерения в виде полинома первой степени. На

рис. 6,б показан результат расчета по одному циклу: серым цветом отражен

график моделируемого оптимального динамического измерения, черным цве-

том — отражено истинное измерение.

0,8

0,6

0,4

0,2

0,02 0,04 0,06 0,08

0,10

0,12 t, c

0,02 0,04 0,06 0,08 0,10

0,12 t, c

0,2

Рис. 6. а - Интервал дискретизации Δ_i = 0,002, полином первой степени; б -

интервал дискретизации Δ_i = 0,001, полином первой степени.

133

1,0

0,8

0,6

0,4

0,2

0,02

0,04

0,06

0,08

0,10

0,12

0,2

0,4

0,6

Рис. 7. Интервал дискретизации Δ_i = 0,0002, полином первой степени.

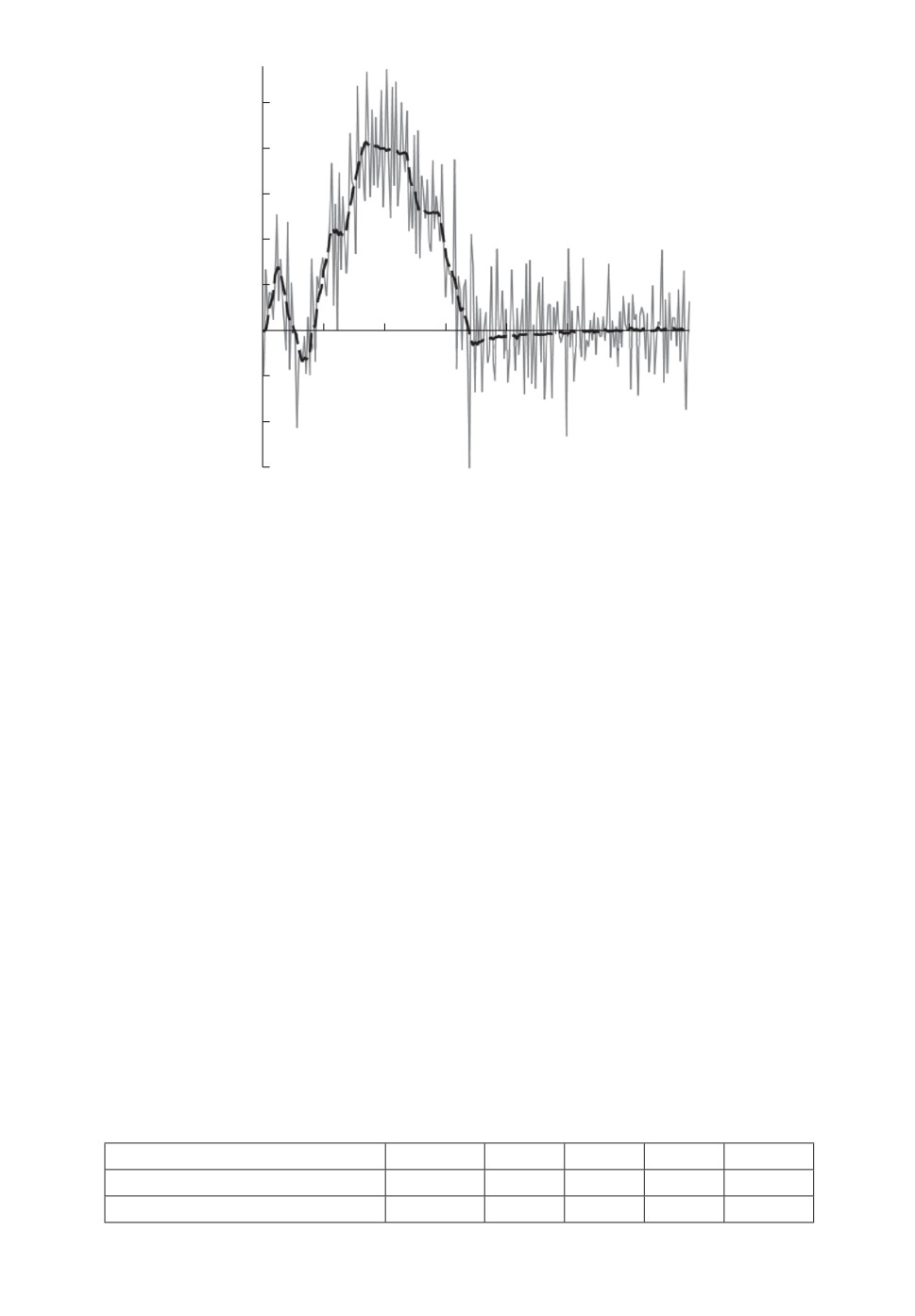
На рис. 7 представлены результаты реализации алгоритма при интерва-

ле дискретизации Δ_i = 0,0002, при котором подмножество множества значе-

ний Y0i для базового расчета содержит 700 точек. Этот интервал дискрети-

зации позволил провести реализацию алгоритма нахождения приближенно-

го оптимального динамического измерения в виде полинома первой степени.

На рис. 7 показан результат расчета по одному циклу: серым цветом отра-

жен график моделируемого оптимального динамического измерения, черным

цветом отражено истинное измерение.

В таблице приведены результаты сравнения погрешностей при нахожде-

нии приближенного оптимального динамического измерения v в зависимости

от выбора шага дискретизации Δ на первом основном цикле. Полученные

значения свидетельствуют о том, что погрешность с увеличением шага дис-

кретизации сначала уменьшается, а затем снова увеличивается.

Сравнение результатов при различных интервалах дискретизации позво-

ляет сделать вывод об их согласовании с известной в области цифровой обра-

ботки сигналов теоремой Котельникова [17], из которой следует, что любой

аналоговый сигнал может быть восстановлен с задаваемой точностью по сво-

им дискретным отсчетам, частота которых f ≥ 2f_c, где f_c - максимальная

частота, которой ограничен спектр реального сигнала.

Таблица. Значения погрешности и времени счета при различных интервалах

дискретизации

Интервал дискретизации Δ, c

0,0002

0,001

0,002

0,004

0,008

Погрешность δ = ∥u - v∥²

101,5218

0,1684

0,0204

0,0236

0,03012

Время счета, c

2760,32

36,62

27,21

20,07

17,69

134

Таким образом, в представляемом алгоритме выбор интервала дискрети-

зации становится, по сути, выбором фильтра на основании

(5.1)

0<Δ≤

2f_c

Получаем, что при Δ₁ = 0,004, f_c = 120 Гц, при Δ₂ = 0,002, f_c = 250 Гц, при

Δ₃ = 0,001, f_c = 500 Гц, Δ₄ = 0,0002, f_c = 2500 Гц. В заключение отметим,

что использование выборок для восстановления сигналов на основе теоремы

отсчетов Котельникова является стандартным приемом [18].

6. Обработка результатов эксперимента

Проведем реализацию описанного алгоритма на примере данных, полу-

ченных в результате стендовых испытаний (см. рис. 2,а). Множество Y0i со-

держит 700 точек. На основании сведений о достаточности f_c = 250 Гц вы-

бираем шаг дискретизации Δ₂ = 0,002 на основании (5.1). Таким образом,

подмножество множества значений Y0i для базового расчета содержит 70 то-

чек. Количество основных циклов равно 10. Приведем результаты реализации

алгоритма для одного из основных циклов.

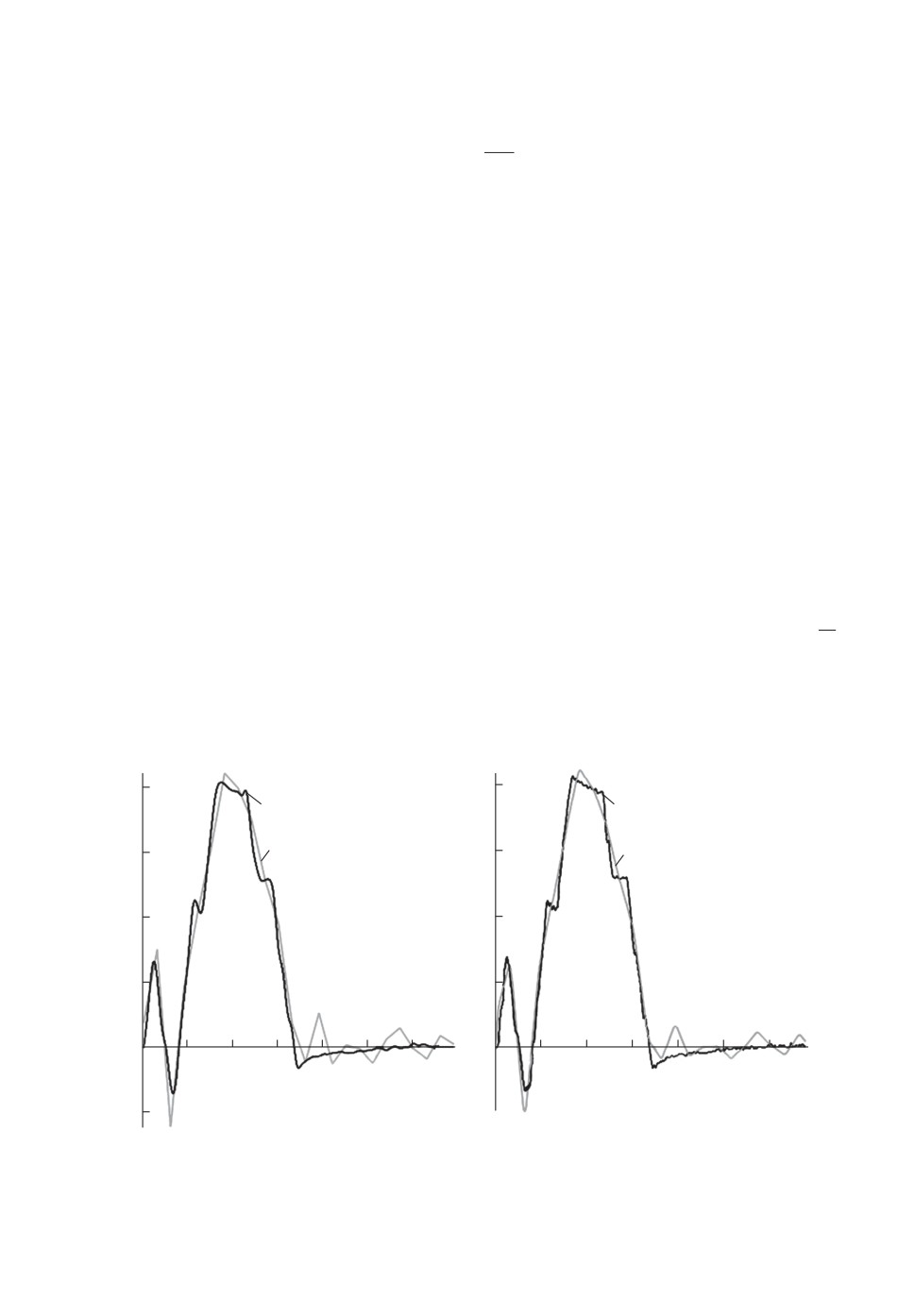
На рис. 8,а для примера представлены результаты базовых расчетов на

четвертом основном цикле. Серым цветом представлено моделируемое опти-

мальное динамическое измерение v4i.

Осреднив результаты, полученные на десяти основных циклах, получим v_i

в каждой точке t_i, а затем интерполированием - моделируемое оптимальное

динамическое измерение v(t). На рис. 8,б представлены графики v(t) (серый

цвет) и истинного измерения (черный цвет).

0,8

0,6

0,4

0,2

0,02 0,04 0,06 0,08 0,10

0,12 t, c

0,02 0,04 0,06 0,08 0,10

0,12 t, c

0,2

Рис. 8. а - Истинное измерение и моделируемое на четвертом основном цикле

алгоритма оптимальное динамическое измерение; б - моделируемое оптималь-

ное динамическое измерение v(t) и истинное измерение.

135

Значительные отклонения моделируемого от истинного измерения наблю-

даются именно “на ступенях” истинного сигнала (см. п. 4), на остальных ча-

стях графика отклонения незначительны. Отметим, что погрешность найден-

ного приближенного оптимального динамического измерения v

δ = ∥u - v∥² = 0,000197.

При этом время счета составило 109,71 c.

7. Заключение

В статье представлен новый алгоритм восстановления динамически иска-

женного сигнала. Алгоритм построен на методах теории оптимальных ди-

намических измерений, численных методах интерполирования и нахождения

средних.

Результаты вычислительного эксперимента сопоставлены с результатами

натурного эксперимента, найденные значения погрешности свидетельствуют

об эффективности предлагаемого метода. Приведенные результаты вычис-

лительной точности при различных шагах дискретизации согласуются с ша-

гом дискретизации, выбранным согласно теореме Котельникова. Предложен-

ный метод позволил сократить время счета более чем в 5 раз при меньшей

мощности персонального компьютера с приемлемой точностью нахождения

оптимального динамического измерения. Кроме того, имеется возможность

распараллеливания процессов, что позволит дальнейшее сокращение времени

счета.

Отметим, что данный численный метод позволит продолжить исследова-

ния в рамках теории оптимальных динамических измерений по следующим

направлениям: моделирование оптимальных динамических измерений со слу-

чайными помехами с построением новых цифровых фильтров; моделирование

нестационарных моделей оптимальных динамических измерений; применение

в алгоритмах решения других обратных задач динамических измерений.

СПИСОК ЛИТЕРАТУРЫ

1. Грановский В.А. Динамические измерения: теория и метрологическое обеспече-

ние вчера и сегодня // Датчики и системы. 2016. № 3 (201). С. 57-72.

2. Ruhm K.H. Measurement Plus Observation — a Modern Structure of Metrology //

21st IMEKO World Congr. on Measurement in Research and Industry. Prague, 2015.

Article ID 116100.

3. Elster C., Eichstädt S., Link A. Uncertainty Evalution of Dynamic Measurements in

Line with the GUM // 19th IMEKO World Congr. 2009. V. 1. P. 98-101.

4. Sommer K.-D., Hqnebeck U.D., Krystek M., et al. Modelling of Dynamic

Measurements for Uncertainty Analysis by Means of Discxretized State-Space

Forms // 19th IMEKO World Congr. 2009. V. 1. P. 290-294.

5. Шестаков А.Л. Методы теории автоматического управления в динамических

измерениях. Челябинск: Издат. центр ЮУрГУ, 2013.

136

Shestakov A.L., Keller A.V., Zamyshlyaeva A.A., Manakova N.A., Zagrebina S.A.,

Sviridyuk G.A. The Optimal Measurements Theory as a New Paradigm in the

Metrology // J. Comp. Eng. Math. 2020. V. 7. No. 1. P. 3-23.

Sagadeeva M.A., Bychkov E.V., Tsyplenkova O.N. The Pyt’ev-Chulichkov Method

for Constructing a Measurement in the Shestakov-Sviridyuk Model // Bulletin of

the South Ural State University. Series: Mathematical Modelling, Programming and

Computer Software. 2020 V. 13. No. 4. P. 68-82.

Шестаков А.Л., Загребина С.А., Манакова Н.А., Сагадеева М.А., Свири-

дюк Г.А. Алгоритм численного нахождения оптимального измерения, искажен-

ного инерционностью, резонансами и деградацией измерительного устройства //

АиТ. 2021. № 1. С. 55-67.

Shestakov A.L., Zagrebina S.A., Manakova N.A., Sagadeeva M.A., Sviridyuk G.A.

Numerical Optimal Measurement Algorithm under Distortions Caused by Inertia,

Resonances, and Sensor Degradation // Autom. Remote Control. 2021. V. 82. No. 1.

P. 41-50.

Загребина С.А. О задаче Шоуолтера-Сидорова // Изв. высш. уч. заведений.

Математика. 2007. № 3. C. 22-28.

10.

Khudyakov Yu.V. On Mathematical Modeling of the Measurement Transducers //

J. Comp. Eng. Math. 2016. V. 3. No. 3. P. 68-73.

11.

Белов A.A., Курдюков А.П. Дескрипторные системы и задачи управления. М.:

Физматлит, 2015.

12.

Zamyshlyaeva A.A., Manakova N.A., Tsyplenkova O.N. Optimal Control in Linear

Sobolev Type Mathematical Models // Bulletin of the South Ural State University.

Series: Mathematical Modelling, Programming and Computer Software. 2020. V. 13.

No. 1. P. 5-27.

13.

Шестаков А.Л., Келлер А.В., Назарова Е.И. Численое решение задачи опти-

мального измерения // АиТ. 2012. № 1. С. 107-115.

Shestakov A.L., Keller A.V., Nazarova E.I. Numerical Solution of the Optimal

Measurement Problem // Autom. Remote Control. 2012. V. 73. No. 1. P. 97-104.

14.

Худяков Ю.В. Алгоритм численного исследования модели Шестакова-Свири-

дюка измерительного устройства с инерционностью и резонансами // Матема-

тические заметки СВФУ. 2013. Т. 20. № 2. C. 211-221.

15.

Keller A.V., Ebel A.A. Parallelization of Numerical Algorithm for Optimum

Dynamic Measurement Problem Solution // Proc. - 2017 2nd Int. Ural Conf. on

Measurements. 2017. V. 2017. P. 372-377.

16.

Келлер А.В. Об алгоритме решения задач оптимального и жесткого управле-

ния // Программные продукты и системы. 2011. № 3. С. 42.

17.

Котельников В.А. О пропускной способности “эфира” и проволоки в электро-

связи // Успехи физических наук. 2006. № 7. C. 762-770.

18.

Зиатдинов С.И. Восстановление сигналов по его выборкам на основе теоремы

отсчетов Котельникова // Изв. высш. уч. заведений. Приборостроение. 2010.

Т. 53. № 5. С. 44-47.

Статья представлена к публикации членом редколлегии А.И. Кибзуном.

Поступила в редакцию 18.04.2021

После доработки 09.06.2021

Принята к публикации 30.06.2021

137