Автоматика и телемеханика, № 2, 2021

Линейные системы

(Ереванский государственный университет)

ОПТИМАЛЬНОЕ ПО БЫСТРОДЕЙСТВИЮ УПРАВЛЕНИЕ

ПЕРЕМЕЩЕНИЕМ СХВАТА ДВУЗВЕННОГО МАНИПУЛЯТОРА

С УЧЕТОМ ТИПА КОНЕЧНОЙ КОНФИГУРАЦИИ

Рассматривается задача оптимального по быстродействию управления

перемещением точечного схвата плоского двузвенного манипулятора с

прямолинейными звеньями равной длины и со вторым статически урав-

новешенным звеном. На плоскости обобщенных координат манипулятора

построены области достижимых конфигураций, позволяющие из двух ко-

нечных конфигураций, соответствующих заданному терминальному по-

ложению схвата, определить ту конфигурацию и тот способ управления

манипулятором, при которых обеспечивается перемещение схвата из на-

чального положения покоя в заданное конечное положение покоя за ми-

нимальное время. Численными расчетами установлено, что оптимальный

выбор типа конечной конфигурации может приводить к значительному

увеличению быстродействия.

Ключевые слова: двузвенный манипулятор, оптимальное по быстродей-

ствию управление, конечный тип конфигурации.

DOI: 10.31857/S000523102102001X

1. Введение

В различных отраслях современного производства широко применяются

двузвенные роботы-манипуляторы. Используются они как самостоятельно,

так и в составе конструкций многозвенных манипуляционных роботов та-

ких, для которых именно эти два звена выполняют основной объем движе-

ний робота при выполнении им различных технологических операций. По-

этому разработка эффективных режимов управления двузвенным роботом-

манипулятором по сей день представляет собой актуальную задачу. Одним

из возможных подходов к рациональному расчету режимов управления явля-

ется их оптимизация по отношению к некоторому критерию качества функ-

ционирования манипулятора (время транспортных операций, энергозатраты

и т.д.). Существенной составляющей при формировании оптимальных алго-

ритмов управления движением двузвенника является учет его конструктив-

ных и геометрических особенностей. Для плоского двузвенного манипуля-

тора каждому положению схвата отвечают две возможные конфигурации,

отличающиеся знаком угла между звеньями. Следовательно, качество пере-

мещения схвата в терминальное положение зависит как от типа конечной

конфигурации, так и от способа управления, приводящего манипулятор в

эту конфигурацию. В [1, 2] для двузвенного манипулятора с безынерционны-

ми звеньями построены оптимальные и субоптимальные законы управления

в двухточечной задаче перемещения схвата с грузом. Выявлена существен-

ная зависимость времени приведения схвата в терминальное состояние от ти-

па конфигурации манипулятора и решена задача выбора оптимального типа

конфигурации. В [3] разработан графоаналитический подход к построению

субоптимальных по быстродействию программных управлений, приводящих

двузвенный манипулятор с произвольными геометрическими и инерционны-

ми характеристиками из начальной конфигурации покоя в произвольную

конечную конфигурацию покоя. Методам оптимизации для решения задачи

управления роботами, в том числе двузвенными манипуляторами, и расчета

их конструктивных параметров посвящены публикации [4-8]. В [9-11, 12] рас-

смотрены модели механического и электромеханического плоскoго двузвен-

ного манипулятора со вторым статически уравновешенным звеном и с про-

извольными инерционными характеристиками. В предположении, что кон-

струкция манипулятора допускает полный поворот звеньев в направлениях

по часовой и против часовой стрелки, установлено, что в одну и ту же конеч-

ную конфигурацию манипулятор можно привести при различных сочетани-

ях поворотов звеньев. Для каждого из двух типов конечных конфигураций

графоаналитической процедурой решена задача выбора направлений пово-

ротов звеньев манипулятора и определения способа управления, при кото-

рых заданный критерий качества (быстродействие [9, 10], энергозатраты [12]

и комбинированный от них функционал [11]) достигает минимального зна-

чения. Прямым вычислением найден оптимальный тип конечной конфигура-

ции. В [13] методом параметрической оптимизации построено субоптимальное

по квадратичному функционалу управление движением плоского двузвенни-

ка с учетом возможных конфигураций манипулятора, соответствующих за-

данным положениям схвата в начале и в конце движения.

В настоящей статье рассматривается механическая модель двузвенного

манипулятора [3], конструкция которого в отличие от [3, 9-12] допускает

лишь пол-оборота вращений звеньев в положительном и отрицательном на-

правлениях. На плоскости обобщенных координат манипулятора построены

области, позволяющие по заданным координатам терминального положения

схвата манипулятора определить тип конечной конфигурации и способ управ-

ления, при которых обеспечивается перемещение схвата из начального поло-

жения покоя в заданное конечное положение покоя за минимальное время.

2. Расчетная модель манипулятора

Рассмотрим механическую двузвенную систему, состоящую из двух аб-

солютно жестких звеньев G₁, G₂ равной длины, соединенных шарниром O₂.

Звено G₁ при помощи шарнира O₁ связано с неподвижным основанием. Шар-

ниры являются идеальными, цилиндрическими, а их оси параллельны друг

другу. На конце второго звена в точке O₃ укреплен схват. Будем предпола-

гать, что линейные размеры схвата много меньше длин звеньев и при исследо-

вании транспортных движений считать схват материальной точкой. Управле-

ние манипулятором осуществляется с помощью двух независимых приводов

D₁, D₂. Привод D₁ осуществляет взаимодействие первого звена с основанием,

а D₂ - взаимодействие между звеньями G₁, G₂ манипулятора. Управляющи-

ми функциями в исследуемой модели манипулятора являются величины M₁,

M₂ - вращающие моменты относительно осей O₁, O₂, развиваемые привода-

ми D₁, D₂ соответственно. Описанная система совершает плоскопараллель-

ное движение в горизонтальной плоскости, перпендикулярной осям шарниров

O₁, O₂.

Уравнения Лагранжа, описывающие движение рассматриваемой системы,

имеют вид [3]:

(I₁ + m₂L²)ϕ1 + m2Llf1(ϕ1,ϕ2,ϕ˙2,ϕ2) = M1 - M2,

I₂ ϕ₂ + m₂Llf₂(ϕ₁,ϕ₂,ϕ˙₁,

ϕ₁) = M₂,

(2.1)

f₁(ϕ₁,ϕ₂,ϕ˙₂,

ϕ₂) =

ϕ₂ cos(ϕ₁ - ϕ₂) +ϕ˙²² sin(ϕ₁ - ϕ₂),

f₂(ϕ₁,ϕ₂,ϕ˙₁,

ϕ₁) =

ϕ₁ cos(ϕ₁ - ϕ₂) -ϕ˙²¹ sin(ϕ₁ - ϕ₂).

Здесь введены следующие обозначения: ϕ₁ - угол между осью O₁x и пря-

мой O₁O₂; ϕ₂ - угол между осью O₁x и прямой O₂C, проходящей через центр

масс C звена G₂; L = |O₁O₂| = |O₂O₃| - длина первого и второго звеньев;

l = |O₂C| - расстояние от оси O₂ до центра масс звена G₂; I₁, I₂ - моменты

инерции звеньев G₁, G₂ относительно осей шарниров O₁, O₂ соответственно;

m - масса звена G₂. Примем, что положительное направление отсчета углов

ϕ₁ и ϕ₂ ведется против часовой стрелки от прямой O₁x.

В данной статье будем рассматривать частный случай манипулятора (2.1),

когда второе звено манипулятора статически уравновешено, т.е. в (2.1) l = 0:

(2.2)

(I₁ + m₂L²)ϕ1 = M1 - M2, I2ϕ2 = M2.

На управляющие моменты M₁, M₂ имеются ограничения

(2.3)

|M₁| ≤ M⁰¹,

|M₂| ≤ M⁰²,

где M⁰¹, M⁰² - заданные постоянные.

3. Постановка задачи

Цель управления манипулятором состоит в приведении схвата в задан-

ное пространственное положение в предположении, что конструкция мани-

пулятора допускает лишь пол-оборота вращений звеньев в положительном

и отрицательном направлениях. Из геометрии двузвенника следует, что при

плоскопараллельном движении положение схвата полностью определяется,

например, декартовыми координатами проекции точки O₃ на горизонталь-

ную плоскость. Задание обобщенных координат ϕ₁, ϕ₂ однозначно определяет

положение точечного схвата, поскольку между декартовыми координатами

проекции точки O₃ и обобщенными координатами ϕ₁, ϕ₂ существует одно-

значная связь

(3.1)

x = L(cosϕ₁ + cosϕ₂), y = L(sinϕ₁ + sinϕ₂

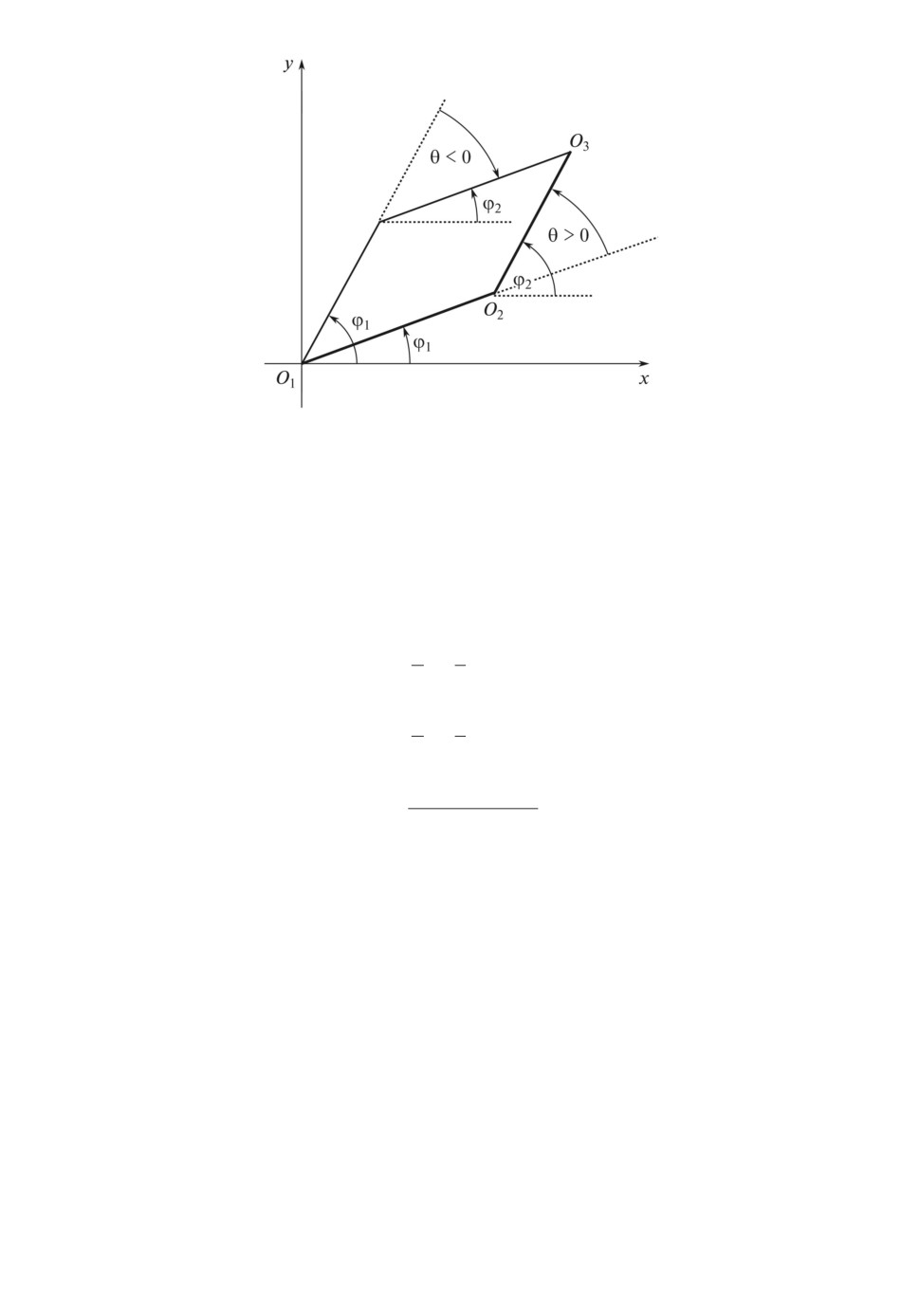
Рис. 1. Положению схвата Q₃ соответствуют две конфигурации двузвенника,

отличающиеся знаком угла между звеньями θ = ϕ₂ - ϕ₁.

Однако углы ϕ₁, ϕ₂ определяются по декартовым координатам x, y неодно-

значно. С учетом конструктивных ограничений двузвенника разрешим систе-

му уравнений (3.1) относительно ϕ₁, ϕ₂ и выберем из них те решения, которые

по модулю не больше π:



|ϕ₁| =arctgy

Kδ + πα(x)signy

π,

≤



(3.2)

|ϕ₂| =arctgy

Kδ + πα(x)signy

π,

≤

)

(x² + y² - 2L

{ 0, x > 0,

K = ±1, δ = arccos

α(x) =

2L²

1, x ≤ 0.

Из (3.2) вытекает, что{каждому положению}схвата (x, y) внутри рабочей

зоны манипулятора R =

(x, y) : x² + y² ≤ 4L²

соответствуют две конфигу-

рации двузвенника, отличающиеся знаком угла между звеньями θ = ϕ₂ - ϕ₁

(рис. 1). Величина δ в (3.2) - угол при вершинах O₁ и O₃ треугольника

O₁O₂O₃. Как следует из (3.2), значениям K = 1 и K = -1 отвечают конфи-

гурации, для которых соответственно θ > 0 и θ < 0, т.е. K = signθ. Конфи-

гурация, отвечающая значению K = 1, 0 < θ < π, показана на рис. 1 жирной

сплошной линией, а конфигурация K = -1, -π < θ < 0 - тонкой сплошной

линией. Если обозначить их через {ϕ₁(x, y), ϕ₂(x, y)}_K , K = ±1, то согласно

(3.2) между углами ϕ₁, ϕ₂, отвечающими различным значениям K, имеется

следующая связь:

(3.3)

ϕ₁(x,y)|_K=-1 = ϕ₂(x,y)|_K=+1, ϕ₂(x,y)|_K=-1 = ϕ₁(x,y)|_K=+1

(в дальнейшем аргументы (x, y) функций ϕ_i(x, y) будут опускаться).

Таким образом, на плоскости обобщенных координат манипулятора

(3.4)

Φ = {ϕ₁,ϕ₂ : -π ≤ ϕ₁,ϕ₂

≤ π}

точки (ϕ₁, ϕ₂), (ϕ₂, ϕ₁), отвечающие конфигурациям

{ϕ₁, ϕ₂}_K=1,

{ϕ₂, ϕ₁}_K=-1 соответственно, симметричны относительно биссектрисы I

и III квадрантов и при этом

(ϕ₁, ϕ₂) ∈ {ϕ₁, ϕ₂ ∈ Φ : ϕ₂ ≥ ϕ₁} = Φ(+1),

(3.5)

(ϕ₂, ϕ₁) ∈ {ϕ₁, ϕ₂ ∈ Φ : ϕ₂ ≤ ϕ₁} = Φ(-1).

Систему (2.2) будем рассматривать при начальных условиях

(3.6)

ϕi(0) = ϕⁱ,

ϕi

(0) = 0, i = 1, 2,

которым согласно (3.1) соответствует начальное положение покоя схвата

x(0) = L(cos ϕ⁰¹ + cos ϕ⁰²) = x⁰,

x(0) = 0,

(3.7)

y(0) = L(sin ϕ⁰¹ + sin ϕ⁰²) = y⁰,

y(0) = 0.

Пусть заданы несовпадающие начальное (x⁰, y⁰) (3.7) и конечное (x^T , y^T )

положения схвата в рабочей зоне м{нипуля}ора R. Так как положению

(x^T , y^T ) отвечают две конфигурации

ϕT1 , ϕ^T

, K = ±1, то в качестве ко-

нечных условий для системы (2.2) рассмотрим условия



(3.8)

ϕi

_K(T) = ϕ^TiK,

ϕi |K

(T ) = 0, i = 1, 2; K = ±1,

которым однозначно соответствует одно и то же положение покоя схвата

(



)

x(T ) = L

cos ϕ^T1

_K + cos ϕ^T2

_K

=x^T,

x(T ) = 0,

(3.9)

(



)

K = ±1.

y(T ) = L

sin ϕ^T1

_K + sin ϕ^T2

_K

=y^T,

y(T ) = 0,

Система (2.2), (2.3) полностью управляема в классе кусочно-непрерывных

функций M₁(t), M₂(t) [14], поэтому при заданных краевых состояниях схвата

(3.7), (3.9) каждой совокупности условий (3.8) (K = ±1) и каждому допусти-

мому управлению M = (M₁(t), M₂(t)) соответствует некоторое время переме-

щения

[{

}

]



(3.10)

T =T ϕ^T1,ϕ^T2

_K,M .

Рассмотрим следующую задачу оптимального по быстродействию управ-

ления перемещением схвата манипулятора с учетом конечного типа конфи-

гурации.

Задача. Определить тип K = ±1 конечной конфигурации (3.8) и закон

изменения ограниченного управления M = (M₁(t), M₂(t)) (2.3), доставляю-

щие минимум

[{

}

]



(3.11)

T^∗ = minminT ϕT1,ϕT2

_K,M

при приведении схвата манипулятора из начального состояния покоя (3.7) в

заданное состояние покоя (3.9).

4. Построение оптимального по быстродействию управления

Внутренний минимум в (3.11) является задачей построения оптимально-

го по быстродействию управления M = (M₁, M₂) системой (2.2), (2.3), (3.6),

(3.8) для фиксированного значения K. При решении этой задачи в краевых

условиях (3.8) параметр{K буде}м опускать, подразумевая тем самым, что

конечная конфигурация

ϕT1 , ϕ^T2

отвечает одному из значений K = +1 или

K = -1.

В (2.2), (2.3), (3.1), (3.6)-(3.9) перейдем к безразмерным переменным

(

))_1/2

(

)

t^′ =

M⁰²/

m₂L²

I^′i = I_i/

m₂L²

M^′i = M_i/M⁰²,

(4.1)

x^′ = x/L, y^′ = y/L, ϕ^′i = ϕ_i - ϕ⁰ⁱ, ϕ^′i0,T = ϕ^0,Ti - ϕ⁰ⁱ, i = 1,2.

Если теперь опустить штрихи, то соотношения (2.2), (2.3), (3.1), (3.2),

(3.6)-(3.9) упростятся: в них получим ϕ^01,2 = 0, L = 1, M⁰² = 1, а система (2.2),

ограничения (2.3) и краевые условия (3.6), (3.8) примут вид:

(4.2)

(I₁ + 1)ϕ1 = M1 - M2, I2ϕ2 = M2,

(4.3)

|M₁| ≤ M⁰¹,

|M₂

| ≤ 1,

(4.4)

ϕi(0) = 0,

ϕi

(0) = 0, i = 1, 2,

(4.5)

ϕi(T ) = ϕⁱ ,

ϕi

(T ) = 0, i = 1, 2.

Заменой переменных

(4.6)

q₁ = (I₁ + 1)ϕ₁ + I₂ϕ₂, q₂ = I₂ϕ₂

система (4.2) приводится к простейшей форме, отвечающей разделению дви-

жений по координатам q₁, q₂:

(4.7)

q₁ = M₁,

q₂ = M₂.

Начальные и конечные условия для системы (4.7) согласно (4.4)-(4.6), име-

ют вид:

(4.8)

q₁(0) = q⁰¹ = 0, q₂(0) = q⁰² = 0,

q_1,2(0) = 0,

(4.9)

q₁(T) = q^T1 = (I₁ + 1)ϕ^T1 + I₂ϕ^T2 , q₂(T) = q^T2 = I₂ϕ^T2 ,

q_1.2(T ) = 0.

Решение задачи об оптимальном по быстродействию управлении для си-

стемы, описываемой отдельно каждым из уравнений (4.7), известно (см. [15])

и имеет вид:

{

M⁰ⁱsign(q^Ti ), t ∈ [0,τ_i),

M^∗i =

-M⁰ⁱsign(q^Ti ), t ∈ [τ_i,T_i],

(4.10)

(



)

qT/M0

T_i = 2τ_i = 2

^1/2 , i = 1, 2; M⁰² = 1.

Управление M^∗i(t) переводит систему, описываемую уравнением q_i = M_i

с ограничением |M_i| ≤ M⁰ⁱ, за минимально время T_i из состояния q_i(0) = 0,

q_i(0) = 0 в состояние q_i(T_i) = q^Ti ,

˙q_i(T_i) = 0.

Заметим, что минимальное значение времени перехода системы (4.7) из

состояния (4.8) в состояние (4.9) не может быть меньше наибольшего из двух

минимальных значений времени перехода, соответствующих рассмотренным

независимым подсистемам (4.7) при соответствующих граничных условиях.

Таким образом, искомое время быстродействия равно

(4.11)

T = max(T₁,T₂

Возможны следующие случаи.

A1. Если T₁ > T₂, то M₁(t) = M^∗1, а M₂(t) является любым допустимым

управлением, осуществляющим требуемый переход за время T₁. При этом на

плоскости (q₁, q₂) неравенству T₁ > T₂ в силу (4.10) отвечает область, опре-

деляемая неравенством



qT/M0

qT

(4.12)

.

A2. Если T₂ > T₁, которому на плоскости (q₁, q₂) отвечает область, опре-

деляемая неравенством



>

(4.13)

q^T2

q^T1 /M01,

то, наоборот, M₂(t) = M^∗2, а M₁(t) является любым допустимым управлением,

осуществляющим требуемый переход за время T₂.

A3. Если T₁ = T₂ = T , то M₁(t) = M^∗1, M₂(t) = M^∗2 только для тех точек

на плоскости (q₁, q₂), для которых



(4.14)

q^T1/M01 =

q^T2

.

В случаях A1 и A2 будем задавать управления M₂(t) и M₁(t) в следующих

формах соответственно:





signq^T2 , t ∈ [0, τ⁽¹⁾²),



M₂(t) =

t ∈ [τ⁽¹⁾²,τ⁽²⁾²),



 -signq^T2 , t ∈ [τ⁽²⁾²,T₁],

(4.15)





M⁰¹signq^T1 , t ∈ [0,τ⁽¹⁾¹),



M₁(t) =

t ∈ [τ⁽¹⁾¹,τ⁽²⁾¹),



 -M⁰¹signq^T1 , t ∈ [τ⁽²⁾¹,T₂],

имеющих по две точки переключения и принимающих по модулю значения,

не превосходящие максимальных.

Интегрируем уравнения (4.7) с краевыми условиями (4.8), (4.9) при управ-

лениях (4.15) на интервалах времени [0, T₂] и [0, T₁]:

q₂(T) = τ⁽¹⁾²τ⁽²⁾²sign(q^T2 ) = q^T2 ,

(4.16)

˙q₂(T) = sign(q^T2 )(τ⁽¹⁾² + τ⁽²⁾² - T₁) = 0,

q₁(T) = τ⁽¹⁾¹τ⁽²⁾¹M⁰¹sign(q^T1 ) = q^T1 ,

(4.17)

˙q₁(T) = M⁰¹sign(q^T1 )(τ⁽¹⁾¹ + τ⁽²⁾¹ - T₂) = 0.

j₂

F₁₂

-p

j₁

-p

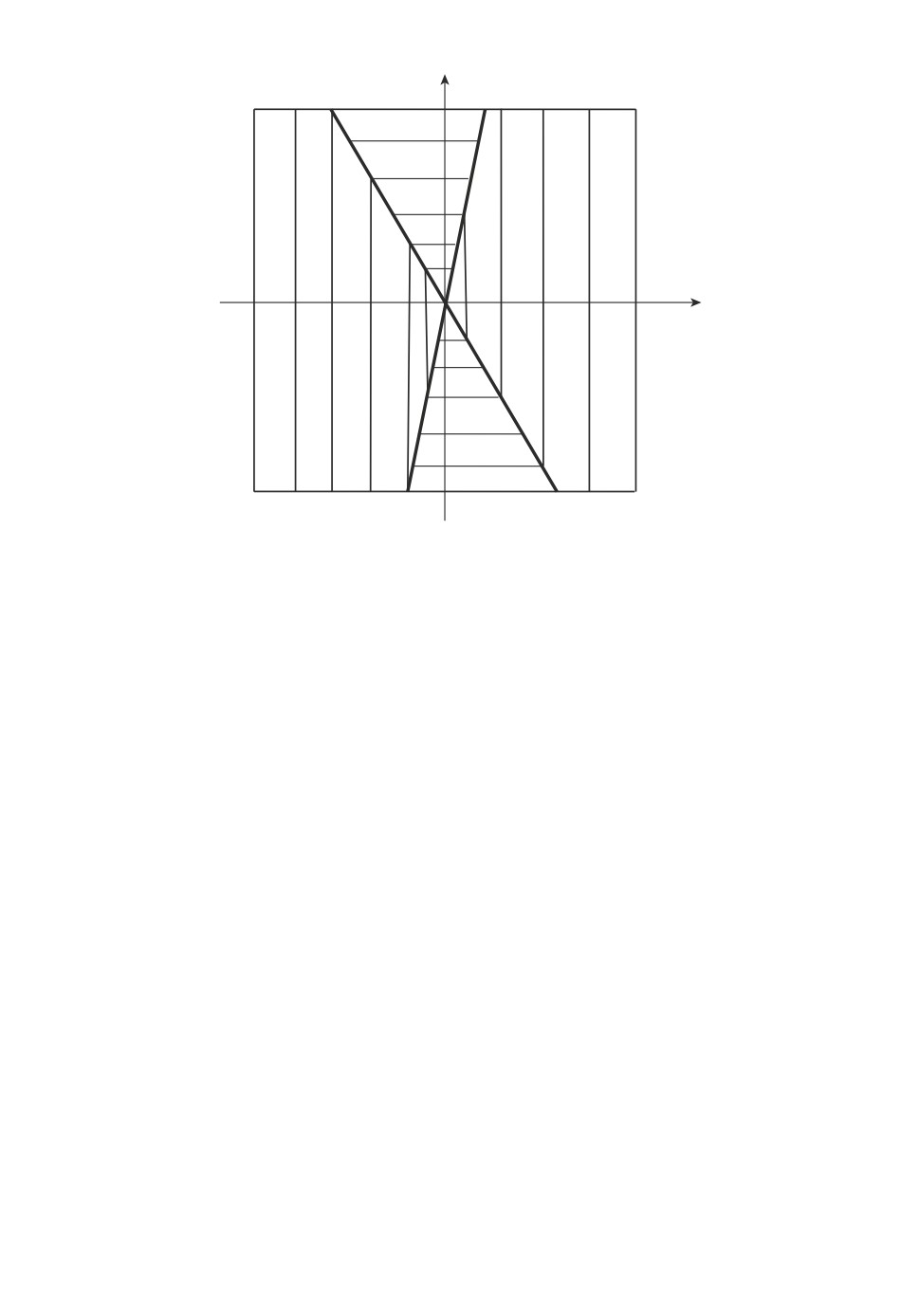
Рис. 2. В областях (Φ⁺¹ ∪ Φ^-1) и (Φ⁺² ∪ Φ^-2) реализуются случаи A1 (T₁ > T₂) и

A2 (T₂ > T₁) соответственно, а в областях Φ₁₂ и Φ₂₁ - случай A3 (T₁ = T₂).

Решение системы (4.16) и (4.17) относительно параметров τ⁽¹⁾², τ⁽²⁾² и

τ⁽¹⁾¹,τ⁽²⁾¹ соответственно не является единственным. Единственность гаранти-

руется условиями τ⁽¹⁾ⁱ ≤ τ⁽²⁾ⁱ, i = 1, 2, в соответствии с (4.15). Разрешив систе-

му (4.16), (4.17) с учетом этих замечаний и переходя к исходным переменным

по формулам (4.6), получим, что в случаях A1, A2 моменты переключения

управлений M₂(t), M₁(t) (4.15) определяются по следующим формулам соот-

ветственно:

(



)1/2



τ⁽¹⁾² = T₁/2 -

T²¹/4 -

I₂ϕ^T2

(



)1/2

(4.18)

(A1, M₂) :τ(2)

= T₁/2 +

T²¹/4 -

I₂ϕ^T2



(



)_1/2

T₁ = 2

(I₁ + 1)ϕ^T1 + I₂ϕ^T2 /M01

(



)_1/2

τ⁽¹⁾¹ = T₂/2 -

T²²/4 -

(I₁ + 1)ϕ^T1 + I₂ϕ^T2 /M01

(



)_1/2

(4.19)

(A2, M₁) :τ(2)

= T₂/2 +

T²²/4 -

(I1 + 1)ϕ^T1 + I₂ϕ^T2/M0

(

)1/2

T₂ = 2

I2ϕ^T2



Неравенствам (4.12) и (4.13) в исходных переменных (4.6) на плоскости

(ϕ₁, ϕ₂) отвечают области (Φ⁺¹ ∪ Φ^-1) и (Φ⁺² ∪ Φ^-2), в которых реализуются

случаи A1 (T₁ > T₂) и A2 (T₂ > T₁) соответственно. На рис. 2 области Φ⁺¹, Φ^-1

заштрихованы вертикальными, а области Φ⁺², Φ^-2 - горизонтальными линия-

ми. В обозначениях этих областей нижний индекс определяет номер управ-

ляющего момента, имеющего одно переключение, а верхний - знак этого

управления на первом интервале. В соответствии со случаем A3 (T₁ = T₂),

на границах Φ₁₂ (изображены жирными линиями) между областями Φ⁺ⁱ, Φ^-i

реализуются режимы управления с одним переключением. Аналитические

выражения областей Φ⁺ⁱ(ϕ₁, ϕ₂), Φ^-i(ϕ₁, ϕ₂), выводимые из (4.12)-(4.14), име-

ют вид:

Φ⁺¹ = {ϕ₁,ϕ₂ ∈ Φ : -Aϕ₁ < ϕ₂ < Bϕ₁, ϕ₁ > 0} ,

(4.20)

Φ^-1 = {ϕ₁,ϕ₂ ∈ Φ : Bϕ₁ < ϕ₂ < -Aϕ₁, ϕ₁ < 0} ,

Φ⁺² = {ϕ₁,ϕ₂ ∈ Φ : Bϕ₁ < ϕ₂,ϕ₁ > 0 и - Aϕ₁ < ϕ₂, ϕ₁ < 0} ,

(4.21)

Φ^-2 = {ϕ₁,ϕ₂ ∈ Φ : ϕ₂ < -Aϕ₁,ϕ₁ > 0 и ϕ₂ < Bϕ₁, ϕ₁ < 0} ,

(4.22)

Φ₁₂ = Φ^+,+1,2 ∪ Φ^+,-1,2 ∪ Φ^-,+1,2 ∪ Φ^-,-1,2,

Φ^+,+1,2 = {ϕ₁,ϕ₂ ∈ Φ : ϕ₂ = Bϕ₁, ϕ₁ > 0} ,

Φ^-,+1,2 = {ϕ₁,ϕ₂ ∈ Φ : ϕ₂ = -Aϕ₁, ϕ₁ < 0} ,

Φ^+,-1,2 = {ϕ₁,ϕ₂ ∈ Φ : ϕ₂ = -Aϕ₁, ϕ₁ > 0} ,

Φ^-,-1,2 = {ϕ₁,ϕ₂ ∈ Φ : ϕ₂ = Bϕ₁, ϕ₁ < 0} ,

(4.23)

A = (I₁ + 1)(M⁰¹ + 1)^-1I^-12, B = (I₁ + 1)(M⁰¹ - 1)^-1I^-12.

В обозначениях областей (4.22) нижние индексы указывают номера управ-

лений с одним переключением, а верхние - знаки этих управлений на первом

интервале.

Замечание. При построении диаграммы (рис. 2) было принято, что ма-

нипулятор характеризуется размерными параметрами, фигурирующими в

(2.2), (2.3),

L = 1 м, m₂ = 10 кг, I₁ = I₂ = (10/3) кг · м²,

(4.24)

M⁰¹ = 2 н · м, M⁰² = 1 н · м,

которые отвечают манипулятору, звенья которого - одинаковые однородные

стержни.

После перехода к безразмерным параметрам согласно (4.1) получим из

(4.24), что

(4.25)

L = 1, m₂ = 1, I₁ = I₂ = 1/3, M⁰¹ = 2, M⁰²

= 1.

Отметим, что суть методики решения поставленной задачи не меняется

при других геометрических и физических параметрах манипулятора.

Подытожив полученные результаты, оптимальный режим управления си-

стемой (4.2)-(4.5) можно представить в виде



(M∗1, M2), (ϕT1 , ϕT2 ) ∈ Φ+1 ∪ Φ-1,

(4.26)

M^∗ =

(M₁, M^∗2), (ϕ^T1 , ϕ^T2 ) ∈ Φ⁺² ∪ Φ^-2,



(M^∗1, M^∗2), (ϕ^T1 , ϕ^T2 ) ∈ Φ₁₂,

где управления M^∗i, M_i, i = 1, 2 определяются формулами (4.10), (4.15),

(4.18), (4.19), а Φ⁺ⁱ, Φ^-i, i = 1, 2, и Φ₁₂ - формулами (4.20)-(4.22).

Таким образом, построенная диаграмма позволяет по заданным значениям

ϕT1 , ϕ^T2 находить тип режима управления, моменты переключения и время

процесса. Тип управления определяется в зависимости от того, какой области

достижимых конечных конфигураций принадлежат данные терминальные

значения ϕ^T1 , ϕ^T2 .

5. Определение оптимального типа конечной конфигурации манипулятора

Перейдем к определению внешнего минимума в (3.11). Пусть конеч-

ное положение схвата (x^T , y^T ) ∈ R зафиксировано. Тогда из формулы (3.2)

найдем две конечные точки (ϕ^T1 , ϕ^T2 ) ∈ Φ(+1), (ϕ^T2 , ϕ^T1 ) ∈ Φ(-1) (3.4), кото-

{

}

рые согласно (3.3) отвечают конфигурациям манипулятора

ϕT1 , ϕ^T

K=+1

{

}

ϕT1 , ϕ^T

соответственно.

K=-1

Введем обозначения:

G₁(1) = {ϕ₁,ϕ₂ ∈ Φ : ϕ₁ ≤ ϕ₂ ≤ Bϕ₁, ϕ₁ > 0} ⊂ Φ⁺¹ ⊂ Φ(1),

G₂(1) = Φ⁺²(ϕ₁,ϕ₂) ⊂ Φ(1),

G₃(1) = {ϕ₁,ϕ₂ ∈ Φ : -ϕ₁ ≤ ϕ₂ ≤ -Aϕ₁, ϕ₁ < 0} ⊂ Φ^-1 ⊂ Φ(1),

(5.1)

{

}

G₄(1) =

ϕ₁,ϕ₂ ∈ Φ : -A^-1ϕ₁ ≤ ϕ₂ ≤ -ϕ₁, ϕ₁ < 0

⊂ Φ^-1 ⊂ Φ(1),

{

}

G₅(1) =

ϕ₁,ϕ₂ ∈ Φ : B^-1ϕ₁ ≤ ϕ₂ ≤ -A^-1ϕ₁, ϕ₁ < 0

⊂ Φ^-1 ⊂ Φ(1),

{

}

G₆(1) =

ϕ₁,ϕ₂ ∈ Φ : ϕ₁ ≤ ϕ₂ ≤ B^-1ϕ₁, ϕ₁ < 0

⊂ Φ^-1 ⊂ Φ(1).

Поскольку области Φ(1), Φ(-1) взаимно симметричны относительно

прямой ϕ₂ = ϕ₁, то при замене ϕ₁ → ϕ₂, ϕ₂ → ϕ₁ области G_i(1) ⊂ Φ(1),

i = 1,...,6, перейдут на симметричные относительно прямой ϕ₂ = ϕ₁ области

Gi(-1) ⊂ Φ(-1), i = 1, . . . , 6, соответственно (см. рис. 3).

Области G_i(1), i = 1, . . . , 6, находятся над прямой ϕ₂ = ϕ₁, изображенной

на рис. 3 штриховой линией, а области G_i(-1), i = 1, . . . , 6, - под прямой

ϕ₂ = ϕ₁. Таким образом, если (ϕ^T1 ,ϕ^T2 ) ∈ G_i(1), то (ϕ^T2 ,ϕ^T1 ) ∈ G_i(-1). Каждой

из этих точек, в зависимости от их принадлежности областям G_i(1), G_i(-1),

1 ≤ i ≤ 6, отвечает оптимальное время перемещения схвата в эту конфигура-

цию при соответствующем оптимальном режиме управления (4.26):

(



)_1/2

T = T₁(ϕT1 ,ϕT2 ) = 2

(I1 + 1)ϕ^T1 + I₂ϕ^T2/M0

если (ϕ^T1 , ϕ^T2 ) ∈ G_1,3,4,5,6(1),

(

)1/2



T = T₂(ϕT1 ,ϕT2 ) = 2

I2ϕ^T2

если (ϕ^T1 , ϕ^T2 ) ∈ G₂(1),

(5.2)

(



)_1/2

T = T₁(ϕT2 ,ϕT1 ) = 2

(I₁ + 1)ϕ^T2 + I₂ϕ^T1 /M01

если (ϕ^T1 , ϕ^T2 ) ∈ G_1,2,3,4,6(-1),

(

)1/2



T = T₂(ϕT2 ,ϕT1 ) = 2

I₂ϕ^T1

если (ϕ^T2 , ϕ^T1 ) ∈ G₅(-1).

j₂

j₂ = -Aj₁

j₂ = Bj₁

j₂ = -j₁

j₂ = j₁

G₂(1)

G₃(1)

G₁(1)

T₂(j₁, j

)

T₁

G₄(1)

T₁

j₂ = A^-1j

G₁(-1)

j₁

j₂ = B^-1

G₅(1)

-p

G₂(-1)

j₁

T₁(j_T, j_T)

G₃(-1)

G₆(1)

T₁

T₂

G₆(-1)

G₅(-1)

G₄(-1)

-p

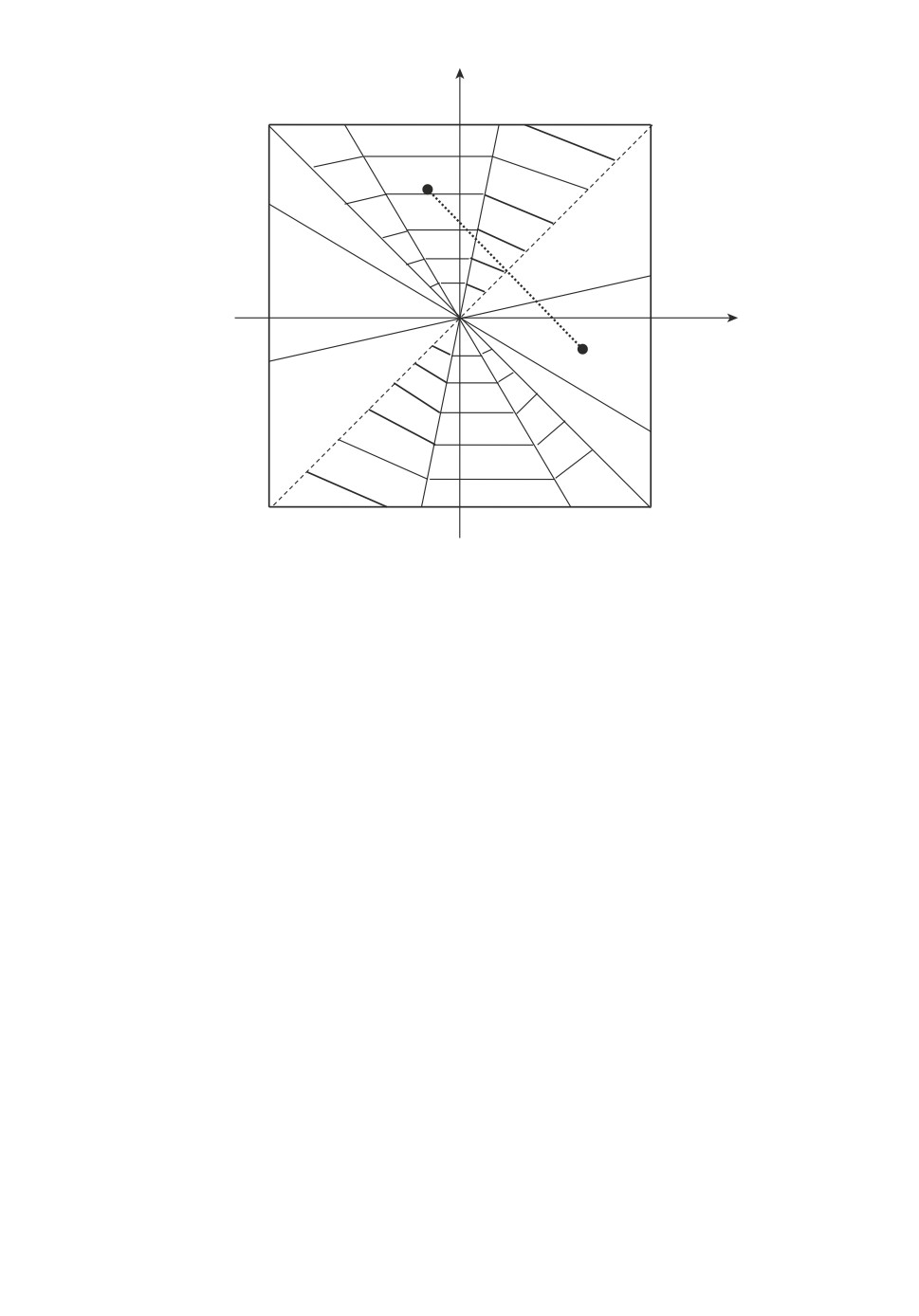
Рис. 3. Диаграмма для определения оптимального типа конечной конфигура-

ции и оптимального типа режима управления.

Учитывая (5.2), вычисление внешнего минимума в (3.11) сводится к вы-

бору оптимальной из двух конечных конфигураций в задаче

[



]



(5.3)

T^∗ = min T(ϕ^T1 ,ϕ^T2 )

_(ϕT

,ϕ^T2 )∈G_i(1) ,T(ϕ2 ,ϕ¹ )

,ϕ^T1 )∈G_i(-1)

1 ≤ i ≤ 6.

Произведя вычисления минимума в (5.3) при числовых значениях (4.25),

в итоге получаем





T₁(ϕ^T1 ,ϕ^T2 ), если (ϕ^T1 ,ϕ^T2 ) ∈ G₁(1) ∪ G₃(1),





T₂(ϕ^T1 ,ϕ^T2 ), если (ϕ^T1 ,ϕ^T2 ) ∈ G₂(1),

(5.4)

T^∗ =



T₂(ϕ^T2 ,ϕ^T1 ), если (ϕ^T2 ,ϕ^T1 ) ∈ G₅(-1),





T₂(ϕ^T2 ,ϕ^T1 ), если (ϕ^T2 ,ϕ^T1 ) ∈ G₄(-1) ∪ G₆(-1).

Расчетные результаты в соответствии с (5.4) представлены на диаграмме

рис. 3, которая позволяет определить оптимальный тип конечной конфигу-

рации и соответствующий оптимальный тип режима управления (4.15), при

помощи которых можно перевести схват манипулятора в заданное конечное

состояние, а также параметры для этого режима из (4.18), (4.19). Тип ко-

нечной конфигурации и режим управления устанавливается в зависимости

от областей, в которых лежат точки (ϕ^T1 , ϕ^T2 ) и (ϕ^T2 , ϕ^T1 ). На рис. 3 области

G_1,2,3(1) и G_4,5,6(-1) заштрихованы.

Приведем числовой пример. Для манипулятора с безразмерными парамет-

рами (4.25) начальные и конечные координаты схвата возьмем в виде

(5.5)

x⁰ = 2, y⁰ = 0, x^T = 1, y^T

= 0,5.

Значениям координат начального и терминального положений схвата (5.5)

соответствуют начальная конфигурация ϕ⁰¹ = ϕ⁰² = 0 и две конечные кон-

фиграции (3.3), которым отвечают две симметричные относительно прямой

ϕ₂ = -ϕ₁ точки на плоскости углов манипулятора (углы даны в радианной

и градусной мерах):

{

}

(5.6)

ϕT1 , ϕ^T

: (ϕ^T1 , ϕ^T2 ) = (-0,514 рад, 1,441 рад) = (-29^◦45^′, 82^◦56^′

K=1

{

}

(5.7)

ϕT1 , ϕ^T

: (ϕ^T2 , ϕ^T1 ) = (1,441 рад, -0,514 рад) = (82^◦56^′, -29^◦45^′

K=-1

Из диаграммы рис. 3 находим, что в рассматриваемом случае (ϕ^T1 , ϕ^T2 ) ∈

∈ G₂(1), a (ϕT2 ,ϕT1 ) ∈ G₂(-1). Следовательно, согласно формуле (5.4) ми-

нимальное время перемещения схвата достигается в точке (5.6), которой

соответствует конечная конфигурация, отвечающая значению K = 1. При

этом следует использовать режим управления M^∗ = (M₁, M^∗2) (4.26), где

M₁ - управление с двумя переключениями в моменты τ⁽¹⁾¹ = 0,0784 (0,1754 c),

τ⁽²⁾¹ = 1,3078 (2,9257 c), M^∗2

с одним переключением в момент τ₂ = 0,6931

(1,5505 c), а оптимальное время перемещения T^∗ = T₂ = 1,3862 (3,1011 c).

В скобках даны размерные значения времен с использованием формул пе-

рехода (4.1). Для сравнения отметим, что если выбрать конечную конфигу-

рацию (5.7), то время перемещения схвата оказывается намного хуже: T^∗ =

= T₁ = 1,8708 (4,1853A).

6. Заключение

На конфигурационной плоскости двузвенного манипулятора со вторым

статически уравновешенным звеном построены области, позволяющие по за-

данным координатам терминального положения схвата манипулятора опре-

делить тип конечной конфиграции и структуру оптимального управления,

приводящего манипулятор в эту конфигурацию, при которых достигается ми-

нимальное значение времени перемещения схвата из начального положения

покоя в произвольное положение покоя рабочей зоны манипулятора. Числен-

ными расчетами установлено, что оптимальный выбор типа конечной конфи-

гурации может приводить к значительному увеличению быстродействия.

СПИСОК ЛИТЕРАТУРЫ

1. Болотник Н.Н., Каплунов А.А. Оптимальные прямолинейные перемещения

груза при помощи двузвенного манипулятора // Изв. АН СССР. Техн. киберн.

1982. № 1. С. 68-74.

2. Болотник Н.Н., Каплунов А.А. Оптимизация управления и конфигураций дву-

звенного манипулятора // Изв. АН СССР. Техн. киберн. 1983. № 4. С. 123-131.

Avetisyan V.V., Bolotnik N.N., Chernousko F.L. Optimal Programmed Motions of a

Two-Link Manipulator // Soviet J. Comput. Syst. Sci. 1985. V. 23. No. 5. P. 65-73.

Akulenko L.D., Bolotnik N.N., Chernousko F.L., Kaplunov A.A. Optimal Control of

Manipulation Robots // IFAC Proc. 1985. V. 17. Iss. 2. P. 311-315.

Chernousko F.L., Akulenko L.D., Bolotnik N.N. Time-Optimal Control for Robotic

Manipulators // Optimal Control Applications and Methods. 1989. V. 10. Iss. 4.

P. 293-311.

Болотник Н.Н., Черноусько Ф.Л. Оптимизация управления манипуляционными

роботами // Изв. АН СССР. Техн. киберн. 1990. № 1. С. 189-238.

Meier E.B., Bryson A.E. Efficient Algorithm for Time-Optimal Control of a Two-

Link Manipulator // J. Guidance, Control and Dynamics. 1990. V. 13. Iss. 5.

P. 859-866.

Chernousko F.L. Optimization in Control of Robots / Computational Optimal Con-

trol. Basel: Birkhause, 1994. P. 19-28.

Аветисян В.В., Овакимян Н.В. Оптимальные плоскопараллельные движения

двузвенного манипулятора // Изв. РАН. Теория и системы управления. 1995.

№ 3. С. 161-168.

10.

Avetisyan V.V., Hovakimyan N.V. Constructing the Regions of Admissible States

of Positioning for a Two-Link Manipulator with Account of Speed Constraints //

J. Comput. Syst. Sci. Int. 1997. V. 36. Iss. 4. P. 638-646.

11.

Аветисян В.В. Оптимизация конфигурации и направлений поворотов звеньев

двузвенного манипулятора по комбинированным критериям качества // Изв.

НАН РА. Механика. 1998. T. 51. № 4. С. 65-71.

12.

Avetisyan V.V. Movements of an Electromechanical Manipulator Robot Optimal

with Respect to Energy Rxpenditure // J. Comput. Syst. Sci. Int. 1996. V. 35.

Iss. 4. P. 679-685.

13.

Demydyuk М.V., Hoshovs’ka N. Parametric Optimization of the Transport Opera-

tions of a Two-Link manipulator // J. Math. Sci. 2019. V. 238. No. 2. P. 174-188.

14.

Овсеевич А.И. О полной управляемости линейных динамических систем //

ПММ. 1989. Т. 53. Вып. 5. С. 845-848.

15.

Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Матема-

тическая теория оптимальных процессов. М.: Наука, 1983.

Статья представлена к публикации членом редколлегии А.А. Галяевым.

Поступила в редакцию 21.05.2020

После доработки 01.08.2020

Принята к публикации 10.09.2020