Автоматика и телемеханика, № 2, 2021

(ОАО “Бортовые аэронавигационные системы”, Москва),

А.М. БРОННИКОВ, д-р техн. наук (bronnikov_a_m@mail.ru)

(Московский государственный технический университет им. Н.Э. Баумана),

И.Ф. ГАМАЮНОВ, канд. техн. наук (ilyagama@gmail.com)

(ВУНЦ ВВС “Военно-воздушная академия

им. проф. Н.Е. Жуковского и Ю.А. Гагарина”, Воронеж)

АНАЛИТИЧЕСКОЕ КОНФИГУРИРОВАНИЕ ИЗБЫТОЧНОЙ

СИСТЕМЫ С УПРАВЛЕНИЕМ ПО РАССОГЛАСОВАНИЮ

Развивается аналитический подход к управлению избыточностью тех-

нических систем на фоне осуществления в системе управления по рас-

согласованию. Новые результаты приводятся в сопоставлении с полу-

ченными ранее основными положениями подхода для случая внешнего

воздействия на избыточную систему. Получены условия допустимости и

формулы альтернативных конфигураций в двух вариантах: как только

достаточный и как необходимый и достаточный. Методические примеры

иллюстрируют применение полученных решений.

Ключевые слова: избыточная система, управление избыточностью, кон-

фигурация системы, допустимая конфигурация, передаточная матрица,

целевая функция, канонизация матриц.

DOI: 10.31857/S0005231021020021

1. Введение

Под конфигурацией избыточного оборудования понимается способ или схе-

ма выборочного соединения компонентов оборудования с целью достижения

заданной цели функционирования [1-5]. Чаще всего перестройке подверга-

ется вычислительная система [6-9], коммуникационная система [10-12] или

несколько систем сразу [13-15].

Одним из наиболее распространенных технических приложений использо-

вания избыточности является синтез отказоустойчивых систем управления,

для которых в случае отказа или повреждения одного из каналов управления

или передачи информации можно перераспределять его функции по остав-

шимся исправным каналам [11, 15].

Авторам не известны работы с постановкой и решением задачи, анало-

гичными рассматриваемой в статье. Так, например, в [15] решается задача

обеспечения неизменности управляющего воздействия на систему за счет ре-

конфигурации регулятора при возникновении отказа органов управления и

не затрагивается задача обеспечения неизменности передаточной матрицы по

рассогласованию. От других работ в области стабилизации свойств линейных

систем за счет управления избыточностью данную статью отличает, прежде

всего, представление традиционного регулятора в цепи обратной связи в ви-

де произведения интерфейсных и интеграционных матриц, что, по мнению

авторов, наиболее соответствует практическим нуждам. Новизной статьи от-

носительно предыдущих работ авторов является использование в качестве

целевой функции передаточной матрицы по рассогласованию.

Аналитический подход к управлению избыточностью оборудования с ли-

нейными стационарными моделями и названный здесь конфигурированием,

охватывает такие вопросы, как:

тестирование альтернативных конфигураций на их допустимость в смыс-

ле наличия возможности достижения целей функционирования системы в

соответствующей конфигурации,

интеграция избыточных компонентов в систему с едиными целями функ-

ционирования в смысле определения настроек системы (в основном алгорит-

мов ее вычислительных средств), обеспечивающих достижение этих целей

при выбранной допустимой конфигурации.

Данная статья нацелена на лаконичное изложение некоторых результа-

тов направления применительно к системам, подверженным внешним воз-

действиям, а также на получение аналогичных результатов для систем с так

называемым управлением по рассогласованию.

2. Исходные положения

Формальным объектом задачи конфигурирования (управления избыточ-

ностью) системы, подвергающейся внешнему воздействию [16, 17], являет-

ся линейная динамическая система, состоящая из объекта управления и из-

быточных в общем случае динамических компонентов комплекса оборудова-

ния (КО), вместе в линейном приближении описываемых уравнением с дис-

кретным временем τ = 1, 2, . . .

(1)

x_τ+1 = Ax_τ + Bu_τ + Gv_τ , x_τ=0 = x₀, y_τ = Dx_τ ,

а также избыточной бортовой интегрированной вычислительной среды,

функционирование которой в линейном приближении описывается форму-

лой

(2)

u_τ = Q(z)y_τ .

Здесь x_τ - метавектор (составной вектор) состояния объекта и компонентов

размерности n на такте τ с известными начальными условиями x₀, u_τ - ме-

тавектор входов компонентов для межкомпонентных связей размерности l,

v_τ - метавектор входов компонентов для внешних воздействий размерности k,

y_τ - метавектор выходов всех компонентов размерности m, A - блочная чис-

ловая матрица собственной динамики объекта и компонентов размеров n × n,

B - блочная числовая матрица эффективности межкомпонентных связей раз-

меров n × l, G - блочная числовая матрица эффективности внешних воздей-

ствий размеров n × k, D - блочная числовая матрица формирования выходов

всех компонентов размеров m × n, z - оператор сдвига во времени на один

такт вперед [18, 19], Q(z) - передаточная матрица размеров l × m (по опера-

тору z) от метавектора выходов компонентов y_τ к метавектору их входов для

межкомпонентных связей u_τ , названная конфигурационной матрицей [16].

В настоящей статье основное внимание сосредоточено на системах с управ-

лением по рассогласованию выходов, в линейном приближении описываемых

уравнением и равенствами с дискретным временем τ = 1, 2, . . .

(3)

x_τ+1 = Ax_τ +Bu_τ +Gv_τ , x_τ=0 = x₀, y_τ = Dx_τ , u_τ = Q(z)(y^задτ -y_τ

где y^задτ - метавектор заданных значений выходов системы.

В задаче управления избыточностью линейной системы числовые матрицы

A, B, G и D в (1) и (3) полагаются фиксированными. Их значения опреде-

ляют динамические свойства как объекта, так и всех (используемых и неис-

пользуемых в текущий момент времени) располагаемых компонентов КО в

разрозненном состоянии.

Конфигурационная матрица Q(z) в (2) и (3) через размещение ненулевых

элементов (соответствует коммутированию входов и выходов соответствую-

щих компонентов) объединяет компоненты КО и объект в единую систему.

Посредством же конкретных значений ненулевых элементов она определя-

ет правила обработки данных вычислительными средствами. Таким образом

осуществляется подчинение функционирования системы (1), (2) или (3) об-

щим целям и удовлетворение предъявляемых требований.

Именно значения конфигурационной матрицы Q(z), а точнее, закономер-

ности возникновения и изменения множества ее в некотором смысле эквива-

лентных значений {Q(z)}_κ, где κ - совокупное обозначение параметров, ва-

рьирование которых порождает это множество, являются предметом поиска,

исследования и практического использования в задаче управления избыточ-

ностью технической системы.

3. Передаточные матрицы системы

В развиваемом подходе требования к динамическим свойствам избыточ-

ной системы связываются со значениями передаточных матриц для вынуж-

денных составляющих:

замкнутой системы (1), (2) от внешних воздействий v_τ к выходам y_τ

[

]

(4)

(z)

= D(zI_n - A - BQ(z)D)^-1

W^vy(z) = wvi.τy_j.τ

m×k

где wvi.τy_j.τ (z) - передаточная функция от i-го входа vi.τ к j-му выходу yj.τ , In -

единичная матрица размеров n × n;

замкнутой системы (3) от заданных значений y^задτ к выходам y_τ

[

]

(5)

Wyзадy(z) = wyj.τ

(z)

= D(zI_n - A + BQ(z)D)^-1

BQ(z).

m×m

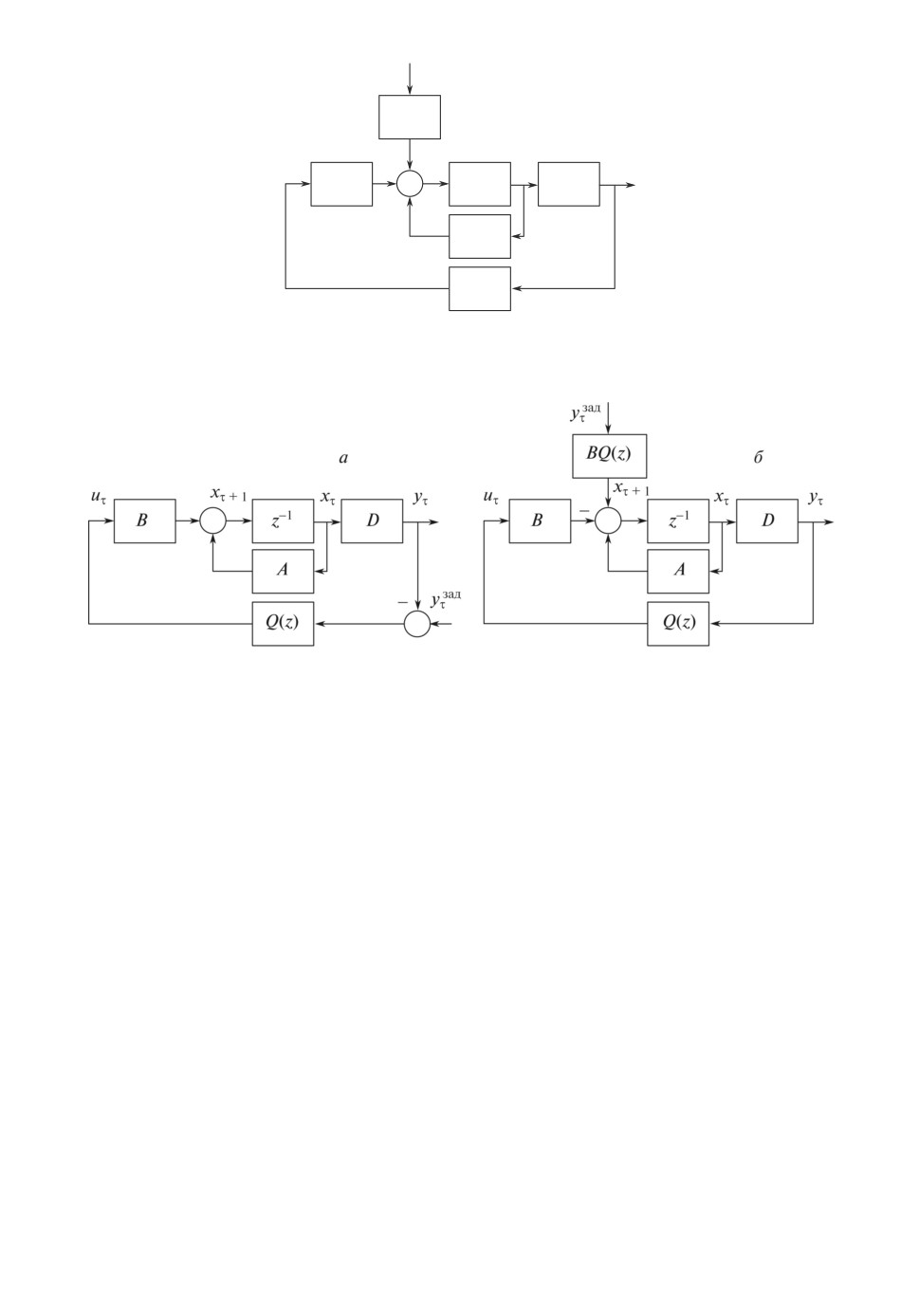
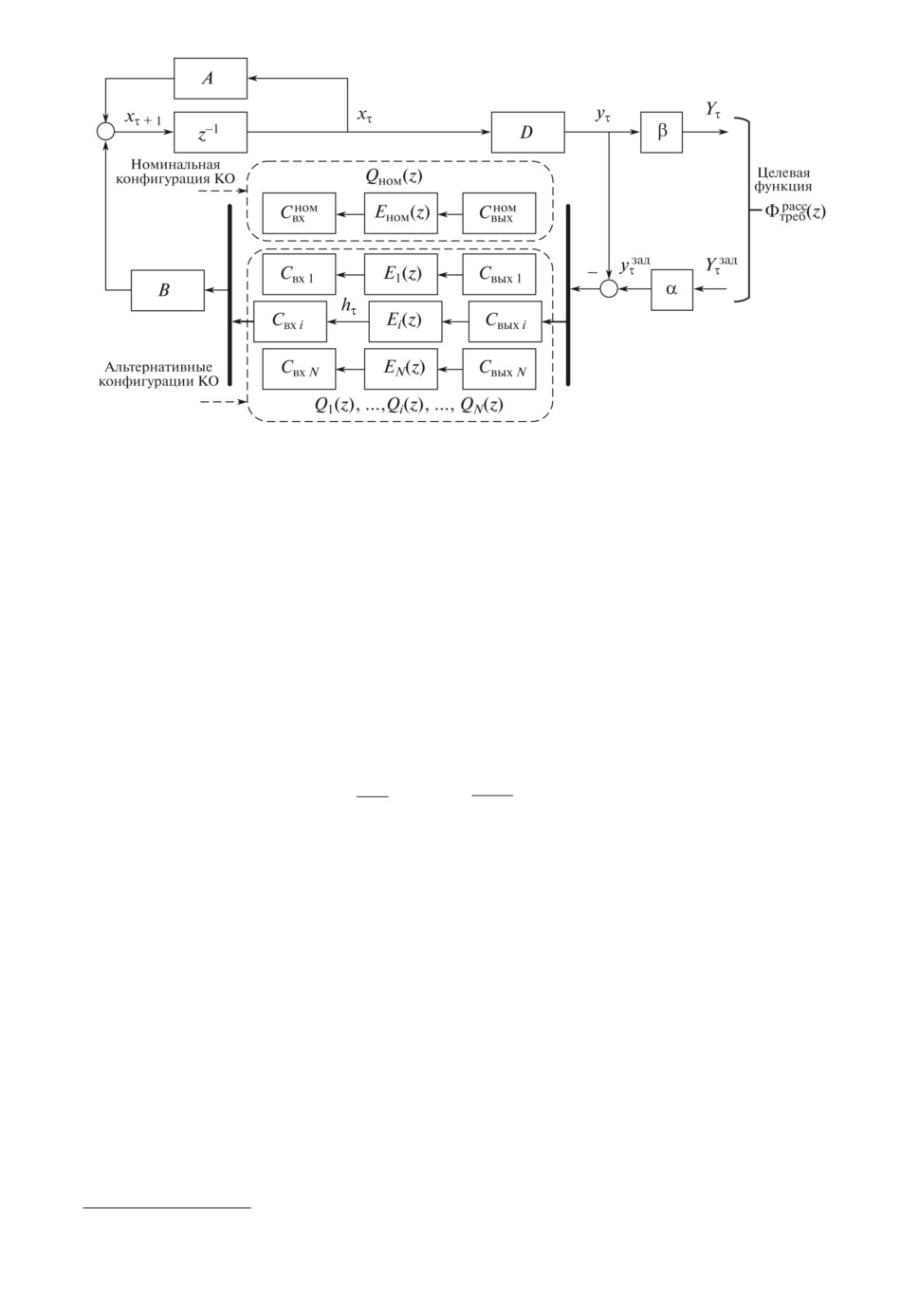
Рисунки 1 и 2 иллюстрируют структуры моделей, соответствующих пе-

редаточным матрицам (4) и (5). В зависимости от конкретных условий рас-

сматривается одна из этих передаточных матриц или они рассматриваются

совместно.

v_t

x_{t + 1}

u_t

x_t

y_t

z^-1

Q(z)

Рис. 1. Структура системы “объект + КО” с внешним воздействием.

Рис. 2. Структуры системы “объект + КО” с управлением по рассогласованию

выходов: а исходная, б преобразованная к виду рис. 1.

Принципиальное различие моделей (4) и (5), определяющее структуры

матричных конструкций в основе решения задачи управления избыточно-

стью, заключается в том, что варьируемая конфигурационная матрица Q(z)

находится либо только в цепи обратной связи (рис. 1) от воздействия v_τ до

выхода системы y_τ , либо присутствует также и в цепи прямой связи (рис. 2)

от y^задτ до y_τ .

4. Формулировка задачи и номинальная конфигурация

Для линейной динамической системы, описываемой передаточными мат-

рицами (4) или (5), вводится понятие целевой функции [17], отражающей

применение системы по назначению. В качестве такой функции для случая

внешних воздействий используются выборочные строки и столбцы переда-

точной матрицы (4) в соответствии с весовыми матрицами α размеров k × g

и β размеров f × m:

(6)

Φ^возд(z) = βW^vy(z)α = βD(zI_n - A - BQ(z)D)^-1

Gα.

В задаче управления по рассогласованию выходов используются выбороч-

ные строки и столбцы передаточной матрицы (5) с весовыми матрицами α

размеров m × g и β размеров f × m:

Φ^расс(z) = βWyзадy(z)α = βD(zIn - A + BQ(z)D)^-1

(7)

BQ(z)α.

Традиционная задача определения обратных связей (в общем случае речь

должна идти о множестве¹ эквивалентных матриц Q(z)), обеспечивающих

требуемое значение Φ^{воздтреб}(z) целевой функции для случая внешнего воздей-

ствия, заключается в разрешении уравнения (6), или значение Φ^{расстреб}(z) - для

случая управления по рассогласованию выходов, связанное с решением урав-

нения (7). Это кратко можно записать диаграммой

Решение (6) или (7)

Φ_треб(z)

=⇒

{Q(z)}_κ.

При постановке задачи о конфигурировании (управлении избыточностью)

КО осуществляется расчленение этой диаграммы на два этапа. Первый из них

заключается в определении любого одного решения Q^{воздном}(z) для уравнения

(8)

Φ^{воздтреб}(z) = βD(zI_n - A - BQ^{воздном}(z)D)^-1

Gα

или Q^номс(z) для уравнения

(9)

Φ^{расстреб}(z) = βD(zI_n - A + BQ^{рассном}(z)D)^-1BQ^{рассном}

(z)α,

названного номинальной конфигурацией КО и устраивающего разработчика.

Для решения таких задач разработан широкий арсенал подходов и мето-

дов, использующих как строгие положения теорий управления и оптимиза-

ции [20-23], так и инженерные приемы и методики, основанные на опыте,

переносе отработанных на прототипах решений и пр. [24]. Примем, что как

минимум по одному решению Q^{воздном}(z) для (8) и Q^номс(z) для (9) существуют.

Второй этап сосредоточен только на порождении множества решений, эк-

вивалентных номинальному в смысле неизменности значения целевой функ-

ции Φ^{воздтреб}(z) или Φ^{расстреб}(z), что записывается диаграммой

Решение (8) или (9)

(10)

Φ_треб(z)

=⇒

Q_ном

=⇒

{Q(z)}_κ

}

Этап 1

Этап 2

Считается, что первый этап выполняется предварительно, и далее все вни-

мание сосредотачивается только на втором этапе. При этом существование

конфигураций Q^возд(z) и Q^расс(z), отличных от номинальных, пока остается

открытым вопросом.

¹ В подавляющем большинстве применений различных подходов либо единственность

решения обеспечивается “излишними” условиями (например, процедуры типа метода наи-

меньших квадратов обеспечивают минимальность квадратичной нормы результата, что с

содержательной стороны не всегда имеет внятное обоснование), либо разработчик не по-

дозревает о существовании других эквивалентных решений поставленной задачи.

5. Формализация и допустимость конфигурации

Исследования показали, что решение уравнений (6) или (7) дает значения

матриц Q(z) с заполненными (не нулевыми) практически всеми их элемента-

ми, что противоречит физическому содержанию задачи, поскольку какая-то

(порой значительная) часть этих элементов должна принимать заведомо ну-

левые значения. Это отражает (формализует) управляемое отключение неко-

торых компонентов комплекса в реализуемой конфигурации системы.

Удачным разрешением указанной ситуации стало [16, 17] представление

конфигурационных матриц в виде произведения

(11)

Q(z) = C_вхE(z)C_вых,

где C_вх и C_вых - распределительные матрицы размеров l × p и q × m, т.е.

матрицы, содержащие бинарные элементы и не более одного единичного эле-

мента в строке, названные интерфейсными матрицами [17], поскольку без

учета задержек моделируют функционирование входных и выходных интер-

фейсов всех компонентов и каналов связи между ними за исключением объек-

та, E(z) - в общем случае рациональная полиномиальная матрица размеров

p × q, моделирующая обработку вычислительными средствами всех посту-

пающих данных и задержек в интерфейсных устройствах и каналах связи,

названная интеграционной матрицей [17].

В выборе интерфейсных матриц C_вх и C_вых, осуществляемом преимуще-

ственно на основе инженерных доводов, заключается процесс конфигуриро-

вания избыточной системы, а определение интеграционной матрицы E(z) пу-

тем решения специальных матричных уравнений составляет процесс интегра-

ции избыточной системы.

Задача конфигурирования избыточной системы, подвергающейся внеш-

нему воздействию v_τ , базирующаяся на уравнении (6) с заданным значени-

ем целевой функции (8), решена ранее. В [25] изложены формальные усло-

вия допустимости возможных конфигураций, задаваемых выбором C_вх и

C_вых, в [26] - решение основного уравнения интеграции для множества ин-

теграционных матриц {E(z)}_κ, соответствующих допустимым конфигураци-

ям и заданной целевой функции, а в [27] - общая методика решения таких

задач.

Далее рассматривается только задача конфигурирования избыточной си-

стемы с управлением по рассогласованию выходов y^задτ - y_τ , связанная с ре-

шением уравнения (7) и заданным значением целевой функции (9).

Как и ранее в задаче с внешним воздействием [25, 26], конфигурацию Q(z)

будем считать допустимой, если при выбранных матрицах C_вх и C_вых в систе-

ме (7) существует возможность (существует соответствующая E(z)) сохране-

ния неизменным значение целевой функции

Φ^{расстреб}(z),

зафиксированное весовыми функциями α, β и номинальной конфигураци-

ей КО Q_ном(z) в соответствии с (9).

6. Управление по рассогласованию

Задача заключается в том, чтобы для целевой функции системы (9) опре-

делить допустимость заданных интерфейсных матриц C_вх, C_вых и при их

допустимости найти множество таких интеграционных матриц E(z), при ко-

торых значение целевой функции Φ^{расстреб}(z) остается неизменным:

βD(zI_n - A + BC_вхE(z)C_выхD)^-1BC_вхE(z)C_выхα = Φ^{расстреб}

(12)

(z).

Уравнение (12) относительно неизвестной матрицы E(z) является основным

уравнением интеграции избыточной системы при управлении по рассогласо-

ванию выходов.

Далее используются обозначения канонизации [20] произвольной матри-

цы S ранга r: S^L и S^R - левый и правый делители нуля максимального ранга,

S^∼L, S^∼R и S^∼ - левый, правый и сводный канонизаторы, удовлетворяющие

тождествам

S^LS = 0, SS^R = 0, S^∼RS^∼L = S^∼ и S^∼LSS^∼R = I_r.

Неединственность указанных матричных образований позволяет отбирать

среди множества альтернатив упрощенные решения (с нулевыми и единич-

ными значениями элементов) для ускорения вычислений и обеспечения на-

глядности примеров [26].

Решение задачи сформулировано в виде двух теорем.

Теорема 1. Достаточным условием существования интеграционных

матриц E(z), обеспечивающих выполнение равенства (12) при заданных ин-

терфейсных матрицах C_вх и [вых, яв]ляется одновременное выполнение двух

условий с блочной матрицей

D α

(13)

BC_вхLBQ^{рассном}(z)[ D α]

= 0,

[

]

[

(14)

BQ^{рассном}(z)

D α

C_вых

D α

= 0,

при этом множество интеграционных матриц E_µ,η(z) описывается форму-

лой

[

](

[

])_∼

{E(z)}_µ,η = (BC_вх)^∼BQ^{рассном}(z)

D α

C_вых

D α

}

Базовое решение

(15)

[

+ BC_вхRµ

+ηC_вых

D α

}

Вариация

Вариация строк

столбцов

где µ и η - произвольные матрицы подходящих размеров, выбор которых

ограничен условием

(16)

det (zI_n - A + BC_вхE_µ,η(z)C_вых

D) = 0.

Только достаточность теоремы 1 обусловлена удовлетворением требования

неизменности раздельно для знаменателя и числителя матричной дроби (12),

что исключает учет возможной компенсации их вариаций и тем самым значи-

тельно сужает множество получаемых решений. Вместе с тем теорема 1 обла-

дает двумя важными достоинствами: относительной вычислительной просто-

той и возможностью получения заведомо физически реализуемых решений,

т.е. решений в виде матриц E(z), степень полиномов числителей которых не

превышает степень полинома знаменателя.

Исчерпывающее же решение задачи дает следующая теорема.

Теорема 2. Необходимым и достаточным условием существования ин-

теграционных матриц E(z), обеспечивающих выполнение равенства (12)

при заданных интерфейсных матрицах C_вх и C_вых, является одновременное

выполнение двух условий разрешимости основного уравнения интеграции

(17)

ℵ(z)

^LBC_вхL (zI_n - A)(βD)^∼Φ^{расстреб}

(z) = 0,

(18)

δ_ξ(z)C_вых (α - Dδ_ξ(z))

и условия существования передаточной матрицы замкнутой системы

(19)

det (zI_n - A + BC_вхE_ξ,ϑ,ψ(z)C_вых

D) = 0,

где

(20)

ℵ(z) = BC_вхL (zI_n - A) βD^R,

матрица δ_ξ(z) принадлежит множеству, вычисляемому по формулам

(21)

{δ(z)}_ξ = (βD)^∼Φ^{расстреб}(z) + βD^Rρ_ξ

(z),

(22)

{ρ(z)}_ξ = -(ℵ(z))^∼BC^L(zI_n - A)(βD)^∼Φ^{расстреб}(z) +

ℵ(z)

^Rξ

| {z

}

Вариация базового

решения на 2-м ярусе

ξ - матрица подходящих размеров с почти произвольными элементами,

обеспечивающими выполнение условий (18) и (19), при этом все множество

интеграционных матриц E_ξ,ϑ,ψ(z) описывается формулой

{E(z)}_ξ,ϑ,ψ = (BC_вх)^∼ (zI_n - A) δ_ξ(z)(C_вых (α - Dδ_ξ(z)))^∼

}

Базовое решение

(23)

+ BC_вхRϑ

+ψ Cвых (α - Dδ_ξ(z))

}

Вариация стролбцов

Вариация строк

на 1-м ярусе

где ϑ и ψ - удовлетворяющие условию² (19) произвольные матрицы подхо-

дящих размеров.

² Строго говоря, условия (15) и (19) могут нарушаться в конечном числе значений z,

называемых полюсами соответствующих передаточных функций.

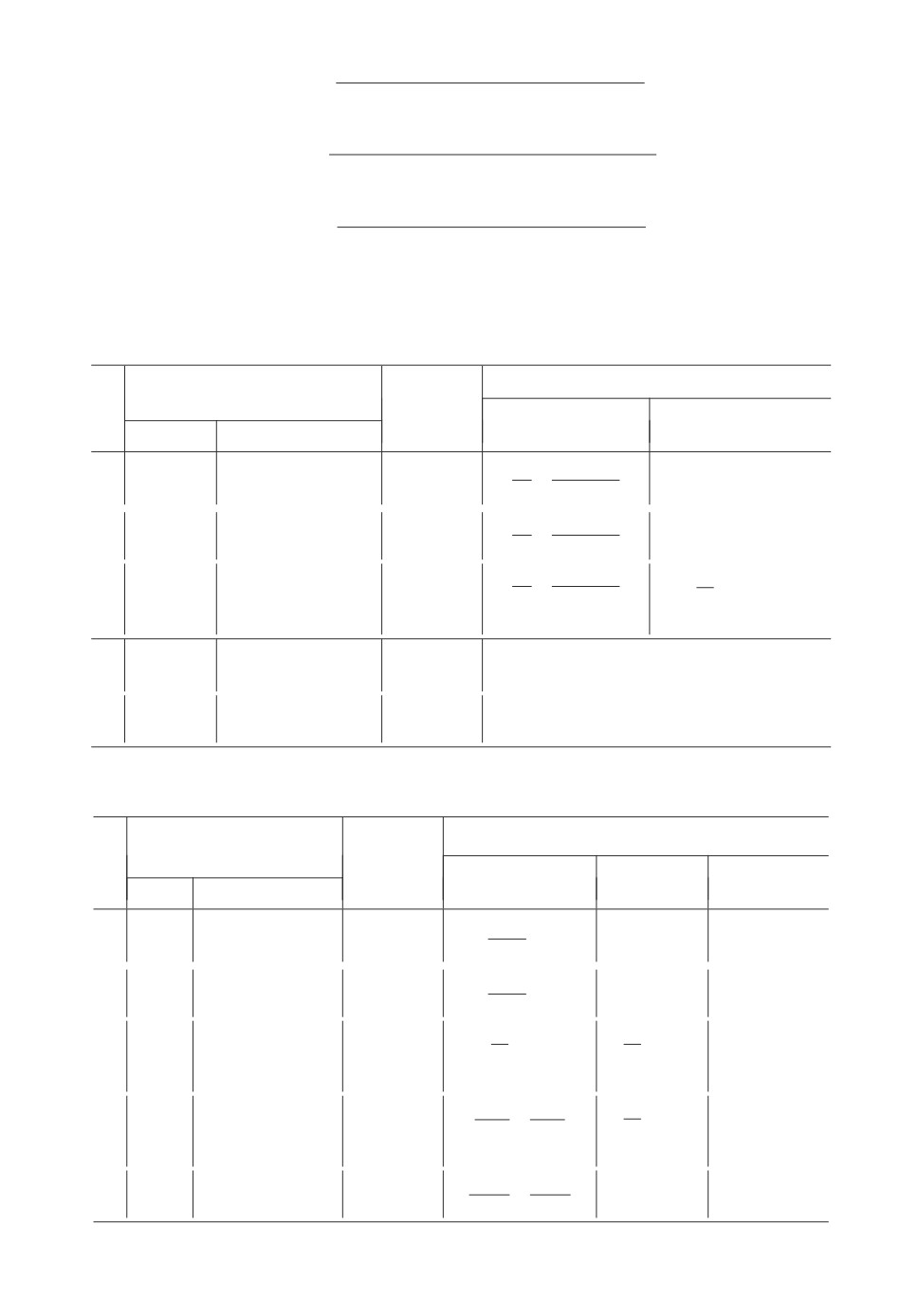
Рис. 3. Общая структура системы “объект + избыточный КО”.

Теорема 2 отличается от теоремы 1 существенно большей сложностью,

связанной с количеством процедур канонизации и “двухъярусностью” варьи-

рования решения: первого путем выбора матриц ϑ и ψ в формуле (23) с про-

веркой условия (19) и второго путем выбора матрицы ξ в формуле (22) с

проверкой условий (18), (19). При этом условие (17) по аналогии с результа-

тами [26] является автономным в том смысле, что не зависит от варьируемых

матриц.

Трудность использования теоремы 2 связана с неявным ограничением вы-

бора матрицы ξ в формуле (22) условиями (18) и (19) через формулу (21).

Способ прямого удовлетворения таких ограничений не найден, но в частных

весьма распространенных случаях при выполнении любого из двух равенств

(24)

βD^R = 0, ℵ(z)^R

матрица δ_ξ(z) принимает единственное значение, а условия (18) и (19) не

зависят от выбора ξ.

Доказательства теорем приведены в Приложении.

Обобщающая иллюстрация решенной задачи показана на рис. 3, где жир-

ными элементами условно показаны коммутационные средства, осуществ-

ляющие подключение эквивалентных по целевой функции номинальной или

одной из N альтернативных конфигураций.

Содержательное объяснение условий (24) сводится к следующему. Вве-

денная в (20) матрица ℵ(z) является фактором связности³ для динамической

системы

(25)

F^hY(z) = βD(zI_n - A)^-1BC_вх,

представляющей собой часть системы (12) от p-мерного выхода h_τ всех вы-

числительных средств КО к тестовым выходам Y_τ при оборванных связях

³ В [20] использован термин “матрица связности”, который здесь корректируется.

КО: E(z) = 0. Согласно теореме 2.4 и определению 2.6 из [20] любое из усло-

вий (24) соответствует отсутствию в системе (25) линейной зависимости вхо-

дов, обусловленной только ее внутренней связностью, т.е. без учета внешней

связности, формализуемой делителем нуля BC_вхR и учитываемой явно в (23).

На рис. 3 показано положение вектора h_τ , относящегося к определению функ-

ции (25).

7. Примеры

Управление самолетом. Пример из [25] с упрощенной моделью продольно-

го движения самолета преобразуем к задаче управления по рассогласованию

выходов (7). Соответствующие матрицы имеют значения:













a₁

a₂









A= a₃ a₄

,B= b1

b₂

,D=



,





a₂

−1 0 1

























α=



,

β^T =













Номинальная конфигурация задана следующими значениями матриц:

[

]

[

]

C^номвх =

C^номвых =





[

]

a₃

a₄ - a_ж

a₃

a₄ - a_ж

,

E_ном(z) =

Q_ном = b₁

b₁

Φ^{расстреб}(z) =a3

z-a_ж

В рамках примера для различных вариантов конфигураций выполнены

вычисления в соответствии теоремами 1 и 2 с привлечением программы

MatLab. Полученные результаты с целью проверки подставлялись в (12). Вы-

борочно результаты вариантов (вариант 0 - номинальный) сведены в табл. 1

и 2, где выполнение условий теорем отмечено символами: “+” выполняется,

“-”

не выполняется.

В табл. 2 введены дополнительные обозначения функций:

a₃ ((z - a₁) (z - a₄) - a₂a₃)

a₃(z - a₁)

(26)

q(z) =

p(z) = -

(z - a₁) (z - a_ж) - a₂a₃

(z - a₁)(z - a_ж) - a₂a₃

a₃ (z - 1)((z - a₁)(z - a₄) - a₂a₃)

r(z) =

(z - 1) ((z - a₁)(z - a_ж) - a₂a₃) - a₂a₃ (z - a₁)

(z - 1) ((z - a₁)(z - a_ж) - a₂a₃)

t(z) =

a₂a₃(z - a₁)

a₃ (z - 1)((z + a₁)(z - a₄) + a₂a₃)

f (z) =

(z - a₁) ((z + 1)(z - a_ж) + a₂a₃)

(z - 1) ((z - a₁)(z - a_ж) - a₂a₃)

s(z) =

a₂a₃(a₁ - 1)

Для варианта 1 далее приводятся некоторые детали вычислений.

Таблица 1. Генерирование альтернативных конфигураций по теореме 1

Условия

Решение по формуле (15)

Конфигурация

№

существ.

Базовое

Вариация

(13), (14)

решение

столбцов

C_вх

C_вых

[

]

[

]

[

]

a₄ - a_ж

b₁

[

]

[

]

[

]

a₄ - a_ж

b₂





]

[

]

[

]

[ a₃

a₄ - a_ж

b₂

b₁

 -b1

[ µ1 µ2 ]

[

]

[

]

Нет решения

[

]

[

]

Таблица 2. Генерирование альтернативных конфигураций по теореме 2

Условия

Решение по формуле (23)

Конфигурация

№

существ.

Базовое

Вариация Вариация

C_вх

C_вых

(17)-(19)

решение

столбцов

строк

[

] [

]

[

]

q (z)

+ + +

ψ[ p(z)

1 ]

b₁

[

] [

]

[

]

q (z)

+ + +

ψ[ p(z)

1 ]

b₂









[

][

]

b₂

[

]

ψ₁

-

+ + +

b₁[ϑ1 ϑ2]

[ p(z) 1]

ψ₂



 



[

][

]

r(z)

b₂

[

]

ψ₁

+ + +

 -

[ϑ₁ ϑ₂]

[ 1 t(z)]

 b₁

b₁

ψ₂

[

] [

]

[

]

f (z) f (z)

+ + +

ψ[ 1

s(z) ]

b₁

Вычисления по теореме 1 (табл. 1). Предварительные расчеты:





BC_вх = b₂

,

BC_вхR = 0,

[

]

[

]

BC^L =

(BC)^∼ =

b₂

[

]

[

]

[

C_вых

D α

C_вых

D α

]^L = 0,





(

[

])



C_вых

D α

^∼ =01

.

Условие (13) выполняется:











[

]

a₃

a₄ - a_ж









 b1 b2

 b1

b₁





= 0.





}

−1 0 1 0

BCвхL

Qном

}

[

]

D α

Условие (14) также выполняется:















a₃

a₄ - a_ж













 b1 b2

 b1

b₁









= 0.





−1

}

−1 0 1 0

}

Qном

}

[

]

Cвых

D α

^[ D α

Решение по формуле (15) единственное:





]

[

]

[ a₃

a₄ - a_ж

(27) E(z) =

 b1 b2



b₁

b₂

}

(BCвх)^∼

Qном





















[









+BC_вх

µ+η C_вых

D α

| {z }





}

−1 0 1 0

}

(

]

Cвых

^[ D α])∼

^[ D α

[

]

a₃

a₄ - a_ж

b₂

Вычисления подтверждают выполнение (16) у вариантов 1 и 2. Следователь-

но, конфигурация строки 1 в табл. 1 является допустимой. Проверка под-

тверждает совпадение Φ^расс(z) и Φ^{расстреб}(z). У вариантов 3 и 4 условие (14) не

выполняется, из чего следует, что конфигурации недопустимы.

Вычисления по теореме 2 (табл. 2). Предварительные расчеты:





[

]

βD =

βD^R =  0 0

,





[

]

z-a₁

(βD)^∼ =  1

,ℵ(z)=

z-1

Фактор связности ℵ(z) обратим, и его оба делителя нуля равны нулю. Усло-

вие (17) выполняется, а вычисления по формуле (22) дают единственное зна-

чение











[

]

z-a₁

a₂





a₃

−a₁



1



ρ(z) =

 z



a₃

z-a₄

z-a_ж

a₂

z-1

| {z

}

z-1

}| {z }

}

Φ^{расстреб}(z)

BCвх

∼

(zIn−A)

(βD)

ℵ^∼= ℵ^-1





a₂a



(z - a₁)(z - a_ж)









a₂a₃

.

(z - 1)(z - a_ж)

Матрица δ_ξ(z) имеет единственное значение





a₂a













a₂a₃



(z - a₁)(z - a_ж)







a₃



(z - a₁)(z - a_ж)





a₃













δ(z) = 1

+ 0 0



a₂a₃





,

z-a_ж

| {z

}









| {z }

расс

}

(z - 1)(z - a_ж)

a₂a₃

(z)

треб

}

(βD)^∼

βD^R

(z - 1)(z - a_ж)

ρ(z)

и, соответственно, матричное выражение, результаты повторной канонизации

которого используются в (20) и (23), принимает тоже единственное значение











a₂a₃



















(z - a₁)(z - a_ж)







[

]

































-



















z-a_ж







}









a₂a₃



Cвых



−1 0 1



| {z }

}

(z - 1)(z - a_ж)



}

δ(z)





(z - a₁)(z - a_ж) - a₂a





(z - a₁)(z - a_ж)







.

a₃

z-a_ж

Канонизация этой матрицы дает:

[

]

(z - a₁)(z - a_ж) - a₂a₃

C_вых (α - Dδ_ξ(z))L =

a₃(z - a₁)

C_вых (α - Dδ_ξ(z))R = 0,

[

]

(z - a₁) (z - a_ж)

(C_вых (α - Dδ_ξ(z)))^∼ =

(z - a₁) (z - a_ж) - a₂a₃

Условие (18) выполняется. Вычисления по формуле (23) в итоге дают мно-

жество решений

[

]

q(z)

[

]

(28)

{E(z)}_ψ =

+ψ

p(z)

b₂

}

Вариация

Базовое решение

строк

где функции q(z) и p(z) принимают значения (26), ψ - произвольное чис-

ло или выражение такие, что выполняется условие (19). Соответствующее

ограничение имеет вид неравенства

a₂ (a₃b₁ - b₂q(z)) - b₁ (z - a₁) (z - a₄)

ψ(z) =

b₁b₂ ((z - a₁) + a₂p(z))

При любых других значениях этой функции условие (19) выполняется, и

конфигурация допустима. Вычисления показывают совпадение Φ^расс(z) и

Φ^{расстреб}(z) у вариантов 1-4.

Множество решений (28) содержит физически реализуемые и не реализуе-

мые элементы, что связано с выбором варьируемого параметра ψ.

Среди решений {E(z)}_ψ присутствует и решение (27), полученное ранее

по теореме 1, в чем можно убедиться, используя в (28) значение параметра

a₄ - a_ж

ψ=

b₁

Пример подтверждает справедливость утверждений теорем 1 и 2, а табл. 1

и 2 демонстрируют более широкие возможности применения теоремы 2.

Методический пример⁴. Рассмотрим следующие матрицы

[

]

[

]

B=D=β=I₂, α=

⁴ Пример подсказан рецензентом статьи.

Таблица 3. Альтернативные конфигурации в методическом примере

Условия

Решение по формуле (23)

№

Конфигурация существ.

Базовое

Вариация

C_вх

C_вых

(17)-(19) решение

столбцов

строк

[

]

[

]

[

]

[

]

-z

ψ₁

+ + +

[ 1z ]

ψ₂

[

]

[

]

[

]

[

]

[

]

-z

ψ₁

+ + +

[ ϑ₁ ϑ₂ ]

[ 1z ]

ψ₂

Значения E(z), не являющиеся решениями

[

]

[

]

[

]

[

]

[

]

-z

ψ₁

+ + -

[ ϑ₁ ϑ₂ ]

[ 1z ]

ψ₂

Пусть задана номинальная конфигурация









z³

z²

z³

z²









Q^{рассном}(z) = I₂



-z2 + 1 z2 + 1



I₂



z² + 1

,

|{z}

C^номвх

C^номвых

}

Eном(z)

[

]_T

Φ^{расстреб}(z) =

Варианты трех конфигураций приведены в табл. 3, где вариант 0 соот-

ветствует номинальной конфигурации при выборе ψ₁(z) = -zz2+1^,ψ2^=0.

Вариант 2 сформирован заведомо неработоспособным, поскольку в (12) для

него имеет место равенство C_выхα = 0.

Применим теорему 2 для варианта 2. Условия (17), (18) выполнены:

[

]

[

]

ℵ(z) = BC_вхL(zI₂ - A) βD^R

zI₂

= 0,

|{z}

[

]

ℵ(z)

^LBC_вхL (zI₂ - A) (βD)^∼Φ^{расстреб}(z) = 1[ 0

zI₂I₂

= 0,

δ(z) = (βD)^∼Φ^{расстреб}(z) = Φ^{расстреб}(z),

[

]

-z

C_вых (α - Dδ_ξ(z)) =

C_вых (α - Dδ_ξ(z))R = 0.

Однако условие (19) не выполняется, в чем можно убедиться следующими

вычислениями:

[

]

[

]

(BC_вх)^∼L =

(BC_вх)^∼R =

[

]

][

]

(BC_вх)^∼ =

[

]

[

][

]

[

][

]

ψ₁

][

]

{E(z)}

zI₂

ϑ₁

ϑ₂

ϑ,ψ

-z

ψ₂

[

]

-z ψ₁

ϑ₁

ϑ₂ + ψ₂

(

[

][

])

[

]

-z ψ₁

det zI₂ +

= det

= 0.

ϑ₁

ϑ₂ + ψ₂

Таким образом, в конфигурации варианта 2 ни одно из вычисленных значе-

ний E(z) не может быть решением задачи из-за невыполнения условия (19).

8. Заключение

Применительно к избыточному комплексу оборудования, реализующему

управление по рассогласованию выходов системы, предложено аналитическое

решение задачи генерирования (тестирования и интеграции) альтернативных

конфигураций, обеспечивающих неизменность целевой функции его функ-

ционирования, зафиксированной в номинальной конфигурации. В отличие

от ранее решенной аналогичной задачи применительно к системе, подвер-

гающейся внешнему воздействию, вновь полученное решение является более

сложным, что выражено в существенно большем числе операций с полино-

миальными матрицами и двумя ярусами их варьирования.

Предлагаемый подход не ограничен исключительно областью линейных

систем. В сочетании с использованием различных приемов декомпозиции и

линеаризации он становится универсальным инструментом для структурных

решений в избыточных системах более широкого круга.

ПРИЛОЖЕНИЕ

Доказательство теоремы 1. Очевидно, что равенство (12), содержа-

щее матричную дробь, будет справедливо, если одновременно выполняются

равенства для знаменателя и правого числителя:

(Π.1)

BC_вхE(z)C_выхD = BQ^{рассном}(z)D, BC_вхE(z)C_выхα = BQ^{рассном}

(z)α.

В блочном форме этим равенствам соответствует запись

[

]

[

]

(Π.2)

BC_вхE(z)C_вых

D α

= BQрассном (z)

D α

Уравнение (П.2) относительно неизвестной матрицы согласно теореме 1.6

из [20] разрешимо, если и только если выполнены условия (13) и (14), а его

решение согласно теореме 1.7 из [20] определяется формулой (15). Равен-

ство (12) имеет смысл, если и только если выполняется условие (16). Вместе

с тем, выполнение первого условия (П.1) гарантирует неизменность знаме-

нателя матричной дроби (12), а значит и существование таких варьируемых

параметров µ и η, при которых детерминантное условие (16) выполняется.

Теорема 1 доказана.

Доказательство теоремы 2. Вводя с учетом (11) замену

(Π.3)

δ(z) = (zI_n - A + BQ(z)D)^-1

BQ(z)α,

перепишем уравнение (12) в виде

(Π.4)

βDδ(z) = Φ^{расстреб}

(z).

Это уравнение всегда разрешимо относительно матрицы δ(z), поскольку

условие существования решения

βD^LΦ^{расстреб}(z) = 0,

соответствующее теореме 1.4 из [20], при подстановке значения Φ^{расстреб}(z) из (9)

становится тождеством:

βD^LβD

(zI_n - A + BQ^{рассном}(z)D)^-1BQ^{рассном}(z)α = 0.

}

Множество решений δ(z) уравнения (П.4) в соответствии с теоремой 1.4

из [20] записывается формулой (22), где ρ - некоторая матрица подходящих

размеров, возможные значения которой уточняются далее.

Теперь перепишем формулу (П.3) следующим образом:

BQ(z)(α - Dδ(z)) = (zI_n - A)δ(z),

куда подставляем (11) и любой из элементов δ_ξ(z) множества (21):

(Π.5)

BCE(z)C (α - Dδ_ξ(z)) = (zI_n - A)δ_ξ

(z).

Одно из условий разрешимости двухстороннего матричного уравнения

(П.5) в соответствии с теоремой 1.7 из [20] записывается в виде равенства

BCвхL (zI_n - A) δ_ξ(z) = 0,

которое с учетом (21) и введением обозначения (20) перепишем в виде

(Π.6)

ℵ(z)ρ = -BC^L (zI_n - A) (βD)^∼Φ^{расстреб}

(z).

Выполнение этого условия явным образом зависит от выбора матрицы ρ, вве-

денной в (21). Решая (П.6) как левостороннее уравнение относительно ука-

занной матрицы, согласно теореме 1.4 [20] получаем условие разрешимости в

виде равенства (17) и решение в виде формулы (22).

Вторым условием разрешимости (П.5) в соответствии с теоремой 1.7 из [20]

является выполнение равенства (18) (обратимый сомножитель (zI_n - A) сле-

ва опущен как не влияющий на результат проверки), а все множество реше-

ний описывается формулой (23).

Однако скрытое в формулах теоремы варьирование знаменателя матрич-

ной дроби (12) требует проверки его существования, т.е. существования таких

варьируемых параметров ξ, ϑ и ψ, при которых выполняется детерминантное

условие (19). Выполнение аналогичного условия для матрицы Q^номс(z) связа-

но с существованием по определению номинальной конфигурации. Теорема 2

доказана.

СПИСОК ЛИТЕРАТУРЫ

Агеев А.М., Бронников А.М., Буков В.Н., Гамаюнов И.Ф. Супервизорный метод

управления избыточностью технических систем // Изв. РАН. Теория и системы

управления. 2017. № 3. С. 59-69.

Буков В.Н., Бронников А.М., Агеев А.М., Гамаюнов И.Ф., Озеров Е.В., Шур-

ман В.А. Концепция управляемой избыточности комплексов бортового оборудо-

вания // Науч. чтения по авиации, посвящ. пам. Н.Е. Жуковского: Матер. XVI

Всерос. науч.-практ. конф. / Гл. ред. С.П. Халютин (11-12 апр. 2019, Москва).

М.: Изд. дом Акад. им. Н.Е. Жуковского, 2019. С. 17-33.

Amato F., Cosentino C., Mattei M., Paviglianiti G. A Direct/Functional Redun-

dancy Scheme for Fault Detection and Isolation on an Aircraft // Aerospace Sci.

Technol. 2006. V. 10. No. 4. P. 338-345.

Bartys M., Patton R.J., Syfert M., Heras S., Quevedo J. Introduction to the

DAMADICS Actuator FDI Benchmark Study // Control Engineering Practice. 2006.

V. 14. No. 6. P. 577-596. Special Issue “Fault Diagnosis of Actuator Systems: the

DAMADICS Benchmark Problem”.

Patton R.J., Uppal F.J., Simani S., Polle B. Reliable Fault Diagnosis Scheme for

a Spacecraft Attitude Control System // J. Risk Reliabil. 2008. V. 222. No. 2.

P. 139-152.

Клюшников В.Ю. Повышение целевой эффективности наноспутников инфор-

мационного обеспечения // Изв. ВУЗов. Приборостроение. 2018. Т. 61. № 5.

С. 414-422.

Gupta S. Dynamic Microcontroller Reconfiguration Delivers More Than

100%

Resource Utilization. URL: https://www.radiolocman.com/review/article.html?di

=148343. (Дата обращения: 26.05.2020).

Филиппов А.К. Современные архитектуры динамически реконфигурируемых

систем обработки информации // Проектирование и технология электронных

средств. 2007. № 2. С. 2-9.

Потомский С.Ю., Полойко Н.А. Архитектура распределенной системы

управления на основе реконфигурируемой многоконвейерной вычислитель-

ной среды L-Net

// Системный администратор.

2014.

№ 10 (143). URL:

http://samag.ru/archive/article/2806. (Дата обращения: 26.05.2020).

10.

Knyazeva N. Improving the Structural Survivability of the Telecommunications Net-

work // Inform. Models Anal. V. 2. 2013. No. 3. P. 275-284.

11.

Hagiyev C., Caliskan F. Fault Diagnosis and Reconfiguration in Flight Control Sys-

tems. Boston: Kluwer Acad. Publ., 2004.

12.

Grebeshkov A.Y., Zuev A.V., Kiporov D.S. Computer Simulation of Average Channel

Access Delay in Cognitive Radio Network // Commun. Computer Inform. Sci. 2016.

V. 678. P. 325-336.

13.

Дегтярев А.Р., Киселев С.К. Отказоустойчивые реконфигурирующиеся ком-

плексы интегрированной модульной авионики // Электротехнические и инфор-

мационные комплексы и системы. 2016. Т. 12. № 1. С. 89-99.

14.

Кулаков А.Ю., Павлов А.Н., Потрясаев С.А., Соколов Б.В. Методы, алгоритмы

и технологии реконфигурации бортовых систем маломассоразмерных космиче-

ских аппаратов // Известия высших учебных заведений. Приборостроение. 2018.

Т. 61. № 7. С. 596-603.

15.

Зыбин Е.Ю., Косьянчук В.В. Аналитический синтез многосвязных отказоустой-

чивых систем управления с упрощенной схемной реализацией // Изв. РАН. Тео-

рия и системы управления. 2010. № 1. С. 108-117.

16.

Агеев А.М. Конфигурирование избыточных комплексов бортового оборудова-

ния // Изв. РАН. Теория и системы управления. 2018. № 4. С. 175-192.

17.

Буков В.Н., Бронников А.М., Агеев А.М., Гамаюнов И.Ф. Аналитический под-

ход к формированию конфигураций технических систем // АиТ. 2017. № 9.

С. 67-83.

18.

Поляк Б.Т., Щербаков П.С. Робастная устойчивость и управление. М.: Наука,

2002.

19.

Методы классической и современной теории автоматического управления. Учеб-

ник в 5 томах. Т. 1: Математические модели, динамические характеристики и

анализ систем автоматического управления / Под ред. К.А. Пупкова, Н.Д. Егу-

пова. М.: Изд-во МГТУ им. Н.Э. Баумана, 2004.

20.

Буков В.Н. Вложение систем. Аналитический подход к анализу и синтезу мат-

ричных систем. Калуга: Изд-во науч. литературы Н.Ф. Бочкаревой, 2006.

21.

Буков В.Н. Адаптивные прогнозирующие системы управления полетом. М.:

Наука, 1987.

22.

Кузовков Н.Т. Модальное управление и наблюдающие устройства. М.: Машино-

строение, 1976.

23.

Красовский А.А., Александров А.Г., Артемьев В.М. и др. Справочник по теории

автоматического управления / Под ред. А.А. Красовского. М.: Наука, 1987.

24.

Авиация ВВС России и научно-технический прогресс: боевые комплексы и си-

стемы вчера, сегодня, завтра / Под. ред. Е.А. Федосова. М.: Дрофа, 2005.

25.

Буков В.Н., Бронников А.М. Тестирование конфигураций избыточных интегри-

рованных комплексов оборудования // АиТ. 2019. № 2. С. 76-95.

26.

Буков В.Н., Бронников А.М., Агеев А.М., Гамаюнов И.Ф. Интеграция комплек-

са оборудования выбранной конфигурации // АиТ. 2019. № 4 С. 105-125.

27.

Буков В.Н., Бронников А.М, Агеев А.М., Гамаюнов И.Ф., Шурман В.А. Гене-

рация альтернативных связей последовательно соединенных подсистем в избы-

точном комплексе оборудования // Изв. РАН. Теория и системы управления.

2020. № 2. С. 53-65.

Статья представлена к публикации членом редколлегии П.С. Щербаковым.

Поступила в редакцию 27.02.2020

После доработки 22.06.2020

Принята к публикации 09.07.2020