Автоматика и телемеханика, № 2, 2021

(Национальный исследовательский университет ИТМО;

Институт проблем машиноведения РАН, Санкт-Петербург)

МЕТОД ПРИТЯГИВАЮЩИХ ЦИЛИНДРОВ.

РЕШЕНИЕ ОБЩЕЙ ЛИНЕЙНОЙ ЗАДАЧИ СЛЕЖЕНИЯ¹

Представлен метод притягивающих цилиндров обобщение метода ин-

вариантных эллипсоидов на случаи задач слежения и наблюдения. На

основе разработанного метода предложен алгоритм расчета параметров

регулятора, обеспечивающего ограниченность ошибки слежения или на-

блюдения в присутствии ограниченных внешних возмущений. Эффектив-

ность предложенного подхода продемонстрирована на примерах.

Ключевые слова: задача слежения, задача наблюдения, подавление воз-

мущений.

DOI: 10.31857/S0005231021020033

1. Введение

Задача подавления ограниченных внешних возмущений на основе метода

инвариантных эллипсоидов ранее рассматривалась в [1-3]. В частности, в [1]

решалась задача стабилизации возмущенной системы с измеряемым состоя-

нием с помощью статического регулятора; в [2] аналогичный подход при-

менялся для стабилизации возмущенной системы с измеряемым выходом

к статическому регулятору был добавлен динамический наблюдатель Люен-

бергера; в [3] аналогичная задача была решена с помощью динамического

регулятора общего вида. Однако во всех этих работах решалась только зада-

ча стабилизации объекта, но не задача слежения.

Распространению метода инвариантных эллипсоидов на задачу слежения

посвящены работы [4, 5], в которых на систему наложен ряд дополнительных

условий. Так, в [4] предполагается, что все компоненты задающего воздей-

ствия измеряемы и могут быть использованы регулятором, а в [5] дополни-

тельно предполагается, что их производные также измеряемы и ограничены.

Отметим, что в обеих работах состояние объекта является измеряемым, а ис-

пользуемый регулятор статическим. В этом смысле работы [4, 5] обобща-

ют [1], но не более поздние [2, 3], в которых уже используется динамический

регулятор при неизмеряемом состоянии объекта.

Целью настоящей работы является обобщение метода инвариантных эл-

липсоидов на случай задачи слежения при использовании динамического ре-

гулятора по выходу. В качестве инструмента используется новый метод, ос-

¹ Результаты разделов 3 и 4 получены при поддержке гранта Российского научного

фонда (проект № 18-79-10104) в ИПМаш РАН. Результаты разделов 5 и 6 получены при

поддержке гранта Президента Российской Федерации (грант № МД-1054.2020.8).

нованный на притягивающих множествах более общего вида, в том числе

неограниченных по части переменных.

В работе использованы следующие обозначения: Sⁿ = {A ∈ R^n×n | A^T = A},

если A ∈ R^m×n, то rangeA = {Ax ∈ R^m | x ∈ Rⁿ}, kerA = {x ∈ Rⁿ | Ax = 0},

A⁺ псевдообратная Мура-Пенроуза (существует у любой матрицы вне за-

висимости от полноты ранга).

2. Мотивирующий пример

В качестве мотивирующего примера рассмотрим неустойчивую систему,

состояющую из объекта первого порядка и наблюдателя первого порядка,

заданную как

{

x(t) = ax(t) + bf(t),

(1)

x(t) = (a - l)x(t) + lx(t),

где x(t) ∈ R - состояние объекта, x(t) ∈ R - состояние наблюдателя, f(t) ∈ R -

внешнее возмущение, |f(t)| ≤ 1, b > 0 и l > a > 0. В качестве выходной пере-

менной объединенной системы (1) рассмотрим ошибку наблюдения

y(t) = x(t) - x(t).

Представленная система неустойчива и не имеет притягивающего эллипсоида

по состоянию. Однако в силу того, что выход y(t) имеет устойчивую динамику

y(t) = (a - l)y(t) + bf(t),

у системы существуют притягивающие эллипсоиды по выходу. Минимальный

притягивающий эллипсоид по выходу (в данном случае - отрезок минималь-

ной длины) может быть найден аналитически как

{

}



b²

(2)

y∈R

y² ≤

(a - l)²

однако в пространстве состояний ему соответствует неограниченное множе-

ство

{

}



(3)

(x, x) ∈ R²

 |x - x| ≤

l-a

не являющееся эллипсоидом. Метод инвариантных эллипсоидов [1] не может

быть непосредственно применен для поиска притягивающего множества (2),

потому как у системы (1) не существует инвариантного эллипсоида по состоя-

нию. Существует, однако, притягивающее подмножество пространства со-

стояний системы в форме полосы (3). Траектория попадает в эту полосу и

затем движется в ней, неограниченно удаляясь от начала координат. Рису-

нок 1 иллюстрирует описанную ситуацию.

Данный пример показывает, что для решения задачи слежения или наблю-

дения в общем случае недостаточно метода инвариантных (притягивающих)

эллипсоидов, разработанного в [1-3] для решения задач стабилизации. Для

обобщения существующего метода на случаи, подобные представленному вы-

ше, в настоящей работе развивается метод притягивающих цилиндров.

Рис. 1. Пример траектории системы. Серым цветом выделено неограниченное

притягивающее подмножество пространства состояний.

3. Геометрические основы метода притягивающих цилиндров

Для описания рассматриваемых в настоящей работе притягивающих под-

множеств введем следующее определение.

Определение 1. Подмножество пространства Rⁿ, заданное как

{



}

(4)

x∈Rⁿ

xTQx ≤ 1

где Q ∈ Sⁿ, Q ≽ 0 и rankQ = k, называется (k, n)-цилиндром.

Прим{ры (k, n)-цлиндро} п{иведены на рис. 2-4. Им соотв}тс{вуют мно-

жества

(x, y) ∈ R²

x2 ≤ 1

(x, y, z) ∈ R³

x2 + (y - z)² ≤ 1

(x, y, z) ∈



}

∈R³

z² ≤1

, каждое из которых можно задать в виде (4), выбрав соответ-

ствующую матрицу Q.

Замечание 1. Отметим, что при k = n множество (4) является эллип-

соидом и что в [1-3] авторами рассматривались притягивающие подмноже-

Рис. 2.

Рис. 3.

Рис. 4.

Рис. 2. Бесконечная полоса - пример (1, 2)-цилиндра.

Рис. 3. Бесконечный цилиндр - пример (2, 3)-цилиндра.

Рис. 4. Слой пространства между двумя плоскостями - пример (1, 3)-цилиндра.

ства именно такого вида. При k < n множество (4) эллипсоидом уже не яв-

ляется, но при этом также может являться притягивающим подмножеством

пространства состояний некоторой системы. В этом смысле метод притягива-

ющих цилиндров является обобщением метода инвариантных (притягиваю-

щих) эллипсоидов.

Сформулируем геометрическое описание (k, n)-цилиндров.

Утверждение 1. Как множество в линейном пространстве (k,n)-ци-

линдр (4) является суммой k-мерного эллипсоида, лежащего в подпростран-

стве rangeQ, и всего подпространства kerQ.

Следствие 1. Как топологическое пространство (k,n)-цилиндр гомео-

морфен прямому произведению замкнутого k-мерного шара и R^n-k.

Доказательства утверждения 1 и следствия 1 приведены в Приложении.

Известно, что образом эллипсоида при линейном отображении является

эллипсоид. Обобщим это утверждение на случай (k, n)-цилиндров.

Утверждение 2. Пусть C ∈ R^m×n, rankC = m. Образом (k,n)-цилинд-

ра (4) при отображении y = Cx является (r, m)-цилиндр

{



}

(

)



y∈R^m

y^TRy ≤ 1 , R = C^+TM

I - (MN)(MN)⁺

MC⁺,

где r = rankR, M = Q^1/2, N = I - C⁺C.

Следствие 2. При n ≥ 2 проекцией (k,n)-цилиндра на произвольную

плоскость является либо вся плоскость, либо полоса (часть плоскости

между двумя параллельными прямыми), либо эллипс (часть плоскости,

ограниченная эллипсом).

Доказательства утверждения 2 и следствия 2 приведены в Приложении.

Изложенные выше утверждения дают читателю базовые представления

о геометрии рассматриваемых в настоящей работе притягивающих подмно-

жеств.

4. Анализ. Метод притягивающих цилиндров

Рассмотрим линейную динамическую систему

(5)

x(t) = Ax(t) + Bf(t),

где x(t) ∈ Rⁿ - вектор состояния, f(t) ∈ R^m - внешнее возмущение, A, B -

вещественные матрицы соответствующих размерностей. Предполагается, что

внешнее возмущение ограничено и что известна матрица G ≻ 0 такая, что

(6)

f^T(t)Gf(t) ≤ 1,

∀t ≥ 0.

Определение 2. Притягивающим (k,n)-цилиндром системы (5)-(6)

называется множество (4) такое, что для всех траекторий системы вы-

полнено

lim sup x^T(t)Qx(t) ≤ 1,

t→+∞

а также, если x(t₀) ∈ (4), то x(t) ∈ (4) при всех t ≥ t₀.

Согласно определению 2, притягивающие (k, n)-цилиндры являются одно-

временно притягивающими и инвариантными подмножествами пространства

состояний.

Сформулируем достаточное условие существования притягивающего ци-

линдра в пространстве состояний системы (5)-(6).

Теорема 1. Если матрица C ∈ R^k×n такова, что

rankC = k, CA(I - C⁺C) = 0,

и если существуют P ≻ 0 и α > 0 такие, что

[

]

PCAC⁺ + (CAC⁺)^TP + αP PCB

≺ 0,

(CB)^TP

-αG

то подмножество {x ∈ Rⁿ | x^TC^TPCx ≤ 1} пространства состояний си-

стемы (5)-(6) является притягивающим (k,n)-цилиндром.

Доказательство теоремы 1 приведено в Приложении.

Замечание 2. Отметим, что в частном случае, при C = I ∈ R^n×n, тео-

рема 1 совпадает с основным результатом работы [1], и тогда притягивающий

(k, n)-цилиндр является инвариантным эллипсоидом.

5. Синтез. Общая линейная задача слежения

5.1. Постановка задачи

Рассмотрим объект управления

{ ˙x(t) = A₁x(t) + B₁u(t) + C₁w(t),

(7)

y(t) = D₁x(t) + E₁u(t) + F₁w(t),

где x(t) ∈ Ra1 - неизмеряемый вектор состояния, u(t) ∈ Rb1 - управление,

w(t) ∈ Rc1 - неизмеряемый вектор возмущений, y(t) ∈ Rb2 - измеряемый вы-

ход, A₁, B₁, C₁, D₁, E₁, F₁ - известные вещественные матрицы соответствую-

щих размерностей.

Пусть эталонная модель задана как

{ ˙x_r(t) = A₂x_r(t) + C₂h(t),

(8)

g(t) = D₂x_r(t),

где x_r(t) ∈ Ra2 - неизмеряемый вектор состояния, h(t) ∈ Rc2 - неизмеряемое

задающее воздействие, g(t) ∈ Rc1 - измеряемый эталонный выход, A₂, C₂,

D₂ - известные вещественные матрицы соответствующих размерностей.

Замечание 3. Формально, эталонную модель можно не выделять в от-

дельную систему, а сделать частью уравнения (7), объединив вектор x(t) с

вектором x_r(t), w(t) с h(t) и y(t) с g(t). Однако в настоящей работе предла-

гается рассмотреть (7) и (8) как две различные модели. Такое разделение не

является обязательным, но помогает лучше понять смысл целевой перемен-

ной z, раскрываемый далее.

Для достижения цели управления предполагается использование регуля-

тора заданного динамического порядка a₃ ∈ N ∪ {0} вида

{

c(t) = A3xc(t) + B3y(t) + C3g(t),

(9)

u(t) = D₃x_c(t) + E₃y(t) + F₃g(t),

где x_c(t) ∈ Ra3 - вектор состояния регулятора, A₃, B₃, C₃, D₃, E₃, F₃ - веще-

ственные матрицы соответствующих размерностей, подлежащие выбору.

Замечание 4. При a₃ = 0 матрицы A₃,B₃,C₃,D₃ пустые, регулятор (9)

является статическим и описывается формулой u(t) = E₃y(t) + F₃g(t). По-

скольку современные компьютерные программы (например, matlab) свобод-

но работают с пустыми матрицами различных размерностей, далее не будем

рассматривать этот случай отдельно, считая его частью общей теории.

Предполагается, что внешние сигналы w(t), h(t) ограничены и что извест-

на матрица G ≻ 0 такая, что

[w(t)]T

[w(t)]

(10)

≤ 1,

∀t ≥ 0.

h(t)

Замечание 5. Консервативность основного результата, который будет

изложен в разделе 5.2, может быть несколько снижена путем замены (10)

на пару ограничений w(t)^TG₁w(t) ≤ 1, h(t)^TG₂h(t) ≤ 1, где G₁, G₂ ≻ 0, или

даже на большее число ограничений, наложенных на отдельные компонен-

ты данных векторов. Однако это приведет к увеличению числа свободных

переменных и усложнению формулировок, не обязательному для настоящей

статьи.

Цель управления формулируется следующим образом: при w(t), h(t) ≡ 0

обеспечить асимптотическую сходимость целевой переменной

(11)

z(t) = K₁x(t) + K₂x_r(t) + K₃x_c

(t)

к нулю. Если же w(t), h(t) ≡ 0, но выполнено условие (10), то перемен-

ная (11) должна асимптотически сходиться к ограниченному множеству ви-

да {z ∈ R^k | z^TP z ≤ 1} и должна быть найдена соответствующая матрица

P ≻ 0. Предполагается, что матрицы K₁ ∈ Rk×a1, K₂ ∈ Rk×a2, K₃ ∈ Rk×a3, за-

]

дающие цель управления, известны и что rank

[K1 K2

K₃

= k. Последнее

условие наложено для удобства и не является огранич[тельным, та]к как его

выполнения всегда можно добиться, убрав из матрицы

K₁

K₂

K₃

линейно

зависимые строки.

Сформулированная таким образом задача в рамках настоящей статьи на-

зывается общей линейной задачей слежения. Отметим несколько частных

случаев:

1. Задача стабилизации. Если K₁ = I, K₂ = K₃ = 0, то при отсутствии

внешних воздействий цель управления принимает вид ∥x(t)∥ → 0. В [3] пока-

зано, что такая задача может быть решена с помощью метода инвариантных

эллипсоидов.

2. Задача слежения. Если K₁ = I, K₂ = -I, K₃ = 0, то при отсутствии

внешних воздействий цель управления имеет вид ∥x(t) - x_r(t)∥ → 0, что со-

ответствует слежению вектора состояния объекта за вектором состояния эта-

лонной модели.

3. Задача наблюдения. Если K₁ = I, K₂ = 0, K₃ = -I, то регулятор (9)

превращается в наблюдатель, вектор состояния которого должен сходиться к

вектору состояния объекта. Если внешние воздействия отсутствуют, то такая

цель управления может быть сформулирована как ∥x_c(t) - x(t)∥ → 0.

Если матрицы K_i выбраны иным образом, то цель управления представ-

ляет собой некоторое сочетание задач стабилизации, слежения и наблюдения

(возможно, по части переменных). Таким образом, поставленная задача син-

теза может быть интерпретирована как одна из этих трех базовых задач,

либо как их комбинация.

Отметим, что на матрицы A₁, B₁, C₁, D₁, F₁, A₂, C₂, D₂ в (7) и (8) не на-

кладывается никаких ограничений. Однако требуется наложить ограничение

на матрицу E₁, связанное с корректностью рассматриваемой обратной свя-

зи. Рассмотрим вспомогательный измеряемый выход y(t) = y(t) - E₁u(t) =

= D₁x(t) + F₁w(t) системы (7), который получается из выражения для y(t),

если убрать слагаемое с E₁. Предположим, что поставленная задача мо-

жет быть решена с помощью регулятора (9), в котором вместо выхода y(t)

используется вспомогательный выход y(t). Тогда после подстановки y(t) =

= y(t) - E₁u(t) получим закон управления в виде

u(t) = (I + E₁E₃)^-1(D₃x_c(t) + E₃y(t) + F₃g(t)) =D3x_c(t)

E₃y(t)

F₃g(t),

для реализации которого необходимо, чтобы матрица (I + E₁E₃)^-1 существо-

вала. Именно это условие и накладывается дополнительно. С учетом ука-

занного свойства при формулировке основного результата достаточно огра-

ничиться случаем E₁ = 0, что и будет сделано, при этом соответствующий

регулятор для общего случая всегда может быть восстановлен.

5.2. Основной результат

Введем вспомогательные обозначения для описания замкнутой системы

















A₁

B₁

C₁

















 0

A₂

0, B=

0

, C =

0

C₂, D=

D1

0,

D₂









]

x(t)





[A3 B3

C₃





[w(t)]

F =

F1

0, X =

s(t) =

xr(t), f(t) =

D₃

E₃

F₃

h(t)

x_c(t)

]

M =A+BXD, N =C+BXF, K =

[K1 K2

K₃

n=a₁ +a₂ +a₃.

Тогда уравнение замкнутой системы (7)-(9), (11) может быть записано как

{

s(t) = Ms(t) + Nf(t),

(12)

z(t) = Ks(t),

при этом ограничение (10) примет вид

(13)

f^T(t)Gf(t) ≤ 1,

∀t ≥ 0.

Перед формулировкой основного результата введем обозначения

H₁ = KAK⁺ + KB(KB)⁺KA(D(K⁺K - I))⁺DK⁺,

H₂ = KC + KB(KB)⁺KA(D(K⁺K - I))⁺F,

(14)

H₃ = KB, H₄ = DK⁺ + D(D(K⁺K - I))⁺DK⁺,

H₅ = F + D(D(K⁺K - I))⁺F.

Сформулируем основной результат в виде теоремы.

Теорема 2. Если матрицы A,B,D,K таковы, что

(15)

KB(KB)⁺KA(D(I - K⁺K))⁺D(I - K⁺K) = KA(I - K⁺

K),

и если существуют P,Q ≻ 0, µ₁,µ₂ ∈ R, α > 0 такие, что PQ = I и

[

]

H₁Q + QH^T1 + αQ H₂

[H₃H^T3

≺µ₁

H^T2

-αG

(16)

[

]

[

]

PH₁ + HT1 P + αP PH₂

H^T4H₄

H^T4H₅

≺µ₂

H^T2P

-αG

H^T5H₄

H^T5H₅

то существует набор X параметров регулятора (9) такой, что подмноже-

ство {s ∈ Rⁿ | s^TK^TPKs ≤ 1} пространства состояний замкнутой систе-

мы (12) является притягивающим (k,n)-цилиндром.

При фиксированных α, P соответствующая матрица X находится как

(17)

X = (KB)⁺KA(D(K⁺K - I))⁺ + Y + (KB)⁺KBY D(D(K⁺K - I))⁺,

где Y - любое решение линейного матричного неравенства

[

]

[

]

PH₁+HT1 P +αP PH₂

PH₃Y H₄ +(PH₃Y H₄)^T PH₃Y H₅

(18)

≺ 0.

H^T2P

-αG

(P H₃Y H₅)^T

Доказательство теоремы 2 приведено в Приложении. Из доказательства,

в частности, следует, что при выполнении условий теоремы матричное нера-

венство (18) всегда имеет решение.

Условие (15) является вполне естественным: оно показывает, как должны

соотноситься между собой параметры объекта (7) и эталонной модели (8),

чтобы решение соответствующей задачи слежения было возможны[. Мож]

но показать, что для задач стабилизации и наблюдения, при K =

]

и K =

-I

соответственно, условие (15) всегда выполнено независи-

]

мо от параметров объекта и эталонной модели. Если же K =

[I -I

, что

соответствует задаче слежения, то условие (15) представляется в виде

B₁B⁺¹(A₁ - A₂)(D^T1D₁ + D^T2D₂)⁺(D^T1D₁ + D^T2D₂) = (A₁ - A₂).

Следует отметить, что выполнение этого условия еще не означает возмож-

ность построения соответствующего регулятора, ведь помимо него должно

быть также выполнено второе условие теоремы 2, связанное с неравенства-

ми (16).

5.3. Вычислительные аспекты

Поскольку на матрицы P и Q, входящие в формулировку теоремы 2, на-

ложено дополнительное ограничение P Q = I, матричные неравенства (16)

не являются линейными даже при фиксированном α и не могут быть непо-

средственно решены с помощью стандартных программных средств, таких

как yalmip или cvx. Однако существует эффективный алгоритм решения

матричных неравенств именно с таким типом нелинейности, который в ли-

тературе можно встретить под названием “Cone complementarity algorithm”

(алгоритм восполнения конуса) [6-9].

Алгоритм 1.

1. Задать i = 0. Зафиксировать параметр α > 0 и найти положительно опре-

деленное решение

P,Q) системы линейных матричных неравенств (16).

2. Положить (R_i, S_i) =

P,Q).

3. Найти положительно определенное решение

P,Q) задачи минимизации:

минимизировать trace(P S_i + QR_i)

[

]

P I

при условиях

≽ 0, (16).

I Q

4. Если выполнено условие остановки (например, величина trace

PS_i+QR_i)

достаточно близка к 2k или величина i достигла предельного значения), пе-

рейти к шагу 5. Иначе увеличить i на единицу и перейти к шагу 2.

5. Принять полученную пару

P,Q) в качестве пары (P,Q), приближенно

удовлетворяющей условиям теоремы 2. Закончить.

В [6] показано, что алгоритм

сходится к паре (P, Q), удовлетво-

ряющей условиям

(16) и доставляющей локальный минимум величине

trace(P Q + QP ). Несмотря на то, что в общем случае выполнение условия

PQ = I не гарантировано, алгоритм широко применяется [6-9] для решения

задач теории управления, в которых возникают подобные матричные нера-

венства.

Применение теоремы 2 на практике во всей полноте предполагает выпол-

нение следующей последовательности действий:

1. Проверить, что для поставленной задачи выполнено условие (15).

2. Применив алгоритм 1, найти взаимообратные P и Q, удовлетворяю-

щие (16).

3. Используя найденную матрицу Q, найти матрицу Y , удовлетворяю-

щую (18).

4. Вычислить матрицу X параметров регулятора по формуле (17).

Однако следует отметить, что нахождение пары взаимообратных матриц

(P, Q) не является обязательным для синтеза регулятора. Если в процессе вы-

полнения алгоритма 1 найдена матрица P такая, что неравенство (18) имеет

решение Y , то нет необходимости далее выполнять алгоритм можно сразу

перейти к вычислению параметров регулятора по формуле (17).

6. Примеры

6.1. Задача слежения

Рассмотрим объект управления (7) с матрицами

]

[-2,99 3,10

[1,5]

[0,15]

A₁ =

B₁ =

C₁ =

-2,10

2,01

0,15

]

D₁ =

-1

E₁ =

[0], F₁ =

и эталонную модель (8) с матрицами

]

[ 0,01 0,1

]

A₂ =

C₂ =

[0], D₂ =[1

-1

-0,1

0,01

Заметим, что объект управления является устойчивым, а эталонная модель,

напротив, неустойчива. Условие (10) предполагается выполненным при G =

= 1.

Пусть динамический порядок a₃ регулятора (9) положен равным 1, а це-

левая переменная (11) задана как

z(t) = x(t) - x_r(t),

что соответствует задаче слежения и выбору матрицы

]

-1

K =

-1 0

Нетрудно проверить, что в этом случае условие (15) выполнено. Тогда в ре-

зультате выполнения алгоритма 1 при α = 0,5 может быть найдена матрица

[

]

1485

-1585

P =

≻0

−1585

1698

и затем по формулам (18), (17) восстановлены параметры

]

B₃

C₃

X =

D₃

E₃

F₃

-2,95

4,95

регулятора (9), который, несмотря на заданный динамический порядок

a₃ = 1, оказывается статическим.

Граница притягивающего цилиндра

Траектория системы

-1

-2

-3

-4

-5

-4

-3

-2

-1

x₁

Рис. 5. Проекция притягивающего (k, n)-цилиндра и траектории замкнутой

системы.

-1

-2

-3

-4

-3

-2

-1

x₁

Рис. 6. Траектория объекта (

), траектория эталонной модели (- -) и границы

допустимого коридора (. . . ).

При моделировании внешнее возмущение было задано как w(t) = sin(0,4t),

]_T

а начальные условия положены равными x(0) =

и x_r(0) =

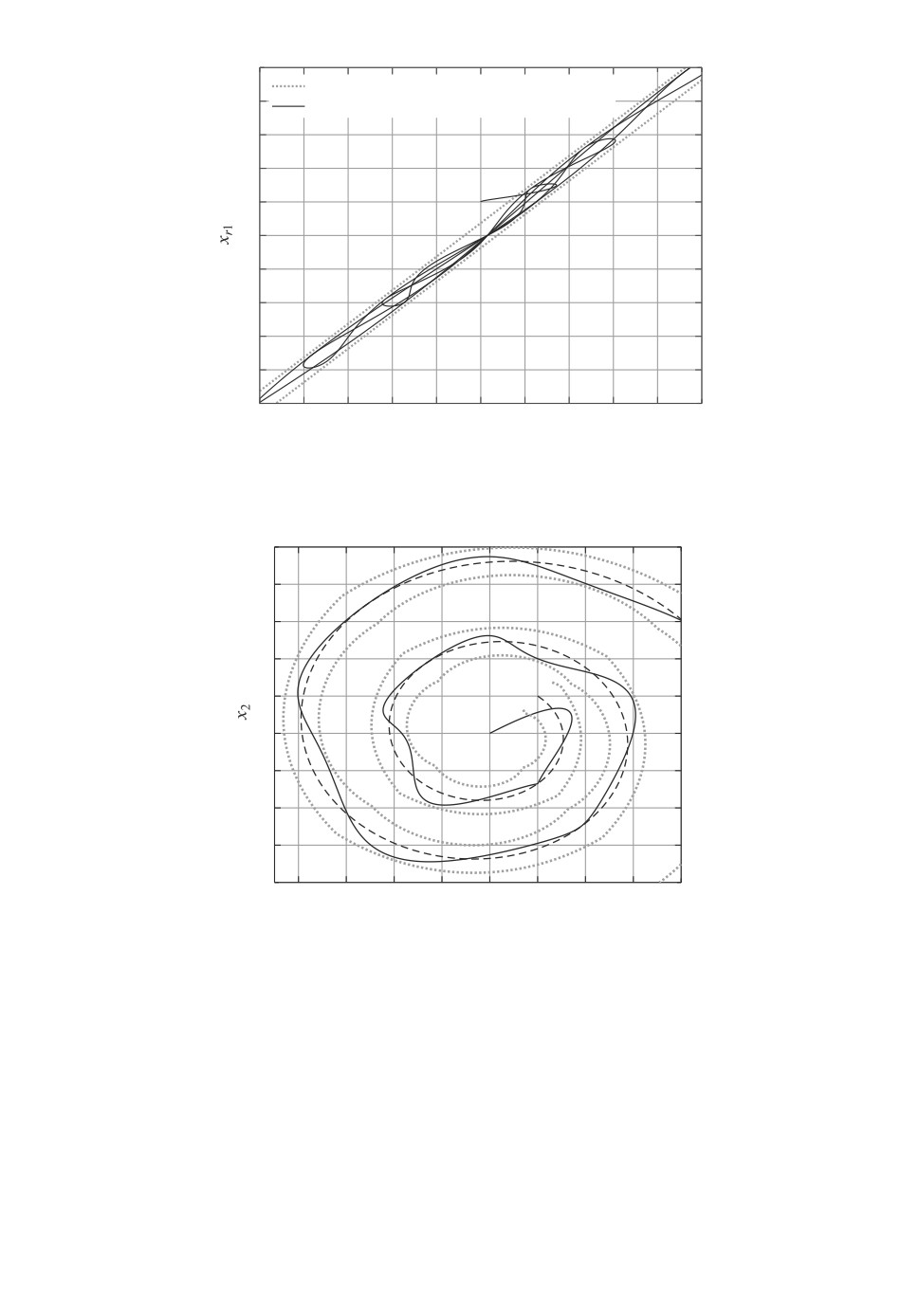
Результаты моделирования представлены на рис. 5, 6. На рис. 5 показана

проекция траектории замкнутой системы: по оси абсцисс отложено значение

первой координаты вектора состояния объекта, а по оси ординат значение

первой координаты вектора состояния эталонной модели. Также показаны

границы полосы, являющейся проекцией притягивающего (k, n)-цилиндра на

эту плоскость.

На рис. 6 показаны траектория x(t) объекта и траектория x_r(t) эталон-

ной модели. На рисунке также отмечены границы “допустимого коридора”,

имеющего следующий смысл: если в данный момент времени каждая из про-

екций траектории замкнутой системы - на плоскость (x₁, x_r1) (см. рис. 5) и

на плоскость (x₂, x_r2) (не приводится, так как выглядит аналогично) на-

ходится внутри соответствующей проекции притягивающего (k, n)-цилиндра,

то траектория x(t) в данный момент времени находится в границах допусти-

мого коридора. Иными словами, тот факт, что траектория объекта, начиная

с какого-то момента, не выходит за границы точечного пунктира, являет-

ся иллюстрацией того, что траектория замкнутой системы попадает внутрь

(k, n)-цилиндра и не покидает его.

6.2. Задача наблюдения

Рассмотрим объект (7) с матрицами













0,168

-0,132

-0,052

A₁ =0,148

-0,152

0,028,B1 = 0,C1 = 0,

0,204

-0,196

-0,006

]

D₁ =

[-0,2 0,8

-0,2

E₁ =

[0], F₁ =[0,02].

Отметим, что объект является неустойчивым. В этом примере эталонная мо-

дель не рассматривается, т.е. все матрицы в (8) пустые. Условие (10) предпо-

лагается выполненным при G = 1.

Пусть динамический порядок a₃ регулятора (9) положен равным 3, а це-

левая переменная (11) задана как

z(t) = x(t) - x_c(t),

что соответствует задаче наблюдения и выбору матрицы





-1

K =0 1 0

-1

0.

-1

Нетрудно проверить, что в этом случае условие (15) выполнено. Тогда в ре-

зультате выполнения алгоритма 1 при α = 0,3 может быть найдена матрица





192

-624

222

P =-624

2051

-732≻0

222

-732

289

и затем по формулам (18), (17) восстановлены параметры









3,970

-15,341

3,750

19,011

A₃ =1,506

-5,585

1,386,B3 =  6,792



0,559

-1,618

0,349

1,777

регулятора (9), который в этой задаче выполняет роль наблюдателя.

Граница притягивающего цилиндра

Траектория системы

-1

x₂

Рис. 7. Проекция притягивающего (k, n)-цилиндра и траектории замкнутой

системы.

-2

x₂

Рис. 8. Траектория объекта (

), траектория эталонной модели (- -) и границы

допустимого коридора (. . . ).

Можно заметить, что для полученных матриц выполнено A₃ = A₁ - B₃D₁,

а значит, структура системы (9) совпадает со структурой наблюдателя Лю-

енбергера

c(t) = A1xc(t) + B3(y(t) - D1xc(t)).

Примечательно, что такая структура не была создана искусственно, а полу-

чилась сама собой в результате выполнения алгоритма 1.

При моделировании внешняя помеха была задана как w(t) =¹² +

+¹²sgn(sin(0,1t)), а начальные условия положены равными x(0) =

[3,2

]_T

и x_c(0) =

[-10

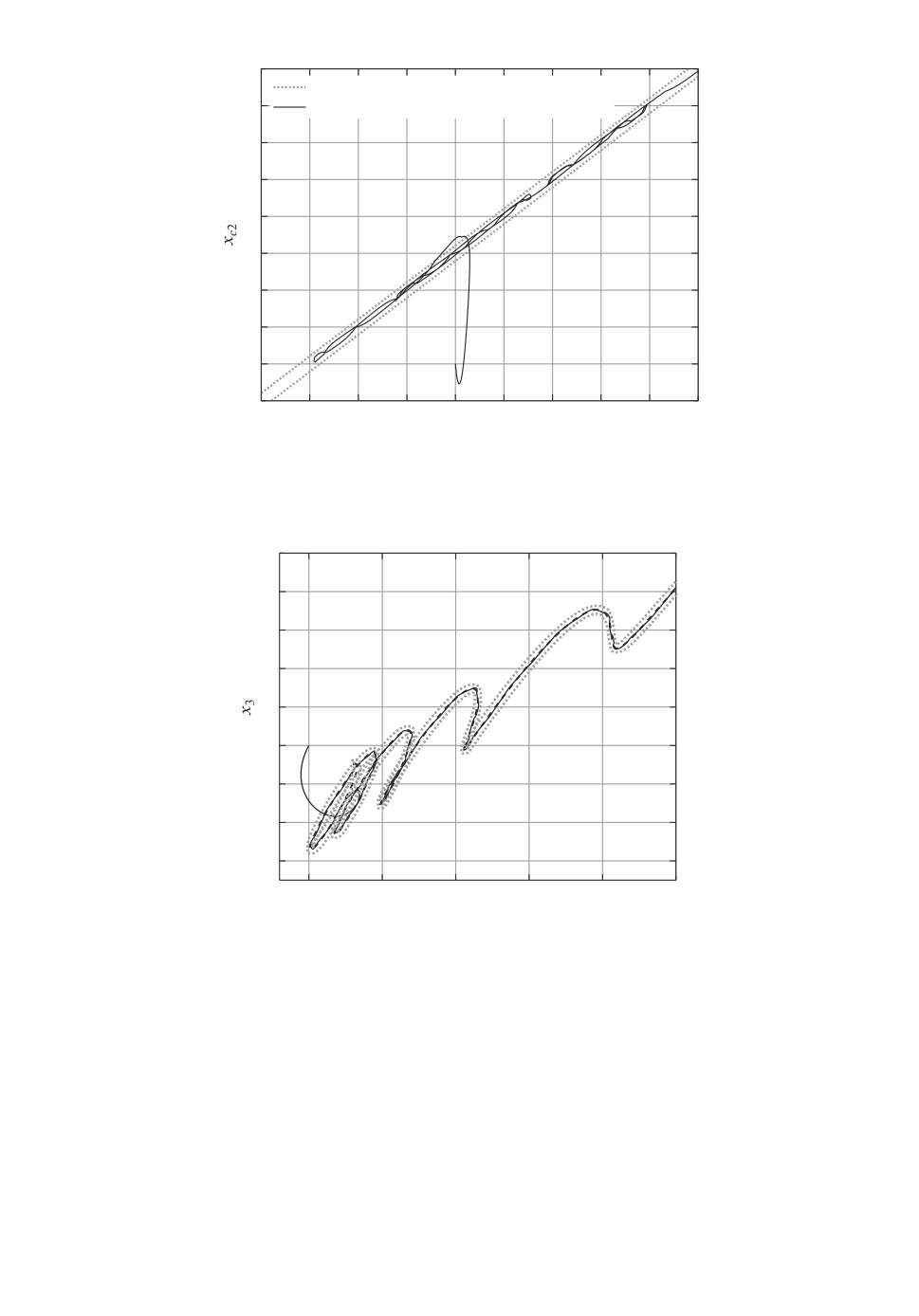
Результаты моделирования представлены на рис. 7 и 8. На рис. 7 показа-

на проекция траектории замкнутой системы: по оси абсцисс отложено зна-

чение второй координаты вектора состояния объекта, а по оси ординат

значение второй координаты вектора состояния регулятора (наблюдателя).

Также показаны границы полосы, являющейся проекцией притягивающего

(k, n)-цилиндра на эту плоскость.

На рис. 8 показаны траектория x(t) объекта и траектория x_c(t) регулятора

(наблюдателя). На рисунке также отмечены границы “допустимого коридо-

ра”, имеющего следующий смысл: если в данный момент времени каждая из

проекций траектории замкнутой системы на плоскость (x₂, x_c2) (см. рис. 7)

и на плоскость (x₃, x_c3) (не приводится, так как выглядит аналогично) на-

ходится внутри соответствующей проекции притягивающего (k, n)-цилиндра,

то траектория x(t) в данный момент времени находится в границах допу-

стимого коридора. Иными словами, тот факт, что траектория наблюдателя

начиная с какого-то момента не выходит за границы точечного пунктира,

является иллюстрацией того, что траектория замкнутой системы попадает

внутрь (k, n)-цилиндра и не покидает его.

7. Заключение

В работе предложено обобщение метода инвариантных эллипсоидов, поз-

воляющее находить притягивающие подмножества пространства состояний

более общего вида. Показано, что предложенный метод может быть исполь-

зован для решения задач стабилизации, слежения и наблюдения, а также их

комбинаций. Предложен алгоритм, позволяющий применять основой резуль-

тат на практике с помощью стандартных программных средств. На числен-

ных примерах продемонстрирована эффективность предложенного подхода.

Автор выражает благодарность Игорю Борисовичу Фуртату и анонимному

рецензенту за ценные замечания, позволившие улучшить форму и содержа-

ние статьи.

ПРИЛОЖЕНИЕ

Доказательство утверждения 1. Матрица Q симметричная, по-

этому пространство Rⁿ можно представить как прямую сумму ее образа и

ядра:

Rⁿ = rangeQ ⊕ kerQ.

Иными словами, для любого x ∈ Rⁿ существует единственное разложение

x = x_r + x_k, x_r ∈ rangeQ, x_k ∈ kerQ.

Тогда (k, n)-цилиндр (4) можно представить как

{

}

{

}

x ∈ Rⁿ | x^TQx ≤ 1

= (x_r + x_k) ∈ Rⁿ | (x_r + x_k)^TQ(x_r + x_k) ≤ 1

{

}

{

}

= (x_r + x_k) ∈ Rⁿ | x^TrQx_r ≤ 1

= x_r ∈ rangeQ | xTr Qx_r ≤ 1

+ kerQ.

Сужение оператора Q на подпространство rangeQ имеет полный ранг. Сле-

довательно, множество {x_r ∈ rangeQ | x^TrQx_r ≤ 1} является k-мерным эллип-

соидом.

Доказательство следствия 1. Символом= обозначим гомеоморфность.

Из того что rangeQ= R^k, kerQ= R^n-k, а множества {x_r ∈ rangeQ | x^TrQx_r ≤ 1}

и kerQ ортогональны друг другу, следует, что

{

}

{

}

x_r ∈ rangeQ | x^TrQx_r ≤ 1

+ kerQ

= x∈R^k |x^Tx≤1 ×Rn-k.

Лемма 1

[10]. Если матрицы A, U, C, V таковы, что обе части равен-

ства

(A + UCV )^-1 = A^-1 - A^-1U(C^-1 + V A^-1U)^-1V A^-1

имеют смысл (все операции определены), то указанное равенство выполне-

но.

Лемма 2

[11]. Для произвольной матрицы A ∈ R^m×n верно, что

lim (A^TA + εI)^-1A^T = A⁺.

ε→0+

Указанное равенство выполнено даже в тех случаях, когда (A^TA)^-1 не су-

ществует.

Доказательство утверждения 2. Воспользуемся полнотой строч-

ного ранга матрицы C и рассмотрим семейство матриц R_ε с параметром ε,

определенных как

(

)_-1

R_ε = C(Q + εI)^-1C^T

ε > 0.

Известно (см. [1]), что если Q ≻ 0, то R = (CQ^-1C^T)^-1. При Q ≽ 0 в силу

непрерывности отображения x → Cx имеем R = lim_ε→0+ R_ε. Cогласно лем-

ме 1

(

)_-1

(Q + εI)^-1 = (εI + MM)^-1 =

I-

M I+

Тогда

)_-1

(

)_-1

R_ε = C(Q + εI)^-1C^T

CC^T -

CM(I +

MM)^-1

MC^T

Заметим, что матрица CC^T обратима. Вновь применяя лемму 1, получаем

R_ε = ε(CC^T)^-1 +

(

)_-1

(

)

+ (CC^T)^-1CM I +

I - C^T(CC^T)^-1C

M MC^T(CC^T)^-1.

Воспользуемся известными равенствами

C^T(CC^T)^-1 = C⁺, I - C^T(CC^T)^-1C = N = N²

и перепишем R_ε в виде

(

)_-1

R_ε = ε(CC^T)^-1 + C^+TM I +

MNNM MC⁺.

Применяя лемму 1, получаем

(

)

(

)

R_ε = ε(CC^T)^-1 + C^+TM I - MN

εI + NMMN

^-1NM MC⁺.

Тогда согласно лемме 2, учитывая, что M = M^T, N = N^T, имеем

(

)

(

)₊

R = lim

R_ε

=C^+TM I - MN

MC⁺.

ε→0+

(

)₊

Наконец заметим, что I - MN

≽ 0 и, следовательно, R ≽ 0.

Доказательство следствия 2. Если C - проекция на R², то m = 2,

r ≤ 2. Значит, образом (k,n)-цилиндра может быть только (0,2), (1,2) или

(2, 2)-цилиндр.

Лемма 3

[12]. Если A ∈ R^n×m, B ∈ R^k×l, C ∈ R^n×l, то матричное урав-

нение

AXB = C

разрешимо относительно X ∈ R^m×k тогда и только тогда, когда

AA⁺CB⁺B = C,

и в этом случае все решения можно параметризовать как

X = A⁺CB⁺ + Y - A⁺AY BB⁺,

где Y ∈ R^m×k - произвольная матрица.

Лемма 4

[13]. Если A ∈ Sⁿ, B ∈ R^m×n и A² = A, то A(BA)⁺ = (BA)⁺.

Лемма 5

[14]. Если A ∈ R^n×m, B ∈ R^k×n, C ∈ Sⁿ, то матричное нера-

венство

AXB + (AXB)^T + C ≺ 0

разрешимо относительно X ∈ R^m×k в том и только в том случае, если

существуют µ₁, µ₂ ∈ R такие, что

C ≺ µ₁AA^T, C ≺ µ₂B^TB.

Доказательство теоремы 1. Введем переменную y(t) = Cx(t) ∈ R^k,

составим уравнение ее динамики

y(t) = CAx(t) + CBf(t)

и найдем условие, при котором оно может быть записано независимо от x(t),

т.е. условие существования матрицы X такой, что

y(t) = XCx(t) + CBf(t) = Xy(t) + CBf(t).

Для этого рассмотрим уравнение CA = XC. В соответствии с леммой 3 оно

разрешимо относительно X в том и только в том случае, если выполнено

условие CA(I - C⁺C) = 0, и тогда все решения могут быть параметризова-

ны как X = CAC⁺ + Y (I - CC⁺), где Y - произвольная матрица соответ-

ствующей размерности. Если дополнительно выполнено условие rankC = k,

то уравнение имеет единственное решение X = CAC⁺.

Так как все соответствующие условия включены в формулировку теоремы,

динамика переменной y(t) может быть записана независимо от x(t) в виде

(Π.1)

y(t) = CAC⁺y(t) + CBf(t).

Обозначим: V = y^TP y. Заметим, что из матричного неравенства

[

]

PCAC⁺ + (CAC⁺)^TP + αP PCB

≺0

(CB)^TP

-αG

следует, что

[y(t)]T [PCAC+ + (CAC+)TP + αP PCB][y(t)]

≤ 0,

∀t ≥ 0,

f (t)

(CB)^TP

-αG f(t)

и тогда

V (t) + αV (t) ≤ αf^T(t)Gf(t),

∀t ≥ 0.

При выполнении условия (6) из этого следует, что

lim sup V (t) ≤ 1

t→+∞

и если V (t₀) ≤ 1, то V (t) ≤ 1 при всех t ≥ t₀. При этом V = x^TC^TP Cx,

C^TPC ≽ 0 и rankC^TPC = k, а значит, подмножество

{



}



x∈Rⁿ

 x^TQx ≤ 1 , Q = C^TPC

пространства состояний системы (5)-(6) является притягивающим (k, n)-ци-

линдром.

Доказательство теоремы

2. В соответствии с теоремой 1 под-

множество {s ∈ Rⁿ | s^TK^TP Ks ≤ 1} системы (12) является притягивающим

(k, n)-цилиндром, если выполнены условия

(Π.2)

KM(I - K⁺

K) = 0,

[

]

PKMK⁺ + (KMK⁺)^TP + αP PKN

(Π.3)

≺ 0.

(KN)^TP

-αG

Для существования регулятора (9) такого, чтобы для замкнутой системы

(12) выполнялось условие (Π.2), необходимо и достаточно, чтобы уравнение

K(A + BXD)(I - K⁺K) = 0

⇔ KBXD(I - K⁺K) = -KA(I - K⁺K)

было разрешимо относительно X. В соответствии с леммой 3 это так в том и

только в том случае, если выполнено

KB(KB)⁺KA(I - K⁺K)(D(I - K⁺K))⁺D(I - K⁺K) =

(Π.4)

= KA(I - K⁺K),

причем все соответствующие матрицы X могут быть параметризованы как

X = (KB)⁺KA(K⁺K - I)(D(I - K⁺K))⁺ +

(Π.5)

+ Y - (KB)⁺KBY D(I - K⁺K)(D(I - K⁺K))⁺,

где Y - произвольная матрица соответствующей размерности. Согласно лем-

ме 4 (Π.4) и (Π.5) равносильны (15) и (17) соответственно.

С учетом выражений M = A + BXD, N = C + BXF условие (Π.3) может

быть переписано в виде

[

]

PKAK⁺ + (KAK⁺)^TP + αP PKC

(KC)^TP

-αG

]

)_T

[PKB

([PKB]

[DK⁺ F] +

[DK⁺ F]

≺0

и после подстановки (17) и применения обозначений (14) представлено как

[

]

PH₁ + HT1 P + αP PH₂

[PH₃]

]

[H4 H5

H^T2P

-αG

(Π.6)

]

)_T

([PH

]

[H4 H5

≺ 0.

Согласно лемме 5 соответствующая матрица Y - а значит, и набор X парамет-

ров регулятора (9) - существует в том и только в том случае, если найдутся

µ₁,µ₂ ∈ R, при которых выполнены матричные неравенства

[

]

PH₁ + HT1 P + αP PH₂

[PH₃H^T3P

(Π.7)

≺µ₁

H^T2P

-αG

[

]

[

]

PH₁ + HT1 P + αP PH₂

H^T4H₄

H^T4H₅

(Π.8)

≺µ₂

H^T2P

-αG

H^T5H₄

H^T5H₅

Заметим, что если матрица Q такова, что P Q = I, то (Π.7) равносильно

[

]

H₁Q + QH^T1 + αQ H₂

[H₃H^T3

(Π.9)

≺µ₁

H^T2

-αG

[

]

Q 0

чтобы увидеть это, достаточно умножить (Π.7) слева и справа на

≻ 0.

Для завершения доказательства осталось заметить, что (Π.8), (Π.9) совпа-

дают с (16), (Π.6) равносильно (18) и что при фиксированных α, P матричное

неравенство (18) является линейным.

СПИСОК ЛИТЕРАТУРЫ

Назин С.А., Поляк Б.Т., Топунов М.В. Подавление ограниченных внешних воз-

мущений с помощью метода инвариантных эллипсоидов // АиТ. 2007. № 3.

С. 106-125.

Nazin S.A., Polyak B.T., Topunov M.V. Rejection of Bounded Exogenous Distur-

bances by the Method of Invariant Ellipsoids // Autom. Remote Control. 2007. V. 68.

No. 3. P. 467-486.

Поляк Б.Т., Топунов М.В. Подавление ограниченных внешних возмущений:

управление по выходу // АиТ. 2008. № 5. С. 72-90.

Polyak B.T., Topunov M.V. Suppression of Bounded Exogenous Disturbances: Out-

put Feedback // Autom. Remote Control. 2008. V. 69. No. 5. P. 801-818.

Хлебников М.В. Подавление ограниченных внешних возмущений: линейный ди-

намический регулятор по выходу // АиТ. 2011. № 4. С. 27-42.

Khlebnikov M.V. Suppression of Bounded Exogenous Disturbances: A Linear Dy-

namic Output Controller // Autom. Remote Control. 2011. V. 72. No. 4. P. 699-712.

Железнов К.О., Хлебников М.В. Применение метода инвариантных эллипсои-

дов для решения линейной задачи слежения // Тр. МФТИ. 2013. Т. 5. № 4.

С. 115-121.

Железнов К.О., Квинто Я.И., Хлебников М.В. Решение задачи слежения для

линейной системы управления на основе метода инвариантных эллипсоидов //

УБС. 2018. № 71. С. 45-60.

El Ghaoui L., Oustry F., AitRami M. A Cone Complementarity Linearization Al-

gorithm for Static Output-Feedback and Related Problems // IEEE Trans. Autom.

Control. 1997. V. 42. No. 1. P. 1171-1176.

Briat C. Linear Parameter-Varying and Time-Delay Systems: Analysis, Observation,

Filtering and Control. Springer, 2015.

Arzelier D., Henrion D., Peaucelle D. Robust State-Feedback D-stabilization via a

Cone Complementarity Algorithm // 6th European Control Conference. Portugal.

2001.

Song X., Zhou S., Zhang B. A Cone Complementarity Linearization Approach to

Robust H_∞-controller Design for Continuous-Time Piecewise Linear Systems with

Linear Fractional Uncertainties // Nonlinear Analysis: Hybrid Systems. 2008. V. 2.

No. 4. P. 1264-1274.

10. Henderson H. V., Searle S. R. On Deriving the Inverse of a Sum of Matrices //

SIAM Rev. 1981. V. 23. No. 1. P. 53-60.

11. Gene G. H., Van Loan C. F. Matrix Computations. Johns Hopkins University Press,

1996.

12. Skelton R.E., Iwasaki T., Grigoriadis K.M. A Unified Algebraic Approach to Linear

Control Design / Nonlinear Analysis. London: Taylor & Francis, Ltd, 1998.

13. Maciejewski A.A., Klein C.A. Obstacle Avoidance for Kinematically Redundant Ma-

nipulators in Dynamically Varying Environments // Int. J. Robot. Res. 1985. V. 4.

No. 3. P. 109-117.

14. Boyd S., El Ghaoui L., Feron E., Balakrishnan V. Linear Matrix Inequalities in

System and Control Theory. Philadelphia: SIAM, 1994.

Статья представлена к публикации членом редколлегии М.В. Хлебниковым.

Поступила в редакцию 02.04.2020

После доработки 15.07.2020

Принята к публикации 10.09.2020