Автоматика и телемеханика, № 2, 2021
© 2021 г. А.А. ЩЕГЛОВА, д-р физ.-мат. наук (shchegl@icc.ru)
(Институт динамики систем и теории управления
имени В.М. Матросова СО РАН, Иркутск)
К ВОПРОСУ О СВЕРХУСТОЙЧИВОСТИ ИНТЕРВАЛЬНОГО
СЕМЕЙСТВА ДИФФЕРЕНЦИАЛЬНО-АЛГЕБРАИЧЕСКИХ
УРАВНЕНИЙ
Рассматривается интервальное семейство дифференциально-алгебраи-
ческих уравнений (ДАУ) в предположениях, гарантирующих совпаде-
ние структуры общего решения каждой из систем данного семейства со
структурой общего решения номинальной системы. Анализ базируется
на преобразовании интервального семейства ДАУ к виду, в котором раз-
делены дифференциальная и алгебраическая части. Данное преобразо-
вание включает в себя обращение интервальной матрицы. В предполо-
жении сверхустойчивости дифференциальной подсистемы номинальных
ДАУ найдена оценка радиуса устойчивости. Получены достаточные усло-
вия робастной устойчивости на основе условия сверхустойчивости диф-
ференциальной части интервального семейства.
Ключевые слова: дифференциально-алгебраические уравнения, интер-
вальные коэффициенты, произвольно высокий индекс неразрешенности,
робастная устойчивость, сверхустойчивость.
DOI: 10.31857/S0005231021020045
1. Введение
Рассматривается система обыкновенных дифференциальных уравнений
(1.1)
A0x′(t) + B0
x(t) = 0, t ∈ T = [0, +∞),
где A0 и B0
заданные вещественные (n × n)-матрицы, x(t)
искомая
n-мерная функция. Предполагается, что det A0 = 0. Cистемы такого рода на-
зываются дифференциально-алгебраическими уравнениями (ДАУ). Важней-
шей характеристикой ДАУ является индекс неразрешенности, отражающий
сложность внутренней структуры системы.
Статья посвящена исследованию асимптотической устойчивости ДАУ с
интервальными коэффициентами.
Анализ робастной устойчивости в случае систем ДАУ существенно слож-
нее, чем для систем обыкновенных дифференциальных уравнений, разрешен-
ных относительно производной (см., например, [1, c. 186-225]). Это связано с
тем, что даже в простейшем случае индекса 1 сколь угодно малое возмущение
коэффициентов ДАУ может привести к нарушению внутренней структуры
системы и к изменению вида общего решения.
55
Публикаций по робастной устойчивости ДАУ относительно немного. Пер-
выми опубликованными исследованиями по данной тематике считаются [2, 3].
Большинство авторов рассматривают только системы с возмущенным мат-
ричным коэффициентом при x(t) [3-7]. Лишь в нескольких публикациях до-
пускаются возмущения матрицы при производной искомой вектор-функции
[2, 8-10]. Отдельные исследования посвящены робастной устойчивости и
оценке радиуса устойчивости нестационарных ДАУ индекса 1 [4, 5, 11]. Вы-
числительный аспект нахождения радиуса устойчивости ДАУ изучался в [12].
Некоторое представление о современном состоянии исследований в области
робастной устойчивости ДАУ дает обзор [13, c. 63-95].
Тем не менее по-прежнему актуальным остается получение результатов по
робастной устойчивости систем произвольно высокого индекса неразрешен-
ности с возмущениями, присутствующими во всех матричных коэффициен-
тах, в частности интервальными. Именно такого рода системам и посвящена
данная статья.
Рассматривается интервальное семейство
(1.2)
(A0 + γΔA) x′(t) + (B0 + γΔB
)x(t) = 0, t ∈ T,
где ΔA = (αi,j)i,j=1,n и ΔB = (βi,j )i,j=1,n матрицы неопределенностей. При
этом
(1.3)
G ≤ ΔA ≤ G, H ≤ ΔB
≤H
(здесь и далее матричные неравенства следует понимать в поэлементном
смысле); G, G, H, H задают масштабы изменения матриц A0 и B0, величина
γ > 0 определяет размах неопределенностей.
Для анализа используется структурная форма ДАУ с разделенными диф-
ференциальной и алгебраической подсистемами. В предположении сверх-
устойчивости дифференциальной подсистемы получена оценка величины γ,
при выполнении которой каждая из систем интервального семейства (1.2)
будет асимптотически устойчива. Кроме того, обоснованы достаточные усло-
вия робастной устойчивости ДАУ (1.1), вытекающие из условия сверх-
устойчивости дифференциальной подсистемы интервального семейства. При
этом, чтобы размерность пространства решений и структура общего реше-
ния ДАУ (1.2) были такими же, как у невозмущенной системы (1.1), на ин-
тервальные возмущения налагаются ограничения в виде конечных соотноше-
ний.
2. Cтруктурная форма для системы
дифференциально-алгебраических уравнений
Для ДАУ (1.1) определим (n(r + 1) × n)-матрицы
Br = col (B0,O,... ,O) ,
(2.1)
Ar = col (A0,B0,O,... ,O) ,
56
(n(r + 1) × nr)-матрицу
O O ... O O
A0
O ... O O
B0
A0
... O O
(2.2)
Λr =
O O ... A0 O
O O ... B0 A0
и (n(r + 1) × n(r + 2))-матрицу
(
)
Dr =
Br Ar Λr
Предположим, что для некоторого r (0 ≤ r ≤ n) в Dr найдется неособен-
ный минор n(r + 1)-го порядка, включающий в себя λ = rank Λr столбцов
матрицы Λr и все столбцы матрицы Ar. Такой минор будем называть раз-
решающим. Обозначим через Mr матрицу, определителем которой является
разрешающий минор.
Разобъем матричные коэффициенты системы (1.1) на блоки:
(2.3)
(A1 A2 ) = A0Q, (B1 B2 ) = B0
Q,
где Q матрица перестановок столбцов такая, что все столбцы матрицы
(2.4)
B2,r = col (B2
,O,... ,O)
являются составляющей частью разрешающего минора, а столбцы матрицы
col (B1, O, . . . , O)
не входят в этот минор. Блоки B2 и A2 имеют размеры n × d, d = nr - λ.
О построении матрицы Q см. [14].
Определение 1. Наименьшее значение r, при котором в матрице Dr
найдется разрешающий минор, называется индексом неразрешенности ДАУ
(1.1).
Лемма 1 [15]. Наличия разрешающего минора в матрице Dr необходимо
и достаточно для существования оператора
d
(d)r
(2.5)
R=R0 +R1
+...+Rr
dt
dt
(Rj
(n × n)-матрицы (j = 0, r)), обладающего свойством: для любой
n-мерной функции ϕ(t) ∈ Cr+1(T )
[
]
d
R A
ϕ(t) + Bϕ(t)
=
dt
(
)
(r+1)
d
(d)
= (R0 R1 . . . Rr) Dr col ϕ(t),
ϕ(t), . . . ,
ϕ(t)
=
dt
dt
(
)
(
)
O O
d
J1
Ed
=
Q-1
ϕ(t) +
Q-1ϕ(t),
En-d O
dt
J2
O
57
где Q
матрица перестановок из (2.3), J1 и J2
некоторые матрицы
соответствующих размеров.
При этом
(2.6)
(R0 R1
... Rr) = (En O ... O)M-1r.
Таким образом, действие оператора (2.5) на систему (1.1) преобразует ее
к виду
(
(
O O
)( x′1(t))
J1
Ed
)( x1(t))
(2.7)
+
= 0,
En-d O
x′2(t)
J2
O
x2(t)
где col (x1(t), x2(t)) = Q-1x(t).
Лемма 2 [14]. Пусть в матрице Dr имеется разрешающий минор и
справедливо равенство
(2.8)
rank Λr+1 = rank Λr
+ n.
Тогда оператор R обладает левым обратным оператором
d
L=L0 +L1
dt
3. Достаточные условия сохранения внутренней структуры
В предположениях леммы 2 существует оператор R вида (2.5), который
преобразует систему (1.1) к структурной форме (2.7) и при этом имеет ле-
вый обратный оператор L. Непосредственно из существования операторов R
и L вытекает эквивалентность в смысле решений систем (1.1) и (2.7). Та-
ким образом, системы (1.1) и (2.7) обладают одними и теми же свойствами
устойчивости.
Для того чтобы иметь возможность проводить анализ устойчивости интер-
вальных ДАУ (1.2), (1.3), опираясь на информацию о структуре и свойствах
системы (1.1) (или, что то же, (2.7)), введем следующее определение.
Определение 2. Будем говорить, что возмущения γΔA и γΔB, под-
чиняющиеся ограничениям (1.3), сохраняют внутреннюю структуру ДАУ
(1.1), если существует оператор
∑ (d
)j
R=
(3.1)
R
j dt
j=0
с интервальными коэффициентами такой, что его действие на систему
(1.2) преобразует ее к виду
(
)(
)
(
O O
x′1(t)
U1
Ed
)( x1(t))
(3.2)
+
= 0,
En-d O
x′2(t)
U2
O
x2(t)
где col (x1(t), x2(t)) = Q-1x(t), U1 и U2 некоторые интервальные матрицы
соответствующих размеров.
58
Найдем условия, при которых для системы (1.2) при каждом выборе воз-
мущений определен операторR.
Аналогично тому, как это было сделано в (2.3), разобъем на блоки все
матрицы, фигурирующие в неравенствах (1.3):
(3.3)
ΔAQ = ( ΔA1 ΔA2 ) , ΔBQ = ( ΔB1 ΔB2
),
(
)
(
)
GQ = G[1] G[2]
,
GQ = G[1] G[2]
,
(
)
(
)
(3.4)
HQ= H[1] H[2]
,
HQ= H[1] H[2]
Здесь Q матрица перестановок из (2.3); блоки ΔA2 , ΔB2 , G[2], G[2], H[2] и
H[2] имеют размеры n × d, также как и блоки A2 и B2 в (2.3).
Обозначим
O O ... O
ΔA O ... O O
ΔB ΔA ... O O
(3.5)
ΔΛr =
,
O O ... ΔB ΔA
O O ... O
O O ... O
G O ... O O
G O ... O
O
H G ... O O
H G ... O
O
(3.6)
,
ΔΛr =
,
ΔΛr=
O O ... H G
O O ... H
G
где ΔΛr задает возмущение матрицы Λr (2.2). По построению
ΔΛr ≤ ΔΛr ≤ ΔΛr.
Пусть QΛ матрица перестановок столбцов, такая что
(
)
Λr QQΛ = Λ[1]r Λ[2]
,
r
где
Q= diag {Q,... ,Q} имеет на главной диагонали r блоков, равных Q;
Λr1]
матрица размеров n(r + 1) × λ, состоящая из столбцов матрицы Λr,
которые входят в разрешающий минор;
Λr2]
матрица размеров n(r + 1) × (nr - λ), состоящая из столбцов, кото-
рые не входят в упомянутый минор.
Введенные обозначения позволяют записать явное представление матри-
цы Mr:
(
)
Mr =B2,r Ar Λr1]
59
Аналогичным образом разобъем на блоки матрицы (3.5) и (3.6):
(
)
ΔΛr QrQΛ = Δ[1]Λ, Δ[2]
,
Λ
(
)
(
)
ΔΛr QrQΛ = Δ[1]Λ, Δ[2]
,
ΔΛr QrQΛ = Δ[1]Λ, Δ[2]
Λ
Λ
Введем в рассмотрение квадратную матрицу порядка n(r + 1)
ΔB2
ΔA1
ΔA2
O ΔB1 ΔB2
O O O
(3.7)
ΔMr =
Δ[1]Λ
,
.
O O O
определяющую возмущение матрицы Mr,
(3.8)
ΔMr ≤ ΔMr ≤ ΔMr,
где
H[2] G[1] G[2]
O H[1] H[2]
O O O
Δ[1]Λ
ΔMr=
r
,
O O O
(3.9)
H[2] G[1] G[2]
O H[1] H[2]
O O O
Δ[1]Λ
ΔMr =
r
.
O O O
Рассмотрим интервальное семейство матриц Mr + γΔMr , в котором каж-
дая из “ точечных” матриц, подчиняется неравенствам
(3.10)
Mr + γΔMr ≤ Mr + γΔMr ≤ Mr + γΔMr.
(
)
Определение 3. Пусть заданы вещественные матрицы S =
si,ji,j=1,n,
S = (si,j)i,j=1,n и семейство интервальных матриц S = (si,j)i,j=1,n:
S≤S≤S.
Определим матрицу abs(S) = (ŝi,j)i,j=1,n , такую что
{
}
ŝi,j = max
|si,j|, |si,j|
60
В соответствии с определением 3 построим матрицу F = abs ( ΔA ΔB ).
Тогда для любой матрицы ΔMr , удовлетворяющей оценке (3.8),
∥ΔMr∥ ≤ ∥F ∥,
где
∑
∥S∥ = max
|sij|
1≤i≤n
j=1
для любой (n × n)-матрицы S с элементами sij.
Утверждение. Пусть
1
(3.11)
γ∥F ∥ <
∥
r
∥
Тогда матрица Mr + γΔMr будет обратима при любых неопределенно-
стях ΔA и ΔB, удовлетворяющих неравенствам (1.3). Кроме того, справед-
ливы оценки:
∥M-1r∥
(3.12)
∥(Mr + γΔMr)-1 ∥ ≤
,
1-γ∥F∥∥
r
∥
∥2∥F∥
r
(3.13)
∥(Mr + γΔMr)-1 - M-1r∥ ≤γ∥
1-γ∥F∥∥
r
∥
Утверждение является очевидным следствием известных результатов
[16, c. 205].
Обозначим через Mr+1 обратимую подматрицу порядка n(r + 2) матри-
цы Dr+1, включающую в себя n + λ столбцов матрицы Λr+1 и все столбцы
матрицы ( B2,r+1 Ar+1 ) (см. (2.4), (2.3), (2.1)).
Теорема 1. Пусть:
1) в матрице Dr существует разрешающий минор;
2) имеет место равенство (2.8);
3) при каждом выборе матриц ΔA и ΔB, подчиняющихся ограничени-
ям (1.3),
(3.14)
(En+d Oλ)M-1rΔ[2]Λ
=O
(индекс при нулевой матрице указывает на число ее столбцов), а матрица
M-1rΔMr обладает структурой
(
)
∗ O
(3.15)
M-1rΔMr =
,
∗
∗
где размеры нулевого блока (n + d) × λ; ∗ обозначает матрицу, явный вид
которой несуществен.
61
Если кроме того
1
(3.16)
γ∥F ∥ <
,
∥M-1r+1∥
то при каждом выборе матриц ΔA и ΔB оператор (3.1), преобразующий
ДАУ (1.2) к виду (3.2), существует, имеет левый обратный оператор
d
L=L0 +L1d
и его коэффициенты вычисляются по формуле
t
(
)
R0
R1
Rr
(3.17)
= (En O )(Mr + γΔMr)-1 .
Доказательство теоремы 1 опущено.
Замечание 1. Нетрудно показать, что неравенство (3.16) гарантирует
оценку (3.11).
4. Оценка радиуса робастной устойчивости ДАУ
В этом разделе в предположениях, обеспечивающих сохранение структу-
ры, получена оценка величины γ, при выполнении которой ДАУ (1.2) будут
асимптотически устойчивы для всех матричных коэффициентов из рассмат-
риваемых интервальных семейств. Эта оценка является следствием формулы
для радиуса сверхустойчивости дифференциальной подсистемы
(4.1)
x′1(t) + U2x1
(t) = 0
интервального семейства (3.2).
Определение 4. Решением ДАУ (1.1) будем называть n-мерную век-
тор-функцию x∗(t) ∈ C1(T), обращающую систему (1.1) в тождество при
подстановке.
При каждом выборе возмущений ΔA и ΔB, подчиняющихся оценкам (1.3),
решение системы (1.2) будем понимать в смысле определения 4.
Определение 5. Интервальное семейство
(1.2) будем называть
асимптотически устойчивым, если при каждом выборе возмущений (1.3)
соответствующая система ДАУ из этого семейства асимптотически
устойчива.
Замечание 2. Как было отмечено выше, в предположениях леммы 2
системы (1.1) и (2.7) обладают одними и теми же свойствами устойчивости.
Пусть дифференциальная подсистема ДАУ (2.7)
(4.2)
x′1(t) + J2x1
(t) = 0
асимптотически устойчива, т.е. любое решение x1(t) этой системы обладает
свойством ∥x1(t)∥ → 0, t → +∞. В свою очередь любое решение алгебраиче-
ской подсистемы находится по формуле x2(t) = -J1x1(t) и, следовательно,
∥x2(t)∥ → 0, t → +∞. Поэтому будем называть систему (2.7) или, что то же,
систему (1.1) асимптотически устойчивой, если этим свойством обладает
система (4.2).
62
Замечание 3. В предположениях теоремы 1 можно провести аналогич-
ные рассуждения в отношении систем (1.2) и (3.2). Существование операторов
R
L гарантирует, что семейства (1.2) и (3.2) имеют одни и те же решения,
так что они и асимптотически устойчивы одновременно. Последнее имеет
место, если этим же свойством обладает каждая система из интервального
семейства (4.1).
В условиях теоремы 1 по построению
U2 = (Od En-d )R0 (B1 + γΔB1 ) ,
где матрицы B1 и ΔB1 определены в (2.3) и (3.3) соответственно,R0 первый
коэффициент дифференциального оператора (3.1), который переводит (1.2)
в систему (3.2).
С учетом (3.17) можно получить представление
(4.3)
U2 = J2 + ΔU2,
(
)
B1
где J2 = ( Od En-d Onr ) M-1r
матричный коэффициент из (2.7)
O
и (4.2), ΔU2 = (δi,j)i,j=1,n-d,
)
(
)(B
1
ΔU2 = ( Od En-d Onr ) (Mr + γΔMr )-1 - M-1r
+
O
(
)
ΔB1
(4.4)
+ γ (Od En-d Onr )(Mr + γΔMr)-1
O
Определение 6. В условиях теоремы 1 будем говорить, что систе-
ма (1.1) робастно устойчива относительно ограничений (1.3), если каждая
система из интервального семейства (1.2) асимптотически устойчива.
Определение 7. Радиусом робастной устойчивости системы
(1.1)
относительно ограничений (1.3) будем называть точную верхнюю грань по
всем значениям параметра γ, при которых интервальное семейство (1.2)
асимптотически устойчиво.
Для матрицы J2 = (ζi,j)i,j=1,n-d из (4.2) определим величину
∑
σ(J2) = min
ζi,i -
|ζi,j| .
1≤i≤n-d
j=1, j=i
Система (4.2) называется cверхустойчивой [1, с. 199], если
(4.5)
σ(J2
) > 0.
Сверхустойчивая система асимптотически устойчива.
По замечанию 2 в предположениях леммы 2 система (1.1) будет асимпто-
тически устойчива, если сверхустойчива система (4.2).
Обратимся к интервальному семейству (4.1).
63
Лемма 3 [1, c. 223]. Пусть система (4.2) сверхустойчива, т.е. имеет
место неравенство (4.5). Интервальное семейство (4.1),(4.3) будет сверх-
устойчиво при всех δi,j:
(4.6)
|δi,j
| ≤ η, i,j = 1,n - d,
тогда и только тогда, когда
σ(J2)
η < η∗ :=
n-d
Величина η∗ называется радиусом сверхустойчивости семейства (4.1),
(4.3), (4.6).
В рассматриваемом случае невозможно априори указать величину η, опре-
деляющую границы изменения элементов матрицы ΔU2 из (4.3), посколь-
ку система (4.1) получена из (1.2) посредством обращения интервальной
матрицы.
Для получения оценки |δi,j | разобъем следующие (n - d) × n(r + 1)-мат-
рицы на блоки размеров (n - d) × n:
(4.7)
(Od En-d Onr )(Mr + γΔMr)-1 = (M0 M1 ... Mr
),
(Od En-d Onr)M-1r =(P0 P1 ... Pr).
Тогда
J2 = P0B1,
(4.8)
ΔU2 = (M0 - P0) B1 + γM0ΔB1.
Используя обозначения для элементов матриц
(4.9)
M0 = (µi,l)i=1,n-d,l=1,n , P0 = (pi,j)i=1,n-d,l=1,n ,
(
)
(
)
(4.10)
B1 = b[1]
,
ΔB1 = β[1]
,
l,j
l,j
l=1,n,j=1,n-d
l=1,n, j=1,n-d
запишем (4.8) поэлементно
∑
∑
(4.11)
δi,j =
(µi,l - pi,l) b[1]l,j + γ
µi,lβ[1]l,j
,
i, j = 1, n - d.
l=1
l=1
Здесь величины µi,l и β[1]l,j являются “точечными” значениями из соответст-
вующих интервалов.
Из (4.11) следует, что
∑
∑
(4.12)
|δi,j| ≤
|µi,l - pi,l||b[1]l,j| + γ
|µi,l||β[1]l,j
|,
i, j = 1, n - d.
l=1
l=1
64
С учетом (3.12) и (3.13)
∑
|µi,l - pi,l| ≤ ∥M0 - P0∥ ≤ ∥ (Mr + γΔMr )-1 - M-1r∥ ≤
l=1
γ∥M-1r∥2∥F ∥
(4.13)
≤
,
1-γ∥F∥∥
r
∥
∑
∥M-1r∥
(4.14)
|µi,l| ≤ ∥M0∥ ≤ ∥ (Mr + γΔMr )-1 ∥ ≤
1-γ∥F∥∥
r
∥
l=1
Обозначим через b∗ максимальный элемент матрицы |B1|:
(4.15)
b∗ =
max
|b[1]l,j
|;
1≤l≤n, 1≤j≤n-d
а через β∗ максимальный элемент матрицы abs(ΔB1 ):
(4.16)
β∗ =
max
abs(β[1]l,j
).
1≤l≤n, 1≤j≤n-d
Введем в рассмотрение величину
[
]
(4.17)
θ = ∥M-1r∥
∥M-1r∥∥F ∥b∗ + β∗
Используя (4.13)-(4.17), оценку (4.12) можно усилить:
γθ
|δi,j | ≤
1-γ∥F∥∥
r
∥
Из замечания 3 следует, что семейство (1.2) будет асимптотически устой-
чиво, если сверхустойчива интервальная система (4.1). Согласно лемме 3 по-
следнее имеет место, когда
γθ
<η∗,
1-γ∥F∥∥
r
∥
откуда получаем искомую оценку радиуса робастной устойчивости систе-
мы (1.1)
∗
η
(4.18)
γ<
θ+η∗∥F∥∥
r
∥
Теорема 2. Пусть выполнены все предположения теоремы 1 и справед-
ливо условие (4.5). Система ДАУ (1.1) будет робастно устойчива относи-
тельно ограничений (1.3), если имеет место неравенство (4.18), в котором
η∗ =σ(J2)n-d, а величина θ находится по формуле (4.17).
65
5. Достаточное условие робастной устойчивости как следствие робастной
сверхустойчивости дифференциальной подсистемы
Положим γ = 1, так что система (1.2) приобретает вид
(5.1)
(A0 + ΔA) x′(t) + (B0 + ΔB
)x(t) = 0, t ∈ T.
Как было показано в разделе 4, в предположениях теоремы 1 каждая си-
стема интервального семейства (5.1) будет асимптотически устойчива, если
тем же свойством обладает и семейство (4.1).
В обозначениях
(4.7),
(2.3) и
(3.3) интервальная матрица U2 =
= (ui,j)i,j=1,n-d из (3.2) и (4.1) находится по формуле
U2 = M0 (B1 + ΔB1).
С использованием (4.9), (4.10)
∑ (
)
ui,j =
µi,l b[1]l,j + β[1]
l,j
l=1
Допустим, удалось получить оценки
(5.2)
ui,j ≤ ui,j ≤ ui,j
,
i, j = 1, n - d.
По определению каждая из систем семейства (4.1) будет сверхустойчива,
если выполняется условие
∑
(5.3)
σ (U2) = min
ui,i -
|ui,j|
> 0.
1≤i≤n-d
j=1,j=i
Поскольку
∑
∑
{
}
ui,i -
|ui,j | ≥ ui,i -
max
|ui,j |, |ui,j|
,
j=1,j=i
j=1,j=i
то неравенство (5.3) будет иметь место, если
∑
{
(5.4)
min
u
-
max
|ui,j|, |ui,j|}
> 0.
i,i
1≤i≤n-d
j=1,j=i
Тем самым доказан следующий результат.
Теорема 3. Пусть γ = 1 и выполнены все предположения теоремы 1.
Если кроме того имеет место неравенство (5.4), то система (1.1) будет
робастно устойчива относительно ограничений (1.3).
66
Пример. В качестве иллюстрации рассмотрим ДАУ
(
)
(
)
0
0
-3 2
(5.5)
x′(t) +
x(t) = 0.
6
-3
2
1
Для этой системы справедливо условие 1 теоремы 1, так как в матрице
-3
2
0
0
0
0
2
1
6
-3
0
0
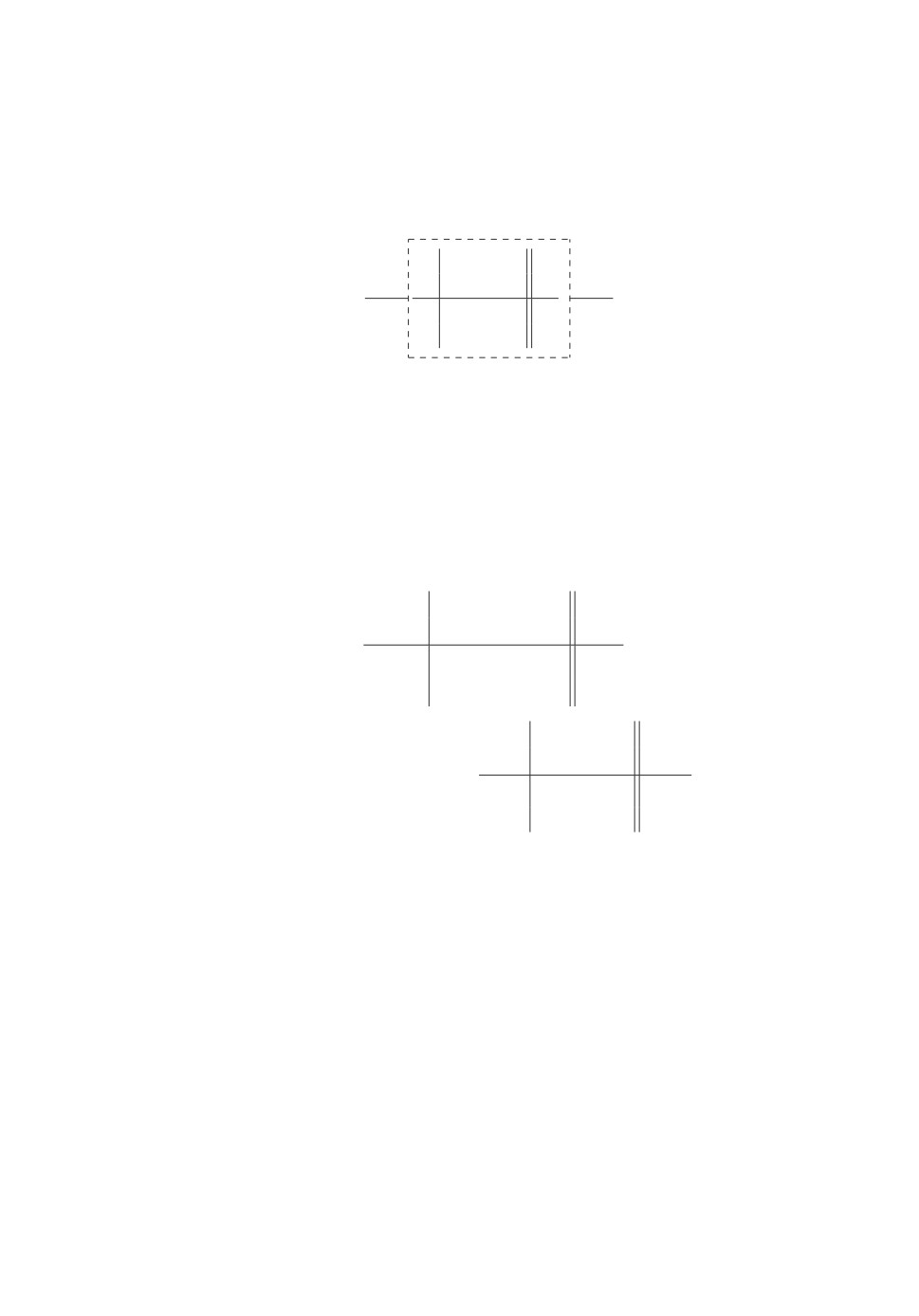
D1 =
0
-3
2
0
0
0
0
0
2
1
6
-3
имеется подматрица M1, обведенная штриховой линией, определителем
котор(й яв)яется разрешающий минор. При этом r = 1, d = 1, Q = E2,
-3
B1 =
, rankΛ1 = λ = 1. Используя явный вид матрицы Λ2, нетрудно
2
вычислить rank Λ2 = 3. Следовательно, условие 2 теоремы 1 тоже выполнено.
Покажем, что для соответствующей интервальной системы (5.1) имеют
место все предположения теоремы 3. Поскольку
1/2
0
0
0
1/3
2/3
1
0
-
M-11 =
,
-1/2
1
2
0
7/36
-7/18
-2/3
1/6
β1,2
α1,1
α1,2
0
0
β2,2
α2,1
α2,2
0
0
Δ[2]Λ =
, ΔM1 =
α1,2
0
,
β1,1
β1,2
α1,1
α2,2
0
β2,1
β2,2
α2,1
то
(En+d Oλ )M-11Δ[2]Λ = col (0,α1,2,2α1,2),
∗ ∗ ∗
0
M-11ΔM1 =∗∗∗α1,1
,
∗
∗
∗
2α1,1
∗
∗
∗
∗
где звездочками обозначены элементы, явный вид которых несуществен. Та-
ким образом, условия (3.14) и (3.15) означают, что
(5.6)
α1,1 = α1,2
= 0.
Равенства (5.6) представляют собой условия сохранения внутренней струк-
туры для интервальных ДАУ (5.1).
67
С учетом (5.6) зададим масштабы изменения коэффициентов системы
(5.5):
(
)
(
)
(
)
0
0
α1,1
α1,2
0
0
(5.7)
≤ΔA =
≤
,
−0,03
-0,025
α2,1
α2,2
0,03
0,025
(
)
(
)
(
)
-0,05
-0,045
β1,1
β1,2
0,05
0,045
(5.8)
≤ΔB =
≤
−0,02
-0,02
β2,1
β2,2
0,02
0,02
Легко видеть, что ∥F ∥ = 0,095. В свою очередь ∥M-12∥ = 10,5 (явное пред-
ставление матрицы M-12 из-за громоздкости приводить не будем). Очевидно,
что неравенство (3.16) выполняется. Таким образом, для рассматриваемых
ДАУ имеют место все предположения теоремы 1.
Найдем оценку радиуса устойч(ости, поль)яс( теор)мой
2. В со-
1/2
0
0
0
d
ответствии с формулой (2.6) R =
+
и в
(2.7)
−1/3
2/3
1
0
dt
J2 = (7/3). Очевидно, что неравенство (4.5) выполнено и η∗ = 7/3. По фор-
муле (4.17) находим θ = 3,66625. Наконец, из (4.18) получаем искомую оценку
7
γ<
≈ 0,52.
13,32625
Проверим для рассматриваемой системы выполнение достаточного усло-
вия робастной устойчивости, предоставляемого теоремой 3. Ввиду того что
U2 = ( u1,1 ), условие (5.4) в данном случае имеет вид u1,1 > 0, где
u1,1 = µ1,1 (-3 + β1,1) + µ1,2 (2 + β2,1),
-1 - β2,2
2+β1,2
µ1,1 =
,
µ1,2 =
,
h
h
h = (2 + β1,2)(6 + α2,1) - (-3 + β1,1)(-3 + α2,2).
Отсюда с учетом (5.7), (5.8) u1,1 =6761935551 > 1,9 > 0. Согласно теореме 3 это
означает, что система (5.5) робастно устойчива относительно ограничений
(5.7), (5.8).
Замечание 4. Следует отметить, что получить явные формулы для фи-
гурантов неравенства (5.4) в общем случае невозможно без дополнительных
предположений о свойствах матрицы Mr + ΔMr , обратная к которой исполь-
зуется для вычисления M0 (см. (4.7)). Интервальный анализ предоставляет
весьма скромные средства для нахождения оценок обратных интервальных
матриц. Например, можно предположить, что Mr + ΔMr и Mr + ΔMr (ΔMr и
ΔMr
“крайние” матрицы для ΔMr (см. (3.8), (3.9)) положительно обратимы,
являются M-матрицами или H-матрицами [17, с. 104-113]. К сожалению, все
эти предположения вступают в противоречие с условиями (5.3), (5.4) и (4.5).
6. Заключение
В статье получены оценка радиуса устойчивости и достаточные условия
робастной устойчивости для ДАУ произвольно высокого индекса неразрешен-
ности с использованием условия сверхустойчивости.
68
Система ДАУ состоит из двух взаимосвязанных частей: подсистемы обык-
новенных дифференциальных уравнений (ОДУ), разрешенной относительно
производной, и подсистемы алгебраических уравнений. Под сверхустойчивос-
тью системы ДАУ понимается сверхустойчивость ее дифференциальной ча-
сти. Таким образом, класс сверхустойчивых ДАУ соизмерим с классом сверх-
устойчивых систем, разрешенных относительно производной. Несмотря на то,
что этот класс довольно узок, понятие сверхустойчивости позволяет полу-
чить простое или явное представление для радиуса робастной устойчивости
систем ОДУ(см., в частности, [18, 19]). Подход к исследованию ДАУ, связан-
ный с предположением о сверхустойчивости, наследует все преимущества и
недостатки, присущие исследованию робастной устойчивости сверхустойчи-
вых систем, разрешенных относительно производной.
Особенностью ДАУ является то, что даже в случае индекса 1 сколь угод-
но малое возмущение коэффициентов может привести к тому, что изменится
размерность дифференциальной и алгебраической подсистем и свойства об-
щего решения возмущенной системы не будут иметь ничего общего со свой-
ствами общего решения номинальной системы [20, c. 7]. Для того чтобы избе-
жать подобной ситуации и гарантировать наследование интервальными ДАУ
свойства устойчивости, на матрицы возмущений накладываются ограничения
(называемые “условиями сохранения структуры”), обеспечивающие совпаде-
ние структуры общего решения возмущенной и номинальной систем. Преиму-
ществом результатов, представленных в данной статье, является то, что ис-
пользованные предположения не накладывают ограничений на внутреннюю
структуру номинальных ДАУ, ориентированы на системы произвольного ин-
декса с возмущениями, присутствующими не только в матрице при x(t), но
и в матрице при производной. Полученные условия робастной устойчивости
носят конструктивный характер и несложны для проверки.
СПИСОК ЛИТЕРАТУРЫ
1. Поляк Б.Т., Щербаков П.С. Робастная устойчивость и управление. М.: Наука,
2002.
2. Byers R., Nichols N.K. On the Stability Radius of a Generalized State-Space Sys-
tem // Linear Algebra Appl. 1993. No. 188-189. P. 113-134.
3. Qiu L., Davisov E.J. The Stability Robustness of Generalized Eigenvalues // IEEE
Trans. Autom. Control. 1992. No. 37. P. 886-891.
4. Chyan C.J., Du N.H., Linh V.H. On Data-Dependence of Exponential Stability
and the Stability Radii for Linear Time-Varying Differential-Algebraic Systems //
J. Differ. Equat. 2008. No. 245. P. 2078-2102.
5. Du N.H., Linh V.H. Stability Radii for Linear Time-Varying Differential-Algebraic
Equations with Respect to Dynamics Perturbations // J. Differ. Equat.
2006.
No. 230. P. 579-599.
6. Fang C.-H., Chang F.-R. Analysis of Stability Robustness for Generalized State-
Space Systems with Structured Perturbations // Syst. Control Lett. 1993. No. 21.
P. 109-114.
7. Lee L., Fang C.-H., Hsieh J.-G. Exact Uninderectional Perturbation Bounds for Ro-
bustness of Uncertain Generalized State-Space Systems: Continuous-Time Cases //
Automatica. 1997. No. 33. P. 1923-1927.
69
8.
De Teran F., Dopico F.M., Moro J. First Order Spectral Perturbation Theory of
Square Singular Matrix Pencil // Linear Algebra Appl. 2008. No. 429. P. 548-576.
9.
Linh V.H., Mehrmann V. Lyapunov, Bohl and Sacker-Sell Spectral Intervals for
Differential-Algebraic Equations // J. Dyn. Differ. Equat. 2009. V. 21. P. 153-194.
10.
Lin Ch., Lam J., Wang J., Yang G.-H. Analysis on Robust Stability for Interval
Descriptor Systems // Syst. Control Lett. 2001. No. 42. P. 267-278.
11.
Berger T. Robustness of Stability of Time-Varying Index-1 DAEs // Math. Control
Signals Syst. 2014. No. 26. P. 403-433.
12.
Benner P., Sima V., Voigt M. L∞-norm Computation for Continuous-Time Descrip-
tor Systems Using Structured Matrix Pencils // IEEE Trans. Autom. Control. 2010.
V. 57. No. 1. P. 233-238.
13.
Du N.H., Linh V.H., Mehrmann V. Robust Stability of Differential-Algebraic Equa-
tions / Surveys in Differential-Algebraic Equations I. Ilchmann A., Reis T. (Eds.).
Berlin-Heidelberg: Springer-Verlag, 2013.
14.
Щеглова А.А., Кононов А.Д. Робастная устойчивость дифференциально-алгеб-
раических уравнений произвольного индекса // АиТ. 2017. № 5. C. 36-55.
Shcheglova A.A., Kononov A.D. Robust Stability of Differential-Algebraic Equations
with an Arbitrary Unsolvability Index // Autom. Remote Control. 2017. V. 78.
P. 798-814.
15.
Щеглова А.А., Кононов А.Д. Устойчивость дифференциально-алгебраических
уравнений в условиях неопределенности // Диффер. уравнения. 2018. Т. 54.
№ 7. С. 881-890.
Shcheglova A.A., Kononov A.D. Stability of Differential-Algebraic Equations under
Uncertainty // Differ. Equat. 2018. No. 7. P. 860-869.
16.
Ланкастер П. Теория матриц. М.: Наука, 1978.
17.
Neumaier A. Interval Methods for Systems of Equations. Cambrige: Cambrige Uni-
versity Press, 1990.
18.
Поляк Б.Т., Щербаков П.С. Сверхустойчивые линейные системы управления I //
АиТ. 2002. № 8. C. 37-53.
Polyak B.T., Shcherbakov P.S. Superstable Linear Control Systems I. Analysis //
Autom. Remote Control. 2002. V. 63. No. 8. P. 1239-1254.
19.
Поляк Б.Т., Щербаков П.С. Сверхустойчивые линейные системы управления
II // АиТ. 2002. № 11. C. 56-75.
Polyak B.T., Shcherbakov P.S. Superstable Linear Control Systems II. Design //
Autom. Remote Control. 2002. V. 63. No. 11. P. 1745-1763.
20.
Чистяков В.Ф., Щеглова А.А. Избранные главы теории алгебро-дифференци-
альных систем. Новосибирск: Наука, 2003.
Статья представлена к публикации членом редколлегии П.С. Щербаковым.
Поступила в редакцию 02.09.2019
После доработки 11.02.2020
Принята к публикации 09.07.2020
70