Автоматика и телемеханика, № 2, 2021
Нелинейные системы
© 2021 г. В.Н. АФАНАСЬЕВ, д-р техн. наук (afanval@mail.ru),
А.П. ПРЕСНОВА (presnova.a.p@yandex.ru)
(Национальный исследовательский университет
“Высшая школа экономики”, Москва)
ПАРАМЕТРИЧЕСКАЯ ОПТИМИЗАЦИЯ НЕЛИНЕЙНЫХ СИСТЕМ,
ПРЕДСТАВЛЯЕМЫХ МОДЕЛЯМИ С ИСПОЛЬЗОВАНИЕМ МЕТОДА
“РАСШИРЕННОЙ ЛИНЕАРИЗАЦИИ”1
Проблема оптимального управления формулируется для класса ди-
намических систем, нелинейные объекты которых представимы в виде
объектов с линейной структурой и параметрами, зависящими от состоя-
ния. Линейность структуры преобразованной нелинейной системы и квад-
ратичный функционал качества позволяют при синтезе оптимального
управления, т.е. параметров регулятора, перейти от необходимости по-
иска решений уравнения Гамильтона-Якоби к уравнению типа Риккати
с параметрами, зависящими от состояния. Основная проблема реализа-
ции оптимального управления связана с проблемой поиска решения та-
кого уравнения в темпе функционирования объекта. Предложен алгорит-
мический метод параметрической оптимизации регулятора, основанный
на использовании необходимых условий оптимальности рассматриваемой
системы управления. Построенные алгоритмы могут использоваться как
для оптимизации самих нестационарных объектов, если для этой цели вы-
делены соответствующие параметры, так и для оптимизации всей управ-
ляемой системы с помощью соответствующей параметрической настрой-
ки регуляторов. Эффективность разработанных алгоритмов продемон-
стрирована на примере медикаментозного лечения пациентов при нали-
чии ВИЧ.
Ключевые слова: нелинейные дифференциальные уравнения, метод рас-
ширенной линеаризации, оптимальное управление, уравнение Гамильто-
на-Якоби-Беллмана, уравнение Риккати с параметрами, зависящими от
состояния, параметрическая оптимизация.
DOI: 10.31857/S0005231021020057
1. Введение
Проблема линеаризации является одной из самых богатых областей иссле-
дований систем управления за последние четыре десятилетия. Самым распро-
страненным методом анализа и синтеза систем с аналитическими (гладкими)
функциями является линеаризация, основанная на разложении нелинейной
1 Работа выполнена при финансовой поддержке Российского фонда фундаментальных
исследований (проект № 19-08-00535).
71
функции в окрестностях точки, определяющей заданный режим, в ряд Тейло-
ра и отбрасыванием нелинейных членов. Начиная с работ А.М. Ляпунова [1],
основные результаты оценки устойчивости нелинейной системы по первому
приближению, а также синтеза управления по первому приближению [2] ос-
нованы на изучении расположения корней характеристического уравнения
системы первого приближения (“некритические задачи”). Однако для “кри-
тических задач” рассмотрения первого приближения недостаточно, управле-
ния же, синтезированные по первому приближению, могут и не обеспечить
устойчивости нелинейной системе.
В отличие от этого метода развиваются методы эквивалентного представ-
ления нелинейных систем, например, метод линеаризации обратной связью
(exact linearization) [3-6] или метод “расширенной линеаризации” (extendent
linearization) [7-10], который и используется в данной статье.
Впервые проблема управления нелинейными объектами с их эквивалент-
ным представлением в виде линейных моделей (State Dependent Coefficient,
SDC) с параметрами, зависящими от состояния, и функционалами, матрицы
штрафа которых также зависят от состояния объекта, была сформулирова-
на в начале 60-х гг. XX столетия в [7]. С конца 90-х гг. прошлого столетия
метод привлекает все большее внимание со стороны ученых и практиков. Пре-
образование исходного нелинейного дифференциального уравнения, которое
описывает исходную систему управления, в систему с линейной структурой,
но с параметрами, зависящими от состояния, и использование квадратичного
функционала качества позволяют при синтезе управления осуществить пере-
ход от уравнения Гамильтона-Якоби-Беллмана к уравнению типа Риккати
с параметрами, зависящими от состояния (State Dependent Riccati Equation,
SDRE). Это и составляет основу SDRE-метода синтеза оптимальных нели-
нейных систем управления [8-10]. Следует отметить, что до настоящего вре-
мени остается ряд вопросов, связанных с неоднозначностью представления
нелинейного объекта в виде модели с линейной структурой и с параметра-
ми, зависящими от состояния. Синтезированные управления с использовани-
ем SDC-модели и квадратичным критерием качества обеспечивают устойчи-
вость модели при любых начальных условиях. Но этого может не быть при
приложении синтезированного таким образом управления к исходной нели-
нейной системе. Таким образом, в общей постановке задачи синтеза не реше-
на задача о глобальной асимптотической устойчивости нелинейной системы
с управлением, синтезированным с использованием ее модели с параметра-
ми, зависящими от состояния. Основная же проблема реализации регулятора,
полученного на основе SDRE-метода, заключается в сложности нахождения
решения алгебраического матричного уравнения Риккати с параметрами, за-
висящими от состояния, в темпе функционирования системы.
Материал статьи размещен в следующем порядке: во втором разделе осу-
ществлена постановка задачи управления нелинейным объектом, описывае-
мым системой обыкновенных дифференциальных уравнений, задан квадра-
тический функционал качества. Для синтеза оптимальных управлений ис-
пользован метод динамического программирования. В третьем разделе об-
суждается метод “расширенной линеаризации”, используемый для синтеза оп-
тимального управления в задаче с заданным временем переходного процесса
72
и синтеза субоптимального управления в задаче с неограниченным временем
окончания переходного процесса. Реализация синтезированного управления
наталкивается на сложность реализации решений матричного уравнения ти-
па Риккати с параметрами, зависящими от состояния системы. В статье для
решения этой проблемы предлагается использовать один из методов алгорит-
мического конструирования систем с неполной информацией [11]. В четвер-
том разделе излагается метод алгоритмического конструирования системы
с параметрической оптимизацией, основанный на применении функции до-
пустимых управляющих воздействий (гамильтонианов). В пятом разделе де-
монстрируется применение полученных теоретических результатов с исполь-
зованием математической модели, описывающей поведение иммунной систе-
мы человека при наличии вируса ВИЧ, в задаче управления подачей пре-
паратов ВААРТ. Представлены результаты математического моделирования
построенной системы.
2. Задача оптимального управления нелинейным
детерминированным объектом
Пусть детерминированная управляемая нелинейная система описывается
обыкновенным дифференциальным уравнением
d
(2.1)
x(t) = f(x(t)) + g(x(t))u(t), x(t0) = x0.
dt
Здесь x(·) = {x(t) ∈ Rn, t ∈ [t0, tf ]} - состояние системы; x ∈ Ωx, x0 ∈ X0 ⊂
⊂Ωx - множество возможных начальных условий системы; u(·) = {u(t) ∈ Rr,
t ∈ [t0,tf]} - управление; вектор-столбец f(x(t)) и матрица g(x(t)) - непре-
рывные функции соответствующих размеров.
Предположение 1. Вектор-функция f(x(t)) - непрерывная диффе-
ренцируемая по x ∈ Ωx, т.е. f(x(t)) ∈ C1(Ωx). Кроме того, будем полагать,
что функции f(x(t)), g(x(t)) такие, что из любых начальных условий (t0, x0) ∈
∈ R+ × Ωx исходит одно и только одно решение уравнения (2.1).
2.1. Задача с заданным временем окончания переходного процесса
Введем функционал качества
tf
∫
1
1
{
}
(2.2)
J (x(·), u(·)) =
xT(tf)Fx(tf ) +
xT(t)Qx(t) + uT(t)Ru(t)
dt.
2
2
t0
Здесь R = RT - положительно определенная матрица, матрицы F = FT и
Q = QT, по крайней мере, положительно полуопределенные.
Предположение 2. Пусть f(x(t)), g(x(t)) - достаточно гладкие функ-
ции такие, что функция Беллмана V (t, x(t)), определенная как
tf
∫
1
{
}
(2.3)
= inf
xT(tf )F x(tf ) +
xT(t)Qx(t) + uT(t)Ru(t)
dt,
u(·)∈U 2
s
73
дифференцируемая функция при любых допустимых управлениях u(·) ∈
∈ L2 [t0,tf].
В силу сделанных выше предположений значение функции V (t, x(t)) есть
решение задачи динамического программирования, связанное с дифферен-
циальным уравнением первого порядка в частных производных Гамильтона-
Якоби-Беллмана [12, 13]
(
)
∂V (t,x(t))
∂V (t,x(t))
(2.4)
+ minH t,x(t),u(t),
= 0,
∂t
u∈U
∂x
где H - гамильтониан
(
)
∂V (t,x(t))
H t,x(t),u(t),
=
∂x
(2.5)
1
{
}
∂V (t,x(t))
=
xT(t)Qx(t) + uT(t)Ru(t)
+
{f(x(t)) + g(x(t))u(t)} .
2
∂x
Функция H (t, x(t), u(t), ∂V (t, x(t))/∂x) определена и непрерывна для t ∈
∈ [t0,tf ].
Оптимальное управление u0(t) в задаче (2.1)-(2.2) является точкой ста-
ционарности гамильтониана (2.5) и определяется соотношением
(
)
(
)
T
∂V (t,x(t))
∂Ht,x(t),u(t),∂V(t,x(t))
∂2H t,x(t),u(t),
∂x
∂x
= 0,
= R ≻ 0,
∂u
∂u2
откуда
}T
{∂V (t,x(t))
(2.6)
u0(t) = -R-1gT(x(t))
,
∂x
где вектор {∂V (t, x(t))/∂x}T является решением уравнения Гамильтона-
Якоби-Беллмана:
∂V (t,x(t))
∂V (t,x(t))
+
f (x(t)) -
∂t
∂x
}T
1 ∂V (t,x(t))
{∂V (t,x(t))
1
(2.7)
-
g(x(t))R-1gT(x(t))
+
xT(t)Qx(t) = 0,
2
∂x
∂x
2
1
V (tf , x(tf )) =
xT(tf )Fx(tf ).
2
Исходная система (2.1) с управлением (2.6) имеет вид
d
{∂V (t,x(t))}T
(2.8)
x(t) = f(x(t)) - g(x(t))R-1gT(x(t))
,
x(t0) = x0.
dt
∂x
74
Лемма 1. Если существует оптимальное управление в задаче (2.1)-
(2.2), то оно единственно и определяется уравнением (2.8), где вектор
{∂V (t, x(t))/∂x}T является решением уравнения (2.7) [14].
Основная трудность реализации управлений в виде (2.6) заключается в
нахождении вектора {∂V (t, x(t))/∂x}T, удовлетворяющего скалярному урав-
нению в частных производных (2.7). В случае успешного решения уравнения
(2.7) управление u(·) осуществляется с использованием принципа обратной
связи по состоянию, т.е. u(t) = u(t, x(t)).
В дальнейшем потребуется знание о поведении га(мильтониана, соотве)т-
ствующее оптимальному управляемому процессу ξ =
x(t), u0(t), t ∈ [t0, tf ]
Лемма 2 [13]. Поведение гамильтониана
(
)
∂V (t,x(t))
H t,x(t),u(t),
=
∂x
(2.9)
1
[
]
∂V (t,x(t))
=
xT(t)Qx(t) + uT(t)Ru(t)
+
[f(x(t)) + g(x(t))u(t)] ,
2
∂x
(
)
соответствующее управляемому процессу ξ =
x(t), u0(t), t ∈ [t0, tf ]
, где
d
x(t) = f(x(t)) + g(x(t))u0(t), x(t0) = x0,
dt
}T
{∂V (t,x(t))
u0(t) = -R-1gT(x(t))
,
∂x
определяется решением уравнения
(
)
∂V (t,x(t))
∂V (t,x(t))
- H t,x(t),u0(t),
= 0,
∂t
∂x
(2.10)
1
V (tf , x(tf )) =
xT(tf )Fx(tf ).
2
2.2. Задача с неопределенным временем окончания переходного процесса
В случае, когда t ∈ [t0, tf ), tf → ∞, функционал качества записывается в
виде
tf
∫
1
{
}
(2.11)
J (x(·), u(·)) = lim
xT(t)Qx(t) + uT(t)Ru(t)
dt.
tf →∞ 2
t0
Здесь Q = QT и R = RT - положительно определенные матрицы.
В этом случае {∂V (x(t))/∂t} = 0 и оптимальное управление и соответст-
вующая траектория системы (2.1) имеют вид
}T
{∂V (x(t))
(2.12)
u(t) = -R-1gT(x(t))
,
∂x
75
}T
d
{∂V (x(t))
(2.13)
x(t) = f(x(t)) - g(x(t))R-1gT(x(t))
,
x(t0) = x0,
dt
∂x
где {∂V (x(t))/∂x}T ищется решением уравнения
∂V (x(t))
1 ∂V (x(t))
{∂V (x(t))}T
f (x(t)) -
g(x(t))R-1gT(x(t))
+
∂x
2
∂x
∂x
(2.14)
1
+
xT(t)Qx(t) = 0.
2
Таким образом, проблема нахождения управления (2.12) полностью зави-
сит от успешного решения уравнения в частных производных (2.14).
Лемма 3.(Значение гамильто)ниана, соответствующее управляемому
процессу ξ =
x(t), u0(t), t ∈ [t0, tf )
, на всем интервале управления посто-
янно, т.е.
(
)
d
∂V (x(t))
H x(t),u0(t),
=
dt
∂x
}T
∂V (x(t))
1 ∂V (x(t))
{∂V (x(t))
(2.15)
=
f (x(t)) -
g(x(t))R-1gT(x(t))
+
∂x
2
∂x
∂x
1
+
xT(t)Qx(t) = 0.
2
3. Метод “расширенной линеаризации” в задаче синтеза управлений
3.1. SDC-представление нелинейной системы
Будем искать решение уравнения Гамильтона-Якоби-Беллмана (2.14),
применив к исходной нелинейной модели управляемого объекта метод “рас-
ширенной линеаризации”. Для этого необходимо сделать несколько предпо-
ложений [8].
Предположение 3. Положим, что при x = 0 выполняются следующие
условия: f(0) = 0 и, кроме этого, g(x(t)) = 0, ∀x(t) ∈ Ωx.
Учитывая сделанные предположения, представим исходную систему (2.1)
с помощью метода “расширенной линеаризации” в виде системы с линей-
ной структурой, параметры которой зависят от состояния объекта (SDC-
представление, State Dependent Coefficient factorization [8-10]). Для этого
представим вектор f(x(t)) в виде
(3.1)
f (x(t)) = A(x(t))x(t).
При таком представлении уравнение объекта (2.1) примет вид
d
(3.2)
x(t) = A(x(t))x(t) + g(x(t))u(t), x(t0) = x0.
dt
76
Такую запись нелинейной управляемой системы (2.1) в виде (3.2) называ-
ют SDC-представлением [8, 9].
Естественно, что такое представление (3.2) для систем, порядок которых
выше первого, не является единственным. Предположим, что в общем случае
матрица-функция f(x(t)) может быть p способами преобразована в произве-
дение матрицы Ai(x(t)) с параметрами, зависящими от состояния, на вектор
состояния x(t), т.е.
(3.3)
f (x(t)) = Ai
(x(t))x(t), i = 1, . . . , p.
Необходимо учесть, что не все полученные таким образом p представлений
вектора f(x(t)) можно использовать при построении системы, эквивалентной
исходной. Модель с параметрами, зависящими от состояния, полученная с
помощью данного преобразования (3.3), должна быть управляема.
Предположение 4. Будем считать, что представление исходной нели-
нейной системы в виде системы с линейной структурой, но с параметрами,
зависящими от состояния, является управляемым в области допустимых зна-
чений [t0, tf ] × Ωx, т.е. пара 〈Aj(x(t)), g(x(t))〉 является поточечно управляе-
мой для всех (t, x) ∈ [t0, tf ] × Ωx.
Следует отметить, что в настоящее время отсутствуют критерии для опре-
деления таких структурных свойств, как управляемость и наблюдаемость
моделей систем, полученных с использованием метода “расширенной лине-
аризации”. Для полученных моделей систем можно провести “поточечную”
проверку на управляемость в некоторой области исследуемого состояния си-
стемы [10, 15].
Сделанные выше предположения 3 и 4 позволят при использовании метода
“расширенной линеаризации” получить представление исходной нелинейной
системы (2.1) в виде модели (3.2), которая имеет линейную структуру и яв-
ляется управляемой.
3.2. Задача с заданным временем окончания переходного процесса
Модифицированное уравнение Гамильтона-Якоби-Беллмана (2.7) имеет
вид
dV (t, x(t))
1 ∂V (t,x(t))
{∂V (t,x(t))}T
=-
g(x(t))R-1gT(x(t))
-
dt
2
∂x
∂x
1
(3.4)
-
xT(t)Qx(t),
2
1
V (tf , x(tf )) =
xT(tf )Fx(tf ).
2
Определим функцию V (t, x(t)) с точностью до положительно определен-
ной симметрической матрицы S(x(t)) в виде
1
(3.5)
V (t, x(t)) =
xT
(t)S(x(t))x(t).
2
77
Перепишем (3.4) с учетом (3.5)
dV (t, x(t))
1
[
]
=-
xT(t)
S(x(t))g(x(t))R-1gT(x(t))S(x(t)) + Q
x(t),
dt
2
(3.6)
1
V (tf , x(tf )) =
xT(tf )Fx(tf ).
2
С учетом того, что {∂V (t,x(t))/∂x}T = S(x(t))x(t), управление (2.6) при-
нимает вид
(3.7)
u0(t) = -R-1gT
(x(t))S(x(t))x(t),
а уравнение модели (3.2) с управлением (3.7) может быть записано как
d
[
]
(3.8)
x(t) =
(x(t)) - g(x(t))R-1gT(x(t))S(x(t))
x(t), x(t0) = x0.
dt
Получим выражение для полной производной по времени от функции
V (t, x(t)), используя ее представление в виде (3.5), а также учитывая вы-
ражение (3.8):
dV (t, x(t))
1
[ dS(x(t))
=
xT(t)
+ S(x(t))A(x(t)) + AT(x(t))S(x(t)) -
dt
2
dt
]
(3.9)
- 2S(x(t))g(x(t))R-1gT(x(t))S(x(t)) x(t),
1
V (tf , x(tf )) =
xT(tf )Fx(tf ).
2
Приравнивая правые части выражений (3.6) и (3.9), получим
dS(x(t))
+ S(x(t))A(x(t)) + AT(x(t))S(x(t)) -
dt
(3.10)
- S(x(t))g(x(t))R-1gT(x(t))S(x(t)) + Q = 0,
S(x(tf )) = F.
Здесь
∑
dS(x(t))
∂S(x(t)) dxi(t)
=
dt
∂xi
dt
i=1
Выражение (3.10) есть уравнение Риккати с параметрами, зависящими от
состояния, и заданным краевым условием на правом конце.
Теорема 1. Даны управляемая модель (3.8) системы (2.1) и функцио-
нал (2.2). Обозначим через J0(t, x(t)) минимальную величину, достигаемую
функционалом J(x(·), u(·)) при оптимальном управлении u0(t), реализован-
ном с использованием обратной связи. Эта величина равна
1
J0(t,x(t)) =
xT(t)S(x(t))x(t), t0 ≤ t ≤ tf .
2
78
Теорема 2. Модель нелинейной системы (2.1), описываемая уравнением
d
[
]
x(t) =
A(x(t)) - g(x(t))R-1gT(x(t))S(x(t))
x(t), x(t0) = x0,
dt
в котором матрица S(x(t)) является симметрической положительно опре-
деленной и находится решением дифференциального уравнения типа Рик-
кати с параметрами, зависящими от состояния (3.10), асимптотически
устойчива.
Доказательства теорем 1 и 2 содержатся в Приложении.
Следует отметить, что асимптотическая стабилизация может не иметь ме-
сто в исходной нелинейной системе (2.1) с синтезированным SDRE-методом
оптимальным управлением вида (3.7) и произвольным начальным состояни-
ем x0 (глобальная асимптотическая стабилизация).
3.3. Задача с неопределенным временем окончания переходного процесса
(субоптимальное управление)
Как это было сделано выше, определим функцию {∂V (x(t))/∂x}T с точ-
ностью до значения матрицы S
⌢(x(t)) в виде
(3.11)
{∂V (x(t))/∂x}T = S⌢
(x(t))x(t),
где S
⌢(x(t)) - симметрическая положительно определенная матрица.
Заменяя в уравнении Гамильтона-Якоби-Беллмана (2.14) {∂V (x(t))/∂x}T
на S
⌢(x(t))x(t) и учитывая, что f(x(t)) = A(x(t))x(t), получим
[
xT(t) AT(x(t))S⌢(x(t)) + ⌢(x(t))A(x(t)) -
]
-S
⌢(x(t))g(x(t))R-1gT(x(t))⌢(x(t)) + Q x(t) = 0
откуда, учитывая что x(t) есть решение уравнения (3.2) с начальным усло-
вием x(t0) = 0, имеем
AT(x(t))S⌢(x(t)) + ⌢(x(t))A(x(t)) -
(3.12)
-S
⌢(x(t))g(x(t))R-1gT(x(t))⌢(x(t)) + Q = 0.
Управление для рассматриваемой задачи принимает вид
(3.13)
u0(t) = -R-1gT(x(t))S⌢
(x(t))x(t).
Запишем исходную систему (2.1) с субоптимальным управлением (3.13)
d
(3.14)
x(t) = f(x(t)) - g(x(t))R-1gT(x(t))S⌢(x(t))x(t), x(t0) = x0.
dt
79
Отметим справедливость сформулированной выше теоремы 1 об асимпто-
тической устойчивости модели с параметрами, зависящими от состояния, и
сделанного замечания относительно глобальной устойчивости исходной нели-
нейной системы.
Для рассматриваемой модели (3.8) исходного объекта (2.1) в случае с от-
крытым интервалом управления можно, используя теоремы 1 и 2, сформу-
лировать соответствующие теоремы о конечном значении функционала при
оптимальном управлении и устойчивости.
Теорема 3. Даны управляемая модель (3.8) системы (2.1) и функцио-
нал (2.11). Обозначим через J0(x(·)) минимальную величину, достигаемую
функционалом J(x(·), u(·)) при оптимальном управлении, реализованном с
использованием обратной связи. Эта величина равна
1
J0(x(t0)) =
xT0S⌢(x0)x0,
2
где положительно определенная симметрическая матрица определяется ре-
шением алгебраического уравнения типа Риккати с постоянными парамет-
рами
AT(x0)S⌢(x0) + ⌢(x0)A(x0) - ⌢(x0)g(x0)R-1gT(x0)⌢(x0) + Q = 0.
Теорема 4. Модель нелинейной системы (2.1), описываемая уравнением
[
]
d
x(t) = A(x(t)) - g(x(t))R-1gT(x(t))S⌢(x(t)) x(t), x(t0) = x0,
dt
в котором матрица S
⌢(x(t)) является симметрической положительно опре-
деленной и находится решением алгебраического уравнения типа Риккати
с параметрами, зависящими от состояния (3.12), асимптотически устой-
чива с положением равновесия в точке x = 0.
Доказательства теорем 3 и 4 аналогичны доказательствам теорем 1 и 2.
Однако отметим, асимптотическая стабилизация может не иметь место в
исходной нелинейной системе (2.1) с синтезированным SDRE-методом субоп-
тимальным управлением вида (3.13) и произвольным начальным состояни-
ем x0 (глобальная асимптотическая стабилизация).
В заключение данного раздела отметим, что выражения для оптимально-
го (3.7) и субоптимального (3.13) управлений нелинейной системой получены.
Однако проблема реализации таких управлений наталкивается на проблему
поиска решения уравнения Риккати с параметрами, зависящими от состояния
системы (3.10) или (3.12), в темпе функционирования системы управления.
Поиск решения этой проблемы, описанный в следующем разделе статьи, ос-
нован на установленных закономерностях поведения гамильтониана при оп-
тимальном управлении и соответствующем состоянии нелинейного объекта
(леммы 2 и 3).
80
4. Конструирование алгоритмов оптимизации нелинейных
неопределенных систем управления
Представлен новый метод формирования алгоритмов оптимизации нели-
нейных неопределенных систем управления, основанный на применении
функций допустимых значений управляющих воздействий (гамильтонианов)
[16]. Под термином “неопределенные системы” понимаются системы с непол-
ной информацией о параметрах и действующих возмущениях [11].
4.1. Общая структура алгоритмов параметрической оптимизации
нелинейных неопределенных систем
Пусть нелинейный управляемый объект описывается дифференциальным
уравнением вида
d
(4.1)
x(t)
f (x(t), u(t), η(t), a(t)), x(t0) = x0,
dt
здесь x(·) = {x(t) ∈ Rn, t ∈ [t0, tf )} - состояние объекта; u(·) = {u(t) ∈ Rr,
{
}
t ∈ [t0,tf)} - управляющие воздействия; η(·) =
η(t) ∈ Δ ⊂ Rk, t ∈ [t0, tf )
-
вектор параметров объекта, подвергающхся ∕озействию неконтролируе-
мых возмущений, при этом известно, что
dη(t)
dt≤maxη∈Δ |dη(t)/dt| = σ,
σi > 0, i = 1,... ,k; вектор параметров объекта, оптимизирующих работу си-
стемы: a(·) = {a(t) ∈ A ⊂ Rp, t ∈ [t0, tf )}. Отметим, что в общем случае k ≥ p.
Выделенные для параметрической оптимизации параметры системы могут
находиться как в самом объекте, так и в регуляторе.
Как следует из лемм 1 и 2, поведение гамильтонианов при оптимальных
управлениях u0(t) и соответствующих траекториях x(t) определяется вполне
определенными выражениями. Это свойство гамильтонианов положим в ос-
нову конструкции алгоритмов оптимизации системы управления.
Сформулируем необходимые условия, при которых функционал качества
достигает минимального значения, основываясь на поведении гамильтониана
вдоль оптимальной траектории. Рассмотрим вначале случай, когда k = p и
параметры a(t) могут “парировать” возмущения η(t), т.е. возможно выполне-
ние условия a(t) - η(t) = 0.
Пусть скалярная функция ϕ(t) соответст(ует значению гамил)ьтониана
при оптимальном управляемом процессе ξ =
x(t), u0(t), t ∈ [t0, tf )
на всем
интервале управления, т.е.
(
)
∂V (x(t))
ϕ(t) = -H x(t), u0(t),
,
∂x
(
)
где H x(t), u0(t),∂V(x(t))
- значение гамильтониана в каждый момент вре-
∂x
мени управления при отсутствии параметрических возмущений (или при пол-
ном их парировании) при оптимальном управлении и соответствующей тра-
ектории системы (4.1).
Введем скалярную функцию ℜ(·) такую, что
(
)
(
)
∂V (x(t))
∂V (x(t))
ℜ x(t),u(t),
,η(t),a(t)
= H x(t),u(t),
,η(t),a(t)
+ ϕ(t).
∂x
∂x
81
Таким образом, условие, которое достигается при a(t) - η(t) = 0,
(
)
∂V (x(t))
(4.2)
ℜ x(t),u0(t),
=0
∂x
есть необходимое условие оптимальности системы управления.
Предположение 5. Необходимые условия оптимальности в задачах
(2.1), (2.2) и (2.1), (2.11), а именно условия вида (4.2), являются и доста-
точными условиями оптимальности.
Это предположение выполняется в случае, когда
а) задача унимодальная, т.е. функционал имеет только один минимум и
отсутствуют другие точки стационарности гамильтониана;
б) исследователь располагает информацией об области нахождения глав-
ного экстремума (минимума) функционала качества, которая соответствует
заданной области допустимых управлений, так что можно рассматривать за-
дачу с одним глобальным минимумом.
Необходимые и достаточные условия оптимальности (4.2) будут исполь-
зоваться в качестве основы при конструировании алгоритмов оптимизации
неопределенных систем [11].
Таким образом, в случае, когда a(t) - η(t) = 0, условие (4.2) выполняться()
не будет, т.е. ℜ x(t), u(t),∂V(x(t))∂x , η(t), a(t)
= 0.
Теорема 5. Пусть неопределенная нелинейная динамическая система
описывается уравнением
d
x(t)
f (x(t), u(t), η(t), a(t)), x(t0) = x0,
dt
где x(t) ∈ Rn -сост∕яние объекта u(t)∕∈ r - управляющие воздействия;
≤maxη∈Δ
η(t) ∈ Δ ⊂ Rk,
dη(t)
dt
dη(t)
dt=σ,σi > 0, i = 1,... ,k - век-
тор параметров объекта, подвергающихся воздействию неконтролируемых
возмущений; a(t) ∈ A ⊂ Rp - вектор параметров объекта, оптимизирую-
щих работу системы. Предполагается также, что при p = k во внутрен-
ней области множества значений параметров A, при соответствующем
u0(t) ∈ U, существуют такие значения a0(t) ∈ A, при которых достигает-
ся заданная цель параметрического управления, т.е.
[
]
[
]
a0(t) = arg minJ(x(t),u0(t),η(t),a(t)) = arg
J (x0(t), u0(t), η(t), a0(t))
∈ A,
a∈A
что соответствует выполнению условия
(
)
∂V (x(t))
ℜ x0(t),u0(t),
,η(t),a0(t)
= 0.
∂x
82
Алгоритм
(
)
T
∂H x(t),u(t),∂V(x(t))∂x,η(t),a(t)
d
a(t) = -
×
dt
∂a
(4.3)
(
)
∂V (x(t))
× ℜ x(t),u(t),
,η(t),a(t)
,
∂x
a(t0) = a0
обеспечивает исходной системе асимптотическое свойство параметриче-
ской оптимизации в смысле заданного функционала качества J(x(t), u(t))
при выполнении условия
(
)
2
(
)
∂H x(t),u(t),∂V(x(t))∂x,η(t),a(t)
∂V (x(t))
(4.4)
ℜ2 x(t),u(t),
,η(t),a(t)
>
∂x
∂a
(
)
(
) ∂H x(t),u(t), ∂V(x(t))∂x,η(t),a(t)
∂V (x(t))
>
ℜ x(t),u(t),
,η(t),a(t)
σ.
∂x
∂η
Отметим, что назначение начального условия a(t0) для алгоритма (4.3) па-
раметрической оптимизации зависит от априорной информации о состоянии
в данный момент времени возмущенных параметров η(t0).
Дадим пояснение о возможности реализации алгоритма (4.3). Как видно,
этот алгоритм содержит неизмеряемую информацию о возмущенных пара-
метрах η(t). Вся информация о возмущенных параметрах и параметрах оп-
тимизации содержится в выражении, описывающем гамильтониан системы.
Действительно:
(
)
∂V (x(t))
H x(t),u(t),
,η(t),a(t)
=
∂x
∂V (x(t))
= L(x(t),u(t)) +
f (x(t), u(t), η(t), a(t)) =
∂x
∂V (x(t))
= L(x(t),u(t)) +
{dx(t)/dt} ,
∂x
так как dx(t)/dt
f (x(t), u(t), η(t), a(t)). Здесь L(x(t), u(t)) - интегрант функ-
ционала (2.2) или (2.11). Таким образом, для реализации алгоритма (4.3)
необходимо располагать информацией о dx(t)/dt.
Как выше отмечалось, количество параметров системы, подвергающихся
возмущениям, может быть больше, чем параметров, на которые возлагается
задача уменьшения наилучшим образом влияния этих возмущений, т.е. в этом
случае k > p. Условие успешной параметрической оптимизации системы в
этом случае формулируется следующей теоремой.
83
Теорема 6. Пусть вектор параметров объекта, подвергающихся воз-
ейст∕и неконтроируе∕ыхвозмущений, отвечает условию η(t) ∈ Δ ⊂ Rk,
dη(t)
≤maxη∈Δ
dη(t)
dt
dt=σ,σi > 0, i = 1,... ,k, а вектор параметров
объекта, оптимизирующих работу системы, есть ap(t) ∈ Ap ⊂ Rp, p < k.
Предполагается, что в области множества значений параметров Ap, выде-
ленных в системе управления для ее оптимизации, при соответствующем
u0p(t) ∈ U существуют такие значения a0p(t) ∈ Ap, при которых достигает-
ся заданная цель параметрического управления, т.е.
[
]
a0p(t) = arg min
Jp(xp(t),u0p(t),η(t),ap(t))
=
(4.5)
a0∈A
[
]
= arg
Jp(x0p(t),u0p(t),η(t),a0p(t))
∈Ap,
что соответствует выполнению условия
(
)
∂V (x(t))
(4.6)
ℜp x0p(t),u0p(t),
,η(t),a0p(t)
= 0.
∂x
Алгоритм
(
)
T
∂H xp(t),u0p(t),∂V(x(t))∂x,η(t),ap(t)
d
ap(t) = -
×
dt
∂ap
(
)
∂V (x(t))
× ℜp xp(t),up(t),
,η(t),ap(t)
∂x
обеспечивает исходной системе асимптотическое свойство параметриче-
ской оптимизации в смысле заданного функционала качества Jp(xp(t), u0p(t)),
(p < k) при выполнении условия
(
)
2
(
)
∂H xp(t),u0p(t),∂V(x(t))∂x,η(t),ap(t)
∂V (x(t))
ℜ2p xp(t),u0p(t),
,η(t),ap(t)
-
∂x
∂ap
(
)
∂V (x(t))
-
ℜp xp(t),u0p(t),
,η(t)
,
∂x
(
)
∂V (x(t))
∂H xp(t),u0p(t),
,η(t),ap(t)
∂x
ap(t)
σ>0.
∂η
Таким образом, выполнение условия (4.5) обеспечивает существование
необходимого условия оптимальности (4.6), которое используется в струк-
туре алгоритма параметрической оптимизации. Доказательство теоремы 6
аналогично доказательству теоремы 5.
Назначение начального условия ap(t0) так же, как и для алгоритма (4.3),
зависит от априорной информации о состоянии в данный момент времени
возмущенных параметров η(t0).
84
4.2. Алгоритмы оптимизации нелинейных систем, линеаризованных
с помощью метода “расширенной линеаризации”
Полученные в разделе
4.1
алгоритмы параметрической оптимизации
неопределенных нелинейных динамических систем применимы для поиска
субоптимального решения задачи построения нелинейной системы управле-
ния, рассмотренной в разделе 3.2 статьи, а именно, для нахождения матрицы
S
⌢(
x(t)), минуя проблемы нахождения решения уравнения Риккати с парамет-
рами, зависящими от состояния (3.5). Для этого представим матрицу S
⌢(x(t))
в виде
(4.7)
S(x(t)) = S0
+ s(t),
здесь матрица S0 находится из решения уравнения Риккати с постоянными
параметрами (при x(t0) = x0)
(4.8)
S(x0)A(x0) + AT(x0)S(x0) - S(x0)g(x0)R-1gT(x0)S(x0
) + Q = 0,
а матрица s(t) - матрица настраиваемых параметров.
В соответствии с изложенным выше способом представления матрицы
S(x(t)) (4.7) запишем алгоритм для нахождения s(t)
d
{∂H (x(t), u(t), [S0 + s(t)] x(t))}T
s(t) = -
ℜ(x(t),u(t),[S0 +s(t)]x(t)) ,
(4.9) dt
∂s
s(t0) = 0,
здесь
ℜ (x(t), u(t), [S0 + s(t)] x(t)) =
(
)
= H (x(t),u(t),[S0 + s(t)]x(t)) - H
x0(t),u0(t),S(x0)x0(t)
,
H (x(t), u(t), [S0 + s(t)] x(t)) =
{
1
=
xT(t) Q - [S0 + s(t)]T g(x(t))R-1gT(x(t))[S0 + s(t)]+
2
}
+ 2[S0 + s(t)]T A(x(t)) x(t),
S(x0) - матрица, при которой выполняется условие
(
)
∂V (x(t))
ℜ x0(t),u0(t),
,η(t),a0(t)
= 0.
∂x
{
∕
}T
Функция чувствительности
∂H (x(t),u(t),[S0 + s(t)]x(t))
∂s
определяет-
ся выражением
{∂H (x(t),u(t),[S0 + s(t)] x(t))}T
=
∂s
[
]
=
-g(x(t))R-1gT(x(t))(S0 + s(t)) + A(x(t))
x(t)xT(t).
85
С учетом (3.7) и (4.7) управление с параметрической оптимизацией при
использовании данного алгоритма принимает вид
(4.10)
u(t) = -R-1gT(x(t))[S0
+ s(t)]x(t).
Система (2.1) с управлением (4.10) принимает вид
d
(4.11)
x(t) = f(x(t)) - g(x(t))R-1gT(x(t)) [S0 + s(t)] x(t), x(t0) = x0,
dt
где матрица S0 определяется решением уравнения (4.8), а матрица s(t) нахо-
дится с использованием алгоритма (4.9).
Таким образом, для исходной нелинейной системы (2.1) решена задача
синтеза субоптимального управления с параметрической оптимизацией регу-
лятора в случае незаданного времени переходного процесса.
5. Демонстрация работы алгоритма параметрической оптимизации
в задаче управления нелинейной системой
Для проверки возможности использования рассмотренных в статье под-
ходов построения систем управления с параметрической неопределенностью
и проверки работоспособности алгоритмов параметрической оптимизации в
этом разделе представлены результаты конструирования системы медика-
ментозного лечения иммунного заболевания ВИЧ. В качестве объекта иссле-
дования была выбрана модель поведения иммунной системы человека при
наличии в ней ВИЧ, предложенная в [17-19]. Модель образуют пять диффе-
ренциальных уравнений:
d
i(t) = λ - di(t) - β(1 - ηu(t))i(t)y(t),
dt
d
y(t) = β(1 - ηu(t))i(t)y(t) - ay(t) - p1z1(t)y(t) - p2z2(t)y(t),
dt
d
(5.1)
z1(t) = c1z1(t)y(t) - b1z1(t),
dt
d
w(t) = c2i(t)y(t)w(t) - c2qy(t)w(t) - b2w(t),
dt
d
z2(t) = c2qy(t)w(t) - hz2(t),
dt
здесь обозначены: i - незараженные Т-клетки иммунной системы, Т-хелперы;
y - зараженные Т-хелперы (вирусы); z1 - Т-киллеры; w - В-лимфоциты; z2 -
иммуноглобулины, клетки-памяти; λ - скорость производства Т-хелперов в
организме. Управление системой (5.1) осуществляется подачей лекарствен-
ных препаратов (u - доза вводимого препарата), максимальная эффектив-
ность которых выражается коэффициентом η. Значения параметров, исполь-
зованных при построении и проведении математического моделирования,
приняты из [18]. Параметры являются безразмерными и усредненными, так
86
как сама модель описывает поведение иммунной системы на качественном
уровне и является безразмерной.
Для примера был рассмотрен очень слабый пациент, имеющий вирус ВИЧ.
Для такого состояния начальные значения примем равными: i = 0,2, y = 2,
z1 = 0,08, w = 0,01, z2 = 0,01. Для рассматриваемой модели иммунной систе-
мы значение концентрации здоровых клеток иммунной системы для нормаль-
ной жизнедеятельности должно быть в диапазоне 8-10. Значения i ≤ 1 гово-
рят о том, что иммунная система не справляется с инфекциями, попадающи-
ми в организм, и состояние пациента близко к стадии наступления СПИДа.
Перепишем систему (5.1) в следующем виде:
d
x(t) = f(x(t)) + g(x(t))u(t),
(5.2)
dt
x(t0) = x0,
где xT(t) = [i(t)y(t)z1(t)w(t)z2(t)],
[-d - βy(t)] i(t)
βi(t)y(t) - ay(t) - p1z1(t)y(t) - p2z2(t)y(t)
f (x(t)) =
c1z1(t)y(t) - b1z1(t)
,
c2i(t)y(t)w(t) - c2qy(t)w(t) - b2w(t)
c2qy(t)w(t) - hz2(t)
βηi(t)y(t)
-βηi(t)y(t)
g(x(t)) =
0
.
0
0
Перепишем систему
(5.2)
в SDC-представлении, учитывая что
( 10
0
0
0
0)T точка равновесия системы (5.1)
d
x(t) = A(x(t))x(t) + g(x(t))u(t), x(t0) = x0,
dt
здесь
A(x(t)) =
-d - βy
-10β
0
0
0
βy
10β - (a + p1z1 + p2z2)
0
0
0
=
0
0
c1y-b1
0
0
,
c2yw
0
0
10c2y - c2qy - b2
0
0
0
0
0
c2qyw -hz
2
где переменные i, y, z1, w, z2, как и в
(5.1), зависят от времени, т.е.
i(t), y(t), z1(t), w(t), z2(t).
87
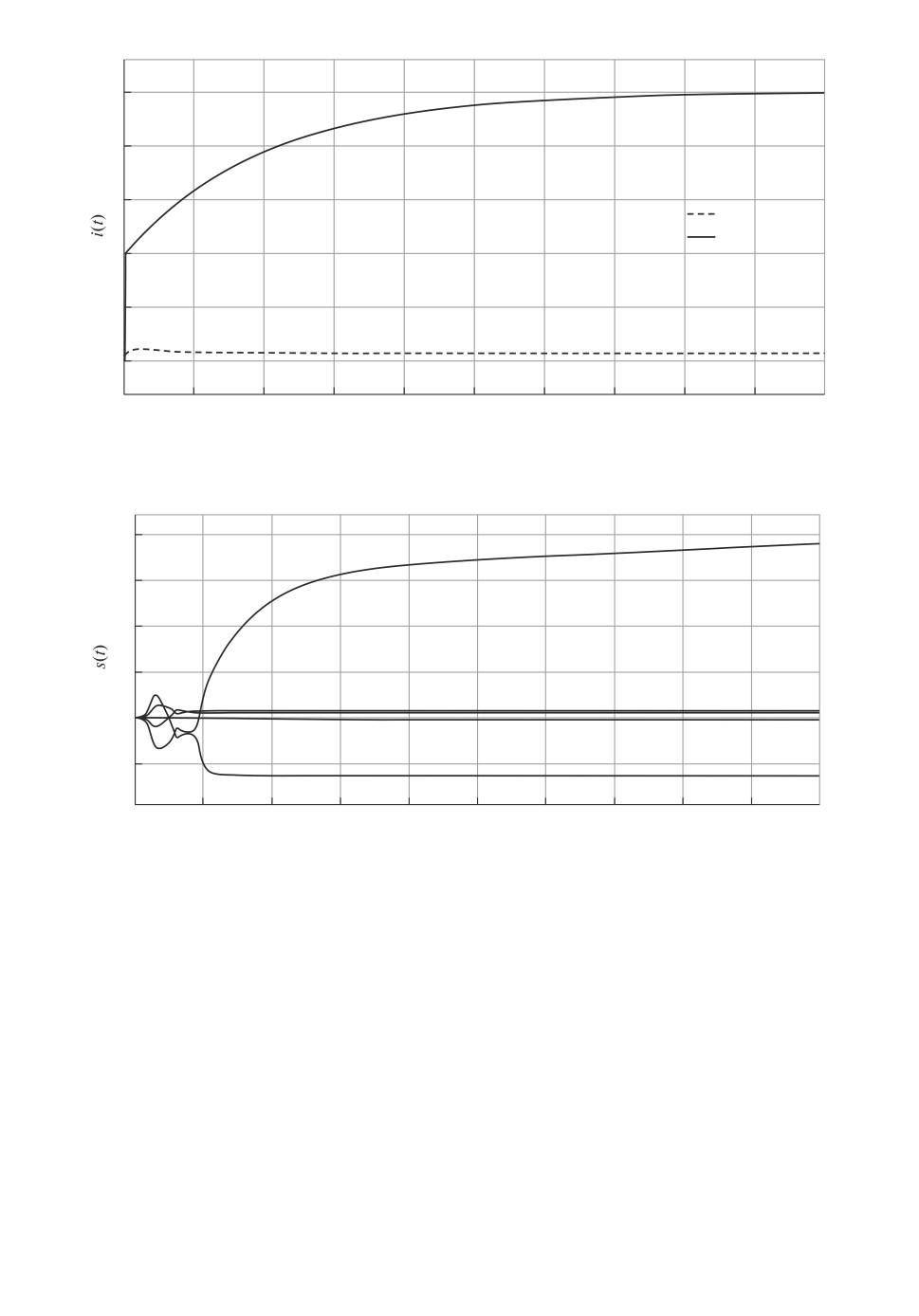
10
8
6
i1(t)
i2(t)
4
2
0
0
5
10
15
20
25
30
35
40
45
50
t
Рис. 1.
80
60
40
20
0
-20
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
t
Рис. 2.
Для назначенных начальных условий и заданных матриц Q, R с исполь-
зованием пакета прикладных программ MATLAB получено решение матрич-
ного уравнения Риккати S0:
113,426
112,15
0
115780
0
112,15
111,7475
0
114460
0
S0 =
0
0
1,25
0
0
.
115780
114460
0
11885 · 104
0
0
0
0
0
1,25
Организация алгоритма оптимизации параметров матрицы s(t) для рас-
сматриваемого примера полностью соответствует приведенному в четвертом
88
разделе статьи (4.7)-(4.11) методу поиска субоптимального решения задачи
построения нелинейной системы управления.
В статье приведены результаты моделирования исходной системы (5.1)
в отсутствие каких-либо управляющих воздействий (без лечения, u = 0) и
с управлениями, синтезированными с использованием алгоритма (4.9), см.
рис. 1 и 2.
Результаты компьютерного моделирования подтверждают эффективность
полученного алгоритмического метода синтеза управлений с параметриче-
ской оптимизацией. Как видно из приведенных результатов моделирования,
разработанное целенаправленное воздействие на иммунную систему, помога-
ет ей установить приемлемый уровень собственных клеток и контролировать
концентрацию зараженных.
ПРИЛОЖЕНИЕ
Доказательство теоремы 1. Подставим в подынтегральную часть
функционала
tf
∫
1
1
{
}
J (x(·), u(·)) =
xT(tf)Fx(tf ) +
xT(t)Qx(t) + uT(t)Ru(t)
dt
2
2
t0
[
]
выражение d
xT(t)S(x(t))x(t)
/dt, компенсировав вне интеграла следующим
[
]
соотношением 0,5
xT(t)S(x(t))x(t) - xT(tf )S(x(tf ))x(tf )
. Получим
1
1
[
]
J (x(·), u(·)) =
xT(tf )Fx(tf ) +
xT(t)S(x(t))x(t) - xT(tf)S(x(tf ))x(tf )
+
2
2
∫
tf
1
{
[
]
}
+
xT(t)Qx(t) + uT(t)Ru(t) + d
xT(t)S(x(t))x(t)
/dt
dt.
2
t
Принимая во внимание то, что
d
[
]
(Π.1)
x(t) =
(x(t)) - g(x(t))R-1gT(x(t))S(x(t))
x(t), x(t0) = x0
dt
и что S(x(tf )) = F , имеем
1
J0(t,x(t)) =
xT(t)S(x(t))x(t), t0 ≤ t ≤ tf .
2
Доказательство теоремы 2. Для доказательства теоремы об асимп-
тотической устойчивости модели (П.1) введем в рассмотрение функцию Ля-
пунова VL(x(t)) такую, что
(Π.2)
ω1 {|x|} ≤ VL(x(t)) ≤ ω2 {|x|} , dVL(x(t))/dt ≤ -ω3
{|x|} , ∀x,
89
где ωi {|x|}, i = 1, 2, 3
- скалярные неубывающие функции такие, что
ωi(0) = 0, ωi {|x|} > 0. Используя вторую теорему Ляпунова, получим, что
при выполнении условия
dVL(x(t))
∂VL(x(t)) dx(t)
(Π.3)
=
≤ -ω3
{|x|}
dt
∂x
dt
система будет устойчива. Назначим VL(x(t)) в виде
VL(x(t)) = xT(t)S(x(t))x(t),
где S(x(t)) - положительно определенная симметрическая матрица, являю-
щаяся решением уравнения Риккати с параметрами, зависящими от состоя-
ния,
dS(x(t))
+ S(x(t))A(x(t)) + AT(x(t))S(x(t)) -
dt
(Π.4)
- S(x(t))g(x(t))R-1gT(x(t))S(x(t)) + Q = 0,
S(x(tf )) = F.
Определим ω3 {|x|} в виде ω3 {|x|} = xT(t)Qx(t), ∀x = 0. Тогда с учетом (П.1)
должно выполняться условие (П.3)
dVL(x(t))
=
dt
[ dS(x(t))
= xT(t)
+ S(x(t))A(x(t)) + AT(x(t))S(x(t)) -
dt
]
- S(x(t))g(x(t))R-1gT(x(t))S(x(t)) + Q x(t) -
- xT(t)S(x(t))g(x(t))R-1gT(x(t))S(x(t))x(t) ≤ 0.
Учитывая (П.4), будем иметь
xT(t)S(x(t))g(x(t))R-1gT(x(t))S(x(t))x(t) ≥ 0.
Это условие выполняется при всех x(t) = 0. Следовательно, модель (П.1)
нелинейной системы (2.1) является асимптотически устойчивой.
Доказательство теоремы 5. Для построения алгоритма парамет-
рической оптимизации системы
d
(Π.5)
x(t)
f (x(t), u(t), η(t), a(t)), x(t0) = x0,
dt
введем функцию Ляпунова
(Π.6)
VL
(η(t), a(t)) =
{ (
)
(
)}2
1
∂V (x(t))
∂V (x(t))
=
ℜ x(t),u(t),
,η(t),a(t)
- ℜ x0(t),u0(t),
=
2
∂x
∂x
(
)
1
∂V (x(t))
=
ℜ2
x(t), u(t),
,η(t),a(t)
2
∂x
90
Тогда для асимптотической параметрической оптимизации ее производная
должна быть отрицательной для случая a(t) - η(t) = 0:
d
(Π.7)
VL
(η(t), a(t)) =
dt
(
)
∂V (x(t))
= ℜ x(t),u(t),
,η(t),a(t)
×
∂x
(
)
∂H x(t),u(t),∂V(x(t))∂x,η(t),a(t)
d
×
η(t) +
∂η
dt
(
)
∂V (x(t))
∂H x(t),u(t),
,η(t),a(t)
∂x
d
+
a(t) < 0,
∂a
dt
так как∂H∂t =∂H0∂t=0,∂∂ηt) =0и∂∂at) =0.
Назначим алгоритм параметрической оптимизации в виде
(
)
T
∂H x(t),u(t),∂V(x(t))∂x,η(t),a(t)
d
a(t) = -
×
dt
∂a
(
)
∂V (x(t))
×ℜ x(t),u(t),
,η(t),a(t)
,
∂x
a(t0) = a0.
При таком назначении алгоритма параметрической оптимизации из усло-
вия (П.14) получим
(
)
(
) ∂H x(t),u(t), ∂V(x(t))∂x,η(t),a(t)d
∂V (x(t))
ℜ x(t),u(t),
,η(t),a(t)
η(t) -
∂x
∂η
dt
(
)
(
) ∂H x(t),u(t), ∂V(x(t))∂x,η(t),a(t)
∂V (x(t))
-ℜ2
x(t), u(t),
,η(t),a(t)
×
∂x
∂a
(
)
∂Hx(t),u(t),∂V(x(t)),η(t),a(t)
∂x
< 0.
×
∂a
Учитывая, что на скорос∕ь изменения озму∕а щих воздействий нало-
жено ограничение, т.е.
dη(t)
dt
≤maxη∈Δ
dη(t)
dt=σ,σi > 0, i = 1,... ,k,
можно записать условие успешного выполнения процесса оптимизации:
(
)
2
(
)
∂H x(t),u(t),∂V(x(t))∂x,η(t),a(t)
∂V (x(t))
ℜ2
x(t), u(t),
,η(t),a(t)
>
∂x
∂a
(
)
(
) ∂H x(t),u(t), ∂V(x(t))∂x,η(t),a(t)
∂V (x(t))
>
ℜ x(t),u(t),
,η(t),a(t)
σ.
∂x
∂η
91
Заключение
В статье для нелинейных динамических систем, представимых моделя-
ми, построенными с использованием метода “расширенной линеаризации”,
и квадратических функционалов качества произведен синтез управляющих
воздействий, реализация которых требует получения решения уравнения
Гамильтона-Якоби-Беллмана. Линейная структура моделей и квадратиче-
ский функционал качества позволяют перейти от уравнения в частных произ-
водных к уравнению типа Риккати с параметрами, зависящими от состояния.
Основная проблема реализации оптимального управления связана с пробле-
мой поиска решения такого уравнения в темпе функционирования объекта.
В статье предложен алгоритмический метод параметрической оптимизации
регулятора, основанный на использовании необходимых условий оптималь-
ности, выраженных в виде поведения гамильтониана на оптимальной траек-
тории системы управления. Построенные алгоритмы могут использоваться
как для оптимизации самих нестационарных объектов, если для этой цели
выделены соответствующие параметры, так и для оптимизации всей управ-
ляемой системы с помощью соответствующей параметрической настройки ре-
гуляторов. Эффективность разработанных алгоритмов продемонстрирована
на примере медикаментозного лечения пациентов при наличии ВИЧ.
СПИСОК ЛИТЕРАТУРЫ
1.
Малкин И.Г. Теория устойчивости движения. М.: УРСС, 2004.
2.
Красовский Н.Н. Некоторые задачи теории устойчивости движения. М.: Изд-во
физ.-мат. лит-ры, 1959.
3.
Isidori A. Nonlinear Control Systems. London: Springer, 1995.
4.
Khalil H.K. Nonlinear Systems. New York: Prentice Hall, 2002.
5.
Mehra R., Chinde V., Kazi K., and Singh N.M. Feedback Linearization of Single-
Input and Multi-Input Control System // Proc. 19th World Congress IFAC. Cape
Town, 2014. P. 5479-5484.
6.
Афанасьев В.Н., Орлов П.В. Субоптимальное управление нелинейным объек-
том, линеаризуемым обратной связью // Изв. РАН ТиСУ. 2011. № 3. С. 13-22.
7.
Pearson J.D. Approximation Methods in Optimal Control // J. Electron. Control.
1962. № 12. Р. 453-469.
8.
Cimen T.D. State-Dependent Riccati Equation (SDRE) Control: A Survey // Proc.
17th World Conf. IFAC. Seoul, 2008. P. 3771-3775.
9.
Mracek C.P., Cloutier J.R. Missile longitudinal autopilot design using the state-
dependent Riccati equation method // Proc. Int. Conf. on Nonlinear Problems in
Aviation and Aerospace. Daytona Beach, 1996. P. 387-396.
10.
Афанасьев В.Н. Управление нелинейными неопределенными динамическими
объектами. М.: URSS, 2015.
11.
Афанасьев В.Н. Динамические системы с неполной информацией: Алгоритми-
ческое конструирование. М.: Наука. Физматлит, 2008.
12.
Беллман Р., Энджел Э. Динамическое программирование и уравнения в част-
ных производных. М.: Изд-во Мир, 1974.
13.
Васильев Ф.П. Методы оптимизации. Кн. 1. М.: МЦНМО, 2011.
92
14. Галеев Э.М., Зеликин М.Ю., Конягин С.В. Оптимальное управление. М.:
МЦНМО, 2008.
15. Гамкрелидзе Р.В. Скользящие режимы в теории оптимального управления //
Тр. МИАН. 1985. Т. 169. С. 180-193.
16. Атанс М., Фалб П. Оптимальное управление. М.: Машиностроение, 1968.
17. Perelson A.S, Kirschner D.E. Dynamics of Hiv Infection of CD4+T Cells // Math.
Biosci. 1993. V. 114. P. 81-125.
18. Wodarz D., Nowak M.A. Specific Therapy Regimes Could Lead to Long-Term Im-
munological Control of HIV // Proc. National. Acad. Sci. 1999. V. 96. P. 14464-
14469.
19. Zurakowski R., Teel A. A Model Predictive Control Based Scheduling Method for
HIV Therapy // J. Theor. Biol. 2006. V. 238. P. 368-382.
Статья представлена к публикации членом редколлегии П.С. Щербаковым.
Поступила в редакцию 08.04.2020
После доработки 06.06.2020
Принята к публикации 10.09.2020
93