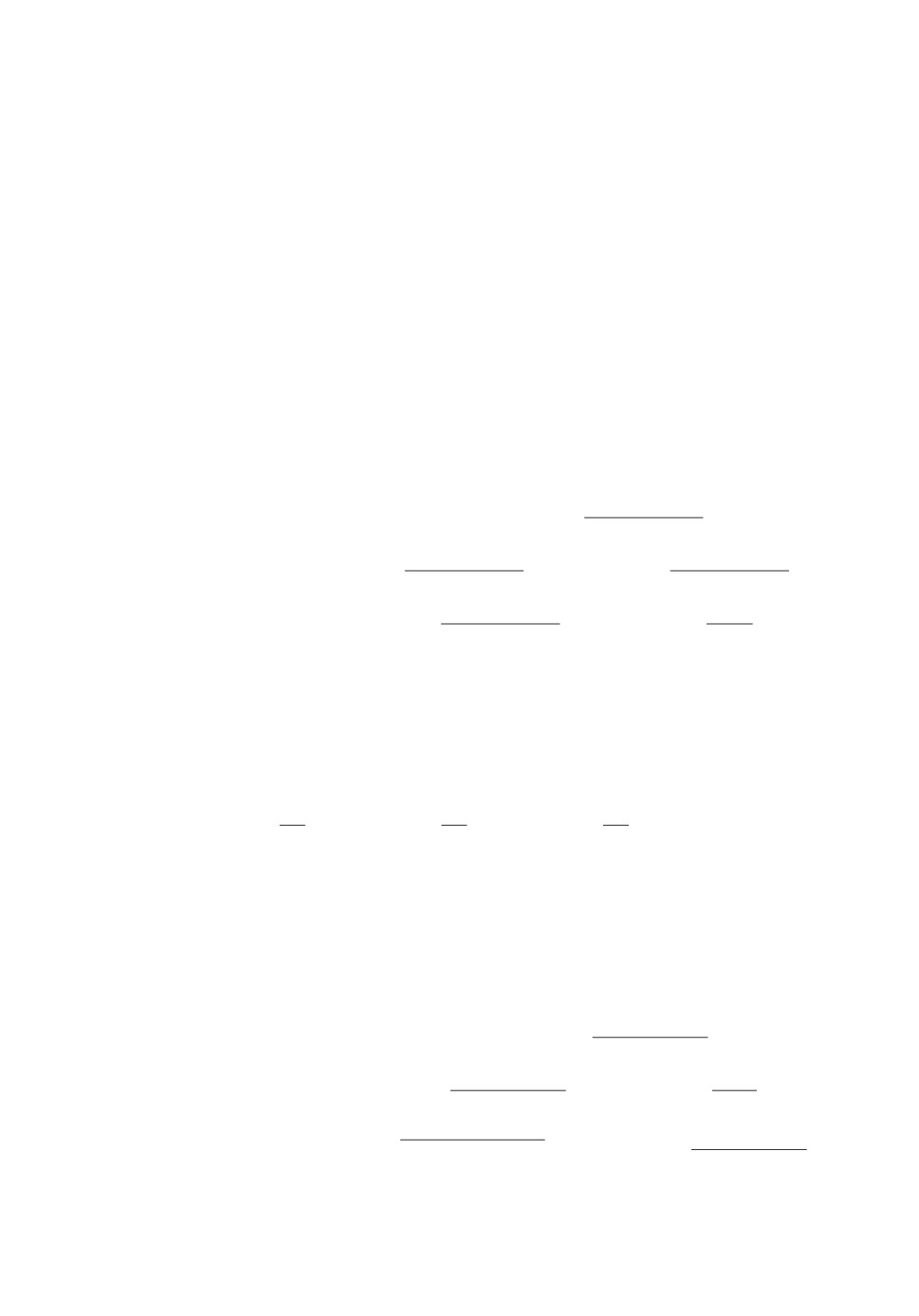Автоматика и телемеханика, № 2, 2021
© 2021 г. А.Е. ШУМСКИЙ, д-р техн. наук (a.e.shumsky@yandex.com),
А.Н. ЖИРАБОК, д-р техн. наук (zhirabok@mail.ru)
(Дальневосточный федеральный университет, Владивосток)
ПРИНЯТИЕ РЕШЕНИЙ ПРИ ДИАГНОСТИРОВАНИИ НЕЛИНЕЙНЫХ
ДИНАМИЧЕСКИХ СИСТЕМ НЕПАРАМЕТРИЧЕСКИМ МЕТОДОМ1
Рассматривается задача диагностирования динамических систем, опи-
сываемых моделями в виде нелинейных дифференциальных уравнений
с неизвестными коэффициентами (параметрами системы). Для решения
задачи применяется непараметрический метод диагностирования, позво-
ляющий исключить влияние неизвестных коэффициентов уравнений на
результаты диагностирования. Приводится изложение сути непараметри-
ческого метода. Предлагается новый метод принятия решений о наличии
и виде дефекта, учитывающий ошибки модели, неконтролируемые воз-
мущающие воздействия, а также шумы измерений. Отличительной осо-
бенностью этого метода является комплексное сочетание метода порого-
вой логики принятия решения и сопоставление сигнала рассогласования
(невязки) с формируемыми в процессе диагностирования сигнатурами де-
фектов.
Ключевые слова: нелинейные динамические системы, диагностирование,
робастность, непараметрический метод.
DOI: 10.31857/S0005231021020070
1. Введение
Современные технические системы ответственного назначения характери-
зуются значительной сложностью, что не позволяет гарантировать безотказ-
ность их функционирования. В связи с этим возникает задача обеспечения
отказоустойчивости подобных систем. Решение последней задачи предпола-
гает, во-первых, диагностирование (обнаружение и локализацию дефектов)
и, во-вторых, парирование выявленных дефектов. Настоящая статья концен-
трируется на проблеме обнаружения и локализации (поиска) дефектов.
Решение задачи диагностирования осуществляется в рамках концепции
аналитической избыточности [1]. Суть этой концепции состоит в предположе-
нии о существовании аналитических зависимостей между входами и выхода-
ми диагностируемой системы, измеряемыми на конечном интервале времени.
Эти зависимости справедливы при исправном функционировании системы.
Дефекты, возникающие в системе, приводят к их нарушению. Как следствие,
задача диагностирования сводится к проверке известных аналитических за-
висимостей посредством соответствующей обработки (в рамках скользящего
временного окна определенной размерности) входов и выходов системы.
1 Работа выполнена при финансовой поддержке Российского научного фонда, проект
№ 16-19-00046-П.
111
Реализация концепции аналитической избыточности предполагает два эта-
па диагностирования. На первом этапе формируется невязка как сигнал рас-
согласования между поведением имеющейся эталонной модели, используемой
для нахождения аналитических зависимостей, и реальным поведением систе-
мы. На втором этапе осуществляется анализ невязки с целью обнаружения
дефектов в системе и определения вида дефекта.
Выделяют два принципиально различных подхода к синтезу генератора
невязки. Первый подход, предполагающий формирование генератора невяз-
ки с замкнутой петлей обратной связи, приводит к использованию наблю-
дателей состояния, разрабатываемых с учетом специфических требований,
предъявляемых задачей диагностирования [2-4]. Достоинством этого подхода
является то, что, помимо собственно генерации невязки, он позволяет также
решить задачу оценивания состояния системы. Последнее может быть важно
для решения различных задач управления в условиях ограниченного наблю-
дения состояния системы.
При использовании второго подхода осуществляется синтез генератора
невязки с разомкнутой петлей обратной связи. Использование второго подхо-
да не позволяет одновременно получать оценки состояния системы, но упро-
щает задачу обеспечения устойчивости невязки. По своим динамическим ха-
рактеристикам формируемая невязка аналогична невязке, получаемой с ис-
пользованием наблюдателя состояния, имеющего конечный отклик на на-
чальное рассогласование. Именно этот подход используется в настоящей ста-
тье.
Помимо дефектов, на невязку могут влиять дестабилизирующие факто-
ры: ошибки эталонной модели, различные внешние неконтролируемые возму-
щающие воздействия, а также шумы измерений. Как следствие, возникает за-
дача обеспечения робастности (нечувствительности принимаемого решения к
дестабилизирующим факторам или крайне низкой чувствительности к этим
факторам по сравнению c чувствительностью к дефектам). Задача обеспе-
чения робастности рассматривалась в ряде работ [5-7]. Принято различать
активные и пассивные методы обеспечения робастности. Первые работают на
этапе формирования невязки и базируются на принципах адаптации, полной
развязки и оптимизации, в то время как вторые используют специальные ме-
тоды принятия решения. В частности, на этапе обнаружения дефектов широ-
ко используются методы пороговой логики принятия решения [5-7], в основе
которых лежит сравнение некоторой нормы сигнала невязки с порогом; пре-
вышение нормой невязки порога рассматривается как факт возникновения
дефекта в системе.
Традиционные активные методы обеспечения робастности имеют ряд
ограничений, влияющих на возможность их практического применения [8].
Специальную группу активных методов составляют так называемые непара-
метрические методы, предложенные в [8] для систем с непрерывным време-
нем, описываемых обыкновенными дифференциальными уравнениями (ли-
нейными и нелинейными) и в [9] для систем с дискретным временем, описы-
ваемых нелинейными разностными уравнениями. Непараметрические мето-
ды позволяют частично снять ограничения традиционных активных методов;
их отличительной особенностью является то, что они обеспечивают форми-
112
рование невязки, не чувствительной к значениям неизвестных постоянных
коэффициентов уравнений (параметров системы). Однако присутствие деста-
билизирующих факторов приводит к необходимости привлечения пассивных
методов обеспечения робастности, обеспечивающих приемлемый компромисс
между минимальной величиной гарантированно обнаруживаемых и локали-
зуемых дефектов, с одной стороны, и отсутствием ложных тревог в силу
действия дестабилизирующих факторов, с другой.
Для обеспечения подобного компромисса в известных работах предлагает-
ся использование адаптивного порога, величина которого устанавливается с
учетом измеряемых сигналов системы [5]. Идея расчета адаптивного порога
для нелинейных динамических систем была сформулирована в [10]. С исполь-
зованием методов теории чувствительности эта идея была распространена
в [7] на случай применения непараметрического метода диагностирования.
В последней работе рассматривались структурированные возмущающие воз-
действия, входящие в описание эталонной модели в качестве дополнитель-
ных неизвестных входов. Для расчета порога в реальном времени за основу
принималось выражение для матрицы чувствительности компонент вектора
невязки к неизвестным входам, представляющим возмущающие воздействия.
Поскольку точное вычисление этой матрицы не представлялось возможным
в силу ее зависимости от компонент вектора состояния системы, не доступ-
ных для непосредственного измерения, было предложено в процессе вычис-
ления порога использовать верхнюю граничную оценку нормы H∞ матри-
цы чувствительности в пространстве Харди [11], определяемую для задан-
ного диапазона изменения значений компонент вектора состояния системы
и зависящую только от измеряемых входов и выходов системы. Недостат-
ком этого решения является определенное завышение величины порога и,
как следствие, занижение чувствительности к дефектам. Кроме того, модель
структурированных возмущающих воздействий не всегда адекватно может
отражать реальную практическую ситуацию.
Предлагаемое в настоящей статье решение позволяет устранить отмечен-
ные недостатки. Его отличительной особенностью является то, что учет воз-
действия дестабилизирующих факторов и формирование адаптивного порога
осуществляется посредством соответствующей обработки уже сформирован-
ного сигнала невязки. Это дает возможность упростить процедуру форми-
рования адаптивного порога для принятия решения об отсутствии дефек-
тов в системе, а также снизить величину этого порога, тем самым увеличив
чувствительность к дефектам. При этом для принятия решения о наличии
дефекта в системе и о виде этого дефекта дополнительно предполагается
осуществлять сопоставление сигнала невязки с сигнатурами этих дефектов.
Для обеспечения единства изложения в рамках одной статьи класс рас-
сматриваемых моделей динамических систем ограничивается моделями с
непрерывным временем, описываемыми нелинейными дифференциальными
уравнениями. Распространение полученных результатов на класс моделей с
дискретным временем, описываемых нелинейными разностными уравнения-
ми, представляется возможным с использованием результатов [9].
113
2. Особенности генерации невязки непараметрическим методом
2.1. Используемые диагностические модели
Пусть диагностируемая система описывается моделью вида
(1)
dx(t)/dt = f(x(t), u(t), a), y(t) = h(x(t), a),
где x(t) ∈ Rn, u(t) ∈ Rp, y(t) ∈ Rl - соответственно векторы состояния, входа
(управления) и измеряемого выхода, a ∈ Rm - вектор коэффициентов (пара-
метров системы), в качестве своих компонент включающий: 1) постоянные
коэффициенты модели, соответствующие точно не известным параметрам
системы, и 2) коэффициенты, имеющие смысл отклонений значений опре-
деленных параметров системы от первоначальных постоянных значений и
принимающие ненулевое значение только в случае возникновения дефектов,
подлежащих обнаружению и локализации; для удобства вектор последних
коэффициентов будем рассматривать как подвектор вектора a и обозначать
как af .
Дополнительно будем предполагать, что дефект в системе приводит к вне-
запному или постепенному отклонению от нуля значения соответствующей
компоненты вектора af (номер компоненты совпадает с номером дефекта).
Будем также придерживаться гипотезы о существовании только однократ-
ных дефектов в системе.
Нелинейные векторные функции f(∗) и h(∗) описывают соответственно
динамику системы и характеристики датчиков. Здесь и ниже символ “звез-
дочка” используется вместо пропущенных с целью упрощения записи аргу-
ментов функций.
Отметим, что в модель (1) не включено описание дестабилизирующих фак-
торов. Учет действия этих факторов будет осуществляться по результатам
обработки вектора невязки, формируемого непосредственно в процессе диа-
гностирования.
Синтез генератора невязки требует осуществления ряда дополнительных
преобразований исходной модели (1). Рассмотрим их.
Сначала осуществляется переход от модели (1) к модели без внутренних
обратных связей
(
)
dx(1)(t)/dt = f(1) y(t), u(t), a ,
(
)
dx(2)(t)/dt = f(2) x(1)(t), y(t), u(t), a ,
(2)
(
)
dx(N)(t)/dt = f(N) x(N-1)(t), x(N-2)(t), . . . , x(1)(t), y(t), u(t), a ,
(
)
(3)
y∗(t) = h∗ x(N)(t),x(N-1)(t),... ,x(1)(t),a
Динамика модели (2) разбита на N частей и x(i)(t) - вектор состояния i-й ча-
сти. Каждая часть зависит от векторов входа и выхода системы, а также век-
торов состояния предыдущих частей. Вектор выхода модели (3) формируется
114
как некоторая функция от векторов состояния частей. Преобразование мо-
дели (1) к модели (2), (3) осуществляется в предположении о существовании
функциональной связи между вектором состояния модели (1) и векторами
состояния частей модели (2):
(4)
x(i)(t) = ϕ(i)
(x(t)),
1≤i≤N,
а также между векторами выхода моделей (1) и (3):
(5)
y∗
(t) = ψ(y(t)),
где ϕ(i)(∗), 1 ≤ i ≤ N и ψ(∗) - некоторые дифференцируемые векторные
функции. Отметим, что решение задачи преобразования исходной модели (1)
к модели (2), (3) было получено в [8] и развито в [7] на основе дифференци-
ально-геометрического подхода [12]. Для удобства читателя краткое изложе-
ние этого результата приведено в Приложении.
На следующем этапе синтеза генератора невязки осуществляется переход
от модели (2), (3) к вход-выходному описанию системы. Для осуществления
такого перехода может потребоваться преобразование компонент функций
f(i)(∗), 1 ≤ i ≤ N, и h∗(∗) к полиномиальному виду. Выполнение этого требо-
вания обеспечивается путем разложения функций более общего вида в ряд.
Допускаемые при этом ошибки рассматриваются как ошибки модели. Особен-
ности структуры модели (2), (3) и полиномиальное представление ее функций
позволят гарантировать получение вход-выходного описания.
Рассмотрим особенности перехода. Для упрощения последующих записей
введем оператор I в соответствии с условием
(
(
))
(6)
I f(j) x(j-1)(t),x(j-2)(t),...,x(1)(t),y(t),u(t),a
=
∫t
(
)
= f(j) x(j-1)(τ),x(j-2)(τ),...,x(1)(τ),y(τ),u(τ),a dτ + x(j)(t0) = x(j)(t).
t0
В силу (6) можно записать
(
)
x(1)(t) = I f(1)(∗) ,
(
( (
)
))
x(2)(t) = I f(2) I f(1)(∗) ,y(t),u(t),a
,
(7)
(
( (
)
(
)
))
x(N)(t) = I f(N) I f(N-1)(∗)
,...,I f(1)(∗) ,y(t),u(t),a
Подставляя (7) в (3), учитывая (5) и осуществляя эквивалентные преобразо-
вания, можно окончательно перейти к вход-выходному описанию системы в
следующем виде:
(8)
ψ(y(t)) = (A + Af )W (t0
,t),
115
где W (t0, t) и A, Af - соответственно вектор-столбец и матрицы такие, что:
1) элементами вектор-столбца W (t0, t) являются функционалы, зависящие от
значений векторов входа и выхода системы, измеряемых на интервале вре-
мени [t0, t]; 2) элементами матрицы A являются полиномы от компонент век-
торов постоянных коэффициентов a, не подверженных влиянию дефектов,
и состояний частей модели (2) x(j)(t0), 1 ≤ j ≤ N, в некоторый “начальный”
момент времени t0; 3) элементами матрицы Af являются полиномы от ком-
понент вектора коэффициентов af и, возможно, других компонент вектора
a и состояний частей модели. Для дальнейшего важно, что при отсутствии
дефектов должно выполняться
(9)
Af
= 0.
С этой целью полиномиальные элементы матрицы Af формируется таким
образом, что каждый терм полиномов в качестве сомножителя включает хотя
бы один коэффициент вектора af .
Модель (8) будем рассматривать как эталонную модель, используемую
для нахождения аналитических зависимостей, проверка выполнения которых
позволит осуществлять обнаружение и поиск дефектов.
2.2. Генерация невязки
Пусть t0, t1, . . . , tL, где ti = t0 + iΔt, 1 ≤ i ≤ L, - некоторые дискретные от-
счеты времени иΔt - период выборки измерений значений входов и выходов
системы. ВыборΔt определяется динамикой (быстродействием) диагности-
руемой системы и вычислительной мощностью средств, используемых для
реализации процесса диагностирования. Чем меньшеΔt, тем меньше будут
временные затраты на обнаружение и определение вида дефекта.
С учетом (9) аналитические зависимости, связывающие входы и выходы
исправной системы на интервале времени TL = [t0, tL] (в рамках размеров
текущего скользящего временного окна), можно записать в виде
(10)
Y (tL) = AV (tL
),
где матрицы
(
)
(11)
Y (tL) =
ψ(y(t1))ψ(y(t2)) . . . ψ(y(tL))
,
(
)
(12)
V (tL) =
W (t0, t1)W (t0, t2) . . . W (t0, tL)
Пусть размер скользящего временного окна выбран таким образом, что
(13)
rank V (tL-1) = rank V (tL
).
В этом случае матрица V (tL) имеет ненулевое ядро [11]. Напомним, что для
любого вектора v(tL), принадлежащего ядру матрицы V (tL), выполняется
равенство V (tL)v(tL) = 0. Поэтому правило проверки аналитических зависи-
мостей (вычисления невязки) может быть предложено в следующем виде
(14)
r(tL) = Y (tL)v(tL), v(tL) ∈ ker V (tL
),
116
где r(tL) - значение вектора невязки, формируемое в момент времени tL и
v(tL) - произвольный вектор, принадлежащий ядру матрицы V (tL). Действи-
тельно, в силу (10) из (14) получаем
(15)
r(tL) = AV (tL)v(tL
) = 0.
Для сведения к минимуму временных затрат на обнаружение дефекта раз-
мер скользящего временного окна должен быть минимально возможным, при
котором выполняется (13). Это достигается за счет применения следующего
алгоритма генерации невязки.
Алгоритм 1 (генерация невязки).
1. Положить L = 1. Вычислить V (t1) = W (t0, t1).
2. Принять L = L + 1. Вычислить V (tL) согласно (12).
3. Проверить выполнение равенства (13). При его невыполнении перейти
к п. 2.
4. Вычислить Y (tL) согласно (11).
5. Вычислить невязку согласно (14).
6. Конец.
Заметим, что вычислительную сложность алгоритма можно уменьшить за
счет исключения п. 3. Действительно, при значении L = Lmax, где величина
Lmax на единицу превышает число столбцов матрицы A, число столбцов мат-
рицы V (tL) превышает число ее строк и матрица V (tL) будет заведомо иметь
ненулевое ядро. Однако в этом случае минимальный размер временного окна
не будет гарантирован.
Дополнительно отметим, что в [13] также рассматривались правила гене-
рации невязки, отличающиеся от правила, представленного формулой (14).
3. Комплексный метод принятия решений
3.1. Пороговая логика
В отсутствие дефектов и дестабилизирующих факторов правило (14) обес-
печивает формирование вектора невязки, равного нулю. На практике из-
за действия различных дестабилизирующих факторов, описание которых не
включено в эталонную модель (8), формируемое значение вектора невязки
будет ненулевым. При этом возникает необходимость ответа на вопрос: “Яв-
ляется ли действие дестабилизирующих факторов единственной причиной
формирования ненулевого вектора невязки?” Для ответа на этот вопрос пред-
лагается использовать пороговую логику принятия решения.
Пусть по результатам вычисления невязки и ее анализа при положениях
скользящего временного окна, предшествующих текущему его положению,
сделан вывод об исправности системы до момента времени t = tL-1 вклю-
чительно, где момент времени tL-1 рассматривается в привязке к текущему
временному положению интервала TL. В этом случае значение порога, ис-
пользуемого для принятия решения в момент времени tL, предлагается вы-
числять по формуле
(
)1/2
(16)
Π(tL) = Π0 + max
r(τ)T r(τ)
,
T∗ = {t0,tL-1
},
τ ∈T∗
117
где верхний индекс T обозначает транспонирование. Постоянную составляю-
щую порога Π0 предлагается определять по результатам моделирования или
натурных испытаний исправной системы в соответствии с требованием от-
сутствия ложных тревог.
Если генерируемое в момент времени tL значение нормы вектора невяз-
ки не превышает порога, принимается решение об отсутствии дефектов в
системе. Поскольку предложенный способ вычисления порога не учитывает
возможное изменение интенсивности действия дестабилизирующих факторов
в момент времени tL, возможно нарушение неравенства
(17)
(rT(tL)r(tL))1/2 ≤ Π(tL)
даже при отсутствии дефектов. Как следствие, принятие окончательного ре-
шения о дефекте в системе требует проведения дополнительной проверки
(см. ниже). Если эта проверка не подтвердит факт присутствия дефекта, то
при следующем положении временного окна будет сформированно большее
значение порога.
Заметим, что предложенный способ вычисления порога позволяет учи-
тывать возможное изменение интенсивности действия дестабилизирующих
факторов в процессе диагностирования, что обеспечивает адаптацию порога
к реальным условиям диагностирования.
3.2. Сопоставление с сигнатурами дефектов
Пусть дефект в системе впервые приводит к ненулевому значению пара-
метра afj в момент времени tL такому, что результатом является нарушение
неравенства (17). При этом матрица A не меняет своего значения, в то вре-
мя как Af = 0. Тогда по-прежнему будет выполняться (15) и, как следствие,
“вклад” дефекта в значение вектора невязки в момент времени tL будет опре-
деляться равенством
(18)
r(tL) = Af W (t0, tL)vL(tL
),
где vL(tL) - значение последней компоненты вектора v(tL).
Предположив, что величина дефекта достаточно мала, воспользуемся ли-
нейным приближением
(
)
f
(19)
Af =
∂Af/∂af
a
j
j
|af=0
Тогда в силу (18) и (19) при отсутствии дестабилизирующих факторов на-
правление вектора невязки будет совпадать с направлением вектора
(
)
(20)
σj(tL) =
∂Af/∂af
W (t0, tL
).
j
|af=0
Вектор σj(tL) назовем сигнатурой j-го дефекта.
Влияние дестабилизирующих факторов на невязку чревато неполным сов-
падением направлений векторов r(tL) и σj (tL). В этом случае вывод о при-
сутствии в системе j-го дефекта может быть сделан на основе оценки угло-
вого расстояния между векторами r(tL) и σj(tL). В качестве такой оценки
118
предлагается использовать абсолютное значение косинуса угла между этими
векторами, рассчитываемое по формуле
|rT(tL) σj (tL)|
(21)
αj(tL) =
(rT(tL) r(tL))1/2 (σTj(tL) σj(tL))1/2
Чем ближе значение αj (tL) к единице, тем больше степень уверенности в том,
что в системе имеет место j-й дефект.
Отметим, что в выражение для частных производных (∂Af /∂afj )|af=0 мо-
гут входить значения неизвестных коэффициентов и компонент векторов
x(j)(t0), 1 ≤ j ≤ N. Для того чтобы иметь возможность вычислять сигна-
туры дефектов непосредственно в процессе диагностирования, предлагается
находить оценки значений этих коэффициентов и компонент векторов для
последующей подстановки их в (20). Нахождение оценок предполагается осу-
ществлять в два этапа: 1) вычисление элементов матрицы A путем прямого
решения уравнения (10) и 2) выражение искомых значений коэффициентов
и компонент векторов через значения элементов матрицы A.
Предположим, что размер скользящего временного окна L является мини-
мальным, таким, что выполняется равенство (13). Тогда матрица V (t0, tL-1),
во-первых, имеет ранг L и, во-вторых, зависит от значений векторов входа
и выхода исправной системы, измеренных на отрезке времени T∗ = [t0, tL-1].
Если матрица V (t0, tL-1) не является квадратной, то, пользуясь представле-
нием
[
]
V1(t0,tL-1)
AV (t0,tL-1) = [A1A2]
,
V2(t0,tL-1)
где V1(t0, tL-1) - квадратная невырожденная матрица, из (10) получим
(22)
A1 = [Y (t0,tL-1) - A2V2(t0,tL-1)]V-11(t0,tL-1
).
При этом для нахождения матрицы A1 потребуется задание матрицы A2 пу-
тем дополнительного определения значений некоторых коэффициентов и не
доступных для непосредственного измерения компонент вектора состояния
системы. Если дополнительно определяемые коэффициенты принимают зна-
чения в пределах известных интервалов (допусков), то для их определения
целесообразно использовать средние значения допусков. Однако при этом бу-
дет возможным осуществлять лишь приближенное вычисление сигнатур де-
фектов. Если дополнительно определяемыми являются значения компонент
состояния системы в момент времени t0, то может потребоваться использо-
вание дополнительного наблюдателя состояния для их оценивания.
Очевидно, что если V (t0, tL-1) - квадратная матрица, то никакого доопре-
деления не требуется и для нахождения матрицы A достаточно положить в
(22) A1 = A, V1(t0, tL-1) = V (t0, tL-1) и A2V2(t0, tL-1) = 0.
3.3. Реализация комплексного метода принятия решения
В приведенных выше соотношениях для вычисления вектора невязки (14),
порога (16), а также значений сигнатуры дефектов и углового расстояния
119
(соотношения (20) и (21) соответственно) используется “внутреннее” время
интервала TL, представляющего скользящее временное окно. Для того чтобы
привязать это “внутреннее” время к текущему времени системы t, достаточно
положить в соответствующих соотношениях
(23)
tL = t, ti = t - (L - i)Δ
t,
0 ≤ i ≤ L - 1.
Рассмотрим особенности совместного использования описанных выше ме-
тодов для принятия решения о наличии дефекта в системе и о виде дефекта.
Во-первых, для реализации метода пороговой логики должна существовать
возможность вычисления в реальном времени: 1) вектора невязки и 2) поро-
га. Вычисление вектора невязки в момент времени t является возможным,
если доступны значения входов и выходов системы на отрезке времени TL,
предшествующем моменту t. Как было показано выше, это требование га-
рантированно выполняется при i ≥ Lmax. Далее, для формирования поро-
га необходимо иметь возможность использовать значения вектора невязки,
сформированные на отрезке времени не менее чем T∗; длина этого отрезка не
превышает (Lmax - 1)Δt.
Во-вторых, должно быть установлено пороговое значение αmin, достаточно
близкое к единице, такое что выполнение неравенства
(24)
αj(t) ≥ αmin
позволяет сделать формальное заключению о присутствии в системе j-го де-
фекта.
Опишем алгоритм, реализующий комплексный подход к принятию реше-
ний.
Алгоритм 2 (принятие решений).
1. Запустить работу алгоритма с момента времени t = tLmax .
2. Положить i = Lmax - 1.
3. Воспользовавшись алгоритмом 1, вычислить вектор невязки r(t).
4. Если i ≥ 1, положить i = i - 1, t = t +Δt и перейти к п. 3.
5. Положить t = t +Δt.
6. Воспользовавшись алгоритмом 1, вычислить вектор невязки r(t).
7. Воспользовавшись соотношением (16), вычислить значение порога Π(t).
8. Если неравенство (17) выполняется, перейти к п. 5.
9. Для каждого j вычислить σj(t) и αj (t) согласно (20) и (21) соответствен-
но.
10. Если ни для одного j неравенство (24) не выполняется, перейти к п. 5.
11. Если для некоторого j и всех i, i = j, выполняется αj(t) > αi(t), при-
нять решение о j-м дефекте в системе.
Приведем ряд комментариев к алгоритму. Выполнение п. 1 гарантирует
наличие информации о входах и выходах системы, достаточной для вычис-
ления невязки на начальном этапе диагностирования. П.п. 2-4 обеспечива-
ют вычисление значений вектора невязки, необходимых для формирования
порога на начальном этапе диагностирования. П.п. 5-10 представляют этап
диагностирования, завершаемый обнаружением дефекта, в то время как при
120
выполнении п. 11 принимается решение о виде дефекта. Заметим, что если
при выполнении этого пункта для некоторой пары дефектов с номерами i и
j имеет место αi(t) ≃ αj (t), то это означает неразличимость этих дефектов в
рамках используемой процедуры диагностирования.
4. Пример
4.1. Формирование эталонной модели
Проиллюстрируем особенности применения полученных результатов на
уже ставшим классическим примере объекта [14], состоящего из трех после-
довательно соединенных баков с площадями поперечного сечения ϑ1, ϑ2 и ϑ3.
Баки соединены между собой трубами с площадями поперечного сечения ϑ4
и ϑ5. В первый бак вливается жидкость, а из последнего через отверстие по-
перечного сечения ϑ6, расположенное в дне третьего бака, вытекает. Модель
объекта представлена системой обыкновенных дифференциальных уравне-
ний
(
)√
dx1(t)/dt = a1u1(t) - a2 - af2
x1(t) - x2(t),
(
)√
(
)√
dx2(t)/dt = a2 - af2
x1(t) - x2(t) - a3 - af3
x2(t) - x3(t),
(25)
(
)√
(
)√
dx3(t)/dt = a3 - af3
x2(t) - x3(t) - a4 - af4
x3(t),
y1(t) = x2(t), y2(t) = x3(t),
где переменные входа u1(t) и состояния x1(t), x2(t), x3(t), x1(t) ≥ x2(t) ≥
≥ x3(t), введены для обозначения соответственно объема поступающей жид-
кости в единицу времени и уровней жидкости в баках. Непосредственно из-
меряемыми являются уровни x2(t) и x3(t). Постоянные коэффициенты - это
a1 = 1/ϑ1, a2 = ϑ4
√2g/ϑ1, a3 = ϑ5√2g/ϑ2, a4 = ϑ6√2g/ϑ3, и g - гравитаци-
онная постоянная. Диагностированию подлежат дефекты, приводящие к за-
сорению труб и, как следствие, уменьшению площади их сечения. На моде-
ли (25) дефекты задаются ненулевыми (положительными) значениями коэф-
фициентов af2 , af3 и af4 .
Рассмотрим поэтапно задачу синтеза эталонной модели. Осуществив пре-
образование (25) к модели без внутренних обратных связей, получим
(
)√
dx(1)1(t)/dt = a1u1(t) - a3 - af3
y1(t) - y2(t),
(
)√
(
)√
dx(1)2(t)/dt = a3 - af3
y1(t) - y2(t) - a4 - af4
y2(t),
(26)
(
)√
(
)√
dx(2)1(t)/dt = a2 - af
x(1)1(t) - 2y1(t) - a3 - af3
y1(t) - y2(t),
2
y1(t) = x(2)1(t), y2(t) = x(1)2(t),
121
при
(
)T
ϕ(1)(x(t)) =
x1(t) + x2(t),x3(t)
,
ϕ(2)(x(t)) = x2(t),
(
)T
ψ(y(t)) =
y1(t),y2(t)
Воспользовавшись соотношением (6) и делая подстановку согласно (7),
запишем
∫
t
(
)∫ t
√
x(1)1(t) = a1 u1(τ)dτ - a3 - af
y1(τ) - y2(τ) dτ + x(1)1(t0),
3
t0
t0
(
)∫t
(
)∫t
√
√
(27)
x(1)2(t) = a3 -af
y1(τ)-y2(τ) dτ - a4 -af
y2(τ) dτ +x(1)2(t0
),
3
4
t0
t0
(
)
(28)
x(2)1(t) = a2 - af
×
2
v
u
τ
∫t
∫
u
(
)∫τ
√
u
×
√a1
u1(τ′)dτ′ - a2 - af
2
y1(τ′) - y2(τ′)dτ′ + x(1)1(t0) - 2 y1(τ) dτ -
t0
t0
t0
(
)∫ t
√
- a3 -af
y1(τ) - y2(τ)dτ + x(2)1(t0).
3
t0
Используем разложение квадратного корня в ряд Маклорена. Положим
∫τ
(
)∫τ
√
(29)
µ(τ) = a1 u1(τ′) dτ′ - a2 - af
y1(τ′) - y2(τ′) dτ′ - 2y1
(τ).
2
t0
t0
Можно показать (посредством моделирования), что для используемых значе-
ний u1(t) и xi(t0), 1 ≤ i ≤ 3, выполняется |µ(τ)/x(1)1(t0)| < 1. Как следствие,
справедлива приближенная запись
√
(
)2
µ(τ)
1
µ(τ)
1
µ(τ)
1+
=1+
-
-
8
x(1)1(t0)
2 x(1)1(t0)
x(1)1(t0)
Ограничившись первыми тремя членами разложения, получим приближен-
ное равенство
t
(
)2
∫
(
)√
µ(τ)
1
µ(τ)
x(2)1(t) = a2 - af
x(1)1(t0)
1+1
-
dτ-
2
8
2 x(1)1(t0)
x(1)1(t0)
t0
(30)
(
)∫t
√
- a3 -af
y1(τ) - y2(τ) dτ + x(2)1(t0).
3
t0
122
С учетом (27) и (29), (30) запишем матрицы эталонной модели (8):
A=
√
(2)
(1)
a1a2
−a2
-a22
x
(t0) a2
x
(t0)
√
√
a2√
-a3
√
1
1
=
2
x(1)1(t0)
x(1)1(t0)
2x(1)1(t0) x(1)1(t0)
2
x(1)1(t0)
x(1)2(t0)
0
0
0
0
a3
0
a21a2
a1a22
-a32
-a22
0
√
√
√
√
8x(1)1(t0) x(1)1(t0)
4x(1)1(t0) x(1)1(t0)
8x(1)1(t0) x(1)1(t0)
2x(1)1(t0) x(1)1(t0)
,
−a4
0
0
0
0
Af =
√
f
(1)
-a1af2
af2
-af2
-2a2af2 +(af2 )2
0
-a
x
(t0)
√
√
√
af
√
2
1
3
=
2
x(1)1(t0)
x(1)1(t0)
2x(1)1(t0) x(1)1(t0)
2
x(1)1(t0)
0
0
0
0
0
-af3
0
−a21af2
a1(-2a2af2 +(af2 )2)
-3a22af2 +3a2(af2 )2-(af2 )3
-a2af2 +(af2 )2
√
√
√
√
0
8x(1)1(t0) x(1)1(t0)
4x(1)1(t0) x(1)1(t0)
8x(1)1(t0) x(1)1(t0)
2x(1)1(t0) x(1)1(t0)
,
af4
0
0
0
0
W (t0, t) =
(
t
t
t
t
∫
∫
∫
∫
∫
√
=
1
t-t0
u1(τ′)dτ′dτ
y1(τ)dτ
y21(τ)dτ
y1(τ) - y2(τ)dτ
t0 t0
t0
t0
t0
(
)2
∫ √
∫
t
√
∫
t
∫
∫t
y1(τ′) - y2(τ′)dτ′dτ
y2(τ)dτ
u1(τ′)dτ′
dτ
t0 t0
t0
t0
t0
(
)
(
)2
∫
∫
√
∫
t
∫ √
∫t
u1(τ′)dτ′
y1(τ′) - y2(τ′)dτ′ dτ
y1(τ′) - y2(τ′)dτ′
dτ
t0
t0
t0
t0
t0
(
)
)T
∫
√
∫t
y1(τ)
y1(τ′) - y2(τ′)dτ′ dτ
t0
t0
Анализ полученных матриц позволяет сделать следующие выводы. Во-
первых, реализуемая в соответствии с алгоритмом 1 процедура генерации
невязки является непараметрической, поскольку не требует знания точных
значений параметров объекта диагностирования (коэффициенты a1 - a4).
Это также обусловливает универсальность процедуры: она пригодна для лю-
бых трехбаковых объектов, независимо от их геометрических размеров. Во-
вторых, матрицы частных производных (∂Af /∂afj )|af=0, 1 ≤ j ≤ 3, зависят
от коэффициентов модели.
Для того чтобы исключить необходимость оценивания значений неизвест-
ных параметров и переменных объекта диагностирования для вычисления
123
матрицы производных (∂Af /∂afj )|af=0, 1 ≤ j ≤ 3, рассмотрим структуру мат-
рицы Af . Несложно видеть, что дефект, соответствующий af2 , влияет только
на первую строку матрицы Af , дефект, соответствующий af4 , влияет только
на вторую строку матрицы Af , в то время как вклад дефекта, соответст-
вующего af3 , в строки матрицы Af одинаков по величине, но различается по
(
)T
(
)T
знаку. Теперь учитывая (20), можно принять σ1 =
1
0
,σ2 =
1
-1
и
(
)T
σ3 =
0
1
. Таким образом, принятие решения не требует знания значений
параметров объекта. Следовательно, процедура принятия решения также яв-
ляется универсальной и пригодна для любых трехбаковых объектов.
4.2. Результаты моделирования
Полученные выше матрицы эталонной модели были использованы для
моделирования в среде пакета MatLab процесса диагностирования трехба-
кового объекта. При моделировании исправного объекта задавались следую-
щие значения параметров объекта: a1 = 1 м-2, a2 = a3 = a4 = 0,4427 м1/2/с.
Генерация невязки и принятие решений осуществлялись на основе алгорит-
мов 1 и 2. Результаты, полученные для исправного объекта, представлены
на рис. 1, где графики а-г описывают поведение соответственно переменных
u(t), y1(t), y2(t) и нормы вектора невязки, а также адаптивного порога. Нера-
венство невязки нулю здесь обусловливается приближенным характером эта-
лонной модели в связи с использованием при ее получении разложения квад-
ратного корня в ряд Маклорена. Значение постоянной составляющей порога
а
б
0,8
4
0,6
3
0,4
2
0,2
1
0
200
400
600
800
1000
0
200
400
600
800
1000
с
с
в
´10-4
г
2,0
2
1,5
1,0
1
Адаптивный порог
Норманевязки
0,5
0
200
400
600
800
1000
0
200
400
600
800
1000
с
с
Рис. 1. Случай исправного функционирования трехбакового объекта.
124
´10-4
а
б
1,0
0,8
0,6
1
0,4
0,2
0
200
400
600
800
1000
0
200
400
600
800
1000
с
с
в
г
1,0
1,0
0,5
0,5
0
0
-0,5
-0,5
-1,0
-1,0
0
200
400
600
800
1000
0
200
400
600
800
1000
с
с
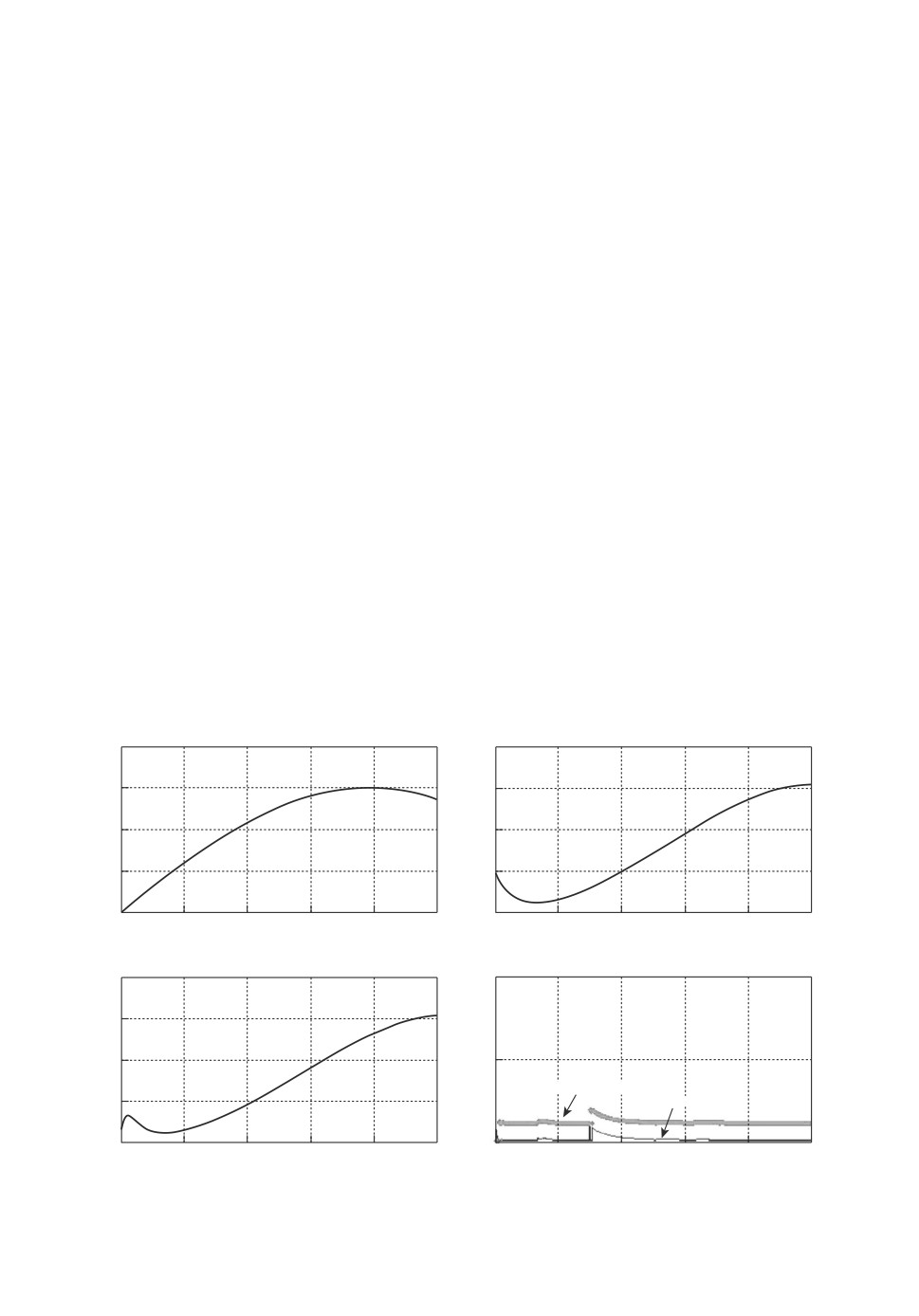
Рис. 2. Первый дефект в трехбаковом объекте.
´10-4
а
б
1,0
0,5
2
0
1
-0,5
-1,0
0
200
400
600
800
1000
0
200
400
600
800
1000
с
с
в
г
1,0
1,0
0,8
0,5
0,6
0
0,4
-0,5
0,2
-1,0
0
200
400
600
800
1000
0
200
400
600
800
1000
с
с
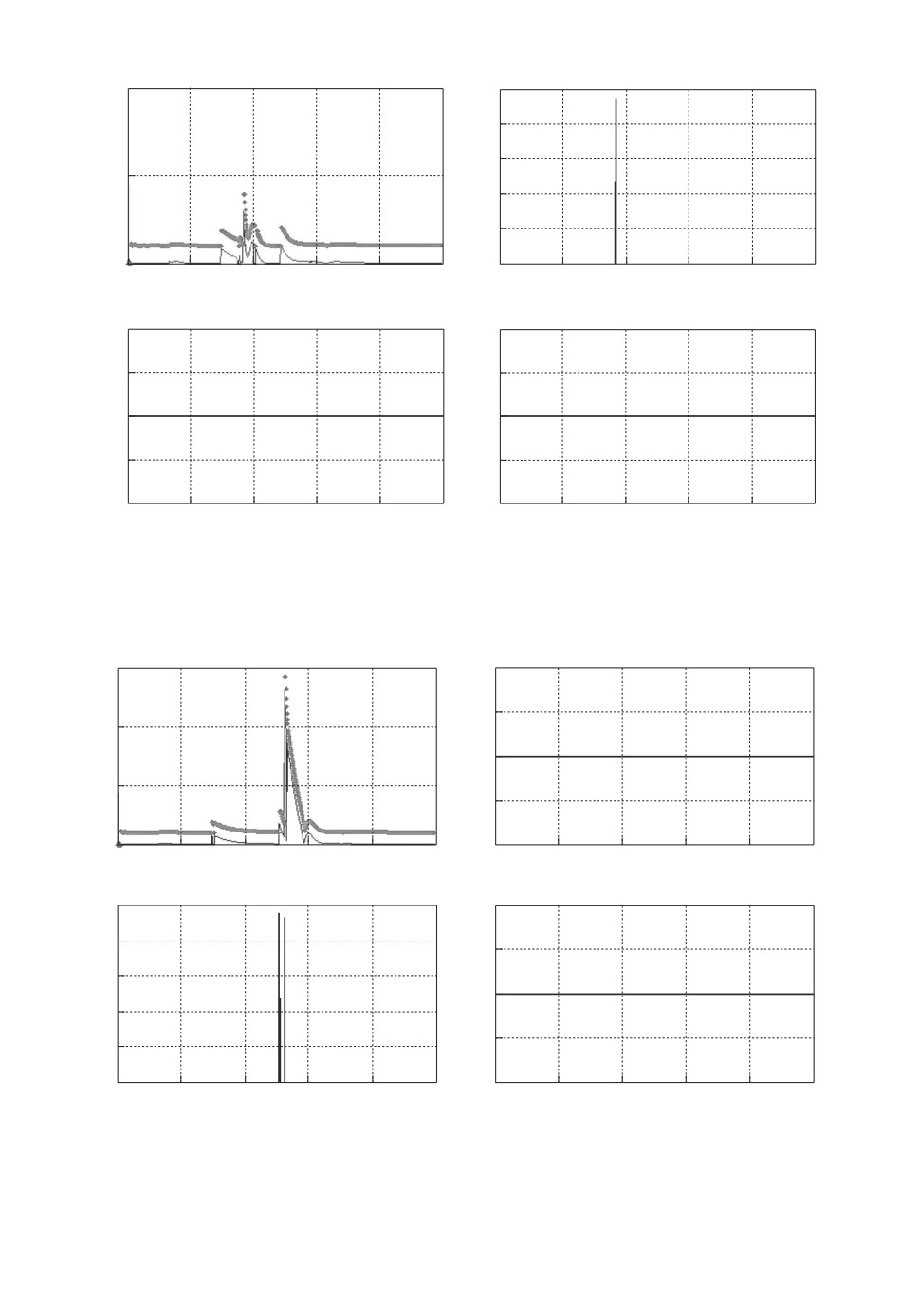
Рис. 3. Второй дефект в трехбаковом объекте.
125
´10-3
а
б
2,5
1,0
2,0
0,5
1,5
0
1,0
-0,5
0,5
-1,0
0
200
400
600
800
1000
0
200
400
600
800
1000
с
с
в
г
1,0
1,0
0,8
0,5
0,6
0
0,4
-0,5
0,2
-1,0
0
200
400
600
800
1000
0
200
400
600
800
1000
с
с
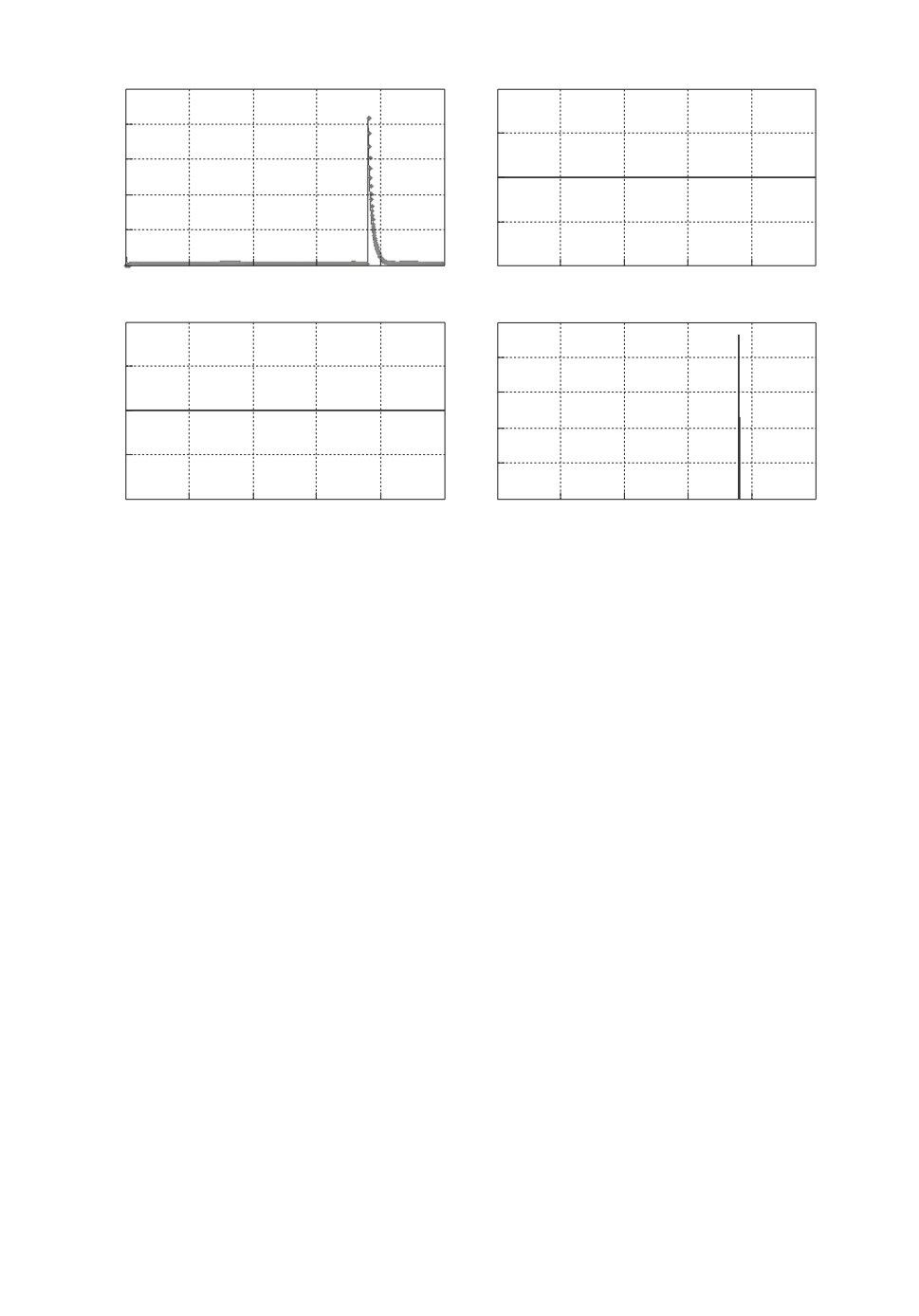
Рис. 4. Третий дефект в трехбаковом объекте.
Π0 = 0,2 × 10-4 выбрано из условия отсутствия ложной тревоги в момент
времени t = 300 с, см. график г.
На рис. 2, 3 и 4 приведены результаты моделирования для случаев возник-
новения в объекте первого, второго и третьего дефектов, приводящих соот-
ветственно к: 1) засорению трубы между первым и вторым баками (значение
коэффициента af2 = 0,1 с момента времени t = 350 с), 2) засорению трубы
между вторым и третьим баками (значение коэффициента af3 = 0,2 с мо-
мента времени t = 500 с) и 3) засорению слива из третьего бака (значение
коэффициента af4 = 0,1 с момента времени t = 700 с). Графики а описывают
поведение нормы сигнала невязки и адаптивного порога. На графиках б -г
приводятся значения угловых расстояний αj , 1 ≤ j ≤ 3, в случае превыше-
ния ими порогового значения αmin = 0,9. Если для некоторого αj порог не
превышается, то на графиках приводится значение αj = 0.
Сопоставление графиков б -г, полученных для различных дефектов, поз-
воляет сделать вывод о возможности локализации всех трех дефектов.
5. Заключение
В работе предложено эффективное решение задачи робастного диагности-
рования нелинейных динамических систем в условиях воздействия дестаби-
лизирующих факторов (ошибок эталонной модели, неконтролируемых внеш-
них возмущающих воздействий и ошибок измерений доступных переменных
системы). Отличительной особенностью этого решения является совместное
использование активного (непараметрический метод генерации невязки) и
126
пассивного (комплексный метод принятия решения о наличии дефекта и ви-
де этого дефекта) подходов к обеспечению робастности.
Новизна статьи состоит в разработке комплексного метода принятия ре-
шения, обеспечивающего определенный компромисс между минимальной ве-
личиной гарантированно обнаруживаемых и локализуемых дефектов и от-
сутствием ложных тревог.
Особенностью комплексного метода является сочетание пороговой логики
принятия решения, использующей адаптивный порог, и сопоставление фор-
мируемого вектора невязки с сигнатурами дефектов, также формируемых
в реальном времени с учетом текущих значений входов и выходов диагно-
стируемой системы. Еще одной особенностью этого метода является ориен-
тированность на получение минимально возможного размера скользящего
временного окна, что должно положительного сказаться на оперативности
принятия решений.
С другой стороны, увеличение размера скользящего временного окна мо-
жет положительно сказаться на подавлении эффекта воздействия дестаби-
лизирующих факторов, носящих случайный характер, за счет следующего:
1) в соотношениях (16), (17) и (21) вместо евклидовой нормы вектора невяз-
ки использовать евклидову норму для среднего значения вектора невязки,
вычисленную на некотором интервале времени; и 2) применить метод наи-
меньших квадратов для оценивания неизвестных параметров системы вме-
сто использования прямого решения, получаемого из уравнения (22). Рацио-
нальный выбор размера скользящего временного окна представляет само-
стоятельную задачу и может рассматриваться как предмет дополнительного
исследования.
В качестве предмета дополнительного исследования также может рассмат-
риваться задача перенесения полученных результатов на случай моделей с
дискретным временем, задаваемых разностными уравнениями.
ПРИЛОЖЕНИЕ
Рассмотрим задачу преобразования модели (1) к модели (2), (3), приняв
во внимание (4) и (5). Дифференцируя обе части равенства (4) по времени,
запишем
(
)
(Π.1)
x(i) =
∂ϕ(i)(x)/∂x
f (x, u, a),
1≤i≤N.
Осуществляя подстановки согласно (2) в левую часть уравнений (Π.1) и учи-
тывая (1) и (4), получим
(
)
f(1)(h(x),u,a) =
∂ϕ(1)(x)/∂x f(x,u,a),
(
)
(
)
f(2) ϕ(1)(x),h(x),u,a
= ∂ϕ(2)(x)/∂x f(x,u,a),
(Π.2)
(
)
(
)
f(N) ϕ(1)(x),... ,ϕ(N-1)(x),h(x),u,a
= ∂ϕ(N)(x)/∂x f(x,u,a).
127
Далее, совместно рассматривая второе уравнение из (1), уравнения (3) и (5),
запишем
(
)
(Π.3)
h∗ ϕ(1)(x),ϕ(2)(x),... ,ϕ(N)(x)
= ψ(h(x,a)).
Уравнения (Π.2) и (Π.3) могут быть непосредственно использованы для на-
хождения функций f(i), 1 ≤ i ≤ N, и h∗ преобразованной модели (2), (3) при
заранее найденных функциях ϕ(i), 1 ≤ i ≤ N, и ψ.
Воспользовавшись языком дифференциальной геометрии [12], опишем
способ нахождения функций ϕ(i), 1 ≤ i ≤ N, обеспечивающих разрешимость
уравнений (Π.2). Пусть Λi обозначает расслоение, введенное для функ-
ции ϕ(i): Λi = span{λ | (∂ϕ(i)/∂x)λ = 0}, где символ “span” обозначает линей-
ную оболочку системы векторов (ковекторов). Пусть также Ωi = Λ⊥i - со-
ответствующее корасслоение, где символ “⊥” обозначает аннигилятор, т.е.
Λ⊥i = {ω ∈ Rn |〈ω,λ〉 = 0 ∀λ ∈ Λi}, и скобки
∑
〈ω, λ〉 =
ωsλs
s
введены для обозначения внутреннего произведения.
Положим fij(x) = f(x, ui, aj ), где ui, 1 ≤ i ≤ v1, aj, 1 ≤ j ≤ v2 - некоторые
фиксированные значения векторов входа u и параметров a, v1 и v2 - конечные
значения такие, что векторная функция f(x, u, a) при любых допустимых
значениях векторов u и a линейно выражается через семейство векторных
функций (полей) F = {fij(x), 1 ≤ i ≤ v1, 1 ≤ j ≤ v2}.
Рассмотрим три операции дифференцирования. Первая операция (диф-
ференцирование Ли) вводится для скалярной функции α и векторного поля
γ ∈ spanF следующим образом:
Lγα = (∂α/∂x)γ.
Вторая операция (скобки Ли) вводится для двух векторных полей λ1 ∈ Λ
и λ2 ∈ Λ, где Λ - некоторое расслоение:
[λ1, λ2] = (∂λ2/∂x)λ1 - (∂λ1/∂x)λ2.
Третья операция вводится для ковекторного поля ω ∈ Ω и векторного по-
ля λ ∈ Λ, где Λ и Ω - некоторые расслоение и корасслоение соответственно;
результатом является ковекторное поле, определяемое следующим образом:
Lλω = λT(∂ωT/∂x)T + ω(∂λ/∂x).
В соответствии с определением расслоения Λi векторная функция ϕ(i) мо-
жет быть найдена посредством интегрирования однородных дифференциаль-
ных уравнений в частных производных:
(
)
(Π.4)
∂ϕ(i)/∂x λ = 0
∀λ ∈ Λi.
128
Необходимые и достаточные условия разрешимости уравнений (Π.4) опреде-
ляются теоремой Фробениуса (см. [12], с. 23). В соответствии с этой теоремой
регулярное (т.е. имеющее постоянный ранг во всей области определения) рас-
слоение интегрируемо, если оно инволютивно (замкнуто) относительно опе-
рации взятия скобок Ли. Процедура интегрирования уравнений (Π.4) также
может быть найдена в [12].
Далее, согласно свойствам приведенных выше операций дифференцирова-
ния (см. [12], с. 10), для ковекторного поля ω ∈ Ωi и векторного поля
⋂
(Π.5)
λ∈Λi = Λj
∩ ker(∂h/∂x), i ≥ 2,
j=1
(при i = 1 принимаем Λ = ker(∂h/∂x)) справедливо
(Π.6)
Lγ〈ω,λ〉 = 〈Lγ
ω,λ〉 + 〈ω,[γ,λ]〉, γ ∈ G.
По построению корасслоения Ωi для λ ∈ Λi и ω ∈ Ωi выполняется 〈ω, λ〉 = 0
и, как следствие,
Lγ〈ω,λ〉 = 0.
Дополнительно положим в (Π.6)
(Π.7)
〈ω, [γ, λ]〉 = 0,
что приведет к
(Π.8)
〈Lγ
ω,λ〉 = 0.
Равенство (Π.8) эквивалентно включению
∑
(Π.9)
Lγω ∈ Ωj
+ span(∂h/∂x).
j=1
При ∂ϕsi)/∂x = ω, где нижний индекс “s” указывает номер компоненты век-
торной функции ϕ(i), это означает, что соответствующая компонента вектор-
ной функции (∂ϕ(i)/∂x)f(∗) может быть выражена через компоненты вектор-
ных функций h(x), ϕ(1)(x), . . . , ϕ(i-1)(x) и векторов u, a. Поскольку это долж-
но выполняться для всех компонент векторной функции (∂ϕ(i)/∂x)f(∗), для
которых найдутся “свои” ковекторы ω, удовлетворяющие (Π.9), существуют
некоторые векторные функции f(i)(∗), 1 ≤ i ≤ N, удовлетворяющие уравне-
ниям (Π.2). При этом равенство (Π.7) может рассматриваться как достаточ-
ное условие разрешимости уравнений (Π.2). Опираясь на вышеизложенное,
приведем алгоритм нахождения функций ϕ(i)(x), 1 ≤ i ≤ N.
Алгоритм 3 (нахождение функций ϕ(i)(x), 1 ≤ i ≤ N).
1. Положить i = 1, сформировать расслоение Λ′1 = ker(∂h/∂x).
129
2. Сформировать расслоение Λi = Λ′i ∩ span{[γ, λ] | γ ∈ G, λ ∈ Λ′i}.
3. Если i ≥ 2 и Λi ⊇ Λi-1, положить N = i и перейти к п. 5.
4. Положить i = i+1 и найти расслоение Λ′i в соответствии с (Π.5). Перейти
к п. 2.
5. Найти векторные функции ϕ(i), 1 ≤ i ≤ N, посредством интегрирова-
ния уравнений (Π.4).
6. Для сокращения размерности получаемой модели исключить из функ-
ций ϕ(i), i ≥ 2, компоненты, функционально зависимые от компонент вектор-
ных функций ϕ(j), 1 ≤ j ≤ i - 1.
Конец.
Отметим следующее. П.п. 1, 2 и 4 алгоритма позволяют формировать рас-
слоения Λi, одновременно удовлетворяющие соотношению (Π.5) и ограниче-
нию (Π.7). Проверка функциональной зависимости (последний пункт алго-
ритма) может быть проведена с использованием анализа ранга соответствую-
щих матриц Якоби (см. [15, с. 112]).
Способ нахождения функции ψ(h(x)), обеспечивающий разрешимость
уравнений (П.3), предполагает интегрирование замкнутого расслоения Λψ⊇
⋂N
⊇ker(∂h/∂x) +
Λi.
i=1
Пример преобразования модели
(25) к модели
(26) приведен в [7,
с. 104-114].
СПИСОК ЛИТЕРАТУРЫ
1. Chow E., Willsky A. Analytical Redundancy and the Design of Robust Failure De-
tection Systems // IEEE Trans. Automat. Contr. 1984. V. 29. P. 603-614.
2. Patton R., Kangethe S. Robust fault diagnosis using eigenstructure assignment of
observers. - In Fault diagnosis in dynamic systems. Theory and application / Eds.
Patton R.J., Frank P.M., Clark R.N. N.Y.: Prentice Hall, 1989. P. 99-154.
3. Ding X., Frank P.M. An adaptive observer-based fault detection scheme for nonlinear
dynamic systems // Proc. 12th World Congress IFAC 1993. V. 8. P. 307-310.
4. De Persis C., Isidori A. A Geometric Approach to Nonlinear Fault Detection and
Isolation // IEEE Trans. Automat. Contr. 2001. V. AC-46. No. 6. P. 853-865.
5. Gertler J. Fault Detection and Diagnosis in Engineering Systems. N.Y.: Marcel
Dekker., 1998.
6. Chen J., Patton R. Robust Model-Based Fault Diagnosis for Dynamic Systems. Lon-
don: Kluwer Academic Publishers., 1999.
7. Шумский А.Е., Жирабок А.Н. Методы и алгоритмы диагностирования и от-
казоустойчивого управления динамическими системами. Владивосток: Изд-во
ДВГТУ, 2009.
8. Shumsky A. Redundancy Relations for Fault Diagnosis in Nonlinear Uncertain Sys-
tems // Int. J. Appl. Math. Comput. Sci. 2007. V. 17. P. 477-489.
9. Жирабок А.Н., Шумский А.Е. Непараметрический метод диагностирования
нелинейных динамических систем // АиТ. 2019. № 2. С. 22-41.
Zhirabok A.N., Shumskii A.E. Nonparametric Method for Diagnosis of Nonlinear
Dynamic Systems // Autom. Remote Control. 2019. V. 80. No. 2. P. 217-233.
10. Seliger R., Frank P.M. Robust residual evaluation by threshold selection and per-
formance index for nonlinear observer-based fault diagnosis // Proc. of IFAC Conf.
Tooldiag’93. Toulose, France. 1993. P. 496-504.
130
11. Ланкастер П. Теория матриц. М.: Наука, 1982.
12. Isidori A. Nonlinear Control Systems. Berlin: Springer Verlag, 1989.
13. Жирабок А.Н., Шумский А.Е., Павлов С.В. Диагностирование линейных дина-
мических систем непараметрическим методом // АиТ. 2017. № 7. С. 3-21.
Zhirabok A.N., Shumskii A.E, Pavlov S.V. Diagnosis of linear dynamic systems by
the nonparametrc method // Autom. Remote Control. 2017. V. 78. No. 7. P. 1173-
1188.
14. Patton R.J., Frank P.M., Clark R.N. Fault diagnosis in dynamic systems. Theory
and applications / N.Y.: Prentice Hall, 1989.
15. Корн Г, Корн Т. Справочник по математике для научных работников и инже-
неров. М.: Наука, 1984.
Статья представлена к публикации членом редколлегии С.А. Красновой.
Поступила в редакцию 02.11.2019
После доработки 14.08.2020
Принята к публикации 10.09.2020
131