Автоматика и телемеханика, № 3, 2021
© 2021 г. П.Ф. ПРЯШНИКОВА, канд. техн. наук (ppf99999@rambler.ru)
(Филиал МГУ им. М.В. Ломоносова в г. Севастополе)
D-РАЗБИЕНИЕ ПРИ ПОЛИНОМИАЛЬНОЙ ЗАВИСИМОСТИ
КОЭФФИЦИЕНТОВ МНОГОЧЛЕНА ОТ ДВУХ ПАРАМЕТРОВ
Предложен метод построения областей устойчивости многочлена, ко-
эффициенты которого полиномиальным образом зависят от двух веще-
ственных параметров. Метод основан на аппроксимации областей D-раз-
биения множеством прямоугольников, на каждом из которых многочлен
имеет одно и то же число нулей в левой полуплоскости.
Ключевые слова: многочлен, устойчивость, D-разбиение, полиномиаль-
ная зависимость.
DOI: 10.31857/S0005231021030028
1. Введение
Одной из задач теории автоматического управления является построение
областей устойчивости многочлена
∑
(1)
a (s, α, β) =
ak (α,β) sk,
k=0
коэффициенты которого ak (α, β) (k = 0, . . . , n) есть функции двух парамет-
ров α и β, определенные на множестве Λ ⊆ R2. Решение этой задачи за-
ключается в определении множества устойчивости Λs, такого что Λs ⊆ Λ и
((α, β) ∈ Λs) ⇔ ((a (s, α, β) = 0) ⇒ (Re (s) < 0)).
В случае произвольных функций ak (α, β) (k = 0, . . . , n) единствен-
ным средством решения поставленной задачи является метод перебора
[1, с. 107-108; 2, с. 136-137]. Метод перебора заключается в том, что вводится
сетка Λc, такая что Λc ⊆ Λ и множество Λc конечно. В каждом узле сетки
(α, β) ∈ Λc устойчивость многочлена (1) проверяется с помощью существую-
щих критериев устойчивости, чаще всего с помощью критериев Рауса или
Гурвица. В результате проверки множество Λc разбивается на два подмноже-
ства Λc = Λcs
⋃Λcu, где множество Λcs состоит из параметров (α,β) устойчи-
вого многочлена, а множество Λcu состоит из параметров (α, β) неустойчивого
многочлена. В качестве искомого множества Λs принимают множество Λcs.
Недостаток метода перебора заключается в том, что Λc есть множество ме-
ры нуль и вопрос об устойчивости многочлена (1) в точках множества Λ\Λc
остается открытым.
В частных случаях функций ak (α, β) (k = 0, . . . , n) задача определения
множества устойчивости Λs решается аналитически или методом D-разбие-
ния. Для возможности решения задачи аналитическим методом зависимо-
сти ak (α, β) (k = 0, . . . , n) должны быть настолько простыми, чтобы усло-
вия известных критериев устойчивости определяли граничные точки мно-
жества Λs в виде известных кривых, например алгебраических кривых вто-
рого порядка. Наиболее известными такими кривыми являются диаграммы
32
Вышнеградского. Примеры других кривых приведены в [3, с. 295; 4, с. 406].
Недостаток аналитических методов заключается в узости класса решаемых
задач.
Метод D-разбиения обычно используется для линейных зависимостей
ak (α,β) = ak,1α + ak,2β + ak,0 (ak,0,ak,1, ak,2 ∈ R) (k = 0,... ,n). Обзор со-
временного состояния метода D-разбиения и библиография представлены
в [5]. В случае линейных зависимостей ak (α, β) может быть найдено пара-
метрическое представление α = α(ω), β = β (ω), ω ∈ [0, +∞), определяющее
множество Γ граничных точек подмножеств множества Λ, все точки (α, β)
каждого из которых соответствуют одному и тому же числу нулей много-
члена (1) в левой полуплоскости. Искомое множество Λs есть объединение
найденных подмножеств, для которых число нулей многочлена (1) в левой
полуплоскости равно n (с учетом кратности нулей). Первый недостаток ме-
тода D-разбиения заключается в том, что параметрическое представление
α = α(ω), β = β (ω) найдено только для линейной зависимости коэффициен-
тов многочлена (1) от параметров α и β. Для полиномиальной зависимости
в [6] предложено использовать методы алгебраической геометрии, позволяю-
щие получить в явном виде уравнение кривой D-разбиения и построить на-
бор точек из каждой связной компоненты D-разбиения. Второй недостаток
заключается в том, что функции α(ω) и β (ω) непрерывного аргумента ω ∈
∈ [0, +∞) заменяют сеточными функциями α(ωq) и β (ωq) соответственно
(0 ≤ ω0 < ω1 < · · · < ωQ = ωmax). Таким образом, задача построения гранич-
ных точек Γs искомого множества Λs решается методом перебора, недостаток
которого отмечен выше.
В статье предлагается метод, который в отличие от известных методов
позволяет с заданной точностью ε определить множество устойчивости Λs
для полиномиальной зависимости коэффициентов многочлена (1) от двух
параметров и при этом не требует замены бесконечных множеств сеточными.
В предлагаемом методе использована идея метода D-разбиения о построении
множеств, соответствующих одному и тому же числу нулей многочлена (1)
в левой полуплоскости. Построение этих областей в предлагаемом методе
принципиально отличается от метода D-разбиения, так как не требует полу-
чения параметрической зависимости α = α(ω), β = β (ω) и не требует замены
бесконечного множества [0, +∞) сеточным.
2. Постановка задачи
Обозначим p(α′, α′′, β′, β′′) = {(α, β)|(α, β) ∈ [α′; α′′] × [β′; β′′]; α′, α′′, β′, β′′ ∈
∈ Λ; α′ < α′′; β′ < β′′} прямоугольник со сторонами, параллельными осям
координат, являющийся подмножеством множества Λ.
Рассматривается многочлен (1), коэффициенты которого зависят от пара-
метров α и β полиномиальным образом
nα,k
nβ,k
∑
∑
(2)
ak (α,β) =
akµναµβν
(k = 0,... ,n)
µ=0 ν=0
на прямоугольнике Λ = p(αmin; αmax; βmin; βmax).
33
Решается задача определения множества устойчивости Λs.
Обозначим
(
)
ps
α′,α′′,β′,β′′
=
{
(
(
))
(
)}
= (α, β) |
(α, β) ∈ p
α′,α′′,β′,β′′
∧
(a (s, α, β) = 0) ⇒ (Re (s) < 0)
прямоугольник на множестве Λ, в каждой точке которого многочлен (1)
упорядоченное множество прямоугольников
=1
⋃
ps (α′,α′′,β′,β′′). Предлагается строить множество Λr =
p так, чтобы
p∈Ps
при заданной точности ε построения множества устойчивости Λs выполня-
лось неравенство
(3)
ρ (Λr, Λs
) ≤ ε,
где ρ есть характеристика близости множеств Λr и Λs. За решение задачи Λs
предлагается принять множество Λr, которое является подмножеством Λs
и в смысле характеристики (3) отличается от Λs на величину, не превосхо-
дящую ε. По сути, речь идет о вписывании в множество устойчивости Λs
прямоугольников ps,q (q = 1, . . . , Qs), на каждом из которых многочлен (1)
устойчив.
Таким образом, решение задачи заключается в определении характеристи-
ки ρ, разработке способа ее вычисления и способа построения прямоугольни-
ков ps,q (q = 1, . . . , Qs).
3. Теоретическая часть
Предлагаемый метод определения множества устойчивости Λs основан на
построении множества прямоугольников P = {pq}Qq=1, такого что:
⋃
1) множество значений параметров Λ =p∈P p;
2) пересечение каждой пары прямоугольников из множества P есть либо
пустое множество, либо одноточечное множество, либо отрезок;
, на каждом элемен-
=1
те которого выполняются достаточные условия непрерывности и отсутствия
нулей вещественных частей всех нулей многочлена (1);
= P\Pa имеет
=1
√
диаметр dp = (α′′ - α′)2 + (β′′ - β′)2, не превосходящий заданного значе-
ния dmax.
Достаточные условия непрерывности вещественных частей нулей много-
члена (1) на прямоугольнике p дает теорема 1.
Теорема 1. Вещественные части всех нулей многочлена (1) непрерыв-
ны на прямоугольнике p, если каждая из точек (α,β) ∈ p не является реше-
нием уравнения
(4)
an
(α, β) = 0.
34
Доказательство теоремы 1 дано в Приложении.
Достаточные условия отсутствия нулей вещественных частей нулей мно-
гочлена (1) на прямоугольнике p дает теорема 2.
Теорема 2. Вещественные части всех нулей многочлена (1) не обра-
щаются в нуль на прямоугольнике p, если каждая из точек (α, β) ∈ p не
является решением уравнения (4) и совокупности
[
Δn-1 (α,β) = 0;
(5)
a0 (α,β) = 0,
где Δn-1 (α, β) есть (n - 1)-й определитель Гурвица.
Доказательство теоремы 2 дано в Приложении.
Следствие. Из теорем 1 и 2 непосредственно следует, что прямо-
угольник p ∈ Pa, если каждая из точек (α, β) ∈ p не является решением
ни одного из уравнений (4), (5).
Левая часть каждого из уравнений (4), (5) есть многочлен вида
mβ
∑∑
d(α,β) =
dµν(α,β);
(6)
µ=0 ν=0
dµν (α,β) = bµναµβν (bµν ∈ R; µ= 0,...,mα; ν= 0,...,mβ).
Достаточные условия отсутствия нулей многочлена (6) на прямоугольнике p
дает теорема 3.
Теорема 3. Многочлен
(6) не имеет нулей на прямоугольнике
p (α′, α′′, β′, β′′), если выполняется условие
p (α′, α′′, β′, β′′) ∈ Pm;
∑
d′µν > 0;
(7)
µ=0 ν=0
mβ
∑∑
d′′µν < 0,
µ=0 ν=0
где Pm
множество прямоугольников, на каждом из которых каж-
дое слагаемое dµν(α,β) (µ = 0,... ,mα; ν = 0,... ,mβ) является монотон-
ной функцией по каждому аргументу, d′µν = min1≤k≤4 dµν(vk), d′′µν =
= max1≤k≤4 dµν(vk), v1 = (α′,β′′), v2 = (α′′,β′′), v3 = (α′′,β′), v4 = (α′,β′).
Доказательство теоремы 3 дано в Приложении.
Для построения множеств Pa и Pb будем рассматривать следующие пре-
образования.
Деление прямоугольника p (α′, α′′, β′, β′′) на два прямоугольника:
{
}
dα(p, λ): p → p′α = p (α′, λ, β′, β′′) ; p′′α = p (λ, α′′, β′, β′′) , λ∈(α′,α′′);
(8)
{
}
dβ (p, λ): p → p′β = p (α′, α′′, β′, λ) ; p′′β = p (α′, α′′, λ, β′′) , λ∈(β′,β′′).
35
(
)
Деление k-го прямоугольника множества P = {pq = p
α′q,α′′q,β′q,β′′q
}Q
на
q=1
два прямоугольника:
{
}
Dα (P,λ,k): p = pk; dα (p,λ) = p′α, p′′
α
;
{
}
P → (P\{pk}) ∪ pk = p′α; pQ+1 = p′′
;
λ ∈ (α′,α′′);
α
(9)
{
}
Dβ (P,λ,k): p = pk; dβ (p,λ) = p′β, p′′
;
β
{
}
P → (P\{pk}) ∪ pk = p′β; pQ+1 = p′′
;
λ ∈ (β′,β′′).
β
(
)
Деление k-го прямоугольника множества P = {pq = p
α′q,α′′q,β′q,β′′q
}Q
по
q=1
стороне с наибольшей длиной на два равновеликих прямоугольника:
(
)
Dα P,(α′k + α′′k)/2,k , если α′′k - α′k ≥ β′′k - β′k;
(10)
D (P,k) =
(
)
Dβ P,(β′k + β′′k)/2,k , если α′′k - α′k < β′′k - β′k.
Перемещение k-го прямоугольника множества P = {pq}Qq=1 в множеств
P =
Q
={pq}
:
q=1
(
)
M P
P,k
:p=pk;
)
(11)
( P)(P\{pk};pq=pq+1(q=k,...,Q-1)
{
}
→
P
P ∪
p˜Q+1 = p
На основании теорем 1-3 и преобразований (8)-(11) предлагается алго-
ритм построения множеств Pa и Pb:
1. Положим Pa = ∅, Pb = {Λ}, q = 0.
2. Преобразуем множество Pb так, чтобы выполнялось включение Pb ⊆
⊆ Pm. С этой целью последовательно находим: Pb = Dα (Pb,0,1), если αmin <
0 < αmax; Pb = Dβ (Pb,0,1), если βmin < 0 < βmax; Pb = Dβ (Pb,0,2), если
αmin < 0 < αmax и βmin < 0 < βmax.
3. Положим q := q + 1.
4. Если q > Qb, заканчиваем выполнение алгоритма.
5. Если на прямоугольнике pb,q для каждого из уравнений (4), (5) тео-
рем 1 и 2 выполняются условия теоремы 3, то с помощью преобразования (11)
M (Pb, Pa, q) перемещаем прямоугольник pb,q из множества Pb в множество Pa
и переходим к п. 4.
6. Если dp,q ≤ dmax, то переходим к п. 3.
7. С помощью преобразования (10) D(Pb, q) производим деление прямо-
угольника pb,q по стороне с наибольшей длиной на два равновеликих прямо-
угольника и переходим к п. 5.
По построению на каждом прямоугольнике pa ∈ Pa выполняются условия
теоремы 4.
36
Теорема 4. Если вещественные части ReS (α,β) всех нулей многочле-
на (1) при полиномиальной зависимости (2) непрерывны и не обращаются
в нуль на прямоугольнике p(α′,α′′,β′,β′′), то на этом прямоугольнике все
вещественные части ReS (α, β) сохраняют знак.
Доказательство теоремы 4 дано в Приложении.
По теореме 4 во всех точках (α, β) ∈ pa многочлен (1) имеет одно и то же
число нулей в левой полуплоскости. Проверяя устойчивость многочлена (1) в
одной из точек каждого прямоугольника pa ∈ Pa, представим множество Pa
в виде Pa = Pr ∪ Pu, где Pr есть множество устойчивых прямоугольников, Pu
есть множество неустойчивых прямоугольников.
Точку (αg, βg) будем называть граничной, если она является решением
хотя бы одного из уравнений (4), (5). Граничные точки D-разбиения образу-
ют подмножество множества граничных точек (αg,βg). Достаточное условие
принадлежности граничной точки (αg, βg) прямоугольнику p (α′, α′′, β′, β′′)
дает теорема 5.
Теорема 5. Прямоугольник p(α′,α′′,β′,β′′) содержит граничную точку
(αg, βg), если хотя бы один из многочленов уравнений (4), (5) принимает в
точках v1 = (α′,β′′), v2 = (α′′,β′′), v3 = (α′′,β′), v4 = (α′,β′) значения разных
знаков.
Доказательство теоремы 5 дано в Приложении.
Множество Pb представим в виде Pb = Pg ∪ Px, где Pg есть множество пря-
моугольников, для которых выполняются условия теоремы 5, Px есть мно-
жество прямоугольников, для которых не выполняются условия теоремы 5.
Множество Pg примем в качестве граничного.
Таким образом множество Λ можно представить в виде Λ = Λr ∪ Λu ∪ Λg ∪⋃
∪Λx, где Λr =p∈Pr p есть объединение устойчивых прямоугольников, Λu =
⋃
⋃
p есть объединение неустойчивых прямоугольников, Λg =
p
= p∈Pu
p∈Pg
есть объединение прямоугольников диаметра не более dmax, содержащих по⋃
крайней мере одну граничную точку, Λx =
p есть объединение прямо-
p∈Px
угольников диаметра не более dmax, для которых не выполняются условия
принадлежности к одному из множеств Pr, Pu, Pg.
Для искомого множества устойчивости Λs справедливы включения
{ Λr ⊆Λs;
(12)
Λs ⊆ Λr ∪ Λg ∪ Λx.
Как было отмечено выше, за область устойчивости будем принимать Λr.
Из (12) следует, что Λr отличается от Λs не более чем на Λg ∪ Λx. Поэтому
за критерий близости множеств Λr и Λs предлагается принять
{S(Λg) + S (Λx), если Λr = ∅;
(13)
ρ (Λr, Λs) =
(S(Λg) + S (Λx))/S (Λr) , если Λr = ∅,
где S(Ω) есть площадь множества Ω. Все площади множеств (13) легко вы-
числяются, так как каждое из множеств есть объединение прямоугольников.
37
Следующая теорема гарантирует, что для любой точки устойчивости
(α0, β0) ∈ Λ многочлена a (s, α, β) существует такое dmax, что эта точка будет
накрыта устойчивым прямоугольником p0 ∈ Pr.
Теорема 6. Если многочлен a(s,α,β) устойчив в точке (α0,β0) ∈ Λ, то
существует такое положительное вещественное число d, что для любо-
го dmax ∈ (0; d) существует устойчивый прямоугольник p0 ∈ Pr, такой что
(α0, β0) ∈ p0.
Доказательство теоремы 6 дано в Приложении.
Объем вычислений предложенного метода определяется числом ариф-
метических операций v1 и v2, необходимых для построения соответственно
многочлена Δn-1 (α, β) и множества прямоугольников P = Pa ∪ Pb. Значе-
ние v1 возрастает при увеличении степеней многочленов a (s, α, β), ak (α, β)
(k = 0, . . . , n) и( за(вис)ит от способа вычисления) определителя(Δn)-1 (α, β).
Значение v2 =
O
n3
+ O (n1) + O (n2) + O (n3)
· O(Q), где O
n3
чис-
ло арифметических операций, необходимых для построения таблицы Рауса,
O (n1), O (n2), O (n3) число арифметических операций, необходимых для
проверки выполнения условий (7) для многочленов соответственно уравнений
(4) и (5), n степень многочлена a (s, α, β); n1, n2, n3 число слагаемых мно-
гочленов левых частей соответственно уравнений (4) и (5); O (·) символ “О -
большое” [7, с. 164]; Q число элементов множества P . Значение v2 возрас-
тает при увеличении степеней многочленов a (s, α, β), ak (α, β) (k = 0, . . . , n).
Значение Q возрастает при увеличении сложности границы D-разбиения и
уменьшении dmax. Сложность границы D-разбиения определяется степеня-
ми и коэффициентами многочленов уравнений (4) и (5), причем, как по-
казывают примеры 1-3, доминирующей может быть зависимость от коэф-
фициентов. Значение dmax выбирается путем последовательного уменьшения
до достижения заданной точности аппроксимации множества устойчивости
Λs множеством прямоугольников Λr. При уменьшении dmax сохраняются все
устойчивые прямоугольники, найденные ранее. Величина ρ (Λr, Λs) есть верх-
няя оценка возможного увеличения площади множества устойчивых прямо-
угольников при дальнейшем уменьшении dmax. Пример 1 иллюстрирует воз-
можность применения предложенного метода с использованием ПЭВМ при
достаточно высоких степенях многочленов a (s, α, β), ak (α, β) (k = 0, . . . , n).
В примере 1 при dmax = 10-3 площадь множества устойчивых прямоуголь-
ников при дальнейшем уменьшении dmax может увеличиться не более чем на
61,8 %, а при dmax = 10-4 может увеличиться не более чем на 3,38 %.
Вычислительные алгоритмы предложенного метода допускают параллель-
ные вычисления, что может быть использовано для снижения времени реше-
ния задачи построения областей устойчивости.
4. Результаты численного эксперимента
Предложенный метод построения областей устойчивости реализован в ви-
де прикладной компьютерной программы в среде разработки Embarcadero
RAD Studio. С помощью разработанной программы решены задачи построе-
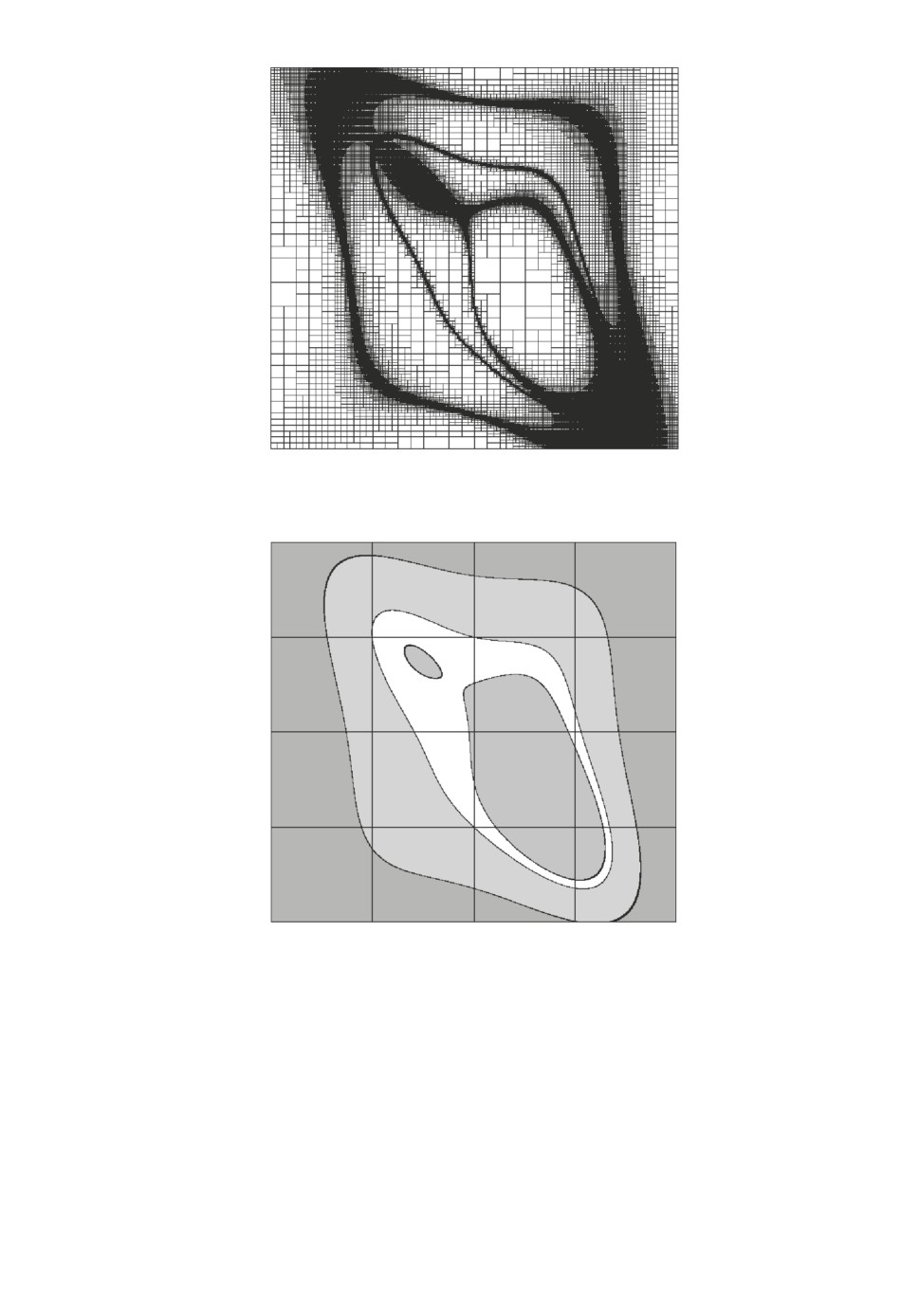
ния областей устойчивости различного уровня сложности. На рис. 2, 4 и 6
множество Λr выделено белым цветом, множество Λu выделено оттенками
38
1,0
0,5
0
-0,5
-1,0
-0,5
0
0,5
1,0
Рис. 1. Множество P примера 1.
1,0
0,5
0
-0,5
-1,0
-0,5
0
0,5
1,0
Рис. 2. D-разбиение примера 1.
серого цвета, множества Λg и Λx выделены черным цветом. Оттенки серого
цвета соответствуют различному числу нулей многочлена в правой полуплос-
кости.
В примере 1 решена задача построения областей устойчивости в простран-
стве параметров (α, β) ∈ [-1; 1] × [-1; 1] многочлена a(s, α, β) = 10(1 + 3α -
- 10αβ + 2α2 + 16α2β2 - 40α4 - 16β4) + 10s + 14s2 + 11s3 + 5,3s4 + 1,6s5 +
+ 0,32s6 +0,039s7 +10-4(27-α4 +β2 +α5β7)·s8 +10-5(8+1,5αβ +α2 -2β2)·s9.
Левые части уравнений (4), (5) имеют соответственно вид a9(α, β) = 10-5(8 +
39
20
10
0
-10
-20
-30
-40
-50
-60
-15
-10
-5
0
5
10
15
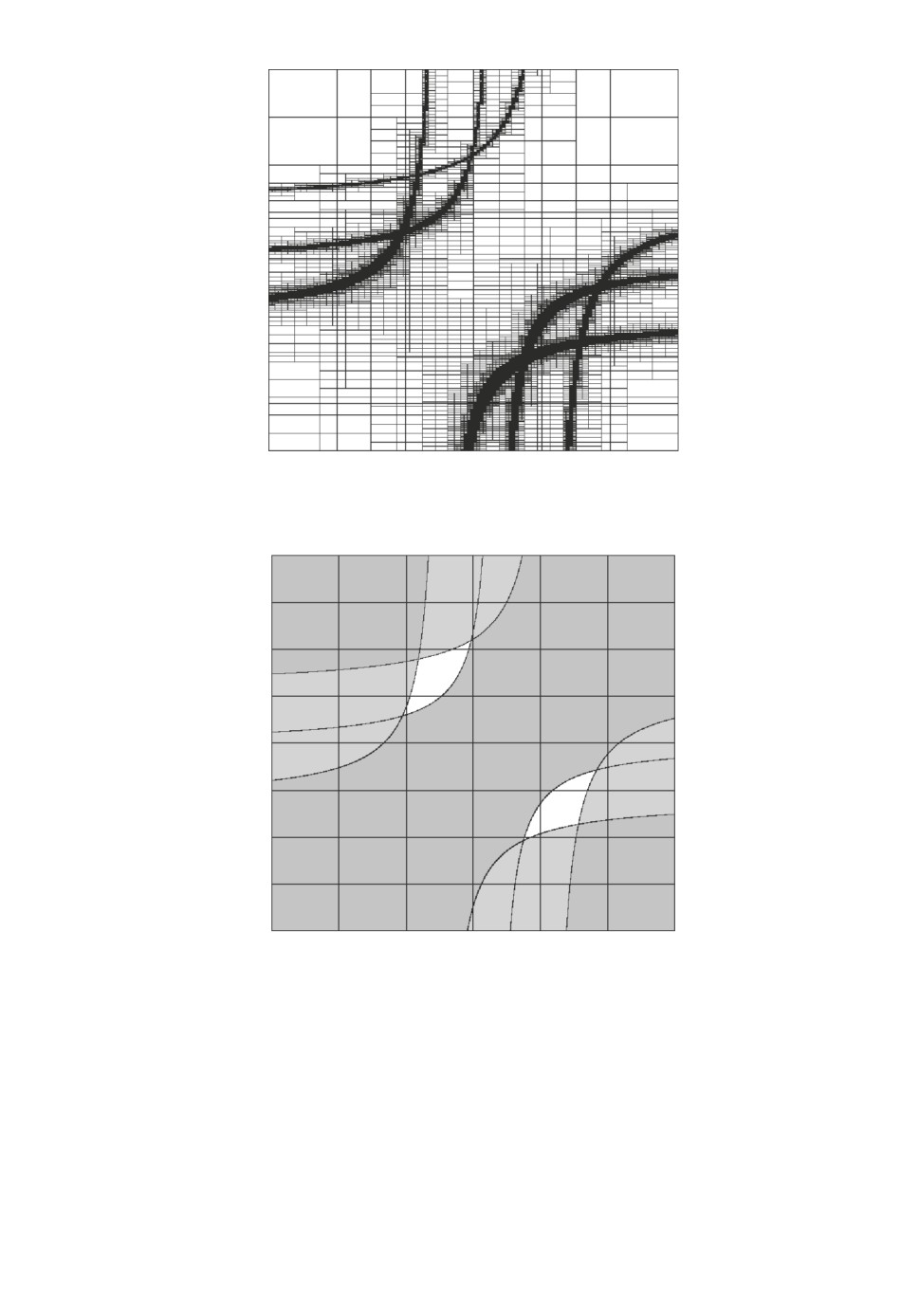
Рис. 3. Множество P примера
2.
20
10
0
-10
-20
-30
-40
-50
-60
-15
-10
-5
0
5
10
15
Рис. 4. D-разбиение примера 2.
+ 1,5αβ + α2 - 2β2), a0(α, β) = 10(1 + 3α - 10αβ + 2α2 + 16α2β2 - 40α4 - 16β4),
Δ8(α,β) = -0,00065075 + ··· + 1,0486 · 10-10β24 + ··· - 1,892 · αβ19 + ··· +
+ 10-12α20β28 +· · ·+2,56·10-10α24 есть многочлен 48-й степени, включающий
454 слагаемых. Изображение множества прямоугольников P при dmax = 10-4
приведено на рис. 1, изображение D-разбиения на рис. 2. Множество P со-
держит 2809726 прямоугольников, ρ (Λr, Λs) = 0,0338. При dmax = 10-3 мно-
жество P содержит 159760 прямоугольников, ρ (Λr, Λs) = 0,618.
40
5
4
3
2
1
0
-1
-2
-3
-4
-5
-4
-3
-2
-1
0
1
2
3
4
5
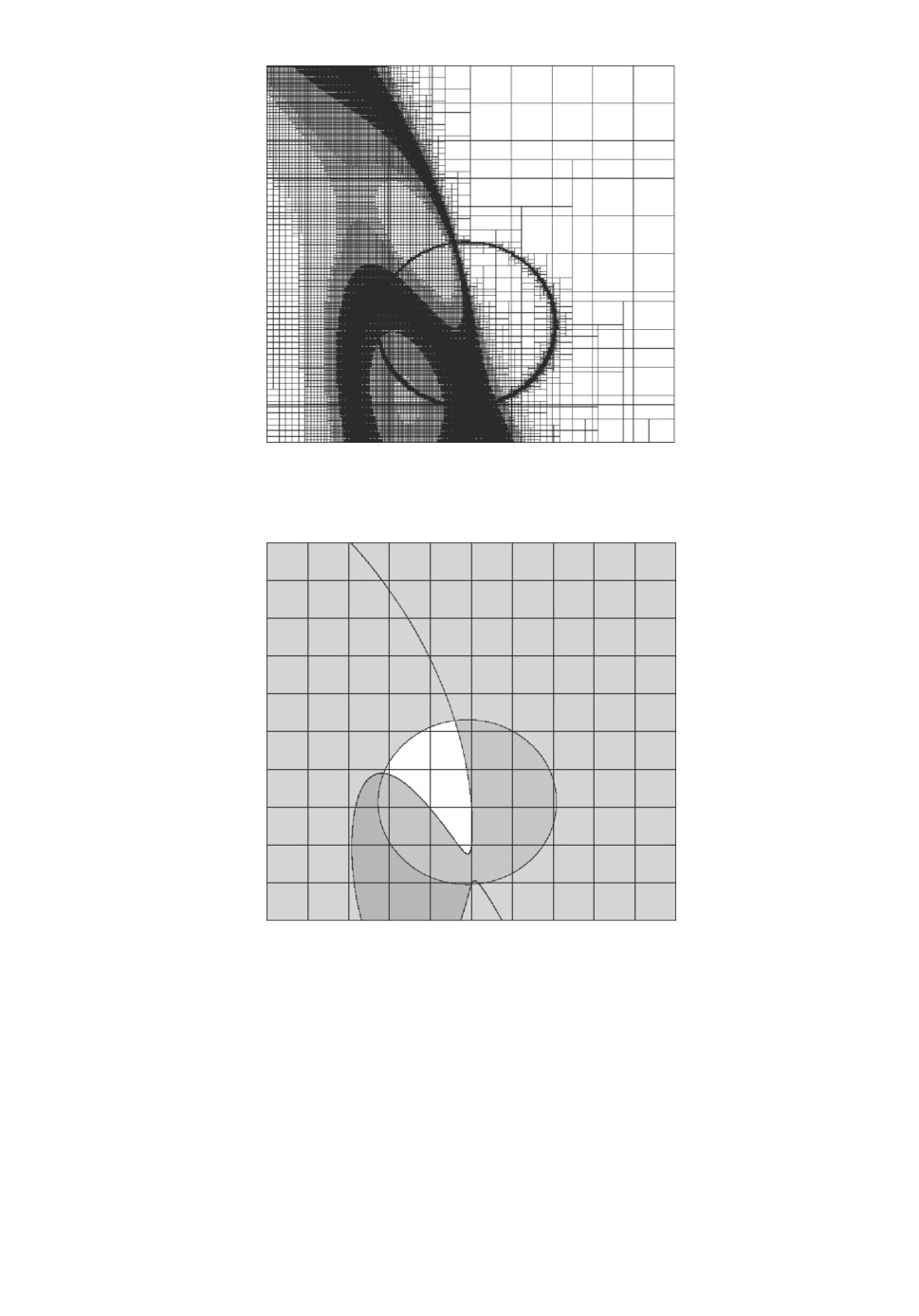
Рис. 5. Множество P примера 3.
5
4
3
2
1
0
-1
-2
-3
-4
-5
-4
-3
-2
-1
0
1
2
3
4
5
Рис. 6. D-разбиение примера 3.
В примере 2 решена задача построения областей устойчивости в про-
странстве параметров (α, β) ∈ [-15; 15] × [-60; 20] дискретной системы A +
(
)
(
)
(
)
α
0
-0,8848
0,4457
0,3914
0,2508
+B
+ C, где A =
, B=
,
0
β
-0,8733
-0,9326
-0,5576
0,0266
(
)
0,1514
0,7854
C =
[5, с. 24, пример 7]. Характеристический много-
−0,4255
-0,8148
член непрерывного аналога рассматриваемой дискретной системы имеет вид
a(s, α, β) = (49,6243+32,4534α-22,8882β+3,95979αβ)+(-53,5986-159,577α+
41
+ 13,6791β - 7,91957αβ)s + (503,974 + 9,2091α + 127,124β + 3,95979αβ)s2. Ле-
вые части уравнений (4), (5) имеют соответственно вид a2(α, β) = 503,974 +
+ 9,2091α + 127,124β + 3,95979αβ, a0(α, β) = 49,6243 + 32,4534α - 22,8882β +
+ 3,95979αβ, Δ1(α, β) = -53,5986 - 159,577α + 13,6791β - 7,91957αβ. Изобра-
жение множества прямоугольников P при dmax = 10-4 приведено на рис. 3,
изображение D-разбиения на рис. 4. Множество P содержит 291837 пря-
моугольников, ρ(Λr, Λs) = 0,078.
В примере 3 решена задача построения областей устойчивос(и в прос)ран-
-α β
стве параметров (α, β) ∈ [-5; 5] × [-5; 5] обратной связи K =
си-
β α
стемы непрерывного времени, заданной матрицами
79
20
-30
-20
0,219
0,9346
-41 -12
17
13
0,047
0,3835
A=
, B=
,
167
40
-60
-38
0,6789
0,5194
33,5
9
-14,5
-11
0,6793
0,831
(
)
0,0346
0,5297
0,0077
0,0668
C =
0,0535
0,6711
0,3834
0,4175
[6, с. 46, пример 4]. Характеристический многочлен этой системы a(s, α, β) =
= (-39,115β2 - 146,0203β - 39,115α2 - 7,8565α + 49,2585) + (-13,8017β2 -
- 101,223β - 13,8017α2 - 366,9898α - 116,492)s + (0,1023β2 + 13,3905β +
+ 0,1023α2 -34,9711α+62,5862)s2 +(-0,8821β-0,7704α+3,0635)s3 +s4. Левые
части уравнений (4), (5) имеют соответственно вид a4(α, β) = 1, a0(α, β) =
= -39,115β2 -146,0203β-39,115α2 -7,8565α+49,2585, Δ3(α,β) = -36367,1-
- 39702β - 13793β2 - 1521,69β3 + 7,77969β4 + 1,24545β5 - 137463α - 56555αβ -
-5815,47αβ2 -189,119αβ3 +1,08776αβ4-86405,5α2 -12995,7α2β-506,74α2β2+
+2,4909α2β3 -18159,2α3 -189,119α3β+2,17547α3β2 -514,515α4 +1,24545α4β+
+ 1,08774α5. Изображение множества прямоугольников P при dmax = 10-5
приведено на рис. 5, изображение D-разбиения на рис. 6. Множество P
содержит 16261342 прямоугольника, ρ(Λr, Λs)= 0,00899.
5. Заключение
В статье предложен новый метод построения областей устойчивости мно-
гочлена в пространстве двух параметров, от которых коэффициенты мно-
гочлена зависят полиномиальным образом. Предложенный метод и разра-
ботанное программное обеспечение могут быть использованы при решении
научных и инженерных задач параметрического анализа и синтеза систем
управления.
ПРИЛОЖЕНИЕ
Доказательство теоремы 1. Если ∀(α,β) ∈ p имеет место нера-
венство an (α, β) = 0, то на прямоугольнике p нули многочлена (1) явля-
ются непрерывными функциями его коэффициентов ak (k = 0, . . . , n) [8,
с. 252-253]. В свою очередь коэффициенты ak (k = 0, . . . , n) при полиноми-
альной зависимости (2) являются непрерывными функциями переменных α
42
и β в R2. Тогда по теореме о непрерывности композиции функций [7, с. 492]
нули многочлена (1) являются непрерывными функциями переменных α и
β на прямоугольнике p. Из непрерывности нулей следует непрерывность их
вещественных частей.
Покажем, что в точках (α, β), в которых an (α, β) = 0, вещественные ча-
сти нулей многочлена (1) могут иметь бесконечный предел. Сделаем замену
переменной s =1ξ , которая при ξ = 0 отображает многочлен (1) в функцию
∑n
f (ξ, α, β) = ϕ (ξ, α, β) /ξn, где ϕ (ξ, α, β) =
an-k (α,β) ξk. В точках (α,β),
k=0
в которых a0 (α, β) = 0, нули многочлена ϕ (ξ, α, β) есть непрерывные функ-
ции переменных α и β. В силу непрерывности, если
lim
an (α,β) = 0,
(α,β)→(α0,β0)
то при (α, β) → (α0, β0) у многочлена ϕ (ξ, α, β) существует бесконечно ма-
лый нуль ξ. При этом у многочлена (1) существует бесконечно большой нуль
s = 1ξ, вещественная часть которого может стремиться к бесконечности, т.е.
не являться непрерывной в точке (α0, β0). Теорема 1 доказана.
Доказательство теоремы 2. Рассмотрим утверждения: A точ-
ка (α, β) не является решением совокупности (5), B вещественные части
нулей многочлена (1) не обращаются в нуль в точке (α, β). Справедливо
утверждение (A ⇒ B) ⇔ (¬A ⇒ ¬B), в силу которого доказательство спра-
ведливости требуемого утверждения A ⇒ B заменим доказательством спра-
ведливости равносильного утверждения ¬B ⇒ ¬A. Если имеет место утвер-
ждение ¬B, при котором в точке (α, β) существует нуль s многочлена (1),
вещественная часть которого равна нулю, то имеет место равенство s = iω
(ω ∈ R). При ω = 0 у многочлена (1) с вещественными коэффициентами су-
ществует комплексно-сопряженный нуль s = -iω, отличный от s. По усло-
вию теоремы an (α, β) = 0 и тогда имеет место формула Орландо [9, с. 465]:
∏1,...,n
Δn-1 (α,β) = (-1)n(n+1)/2an-1n (α,β)·
(sk (α, β) + sq (α, β)). Так как s +
k<q
+ s = 0, то из формулы Орландо следует Δn-1 (α,β) = 0. Если ω = 0, то
многочлен (1) имеет нуль s = 0, откуда следует a0 (α, β) = 0. Теорема 2 дока-
зана.
Доказательство теоремы 3. По условию теоремы каждое слагае-
мое dµν (α, β) (µ = 0, . . . , mα; ν = 0, . . . , mβ) является монотонной функци-
ей по каждому аргументу на прямоугольнике p, следовательно принимает
наибольшее и наименьшее значения в вершинах прямоугольника, так что
d′µν = min(α,β)∈p dµν(α,β), d′′µν = max(α,β)∈p dµν(α,β). Тогда для любой точки
(α, β) ∈ p имеют место неравенства
mβ
mβ
∑∑
∑∑
d(α,β) =
dµν(α,β) ≥
d′µν;
µ=0 ν=0
µ=0 ν=0
(Π.1)
mβ
mβ
∑∑
∑∑
(α, β) =
dµν(α,β) ≤
d′′µν.
d
µ=0 ν=0
µ=0 ν=0
Если выполняется первое из неравенств совокупности (7), то из первого нера-
венства системы (П.1) следует, что d (α, β) > 0 для любой точки (α, β) ∈ p и,
следовательно, многочлен d (α, β) не имеет нулей на прямоугольнике p. Если
43
выполняется второе из неравенств совокупности (7), то из второго неравен-
ства системы (П.1) следует, что d (α, β) < 0 для любой точки (α, β) ∈ p и,
следовательно, многочлен d (α, β) не имеет нулей на прямоугольнике p. Тео-
рема 3 доказана.
Для доказательства теорем 4 и 5 используется теорема П.1.
Теорема П.1 [7, с. 495]. Если функция f : E → R, непрерывная на
связном множестве E, принимает в точках a, b ∈ E значения f (a) = A,
f (b) = B, то для любого числа C, лежащего между A и B, найдется точка
c ∈ E, в которой f (c) = C.
Доказательство теоремы 4. Аналогично, как и при доказатель-
стве теоремы 2, рассмотрим утверждения: A непрерывные вещественные
части ReS (α, β) всех нулей многочлена (1) не обращаются в нуль на прямо-
угольнике p, B все вещественные части ReS (α, β) сохраняют знак на пря-
моугольнике p. Заменим доказательство справедливости требуемого утвер-
ждения A ⇒ B доказательством справедливости равносильного утвержде-
ния ¬B ⇒ ¬A. Предположим, что имеет место утверждение ¬B, при кото-
ром на прямоугольнике p существуют точки (α1, β1) и (α2, β2), в одной из
которых функции ReS (α, β) положительна, а в другой отрицательна. Ес-
ли в теореме П.1 положить E = p, f = ReS (α, β), a = (α1, β1), b = (α2, β2),
A = ReS (α1,β1), B = ReS (α2,β2), C = 0, то будут выполнены все условия
этой теоремы. Тогда по теореме П.1 на прямоугольнике p существует точка
c = (α0,β0), в которой ReS (α0,β0) = 0. Теорема 4 доказана.
Доказательство теоремы 5. По условию теоремы существует пара
точек, например v1, v2, в которых один из многочленов d (α, β) принимает зна-
чения разных знаков. Тогда теорема 5 является прямым следствием теоремы
П.1, если положить E = p, f = d (α, β), a = v1, b = v2, A = d (v1), B = d (v2),
C = 0. Теорема 5 доказана.
Доказательство теоремы
6.
Рассмотрим многочлен (6), каж-
дое слагаемое которого dµν (α, β) (µ = 0, . . . , mα; ν = 0, . . . , mβ ) есть непре-
рывная функция аргументов α и β. В силу непрерывности для точ-
ки (α0, β0) ∈ R2 и для любого ε > 0 существует круг Vrµν (α0, β0) ={
√
}
= (α, β) ∈ R2 | (α - α0)2 + (β - β0)2
≤ rµν радиуса rµν > 0 с центром
в точке (α0, β0), такой что ∀ (α, β) ∈ Vrµν (α0, β0) выполняется неравенство
ν=mβ
|dµν (α, β) - dµν (α0, β0)| < ε. Если положить r = min {rµν }µ=mα;
, то на
µ,ν}0
{
√
круге Vr (α0, β0) = (α, β) ∈ R2 | (α - α0)2 + (β - β0)2 ≤ r выполняется
система неравенств
(Π.2)
|dµν (α, β) - dµν (α0, β0)| < ε (µ = 0, . . . , mα; ν = 0, . . . , mβ
).
Круг Vr (α0, β0) есть компакт, в силу чего непрерывная функция dµν (α, β)
достигает на круге своих наименьшего и наибольшего значений dµν,min =
= min
dµν(α,β) = dµν(αµν,min,βµν,min); dµν,max =
max dµν (α, β) =
(α,β)∈Vr (α0,β0)
(α,β)∈Vr (α0,β0)
= dµν(αµν,max,βµν,max), где (αµν,min,βµν,min) ∈ Vr (α0,β0) и (αµν,max,βµν,max) ∈
44
∈ Vr (α0,β0). Тогда при (α,β) = (αµν,min,βµν,min) неравенства (П.2) принима-
ют вид
(Π.3)
dµν (α0,β0) - dµν,min < ε(µ = 0,... ,mα; ν = 0,... ,mβ
),
при (α, β) = (αµν,max, βµν,max) неравенства (П.2) принимают вид
(Π.4)
dµν,max - dµν (α0,β0) < ε(µ = 0,... ,mα; ν = 0,... ,mβ
).
Суммируя неравенства (П.3) по µ = 0, . . . , mα, ν = 0, . . . , mβ, получим в
∑mα ∑mβ
∑mα ∑mβ
качестве следствия неравенство
dµν(α0,β0)-
dµν,min <
µ=0
ν=0
µ=0
ν=0
< (mα + 1) (mβ + 1) ε, равносильное неравенству
∑
(Π.5)
dµν,min > d(α0,β0) - (mα + 1) (mβ
+ 1) ε.
µ=0 ν=0
Аналогично из неравенств (П.4) следует неравенство
∑
(Π.6)
dµν,max < d(α0,β0) + (mα + 1) (mβ
+ 1) ε.
µ=0 ν=0
Если d(α0, β0) > 0, то можно положить ε = d(α0, β0)(2(mα + 1)(mβ + 1))-1,
и тогда из неравенства (П.5) следует, что существует круг Vr′ (α0, β0), на
котором выполняется неравенство
∑
d(α0,β0)
(Π.7)
dµν,min >
> 0.
2
µ=0 ν=0
Если d(α0, β0) < 0, то можно положить ε = -d(α0, β0)(2(mα + 1)(mβ + 1))-1,
и тогда из неравенства (П.6) следует, что существует круг Vr′′ (α0, β0), на
котором выполняется неравенство
∑
d(α0,β0)
(Π.8)
dµν,max <
< 0.
2
µ=0 ν=0
Из устойчивости многочлена a (s, α, β) в точке (α0, β0) по критерию
устойчивости Гурвица следует, что все значения a0 (α0, β0), an (α0, β0),
Δn-1 (α0,β0) или все положительны, или все отрицательны. Каждая из функ-
ций a0 (α, β), an (α, β), Δn-1 (α, β) есть многочлен вида (6), в силу чего для
этих функций существует круг Vr (α0, β0), на котором выполняется одно из
неравенств (П.7) или (П.8). Положим d = r, выберем dmax ∈ (0; d) и постро-
им множество прямоугольников P = Pa ∪ Pb. Пусть p есть прямоугольник
из множества P , которому принадлежит точка (α0, β0). Если предположить,
что прямоугольник p ∈ Pb, то справедливо неравенство dp ≤ dmax < d, сле-
довательно p ⊆ Vr (α0, β0). Тогда на прямоугольнике p выполняется одно из
неравенств (П.7) или (П.8) и, следовательно, p ∈ Pa. Полученное противоре-
чие доказывает, что p ∈ Pa. На каждом прямоугольнике множества Pa много-
член a (s, α, β) или устойчив, или неустойчив. Поскольку многочлен a (s, α, β)
устойчив в точке (α0, β0) ∈ p, то p есть устойчивый прямоугольник, покры-
вающий точку (α0, β0). Теорема 6 доказана.
45
СПИСОК ЛИТЕРАТУРЫ
1. Чернецкий В.И., Дидук Г.А., Потапенко А.А. Математические методы и алго-
ритмы исследования автоматических систем. Л.: Энергия, 1970.
2. Савин М.М., Елсуков В.С., Пятина О.Н. Теория автоматического управления.
Ростов на Дону: Феникс, 2007.
3. Егоров А.И. Обыкновенные дифференциальные уравнения с приложениями. М.:
Физматлит, 2005.
4. Dorf R., Bishop R. Modern Control Systems. New Jersey: Prentice Hall, 2011.
5. Грязина Е.Н., Поляк Б.Т., Тремба А.А. Современное состояние метода D-раз-
биения // АиТ. 2008. № 2. С. 3-40.
Gryazina E.N., Polyak B.T., Tremba A.A. D-decomposition Technique State-of-the-
art // Autom. Remote Control. 2008. V. 69. No. 12. P. 1991-2026.
6. Васильев О.О. Исследование D-разбиений методами вычислительной веще-
ственной алгебраической геометрии // АиТ. 2012. № 12. С. 36-55.
Vasil’ev O.O. Study of D-decompositions by the Methods of Computational Real-
valued Algebraic Geometry // Autom. Remote Control. 2012. V. 73. No. 12.
P. 1978-1993.
7. Зорич В.А. Математический анализ. Ч. 1. М.: МЦНМО, 2012.
8. Кострикин А.И. Введение в алгебру. Ч. 1. Основы алгебры. М.: Физматлит,
2000.
9. Гантмахер Ф.Р. Теория матриц. М.: Физматлит, 2010.
Статья представлена к публикации членом редколлегии П.С. Щербаковым.
Поступила в редакцию 11.08.2017
После доработки 10.06.2020
Принята к публикации 09.07.2020
46