Автоматика и телемеханика, № 3, 2021

(Институт проблем управления им. В.А. Трапезникова РАН, Москва)

СМЕШАННАЯ РОБАСТНОСТЬ: АНАЛИЗ СИСТЕМ

С НЕОПРЕДЕЛЕННЫМИ ДЕТЕРМИНИРОВАННЫМИ

И СЛУЧАЙНЫМИ ПАРАМЕТРАМИ

НА ПРИМЕРЕ ЛИНЕЙНЫХ СИСТЕМ¹

Рассматривается вопрос робастности линейных систем с постоянными

коэффициентами. Существуют методы и инструменты анализа устойчи-

вости систем со случайными либо детерминированными неопределенно-

стями. При этом нет подходов для анализа систем, содержащих оба типа

параметрической неопределенности. В статье проводится классификация

типов робастности и вводится новый тип

“смешанная параметрическая

робастность”, включающий несколько вариаций. Предлагаемые постанов-

ки задач о смешанной робастности могут рассматриваться как проме-

жуточные варианты между классическим детерминированным и вероят-

ностным подходами к робастности. Перечислены несколько случаев, в ко-

торых поставленные задачи легко решаются. В общем случае применимы

проверки устойчивости робастных систем с помощью сценарного подхо-

да, однако эти проверки могут быть вычислительно сложными. Для вы-

числения искомой вероятности устойчивости предложен простой графо-

аналитический подход, основанный на робастном D-разбиении. Этот спо-

соб подходит для случая небольшого числа случайных параметров. Ито-

говая оценка вероятности устойчивости вычисляется детерминированным

способом и может быть найдена с произвольной точностью. Описаны при-

ближенные способы решения поставленных задач. Приведены примеры и

обобщение смешанной робастности на другие типы систем.

Ключевые слова: смешанная робастность, детерминированная робаст-

ность, вероятностная робастность, линейные системы, устойчивость.

DOI: 10.31857/S000523102103003X

1. Введение

В основном в статье рассматриваются динамические системы с постоян-

ными коэффициентами и робастность устойчивости относительно неопреде-

ленности². Во введении намеренно не оговорен точный класс систем, здесь

¹ Работа выполнена при частичной финансовой поддержке Российского научного фонда

(проект № 16-11-10015).

² В общем случае предлагаемые постановки задач подходят для любых систем, зави-

сящих от параметров, см. подробнее заключительный раздел 6. Допустимо рассматривать

и непараметрическую неопределенность, но формальное описание соответствующих задач

затруднено. Обобщение смешанной робастности на другие свойства системы или критерии

качества, помимо устойчивости, тривиально.

изложены принципиальные подходы к постановкам и решению задач робаст-

ности. Далее эти подходы демонстрируются на примере робастной устойчиво-

сти. Без потери общности читатель может рассматривать экспоненциальную

(асимптотическую) устойчивость линейной системы с одним входом и одним

выходом, заданной дробно-рациональной передаточной функцией.

Основная цель работы состоит в описании нового вида неопределенности

смешанной неопределенности и сопутствующей ей робастности систем. Этот

вид объединяет два типа неопределенности разной природы: детерминиро-

ванной и случайной.

Статья организована следующим образом: после обзорного введения с опи-

санием различных типов робастности в разделе 2 предлагается новый тип

робастности смешанная робастность. Формулировки трех подтипов зада-

чи о смешанной робастности приведены в разделе 3 на примере задачи о

робастной устойчивости. Там же для некоторых из них описан известный

способ решения с помощью сценарного подхода. В разделе 4 для случая

маломерного случайного параметра предлагается использовать графический

(графо-аналитический) подход, основанный на технике робастного D-разбие-

ния. В подразделе 3.3 предложены процедуры приближенного решения. При-

меры приведены в разделе 5. В заключении приведен ряд направлений раз-

вития поставленных задач.

1.1. Терминология робастности

Широко используемый в теории управления термин “робастность”³ мож-

но понимать по-разному в зависимости от контекста и области применения.

Как правило, он используется в качестве характеристики или свойства (ро-

бастные регуляторы, робастные системы, робастное управление, робастная

стабилизация, робастное оценивание и др.), но в контексте статьи этот тер-

мин будет рассмотрен как самостоятельный, поскольку интерес представляют

разновидности робастности.

Введенный в статистике Боксом и популяризированный Хубером в кон-

тексте “устойчивости”, “стабильности” и “грубости” оценок, термин стал ис-

пользоваться и в теории управления.

Формирование классической теории робастности состоялось в 80-х гг. XX в.

В первую очередь исследовалась робастная устойчивость полиномов и мат-

риц, см., например, дискуссию по проблеме робастности, состоялось на 11-м

Международном конгрессе по автоматическому управлению IFAC [2]. Позд-

нее к ним добавилась H_∞-теория, M-Δ и µ-анализ, обобщающие различ-

ные виды неопределенности. Систематический обзор результатов представ-

лен в [3-5].

В русском языке термин установился не сразу. Понятие “грубости”, соот-

ветствующее переводу английского “robust”, было введено в лексикон теории

управления Андроновым в немного другом контексте (ему соответствует об-

ратное свойство

“хрупкость”). Стало ясно, что нужно слово, описывающее

³ Англоязычный термин robustness (robust) трактуется еще более разнообразно. На рус-

ском языке термин робастность по отношению к системам управления был систематически

использован в монографии [1].

сохранение свойств при изменении системы или, если смотреть с другой сто-

роны, сохранение свойств множества систем.

В итоге появился новый термин

“робастность”, который активно ис-

пользовал в своих работах Я.З. Цыпкин и его ученики [6, 7]. Популяризации

термина во многом способствовала монография [1], по сути, закрепившая его.

Вместе с этим для обозначения задач робастности продолжают использовать-

ся синонимы “грубость”, “нечувствительность” и др. [8].

Каким образом можно выделить класс задач, связанных с робастностью?

Неформально “робастностью” называется свойство нечувствительности (си-

стемы) по отношению к неопределенности. Далее приведены две устоявшиеся

характеристики робастности, а затем два основных типа неопределенно-

сти: детерминированная и вероятностная. На их основе предлагается ввести

новый, смешанный тип робастности, также удовлетворяющий указанным ха-

рактеристикам.

Во-первых, “робастность” определяется относительно неопределенности,

которая может быть параметрической или непараметрической. Непараметри-

ческая включает в себя “немоделируемую динамику”, описываемую в частот-

ной области (H_∞-теория, QFT), структурную неопределенность (например,

M -Δ и µ-анализ) и даже внешние помехи. Часто неопределенность задается

посредством номинальной системы и присутствующего в ней возмущения⁴.

В статье рассматривается параметрическая статическая неопределен-

ность. Истинное значение параметра считается неизвестным, но зафиксиро-

ванным в течение времени. Тем самым можно говорить о параметрической

робастности. В этом случае система и ее характеристики явно или неяв-

но зависят от n-мерного вещественного вектора q ∈ Rⁿ, комплекснозначная

неопределенность рассматривается аналогично.

Классическое детерминированное описание неопределенности как множе-

ства позже было дополнено вероятностной постановкой, с помощью случай-

ных величин. В подразделах 1.2.1 и 1.2.2 эти типы параметрической неопре-

деленности и связанные с ними задачи описаны подробнее.

Во-вторых, робастность определяется относительно желаемого/требуе-

мого свойства системы. Помимо привычной робастной устойчивости, таким

свойством может быть выполнение заданного критерия качества, удовлетво-

рение фазовым ограничениям или даже сохранение определенных статисти-

ческих характеристик системы [3]. Можно рассуждать о робастности “такого-

то свойства” по отношению к “такой-то неопределенности”.

Упомянем, что в статистике и анализе данных, где возник термин “робаст-

ность”, он понимается в более узком смысле: как чувствительность/нечувст-

вительность к отклонениям распределений и выбросам [7].

⁴ Здесь термин “возмущение” используется не для описания внешнего воздействия, а

как изменение параметров или иных характеристик системы. Исторически способность си-

стемы противодействовать внешним возмущениям или подавлять внешние шумы с задан-

ными, определенными характеристиками редко называется робастностью. Вместе с этим

способность системы сохранять заданное свойство при разных характеристиках внешних

сигналов называться робастностью может (робастность относительно вариативности этих

характеристик). Граница между этими случаями размыта, устоявшегося общепринятого

понимания применимости термина “робастность” нет.

1.2. Задачи робастности

Задача робастного синтеза состоит в том, чтобы сделать систему “ро-

бастной”, т.е. удовлетворить конкретный критерий для конкретной неопреде-

ленности. Например, надо найти регулятор заданной структуры, стабилизи-

рующий систему, параметры которой известны в некоторых пределах, и т.п.

Полученный регулятор называется “робастным”, в данном случае робастно

стабилизирующим.

В основе задачи синтеза лежит задача робастного анализа, которая состо-

ит в проверке заданного критерия (например, устойчивости) для заданной

неопределенности. Далее “задачей о робастности” называется именно задача

робастного анализа и ее вариации.

Для постановки задачи анализа существенно то, как именно проверяется

требуемый критерий в зависимости от типа неопределенности. Эта провер-

ка может быть бинарной (выполняется/не выполняется), шкалированной или

вероятностной. Рассмотрим эти задачи подробнее на примере анализа устой-

чивости.

1.2.1. “Классический” робастный параметрический анализ

(бинарный, гарантирующий подход)

Параметрическую неопределенность удобно задавать параллелепипедом

(брусом), эллипсоидом, шаром в какой-либо норме или иным заданным мно-

жеством Q ⊂ Rⁿ. Например, характеристический полином системы может

иметь интервальные коэффициенты, которые и являются неопределенными

параметрами. Данное множество обычно содержит номинальное значение па-

раметра q₀ ∈ Q, задающего номинальную систему. Напомним, что в статье

рассматривается статическая параметрическая неопределенность, т.е. пара-

метр, будучи неизвестным, не меняется с течением времени.

Задача робастной устойчивости состоит в проверке устойчивости систе-

мы для каждого элемента из множества возможных значений (множества

неопределенности):

Параметрическая система

Система устойчива

(1)

“робастно устойчива”

для всех q ∈ Q.

Этот подход реализует концепцию гарантированной устойчивости, прини-

мающий во внимание все “наихудшие” варианты (worst-case) неопределенно-

сти. Будем называть подобный вид робастности детерминированной робаст-

ностью, а задачу задачей о детерминированной робастности. Результат

анализа бинарный: либо робастность есть, либо ее нет.

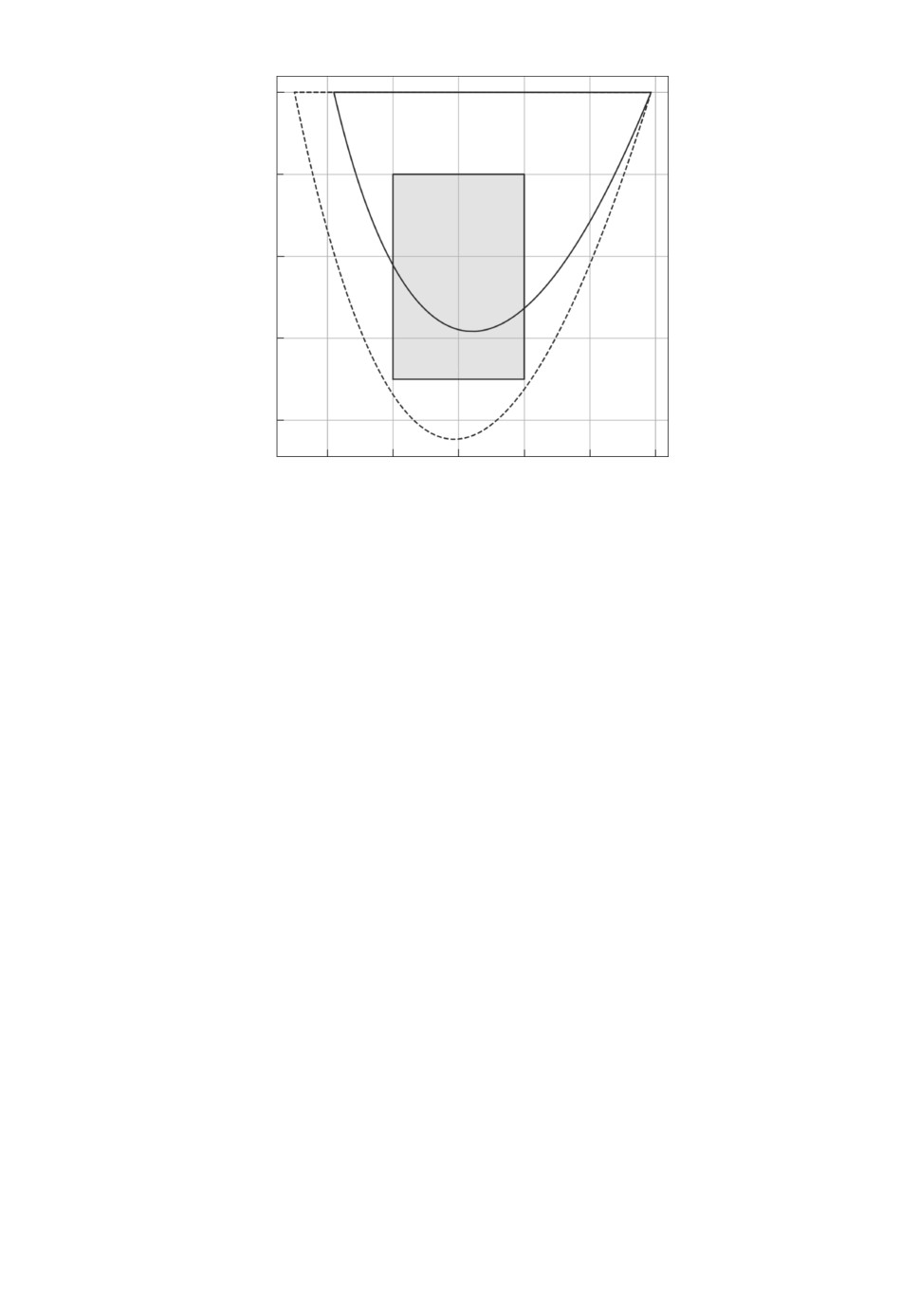
В качестве примера можно рассмотреть прямоугольник на рис. 1 как мно-

жество неопределенных параметров Q и устойчивость в качестве критерия.

Каждое значение параметра точка в двумерном пространстве (q₁, q₂) со-

ответствует либо устойчивой, либо неустойчивой системе. Пусть множества

“устойчивых” и “неустойчивых” параметров разделены некоторой “погранич-

ной” линией, отсекающей часть прямоугольника-неопределенности. Посколь-

ку часть множества Q принадлежит области неустойчивых параметров, то

Устойчивость

Неустойчивость

q₁ или d₁

Рис. 1. Иллюстрация детерминированного и вероятностного подхода. Сплош-

ная линия обозначает границу прямоугольного множества неопределенности.

Штриховая линия обозначает границу между “устойчивыми” и “неустойчивы-

ми” параметрами. Серая часть прямоугольника соответствует значениям па-

раметров из множества неопределенности, при которых система неустойчива.

решением задачи детерминированной робастной устойчивости будет “Нет”:

система не робастно устойчива.

Проверка детерминированной робастности (а тем более решение задачи

робастного синтеза) в большинстве случае является принципиально сложной

задачей. Для анализа устойчивости существует ряд успешно разрешенных

вопросов, таких как Теорема о вершинах, Реберная теорема или знамени-

тый результат Харитонова о сведении анализа устойчивости интервального

семейства полиномов к анализу всего четырех полиномов [5, 9]. Однако эти

случаи являются скорее исключением, чем правилом. Для большинства ин-

тервальных случаев эта задача является NP-полной, например, для анализа

робастности по отношению к неопределенности-многограннику может потре-

боваться перебор всех вершин этого множества, а число вариантов перебора

экспоненциально растет с размерностью [10, 11].

Помимо сложности решения задачи о классической робастности, критике

подвергалась сама постановка: почему множество допустимых неопределен-

ных параметров выбирается тем или иным, каков размер этого множества?

Например, если неопределенность задана шаром, то как выбирать его ради-

ус? Отметим, что в классическом робастном анализе есть важная задача о

радиусе робастной устойчивости (robustness margin), состоящая в определе-

нии максимального размера множества неопределенности заданной формы,

сохраняющего устойчивость [1, 5].

Для полноты картины следует упомянуть подход, описывающий робаст-

ность не-бинарного критерия качества, например перерегулирования. В зави-

симости от размера множества неопределенности Q значение критерия будет

“деградировать” (ухудшаться при увеличении размера) [12]. Кривая деграда-

ции в зависимости от размера неопределенности дает полезную информацию

для принятия решений. Такой подход назван шкалированной, модулирован-

ной робастностью (modulated robustness) [13]. Для бинарного же критерия,

такого как устойчивость, переход от устойчивости к неустойчивости “мгно-

венный” и определяет радиус робастной устойчивости.

Кроме того, множества неопределенности часто формируются исходя из

грубых верхних и нижних оценок внутренних параметров, что неизбежно вле-

чет консерватизм решения. Еще одной проблемой классического робастного

анализа является встречающаяся “сосульчатая” (icicle) геометрия множества

неустойчивых параметров [13]. В этом случае есть параметры, близкие к но-

минальным, делающие систему неустойчивой, и радиус робастной устойчи-

вости близок к нулю. Но при этом объем множества таких “неустойчивых”

параметров может быть пренебрежимо мал по сравнению со всем множеством

неопределенности.

Таким образом, будучи несомненно полезным и важным подходом к иссле-

дованию и синтезу систем управления, классический, гарантирующий подход

к робастности имеет свои ограничения.

1.2.2. Вероятностный робастный параметрический анализ

(случайные параметры)

Для преодоления указанных проблем был предложен вероятностный под-

ход. В этом подходе неопределенность в системе считается вероятностной,

представленной случайным вектором δ ∈ R^m [14]. Этот вектор имеет некото-

рое распределение на множестве Δ ⊂ R^m, являющемся носителем (функции)

распределения. Для простоты⁵ обозначим такой вид неопределенности вместе

с его распределением как δ ∼ Δ. Существенно, что в данном подходе разреша-

ется потеря устойчивости (как правило, небольшая), которая описывается в

терминах теории вероятности.

Задача вероятностного анализа робастной устойчивости состоит в нахож-

дении вероятности устойчивости p^∗ по отношению к случайной неопределен-

ности δ:

[

]

(2)

p^∗ = Prob_δ∼Δ

Система устойчива для данного δ

Эта вероятность равна мере множества “устойчивых” параметров, т.е. зна-

чений, при которых система устойчива. Будем называть этот вид устойчиво-

сти по отношению к “случайной” неопределенности вероятностной робаст-

ностью. Это уже не бинарное свойство, оно сопровождается своим значением

вероятности.

Вероятность логического утверждения, зависящего от случайной перемен-

ной δ, понимается как мера множества, на котором это утверждение истинно.

Она равна интегралу Лебега от индикаторной функции этого утверждения,

принимающей значения 0, если утверждение ложно, и 1, если истинно. Будем

предполагать, что утверждение алгоритмически разрешимо (индикаторная

функция вычислима в точках носителя и на его подмножествах). Автор на-

⁵ Строго говоря, распределение задается тройкой (Δ, F, P) с множеством элементарных

событий Δ, сигма-алгеброй его подмножеств F и вероятностной мерой P : F → [0, 1], но для

краткости избыточные обозначения опущены. Далее мера обозначается символом µ. Ис-

пользуется традиционная мера Лебега, а обозначение распределения ассоциируется с мно-

жеством Δ. Рассматриваемые множества неопределенности предполагаются измеримыми.

Можно рассматривать как абсолютно непрерывные распределения, заданные функцией

плотности распределения, так и дискретные распределения либо их смесь. В контексте

робастного анализа с вероятностной точки зрения важен их носитель и (кумулятивная)

функция распределения.

меренно не использовал термин “стохастическая робастность”, так как этот

термин более широкий и используется чаще по отношению к устойчивости

систем со случайными процессами. Следует особо отметить, что система не

обладает стохастической динамикой, но часть ее параметров является реали-

зацией конечномерной случайной величины δ.

Задача о вероятностной робастности (2) связана с детерминированной ро-

бастностью (1) несколькими путями.

Во-первых, следуя подходу [15], предлагается методически заменять де-

терминированную неопределенность q ∈ Q случайной неопределенностью δ

той же размерности, равномерно распределенной на множестве Q (тем самым

полагая Δ = Q). Таким образом, “трудная” задача о детерминированной ро-

бастности (включая задачи синтеза) заменяется полиномиально сложной [16].

Это связано с тем, что можно эффективно вычислять вероятность устойчи-

вости (2) методом Монте-Карло (см. подраздел 3.2 с подробностями). Оче-

видно, что новая задача имеет другое содержание, но ее решение может быть

интерпретировано в контексте исходной детерминированной задачи. В слу-

чае единичной вероятности устойчивости p^∗ = 1 результат можно тракто-

вать⁶ как детерминированную робастность по отношению к множеству Q,

совпадающему с Δ. Если же вероятность устойчивости меньше единицы, то

это соответствует отсутствию детерминированной робастной устойчивости.

Полученный результат может привести к разумной корректировке постанов-

ки исходной задачи, например, в виде рекомендации уменьшить множество

неопределенных параметров.

Во-вторых, неопределенность может быть вероятностной изначально, т.е.

описывать случайность значений параметров. В этом случае распределение

уже не обязательно равномерное. Согласно классическому подходу к робаст-

ности, в качестве множества неопределенности выбирается либо весь носи-

тель случайных параметров, либо его доверительное множество высокой ве-

роятности (множество квантили). В обоих случаях в постановку вносится

консерватизм, сопровождаемый вопросами выбора уровня квантили и вы-

бора соответствующего доверительного множества. В то же время исходная

вероятностная задача анализа может быть эффективно решена напрямую,

и ответом является вероятность устойчивости. Более того, для успешного

решения достаточно иметь генератор выборки распределения случайных па-

раметров/систем, а не его аналитическое описание [12]. Этот же подход ис-

пользуется для вероятностных задач синтеза, см. [17].

Ключевая идея использовать или вводить случайность неопределенных

параметров получила должную популярность: основная монография [12]

была переиздана спустя 8 лет. Подход получил широкое распространение и

в приложениях, поскольку он строго обосновывает идеи рандомизации при

анализе и синтезе систем управления.

Рассмотрим тот же рис. 1. Пусть прямоугольник является носителем Δ

с равномерным распределением случайного параметра δ. Тогда решение за-

дачи вероятностного робастного анализа (2) дается в точности отношением

⁶ С точностью до множеств нулевой вероятности. В зависимости от задачи эта разница

может быть ничтожной либо, наоборот, существенной.

площади незаштрихованной части прямоугольника к его общей площади. На-

ряду с вероятностью устойчивости удобно использовать вероятность потери

устойчивости 1 - p^∗. Для равномерного распределения она равна доле за-

штрихованной части прямоугольника, т.е. 2 %.

Оценка вероятности устойчивости (2) может быть выполнена несколькими

способами.

Во-первых, если дано описание множества устойчивых параметров, то ме-

ру этого множества можно найти явно. Для равномерного распределения это

задача геометрической вероятности: надо найти отношение объемов устойчи-

вых параметров в носителе к объему самого носителя Δ. Эта же величина мо-

жет быть вычислена с помощью объема множества неустойчивых параметров

(см. формулу (13) далее). Сами объемы могут быть найдены аналитически

или численно.

Во-вторых, оценка вероятности p^∗ может быть сделана эмпирически с по-

мощью случайной выборки на множестве неопределенности согласно сопут-

ствующему ему распределению. Для равномерного распределения отношение

подмножеств оценивается отношением числа точек, попавших в каждое из

подмножеств. Этот подход является самым известным и мощным инструмен-

том для решения вероятностных задач анализа и синтеза. В теории управле-

ния он известен как сценарный подход и использует идею рандомизации, см.

подробнее подраздел 3.2. В его основе лежит метод типа Монте-Карло, вклю-

чающий вычисление необходимого размера выборки для достижения задан-

ного качества оцениваемой вероятности [14, 17]. Обширная коллекция ран-

домизированных алгоритмов для решения вероятностных задач управления

приведена в монографии [12] и в ее библиографическом списке. Сценарный

подход может быть использован и для решения задач синтеза, которые в

статье не рассматриваются.

Отметим, что существуют способы формирования выборки для сложных и

неявно заданных множеств неопределенности. В них используются реализа-

ции метода Монте-Карло в марковских цепях, организованные как случайное

блуждание “биллиардного” типа (Billiard Walk) или “удар-отход” (Hit-and-

Run) [18].

Есть и обратная зависимость между вероятностной и детерминированной

робастностью. Задачу о вероятностной робастности можно приближенно ре-

шать детерминированными методами. Для фиксированного значения вероят-

ности p выбирается множество квантили Q_p : Prob_δ∼Δ[δ ∈ Q_p] = p, и для него

проверяется робастная устойчивость. Если система оказывается устойчивой

(в детерминированном смысле относительно Q_p), то вероятность робастной

устойчивости не меньше p. Подбор уровня и множества квантили остается во

многом эвристической процедурой, во многом из-за “сосульчатого” множества

неопределенных параметров.

2. Смешанная робастность

В данном разделе неформально вводится концепция смешанной робаст-

ности, совмещающей два вышеупомянутых типа робастности. Строгие фор-

мулировки приведены в разделе 3.

Рассмотрим линейную систему с постоянными коэффициентами, имею-

щую и детерминированную параметрическую неопределенность q, и случай-

ную δ. Параметры принадлежат своим множествам q ∈ Q ⊂ Rⁿ, δ ∈ Δ ⊆ R^m.

Случайный вектор δ распределен на множестве Δ и обозначается как δ ∼ Δ.

Параметры распределения здесь несущественны и опущены.

Начнем с простого случая: пусть распределение случайного параметра δ

не зависит от значения параметра q (также неопределенного). Анализ устой-

чивости таких систем включает в себя и вероятностную, и гарантирующую

части. Соответственно задача является смесью детерминированной (1) и ве-

роятностной (2) задач. Она состоит в нахождении вероятности

(3)

Prob_δ∼Δ

[Система устойчива для данного δ и всех q ∈ Q].

Формально поставленная задача может называться задачей о “вероятност-

ной робастности”. В конце концов, это и есть задача вероятностного анали-

за устойчивости типа (2), сформулированная с более сложным утверждением

“Система робастно устойчива (по q на множестве Q) для данного δ” вместо

“Система устойчива для данного δ”. Ее разрешимость с помощью сценарно-

го подхода и связь с известными способами решения обсуждается в подраз-

деле 3.2. Более того, эта задача подпадает под обобщенную формулировку

задачи 6.4 из [12] о вычислении (вероятностного) показателя качества систе-

мы. Вместе с этим существуют более удобные методы вычисления вероятно-

сти (3), использующие особенность постановки.

Во избежания двусмысленности термина “робастность” предпочтительно

использовать термин смешанная параметрическая робастность. Этот тер-

мин подчеркивает не только параметрическую форму неопределенности, но

и существенную роль разных типов неопределенности: случайной и не слу-

чайной. Поскольку далее рассматриваются только параметрические неопре-

деленности, уточнение “параметрическая/ие” опускается.

В общем случае параметры этих двух видов могут быть зависимыми или

подчиненными друг другу, см. раздел 3 статьи. Соответствующие постанов-

ки задач являются также новыми. В разделе 4 предложен ряд подходов к

решению, специфичных для задач смешанной робастности.

Отметим, что довольно часто встречаются задачи, в которых детер-

минированная параметрическая робастность смешивается с вероятностной

динамической неопределенностью в шуме/возмущениях/ограничениях, см.

[19-23]. Такие неопределенности также известны под именем структуриро-

ванно-неструктурированных возмущений (structured-unstructured perturba-

tion) [24]. Другим примером смешивания с зависимыми случайными и не

случайными переменными являются задачи оптимизации с квантильными

ограничениями, но в них преследуется иная цель. В то же время комбинация

случайных и не случайных неопределенных параметров изучалась редко или

неявно, для других задач или в другом контексте, в частности для упрощения

задачи синтеза регулятора [25] или для оценки некоторого распределения [26].

Далее понятие смешанной робастности проводится на примере анализа

линейных систем управления с постоянными коэффициентами, содержащих

смешанную (гибридную, совместную) параметрическую неопределенность.

2.1. Мотивирующие факторы для введения

смешанной параметрической робастности

Деление между детерминированными и случайными параметрами возни-

кает в нескольких случаях.

Во-первых, в системе эти параметры могут иметь различную природу. На-

пример, случайный параметр δ представляет неопределенность в регуляторе

(неточность реализации), в то время как параметр q отвечает за неопределен-

ность в управляемой системе либо наоборот. В [25] подобное разделение было

сделано искусственно для не робастной задачи синтеза регулятора. В этом

случае часть параметров регулятора случайно выбирались по методу Монте-

Карло, а области устойчивости по остальным параметрам легко вычислялись.

Основной идеей являлся случайный, рандомизированный подбор регулято-

ров, этот подход не был связан с анализом робастности.

Во-вторых, выделение нескольких параметров из общего числа варьируе-

мых параметров полезно для более глубокого исследования системы. Этот

выбор может быть сделан вручную для оценки так называемой “модулиро-

ванной” (шкалированной) робастности по отношению к выбранным парамет-

рам либо для оценки потери качества при изменении множества неопреде-

ленности [12, 13]. Случайность выделенных параметров может быть навязана

искусственно [16]. С одной стороны, эта случайность моделирует нежесткие

ограничения, а с другой отражает априорные представления о неопреде-

ленности. В зависимости от задачи случайный параметр можно рассматри-

вать, например, как равномерно или нормально распределенный, с несим-

метричным распределением, представленный смесью распределений и т.д.

Такой подход помогает не только формализовать априорные представления

о неопределенности, но также помогает убедиться в отсутствии хрупкости,

т.е. негативной чувствительности системы к малым изменениям выбранных

параметров. А параметры, найденные с помощью оптимизации (без учета

робастности), часто именно такие, подробнее об этом эффекте см. [27].

В-третьих, предложенная постановка может возникнуть, если некоторая

часть неопределенных параметров ограничена “жестко” (q), а другие пара-

метры ограничены “мягко” (δ). Действительно, даже если использовать ве-

роятностный подход, не обязательно ожидать, что все неопределенные пара-

метры представимы случайными величинами. Этот случай включает в себя

нечеткие неопределенности, которые, например, могут быть смоделированы

как сумма интервального и случайного значений. При этом привлекать спе-

циальный аппарат нечеткого исчисления не требуется.

В-четвертых, задача о смешанной робастности является результатом ча-

стичной рандомизации, при которой только некоторые из исходно детерми-

нированных неопределенных параметров заменяются случайными.

Основным результатом статьи является постановка задач для смешанной

параметрической робастности, включающей различные типы неопределенно-

сти. В случае нескольких случайных параметров для решения этой задачи

предлагается использовать графо-аналитический подход.

Предложенное понятие смешанной робастности по сложности заполняет

промежуток между детерминированными задачами и изложенными в [12,

гл. 6] идеями вероятностного анализа этих задач. Тем самым можно найти

компромисс между сложностью (вложенной) задачи о детерминированной

робастности и “неуверенностью” (т.е. случайностью исхода) решения вероят-

ностной задачи о робастности.

Подчеркнем схожесть и отличия между предложенными задачами о сме-

шанной робастности и вероятностным вычислением показателя качества из

[12, гл. 6]. В то время как задача 6.1 в [12] поставлена относительно произ-

вольного критерия, в приведенных примерах предполагается, что случайно

распределенный параметр δ это единственная неопределенность. Затем

эта неопределенность исследуется вероятностными методами с учетом детер-

минированных ограничений на нее. Таким образом, одна из задач ставится

как поиск вероятности⁷

[

]

Prob_δ∼Δ

P (s, δ) гурвицев и δ ∈ Q

В предложенной же задаче о смешанной робастности (3) критерий, пара-

метризованный случайной переменной δ, включает внутреннюю робастность

по отношению к другой неопределенности q. Тем самым простейшая задача

о смешанной робастности одновременно охватывает две различные группы

“робастности”: внутреннюю по отношению к параметру q и внешнюю по отно-

шению к параметру δ. Если бы δ был тоже детерминированным (в контексте

классической робастности), либо параметр q был бы случайным, то в итоге

задача свелась бы к классической детерминированной постановке (1) или к

полностью вероятностной постановке (2) соответственно.

Помимо рассмотренного примера независимых случайных и неслучайных

параметров, возникают два новых типа смешанной робастности: случайные

параметры могут зависеть от неслучайных и наоборот множество неопре-

деленности детерминированных параметров само может быть случайным, по-

дробнее см. раздел 3.

Смешивание разных типов параметрической робастности и их взаимосвязь

в задачах автоматического управления являются новыми. С другой стороны,

идея вычисления вероятности попадания случайного параметра δ в “хоро-

шее” или “плохое” множество хорошо известна, см., например, [12, раздел 6.2].

Трудность состоит в удобном описании этих множеств. Для случая маломер-

ного случайного параметра эта задача решена в разделе 4 с помощью робаст-

ного D-разбиения.

3. Постановка задач о смешанной робастности

Рассмотрим замкнутую линейную систему с постоянными коэффициен-

тами без запаздывания⁸ с двумя типами параметров: детерминированными

q ∈ Q ⊂ Rⁿ и случайными δ ∼ Δ ⊆ R^m. Случайная величина δ распределена

⁷ Значение показателя качества в постановке заменено на критерий устойчивости для

краткости. Упомянутая глава содержит много других идей анализа, например изучение

деградации критерия качества (при случайных параметрах) и т.п., см. также похожий

подход к “шкалированной” робастности в [13].

⁸ Расширения на другие типы систем представлены в разделе 6.

на множестве Δ с некоторой вероятностной мерой (равномерной, нормальной

и т.д.). Еще раз подчеркнем, что предложенные постановки имеют смысл не

только для задач устойчивости, но и для любых желаемых свойств системы.

Устойчивость рассматриваемой системы определяется корнями характе-

ристического полинома, коэффициенты которого зависят от параметров

P (s, q, δ) = a₀(q, δ)s^k + . . . + a_k(q, δ).

Для устойчивости непрерывной системы этот полином должен быть гурви-

цевым, т.е. все его корни s_i должны иметь отрицательную вещественную

часть Re s_i < 0. Для устойчивости дискретной системы аналогичный поли-

ном P (z, q, δ) должен быть шуровским, т.е. все корни должны находиться

внутри единичного круга |z_i| < 1. Без потери общности далее рассматрива-

ется только непрерывный случай, и устойчивость системы отождествляется

со свойством Гурвица ее характеристического полинома.

Задача анализа смешанной параметрической робастности состоит в том,

чтобы найти вероятность устойчивости по случайной переменной δ при на-

личии неопределенности q. Поскольку в общем случае случайные и детерми-

нированные параметры могут быть зависимыми друг от друга, приведем три

постановки задачи о смешанной робастности.

В самом простом варианте случайная и детерминированная неопределен-

ности полностью независимы, т.е. задача имеет форму (3). Пусть это и самый

простой способ смешивания, но он является новым. Здесь неопределенные па-

раметры равноправны.

I. Задача о независимой смешанной параметрической робастности

(Q-Δ робастность).

Пусть заданы случайный параметр δ ∼ Δ ⊆ R^m и множество неопреде-

ленности Q ⊂ Rⁿ, а также характеристический полином системы с посто-

янными коэффициентами P (s, q, δ). Требуется найти вероятность устой-

чивости

[

]

(4)

p^∗

= Prob_δ∼Δ P (s, q, δ) гурвицев для всех q ∈ Q .

В статье эта и последующие значения вероятности называются вероятно-

стями смешанной робастности или вероятностями смешанной робастной

устойчивости.

Далее, множество возможных параметров Q для детерминированной

неопределенности может зависеть от случайного параметра δ, т.е., строго

говоря, само быть случайным. Тем самым детерминированная неопределен-

ность подчинена случайной.

II. Смешанная задача робастности с зависимостью первого типа (Q(Δ)

робастность).

Пусть заданы случайный параметр δ ∼ Δ⊆R^m, значения которого связа-

ны с множествами неопределенности Q(δ)⊂Rⁿ, и характеристический по-

лином системы с постоянными коэффициентами P (s, q, δ). Требуется най-

ти вероятность устойчивости

[

]

(5)

p^∗ = Prob_δ∼Δ P(s,δ,q)гурвицев для всех q ∈ Q(δ) .

Отметим, что характеристический полином зависит не только от слу-

чайного множества неопределенности q, но и от самого случайного пара-

метра δ. Можно рассматривать форму записи задачи только со случай-

ным множеством (без неопределенности δ в характеристическом полиноме)

[

]

P (s, q) гурвицев для всех q ∈Q(δ) . Легко показать, что эти постановки эк-

вивалентны.

Наконец, случайный параметр δ (по существу его распределение и носи-

тель) может зависеть от значения детерминированной неопределенности. Эту

постановку можно рассматривать как поиск “наихудшего” варианта неопре-

деленности. При этом неопределенность понимается в расширенном смысле

и включает неопределенность в распределении Δ(q).

III. Смешанная задача робастности с зависимостью второго типа (Δ(Q)

робастность).

Пусть заданы множество неопределенных параметров Q ⊂ Rⁿ и семей-

ство случайных параметров δ ∼ Δ(q) ⊆ R^m, параметризованное с помощью

q ∈ Q. Для характеристического полинома системы с постоянными коэф-

фициентами P (s, q, δ) найти гарантированную вероятность устойчивости

[

]

(6)

p^∗ = inf

Prob_δ∼Δ(q) P (s, q, δ) гурвицев .

q∈Q

Эта постановка охватывает параметрические семейства распределений

как частный случай, при котором меняются только параметры, но не но-

ситель. Для удобства положим, что указанный минимум достигается (на-

пример, если Q компактно, а распределение задано функцией распределе-

ния, равномерно непрерывной по параметру q). Вместе с этим предложен-

ная постановка более общая, так как устойчивость системы может зави-

сеть не только от параметризованного распределения случайного параметра

(min_q∈Q Prob_δ∼Δ(q)[P (s, δ) гурвицев]), но детерминированный параметр мо-

жет также влиять на устойчивость непосредственно, например, частью ком-

понент, к примеру min_(qa_,qb_)∈Q Prob_δ∼Δ(qa₎[P (s, q^b, δ) гурвицев].

Как частный случай, в третий тип попадает задача с фиксированным рас-

пределением, при котором неопределенность входит только в сам характери-

стический полином:

minProbδ∼Δ[P(s,q,δ) гурвицев].

q∈Q

Несмотря на то что в такой постановке оба типа параметров независимы,

эта задача принципиально отличается от задачи о Q-Δ робастности (4). Ее

также можно интерпретировать как задачу о нахождении гарантированно-

го “среднего” показателя устойчивости, понимая вероятность устойчивости

Prob_δ∼Δ[P(s,q,δ) гурвицев] как “усредненное значение устойчивости” по мно-

жеству Δ. Схожий подход к минимизации не бинарного критерия описан

в [13]. Отметим, что попутно может быть определено “наихудшее” с точки

зрения устойчивости значение параметра q^∗ ∈ Arg min_q∈Q(· · · ). Такое значе-

ние параметра может быть не единственным, даже если минимум достижим.

Если минимум не достигается, возможна постановка задачи о нахождении

предельной точки или локализации области “наихудших” параметров.

С точки зрения разрешимости поставленных задач самой простой, по-

видимому, является задача о Q-Δ робастности с независимыми неопреде-

ленностями (4). Методы, подходящие для решения задачи о Q(Δ) робастно-

сти (5), также подходят и для нее. Задача о Δ(Q) робастности с обратной

зависимостью имеет принципиально другую природу. По-видимому, она наи-

более трудоемка (за исключением дискретного случая, см. подраздел 4.3).

Для нее в подразделе 3.3 предлагается использовать приближенный метод.

Далее перечислены несколько способов решения поставленных задач о

смешанной робастности с помощью известных методов. В подразделе 3.3

предложены методы приближенного решения. В разделе 4 задачу анализа

о независимой Q-Δ робастности предлагается решать в два этапа с помощью

вспомогательной задачи синтеза.

3.1. Аналитическое решение

Для первых двух задач о смешанной робастности (Q-Δ и Q(Δ)) можно

формально описать внутренний критерий с помощью индикаторной функции

устойчивости

(7)

F (δ) = I[P (s, q, δ) робастно устойчив].

Здесь робастность подразумевается либо для фиксированного множества

неопределенности Q, либо для параметризованного Q(δ). Для разных зна-

чения δ ∈ Δ вычисление этой функции сводится к различным задачам о де-

терминированной робастности. В этом случае решение задачи о смешанной

робастности (4) записывается как

∫

(8)

p^∗ =

F (δ)dµ,

т.е. как мера множества робастно стабилизирующих параметров Δ_good ∋ δ.

Здесь использована мера Лебега µ, лежащая в основе распределения случай-

ного параметра.

Однако функция F редко доступна в явном виде, поскольку ее вычисление

включает детерминированную задачу о робастной устойчивости (1), которая

может быть трудоемка.

Аналогично характеризуется прямой способ решения задачи Δ(Q)-робаст-

ности. Если вероятность устойчивости в п[раметризованных ]вероятност-

ных задачах робастности p^∗(q) = Prob_δ∼Δ(q)

P (s, q, δ) гурвицев

имеет яв-

ный вид, то решение можно получить с помощью задачи оптимизации p^∗ =

= min_q∈Q p^∗(q), в общем случае невыпуклой и негладкой.

3.2. Сценарный подход (выборка методом Монте-Карло)

Следуя идее рандомизации в вероятностном анализе, для оценки вероят-

ности (8) может быть использован сценарный подход (выборочный, эмпири-

ческий) [14]. Надо выбрать N случайных образцов δⁱ, i = 1, . . . , N, согласно

распределению параметра δ и получить долю устойчивых систем, которую

можно записать с помощью индикаторной функции устойчивости как

∑

p∗ =

F (δⁱ).

i=1

В этом случае неравенство

(9)

|p^∗ - p^∗

|<ε

будет выполнено с вероятностью 1 - 2e-2ε2N ≡ 1 - θ для любой точности

(accuracy) ǫ ∈ (0, 1). Эта вероятность характеризуется уровнем достоверно-

сти (confidence level) θ. Достаточного числа образцов, необходимого для до-

стижения (высокой) вероятности 1 - θ с данной (также высокой) точностью ε

оценки (8) дается верхней оценкой Чернова [14]:

⌈1

⌉

(10)

N =

2ε

Например, для достижения точности ε = 0,01 и уровня достоверности θ =

= 10^-7 нужны 84057 образцов.

Формирование выборки является отдельной задачей, легко решаемой для

произвольных непрерывных маломерных распределений (например, методом

обращения или отсечения), некоторых распределений векторов и матриц, а

также для дискретных распределений [12, главы 14, 16, 18].

Размер выборки может быть значительно уменьшен, если использовать

свойство выпуклости критерия. Априори ожидать выпуклости индикаторной

функции устойчивости (7) нельзя из-за подзадачи о робастной устойчивости.

Таким образом, для достоверного вычисления вероятности устойчивости ти-

пичный размер выборки должен быть велик, что особенно затрудняет при-

менение сценарного подхода для задач смешанной робастности.

Как уже упоминалось в разделе 1, в общем случае каждая подзадача слож-

на. Для прямого же применения сценарного подхода данные задачи должны

легко решаться для каждого элемента выборки. И действительно, такие слу-

чаи есть.

Робастная устойчивость полинома с независимыми интервальными коэф-

фициентами может быть проверена аналитически с помощью теоремы Хари-

тонова [9]. В этом случае для образца δⁱ каждый из коэффициентов a_j (q, δⁱ)

должен независимо меняться в интервалах a_j (δⁱ) ≤ a_j (q, δⁱ) ≤ a_j (δⁱ). То-

гда достаточно проверить гурвицевость четырех “угловых” полиномов. От-

метим, что эта проверка верна только для характеристического полинома

системы непрерывного времени, для дискретного случая аналогичного ре-

зультата нет [28].

Отметим также, что для любого числа образцов полученная оценка (9)

эмпирическая и всегда будет выполнена не гарантированно, а лишь с большой

долей уверенности, заданной параметром θ.

3.3. Приближенные методы

Задачи о смешанной робастности подразумевают ответ в виде численного

значения, поэтому альтернативой точному решению могут служить верхние

и нижние границы вероятности устойчивости.

Можно использовать простые необходимые или достаточные условия ро-

бастной устойчивости для вычисления функции F (δⁱ), что приведет к ниж-

ним или верхним границам вероятности смешанной робастности. Так, если

вместо индикаторной функции устойчивости F (δⁱ) в формуле (8) использо-

вать индикаторную функцию необходимого критерия устойчивости, то это

даст верхнюю границу вероятности устойчивости. Соответственно исполь-

зование достаточного критерия устойчивости даст нижнюю границу веро-

ятности (8). В контексте сценарного подхода вычисление критериев может

быть намного проще проверки робастной устойчивости, при этом оценка ве-

роятности (9) будет односторонней, а необходимые или достаточное условия

устойчивости могут быть слишком консервативными и в результате давать

грубые оценки вероятностей смешанной робастности.

Задачу о Q(Δ) робастной устойчивости с зависимыми параметрами можно

приближенно решать как задачу с независимыми параметрами. Во-первых,

если итоговое множество ограничено, то можно получить верхнюю и нижнюю

границу, объединяя или пересекая множества неопределенности:

[

]

⋃

p^∗II ≥ p^∗I,∪ = Prob_δ∼Δ P(s,q,δ) гурвицев для всех q ∈ Q =

Q(δ)

δ∈Δ

[

]

⋂

p^∗II ≤ p^∗

I,∩

= Prob_δ∼Δ P (s, q, δ) гурвицев для всех q ∈ Q =

Q(δ)

δ∈Δ

Во-вторых, в контексте сценарного подхода для решения задачи о Q(Δ) ро-

бастности в качестве нижней оценки вероятности устойчивости можно ис-

пользовать решение задачи о Q-Δ робастности относительно объединения⋃

множеств Q =_i=1,...,N Q(δⁱ).

Для всех трех типов задач о смешанной робастности применима идея

аппроксимации носителя случайного распределения с помощью множества

квантили, упомянутая в конце подраздела 1.2.2. Так, если для фиксирован-

ного p и множества Q_p : Prob_δ∼Δ[δ ∈ Q_p] ≥ p полином P (s, q, δ) робастно

устойчив в классическом смысле по отношению к q ∈ Q, δ ∈ Q_p, то вероят-

ность робастной устойчивости (4) с независимыми параметрами не меньше p.

Для задачи (5) о Q(Δ) робастности надо проверять робастную устойчивость

характеристического полинома по отношению к q ∈ ∪δ∈Qp Q(δ), δ ∈ Q_p. На-

конец, этот прием можно использовать для задачи (6) о Δ(Q) робастности,

выбрав Q_p : ∀q ∈ Q, Prob_δ∼Δ(q)[δ ∈ Q_p] ≥ p.

3.4. Робастное D-разбиение

Рассмотрим метод синтеза маломерных систем управления, который будет

полезен для решения задач о смешанной робастности: задачу о робастной

D-устойчивости [29].

Пусть интересующая нас система с постоянными коэффициентами зависит

от параметров d ∈ R^m и неопределенности q ∈ Q ⊂ Rⁿ. Ее характеристиче-

ский полином P (s, q, d). Предположим, что множество локализации корней D

в комплексной плоскости также является частью постановки задачи. Для за-

дачи робастной стабилизации непрерывных систем это левая комплексная

полуплоскость D = {s : Re s < 0} ⊂ C и т.д.

Цель задачи синтеза состоит в том, чтобы предоставить такое значение

параметра d, при котором все корни характеристического полинома P (s, q, d)

лежат в множестве D для всех допустимых неопределенностей:

(11)

d^∗ : Все корни полинома P(s,q,d^∗

) лежат в D для всех q ∈ Q.

Данная задача иногда называется задачей о робастном расположении кор-

ней или задачей синтеза о робастной кластеризации (локализации). Надле-

жащим выбором множества D можно решать различные задачи синтеза:

а) о робастной стабилизации систем непрерывного времени (D левая

комплексная полуплоскость),

б) о робастной стабилизации дискретных систем (D внутренность еди-

ничного круга),

в) о робастной стабилизации с ограниченной колебательностью (D явля-

ется сектором в левой комплексной полуплоскости)

и т.д.

Есть разные способы решения этой задачи от алгебраических и оптими-

зационных до основанных на линейных матричных неравенствах. В практи-

чески каждом из этих подходов выдается единственное значение d^∗, которое

является “наилучшим” по отношению к дополнительно выбранному крите-

рию.

Альтернативным подходом является описание всего множества робастно

стабилизирующих параметров, которые удовлетворяют задаче (11):

{

}

D_stab = d^∗ : Все корни полинома P(s,q,d^∗) лежат в D для всех q ∈ Q

Робастное D-разбиение является графо-аналитическим методом и чаще все-

го применяется для одно- и двухмерных параметров. Он позволяет неявно

изобразить множество устойчивых параметров D_stab ⊆ R^m, а точнее, его гра-

ницу [29]. Эта граница строится с помощью принципа исключения нуля и

“заметания” (перебора по сетке) обобщенных частот либо с помощью анали-

тического вывода уравнений, см. [30-33] и цитируемые там источники.

Основным ограничением практического применения робастного D-разбие-

ния является низкая размерность пространства параметров. Обычно оно мо-

жет быть сделано для m = 1, 2 или максимум для трех параметров.

Снова отметим, что указанная задача является задачей синтеза. Она же

может быть ключевым компонентом для решения задачи анализа смешанной

робастности с независимыми параметрами (4).

4. Основные результаты

Для решения задачи о смешанной робастности с независимыми параметра-

ми (4) или зависимостью первого типа (5) предлагается отказ от сценарного

подхода в части формирования подзадач робастного анализа. В общем слу-

чае для решения задач о смешанной робастности с зависимыми параметрами

предлагается использовать аппроксимации из подраздела 3.3.

Наличие дискретной неопределенности (случайной и/или детерминиро-

ванной) существенно упрощает решение задач о смешанной робастности.

4.1. Смешанная робастность с независимыми группами

детерминированных и случайных параметров (Q-Δ робастность)

Идея состоит в том, чтобы рассматривать случайный параметр δ как де-

терминированный и для него найти множество “хороших”, “робастно устой-

чивых” параметров

{

}

Δ_stab = δ : F(δ) = 1

{

}

= δ : система робастно устойчива для всех q ∈ Q .

Напомним, что искомая вероятность смешанной робастной устойчивости (4)

является вероятностной мерой этого множества. Единственным ограничени-

ем подхода является требование его измеримости.

Для нахождения этого множества предлагается использовать⁹ робастное

D-разбиение в пространстве случайной неопределенности δ ∈ R^m по отноше-

нию к “жестко” ограниченной неопределенности q ∈ Q. Каждая точка множе-

ства Δ_stab ≡ D_stab обеспечивает робастную устойчивость характеристическо-

го полинома по отношению к детерминированной неопределенности q. Затем

решение задачи (4) вычисляется как (вероятностная) мера этого множества.

Предлагается следующий алгоритм решения задачи о смешанной робаст-

ности (4). Он записан в терминах устойчивости линейной системы с постоян-

ными параметрами, но тривиально модифицируется на иные свойства систем.

Алгоритм 1. Решение задачи о независимой смешанной робастности

(Q-Δ робастности).

Шаг 1. Найти множество робастно стабилизирующих параметров Δ_stab по

отношению к детерминированной неопределенности q

Δ_stab = {δ : P(s,q,δ) гурвицев для всех q ∈ Q}.

Шаг 2. Для данной случайной неопределенности δ ∼ Δ вычислить вероят-

ность устойчивости как

(12)

p^∗ = Prob_δ∼Δ[δ ∈ Δ_stab] = µ(Δ_stab

Подчеркнем, что каждый шаг алгоритма может быть выполнен незави-

симо с помощью любого подходящего метода. Например, оценка вероятно-

сти (12) на шаге 2 может быть сделана методом Монте-Карло (по сути, тем

⁹ Этот способ особенно хорошо подходит для анализа робастности любого свойства си-

стемы, определяемого расположением корней характеристического полинома.

же сценарным подходом). Этот подход отличается от прямого сценарного

подхода из подраздела 3.2. На шаге 2 каждый случайно выбранный обра-

зец δⁱ должен быть проверен на принадлежность конструктивно описанному

множеству Δ_stab, в то время как в прямом сценарном подходе для каждого

образца должна решаться подзадача о детерминированной робастности.

Если распределение случайной неопределенности δ равномерно на Δ, то

геометрическая вероятность (12) вычисляется как отношение объемов (пло-

щадей) множеств

Vol(Δ ∩ Δ_stab)

Vol(Δ \ Δ_stab)

(13)

p^∗ =

=1-

Vol(Δ)

При использовании робастного D-разбиения граница множества Δ_stab зада-

ется поточечно (численно либо сеткой при аналитическом задании границы),

тем самым это множество аппроксимируется многоугольником или набором

многоугольников, площадь которых может быть найдена точно. Уменьшая

сетку, эта аппроксимация позволяет найти площадь Δ_stab с требуемой точно-

стью.

Для не равномерного распределения задача (12) о численном нахождении

меры множества Δ_stab может быть нетривиальной даже при аналитическом

описании множества. В одномерном случае задача решается явно (см. под-

раздел 4.2), в двухмерном и трехмерном случаях можно использовать пере-

бор одного или двух параметров. Вопрос о точности полученных сеточных

аппроксимаций и используемых квадратурных формул требует отдельного

рассмотрения.

Основным недостатком предлагаемого подхода является низкая размер-

ность случайного параметра δ. Выполнимость первого шага ограничена при-

менимостью техники анализа пространства параметров, такого как робастное

D-разбиение, поскольку множество Δ_stab может быть конструктивно постро-

ено только в одно-, дву- и (максимум) трехмерных случаях.

Другой особенностью является численная сложность построения самого

множества Δ_stab. Если параметры q, δ входят в коэффициенты характери-

стического полинома аффинно, то робастное D-разбиение можно построить

численно или аналитически [29, 30, 32]. В противном случае построение ро-

бастного D-разбиения может быть сложной задачей само по себе. В таких

случаях предлагается использовать внутренние или внешние приближения

множества Δ_stab, получая для них соответственно нижние и верхние оценки

вероятности (12).

Для задачи о смешанной Q(Δ) робастности (с зависимостью первого типа)

можно применять этот же алгоритм 1, если на первом шаге удается найти

множество робастно стабилизирующих параметров Δ_stab с учетом зависимо-

сти:

Δ_stab = {δ : P(s,q,δ) гурвицев для всех q ∈ Q(δ)}.

Далее перечислены несколько случаев, в которых задача о смешанной ро-

бастности или ее подзадачи могут быть решены явно.

4.2. Скалярная случайная неопределенность

Пусть случайный параметр системы одномерен: δ ∈ R¹. Если множество

Δ_stab непусто, то оно может быть представлено как объединение непересека-

ющихся отрезков¹⁰ (a_i,b_i], i = 1,..., где a_i < b_i и b_i < a_i+1.

Эти интервалы могут быть найдены разными способами, например с помо-

щью одномерного робастного D-разбиения [29] или так называемым методом

“разведчика устойчивости” (Stability Feeler), предложенным в [34].

Таким образом, система является робастно устойчивой для некоторого

значения δ тогда и только тогда, когда существует интервал i : a_i < δ ≤ b_i.

Значение индикаторной функции устойчивости (7) тривиально вычисляется

{

1, если ∃i : δ ∈ (a_i, b_i],

F (δ) =

в противном случае.

Для найденных отрезков робастной устойчивости задача о смешанной ро-

бастности (4) имеет очевидное решение (8):

∑

(

)

(14)

p^∗ =

CDF(b_i) - CDF(a_i)

i=1,...

т.е. является суммой вероятностей попадания неопределенного параметра δ в

каждый из отрезков (a_i, b_i]. Решение записано с помощью одномерной функ-

ции распределения неопределенного параметра δ

CDF(a) = Prob_δ∼Δ[δ ≤ a].

4.3. Дискретная неопределенность

Пренебрегая переходными процессами, анализ робастности системы с пе-

реключениями можно свести к анализу системы с дискретной неопределен-

ностью. Аналогичным образом конечный набор однотипных систем может

быть записан в виде одной системы с добавлением в нее неопределенного

дискретного параметра.

Анализ смешанной робастности значительно упрощается при наличии дис-

кретной неопределенности любого типа. Приемы, подобные перечисленным

далее, можно использовать в случаях, когда дискретны только некоторые

компоненты случайного и/или детерминированного параметров.

4.3.1. Дискретная детерминированная неопределенность

Если число различных значений детерминированных параметров конечно

и невелико (например, не превышает K), то подзадачи робастного анализа

¹⁰ Первый и последний отрезки могут иметь бесконечную длину, например быть (-∞, b1].

Также эти отрезки могут быть открытыми или полуоткрытыми, например для каких-то j

быть [aj , bj ], для других (aj , bj ) и т.д. Разница между этими случаями имеет меру нуль и для

абсолютно непрерывного распределения δ не влияет на вычисление вероятности. Однако

в случае дискретного или смешанного распределения эти нюансы необходимо учитывать.

Q-Δ и Q(Δ) робастной устойчивости (4), (5) сводятся к проверке устойчи-

вости небольшого числа полиномов. В этом случае разумно применять пря-

мой сценарный подход из подраздела 3.2, решая эту подзадачу для конеч-

ного же числа образцов δⁱ, i = 1, . . .: “P (s, δⁱ, q^i,k) гурвицев для всех k ∈ K_i ⊆

⊆ 1, . . . , K”.

Задача Δ(Q) о смешанной робастности сводится к перебору и решению

конечного числа подзадач о вероятностной робастности

[

]

“Probδ∼Δk P (s, q^k, δ) гурвицев , k = 1, . . . , K”.

4.3.2. Дискретная случайная неопределенность

Пусть распределение задано набором значений δ^j вместе с вероятностями

p_j = Prob_δ∼Δ[δ = δ^j], j = 1,... Если множество допустимых значений δ^j ко-

нечно и имеет небольшой размер, j = 1, . . . , M, то связанная с ним задача о

смешанной Q(Δ) (или Q-Δ) робастности может быть решена явно.

Алгоритм 2. Решение задачи о смешанной Q(Δ) робастности c дискрет-

ной случайной неопределенностью (5).

Пусть задана случайная величина δ, принимающая значения δ^j с вероят-

ностями p_j , и характеристической полином системы P (s, q, δ) зависит также

от неопределенного параметра q ∈ Q(δ).

Для каждого j = 1, . . . , M решить задачу о детерминированной робастно-

сти и вычислить

∑

[

]

p^∗ =

p_j · I P(s,q,δ^j) гурвицев для всех q ∈ Q(δ^j) .

j=1

Технически, этот подход похож на сценарный, но число “образцов” ограни-

чено, а в результате будет получено точное решение. Анализ распадается на

M независимых подзадач о детерминированной робастности и его сложность

зависит от сложности решения этих подзадач. Как и в случае сценарного

подхода, эти подзадачи можно решать параллельно.

Отметим, что этот результат не зависит от размерности случайной неопре-

деленности δ.

Алгоритм 2 применим не только к задаче (5) о смешанной робастности c

зависимостью, но и к задаче (4) с независимыми параметрами.

Можно аппроксимировать решение, отбросив ряд “маловероятных” значе-

ний параметра δ, и тем самым получить нижнюю оценку вероятности устой-

чивости. Так же можно поступить, если множество дискретных значений бес-

конечно.

4.3.3. Дискретная случайная и дискретная детерминированная

неопределенность

Данный случай примечателен тем, что в случае конечного числа значений

параметров все три варианта задачи о смешанной робастности: Q-Δ, Q(Δ) и

Δ(Q) легко решаются.

В задаче о Q-Δ робастности случайный параметр задан набором значе-

ний δ^j вместе с вероятностями p_j = Prob_δ∼Δ[δ = δ^j ], j = 1, . . . , M, а детерми-

нированный набором Q = {q^k, k = 1, . . . , K}. Решение дается формулой

∑ K∏ [

]

p^∗ =

p_j ·

I P(s,q^k,δ^j) гурвицев .

j=1

k=1

В задаче о Q(Δ) робастности детерминированный параметр задан набором

с двумя индексами {q^j,k, k = 1, . . . , K_j } для каждого j = 1, . . . , M. Решение

дается аналогичной формулой

∏ [

]

p^∗ =

p_j ·

I P(s,q^j,k,δ^j) гурвицев .

j=1

k=1

Наконец, в задаче о Δ(Q) робастности детерминированная неопределен-

ность задана набором {q^k, k = 1, . . . , K}, а случайная - наборами значений

{δ^k,j , j = 1, . . . , M_k}, k = 1, . . . , K, c вероятностями p_k,j = Probδ∼Δk [δ = δ^k,j],

j = 1,...,M_k. В этом случае решение дается формулой

M_j

∑

[

]

p^∗ = min

p_k,j · I P(s,q^k,δ^k,j) гурвицев .

k=1,...,K

j=1

5. Примеры

В первых трех примерах рассматриваются задачи о независимой смешан-

ной робастности (Q-Δ робастности), далее в примерах решаются задачи о

зависимой смешанной робастности. В четвертом примере рассмотрена зада-

ча о зависимости первого типа (Δ(Q) робастность), а в пятом - зависимость

второго типа (Δ(Q) робастность). В последних примерах активно использу-

ется возможность описать множество устойчивости анализируемой системы

на расширенном множестве неопределенностей Q × Δ.

5.1. Скалярная случайная неопределенность

Рассмотрим немного измененный пример 2 из [34] об устойчивости дис-

кретных систем. Объект управления с передаточной функцией G(z, K), вклю-

чающей коэффициент усиления, стабилизируется управлением с обратной

связью с помощью регулятора C(z, q₁, q₂):

G(z, K) =

1 + 3z

8,5 + 3,5z

C(z, q₁, q₂) =

1 + (8 + q₁)z + (6 + q₂)z²

Каждый из неопределенных параметров q₁, q₂ находится в интервале [-1, 1].

Задача о смешанной робастности состоит в том, чтобы определить веро-

ятность устойчивости, рассматривая коэффициент усиления обратной свя-

зи K как нормально распределенную случайную величину со средним 2 и

стандартным отклонением 0,1. Устойчивость определяется критерием Шура-

Кона (а не Гурвица) для характеристического полинома

(

)

P (z, q, K) = K(8,5 + 3,5z) + (1 + 3z)

1 + (8 + q₁)z + (6 + q₂)z²

В [34] определена робастная устойчивость этой системы при K ∈

∈ [-0,11, 2,21], что соответствует первому шагу алгоритма 1. Формула (14)

для нормального распределения принимает вид

∫

p^∗ =

√

e-2

·(0,1)2 dK =

0,1

2π

−0,11

(

)

))

( 2,21 - 2

(-0,11 - 2

erf

√

- erf

√

= 0,982.

0,1

В результате получена точная вероятность смешанной робастной устойчи-

вости.

5.2. Двумерная случайная неопределенность

Рассмотрим пример с замкнутой системой, имеющей характеристический

полином

(

)

(15)

P (s, q, δ) =

(1 + q₁)s² + (1 + q₂)s - 1

s + (s - 15)(δ₁s + δ₂ - 0,3s²

Детерминированная неопределенность q ограничена эллипсом 100q²¹ + 25q²² ≤

≤ 9, в то время как случайный неопределенный параметр δ равномерно

распределен в заштрихованном прямоугольнике (см. рис. 2): δ₁ ∼ [-4, -2],

δ₂ ∼ [-7,-2]. Этот параметр представляет неопределенность коэффициентов

ПИ-регулятора. Цель состоит в решении задачи (4) о смешанной робастности

при данных независимых неопределенностях.

Штриховая линия на рис. 2 дает границу множества устойчивости для но-

минальной системы (q₁ = q₂ = 0). Поскольку все возможные случайные па-

раметры попадают в это множество устойчивости, то номинальная система

будет робастно устойчива с вероятностью единица по отношению к неопре-

деленности δ.

При наличии эллиптически ограниченной неопределенности q область

устойчивости Δ_stab уменьшается, так как она соответствует робастной устой-

чивости. Следуя первому шагу алгоритма 1 из раздела 4, это множество по-

строено с помощью робастного D-разбиения. Границы Δ_stab изображены на

рис. 2 сплошной линией. Видно, что существуют значения неопределенности

δ ∈ Δ \ Δ_stab вне этой области.

Для равномерного распределения второй шаг алгоритма 1 становится за-

дачей о вычислении геометрической вероятности. В итоге решение задачи о

d₂

-2

D_stab

-4

-6

D\D_stab

-8

-5

-4

-3

-2

-1

d₁

Рис. 2. Номинальное и робастное D-разбиение для характеристического поли-

нома (15). Штриховая линия граница номинального D-разбиения. Сплош-

ная линия граница робастного D-разбиения. Серый прямоугольник но-

ситель (Δ) равномерно распределенной неопределенности δ, разделенный на

множество “хороших” (Δ_stab) и “плохих” (Δ \ Δ_stab) параметров.

смешанной робастности сводится к вычислению площадей 13. В этом примере

вероятность смешанной робастности равна p^∗ = 0,68901.

Для сравнения эта вероятность была оценена с помощью сценарного под-

хода: для точности ε = 0,01 и уровня достоверности θ = 10^-7 на множестве Δ

согласно равномерному распределению и оценке (10) были выбраны 84507 об-

разцов случайных параметров δⁱ. Для каждого образца была проверена ро-

бастная устойчивость полинома P (s, q, δⁱ). В 57856 случаях полином был ро-

бастно устойчив, что приводит к оценке p^∗ = 0,68830, лежащей в пределах

точности |p^∗ - p^∗| = 7,2 · 10^-4 < ε.

5.3. Скалярные случайные и детерминированные неопределенности

Рассмотрим линейную систему с характеристическим полиномом, завися-

щую от скалярных неопределенных параметров q и δ:

(16)

P (s, q, δ) = s³ + (2 - |q - δ|)s² + 2s²

+ 3.

Полином устойчив при |q - δ| < 0,5, что геометрически соответствует полосе

между прямыми q - δ = 0,5 и q - δ = -0,5, см. рис. 3 слева.

Далее приведены различные связи между этими двумя параметрами, де-

монстрирующие все варианты задач о смешанной робастности (4), (5), (6).

Детерминированный

параметр q

1,0

1,75

1,60

0,8

1,40

0,6

1,20

0,4

1,00

0,2

0,80

0,2

0,4

0,6

0,8

1,0

0,25

0,50

0,75

1,00

1,25

1,50

1,75

2,00

Cлучайный параметр d

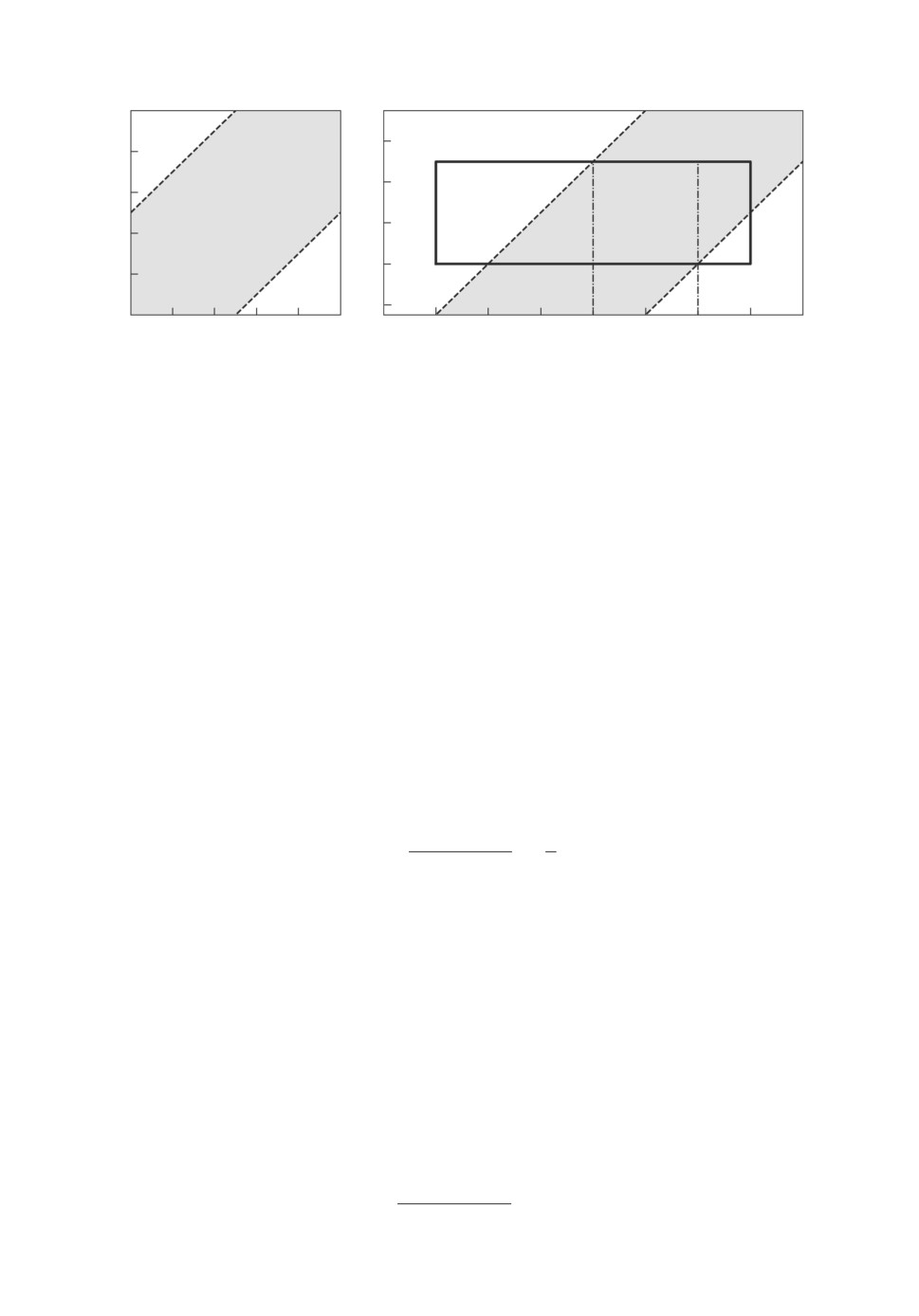
Рис. 3. Пример 3. Серые области с пунктирным границами множества устой-

чивости. Слева: область устойчивости полинома (16). Справа: иллюстрация

решения задачи из подраздела 5.3.1 о Q-Δ робастности с равномерным рас-

пределением случайного параметра. Штрихпунктирные линии по пересече-

нию границ множества неопределенных параметров и множества устойчиво-

сти определяют подходящий отрезок [1, 1,5] для случайного параметра.

5.3.1. Независимая смешанная робастность (Q-Δ робастность)

Рассмотрим задачу о (Q-Δ робастности (4). Пусть множество значений

детерминированного параметра задано интервалом Q = [1, 1,5], а случайный

параметр равномерно распределен на отрезке Δ = [0,25, 1,75], см. рис. 3,

справа.

Здесь применим двухэтапный алгоритм 1 из раздела 4. Полином (16) ро-

бастно устойчив (по q ∈ Q) для всех δ ∈ Δ_stab = [1, 1,5]. Вне этого отрезка

существуют значения q ∈ Q, нарушающие устойчивость. Согласно (12), (13)

вероятность смешанной Q-Δ робастности вычисляется в явном виде как от-

ношение длин отрезков Δ_stab и Δ:

1,5 - 1

p^∗ =

1,75 - 0,25

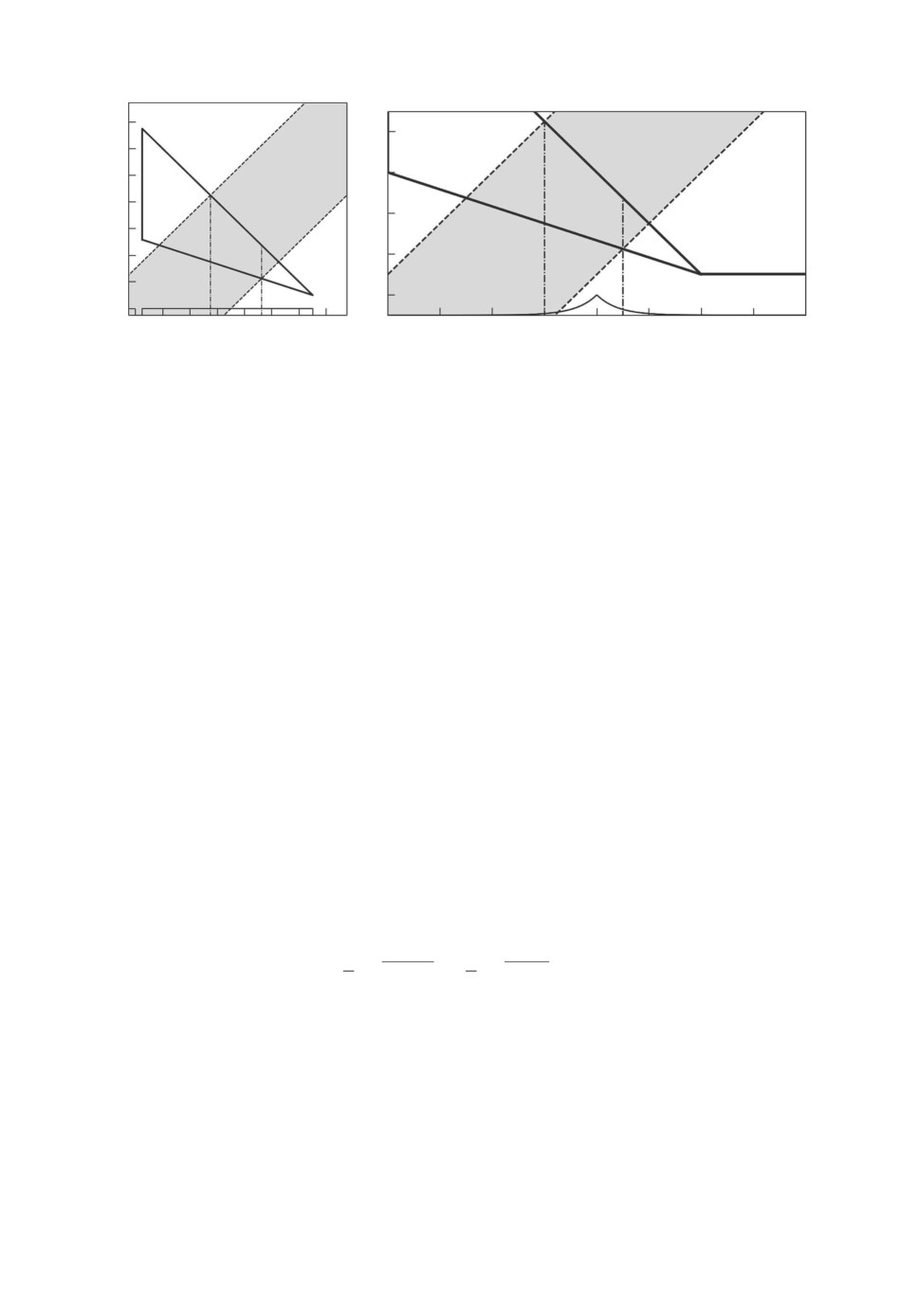
5.3.2. Смешанная робастность с зависимостью первого типа

(Q(Δ) робастность), первый вариант

Пусть случайный параметр δ равномерно распределен на отрезке Δ =

= [0,25, 1,5]. Множество значений детерминированного параметра представ-

ляет собой случайное множество Q(δ) = [1 - δ/3, 2 - δ], см. рис. 4, слева.

В данном случае можно также применить модифицированный алгоритм 1,

описанный в конце раздела 4. Полином (16) робастно устойчив (по q ∈ Q(δ))

при значениях δ ∈ Δ_stab = [0,75, 1,125]. Как и в примере из подраздела 5.3.1,

вероятность смешанной Q(Δ) робастности вычисляется как отношение отрез-

ков

1,125 - 0,75

p^∗ =

= 0,3.

1,5 - 0,25

Детерминированный

параметр q

1,8

1,2

1,6

1,4

1,0

1,2

0,8

1,0

0,8

0,6

0,4

0,2

0,6

1,0

1,4

0,25

0,50

0,75

1,00

1,25

1,50

1,75

2,00

Cлучайный параметр d

Рис. 4. Серые области с пунктирным границами множества устойчивости.

Сплошные линии границы множества неопределенности. Штрихпунктир-

ные линии определяют края отрезков случайных параметров (границы мно-

жеств Δ_stab = [0,75, 1,125], одинаковых в обоих случаях). Цифрой 1 схема-

тически обозначены плотности распределения случайного параметра. Слева:

пример 5.3.2, первый вариант Q(Δ) робастности с равномерным распреде-

лением случайного параметра. Справа: пример 5.3.3, второй вариант Q(Δ)

робастности с распределением Лапласа случайного параметра.

5.3.3. Смешанная робастность с зависимостью первого типа

(Q(Δ) робастность), второй вариант

В этом варианте случайный параметр δ имеет распределение Лапласа с

коэффициентом сдвига 1 и коэффициентом масштаба 0,1. Носитель Δ = R

не ограничен. Множество значений детерминированного параметра представ-

ляет собой случайное множество: отрезок Q(δ) = [1 - δ/3, 2 - δ], если δ < 1,5,

или одну точку Q(δ) = {0,5} для δ ≥ 1,5, см. рис. 4, справа.

Двухэтапный алгоритм 1 применим и в этом случае, множество Δ_stab то

же и по построению не зависит от распределения. Для скалярной случай-

ной неопределенности и известного закона распределения можно использо-

вать (14):

p^∗ = CDF_Laplace(1,125) - CDF_Laplace(0,75) =

1,125-1

0,1

=1-

e^-

e-1

= 0,8157.

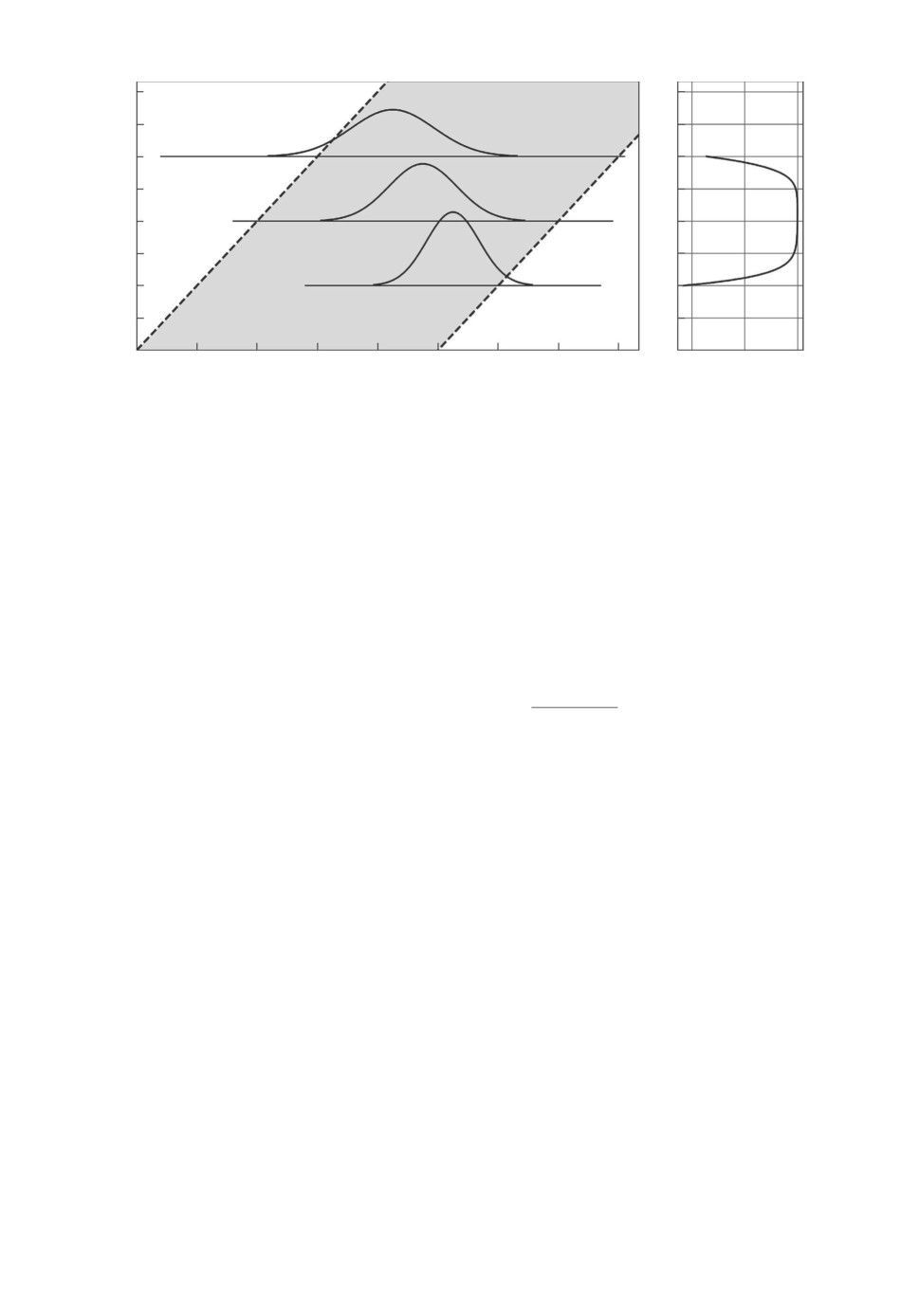
5.3.4. Смешанная робастность с зависимостью второго типа

(Δ(Q) робастность)

Рассмотрим детерминированный параметр q ∈ Q = [0,7, 1,1] и случайный

параметр δ c нормальным распределением N (δ₀, σ). Параметры распределе-

ния зависят от детерминированного параметра: среднее δ₀ = 1,4 - 0,5q, сред-

неквадратичное отклонение σ = q/8, см. рис. 5. Отметим, что параметр q не

только влияет на распределение, но и входит в характеристический поли-

ном (16) явно.

Детерминированный параметр q

1,3

1,2

1,1

1,0

0,9

0,8

0,7

0,6

0,5

0,2

0,4

0,6

0,8

1,0

1,2

1,4

1,6

0,96

0,98

1,00

Cлучайный параметр d

p(q)

Рис. 5. Пример 5.3.4. Слева: пример Δ(Q) робастности с нормальным рас-

пределением случайного параметра. Серая область с пунктирным граница-

ми множество устойчивости. 1, 2, 3 схематически проиллюстрированы

три плотности распределения случайной величины δ для разных значений

параметра q = 1,1, 0,9, 0,7. Справа: связь между вероятностью устойчивости

p(q) (ось абсцисс) и параметром q (ось ординат).

Вероятность устойчивости Prob_δ∼Δ(q) [Полином (16) гурвицев] можно най-

ти в явном виде по формуле (14), учитывая, что области устойчивости зада-

ются отрезками D_stab(q) = [q - 0,5, q + 0,5]:

∫

δ-(1,4-0,5q)

p(q) = Prob_δ∼Δ(q) =

2(q/8)2

dδ.

q-0,5

График этой вероятности приведен на рис. 5 справа. Решением задачи о

смешанной Δ(Q) робастности является минимальное значение вероятности

устойчивости p = 0,9568 при “наихудшем” q = 0,7.

6. Заключение и расширения

В статье проведен обзор различных типов параметрической робастности.

На примере исследования устойчивости систем с детерминированной и слу-

чайной неопределенностями предложены постановки задачи о смешанной ро-

бастности.

Задачи отличаются взаимозависимостью детерминированных и случай-

ных групп параметров. Заменой критерия эти постановки элементарно обоб-

щаются на другие свойства системы, например на (робастную) апериодич-

ность и пр. Можно исследовать иные зависимости детерминированных и слу-

чайных параметров, в том числе их иерархические графы.

Предлагается алгоритм, разделяющий решение основной задачи о смешан-

ной робастности на два независимых этапа. На первом этапе метод анализа

в пространстве параметров описывает подмножество “хороших” случайных

параметров. На втором этапе используется другой метод, который аналити-

чески, численно или методом Монте-Карло оценивает вероятность попадания

случайного параметра в указанное множество.

Используемый на первом этапе метод робастного D-разбиения позволяет

решать и другие задачи о смешанной робастности.

Во-первых, помимо устойчивости можно проверять нечувствительность к

параметрическим возмущениям заданных показателей качества, например

запаса устойчивости по усилению и фазе, коэффициента демпфирования и

т.п. Эти возможности открываются благодаря тому, что подобные показатели

определяются расположением корней характеристического полинома или ха-

рактеризуются с помощью частотных методов. Одновременная робастность

по отношению к нескольким критериям качества исследуется аналогично.

Во-вторых, наряду с линейными системами непрерывного времени предло-

женный подход позволяет исследовать смешанную робастную устойчивость

иных типов линейных систем с постоянными параметрами. Так, устойчивость

дискретных систем определяется свойством Шура характеристического поли-

нома; устойчивость систем с запаздыванием определяется свойством Гурвица

характеристического квазиполинома; достаточное условие устойчивости си-

стем дробного порядка также описывается расположением корней “полинома”

с нецелыми степенями.

Кроме точных решений, в подразделе 3.3 предложен ряд процедур, позво-

ляющих решать задачи о смешанной робастности приближенно.

Помимо решенных, поставлен ряд открытых вопросов: как эффективно

решать задачи (5) и (6) о смешанной робастности с зависимыми детерми-

нированными и случайными параметрами? Насколько хорошо их удается ре-

шать приближенными методами? На примере из подраздела 5.3 показано, что

решение задач смешанной робастности упрощается, если известно подмноже-

ство Q×Δ объединенного набора параметров, на котором система устойчива.

Как описать это множество для иных свойств системы, аналогично тому, как

аппарат D-разбиения используется для устойчивости?

Автор выражает сердечную признательность Б.Т. Поляку за поддержку

при подготовке статьи, а также благодарит анонимного рецензента, замеча-

ния которого позволили существенно улучшить статью.

СПИСОК ЛИТЕРАТУРЫ

1. Поляк Б.Т., Щербаков П.С. Робастная устойчивость и управление. М.: Наука,

2002.

2. Дискуссия по проблеме робастности в системах управления // АиТ. 1992. № 1.

С. 165-176.

Discussion on Robustness Problems in Control Systems // Autom. Remote Control.

1992. V. 53. No. 1. P. 134-142.

3. Weinmann A. Uncertain Models and Robust Control. Springer, 1991.

4. Barmish B.R. New Tools for Robustness of Linear Systems. Macmillan Coll Div.,

1993.

5. Bhattacharyya S.P., Chapellat H., Keel L.H. Robust Control: The Parametric Ap-

proach. Prentice Hall, 1995.

Поляк Б.Т., Цыпкин Я.З. Робастная устойчивость линейных систем

ВИНИТИ. Итоги науки и техники. Сер. Технич. кибернетика. 1991. Т. 32.

С. 3-31.

Ершов А.А. Стабильные методы оценки параметров (обзор) // АиТ. 1978. № 8.

С. 66-100.

Ershov A.A. Stable Methods of Estimating Parameters (Survey) // Autom. Remote

Control. 1979. V. 39. No. 8. P. 1152-1181.

Браверман М.Э., Розоноэр Л.И. О грубости линейных динамических систем. I //

АиТ. 1991. № 11. С. 17-23.

Braverman M.E., Rozonoer L.I. Robustness of linear dynamic systems. I // Autom.

Remote Control. 1991. V. 52. No. 11. P. 1493-1498.

Харитонов В.Л. Об асимптотической устойчивости положения равновесия се-

мейства систем линейных дифференциальных уравнений // Дифф. уравнения.

1978. Т. 14. № 11. С. 2086-2088.

10.

Nemirovskii A. Several NP-hard Problems Arising in Robust Stability Analysis //

Math. Cont. Signals Syst. 1993. V. 6. No. 2. P. 99-105.

11.

Poljak S., Rohn J. Checking Robust Nonsingularity is NP-hard // Math. Cont. Sig-

nals Syst. 1993. V. 6. No. 1. P. 1-9.

12.

Tempo R., Calafiore G., Dabbene F. Randomized Algorithms for Analysis and Con-

trol of Uncertain Systems: with Applications. Springer, 2013.

13.

Garatti S., Campi M.C. Modulating Robustness in Control Design: Principles and

Algorithms // IEEE Cont. Syst. Mag. 2013. V. 33. No. 2. P. 36-51.

14.

Tempo R., Bai E.W., Dabbene F. Probabilistic Robustness Analysis: Explicit Bounds

for the Minimum Number of Samples // Proc. 35th IEEE Conf. Dec. and Cont. 1996.

V. 3. P. 3424-3428.

15.

Barmish B.R., Lagoa C.M. The Uniform Distribution: A Rigorous Justification for

Its Use in Robustness Analysis // Math. Cont. Signals Syst. 1997. V. 10. No. 3.

P. 203-222.

16.

Bai E.W., Tempo R., Fu M. Worst-case Properties of the Uniform Distribution and

Randomized Algorithms for Robustness Analysis // Proc. 1997 American Contr.

Conf. 1997. V. 1. P. 861-865.

17.

Calafiore G.C., Campi M.C. The Scenario Approach to Robust Control Design //

IEEE Trans. Autom. Cont. 2006. V. 51. No. 5. P. 742-753.

18.

Gryazina E., Polyak B. Random Sampling: Billiard Walk Algorithm // Europ. J.

Oper. Res. 2014. V. 238. No. 2. P. 497-504.

19.

Fan M.K.H., Tits A.L., Doyle J.C. Robustness in the Presence of Mixed Parametric

Uncertainty and Unmodeled Dynamics // IEEE Trans. Autom. Cont. 1991. V. 36.

No. 1. P. 25-38.

20.

Jayasuriya S. Frequency Domain Design for Robust Performance Under Parametric,

Unstructured, or Mixed Uncertainties // J. Dyn. Syst. Meas. Cont. 1993. V. 115.

No. 2B. P. 439-451.

21.

Reinelt W., Ljung L. Robust Control of Identified Models with Mixed Parametric and

Non-parametric Uncertainties / Proc. 2001 Europ. Cont. Conf. 2001. P. 3564-3569.

22.

Vitus M.P., Zhou Z., Tomlin C.J. Stochastic Control with Uncertain Parameters

via Chance Constrained Control // IEEE Trans. Autom. Cont. 2016. V. 61. No. 10.

P. 2892-2905.

23.

da Silva de Aguiar R.S., Apkarian P., Noll D. Structured Robust Control against

Mixed Uncertainty // IEEE Trans. Cont. Syst. Tech. 2018. V. 26. No. 5. P. 1771-

1781.

24.

Chapellat H., Dahleh M.A., Bhattacharyya S.P. Robust Stability under Structured

and Unstructured Perturbations // IEEE Trans. Autom. Cont. 1990. V. 35. No. 10.

P. 1100-1108.

25.

Fujisaki Y., Oishi Y., Tempo R. Mixed Deterministic/Randomized Methods for

Fixed Order Controller Design // IEEE Trans. Autom. Cont. 2008. V. 53. No. 9.

P. 2033-2047.

26.

Wu D., Gao W., Song C., Tangaramvong S. Probabilistic Interval Stability Assess-

ment for Structures with Mixed Uncertainty // Struct. Safety 2016. V. 58. P. 105-118.

27.

Keel L.H., Bhattacharyya S.P. Robust, Fragile, or Optimal? // IEEE Trans. Autom.

Cont. 1997. V. 42. No. 8. P. 1098-1105.

28.

Джури Э.И. Робастность дискретных систем // АиТ. 1990. № 5. С. 3-28.

Jury E.I. Robustness of Discrete Systems // Autom. Remote Control. 1990. V. 51.

No. 5. P. 571-592.

29.

Петров Н.П., Поляк Б.Т. Робастное D-разбиение // АиТ. 1991. № 11. С. 41-53.

Petrov N.P., Polyak B.T. Robust D-partition // Autom. Remote Control. 1991.

V. 52. No. 11. P. 1513-1523.

30.

Тремба А.А. Робастное D-разбиение при l_p-ограниченных параметрических

неопределенностях // АиТ. 2006. № 12. С. 21-35.

Tremba A.A. Robust D-decomposition under l_p-bounded Parametric Uncertainties //

Autom. Remote Control. 2006. V. 67. No. 12. P. 1878-1892.

31.

Siljak D.D. A Robust Control Design in the Parameter Space // Proc. 1992 IEEE

Int. Symp. Circuits Syst. 1992. V. 6. P. 2723-2727.

32.

Hwang C., Hwang L., Hwang J. Robust D-partition // J. Chinese Inst. Eng. 2010.

V. 33. No. 6. P. 811-821.

33.

Mihailescu-Stoica D., Schrödel F., Adamy J. All Stabilizing PID Controllers for

Interval Systems and Systems with Affine Parametric Uncertainties / 11th Asian

Cont. Conf. (ASCC). 2017. P. 576-581.

34.

Matsuda T., Mori T. Stability Feeler: A Tool for Parametric Robust Stability Anal-

ysis and Its Applications // IET Control Theory Applications 2009. V. 3. No. 12.

P. 1625-1633.

Статья представлена к публикации членом редколлегии П.С. Щербаковым.

Поступила в редакцию 08.06.2020

После доработки 01.09.2020

Принята к публикации 10.09.2020