Автоматика и телемеханика, № 3, 2021

Нелинейные системы

(Институт проблем машиноведения РАН, Санкт-Петербург),

П.А. ГУЩИН, канд. техн. наук (guschin.p@mail.ru)

(Губкинский университет, Москва)

ДИСКРЕТНОЕ ПО ПРОСТРАНСТВЕННОЙ ПЕРЕМЕННОЙ

УПРАВЛЕНИЕ СКАЛЯРНЫМИ ЛИНЕЙНЫМИ

РАСПРЕДЕЛЕННЫМИ ОБЪЕКТАМИ ПАРАБОЛИЧЕСКОГО

И ГИПЕРБОЛИЧЕСКОГО ТИПОВ¹

Предложен дискретный по пространственной переменной закон управ-

ления некоторым классом систем, которые описываются скалярными ли-

нейными дифференциальными уравнениями параболического и гипербо-

лического типов с неизвестными параметрами и возмущениями. Доступно

конечное множество дискретных измерений (по пространственной пере-

менной) состояния объекта. Закон управления зависит от функции, ко-

торая зависит от пространственной переменной и от конечного набора

измерений состояния объекта. Приведены примеры данной функции, ко-

торая позволяет реализовать управляющий сигнал лишь на отдельных

интервалах по пространственной переменной и обеспечивать меньшие за-

траты на управление по сравнению с некоторыми другими аналогами.

Доказана экспоненциальная устойчивость замкнутой системы и робаст-

ность по отношению к интервально неопределенным параметрам объек-

та и внешним ограниченным возмущениям. Численные примеры моде-

лирования подтвердили результаты расчетов и показали эффективность

предложенного алгоритма по сравнению с некоторыми существующими

аналогами.

Ключевые слова: статический закон управления, линейное дифференци-

альное уравнение в частных производных, функционал Ляпунова, линей-

ное матричное неравенство, экспоненциальная устойчивость.

DOI: 10.31857/S0005231021030041

1. Введение

В статье рассматривается некоторый класс линейных дифференциаль-

ных уравнений параболического и гиперболического типов с распределен-

ным управлением. Такие уравнения могут описывать, например, конвекци-

онно-дифузионные процессы, вращающуюся стойку компрессора с приводом

впрыска воздуха, распространение тепла в стержне, колебание струны и т.д.

¹ Результаты раздела 3 получены при поддержке Российского научного фонда (проект

№ 18-79-10104) в ИПМаш РАН. Результаты разделов 4 и 5 получены при поддержке Рос-

сийского фонда фундаментальных исследований (проект № 19-08-00246) в ИПМаш РАН.

Результаты разделов 6 и 7 получены при поддержке гранта Президента РФ (проект № МД-

1054.2020.8) в ИПМаш РАН.

Реализуемое конечномерное управление с использованием преобразования

Фурье и метода Галеркина рассмотрено в публикациях [1-3]. Для линейных

параболических систем в [4] предложен метод управления, основанный на

движущихся датчиках и актуаторах вдоль пространственной координаты.

В [5, 6] для подобных систем предложено адаптивное управление с использо-

ванием процедуры бэкстеппинга, которое достаточно трудоемко в расчете и

реализации.

В отличие от [1-6] в настоящей статье будет предложен способ формиро-

вания закона управления с использованием дискретизации сигнала измере-

ния по пространственной переменной. Для конечномерных систем подобный

подход изучался в течение нескольких последних десятилетий в качестве дис-

кретизации по уровню измеряемого сигнала [7-10] и др. В отличие от непре-

рывного управления, такое дискретное управление не учитывает поведение

объекта между выборками, зато в ряде случаев оно позволяет решить ряд

технических задач: управление через цифровые каналы связи, управление

с ограничением на информационные каналы связи и т.п. В данной статье

дискретизация по пространственной переменной позволит получить реали-

зуемый сигнал управления.

Наблюдаемость систем с дискретными пространственными измерения-

ми изучена в [11]. Дискретное по пространственной переменной управле-

ние бесконечномерными системами рассмотрено, например, в [12-15]. Мето-

ды [12, 13] неприменимы к неизвестным параметрам системы и не содержат

количественного анализа устойчивости замкнутой системы и скорости схо-

димости решений. В отличие от [12, 13] в [14, 15] предложен метод управ-

ления системами параболического типа с неизвестными параметрами с ис-

пользованием линейных матричных неравенств (ЛМН) для анализа экспо-

ненциальной устойчивости. Однако решения [12-15] не учитывают наличие

возмущений.

В настоящей статье, как и в [12-15], будет предложен метод управле-

ния с дискретизацией по пространственной переменной. Однако, в отличие

от [12-15], предложенный закон управления позволит формировать различ-

ные конфигурации регулируемого сигнала по пространственной переменной.

Например, по сравнению с [14, 15] предложенный закон управления не тре-

бует своей реализации по всей пространственной переменной, а стабилиза-

ция объекта может осуществляться с меньшими затратами на регулируе-

мый сигнал. В отличие от [12-15] будет показана экспоненциальная устой-

чивость замкнутой системы для систем параболического и гиперболическо-

го типов в условиях возмущений с использованием ЛМН. Будут приведены

численные примеры моделирования и сравнительный анализ эффективности

предложенного алгоритма с решением [14, 15] для систем параболического

типа.

В статье используются следующие обозначения: Rⁿ евклидово простран-

ство размерности n с нормой | · |; R^n×m множество всех n × m веществен-

ных матриц; P > 0 и P ∈ R^n×n означает, что P

симметрическая поло-

жительно определенная матрица; симметричные элементы симметрической

матрицы будут обозначаться ∗. Непрерывно дифференцируемые функции по

всем аргументам будут обозначаться как функции класса C¹. Нижние индек-

∂²z

сы обозначают частные производные z_ξ =^∂z

и z_ξξ =

. L₂(0,l)

гильбер-

∂ξ

∂ξ²

тово пространство с квадратично интегрируемыми функциями z(ξ), ξ ∈ [0, l]

∫l

с соответствующей нормой ∥z∥2L2 =

z²(s)ds. H₁(0,l)

пространство Со-

болева абсолютно непрерывных скалярных функций z : [0, l] → R с нормой

∫l

∥z∥2H1 =

z^2s(s)ds и z_ξ ∈ L₂(0,l). H₂(0,l)

пространство Соболева скаляр-

ных функций z : [0, l] ∈ R с абсолютно непрерывными производными z_ξ, нор-

∫l

мой ∥z∥2H2 =

z^2ss(s)ds и z_ξξ ∈ L₂(0,l).

2. Постановка задачи

2.1. Модели объектов

1. Пусть первый класс исследуемых объектов описывается скалярным ли-

нейным дифференциальным уравнением параболического типа

z_t(x,t) = a₁z_xx(x,t) + a₂z_x(x,t) + φz(x,t) + u(x,t) + f(x,t),

(1)

x ∈ [0, l], l > 0,

с граничными условиями Дирихле

(2)

z(0, t) = z(l, t) = 0

или смешанными граничными условиями

(3)

z_x

(0, t) = γz(0, t), z(l, t) = 0, γ ≥ 0.

Здесь t ≥ 0, z : [0, l] × [0, ∞) → R состояние объекта, u(x, t) сигнал управ-

ления, f(x, t)

возмущение класса C¹. Коэффициенты a₁, a₂, φ и функ-

ция f(x, t) неизвестны, но известны границы интервалов, которым они при-

надлежат:

0 < a₁ ≤ a₁ < ∞, a₂ ≤ a₂ ≤ a₂, φ ≤ φ ≤ φ,

|f(x, t)|

Величина γ в (3) может быть неизвестной.

Замечание 1. При u(x,t) = 0 уравнение

(1) описывает конвекци-

онно-дифузионные процессы, а при a₁ = 1, a₂ = 0 и φ = 0 процессы диф-

фузии. В [2] уравнением (1) описывается вращающаяся стойка компрессора

с приводом впрыска воздуха u(x, t), где z(x, t) осевой поток через компрес-

сор. При u(x, t) = 0 и a₂ = 0 краевая задача (1), (2) описывает распростране-

ние тепла в однородном одномерном стержне с фиксированной температурой

на концах, где a₁ и φ коэффициенты теплопроводности и теплообмена с

окружающей средой соответственно, z(x, t) - значение температуры в момент

времени t в точке x.

2. Пусть второй класс исследуемых объектов описывается скалярным ли-

нейным дифференциальным уравнением гиперболического типа в виде

z_tt(x,t) = a₁z_xx(x,t) + a₂z_x(x,t) + φz(x,t) - bz_t(x,t) + u(x,t) + f(x,t),

(4)

x ∈ [0, l],

с граничными условиями Дирихле (2) или смешанными граничными условия-

ми (3). В (4) b > b > b > 0, где вершины b и b известны. Остальные константы

и функции в (4) принимают те же значения, что и в (1).

Замечание 2. При u(x,t) = 0 и a₂ = 0 краевая задача (4), (2) описывает

колебания однородной струны с фиксированными концами и рассеиванием

энергии, где a₁, b и φ коэффициенты упругости, диссипации и жесткости

соответственно, z(x, t) и z_t(x, t) прогиб и скорость струны соответственно

в момент времени t в точке x.

2.2. Цель управления

Для решения задачи разобьем отрезок [0, l] на N подинтервалов, необяза-

тельно равной длины, и обозначим:

(5)

0=x₀ <x₁ <...<x_N =l, Δ≥x_j+1 -x_j

j = 0,...,N - 1.

Здесь Δ известная константа. Предположим, что N сенсоров расположе-

ны внутри данных подинтервалов, т.е. доступны измерению только сигна-

лы z(x_j , t), где x_j ∈ (x_j , x_j+1), j = 0, . . . , N - 1.

Цель управления состоит в разработке дискретного по пространствен-

ной переменной x закона управления, который обеспечит экспоненциальную

устойчивость замкнутой системы для (1) и (4).

3. Синтез закона управления

Зададим закон управления в виде

u(x, t) = -KF^j(z(x_j , t), x, t),

(6)

x ∈ [x_j,x_j+1),

x_j ∈ (x_j,x_j+1), j = 0,... ,N - 1,

где K > 0, функция F^j (z(x_j , t), x, t) удовлетворяет следующим условиям:

(а) F^j (z(x_j , t), x, t) класса C¹ для любых t ≥ 0 и x ∈ [0, l];

(б) производная

Fjx (z(xj , t), x, t) ограничена для любых t ≥ 0 и x ∈ [0, l];

(в) F^j (z(x_j , t), x_j , t) = z(x_j , t), x_j ∈ (x_j , x_j+1), j = 0, . . . , N - 1.

Условие (а) требуется для решения краевой задачи (см. раздел 6). Тре-

бования (б) и (в) необходимы для доказательства устойчивости замкнутой

системы и ограниченности всех сигналов в ней. Приведем примеры функции

F^j(z(x_j,t),x,t).

Пример 1. Пусть

F^j(z(x_j,t),x,t) = ϕ^j(z(x_j,t),x,t)z(x_j,t),

где ϕ^j (z(x_j , t), x, t) класса C¹, ϕ^x(z(x_j , t), x, t)z(x_j , t) ограничена для любых x

и t, а также ϕ^j(z(x_j,t), x_j,t) = 1. В частности, если ϕ^j(z(x_j,t),x,t) = 1 для

любых x и t, то получим закон управления из [14, 15]. Далее рассмотрим

примеры других функций ϕ^j (z(x_j , t), x, t).

j ^j(z(-_j, t), x, t)

a₁

a₂

x_j

x_{j + 1}

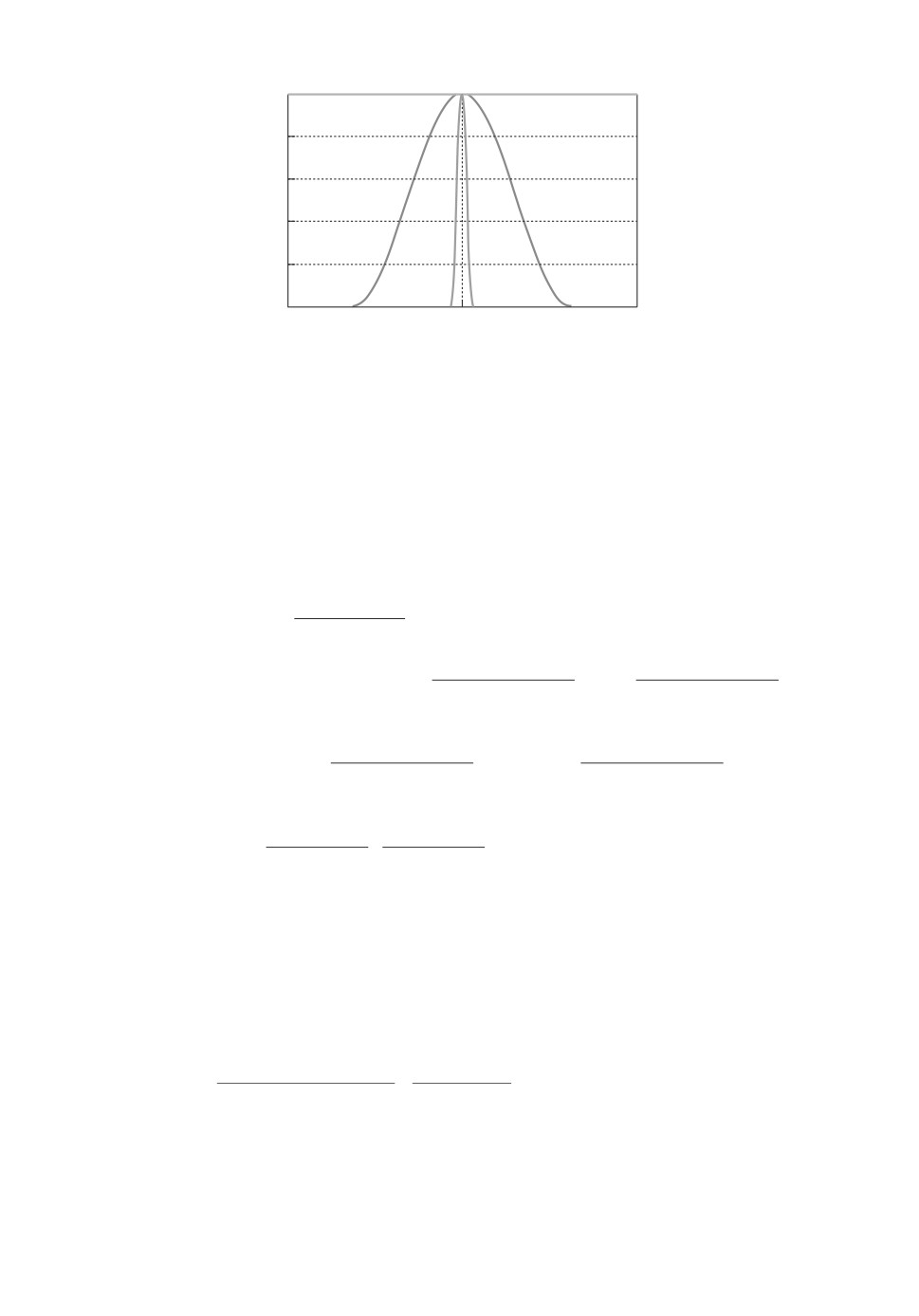
Рис. 1. График функции ϕ^j (z(x_j , t), x, t) из примера 2 (при z(x_j , t) =

= const > 0) на интервале x ∈ [x_j, x_j+1) при различных значениях

α > 0 ((α = α₁) < (α = α₂)).

Пример 2. В

[14, 15] u(x, t) = 0 на всем интервале

[x_j , x_j+1), если

z(x_j,t) = 0. Приведем пример, когда u(x,t) = 0 лишь на части интервала

[x_j, x_j+1) при z(x_j , t) = 0. Пусть в примере 1 функция ϕ^j задана в виде

(7)

ϕj (z(x_j

,t),x,t) =



(

)



α(x - x_j)

0,5 + 0,5 cos



1 + z²(x_i,t)



[

]



π(1 + z²(x_j , t))

x∈

x_j -

;x_j +

=



[

) (

)



(1 + z²(x_j , t))

π(1 + z²(x_j , t))

0, x ∈ x_j ; x_j -π

∪

x_j +

;x_j+1

Здесь α > 0 д{таточно большое числ}, которое может быть выбрано из

x_j-x_j

x_j+1-x_j

условия α > max

. Очевидно, что ϕ^j (z(x_j , t), x_j , t) =

π(1+z²(x_j ,t))

= 1, ϕ^j (z(x_j , t), x, t) класса C¹ и ϕ^x(z(x_j , t), x, t)z(x_j , t) ограничена для любых

t ≥ 0, x ∈ [0,l] и z(x_j,t) ∈ R. Графики функции (7) приведены на рис. 1.

Пример 3. В (7) переход между значениями ϕ^j зависит от z(x_j,t). Далее

приведем пример, исключающий данную зависимость. Зададим в примере 2

функцию ϕ^j в виде

ϕj (z(x_j , t), x, t) =

{

(8)

(1+z2(xj ,t))(β2-(x-xj )2)

βj(1+z2(xj,t)) ,

x∈(x_j -β_j;x_j +β_j),

= e

0, x ∈ [x_j; x_j - β_j ] ∪ [x_j + β_j ; x_j+1) .

Здесь α > 0, β_j ≤ min{x_j+1 - x_j, x_j - x_j }. В отличие от (7) в (8) переход меж-

ду значениями функции не зависит от z(x_j , t), а зависит только от β_j . Оче-

видно, что ϕ^j (z(x_j , t), x_j , t) = 1, функция ϕ^j (z(x_j , t), x, t) класса C¹, а также

j ^j(z(-_j, t), x, t)

a₁

a₂

x_j

x_i

x_{j + 1}

Рис. 2. График функции ϕ^j (z(x_j , t), x, t) из примера 3 (при z(x_j , t) =

= const > 0) на интервале x ∈ [x_j, x_j+1) при различных значениях

α > 0 ((α = α₁) < (α = α₂)).

ϕx(z(x_j , t), x, t)z(x_j , t) ограничена для любых t ≥ 0, x ∈ [0, l] и z(x_j , t) ∈ R.

Графики функции (8) приведены на рис. 2.

Замечание 3. В [14] использовался закон управления u(x,t)=-Kz(x_j,t),

x_j = 0,5(x_j + x_j+1), x ∈ [x_j,x_j+1), j = 0,... ,N - 1, что является частным слу-

чаем (6) (см. пример 1). Если функцию F^j (z(x_j , t), x, t) выбрать как в приме-

рах 2 или 3, то из рис. 1 и 2 видно, что площадь под кривой ϕ^j (z(x_j , t), x, t) = 1

для [14] может быть существенно больше, чем площадь под остальными кри-

выми. Таким образом, предложенный закон управления может стабилизиро-

вать объект (1) при меньших затратах на управление, что далее будет про-

демонстрировано на численных примерах.

Пример 4. Приведем пример управления, близкого к граничному. Пусть

N = 2. Тогда отрезок [0,l] имеет следующее разбиение: 0 = x₀ < x₁ = l. Если

выбрать единственную на отрезке [0, l] функцию (7) или (8) с достаточно

большим значением α и точкой x₀, достаточно близкой к левому или правому

концу отрезка [0, l], то получим управление, близкое к граничному. Если взять

N = 3, то можно две точки x₀ и x₁ выбрать достаточно близко к левому и

правому концам соответственно.

4. Основной результат для системы параболического типа (1)

Подставим (6) в (1) и запишем уравнение замкнутой системы:

z_t(x,t) = a₁z_xx(x,t) + a₂z_x(x,t) + f(x,t) -

(9)

- (K - φ)z(x, t) + K[z(x, t) - F^j (z(x_j , t), x, t)],

x ∈ [x_j,x_j+1), j = 0,... ,N - 1.

Теорема 1. Рассмотрим замкнутую систему (9) при граничных усло-

виях (2) или (3). Пусть для заданных коэффициентовR > 0, Δ > 0, δ > 0,

K > 0 будут разрешимы следующие два линейных матричных неравенства:

(10)

Ψ (a₂ = a₂) ≤ 0, Ψ (a₂ = a₂

) ≤ 0,

где





-2K + 2φ + 2δ + KR

a₂









∗

-2a₁ +4Δ2

KR^-1

-4Δ2KR-1



π²



(11)

Ψ=

.



∗

-β₁







∗

-β₂ +4Δ2

KR^-1

π²

Тогда будет выполнено следующее неравенство

(12)

∥z(·, t)∥^2L

≤ e^-2δt∥z(·,0)∥^2L

2δ

где

∫

∑

γ = β1 sup

f²(x,t)dx + β₂ sup

(F^jx (x, t))²dx.

t≥0

j=0 x_j

Перед доказательством теоремы 1 рассмотрим две вспомогательные лем-

мы.

Лемма 1 (расширенное неравенство Виртингера). Пусть z ∈ H₁(0,l)

скалярная функция,

0=χ₀ <χ₁ <...χ_n-1 <χ_n =l и Δ≥χ_i -χ_i+1, i=

= 0, . . . , n - 1. Если z(χ_i) = 0, i = 1, . . . , n - 1, тогда

∫

4Δ²

(13)

z²(ξ)dξ ≤

z^2ξ

(ξ)dξ.

π²

Доказательство. Перепишем левую часть неравенства (13) в виде

χ₁

∫

∑

z²(ξ)dξ = z²(ξ)dξ +

z²(ξ)dξ +

z²(ξ)dξ.

i=1 χ_i

χ_n-1

Применяя неравенство Виртингера [16] к каждому интегральному выраже-

нию, получим

χ₁

∫

∑

z²(ξ)dξ +

z²(ξ)dξ ≤

χ_n-1

i=1 χ_i





χ₁

∫

∑

4Δ

4Δ²



≤

z^2ξ(ξ)dξ +

z^2ξ(ξ)dξ ≤

z^2ξ(ξ)dξ.

π²

χ_n-1

i=1 χ_i

Лемма 1 доказана.

Лемма 2. Пусть функция V : [t₀,∞) → [0,∞) дифференцируема на

[t₀, ∞) и задано дифференциальное неравенство

(14)

(t) ≤ -δV (t) + f(t),

где δ > 0 и sup |f(t)| = β. Тогда справедливо следующее неравенство

t≥t₀

(15)

V (t) ≤ e-δ(t-t0 )V (t₀) +

t≥t₀.

Доказательство. Обозначим

y(t) = e-δ(t-t0 )V (t₀) +

t≥t₀.

Легко проверить, что функция y(t) является решением дифференциального

уравнения

(16)

y(t) = -δy(t) + β, t ≥ t₀.

Воспользуемся принципом сравнения и покажем, что V (t) ≤ y(t) для любых

t ≥ t₀. Пусть ε₁ > ε₂ > ... > ε_n > ...

последовательность положительных

чисел таких, что lim_n→∞ ε_n = 0⁺. Тогда функция

ε_n

(17)

y_n(t) = -δy(t) +

является решением дифференциального уравнения

(18)

y(t) = -δy(t) + β + ε_n.

Предположим, что существует t^∗ > t₀, такое что

(19)

t^∗ = inf{t > t₀ : V (t) ≥ y_n

(t)}.

Тогда V (t^∗) ≥ y_n(t^∗) и V (t) < y_n(t) при t₀ ≤ t ≤ t^∗. Из (14) и (18) имеем

V (t^∗) < y_n(t^∗). С другой стороны, из V (t) < y_n(t) при t < t^∗ и V (t^∗) = y_n(t^∗)

следует, что

V (t^∗) ≥ y_n(t^∗). Пришли к противоречию. Значит, V (t) < y_n(t)

для всех t ≥ t₀ и n = 1, 2,

Следовательно, V (t) ≤ lim_n→∞ y_n(t) = y(t) при

всех t ≥ t₀. Доказательство леммы 2 закончено.

Доказательство теоремы 1. Для анализа устойчивости замкнутой

системы (9) рассмотрим следующий функционал Ляпунова

∫l

(20)

V (t) = z²

(x, t)dx.

Дифференцируя V (t) по времени вдоль траекторий (9), составим следующее

выражение

∫l

[

V (t) + 2δV (t) = 2

a₁z(x,t)z_xx(x,t) + a₂z(x,t)z_x(x,t) -

]

(21)

− (K - φ)z²(x, t) + z(x, t)f(x, t) dx +

∫

∑

[

]

+ 2K

z(x, t) z(x, t) - F^j (x, t)

+ 2δ z²(x, t)dx,

j=0 x_j

где ради краткости в доказательстве обозначим F^j (z(x_j , t), x, t) = F^j (x, t).

С учетом граничных условий (2) или (3) проинтегрируем по частям первое

слагаемое в (21):

∫l

2a₁

z(x, t)z_xx(x, t)dx =

(22)

∫

_l



= 2a₁z(x, t)z_x(x, t)

- 2a₁

z²

(x, t)dx ≤ -2a₁ z^2x(x, t)dx.

Используя неравенство Юнга для предпоследнего слагаемого в (21), полу-

чим

∫

[

]

∑

z(x, t) z(x, t) - F^j (x, t) dx ≤

j=0 x_j

(23)

∫l

∫

∑

[

]₂

≤ K R z²(x,t)dx + K R-1

z(x, t) - F^j (x, t)

dx.

j=0 x_j

Согласно условию (в) z(x, t) = F^j(x, t) в точке x = x_j. Тогда применяя лем-

му 1 к (23), получим

∫

[

]₂

∑

KR^-1

z(x, t) - F^j(x, t)

dx ≤

j=0 x_j

(24)

∫

∑

[

]

4Δ

≤

KR^-1

z^2x(x,t) - 2z_x(x,t)F^jx(x,t) + (F^jx(x, t))2

dx.

π²

j=0 x_j

Обозначим η_j = col{z(x, t), z_x(x, t), f(x, t),

Fjx (x, t)}. Применяя (22)-(24)

к (21), получим

∫^l

∫

∑

V (t) + 2δV (t) - β₁ f²(x, t)dx - β2

F^jx(x,t)dx ≤

j=0 x_j

(25)

∫

∑

≤

η^TjΨη_jdx,

j=0 x_j

где Ψ задана в (11). Матрица (11) аффинна по отношению к параметру a₂.

Значит, согласно [17] если выполнены ЛМН (10) в вершинах a₂ = {a₂, a₂}, то

ЛМН Ψ ≤ 0 будет выполнено для любых a₂ ∈ [a₂, a₂]. Следовательно, будет

выполнено неравенство

∫l

∫

∑

(26)

V (t) + 2δV (t) - β₁ f²(x, t)dx - β2

F^jx

(x, t)dx ≤ 0.

j=0 x_j

Воспользовавшись леммой 2, решение дифференциального неравенства (26)

определим в виде

(27)

V (t) ≤ V (0)e^-2δt +

2δ

Тогда из (27) следует (12). Теорема 1 доказана.

5. Основной результат для системы гиперболического типа (4)

Подставим (6) в (4) и запишем уравнение замкнутой системы:

z_tt(x,t) = a₁z_xx(x,t) + a₂z_x(x,t) - bz_t(x,t) + f(x,t) -

[

]

(28)

- (K - φ)z(x, t) + K z(x, t) - F^j (z(x_j , t), x, t) ,

x ∈ [x_j,x_j+1), j = 0,... ,N - 1.

Теорема 2. Рассмотрим замкнутую систему (28) при граничных усло-

виях (2) или (3). Пусть для заданных коэффициентов p ∈ (-0,5; 0,5),R > 0,

Δ > 0, δ > 0, K > 0 будут разрешимы следующие линейные матричные нера-

венства в соответствующих вершинах:

(

)

(29)

Ψ φ = {φ,φ},a₂ = {a₂,a₂},b = {b,b}

≤ 0,

где





Ψ₁₁

0,5pa₂

Ψ₁₃

0,5p





4Δ²







∗

Ψ₂₂

a₂

KR^-1





π²





∗

Ψ₃₃



Ψ=









∗

-β₁









4Δ

∗

-β₂ +

KR^-1

(30)

π²

Ψ₁₁ = -0,5p(K - φ) + 0,25KRp² + 2δ,

Ψ₁₃ = 1 - 0,5pb - K + φ + KRp,

4Δ

Ψ₂₂ = -pa₁ +

KR^-1,

π²

Ψ₃₃ = 0,5p - 2b + 0,5KR.

Тогда будет выполнено неравенство (12), параметры которого расчиты-

ваются с учетом (29).

Доказательство. Для анализа устойчивости замкнутой системы (28)

рассмотрим функционал Ляпунова в виде

∫^l

[

]

(31)

V (t) =

a₁z^2x(x,t) + z²(x,t) + pz(x,t)z_t(x,t) + z^2t(x,t)

dx.

При p ∈ (-0,5; 0,5) будет справедливо неравенство z² + pzz_t + z^2t ≥ 0. Значит,

V (t) ≥ 0. Дифференцируя V (t) по времени вдоль траекторий (28), составим

выражение

∫l

[

V (t) + 2δV (t) = 2

a₁z_x(x,t)z_xt(x,t) + z(x,t)z_t(x,t) + 0,5pz^2t(x,t) +

[

][

+ 0,5pz(x, t) + z_t(x, t) a₁z_xx(x, t) + a₂z_x(x, t) -

]

- bz_t(x, t) + f(x, t) - (K - φ)z(x, t) dx +

(32)

∫

∑

[

][

]

+ 2K

0,5pz(x, t) + z_t(x, t) z(x, t) - F^j (x, t)

j=0 x_j

∫l

+ 2δ z²(x, t)dx,

где ради краткости в доказательстве обозначим F^j (z(x_j , t), x, t) = F^j (x, t).

С учетом граничных условий (2) или (3), проинтегрируем по частям первое

слагаемое в (32):

∫l

2a₁

z_x(x,t)z_xt(x,t)dx =

∫

_l



(33)

= 2a₁z_x(x, t)z_t(x, t)

- 2a₁

z_t(x,t)z_xx(x,t)dx =

∫l

= -2a₁

z_t(x,t)z_xx(x,t)dx.

Используя неравенство Юнга для предпоследнего слагаемого в (32), полу-

чим

∫

∑

[

][

]

0,5pz(x, t) + z_t(x, t) z(x, t) - F^j (x, t) dx ≤

j=0 x_j

∫^l

[

]₂

(34)

≤KR

0,5pz(x, t) + z_t(x, t)

dx +

∫

∑

[

]₂

+KR-1

z(x, t) - F^j (x, t)

dx.

j=0 x_j

Так как z(x, t) = F^j (x, t) в точке x = x_j (см. условие (в)), то, применяя

лемму 1 к (34), получим (24). Обозначим

ηj = col{z(x, t), zx(x, t), zt(x, t), f(x, t),

(x, t)}.

Применяя (22), (33), (34) и (24) к (32), запишем результат в виде

∫l

∫

∑

V (t) + 2δV (t) - β₁ f²(x, t)dx - β2

F^jx(x,t)dx ≤

j=0 x_j

(35)

∫

∑

≤

ηTj Ψη_jdx.

j=0 x_j

ЗдесьΨ задано в (30). МатрицаΨ аффинна по отношению к параметрам φ,

a₂ и b. Согласно [17] если выполнены ЛМН (29) в вершинах φ = {φ,φ}, a₂ =

= {a₂, a₂} и b = {b, b}, то ЛМН

Ψ≤ 0 выполнено для любых φ ∈ [φ,φ],

a₂ ∈ [a₂,a₂] и b ∈ [b,b]. Следовательно, будет выполнено неравенство (35).

Воспользовавшись леммой 2, решение дифференциального неравенства (35)

можно записать в виде (27). Тогда из (27) следует неравенство (12), парамет-

ры которого расчитываются с учетом (29). Теорема 2 доказана.

6. Решение краевой задачи

Покажем, что существуют решения уравнений (9) и (28), удовлетворяю-

щие граничным условиям (2) или (3).

6.1. Замкнутая система (9)

Сначала рассмотрим уравнение (9) с граничными условиями (2). Крае-

вую задачу (9), (2) можно сформулировать как абстрактную неоднородную

задачу Коши в гильбертовом пространстве H = L₂(0, l) в виде

(36)

Ż(t) = Az(t) + F (t, z(t)), z₀

= z(0) ∈ D(A).

Здесь оператор

∂²

∂

A=a₁

+a₂

+φ

∂x²

∂x

имеет область определения

D(A) = {z ∈ H₂(0, l) : z(0) = z(l) = 0},

F (t, z(t)) = f(t) + u(t),

функция u(t) задана в (6). Согласно теореме 1, [18] и [19] инфинитезималь-

ный оператор A генерирует строго непрерывную экспоненциально устойчи-

вую полугруппу (C₀-полугруппу) T (t). Тогда краевая задача (36) может быть

сформулирована как краевая задача на полубесконечном интервале [0, ∞) и

ее решения могут быть найдены как решения интегрального уравнения

∫t

(37)

z(t) = T (t)z(0) +

T (t - s)F (s, z(s))ds.

Так как функция F (t, z(t)) класса C¹, то согласно теореме 3.1.3 из [19] су-

ществует единственное решение (36), которое удовлетворяет интегральному

уравнению (37). Краевая задача при смешанных граничных условиях (3) ре-

шается аналогично.

6.2. Замкнутая система (28)

Теперь рассмотрим уравнение (28) с граничными условиями (2) или (3).

Запишем сначала краевую задачу (28), (2) как абстрактную неоднородную

задачу Коши в гильбертовом пространстве H = L₂(0, l) в виде

(38)

ξ(t) =

Aξ(t)

F (t, ξ(t)), ξ₀ = ξ(0) ∈

где ξ = col{z, z_t}, оператор







A=

∂²

-b

a₁ ∂x2^+φ

имеет область определения

A) = {ξ ∈ H₂(0,l) : ξ(0) = ξ(l) = 0},

F (t, ξ(t)) = [0 1]^T [f(t) + u(t)],

функция u(t) задана в (6). Согласно теореме 1, [18] и [19] инфинитезимальный

оператор A генерирует строго непрерывную экспоненциально устойчивую

полугруппу (C₀-полугруппу) T (t). Следовательно, дальнейшие рассуждения

для уравнения (38) аналогичны рассуждениям для (36) в подразделе 6.1.

7. Численное исследование предложенной схемы управления

7.1. Моделирование системы управления

Пусть l = 1. Для моделирования систем (1) и (4) разделим отрезок [0, 1]

на 160 подынтервалов одинаковой длины. Тогда шаг дискретизации по про-

странственной переменной D = 1/160. Производные первого и второго по-

рядков по пространственной переменной от функции z(x, t) вычисляются в

точках 0 = x₀ < x₁ < . . . x_l < . . . < x₁₆₀ с помощью формул

z(x_k+1, t) - z(x_k, t)

z_x(x_k,t) =

z(x_k+1, t) - 2z(x_k, t) + z(x_k-1, t)

z_xx(x_k,t) =

D²

Для формирования закона управления (6) разделим отрезок [0, 1] пооче-

редно на N = 2 и на N = 10 равных подынтервалов (см. (5)).

Рассмотрим системы (1) и (4) при граничных условиях Дирихле (2) и

a₁ ≥ 0,5, a₂ ∈ [-5,5], φ ∈ [-5,5], b = [-5,-1], |f(x,t)| ≤ 20 для любых x и t.

Матричные неравенства (10) и (29) разрешимы при K ≥ 100.

7.2. Результаты моделирования для системы (1)

В (1) выберем a₁ = 1, a₂ = -1, φ = 5, f(x, t) = 0,2[sin(30kt) + sin(2kt)],

k = 0,...,160 и z(x,0) = sin(πx_k). Для моделирования алгоритмов управ-

ления рассмотрим два разбиения: N = 2 и N = 10 (см. (5)). Пусть x_j =

= 0,5(x_j + x_j+1). В законе управления (6) выберем функцию F^j (z(x_j , t), x, t)

из примера 3, где α = 10³, а также β_j = 1/8 при N = 2 и β_j = 1/80 при N =

= 10.

На рис. 3-5 представлены решения (1) и графики u(x, t) для:

1) закона управления u(x, t) = -Kz(x_j, t) из [14, 15] при K = 100;

2) предложенного закона управления (6) при K = 100;

3) предложенного закона управления (6) при K = 500.

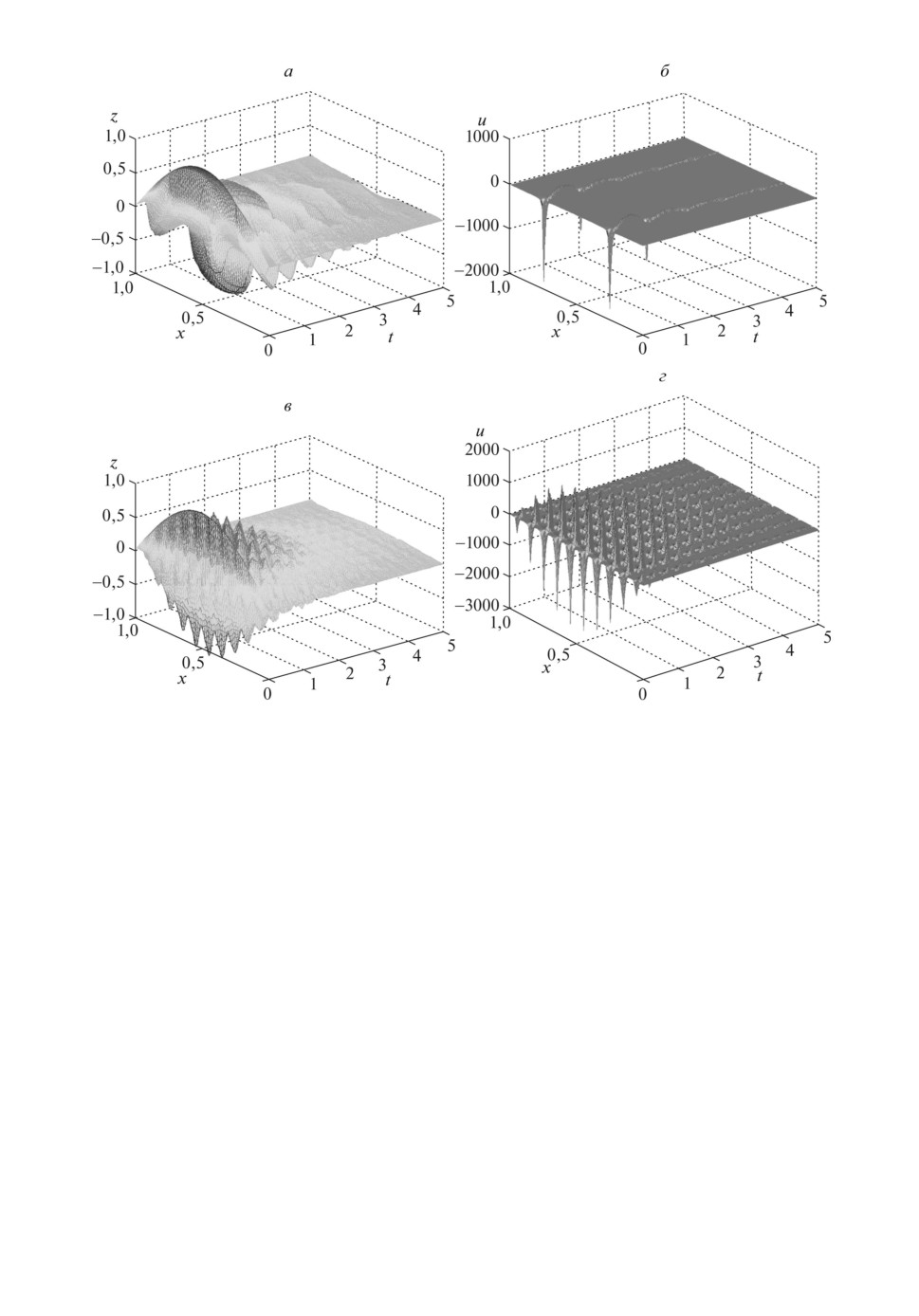
Из рис. 3 и 4 видно, что качество управления по z(x, t) для предложенного

закона управления незначительно уступает качеству управления для алго-

ритма из [14, 15]. При этом предложенный алгоритм обеспечивает экспонен-

циальную устойчивость по z(x, t) в условиях возмущений. Если же увеличить

коэффициент K в предложенном законе управлении в 5 раз, то амплитуда

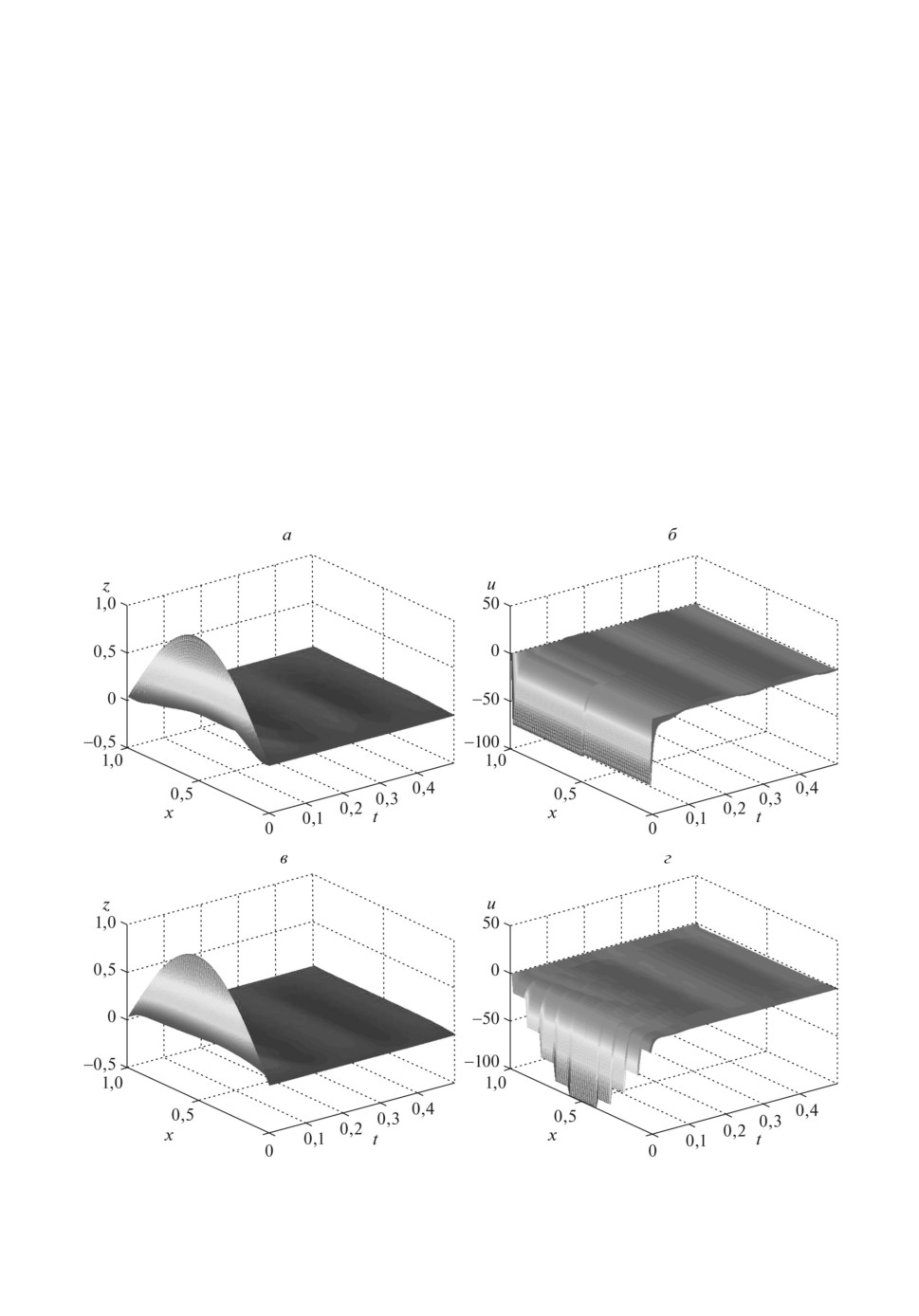
Рис. 3. Пространственно-временные графики по z(x, t) и u(x, t) для [14, 15]

при N = 2 (а, б ) и N = 10 (в, г) при K = 100.

140

120

100

0,1

0,2

0,3

0,4

0,5

0,1

0,2

0,3

0,4

0,5

Рис. 6. Разница затрат на управление при N

= 2

(а) и N = 10 (б ) меж-

ду использованием закона управления из [14,

15] и предложенным законом

управления соответственно при K = 100.

0,1

0,2

0,3

0,4

0,5

Рис. 7. Разница затрат на управление при N = 10 между использованием за-

кона управления из [14, 15] при K = 100 и предложенным законом управления

при K = 500.

управления также возрастет примерно в 5 раз, но при этом скорость экспонен-

циальной сходимости и качество подавления возмущения в установившемся

режиме будет выше, чем у алгоритма из [14, 15] при K = 100.

Теперь проанализируем затраты на управление. На рис. 6 и 7 представлена

интегральная разность вида

∫

∑

I =

(|u_F&B(x_j , s)| - |u_proposed(x_j, s)|) ds,

j=0 0

где u_F&B(x_j , t) - закон управления [14], u_proposed(x_j , t) - предложенный закон

управления. Из рис. 6 и 7 видно, что затраты на управление у предложенного

алгоритма меньше, чем у [14]. При этом предложенный закон управления

принимает ненулевые значения лишь на части пространственной переменной,

в то время как управление [14, 15] требует реализации на протяжении всей

пространственной переменной, см. рис. 3-5.

Отметим, что результаты моделирования для функции F^j(z(x_j , t), x, t) из

примера 2 с α = 100 сопоставимы с результатами, полученными для функции

F^j(z(x_j,t),x,t) из примера 3, поэтому они не приводятся.

7.3. Результаты моделирования для системы (4)

При моделировании (4) выберем a₁ = 1, a₂ = -1, b = -1, φ = 5 и f(x, t) =

= 0,2[sin(30kt) + sin(2kt)], k = 0, . . . , 160, z(x, 0) = sin(πx_k) и z_t(x, 0) = 0. В за-

коне управления (6) зададим параметры как в подразделе 7.2. На рис. 8

и 9 представлены решения (4) и графики u(x,t) для предложенного зако-

на управления (6) при K = 100 и K = 500, а также при N = 2 и N = 10. Из

рис. 8 и 9 видно, что предложенный алгоритм обеспечивает экспоненциаль-

ную устойчивость по z(x, t) в условиях возмущений. Результаты моделиро-

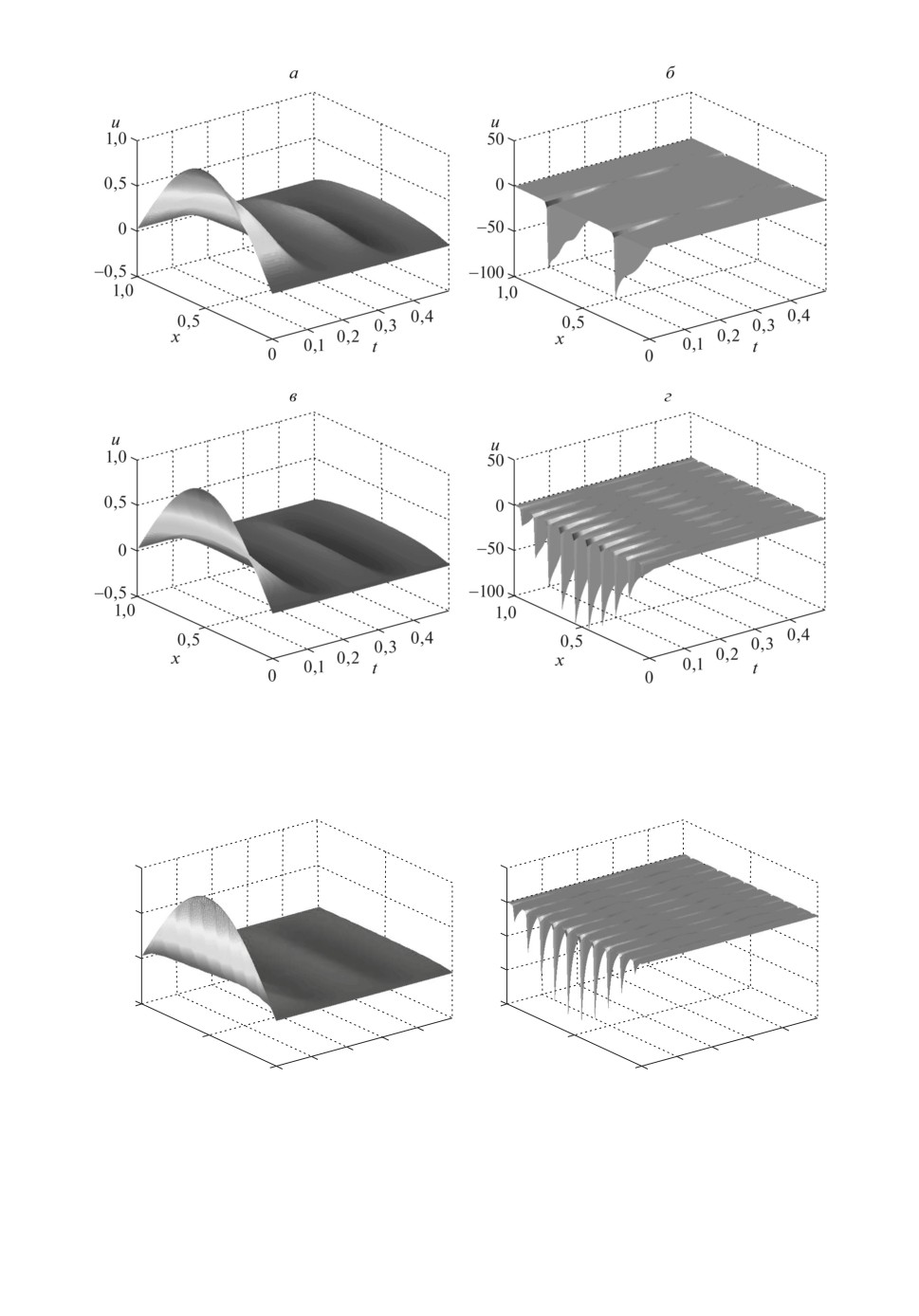
Рис. 8. Пространственно-временные графики по z(x, t) и u(x, t) для предло-

женного алгоритма при N = 2 (а, б ), N = 10 (в, г) и K = 100.

Рис. 9. Пространственно-временные графики по z(x, t) и u(x, t) для предло-

женного алгоритма при N = 2 (а, б ), N = 10 (в, г) и K = 500.

вания для функции F^j(z(x_j , t), x, t) из примера 3 с α = 100 сопоставимы с

результатами, полученными для функции F^j (z(x_j , t), x, t) из примера 2, по-

этому они не приводятся.

8. Заключение

Предложен дискретный по пространственной переменной закон управле-

ния скалярными линейными дифференциальными уравнениями параболиче-

ского и гиперболического типов с интервально неопределенными параметра-

ми и внешними ограниченными возмущениями. Для синтеза закона управ-

ления используется конечный набор измерений выходного сигнала. Закон

управления зависит от функции, зависящей от пространственной коорди-

наты и текущего измерения. Данная функция позволяет достигать разных

свойств, например обеспечивать пониженные затратами на управление или

реализовывать управление, близкое к граничному. Доказана экспоненциаль-

ная устойчивость замкнутых систем и робастность по отношению к парамет-

рам и внешним возмущениям.

Численные примеры моделирования подтвердили результаты расчетов и

показали эффективность предложенного алгоритма по сравнению с резуль-

татом [14, 15] в том смысле, что при меньших затратах на управление можно

повысить скорость сходимости решений и повысить качество регулирования

в установившемся режиме.

СПИСОК ЛИТЕРАТУРЫ

Candogan U.O., Ozbay H., Ozaktas H.M. Controller Implementation for a Class

of Spatially-varying Distributed Parameter Systems // IFAC Proceedings Volumes

(Proc. 17th IFAC World Congr.). 2008. V. 41. No. 2. P. 7755-7760.

Hagen G., Mezic I. Spillover Stabilization in Finite-dimensional Control Observer

Design for Dissipative Evolution Equations // SIAM J. Control Optim. 2003. V. 42.

No. 2. P. 746-768.

Smagina E., Sheintuch M. Using Lyapunov’s Direct Method for Wave Suppression

in Reactive Systems // Syst. Control Lett. 2006. V. 55. No. 7. P. 566-572.

Demetriou M.A. Guidance of Mobile Actuator-plus-sensor Networks for Improved

Control and Estimation of Distributed Parameter Systems // IEEE Trans. Automat.

Control. 2010. V. 55. P. 1570-1584.

Smyshlyaev A., Krstic M. On Control Design for PDEs with Spacedependent Diffu-

sivity or Time-dependent Reactivity // Automatica. 2005. V. 41. P. 1601-1608.

Krstic M., Smyshlyaev A. Adaptive Boundary Control for Unstable Parabolic PDEs-

part I: Lyapunov Design // IEEE Trans. Automat. Control. 2008. V. 53. P. 1575-

1591.

Delchamps D.F. Extracting State Information from a Quantized Output Record //

Syst. Control Lett. 1989. V. 13. P. 365-372.

Brockett R.W., Liberzon D. Quantized Feedback Stabilization of Linear Systems //

IEEE Trans. Automat. Control. 2000. V. 45. P. 1279-1289.

Baillieul J. Feedback Coding for Information-Based Control: Operating near the

Data Rate Limit // Proc. 41st IEEE Conf. Decision Control, Las Vegas, Nevada,

USA, 2002. P. 3229-3236.

10.

Zheng B.-C., Yang G.-H. Quantized Output Feedback Stabilization of Uncertain Sys-

tems with Input Nonlinearities via Sliding Mode Control // Int. J. Robust Nonlinear

Control. 2012. V. 24. No. 2. P. 228-246.

11.

Khapalov A.Y. Continuous Observability for Parabolic System under Observations of

Discrete Type // IEEE Trans. Automat. Control. 1993. V. 38. No. 9. P. 1388-1391.

12.

Cheng M.B., Radisavljevic V., Chang C.C., Lin C.F., Su W.C. A Sampled Data

Singularly Perturbed Boundary Control for a Diffusion Conduction System with

Noncollocated Observation // IEEE Trans. Automat. Control. 2009. V. 54. No. 6.

P. 1305-1310.

13.

Logemann H., Rebarber R., Townley S. Generalized Sampled-data Stabilization of

Well-posed Linear Infinite-dimensional Systems // SIAM J. Control Optim. 2005.

V. 44. No. 4. P. 1345-1369.

14.

Fridman E., Blighovsky A. Robust Sampled-data Control of a Class of Semilinear

Parabolic Systems // Automatica. 2012. V. 48. P. 826-836.

15.

Liu K., Fridman E., Xia Y. Networked Control under Communication Constraints:

A Time-Delay Approach. Springer International Publishing, Advances in Delays and

Dynamics, 2020.