Автоматика и телемеханика, № 3, 2021

Управление в технических системах

(Makarovskikh.T.A@susu.ru),

А.В. ПАНЮКОВ, д-р. физ. мат. наук (paniukovav@susu.ru)

(Южно-Уральский государственный университет (НИУ), Челябинск)

ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ ДЛЯ ЗАДАЧИ ПОСТРОЕНИЯ

ТРАЕКТОРИИ ДВИЖЕНИЯ РЕЖУЩЕГО ИНСТРУМЕНТА

ДЛЯ CAD/CAM СИСТЕМ ТЕХНОЛОГИЧЕСКОЙ ПОДГОТОВКИ

ПРОЦЕССОВ РАСКРОЯ¹

Большинство исследований, касающихся траекторий инструмента для

режущих машин, посвящены определению траектории при поконтурном

вырезании. Современные ресурсосберегающие технологии резки листо-

вых материалов позволяют совмещать контуры вырезаемых деталей, что

уменьшает количество отходов материала и сокращает длину резки. Од-

нако совмещение границ вырезаемых контуров является источником ря-

да ограничений, формализуемых в терминах плоских графов: (1) упо-

рядоченное охватывание, (2) самонепересекающаяся траектория резания.

В статье рассмотрены основные структуры данных и алгоритмы, исполь-

зуемые в разрабатываемой CAD/CAM системе технологической подго-

товки процессов раскроя, допускающей раскройный план с совмещенны-

ми контурами, и программное обеспечение, которое для решения задачи

маршрутизации по раскройному плану строит гомеоморфный образ гра-

фа, решает данную задачу и интерпретирует результаты решения.

Ключевые слова: вырезание из листового материала, раскройный план,

совмещение фрагментов контуров деталей, плоский граф, маршрут, ал-

горитм, структуры данных, программное обеспечение.

DOI: 10.31857/S0005231021030077

1. Введение

Лазерная резка является одной из основных современных технологий, ис-

пользуемых при обработке листового материала, что делает актуальной зада-

чу определения траектории движения режущего инструмента. Задача опре-

деления траектории заключается в определении точной последовательности

резов. Развитие автоматизации производства привело к появлению техно-

логического оборудования с числовым программным управлением, исполь-

зуемого для резки листовых материалов. Новые технологии позволяют осу-

ществлять вырезание по произвольной траектории с достаточной для практи-

ки точностью. Преимуществом при использовании лазерной резки является

¹ Статья выполнена при поддержке Правительства РФ (Постановление № 211 от

16.03.2013 г.), Cоглашение № 02.A03.21.0011 и Министерства науки и высшего образова-

ния РФ (государственное задание FENU-2020-0022).

123

минимальность таких показателей, как ширина реза и термические деформа-

ции. Целью задачи определения маршрута резки является поиск такого пути

режущего инструмента, при котором выполняются условия предшествова-

ния, а время, затраченное на вырезание, минимально [1].

Основными ограничениями при лазерной резке являются: (1) все элементы

внутренних контуров должны быть вырезаны прежде, чем будет полностью

пройден охватывающий их контур (условие OE-охватывания [2]); (2) следует

избегать пересечения траектории резки, касания допустимы (NOE-ограни-

чение [1, 3]); (3) в процессе лазерной резки происходит нагревание метал-

лического листа, поэтому необходимо учитывать термальные эффекты [4];

(4) ограничения на расположение точки врезки (построение PPOE-покры-

тия [5]); (5) общее время, требуемое на выполнение резки, представляющее

суммарное время для осуществления всех вырезаний, время на выполнение

холостых переходов и время на врезку желательно сокращать.

В [1, 6] приводится классификация задач маршрутизации режущего ин-

струмента и отмечается, что технологии ECP (Endpoint Cutting Problem) и

ICP (Intermittent Cutting Problem) за счет возможности совмещения границ

вырезаемых деталей позволяют сократить расход материала, длину резки

и длину холостых проходов [1]. Проблемы уменьшения отходов материала и

максимального совмещения фрагментов контуров вырезаемых деталей реша-

ются на этапе составления раскройного плана.

Несмотря на очевидные преимущества технологий ECP и ICP, в настоящее

время большинство отечественных [7-11] и зарубежных [1, 6, 12, 13] публи-

каций посвящено развитию технологии GTSP (General Travelling Salesman

Problem), которая не предполагает совмещение контуров вырезаемых дета-

лей. При использовани технологии GTSP длина траектории будет равна сум-

ме периметров всех контуров, а количество точек врезки количеству конту-

ров, при этом проблема выполнения отмеченных выше условий оказывается

тривиальной.

Для определения последовательности резки фрагментов раскройного пла-

на не используется информация о форме детали, поэтому все кривые без са-

мопересечений и соприкосновений на плоскости, представляющие форму де-

талей, интерпретируются в виде ребер графа, представляющего гомеоморф-

ный образ раскройного плана, а все точки пересечений и соприкосновений

представляются в виде вершин этого графа.

Гомеоморфным образом раскройного плана является плоский граф G с

внешней гранью f₀ на плоскости S. Для любой части J графа G (т.е. J ⊆

⊆ G) обозначим через Int (J) теоретико-множественное объединение его внут-

ренних граней (объединение всех связных компонент S \ J, не содержащих

внешней грани). Если J считать пройденной частью маршрута режущего ин-

струмента (очевидно, что J - плоский граф), то Int(J) интерпретируется как

отрезанная от листа часть. Множества вершин, ребер и граней графа J будем

обозначать через V (J), E(J) и F (J) соответственно.

Топологическое представление плоского графа G на плоскости S с точно-

стью до гомеоморфизма определяется заданием для каждого ребра e ∈ E(G)

следующих функций [2, 3]: v_k(e), k = 1, 2, вершины, инцидентные ребру e;

124

l_k(e), k = 1,2, ребра, полученные вращением ребра e против часовой стрел-

ки вокруг вершины v_k(e); r_k(e), k = 1, 2, ребра, полученные вращением реб-

ра e по часовой стрелке вокруг вершины v_k(e); f_k(e) грань, находящаяся

справа при движении по ребру e от вершины v_k(e) к вершине v_3-k(e), k = 1, 2.

Таким образом, используя известные координаты прообразов вершин гра-

фа G и размещения фрагментов раскройного плана, являющихся прообраза-

ми ребер графа G, любой маршрут в графе G можно интерпретировать как

траекторию режущего инструмента.

2. Представление исходных данных в программе

Как правило, раскройный план содержит большие группы однотипных

деталей, а для описания размещения детали на раскройном плане достаточно

указания величин (x, y, ϕ), где (x, y) координаты базовой точки этой детали

(обычно это начало координат, к которым привязаны координаты остальных

точек), ϕ - угол поворота детали вокруг ее базовой точки. Поэтому разумно

иметь базу данных типовых деталей.

Основными примитивными элементами траекторий маршрута резки явля-

ются отрезки прямых и дуги окружностей. Целая окружность представляет-

ся как объединение двух дуг с центральными углами ϕ и 2π - ϕ, ϕ > 0. Для

идентификации таких примитивов достаточно указать координаты (x₁, y₁)

и (x₂, y₂) крайних точек v₁ и v₂ соответственно, а также tg(ϕ/4), где ϕ

центральный угол дуги (v₁, v₂) окружности, проходящей от точки v₁ до точ-

ки v₂ (очевидно, что для отрезка можно считать tg(ϕ/4) = 0). С формальной

точки зрения плоская деталь представляет часть плоскости, ограниченной

внешней границей и внутренними границами по числу дыр. Каждая грани-

ца представляет замкнутый контур, состоящий из такой последовательности

примитивов, что начало следующего совпадает с концом предыдущего.

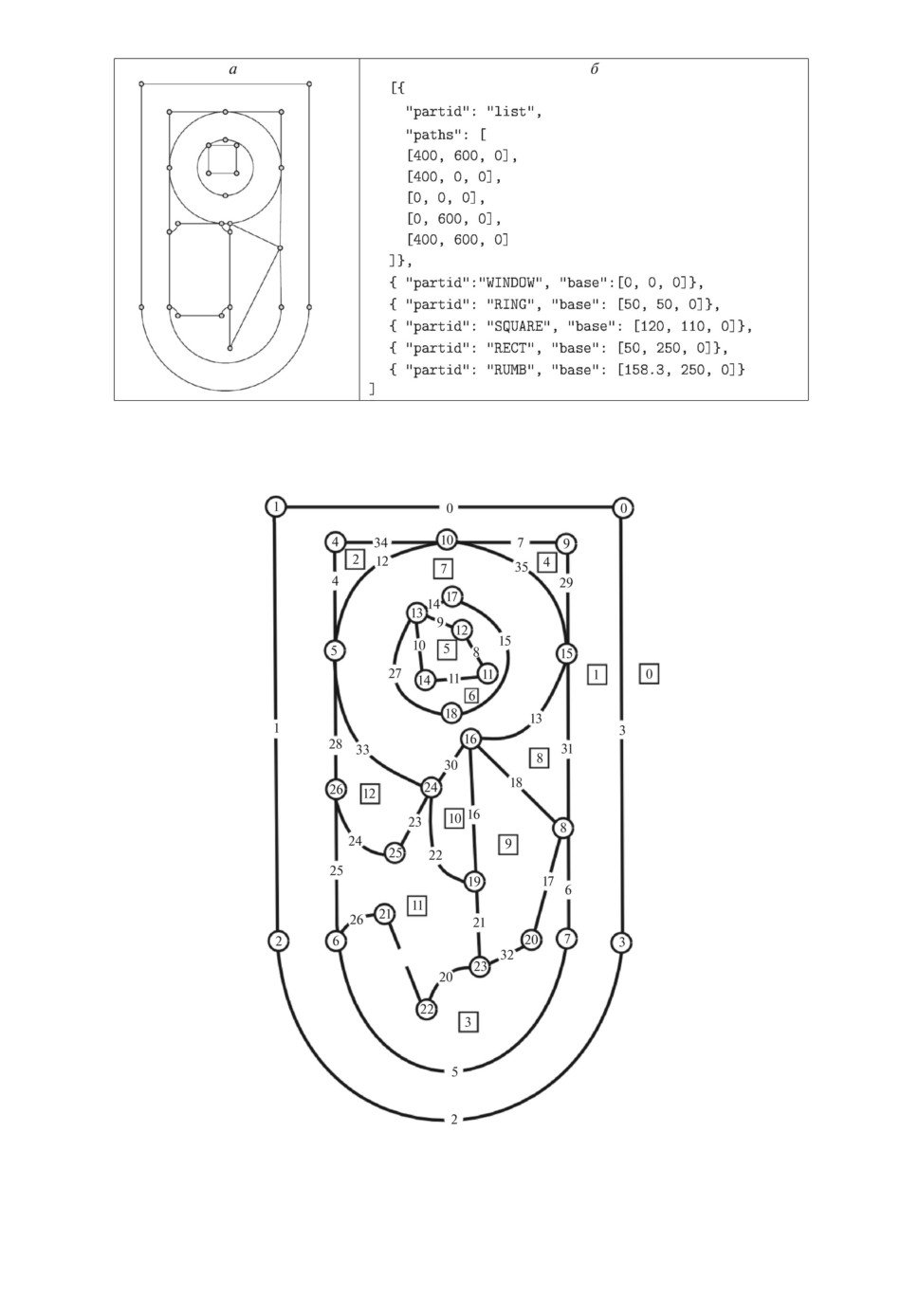
Для представления данных о детали используется формат JSON [14]. На

рис. 1 представлены примеры деталей и их описания. Описание каждой дета-

ли содержит ее имя в ключевом поле partid и список контуров в поле paths.

Каждый контур представляет из себя трехэлементный массив, состоящий из

двух координат концов и значения tg(ϕ/4). Декартовы координаты конечной

точки одного примитива являются координатами начальной точки следую-

щего. Очевидно, что такое представление декартовых координат позволяет

легко определять замкнутые контуры (начальные координаты первого при-

митива совпадают с конечными координатами последнего). Примеры опи-

саний деталей, состоящих из нескольких контуров, число которых больше

единицы, приведено на рис. 1,а и 1,д.

Первым объектом при таком представлении данных будет определение ли-

ста, содержащего раскройный план, а все последующие объекты описания

деталей, координаты их опорной точки и ориентция.

Пример раскройного плана с совмещенными границами контуров деталей

представлен на рис. 2,а.

Для определения последовательности резки фрагментов раскройного пла-

на не используется информация о форме детали, поэтому все кривые без са-

125

мопересечений и соприкосновений в описании формы деталей можно интер-

претировать как ребра графа, а все точки пересечений и соприкосновений

как вершины графа. Для получения представления плоского графа, позво-

ляющего восстановить с точностью до гомеоморфизма исходный раскройный

план, необходимо и достаточно в каждой вершине зафиксировать цикличе-

ский порядок на множестве инцидентных ей ребер. На рис. 3 представлен го-

меоморфный образ раскройного плана, изображенного на рис. 2,a. Структу-

ры данных, используемые для представления гомеоморфного образа, должны

включать всю необходимую информацию для эффективной работы алгорит-

мов маршрутизации и интерпретации построенных маршрутов [15, 16]. На ли-

стинге 1 представлены структуры данных для представления гомеоморфного

образа раскройного плана в виде плоского графа.

Листинг 1. Структуры данных для гомеоморфного образа раскройного плана

struct

Vert {// Вершина графа

double x, y; // координаты вершины

int sv; // номер компоненты связности содержащей вершину

int rank; // ранг вершины

double dpth; // глубина вершины (скорректированный ранг)

int deg; // степень вершины

int mark; // метка для поиска в ширину в алгоритмах

};

struct

Edge { // ребро графа

int rank; // ранг ребра

int dpth; // глубина ребра (скорректированный ранг)

int v1, v2; // номера инцидентных вершин в контейнере

vector<Vert> V

double x_0, y_0, r; // координаты центра дуги и ее радиус

double v1_ang, v2_ang; // центральные углы возможных дуг

double v1_ta4, v2_ta4; // тангенсы четвертей соответствующих дуг

int l1,l2,r1,r2; // номера возможных смежных ребер

в vector<Edge> E

int sv; // номер компоненты связности в контейнере

vector<Connect> Sv

int cycle1, cycle2; // номера контуров в контейнере

vector<Cycle> C

int f1, f2; // номера граней, инцидентных ребру,

в vector<Face> F

int mark; // метка для поиска в ширину в алгоритмах

};

struct

Face { // Грань графа

int number; // номер грани (детали, отверстия, дополнительной)

int dpth; // глубина грани

};

struct

Connect { // Компонента связности

int v; // одна из вершин компоненты (номер в vector<Vert> V)

int outcycle; // номер охватывающего контура в vector<Cycle> C

int up; // смежная охватывающая компонента

(номер в vector<Connect> Sv)

int rank; // ранг компоненты

Connect ( ):v(-1),outcycle(-1),up(-1),rank(-1){}; // конструктор

};

128

struct Cycle { // контур внешней или внутренней грани графа

int v; // номер вершины контура в контейнере vector<Vert> V

int e; // номер ребра в контейнере vector<Edge> E, инцидентного v

int f; // номер грани в контейнере vector<Face>

vector<int> vertexes; // отсортированные в порядке обхода вершины

vector<int> edges; // ребра цикла, отсортированные в порядке обхода

Cycle (int vtx, int edg) : v(vtx), e(edg), f(-1) { }; // конструктор

Cycle ( ) : v(-1), e(-1), f(-1) {}; // конструктор по умолчанию

};

Структура Vert содержит поля с указанием декартовых координат соот-

ветствующей точки на раскройном плане и ряд вспомогательных полей. Эти

данные необходимы для интерпретатора маршрута и при заполнении полей

структуры Edge. Поля структуры Edge содержит номера v1, v2 инцидентных

вершин, номера f1, f2 инцидентных граней, номера l1, l2, r1, r2 соседних в

циклическом порядке ребер, значения v1_ta4, v2_ta4 величины tg(ϕ/4), где

ϕ - центральный угол дуг (v₁,v₂) и (v₂,v₁) соответственно, а также вспо-

могательные величины. Структура Face ставит в соответствие объекты на

раскройном плане с гранями его гомеоморфного образа. Структура Connect

используется для идентификации компонент связности гомеоморфного об-

раза раскройного плана. Структура Cycle используется для идентифика-

ции контуров, являющихся границами граней. Контейнеры для приведенных

структур, другие вспомогательные данные, все используемые методы их за-

полнения и алгоритмы маршрутизации инкапсулированы в класс DataHolder

[15-17].

3. Маршрутизация в связных графах

Использование плоского графа в качестве гомеоморфного образа модели

раскройного плана позволяет формализовать технологические ограничения

на порядок вырезания фрагментов плана резки: во-первых, граф G содер-

жит образы всех возможных элементов траектории инструмента; во-вторых,

маршрут резки должен удовлетворять условию упорядоченного охватыва-

ния, т.е. отрезанная от листа часть не должна требовать дополнительных

разрезаний [2]; в-третьих, должны отсутствовать самопересечения траекто-

рии резки [3].

Допустимый маршрут формализуется как упорядоченная последователь-

ность OE-цепей, покрывающая граф [2, определения 4-5].

Определение OE-покрытия вполне конструктивно, доказательством это-

го факта является эффективность алгоритмов, рассмотренных в [2]. Если

связный граф G не является эйлеровым, то он содержит 2k, k ≥ 1, вершин

нечетной степени. В этом случае OE-маршрут состоит из k реберно-непересе-

кающихся цепей. Задача построения такого маршрута решается алгоритмом

OE-Router [18]. При этом в построенном маршруте длина холостых перехо-

дов (т.е. переходов между концом текущей цепи и началом следующей цепи)

может не быть оптимальной. Если плоский граф G, представляющий образ

раскройного плана, не содержит мостов (т.е. ребер, инцидентных одной гра-

ни), то возможно построить OE-маршрут, в котором ребра произвольного

129

Таблица 1. Алгоритмы построения OE-маршрутов

Название алгоритма

Вычислительная сложность

Eulerian OE-cycle (рекурсивный алгоритм) [2] O(|V |²)

Eulerian OE-cycle (алгоритм OE-Cycle) [2]

O(|E| · log₂|V |)

OE-Postman Route (алгоритм CPP_OE)

O(|E| · |V |)

OE-Router [18]

O(|E| · log₂|V |)

M-OE-Router [2]

O(|V |²)

паросочетания M на подмножестве V_odd ⊂ V (G) множества вершин нечет-

ной степени и только они соответствуют холостым движениям. Выбор крат-

чайшего паросочетания M позволяет найти маршрут с минимальной длиной

холостых переходов. Отметим, что связные плоские графы, являющиеся об-

разами раскройных планов, как правило, не содержат мостов. Поэтому если

M является кратчайшим паросочетанием, то алгоритм M-OE-Router строит

маршрут с минимальной длиной холостых переходов.

Если граф G, представляющий гомеоморфный образ раскройного плана,

связен и не содержит мостов, то алгоритм M-OE-Router точно решает задачу,

но требует определения кратчайшего паросочетания. Алгоритм OE-Router

решает задачу для любого графа G, используя жадную стратегию выбора

холостого хода. Полный перечень алгоритмов построения OE-маршрутов для

связных графов приведен в табл. 1.

4. NOE-маршрутизация

Задача построения эффективных алгоритмов нахождения непересекаю-

щихся цепей в плоских графах является открытой: некоторые попытки ре-

шить данную задачу были предприняты в [19]. В [20] предложено решение

задачи для плоского связного 4-регулярного графа.

Определение 1. Эйлеров цикл C в плоском графе G называется само-

непересекающимся, если он гомеоморфен циклическому графуG, представ-

ляющему плоскую жорданову кривую без самопересечений. Циклический

графG может быть получен из графа G с помощью применения O(|E(G)|)

операций расщепления вершин.

Общим случаем является решение задачи построения самонепересекаю-

щейся OE-цепи (или NOE-цепи, non-intersecting OE-trail) [21].

Определение 2. Будем говорить, что цепь является NOE-цепью, ес-

ли она одновременно является OE-цепью и самонепересекающейся цепью.

Определение 3. Систему переходов [22] цепи, соответствующую са-

монепересекающейся цепи, будем называть системой непересекающихся пе-

реходов.

Доказательство того факта, что для системы переходов, соответствующей

самонепересекающемуся эйлерову циклу, существует такая начальная верши-

на и такое конечное ребро, смежное внешней грани, для которых построенный

цикл будет OE-циклом, во многом схоже с доказательством теоремы 1 в [20]

для 4-регулярного графа G, и представляет алгоритм построения NOE-цепи.

130

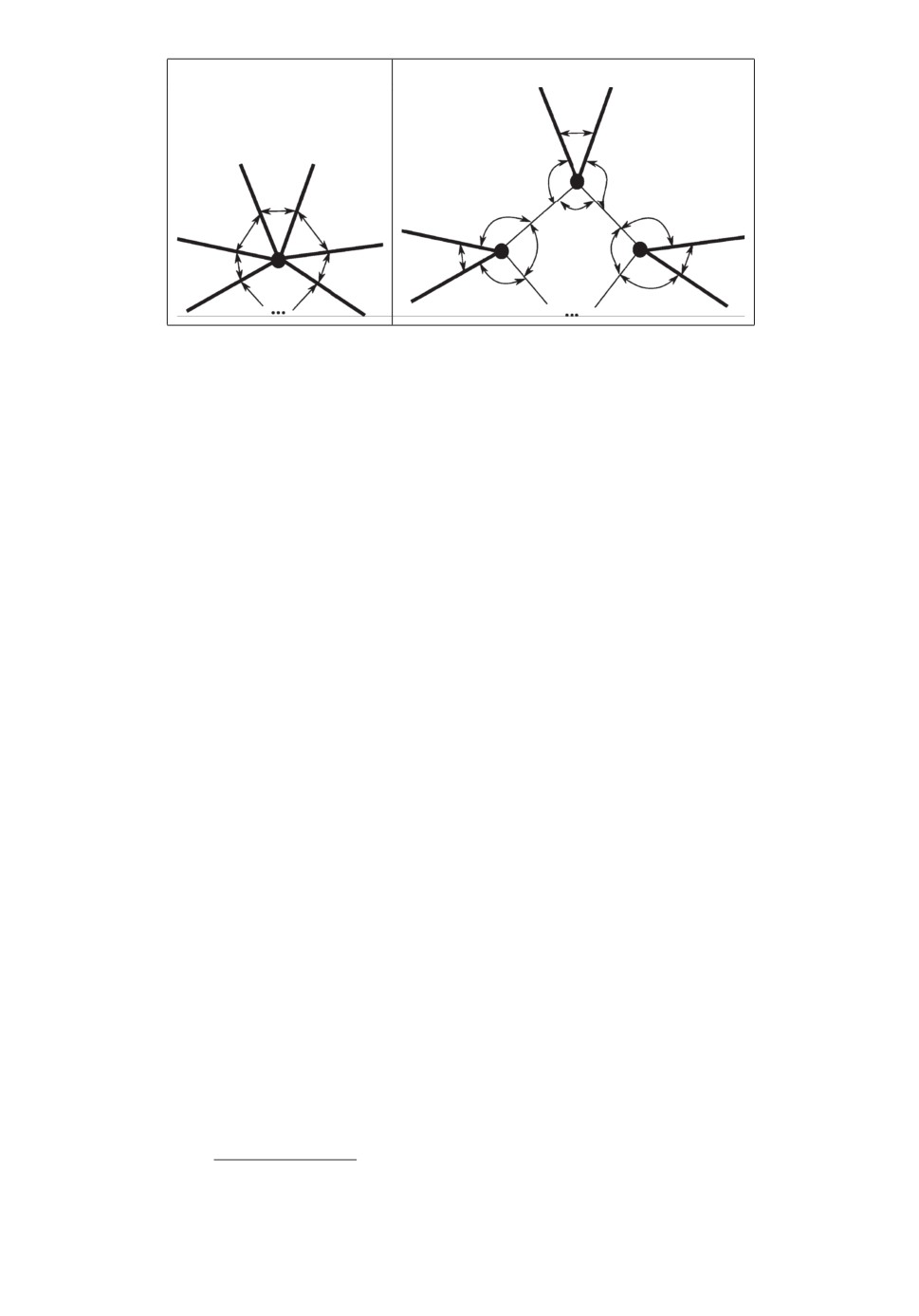
Рис. 4. a Исходные указатели на соседние ребра в расщепляемой вершине.

б Расщепление вершины (жирными линиями показаны ребра графа G, тон-

кими линиями - дополнительные (фиктивные) ребра) и модификация указа-

телей в соответствии с расщеплением.

Для построения самонепересекающейся эйлеровой OE-цепи (или цикла) в

плоском эйлеровом графе (в дальнейшем эту цепь будем называть NOE-це-

пью (non-intersecting OE-chain)), для которой не задано фиксированной си-

стемы переходов, можно поступить следующим образом [21].

На множестве вершин V (G) определим булеву функцию

{

true, если вершина просмотрена;

Checked(v) =

false в противном случае.

При инициализации этой функции все вершины из V (G) объявляются как

непросмотренные.

Функция Non-intersecting(G) (алгоритм 1) расщепляет в графе G все

вершины v ∈ V (G), deg(v) = 2n, n ≥ 3, на n искусственных вершин степени 4

и вводит n искусственных ребер, инцидентных полученным после расщепле-

ния вершинам и образующим цикл (рис. 4). Для выполнения указанных пре-

образований необходимо просмотреть все функции v_k(e), k = 1, 2, определен-

ные для всех ребер e, и внести требуемые модификации во всю систему коди-

рования графа. В теле функции используется процедура Handle (e, v_k(e), k)

(алгоритм 2), которая обрабатывает каждую непросмотренную вершину гра-

фа G. Обработка заключается в расщеплении вершины v_k(e) в соответствии

с рис. 4,a и 4,б.

Алгоритм 1. Функция Non-intersecting (G)

Require: плоский эйлеров граф G;

Ensure: плоский связный 4-регулярный граф G^∗;

1: for all (e ∈ E(G) ) do

⊲ Просмотреть все ребра графа

k = 1;

⊲ Обработать последовательно функции с индексом 1, а

затем - 2

while (k ≤ 2) do

if (Checked(v_k(e))) then ⊲ Если вершина не была обработана ранее

Handle (e, v_k(e), k);

⊲ Обработать вершину

end if

131

k + +;

end while

9: end for

10: Return G^∗;

Алгоритм 2. Процедура Handle (e,v,k)

⊲ Проход 1: Определение степени вершины v

2: e_first = e;

3: d = 0;

⊲ Степень вершины

4: repeat

⊲ Просмотреть все ребра

le = l_k(e);

⊲ Найти смежное ребро, заданное функцией l_k(e)

if (v_k(le) = v) then

REPLACE(le);

end if

e = le;

⊲ Учесть текущее ребро при подсчете степени

10:

d = d + 1;

⊲ и перейти к следующему

11: until (e = e_first);

12:

⊲ Проход 2: Расщепление вершин, степень которых выше 4

13: if (d > 4) then

14:

e = e_first; le = lk (e); fl=new EDGE; fle = fl; e_first = e; e_next = lk (le);

15:

repeat

16:

e = e_next; le = lk (e); fr = fl; fl=new EDGE; e_next = lk (le);

17:

Pointers(e, le, fr, fl);

⊲ Расставить указатели для ребер

18:

until (l_k(le) = e_first);

19:

Pointers(e_first, l_k(e_first), fle, fe);

⊲ Расставить указатели для ребер

20: end if

Введенные процедурой Handle n искусственных вершин и n искусственных

ребер, инцидентных этим вершинам, образуют цикл. В результате обработ-

ки всех вершин графа G получим модифицированный граф G^∗, являющийся

плоским связным 4-регулярным графом. Для G^∗ можно применить алгоритм

AOE-TRAIL( ), который построит в нем AOE-цепь T^∗. Если затем в T^∗ все ис-

кусственные ребра и инцидентные им вершины, полученные при расщеплении

вершины v, заменить на v, то получим NOE-цепь T в исходном графе G. По-

лученная после удаления ребер цепь будет принадлежать классу OE, так как

процедура удаления ребер не нарушает порядка следования оставшихся ребер

в цепи, что исключает появление цикла, охватывающего еще непройденные

ребра.

5. Маршрутизация для несвязных графов

Если раскройный план содержит детали с отверстиями, а также дру-

гие детали, расположенные в этих отверстиях, то плоский граф G =

= (V (G), F (G), E(G)), представляющий гомеоморфный образ раскройного

плана, оказывается несвязным. Поскольку вырезанные фрагменты содержат

прообразы охваченных граней графа, то требования к маршруту резки, га-

рантирующие выполнение OE-ограничения, можно формализовать в терми-

132

Таблица 2. Алгоритмы построения OE-маршрутов

для несвязных графов

Название алгоритма Вычислительная сложность

MultiComponent

O(|E| · log₂|V |)

Bridging

O(|E| · log₂|V |)

DoubleBridging

O(|V |²)

FaceCutting

O(|E| · log₂|V |)

нах графа G^′ = (F (G), V (G), E(G)), двойственного графу G [2]: необходимо,

чтобы порядок обхода граней графа G (т.е. вершин графа G^′) являлся рас-

ширением отношения частичного порядка ≺:

(

)

(f_i ≺ f_j)

⇔ f_j принадлежит кратчайшей цепи T^f

между f_i и f₀

G^′

где f₀

внешняя (бесконечная) грань плоского графа G. Перечень алгорит-

мов построения OE-маршрутов для несвязных графов приведен в табл. 2.

Для построения OE-покрытия в несвязаном графе реализованы следующие

подходы: (1) определение допустимого обхода компонент связности графа G;

(2) пополнение множества ребер E(G) до множества E(G), гдеG - плоский

связный граф.

Первый подход реализуется алгоритмом MultiComponent, в котором на-

хождение искомого OE-маршрута заключается в независимом построе-

нии OE-маршрутов для каждой компоненты связности и последующем их

объединении в результирующий маршрут в порядке уменьшения рангов

компонент связности. Второй подход реализуется алгоритмами Bridging,

DoubleBridging и FaceCutting и основан на добавлении мостов в разделяю-

щих гранях.

Определение 4

[18]. Грань f ∈ F (G) называется разделяющей, если

граф G^′ \ {f} - несвязный.

Пусть графG получен из графа G добавлением между компонентами связ-

ности минимального по мощности и по длине множестваE мостов, принад-

лежащих разделяющим граням. Очевидно, что такие ребра в графе G^′ будут

являться ребрами остовного дерева минимального веса. Полученный таким

образом граф

G является плоским связным графом, для которого можно

построить OE-маршрут M(G) с помощью алгоритма OE-Router [18].

При этом OE-маршрут M(G) строится по маршруту M(G) удалением ре-

бер введенного множестваE. При этом получим множество цепей, представ-

ляющих OE-покрытие исходного несвязного графа. Указанный подход реа-

лизует алгоритм Bridging.

Чтобы обеспечить возможность применения алгоритма M-OE-Router, до-

статочно дополнить граф G до графаG включением множества реберE =

= ∪_e∈˜E{e₁ = e, e₂ = e}, т.е. включением двух дубликатов для каждого ребра

e ∈E. Указанный подход в совокупности с алгоритмом M-OE-Router реали-

зует алгоритм DoubleBridging.

Теорема 1. Если в каждой компоненте связности G_k графа G степени

вершин, инцидентных разделяющим граням графа G, четны, то маршрут с

133

минимальной длиной дополнительных построений реализуется алгоритмом

DoubleBridging.

Доказательство. Очевидно, что обход каждой компоненты связности

должен заканчиваться на внешней границе. Если предположить, что обход

компоненты связности начинается из вершины, не принадлежащей внешней

границе, то завершится данный фрагмент OE-покрытия в вершине нечет-

ной степени, не принадлежащей границе. Поскольку на границе нет вершин

нечетной степени, то в соответствии с определением OE-маршрута часть гра-

фа, содержащая внешнюю границу, останется непройденной. В оптимальном

решении (полученном алгоритмом M-OE-Router) компоненты будут связаны

парами кратных ребер. Причем, суммарный вес всех связывающих ребер ми-

нимален. Теорема доказана.

Очевидно, что длина введенных мостов в алгоритме DoubleBridging не

меньше удвоенной длины кратчайшего остова в разделяющей грани.

Еще одним способом получения связного графа без мостов является рас-

щепление вершин, инцидентных разделяющей грани, с помощью гамильто-

нова цикла (алгоритм FaceCutting). Такой подход представляется наиболее

целесообразным, поскольку, во-первых, на практике размерность задачи ком-

мивояжера сопоставима с оценками степеней соответствующих разделяющих

граней (т.е. достаточно низкая); во-вторых, в соответствии с метрикой гра-

фа G даже приближенный полиномиальный алгоритм Кристофидеса [23] для

задачи коммивояжера строит гамильтонов цикл в разделяющей грани с дли-

ной, не превышающей удвоенной длины кратчайшего остова.

6. Пример

В табл. 3 (левый столбец) приведено оптимальное NOE-покрытие рас-

кройного плана рис. 2 упорядоченной последовательностью OE-цепей. Пер-

вая цепь проходит через квадрат и внутреннюю границу кольца. Вторая по

правой стороне прямоугольника, по внешней границе кольца, и завершается

вырезание треугольником и прямоугольником. Третья цепь завершает внут-

ренний контур окна. Четвертая проходит по внешнему контуру окна. Код тра-

ектории инструмента в терминах JSON представлен в правом столбце табл. 3.

Каждая отдельная цепь соответствует определенной части траектории непре-

Таблица 3. Оптимальное NOE-покрытие раскройного плана рис. 2 упорядоченной

последовательностью OE-цепей

Цепь

JSON-код цепи

{ "partid": "chain_1",

"paths": [

chain 1:

[150.0,100.0,-0.162278], [120.0,110.0,-0.0],

v17 e14 v13 e9 v12

[170.0,110.0,-0.0], [170.0,160.0,-0.0],

e8 v11 e11 v14 e10

[120.0,160.0,-0.0], [120.0,110.0,-0.720759],

v13 e27 v18 e15 v17

[150.0,200.0,-1.0], [150.0,100.0,0]

]},

134

Таблица 3 (окончание)

{ "partid": "chain_1",

"paths": [

[150.0,400.0,0.0], [150.0,265.0,-0.0],

chain 2:

[150.0,250.0,0.0375], [135.0,250.0,0.374006],

v23 e21 v19 e16 v16

[50.0,150.0,0.4142], [150.0,50.0,0.4142],

e30 v24 e33 v5 e12

[250.0,150.0,0.4142], [150.0,250.0,-0.0],

v10 e35 v15 e13 v16

[250.0,300.0,-0.0], [150.0,475.0,-0.0],

e18 v8 e17 v20 e32

[150.0,400.0,-0.414213],[135.0,415.0,-0.0],

v23 e20 v22 e19 v21

[65.0,415.0,-0.414213], [50.0,400.0,-0.0],

e26 v6 e25 v26

[50.0,265.0,0]

]},

{ "partid": "chain_3",

"paths": [

chain 3:

[150.0,265.0,0.414213], [135.0,250.0,0.0],

v19 e22 v24 e23 v25

[65.0,250.0,0.414213], [50.0,265.0,-0.0],

e24 v26 e28 v5 e4

[50.0,150.0,-0.0], [50.0,50.0,-0.0],

v4 e34 v10 e7 v9 e29

[150.0,50.0,-0.0], [250.0,50.0,-0.0],

v15 e31 v8 e6 v7 e5

[250.0,150.0,-0.0], [250.0,300.0,-0.0],

[250.0,400.0,1.0],

[50.0,400.0,0]

]},

{ "partid": "chain_4",

"paths": [

chain 4:

[300.0,0.0,0.0],

[0.0,0.0,0.0],

v0 e0 v1 e1 v2 e2 v3

[0.0,400.0,-1.0], [300.0,400.0,0.0],

e3 v0

[300.0,0.0,0]

] }

рывной резки. Она представляет собой последовательность трехэлементных

массивов, содержащих координаты текущей начальной точки примитива, а

также значение для нее. При вырезании деталей в соответствии с найденной

последовательностью цепей соблюдаются все технологические ограничения.

7. Заключение

Технология, допускающая совмещение границ вырезаемых деталей

современная ресурсосберегающая технология резки. Известны алгоритмы

маршрутизации, когда на маршрут движения режущего инструмента одно-

временно наложены следующие технологические ограничения: (1) отрезан-

ная от листа часть не требует дополнительных разрезаний, (2) отсутствуют

самопересечения траектории резки.

В статье дано решение проблемы эффективной программной реализации

этих алгоритмов: представлены результаты авторов, использованные при раз-

работке функциональных элементов комплекса программ автоматизирован-

ной системы технологической подготовки процессов раскроя листового мате-

риала.

135

СПИСОК ЛИТЕРАТУРЫ

Dewil R., Vansteenwegen P., Cattrysse D. A Review of Cutting Path Algorithms

for Laser Cutters // Int. J. Adv. Manuf. Technol. 2016. V. 87. P. 1865-1884.

https://doi.org/10.1007/s00170-016-8609-1

Макаровских Т.А., Панюков А.В., Савицкий Е.А. Математические модели и ал-

горитмы маршрутизации для САПР технологической подготовки процессов рас-

кроя // АиТ. 2017. № 5. С. 123-140. https://doi.org/10.1134/S0005117917050095

Makarovskikh Т.А., Panyukov A.V., Savitsky E.A. Mathematical Models and Rout-

ing Algorithms for CAD Technological Preparation of Cutting Processes // Autom.

Remote Control. 2017. V. 78. No. 4. P. 868-882.

Makarovskikh T., Panyukov A. The Cutter Trajectory Avoiding Intersections of

Cuts // IFAC-PapersOnLine. 2017. V. 50. Iss. 1. P. 2284-2289.

https://doi.org/10.1016/j.ifacol.2017.08.226

Li X., Liu Zh., Wang F., Yi B., Song Y. Combining Physical Shell Mapping and

Reverse-Compensation Optimisation for Spiral Machining of Free-Form Surfaces //

Int. J. Prod. Rts. 2018. https://doi.org/10.1080/00207543.2018.1512763

Makarovskikh T., Panyukov A. Development of Routing Methods for Cutting out

Details // CEUR Workshop Proc. 2018. V. 2098. P. 249-263.

http://ceur-ws.org/Vol-2098/paper22.pdf

Dewil R., Vansteenwegen P., Cattrysse D., Laguna M., Vossen T. An Improvement

Heuristic Framework for the Laser Cutting Tool Path Problem // Int. J. Prod. Rts.

2015. V. 53. Iss. 6. P. 1761-1776. https://doi.org/10.1080/00207543.2014.959268.

Petunin A., Stylios C. Optimization Models of Tool Path Problem for CNC Sheet

Metal Cutting Machines // IFAC-PapersOnLine. 2016. V. 49. P. 23-28.

https://doi.org/10.1016/j.ifacol.2016.07.544

Petunin A., Chentsov A.G., Chentsov P.A. About Routing in the Sheet Cutting //

Bulletin of the South Ural State University, Series: Mathematical Modelling, Pro-

gramming and Computer Software. 2017. V. 10 (3). P. 25-39.

https://doi.org/10.14529/mmp170303

Chentsov A.G., Grigoryev A.M., Chentsov A.A. Solving a Routing Problem with the

Aid of an Independent Computations Scheme // Bulletin of the South Ural State

University, Series: Mathematical Modelling, Programming and Computer Software.

2018. V. 11 (1). P. 60-74. https://doi.org/10.14529/mmp180106

10.

Khachay M., Neznakhina K. Towards Tractability of the Euclidean Generalized

Travelling Salesman Problem in Grid Clusters Defined by a Grid of Bounded

Height // Communications in Comput. and Inform. Sci. 2018. V. 871. P. 68-77.

https://link.springer.com/chapter/10.1007/978-3-319-93800-4_6

11.

Chentsov A., Khachay M., Khachay D. Linear Time Algorithm for Precedence

Constrained Asymmetric Generalized Traveling Salesman Problem

// IFAC-

PapersOnLine. 2016. V. 49. P. 651-655. https://doi.org/10.1016/j.ifacol.2016.07.767

12.

Hoeft J., Palekar U. Heuristics for the Plate-cutting Traveling Salesman Problem //

IIE Transactions. 1997. V. 29. P. 719-731. https://doi.org/10.1023/A:1018582320737

13.

Dewil R., Vansteenwegen P., Cattrysse D. Construction heuristics for generating

tool paths for laser cutters // Int. J. Prod. Rts. 2014. V. 52 (20). P. 5965-5984.

https://doi.org/10.1080/00207543.2014.895064

14.

Crockford D. The Application/json Media Type for JavaScript Object Notation

(JSON). Internet Engineering Task Force, 2006.

https://www.rfc-editor.org/info/rfc4627

136

15.

Макаровских Т.А., Панюков А.В., Савицкий Е.А. Программное обеспечение для

задачи построения траектории движения режущего инструмента // Тр. XVIII-й

Междунар. молодeжной конф. “Системы проектирования, технологической под-

готовки производства и управления этапами жизненного цикла промышленного

продукта (CAD/CAM/PDM-2018”. 2018. С. 172-176.

16.

Макаровских Т.А., Панюков А.В., Савицкий Е.А. Задача построения движения

режущего инструмента: программная реализация // Тр. XIII Всеросс. совеща-

ния по проблемам управления (ВСПУ-2019). Под общей редакцией Д.А. Нови-

кова. 2019. С. 2650-2654.

17.

Makarovskikh T.A., Panyukov A.V., Savitskiy E.A. Software Development for Cut-

ting Tool Routing Problems // Procedia Manufacturing. 2019. V. 29. P. 567-574.

https://doi.org/10.1016/j.promfg.2019.02.123

18.

Makarovskikh T.A., Panyukov A.V., Savitskiy E.A. Mathematical Models and Rout-

ing Algorithms for Economical Cutting Tool Paths // Int. J. Prod. Rts. 2018.

V. 56 (3). P. 1171-1188. https://doi.org/10.1080/00207543.2017.1401746.

19.

Manber U., Bent S.W. On Non-intersecting Eulerian Circuits // Discrete Applied

Mathematics. 1987. V. 18. P. 87-94. https://doi.org/10.1016/0166-218X(87)90045-X

20.

Макаровских Т.А. Программное обеспечение для построения A-цепей с упорядо-

ченным охватыванием в плоском связном 4-регулярном графе // Вестн. Южно-

Уральского гос. ун-та. Сер. Вычислительная математика и информатика. 2019.

Т. 8. № 1. С. 36-53. https://doi.org/10.14529/cmse190103

21.

Макаровских Т.А. Построение самонепересекающихся OE-маршрутов в плоском

эйлеровом графе // Вестн. Южно-Уральского гос. ун-та. Сер.: Вычислительная

математика и информатика. 2019. Т. 8. № 4. C. 30-42.

https://doi.org/10.14529/cmse190403

22.

Макаровских Т.А. О числе OE-цепей для заданной системы переходов // Вест-

ник Южно-Уральского гос. ун-та. Сер.: Математика. Механика. Физика. 2016.

Т. 8. № 1. С. 5-12. https://doi.org/10.14529/mmph160101

23.

Garey M.R., Johnson D.S. Computer and intractability: a guide to the theory of

NP-completeness, 1979.

Статья представлена к публикации членом редколлегии А.А. Лазаревым.

Поступила в редакцию 26.06.2019

После доработки 10.04.2020

Принята к публикации 09.07.2020

137