Автоматика и телемеханика, № 4, 2021

Обзоры

О.Г. АНДРИАНОВА, канд. физ.-мат. наук (andrianovaog@gmail.com)

(Институт проблем управления им. В.А. Трапезникова РАН, Москва;

Национальный исследовательский университет

“Высшая школа экономики”, Москва),

А.А. БЕЛОВ, канд. физ.-мат. наук (a.a.belov@inbox.ru),

Д.А. ГОЛЬДИН, канд. техн. наук (goldind@ipu.ru)

(Институт проблем управления им. В.А. Трапезникова РАН, Москва)

МЕЖДУ LQG/H₂ И H_∞ ТЕОРИЯМИ УПРАВЛЕНИЯ¹

В обзоре обсуждаются различные подходы в теории управления, воз-

никавшие на протяжении последних десятилетий, которые отражают же-

лание найти компромисс между LQG/H₂ теорией управления и H_∞ тео-

рией управления. К таким теориям можно отнести теорию регуляторов,

чувствительных к риску (risk sensitive), теорию субоптимального управ-

ления с ограничением на функционал H_∞ энтропии, теорию смешанного

H₂/H_∞ управления, теорию минимаксного LQG управления, анизотро-

пийную теорию и некоторые другие. Более подробно в обзоре обсуждается

анизотропийная теория управления, которая в рамках одной постановки

задачи включает в себя и LQG/H₂ и H_∞ теории.

Ключевые слова: линейные системы, подавление влияния внешних возму-

щений, робастное управление, робастная фильтрация, робастная стабили-

зация, субоптимальное управление, оптимальное управление, теория ин-

формации, окрашенный шум, робастная устойчивость, системы с неопре-

деленностями, дескрипторные системы, частотная теорема.

DOI: 10.31857/S0005231021040024

1. Введение

На разных этапах развития теории автоматического управления линейны-

ми стационарными системами разработчики предъявляли различные требо-

вания к функционированию систем управления. На начальном этапе базовой

задачей, стоявшей перед разработчиками систем автоматического управле-

ния, являлась задача обеспечения устойчивости замкнутой системы. По мере

усложнения целей функционирования систем управления к системам предъ-

являлись более сложные требования: обеспечение заданных характеристик

переходных процессов, оптимизация некоторых параметров и характеристик

замкнутой системы управления и т.д. Все это привело к появлению теории

¹ Работа выполнена при финансовой поддержке Российского фонда фундаментальных

исследований (проект № 19-18-50330).

оптимального управления, использующей традиционные и новые методы оп-

тимизации.

Одной из важных характеристик систем управления является энергия,

которую система затрачивает в процессе своего функционирования. Если

система описывается с помощью дифференциальных уравнений, в которые

управление входит как параметр, то энергия представляет собой интеграл

от квадратичной формы, аргументами которой являются состояние объекта

и управление, построенное для него. В случае дискретного описания управ-

ляемой системы энергией будет некоторая сумма, являющаяся аналогом ин-

теграла в непрерывном случае. Задача минимизации энергии, потребляемой

управляемой системой, является одной из важнейших задач теории опти-

мального управления, нашедшей свое применение при синтезе управления

для многих технических систем. Энергия является некой усредненной харак-

теристикой системы управления. Математическая модель такого критерия

качества может быть представлена в виде H₂ нормы замкнутой системы.

Среди множества других критериев качества можно выделить критерий по-

давления влияния наихудшего в заданном классе воздействия, действующего

на систему. Обеспечение подавления влияния наихудшего возмущения явля-

ется чрезвычайно важной задачей при проектировании систем автоматиче-

ского управления объектами, к которым предъявляются требования работо-

способности при экстремальных условиях: системы управления самолетами,

ядерными реакторами, аварийными ситуациями и т.д. Системы управления

с такими критериями качества относятся к минимаксным (игровым) систе-

мам. Математической моделью такого критерия качества является H_∞ норма

замкнутой системы.

Оба этих критерия могут рассматриваться как разные способы подавления

влияния внешних возмущений для линейной задачи при различных предпо-

ложениях на входные сигналы, действующие на систему.

В процессе работы над этими задачами в их решении обнаружились об-

щие моменты. Это навело исследователей на мысль, что должна существо-

вать теория, которая в определенном смысле обобщает эти две задачи и при

этом каждая из задач будет являться ее частным случаем. Данная работа

посвящена обзору различных задач теории автоматического управления, ко-

торые в той или иной степени разрабатывали теорию, обобщающую H₂ и H_∞

методы построения регуляторов для линейных систем.

Первая часть настоящего обзора посвящена различным теориям, постро-

енным во второй половине прошлого века, которые в той или иной степени

являются развитием классических постановок H₂ и H_∞ теорий автоматиче-

ского управления.

Вторая часть обзора в основном посвящена робастной стохастической тео-

рии управления с анизотропийным функционалом качества, которая была

создана И.Г. Владимировым, решившей задачу построения теории управле-

ния, лежащей между H₂ и H_∞ теориями. При этом обе эти теории являются

частными (предельными) случаями анизотропийной теории управления.

В конце обзора рассматриваются задачи минимаксного LQG управления,

по своей идеологии близкие к идеологии построения анизотропийного управ-

ления. В постановке задач минимаксного LQG управления также использует-

ся теоретико-информационная характеристика двух случайных сигналов

относительная энтропия. Однако в отличие от анизотропийной теории, где

понятие относительной энтропии используется для формирования критерия

качества системы управления, в минимаксном LQG управлении эта характе-

ристика сигналов используется для описания ограничений в системе.

Несмотря на близость задач управления и фильтрации [147, 149, 150], авто-

ры не включили в обзор работы по фильтрации с H₂, H_∞ и анизотропийными

критериями, так как это значительно увеличило бы объем этого обзора без

изложения существенно новых идей. Постановки и решения задач анизотро-

пийной фильтрации можно найти в [62, 63], идеи H_∞ фильтрации описаны,

например, в [9, 10]. Задачи смешанной H₂/H_∞ фильтрации, подразумеваю-

щей H₂ норму в качестве критерия минимизации и обеспечение заданного

уровня подавления внешнего возмущения, были решены в [247].

В основе анизотропийной теории управления лежат теоретико-информа-

ционные идеи описания неопределенности сигналов в системах управления,

основанные на понятии энтропии. В последнее время теоретико-информаци-

онному описанию неопределенности в различных работах уделено достаточно

большое внимание. В частности, работа [46] посвящена минимизации и мак-

симизации относительной энтропии в различных дисциплинах, однако в ней

ни слова не говорится об описании неопределенностей сигналов в системах

управления в терминах относительной энтропии. Данный обзор имеет своей

целью закрыть этот пробел.

По образному выражению из введения к книге [108] “теория информации

отвечает на два фундаментальных вопроса: каково предельное сжатие дан-

ных (ответ: энтропия) и какова предельная скорость передачи данных (ответ:

пропускная способность канала)”. Теория управления также обеспечивает два

основных требования к системам управления: построение устойчивых систем

и гарантию выбранного качества систем. И теория информации, и теория

управления имеют дело с моделями сигналов. В теории управления сигна-

лы в основном рассматриваются в роли входов и выходов собственно систем

управления (объект плюс регулятор), созданию которых и посвящена тео-

рия. В теории информации сигналы и их характеристики служат основным

предметом исследования.

В теории информации в основном исследуются сигналы, имеющие стоха-

стическую природу. Введение в теорию управления вероятностного описания

приблизило модели систем управления к реальным техническим системам.

В вероятностных терминах можно описывать как внешние сигналы, дейст-

вующие на объект, так и сигналы внутри объекта управления. Соответствен-

но, и неопределенности в системе следует описывать подобным способом.

Описание систем управления с помощью вероятностных характеристик

уже подразумевает некую неопределенность. Как отмечал в своей рабо-

те А.А. Красовский [33], “статистическое рассмотрение позволяет построить

некий мост от динамики систем к информационному описанию процессов в

системах управления. Этот мост заключается в том, что переходные процес-

сы получают описание в информационных терминах”. Однако можно ввести

неопределенности в описание характеристик случайного процесса, участвую-

щего в описании управляемой системы. Известно, что наиболее полной харак-

теристикой случайного процесса является плотность распределения вероят-

ностей. Неизвестные характеристики плотности распределения вероятностей

входного случайного сигнала или случайных начальных условий являются

неопределенностью в вероятностном описании системы, а различные моде-

ли описания неизвестных характеристик плотности позволяют ставить и ре-

шать содержательные задачи теории управления в присутствии неопределен-

ности [3]. Например, в книге Г.П. Тартаковского [60] рассматриваются задачи

оценивания параметров и фильтрации случайных процессов, стохастического

управления, в том числе при наличии априорной неопределенности.

Идеи применения теории информации стали появляться в 60-е годы XX в.

В своей книге [66] А.А. Фельдбаум указывал на большие возможности приме-

нения теоретико-информационных методов в теории управления. Во введе-

нии к своей книге [57] А.В. Солодов отмечал важность привлечения информа-

ционных характеристик сигналов для постановки задач управления. В книге

описано применение информационных характеристик к оценкам системы ав-

томатического управления, рассмотрена пропускная способность систем при

наличии помех. Однако никаких попыток ввести информационные характе-

ристики в описание модели управления или в критерии качества в то время

сделано не было.

Взаимосвязь теории информации и теории управления может рассматри-

ваться в двух направлениях. Первое направление хорошо описано в обзоре [2].

Это введение объектов исследования теории информации в описание объек-

та управления (например, канала связи), что приводит к необходимости ис-

следования традиционных задач теории управления с учетом изменившихся

моделей. Второе направление влияния теории информации на теорию управ-

ления состоит в привлечении хорошо развитого аппарата теории информации

для описания множества сигналов, циркулирующих в системе, и не только на

ее входе и выходе, но и внутри объекта управления. Учет теоретико-вероят-

ностных характеристик входных сигналов и сигналов внутри объекта управ-

ления является основой анизотропийной теории управления, обзору работ по

которой посвящена вторая часть настоящей статьи.

Авторы в основном придерживаются временной последовательности появ-

ления рассматриваемых в обзоре работ.

В работе использованы следующие обозначения: Z кольцо целых чисел,

R поле вещественных чисел, C поле комплексных чисел, E матема-

тическое ожидание, cov ковариационная матрица, ⊗ произведение Кро-

некера, diag(i₁, . . . , i_N ) диагональная матрица порядка N, на главной диа-

гонали которой стоят числа i₁, . . . , i_N , | · | евклидова норма вектора, L^m2

класс m-мерных квадратично интегрируемых случайных последовательно-

стей, l₂

класс квадратично суммируемых случайных последовательностей,

L^m2

класс R^m-мерных случайных распределенных абсолютно непрерывно

векторов с конечным вторым моментом, D(p ∥ q) относительная энтропия

или расстояние Кульбака-Лейблера [34] между двумя распределениями p и q,

A(w) анизотропия случайного вектора w, A(W ) средняя анизотропия

случайной последовательности W , |||F |||_a анизотропийная норма системы F

с уровнем средней анизотропии входной последовательности a.

H^m×m2 обозначает пространство Харди аналитических в открытом еди-

{

}

ничном круге

z ∈ C¹ : |z| < 1

на комплексной плоскости матричных функ-

ций G, имеющих конечную H₂-норму



_1/2

∫

((

)_∗

)

∥G∥₂ =1

G(ω)

G(ω) dω

2π

(

)

где черезG(ω) = lim_r→1-0 G

re^iω

, ω ∈ Ω = [-π;π], обозначено угловое гра-

ничное значение функции

∑

(1.1)

G(z) = g_k z^k,

k=0

g_k

импульсная переходная характеристика, (·)^∗ обозначает комплексное

сопряжение.

H^m×m∞ (RH^m×m∞) обозначает пространство Харди (правильных) аналити-

ческих в открытом единичном круге передаточных функций H(z) дискретной

системы, с нормой

(1.2)

∥H∥_∞ = sup

σ(H(z)),

|z|<1

где σ(·) обозначает максимальное сингулярное значение матрицы.

2. Обзор современных подходов к понижению влияния внешних

возмущений в линейных системах

В 50-е гг. двадцатого века на основе фундаментальной работы [32] по тео-

рии линейной фильтрации в дискретном времени, опубликованной в 1941 г.

академиком А.Н. Колмогоровым, и подобной теории, независимо разработан-

ной крупным американским математиком Н. Винером, рассмотревшим зада-

чи линейной фильтрации сигналов, а также их экстраполяции и интерполя-

ции для непрерывного времени [233], появились исследования по применению

вероятностных методов в теории фильтрации и позже в теории автоматиче-

ского управления. Подробнее об этом можно узнать в [19].

Ранее, как правило, предполагалось, что сигналы, функционирующие в

системе управления, имеют детерминированный характер. Основой теории

Винера-Колмогорова была спектральная теория случайных процессов, раз-

вившаяся из фундаментальной работы А.Я. Хинчина [68], в которой было

установлено, что корреляционная функция случайного процесса и его энер-

гетический спектр мощности связаны преобразованием Фурье. Теория, из-

ложенная в книге Н. Винера, была очень сложна для понимания инженера-

ми, которые в те годы не имели для этого необходимой математической под-

готовки. Известные американские ученые Г.В. Боде и К. Шеннон в 1950 г.,

используя интуитивно понятные соображения, дали упрощенное изложение

этой теории [98]. Совершенно другой подход к проблемам выделения сигна-

ла на фоне шума, отличный от теории Колмогорова-Винера, применимый и

к проблемам оптимальной линейной фильтрации сигналов, был предложен

Р.Л. Стратоновичем в 1959 г. [58]. Теория Р.Л. Стратоновича основывалась

на представлении случайных процессов, моделирующих как полезный сиг-

нал, так и шум с помощью дифференциальных уравнений (уравнений состоя-

ния). Независимо от Р.Л. Стратоновича законченные результаты оптималь-

ной линейной фильтрации как в дискретном, так и в непрерывном времени

получили в 1961 г. американские ученые Р.Е. Калман и Р.С. Бьюси [149, 150].

Для гауссовских и марковских случайных процессов Р.Л. Стратоновичем,

Р.Е. Калманом и Р.С. Бьюси были выведены дифференциальные уравнения,

определяющие структуру оптимального фильтра, на вход которого посту-

пает принимаемый сигнал, и матричное уравнение Риккати, определяющее

точность его оценки. Наличие дифференциальных уравнений оценки вместо

интегральных предоставляет определенные практические преимущества, так

как дифференциальные уравнения решаются намного легче с помощью ана-

логовой или цифровой техники, чем интегральные.

Введение в теорию управления сигналов, имеющих вероятностные харак-

теристики, позволило ставить и решать новый класс задач теории управле-

ния. Одним из ярких результатов того времени явилась теория построения

регуляторов для линейных систем с квадратичным критерием качества, обес-

печившая мощный инструмент для синтеза многомерных систем управления.

Так называемая LQG задача (Р.E. Калман [28, 148]) (аббревиатура LQG соот-

ветствует первым буквам английских слов в выражении “линейно-квадратич-

ная гауссовская”) это задача построения управления для объекта с линей-

ной динамикой, возбужденной аддитивным гауссовским шумом, и критерием

качества, который является математическим ожиданием положительно полу-

определенной квадратичной формы и содержит интересную особенность. Ли-

нейный регулятор, являющийся решением этой задачи, оказывается линейной

функцией состояния и идентичен регулятору в задаче, в которой отсутствует

гауссовский шум. Такая задача называется задачей построения LQR регу-

лятора (аббревиатура LQR соответствует первым буквам английских слов в

выражении “линейно-квадратичный регулятор”). Эта задача была решена в

работах А.М. Летова [41-44].

Напомним постановку и решение задачи LQG оптимизации для динами-

ческой линейной системы, заданной в непрерывном времени в следующем

виде:

(2.1)

x(t) = A(t) x(t) + B(t)u(t) + v(t),

(2.2)

y(t) = C(t)x(t) + w(t),

где x вектор состояния системы, u вектор управления, y измеряемый

выход, используемый для построения управления. На систему также действу-

ют аддитивные гауссовские белые шумы v(t) и w(t)². Для заданной системы

² Формулы (2.1)-(2.2) являются символической (инженерной) записью случайных про-

цессов, представленных в интегральной форме, которая включает стохастический интеграл

Ито [143].

требуется найти такую последовательность u(t), которая в каждый момент

времени t линейно зависит только от предыдущих значений y(t^′), 0 ≤ t^′ < t,

и минимизирует следующий критерий качества:





∫

(

)

J = E x^T(T)Fx(T) +

x^T(t)Q(t)x(t) + u^T(t)R(t)u(t)

dt ,

F ≥ 0, Q(t) ≥ 0, R(t) > 0.

Время (горизонт) T может быть как конечным, так и бесконечным. Если

T → ∞, то первым членом x^T(T)Fx(T) нужно пренебречь. Для того чтобы

функционал качества J не стремился в этом случае к бесконечности, имеет

смысл рассмотреть новый функционал, равный^JT .

LQG регулятор, который решает поставленную задачу, удовлетворяет

уравнениям

(2.3)

x(t) = A(t)x(t) + B(t)u(t) + L(t)(y(t) - C x(t)),

x(0) = E [x(0)],

(2.4)

u(t) = -K(t)x(t).

Матрица L(t) называется коэффициентом усиления Калмана и ассоциируется

с фильтром Калмана, представленным уравнением (2.3). В каждый момент

времени фильтр генерирует оценку x(t) состояния x(t), используя измерения

и входы. Коэффициент усиления L(t) определяется матрицами A(t), C(t),

V (t), W (t), две последние являются ковариационными матрицами v(t) и w(t),

а также E (x(0)x^T(0)). Коэффициент усиления Калмана может быть найден

из следующего матричного дифференциального уравнения Риккати:

(t) = A(t)P (t) + P (t)A^T(t) - P (t)C^T(t)W^-1(t)C(t)P (t) + V (t),

P (0) = E (x(0)x^T(0)).

При известном решении P (t), 0 ≤ t ≤ T , коэффициент усиления Калмана ра-

вен

L(t) = P (t)C^T(t)W^-1(t).

Матрица обратной связи K(t) определяется с помощью матриц A(t), B(t),

Q(t), R(t) и F и может быть найдена из матричного дифференциального

уравнения Риккати

- S(t) = A^T(t)S(t) + S(t)A(t) - S(t)B(t)R^-1(t)B^T(t)S(t) + Q(t),

S(T ) = F.

При найденном S(t), 0 ≤ t ≤ T , матрица K(t) равна R^-1(t)B^T(t)S(t).

Полученные матричные уравнения Риккати очень похожи за исключением

того, что первое решается в прямом времени, а второе в обратном. Первое

уравнение дает возможность найти решение задачи линейно-квадратичного

оценивания (LQE), а второе задачу поиска линейно-квадратичного регу-

лятора (LQR). Вместе эти две задачи представляют собой задачу линейно-

квадратичного гауссовского управления (LQG). Задачи оценивания (LQE) и

поиска регулятора (LQR) могут быть решены отдельно, эта идея получила

название принципа разделения.

Когда матрицы A(t), B(t), C(t), Q(t), R(t), V (t), W (t) не зависят от вре-

мени, а T → ∞, закон управления становится стационарным, а динамические

уравнения Риккати могут быть заменены алгебраическими [54, 55].

2.1. LQG, LEQG и регуляторы, чувствительные к риску

Приведем формулировку и схему решения LQG задачи для линейной

нестационарной системы управления, описываемой следующими уравнения-

ми:

(2.5)

x_k+1 = A_kx_k + B_ku_k + w_k,

(2.6)

y_k = C_kx_k + v_k

0≤k<N,

с нулевым начальным условием x₀ = 0. Здесь k является индексом времени,

а w_k, v_k представляют собой независимые дискретные гауссовские случайные

процессы с ковариационными матрицами W_k, V_k соответственно.

Функционал качества задается следующим выражением:

(

)

∑

(

)

(2.7)

J =E x^TNFx_N +

x^Tk Q_kx_k + u^Tk R_ku_k

k=0

F ≥ 0, Q_k ≥ 0, R_k > 0.

Требуется найти регулятор, стабилизирующий замкнутую систему и ми-

нимизирующий функционал качества (2.7).

Регулятор в LQG задаче задается равенством

(2.8)

u_k = -L_k x_k,

где x_k является оценкой x_k. Оценка x_k состояния x_k вычисляется с помощью

решения разностного уравнения Риккати. Матрица обратной связи L_k так-

же находится с помощью решения разностного уравнения Риккати. Таким

образом, для получения управления (2.8), минимизирующего функционал

качества (2.7), надо решить два разностных уравнения Риккати. Если все

матрицы в формулировке задачи стационарны и если горизонт N стремит-

ся к бесконечности, дискретный LQG регулятор становится стационарным.

В этом случае разностные уравнения Риккати заменяются соответствующи-

ми алгебраическими уравнениями. Причем уравнения для определения x_k

и L_k можно решать независимо, т.е. раздельно. В теории LQG управления

принцип разделения, не верный в детерминированных системах и более фор-

мально известный как принцип разделения оценки и контроля, утверждает,

что задача создания оптимальных LQG регуляторов по принципу обратной

связи для стохастической системы может быть решена путем разработки оп-

тимального наблюдателя состояния системы, который подставляется в оп-

тимальный детерминированный регулятор. Таким образом, проблема может

быть разбита на две отдельные части, что облегчает синтез. Этот важный

в LQG дискретной задаче принцип разделения подробно описан, например,

в [48, 67].

Критерий качества (2.7), используемый в постановке задачи поиска оп-

тимального LQG регулятора, в стационарном случае идентичен H₂ норме

передаточной функции замкнутой системы. Таким образом, решение опти-

мальной LQG задачи подразумевает минимизацию H₂ нормы замкнутой си-

стемы. В данной ситуации можно говорить о решении H₂ оптимальной задачи

управления.

Обратим внимание, что описанная выше задача не имеет неопределен-

ностей ни в описании модели объекта, ни в описании входных возмущений,

так как гауссовская входная последовательность полностью определена своей

функцией плотности распределения вероятностей.

LQG и LQR задачам посвящено огромное количество литературы во всем

мире. Обширная библиография приведена в [80]. В России наиболее популяр-

на была монография Х. Квакернаака и Р. Сивана [29], в которой изложены

эти задачи как для непрерывных, так и для дискретных систем управления.

Описание вычислительных процедур можно найти в [83, 220].

В июне 1971 г. вышел первый тематический выпуск журнала IEEE Tran-

sactions on Automatic Control. Этот выпуск был полностью посвящен различ-

ным аспектам LQG управления и, по словам его редактора, подводил итоги

как теоретических и алгоритмических, так и возможных практических аспек-

тов этой задачи [84]. Однако уже в этом номере появились работы [84, 194],

ставившие под сомнение универсальность этой теории. По образному выра-

жению Д.С. Бернштейна [96] “LQG теория и ее техника уравнений Риккати

очень похожа на здание, состоящее из одних стальных рам, очень жесткое

и очень ограниченное”.

В реальных задачах LQG регулятор работал достаточно хорошо, если ад-

дитивная помеха была гауссовским белым шумом. Однако если у входного

возмущения была достаточно большая временная ковариация, т.е. шум не

белый, то LQG регуляторы не удовлетворяли требованиям, предъявляемым

к замкнутым этими регуляторами системам управления. Интуитивно было

понятно, что в случае большой ковариации входного возмущения другие ре-

гуляторы должны работать лучше, чем LQG. Это соображение подводило

разработчиков систем управления к мысли учитывать при построении регу-

ляторов свойства случайных сигналов, циркулирующих в системе управле-

ния. Одним из подходов к учету отличия входного случайного сигнала от

белого шума был подход, основанный на изменении критерия качества (оп-

тимальности) для системы управления.

Этот подход впервые применил Д. Джекобсон в 1973 г. в [144]. В этой ста-

тье автор впервые предложил использовать экспоненциально-квадратичный

функционал качества. Задачу с критерием качества, в который входит экс-

понента, стали называть LEQG задачей (линейной, экспоненциально-квад-

ратичной, гауссовской).

В [144] рассматривалась линейная стационарная система с наблюдаемым

вектором состояния

x_k+1 = Ax_k + B₁w_k + B₂u_k,

y_k = x_k,

где x_k вектор состояния, y_k наблюдаемый вектор, u_k вектор управле-

ния, w_k гауссовский шум, постоянные матрицы A, B₁, B₂ имеют соответ-

ствующие размерности. Вводилась квадратичная форма

∑

(2.9)

G = x^TNΠx_N + (xTk Q_kx_k + uTk R_ku_k

k=0

Задача состояла в построении регулятора, минимизирующего функционал,

равный

[

{

}]

Υ_N = σE exp σ

причем параметр σ принимал значения ±1. Значение -1 соответствовало

так называемой LE - G задаче, а +1 LE + G постановке. Когда интенсив-

ность шума стремилась к бесконечности, оптимальные коэффициенты усиле-

ния для LE - G задачи стремились к нулю, т.е. при таком входном воздей-

ствии практически невозможно было уменьшить значение критерия качества

за счет подачи управляющего сигнала. В задаче LE + G оптимальный регу-

лятор переставал существовать, если интенсивность шума была достаточно

большой (т.е. критерий качества стремился к бесконечности независимо от

управляющего входа). Регулятор получался линейной функцией состояния

u_k = K(Σ_k)x_k,

причем коэффициент K(Σ_k) зависел от Σ_k ковариационной матрицы w_k.

Более того, прямыми вычислениями Джекобсон впервые показал, что струк-

тура соответствующего регулятора является той же, что и структура регуля-

тора для задачи управления в динамической игре. Этот интересный результат

впервые установил связь между задачами управления в динамических детер-

минированных играх и задачами управления, основанными на минимизации

стохастических функций качества.

В отсутствие шума решение этой задачи совпадало с LQR задачей. Однако

в присутствии шума оптимальные регуляторы в задаче Джекобсона с экспо-

ненциальным критерием качества отличались от регуляторов в LQG задаче.

И хотя, как и в случае LQG задачи, эти регуляторы являлись линейными

функциями переменных состояния, они определенно зависели от ковариа-

ционной матрицы аддитивного гауссовского шума. Для малых ковариаций

решения этих задач были близки, но для больших заметно разнились.

Подчеркнем, что в задаче Джекобсона отсутствуют неопределенности в

описании объекта и входных возмущений.

Вплоть до работы П. Уиттла [229] общий случай (случай наблюдения

неполного вектора состояний) не был решен. Уиттл рассматривал модель

объекта в виде

x_k+1 = Ax_k + Bu_k + ε_k,

y_k = Cx_k + η_k,

где ε_k и η_k являются входным возмущением и шумом измерений соответствен-

но. Предполагалось, что последовательность векторов {[ε^Tk, η^Tk]^T} являлась

гауссовским белым шумом с совместной ковариационной матрицей

[

]

N 0

cov[ε^Tk, η^Tk] =

Вводилась следующая квадратичная форма:

∑

G = x^TTΠx_T + (xTk Qx_k + uTk Ru_k).

k=0

Функционал качества выбирался в виде

(

)

(2.10)

γ(θ) = -2θ^-1 log E e^-1/2θG

Матрицы N, M, R, Q, Π положительно определенные, θ действительный

скаляр.

Если величина θVar(G) мала (здесь Var(G) дисперсия), то γ(θ) ∼ E(G)-

- 1/4θVar(G). Это иллюстрирует тот факт, что случаи θ = 0 , θ > 0 и θ < 0

соответствуют поведению, нейтральному к риску, предпочитающему риск и

не охотно относящемуся к риску соответственно в задачах оптимизации [97].

Параметр θ Уиттл назвал параметром чувствительности к риску и продемон-

стрировал, что, выбирая этот параметр слишком большим, можно прийти к

ситуации, в которой критерий качества может принимать бесконечные зна-

чения. Из приведенных выше рассуждений следует, что γ(0) является тра-

диционным критерием и E (G) является предельным значением для γ(θ) при

стремлении θ к 0 с обеих сторон.

Уиттл показал, что оптимальный регулятор является линейной функци-

ей оценки состояния, получаемой с помощью модифицированного фильтра

Калмана.

Задача построения управления путем минимизации экспоненциально-

квадратичного функционала задача построения управления, чувствитель-

ного к риску (risk-sensitive problem), изучалась в различных интерпрета-

циях в [93, 103, 104, 145, 229, 230, 232].

Однако LQG и LEQG теории были весьма ограничены в своих приложе-

ниях к синтезу реальных технических систем управления. В конце 70-х годов

была указана причина ограниченных возможностей LQG теории [114]. Эта

причина состояла в том, что регуляторы, построенные в рамках этой теории,

плохо работали в присутствии неучтенных при синтезе неопределенностей

объекта, даже если эти неопределенности были малы. Говоря современным

языком, системы управления, замкнутые LQG регулятором, были не робаст-

ны относительно некоторых неточностей в описании объекта. Необходимо

подчеркнуть, что с понятием неточности в описании модели объекта или

входных сигналов в рассмотрение специалистов по теории управления вхо-

дит и описание класса тех неопределенностей, которые так или иначе долж-

ны быть определены. Под неопределенностью описания объекта управления

будем понимать параметрическую неопределенность в описании коэффици-

ентов математической модели, неструктурированную (структурированную)

неопределенность в описании модели объекта, а также неопределенность в ви-

де так называемой M-Δ конфигурации в соответствии с современной класси-

фикацией неопределенностей. Более подробно об описании моделей неопреде-

ленностей можно прочитать в [6, 52, 53, 174, 191]. Неопределенность в описа-

нии сигналов в системе управления определим в теоретико-информационных

терминах несколько позже.

2.2. H_∞ оптимальные и субоптимальные регуляторы

Попытки обойти изъяны теории построения регуляторов для линейных

систем с квадратичным критерием качества [115] привели к возрождению

частотного подхода в форме теории H_∞ оптимизации [250].

В своей пионерской работе [250] для построения регуляторов Д. Зеймс

предложил использовать другой критерий качества H_∞ норму замкну-

той системы. Использование этой нормы в известном смысле обеспечивало

робастную устойчивость системы. Идея этого способа обеспечения робаст-

ной устойчивости основана на известном круговом свойстве индуцированной

нормы оператора (см., например, [25]) и на связи между устойчивостью си-

стемы управления и условием обеспечения сжимаемости оператора системы

(его норма должна быть меньше 1). Если ∥A∥_ind является индуцированной

нормой оператора A, то

(2.11)

∥AB∥_ind ≤ ∥A∥_ind∥B∥_ind.

Если в качестве A понимать оператор системы, а в качестве B оператор

неопределенности Δ, тогда требование выполнения условия

∥A∥_ind∥Δ∥_ind < 1

обеспечивает устойчивость последовательно соединенных операторов систе-

мы и неопределенности. Причем “размер” неопределенности, при которой со-

вокупная система остается устойчивой, определяется “размером” системы

∥Δ∥_ind < 1/∥A∥_ind.

Если в качестве индуцированной нормы оператора взять индуцированную

l₂ норму оператора (т.е. H_∞ норму), тогда неравенство (2.11) перепишется в

Рис. 1. Нижнее дробно-линейное преобразование L(F, K).

виде

(2.12)

∥AB∥_∞ ≤ ∥A∥_∞∥B∥_∞.

Последнее неравенство тесно связано с так называемой теоремой о малом

усилении (small gain theorem), опубликованной Зеймсом в 1966 г. [248, 249].

Приведем формальную постановку задачи построения управления по кри-

терию минимума H_∞ нормы замкнутой системы.

Пусть разомкнутая система F имеет n-мерное внутреннее состояние x_k,

связанное с m₁-мерным возмущением w_k, m₂-мерным управлением u_k,

p₁-мерным управляемым сигналом z_k и p₂-мерным наблюдением y_k уравне-

ниями

x_k+1 = Ax_k + B₁w_k + B₂u_k,

(2.13)

z_k = C₁x_k + D₁₁w_k + D₁₂u_k,

y_k = C₂x_k + D₂₁w_k,

-∞ < k < +∞,

где A, C_i, B_j и D_ij постоянные матрицы соответствующих размеров. Си-

стема F имеет блочную структуру

[

]

F₁₁

F₁₂

(2.14)

F =

F₂₁

F₂₂

Система F , а также ее подсистемы F_ij в (2.14) имеют следующие реализации

в пространстве состояний:





A B₁

B₂

.

(2.15)

F ∼C1 D11

D₁₂

C₂

D₂₁

Если управляющий сигнал U формируется по наблюдению Y регулято-

ром K, являющимся физически реализуемой линейной стационарной (не обя-

зательно устойчивой) системой, т.е. U = K ⊗ Y , то передаточная функция

от W к Z получающейся замкнутой системы представляет собой нижнее

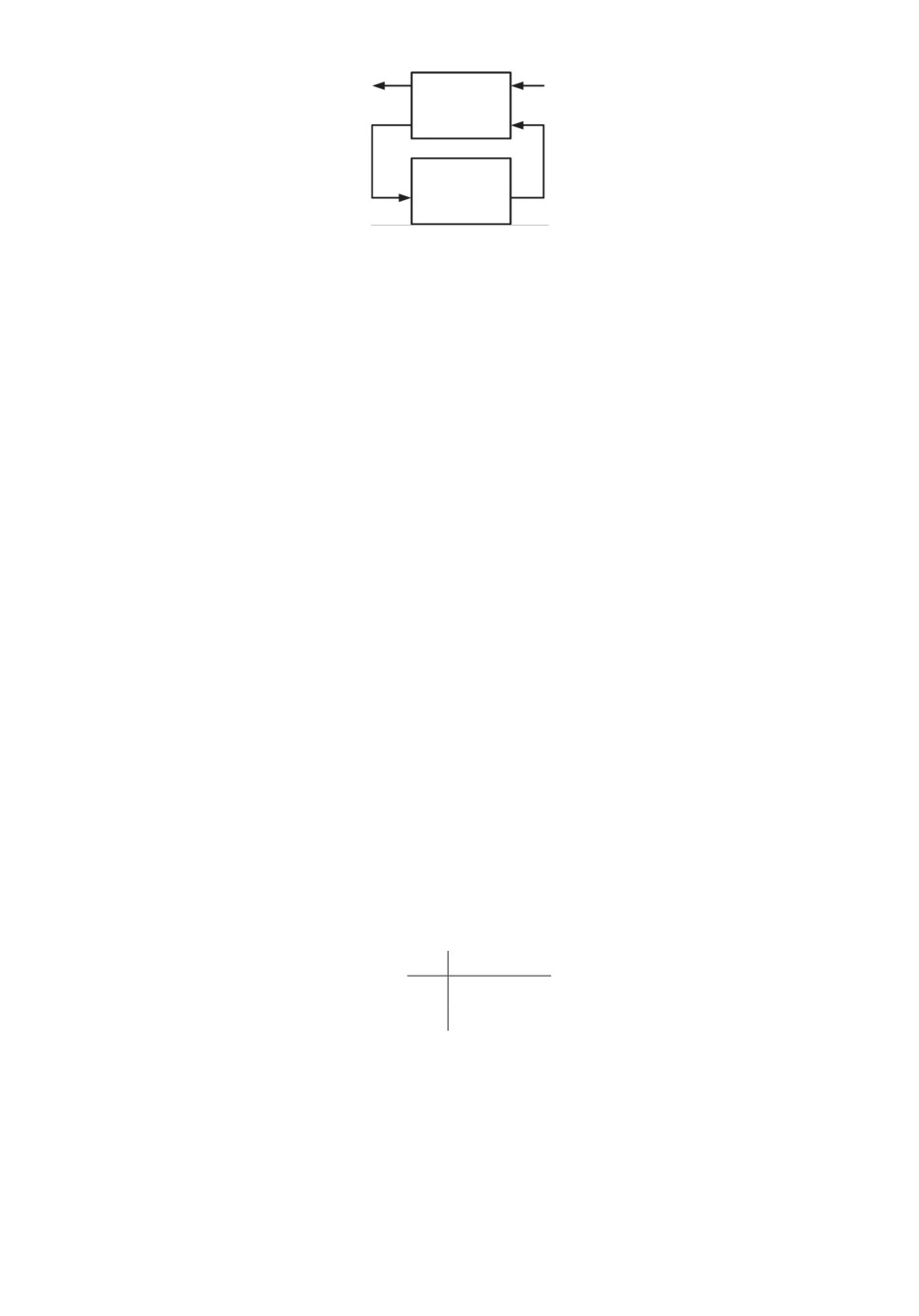
дробно-линейное преобразование пары (F, K) (см. рис. 1):

(2.16)

L(F, K) = F₁₁ + F₁₂ K (Ip2 - F₂₂K)^-1 F₂₁.

Задача построения оптимального H_∞ управления состоит в построении

регулятора, обеспечивающего минимум H_∞ нормы, замкнутой этим регуля-

тором системы, от W к Z. Другими словами, оптимальный H_∞ регулятор

должен обеспечивать условие

||L(F, K)||_∞ → inf .

В частотной области H_∞ норма линейной системы может быть интерпрети-

рована как максимальное значение АЧХ системы. Хорошо известно, что ре-

шение задачи синтеза H_∞ регулятора в частотной области сводится к поиску

матричных передаточных функций замкнутой системы с более равномерной

АЧХ на всем диапазоне частот [121]. В отечественной литературе подобная

интерпретация H_∞ нормы носит название равномерно-частотного показате-

ля [11].

Решение оптимальной H_∞ задачи управления сводится к решению доста-

точно известной в теории управления задачи слежения за моделью (model

matching problem) в H_∞ метрике (метрике пространствa Харди). Для систем

с одним входом и одним выходом (SISO) это решение описано в моногра-

фии [118] путем сведения задачи слежения за моделью к интерполяцион-

ной задаче Неванлинны-Пика. Для систем с многими входами и выходами

(MIMO) решение задачи слежения за моделью и, следовательно, H_∞ опти-

мальной задачи сводится к известной задаче Нехари. Построение H_∞ опти-

мальных регуляторов методом сведения этой задачи к задаче Нехари изло-

жено в [121], а также в [192]. В России решение задачи H_∞ оптимизации

посредством решения задачи Нехари было описано в [51].

Несмотря на привлекательность H_∞ регуляторов, алгоритмы построения

оптимального H_∞ управления были достаточно сложны для восприятия ин-

женерами-разработчиками систем управления на рубеже 80-х годов прошло-

го века. Кроме того, эти алгоритмы обладали в глазах инженеров большим

недостатком: оптимальный регулятор мог иметь порядок значительно больше

порядка самой системы.

Существенным моментом в построении H_∞ теории управления явился пе-

реход от оптимальной H_∞ задачи к субоптимальной. Решение субоптималь-

ной H_∞ задачи в наиболее полном виде в пространстве состояний для слу-

чая непрерывного времени опубликовано в знаменитой “работе четырех ав-

торов” [117] и для дискретного случая в [139]. Решения задачи H_∞ субоп-

тимального управления напоминают решения классической LQG задачи. За

счет сведения решения задачи H_∞ субоптимального управления к решению

двух уравнений Риккати вычислительная сложность решения субоптималь-

ной задачи получилась значительно меньше, чем решение оптимальной зада-

чи. Решение H_∞ субоптимальной задачи с помощью двух уравнений Риккати

стали называть “2-Риккати подходом”.

Решение дискретной задачи H_∞ субоптимального управления всегда мо-

жет быть получено с использованием хорошо известного преобразования

1+s

1-s

Это преобразование переводит функции, аналитические в полуплоскости, в

функции, аналитические в единичном круге. Более того, Ганкелева норма

и H_∞ норма передаточной функции являются инвариантными относитель-

но этого преобразования. По этой причине субоптимальный H_∞ регулятор

может быть получен с использованием следующей процедуры. Преобразу-

ем дискретный объект G(z) в соответствующий непрерывный объектG(s) =

(

)

1+s

. Построим регулятор в задаче с непрерывным временемK(s), ко-

1-s

торый преобразуется в регулятор с дискретным временем с использованием

обратного преобразования. Описанная процедура теоретически корректна.

Однако сложность ее выполнения сравнима с получением необходимых урав-

нений напрямую. Более того, использование преобразования невозможно для

систем, имеющих полюса в точке -1. Для таких систем требуется другое би-

линейное преобразование.

Как было сказано выше, решение субоптимальной H_∞ задачи управле-

ния сводится к решению двух связанных уравнений Риккати, в которые вхо-

дит параметр γ, задающий ограничение на верхнюю границу критерия каче-

ства H_∞ норму замкнутой системы, т.е.

∥T_zw∥_∞ ≤ γ,

где T_zw передаточная функция замкнутой системы от возмущающего входа

к управляемому выходу.

Заметим, что для H_∞ субоптимальных регуляторов справедливо утвер-

ждение, аналогичное принципу разделения при синтезе H₂ оптимального ре-

гулятора. H_∞ субоптимальный регулятор с обратной связью по выходу яв-

ляется оценивателем по выходу в случае закона управления по вектору со-

стояния в присутствии “наихудшего случая” возмущения. Этот принцип не

означает возможность автономно решать задачу оценивания и управления,

как в случае H₂ задачи, однако в случае наихудшего возмущения, равного

нулю, принцип разделения в H_∞ задаче становится принципом разделения в

H₂ задаче.

Решение H_∞ субоптимальной задачи входит в различные компьютерные

пакеты для разработки систем управления, например в известный MATLAB

Robust Control Toolbox [254].

2.3. Робастная устойчивость (в H_∞ теории управления)

Важнейшей целью в синтезе систем управления является обеспечение

устойчивости замкнутых систем. Это минимальное требование к любо-

му регулятору. В реальности же поведение объекта управления может отли-

чаться от поведения его математической модели (называемой номинальным

объектом). Эти отличия могут быть вызваны округлением или недостаточ-

ной точностью приборов для измерения параметров системы, технологиче-

ским разбросом характеристик компонент объекта управления, нелинейной

или неучтенной динамикой и т.д. Отличие между реальным объектом и его

номинальной моделью называется ошибкой моделирования или неопределен-

ностью системы. Из-за наличия неопределенностей в системе синтезируемый

регулятор должен не только стабилизировать номинальный объект управле-

ния, но должен также стабилизировать семейство систем, которое состоит из

области неопределенности вокруг номинальной модели в предположении, что

реальный объект входит в это семейство.

Необходимость стабилизировать систему с неопределенностью определила

концепцию робастной устойчивости: замкнутая система остается устойчивой

при наличии неопределенностей из некоторого известного наперед множе-

ства. Методы H_∞ теории управления способствовали получению значитель-

ных результатов в области робастной стабилизации объектов с неопределен-

ными параметрами.

Существует много способов описания неопределенности в системах управ-

ления. Для знакомства с большинством описаний этих неопределенностей

авторы рекомендуют работу [191], в которой перечислены и определены ос-

новные способы описания неопределенностей. Достаточно распространенным

способом описания меры неопределенности является L_∞ норма.

В H_∞ теории управления принято моделировать неопределенность пере-

даточной функцией, отдельной от передаточной функции номинального объ-

екта. Такой подход впервые для аддитивных и мультипликативных неопреде-

ленностей был применен в [106, 116] и для неопределенностей в виде взаимно

простых множителей (факторов) в [222, 223].

Используя нижнее дробно-линейное преобразование пары (F, Δ), задавае-

мое формулой (2.16), определим вид матрицы F для основных типов неструк-

турированных неопределенностей, следуя монографии [132]:

[

]

1) аддитивной неопределенности соответствует матрица F =

, где

I G_O

GO передаточная функция номинального объ[кта;

]

-G_O G_O

2) обратной аддитивной неопределенности F =

;

-G_O G_O

[

]

3) входной мультипликативной неопределенности F =

;

GO GO

[

]

4) выходной мультипликативной неопределенности F =

;

I G_O

5) обратной входной мультипликативной неопределенности

[

]

-I I

F =

;

-G_O G_O

6) обратной выходной мультипликативной неопределенности

[

]

-I G_O

F =

;

-I G_O

7) левой неопределенности в виде взаимно простых факторов

 [

]

[

]



-M-1

-G_O





F =



,

M-1

Рис. 2. Верхнее дробно-линейное преобразование U(F, Δ).

где G_O =M-1

N левая взаимно простая факторизация номинального

объекта, F = (M +ΔM )^-1

N + ΔN) передаточная функция возмущен-

[

]

ного объекта, Δ =

Δ_M

Δ_N

;

8) правой неопределенности в виде взаимно простых факторов

[ [

]

M-1

-M-1 0

F =

[

]

-G_O I

[

]

Δ_M

где G_O

NM-1, F =

N + ΔN)(M+ ΔM)^-1, Δ =

Δ_N

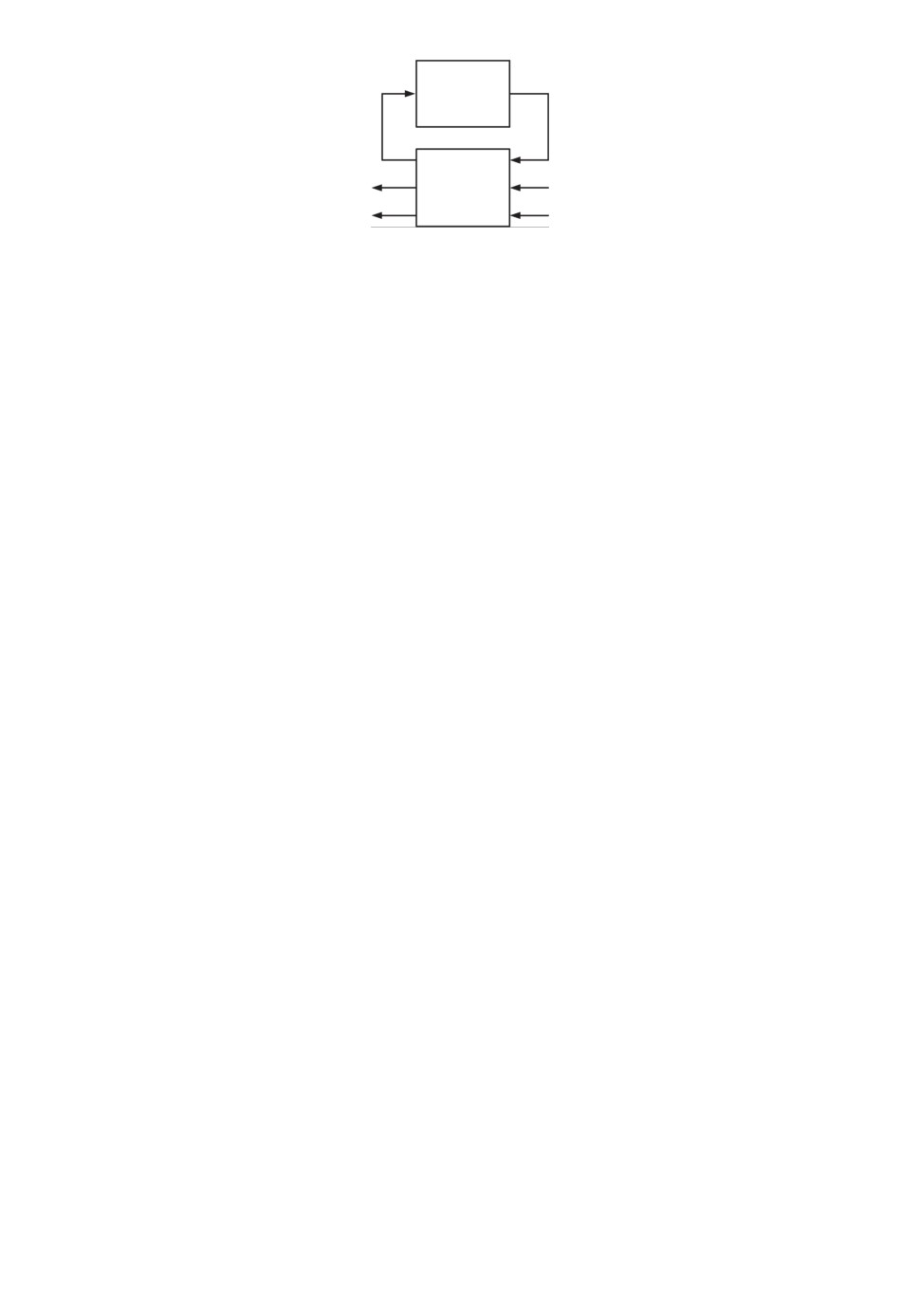
На рис. 2 схематично представлено так называемое верхнее дробно-линей-

ное преобразование. Оно задается следующей формулой:

(2.17)

U (F, Δ) = F₂₂ + F₂₁Δ(I_n - F₁₁Δ)^-1F₁₂.

При обратимой (I_n - F₁₁Δ) систему с тремя неопределенностями (адди-

тивной, мультипликативной и неопределенностью в виде взаимно простых

факторов) можно представить в виде верхнего дробно-линейного преобра-

зования так называемого стандартного объекта F [174], представленного в

блочном виде (2.14), и неопределенности Δ.

Во всех описанных выше типах неопределенностей предполагается, что

Δ не имеет определенной структуры. Рассмотрим теперь структуриро-

ванную неопределенность, включающую в себя немоделируемую динамику

(неструктурированную неопределенность) и параметрическую неопределен-

ность. В этом случае система с неопределенностью может быть представлена

верхним дробно-линейным преобразованием (2.17), где

Δ = diag(δ₁Ir1, ..., δ_sIrs, Δ₁, ..., Δ_f),

δ_i ∈ C, Δ_i ∈ Chj×hj , Σ^si=1r_i + Σ^fj=1h_j = n, где n порядок Δ.

В [174] приведены необходимые и достаточные условия робастной стабили-

зируемости номинального объекта при наличии неопределенностей. Это усло-

вие подразумевает выполнение теста на H_∞ норму передаточной функции си-

стемы. Математической основой для этого теста для разных классов неопре-

деленностей является уже упоминаемая теорема о малом усилении [248, 249]

и круговое свойство индуцированных норм (2.11) [25].

Робастные регуляторы могут быть найдены с помощью процедуры реше-

ния задачи H_∞ оптимизации, поставленной в [250].

Целью данной работы не является подробное изложение задач робаст-

ного анализа и синтеза, так как этому вопросу посвящено много литерату-

ры [120, 130, 205, 252]. Здесь необходимо было сформулировать основные по-

нятия робастного анализа, чтобы далее была возможность при изложении

этих вопросов в рамках анизотропийной теории управления ссылаться на ре-

зультаты, полученные, в частности, в H_∞ теории управления. Более подробно

о задачах робастного анализа и синтеза можно прочесть в недавно вышедшем

обзоре [191].

В конце 80-х годов была создана теория робастного управления (H_∞ оп-

тимального и H_∞ субоптимального управления) для систем в пространстве

состояний. В рамках этой теории был четко определен класс неопределенно-

стей, которые надо учитывать при построении систем управления.

Необходимость описания классов неопределенностей была давно понята

специалистами по теории управления. Существует много работ, в которых

так или иначе определяются неопределенности в теории управления, но здесь

представляют интерес неопределенности в описании системы, которая фигу-

рирует в задаче H_∞ оптимизации [100, 157, 228, 236, 240, 243].

В рамках этих теорий можно было, используя теорему о малом усилении,

гарантированно обеспечивать робастность замкнутой системы.

Теориям H_∞ оптимального и H_∞ субоптимального управления посвящено

огромное количество монографий, вышедших как за рубежом, так и в России.

Из них стоит упомянуть книги [118, 121, 130, 205, 252], вышедшие на Западе.

На русском языке выходили обзоры [51, 76, 77], которые сейчас стали библио-

графической редкостью. H_∞ оптимальное и H_∞ субоптимальное управление

упомянуто в монографиях [8, 35, 52, 78].

2.4. H₂ субоптимальные и робастные регуляторы

Естественно предположить, что постановка задач синтеза H₂ субопти-

мального управления должна была возникнуть в начале 60-х годов вслед

за постановками и решениями H₂ оптимальных задач [41, 148]. Однако ис-

торически активное исследование субоптимальных и робастных H₂ регуля-

торов началось значительно позже, в 90-x годах прошлого века. По мнению

авторов, на это повлияли два фактора. Первый появившиеся численные

методы решения линейных матричных неравенств [101, 184] и задач выпук-

лой оптимизации [102], второй развитие методологии и методики решения

задач робастного и субоптимального H_∞ управления [101]. Поэтому раздел,

посвященный H₂ субоптимальным робастным регуляторам, помещен после

раздела, посвященного H_∞ регуляторам.

Как указывается во введении к статье [170], “в практической задаче мо-

жет оказаться, что оптимальный H₂ регулятор для заданного конкретного

объекта может не существовать. То есть данный объект не может удовлетво-

рять необходимым и достаточным условиям для существования оптимально-

го H₂ управления” (для более детальной информации см., например, [195]).

Тогда разработчик вынужден искать неоптимальный регулятор. При отсут-

ствии формального определения субоптимального регулятора любой регу-

лятор, который обеспечивает внутреннюю устойчивость системы, замкнутой

контуром, может быть истолкован как субоптимальный регулятор. Однако

определение субоптимальности естественно дать через достижение H₂ нормы

(или любой указанной нормы) выбранной передаточной функции ограниче-

ния

∥T_zw∥₂ ≤ γ,

где T_zw матрица передаточных функций замкнутой системы от W к Z, γ

допустимая мера усиления возмущения.

В [195] дается краткое описание субоптимальной задачи H₂ управления.

Эта работа решает задачу синтеза регулятора, такого что H₂ норма замкну-

той системы сколь угодно близка к оптимальному значению. Теоретическое

решение этой проблемы обеспечивается с помощью теории возмущений.

Перечислим результаты лишь некоторых работ, посвященных синтезу H₂

управления. В [170] построено субоптимальное управление по состоянию и

с использованием трех различных дифференциальных оценивателей (про-

гнозирования, оценивания текущего состояния и оценивателя пониженного

порядка) для дискретных стационарных систем. Динамический компенсатор

для дискретных систем, обеспечивающий устойчивость и желаемое поведение

системы, разработан в [154]. Вопросы робастного H₂ оценивания для систем с

ограниченными по норме и политопическими неопределенностями были рас-

смотрены в [235]. Управление по выходу для систем с неопределенностями

предложено в [197].

Предлагаемый читателю обзор ни в коей мере не может рассматриваться

как изложение LQG, H₂, H_∞, а также связанных с этими задачами других

теорий, поскольку имеет целью только изложить фактические работы, кото-

рые появились в этом направлении. Тем не менее сформулировать вышеупо-

мянутые задачи следовало.

2.5. Редукция моделей в H₂ и H_∞ теориях управления

Решение описанных выше задач сводится к нахождению оптимально-

го (субоптимального) регулятора полного порядка, равного порядку моде-

ли объекта управления. В технических приложениях очень часто возника-

ет необходимость построения регулятора пониженного (заданного) порядка

меньшего, чем порядок модели. Стоит отметить, что задача синтеза такого

регулятора является достаточно трудной, так как зачастую при ее решении

нарушается выпуклость полученных условий относительно параметров ре-

гулятора. Методы синтеза регуляторов пониженного порядка разделяют на

прямые и косвенные. При использовании прямых методов параметры регу-

лятора пониженного порядка сразу вычисляются с помощью процедуры оп-

тимизации или какой-либо другой процедуры. В косвенных подходах либо

сначала строится регулятор полного порядка, который впоследствии редуци-

руется, либо сначала редуцируется модель объекта управления, для редуци-

рованной модели строится регулятор полного порядка, а потом этот регуля-

тор используется для управления исходной моделью. Остановимся подробнее

на косвенных методах.

Редукция модели объекта управления является одной из классических за-

дач теории управления, вопросам редукции посвящено большое количество

литературы, например, [86, 125, 128, 134, 136, 137, 146, 169, 175, 177, 182, 234,

242, 251].

Существующие методы редукции можно сгруппировать по трем основ-

ным направлениям. К первому направлению относятся методы, основанные

на отсечении или отбрасывании некоторых уравнений, описывающих систе-

му [146, 175, 177, 182]. Работы [146, 182] посвящены понижению порядка с

помощью отсечения LQG и H_∞ регуляторов соответственно. Редукция при-

меняется к замкнутым оптимальным системам, а к диагональному виду при-

водятся решения алгебраических уравнений Риккати фильтрации и управ-

ления, соответствующие LQG и H_∞ задачам. Несмотря на то что методы

в [146, 175, 177, 182] разработаны для непрерывных систем, они могут быть

легко модифицированы на случай дискретных [252]. Следует отметить, что

техника отсечения приводит к некоторой потере качества замкнутой систе-

мы и накладывает ограничения на пониженный порядок регулятора. Эти

ограничения связаны с возможной неустойчивостью замкнутой регулятором

пониженного порядка системы полного порядка.

Второе направление составляют методы оптимальной аппроксимации ли-

нейной системы моделью пониженного порядка с использованием различных

критериев качества [86, 134, 136, 137, 169, 182, 234, 242]. В качестве крите-

риев могут быть использованы, например, квадратичный критерий ошиб-

ки аппроксимации [134, 137, 234], H₂ норма модели ошибки аппроксима-

ции [136, 242], H_∞ норма [86] и другие критерии [169].

Наконец, третье направление включает в себя комбинированные методы

редукции и оптимальной аппроксимации. К их числу относятся, например,

оптимальная аппроксимация линейных стационарных систем по норме Ган-

келя, предложенная в [125] и развитая для аппроксимации на определенных

диапазонах частот в [134]. В [128] рассматриваются методы редукции H_∞ ре-

гуляторов, позволяющие сохранить неизменное значение H_∞ нормы замкну-

той системы с регулятором пониженного порядка и обеспечивающие устой-

чивость этой системы. Эти методы основаны на усечении взаимно простых

факторов передаточной функции регулятора с последующей аппроксимацией

редуцированных факторов дробно-рациональными функциями.

3. Общая парадигма H₂ и H_∞ теорий управления

Для линейных стационарных систем наиболее известными методами по-

давления влияния внешних возмущений являются H₂ и H_∞ подходы, в ко-

торых критерием качества замкнутой системы является норма передаточ-

ной функции от возмущения к управляемому выходу. Стоит отметить, что

H_∞ норма является индуцированной, в то время как H₂ таковой не являет-

ся. В H₂ задаче возмущение всегда определенного вида гауссовский белый

шум с нулевым средним и единичной ковариационной матрицей, в то время

как в H_∞ оно наихудшее. В случае H_∞ управления минимизируется мак-

симальная (по всему диапазону частот) норма передаточной матрицы (как

коэффициент усиления внешнего возмущающего воздействия).

Рис. 3. Система F , замкнутая регулятором K.

Вследствие того, что H_∞ теория работает с широким классом возмущений,

в рамках этой теории можно ставить и решать различные задачи управле-

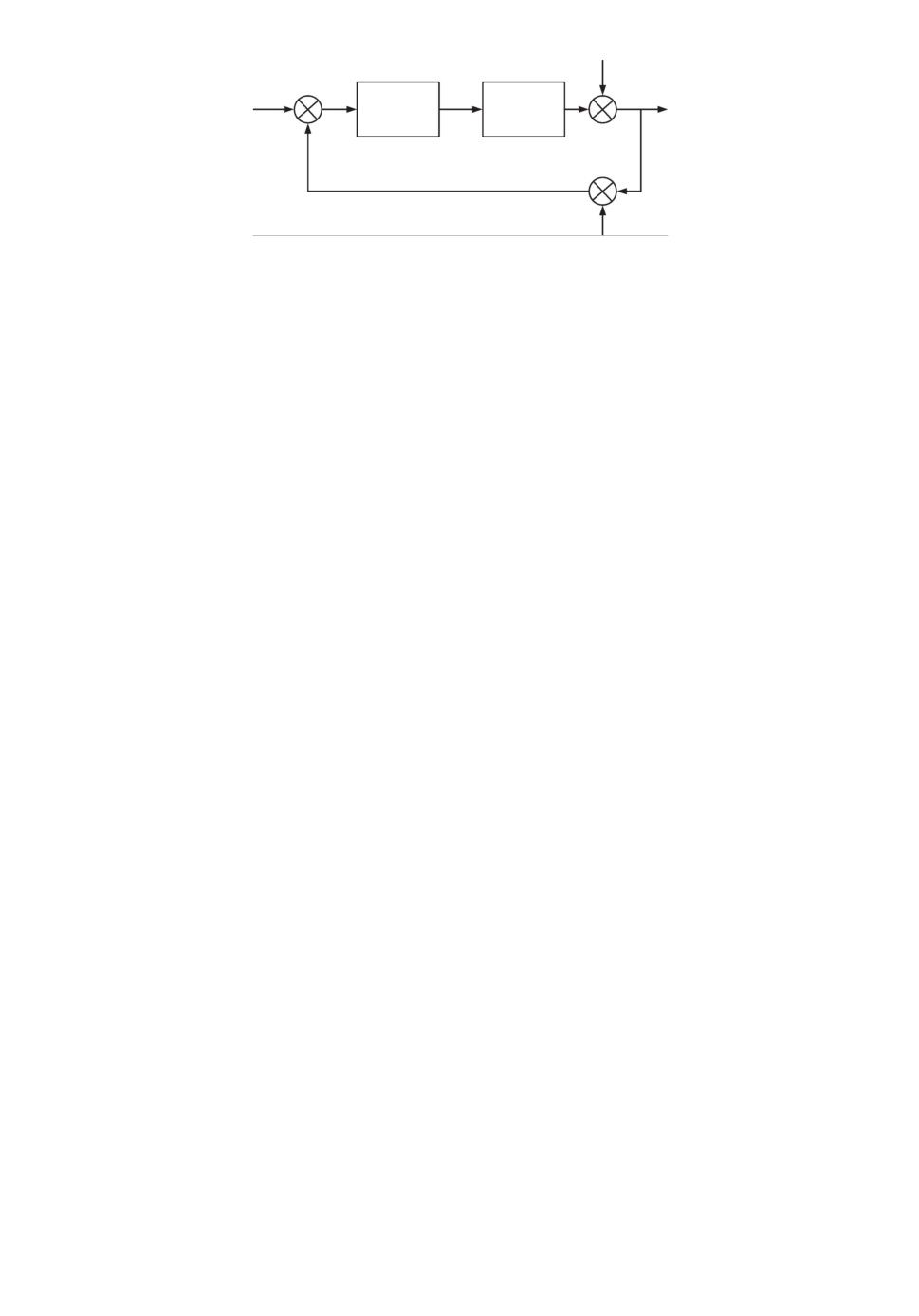
ния. Рассмотрим их формулировки для замкнутой системы, изображенной

на рис. 3. Здесь F

объект управления, K закон управления, который

требуется построить, r

задающее воздействие, y выход системы, u

управление, e сигнал ошибки между задающим воздействием и выходом

системы, d возмущение и n шум измерений. Сигналы выхода, управления

и ошибки генерируются следующим образом:

y = (I + FK)^-1FKr + (I + FK)^-1d - (I + FK)^-1GKn,

u = K(I + FK)^-1r - K(I + FK)^-1d - K(I + FK)^-1n,

e = (I + FK)^-1r - (I + FK)^-1d - (I + FK)^-1n.

Будем предполагать, что сигналы r, d, n обладают ограниченной энергией

и были нормализованы, т.е. лежат в единичном шаре пространства L₂. Од-

нако точно не известна природа этих сигналов. При указанных допущениях

можно синтезировать стабилизирующие регуляторы K для решения следую-

щих задач с минимизацией H_∞ норм соответствующих систем:

• задача слежения, ∥(I + F K)^-1F K∥_∞;

• ослабление влияния внешних возмущений, ∥(I + F K)^-1∥_∞;

• подавление шумов, ∥ - (I + F K)^-1F K∥_∞;

• снижение энергии управления, ∥K(I + F K)^-1∥_∞.

Ниже будут использованы обозначение LQG/H₂ или просто H₂ для обо-

значения более общей, чем LQG задачи, H₂ задачи. О вложении LQG

задачи в H₂ задачу можно прочитать в разных работах, например в [99].

Общая парадигма задач LQG/H₂ и H_∞ управления представлена на

рис. 1.

Здесь F объект управления, K регулятор, W и Z соответственно

внешний вход и управляемый выход системы, Y и U наблюдаемый выход и

управление, T_zw передаточная функция (матрица передаточных функций)

замкнутой системы от W к Z. В обеих задачах надо построить управление,

которое минимизирует соответствующий задаче критерий качества.

В дальнейшем будут рассмотрены дискретные модели систем управления.

Общий взгляд на H₂ и H_∞ задачи теории управления в свете представ-

ленной на рис. 1 парадигмы удобно изложить как различные интерпретации

задачи понижения влияния внешних возмущений.

Стандартная задача H₂ оптимизации состоит в нахождении регулятора K

(см. рис. 1), который

• стабилизирует замкнутую систему;

• минимизирует H₂ норму передаточной функции (матрицы передаточных

функций) T_zw замкнутой системы от W к Z, т.е.

(3.1)

∥T_zw∥₂

→ min.

Стандартная задача H_∞ оптимизации состоит в нахождении регулятора K

(см. рис. 1), который

• стабилизирует замкнутую систему;

• минимизирует H_∞ норму передаточной функции (матрицы передаточных

функций) T_zw замкнутой системы от W к Z, т.е.

(3.2)

∥T_zw∥_∞ = sup σ(T_zw

(z)) → min .

|z|<1

Сформулированную задачу (как и всякую минимаксную задачу) можно

рассматривать как антагонистическую игру двух игроков, в качестве первого

из которых выступает разработчик системы управления, выбирающий регу-

лятор K, а в качестве второго природа (которая максимизирует влияние

помехи на коэффициент усиления системы) [87].

Обычно рассматривают субоптимальную H_∞ задачу, которая отличается

от сформулированной выше оптимальной требованием, чтобы

(3.3)

∥T_zw∥_∞

≤ γ,

где γ ≥ γ_opt. Если величина γ задана наперед и окажется, что γ ≤ γ_opt, то

задача субоптимального синтеза не будет иметь решения.

Прозрачна частотная интерпретация задач H₂ и H_∞ оптимизации для си-

стем с одним входом и одним выходом. H_∞ регуляторы синтезируются, что-

бы минимизировать максимальное значение амплитудно-частотной характе-

ристики замкнутой системы, в то время как H₂ управление минимизирует

среднюю величину амплитуды по всем частотам.

Теории оптимального и субоптимального управления по критерию мини-

мума H_∞ нормы замкнутой системы обеспечивали выполнение ограничений

на понижение влияния внешних возмущений [188] в числе прочих целей. За-

мечательно, что теория H_∞ субоптимального управления базировалась на

решении уравнений Риккати, содержащих некоторый параметр, и была очень

похожа на теорию синтеза линейных регуляторов для линейных систем с

квадратичным критерием качества [117]. В случае, когда значение этого пара-

метра стремилось к бесконечности, уравнения для синтеза H_∞ субоптималь-

ного регулятора стремились к уравнениям Риккати для LQG задачи. Однако

H_∞ оптимальные регуляторы, являясь минимаксными, т.е. рассчитанными

на наихудший случай входных возмущений, имеют свои естественные недо-

статки для реализации минимума критерия качества величина управления

порой становится очень большой и такие системы трудно реализуемы. Вдо-

бавок системы с H_∞ критерием качества являются очень консервативными.

Субоптимальные H_∞ регуляторы, которые гарантируют то, что индуци-

рованная норма оператора замкнутой системы ниже фиксированной грани-

цы γ, не единственны. Действительно, все регуляторы, достигающие задан-

ной границы на норму передаточной функции замкнутой системы, могут

быть выражены в терминах дробно-линейного преобразования [193] регулято-

ра K_c (известного, как “центральный” [117]) и свободного параметра Q ∈ H_∞,

∥Q∥_∞ < 1. Хотя каждый выбор параметра Q гарантирует ограничение на

норму, интересно выяснить, когда существует такой параметр Q, при кото-

ром полученный регулятор будет минимизировать дополнительный функцио-

нал качества для замкнутой системы. Естественный выбор вспомогательного

функционала H₂ норма передаточной функции замкнутой системы. Одним

из недостатков H_∞ управления является тот факт, что качество замкнутой

системы, обычно ассоциированное с H₂ нормой передаточной функции замк-

нутой системы, приносится в жертву свойству робастности замкнутой систе-

мы, гарантированному H_∞ регуляторами. Обе концепции, рассматриваемые

в отдельности (H₂ и H_∞ управление), не являются удовлетворительными с

инженерной точки зрения. Разработчики предпочитают компромиссы.

Эти компромиссы между достоинствами и недостатками LQG и H_∞ тео-

рий можно разделить на два направления. Первое направление минимиза-

ция H₂ нормы замкнутой системы с ограничениями на H_∞ норму, второе

минимизация H_∞ нормы замкнутой системы с одновременной минимизацией

верхней границы функционала качества, используемого в H₂ задаче опти-

мального управления.

4. Компромиссы между LQG и H_∞

Одной из первых работ, которая относится к первому из вышеперечис-

ленных компромисов, была работа Бернштейна и Хаддада [95], ставившая

задачу построения LQG регулятора, обеспечившего вместе с тем и ограниче-

ния на H_∞ норму передаточной функции замкнутой системы. Метод синтеза

таких регуляторов приводил к решению трех связанных модифицированных

уравнений Риккати. Связность этих уравнений иллюстрирует разрыв прин-

ципа разделения для LQG задачи с H_∞ ограничением. Важно отметить, что

два из указанных трех уравнений Риккати, через решение которых строятся

матрицы оптимальных регуляторов, являются уже известными, так как они

идентичны уравнениям для решения LEQG задачи, исследованной в [93]. Тем

самым прослеживается явная связь между LQG задачей с ограничением на

H_∞ норму передаточной функции замкнутой системы и LEQG задачей.

Опишем круг вопросов, относящихся ко второму направлению описанных

выше компромиссов. Как хорошо известно, H_∞ субоптимальное управление

не единственно и может быть неким способом параметризовано [126]. Однако

если на множестве субоптимальных регуляторов поставить задачу максими-

зации так называемого функционала H_∞ энтропии

∞

∫



(

)

(4.1)

J (γ, F ) = -

φ(ω) ln det

I_m - γ^-2 (F(jω))^∗ F(jω)

dω,

2π

−∞

здесь γ

величина, ограничивающая H_∞ норму передаточной функции

замкнутой системы F (s), аналогичного введенному Аровым и Крейном функ-

ционала энтропии в задачах продолжения [4, 5], то получаемый регулятор

(являющийся решением субоптимальной задачи и максимизирующий функ-

ционал H_∞ энтропии) оказывается единственным [178]. Этот регулятор яв-

ляется так называемым центральным регулятором. Более того, в [126] бы-

ло показано, что задача синтеза регулятора, предполагающего минимизацию

H_∞ энтропии, в определенном смысле эквивалентна задаче синтеза регулято-

ра по критерию минимизации функционала чувствительности к риску (2.10).

Тот же результат был получен другим методом в [231].

Известно [180], что H_∞ энтропия является некой мерой рассогласования

между H₂ и H_∞ оптимальностью. Так, H_∞ энтропия является верхней гра-

нью H₂ нормы замкнутой системы, таким образом минимизация интеграла

H_∞ энтропии приводит к достижению максимального значения в функцио-

нале качества в H₂(LQG) задаче. Заметим, что можно выбрать H_∞ субопти-

мальный регулятор в непрерывном времени, который приводит к неограни-

ченной H₂ норме замкнутой системы. Факт важности задачи минимизации

H_∞ энтропийного функционала привлек большое внимание специалистов по

H₂ и H_∞ управлению, так как появилась надежда, что, минимизируя функ-

ционал H_∞, разработчик в то же время минимизирует H₂ критерий качества.

Насколько известно авторам, этот факт еще не доказан, хотя и не опроверг-

нут.

После появления работ [127, 178, 179] был опубликован целый ряд иссле-

дований, посвященных построению регуляторов, имеющих ограничение на

H_∞ норму замкнутой системы и максимизирующих функционал H_∞ энтро-

пии. Так, в [138] для дискретного времени в пространстве состояний получе-

ны формулы для регулятора, обеспечивающего ограниченность H_∞ нормы

замкнутой системы параметром γ и минимизирующего функционал H_∞ эн-

тропии. Решение получено переформулировкой задачи в непрерывном вре-

мени и применением билинейного преобразования, конформно переводящего

единичный диск в левую полуплоскость. В [181] дано альтернативное [126]

решение задачи минимизации функционала энтропии с требованием ограни-

ченности H_∞ нормы и устойчивости замкнутой системы, которое получено

сведением первоначальной задачи с помощью параметризации Юлы-Кучеры

(см., например, [130]) к задаче слежения за моделью [121] и затем к так на-

зываемой задаче расстояния. В [140] задача поиска регулятора, минимизи-

рующего энтропийный интеграл и при ограничении на H_∞ норму замкнутой

системы сводится к решению двух вспомогательных задач (так называемых

задач полной информации и оценки выхода) и далее применению принципа

разделения. В [239] рассматривалась задача синтеза статического регулятора

по выходу, минимизирующего функционал H_∞ энтропии и обеспечивающего

заданное ограничение на H_∞ норму замкнутой системы. Решение задачи сво-

дится к решению связанных уравнений Риккати и Ляпунова. Подход близок

к подходу работы [95].

В [122] для непрерывных сингулярно-возмущенных систем рассматрива-

лось статическое робастное управление по выходу, минимизирующее функ-

ционал H_∞ энтропии замкнутой системы. Требовалось, чтобы регулятор

обеспечивал ограничения на H_∞ норму замкнутой системы и минимизиро-

вал H_∞ энтропию замкнутой системы для достаточно малых значений син-

Рис. 4. Смешанная задача H₂/H_∞ управления.

гулярного возмущения ε. Оптимальный коэффициент усиления регулятора

синтезируется на базе обобщенных уравнений Риккати и Ляпунова с сим-

метричными 2 × 2 блоками, которые связаны между собой. Если ε → 0, то

оптимальный регулятор один из тех, которые минимизируют H_∞ энтропию

замкнутой непрерывной системы.

Понятие энтропии, использовавшееся в H_∞ оптимизации, для дискретных

систем было распространено на нестационарный случай [141]. Это обобщение

не тривиально, так как H_∞ энтропия для стационарной системы определяется

в терминах передаточной функции замкнутой системы, которых не существу-

ет для нестационарных систем. Энтропия для нестационарных дискретных

систем была определена в терминах теории операторов c привлечением фун-

даментальных теорем о факторизациях. В [186] была решена задача построе-

ния управления, минимизирующего энтропийный функционал для нестацио-

нарных дискретных систем, а в [187] получена взаимосвязь между задачей

минимизации энтропии для нестационарных систем и задачей минимизации

функции чувствительности к риску для таких систем.

Уже упомянутая работа Бернштейна и Хаддада [95], ставшая первой по-

пыткой найти компромисс между робастной устойчивостью (хорошо извест-

ный факт, что величина H_∞ нормы отвечает за робастную устойчивость

замкнутой системы теорема о малых приращениях) и подавлением случай-

ного возмущения в виде белого шума в соответствии с квадратичным крите-

рием качества (величиной H₂ нормы), породила целое направление в теории

робастного управления, которое называется смешанным H₂/H_∞ управлени-

ем. Как отмечалось в книге [107], такие регуляторы представляют собой же-

лаемый компромисс между H₂ и H_∞ теориями управления.

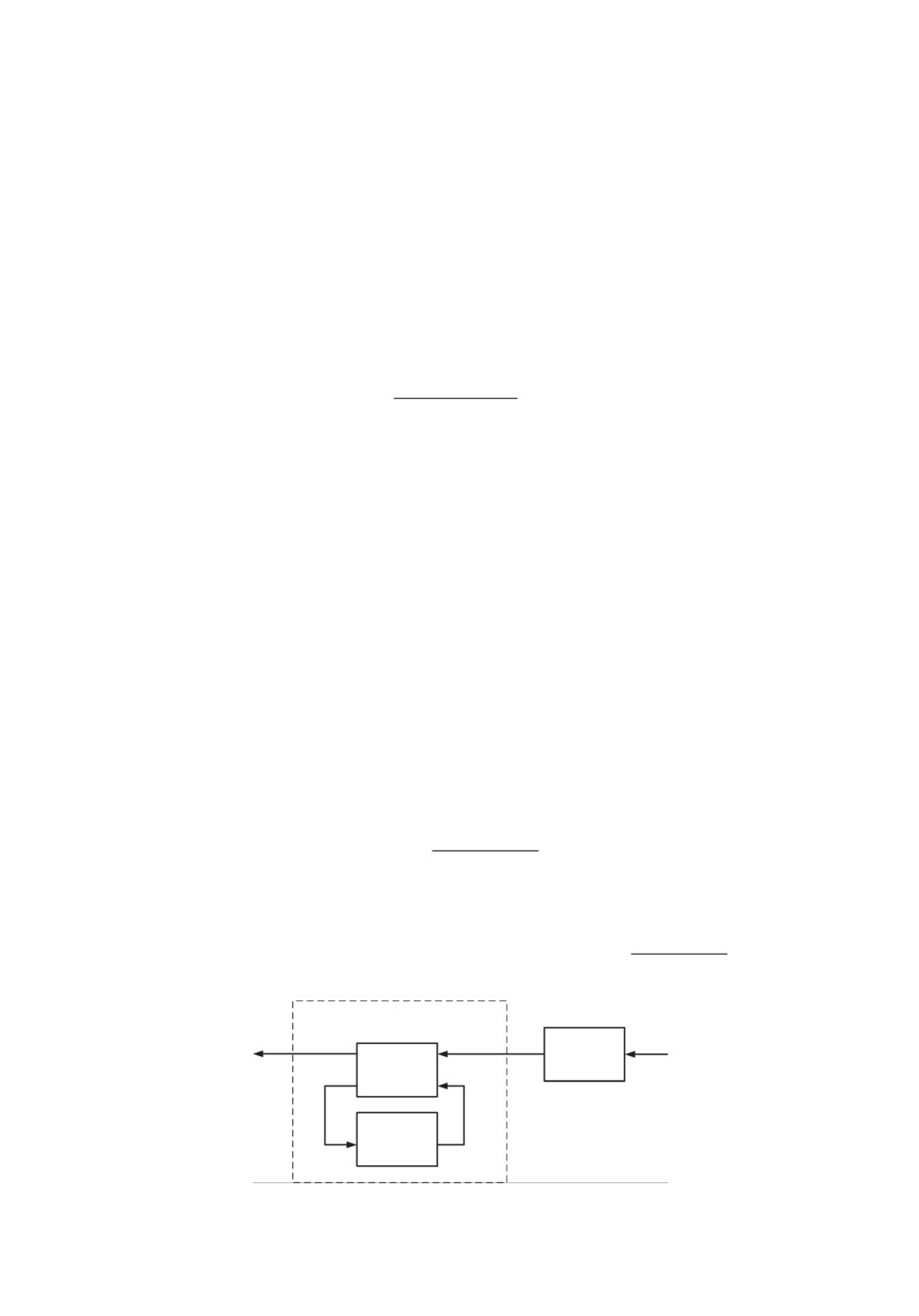
Изложим кратко парадигму смешанного H₂/H_∞ управления, следуя [155]

(см. рис. 4).

Здесь, как и на предыдущем рисунке, F - объект управления, K - регуля-

тор, Tziw_i , i = 0, 1 - передаточная матрица замкнутой системы от Wi к Zi.

Задача смешанного H₂/H_∞ управления - найти внутренне стабилизирующий

регулятор K, минимизирующий ∥Tz0w₀ ∥2 и обеспечивающий ∥Tz₁w₁ ∥∞ < γ.

Задача управления, рассмотренная в [95], получается из задачи смешан-

ного H₂/H_∞ управления при W₀ = W₁ = W . Вместо минимизации ∥Tz0w∥2

в [95] решается задача синтеза LQG регулятора с ограничением на H_∞ нор-

му замкнутой системы, которую называют смешанным H₂/H_∞ критерием

качества.

В [179] показано, что в случае W₀ = W₁ = W и Z₀ = Z₁ = Z задача в [95]

эквивалентна задаче минимизации энтропии [127].

Дальнейшее развитие теория смешанного H₂/H_∞ управления нашла в ра-

ботах [119, 253]. В предисловиях к этим работам говорится, что одной из мо-

тивировок написания работ является желание получить общую постановку

для задач H₂ и H_∞ оптимизации аналогично тому, как решения этих задач

проводятся по близкой схеме (см. [117]). Забегая вперед, отметим, что в рам-

ках анизотропийной теории управления, описанной ниже, общая постановка

задач H₂(LQG) и H_∞ оптимизации была получена. Задачи, поставленные и

решенные в [253] и [119], являются в определенной степени дуальными резуль-

татам работы [95]. В [176] было получено решение стохастической смешанной

H₂/H_∞ задачи для дискретного случая.

Недавно была опубликована работа [30], в которой предложен один из

подходов к созданию общей теории H₂/H_∞ управления для систем с детер-

минированными входами. В работе вводится характеристика оператора из

пространств входов в пространство выходов, названная H_∞/γ₀ нормой. Эта

новая норма существенным образом зависит от входящей в ее определение

матрицы R. В крайних случаях при отсутствии одного из входов введенная

норма превращается в одну из оставшихся норм. Подход напоминает ранее

предложенный подход с введением коэффициента усиления в виде суммы

взвешенных норм λ|| · ||₂ + (1 - λ)|| · ||_∞, λ ∈ [0, 1]. В указанной работе также

синтезирован оптимальный закон управления по состоянию, минимизирую-

щий введенную H_∞/γ₀ норму.

Необходимо отметить работы [85, 185], в которых показана связь между

задачами минимизации H_∞ энтропии и смешанным H₂/H_∞ управлением для

стационарных и нестационарных систем управления соответственно. Авторам

бы не хотелось в этом обзоре углубляться в строгое определение смешанной

задачи H₂/H_∞ управления в нестационарном случае, читатель может найти

необходимые сведения в процитированных выше работах.

5. Анизотропийная теория управления начальный период

В этом разделе будут кратко приведены некоторые понятия теории инфор-

мации, необходимые для изложения основ анизотропийной теории управле-

ния; введены основные понятия анизотропийной теории управления: поня-

тия анизотропии вектора, средней анизотропии последовательности, анизо-

тропийной нормы системы; сформулирована задача синтеза оптимального

анизотропийного регулятора и описано ее решение.

5.1. Необходимые (некоторые) сведения из теории информации

Пусть X будет дискретной случайной величиной с алфавитом X , и пусть

задана функция вероятностной меры p(x) = Pr{X = x}, x ∈ X .

Энтропия H(X) случайной переменной X определяется как

∑

(5.1)

H(X) = -

p(x) log p(x) = -E (log p(x)) .

x∈X

Энтропия представляет собой характеристику одной случайной величины.

Пусть теперь на одном множестве заданы два вероятностных распределения

p(x) и q(x).

Относительная энтропия или расстояние Кульбака-Лейблера между

двумя распределениями p(x) и q(x) определяется как

(

)

p(x)

(5.2)

D(p ∥ q) = E_p log

q(x)

где E_p(Φ) математическое ожидание функции Φ, определенное по правилу

∑

E_p(Φ) =

p(x)Φ(x).

x∈X

Свойства относительной энтропии

• Пусть p(x), q(x), x ∈ X будут два распределения вероятностей (две меры).

Тогда

D(p ∥ q) ≥ 0.

Равенство нулю выполняется, если p(x) = q(x) для всех x.

• В общем случае

D(p ∥ q) = D(q ∥ p).

Рассмотрим две случайных величины X и Y с совместной функцией ве-

роятностей p(x, y) и функциями вероятностей p(x) и p(y).

Взаимной информацией I(X; Y ) называется относительная энтропия меж-

ду совместным распределением и произведением распределений p(x)p(y), т.е.

(

)

∑

p(x, y)

(5.3)

I(X; Y ) = D(p(x, y) ∥ p(x)p(y)) =

p(x, y) log

p(x)p(y)

x∈X y∈Y

Определим важную для дальнейшего изложения дифференциальную эн-

тропию случайной величины. Пусть X непрерывная m-мерная случайная

величина, f(x) плотность распределения вероятностей для X. Множество,

где f(x) > 0, называется опорным множеством на X.

Дифференциальная энтропия h(X) для X c плотностью распределения

f (X) определяется как

∫

h(X) = -E (log f(X)) = - f(X) log f(X) dX,

где S опорное множество случайной переменной.

По аналогии с дискретным случаем определим относительную энтропию.

Относительная энтропия или расстояние Кульбака-Лейблера D(f ∥ g)

между плотностями f(x) и g(x) определяется как

∫

(f(x))

(5.4)

D(f ∥ g) = f(x) log

dx₁ · · · dx_m.

g(x)

R^m

Свойства относительной энтропии

1) D(f ∥ g) конечна, если опорное множество функции f(x) содержится в

опорном множестве g(x).

2) D(f ∥ g) ≥ 0, причем равенство достигается, если f = g.

3) Справедливо соотношение 0 log⁰⁰ = 0.

Для непрерывных случайных величин определим взаимную информацию.

Пусть X и Y две случайные m-мерные величины с совместной функци-

ей распределения плотности вероятностей f(x, y) и функциями плотностей

вероятностей f(x) и f(y).

Взаимная информация I(X; Y ) определяется как

I(X; Y ) = D(f(x, y) ∥ f(x)f(y)) =

∫

(

)

f (x, y)

= f(x,y)log

dx₁ · · · dx_mdy₁ · · · dy_m.

f (x)f(y)

R^2m

Понятие относительной энтропии играет большую роль не только в тео-

рии информации (сжатие данных), но и в различных других научных дисци-

плинах, таких как статистическая физика, теория вероятностей, финансовая

математика [46]. В следующем разделе покажем, какую роль это понятие иг-

рает в теории управления. Более подробно о введенных определениях и их

свойствах можно прочесть в [59, 108, 129].

Пожалуй, первой работой, которая строго использовала теоретико-ин-

формационные понятия в постановках задач управления, была работа

1988 г. [198]. В ней предлагалось искать оптимальное управление из условия

максимизации дифференциальной энтропии, связанной с функцией распре-

деления вероятностей, построенной на множестве управлений. В этой работе

было показано, что оптимизация среднего функции потерь эквивалентна ми-

нимизации энтропии управления при условии наихудшей функции плотности

энтропии.

В [151] в роли критерия качества для построения управления была пред-

ложена относительная энтропия. Это направление в теории управления раз-

вивается достаточно успешно [152, 153]. Заметим, что концепция анизотро-

пийного управления, также основанная на понятии относительной энтропии

(расстоянии Кульбака-Лейблера), была предложена И.Г. Владимировым дву-

мя годами ранее в [201].

5.2. Ключевые определения анизотропийной теории

Понятия анизотропии случайного вектора, средней анизотропии после-

довательности случайных векторов, а также анизотропийной нормы линей-

ной стационарной системы впервые появились в 1994 г. в [201]. Анизотро-

пия случайного вектора определяется как минимальная относительная эн-

тропия (расстояние Кульбака-Лейблера) между плотностью распределения

случайного вектора и плотностью распределения гауссовского сигнала с ну-

левым средним и скалярной ковариационной матрицей [24]. Средняя ани-

зотропия бесконечной последовательности случайных векторов определяет-

ся через анизотропию элемента последовательности аналогично тому, как

определяется энтропия на степень свободы (термин заимствован из [60]). Эн-

тропия на степень свободы есть предел отношения энтропии n случайных

величин к числу n при стремлении числа n к бесконечности. Энтропия на

степень свободы также называется энтропией стационарного источника на

сообщение [31]. Аналогом этого понятия в английском языке служит термин

¾entropy rate¿ [108]. Средняя анизотропия определяется как предел отноше-

ния анизотропии вектора, составленного из n случайных векторов, к числу n

при стремлении числа n к бесконечности.

Определение анизотропии случайного вектора.

Напомним, что L^m2 это класс R^m-мерных случайных распределенных

абсолютно непрерывно векторов с конечным вторым моментом.

Для любого λ > 0 обозначим через p_m,λ функцию плотности распределе-

ния вероятностей на R^m гауссовского сигнала с нулевым средним и скалярной

ковариационной матрицей λI_m

(

)

|x|²

(5.5)

p_m,λ(x) = (2πλ)^-m/2 exp

x∈R^m.

2λ

Для любого w ∈ L^m2 с функцией плотности распределения вероятностей

f : R^m → R₊ его относительная энтропия относительно (5.5) принимает вид

[49]

f (w)

E|w|

(5.6)

D (f ∥ p_m,λ) = E ln

= -h(w) +

ln(2πλ) +

p_m,λ(x)

2λ

где

∫

(5.7)

h(w) = -E ln f(w) = -

f (w) ln f(w)dw

R^m

дифференциальная энтропия случайного вектора w.

Определение 1. Анизотропия A(w) случайного вектора w ∈ L^m2 опре-

деляется как минимальное информационное уклонение его распределения от

гауссовских распределений на R^m с нулевым средним и скалярными ковариа-

ционными матрицами

(5.8)

A(w) = minD (f ∥ pm,λ

λ>0

Непосредственное вычисление показывает, что минимум в (5.6) по всевоз-

можным λ > 0 достигается при λ = E|w|²/m и, следовательно,

)

( 2πe

(5.9)

A(w) = minD (f ∥ pm,λ) =

E|w|²

− h(w).

λ>0

Свойства анизотропии

Пусть G^m(Σ) класс R^m-мерных гауссовских случайных векторов w с

Ew = 0 и cov(w) = Σ, det Σ = 0, соответствующая функция плотности рас-

пределения вероятности

(

)

p(w) = (2π)^-m/2(det Σ)^-1/2 exp

∥w∥²

Σ^-1

√

∥x∥_Q =

x^⊤Qx (полу-) норма вектора x, индуцированная положительно

(полу-) определенной симметричной матрицей Q > 0. Тогда

(a) для любой положительно определенной матрицы Σ ∈ R^m×m

{

}

mΣ

(5.10)

min

A(w) : w ∈ L^m2, E(ww^⊤) = Σ

ln det

trΣ

причем минимум достигается лишь на w ∈ G^m(Σ);

(b) для любого w ∈ L^m2 имеем A(w) ≥ 0, причем A(w) = 0 тогда и только

тогда, когда w ∈ G^m(λI_m);

ной гомотетии вектора w, т.е. A(λUw) = A(w) для любого скаляра

λ ∈ R \ {0} и любой ортогональной матрицы U ∈ R^m×m.

Средняя анизотропия гауссовского сигнала

Пусть V = {v_k}_k∈Z дискретный m-мерный гауссовский белый шум с ну-

левым математическим ожиданием и единичной ковариационной матрицей:

(

)

Ev_k = 0, E

v_kv^Tk

=I_m,

-∞ < k < +∞.

Рассмотрим m-мерную стационарную гауссовскую последовательность

W = {w_k}_k∈Z = G ⊗ V,

получаемую из белого шума V посредством формирующего фильтра G с им-

пульсной переходной характеристикой g_k ∈ R^m×m, k ≥ 0:

∑

w_j = g_k v_j-k,

-∞ < j < +∞.

k=0

Такой фильтр отождествляется со своей передаточной функцией

∑

G(z) = g_k z^k,

k=0

которая предполагается лежащей в пространстве Харди H^m×m2.

Последовательность W имеет нулевое математическое ожидание и спек-

тральную плотность

(

)_∗

(5.11)

S(ω) =

G(ω)

ω ∈ Ω = [-π;π].

2π

Выделим из последовательности W подпоследовательность размерности

N×m





w₀





W_0:N-1 =



,

w_N-1

каждый вектор w_i принадлежит R^m при i = 0, (N - 1).

Определение 2. Средняя анизотропия последовательности W опреде-

ляется следующим образом [20]:

A(W_0:N-1)

A(W ) = lim

N→+∞

В [20] также доказано, что средняя анизотропия последовательности W =

= G ⊗ V может быть определена как

∫

(

)

(

)_∗

(5.12)

A(G) = -

ln det

G(ω)

dω.

4π

∥G∥²

Функционал (5.12) принимает неотрицательные конечные значения, как толь-

ко формирующий фильтр G ∈ H^m×m2 имеет максимальный (точнее, полный

строчный) ранг, т.е.

rankG(ω) = m для почти всех ω ∈ Ω.

Если же фильтр G не максимального ранга, то A(G) = +∞. Отметим,

A(G) = 0 в том и только в том случае, если формирующий фильтр G яв-

ляется с точностью до ненулевого постоянного множителя системой полного

пропускания, т.е. если последовательность W

гауссовский белый шум со

скалярной ковариационной матрицей.

Как видно, средняя анизотропия (5.12) является характеристикой вероят-

ностного распределения гауссовской последовательности W = G ⊗ V , а не ее

индивидуальных траекторий.

Заметим также, что функционал средней анизотропии A(G) инвариан-

тен относительно преобразования G → αU1GU2 с произвольными нену-

левым постоянным множителем α ∈ R и системами полного пропускания

U₁,U₂ ∈ H^m×m2 (для которых матрицы

U₁(ω),

U₂(ω) унитарны при почти

всех ω ∈ Ω). В частности, это означает, что A(G) полностью определяется

функциями собственных значений спектральной плотности (5.11), которые с

точностью до постоянного множителя

совпадают с квадратами функций

2π

сингулярных значенийG.

Имеются глубокие связи функционала средней анизотропии (5.12) с теоре-

тико-информационным подходом к количественному описанию хаоса, осно-

ванным на колмогоровской ǫ-энтропии вероятностных распределений [26, 65],

с одной стороны, и с принципом изотропности конечномерного евклидова

пространства

с другой. Читатель, интересующийся подробностями этих

связей, отсылается к работам И.Г. Владимирова [20, 56]. Упомянутые связи

позволяют интерпретировать среднюю анизотропию (5.12) различными (но

генетически едиными) способами.

Здесь заметим лишь, что

(5.12) можно рассматривать как количе-

ственный показатель трудности генерации гауссовских последовательностей

W = G ⊗ V в природных условиях.

C использованием многомерной версии формулы Колмогорова-Сеге [27]

в [113] получена формула для вычисления средней анизотропии случайной

последовательности, сгенерированной с помощью формирующего фильтра из

гауссовского белого шума. Фильтр задается своим (A, B, C, D) представлени-

ем. Для вычисления средней анизотропии необходимо получить решения ал-

гебраического уравнения Риккати и уравнения Ляпунова, в которые входят

матрицы A, B, C, D формирующего фильтра.

На базе результатов, полученных в [69], в [207] вычисление средней ани-

зотропии сведено к решению линейных матричных неравенств. Задача из-

менения средней анизотропии в различных соединениях линейных фильтров

была рассмотрена в [163].

В рамках теории анизотропийного управления решена и обратная задача:

имея заданный уровень средней анизотропии (цветности) на выходе форми-

рующего фильтра построить характеристики фильтра. Алгоритмы решения

обратной задачи изложены в [38, 166].

Анизотропийная норма системы

Рассмотрим устойчивую линейную дискретную систему F , заданную в

пространстве состояний в следующем виде:

(5.13)

x_k+1 = Ax_k + Bw_k,

(5.14)

y_k = Cx_k + Dw_k,

где x_k ∈ Rⁿ вектор состояния системы, W = {w_k}_k∈Z стационарная гаус-

совская последовательность m-мерных векторов с ограниченным уровнем

средней анизотропии A(W ) ≤ a (a ≥ 0) и нулевым средним, y_k ∈ R^p вы-

ход системы.

Обозначим через Y = {y_k}_k∈Z выходную последовательность систе-

мы (5.13)-(5.14). Определим мощностную норму последовательности Y фор-

мулой

∑

∥Y ∥_P =

√ lim

E|y_k|2.

N→∞ N

k=0

Предполагая, что ∥Y ∥_P и ∥W ∥_P конечные, определим для заданной систе-

мы F с входным сигналом W = {w_k}_k∈Z среднеквадратичный коэффициент

усиления (СККУ ) в виде

∥Y ∥_P

Q(F, W ) =

∥W ∥_P

Определение 3. Для заданной величины a ≥ 0 анизотропийной нор-

мой системы F называют

(5.15)

|||F |||_a = sup

Q(F, W ).

A(W )≤a

Таким образом, анизотропийная норма системы |||F |||_a задает стохастический

коэффициент усиления системой F входного сигнала W .

Свойства анизотропийной нормы системы

Для F ∈ H^∞×m ее a-анизотропийная норма является неубывающей функ-

цией параметра a ≥ 0, удовлетворяющей неравенствам

(5.16)

∥F ∥₂/√m = |||F|||0 ≤ |||F|||a ≤ lim

|||F |||_a = ∥F ∥_∞.

a→+∞

Вычисление нормы |||F |||_a для a > 0 представляет интерес, лишь если

(5.17)

∥F ∥₂ <

√m∥F∥_∞.

∥F ∥₂ =

√m∥F∥_∞ тогда и только тогда, когда F^⊤F = λI_m для некоторого

λ ≥ 0. В частности, (5.17) выполнено, если F = 0 и p < m.

Анизотропийная норма не обладает круговым свойством (2.11), однако

в [113] доказано следующее свойство псевдомультипликативности анизотро-

пийной нормы:

для любого a ≥ 0 и любых систем F ∈ H^∞×m и G ∈ H^m×m∞

(5.18)

|||F G|||_a ≤ |||F |||_b |||G|||_a,

где

(5.19)

b = a + A(G) + m ln

(√m |||G|||_a/∥G∥₂) .

В [22] представлена асимптотика поведения анизотропийной нормы при

уровне средней анизотропии a, стремящемся к нулю и к бесконечности (при

стремлении анизотропийной нормы к H₂ и H_∞ норме соответственно).

В [113, 224] представлены формулы и приведен численный алгоритм для

вычисления анизотропийной нормы в частотной области и в пространстве со-

стояний. Для вычисления анизотропийной нормы системы F в пространстве

состояний необходимо решить матричные алгебраические уравнения Рикка-

ти и Ляпунова, а также алгебраическое уравнение специального вида. В пер-

вые два уравнения входят параметры матриц (A, B, C, D) представления си-

стемы, во второе входят матрицы, являющиеся решениями вышеназванных

алгебраических уравнений Риккати и Ляпунова, а также параметр уровня

средней анизотропии сигнала на входе системы F .

Численный алгоритм для вычисления анизотропийной нормы системы ос-

нован на методе ньютоновских итераций и имеет достаточно высокую вычис-

лительную сложность. Для преодоления этого недостатка в более поздних

работах [70, 207] предложены новые способы оценки анизотропийной нор-

мы методами выпуклой оптимизации. Результат, сформулированный в [70],

позволяет оценивать анизотропийную норму системы с применением совре-

менных вычислительных пакетов, решающих задачи полуопределенного про-

граммирования.

5.3. Оптимальная анизотропийная задача и ее решение

В [21] и [201] для стационарных систем была поставлена задача синтеза

регулятора, минимизирующего анизотропийную норму замкнутой системы,

которая была решена в [225].

Пусть задана система F , изображенная на рис. 5 и имеющая описание в

пространстве состояний (2.13). Внешнее возмущение является последователь-

ностью случайных векторов с уровнем средней анизотропии a.

Сформулируем анизотропийную задачу оптимизации.

Задача 1. Для заданных системы (2.13) и уровня a ≥ 0 средней ани-

зотропии входного возмущения W найти регулятор K, минимизирующий

a-анизотропийную норму передаточной функции замкнутой системы (2.16):

}

{ ∥L(F, K)G∥₂

(5.20)

|||L(F, K)|||_a ≡ sup

: G∈G_a

→ inf .

∥G∥₂

K∈K

Здесь G_a обозначает множество фильтров, на выходе которых сигнал с

уровнем средней анизотропии, меньшим или равным a, K множество ста-

билизирующих регуляторов.

По аналогии с задачами H₂ и H_∞ оптимизации (3.1) и (3.2) задача анизо-

тропийной оптимизации может быть переформулирована как

|||T_zw|||_a → min .

Сформулированную проблему (как и задачу H_∞ оптимизации) можно рас-

сматривать как антагонистическую игру двух игроков, в качестве первого из

которых выступает управление (регулятор K), а в качестве второго фор-

мирующий фильтр G, генерирующий входное возмущение W . Рассмотрим

множества

K^⋄a(G)= Arg min

∥L(F, K)∥₂, G ∈ G_a,

K∈K(F )

G^⋄a(K)= Arg max∥L(F,K)∥2 , K ∈ K(F).

G∈Ga

∥G∥₂

План решения сформулированной задачи состоит в следующем. Если для си-

стемы F и заданного уровня средней анизотропии a научиться строить ¾наи-

худший¿ фильтр G ∈ G^⋄a(K), который максимизирует∥L(F,K)G∥2 , то задача_∥G∥

+(F, K)

G ÎG_a

Рис. 5. Иллюстрация задачи стохастической H_∞-оптимизации.

сводится к задаче построения оптимального регулятора K, который при этом

наихудшем фильтре минимизирует ∥L(F, K) G∥₂.

Алгоритм синтеза приводит к необходимости решения системы уравне-

ний, состоящей из трех алгебраических уравнений Риккати, уравнения Ляпу-

нова и алгебраического уравнения специального вида. Одно алгебраическое

матричное уравнение Риккати, матричное уравнение Ляпунова и уравнение

специального вида необходимы для построения наихудшего фильтра, остав-

шиеся два алгебраических уравнения Риккати выполняют ту же роль, что и

два алгебраических уравнения в LQG/H₂ или H_∞ теориях. Одно из уравне-

ний необходимо для решения задачи построения оценки вектора состояния

системы x, а второе собственно для построения управления. Причем все

эти уравнения являются связанными. В [172] описан метод гомотопий для

решения связанных уравнений Риккати.

В [112] разработан метод гомотопий для решения системы уравнений, необ-

ходимых для синтеза анизотропийного регулятора. Описание применения ме-

тода гомотопий в анизотропийной теории управления, в частности, исполь-

зование метода гомотопий с ньютоновскими итерациями изложено в [23].

Как было установлено выше, и H_∞ оптимальная задача, и анизотропий-

ная оптимальная задача являются игровыми. В силу неравенства (5.16) ани-

зотропийный регулятор занимает промежуточное место между LQG/H₂ и

H_∞ регуляторами. Это наводит на мысль, что и LQG регулятор является

минимаксным. Это действительно так, потому что гауссовский белый шум

(сигнал на входе системы в LQG задаче) является наихудшим возмущением

по критерию максимума энтропии входного сигнала (см. [108]).

5.4. Некоторые свойства анизотропийных регуляторов

Как и следовало ожидать, системы управления, замкнутые анизотропий-

ными регуляторами, являются более робастными, чем системы, замкнутые

H₂ регуляторами, и менее консервативными, чем системы, замкнутые H_∞ ре-

гуляторами. В [23, 35, 159] рассматривались сравнения возможностей H₂, H_∞

и анизотропийных регуляторов в задаче подавления внешнего возмущения

типа “сдвига ветра” при посадке самолета. Анизотропийные регуляторы по-

казали значительные преимущества по сравнению с H_∞ регуляторами в во-

просах энергозатрат на управление. Одновременно с этим анизотропийные

регуляторы оказались более робастными относительно H₂ регуляторов.

Напомним, что LQG/H₂ оптимальная задача имеет единственное реше-

ние, решение H_∞ оптимальной задачи не единственно. Решение оптимальной

анизотропийной задачи также является единственным.

Отметим очень важное свойство анизотропийных регуляторов. По анало-

гии с рассмотренной выше задачей построения H_∞ регуляторов, минимизи-

рующих энтропийный функционал (4.1), между энтропийным функционалом

и анизотропией также существует связь. В [45] было установлено, как можно

трактовать энтропийный функционал с точки зрения теоретико-информаци-

онного подхода. В этой работе было показано, что анизотропийный регулятор

также минимизирует H_∞ энтропию замкнутой системы для некоторого фик-

сированного значения параметра γ.

Выше были рассмотрены хорошо известные из литературы принципы раз-

деления в LQG/H₂ теории оптимального управления (см., например, [47, 48])

и в H_∞ теории субоптимального управления (см., например, [117, 130]). За-

мечательно то, что и в анизотропийной теории тоже можно сформулировать

принцип разделения. Этот принцип в анизотропийной теории может выгля-

деть так: “Оптимальный анизотропийный регулятор полного порядка явля-

ется оптимальным оценивателем оптимального закона управления в зада-

че с полной информацией о векторе состояния системы для случая наихуд-

шего входа.”

Заметим, что принцип разделения не означает независимости уравнений

Риккати. Он скорее близок к принципу разделения в задаче H_∞ субопти-

мального управления. Здесь задача синтеза оценивателя и задача синтеза

статического регулятора в виде обратной связи не могут быть решены неза-

висимо друг от друга. Более подробно об этом написано в [225].

6. Развитие анизотропийной теории

В данном разделе речь пойдет о развитии робастной анизотропийной тео-

рии управления, взявшей за основу определения и концепции предыдущего

раздела, с начала 2000-х годов. Будут приведены постановки и решения сле-

дующих задач: робастная устойчивость, синтез анизотропийных регуляторов

для систем с параметрическими неопределенностями, построение субопти-

мального управления методами выпуклой оптимизации, построение анизо-

тропийной теории анализа и синтеза для дескрипторных систем, систем с

нецентрированными входными сигналами и нестационарных систем, реше-

ние задач анизотропийной фильтрации.

6.1. Робастная устойчивость в анизотропийной теории

Как было указано в свойствах анизотропийной нормы, она не обладает

круговым свойством (2.11). Однако существует аналог этого свойства. На

базе соотношений (5.18), (5.19) в [36, 37] проведено исследование робастной

устойчивости в анизотропийной теории.

Рассмотрим оператор F , задающий вход-выходные соотношения в виде

[

]

[

][

]

z₁

F₁₁

F₁₂

w₁

(6.1)

z₂

F₂₁

F₂₂

w₂

Здесь w₁ ∈ R^m, w₂ ∈ R^p входы системы, z₁ ∈ R^m, z₂ ∈ R^q выходы систе-

мы, причем z₁ не обязательно является измеряемым.

Система (6.1) называется внутренне устойчивой, если матричная переда-

точная функция от входа (w₁, w₂)^T ∈ R^m+p к выходу (z₁, z₂)^T ∈ R^m+q асимп-

тотически устойчива [130], что эквивалентно тому, что передаточные функ-

ции Fz1w₁ , Fz₁w₂ , Fz₂w₁ , Fz₂w₂ аналитичны вне единичного круга. Fz_iw_j пе-

редаточная функция от входа w_i к выходу z_j , i, j = 1, 2.

Задача 2. Для заданного номинального объекта F найти диапазон изме-

нения неопределенности его параметров Δ, количественно измеряемый анизо-

z₁

w₁

z₂

w₂

Рис. 6. F -Δ конфигурация.

тропийной нормой, при котором система с неопределенностью будет являться

внутренне устойчивой.

Последнее будет означать робастность объекта F по отношению к неопре-

деленности Δ.

Введем класс допустимых неопределенностей

{

}

D_a(ǫ) =

Δ:Δ∈RH^m×m∞ :

|||Δ|||_a < ǫ

Далее всюду Δ(jω) означает предел

(

)

Δ(jω) = lim Δ

re^jω

ω ∈ [-π;π].

r→1-0

Будем говорить, что неопределенность Δ является допустимой для объек-

та F, если Δ ∈ RH^m×m∞ и система U(F,Δ) вида (2.17) внутренне устойчивы.

Теорема 1. Рассмотрим систему U(F,Δ) представленную на рис. 6,

где Δ : L^m2 → L^m2 и F : L^m+p2 → L^m+q2

каузальные линейные системы и

вход-выходные соотношения задаются посредством (6.1).

Пусть

• F устойчива и

(6.2)

|||F₁₁|||_c < ǫ^-1,

√

где c = a + m ln

, σ(Δ) =

λ_min(Δ^∗Δ)

минимальное

ess inf σ(Δ(jω))

−π≤ω≤π

сингулярное значение оператора Δ, ǫ некоторая положительная кон-

станта.

• Уровень анизотропии a определяется по формуле

mΣ

(6.3)

a=-

ln det

- mln

trΣ

ess sup σ(Δ(jω))

-π≤ω≤π

где Σ = (I_m - qF^∗11F₁₁)^-1, а параметр q ∈ [0, ∥F₁₁∥^-2∞) является решением

неравенства

]

[(

)

(6.4)

tr I_m - ǫ²F^∗11F₁₁

(I_m - qF^∗11F₁₁

)^-1

≤ 0.

Тогда для всех Δ ∈ D_a(ǫ) замкнутая система U(F, Δ) внутренне устойчива.

Теорема 1 дает достаточные условия робастности объектов, неопределен-

ность которых ограничена по анизотропийной норме. Данная теорема позво-

ляет ослабить консервативное условие ∥F₁₁∥_∞ < 1/ǫ теоремы о малом усиле-

нии, заменив его на условие (6.2). Уровень анизотропии a в данном случае

показывает, насколько можно понизить требования теоремы о малом усиле-

нии, не потеряв при этом робастную устойчивость.

Можно указать, как находить граничный уровень анизотропии a, обес-

печивающий внутреннюю устойчивость при выполнении (6.2), по заданной

реализации номинального объекта. Нахождение подходящего уровня анизо-

тропии сводится к задаче оптимизации max q при нелинейных ограничениях.

Подробно об этом можно прочесть в [37].

На базе предыдущей теоремы можно для заданной системы с различными

типами неопределенности (аддитивной, мультипликативной, неопределенно-

сти в виде взаимно простых факторов) [130] находить возможный разброс

параметров, точное значение которых неизвестно. Приведем аналог теоремы

Гловера-МакФарлейна [174] о робастной стабилизируемости [51] системы с

аддитивной неопределенностью.

Теорема 2. Рассмотрим систему L(F + Δ,K), с номинальным объек-

том F , аддитивной неопределенностью Δ и регулятором K, где Δ: l₂ → l₂

аддитивные возмущения, F : l₂ → l₂ номинальный объект, K : l₂ → l₂

регулятор и Δ, F, K линейные каузальные системы. Пусть также от-

носительно неопределенности известно ее максимальное сингулярное чис-

ло обусловленности ψ = ess sup cond (Δ^∗Δ). Регулятор K стабилизирует

-π≤ω≤π

F + Δ, если:

1) регулятор K стабилизирует номинальный объект, т.е. система

L(F, K) устойчива,

(

)

2) Δ ∈ D_a

для некоторого a ∈ [0, ∞).

|||K(I - F K)^-1|||a+mlnψ

Аналогичные результаты получены в анизотропийной теории с ненулевым

матожиданием входного возмущения [167].

6.2. Субоптимальное анизотропийное управление,

построение регуляторов пониженного

и заданного порядков

Аналогично тому, как в H₂ и H_∞ теориях управления вслед за оптималь-

ными постановками появились постановки, а затем и решения субоптималь-

ных задач, а также задач построения регуляторов пониженного и заданного

порядков, такая же ситуация сложилась и в анизотропийной теории. Субоп-

тимальные регуляторы стабилизируют замкнутую систему и обеспечивают

ограниченность ее анизотропийной нормы заданным значением, т.е. гаран-

тируют подавление случайных внешних возмущений, средняя анизотропия

которых не превосходит некоторого заданного уровня. В отличие от синтеза

оптимального анизотропийного регулятора решение субоптимальных задач

приводит к множеству регуляторов, оставляя дополнительные степени сво-

боды для определения некоторых дополнительных требований к замкнутой

системе с целью достижения желаемого качества управления.

6.2.1. Частотная теорема в анизотропийной теории

Ключевым шагом в теории построения субоптимальных анизотропийных

регуляторов является частотная теорема, сформулированная как в терминах

уравнения Риккати [164], так и в терминах матричных неравенств [70].

Кратко изложим анизотропийную частотную теорему, следуя [70].

Модель дискретной линейной стационарной системы F ∈ H^∞×m с m-мер-

ным входом W , n-мерным состоянием X и p-мерным выходом Z имеет вид

]

[x_k+1

[A B][x_k ]

(6.5)

z_k

C D w_k

где размерности вещественных матриц A, B, C, D согласованы и матрица A

является Шуровой (ρ(A) < 1). Предполагается, что входная последователь-

ность W есть стационарная последовательность гауссовских случайных век-

торов с ограниченной средней анизотропией a ≥ 0. Задача состоит в следую-

щем.

Задача 3. Для заданной системы F, уровня средней анизотропии входно-

го возмущения a ≥ 0 и числа γ > 0 проверить выполнение условия |||F |||_a < γ,

где |||F |||_a

анизотропийная норма системы F, определяемая (5.15).

Теорема 3. Пусть F ∈ H^∞×m система с реализацией в пространстве

состояний (6.5), a-анизотропийная норма (5.15) системы F строго ограни-

чена заданным пороговым значением γ > 0, т.е.

|||F |||_a < γ,

если существует η > γ², такое что неравенство

(

)_1/m

(6.6)

η - e-2a det(ηI_m - B^TΦB - D^TD)

<γ²

выполняется для вещественной (n × n)-матрицы Φ = Φ^T ≻ 0, удовлетво-

ряющей ЛМН

[

]

A^TΦA - Φ + C^TC A^TΦB + C^TD

(6.7)

< 0.

B^TΦA + D^TC B^TΦB + D^TD - ηI_m

Систему неравенств (6.6) и (6.7) можно решить с помощью свободно рас-

пространяемых программных пакетов, например [171] с программой-реша-

телем [206] для системы Matlab и Scilab. Этот метод вычисления a-анизо-

тропийной нормы не использует решения сложной системы перекрестно свя-

занных уравнений с помощью вычислительного алгоритма на основе метода

гомотопий.

В случае a → +∞ ЛМН (6.7) можно привести к виду





A^T ΦA -Φ

A^T ΦB

C^T





(6.8)

 B^TΦA BTΦB - γIm DT

 < 0,

-γI_p

хорошо известному в контексте H_∞ управления для дискретных си-

стем (см., например, [111, 123]). Этот факт тесно связан со сходимостью

lim_a→+∞ |||F |||_a = ∥F ∥_∞, благодаря чему неравенство |||F |||_a < γ “аппрокси-

мирует”

(6.9)

∥F ∥_∞

<γ

для достаточно больших значений a. Таким образом, при a → +∞ теорема 3

становится частотной теоремой для H_∞ нормы, устанавливающей эквива-

лентность между выполнением (6.9) и существованием положительно опре-

деленного решения ЛМН (6.8).

Частотная теорема для анизотропийной нормы в терминах неравенств яв-

ляется ключевым результатом, который применяется для решения задач син-

теза анизотропийных субоптимальных регуляторов методами выпуклой оп-

тимизации и полуопределенного программирования, описанных в следующем

разделе.

6.2.2. Построение субоптимальных анизотропийных регуляторов

Объект управления представлен дискретной линейной стационарной мо-

делью F с n_x-мерным состоянием X, m_w-мерным входом возмущения W,

m_u-мерным входом управления U, p_z-мерным управляемым выходом Z и

p_y-мерным измеряемым выходом Y :











x_k+1

A B_w B_u

x_k

= 



,

(6.10)

F : z_k

C_z D_zw D_zu

w_k

y_k

C_y D_yw

u_k

где размерности всех матриц согласованы, p_z ≤ m_w, пара матриц (A, B_u) яв-

ляется стабилизируемой, а пара (A, C_y) детектируемой.

Предполагается, что средняя анизотропия (5.12) последовательности W

не превосходит известного неотрицательного уровня a.

Регулятор заданного порядка по измеряемому выходу в форме динамиче-

ского компенсатора имеет следующий вид:

[

]

[

][

]

ξ_k+1

A_c B_c

ξ_k

(6.11)

K :

u_k

C_c D_c

y_k

где ξ_k n_ξ-мерный вектор состояния, стабилизирующий замкнутую систему

и гарантирующий некоторый заданный уровень качества подавления внеш-

них возмущений. Предполагается, что для объекта управления (6.10) и регу-

лятора (6.11) выполняется условие Кимуры [158] порядка n_ξ:

n_ξ > n_x - m_u - p_y.

Выполнение этого условия гарантирует существование стабилизирующего ре-

гулятора заданного порядка n_ξ.

Общая постановка задачи синтеза анизотропийного субоптимального ре-

гулятора заданного порядка следующая.

Задача 4. Для заданных объекта управления F с моделью в простран-

стве состояний (6.10), уровня средней анизотропии a ≥ 0 входного возмуще-

ния W и некоторого желаемого порогового значения γ > 0 найти дискретный

линейный стационарный регулятор по выходу K с моделью в пространстве

состояний (6.11), стабилизирующий замкнутую систему и гарантирующий,

что ее a-анизотропийная норма не превосходит порогового значения γ, т.е.

|||T_zw|||_a < γ.

В рамках анизотропийной теории управления получено решение общей

задачи синтеза регулятора заданного порядка и рассмотрены три важных

частных случая структуры объекта и регулятора [72]: регулятор в виде ста-

тической обратной связи по состоянию для объекта, состояние которого изме-

ряется точно [212]; динамический регулятор полного порядка по измеряемому

выходу; регулятор в виде статической обратной связи по измеряемому выхо-

ду объекта управления. Для решения задачи синтеза применяется критерий

проверки условия ограниченности анизотропийной нормы системы заданным

пороговым значением для модели в пространстве состояний. Этот критерий

частотная теорема для анизотропийной нормы сформулирован в предыду-

щем разделе обзора. В [208, 209] предложена техника редукции оптимального

анизотропийного регулятора, являющегося решением задачи анизотропийной

стохастической H_∞ оптимизации полного порядка [210]. На основе методов

выпуклой оптимизации в [71] решена задача синтеза субоптимального анизо-

тропийного регулятора заданного порядка в виде динамического компенса-

тора.

6.2.3. Многоканальная задача анизотропийного управления

В рамках концепции построения субоптимальных регуляторов в [73] рас-

сматривается задача синтеза анизотропийного управления для дискретной

линейной стационарной системы, в которой определенные вход-выходные ка-

налы сгруппированы вместе с учетом технических особенностей системы или

близости свойств сигналов.

Предположим, что в векторе управляемого выхода Z объекта управления

(6.10) с учетом требований технического проектирования выделены N групп

каналов управляемых выходов Z_j (состоящих в минимальном случае из одно-

го канала). Пусть в векторе внешнего входа W также выделены N групп кана-

лов внешних входов W_j. Одинаковые группы каналов управляемых выходов

Z_j = Z_i или внешних входов W_j = W_i считаются различными при j = i. Ана-

логичное разбиение входа и выхода объекта управления на группы каналов

предлагается в [199, 200] в гораздо более широкой постановке задачи много-

канального управления. Разбиение каналов по группам может осуществлять-

ся с учетом технических особенностей системы (например, эталонные сигна-

лы/внешние возмущения/шумы измерений) или близости свойств сигналов

Z₁

W₁

Z_N

W_N

Рис. 7. Замкнутая система в многоканальной задаче.

(например, слабо/сильно коррелированные сигналы). Для каждой из групп

каналов внешних входов W_j предполагается, что средняя анизотропия (5.12)

последовательности W_j не превосходит известного неотрицательного уров-

ня a_j, j = 1, . . . , N. Синтезируемый анизотропийный регулятор одновремен-

но обеспечивает заданные уровни подавления возмущений для определенных

групп каналов. Такие задачи будем называть многоканальными.

Пусть T_zw(z) обозначает матричную передаточную функцию от внеш-

него входа W к управляемому выходу Z замкнутой системы с регулято-

ром заданного порядка K в форме динамического компенсатора (6.11) с

n_ξ-мерным состоянием Ξ = {ξ_k}_k∈Z, стабилизирующим замкнутую систему

(рис. 7) и обеспечивающим некоторый заданный уровень подавления внеш-

них возмущений или заданное качество отслеживания эталонных сигналов.

Матричная передаточная функция замкнутой системы T_zw(z) задана ниж-

ним дробно-линейным преобразованием вида (2.16) для пары (F, K). Тогда

Tzjw_j (z) := LjTzw(z)Rj матричная передаточная функция от группы внеш-

них входов W_j к группе управляемых выходов Z_j , j = 1, . . . , N, где L_j , R_j

вещественные матрицы выбора групп входов и выходов соответственно. Пред-

полагается, что для объекта управления (6.10) и регулятора (6.11) выпол-

няется условие Кимуры n_ξ > n_x - m_u - p_y, что гарантирует существование

стабилизирующего регулятора заданного порядка n_ξ.

Постановка многоканальной задачи синтеза анизотропийного субопти-

мального регулятора заданного порядка следующая.

Задача 5. Для заданных объекта управления F с моделью в простран-

стве состояний (6.10), уровней средней анизотропии aj ≥ 0 групп внеш-

них входов W_j и некоторого набора желаемых пороговых значений γ_j > 0,

j = 1,...,N, найти дискретный линейный стационарный регулятор по выхо-

ду K с моделью в пространстве состояний (6.11), стабилизирующий замкну-

тую систему и обеспечивающий одновременное выполнение условий

(6.12)

|||Tzj w_j |||aj < γj.

Решение многоканальных задач имеет достаточно важное прикладное зна-

чение. Разработанная методика построения анизотропийных регуляторов для

многоканальных задач была применена к решению многоканальной задачи

анизотропийного управления угловым положением гиростабилизированной

платформы с переменным кинетическим моментом гироблока под воздей-

ствием внешних возмущений в условиях шумов измерений [211].

6.3. Синтез анизотропийных регуляторов для объектов

с параметрической неопределенностью

Естественно поставить задачу синтеза анизотропийных регуляторов для

систем, в которых объект подвергается некоторым возмущениям, в частно-

сти параметрическим, т.е. поставить задачу синтеза, аналогичную задаче по-

строения H₂ регуляторов для возмущенных объектов, упомянутую выше в

разделе 2.4.

Подробно содержание этого раздела опубликовано в [37]. Рассмотрим ли-

нейную дискретную стационарную систему F , описываемую уравнениями

x_k+1 = (A + F₁Ω_kE₁) x_k + (B₁ + F₂Φ_kE₂)w_k + (B₂ + F₃Ψ_kE₃)u_k,

(6.13)

z_k = C₁x_k + D₁₂u_k,

y_k = C₂x_k + D₂₁w_k,

где k ∈ Z, E |x_-∞|² < +∞, x_k ∈ Rⁿ состояние, z_k ∈ Rp1 управляемый вы-

ход, u_k ∈ Rm2 вектор управления, w_k ∈ Rm1 возмущение, y_k ∈ Rp2 на-

блюдаемый выход. Все входящие в систему (6.13) матрицы известны за ис-

ключением матриц Ω_k, Φ_k, Ψ_k, отвечающих неизвестным параметрам, о ко-

торых известно только то, что они удовлетворяют следующим ограничениям:

(6.14)

Ω^TkΩ_k ≤ I, Φ^TkΦ_k ≤ I, Ψ^TkΨ_k

≤ I, k ∈ Z,

где I обозначает единичную матрицу подходящей размерности.

Передаточная функция замкнутой системы от входа W = {w_k}_k∈Z к вы-

ходу Z = {z_k}_k∈Z задается согласно (2.16) нижним дробно-линейным преоб-

разованием пары (F, K)

L(F, K) = F₁₁ + F₁₂K(I - F₂₂K)^-1F₂₁.

Априорная информация о вероятностном распределении последовательно-

сти W состоит в следующем: W является стационарной гауссовской случай-

ной последовательностью, средняя анизотропия которой ограничена сверху

неотрицательным параметром a. Обозначим множество таких последователь-

ностей через W_a.

{

}

Введем Δ_k = diag

Ω_k, Φ_k, Ψ_k

матрицу всех неопределенностей в си-

стеме, тогда совокупность неравенств (6.14) может быть записана в виде

(6.15)

Δ^TkΔ_k

≤ I, k ∈ Z.

Неопределенность Δ_k, удовлетворяющую (6.15), будем называть допустимой.

Множество всех допустимых неопределенностей для системы F обозначим

через ID:

{

}

(6.16)

ID =

Δ_k = diag

Ω_k, Φ_k, Ψ_k

Δ^TkΔ_k ≤ I, k ∈ Z

Перед постановкой задачи введем понятия неупреждающего и допустимо-

го регулятора.

Линейный регулятор K называется строго неупреждающим, если для лю-

бого k управление u_k зависит только от предшествующих наблюдений y_j,

j ≤ k. Регулятор K называется допустимым, если он строго неупреждаю-

щий и внутренне стабилизирует замкнутую систему L(F, K). Множество всех

допустимых регуляторов для данной системы F обозначим через K.

Сформулируем теперь робастную стохастическую задачу H_∞ -оптимиза-

ции для системы с параметрической неопределенностью.

Задача 6. Для заданной системы (6.13) и верхней границы a ≥ 0 уровня

анизотропии входа найти допустимый регулятор K ∈ K, который миними-

зирует максимальное значение a-анизотропийной нормы замкнутой системы

L(F, K) по всем неопределенностям Δ_k ∈ ID, т.е. доставляет минимум функ-

ционалу качества

(6.17)

J₀(K) = sup |||L(F,K)|||_a.

Δ_k∈ID

Оптимальная задача (6.17) эквивалентна оптимальной задаче

(6.18)

sup sup

∥Z∥^2P → inf .

K∈K

Δ_k∈ID W∈BWa

Здесь BW_a множество нормированных входных сигналов с ограниченной

средней анизотропией:

BW_a = {W ∈ W_a : ∥W∥_P = 1} .

Решение сформулированной задачи производится путем погружения ее в

более общую задачу H_∞ оптимизации. У новой задачи объектом является

невозмущенный объект из задачи 6, влияние параметрической неопределен-

ности заменяется новым дополнительным входом в объект.

Показано, что значение функционала качества новой задачи мажорирует

значение функционала качества первоначальной задачи.

Решение новой более общей задачи сводится к решению четырех связан-

ных алгебраических уравнений Риккати, уравнению Ляпунова и уравнению

специального вида. Для их решения представлен модифицированный метод

гомотопий [162].

Основным недостатком предложенной методики является высокая вычис-

лительная сложность метода гомотопий. Данный недостаток был преодолен с

применением матричных неравенств. Условия синтеза статических и динами-

ческих регуляторов на основе методов выпуклой оптимизации были сформу-

лированы в [75] для системы с дробно-линейными неопределенностями вида









x_k+1

A B_w B_u

(6.19)

 z_k

= 

C_z D_zw D_zu

+

y_k

C_y D_yw









B_Δ

[

Δ(Ip

] wkk

,

+ D_zΔ

- D_ΔΔΔ)^-1

C_Δ D_Δw D_Δu

D_yΔ

u_k

где x_k n_x-мерный вектор состояния, w_k m_w-мерная случайная стацио-

нарная последовательность с ограниченным уровнем средней анизотропии

A(W ) ≤ a, u_k m_u-мерное управление, z_k p_z-мерный управляемый выход,

y_k p_y-мерный измеряемый выход. Отметим, что p_z ≤ m_w, пара (A, B_u) ста-

билизируема, а пара (A, C_y) детектируема. Стационарная неопределенность

Δ ∈ RmΔ×pΔ для заданного γ > 0 удовлетворяет условию Δ^TΔ ≤ γ^-2IpΔ.

Очевидно, что данная постановка обобщает задачу для объекта, записанного

в форме (6.13).

Для решения задачи с использованием верхнего дробно-линейного преоб-

разования были введены дополнительные m_Δ-мерный вход неопределенно-

сти wΔk и p_Δ-мерный выход неопределенности zΔk такие, что wΔk = ΔzΔk и

E |wΔk |² ≤ γ^-2E |zΔk |².

В [213] для аналогичной системы была решена задача синтеза робастного

субоптимального анизотропийного регулятора по состоянию без увеличения

размерности задачи.

Приведем теперь постановку задачи, следуя [17]. В качестве объекта

управления рассматриваются дискретные системы, заданные в пространстве

состояний в виде

(6.20)

x_k+1 = A^Δx_k + B^Δww_k + B_uu_k,

(6.21)

y_k = C^Δyx_k + D^Δyww_k,

(6.22)

z_k = C^Δzx_k + D^Δzww_k + D_zuu_k,

где x_k ∈ Rⁿ вектор состояния, u_k ∈ Rm1

управление, w_k ∈ R^m слу-

чайная стационарная последовательность с ограниченным уровнем средней

анизотропии A(W ) ≤ a, y_k ∈ R^p измеряемый выход, z_k ∈ Rp1 управляе-

мый выход, A^Δ = A + M_AΔN_A, B^Δw = B_w + M_BΔN_B, C^Δz = C_z + M_C ΔN_C,

C^Δy = C_y + M_CyΔN_Cy, D^Δyw = D_yw + M_DyΔN_Dy, D^Δzw = D_zw + M_DΔN_D. Мат-

рицы A, B_w, B_u C, D_w, C_z, D_zw, D_zu, M_A, N_A, M_B, N_B, M_C , N_C , M_D, N_D,

M_Cy, N_Cy, M_Dy и N_Dy постоянные соответствующих размерностей.

Матрица Δ ∈ R^q×q неизвестная, ограниченная по спектральной норме

σ(Δ) ≤ 1, т.е. Δ^TΔ ≤ I_q.

Можно показать, что в определенных случаях параметрические неопреде-

ленности объекта управления (6.19) могут быть представлены также и в фор-

ме (6.20)-(6.22). Однако данные классы не тождественны. Так, если матрица

D_ΔΔ = 0 в выражении (6.19), то дробно-линейные неопределенности явля-

ются подмножеством множества неопределенностей из класса (6.20)-(6.22).

В случае же, если D_ΔΔ = 0, неопределенности принадлежат разным множе-

ствам.

Для системы (6.20)-(6.22) были получены условия для синтеза статиче-

ских робастных субоптимальных анизотропийных регуляторов по состоянию

(u_k = F x_k) и по выходу (u_k = Ky_k).

6.4. Анизотропийная теория дескрипторных систем

Как говорилось выше, системы управления, замкнутые анизотропийны-

ми регуляторами, лежат “между” системами, замкнутыми H₂ регуляторами,

и системами, замкнутыми H_∞ регуляторами. Дескрипторные системы явля-

ются обобщением обыкновенных динамических систем, так как в своей моде-

ли содержат не только разностные или дифференциальные уравнения, но и

алгебраические связи между переменными состояния. Термин “дескриптор-

ный” пришел из зарубежной литературы, так как переменными состояния

таких систем являются физические величины (отсюда термин “descriptor”

описатель). Дескрипторные системы имеют больше приложений, чем обык-

новенные системы, поэтому обобщение известных для обыкновенных систем

теорий явилось естественным развитием теории управления. Известны тео-

рии построения H₂ и H_∞ регуляторов для линейных дискретных дескриптор-

ных систем [92, 105, 109, 110, 142, 237, 238]. Естественно желание построить

анизотропийную теорию для дискретных дескрипторных систем.

В пространстве состояний модель линейного стационарного объекта управ-

ления в дескрипторной форме имеет вид

(6.23)

Ex_k+1 = Ax_k + Bw_k,

(6.24)

y_k = Cx_k + Dw_k.

Основным отличием данной формы записи от обыкновенных систем явля-

ется присутствие в левой части матричного сомножителя E. При этом матри-

ца E предполагается вырожденной. Из-за вырожденности матрицы E отсут-

ствует возможность записать уравнения (6.23)-(6.24) в форме (5.13)-(5.14).

Это приводит к появлению у дескрипторных систем поведения, не характер-

ного для систем обыкновенных, а именно (см. [92, 221]):

• передаточная функция дескрипторной системы может не являться строго

правильной;

• для произвольных ограниченных начальных условий временная характе-

ристика дескрипторных систем может проявлять импульсное или непри-

чинное поведение вместе;

• дескрипторные системы обычно содержат три типа мод: ограниченные ди-

намические моды, неограниченные динамические моды и нединамические

моды; нежелаемое импульсное поведение в дескрипторных системах может

генерироваться неограниченными динамическими модами;

• даже если дескрипторная система является безымпульсной, она все рав-

но может иметь разрывы первого рода из-за несогласованных начальных

условий.

Подробнее о дескрипторных систем дискретного и непрерывного времени

можно прочесть в [13, 15, 109].

Из-за вышеперечисленных особенностей построение анизотропийной тео-

рии для таких систем не является тривиальным обобщением анизотропийной

теории для обыкновенных систем.

Первой задачей, которая была решена в рамках построения анизотропий-

ной теории для дискретных дескрипторных систем, была задача вычисления

анизотропийной нормы дескрипторной системы [12]. Для вычисления ани-

зотропийной нормы необходимо решить алгебраическое матричное уравне-

ние Риккати, уравнение Ляпунова и уравнение специального вида. В эти три

уравнения входили параметры обыкновенной системы, эквивалентной дан-

ной дескрипторной системе. В [90] предложен алгоритм вычисления анизо-

тропийной нормы дискретной дескрипторной системы с помощью выпуклой

оптимизации. Задачи анализа для дескрипторных систем, на вход которых

поступает случайная гауссовская последовательность с ненулевым математи-

ческим ожиданием, рассмотрены в [81].

Первая работа по синтезу оптимального анизотропийного управления для

дескрипторных систем [89] была посвящена построению управления при на-

личии информации обо всем векторе состояния и сводилась к решению двух

алгебраических матричных уравнений Риккати, матричного уравнения Ля-

пунова и уравнения специального вида. В [14] поставлена и решена задача

синтеза оптимального анизотропийного регулятора по выходу. Решение за-

дачи свелось к двухшаговой процедуре синтеза управления: на первом шаге

производились каузализация системы и ее приведение к форме эквивалент-

ной обыкновенной системы, а на втором шаге применялась известная мето-

дика решения задачи синтеза для обыкновенной системы.

В [1] получены условия ограниченности анизотропийной нормы дескрип-

торной системы на основе решения обобщенного уравнения Риккати и про-

верки ряда неравенств. В [82] задача субоптимального управления по состоя-

нию и вектору полной информации (состояние и возмущение) решена с по-

мощью обобщенных алгебраических уравнений Риккати. В [16] предложена

новая методика вычисления анизотропийной нормы и поиска субоптимально-

го анизотропийного регулятора по состоянию на основе строгих матричных

неравенств.

Более подробно с поставленными и решенными задачами анизотропийно-

го управления для дескрипторных систем можно ознакомиться в моногра-

фии [91].

6.5. Анизотропийный анализ систем с нецентрированными

входными сигналами

Как было сказано выше, в первоначальных постановках задач анизотро-

пийных анализа и синтеза [20, 21, 24, 70, 164, 225] в качестве внешних входных

возмущений рассматривались стационарные эргодические последовательно-

сти гауссовских случайных векторов с нулевыми математическими ожида-

ниями. Равенство нулю математических ожиданий означает, что средняя на

бесконечном интервале ошибка, обусловленная наличием такого рода возму-

щений, зависит только от ковариационных матриц векторов последователь-

ности. Однако в реальных ситуациях, при различных сбоях в оборудовании

или наличии нетривиального внешнего возмущения, средние значения векто-

ров возмущения отличны от нуля. В связи с этим в рамках анизотропийной

теории имеет смысл в качестве внешнего возмущения рассматривать стацио-

нарные эргодические последовательности гауссовских случайных векторов

с ненулевыми средними. Предположение о наличии у векторов последова-

тельности постоянного (одного и того же) математического ожидания не на-

рушает свойств стационарности и эргодичности последовательности. Более

того, при определенных условиях эти свойства сохраняются и при перемен-

ных во времени математических ожиданиях. Таким образом, при рассмотре-

нии в анизотропийной теории случая ненулевого математического ожидания

у векторов входной последовательности фактически происходит расширение

границ ее применения. Идея построения анизотропийной теории с ненулевым

матожиданием входного сигнала принадлежит М. Карни [165].

Для построения анизотропийной теории управления с нецентрированны-

ми входными случайными сигналами необходимо скорректировать определе-

ния анизотропии, средней анизотропии и анизотропийной нормы в случае,

когда векторы входного возмущения имеют ненулевые математические ожи-

дания. Далее нужно рассмотреть вопросы анализа и получить алгоритмы

вычисления анизотропии, средней анизотропии и анизотропийной нормы в

частотной области и пространстве состояний. Окончательной целью являет-

ся построение методов синтеза анизотропийных регуляторов для систем, на

вход которых поступает нецентрированная случайная последовательность.

Рассмотрим два гауссовских m-мерных случайных вектора w и v с плотно-

стями распределений

{

}

(

)_-1/2

f (x) =

(2π)^m det(Σ)

exp

(x - µ)^TΣ^-1(x - µ)

{

}

(

)_-m/2

x^Tx

p_λ(x) =

2πλ

exp

x∈R^m,

2λ

соответственно. Случайный вектор w имеет ненулевое математическое ожи-

дание E[w] = µ = 0 и ковариационную матрицу cov(w) = Σ = Σ^T ≻ 0, в то

время как математическое ожидание вектора v равно нулю, а его ковариаци-

онная матрица скалярная: cov(v) = λI_m. В качестве меры отличия w от v,

как и ранее, будет выступать относительная энтропия (5.4), равная в данном

случае

tr(Σ) + |µ|

(6.25)

D(f||p_λ) = -h(w) +

ln(2πλ) +

2λ

так как E[|w|²] = tr(Σ) + |µ|².

Анизотропия случайного вектора определяется как минимальное в смыс-

ле параметра λ > 0 значение относительной энтропии D(f||p_λ):

A(w) = minD(f||pλ),

λ>0

что с учетом (6.25) приводит к

(

)

mΣ

A(w) = -

ln det

tr(Σ) + |µ|²

Сравнение полученной формулы для анизотропии случайного вектора w с

ненулевым математическим ожиданием µ и выражения (5.10), определяюще-

го анизотропию случайного вектора с нулевым математическим ожиданием,

позволяет заключить, что

)

( tr(Σ) + |µ|

A(w)|_µ=0 = A(w)|_µ=0 +

ln det

tr(Σ)

Иными словами, наличие математического ожидания всегда увеличивает ме-

ру отличия w от множества эталонных случайных векторов с плотностями

{p_λ(x): λ > 0}. Более того, для двух различных случайных векторов w₁ и w₂

с математическими ожиданиями µ₁ и µ₂ и равными ковариационными матри-

цами cov(w₁) = cov(w₂) = Σ анизотропия тем больше, чем больше евклидова

норма математического ожидания:

A(w₁) ≥ A(w₂)

⇔

|µ₁| ≥ |µ₂|.

В случае ненулевого математического ожидания средняя анизотропия до-

пускает представление

∫

(

)

mS(ω)

(6.26)

A(W ) = -

ln det

dω,

4π

∥G∥²²

+ |M|²

-π

где для вектора M справедливо

(

)

(6.27)

D_g + C_g(I - A_g)^-1B_g

µ,

а матрицы A_g, B_g, C_g, D_g задают формирующий фильтр G в пространстве

состояний следующим образом:

x_k+1 = A_gx_k + B_g(v_k + µ),

(6.28)

w_k = C_gx_k + D_g(v_k + µ).

Алгоритм вычисления средней анизотропии при ненулевом математиче-

ском ожидании аналогичен алгоритму вычисления средней анизотропии в

случае центрированного возмущения [113, 207].

Следующая формула устанавливает связь между значением средней ани-

зотропии последовательности с ненулевыми матожиданиями и средней ани-

зотропии последовательности с нулевыми математическими ожиданиями:

)

( ∥G∥²² + |M|

(6.29)

A(W ) = A_o(W ) +

∥G∥²

где ∥G∥²² = tr(Σ) H₂ норма передаточной функции G(z).

Рассмотрим линейную дискретную стационарную систему F ∈ H^∞×m с

m-мерным входом W , с p-мерным выходом Z и постоянными матрицами

A∈R^n×n,B∈R^n×m,C ∈R^p×n,D∈R^p×m:

x_k+1 = Ax_k + Bw_k,

(6.30)

z_k = Cx_k + Dw_k.

Передаточная функция такой системы равна F (z) = D+C(z^-1I_n -A)^-1B.

В качестве входа W будем рассматривать последовательность с ограниченной

сверху числом a ≥ 0 средней анизотропией, т.е. последовательность, сгенери-

рованную формирующим фильтром (6.28) из множества

{

}

G_a = G ∈ H^m×m2 : A(G) ≤ a .

Анизотропийная норма системы (6.30) равна

√

∥F G∥²² + |F|

(6.31)

|||F |||_a =

sup Q(F,W) = sup

W: A(W)≤a

G∈Ga

∥G∥²² + |M|²

где M и F математические ожидания соответственно векторов входной и

выходной последовательностей W и Z на стационарном режиме:

(

)

M = lim

E[w_k] =

D_g + C_g(I - A_g)^-1B_g

µ,

k→∞

(

)

F = lim

E[z_k] =

D + C(I - A)^-1B

k→∞

Идеи построения анизотропийных регуляторов с нецентрированными

входными возмущениями были опубликованы в [168].

6.6. Анизотропийная теория для нестационарных систем

В последние годы развивается подход к построению теории анизотропий-

ного робастного управления и фильтрации в нестационарных системах. В [24]

впервые была рассмотрена задача анизотропийного анализа робастного каче-

ства линейных нестационарных дискретных систем на конечном временном

интервале. В этой работе были даны определения анизотропии и анизотро-

пийной нормы, которые соответствовали новым задачам нестационарной ани-

зотропийной теории управления на конечном горизонте.

Следующей важной работой в построении анизотропийной теории для

систем на конечном горизонте в субоптимальной постановке явилась рабо-

та [173]. Определения анизотропии случайного вектора и анизотропийной

нормы дискретной линейной нестационарной системы, введенные в [24], яв-

ляются основой для решения задач анизотропийного управления и фильтра-

ции на конечном временном интервале. В [173] сформулированы необходи-

мые и достаточные условия ограниченности анизотропийной нормы системы

с переменными параметрами, предполагающие решение разностного уравне-

ния Риккати и неравенства относительно детерминанта положительно опре-

деленной матрицы. На основе этого критерия в [74] поставлена и решена

задача синтеза анизотропийного регулятора для дискретной линейной неста-

ционарной системы, гарантирующего ограниченность анизотропийной нормы

замкнутой системы заданным пороговым значением на конечном временном

интервале. Получены достаточные условия существования анизотропийно-

го регулятора с переменными параметрами, гарантирующего ограниченность

анизотропийной нормы замкнутой дискретной линейной нестационарной си-

стемы заданным пороговым значением на конечном временном отрезке. Эти

условия определяют алгоритм вычисления матрицы параметров регулятора

из рекуррентного решения систем матричных неравенств или последователь-

ности оптимизационных задач.

Задача анализа нестационарной линейной системы на конечном интервале

времени при нецентрированных входных возмущениях была решена в [40].

В этой работе было показано, что вычисление анизотропийной нормы ука-

занного класса систем в пространстве состояний связано с решением систем

разностных матричных уравнений и уравнения специального вида. Решение

задачи синтеза субоптимального управления для нестационарных систем на

конечном горизонте было получено в [74].

6.7. Анизотропийная фильтрация

Как известно, вместе с H₂ и H_∞ теориями управления развивались и H₂

и H_∞ теории фильтрации [79, 147, 204]. Этим теориям фильтрации при-

сущи все особенности, имеющиеся в соответствующих теориях управления.

В калмановской фильтрации предполагается, что модель динамики процесса

и статистические характеристики шумов модели и измерения точно извест-

ны. Дисперсия ошибки оценивания (фильтрации) является квадратичным

критерием оптимальности. Фильтр Калмана, обеспечивающий минимальную

дисперсию ошибки оценивания, является оценивателем состояния системы.

Минимизация или ограничение дисперсии ошибки фильтрации эквивалент-

на минимизации или ограничению H₂ нормы оператора ошибки фильтрации.

Также известно, что фильтр Калмана (или H₂ фильтр), синтезированный для

заданной модели, не является робастным, т.е. может потерять устойчивость

при малых изменениях математической модели объекта.

В случае, когда априорная информация о модели объекта и статистиче-

ских свойствах шумов модели и измерения не известна точно, может исполь-

зоваться H_∞ критерий. Фильтр, синтезированный по критерию ограниченно-

сти H_∞ нормы, гарантирует, что H_∞ норма оператора, связывающего вход-

ной сигнал возмущения и ошибку оценивания, не превышает заданного поло-

жительного числа. Алгоритмы H_∞ фильтрации принадлежат классу мини-

максных алгоритмов, при которых минимизируется ошибка оценивания для

наихудшего случая (см., например, [131, 135, 183, 203, 204]).

Стоит отметить, что алгоритмы фильтрации в этих теориях рассматрива-

ются как на конечном, так и на бесконечном горизонтах [135].

Как и в случае управления, оптимальные H₂ и H_∞ фильтры эффективно

функционируют только в том случае, когда входные сигналы принадлежат

тем классам, которые предполагались при создании этих теорий. Примене-

ние H₂ оценивателя в случае с сильно “окрашенным” входным возмущением

обычно приводит к неудовлетворительным ошибкам оценивания, а H_∞ оцени-

ватель, рассчитанный на наихудший случай, при входном возмущении в виде

белого или слабо “окрашенного” шума является излишне перестраховочным

(консервативным) [214].

Одним из направлений по синтезу менее консервативных, чем H_∞ филь-

тры, и более робастных, чем H₂ фильтры, являются так называемые “смешан-

ные” H₂/H_∞ фильтры (см., например, [119, 133, 156, 253]). В данном подходе

минимизируется H₂ критерий при заданном ограничении на H_∞ критерий.

Методы H₂, H_∞ и смешанной H₂/H_∞ фильтрации основываются на реше-

ниях уравнений Риккати или линейных матричных неравенств (см., напри-

мер, [8, 101]). Достижение компромисса между H₂ оптимальными и H_∞ оп-

тимальными фильтрами рассматривается в задаче обобщенной H_∞ фильтра-

ции [9], в которой минимизируется совместное влияние неизвестных началь-

ных условий и неизмеряемого внешнего возмущения на ошибку оценивания.

Для линейных нестационарных систем предложены алгоритмы синтеза неста-

ционарных фильтров, которые основываются на рекуррентном решении си-

стемы разностных линейных матричных неравенств [124]. При этом решение

системы линейных матричных неравенств необходимо на каждом шаге.

Первой работой по анизотропийной оптимальной фильтрации для стацио-

нарных систем на бесконечном горизонте была [227].

Задача оптимальной анизотропийной фильтрации для линейных неста-

ционарных дискретных систем на конечном горизонте решена в [226]. Она

сводится к решению двух разностных уравнений Риккати в прямом и обрат-

ном времени.

В [61] решена задача анизотропийной субоптимальной фильтрации мето-

дами выпуклой оптимизации.

Работа [173] позволила решить задачу анизотропийной фильтрации для

линейных нестационарных систем на конечном горизонте для частного слу-

чая равенства размерностей оцениваемого выхода и внешнего возмуще-

ния [241]. При решении последней задачи в [241] вводится скалярная вспомо-

гательная матричная переменная, которая приводит к существенному увели-

чению консерватизма.

В [63] сняты ограничения на равенства размерностей оцениваемого вы-

хода и внешнего возмущения [241], решена задача робастной фильтрации

на конечном горизонте для линейной дискретной нестационарной системы

с наблюдаемым и оцениваемым выходами с неточно известным вероятност-

ным распределением входного возмущения. Величина ошибки оценивания ко-

личественно характеризуется анизотропийной нормой. Задача нахождения

субоптимального анизотропийного оценивателя сводится к задаче выпуклой

оптимизации. Приведен алгоритм поиска субоптимального анизотропийного

оценивателя, который основывается на рекуррентном решении системы мат-

ричных неравенств.

В [215] рассматривалась задача стохастической анизотропийной робаст-

ной фильтрации на бесконечном горизонте для линейной дискретной стацио-

нарной системы, подверженной влиянию нецентрированного случайного воз-

мущения с неточно известным вероятностным распределением. В терминах

матричных неравенств доказано достаточное условие строгой ограниченно-

сти анизотропийной нормы линейной дискретной стационарной системы за-

данным пороговым значением (частотная теорема). Сформулировано доста-

точное условие существования оценивателя, гарантирующего ограниченность

анизотропийной нормы оператора ошибки оценивания заданным пороговым

значением.

Решение задачи фильтрации для линейной дискретной нестационарной си-

стемы на конечном горизонте было получено в [64], где предполагалось, что

внешнее возмущение имеет ограниченную сверху анизотропию и дополни-

тельно удовлетворяет двум ограничениям на моменты. Решение задачи ос-

новывается на критерии ограниченности анизотропийной нормы системы и

сводится к поиску решения задачи выпуклой оптимизации.

6.8. Другие теории, имеющие отношение к относительной энтропии

В теории минимаксного LQG управления относительная энтропия рас-

сматривается для описания неопределенности объекта управления. Пара-

Рис. 8. К описанию неопределенностей в задаче минимаксного LQG.

метрические неопределенности, к которым можно отнести нелинейности,

неучтенную и немоделируемую динамику, а также интервальные допуски на

параметры системы, выделяются в структуру, показанную на рис. 8.

Математически неопределенность объекта управления описывается в ви-

де:

x_k+1 = Ax_k + Bu_k + D w_k,

z_k = E₁x_k + E₂u_k,

y_k = Cx_k + v_k.

Здесь начальные условия x₀ и шумы w_k и v_k случайные процессы, опре-

деляемые неизвестной функцией распределения вероятностей ν(·). Данная

задача рассматривается на конечном горизонте, т.е. k = 0, N . Относитель-

ная энтропия в данном случае определяет “расстояние” между гауссовскими

функциями распределения µ(·) и ν(·). Матрицы E₁ и E₂ являются извест-

ными и участвуют в формировании неопределенности. При этом функция

распределения вероятностей ν(·) определяет допустимые возмущения, если

справедливо неравенство:

[

]

(

)

∑

(6.32)

ν(·)∥µ(·)

−E_ν

∥z_k∥² + d

≤ 0,

k=0

где d > 0 постоянная скалярная величина, E_ν условное математическое

ожидание относительно ν(·), а D(ν(·)∥µ(·)) относительная энтропия между

функциями распределения вероятностей µ(·) и ν(·), определяемая выражени-

ем

∫



ν(η)

(

)

ν(η) log

dη, если ν(η) ≪ µ(η) и log

∈L₁,

µ(η)

(6.33) R

ν(·)∥µ(·)

^Ω+∞ в противном случае.

Запись ν(η)≪µ(η) означает, что функция распределения вероятности ν(η)

абсолютно непрерывна относительно функции µ(η).

Задача минимаксного управления в данной постановке заключается в по-

иске наихудшего значения математического ожидания квадратичного функ-

ционала качества при ограничениях (6.33) и выражается в виде

V_τ = inf supE_ν[J_τ ],

K∈Λ ν(·)

где

∑[

]

J_τ =

x^TN+1Q_N+1x_N+1 +

x^TkQ_k + u^TRuk

k=0

[

]

(

)

∑

-τ R

ν(·)∥µ(·)

−d-E_ν

∥z_k∥2

k=0

Относительная энтропия в данном случае используется, чтобы характе-

ризовать неопределенность в объекте. Однако она, как и в описанных чуть

выше работах по анизотропийной теории управления, относится к описа-

нию неопределенности входного сигнала, действующего на систему и фор-

мируемого в том числе за счет неопределенности объекта управления. Та-

ким образом, ставится задача поиска оптимального управления, минимизи-

рующего некий функционал качества при ограничениях на относительную

энтропию входного вероятностного сигнала. Эта задача сводится к построе-

нию управления при наихудшем в смысле относительной энтропии входном

сигнале. Такое управление авторы назвали минимаксным. В отличие от ра-

бот по анизотропийной теории управления в серии работ по минимаксно-

му управлению рассматриваются как дискретные описания систем управле-

ния [189, 190, 202, 219, 245, 246], так и описания системы в виде стохастических

дифференциальных уравнений [217, 218]. Аналогом описания неопределенно-

сти для систем, заданных стохастическими дифференциальными уравнения-

ми, является описание с помощью интегральных квадратичных ограничений.

В рамках такого подхода были решены задачи минимаксного управления и

фильтрации на конечном горизонте [217, 245].

Содержательные результаты в минимаксной теории управления получены,

когда система является линейной, а распределение входного сигнала являет-

ся гауссовским. В этом случае решение минимаксной линейно-квадратичной

задачи сводится к задаче оптимального управления, чувствительного к рис-

ку [229]. С описанными выше работами сильно коррелируют работы [189]-

[202], в которых также используется информационная характеристика от-

носительная энтропия.

7. Заключение

Основной целью данной работы было провести обзор того, как во второй

половине XX века развивались и модифицировались классические постанов-

ки задач H₂ и H_∞ управления, как появились минимаксные задачи, а также

их связь со стохастической робастной теорией управления с анизотропийным

критерием качества, созданной И.Г. Владимировым и развиваемой научной

школой А.П. Курдюкова более 20 лет.

Авторы просят прощения за неполное освещение всех подходов, лежащих

между задачами H₂ и H_∞ оптимального и субоптимального управления. Ро-

бастные стохастические идеи и постановки задач приведены в обзоре в той

степени, которая позволяет акцентировать особенность описываемого подхо-

да и соотносить его с анизотропийной теорией.

В завершение обзора хотелось бы отменить дальнейшее направление

развития анизотропийной теории, основным объектом рассмотрения кото-

рой являются линейные системы дискретного времени. В недавних работах

В.А. Бойченко и А.П. Курдюкова [18, 160] была сделана попытка расширить

область применимости анизотропийной теории на случай внешних возмуще-

ний в виде дискретных и непрерывных случайных процессов с конечной l₂/L₂

или мощностной нормой. Для этого было введено понятие σ-энтропии слу-

чайного сигнала и определение σ-энтропийной нормы системы. Аксиоматика

данной теории была построена на основе понятия корреляционной свертки

случайного сигнала, которая позволяет работать как со стационарными, так

и с нестационарными случайными процессами, используя матрицу спектраль-

ной плотности, которая инкапсулирует все различия, явившиеся следствием

выбора l₂/L₂ или мощностной нормы дискретного или непрерывного сигнала.

Полученные результаты σ-энтропийного анализа верны для систем и непре-

рывного, и дискретного времени. В дальнейшем планируется развивать это

направление, переходя к постановке и решению задач синтеза.

СПИСОК ЛИТЕРАТУРЫ

Андрианова О.Г., Белов А.А., Курдюков А.П. Условия ограниченности анизо-

тропийной нормы дескрипторной системы // Известия РАН. Теория и системы

управления. 2015. № 1. С. 29-40.

Андриевский Б.Р., Матвеев А.С., Фрадков А.Л. Управление и оценивание при

информационных ограничениях: к единой теории управления, вычислений и

связи // АиТ. 2010. № 4. С. 34-99.

Andrievsky B.R., Matveev A.S., Fradkov A.L. Control and Estimation Under Infor-

mation Constraints: Toward a Unified Theory of Control, Computation and Com-

munications // Autom. Remote Control. 2010. V. 71. P. 572-633.

Аоки М. Оптимизация стохастических систем. М.: Наука, 1971.

Аров Д.З., Крейн М.Г. Задача поиска минимума энтропии в проблеме продол-

жения // Функцион. анализ и его приложения. 1981. Т. 4. С. 73-75.

Аров Д.З., Крейн М.Г. О вычислении энтропийных интегралов и их минимумов

в обобщенных проблемах продолжения // Acta Scienta Matematica. 1983. Т. 45.

C. 33-50.

Афанасьев В.Н. Управление неопределенными динамическими объектами. М.:

Физматлит, 2008.

Баландин Д.В., Коган М.М. Алгоритмы синтеза робастного управления дина-

мическими системами. Нижний Новгород, 2007.

Баландин Д.В., Коган М.М. Синтез законов управления на основе линейных

матричных неравенств. М.: Физматлит, 2007.

Баландин Д.В., Коган М.М. Обобщенная H_∞-оптимальная фильтрация при

внешнем и начальном возмущениях // Дифференциальные уравнения. 2012.

Т. 48. № 11. С. 1507-1514.

10.

Баландин Д.В., Коган М.М. Минимаксная фильтрация: γ₀-оптимальные на-

блюдатели и обобщенные H_∞-оптимальные фильтры // АиТ. 2013. № 4.

С. 43-58.

Balandin D.V., Kogan M.M. Minimax Filtering: γ₀-optimal Observers and Gener-

alized H_∞-optimal Filters // Autom. Remote Control. 2013. V. 74. P. 575-587.

11.

Барабанов А.Е., Первозванский А.А. Оптимизация по равномерно-частотным

показателям (H_∞-теория) // АиТ. 1992. № 9. C. 3-32.

Barabanov A.E., Pervozvanskii A.A. Optimization with respect to uniform-

frequency indices (H_∞-theory) // Autom. Remote Control. 1992. V. 53. No. 9.

P. 1301-1327.

12.

Белов А.А., Курдюков А.П. Вычисление анизотропийной нормы дескрипторной

системы // АиТ. 2010. № 6. C. 51-63.

Belov A.A., Kurdyukov A.P. Calculation of the Anisotropic Norm of the Descriptor

System // Autom. Remote Control. 2010. V. 71. P. 1022-1033.

13.

Белов А.А., Курдюков А.П. Линейные дескрипторные системы дискретного

времени. М.: ИПУ РАН, 2011.

14.

Белов А.А. Синтез анизотропийных регуляторов для дескрипторных систем по

выходной переменной // АиТ. 2013. № 11. С. 84-99.

Belov A.A. Anisotropic Controller Design for Descriptor Systems with Respect to

the Output Variable // Autom. Remote Control. 2013. V. 74, No. 11. P. 1838-1850.

15.

Белов А.А., Курдюков А.П. Дескрипторные систеы и задачи управления. М.:

Физматлит, 2015.

16.

Белов А.А., Андрианова О.Г. Синтез субоптимальных анизотропийных регуля-

торов по состоянию для дескрипторных систем на основе линейных матричных

неравенств // АиТ. 2016. № 10. С. 40-56.

Belov A.A., Andrianova O.G. Anisotropy-Based Suboptimal State-Feedback Con-

trol Design Using Linear Matrix Inequalities // Autom. Remote Control. 2016.

V. 77. No. 10. P. 1741-1754.

17.

Белов А.А., Андрианова О.Г. Синтез робастного управления параметрически

неопределенными линейными системами для подавления случайных внешних

возмущений // АиТ. 2020. № 4. С. 94-109.

Belov A.A., Andrianova O.G. Robust Control Design for Suppressing Random Ex-

ogenous Disturbances in Parametrically Uncertain Linear Systems // Autom. Re-

mote Control. 2020. V. 81. No. 4. P. 649-661.

18.

Бойченко В.А. Анизотропийный анализ в случае ненулевых начальных усло-

вий // Управление большими системами. 2017. № 67. С. 32-51.

19.

Быховский М.А. Пионеры информационного века. История развития теории

связи. М.: Техносфера, 2006.

20.

Владимиров И.Г., Курдюков А.П., Семенов А.В. Анизотропия сигналов и эн-

тропия линейных стационарных систем // ДАН. 1995. Т. 342. № 5 С. 583-585.

21.

Владимиров И.Г., Курдюков А.П., Семенов А.В. Стохастическая проблема

H∞ -оптимизации // ДАН. 1995. Т. 343. № 5. C. 607-609.

22.

Владимиров И.Г., Курдюков А.П., Семенов А.В. Асимптотика анизотропийной

нормы линейных стационарных систем. // АиТ. 1999. № 3. С. 78-87.

Vladimirov I.G., Kurdyukov A.P., Semenov A.V. Asymptotics of the Anisotropic

Norm of Linear Time-Independent Systems // Autom. Remote Control. 1999. V. 60.

No. 3. P. 359-366.

23.

Владимиров И.Г., Курдюков А.П., Максимов Е.А., Тимин В.Н. Анизотропий-

ная теория управления новый подход к стохастическому робастному управ-

лению // Труды IV конференции “Идентификация систем и задачи управле-

ния” Пленарный доклад. Москва, Январь 25-28, 2005. С. 9-32.

24.

Владимиров И.Г., Даймонд Ф., Клоеден П. Анизотропийный анализ робастного

качества линейных нестационарных дискретных систем на конечном времен-

ном интервале // АиТ. 2006. № 8. C. 92-111.

Vladimirov I.G., Diamond Ph., Kloeden P.E. Anisotropy-Based Robust Perfor-

mance Analysis of Finite Horizon Linear Discrete Time Varying Systems // Autom.

Remote Control. 2006. V. 67. No. 8. P. 1265-1282.

25.

Гантмахер Ф.Р. Теория матриц. М.: Наука, 1966.

26.

Гельфанд И.М., Колмогоров А.Н., Яглом А.М. Информация и энтропия для

непрерывных распределений. Труды III Всесоюзного математического съезда,

Москва, 1958. Т. 3. С. 300-320.

27.

Ибрагимов И.А., Розанов Ю.А. Гауссовские случайные процессы. М.: Наука,

1970.

28.

Калман Р.Е. Об общей теории систем управления, Труды I Конгресса IFAC,

Т. 2, Изд-во АН СССР, М.: 1961.

29.

Квакернаак Х., Сиван Р. Линейные оптимальные системы управления. М.:

Мир, 1977.

30.

Коган М.М. Синтез оптимального и робастного управления с H_∞/γ₀ критери-

ем // АиТ. 2016. № 8. C. 3-23.

Kogan M.M. Design of Optimal and Robust Control with H_∞/γ₀ Performance Cri-

terion // Autom. Remote Control. 2016. V. 77. P. 1317-1333.

31.

Колесник В.Д., Полтырев Г.Ш. Курс теории информации. М.: Наука, 1982.

32.

Колмогоров А.Н. Интерполирование и экстраполирование стационарных слу-

чайных последовательностей // Изв. Акад. наук СССР, сер. Матем. 1941. Т. 5.

№ 1. С. 3-14.

33.

Красовский А.А. Статистическая теория переходных процессов в системах

управления. М.: Наука, 1968.

34.

Кульбак С. Теория информации и статистика М.: Мир, 1967.

35.

Курдюков А.П., Владимиров И.Г., Тимин В.Н. Элементы теории робастного

и стохастического робастного управления. Том 3 “Синтез регуляторов систем

автоматического управления” в учебнике “Методы классической и современ-

ной теории автоматического управления”, М.: Изд. ГТУ им. Н.Э. Баумана,

С. 385-480, 2004.

36.

Курдюков А.П., Максимов Е.А. Робастная устойчивость линейных дискретных

систем с неопределенностью, ограниченной по анизотропийной норме // АиТ.

2004. № 12. С. 129-143.

Kurdyukov A.P., Maksimov E.A. Robust Stability of Linear Discrete Stationary

Systems with Uncertainty Bounded in the Anisotropic Norm // Autom. Remote

Control. 2004. V. 65. P. 1977-1990.

37.

Курдюков А.П., Максимов Е.А. Решение стохастической задачи H_∞ -оптимиза-

ции для линейных систем с параметрической неопределенностью // АиТ. 2006.

№ 8. C. 112-141.

Kurdyukov A.P., Maximov E.A. Solution of the Stochastic H_∞ -optimization Prob-

lem for Discrete Time Linear Systems Under Parametric Uncertainty // Autom.

Remote Control. 2006. V. 67. P. 1283-1310.

38.

Кустов А.Ю., Курдюков А.П. Синтез формирующего фильтра, обеспечиваю-

щего на своем выходе заданный уровень средней анизотропии // АиТ. 2013.

№ 3. С. 51-66.

Kustov A.Yu., Kurdyukov A.P. Shaping Filter Design with a Given Mean

Anisotropy of Output Signals // Autom. Remote Control. 2013. V. 74. P. 358-371.

39.

Кустов А.Ю. Анизотропийный анализ в случае ненулевого математического

ожидания входного возмущения // Управление большими системами: сборник

трудов (электронный журнал). М.: ИПУ РАН, 2014. Вып. 50. С. 6-23.

40.

Кустов А.Ю., Тимин В.Н. Анизотропийный анализ нестационарных систем на

конечном интервале времени при нецентрированном возмущении // АиТ. 2017.

№ 6. С. 18-35.

Kustov A.Yu., Timin V.N. Anisotropy-Based Analysis for Finite Horizon Time-

Varying Systems with Non-centered Disturbances // Autom. Remote Control. 2017.

V. 78. P. 974-988.

41.

Летов А.М. Аналитическое конструирование регуляторов. I // АиТ. 1960.

Т. 21. № 4. C. 436-441.

42.

Летов А.М. Аналитическое конструирование регуляторов. II // АиТ. 1960.

Т. 21. № 5. C. 561-568.

43.

Летов А.М. Аналитическое конструирование регуляторов. III // АиТ. 1960.

Т. 21. № 6. C. 661-665.

44.

Летов А.М. Аналитическое конструирование регуляторов. IV // АиТ. 1961.

Т. 22. № 4. C. 425-435.

45.

Максимов Е.А. О связи задачи синтеза анизотропийных регуляторов с класси-

ческими задачами оптимального управления // АиТ. 2007. № 9. С. 134-144.

Maksimov E.A. On the Relationship Between the Problem of Anisotropy-Based

Controller Synthesis and Classical Optimal Control Problems // Autom. Remote

Control. 2007. V. 68. P. 1594-1603.

46.

Маслов В.П.,Черный А.С. О минимизации и максимизации энтропии в различ-

ных дисциплинах // Теория вероятностей и ее применения. 2003. Т. 48. № 3.

С. 467-486.

47.

Острем К.Ю. Введение в стохастическую теорию управления. М.: Мир, 1973.

48.

Первозванский А.А. Курс теории автоматического управления. М.: Наука,

1986.

49.

Пинскер М.С. Количество информации о гауссовском случайном процессе, со-

держащейся во втором процессе, стационарно с ним связанном // ДАН. 1954.

Т. 98. С. 213-216.

50.

Позняк А.С., Себряков Г.Г., Семенов А.В., Федосов Е.А. H_∞-теория управле-

ния: феномен, достижения, перспективы, открытые проблемы. М: ГосНИИАС,

Институт проблем управления АН СССР, 1990.

51.

Позняк А.C. Лекции по основам H_∞ оптимального управления. М.: Изд.

МФТИ, 1991.

52.

Поляк Б.Т., Щербаков П.С. Робастная устойчивость и управление. М.: Наука,

2002.

53.

Поляк Б.Т., Хлебников М.В., Щербаков П.С. Управление линейными система-

ми при внешних возмущениях. М.: ЛЕНАНД, 2014.

54.

Пугачёв В.С., Синицын И.Н. Стохастические дифференциальные системы.

Изд. 2-е, доп., М.: Наука, 1990.

55.

Сейдж Э., Мелc Дж. Теория оценивания и ее применение в связи и управле-

нии. Пер с англ. под ред. проф. Б. Р. Левина. М.: Связь, 1976.

56.

Семенов А.В., Владимиров И.Г., Фурлетов М.Ю., Мещеряков О.Г. Методы

стохастической H_∞-оптимизации в приложении к проблемам конструирова-

ния робастных регуляторов и фильтров. Технический отчет № 184 (1390)-94,

М.: ГосНИИАС, 1994.

57.

Солодов А.В. Теория информации и ее применение к задачам автоматического

управления и контроля. М.: Наука, 1967.

58.

Стратонович Р.Л. К теории оптимальной нелинейной фильтрации случайных

функций // Теория вероятностей и ее применение. 1959. Т. 4. № 2. С. 239-242.

59.

Стратонович Р.Л. Теория информации. М.: Советское радио, 1975.

60.

Тартаковский Г.П. Теория информационных систем. М.: Физматкнига, 2005.

61.

Тимин В.Н., Чайковский М.М., Курдюков А.П. Решение задачи анизотропий-

ной субоптимальной фильтрации методом выпуклой оптимизации // ДАН.

2012. Т. 444. № 6. С. 612-615.

62.

Тимин В.Н. Субоптимальная анизотропийная фильтрация линейных дискрет-

ных стационарных систем // АиТ. 2013. № 11. С. 3-19.

Timin V.N. Anisotropy-Based Suboptimal Filtering for the Linear Discrete Time-

Invariant Systems // Autom. Remote Control. 2013. V. 74. P. 1773-1785.

63.

Тимин В.Н., Курдюков А.П. Субоптимальная анизотропийная фильтрация на

конечном горизонте // АиТ. 2016. № 1. С. 5-29.

Timin V.N., Kurdyukov A.P. Suboptimal Anisotropic Filtering in a Finite Hori-

zon // Autom. Remote Control. 2016. V. 77. P. 1-20.

64.

Тимин В.Н., Кустов А.Ю., Курдюков А.П., Гольдин Д.А., Вершинин Ю.А.

Субоптимальная анизотропийная фильтрация для линейных дискретных

нестационарных систем с нецентрированным внешним возмущением // АиТ.

2019. № 1. С. 3-20.

Timin V.N., Kustov A.Y., Kurdyukov A.P. et al. Suboptimal Anisotropic Filter-

ing for Linear Discrete Nonstationary Systems with Uncentered External Distur-

bance // Autom. Remote Control. 2019. V. 80. P. 1-15.

65.

Тихомиров В.М. Работы А.Н. Колмогорова по ǫ-энтропии функциональных

классов и суперпозициям функций // Успехи математических наук. 1963,

Т. XVIII. № 5(113). C. 55-92.

66.

Фельдбаум А.А. Основы теории оптимальных автоматических систем. М.: Нау-

ка, 1966.

67.

Фомин В.Н. Методы управления линейными дискретными объектами. Л.: ЛГУ,

1985.

68.

Хинчин А.Я. Теория корреляции стационарных стохастических процессов //

Успехи мат. наук. 1938. № 5. C. 42-51.

69.

Чайковский М.М. Нахождение сильно минимизирующего ранг решения линей-

ного матричного неравенства // АиТ. 2007. № 9. C. 96-105.

Tchaikovsky M.M. Finding the Strongly Rank-Minimizing Solution to the Linear

Matrix Inequality // Autom. Remote Control. 2007. V. 68. P. 1559-1567.

70.

Чайковский М.М., Курдюков А.П. Критерий строгой ограниченности анизо-

тропийной нормы заданным значением в терминах матричных неравенств //

ДАН. 2011. Т. 441. № 3. С. 318-321.

71.

Чайковский М.М. Синтез анизотропийных субоптимальных регуляторов задан-

ного порядка на основе полуопределенного программирования и алгоритма по-

иска взаимообратных матриц // Управление большими системами. 2012. № 39.

С. 95-137.

72.

Чайковский М.М. Синтез анизотропийных регуляторов методами выпуклой оп-

тимизации и полуопределенного программирования // Управление большими

системами. 2013. № 42. С. 100-152.

73.

Чайковский М.М. Многоканальные задачи синтеза анизотропийных регулято-

ров // АиТ. 2016. № 8. С. 43-65.

Tchaikovsky M.M. Multichannel Synthesis Problems for Anisotropic Control // Au-

tom. Remote Control. 2016. V. 77. No. 8. P. 1351-1369.

74.

Чайковский М.М., Тимин В.Н. Синтез анизотропийного субоптимального

управления для линейных нестационарных систем на конечном временном ин-

тервале // АиТ. 2017. № 7. C. 39-56.

Tchaikovsky M.M., Timin V.N. Synthesis of Anisotropic Suboptimal Control for

Linear Time-Varying Systems on Finite Time Horizon // Autom. Remote Control.

2017. V. 78. No. 7. P. 1203-1217.

75.

Чайковский М.М., Курдюков А.П. Анизотропийное субоптимальное управле-

ние для систем с дробно-линейной неопределенностью // АиТ. 2018. № 6.

С. 172-190.

Tchaikovsky M.M., Kurdyukov A.P. Anisotropic Suboptimal Control for Systems

with Linear-Fractional Uncertainty // Automation and Remote Control. 2018.

V. 79. No. 6. P. 1100-1116.

76.

Новые перспективные методы проектирования многомерных динамических си-

стем управления. Обзор. Под редакцией Е.А. Федосова, ГосНИИАС, 1989.

77.

Конструирование робастных систем управления с использованием методов

H_∞-оптимизации. Обзор. Под редакцией Е.А. Федосова, ГосНИИАС, 1991.

78.

Методы робастного, нейро-нечеткого и адаптивного управления. М.: Изд.

МГТУ им. Н.Э. Баумана, 2002.

79.

Anderson B.D.O., Moore J.B. Optimal filtering. Englewood Cliffs. N.J.: Prentice

Hall. 1979.

80.

Anderson B. and Moore J.B. Optimal Control: Linear Quadratic Methods. Prentice-

Hall. 1990.

81.

Andrianova O.G., Kurdyukov A.P., Belov A.A., Kustov A.Y. Anisotropy-Based

Analysis for Descriptor Systems with Nonzero-Mean Input Signals // 2014 Euro-

pean Control Conference (ECC). Strasbourg. 2014. P. 430-435.

82.

Andrianova О.G., Belov А.A. A Riccati Equation Approach to Anisotropy-Based

Control Problem for Descriptor Systems: State Feedback and Full Information

Cases // 2015 European Control Conference (ECC). Linz. 2015. P. 3226-3231.

83.

Arnold W.F., Laub A.J. Generalised Eigenproblem Algorithms and Software for

Algebraic Riccati Equations // Proc. IEEE. 1984. V. 72. No. 12. P. 1746-1754.

84.

Athans M. Editorial on the LQG Problem // IEEE Trans. Automat. Control. 1971.

V. 16. P. 528.

85.

Baeyens E., Khargonekar P.P. Some Examples in Mixed H₂/H_∞ Control //

Proc. 1994 American Control Conference ACC ’94. Baltimore. MD. USA. 1994.

P. 1608-1612.

86.

Baratchart L., Leblond J., Partington J.R. Hardy Approximation to L_∞ Functions

on Subsets of the Circle // Constr. Approx. 1996. V. 12. P. 423-435.

87.

Basar T., Bernhard P. H_∞-Optimal Control and Related Minimax Design Prob-

lems: a Dynamic Game Approach, Boston: Birkhauser, 1995.

88.

Bedioui N., Salhi S., Ksouri M. H₂ Performance via Static Output Feedback for

a Class of Nonlinear Systems // Proc. IEEE International Conference on Signals,

Circuits and Systems (SCS). 2008. P. 1-6.

89.

Belov A.A. Anisotropy-Based Control for Discrete-Time Descriptor Systems via

State Feedback // Proc. 14th International Student Olympiad on Automatic Con-

trol, Saint-Petersburg. 2011. P. 134-140.

90.

Belov A., Andrianova O. Computation of Anisotropic Norm for Descriptor Systems

Using Convex Optimization // 2013 International Conference on Process Control

(PC), Strbske Pleso. P. 173-178.

91.

Belov A.A., Andrianova O.G., Kurdyukov A.P. Robust Anisotropy-Based Control:

Control of Discrete-Time Descriptor Systems, Cham: Springer International Pub-

lishing, 2018.

92.

Bender D.J., Laub A.J. The Linear-Quadratic Optimal Regulator for Descriptor

Systems // IEEE Trans. Automat. Control. 1987. V. 32. P. 672-687.

93.

Bensoussan A., van Schuppen J.H. Optimal Control of Partially Observable

Stochastic Systems with an Exponential-of-Integral Performance Index // SIAM

J. Control Optim. 1985. V. 23. No. 4. P. 599-613.

94.

Berkenkamp F., Schoellig A.P. Derivation of a Linear, Robust H₂ Controller

for Systems with Parametric Uncertainty. ETH Zurich. Tech. Rep.

2015.

https://doi.org/10.3929/ethz-a-010405770.

95.

Bernstein D.S., Haddad W.M. LQG Control with an H_∞ Performance Bound: A

Riccati Equation Approach // IEEE Trans. Automat. Control. 1989. V. 34. No. 3.

P. 293-305.

96.

Bernstein D.S. Review of Minimum Entropy H_∞ Control // IEEE Trans. Automat.

Contr. 1992. V. 37. No. 8. P. 1276-1277.

97.

Bertsekas D.P. Dynamic Programming and Stochastic Control. Academic Press,

New York. 1976.

98.

Bode H.W., Shannon C.E. A Simplified Derivation of Linear Least-Square Smooth-

ing and Prediction Theory // Proc. IRE. 1950. No. 4. P. 417-425.

99.

Bosgra O.H., Kvakernaak H. Design Methods for Control Systems, Course notes,

Dutch Institute for Systems and Control. V. 67. 2001.

100.

Boukas H., Shi P. H_∞ Control for Discrete-Time Linear Systems with Frobenius

Norm-Bounded Uncertainties // Automatica. 1999. V. 35. No. 9. P. 1625-1631.

101.

Boyd S., Ghaoui L.E., Feron E., and Balakrishnan V. Linear Matriz Inequalities

in System and Control Theory // 1994. SIAM Studies in Applied Mathematics.

SIAM, Philadelphia. http://dx.doi.org/10.1137/1.9781611970777.

102.

Boyd S., Vandenberghe L. Convex Optimization. Cambridge University Press. 2004.

103.

Campi M.C., James M.R. Risk-Sensitive Control: a Bridge Between H₂ and H_∞

Control // Proc. 32nd IEEE Conference on Decision and Control. San Antonio.

TX. USA. 1993. V. 3. P. 2179-2180.

104.

Campi M.C., James M.R. Nonlinear Discrete-Time Risk-Sensitive Optimal Con-

trol // Int. J. Robust Nonlinear Control. 1996. V. 6. P. 1-19.

105.

Yung C.-F., Wang C.-C., Wu P.-F., Wang H.-S. Bounded Real Lemma for Discrete-

Time Descriptor Systems // IFAC Proc. Volumes. 2008. V. 41. No. 2. P. 9982-9986.

106.

Chen M., Desoer C. Necessary and Sufficient for Robust Stability of Linear Dis-

tributed Feedback Systems // Int. J. Control. 1982. V. 35. No. 2. P. 255-267.

107.

Colaneri P., Geromel J.C., Locatelli A. Control Theory and Design. A RH₂ and

RH_∞ Viewpoint. Academic press, 1997.

108.

Cover T.M., Thomas J.A. Elements of Information Theory. Wiley & Sons, Inc.

1991.

109.

Dai L. Singular Control Systems. Lecture notes in control and information sciences.

New York: Springer-Verlag, 1989.

110.

Dai L. Filtering and LQG Problems for Discrete-Time Stochastic Singular Sys-

tems // IEEE Trans. Automat. Control. 1989. V. 34. No. 10. P. 1105-1108.

111.

De Souza C.E., and Xie L. On the Discrete-Time Bounded Real Lemma with Appli-

cation in the Characterization of Static State Feedback H_∞ Controllers // Systems

& Control Lett. 1992. V. 18. P. 61-71.

112.

Diamond P., Kurdjukov A., Semyonov A. and Vladimirov I. Homotopy Meth-

ods and Anisotropy-Based Stochastic H_∞-optimization of Control Systems //

CADSMAP Report 97-14, December 1997, The University of Queensland, Aus-

tralia. P. 1-22.

113.

Diamond P., Vladimirov I., Kurdjukov A., Semyonov A. Anisotropy-Based Per-

formance Analysis of Linear Discrete Time Invariant Control Systems // Int. J.

Control. 2001. V.74. No. 1. P. 28-42.

114.

Doyle J.C. Guaranteed Margins for LQG Regulators // IEEE Trans. Automat.

Contr. 1978. V. 23. No. 4. P. 756-757.

115.

Doyle J.C., Stein G. Robustness with Observers // IEEE Trans. Automat. Contr.

1979. V. 24. No. 4. P. 607-611.

116.

Doyle J.C., Stein G. Multivariable Feedback Design: Concepts for a Classi-

cal/Modern Synthesis // IEEE Trans. Automat. Contr. 1981. V. 26. P. 4-16.

117.

Doyle J.C., Glover K., Khargonekar P.P., Francis B.A. State-Space Solutions to

Standard H₂ and H_∞ Control Problems // IEEE Trans. Automat. Contr. 1989.

V. 34. No. 8. P. 831-847.

118.

Doyle J.C., Francis B.A., Tannenbaum A.R. Feedback Control Theory. Maxwell

MacMillan Internat, New York, 1992.

119.

Doyle J., Zhou K., Glover K., Bodenheimer B. Mixed H₂ and H_∞ Performance

Objectives II: Optimal control // IEEE Trans. Automat. Control. 1994. V. 39.

No. 8. P. 1575-1586.

120.

Dullerud G.E., Paganini F.G. A Course in Robust Control Theory. A convex ap-

proach. New York: Springer-Verlag, 2000.

121.

Francis B.A. A Course in H_∞-Control Theory. Lecture Notes in Control and Infor-

mation Sciences. 1987. V. 88. Springer-Verlag, Berlin.

122.

Fridman E., Shaked U. Robust H_∞ Minimum Entropy Static Output-Feedback

Control of Singularly Perturbed Systems // Automatica. 2000. V. 36. P. 1181-1188.

123.

Gahinet P., Apkarian P.A. Linear Matrix Inequality Approach to H_∞ Control //

Int. J. Robust Nonlinear Control. 1994. V. 4. No. 4. P. 421-448.

124.

Gershon E., Shaked U., Yaesh I. H_∞ Control and Estimation of State-Multiplicative

Linear Systems. London: Springer, 2005.

125.

Glover K. All-optimal Hankel Norm Approximations of Linear Multivariable Sys-

tems and Their L_∞-error Bounds // Int. J. Control. 1984. V. 39. P. 1115-1193.

126.

Glover K., Doyle J. State-Space Formulae for All Stabilizing Controllers That Sat-

isfy an H_∞-norm Bound and Relations to Risk Sensitivity // Systems & Control

Lett. 1988. V. 11. P. 167-172.

127.

Glover K., Mustafa D. Derivation of the Maximum Entropy H_∞ Controller and a

State-Space Formula for its Entropy // Int. J. Control. 1989. V. 50. P. 899-916.

128.

Goddard P.J., Glover K. Controller Approximation: Approaches for Preserving H_∞

Performance // IEEE Trans. Automat. Contr. 1998. V. 43. No. 7. P. 858-871.

129.

Gray R.M. Entropy and Information Theory. Springer US, 2011.

130.

Green M., Limebeer D.J.N. Linear Robust Control. Pearson Education Inc., 1995.

131.

Grimble M.J., Elsayed A. Solution of the H_∞ Optimal Linear Filtering Problem

for Discrete-Time Systems // IEEE Trans. Acoust. Speech Signal Processing. 1990.

V. 38. No. 7. P. 1092-1104.

132.

Gu Da-W, Petkov P.H., Konstantinov M.M. Robust Control Design with MAT-

LABR // Advanced Textbooks in Control and Signal Processing. 2005. Springer-

Verlag, Berlin, Heidelberg.

133.

Haddad W.M., Bernstein D.S., Mustafa D. Mixed-Norm H₂/H_∞ Regulation and

Estimation: the Discrete-Time Case // Systems & Control Lett. 1991 V. 16. No. 4

P. 235-247.

134.

Halevi Y. Frequency Weighted Model Reduction via Optimal Projection // IEEE

Trans. Automat. Contr. 1992. V. 37. No. 10. P. 1537-1542.

135.

Hassibi B., Sayed A., Kailath T. Indefinite Quadratic Estimation and Control: A

Unified Approach to H₂ and H_∞ Theories. SIAM, 1999.

136.

Huang X.-X., Yan W.-Y., Teo K. L. H₂ Near-Optimal Model Reduction // IEEE

Trans. Automat. Contr. 2001. V. 46. No. 8. P. 1279-1284.

137.

Hyland D.C., Bernstein D.S. The Optimal Projection Equations for Model Reduc-

tion and the Relationships Among the Methods of Wilson, Skelton, and Moore //

IEEE Trans. Automat. Contr. 1985. V. 30. No. 12. P. 1201-1211.

138.

Iglesias P.A., Mustafa D., Glover K. Discrete Time H_∞ Controllers Satisfying a

Minimum Entropy Criterion // Systems & Control Lett. 1990. V. 14. P. 275-286.

139.

Iglesias P.A., Glover K. State-Space Approach to Discrete-Time H_∞ Control //

Int. J. Control. 1991. V. 54. No. 5. P. 1031-1073.

140.

Iglesias P.A., Mustafa D. State-Space Solution of the Discrete-Time Minimum En-

tropy Control Problem Via Separation // IEEE Trans. Automat. Contr. 1993. V. 38.

No. 10. P. 1525-1530.

141.

Iglesias P.A. An Entropy Formula for Time-Varying Discrete-Time Control Sys-

tem // SIAM J. Control Optim. 1996. V. 34. No. 5. P. 1691-1706.

142.

Ishihara J.Y., Terra M.H., Sales R.M. The Full Information and State Feedback

H₂ Optimal Controllers for Descriptor Systems // Automatica. 2003. V. 39. No. 3.

P. 391-402.

143.

Ito K. Stochastic Integral // Proc. Imp. Acad. 1944. V. 20. No. 8. P. 519-524.

144.

Jacobson D.H. Optimal Stochastic Linear Systems with Exponential Performance

Criteria and Their Relation to Deterministic Differential Games // IEEE Trans.

Automat. Contr. 1973. V. 18. No. 2. P. 124-131.

145.

Jacobson D.H. Extensions of Linear-Quadratic Control, Optimization and Matrix

Theory. New York: Academic Press, 1977.

146.

Jonckheere E., Silverman L. A New Set of Invariants for Linear Systems-

Application to Reduced Order Compensator Design // IEEE Trans. Automat.

Contr. 1983. V. 28. No. 10. P. 953-964.

147.

Kalman R.E. A New Approach to Linear Filtering and Prediction Problems //

Trans. ASME. (J. Basic Eng.). 1960. V. 82. P. 34-45.

148.

Kalman R.E. Contributions to the Theory of Optimal Control // Bol. Soc. Mat.

Mexanicana. 1960. No. 5. P. 102-119.

149.

Kalman R.E. New Methods and Results in Linear Prediction and Filtering Theory.

Baltimore: RIAS Tech. Rep. 1961. P. 1-61.

150.

Kalman R.E., Bucy R. New Results in Linear Filtering and Prediction Theory //

ASME J. Basis Eng. 1961. V. 83. P. 95-108.

151.

Karny M. Towards Fully Probabilistic Control Design // Automatica. 1996. Vol. 32.

P. 1719-1722.

152.

Karny M., Guy T.V. Fully Probabilistic Control Design // Systems & Control Lett.

2006. V. 55. No. 4. P. 259-265.

153.

Karny M., Kroupa T. Axiomatisation of Fully Probabilistic Design // Information

Sciences. 2012. V. 186. No. 1. P. 105-113.

154.

Kapila V., Haddad W.M. H₂ Stable Stabilization for Discrete-Time Systems //

Proc. 1995 34th IEEE Conference on Decision and Control. New Orleans. LA. USA.

1995. V. 2. P. 1933-1934.

155.

Khargonekar P.P., Rotea M.A. Mixed H₂/H_∞ Control: A Convex Optimization

Approach // IEEE Trans. Automat. Contr. 1991. V. 36. No. 7. P. 824-837.

156.

Khargonekar P.P., Rotea M.A., Baeyens E. Mixed H₂/H_∞ Filtering // Int. J.

Robust Nonlinear Control. 1996. V. 6. P. 313-330.

157.

Kim S.W., Seo C.J., Kim B.K. Robust and Reliable H_∞ Controllers for Discrete-

Time Systems with Parameter Uncertainty and Actuator Failure // Int. J. Syst.

Sci. 1999. V. 30. No. 12. P. 1249-1258.

158.

Kimura H. Pole Assignment by Gain Output Feedback // IEEE Trans. Automat.

Contr. 1975. Vol. 20. No. 4. P. 509-516.

159.

Kurdyukov A.P., Pavlov B.V., Timin V.N., Vladimirov I.G. Longitudinal

Anisotropy-Based Flight Control in a Wind Shear // IFAC Proc. Volumes. 2004.

V. 37. No. 6. P. 423-426.

160.

Kurdyukov A.P., Boichenko V.A. A Spectral Method of the Analysis of Linear

Control Systems //Int. J. Appl. Math. Comput. Sci. 2019. V. 29. No. 4. P. 667-679.

161.

Kurdyukov A.P., Maximov E.A., Tchaikovsky M.M. Homotopy-Based Algorithm for

Computing Stochastic H_∞ -optimal Controller for LTI-System with Uncertainty //

7-th Int. Scientific-Technical Conf. Process Control 2006. Pardubice (Czech Repub-

lic), 2006. CD-ROM.

162.

Kurdyukov A.P., Maximov E.A., Tchaikovsky M.M. Homotopy Method for Solving

Anisotropy-Based Stochastic H_∞ -optimization Problem with Uncertainty // IFAC

Proc. Volumes. V. 39. No. 9. 2006. P. 327-332.

163.

Kurdyukov A.P., Vladimirov I.G. Propogation of mean Anisotropy of Signals in

Filter Connections // IFAC Proc. Volumes. V. 41. No. 2. P. 6313-6318.

164.

Kurdyukov A.P., Maximov E.A., Tchaikovsky M.M. Anisotropy-Based Bounded

Real Lemma // Proc. of the 19-th International Symposium MTNS. Budapest.

Hungary. 2010. P. 2391-2397.

165.

Kurdyukov A.P., Kustov A.Yu., Tchaikovsky M.M., Karny M. The Concept of Mean

Anisotropy of Signals with Nonzero Mean // Proc. 2013 Int. Conf. on Process

Control (PC). Strbske Pleso. 2013. P. 37-41.

166.

Kurdyukov A.P., Kustov A.Y. Constructing Signals with Prescribed Mean

Anisotropy Level // IFAC Proc. Volumes. V. 46. No. 11. 2013. P. 489-494.

167.

Kurdyukov А.P., Kustov А.Y., Yurchenkov А.V. Robust Stability in Anisotropy-

Based Theory with Non-Zero Mean of Input Sequence // Proc. 21st Int. Sympo-

sium on Mathematical Theory of Networks and Systems (MTNS 2014). Groningen.

Netherlands. 2014. P. 208-214.

168.

Kustov A. Anisotropy-Based Analysis and Synthesis Problems for Input Distur-

bances with Nonzero Mean // Proc. 2014 15th International Carpathian Control

Conference (ICCC). Velke Karlovice. 2014. P. 291-295.

169.

Li R.-C., Bai Z. Structure-Preserving Model Reduction Using a Krylov Subspace

Projection Formulation // Commun. Math. Sci. 2004. V. 3. No. 2. P. 179-199.

170.

Lin Z., Saberi A., Sannuti P., Shamash Y.A. A Direct Method of Constructing H₂

Suboptimal Controllers Discrete-Time Systems // Proc. 36th IEEE Conference

on Decision and Control. San Diego. CA. USA. V. 2. 1997. P. 1008-1013.

171.

Löfberg J. YALMIP: A Toolbox for Modeling and Optimization in Mat-

lab

// Proc. CACSD Conference, Taipei, Taiwan,

2004. Available from

http://users.isy.liu.se/johanl/yalmip/.

172.

Mariton M., Bertrand R. A Homotopy Algorithm for Solving Coupled Riccati Equa-

tions // Optimal. Contr. Appl. Meth. 1985. V. 6. No. 4. P. 351-357.

173.

Maximov E.A., Kurdyukov A.P., Vladimirov I.G. Anisotropic Norm Bounded Real

Lemma for Linear Time-Varying System // IFAC Proc. Volumes. 2011. V. 44. No. 1.

P. 4701-4706.

174.

McFarlane G.C., Glover K. Robust Controller Design Using Normalized Coprime

Factor Plant Description. Lecture Notes in Control and Information Sciences,

Springer-Verlag, Berlin etc. 1990.

175.

Meyer D.G. Fractional Balanced Reduction: Model Reduction via Fractional Rep-

resentation // IEEE Trans. Automat. Contr. 1990. V. 35. No. 12. P. 1341-1345.

176.

Miradore R., Ricci G. Mixed H₂/H_∞ Control: the Discrete-Time Case // Systems

& Control Lett. 2005. V. 54. No. 1. P. 1-13.

177.

Moore B.C. Principal Component Analysis in Linear Systems: Controllability, Ob-

servability and Model Reduction // IEEE Trans. Automat. Contr. 1981. V. 26.

No. 1. P. 17-32.

178.

Mustafa D., Glover K. Controllers which Satisfy a Closed-Loop H_∞-norm Bound

and Maximize an Entropy Integral // Proc. 27th IEEE Conference on Decision and

Control. Austin. TX. USA. 1988. V. 2. P. 959-964.

179.

Mustafa D. Relations Beetwen Maximum Entropy/H_∞ Control and Combined

H_∞/LQG Control // Systems & Control Lett. 1989. V. 12. No. 3. P. 193-203.

180.

Mustafa D., Glover K. Minimum Entropy H_∞-Control. Lecture Notes in Control

and Information Sciences, Springer-Verlag, Berlin etc. 1991.

181.

Mustafa D., Glover K., Limebeer D.J.N. Solutions to the H_∞ General Dis-

tance Problem which Minimize an Entropy Integral // Automatica. 1991. V. 27.

P. 193-199.

182.

Mustafa D., Glover K. Controller Reduction by H_∞-Balanced Truncation // IEEE

Trans. Automat. Contr. 1991. V. 36. No. 6. P. 668-682.

183.

Nagpal K.M., Khargonekar P.P. Filtering and Smoothing in an H_∞-setting // IEEE

Trans. Automat. Contr. 1991. V. 36. No. 2. P. 152-166.

184.

Nesterov Y., Nemirovski A. Interior-Point Polynomial Methods in Convex Program-

ming // Studies in Applied Mathematics, SIAM, Philadelphia, PA. 1994.

185.

Peters M.A., Iglesias P.A. Connections Between Minimum Entropy Control and

Mixed H₂/H_∞ Control for Time-Varying Systems // Systems & Control Lett. 1995.

V. 26 P. 341-347.

186.

Peters M.A., Iglesias P.A. Minimum Entriopy Control For Discrete-time Time-

Varying Systems // Automatica. 1997. V. 33. P. 591-605.

187.

Peters M.A., Iglesias P.A. The Relationship Between Minimum Entropy Con-

trol and Risk-Sensitive Control for Tite-Varing Systems // IEEE Trans. Automat.

Contr. 1999. V. 44. P. 1065-1069.

188.

Petersen I.R. Disturbance Attenuation and H_∞ Optimization: A Design Method

Based on the Algebraic Riccati Equation // IEEE Trans. Automat. Contr. 1987.

V. 32. No. 5. P. 427-429.

189.

Petersen I.R., James M.R., Dupuis P. Minimax Optimal Control of Stochastic

Uncertain Systems with Relative Entropy Constraints // IEEE Trans. Automat.

Contr. 2000. V. 45. No. 3. P. 398-412.

190.

Petersen I.R. Minimax LQG Control // Int. J. Math. Comput. Sci. 2006. V. 16.

No. 3. P. 309-323.

191.

Petersen I.R., Tempo R. Robust Control of Uncertain Systems: Classical Results

and Recent Developments // Automatica. 2014. V. 50. No. 5. P. 1315-1335.

192.

Poznyak A.S. Advanced Mathematical Tools for Automatic Control Engineers: De-

terministic Techniques. Elsevier, 2008.

193.

Redheffer R. On a Certain Linear Fractional Transformation // J. Math. Phys.

1960. V. 39. P. 269-286.

194.

Rosenbrock H.H., McMorran P.D. Good, Bad, or Optimal? // IEEE Trans.

Automat. Contr. 1971. V. 16. No. 6. P. 552-554.

195.

Saberi A., Sannuti P., Chen B.M. H₂ Optimal Control. London: Prentice Hall

International, 1995.

196.

Saberi A., Stoorvogel A., Sannuti P. Control of Linear Systems with Regulation

and Input Constraints. London: Springer-Verlag, 2000.

197.

Sadabadi M.S., Alireza K. An LMI Formulation of Fixed-Order H_∞ and H₂ Con-

troller Design for Discrete-Time Systems with Polytopic Uncertainty // 52nd IEEE

Conf. on Decision and Control. 2013. P. 2453-2458.

198.

Saridis G.N. Entropy Formulation of Optimal and Adaptive Control // IEEE Trans.

Automat. Control. 1988. V. 33. No. 8. P. 713-721.

199.

Scherer C.W., Gahinet P., Chilali M. Multiobjective Output-Feedback Control via

LMI Optimization // IEEE Trans. Automat. Contr. 1997. V. 42. No. 7. P. 896-911.

200.

Scherer C.W. An Efficient Solution to Multi-Objective Control Problems with LMI

Objectives // Systems & Control Lett. 2000. V. 40. No. 1. P. 43-57.

201.

Semyonov A.V., Vladimirov I.G., Kurdjukov A.P. Stochastic Approach to H_∞-

optimization // Proc. 33rd IEEE Conf. on Decision and Control. Florida(USA),

1994. V. 3. P. 2249-2250.

202.

Shaiju A.J., Petersen I.R. Formulas for Discrete Time LQR, LQG, LEQG and

Minimax LQG Optimal Control Problems // IFAC Proc. Volumes. 2008. V. 41.

No. 2. P. 8773-8778.

203.

Shaked U., Theodor Y. H_∞-optimal Estimation: A Tutorial // Proc. 31st IEEE

Conf. on Decision and Control. Tucson. AZ. USA. 1992. V. 2. P. 2278-2286.

204.

Simon D. Optimal State Estimation: Kalman, H_∞, and Nonlinear Approaches. New

Jersey: John Wiley and Sons, 2006.

205.

Stoorvogel A.A. The H_∞ Control Problem: a State Space Approach. 2000.

206.

Sturm J.F. Using SeDuMi 1.02, a Matlab Toolbox for Optimization Over Symmetric

Cones // Optimization Methods and Software. 1999. V. 11. P. 625-653.

207.

Tchaikovsky M.M., Kurdyukov A.P. On Computing Anisotropic Norm of Linear

Discrete-Time-Invariant System via LMI-Based Approach // Archives of Control

Sciences. 2006. V. 16. No. 3. P. 257-281.

208.

Tchaikovsky M., Kurdyukov A. Stochastic Robust Controller Reduction by

Anisotropic Balanced Truncation // 2009 IEEE Control Applications (CCA) &

Intelligent Control (ISIC). St. Petersburg. 2009. P. 1772-1777.

209.

Tchaikovsky M. Anisotropic Balanced Truncation Application to Reduced-Order

Controller Design // Proc. 17th Int. Conf. on Process Control’09. Strbske Pleso.

Slovakia. 2009. P. 14-27.

210.

Tchaikovsky M., Kurdyukov A. On Simplifying Solution to Normalized Anisotropy-

Based Stochastic H_∞ Problem // IFAC Proc. Volumes. V. 42. No. 6. 2009.

P. 161-166.

211.

Tchaikovsky M.M., Kurdyukov A.P., Nikiforov V.M. LMI-Based Design of Mul-

tichannel Anisotropic Suboptimal Controllers with Application to Control of Gy-

rostabilized Platform // Proc. IEEE Int. Conf. on Control Applications (CCA-2012,

Dubrovnik). Dubrovnik: IEEE (Catalog Number: CFP12CCA-USB). 2012. P. 1455-

1460.

212.

Tchaikovsky M.M. Static Output Feedback Anisotropic Controller Design by LMI-

Based Approach: General and Special Cases // Proc. 2012 American Control Con-

ference (ACC). Montreal. QC. 2012. P. 5208-5213.

213.

Tchaikovsky M.M., Kurdyukov A.P. On Upper Estimate of Anisotropic Norm of

Uncertain System with Application to Stochastic Robust Control // Int. J. Control.

2018. V. 91. No. 11. P. 2411-2421.

214.

Theodor Y., Shaked U., de Souza C.E. A Game Theory Approach to Robust Dis-

crete-Time H_∞ Estimation // IEEE Trans. Signal Proc. 1994. V. 42. P. 1486-1495.

215.

Timin V.N., Kustov A.Yu. Suboptimal Anisotropy-Based/H_∞ Filtering for LDTI

Systems with Nonzero-Mean Input // 2015 20th Int. Conf. on Process Control (PC).

Strbske Pleso. 2015. P. 147-151.

216.

Trentelman H., Stoorvogel A.A., Hautus M. Control Theory for Linear Systems.

Communication and Control Engineering, Springer-Verlag London, 2001.

217.

Ugrinovskii V.A., Petersen I.R. Finite Horizon Minimax Optimal Control of

Stochastic Partially Observed Time Varying Uncertain Systems // Math. Contr.

Signals Syst. 1999. V. 12. No. 1. P. 1-23.

218.

Ugrinovskii V.A., Petersen I.R. Minimax LQG Control of Stochastic Partially Ob-

served Uncertain Systems // SIAM J. Control Optim. 2002. V. 40. No. 4. P. 1189-

1226.

219.

Ugrinovskii V.A., Petersen I.R. Robust Output Feedback Stabilization via Risk-

Sensitive Control // Automatica. 2002. V. 38. No. 3. P. 945-955.

220.

Van Dooren P.V. A generalized eigenvalue approach for solving Riccati equation //

SIAM J. Sci. Stat. Comp. 1981. V. 2. P. 121-135.

221.

Verghese G.C., Levy B.C., Kailath T. A Generalized State-Space for Singular Sys-

tems // IEEE Trans. Automat. Control. 1981. V. 26. P. 811-831.

222.

Vidyasagar M. Control System Synthesis: a Factorization Approach. Cambridge,

MA: MIT Press, 1985.

223.

Vidyasagar M., Kimura H. Robust Controllers for Uncertain Linear Multivariable

Systems // Automatica. 1986. V. 22. No. 1. P. 85-94.

224.

Vladimirov I.G., Kurdjukov A.P., Semyonov A.V. On Computing the Anisotropic

Norm of Linear Discrete-Time-Invariant Systems // IFAC Proc. Volumes. 1996.

V. 29. No. 1. P. 3057-3062.

225.

Vladimirov I.G., Kurdjukov A.P., Semyonov A.V. State-Space Solution to

Anisotropy-Based Stochastic H_∞ -optimization Problem // Proc. 13th IFAC World

Congress. San-Francisco(USA). 1996. P. 427-432.

226.

Vladimirov I., Diamond P. Robust Filtering in Finite Horizon Linear Discrete Time

Varying Systems by Minimum Anisotropic Norm Criterion // CADSMAP Res.

Report 01-05. 2001.

227.

Vladimirov I. Anisotropy-Based Optimal Filtering in Linear Discrete time Invariant

Systems. Center for Applied Dynamical Systems //

http://arxiv.org/abs/1412.3010, December 2014.

228.

Wang S.-Y., Gao Z.-F., Qiu J.-Q., He H.-K. Observer-Based Robust H_∞ Control

of a Class of Discrete Time Systems with State Uncertainties // Proc. 2009 Int.

Conf. Machine Learning and Cybernetics. Hebei. 2009. P. 1949-1953.

229.

Whittle P. Risk-Sensitive Linear/Quadratic/Gaussian Control // Adv. Appl. Prob.

1981. V. 13. No. 4. P. 764-777.

230.

Whittle P., Kuhn J. A Hamiltonian Formulation of risk-sensitive Linear/Quadra-

tic/Gaussian Control // Int. J. Control. 1986. V. 43. No. 1. P. 1-12.

231.

Whittle P. Entropy-Minimising and Risk-Sensitive Control Rules // Systems &

Control Lett. 1989. V. 13. No. 1. P. 1-7.

232.

Whittle P. Risk-Sensitive Optimal Control. New York: John Wiley and Sons, 1990.

233.

Wiener N. Extrapolation, Interpolation and Smoothing of Stationary Time Series.

New York: John Wiley and Sons, 1949.

234.

Wilson D. A. Optimum Solution of Model-Reduction Problem // Proc. IEE. 1970.

V. 117. No. 6. P. 1161-1165.

235.

Xie L. On Robust H₂ Estimation // ACTA Automatica Sinica. 2005. V. 31. No. 1.

P. 1-12.

236.

Xu S., Chen T. Robust H_∞ Control for Uncertain Discrete-Time Systems with

Time-Varying Delays via Exponential Output Feedback Controllers // Systems &

Control Lett. 2004. V. 51. No. 3-4. P. 171-183.

237.

Xu S., Lam J. Robust Control and Filtering of Singular Systems. Lecture Notes in

Control and Information Sciences. Berlin: Springer-Verlag, 2006.

238.

Yaesh I., Shaked U. A Transfer Function Approach to the Problems of Discrete-

Time Systems: H_∞ -optimal Linear Control and Filtering // IEEE Trans. Automat.

Contr. 1991. V. 36. No. 11. P. 1264-1271.

239.

Yaesh I., Shaked U. Minimum Entropy Static Output-Feedback Control with an

H_∞-norm Performance Bound // IEEE Trans. Automat. Contr. 1997. V. AC-42.

No. 6. P. 853-858.

240.

Yaesh I., Shaked U. Robust Reduced-Order Output-Feedback H_∞ Control // IFAC

Proc. Volumes. V. 42. No. 6. 2009. P. 155-160.

241.

Yaesh I., Stoica A.-M. Linear Time-Varying Anisotropic Filtering its Application to

Nonlinear Systems State Estimation // 2014 European Control Conference (ECC).

Strasbourg. 2014. P. 975-980.

242.

Yan W.-Y., Lam. J. An Approximate Approach to H₂ Optimal Model Reduction //

IEEE Trans. Automat. Contr. 1999. V. 44. P. 1341-1358.

243.

Yang R., Lu L., Xie L. Robust H₂ and H_∞ Control of Discrete-Time Systems with

Polytopic Uncertainties via Dynamic Output Feedback // Int. J. Control. 2005.

V. 78. P. 1285-1294.

244.

Yoon M.G., Ugrinovskii V.A. Robust Tracking Problem for Continuous Time

Stochastic Uncertain Systems // 42nd IEEE Int. Conf. on Decision and Control

(IEEE Cat. No.03CH37475). Maui. HI. 2003. V. 1. P. 282-287.

245.

Yoon M.G., Ugrinovskii V.A., Petersen I.R. Robust Finite Horizon Minimax Fil-

tering for Stochastic Discrete Time Uncertain Systems // Systems & Control Lett.

2004. V. 52. No. 2. P. 99-112.

246.

Yoon M.G., Ugrinovskii V.A., Petersen I.R. On the Worst-Case Disturbance of

Minimax Optimal Control // Automatica. 2005. V. 41. P. 847-855.

247.

Li Y., Xu J.-M., Xu Ch. H₂/H_∞ Optimal Filter Design for Linear Discrete-Time

Systems // Fifth World Congress on Intelligent Control and Automation (IEEE

Cat. No.04EX788). Hangzhou. China. 2004. V. 2. P. 1597-1600.

248.

Zames G. On the Input-Ouput Stability of Nonlinear Time-Varying Feedback Sys-

tems, Part I: Conditions Derived Using Concepts of Loop Gain, Conicity and Pos-

itivity // IEEE Trans. Automat. Contr. 1966. V. 11. No. 2. P. 228-238.

249.

Zames G. On the Input-Ouput Stability of Nonlinear Time-Varying Feedback Sys-

tems, Part II: Conditions Involving Circles in the Frequency Plane and Sector Non-

linearities // IEEE Trans. Automat. Contr. 1966. V. 11. No. 3. P. 465-476.