Автоматика и телемеханика, № 4, 2021
Нелинейные системы
© 2021 г. А.И. МАЛИКОВ, д-р физ.-мат. наук (a_i_malikov@mail.ru)
(Казанский национальный исследовательский технический
университет им. А.Н. Туполева КАИ)
ОЦЕНИВАНИЕ СОСТОЯНИЯ И СТАБИЛИЗАЦИЯ
НЕЛИНЕЙНЫХ СИСТЕМ С ДИСКРЕТНЫМ УПРАВЛЕНИЕМ
И НЕОПРЕДЕЛЕННЫМИ ВОЗМУЩЕНИЯМИ1
Рассматриваются непрерывные системы с дискретным управлением с
неопределенными нелинейностями, подверженные воздействию ограни-
ченных внешних возмущений. На основе метода квадратичных функций
Ляпунова, матричных систем сравнения и техники дифференциальных
линейных матричных неравенств развивается подход к задачам оцени-
вания состояния, подавления начальных отклонений и неопределенных
возмущений с помощью обратной связи по состоянию, доступному в дис-
кретные моменты времени. Предлагается способ синтеза периодического
и апериодического дискретного управления, обеспечивающий на конеч-
ном интервале принадлежность заданному множеству траекторий исход-
ной системы при любых возмущениях, ограниченных по L∞ норме.
Ключевые слова: непрерывные системы с липшицевыми нелинейностями,
неопределенные возмущения, оценивание состояния, дискретное управле-
ние, дифференциальные линейные матричные неравенства.
DOI: 10.31857/S0005231021040048
1. Введение
В обширной литературе по синтезу управления область, которой уделя-
ется мало внимания, это управление системами с дискретными данными.
В этой задаче объект с непрерывным временем обычно управляется алго-
ритмом обратной связи с дискретным временем. Устройство дискретизации
и квантования обеспечивает согласование между непрерывным временем и
дискретным временем. Одним из способов решения проблемы дискретного
управления является реализация алгоритма непрерывного управления с до-
статочно малым периодом дискретизации. Однако аппаратное обеспечение,
используемое для дискретизации и проведения измерений на объекте или
вычисления управляющего воздействия с обратной связью, может сделать
невозможным сокращение периода выборки до уровня, который гарантиру-
ет приемлемые характеристики замкнутой системы. В этом случае становит-
ся интересным исследовать применение алгоритмов дискретного управления,
основанных на модели процесса с непрерывным временем.
1 Работа выполнена при поддержке Российского фонда фундаментальных исследований
(проект № 18-08-01045а).
96
В последнее время дискретное управление широко применяется в циф-
ровых и сетевых системах [1-6]. Большое внимание уделяется анализу их
устойчивости [7-21]. Как отмечено в [1], существуют три основных подхода
к анализу устойчивости и синтезу системы с дискретными данными, осно-
ванные на технике линейных матричных неравенств (ЛМН). Первый подход
связан с представлением системы с дискретными данными в виде системы с
запаздыванием [1, 2, 5-7]. Такой подход в основном применяется для линей-
ных систем с дискретными данными при постоянной или изменяющейся во
времени дискретизацией. Условия устойчивости таких систем получены с по-
мощью функционалов Ляпунова-Красовского или функций типа Ляпунова-
Разумихина [2].
Во втором подходе [8, 9, 13, 17 и др.] исходная система с дискретными
данными представляется как система с импульсами. Выбирая кусочно-зави-
симый от времени функционал Ляпунова-Красовского или разрывный функ-
ционал Ляпунова-Красовского, можно получить менее консервативные усло-
вия устойчивости [14, 15, 18, 21, 22].
Следует отметить, что, хотя некоторые менее консервативные критерии
устойчивости могут быть получены с использованием вышеупомянутых двух
подходов, выбранные функционалы Ляпунова-Красовского обычно сложны.
Так как полученные ЛМН требуют при решении большего количества ска-
лярных и матричных переменных, общая вычислительная сложность крите-
риев устойчивости определенно намного выше.
Третий подход - это подход с дискретным временем [1, 2, 10-12, 17, 19, 20],
при котором система с дискретными данными эквивалентно преобразуется в
конечномерную систему с дискретным временем, в которой сохраняется ин-
формация о состоянии системы между моментами дискретизации. Системы с
апериодическими дискретными данными также изучались в дискретной вре-
менной области. В частности, линейные системы с постоянными коэффици-
ентами с апериодической дискретизацией были проанализированы с исполь-
зованием модели линейной системы с дискретным временем с переменным
параметром. Эффект дискретизации может быть смоделирован с помощью
оператора, а проблема устойчивости может быть решена в рамках подхо-
да устойчивости входа/выхода [1, 2, 19]. В данной статье используется вто-
рой подход для решения задачи оценивания состояния и синтеза дискретного
управления.
Как было отмечено в обзоре [1], несмотря на то что в публикациях были
представлены значительные достижения в этой области, проблемы, связан-
ные как с основами таких систем, так и с выводом конструктивных методов
анализа устойчивости, остаются открытыми даже для случая линейной си-
стемы. Следует также отметить, что не все предлагаемые в литературе кри-
терии устойчивости, представленные в виде ЛМН, могут быть применены
для синтеза дискретного управления.
Обычно в основу способов синтеза дискретного управления полагается
обеспечение устойчивости (асимптотической, экспоненциальной) [6-8, 10, 12,
17, 23] или оптимального качества по H2 или H∞ критериям исходной непре-
рывной системы [24-28]. При этом рассматриваются, как правило, линейные
97
системы без учета возмущений. В [29] показатели H2 и H∞ качества опреде-
ляются и выражаются через дифференциальные линейные матричные нера-
венства (ДЛМН). На основе принципа оптимальности Беллмана, выражен-
ного в терминах уравнения динамического программирования, связанного
с интервалом времени, соответствующим двум последовательным моментам
выборки, предлагаются способы синтеза оптимальных H2 и H∞ регуляторов
полного порядка с обратной связью по выходу периодических дискретных
данных для линейных инвариантных систем с непрерывным временем. Зада-
чи синтеза оптимальных регуляторов решаются путем преобразования всех
ограничений в ЛМН и использования методов полуопределенного програм-
мирования. В [30] предложены способы синтеза стабилизирующих динамиче-
ских регуляторов с обратной связью по выходу для класса линейных аперио-
дических импульсных систем. Условия синтеза сформулированы в виде ЛМН,
зависящих от времени, которые могут быть решены численно с использовани-
ем методов релаксации матричных сумм квадратов. Полученные результаты
применены для синтеза динамических регуляторов с обратной связью по вы-
ходу для систем с апериодическими дискретными данными. В [31] подход с
использованием векторной функции Ляпунова для 2D систем используется
для получения условий устойчивости импульсной системы, а затем решается
задача синтеза робастного управления на основе наблюдателя для линейных
систем с дискретными данными.
Цель данной статьи представить способы оценивания состояния и синте-
за дискретного управления для класса непрерывных систем с липшицевыми
нелинейностями и неопределенными ограниченными по норме возмущения-
ми. При этом исходная непрерывная модель представляется в виде системы
с импульсным изменением координат состояния. Предложенный в [32, 33]
и развитый в [34, 35] подход с использованием функции Ляпунова с изме-
няющимися коэффициентами и ДЛМН применяется для решения задач оце-
нивания состояния, анализа ограниченности на конечном интервале и син-
теза дискретного управления одного класса нелинейных систем при учете
неопределенных возмущений. В результате задачи оценивания состояния и
синтеза дискретного управления сводятся к совокупности задач оптимиза-
ции с ЛМН, получающихся при кусочно-линейной аппроксимации решения
ДЛМН [36]. Рассматриваются случаи периодического и апериодического дис-
кретного управления. На примере линейной системы второго порядка прово-
дится сопоставление предлагаемого подхода с другими известными методами.
Результаты применяются для стабилизации однозвенного манипулятора с по-
мощью как периодического, так и апериодического дискретного управления.
2. Непрерывная система с дискретным управлением
Рассматривается система с дискретным управлением
(1)
x(t) = A(t)x(t) + D(t)w(t) + Φ(t)ϕ(t, x(t)) + B(t)u(t),
где x ∈ Rn
вектор состояния, w(t) ∈ W ⊂ Rr
вектор неопределенных
внешних возмущений, u ∈ Rm, u(t) = K(tk)x(tk), t ∈ [tk, tk+1) вектор управ-
ления в форме обратной связи по состоянию, измеряемому в дискретные
98
моменты времени tk ∈ Θ = {t0, tk = tk-1 + hk, k = 1, . . . , N - 1}, hk
шаг
выборки измерений, A ∈ Rn×n, B ∈ Rn×m, D ∈ Rn×r, Φ ∈ Rn×q
извест-
ные матрицы с постоянными или непрерывными и ограниченными элемен-
тами при всех t ∈ T , T = [t0, tN ], t0, tN
начальный и конечный моменты
времени.
Нелинейная векторная функция ϕ(t, x) является непрерывной и удовлет-
воряет ограничению
(2)
∥ϕ(t, x)∥2 ≤ µ0 + µ1 ∥Cf (t)x∥2 ∀t ∈ T, x ∈ Rn,
где Cf (t)x ∈ Rq×n
известная матрица с ограниченными элементами при
всех t ∈ T . Здесь и далее ∥·∥ означает евклидову норму вектора, µ0, µ1 ≥ 0
заданные константы.
Предположим, что неопределенные возмущения являются непрерывными
и ограниченными в каждый момент времени функциями:
(3)
W = {w(t) ∈ Rr
: ∥w(t)∥ ≤ 1 ∀t ∈ T}.
3. Задача оценивания состояния
Пусть в начальный момент времени состояние системы x(t0) = x0 принад-
лежит заданному эллипсоиду
{
}
(4)
E(Q0) =
x∈Rn :xTQ-10x≤1
,
где Q0
заданная положительно определенная матрица, индекс T знак
транспонирования.
Требуется найти оценку в виде эллипсоида, ограничивающего множе-
ство состояний исходной системы (1) на рассматриваемом интервале [t0, tN ].
В дальнейшем будет предложен способ синтеза дискретного управления, обес-
печивающего минимизацию следа матрицы эллипсоида, ограничивающего со-
стояние или выход рассматриваемой системы.
Задача оценивания состояния решается с использованием второго под-
хода, при котором исходная система с дискретным управлением представ-
ляется как импульсная система [1]. Определим переменные u(t) = Kx(tk) и
z(t) = (xT(t), uT(t))T. Тогда систему (1) можно представить как систему с
импульсами
(5)
Ż(t) = Az(t)z(t) + Dz(t)w(t) + Φz(t)ϕ(t, x(t)), t = tk,
(6)
z(tk) = Jz(tk)z(tk - 0), t = tk
∈ Θ,
где
[
]
[
]
A(t) B(t)
D(t)
Az(t) =
,
Dz(t) =
,
0
0
0
[
]
[
]
Φ(t)
I
0
Φz(t) =
,
Jz(tk) =
0
K(tk)
0
99
При этом z(t0) = z0 = (xT0, uT0) ∈ E(Qz0), где Qz0 = diag(Q0, KQ0KT), x(t) =
= Cz(t), C = ( In
0m ), In единичная (n×n)-матрица. Обозначим Cfz(t) =
= [Cf (t), 0]. В дальнейшем для краткости опускаем зависимость от t или tk
у матриц Az(t), Dz(t), Φz(t), Cfz(t), Jz(tk).
На интервалах непрерывности [tk, tk+1) (k = 0, 1, . . . , N - 1) для оценива-
ния состояния будут использоваться теоремы 1 и 2 из [34], которые здесь
приводятся для указанных интервалов.
Теорема 1 [34]. Если существует решение Q(t) = Q(t,tk,Qk) > 0 диф-
ференциального матричного уравнения
1
dQ(t)/dt = Az(t)Q(t) + Q(t)ATz + αQ(t) +
DzDTz +
α - µ0/β
(7)
µ1
+ βΦzΦTz +
Q(t)CTfzCfzQ(t)
β
при t ∈ [tk,tk+1) и β > 0, α > µ0/β, то эллипсоид E(Q(t)) является ограни-
чивающим для траекторий системы (5), стартующих из начального эллип-
соида E(Qk), т.е.
z(t, tk, z(tk)) ∈ E(Q(t)) при всех t ∈ [tk, tk+1).
Здесь Q(t0) = Qz0, β, α свободные параметры, которые в общем случае
могут зависеть от времени.
Доказательство теоремы 1 представлено в [34]. Там же были доказаны
утверждения о существовании и ограниченности положительно определен-
ных решений уравнения (7) при фиксированных значениях параметров α и β.
Вопрос же выбора значений α и β не был рассмотрен. Однако ими можно рас-
порядиться для получения оценки, оптимальной в каждый момент времени
по критерию следа матрицы Q(t) = Q(t, tk, Qk), определяющего сумму длин
полуосей ограничивающего эллипсоида E(Q(t)). Это обеспечивается миними-
зацией следа матрицы правой части (7) по β, α при всех t ∈ [tk, tk+1).
Лемма. Пусть матрицы Φz, Dz имеют хотя бы по одному ненулевому
элементу при всех t ∈ [tk, tk+1). Тогда если существует на [tk, tk+1) решение
Q(t) = Q(t, tk, Qk) > 0 уравнения (7), где
√
Q(t))
µ0trace(Q(t)) + µ1trace(Q(t)CTfzCfz
β(Q(t)) =
,
trace(ΦzΦTz)
(8)
√
µ0
trace(Dz DTz)
α(Q(t)) =
+
,
β(Q(t))
trace(Q(t))
то эллипсоид E(Q(t)), ограничивающий состояния системы (5), будет оп-
тимальным по критерию trace(Q(t)) → min при каждом t ∈ [tk,tk+1).
Q(t),β(t)
Доказательство леммы дано в Приложении.
100
Замечание 1. При подстановке выражений (8) уравнение (7) становится
существенно нелинейным. При практических применениях оно может быть
решено численно. Исследование же вопросов существования и свойств реше-
ний этого уравнения выходит за рамки данной статьи. Здесь предлагается
ограничиться заданием на каждом интервале [tk, tk+1) фиксированных зна-
чений параметров β(Q(tk)), α(Q(tk)), определяемых по формулам (8) в мо-
менты tk, k = 0, . . . , N - 1. В этом случае согласно леммам 1 и 2 из [34] (7)
будет являться матричной системой сравнения (МСС) для (5), а ее решение
Q(t) = Q(t, tk, Qk) при условии Q(tk) = Qk > 0 будет положительно опреде-
ленным. Ясно, что такое решение будет определять эллипсоид E(Q(t)), огра-
ничивающий траектории системы (5), стартующие из эллипсоида E(Q(tk)),
который, однако, не будет оптимальным при всех t ∈ [tk, tk+1). Поэтому для
оценивания состояния здесь будет использоваться подход, основанный на чис-
ленном решении задачи оптимизации с ДЛМН.
Теорема 2 [34]. Если при некотором заданном α > 0 существует реше-
ние Q(t) = Q(t,tk,Qk) > 0, β(t) > α/µ0 дифференциального матричного нера-
венства
-dQ(t)/dt + AzQ(t) + Q(t)ATz + αQ(t) + βΦz ΦTz Dz Q(t)CTfz
0
DTz
-αI
0
I
(9)
β(t)
≤0
CfzQ(t)
0
-
I
0
µ1
β(t)
0
I
0
-
I
µ0
при t ∈ [tk,tk+1), то эллипсоид E(Q(t)) является ограничивающим для тра-
екторий системы (5), стартующих из начального эллипсоида E(Qk).
Доказательство теоремы 2 представлено в [34].
Как отмечено в [34], положительно определенное решение уравнения (7)
при некоторых α > 0, β(t) ≥ µ0/α на рассматриваемом интервале времени
(в данном случае [tk, tk+1)) будет являться решением дифференциального
матричного неравенства (9) при тех же значениях β, α. При тех же β, α мо-
гут существовать и другие решения (9), которые будут определять эллипсоид,
ограничивающий траектории системы (5). При фиксированном α > 0 нера-
венство (9) становится линейным по переменным Q(t) и β(t) и оптимальный
ограничивающий эллипсоид будет определяться из решения следующей зада-
чи оптимизации trace(Q(t)) → min при ограничениях Q(t) > 0, β(t) > µ0/α
Q(t),β(t)
и ДЛМН (9). Такое оптимальное решение будет зависеть от параметра α.
Чтобы решение было оптимальным и по α, следовало бы добавить еще од-
номерную оптимизацию по α из заданного диапазона. Однако это еще более
усложняет задачу нахождения оптимального ограничивающего эллипсоида.
Поэтому значение параметра α предлагается вычислять только в дискретные
моменты tk из (8) по известной в этот момент матрице Q(tk), а затем при
αk = α(Q(tk)) решать задачу оптимизации trace(Q(t)) → min при ограни-
Q(t),β(t)
чениях Q(t) > 0, β(t) > µ0/αk и ДЛМН (9). Далее будет показано, каким об-
101
разом эта задача оптимизации сводится в результате дискретизации к сово-
купности задач оптимизации с ограничениями в виде ЛМН.
В моменты tk, k = 1, . . . , N, поведение системы представлено линейным
разностным уравнением (6). В этом случае для оценивания состояния будет
использоваться теорема 1 из [35], которая здесь приводится применительно
к линейному разностному уравнению (6).
Теорема 3. Чтобы эллипсоид E(Q(tk+1)) ограничивал состояния систе-
мы в момент tk+1 при условии, что z(tk+1 - 0) ∈ E(Q(tk+1 - 0)), достаточ-
но, чтобы существовало решение Q(tk+1) > 0 разностного линейного мат-
ричного неравенства (РЛМН)
(
)
Q(tk+1)
JzQ(tk+1 - 0)
(10)
≥ 0.
Q(tk+1 - 0)JTz Q(tk+1 - 0)
Доказательство теоремы 3 для более общего случая дискретной системы
с неопределенными возмущениями представлено в [35].
Рассмотрим теперь ряд случаев относительно параметра выборки hk:
1. Все значения hk равны hk = h > 0, k = 1, . . . , N, h постоянный период
выборки;
2. Все значения hk > 0, k = 1, . . . , N , известны (переменный период выбор-
ки);
3. Значения hk > 0, k = 1, . . . , N, неизвестны и могут изменяться в интер-
вале [hmin, hmax], где 0 < hmin < hmax, hmin, hmax известны.
Рассмотрим сначала случай 1 с периодическими выборками (импульса-
ми), т.е. tk+1 - tk = h = const. Случай 2 при переменных, но известных hk
рассматривается аналогично.
Справедливо следующее утверждение.
Теорема 4. Эллипсоид E(Q(t)), где Q(t) = Q(t,t0,Qz0) решение мат-
ричной системы дифференциальных уравнений (7) с РЛМН (10) или зада-
чи оптимизации trace(Q(t, t0, Qz0)) → min с ограничениями ДЛМН
(9) и
РЛМН (10) будет ограничивающим для состояний системы (5), (6), а эл-
липсоид с матрицей CQ(t, t0, Qz0)CT будет ограничивающим для состояний
исходной системы (1) с дискретным управлением при всех нелинейностях
из (2) и возмущениях из (3).
Доказательство основывается на последовательном применении теорем 1
и 2 на интервалах непрерывности [tk, tk+1) (k = 0, 1, . . . , N - 1) для по-
лучения матрицы Q(t, tk, Q(tk)) > 0 эллипсоида, ограничивающего состоя-
ние z(t, tk, x(tk)) системы (5), (6) с начальными данными из эллипсоида
с матрицей Q(tk) при всех нелинейностях из (2) и возмущениях из (3),
и применении теоремы 3 в точках tk+1, (k = 0, 1, . . . , N - 1) для получе-
ния матрицы Q(tk+1) > 0, ограничивающей состояние z(tk+1, tk, x(tk)) систе-
мы (5), (6) после импульса при условии z(tk+1 - 0, tk, x(tk)) ∈ E(Q(tk+1 - 0)).
Здесь Q(tk+1 - 0) = Q(tk + h, tk, Qk)
матрица эллипсоида, ограничиваю-
щего состояние системы (5), (6) непосредственно перед импульсом в мо-
мент tk+1. Она определяется как решение дифференциального матричного
102
уравнения (7) или задачи оптимизации trace(Q(t, tk, Qk)) → min с ДЛМН (9)
на [tk, tk+1).
Таким образом, в случае периодического дискретного управления со-
стояние системы (5), (6) с начальными данными из эллипсоида E(Qz0)
будет ограничено эллипсоидом с матричной функцией Q(t, t0, Qz0), яв-
ляющейся решением МСС (7) с РЛМН (10) или задачи оптимизации
trace(Q(t, t0, Qz0)) → min с ограничениями ДЛМН (9) и РЛМН (10) при t ∈ T .
При численном решении задачи оптимизации проводится дискретизация
ДЛМН (9) на рассматриваемом интервале [t0, tN ]. Производная dQ(t)/dt на
интервале [tk, tk+1) считается постоянной и представляется как dQ(t)/dt =
= Z(tk), где tk = t0 + kh, k = 1, . . . , N, и N есть целая часть отношения
(tN - t0)/h. Тогда для t ∈ [tk, tk+1) матрица Q(t) определится как
(11)
Q(t) = Q(tk) + (t - tk)Z(tk
),
причем Q(t0) = Qz0. Для того чтобы матрица Q(t) удовлетворяла неравен-
ству Q(t) > 0 и ДЛМН (9) при всех t ∈ [tk, tk+1), необходимо и достаточ-
но, чтобы она удовлетворяла им в двух крайних точках t ∈ {tk, tk + h}, т.е.
при каждом k = 0, . . . , N - 1 одновременно должны выполняться неравен-
ства [36]:
(12)
Q(tk) > 0, Q(tk
+ h) > 0,
T
-Z(tk)+AzQ(tk)+Q(tk)Az +αkQ(tk)+βΦzΦz Dz Q(tk)C
fz
0
DTz
-αkI
0
I
(13)
β(tk)
≤ 0,
CfzQ(tk)
0
-
I
0
µ1
β(tk)
0
I
0
-
I
µ0
-Z(tk)+AzQ(tk +h)+Q(tk +h)Az+
Dz Q(tk + h)Cfz
0
+ αQ(tk + h) + βΦz Φz
DTz
-αkI
0
I
(14)
≤ 0,
β(tk)
CfzQ(tk + h)
0
-
I
0
µ1
β(tk)
0
I
0
-
I
µ0
где Q(tk + h) = Q(tk) + hZ(tk) = Q(tk+1 - 0), αk = α(Q(tk)) из (8) и матрицы
Az, Dz, Φz, Cfz берутся в момент tk.
В результате линейной аппроксимации (11) решения ДЛМН (9) нахож-
дение матрицы Q(t) > 0 эллипсоида, ограничивающего состояния системы,
сводится к последовательному решению совокупности задач оптимизации:
trace(Q(tk+1)) →
min
при ЛМН ограничениях (10), (12)-(14)
Q(tk+1)>0,β(tk+1)≥µ0/αk
для k = 0, . . . , N - 1. На первой итерации при k = 0 по заданной матри-
це Q(t0) = Q0 и α0 в результате решения указанной задачи оптимизации с
103
ЛМН вычисляются матрицы Q(t0 + h) и Q(t1) с минимальным следом, кото-
рые определяют матрицу эллипсоида, ограничивающего состояния системы
(5), (6) на интервале [t0, t1]. Затем при k = 1, 2, . . . , N - 1 по матрице Q(tk)
вычисляются αk и матрицы Q(tk + h) и Q(tk+1), которые определяют матри-
цу эллипсоида, ограничивающего состояния системы (5), (6) на последующих
интервалах [tk, tk+1].
Для численного решения на каждой итерации задач оптимизации с ЛМН
используются программные средства полуопределенного программирования
(CVX, Sedumi, Yalmip и др.). Они позволяют решать такую задачу для си-
стемы размерности порядка 20 за доли секунды. Общее время, требуемое для
численного решения всей совокупности задач и получения эллипсоидальных
оценок, будет зависеть от длительности рассматриваемого интервала времени
и шага дискретизации ДЛМН.
Замечание 2. С целью более точной аппроксимации решения зада-
чи оптимизации с ДЛМН на интервалах [tk, tk+1) рекомендуется решать
задачу с шагом hki = h/M, где M > 1 количество промежуточных то-
чек дискретизации интервала [tk, tk+1). В этом случае значение матри-
цы Q(tk + h) = Q(tk+1 - 0) определится как Q(tk + h) = Q(tk) + hZks, где
∑
Zks =
Z(tki)/M среднее значение производной на интервале [tk, tk+1),
i=0
tki = tk + ihki.
Рассмотрим теперь случай 3, когда система (5), (6) является апериоди-
ческой, т.е. импульсы происходят в нерегулярные моменты времени. Пусть
выполнено ограничение в виде интервала времени для последовательности
моментов импульсов, т.е. tk+1 - tk = hk ∈ [hmin, hmax]. Пусть t ∈ [tk, tk+1] и θ ∈
∈ [0, hmax - hmin].
Так же как в случае 1, при t ∈ [tk, tk+1) = [tk, tk + hmin + θ) может быть по-
{
)
лучена оценка в виде эллипсоида E(t) =
x : xTQ-1(t)x ≤ 1
, если при неко-
торых β(tk) > 0, α(tk) ≥ µ0/β(tk) найдется положительно определенное ре-
шение Q(t) > 0 матричной системы сравнения (7) или дифференциального
линейного матричного неравенства (9) при t ∈ [tk, tk+1), k = 0, 1, 2, . . . , N - 1.
Однако момент возникновения каждого следующего импульса tk+1 является
неопределенным и может изменяться в интервале [tk + hmin, tk + hmax]. В дан-
ном случае эллипсоид, ограничивающий состояние системы в момент tk+1,
должен гарантированно содержать все эллипсоиды, которые будут получены
при импульсном воздействии из эллипсоидов, ограничивающих состояния до
момента tk+1 при всех tk+1 = tk + hk ∈ [tk + hmin, tk + hmax]. Поэтому (10) за-
меняется неравенством
(15)
Q(tk+1) ≥ JQ(tk + hmin + θ)JT,
которое должно быть выполнено при любом θ ∈ [0, hmax - hmin]. Проверка
этого неравенства затруднена, однако при использовании линейной аппрок-
симации решения задачи оптимизации trace(Q(t)) → min при ДЛМН ограни-
чениях (9) в виде Q(tk + hmin + θ) = Q(tk) + (hmin + θ)Z(tk) матричное нера-
венство (15) будет линейным по переменной θ ∈ [0, hmax - hmin]. Поэтому оно
будет выполнено при любых θ ∈ [0, hmax - hmin] тогда и только тогда, когда
104
выполняется одновременно в двух крайних точках рассматриваемого интер-
вала, т.е. при θ ∈ {0, hmax - hmin}:
(16)
Q(tk+1) ≥ JQ(tk + hmin)JT, Q(tk+1) ≥ JQ(tk + hmax)JT.
Здесь матрицы Q(tk + hmin), Q(tk + hmax) определяются из (11), вычисленных
при t = tk + hmin и t = tk + hmax соответственно.
Таким образом, в случае апериодического дискретного управления состоя-
ние системы (5), (6) с начальными данными из эллипсоида E(Qz0) будет
ограничено эллипсоидом с матричной функцией Q(t, tk, Qk) на интервалах
непрерывности [tk, tk+1) и эллипсоидом с матрицей Qk+1 при t = tk+1. Мат-
рица Q(t, tk, Qk) определяется из (11), где Z(tk), а также матрицы Q(tk +hk) и
Qk+1 вычисляются в задаче оптимизации trace(Q(tk+1)) →
min
Q(tk+1)>0,βk>µ0/αk
с ЛМН ограничениями (12)-(14) и (16).
Отметим, что оценку для вектора состояния x(t) исходной системы (1) с
дискретным управлением, с нелинейностями из (2) и возмущениями из (3)
при x(t0) из (4) будет определять эллипсоид с матрицей CQ(t, t0, Qz0)CT.
4. Задача об ограниченности относительно заданных множеств
{
}
Обозначим множество начальных состояний E(R0) =
x ∈ Rn: xTR-10x ≤ 1
{
}
и множество допустимых траекторий E(R(t)) =
x ∈ Rn : xTR-1(t)x ≤ 1
,
R0,R(t) известные симметрические положительно определенные матрицы,
t ∈ T. Так же как в [32], вводится определение.
Определение. Будем говорить, что система с дискретными данны-
ми (5), (6) обладает на t ∈ T свойством ограниченности относительно за-
данных множеств {E(R0), E(R(t))}, если для всех z0 ∈ E(R0) существуют
на t ∈ T решения z(t) = z(t,t0,x0) системы (5), (6) с начальными данны-
ми z(t0) = z0, для которых имеет место z(t,t0,z0) ∈ E(R(t)) при всех t ∈ T,
всех нелинейностях из (2) и возмущениях из (3).
Отметим, что аналогичное определение было введено в [32] для линей-
ных неавтономных систем, где были получены необходимые и достаточные
условия в терминах разрешимости дифференциальных линейных матрич-
ных неравенств. Такое же динамическое свойство изучалось применительно
к непрерывным в [34] и дискретным в [35] нелинейным липшицевым систе-
мам с неопределенными возмущениями. Особенностью данного динамическо-
го свойства является то, что оно определяет как качественное поведение, так
и дает количественные оценки, поскольку в его определении указываются
конкретные множества начальных данных и множества, которым должны
принадлежать траектории системы с этими начальными данными.
С учетом полученных выше эллипсоидальных оценок состояния для систе-
мы с дискретными данными (5), (6), приходим к следующему утверждению.
Теорема 5. Система (5), (6) с периодическими (апериодическими) им-
пульсами обладает на [t0, tN ] свойством ограниченности относительно
заданных множеств {E(R0), E(R(t))}, если существует решение Q(t) =
105
= Q(t,t0,Qz0) МСС (7) с РЛМН (10) или ДЛМН (9) с РЛМН (10) (соот-
ветственно задачи оптимизации trace(Q(tk+1)) →
min
с ЛМН
Q(tk+1)>0,β≥µ0/αk
ограничениями (12)-(14) и (16)) с начальными данными Q0 ≥ R0, удовле-
творяющее неравенству Q(t) ≤ R(t) для всех t ∈ T .
При выполнении условий теоремы 5 исходная система (1) с дискретным
управлением будет обладать ограниченностью относительно заданных мно-
жеств {E(CR0CT), E(CR(t)CT)}.
5. Задача синтеза дискретного управления, обеспечивающего
ограниченность непрерывной системы
Рассмотрим систему (1) с управлением, которое должно удовлетворять
ограничению
{
}
(17)
u(t) ∈ u : uTU-1u ≤ 1
,
t∈T,
где U заданная симметрическая положительно определенная (m × m)-мат-
рица.
Задача состоит в нахождении управления в виде обратной связи по со-
стоянию, доступному в дискретные моменты времени tk, k = 0, 1, . . . , N - 1:
(18)
u(t) = K(tk)x(tk), t ∈ [tk, tk+1
),
k = 0,1,...,N - 1,
стабилизирующего замкнутую систему и подавляющего начальные отклоне-
ния и воздействие внешних возмущений в смысле минимальности ограни-
чивающего эллипсоида для состояний или обеспечивающего ограниченность
замкнутой системы. Здесь K матрица коэффициентов усиления дискрет-
ного регулятора.
Задача синтеза с учетом рассмотренного в разделе 3 способа численного
решения ДЛМН (9) сводится к задаче оптимизации критерия при ограниче-
ниях в виде разностных линейных матричных неравенств. В качестве крите-
рия берется след матрицы, определяющий размер ограничивающего состоя-
ния эллипсоида в дискретные моменты времени tk, k = 1, 2, . . . , N.
Представим исходную систему с дискретным управлением (18) в виде (5) с
импульсами (6). Искомая матрица коэффициентов усиления регулятора вхо-
дит только в разностное уравнение для импульсов (6). Представим его в виде
(
)
(19)
z(tk) = Jzz(tk - 0) =
J + BK(tk)C z(tk - 0), tk
∈ Θ,
где
(
)
(
)
I
0
0
(
)
B=
J =
,
,
C =
I
0
,
z(t0 - 0) = z(t0) ∈ E(Qz0),
0
0
I
Qz0 > 0
заданная матрица эллипсоида, ограничивающего начальные состо-
яния.
106
Справедлива следующая теорема.
Теорема 6. Пусть при Q(t0-0) = Qz0, αk = α(Q(tk-0)) из (8) и всех tk,
k = 0,1,... ,N -1, найдутся решения Q(tk), Q(tk+1-0) = Q(tk+h) = Q(tk)+
+ hZ(tk), Y (tk) задачи
trace[Q(tk+1 - 0)] → min
при ограничениях (12)-(14) и
(
)
Q(tk)
JQ(tk - 0)CT +BYk)
(20)
≥0
CQ(tk - 0
JT + YTk
BT
CQ(tk - 0)CT
(
)
U
Yk
(21)
≥ 0,
YTk
CQ(tk - 0)CT
где минимизация проводится по матричным переменным Q(tk), Yk ∈ Rm×n,
Z(tk) ∈ Rn×n, скалярной переменной β(tk) > µ0/αk, определяет согласно (11)
матрицу Q(t) ограничивающего эллипсоида для вектора состояния z(t)
и зависимую от времени матрицу коэффициентов дискретного управле-
ния по состоянию K(tk) = Yk(CQ(tk - 0)CT)-1. Если, кроме того, матри-
ца Q(t) удовлетворяет дополнительно ограничениям Qz0 ≥ R0 и Q(t) ≤ R(t)
для всех t ∈ [t0, t0 + Nh], где R0 и R(t)
заданные положительно опре-
деленные симметрические матрицы, то искомое управление
(18) обес-
печивает ограниченность замкнутой системы относительно множеств
{E(R0), E(R(t))}.
Доказательство теоремы 6 дано в Приложении.
В случае апериодического дискретного управления (tk+1 - tk = hk ∈
∈ [hmin, hmax]) с учетом полученных в разделе 3 оценок состояния задача син-
теза сводится к подобной задаче оптимизации trace[Q(tk+1 - 0)] → min при
ЛМН ограничениях (12)-(14) и (20), (21) с той лишь разницей, что добавля-
ются дополнительные ограничения на матрицу Q(tk+1 - 0):
(22)
Q(tk+1 - 0) ≥ Q(tk) + hminZ(tk), Q(tk+1 - 0) ≥ Q(tk) + hmaxZ(tk
).
Замечание 3. С целью уменьшения погрешности при линейной аппрок-
симации решения задачи оптимизации с шагом, равным периоду дискретного
управления, предлагается аппроксимировать решение задачи оптимизации на
каждом дискретном интервале [tk, tk+1) с более мелким шагом, чем период
дискретного управления, т.е. hi = (tk+1 - tk)/M = h/M, где M количество
промежуточных точек интервала [tk, tk+1). В результате исходная задача оп-
тимизации заменяется следующей:
trace (Q (tk+1 - 0)) → min с ЛМН ограничениями
(
)
(
)
Q (tkj) = Q
tk(j-1)
+ (j - 1) hiZ
tk(j-1)
> 0,
107
-Z(tk(j-1)) + AzQ(tk(j-1)) + Q(tk(j-1))ATz+
Dz Q(tk(j-1))CTfz
0
+ αkjQ(tk(j-1)) + βΦzΦT
z
DTz
-αkjI
0
I
≤ 0,
βkj
CfzQ(tk(j-1))
0
-
I
0
µ1
βkj
0
I
0
-
I
µ0
-Z(tk(j-1)) + AzQ(tkj) + Q(tkj)ATz
+
Dz Q(tkj)CTfz
0
+ αkjQ(tkj) + βΦzΦT
z
DTz
-αkjI
0
I
≤ 0,
βkj
CfzQ(tkj)
0
-
I
0
µ1
βkj
0
I
0
-
I
µ0
при всех j = 1, 2, . . . , M и ЛМН
(
)
Q(tk)
JQ(tk - 0
CT +BYk)
≥ 0,
CQ(tk - 0
JT + YTk
BT
CQ(tk - 0
CT
где tkj = tk(j-1) +(j -1)hi, αkj = α(Q(tkj )) и матрицы Az, Dz, Φz, Cfz берутся
в момент tkj.
6. Численные примеры
Для сравнения рассмотрим часто встречающийся пример из [6] линейной
системы с дискретным управлением со значениями параметров:
[
]
[
]
[
]
0
1
0
A=
,
B=
,
K =
-3,75
-11,5
0
-0,1
0,1
Среди разрабатываемых подходов [6, 7, 9, 14, 16, 17] наибольшая верх-
няя оценка h = 1,7294 периода дискретного управления с постоянными ко-
эффициентами K была получена в [18] с использованием так называемого
петлевого функционала с граничными условиями. Применение предложен-
ного здесь подхода при численном решении МСС (7), принимающей вид
dQ(t)/dt = AzQ + QATz для линейной системы без возмущений, с РЛМН (10),
получена такая же верхняя граница рассматриваемого дискретного управле-
ния, при котором эллипсоидальные оценки множества решений с начальными
данными из заданного эллипсоида через некоторый промежуток времени стя-
гиваются к началу координат, что соответствует поведению асимптотически
устойчивой системы.
108
2
1
0
-1
-2
-3
-2
-1
0
1
2
3
x1
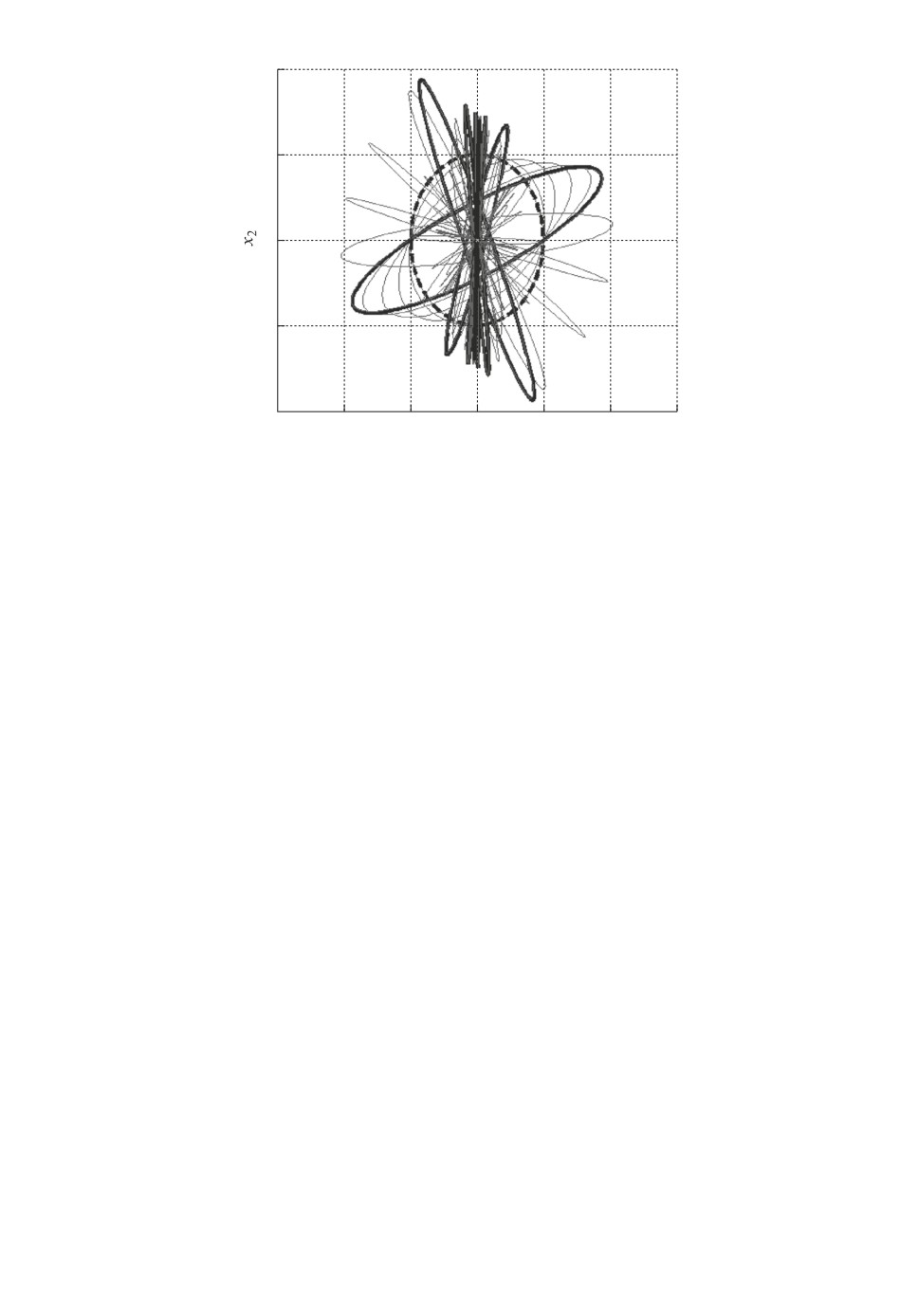
Рис. 1. Эллипсоидальные оценки множества состояний системы с периодиче-
ским (h = 1,7294) дискретным управлением.
Следует отметить, что в [18] с помощью достаточно сложного, так назы-
ваемого петлевого функционала анализ асимптотической устойчивости ли-
нейной автономной системы без возмущений сводился к разрешимости задачи
оптимизации с ЛМН, в которой наряду с обычными переменными появляет-
ся большое количество вспомогательных матричных переменных. При этом
существенно возрастает размерность ЛМН. В отличие от [18] предлагаемый
подход применительно к линейным системам без возмущений позволяет све-
сти задачу оценивания состояния (а также анализа асимптотической устой-
чивости) к совокупности задач оптимизации с ЛМН, в которых отсутствуют
какие-либо вспомогательные переменные, что приводит к сокращению вы-
числений.
На рис. 1 толстыми сплошными линиями показаны эллипсы, ограничи-
вающие состояния рассматриваемой системы в дискретные моменты време-
ни tk = kh, k = 1, . . . , N , при h = 1,7294, а тонкими сплошными линиями
в [роме ]уточные моменты времени. Начальный эллипс с матрицей Q0 =
1
0
=
показан штриховой линией.
0
1
Пусть теперь период дискретного управления задан как h = 5 c. В резуль-
тате решения задачи оптимизации trace(Q(tk+1)) → min с ЛМН ограниче-
ниями (12)-(14) и (22) при каждом k = 0, 1, . . . , 19 были получены коэффи-
циенты усиления K(tk) дискретного управления, которое обеспечивает огра-
ниченность на интервале [0, 70 c] траекторий рассматриваемой системы, с
начальными данными из эллипса с матрицей Q0 (показан на рис. 2,а тол-
стой штриховой линией). Тонкими сплошными линиями показаны эллипсы,
ограничивающие состояния в точках дискретизации tk указанного интервала
времени. При этом эллипсы сначала при каждом tk ∈ [0, 25 c) расширяются
(по критерию trace(Q(tk)), а во второй части интервала [0, 70 c] медленно
сжимаются.
109
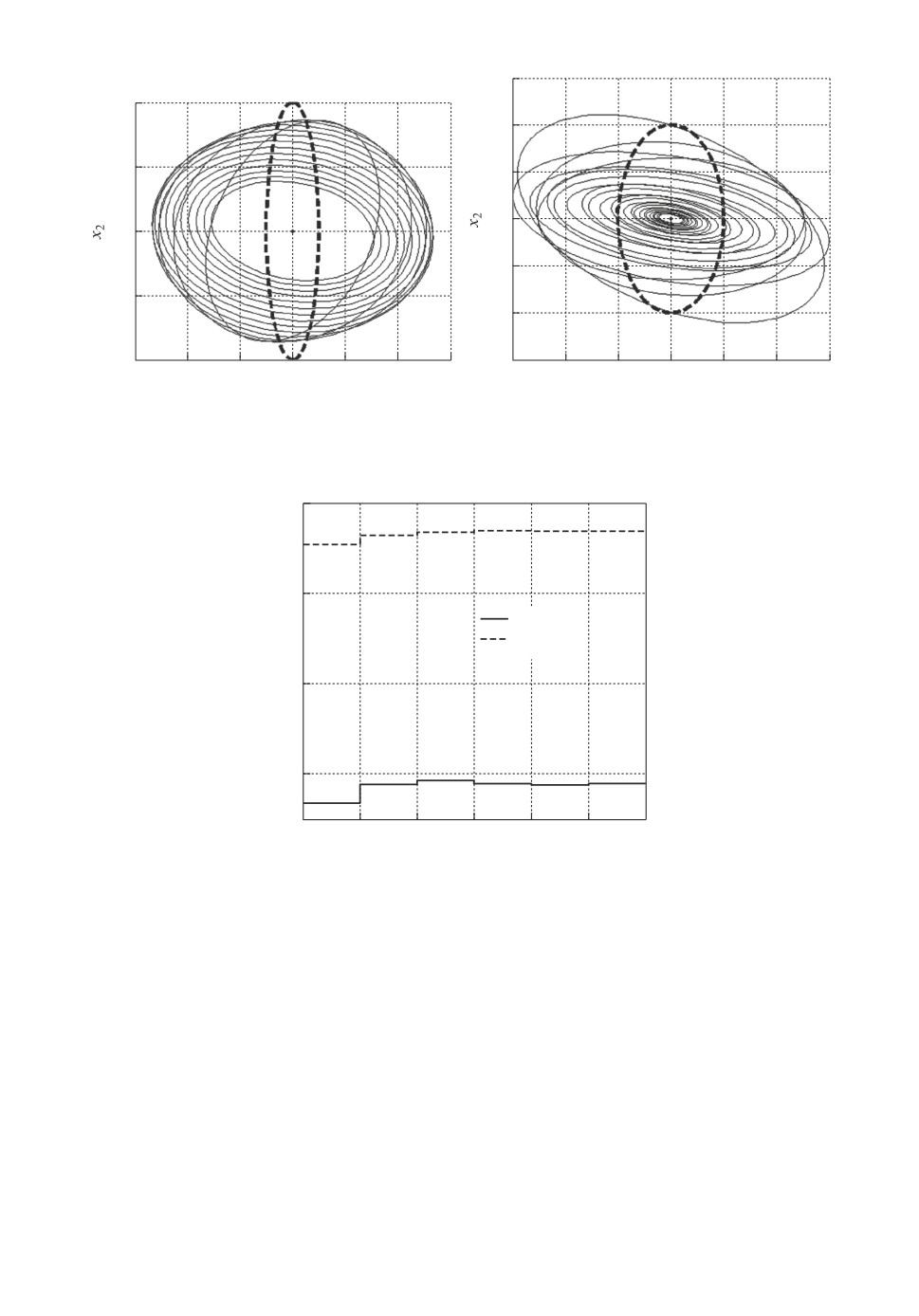
а
б
1,5
1,0
1,0
0,5
0,5
0
0
-0,5
-0,5
-1,0
-1,0
-1,5
-6
-4
-2
0
2
4
6
-3
-2
-1
0
1
2
3
x1
x1
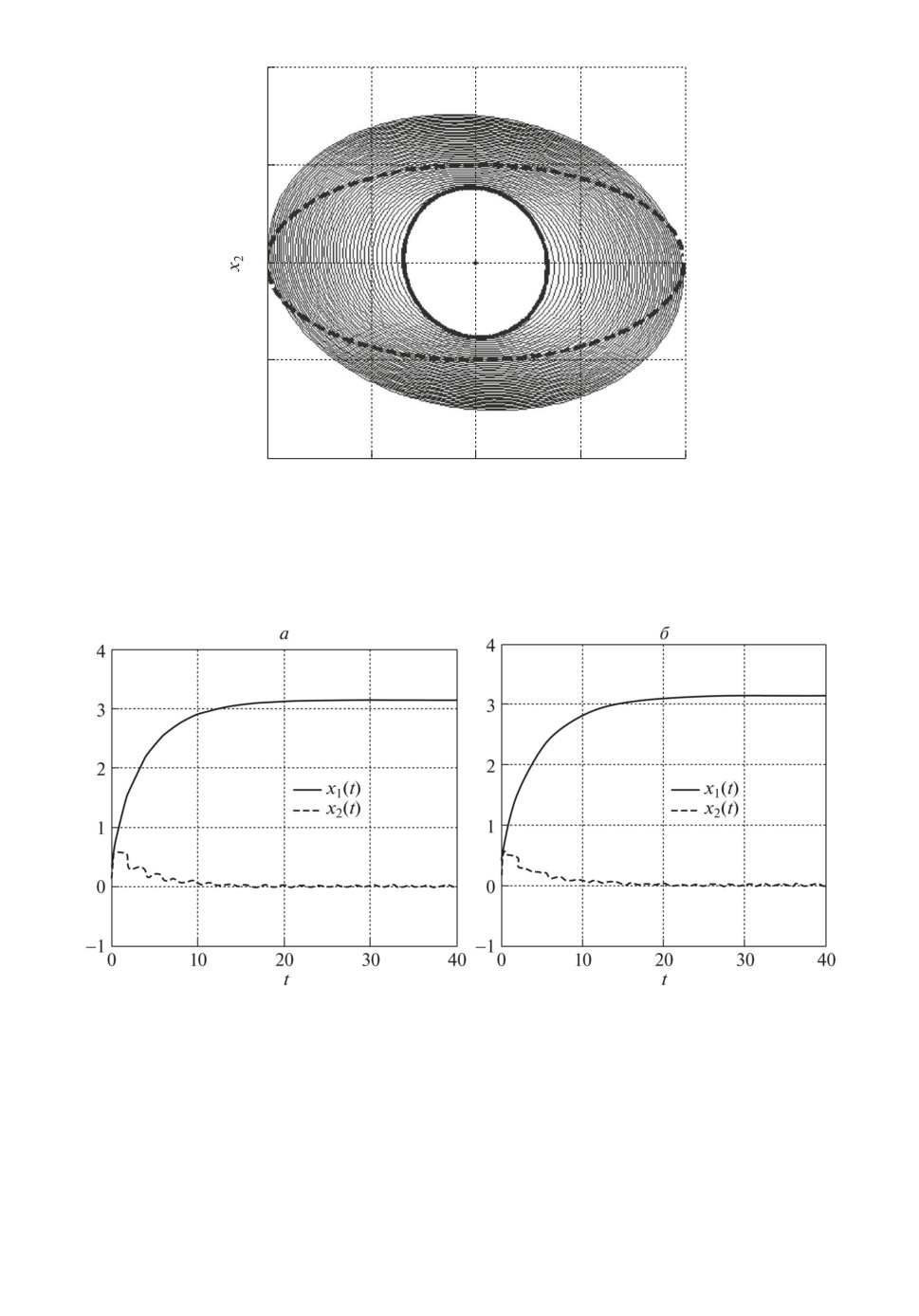
Рис. 2. Эллипсоидальные оценки множества состояний системы с периодиче-
ским (h = 5 с) дискретным управлением.
-0,2
-0,6
K1(t)
K2(t)
-1,0
-1,4
0
5
10
15
20
25
30
t
Рис. 3. Изменения коэффициентов усиления периодического (h = 5 с) дискрет-
ного управления.
С использованием замечания 2 при hi = h/5 = 1 c были получены коэффи-
циенты дискретного управления и эллипсоидальные оценки состояния, кото-
рые представлены на рис. 2,б . Штриховой линией показан начальный эллипс,
а тонкими сплошными линиями эллипсы, ограничивающие состояния в
дискретные tk и промежуточные tki моменты времени рассматриваемого ин-
тервала [0, 70 c].
Сравнивая рис. 2,а и 2,б , можно отметить, что полученное периодическое
дискретное управление обеспечивает после t = 5 c постепенное сжатие эллип-
соидальных оценок, причем более эффективное (по критерию следа матрицы
эллипса) при использовании замечания 2. На рис. 3 изображены графики из-
менения коэффициентов усиления дискретного управления.
110
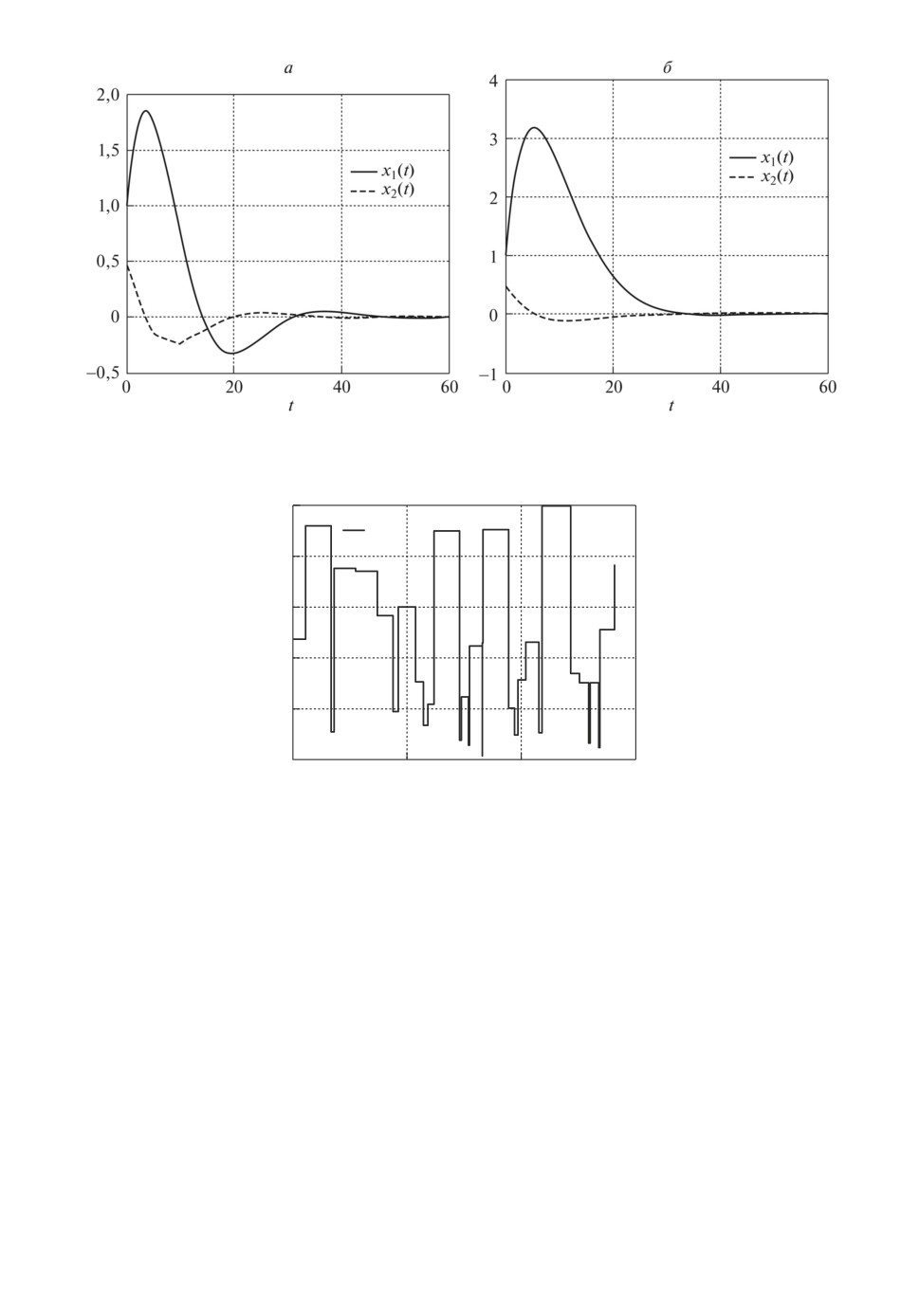
Рис. 4. Изменения координат состояния рассматриваемой системы (а) с пе-
риодическим, (б ) с апериодическим дискретным управлением.
10
h(t)
8
6
4
2
0
40
80
120
t
Рис. 5. Изменение шага дискретизации в системе с апериодическим дискрет-
ным управлением.
В результате решения задачи оптимизации из теоремы 6 для системы с
апериодическим дискретным управлением (hmin = 0,01 c; hmax = 10 c) полу-
чены коэффициенты усиления K = [ -0,0617
-0,4326 ], при которых обес-
печивается сначала расширение, а после 10 с медленное сжатие эллипсои-
дальных оценок. На рис. 4,a показаны изменения координат состояния рас-
сматриваемой системы с полученным периодическим (h = 5 с) дискретным
управлением, а на рис. 4,б
с апериодическим дискретным управлением
при изменении шага дискретизации hk ∈ [hmin, hmax], задаваемого с помощью
датчика случайных чисел (показано на рис. 5).
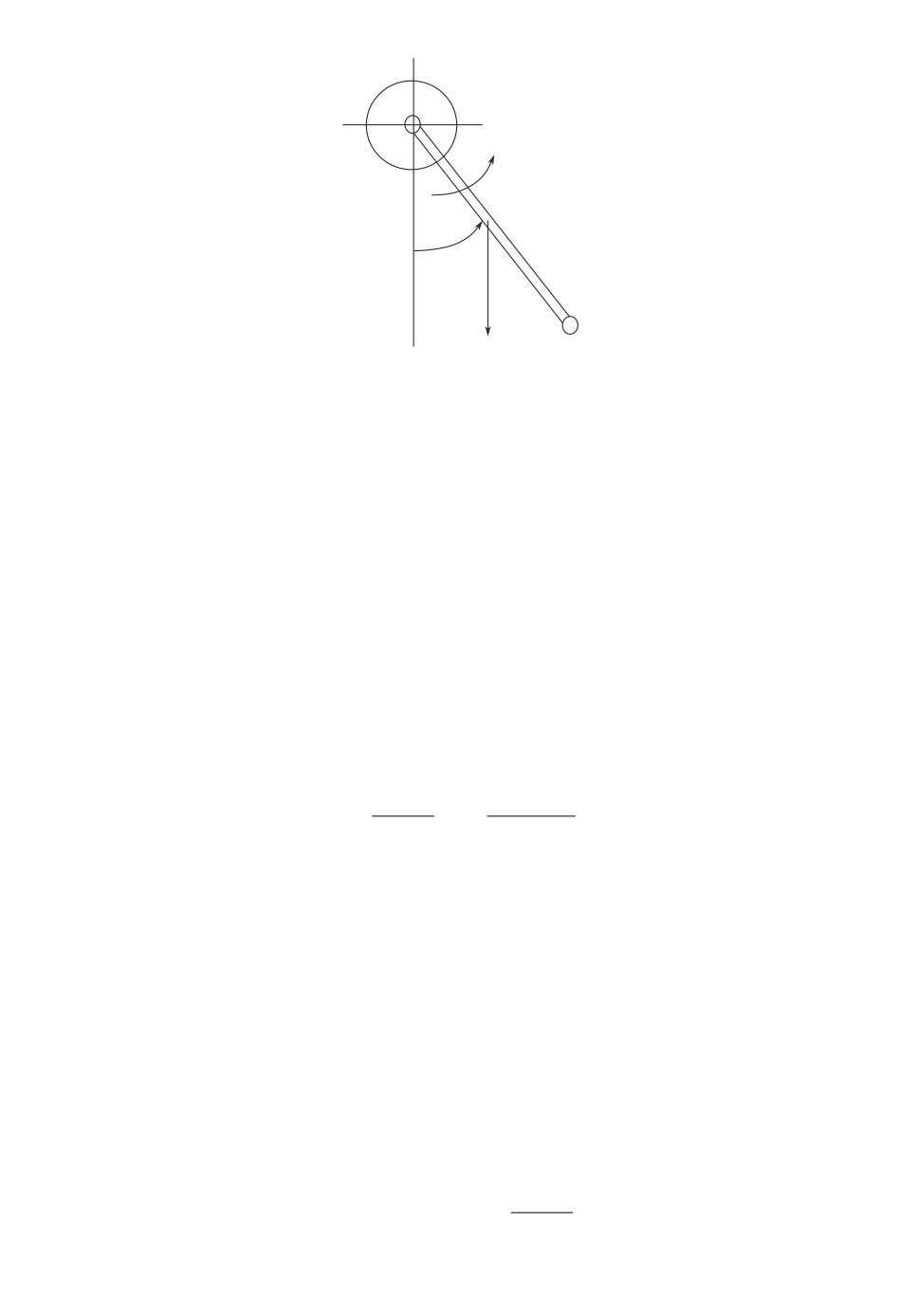
7. Приложение к однозвенному манипулятору
Рассматривается манипулятор с одним звеном, который через редуктор
соединен с выходным валом двигателя постоянного тока [37]. Предполагается,
что движение манипулятора происходит в вертикальной плоскости (рис. 6).
111
q1
q1
m1g
Рис. 6. Кинематическая схема однозвенного манипулятора.
Обозначим θ1 угол отклонения от вертикальной оси,˙θ1 = dθ1/dt уг-
ловая скорость звена манипулятора. Предполагается, что известны значения
θ1,
θ1 только в дискретные моменты времени tk ∈ Θ.
Уравнение динамики манипулятора имеет вид
(23)
(m1l21 + Ip1)θ1 = -m1gl1 sin θ1 + T1 - Bθ1
˙θ1 - w1.
Здесь m1, l1, Ip1 масса, расстояние до центра масс и момент инерции зве-
на, Bθ1
коэффициент пропорциональности момента вязкого трения, w1
неопределенное возмущение, вызванное моментами сопротивления, сухого
трения и других неучтенных моментов, T1 момент, создаваемый двига-
телем постоянного тока.
Пренебрегая электромагнитными переходными процессами в якорной об-
мотке двигателя и полагая, что момент двигателя пропорционален напряже-
нию якорной обмотки, выражение для момента представляется в виде
2
KgKm
(KgKm)
(24)
T1 =
V1 -
θ1,
R
R
где Kg, Km, R коэффициенты редукции, пропорциональности и активное
сопротивление обмотки двигателя, V1 управляющее напряжение. Таким об-
разом, момент, приложенный к звену, является функцией входного напряже-
ния якорной обмотки двигателя. Второй член пропорционален угловой скоро-
сти со знаком минус потому, что ЭДС вращения вызывает противодействую-
щий момент по сравнению с моментом, создаваемым входным напряжением.
Положение равновесия для манипулятора определяется из уравнения
-m1gl1 sin θ1 + T1 = 0.
Если требуется стабилизировать манипулятор в заданном положении θ10,
то необходимо приложить управляющий момент T0 = m1gl1 sin θ10. Тогда
из (24) получаем выражение для установочного значения напряжения для
выбранного положения:
R
V0 = m1gl1 sinθ10
KgKm
112
Введем обозначения для отклонений от невозмущенного движения θ10 и от
установочных значений момента и напряжения:
θ=
θ=θ1 -θ10,
θ1,
θ=θ1, T = T1 - T0, V = V1 - V0.
После подстановки (24) в (23) с учетом обозначения β = KgKm получаем
уравнение движения манипулятора в отклонениях от требуемого положения
равновесия θ10:
(
)
β2
-m1gl1[sin(θ + θ10) - sin(θ10)] - Bθ1 +
˙θ+βRV -w
R
θ=
m1l21 + Ip1
Определим вектор состояния x = (θ,˙θ)T и управление u(tk) = V (tk) =
= K(tk)x(tk). Тогда исходное уравнение представляется в виде (1), где
0
1
A=
,
m1gl1
Bθ1 +β2R
-
m1l21 + Ip1
m1l21 + Ip1
0
0
0
B=
β
, D1 =
-1
, Φ= -m1gl1
,
R(m1l21 + Ip1)
m1l21 + Ip1
m1l21 + Ip1
(
)
Cf =
1
0
,
ϕ(θ) = sin(θ + θ10) - sin(θ10) - θ.
Моделирование системы с регуляторами проводилось при значениях пара-
метров: l = 0,5; IP = 0,05; g = 9,8; R = 2,6; Kg = 3,7; Km = 3,835; Bθ = 0,025.
Пусть требуется стабилизировать звено манипулятора в вертикальном по-
ложении θ10 = π. При таком θ10 нелинейность ϕ(θ) удовлетворяет условию (2)
при µ0 = 0, µ1 ≤ 1.
С использованием теоремы 6 в результате решения совокупности задач
оптимизации с ЛМН при α = 0,0043, β = 1,0296 было получено периодиче-
ское с h = 2 c дискретное управление с постоянными коэффициентами уси-
ления K = [ -3,2518
-0,0025] , которое обеспечивает на конечном интерва-
ле [0 100 c] стабилизацию манипулятора с начальными данными из эллипса
[
]
1
0
с матрицей Q0 =
. На рис. 7 представлены эллипсоидальные оценки
0
1
состояния однозвенного манипулятора с периодическим дискретным управ-
лением. Начальный эллипс с матрицей Q0 обозначен толстой штриховой ли-
нией. Тонкими сплошными линиями показаны эллипсы, ограничивающие со-
стояние в дискретные [ оменты времени t] k = 1, 2, . . . , 50. Предельный эл-
0,1193
-0,0159
липс с матрицей Q0 =
, к которому стягиваются оценки
-0,0159
0,5904
состояния при t ≥ 90 c, обозначен толстой сплошной линией.
113
2
1
0
-1
-2
-1,0
-0,5
0
0,5
1,0
x1
Рис. 7. Оценки множества состояний однозвенного манипулятора с периоди-
ческим дискретным управлением при действии возмущений.
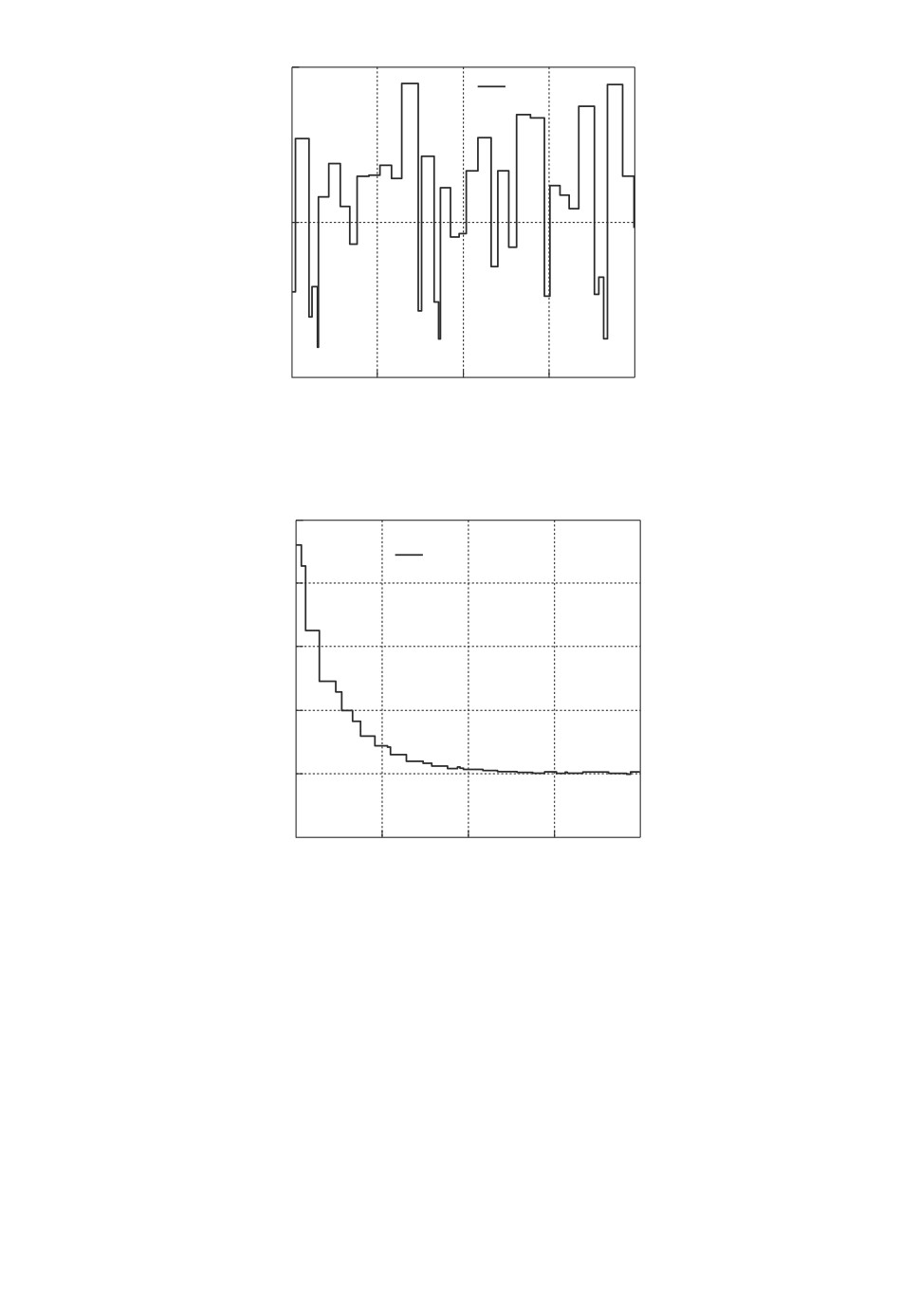
Рис. 8. Изменения координат состояния однозвенного манипулятора (а) с пе-
риодическим дискретным управлением, (б ) с апериодическим дискретным
управлением при действии возмущений.
На рис. 8,а и 8,б показаны изменения координат состояния однозвенно-
го манипулятора соответственно с периодическим и апериодическим дис-
кретным управлением при действии возмущения, заданного в виде w(t) =
= sin(2cos(3t)).
114
2
h(t)
1
0
10
20
30
40
t
Рис. 9. Изменение шага дискретизации в системе с апериодическим дискрет-
ным управлением.
8
u(t)
6
4
2
0
-2
0
10
20
30
40
t
Рис. 10. Изменение апериодического дискретного управляющего сигнала.
На рис. 9 и 10 представлены соответственно изменения шага дискретиза-
ции и управляющего сигнала в системе с апериодическим дискретным управ-
лением при действии возмущений.
8. Заключение
Для непрерывных систем с липшицевыми нелинейностями, неопределен-
ными возмущениями и дискретным управлением предложены способы оце-
нивания состояния в виде эллипсоидов, ограничивающих состояния для про-
цессов с начальными данными из заданного эллипсоида. Исходная система с
дискретным управлением представлена как импульсная система. С исполь-
115
зованием квадратичной функции Ляпунова с изменяющимися параметра-
ми получены условия ограниченности на конечном интервале в виде разре-
шимости дифференциального матричного уравнения и задачи оптимизации
с дифференциально-разностными линейными матричными неравенствами.
При кусочно-линейной аппроксимации решения ДЛМН задачи оценивания
состояния и синтеза как периодического, так и апериодического дискретного
управления сведены к совокупности задач оптимизации с ЛМН, для числен-
ного решения которых применены методы полуопределенного программиро-
вания. Для сравнения рассмотрен пример линейной системы второго порядка
без возмущений. Для него известными методами была ранее получена верх-
няя граница периода дискретного управления с постоянными коэффициен-
тами, при которых обеспечивается асимптотическая устойчивость. Такая же
верхняя граница получена с применением предложенного подхода при сокра-
щении количества варьируемых переменных в задаче оптимизации. Кроме
того, данный подход позволяет получать на конечном интервале времени эл-
липсоидальные оценки множества состояний исходной нелинейной системы
с дискретным управлением и неопределенными возмущениями, синтезиро-
вать дискретное управление, обеспечивающее свойство ограниченности отно-
сительно заданных множеств. Результаты применены для оценивания состоя-
ния и синтеза периодического и апериодического дискретного управления,
обеспечивающего стабилизацию на конечном интервале времени однозвенно-
го манипулятора, представленного нелинейной моделью с неопределенными
возмущениями.
ПРИЛОЖЕНИЕ
Доказательство леммы. Чтобы скалярная переменная trace(Q(t)),
зависящая от времени и параметров, принимала наименьшее значение при
каждом t ∈ [tk, tk+1), достаточно, чтобы ее производная d(trace(Q(t)))/dt бы-
ла минимальной по параметрам β > 0, α > µ0/β при всех t ∈ [tk, tk+1). По-
скольку d(trace(Q(t)))/dt = trace(dQ(t)/dt), то приходим к следующей задаче
оптимизации:
(
)
β
µ1
(Π.1) trace AzQ + QATz + αQ +
DzDTz +βΦzΦTz +
QCTfzCfzQ
→
αβ - µ0
β
→ min.
α,β
Так как trace(AzQ + QATz) не зависит от α и β, то минимум для (П.1) (если
существует) будет отличаться от минимума функции F (α, β) = αtrace(Q)+
+ βαβ-µ
CfzQ) на постоянную при
0
trace(DzDTz) + βtrace(ΦzΦTz) +µ1βtrace(Q
fz
каждом t величину trace(AzQ + QATz). По условиям леммы матрицы Φz
и Dz имеют хотя бы по одному ненулевому элементу при каждом t ∈
∈ [tk, tk+1). Величины trace(DzDTz ) и trace(ΦzΦTz ) будут положительными
при всех t ∈ [tk, tk+1), так как они представляют собой квадрат нормы Фро-
бениуса для матриц DTz и ΦTz соответственно. Матрица Q(t) является по-
ложительно определенной при всех t ∈ [tk, tk+1), так что trace(Q(t)) > 0 и
trace(QCTfzCfzQ) ≥ 0. Функция F (α, β) определена, непрерывна, непрерывно
116
дифференцируема, ограничена снизу F (α, β) > 0 в открытой выпуклой обла-
сти β > 0, α > µ0/β. Проверим условие выпуклости функции F (α, β) по α, β.
Для этого вычислим частные производные второго порядка для F (α, β) по
параметрам β, α:
2
β
(Π.2)
∂ trace(dQ(t)/dt)/∂α = trace(Q(t)) -
trace(DzDTz
),
(αβ - µ0)2
µ1
(Π.3)
∂ trace(dQ(t)/dt)/∂β = -
trace(QCTfzCfz
Q) -
β2
µ0
−
trace(DzDTz) + trace(ΦzΦTz),
(αβ - µ0)2
3
2β
∂2trace(dQ(t)/dt)/∂α2 =
trace(DzDTz),
(αβ - µ0)3
2βµ0
∂2trace(dQ(t)/dt)/∂α∂β = ∂2trace(dQ(t)/dt)/∂β∂α =
trace(DzDTz),
(αβ - µ0)3
2µ1
2µ0α
∂2trace(dQ(t)/dt))/∂β2 =
trace(QCTfzCfzQ) +
trace(DzDTz).
β3
(αβ - µ0)3
Легко видеть, что матрица вторых производных (гессиан)
[
]
2
β3
µ0β
∇2F(α,β) =
trace(DzDTz)
+
(αβ - µ0)3
µ0β µ0α
[
]
0
0
+
0
2µ1trace(QCTfzCfzQ)/β3
является положительно определенной при всех β > 0, α > µ0/β. Согласно
теореме 5 из [38, c. 163], функция F (α, β) является выпуклой по парамет-
рам β, α из области определения. Известно, что если выпуклая функция
имеет минимум внутри открытой выпуклой области, то этот минимум бу-
дет глобальным. Для нахождения минимума определим стационарные точ-
ки, используя необходимые условия экстремума функции [38]. Приравнивая
производные (П.2), (П.3) нулю, получаем:
2
β
(Π.4)
trace(Q(t)) =
trace(DzDTz
),
(αβ - µ0)2
µ1
µ0
(Π.5)
trace(ΦzΦTz) =
trace(QCTfzCfzQ) +
trace(DzDTz
).
β2
(αβ - µ0)2
Уравнение (П.5) c учетом (П.4) принимает вид
1
[
]
trace(ΦzΦTz) =
µ0trace(Q(t)) + µ1trace(QCTfzCfzQ)
β2
Отсюда находится β(Q(t)) как в (8). Далее из первого уравнения находим
(αβ - µ0)2 =β2trace(Dz Dz)trace(Q(t)) и, извлекая квадратный корень из обеих частей,
117
получаем второе в (8) выражение для α(Q(t)). Так что (8) является един-
ственным решением уравнений (П.2), (П.3) при β > 0, α > µ0/β.
Выше было показано, что матрица вторых частных производных является
положительно определенной при всех β > 0, α > µ0/β, а значит, и для β, α
из (8). Таким образом, согласно достаточным условиям [38] полученные выра-
жения (8) действительно доставляют глобальный минимум d(trace(Q(t)))/dt
при каждом t ∈ [tk, tk+1), что завершает доказательство леммы.
Доказательство теоремы 6. В случае периодического дискрет-
ного управления (hk = h = const > 0), как показано в разделе 3, задача по-
строения оценки состояния сводится к совокупности задач оптимизации
trace(Q(tk+1 - 0)) → min с ЛМН ограничениями (10), (12)-(14) для всех k =
= 0, . . . , N - 1. С учетом (19) матричное неравенство (10) здесь принимает
вид
(
)
Q(tk)
J + BK(tk)C)Q(tk - 0)
≥ 0.
Q(tk - 0)
J + BK(tk)C)T
Q(tk - 0)
Далее, умножая последнее неравенство слева на матрицу diag(I, C), а
справа на diag(I, CT) и вводя замену Yk = K(tk)CQ(tk - 0)CT, приходим
к РЛМН (20) относительно матричных переменных Q(tk), Q(tk+1 - 0) и Yk.
Ограничение на управление (17) обеспечивается ЛМН (21). Отметим, что
параметр αk при каждом k = 0, 1, 2, . . . , N - 1 определяется из (8) по извест-
ной после k-й итерации матрице Q(tk - 0), а матрица CQ(tk - 0)CT будет
положительно определенной, так как является верхним левым блоком раз-
мерности (n × n)-матрицы Q(tk - 0). Теорема 6 доказана.
Автор выражает благодарность А.И. Матасову за ряд ценных замечаний
по статье.
СПИСОК ЛИТЕРАТУРЫ
1. Hetel L., Fiter C., Omran H., Seuret A., Fridman E., Richard J.-P., Niculescu S.
Recent Developments on the Stability of Systems with Aperiodic Sampling: an
Overview // Automatica. 2017. V. 76. P. 309-335.
2. Seuret A. Contributions to the Stability Analysis and Control of Networked Systems.
Automatic Control Engineering. Université Toulouse 3 Paul Sabatier, 2017.
3. Hespanha J.P., Naghshtabrizi P., Xu Y. A Survey of Recent Results in Networked
Control Systems // Proc. IEEE. 2007. V. 95 (1). P. 138-162.
4. Zhang X.-M., Han Q.-L., Yu X. Survey on Recent Advances in Networked Control
Systems // IEEE Trans. Ind. Inf. 2016. V. 12. P. 1740-1752.
5. Lee T., Wu Z.-G., Park J. Synchronization of a Complex Dynamical Network with
Coupling Time-Varying Delays via Sampled-Data Control // Appl. Math. Comput.
2012. V. 219 (3). P. 1354-1366.
6. Fridman E., Seuret A., Richard J.-P. Robust Sampled-Data Stabilization of Linear
Systems: An Input Delay Approach // Automatica. 2004. V. 40. P. 1441-1446.
7. Fridman E. A Refined Input Delay Approach to Sampled-Data Control // Automat-
ica. 2010. V. 46. P. 421-427.
118
8.
Naghshtabrizi P., Hespanha J., Teel A. On the Robust Stability and Stabilization of
Sampled-Data Systems: A Hybrid System Approach. // Proc. 45th IEEE Conf. on
Decision and Control, San Diego, CA, USA, 13-15 December 2006. P. 4873-4878.
9.
Naghshtabrizi P., Hespanha J.P, Teel A.R. Exponential Stability of Impulsive Sys-
tems with Application to Uncertain Sampled-Data Systems // Syst. Control Lett.
2008. V. 57. P. 378-385.
10.
Suh Y. Stability and Stabilization of Nonuniform Sampling Systems // Automatica.
2008. V. 44. P. 3222-3226.
11.
Fujioka H. A Discrete-time Approach to Stability Analysis of Systems with Aperi-
odic Sample-and-hold Devices // IEEE Trans. Automat. Control. 2009. V. 54 (10).
P. 2440-2445.
12.
Oishi Y., Fujioka H. Stability and Stabilization of Aperiodic Sampled-Data Con-
trol Systems Using Robust Linear Matrix Inequalities // Automatica. 2010. V. 46.
P. 1327-1333.
13.
Chen W.-H., Zheng W.X. Input-to-State Stability for Networked Control Systems
via an Improved Impulsive System Approach // Automatica. 2011. V. 47. P. 789-796.
14.
Seuret A. A Novel Stability Analysis of Linear Systems under Asynchronous Sam-
pling // Automatica. 2012. V. 48. P. 177-182.
15.
Zhang C.-K., Jiang L., He Y., Wu H., Wu M. Stability Analysis for Control Sys-
tems with Aperiodically Sampled Data Using an Augmented Lyapunov Functional
Method // IET Control Theory Appl. 2012. No. 7. P. 1219-1226.
16.
Seuret A., Peet M.M. Stability Analysis of Sampled-Data Systems Using Sum of
Squares // IEEE Trans. Automat. Control. 2013. V. 58 (6). P. 1620-1625.
17.
Briat C. Convex Conditions for Robust Stability Analysis and Stabilization of Linear
Aperiodic Impulsive and Sampled-Data Systems under Dwell-Time Constraints //
Automatica. 2013. V. 49. P. 3449-3457.
18.
Seuret A., Briat C. Stability Analysis of Uncertain Sampled-Data Systems with
Incremental Delay Using Looped Functionals // Automatica. 2015. V. 55. P. 274-278.
19.
Omran H., Hetel L., Petreczky M., Richard J.P., Lamnabhi-Lagarrigue F. Stability
Analysis of Some Classes of Input-Affine Nonlinear Systems with Aperiodic Sampled-
Data Control // Automatica. 2016. V. 70. P. 266-274.
20.
Jiang X., Yin Z., Wu J. Stability Analysis of Linear Systems Under Time-Varying
Samplings by a Non-Standard Discretization Method. // Electronics. 2018. V. 7 (10).
P. 1-11.
21.
Xiao S.-P., Lian H., Teo K., Zeng H.-B., Zhang X.-H. A New Lyapunov Functional
Approach to Sampled-Data Synchronization Control for Delayed Neural Networks //
J. Franklin Inst. 2018. P. 8857-8873.
22.
Park J.M., Park P.G. An Improved Stability Criterion for Linear Systems with
Multi-Rate Sampled Data // Nonlinear Analysis: Hybrid Systems. 2020. V. 38.
P. 100947.
23.
Sevim U., Goren-Sumer L. Singular Value Assignment for Nonuniformly Sampled
Systems: Stabilization and Control. arXiv:1706.00967v2 [math.DS] 29 Jun 2020.
24.
Khargonekar P.P., Sivashankar N. H2 optimal Control for Sampled-Data Systems //
Syst. Control Lett. 1991. V. 17. No. 6. P. 425-436.
25.
Hu L.S., Lam J., Cao Y.Y., Shao H.H. An LMI Approach to Robust H2 Sampled-
Data Control for Linear Uncertain Systems // IEEE Trans. Syst., Man and Cyber-
netics, Part B: Cybernetics. 2003. V. 33. No. 1. P. 149-155.
26.
Kim J.H., Hagiwara T. Extensive Theoretical/Numerical Comparative Studies on
H2 and Generalized H2 Norms in Sampled-Data Systems // Int. J. Control. 2017.
V. 90. No. 11. P. 2538-2553.
119
27.
Kim J.H., Hagiwara T. Upper/Lower Bounds of Generalized H2 Norms in Sampled-
Data Systems with Convergence Rate Analysis and Discretization Viewpoint // Syst.
Control Lett. 2017. V. 107. P. 28-35.
28.
Бирюков Р.С. Обобщенное H2-управление линейным непрерывно-дискретным
объектом на конечном горизонте // АиТ. 2020. № 8. С. 40-53.
Birukov R.S. Generalized H2-optimal Control of Continuous-Discrete Linear Plant
on a Finite Horizont // Autom. Remote Control. 2020. V. 81. No. 8. P. 1394-1404.
29.
Geromel J.C., Colaneri P., Bolzern P. Differential Linear Matrix Inequality in Op-
timal Sampled-Data Control // Automatica. 2019. V. 100. P. 289-298.
30.
Holicki T., Carsten W., Scherer C.W. Output Feedback Synthesis for a Class of
Aperiodic Impulsive Systems. arXiv:1910.03486v3 [math.OC] 21 Jun 2020.
31.
Rios H., Hetel L., Efimov D. Robust Output-feedback Control for Uncertain Linear
Sampled-Data Systems: A 2D Impulsive System Approach // Nonlinear Analysis:
Hybrid Systems, 2019. P. 177-201.
32.
Amato F., Ambrosino R., Ariola M., Cosentino C., De Tommasi G. Finite Time
Stability and Control. London: Springer-Verlag, 2014.
33.
Amato F., De Tommasi G., Pironti A. Finite-time Stability: an Input-output Ap-
proach. N.Y.: Wiley, 2018.
34.
Маликов А.И. Оценивание состояния и стабилизация непрерывных систем с
неопределенными нелинейностями и возмущениями // АиТ. 2016. № 5. С. 19-36.
Malikov A.I. State Estimation and Stabilization of Continuous Systems with Uncer-
tain Nonlinearities and Disturbances // Autom. Remote Control. 2016. V. 77. No. 5.
P. 764-778.
35.
Маликов А.И. Оценивание состояния и стабилизация дискретных систем с
неопределенными нелинейностями и возмущениями // АиT. 2019. № 11. С. 59-82.
Malikov A.I. State Estimation and Stabilization of Discrete-time Systems with Un-
certain Nonlinearities and Disturbances // Autom. Remote Control. 2019. V. 80.
No. 11. P. 1976-1995.
36.
Маликов А.И., Дубакина Д.И. Численные способы решения задач оптимизации
с дифференциальными линейными матричными неравенствами // Изв. ВУЗов.
Математика. 2020. № 4. С. 74-86.
Malikov A.I., Dubakina D.I. Numerical Methods for Solving Optimization Problems
with Differential Linear Matrix Inequalities // Izv. Vyssh. Uchebn. Zaved. Mat. 2020.
No. 4. P. 74-86.
37.
Маликов А.И. Синтез наблюдателей состояния по результатам измерений для
нелинейных липшицевых систем с неопределенными возмущениями //АиT.
2017. № 5. С. 16-35.
Malikov A.I. State Observer Synthesis by Measurement Results for Nonlinear Lips-
chitz Systems with Uncertain Disturbances // Autom. Remote Control. 2017. V. 78.
No. 5. P. 782-797.
38.
Васильев В.П. Методы оптимизации. М.: Факториал Пресс, 2002.
Статья представлена к публикации членом редколлегии А.И. Матасовым.
Поступила в редакцию 11.09.2020
После доработки 21.11.2020
Принята к публикации 08.12.2020
120