Автоматика и телемеханика, № 4, 2021

П.А. ГУЩИН, канд. техн. наук (guschin.p@mail.ru)

(Институт проблем машиноведения РАН, Санкт-Петербург),

УПРАВЛЕНИЕ ДИНАМИЧЕСКИМИ ОБЪЕКТАМИ

С ГАРАНТИЕЙ НАХОЖДЕНИЯ РЕГУЛИРУЕМОГО СИГНАЛА

В ЗАДАННОМ МНОЖЕСТВЕ¹

Предложен метод управления динамическими системами, позволяю-

щий гарантировать нахождение выходного сигнала объекта в заданном

множестве в любой момент времени. Для решения задачи используется

специальная замена координат, позволяющая свести исходную задачу с

ограничениями к задаче исследования на устойчивость по вход-состоянию

новой расширенной системы без ограничений. Приведены примеры заме-

ны координат и синтезированы алгоритмы управления линейными объ-

ектами и системами с секторной нелинейностью при наличии параметри-

ческой неопределенности и возмущений. Полученные результаты сопро-

вождаются моделированием, иллюстрирующим эффективность предло-

женного метода и подтверждающим теоретические выводы.

Ключевые слова: динамическая система, замена координат, устойчивость,

управление.

DOI: 10.31857/S000523102104005X

1. Введение

Задача управления объектами с обеспечением желаемого качества пере-

ходных процессов по регулируемой переменной является одной из основ-

ных задач теории автоматического управления. В условиях определенности

параметров модели объекта существует ряд классических методов: методы

управления с заданным расположением собственных чисел замкнутой систе-

мы, методы управления с обеспечением желаемых частотных характеристик

замкнутой системы, методы оптимального управления и т.д., см., напри-

мер, [1-4]. Вопрос улучшения оценки сверху для отклонения регулируемой

переменной в линейных параметрически определенных системах с ненулевы-

ми начальными условиями до сих пор остается актуальным [5-7].

Для управления в условиях параметрической неопределенности и возму-

щений можно выделить методы адаптивного и робастного управления, где

качество регулирования задается эталонным сигналом, см., например, [8-10].

¹ Результаты разделов 3-5 получены при поддержке гранта Российского научного

фонда (проект № 18-79-10104) в Институте проблем машиноведения РАН. Результаты

раздела 6 получены при поддержке гранта Президента Российской Федерации (грант

№ МД-1054.2020.8) в Институте проблем машиноведения РАН.

121

Однако методы [8-10] не гарантируют заданного отклонения регулируемого

сигнала от эталонного в переходном режиме. Если начальные условия объ-

екта неизвестны, то в начальный момент времени данные отклонения могут

быть произвольно большими. Методы [8-10] гарантируют только заданное от-

клонение регулируемой переменной от эталонного сигнала в установившемся

режиме.

Метод [11] позволяет гарантировать нахождение фазовых траекторий си-

стемы в некотором наименьшем эллипсоиде в переходном и установившемся

режимах. Однако данный эллипсоид остается одним и тем же в любой момент

времени, что может давать грубое качество регулирования в переходном и в

установившемся режимах.

В [12] рассмотрено применение адаптивного управления с обеспечением

регулируемой переменной в заданных множествах, которые могут быть раз-

ными для переходного и установившегося режимов. Данные множества за-

даются последовательностью прямоугольников, где высота каждого прямо-

угольника соответствует желаемому максимальному отклонению выходной

переменной объекта от положения равновесия, а длина прямоугольника

желаемому времени нахождения выходной переменной объекта в соответ-

ствующем прямоугольнике. Однако прямоугольные области в [12] достаточно

грубые и алгоритм применим только для объектов со скалярными входными

и выходными сигналами.

В отличие от [12] в [13] предложен метод управления с гарантией нахож-

дения регулируемой переменной в заданном криволинейном множестве для

объектов с векторными входными и выходными сигналами. Однако реализа-

ция данного метода требует знания знака и множества начальных условий

объекта, а полученные верхние и нижние оценки переходных процессов до-

статочно грубые в том смысле, что определяются одной функцией с разными

знаками. Причем верхние и нижние оценки должны асимптотически сходить-

ся к некоторым константам. В настоящее время результат [13] имеет большое

количество обобщений на разного рода системы, см. например, [14-16], но

все вышеперечисленные особенности метода [13] остаются справедливыми и

в [14-16].

Настоящая статья сфокусирована на получении нового метода управления

с обеспечением регулируемой переменной в заданном множестве. В отличие

от [13] целевое множество не будет зависеть от знака значений начальных

условий, а требуется только знание множества начальных значений объекта

управления. По сравнению с [12, 13] конфигурация заданного множества мо-

жет задаваться произвольными ограниченными непрерывно-дифференцируе-

мыми функциями, для которых не требуется асимптотическая сходимость.

В результате полученный метод позволит существенно расширить класс ре-

шаемых задач в смысле качества переходных процессов в отличие от [12, 13].

Статья организована следующим образом. В разделе 2 приведен класс ис-

следуемых объектов и поставлена цель управления в виде принадлежности

выходного сигнала объекта заданному множеству. Раздел 3 содержит основ-

ной результат, где предложена специальная замена координат, которая поз-

воляет свести исходную задачу с ограничениями к задаче исследования на

122

устойчивость по вход-состоянию новой расширенной динамической системы

без ограничений. Также в разделе 3 приведены примеры такой замены ко-

ординат. Возможность использования предложенного метода продемонстри-

рована в дальнейших разделах для некоторых видов систем. Так, в разде-

ле 4 предложен алгоритм управления по состоянию линейными объектами с

известными параметрами и неизвестным внешним ограниченным возмуще-

нием. Раздел 5 содержит синтез закона управления, который не зависит от

параметров объекта, где сам объект описывается динамической системой с

секторной нелинейностью и возмущениями. Раздел 6 иллюстрирует приме-

нимость предложенной схемы для объекта управления с произвольной отно-

сительной степенью. Разделы 4-6 сопровождаются моделированием, иллюст-

рирующим эффективность предложенного метода, и анализом полученных

результатов.

2. Постановка задачи

Рассмотрим динамическую систему

x = F(x,u,t),

(1)

y = h(x),

где t ≥ 0, x ∈ Rⁿ

вектор состояния, u ∈ R^m

сигнал управления, y =

= col {y₁, . . . , y_v} выходной сигнал, вектор-функция F определена для всех

x, u и t, кусочно-непрерывна и ограничена по t, h(x) непрерывно-диффе-

ренцируемая функция по x. Объект управления (1) управляемый и наблю-

даемый для любого x ∈ Rⁿ.

Требуется разработать закон управления, который обеспечит нахождение

выходного сигнала объекта y(t) в следующем множестве

{

}

(2)

Y = y ∈ R^v : g_i(t) < y_i(t) < g_i(t), i = 1,...,v

для любых t ≥ 0,

где g_i(t) и g_i(t)

ограниченные функции вместе со своими первыми произ-

водными по времени. Данные функции выбираются разработчиком исходя

из требований работы системы. Например, при управлении электрическим

генератором [17] требуется поддержание частоты w(t) и выходного напряже-

ния V (t) в заданных пределах: w < w(t) < w и V < V (t) < V .

3. Метод решения. Основной результат

Введем замену выходной переменной y в виде

(3)

y(t) = Φ(ε(t), t),

где ε(t) ∈ R^v непрерывно-дифференцируемая вектор-функция по t, функ-

ция Φ(ε, t) = col {Φ₁(ε, t), . . . , Φ_v(ε, t)} удовлетворяет следующим условиям:

(а) g_i(t) < Φ_i(ε, t) < g_i(t), i = 1, . . . , v для любых t ≥ 0 и ε ∈ R^v;

123

2,0

S(e) =--

+ 1

|e| + 1

1,5

1,5e^e + 0,5

S(e) =

---------

e^e + 1

1,0

0,5

-5

1,5e^ε + 0,5

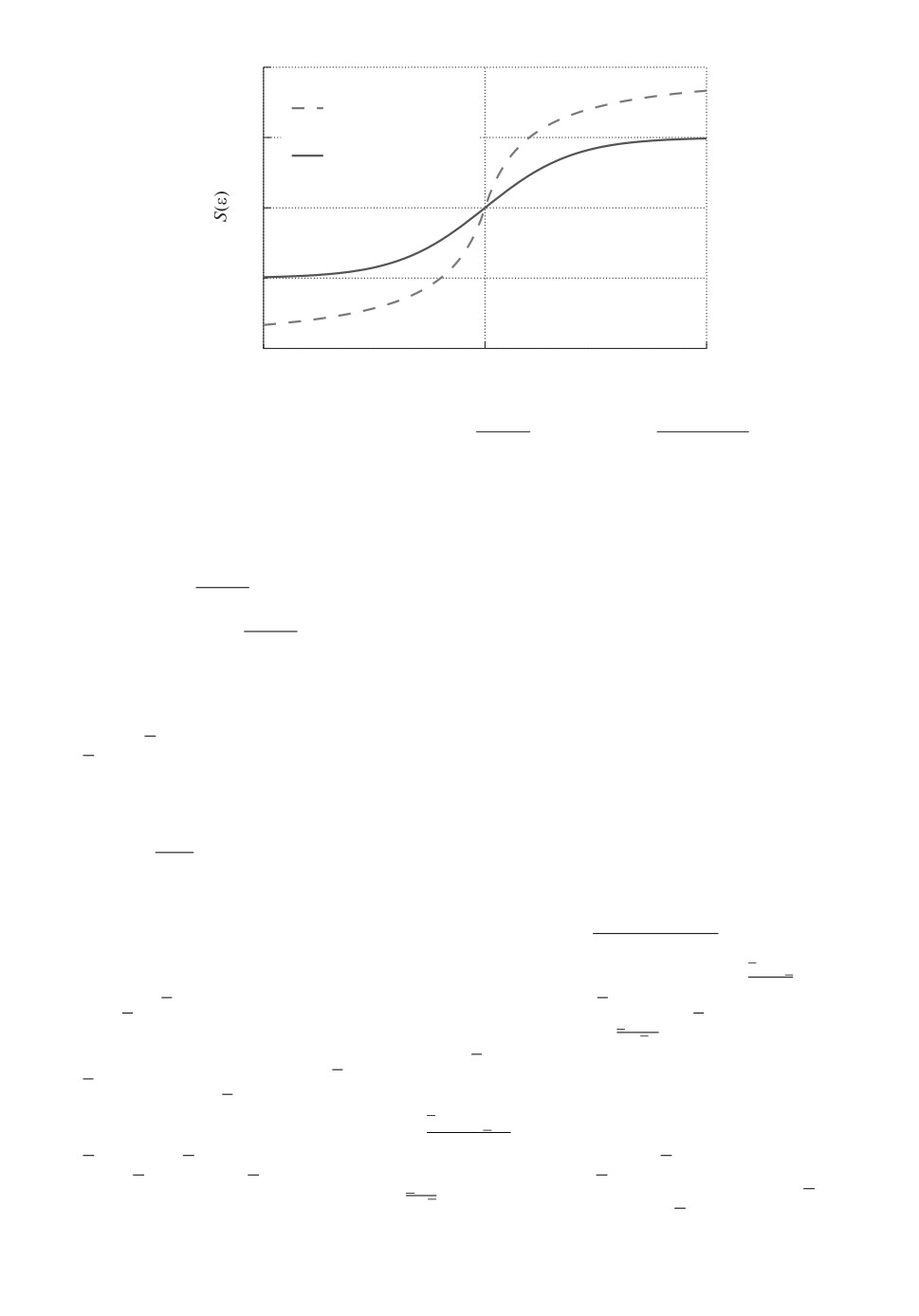
Рис. 1. Примеры функции S(ε) =

+ 1 и S(ε) =

1 + |ε|

e^ε + 1

(б) существует обратное отображение ε = Φ^-1(y, t) для любых y ∈ Y и

t ≥ 0;

(в) функция Φ(ε, t) непрерывно-дифференцируемая по ε и t, а также

(

)

∂Φ(ε,t)

det

= 0 для любых y ∈ Y и t ≥ 0;

∂ε

(г) функция^{∂Φ(ε,t)∂t} ограничена по t ≥ 0 для любых ε ∈ R^v.

Приведем четыре примера функции Φ(ε, t), где в примерах 1 и 2 верхняя

и нижняя границы множества будут зависеть от одной функции g(t), а в

примерах 3 и 4 границы множества будут заданы независимыми функциями

g(t) и g(t).

Пример 1. Пусть Φ(ε,t) = g(t)S(ε), где в данном случае функция S(ε) ∈

∈ R определяет замену координат, а функция g(t) ∈ R задает качество пере-

ходных процессов. Дополнительно, g(t) = 0 и ġ(t) ограниченные функции,

S(ε) =^ε1+|ε| + r (см. пример функции S(ε) на рис. 1 для r = 1). Так как из (3)

y(t) = g(t)S(ε), то переменная y(t) содержится в множестве (r - 1)g(t) <

< y(t) < (r+1)g(t) при g(t) > 0 или в множестве (r+1)g(t) < y(t) < (r-1)g(t)

y-rg

при g(t) < 0. Обратное отображение имеет вид ε =

g-(y-rg) sign(ε)

Пример 2. Зададим в примере 1 функцию S(ε) в виде S(ε) = reε+reε+1 , где

0 < r < r (см. пример функции S(ε) на рис. 1 для r = 1,5 и r = 0,5). Тогда

из (3) обратное преобразование выглядит как ε = ln^rg-yy-rg . Переменная y(t)

находится в множестве rg(t) < y(t) < rg(t) при g(t) > 0 или в множестве

rg(t) < y(t) < rg(t) при g(t) < 0.

, где Φ(ε, t) ∈ R, ε ∈ R, функции

g(t), g(t), ġ(t)и ġ(t) ограниченные для любого t и g(t) < g(t). С учетом (3)

обратное преобразование ε = ln^g-yy-g будет выполнено при g(t) < y(t) < g(t)

для любых t.

124

Пример 4. Зададим Φ(ε,t) в виде

{

g(t) + 0,5(g(t) - g(t))e^-ε, ε ≥ 0,

Φ(ε, t) =

g(t) + 0,5(g(t) - g(t))e^ε,

ε < 0,

где остальные функции, как и в примере 3. Принимая во внимание (3), об-

ратное преобразование примет вид



g-g



ln

0≤y<g,

2(g - y)

ε=

2(y - g



ln

g < y < 0.

g-g

Значит, g(t) < y(t) < g(t) для любых t.

Теперь определим динамику по переменной ε для исследования устойчиво-

сти замкнутой системы. Для этого найдем по(ную п)изводную по времени

∂Φ(ε,t)

от (3) в виде y =^{∂Φ(ε,t)∂ε} ε +^{∂Φ(ε,t)∂t} . Так как det

= 0 (см. условие (в)),

∂ε

то перепишем последнее равенство как

)

)-1 (

(∂Φ(ε,t)

∂Φ(ε,t)

(4)

ε=

∂ε

∂t

Выражение (4) содержит сигнал управления u(t), так как y =^∂h(x)∂x F (x, u, t)

из (1). Теперь сформулируем основной результат статьи.

Теорема 1. Пусть для преобразования (3) выполнены условия (а)-(г).

Если существует такой закон управления u, что решения (4) ограничены,

то y(t) ∈ Y_α ⊂ Y. Если при выбранном законе управления решения (4) неогра-

ниченны, то y(t) ∈ Y.

Доказательство. Пусть выбран закон управления так, что решения

уравнения (4) ограничены, т.е. |ε(t)| < N при любом t, где 0 < N < ∞. Тогда

в силу преобразования (3) и условия (а) следует, что

{

}

y∈Y_α =

y ∈ R^v : M_i(t) < y_i(t) < M_i(t), i = 1,...,v

где M_i(t) = inf {Φ_i(ε, t)} и M_i(t) = sup {Φ_i(ε, t)} для любых t ≥ 0. Посколь-

|ε|<N

ку (3) является взаимно однозначным отображением, то M_i(t) < g_i(t) и

M_i(t) > g_i(t), значит, Y_α ⊂ Y. Пусть теперь закон управления не обеспечи-

вает ограниченность решения (4), т.е. ε(t) ∈ R^v. Тогда в силу преобразова-

ния (3), а также условий (а) и (2) имеем, что y ∈ Y, где g_i(t) = inf

{Φ_i(ε, t)}

ε∈R^v

и g_i(t) = sup{Φ_i(ε,t)}. Теорема 1 доказана.

ε∈R^v

Теорема 1 позволяет перейти от задачи управления (1) с ограничения-

ми (2) к задаче управления (4) без ограничений. Следующие разделы демон-

стрируют возможность применения предложенного метода для некоторых

типов задач.

125

4. Управление линейным объектом с известными параметрами и

измеряемым вектором состояния в условиях возмущений

Пусть объект управления описывается следующим линейным дифферен-

циальным уравнением:

x = Ax + Bu + Df,

(5)

y = Lx.

Здесь x ∈ Rⁿ, u ∈ R, y ∈ R, f ∈ R^l неизвестное ограниченное возмущение,

матрицы A ∈ R^n×n, B ∈ Rⁿ и L ∈ R^1×n известны, а матрица D ∈ R^n×l неиз-

вестна. Пара (A, B) управляема и пара (L, A) наблюдаема. Объект (5) имеет

относительную степень, равную единице (LB = 0 [10]).

Сформулируем результат, который содержит ¾простейший¿ закон управ-

ления в смысле ¾удобства¿ анализа замкнутой системы на устойчивость.

Теорема 2. Предположим, что для преобразования (3) выполнены усло-

вия (а)-(г),^{∂Φ(ε,t)∂ε} > 0 для любых ε и t, а также существует вектор T ∈ Rⁿ

такой, что матрица A - B(LB)^-1LA - T L гурвицева. Тогда для любого

K > 0 закон управления

(6)

u = -(LB)^-1

[LAx + Kε]

обеспечивает выполнение целевого условия (2).

Замечание 1. Отметим, что модель (5) с гурвицевой матрицей A-

-B(LB)^-1LA - TL может описывать ряд технических систем. Например,

дистилляционная колонна [18], [4, с. 569], где сигнал управления расход

орошения, а регулируемый сигнал состав легких фракций верха колонны;

летательный аппарат [4, с. 565] на различных высотах и числах Маха, где u

управление рулями высоты, y вертикальное ускорение; электрический дви-

гатель постоянного тока [19], где сигнал управления входное напряжение,

выходной сигнал угловая скорость, и т.д.

Доказательство. Принимая во внимание преобразование (3) и урав-

нение объекта (5), перепишем выражение (4) в виде

)_-1

(∂Φ(ε,t)

(7)

ε=

(LAx + LBu + ψ) ,

∂ε

где ψ = LDf -^{∂Φ(ε,t)∂t}

ограниченная функция по ε и t. Подставив закон

управления (6) в первое уравнение (5) и уравнение (7), а также добавив в по-

лученном выражении слагаемое T Φ(ε, t) - T Lx(t) = 0 (которое справедливо

в силу (3) и второго уравнения (5)), получим

(8)

x = (A - B(LB)^-1LA - TL)x - KB(LB)^-1

ε + Df + TΦ(ε,t),

)_-1

(∂Φ(ε,t)

(9)

ε=

[-Kε + ψ] .

∂ε

126

Введение вектора T позволяет рассматривать неустойчивые объекты (5). Ис-

следуем уравнение (9) на устойчивость по вход-состоянию. Для этого выберем

функцию Ляпунова вида V = 0,5ε². Подставив (9) в условие

)_-1

(∂Φ(ε,t)

(∂Φ(ε,t))-1

+ 2αV

- βψ²

≤ 0, где α > 0 и β > 0,

∂ε

[

][

]

-K + α 0,5

получим -(K - α)ε² + εψ - βψ² ≤ 0 или в виде [ε ψ]

≤ 0.

0,5

-β ψ

[

]

-K + α 0,5

Последнее неравенство будет выполнено, если матрица

будет

0,5

-β

отрицательно определенной, что равносильно выполнению условий K > α и

(K - α)β > 0,25. Поскольку K заданное число, то для него всегда найдутся

α и β такие, что данные условия будут выполнены. Значит, сигнал ε(t) бу-

дет ограниченным. Если матрица A - B(LB)^-1LA - T L гурвицева, то в силу

ограниченности функций ε(t), Φ(ε, t) и f(t) сигнал x(t) будет ограниченным.

Значит, закон управления u, определенный в (6), будет ограничен. Тогда из

теоремы 1 следует, что целевое условие (2) будет выполнено. Теорема 2 до-

казана.

Пример 5. Продемонстрируем теперь качество переходных процессов на

примере управления объектом, параметры которого заданы в виде

[

]

[

]

[

]

[

]

x(0) =

(10)

(

)

d(t)

f (t) = 0,1 + sin(3t) + sat

0,3

где sat(·) функция насыщения, сигнал d(t) смоделирован в Matlab Simulink

с помощью блока “Band-Limited White Noise” с мощностью шума 0,1 и вре-

менем выборки 0,1. Требуется обеспечить принадлежность выходного сиг-

нала y(t) множеству rg(t) < y(t) < rg(t), где r = 0,8 и r = 1, а функция g(t)

будет определена ниже.

Матрица A - B(LB)^-1LA - T L гурвицева, например, при любом T =

= [T₁ T₂]^T, где T₁ > 0 и T₂ > 0. Зададим K = 1 в (6). Определим функ-

цию Φ(ε, t), как в примере 2, задав g(t) в виде

(11)

g(t) = (g₀ - g_∞)e^-kt + g_∞.

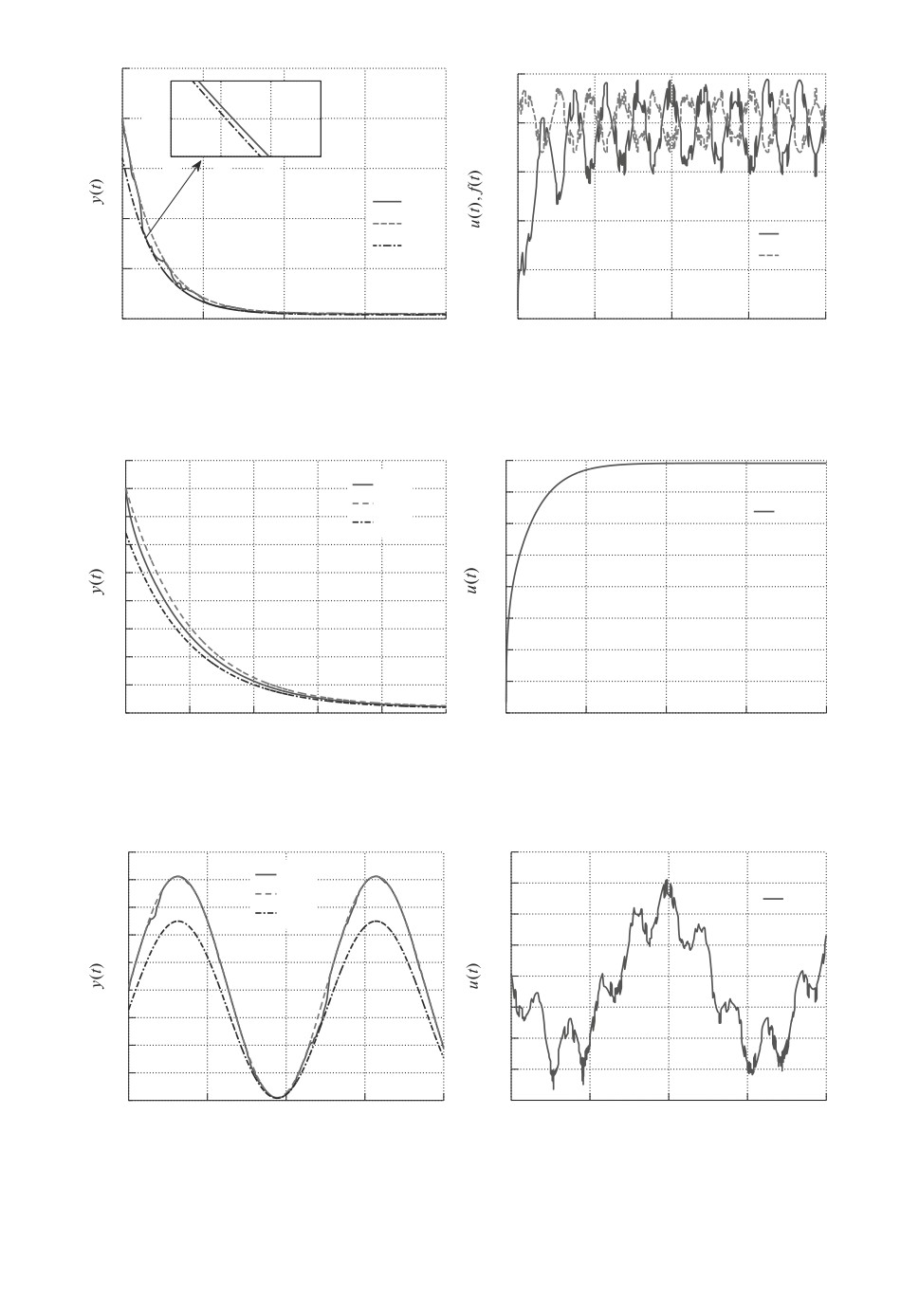
Здесь g₀ = y(0) + 0,01, g_∞ = 0,1 и k = 0,5. На рис. 2 приведены результаты

переходных процессов по y(t), u(t) и f(t). Колебания сигнала управления

на рис. 2 вызваны наличием возмущения f. Причем, как видно из рис. 2

(справа), после 3 с с начала работы системы амплитуда колебаний сигнала

управления соизмерима с величиной возмущения. На рис. 3 представлены

результаты моделирования при отсутствии возмущения (f = 0). Таким обра-

зом, для стабилизации объекта в заданном множестве не требуется большого

значения управляющего сигнала.

127

Отметим, что на рис. 2 (и в последующих примерах) выходные сигналы не

достигают границ желаемого множества, что согласуется с теоретическими

выводами и что читатель может легко проверить путем моделирования. Для

иллюстрации сказанного на рис. 2 приведен фрагмент рисунка в увеличенном

масштабе.

В отличие от [13] и рис. 2, 3, где границы целевого множества сходятся к

некторым числам, теперь обеспечим принадлежность выходного сигнала y(t)

ранее заданному множеству 0,8g(t) < y(t) < g(t), где функция g(t) не имеет

предела:

(12)

g(t) = g₀ sin(kt) + g₀ + g_∞.

На рис. 4 приведены результаты моделирования по y(t) и u(t).

Из рис. 2-4 видно, что при r > 0 и r > 0 значение y = 0 недостижимо в си-

лу преобразования координат из примера 2. Нулевое значение y может быть

достигнуто только при r < 0 и r > 0 (с учетом g(t) > 0). Однако в таком слу-

чае заданное множество будет более грубым по сравнению с множествами из

рис. 2-4, поскольку нижняя граница желаемого множества будет находиться

в отрицательной области значений y. Данная проблема будет преодолена в

последующих примерах при использовании замены координат из примера 3.

5. Управление объектом по выходу с секторной нелинейностью

в условиях возмущений

Рассмотрим объект управления вида

x = Ax + Gϕ(x) + Bu + Df,

(13)

y = Lx.

Здесь x ∈ Rⁿ, u ∈ R^m, y ∈ R^v (v ≤ m), f ∈ R^l неизвестная ограниченная

функция, A ∈ R^n×n, G ∈ R^n×k, B ∈ R^n×m, D ∈ R^n×l и L ∈ R^v×n извест-

ные матрицы, неизвестная нелинейность ϕ(x) ∈ R^k удовлетворяет условию

|ϕ(x)| ≤ C|x|, C > 0 известная константа. Пара (A, B) управляема и па-

ра (L, A) наблюдаема. Объект (13) имеет строгую относительную степень

(от англ. ¾strict relative degree¿), равную единице (т.е. L_iB_j = 0, где L_i

i-я строка матрицы L и B_j i-я строка матрицы B, i, j = 1, . . . , n [20, 21]).

Требуется разработать алгоритм управления, обеспечивающий выполнение

целевого условия (2).

Зададим закон управления в виде

(14)

u=K₁y+K₂

ε,

где K₁ ∈ R^m×v и K₂ ∈ R^m×v выбираются разработчиком. В частности, K₁

и K₂ можно выбирать при условии, что матрицы A + BK₁L и LBK₂ гур-

вицевы. Принимая во внимание (3) и (14), а также добавив в полученном

выражении слагаемые T₁Lx - T₁Φ(ε, t) = 0 и T₂Lx - T₂Φ(ε, t) = 0 (которые

129

справедливы в силу (3) и второго уравнения (13)), перепишем (4) и (13) в

виде

x = (A + BK₁L + T₁L)x + BK₂ε + Gϕ(x) + Df - T₁Φ(ε,t),

)_-1 [

(∂Φ(ε,t)

ε=

LBK₂ε + (LA + LBK₁L + T₂L)x +

(15)

∂ε

]

∂Φ(ε,t)

+ LGϕ(x) + LDf -

- T₂Φ(ε,t)

∂t

Здесь T₁ ∈ R^n×v, T₂ ∈ R^v×v, I единичная матрица. Введение матриц T₁ и

T₂ позволяет исследовать неустойчивые объекты (13).

Из второго уравнения (15) следует, что условие v ≤ m (т.е. dim ε ≤ dim u)

и единичная строгая относительная степень (13) позволит закону управле-

ния (14) обеспечить ограниченность ε(t). Введем новые обозначения

{

}

∂Φ(ε,t)

x_e = col {x, ε}, f_e = col f,

, Φ(ε,t)

∂t





A+BK₁L+T₁L

BK₂





A_e(ε,t) =

(∂Φ(ε,t))-1

(∂Φ(ε,t))-1

,

(LA + LBK₁L + T₂L)

LBK₂

∂ε





(16)





Ge(ε, t) =

(∂Φ(ε,t))-1

,

∂ε





-T₁





D_e(ε,t) =

(∂Φ(ε,t))-1

(∂Φ(ε,t))-1



LD -

T₂

∂ε

и перепишем (15) в виде

(17)

x_e = A_e(ε,t)x_e + G_e(ε,t)ϕ(x) + D_e(ε,t)f_e.

Теорема 3. Предположим, что для преобразования (3) выполнены усло-

вия (а)-(г),^{∂Φ(ε,t)∂ε} > 0 для любых ε и t. Пусть для заданных α > 0, K₁, K₂,

T₁ и T₂ существует коэффициент β > 0 и матрица P = P^T > 0 такие, что

выполнено матричное неравенство





A_e(ε,t)^TP + PA_e(ε,t) + αP + C²E^TE PG_e(ε,t) PD_e(ε, t)

(18)



∗

-1



≤ 0.

∗

-βI

Здесь

“ ∗” определяет симметричный блок симметричной матрицы,

E = [I 0]. Тогда закон управления (14) обеспечивает выполнение целевого

условия (2).

130

Доказательство. Для анализа устойчивости (17) зададим функцию

Ляпунова в виде V = x^TeP x_e, где P = P^T > 0. С учетом (17), подставив вы-

ражение для V в неравенство

(19)

+ αV - βfTe f_e

≤ 0,

получим

[

]

x^Te

A_e(ε,t)^TP + PA_e(ε,t) + αP

x_e +

(20)

+ 2xTe P G_e(ε, t)ϕ(x) + 2xTe P D_e(ε, t)f_e - βfTe f_e ≤ 0.

Введем новый вектор z = col {x_e, ϕ(x), f_e} и перепишем неравенство (20)

в виде





A_e(ε,t)^TP + PA_e(ε,t) + αP PG_e(ε,t) PD_e(ε,t)



(21)

z^T 

∗

z ≤ 0.

∗

-βI

По условию задачи ϕ²(x) ≤ C²x^TeE^TEx_e. Перепишем данное условие в ви-

де





C²E^TE



(22)

z^T 

∗

-1 0z ≥ 0.

∗

Согласно S-процедуре неравенства (21) и (22) будут одновременно выполне-

ны, если будет выполнено неравенство (18). Значит, из условия (19) функ-

ция x_e(t) ограничена, следовательно, сигналы x(t) и ε(t) ограничены. Тогда

закон управления (14) будет ограниченным. В силу теоремы 1 цель управле-

ния (3) будет выполнена. Теорема 3 доказана.

Пример 6. Продемонстрируем качество управления на объекте с двумя

входами и двумя выходами со следующими параметрами:













A= 0

,B= 11,D= 1,

0,1

-2 -3





[

]

,ϕ(x)=sin(x),

G= 0

0,1

возмущение f(t) определено в (10).

[

]

Параметры регулятора (14) зададим в виде K₁ = 0,01

, K₂ =

−1 -1

[

]

[

]

[

]

1,5

-1,75

. Дополнительно выберем T₁ =

и T₂ =

−1

131

Пусть Φ(ε, t) = diag {Φ₁(ε₁, t), Φ₂(ε₂, t)}, где Φ_i определены, как в приме-

ре 3, т.е.

ε_i + g

g_i(t)e

(t)

Φ_i(ε_i,t) =

i = 1,2.

e^εi + 1

Значит, Φ(ε, t) > 0 для любых ε и t. Тогда

∂Φ_i(ε_i,t)

eεi(g_i(t) - g

(t))

> 0,

∂ε_i

(e^εi + 1)²

(

)_-1

∂Φ_i(ε_i,t)

так как g_i(t) > g

(t). Дополнительно,

→ +∞ при ε → +∞ и

∂ε_i

(

)_-1 

∂Φ_i(ε_i,t)



наименьшее значение



> 0. Согласно [22], если

∂ε_i

g_i(t)-g

(t)

ε=0

выполнено линейное матричное неравенство в вершинах политопа, то и

внутри политопа линейное матричное неравенство будет выполнено. В рас-

сматриваемом случае при каждом фиксированном∂Φi(εi,t) матричное нера-_∂ε

венство (18) является линейным. Однако политоп не замкнутый, так как

(

)_-1

∂Φ_i(ε_i,t)

→ +∞ при ε → +∞. Численное моделирование при увеличении

∂ε_i

(

)_-1

∂Φ_i(ε_i,t)

показало, что собственные числа матрицы P сходятся к некото-

∂ε_i

рым положительным значениям. В вершинах

матричное неравен-

g_i(t)-g

(t)

ство (18) также выполнено.

Зададим параметры функции Φ(ε, t) в виде

g₁(t) = (g₀ - g₁)e^-kt + g₁,

g₂(t) = (g₀ - g₂)cos(kt) + g₄,

(23)

g₁(t) = (g₀ - g₂)e^-kt + g₃,

g₂(t) = cos(kt) + g₅,

√

где g₀ =

y^T(0)y(0) + 0,01, g₁ = 0,1, g₂ = 2, g₃ = -0,2, g₄ = g₀ - 0,1, g₅ = 0,8

и k = 0,5.

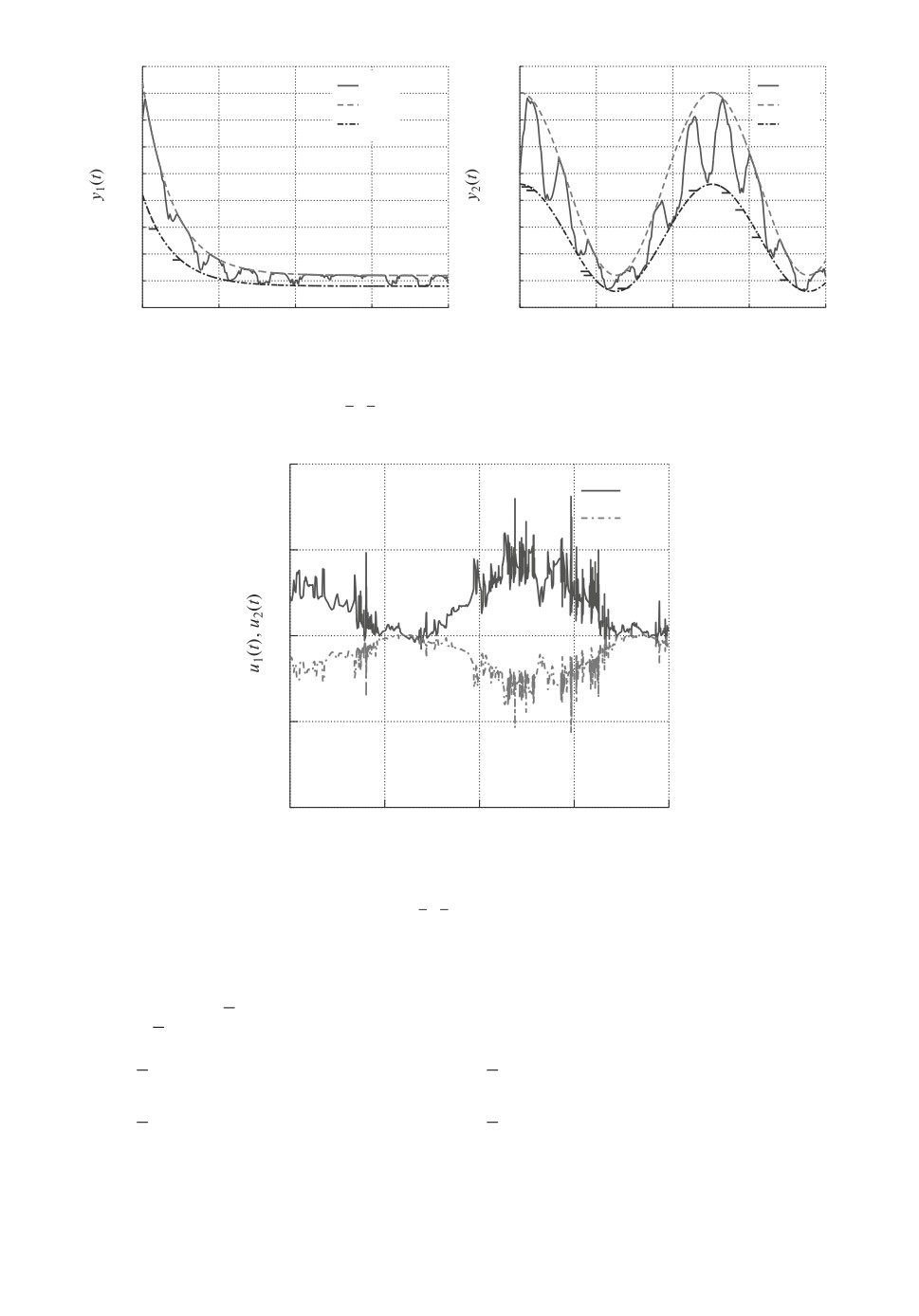
На рис. 5, 6 приведены результаты переходных процессов по y₁(t) , y₂(t) и

u(t) = col {u₁(t), u₂(t)} при x(0) = col {⁵³ ,²³ , -1}.

Исследования робастности замкнутой системы с законом управления u =

= K₁y + K₂ε по отношению к параметрам объекта (5) путем моделирования

показали, что замкнутая система соханяет устчивостьи обеспечива вы-

полнение цели управления при A = 0

 и G= 0

,где

a₁

a₂

a₃

g_ϕ1

g_ϕ2

g_ϕ3

a₁ ∈ [-5;0,1], a₂ ∈ [-5;-2], a₃ ∈ [-5;-3], b∈ [0,5;10] и g_ϕ1 ∈ [-3;3], g_ϕ2 ∈ [-3;3]

и gϕ3 ∈[-3;3].

Исследование робастности по отношению к начальным значениям объекта

показало следующее. Согласно условиям (3) и (a) начальные значения y_i(0)

должны быть согласованы с неравенствами g_i(0) < y_i(0) < g_i(0), i = 1, 2. Од-

нако начальные условия могут иметь существенную неопределенность, и ес-

ли они оказались на границе заданной области или за ее пределами, то закон

132

4,0

y₁(t)

y₂(t)

3,5

1(t)

2(t)

3,0

g₁(t)

3,0

g₂(t)

2,5

2,0

1,5

1,0

0,5

-0,5

Рис. 5. Переходные процессы по y₁(t) и y₂(t) для функции Φ(ε, t) с парамет-

рами (23) при x(0) = col {⁵³ ,²³ , -1}.

u₁(t)

u₂(t)

-10

-20

Рис. 6. Переходные процессы по u(t) = col {u₁(t), u₂(t)} для функции Φ(ε, t) с

параметрами (23) при x(0) = col {⁵³ ,²³ , -1}.

управления будет неработоспособным в силу того, что обратная функция не

существует при таких значениях (см. пример 3). Для решения данной про-

блемы g_i(t) и g_i(t) в (23) можно задавать c ¾запасом¿ в начальный момент

времени, например в виде

g₁(t)=(g₀ -g₁)e^-kt +g₁ +g₆e-k0t, g₂(t)=(g₀ -g₂)cos(kt)+g₄ +g₆e-k0t,

(24)

g₁(t)=(g₀ -g₂)e^-kt +g₃ -g₆e-k0t, g₂(t)=cos(kt)+g₅ -g₆e-k0t,

где g₆ > 0 и k₀ > 0. Причем для покрытия большой области начальных зна-

чений с обеспечением нахождения выходных переменных объекта в множе-

стве (23) необходимо g₆ и k₀ выбирать достаточно большими числами. Ре-

зультаты моделирования по выходным сигналам y₁(t) и y₂(t) представлены

133

y₁(t)

y₂(t)

1(t)

2(t)

g₁(t)

g₂(t)

-1

-2

-20

Рис. 7. Переходные процессы по y₁(t) и y₂(t) для функции Φ(ε, t) с парамет-

рами (24) при x(0) = col {¹⁰³ , -⁵³ , -1}.

y₁(t) : g = 1

y₂(t) : g = 1

y₁(t) : g = 10

y₂(t) : g = 10

y₁(t) : g = 100

y₂(t) : g = 100

-1

Рис. 8. Переходные процессы по y₁(t) и y₂(t) при γ = 1, γ = 10 и γ = 100 при

x(0) = col {1 1 0}.

на рис. 7 при g₆ = 3 и k₀ = 2 (значения g₆ и k₀ не выбраны достаточно больши-

ми числами для иллюстрации результата на рисунке) в (24), а также x(0) =

= col {¹⁰³ , -⁵³ , -1}.

Анализ результатов моделирования также показал, что если:

1) время переходного процесса по y(t) соизмеримо со временем переходного

процесса по ε(t);

2) функция |f(t)| принимает большие значения,

то переходные процессы по y могут протекать почти на границах g(t) и

g(t). Из выражения ε = ln^g-yy-g следует, что величина |ε(t)| может принимать

большие значения, а значит, возрастет вычислительная нагрузка на систему

управления. В результате увеличивается работа Matlab/Simulink, а иногда

Matlab/Simulink выдает ошибку в вычислениях. Для предотвращения дан-

ной проблемы рекомендуется выбирать настраиваемые параметры так, что-

бы переходные процессы по ε(t) протекали быстрее, чем по y(t). Это также

134

позволит повысить робастность по отношению к параметрической неопреде-

ленности в объекте и влиянию возмущения f. Так, из рис. 8 видно, что при

увеличении γ > 0 в законе управления u = K₁y + γK₂ε переходные процессы

по y отдаляются от границ g(t) и g(t).

6. Динамический регулятор для объектов со скалярным входным и

выходным сигналами и произвольной относительной степенью

Результаты разделов 4 и 5 справедливы при относительной степени объек-

та, не превышающей единицы. Хорошо известно, что управление объектами

со скалярными входными и выходными сигналами и с произвольной отно-

сительной степенью в условиях параметрической неопределенности является

сложной задачей относительно обоснования работоспособности алгоритма,

см., например, [23, 24]. Поскольку основная цель статьи обеспечение целе-

вого условия (2) с применением нового преобразования (3), то в настоящем

разделе ради простоты выводов рассматривается объект со скалярными вход-

ным и выходным сигналами и с известными параметрами, но с произвольной

относительной степенью. В численном примере будет продемонстрирована

работоспособность алгоритма по отношению к параметрической неопреде-

ленности.

Пусть объект управления описывается уравнением

(25)

Q(p)y(t) = R(p)u(t) + f(t).

Здесь y ∈ R выходной сигнал, u ∈ R сигнал управления, f ∈ R ограни-

ченное возмущение, Q(p) и R(p) линейные дифференциальные операторы с

известными коэффициентами, Q(λ) гурвицевый полином, λ комплексная

переменная, p =^ddt оператор дифференцирования. Требуется разработать

алгоритм управления, обеспечивающий выполнение целевого условия (2).

Подставив y(t) из (25) в (4), получим

)

(∂Φ(ε,t))-1 (pR(p)

pD(p)

∂Φ(ε,t)

(26)

ε=

u(t) +

f (t) -

∂ε

Q(p)

∂t

Закон управления u = -^Q(p)pR(p) Kε, где K > 0, позволил бы свести уравне-

(

)_-1 (

)

∂Φ(ε,t)

ние (26) к виду ε =

-Kε +^pD(p)Q(p)f(t) -^∂Φ(ε,t)

, решение которо-

∂ε

∂t

го было бы ограниченным при^{∂Φ(ε,t)∂ε} > 0. Обозначим относительную степень

объекта (25) через ρ = deg Q(p) - deg R(p). Тогда приведенный закон управ-

ления не реализуем при ρ > 1 из-за требований к наличию ρ - 1 производных

от сигнала ε(t). Поэтому зададим закон управления в виде

Q(p)

(27)

u=-

Kε.

R(p)[p(µp + 1)^ρ-1 + aµ]

Здесь достаточно малое число µ > 0 и коэффициент a > 0 выбираются из

условия гурвицевости полинома λ(µλ + 1)^ρ-1 + aµ. Учитывая (27), перепи-

135

шем (25) и (26) как

D(p)

(28)

y(t) = -K

ε(t) +

f (t),

p(µp + 1)^ρ-1 + aµ

Q(p)

)_-1 (

)

(∂Φ(ε,t)

p - p(µp + 1)^ρ-1

- aµ

(29)

ε=

-Kε - K

ε+φ

∂ε

p(µp + 1)^ρ-1 + aµ

где φ =^pD(p)Q(p) f(t) -^{∂Φ(ε,t)∂t}

ограниченная функция.

Теорема 4. Пусть для преобразования (3) выполнены условия (а)-(г),

∂Φ(ε,t)

> 0 для любых ε и t. Тогда существуют коэффициенты µ₀ и a такие,

∂ε

что при µ < µ₀ полином λ(µλ + 1)^ρ-1 + aµ гурвицев и закон управления (27)

обеспечивает выполнение целевого условия (2).

Доказательство. Рассмотрим уравнение (29), которое является регу-

лярно возмущенным при малом параметре µ. Перепишем (29) при µ = 0 в

виде

)_-1

(∂Φ(ε,t)

ε=

(30)

(-Kε + φ) .

∂ε

Для анализа устойчивости (30) зададим функцию Ляпунова как V = 0,5ε².

(

)_-1

(

)_-1

∂Φ(ε,t)

Проверим условиеV + 2αV

-β

φ² < 0, где α > 0 и β > 0.

∂ε

Подставив V и (30) в последнее неравенство, получим -(K - α)ε² + εφ -

-βφ² < 0. Данное неравенство будет выполнено при выполнении условия

K > α и (K - α)β > 0,25 (см. доказательство теоремы 2). Поскольку α и β

произвольные числа, то всегда можно обеспечить выполнение данных усло-

вий при заданном K. Следовательно, решение уравнения (30) предельно

ограниченное. Значит, согласно теореме 2.2 из [25] существует µ₀ такое, что

при µ < µ₀ выполнено условие |ε(t) - ε(t)| < O(µ), где lim_µ→0 O(µ) = 0. В ре-

зультате при µ < µ₀ решение уравнения (29) также предельно ограничен-

ное. Тогда в силу ограниченности f(t) и ε(t), а также гурвицевости Q(λ)

и λ(µλ + 1)^ρ-1 + aµ сигнал y(t) будет ограниченным из (28). Значит, закон

управления u будет ограничен из (27). Тогда из теоремы 1 следует, что целе-

вое условие (3) будет выполнено. Теорема 4 доказана.

Пример 7. Пусть параметры объекта управления (25) определены в виде

Q(p) = (p + 1)³, R(p) = 1 и возмущение f(t) задано в (10).

Параметры регулятора (14) зададим в виде K = 3, µ = 0,01 и a = 0,1. То-

гда закон управления (27) будет выглядеть как

3(p + 1)

(31)

u=-

ε.

p(0,01p + 1)² + 10^-3

{

2 cos(t) + 0,2,

0 ≤ t ≤ 2π,

2 cos(t) - 0,2,

0 ≤ t ≤ 2π,

g(t) =

2,2,

t > 2π;

1,8,

t > 2π.

136

y(t)

(t)

g(t)

-1

-2

-3

Рис. 9. Переходные процессы по y(t).

500

u(t)

-5

-500

Рис. 10. График сигнала u(t).

Результаты моделирования показали, что закон управления (31) обеспечива-

ет цель управления (2). Моделирование также показало, что замкнутая си-

стема робастна по отношению к параметрическим неопределенностям. Так,

на рис. 9, 10 приведены результаты переходных процессов по y(t) и u(t) при

y(0) = 2, py(0) = p²y(0) = 1, неустойчивом полиноме Q(λ) = (λ - 1)³ и регу-

ляторе (31). Начальные всплески сигнала управления обусловлены рассогла-

сованием начальных условий в регуляторе и в объекте управления. Однако

после отработки регулятором рассогласования начальных условий дальней-

ший график управления принимает ¾небольшие¿ значения, которые соответ-

ствуют выходному сигналу в заданном множестве.

7. Заключение

Разработан новый метод управления динамическими системами, позво-

ляющий гарантировать нахождение выходной переменной объекта управле-

137

ния в заданном множестве. Для решения задачи предложена специальная

замена координат, позволяющая свести исходную задачу с ограничениями к

задаче исследования на устойчивость по вход-состоянию новой расширенной

динамической системы без ограничений. Приведены примеры замены коорди-

нат и алгоритмы управления линейными объектами и динамическими систе-

мами с секторной нелинейностью. Полученные результаты сопровождаются

моделированием, иллюстрирующим эффективность предложенного метода и

подтверждающими аналитические выводы.

Отметим, что основной результат, сформулированный в теореме 1, спра-

ведлив для объектов с произвольной размерностью входных и выходных сиг-

налов. Однако решение, полученное в разделе 5, не позволяет управлять объ-

ектами с размерностью выходного сигнала больше, чем размерность сигнала

управления. Для управления такими объектами существует ряд решений, см.,

например, [26, 27] и список литературы в них. Применение методов [26, 27]

и теоремы 1 может быть отдельным исследованием по управлению объек-

тами с размерностью выходного сигнала больше, чем размерность сигнала

управления.

СПИСОК ЛИТЕРАТУРЫ

Первозванский А.А. Курс теории автоматического управления. М.: Наука, 1986.

Теория автоматического управления: Учеб. для вузов по спец. “Автоматика и

телемеханика”. В 2-х ч. Под ред. А.А. Воронова. М.: Высш. шк., 1986.

Поляк Б.Т., Хлебников М.В., Рапопорт Л.Б. Математическая теория автома-

тического управления, учебное пособие. М.: Ленанд, 2019.

Афанасьев В.Н., Колмановский В.Б., Носов В.Р. Математическая теория кон-

струирования систем управления. М.: Высш. шк., 2003.

Баландин Д.В., Коган М.М. Метод функций Ляпунова в синтезе законов управ-

ления при интегральном и фазовых ограничениях // Дифференц. уравнения.

2009. Т. 45. № 5. С. 655-664.

Whidborne J.F., Amar N. Computing the Maximum Transient Energy Growth //

BIT Numerical Math. 2011. V. 51. No. 2. P. 447-557.

Поляк Б.Т., Тремба А.А., Хлебников М.В., Щербаков П.С., Смирнов Г.В. Боль-

шие отклонения в линейных системах при ненулевых начальных условиях //

АиТ. 2015. № 6. С. 18-41.

Polyak B.T., Tremba A.A., Khlebnikov M.V., Shcherbakov P.S., Smirnov G.V. Large

Deviations in Linear Control Systems with Nonzero Initial Conditions // Autom.

Remote Control. 2015. V. 76. No. 6. P. 957-976.

Tao G. Adaptive Control Design and Analysis. John Wiley & Sons, 2003.

Андриевский Б.Р., Бобцов А.А., Фрадков А.Л. Методы анализа и синтеза нели-

нейных систем управления. Ижевск: Ин-т компьют. исслед., 2018.

10.

Мирошник И.В., Никифоров В.О., Фрадков А.Л. Нелинейное и адаптивное

управление сложными динамическими системами. СПб.: Наука, 2000.

11.

Поляк Б.Т., Хлебников М.В., Щербаков П.С. Управление линейными система-

ми при внешних возмущениях: Техника линейных матричных неравенств. М.:

Ленанд, 2014.

12.

Miller D.E., Davison E.J. An Adaptive Controller Which Provides an Arbitrarily

Good Transient and Steady-State Response // IEEE Trans. Autom. Control. 1991.

V. 36. No. 1. P. 68-81.

138

13.

Bechlioulis C.P., Rovithakis G.A. Robust Adaptive Control of Feedback Linearizable

MIMO Nonlinear Systems With Prescribed Performance // IEEE Trans. Autom.

Control. 2008. V. 53. No. 9. P. 2090-2099.

14.

Bu X., He G., Wei D. A new prescribed performance control approach for uncertain

nonlinear dynamic systems via back-stepping // J. Franklin Institut. 2018. V. 355.

No. 17. P. 8510-8536.

15.

Yin Z., Luo J., Wei C., Yin Z., Luo J., We C. Robust Prescribed Performance

Control for Euler-Lagrange Systems with Practically Finite-Time Stability // Eur.

J. Control. 2020. V. 52. P. 1-10.

16.

Du P., Zhou Q., Liang H., Du P., Zhou Q., Liang H. Neural adaptive prescribed

performance control for interconnected nonlinear systems with output dead zone //

Int. J. Robust and Nonlinear Control. 2019. https://doi.org/10.1002/rnc.4802

17.

Павлов Г.М., Меркурьев Г.В. Автоматика энергосистем. СПб.: Издание Центра

подготовки кадров РАО “ЕЭС России”, 2001.

18.

Буяхияуй К., Григорьев Л.И., Лаауад Ф., Хелласи А. Оптимальное нечеткое

управление для снижения энергопотребления в дистилляционных колоннах //

АиТ. 2005. № 2. С. 36-45.

Bouyahiaoui C., Grigoriev L.I., Laaouad F., Khelassi A. Optimal Fuzzy Control to

Reduce Energy Consumption in Distillation Columns // Autom. Remote Control.

2005. V. 66. No. 2. P. 200-208.

19.

Ruderman M., Krettek J., Hoffmann F., Bertram T. Optimal State Space Control of

DC Motor // Proc. 17th World Congress The International Federation of Automatic

Control, Seoul, Korea, 2008. P. 5796-5801.

20.

Isidori A. Nonlinear Control Systems. Springer, 1995.

21.

Фомичев В.В., Ильин А.В., Коровин С.К. Методы робастного обращения дина-

мических систем. М.: Физматлит, 2009.

22.

Fridman E. A refined input delay approach to sampled-data control // Automatica.

2010. V. 46. P. 421-427.

23.

Бобцов А.А. Алгоритм робастного управления в задаче слежения за эталонным

сигналом // АиТ. 2003. № 6. С. 104-113.

Bobtsov A.A. A Robust Control Algorithm for Tracking the Reference Signal //

Autom. Remote Control. 2003. V. 64. No. 6. P. 943-950.

24.

Цыкунов А.М. Алгоритмы робастного управления с компенсацией ограниченных

возмущений // АиТ. 2007. № 7. С. 103-115.

Tsykunov A.M. Robust Control Algorithms with Compensation of Bounded Pertur-

bations // Autom. Remote Control. 2007. V. 68. No. 7. P. 1213-1224.

25.

Васильева А.Б., Бутузов В.Ф. Асимптотические разложения решений сингу-

лярно возмущенных уравнений. М.: Наука, 1973.

26.

Liu X., Gu G., Zhou K. Robust stabilization of MIMO nonlinear systems by back-

stepping // Automatica. 1999. V. 35. P. 987-992.

27.

Estrada A., Fridman L., Iriarte R. Combined backstepping and HOSM control design

for a class of nonlinear MIMO systems // Int. J. Robust and Nonlinear Control. 2017.

V. 27. No. 4. P. 566-581.

Статья представлена к публикации членом редколлегии П.С. Щербаковым.

Поступила в редакцию 23.03.2020

После доработки 17.06.2020

Принята к публикации 09.07.2020

139