Автоматика и телемеханика, № 4, 2021

Интеллектуальные системы управления,

анализ данных

(Институт системного анализа Федерального исследовательского центра

“Информатика и управление” РАН, Москва;

Национальный исследовательский университет

“Высшая школа экономики”, Москва;

Московский физико-технический институт),

В.Ю. ПОЛИЩУК, канд. техн. наук (liquid_metal@mail.ru)

(Институт мониторинга климатических и экологических систем СО РАН;

Национальный исследовательский Томский политехнический университет),

Ю.С. ПОПКОВ, д-р техн. наук (popkov@isa.ru)

(Институт системного анализа Федерального исследовательского центра

“Информатика и управление” РАН, Москва;

Брауде Колледж университета Хайфы, Кармиель, Израиль;

Институт проблем управления им. В.А. Трапезникова РАН, Москва),

Ю.М. ПОЛИЩУК, д-р физ.-мат. наук (yupolishchuk@gmail.com),

А.В. МЕЛЬНИКОВ, д-р техн. наук (melnikovav@uriit.ru),

Е.С. СОКОЛ (eugen137@gmail.com)

(Югорский НИИ информационных технологий, Ханты-Мансийск)

МЕТОД ЭНТРОПИЙНО-РАНДОМИЗИРОВАННОГО

ВОССТАНОВЛЕНИЯ ПРОПУЩЕННЫХ ДАННЫХ¹

Статья посвящена проблеме восстановления пропусков в коллекциях

данных для задач машинного обучения. Предложен новый рандомизиро-

ванный метод восстановления пропущенных данных, основанный на тех-

нологии энтропийно-робастного оценивания и генерации ансамблей слу-

чайных величин. Предложенный метод схож с использованием вспомога-

тельной регрессии для восстановления пропущенных значений, но в от-

личие от последней в случае энтропийного оценивания не накладываются

дополнительные ограничения на функцию правдоподобия ошибок в вы-

борке и допустимы малые объемы данных, что становится крайне акту-

альным в задачах, когда объем данных для обучения ограничен, а про-

пуски встречаются не систематически. Предложенный метод применяет-

ся для восстановления пропущенных данных о площадях термокарстовых

озер арктической зоны РФ, измеряемых по спутниковым снимкам.

Ключевые слова: восстановление пропусков, энтропийное оценивание,

рандомизированное машинное обучение, термокарстовые озера, Аркти-

ка.

DOI: 10.31857/S0005231021040061

¹ Работа выполнена при финансовой поддержке Российского фонда фундаментальных

исследований (проекты №№ 19-07-00282, 20-07-00223). Работа выполнена в рамках госбюд-

жетной темы.

140

1. Введение

В прикладных задачах анализа данных нередко возникает необходимость

работы с выборками данных, содержащих пропущенные значения. Пропус-

ки в данных могут быть следствием самых различных причин, от отказа

респондентов отвечать на вопросы анкеты до технических сбоев измеритель-

ных датчиков или программного обеспечения. Наличие пропусков в данных

приводит к искажению результатов анализа и, следовательно, требует до-

полнительной обработки. Кроме того, большинство современных алгоритмов

машинного обучения не поддерживают наличие пропусков в данных, что при-

водит к необходимости восстановления пропущенных значений.

Проблеме неполноты данных посвящено множество публикаций по стати-

стике [1-4], и в различных сферах прикладного анализа данных, например

в медицине [5], образовании [6] и др. [7, 8]. В частности, в [5] приводится

один из наиболее полных обзоров современных методов анализа в условиях

наличия пропусков в данных, книга содержит подробную теорию и примеры

реализации и тестирования методов для клинических данных.

Различают три механизма появления пропусков в данных [2]:

• Полностью случайные пропуски (Missing Completely At Random,

MCAR) механизм, при котором вероятность появления пропущен-

ных значений одинакова для всех объектов выборки. Например, если

на предприятии не измеряют характеристики некоторых случайно вы-

бранных устройств;

• Случайные пропуски (Missing At Random, MAR) механизм, при ко-

тором вероятность появления пропусков может быть выявлена на ос-

нове имеющейся в выборке информации. Например, если не измеря-

ются характеристики устройств с определенными критериями по весу,

габаритам и пр.;

• Неслучайные пропуски (Missing Not At Random, MNAR) в этом слу-

чае наличие пропусков в данных является дополнительной характери-

стикой объекта и не может игнорироваться при анализе. Например,

если оказывается невозможным измерить характеристики уже вышед-

ших из строя устройств.

Существует два основных подхода к анализу неполных данных. Пер-

вый подход подразумевает отбрасывание пропусков, полное или частичное

(Listwise/pairwise deletion), в зависимости от требований алгоритма анали-

за [9]. Это наиболее простой в реализации способ, но применяемый исклю-

чительно для полностью случайных (MCAR) пропусков, когда исключение

одного или нескольких объектов не приводит к нарушению репрезентатив-

ности выборки. Кроме того, данный способ не подойдет для выборок малых

объемов и выборок с высокой долей пропусков.

Второй подход предполагает восстановление пропущенных значений, т.е.

вставку (импутирование) некоторых значений на места пропусков. Согласно

классификации, приведенной в [1], различают простые и сложные методы

импутирования. К простым относятся замещения пропусков специальными

значениями, например нулями, средними или медианными значениями по

признаку, модой или новой категорией для дискретных и категориальных

141

признаков [10]. Такие способы восстановления пропущенных значений наи-

более распространены на практике благодаря своей простоте реализации, но

подходят преимущественно для случайных пропусков (MAR). Также в эту

группу методов входит использование вспомогательной регрессии для при-

знаков, метода ближайших соседей (HotDeck [11], kNN [12]) и метода k-сред-

них (k-means [13]) для поиска подходящего значения на место пропуска.

К сложным методам импутирования относятся итеративные алгоритмы,

предполагающие оптимизацию некоторого функционала, отражающего точ-

ность расчета подставляемых значений. Причем оптимизация функционала

может проводиться как глобально, т.е. по всем объектам выборки (метод

Бартлетта [4], ЕМ-оценивание [14, 15] и Resampling [4]), так и локально, когда

для подбора пропущенного значения используются только близкие объекты

(алгоритмы Zet [16, 17] и ZetBraid [18]).

Так или иначе, любые алгоритмы импутирования предполагают исполь-

зование имеющейся информации для заполнения пропусков, что приводит к

искажению статистических характеристик выборки в сторону характеристик

только полных наблюдений. Кроме того, замещение пропусков вносит в вы-

борку определенную долю искусственных данных, которые в свою очередь

приводят к смещению значимости получаемых на их основе результатов [19].

Для борьбы с данными недостатками в публикациях [20-22] был пред-

ложен метод множественного импутирования, предполагающий замещение

пропусков несколькими возможными значениями, с каждым из которых бу-

дет формироваться отдельный массив данных для обучения и анализа. Мно-

жественное импутирование призвано отразить присущую реальным данным

неопределенность при подстановке пропущенных значений. Поэтому резуль-

таты анализа получившихся массивов данных приводятся в терминах сред-

них значений, дисперсионного разброса и доверительных интервалов. На ана-

логичной идее усреднения основаны также методы стохастической регрессии

для восстановления пропусков и популярная в последнее время технология

размножения выборки bootstrap [23].

Таким образом, существующие методы работы с пропущенными данными

различаются по качеству восстановления, сложности реализации и критери-

ям применимости. Наиболее интуитивными и простыми в реализации явля-

ются отбрасывание пропусков и импутирование специальными значениями,

более технологичными и универсальными являются поиск ближайших сосе-

дей и восстановление регрессией, а наиболее робастными оказываются сто-

хастические методы, основанные на многократном повторении и усреднении

результатов анализа.

В данной статье предложен новый метод восстановления пропущенных

данных, основанный на энтропийно-робастном оценивании и генерации ан-

самблей случайных величин [24, 25]. В результате оценивания восстанавли-

ваются плотности распределения вероятностей как для параметров модели,

так и для шумов измерений, что позволяет восстановить пропущенные зна-

чения с помощью семплирования случайных величин.

142

2. Структура процедуры рандомизированного восстановления

пропущенных данных

Рассмотрим состав и свойства информационного обеспечения задачи ма-

шинного обучения. Обучающая коллекция состоит из данных о функциони-

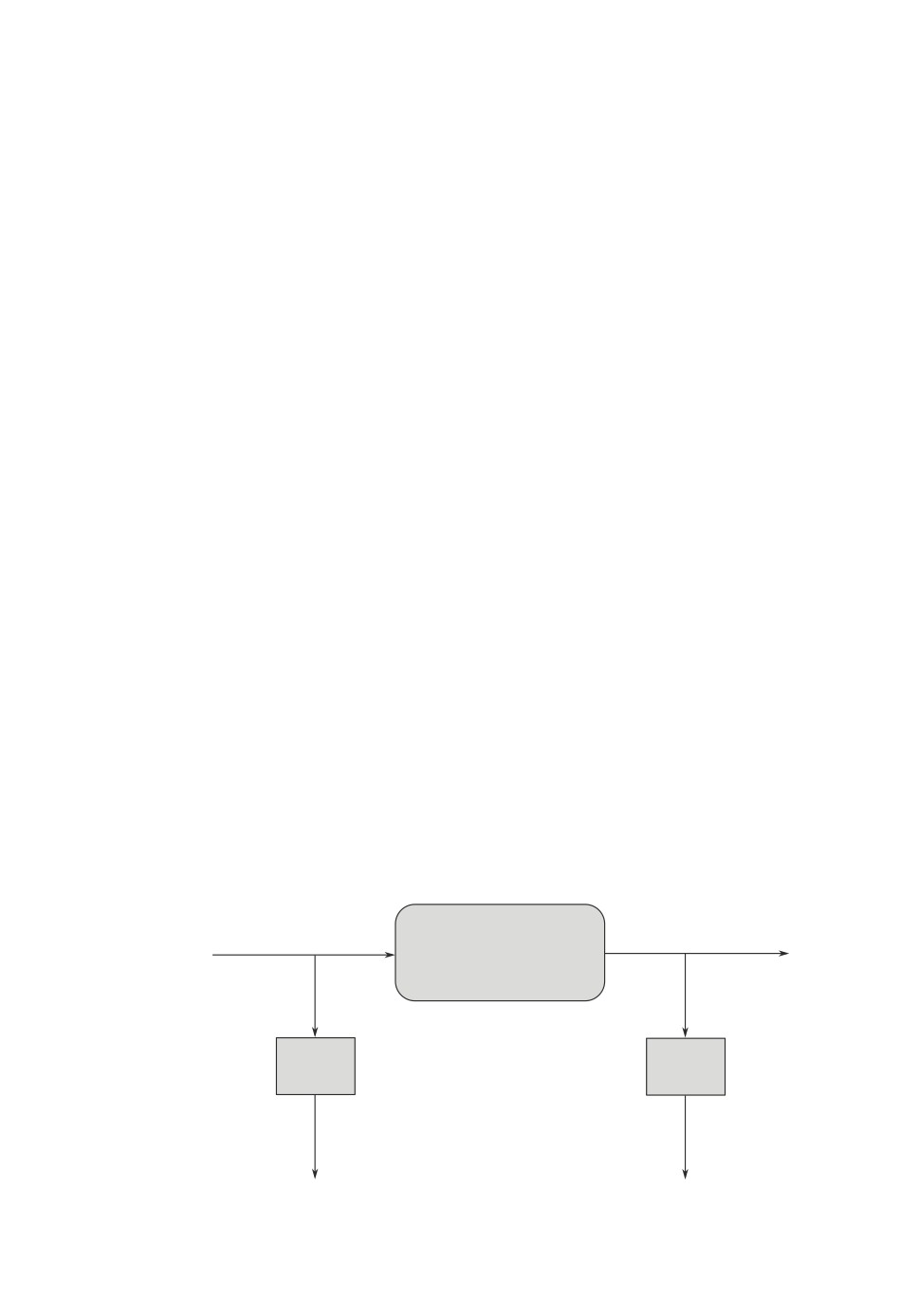
ровании исследуемого объекта О (рис. 1) и его измеренных входа x(t) ∈ R^m

и выхода y(t) ∈ Rⁿ объекта О. Переменные x(t), y(t) сопровождаются изме-

рительными ошибками η(t) ∈ R^m и ξ(t) ∈ Rⁿ соответственно. Обычно инфор-

мация о них гипотетическая. Обычно предполагается, что они в обучающей

коллекции присутствуют аддитивно:

(2.1)

x(t) = x⁰(t) + η(t);

y(t) = y⁰

(t) + ξ(t),

где x⁰(t), y⁰(t)

“чистые” переменные.

Будем полагать, что измерения входа и выхода осуществляются в одной

временной шкале t = kh с шагом h и на одинаковом временном интервале

T = [0,T]. Следовательно, реальная обучающая коллекция состоит из мат-

рицы данных о входе и выходе объекта О.

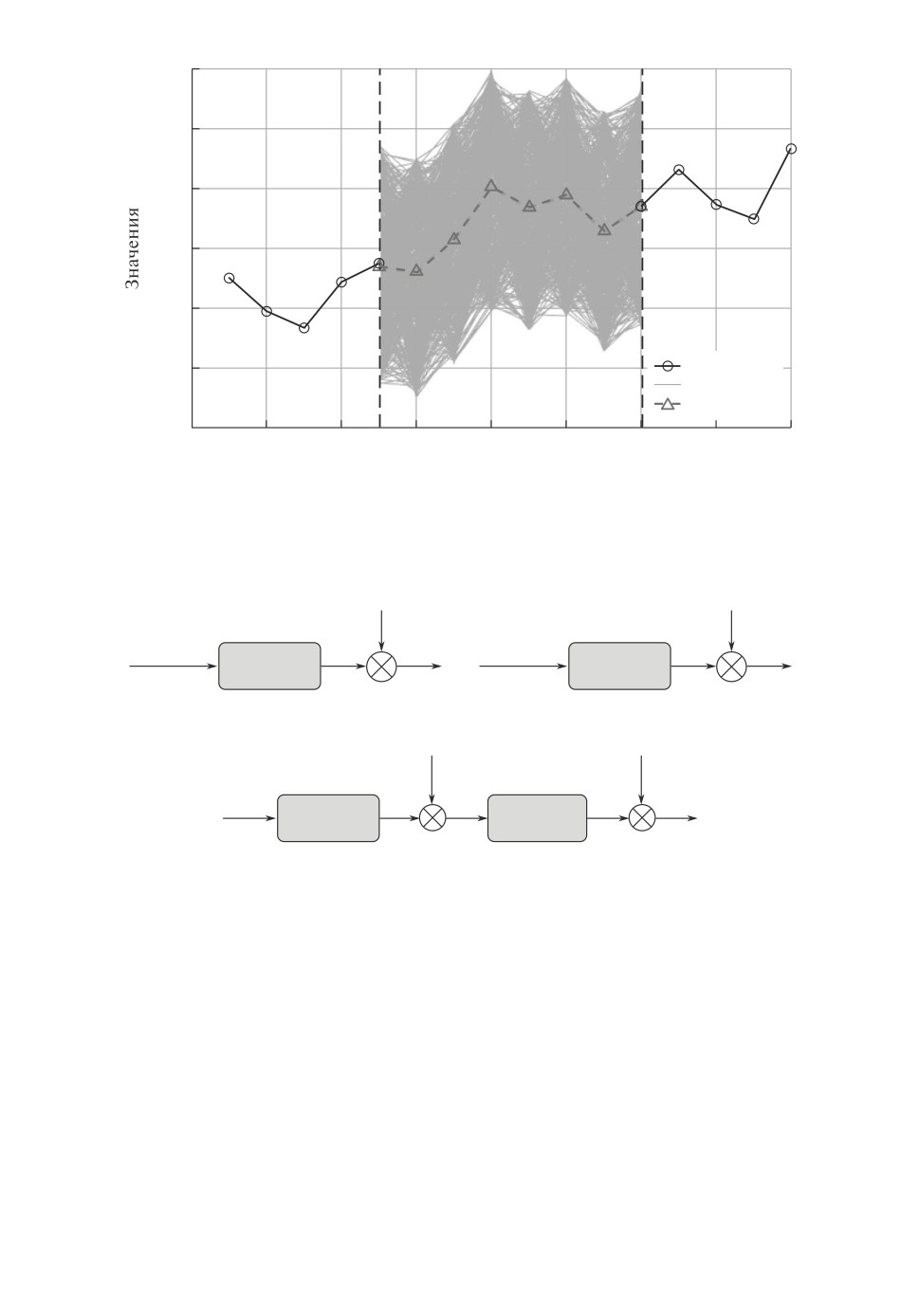
Наборы данных о входе и выходе могут иметь пропуски (рис. 2, интервал

[k^-, k⁺]). Возможны три ситуации пропусков: в выходных, входных, и в вы-

ходных и входных данных (необязательно в одни и те же моменты времени).

Основная идея рандомизированного восстановления пропущенных данных

состоит в том, чтобы пропуски заменить ансамблем пропущенных данных

(АПД) случайными значениями компонент входа и выхода (см. рис. 2),

оптимизированным с учетом имеющихся измерений. При этом используется

параметризованная рандомизированная модель (РПМ) объекта, вероятност-

ные характеристики которой плотности распределение вероятностей ее па-

раметров (ПРВ) определяются посредством MEE-оценивания (Maximum

Entropy Estimation) [26].

Генерация оптимизированных АПД осуществляется путем сэмплирования

оптимальных ПРВ [27]. Синтезированный АПД позволяет использовать его

непосредственно для решения различных задач машинного обучения, либо

определять его численные характеристики: средние, медианные, дисперсион-

Вход

Выход

Объект

Измерительное

ИУ

Устройство

Ошибки h[kh]

Ошибки x[kh]

x[kh]

y[kh]

Рис. 1. Блок-схема процедуры измерения данных об объекте.

143

0,78

0,77

0,76

0,75

0,74

Данные

0,73

АПД

Средняя

0,72

Время

Рис. 2. Пример построения ансамбля пропущенных данных (АПД).

y[kh]

x[kh]

РПМ-О

РПМ-В

x[kh]

^[kh]

x[kh]

y[kh]

h[kh]

РПМ-В

РПМ-О

^[kh]

Рис. 3. Блок-схемы моделей РПМ.

ные трубки, интерквантильные множества данных и т.д. Иллюстрация этой

идеи представлена на рис. 2.

В ситуации, когда пропуски имеют место в выходных данных, процедура

использует входные данные x[kh], РПМ-О и выходные данные с пропуска-

ми y[kh] для вычисления энтропийно-оптимальных ПРВ (рис. 3,а) и генера-

ции ансамбля Y восстановленных входных данных.

Если имеют место пропуски во входных данных, то для их восстановле-

ния используется дополнительная РПМ-В со входом в виде оптимизирован-

ной последовательности независимых случайных векторов η[kh] и входные

данные с пропусками x[kh]. Для определения ПРВ параметров и указанной

последовательности используется MEE-оценивание. Они позволяют генери-

144

ровать ансамбль E случайных векторов η[kh] и ансамбль X восстановленных

входных данных (рис. 3,б ).

И наконец, если пропуски имеют место и во входных, и в выходных дан-

ных, то сначала восстанавливаюся ансамбли E случайных векторов η[kh] и

входных данных X , которые затем используются для восстановления ансам-

блей выходных данных Y (рис. 3,в).

Совокупность методов рандомизированного восстановления пропущенных

данных будем обозначать RRMD Random Restored Missing Data.

3. Алгоритмы оптимизации АПД

1. Пропуски в выходных данных.

Пусть на дискретном интервале наблюдения τ = [0, N] имеется набор

входных данных x ∈ R^m без пропусков x[0], . . . , x[N] и набор выходных

данных y ∈ Rⁿ с пропусками y[0], . . . , y[k^- - 1], y[k⁺ + 1], . . . , y[N]. Данные

y[k^-], . . . , y[k⁺] отсутствуют.

Из набора входных данных образуем матрицу

(3.1)

X_(k-̺)

= [x[k - ̺], x[k - ̺ + 1], . . . , x[k]]

с параметром ρ < N.

Выходные данные содержат аддитивные ошибки ξ[k] ∈ Rⁿ интервального

типа:

(3.2)

ξ[k] ∈ Ξ_k = [ξ^-, ξ⁺

Вероятностные свойства ошибок характеризуются функциями ПРВ Q_k(ξ[k]),

k = 0,N, которые предполагаются непрерывно-дифференцируемыми.

В общем случае связь между входом и выходом объекта О описывается

рандомизированной параметризованной динамической моделью РДМ-О:

(

)

(3.3)

ŷ[k] = B

a,X_(k-̺)

где B нелинейный функционал со случайными параметрами a ∈ R^r интер-

вального типа:

(3.4)

a ∈ A = [a^-,a⁺

Вероятностные свойства параметров характеризуются функцией ПРВ P (a),

которая предполагается непрерывно-дифференцируемой.

Наблюдаемый выход РДМ-О

(3.5)

v[k] = ŷ[k] + ξ[k], k = 0, N .

Для определения оптимальных ПРВ воспользуемся алгоритмом рандоми-

зированного машинного обучения (РМО) [25], который в данном случае имеет

145

вид:

∫

H[P (a), Q(ξ)] = - P (a) ln P (a)da -

∫

∑

(3.6)

Q_k(ξ[k])ln Q_k

(ξ[k])dξ[k] ⇒ max,

k=0Ξ

∫

P (a)da = 1;

Q_k(ξ[k])dξ[k] = 1, k = 0,N,

Ξ_k

∫

(

)

P (a)B

a,X_(k-̺)

da + Q_k(ξ[k])ξ[k]dξ[k] = y[k],

Ξ_k

k = k^-,...,k⁺; k = 0,N.

Учитывая, что ПРВ непрерывно-дифференцируемые функции и задача

(3.6) относится к ляпуновскому классу функциональных оптимизационных

задач [28], можно получить ее аналитическое решение, параметризованное

множителями Лагранжа θ⁽⁰⁾, . . . , θk--1, θk++1, . . . , θ^(N):

[

]

∑

(

)

exp -

〈θ^(k), B

a,X_(k-̺)

〉

k=0

(3.7)

P^∗(a,θ) =

P(θ)

(

)

exp

-〈θ^(k), ξ[k]〉

Q^∗k(ξ[k],θ^(k)) =

k = k^-,...,k⁺; k = 0,N.

Q_k(θ^(k))

Здесь

[

]

∫

∑

(

)

(3.8)

P(θ) = exp

〈θ^(k), B

a,X_(k-̺)

〉

da,

k=0

∫

(

)

Q_k(θ^(k)) = exp -〈θ(k), ξ[k]〉 dξ[k],

k = k^-,...,k⁺; k = 0,N.

Ξ_k

Множители Лагранжа определяются из системы уравнений

M_k(θ)

N_k(θ^(k))

(3.9)

= y[k],

k=k^-,...,k⁺

; k = 0,N,

P(θ)

Q_k(θ^(k))

где

[

]

∫

∑

(

)

(

)

(3.10)

M_k(θ) = exp

〈θ^(k), B

a,X_(k-̺)

〉 B

a,X_(k-̺)

da,

k=0

∫

(

)

(3.11)

N_k(θ^(k)) = exp -〈θ(k), ξ[k]〉

ξ[k]dξ[k].

Ξ_k

146

2. Пропуски во входных данных.

Восстановление пропусков во входных данных представляет собой более

сложную задачу, чем то же самое для входных данных. Причина состоит

в том, что механизм происхождения входных данных и источник его воз-

буждения неизвестны. В терминах используемого здесь подхода, неизвестны

модель, которая может генерировать указанные входные данные, и возбуж-

дающий ее процесс. Все это повышает уровень неопределенности в данной

задаче, что мотивирует применение рандомизированного подхода.

Реализация его состоит в использовании последовательности независимых

случайных векторов ζ[k] ∈ R^q (k = 0, N) со специальными вероятностными

характеристиками и рандомизированной параметризованной модели, выбор

которой определяется ее степенью сложности².

Итак, рассмотрим интервал наблюдения τ = [0, N] и набор входных

данных x ∈ R^m с пропусками x[0], . . . , x[k^- - 1], x[k⁺ + 1], . . . , x[T ]. Данные

x[k^-], . . . , x[k⁺] отсутствуют.

Для восстановления пропущенных входных данных будем полагать, что

они являются результатом преобразования последовательности независимых

случайных векторов ζ[k] ∈ R^q, k ∈ τ . Будем полагать, что векторы ζ[k]

интервального типа, т.е.

(3.12)

ζ[k] ∈ Z_k = [ζ^-[k], ζ⁺

[k]],

k = 0,N.

В силу неопределенности и недостаточности знаний о процессе и его преоб-

разовании будем использовать его рандомизированную параметризованную

модель (РПМ-В)

(

)

(3.13)

x[k] = F

c, Z_(k-ρ)

где F нелинейный векторный функционал со случайными параметрами

c ∈ R^s и входом матрицей, составленной из столбцов векторов ζ[k] ∈ R^q,

с размером (q × ρ):

(3.14)

Z_(k-ρ)

= [ζ[k - ρ], ζ[k - ρ + 1], . . . , ζ[k]] .

Введем матрицу

[

]

(3.15)

Z =

Z_(-ρ),Z_(1-ρ),... ,Z_(N-ρ)

характеризующую вход РПМ-В (3.13) на интервале k = 0, N . Матрица Z -

случайная, интервального типа:

⋃

(3.16)

Z ∈ Z = Z_k = [Z^-,Z⁺

k=0

Случайные параметры модели

(3.17)

c ∈ C = [c^-,c⁺

² Возможно, потребуется перебор и тестирование разных моделей.

147

Вероятностные свойства параметров c и матрицы Z (3.15) характеризуются

функцией совместной плотности распределения вероятностей (ПРВ) W (c, Z),

которая определена на множестве

⋃

(3.18)

F =C

и п редполагается непрерывно-дифференцируемой.

Пусть имеющиеся входные данные x[k] содержат ошибки η[k] ∈ R^m интер-

вального типа:

(3.19)

η[k] ∈ E_k = [η^-, η⁺

Вероятностные свойства ошибок характеризуются функциями ПРВ G_k(η[k]),

k = 0,N, которые предполагаются непрерывно-дифференцируемыми.

Наблюдаемый выход РПМ-В

(3.20)

z[k] = x[k] + η[k], k = 0, N .

Отсюда видно, что для восстановления пропущенных входных данных ис-

пользуется похожая с РДМ-О модель, но со случайным входом ζ[k].

Воспользуемся алгоритмом РМО [25] для определения функций ПРВ

W (c, Z) и G_k(ζ[k]), k = 0, N , который в данном случае имеет вид:

∫

H[W (c, Z), G(η)] = - W (c, Z) ln W (c, Z) dc dZ-

∫

∑

(3.21)

Gk(η[k]) ln Gk(η[k])dη[k] ⇒ max,

k∈KE

∫

W (c, Z) dc dZ = 1;

Gk(η[k])dη[k] = 1,

E_k

∫

(

)

W (c, Z)F

c, Z_(k-ρ)

dc dZ + G_k(η[k])η[k]dη[k] = x[k],

E_k

k ∈ K,

где множество индексов K = 0, N не содержит значения k = k^-, . . . , k⁺.

Эта задача того же класса, что и (3.6). Ее решение имеет вид

[

]

∑

(

)

exp -

〈λ^(k), F

c, Z_(k-ρ)

〉

k∈K

(3.22)

W^∗(c,Z,λ) =

W(λ)

(

)

exp

-〈λ^(k), η[k]〉

G∗k(η[k], λ^(k)) =

G_k(λ^(k))

k ∈ K,

148

где

[

]

∫

∑

(

)

W(λ) = exp

〈λ^(k), F

c, Z_(k-ρ)

〉 dc,

k∈K

(3.23)

∫

(

)

G_k(λ^(k)) = exp

-〈λ^(k), η[k]〉 dη[k].

E_k

В этих равенствах λ^(k) вектор множителей Лагранжа, соответствующий

k-му балансовому ограничению. Он определяется из системы уравнений:

M_k(λ)

S_k(λ^(k))

(3.24)

= x[k], k = k^-, . . . , k⁺

;k ∈ K,

W(λ)

G_k(λ^(k))

где

[

]

∫

∑

(

)

(

)

M_k(λ) = exp -

〈λ^(k), F

c, Z_(k-ρ)

〉 F

c, Z_(k-ρ)

dcdZ,

^k∈K∫

(

)

(3.25)

S_k(λ^(k)) = exp -〈λ(k), η[k]〉

η[k]dη[k].

E_k

3. Пропуски во входных и выходных данных.

В этом случае описанные процедуры применяются последовательно: сна-

чала алгоритм (3.21), а затем алгоритм (3.6).

В результате применения упомянутых алгоритмов отдельно или последо-

вательно получаем

• энтропийно-оптимальные функции ПРВ параметров соответствующих мо-

делей: P^∗(a), W^∗(c);

• энтропийно-оптимальные функции ПРВ измерительных шумов:

Q^∗k(ξ[k]),G^∗k(η[k]), k = 1,N;

• энтропийно-оптимальную функцию ПРВ рандомизированной входной по-

следовательности K^∗k(ζ[k]), k = 1, N .

4. Сэмплирование оптимальных функций ПРВ

Сэмплирование предполагает трансформацию функции ПРВ в соответ-

ствующую последовательность случайных векторов. В данной процедуре это

есть способ реализации ансамблей случайных векторов на участках пропу-

щенных данных.

Общий метод генерации последовательностей случайных векторов с за-

данной функцией ПРВ изложен в [29]. Он используется для сэмплирова-

ния последовательностей соответствующих случайных векторов-параметров

РПМ-О, РПМ-В и векторов-шумов измерений и генерирования ансамблей

восстановленных данных с помощью метода Монте-Карло [30].

149

Полезными характеристиками ансамблей являются:

эмпирические функции ПРВ P_k(v_rst[k]), W_k(z_rst[k]) для восстановлен-

ных выходных и входных данных соответственно;

эмпирические функции РВ:

∑

P_k(v^(i)rst[k]) =

P_k(v^(j)rst[k]) для выходных данных;

j=1

∑

(4.1)

W_k(z^(i)rst[k]) =

W_k(v^(j)rst

[k]) для входных данных.

j=1

Востребованными для решения задач машинного обучения являются на-

боры восстановленных данных, которые являются интегральными характе-

ристиками ансамбля случайных траекторий.

1. Данные, соответствующие максимумам ПРВ параметров и шумов

(max-pn):

восстановленные выходные данные

ŷ_rst[k] = B(a^∗,X_(k-ρ)), a^∗ = arg max P^∗(a),

(4.2)

ξ_rst[k] = arg maxQ^∗k

(ξ[k]),

v_rst[k] = ŷ_rst[k] + ξ_rst[k],

k = 0,N;

восстановленные входные данные

x_rst[k] = F(c^∗,Z^∗(k-ρ)), c^∗ = arg max W^∗(a),

Z^∗(k-ρ) = [ζ^∗[k - ρ],... ,ζ^∗[k]], ζ^∗[k] = arg max K^∗k(ζ[k]),

(4.3)

η_rst[k] = arg max G^∗k

(η[k]),

zrst[k] = xrst[k] + ηrst[k],

k = 0,N.

2. Данные, соответствующие максимумам эмпирических ПРВ наблюдае-

мых траекторий для k = 0, N (max-ePDF):

восстановленные выходные данные

(4.4)

v_rst[k] = arg maxP_k(v_rst

[k]), k = 0, N;

восстановленные входные данные

(4.5)

žrst[k] = arg max Wk(zrst

[k]), k = 0, N .

3. Данные, соответствующие средней по ансамблю траектории (mean)

(M количество траекторий в ансамбле):

восстановленные выходные данные

∑

(4.6)

v_rst[k] =

v^(i)rst

[k], k = 0, N;

i=1

150

восстановление входных данных

∑

(4.7)

zrst[k] =

z(i)rst

[k], k = 0, N .

i=1

4. Данные, соответствующие медианной по ансамблю траектории (med)

(M количество траекторий в ансамбле):

восстановление выходных данных:

∑

(4.8)

v(j∗)rst[k] ⇒

P_k(v^(j)rst[k]) =

P_k(v^(j)rst

[k]);

j=1

j=j^∗+1

восстановление входных данных:

∑

(4.9)

z(j∗)rst[k] ⇒

W_k(z^(j)rst[k]) =

W_k(z^(j)rst

[k]).

j=1

j=j^∗+1

5. Восстановление пропусков данных дистанционного зондирования

состояния термокарстовых озер арктической зоны

Термокарстовые озера, расположенные в арктической зоне, являются ос-

новным природным источником эмиссии метана, который считается вторым

по значимости парниковым газом, влияющим на изменение климата Зем-

ли [31]. Арктические зоны России и Канады являются основными регио-

нами наиболее динамичных изменений вечной мерзлоты и термокарстовых

озер. Поэтому изменения площади озер являются важными для прогнозиро-

вания динамики выбросов метана. Для получения данных о площадях озер

используются космические снимки Landsat и средства их дешифрирования в

геоинформационной системе ArcGIS. Климатические данные (среднегодовая

температура и годовая сумма осадков) получены с использованием систем

реанализа метеоданных ERA-40, ERA-Interim [32]. Пространственная струк-

тура данных состоит из 30 тестовых участков, расположенных в трех зонах

вечной мерзлоты Западной Сибири: сплошной (С continuous), прерывистой

(D - discontinuos) и островной (I insular).

Однако данные о текущем состоянии озер, в частности об их площади и

форме, а также климатические данные (например, температура и осадки)

регистрируются нерегулярно, а их преобразование от источника измерений

до компьютерных атрибутов сопровождается существенными ошибками.

Многочисленными экспериментальными исследованиями с применением

методов математической статистики показано, что основными факторами,

влияющими на величину площади термокарстовых озер, являются среднего-

довая температура воздуха T [t] и годовая сумма осадков R[t] (t календар-

ный год) [33].

1. Данные.

Данные по температур

T, осадкам

R и площади озе

S в календарной

и в дискретной временных шкалах представлены в [34]. В настоящей статье

151

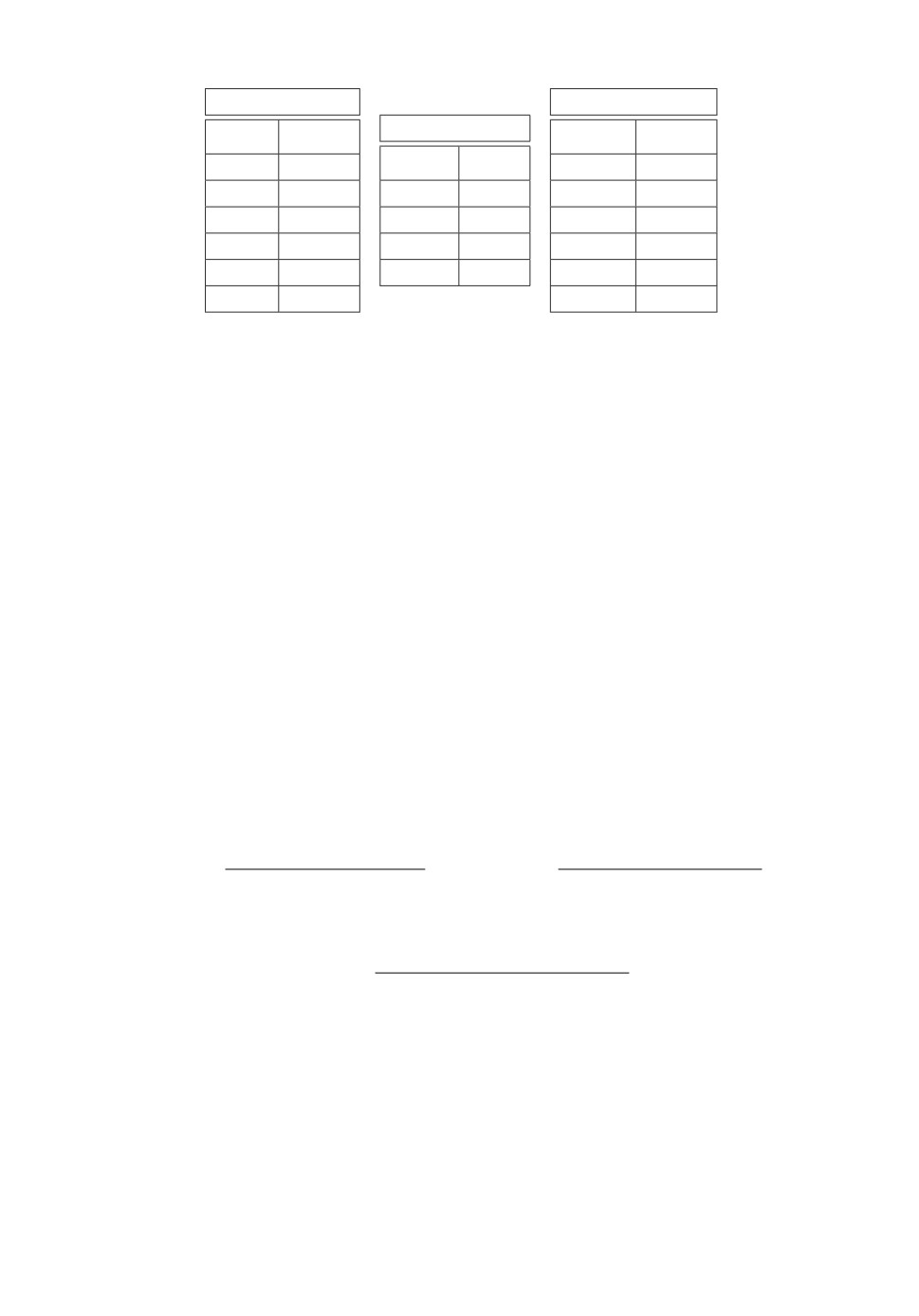
Таблица 1. Данные площади тестовых участков

Участок D - 9

Участок I - 5

Участок C - 24

Год Площадь, га

1973

13,88

Год Площадь, га

1973

67,90

1987

14,29

1977

25,62

1984

68,89

1988

15,36

1981

22,59

1988

64,27

2001

15,40

1988

24,24

2001

62,36

2002

14,15

1999

23,81

2003

62,31

2003

14,50

2001

22,96

2007

66,96

2006

13,88

2006

23,76

2007

13,01

используются данные для трех участков I - 5, D - 9, C - 24, данные по пло-

щади представлены в табл. 1, а данные по температуре и количеству осадков

приведены в Приложении в табл. П.1.

Данные охватывают временной интервал [1973-2007], или k = 1, 35. Преоб-

разуем их к нормализованной форме, т.е. отобразим их значения на числовой

отрезок [0, 1]:

S_min

T_min

R-Rmin

(5.1)

S_r =

T_r =

R_r =

S_max

S_min

T_max

T_min

R_max -Rmin

Данные о площади озер на соответствующих участках с пропусками:

• участок I - 5: обучающая коллекция

S^(I-5)r,LM[k],

k ∈ K^(I-5)LM = {1,12,16,29,31,35};

• участок D - 9: обучающая коллекция

S^(D-9)r,LM[k],

k ∈ K^(D-9)LM = {1,16,29,35};

тестовая коллекция

S^(D-9)r,T[k],

k ∈ K^(D-9)T = {15,30,31,34};

• участок C - 24: обучающая коллекция

S^(C-24)r,LM[k],

k ∈ K^(C-24)LM = {5,9,16,27,29,34}.

Данные по площади озер на участках I - 5, C - 24 будут использованы

для обучения соответствующих моделей и восстановления пропущенных дан-

ных, данные по участку D - 9 для обучения модели (K^(D-9)LM) и тестирова-

ния (K^(D-9)T) восстановленных данных.

152

2. Модель.

Восстановление пропущенных данных на трех обозначенных выше зонах и

участках осуществляется единой по структуре моделью линейной регрессии

вида

(5.2)

[k] = αT [k] + βR[k] + ξ[k], k = 0, N ,

где параметры α, β случайные, независимые, интервального типа:

(5.3)

α ∈ A = [α^-,α⁺], β ∈ B = [β^-,β⁺

Для принятых тестовых участков границы интервалов одинаковые³:

A[0; 1], B = [0; 1].

Вероятностные свойства параметров характеризуются функциями ПРВ

P (α), F (β).

Шум также нормализованный и интервальный

(5.4)

ξ[k] ∈ Ξ = [ξ^-, ξ⁺

] = [-0,15;0,15]

с функциями ПРВ Q_k(ξ[k]), k ∈ K.

3. А л г о р и т м РМО.

Общая форма алгоритма обучения модели имеет вид

∫

H = - P(α)lnP(α)dα - F(β)lnF(β)dβ -

∫

∑

(5.5)

Q_k(ξ[k])ln Q_k

(ξ[k])dξ[k] ⇒ max,

k∈KΞ

нормировка

∫

(5.6)

P (α)dα = 1,

F (β)dβ = 1,

Q_k

(ξ[k])dξ[k] = 1, k ∈ K,

Ξ_k

эмпирические балансы

∫

(5.7)

P (α)αT [k]dα + F (β)βR[k]dβ + Q_k(ξ[k])ξ[k]dξ[k] = S_r

[k], k ∈ K.

Ξ_k

Решение задачи (5.5)-(5.7) имеет вид

exp (-αl_r(θ))

exp (-βh_r(θ))

P^∗(α,θ) =

F^∗(β,θ) =

P(θ)

F (θ)

exp(-θ_kξ[k])

(5.8)

Q_k(ξ[k],θ_k) =

k ∈ K,

Q_k(θ_k)

где θ = {θ_k, k ∈ K} множители Лагранжа,

³ Границы интервалов косвенно влияют на качество восстановленных данных, измеряе-

мого принятым функционалом. Для выбора границ можно воспользоваться его численной

оптимизацией.

153

Таблица 2. Расчетные данные по тестовым участкам

Участок I - 5

Участок C - 24

Участок D - 9

K^(I-5)LM θ/10³

K^(C-24)LM θ/10³

0,0015

K^(D-9)LM θ/10³

4,73

2,99

-2,13

-0,734

-0,0278

4,73

-0,0102

-0,356

0,0321

-1,07

-4,73

-1,56

-0,076

3,26

-0,0042

нормировочные коэффициенты

∫

P(θ) = exp (-αl_r(θ)) dα;

F (θ) = exp (-βh_r(θ)) dβ;

∫

(5.9)

Q_k(θ_k) = exp(-θ_k

ξ[k])dξ[k],

k ∈ K,

показатели экспонент

∑

(5.10)

l_r(θ) =

θ_kT[k], h_r(θ) =

θ_k

R[k].

k∈K

Множители Лагранжа определяются из системы уравнений

(5.11)

L(θ)T [k] + K(θ)R[k] + V_k(θ_k) = S_r

[k], k ∈ K,

где

∫

α exp (-αl_r(θ)) dα

β exp (-βh_r(θ)) dβ

L(θ) =α-

K(θ) =

P(θ)

F (θ)

∫

ξ[k] exp (-θ_kξ[k]) dξ[k]

ξ^-[k]

(5.12)

V_k(θ_k) =

Q_k(θ_k)

В табл. 2 приведены результаты обучения по тестовым участкам I - 5,

D - 9, C - 24.

В силу линейности модели (5.2) все энтропийно-оптимальные функции

ПРВ экспоненциальные:

• участок I - 5:

P^∗(α) = 7,28exp(-7,27α), F^∗(β) = 0,0448exp(4,65β),

(5.13)

α^mean = 0,137; β^mean

= 0,795;

154

1,2

1,0

0,8

0,6

0,4

0,2

data

test

mean

std

-0,2

1970

1975

1980

1985

1990

1995

2000

2005

2010

Год

Рис. 4. Восстановление пропущенных данных на участке D - 9.

• участок D - 9:

P^∗(α) = 0,476exp(0,543α), F^∗(β) = 0,0462exp(4,60β),

(5.14)

α^mean = 0,178; β^mean

= 0,783;

• участок C - 24:

P^∗(α) = 1,84exp(-1,37α), F^∗(β) = 1,14exp(-0,272β),

(5.15)

α^mean = 0,389; β^mean

= 0,477.

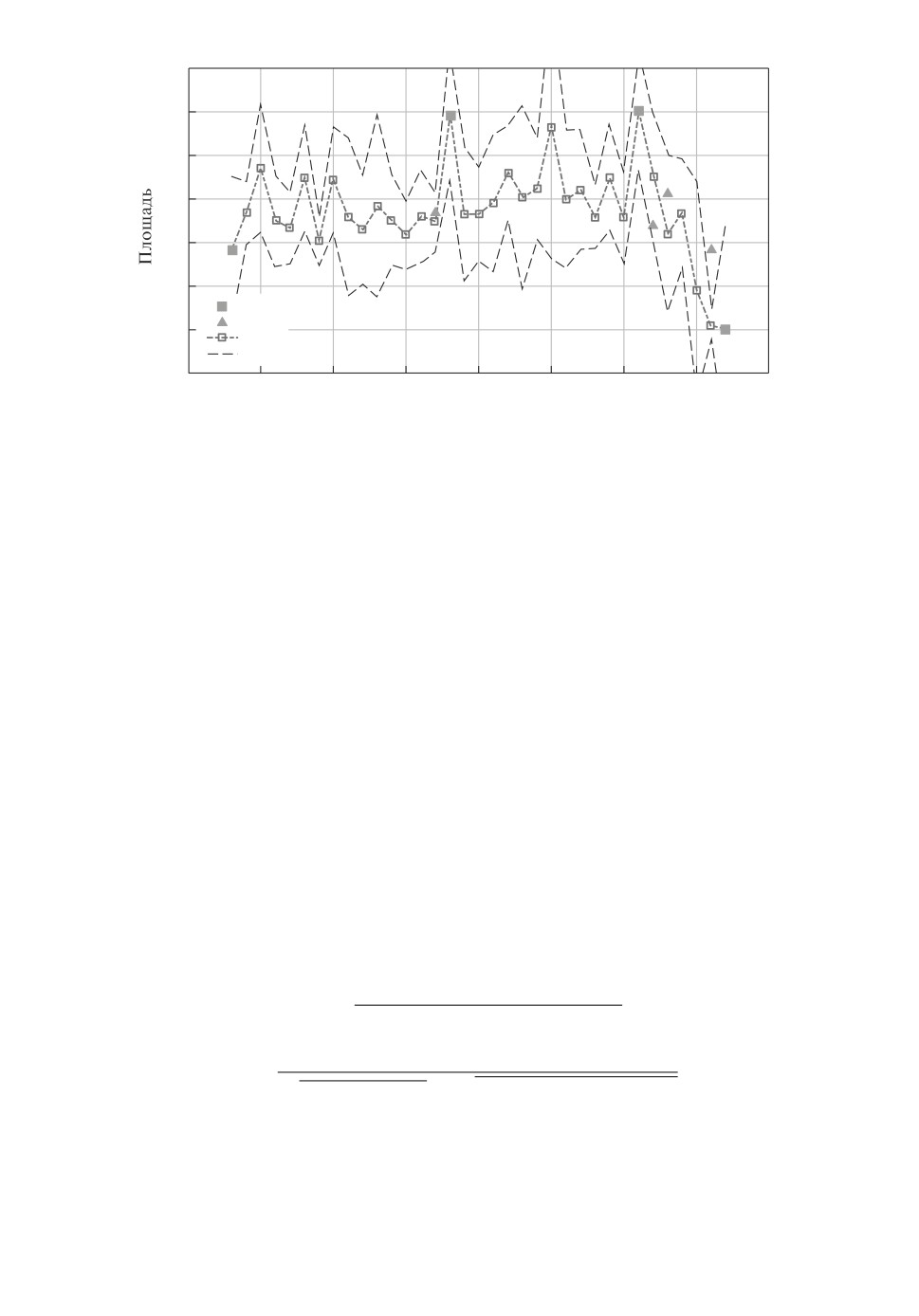
4. Тестирование для участка D - 9.

Для участка D - 9 имеются данные K^(D-9)T, которые будем использовать

для оценки качества восстановления данных на этом участке.

Имея набор энтропийно-оптимальных ПРВ (5.14), сэмплируем их и, вы-

числяя для каждого сэмпла траектори

S[k], формируем ансамбль случай-

ных траекторий на интервале k ∈ [1, 35] (рис. 4). На этом же интервале пока-

зана средняя по ансамблю траектория mean[k], которая принята за траекто-

рию восстановленных данных.

Качество восстановления характеризуется относительной ошибкой

√

(

)₂

∑

[k]

S[k] - S^(D-9)r,T

(D-9)

k∈K_T

(5.16)

δ=

√

(

)₂ .

√ ∑

∑

S²[k] +

S^(D-9)r,T[k]

(D-9)

k∈K^(D-9)

k∈K_T

Для участка D - 9 относительная ошибка δ ≈ 0,23. Поскольку сформирован

ансамбль траекторий восстановленных данных, то по нему можно определить

и другие типы траекторий и доверительные области (см. п. 5).

155

а I - 5

1,2

1,0

0,8

0,6

0,4

0,2

data

mean

std

-0,2

1970

1975

1980

1985

1990

1995

2000

2005

2010

Год

б С - 24

1,2

1,0

0,8

0,6

0,4

0,2

data

mean

std

-0,2

1970

1975

1980

1985

1990

1995

2000

2005

2010

Год

Рис. 5. Восстановление пропущенных данных на участках I - 5 (а) и C - 24 (б ).

5. Генерация восстановленных данных.

Для модели (5.2) производилось сэмплирование функций ПРВ параметров

согласно (5.13) и (5.15). Для каждого сэмпла вычислялась траектори

S[k],

k∈K, иформировался ансамбл

S случайных траекторий.

Полезными вероятностными характеристиками ансамбля являются функ-

ции эмпирической плотности U_k

S[k]) (гистограммы), определенные на мно-

жестве S_k =

S^-[k]

S⁺[k]], где

S^-[k] = mi

S[k],

S⁺[k] = ma

S[k]. Перемен-

ная k ∈ K^(I-5) для участка I - 5 и k ∈ K^(C-24) для участка C - 24.

Определялись следующие числовые характеристики ансамбля траекто-

рии:

максимумов гистограмм

(5.17)

max[k] = maxU_k(S

[k]), k ∈ T ;

156

медиан

∫

(5.18)

U_k

S[k])

S[k] =

U_k

S[k])dS

[k], k ∈ T ;

S[k]^-

med[k]

средних

∫

(5.19)

mean[k] =

S[k] U_k

S[k])dS

[k].

S[k]^-

На рис. 5,а и 5,б показаны ансамбли и графики соответствующих траекто-

рий.

6. Заключение

Предложен новый метод восстановления пропущенных данных, состоящий

в генерации ансамбля случайных траекторий, формируемых рандомизиро-

ванной параметризованной моделью, обученной с привлечением имеющих-

ся данных. Для пропусков в выходных данных развит алгоритм рандоми-

зированного машинного обучения, основанный на технике MEE-оценивания

функций ПРВ параметров модели и шумов измерений. В случае пропусков во

входных данных развит метод восстановления, использующий аналогичную

рандомизированную параметризованную модель и специальный оптимизиро-

ванный шум. С помощью техники MEE-оценивания определяются функции

ПРВ параметров модели и шума.

Предложенный метод сочетает преимущества подходов параметрического

оценивания с заданной моделью процесса и непараметрического оценивания

при неизвестных характеристиках шумов измерений, что обеспечивает ро-

бастность метода, но может в определенных случаях приводить к завышен-

ным ошибкам восстановления. Робастность также обеспечивается и процеду-

рой генерации энтропийно-оптимизированных траекторий путем сэмплиро-

вания соответствующих функций ПРВ.

ПРИЛОЖЕНИЕ

Таблица П.1. Данные о температуре и осадках для тестовых участков

Участок I - 5

Участок D - 9

Участок C - 24

Год

1973

-1,00

650,30

–3,50

580,80

–11,00

372,40

1974

-3,50

494,25

–6,00

494,30

–12,00

211,00

1975

-2,00

684,80

–4,00

579,00

-9,50

220,50

1976

-2,50

487,30

–4,50

442,50

–10,00

263,40

1977

-2,50

486,50

–5,00

432,60

–11,00

216,70

1978

-3,50

706,40

–4,50

562,70

–11,00

275,40

1979

-2,00

700,10

-6,00

414,40

-12,50

342,90

157

Таблица П.1. (окончание)

1980

-2,50

556,50

–4,50

556,50

–11,00

216,00

1981

-1,00

534,60

–3,00

427,30

-9,00

209,30

1982

-2,50

489,95

–4,00

409,90

–11,00

303,10

1983

-1,00

578,80

–2,50

448,80

-9,50

318,80

1984

-2,50

465,05

–4,50

444,20

–9,50

319,20

1985

-3,50

482,20

–5,00

412,90

–9,50

274,20

1986

-3,50

577,30

–4,50

456,00

–9,50

274,00

1987

-2,50

467,50

–6,00

467,50

–11,00

253,60

1988

-1,00

501,20

–3,50

390,30

–10,00

390,30

1989

-1,00

487,70

–3,50

444,40

–11,00

357,70

1990

-2,50

462,10

–4,50

462,10

–11,00

323,00

1991

-1,00

551,50

–3,50

473,80

–11,00

396,20

1992

-3,50

585,30

–5,00

585,30

–11,00

381,80

1993

-1,00

471,50

–2,50

471,50

-8,50

402,70

1994

-2,50

562,50

–4,50

532,75

–11,00

324,60

1995

0,50

578,90

–1,00

640,50

-6,00

332,60

1996

-1,00

571,35

–3,50

485,90

–7,50

372,10

1997

-2,50

521,10

–4,00

521,10

–9,50

299,80

1998

-3,50

544,80

–6,00

480,70

–11,00

288,10

1999

-2,50

563,15

–4,50

563,15

-8,50

369,50

2000

-1,00

561,30

–4,50

453,30

–9,50

291,20

2001

-2,00

430,20

–4,00

511,60

–9,50

267,40

2002

-2,06

520,15

–4,02

555,80

–9,82

270,50

2003

-0,48

429,20

–2,92

378,90

–9,05

177,80

2004

-1,80

338,40

–4,13

457,80

–9,78

159,20

2005

0,44

343,90

–1,66

199,50

–8,02

247,70

2006

-2,78

222,00

–5,44

168,30

–9,24

222,00

2007

0,14

325,40

-1,77

285,75

-7,51

246,10

СПИСОК ЛИТЕРАТУРЫ

1. Загоруйко Н.Г. Методы распознавания и их применение. М.: Сов. Радио, 1972.

2. Литтл Р.Дж.А., Рубин Д.Б. Статистический анализ данных с пропусками. М.:

Финансы и статистика, 1990.

3. Загоруйко Н.Г. Прикладные методы анализа данных и знаний. Новосибирск:

ИМ СО РАН, 1999.

4. Злоба Е., Яцкив И. Статистические методы восстановления пропущенных дан-

ных // Computer Modeling & New Technologies. 2004. V. 6. P. 55-56.

5. Molenberghs G., Kenward M.G. Missing Data in Clinical Studies. Chichester, UK.,

John Wiley & Sons, 2007. P. 47-50.

6. Cheema J. A Review of Missing Data Handling Methods in Education Research //

Review of Educational Research. 2014. No. 4. P. 487-508.

7. Круглов В.В., Абраменкова И.В. Методы восстановления пропусков в массивах

данных // Методы восстановления пропусков в массивах данных. 2005. № 2.

8. Van Buuren S. Flexible Imputation of Missing Data. Chapman and Hall/CRC; 1 ed.,

2012.

9. Enders C. Applied Missing Data Analysis. N.Y.-London, 2010.

158

10.

Schafer J.L., Schenker N. Inference with Imputed Conditional Means // Journal of

the American Statistical Association. 2000. V. 95. No. 449. P. 144-154.

11.

Mander A., Clayton D. HotDeck Imputation. Stata Technical Bulletin. 1999. V. 51.

P. 32-34.

12.

Batista G.E.A.P.A., Monard M.C. K-Nearest Neighbour as Imputation Method:

Experimental Results. Technical report, ICMC-USP, 2002.

13.

Dan Li, Jitender Deogun, William Spaulding, Bill Shuart. Towards Missing Data

Imputation: A Study of Fuzzy K-means Clustering Method // S. Tsumoto, et al.

(Eds.): RSCTC 2004. LNAI 3066. 2004. P. 573-579.

14.

Dempster A.P., Laird N.M., Rubin D.B. Maximum Likelihood from Incomplete Data

via the EM Algorithm // Journal of the Royal Statistical Society. 1977. V. 39. P. 1-38.

15.

Zhou X.-Y., Lim J.S. EM Algorithm with GMM and Naive Bayesian to Implement

Missing Values // Advanced Science and Technology Lett. 2014. V. 46. P. 1-5.

16.

Загоруйко Н.Г., Елкина В.Н., Тимеркаев В.С. Алгоритм заполнения пропус-

ков в эмпирических таблицах (алгоритм Zet) // Эмпирическое предсказание и

распознавание образов. Новосибирск: 1975. Вып. 61: Вычислительные системы.

С. 3-27.

17.

Снитюк В.Е. Эволюционный метод восстановления пропусков в данных. Сбор-

ник трудов VI Межд. конф. “Интеллектуальный анализ информации”, Киев:

2006. С. 262-271.

18.

Алгоритм ZetBraid // Информационные интеллектуальные системы.

2008.

Вып. 40.

19.

Rubin D.B. Multiple Imputation for Nonresponse in Surveys. N.Y.: Willey, 1987.

P. 64-66.

20.

Rubin D.B. Multiple Imputation After 18+ Years // Journal of the American Sta-

tistical Association. 1996. No. 91. P. 473-489.

21.

Lipsitz S.R., Lue Ping Zhao, Molenberghs G.A. Semiparametric Method of Multiple

Imputation // Journal of the Royal Statistical Society. Ser. B (Statistical Method-

ology). 1998. V. 60. No. 1. P. 127-144.

22.

Horton N.J., Lipsitz S.R. Multiple Imputation in Practice: Comparison of Software

Packages for Regression Models with Missing Variables // The American Statistician.

2001. V. 55. No. 3. P. 244-254.

23.

Efron B. Missing Data, Imputation, and the Bootstrap // Journal of the American

Statistical Association. 1994. V. 89. No. 426. P. 463-475.

24.

Popkov Y.S., Dubnov Y.A., Popkov A.Y. New Method of Randomized Forecast-

ing Using Entropy-Robust Estimation: Application to the World Population Predic-

tion // Mathematics. 2016. V. 4. Iss. 1. P. 1-16.

25.

Попков Ю.С., Попков А.Ю., Дубнов Ю.А. Рандомизированное машинное

обучение. М.: УРСС, 2019.

26.

Попков Ю.С. Асимптотическая эффективность оценок максимальной энтро-

пии // ДАН. Математика, Информатика, Процессы управления. 2020. Т. 493.

С. 100-103.

27.

Geweke J., Hisashi T. Note on the Sampling Distribution for the Metropolis-

Hastings Output // Joutnal of American Statistical Association. 2003. V. 96. (453).

P. 270-281.

28.

Иоффе А.Д., Тихомиров В.М. Теория экстремальных задач. М.: Наука, 1974.

29.

Дарховский Б.С., Попков Ю.С., Попков А.Ю., Алиев А.С. Метод генерации

случайных векторов с заданной функцией плотности распределения вероятно-

стей // АиТ. 2018. Вып. 9. С. 31-45.

159

Darkhovsky B.S., Popkov Yu.S., Popkov A.Yu., Aliev A.S. A Method of Generating

Random Vectors with a Given Probability Density Function // Autom. Remote

Control. 2018. V. 79. P. 1569-1581.

30. Rubinstein R.Y., Kroese D.P. Simulation and Monte Carlo Method. John Wiley and

Sons, 2007.

31. Полищук В.Ю., Полищук Ю.М. Геоимитационное моделирование полей термо-

карстовых озер в зонах мерзлоты. Ханты-Мансийск: УИП ЮГУ, 2013.

32. Polishchuk Y.M., Muratov I.N., Polishchuk V.Y. Remote Research of Spatiotemporal

Dynamics of Thermocarst Lakes Fields in Siberian Permafrost / The Arctic: Current

Issues and Challenges (Eds. Pokrovsky O.S., Kirpotin S.N., Malov A.I.). N.Y.: Nova

Science Pbl., 2020. P. 208-237.

33. Попков Ю.С., Волкович В., Мельников А.В., Полищук Ю.М. Методологиче-

ские вопросы использования рендомизированного машинного обучения для

прогнозирования динамики термокарстовых озер Арктики // Вестн. Южно-

Уральского гос. ун-та. Сер. “Компьютерные технологии, управление, радиоэлек-

троника”. 2019. Т. 19. Вып. 4. С. 5-12.

34. Электронный ресурс,

URL: https://cloud.uriit.ru/index.php/s/0DOrxL9RmGqXsV0.

Статья представлена к публикации членом редколлегии А.И. Михальским.

Поступила в редакцию 24.07.2020

После доработки 27.10.2020

Принята к публикации 08.12.2020

160