Автоматика и телемеханика, № 5, 2021

Нелинейные системы

А.А. ГАЛЯЕВ, чл.-корр. РАН (galaev@ipu.rssi.ru)

(Институт проблем управления им. В.А. Трапезникова РАН, Москва)

ПЕРЕХВАТ ПОДВИЖНОЙ ЦЕЛИ МАШИНОЙ ДУБИНСА

ЗА КРАТЧАЙШЕЕ ВРЕМЯ¹

Задача перехвата движущейся по предписанной траектории цели ма-

шиной Дубинса сформулирована и формализована как задача оптималь-

ного управления по критерию быстродействия с произвольным направ-

лением скорости машины при перехвате. Уточнены имеющиеся в лите-

ратуре условия, при которых оптимальной траекторией является геоде-

зическая линия, проведенная из начального положения машины в точку

перехвата. Получены алгебраические уравнения для вычисления опти-

мального времени перехвата. На основе этих уравнений произведен син-

тез оптимального управления. Разработан программный модуль для по-

строения оптимальных траекторий машины при различных траекториях

движения цели.

Ключевые слова: машина Дубинса, множество достижимости, перехват

подвижной цели, движение в условиях ветра, задача быстродействия, гео-

дезическая линия.

DOI: 10.31857/S0005231021050019

1. Введение

Первые работы по поиску линии, соединяющей две заданные точки

и имеющей ограниченную кривизну и минимальную длину, принадлежат

А.А. Маркову. В [1] он рассмотрел четыре задачи о прокладке железнодо-

рожных путей. Первая задача была сформулирована как поиск линии, со-

единяющей две точки на плоскости и имеющей кратчайшую длину и ограни-

ченную кривизну, причем в первой точке фиксировано направление выхода

этой линии. Соответствующая кратчайшая траектория называется геодези-

ческой линией. Не умаляя общности, можно считать минимальный радиус

кривизны такой линии единичным.

Первая задача Маркова может быть переформулирована как задача наи-

скорейшего достижения финальной точки подвижным объектом с постоянной

по модулю скоростью и ограниченной маневренностью. В такой постановке

задачу рассматривал Р. Айзекс в [2] для иллюстрации примера универсаль-

ной поверхности в задаче о шофeре-убийце с неподвижным пешеходом. В [3]

Ю.И. Бердышев, используя принцип максимума Понтрягина, получил пол-

ное аналитическое решение этой задачи в том случае, когда рассматриваемый

объект ограниченной маневренности точечный. Помимо этого, в [3] приведено

¹ Работа выполнена при финансовой поддержке Молодeжной научной школы Института

проблем управления им. В.А. Трапезникова РАН.

решение задачи о наискорейшем попадании из заданного начального состоя-

ния на окружность с нормальным к ней в конечный момент времени векто-

ром скорости при условии достаточной удаленности начального положения

объекта от центра этой окружности. Результат Ю.И. Бердышева дополняет

результаты А.А. Маркова аналитическими выражениями для оптимального

управления. Решение первой задачи Маркова получено и для некоторых бо-

лее общих случаев: когда подвижный объект имеет форму окружности или

отрезка [4, 5]; когда вводится дополнительное управление производной моду-

ля скорости [6, 7]; когда на подвижный объект действует постоянное возму-

щение [8].

В [9] Л.Э. Дубинс произвел классификацию оптимальных траекторий дви-

жения в задаче поиска линии наименьшей длины и ограниченной кривизны

при заданном направлении выхода из начальной точки и заданном направ-

лении прихода в конечную точку. Подробное аналитическое решение этой

задачи получил T. Pecsvaradi в [10]. Позднее этот результат был переоткрыт

другой группой исследователей [11]. Кратчайшую траекторию в такой задаче

называют ¾путь Дубинса¿, а соответствующий подвижный объект с ограни-

ченной маневренностью называют ¾машина Дубинса¿ (первые аналогии с

машиной проводил, по-видимому, Р. Айзекс).

Для некоторых приложений [12, 13], использующих модель машины Ду-

бинса, важную роль занимает понятие множества достижимости. В декарто-

вых координатах (x, y) граница множества достижимости ¾в момент¿ описа-

на в [14], а ¾к моменту¿ в [15]. Построение и анализ множеств достижимо-

сти в трехмерном пространстве состояний для машины Дубинса произвели

В.С. Пацко и др. [16, 17]. В данной работе использованы некоторые свойства

проекции на декартову плоскость множества достижимости ¾в момент¿ для

машины Дубинса (замкнутость, непрерывность границ или их частей, смена

связности).

В отличие от [18] в настоящей работе рассматривается не игровая задача

наискорейшего перехвата подвижной цели машиной Дубинса. Предполага-

ется, что цель движется по произвольной и заранее известной непрерывной

траектории. В сравнении с [19, 20] управление считается ограниченной функ-

цией времени.

Подобная задача встречалась сразу в нескольких работах, и авторы огра-

ничивались лишь частичным еe решением. В [21] для игры ¾двух автомо-

билей¿ установлены необходимые и достаточные условия поимки цели при

любых начальных условиях. В неигровом случае предписанных движений це-

ли эти условия носят достаточный характер. В [22] установлены достаточные

условия того, что оптимальной траекторией будет линия типа ¾дуга-прямая¿.

Эти условия накладывают ограничения на отношение минимального радиуса

кривизны траектории машины и расстояния между целью и машиной в на-

чальный момент времени. В [7, 23] синтезировано управление для перехвата

цели по геодезической линии, проведенной из начала движения машины в

точку перехвата, причем полагается, что цель движется по прямой c посто-

янной скоростью. В [24] приведен алгоритм поимки движущейся по прямой

цели машиной Дубинса, которая выбирает кратчайшую траекторию из клас-

са ¾дуга-прямая¿.

Авторы работ [25, 26] выделили сразу несколько утверждений, связанных

с рассматриваемой в настоящей работе задачей. Во-первых, они установили,

что если траектория цели не попадает в круги единичного радиуса, которые

касаются вектора скорости машины Дубинса в начальный момент времени,

то перехват за кратчайшее время осуществляется по геодезической линии.

Во-вторых, если траектория все же попадает в эти круги, то возможны слу-

чаи, когда оптимальный перехват осуществляется не по геодезической линии.

Также авторы приводят оценки сверху и снизу для оптимального времени пе-

рехвата.

В некоторых работах рассмотрены задачи бокового перехвата подвижной

цели. В таких задачах угол перехвата фиксирован в конечный момент време-

ни. Например, в [27] получено решение для задачи наискорейшего перехвата

под прямым углом, а в [28] рассмотрен случай перехвата за минимальное вре-

мя, заканчивающийся попаданием в движущуюся по окружности цель сза-

ди. В обеих работах предполагается, что цель достаточно удалена от объекта

управления в начальный момент времени.

2. Постановка задачи

Будем описывать управляемый подвижный объект моделью машины Ду-

бинса [3, 15]. Выберем единицы измерения длины и времени так, чтобы ско-

рость и минимальный радиус кривизны траектории машины были равны еди-

нице. В этом случае динамика машины в декартовой системе координат опи-

сывается следующей системой:

{

x = cosϕ;

ϕ = u;

(2.1)

y = sinϕ;

|u(t)| ≤ 1.

Здесь (x(t), y(t)) положение машины на декартовой плоскости, ϕ(t) угол

еe скорости с осью абсцисс, u(t) управление в момент времени t. Положим

все начальные условия для системы (2.1) фиксированными:

(2.2)

x(0) = 0, y(0) = 0, ϕ(0) =

Пусть непрерывная вектор-функция E(t) = (x_E(t), y_E (t)) задает траекторию

движения цели на декартовой плоскости. Терминальные условия поимки вы-

глядят следующим образом:

(2.3)

= y(T) = y_E

(T ).

Здесь T ∈ R⁺⁰ время движения из начальной точки в точку перехвата. По-

ставим задачу поимки цели за кратчайшее время как задачу поиска опти-

мального управления в классе кусочно-постоянных функций:

∫T

= dt → min .

Из теоремы 1 статьи [14] следует, что класса кусочно-постоянных функций

будет достаточно.

Далее будут использованы обозначения из [11] для именования классов

траекторий: букве C соответствует движение по дуге окружности (circle arc)

единичного радиуса; букве S движение по отрезку (straight line segment).

Тогда CS это класс траекторий, состоящих из дуги окружности единично-

го радиуса и отрезка, а CC это класс траекторий, состоящих из двух дуг

разных окружностей единичного радиуса. Все стыки дуг и отрезков подра-

зумеваются гладкими. В работе будет показано, что траекторий из классов

CS и CC достаточно для осуществления оптимального перехвата. На месте

буквы C может стоять буква L или R для указания направления разворо-

та (левый и правый развороты соответственно). При движении по прямой

u(t) = 0; при L-развороте u(t) = 1; при R-развороте u(t) = -1. Круги еди-

ничного радиуса, касающиеся вектора скорости машины в начальный момент

времени, будем обозначать через D_L и D_R.

Подобно [14] будем обозначать через R(t) множество достижимости маши-

ны Дубинса в момент времени t на плоскости геометрических координат, а

через B(t) границу этого множества. Решение задачи с неподвижной целью

полностью исследовано в [3, 14, 15] и получено подробное описание множе-

ства R(t) [14], поэтому вместо применения принципа максимума Понтрягина

воспользуемся свойствами этого множества для синтеза оптимального управ-

ления в задаче с подвижной целью. В разделе 3 выписаны алгебраические

соотношения, описывающие B(t); из множества B(t) выделено подмножество

точек B_G(t), в которые машина попадает в момент t по геодезической линии;

найден порог времени, после которого оптимальные геодезические траекто-

рии принадлежат только классу CS. В разделе 4 доказано, что, за исключени-

ем только одной ситуации, оптимальная точка перехвата лежит на B(t); выве-

дены уравнения для вычисления оптимального времени перехвата; приведен

алгебраический критерий того, что перехват осуществляется по геодезиче-

ской линии. В разделе 5 описан алгоритм синтеза оптимального управления,

опирающийся на решение нелинейных алгебраических уравнений, а также

приведены результаты численного моделирования оптимального перехвата

для различных траекторий движения цели.

3. Граница множества достижимости

Рассмотрим управления, ведущие на границу B(t) множества достижимо-

сти R(t). В [14, с. 212] показано, что любая точка из B(t) может быть достиг-

нута по траектории длины t из классов CS, CC. Управления, отвечающие

этим траекториям, ведут на B(t) и могут быть кратко описаны с помощью

следующей леммы, которая естественным образом следует из теоремы 4 ста-

тьи [14].

Лемма 1. Каждая точка B(T) в момент T может быть достигнута

с помощью управления

{

t ∈ [0,τ];

(3.1)

u(t) =

−σs,

t ∈ (τ,T],

где s ∈ {-1, 1}, σ ∈ {0, 1}, τ ∈ [0, T ], τ ≤ 2π.

Действительно, если σ = 0, то управлению (3.1) отвечают траектории типа

CS; если σ = 1, то траектории типа CC; если s = 1, то начальный разворот

направлен налево; если s = -1, то направо. Число τ называется моментом

переключения управления.

Далее через B_Λ(t) будут обозначаться подмножества B(t), на которые в мо-

мент t можно попасть, используя управление типа Λ ∈ {LS, RS, LR, RL}. Так-

же обозначим: B_CS(t) = B_LS(t) ∪ B_RS (t) и B_CC (t) = B_LR(t) ∪ B_RL(t). Дальней-

шее изложение текущего раздела существенно повторяет полученные в [14]

результаты, но в более удобной для задачи перехвата форме, а также уточ-

няет их.

Рассмотрим сначала управления, ведущие на B_CS (T ). Проинтегрируем

уравнения динамики (2.1) при начальных условиях (2.2) для управления (3.1)

при σ = 0:

{

sx_T + 1 = -(T - τ)sin τ + cos τ;

(3.2)

y_T = (T - τ)cos τ + sinτ.

Определим функцию знака следующим образом:





1, x > 0;

0, x = 0;

-1, x < 0.

Согласно [3, 15], для того чтобы (x_T , y_T ) ∈ B_CS (T ), требуется выполнение s =

= -sgn x_T , кроме случая, когда x_T = 0 и y_T < 0. Это означает, по какую сто-

рону от оси ординат лежит точка (x_T , y_T ), туда же и должна поворачивать

машина Дубинса в течение времени τ < 2π. Если (x_T , y_T ) лежит на отрица-

тельной части оси ординат, то начальное направление поворота произвольно,

т.е. s = ±1. Подставляя s в первое равенство (3.2), получим уравнение

|x_T | = (T - τ) sin τ - (cos τ - 1) ≥ 0,

которое при фиксированном T дает ограничение на время переключения τ.

Введем обозначения:

= -(T - τ)sin τ + (cos τ - 1);

= (T - τ) cos τ + sin τ.

С помощью этих обозначений можно выписать явный вид для подмножеств

B_CS(T):

B_LS(T) = {(x_LS(τ,T),y_LS(τ,T))| τ ∈ [0,T], τ < 2π,x_LS(τ,T) ≤ 0};

B_RS(T) = {(x_RS(τ,T),y_RS(τ,T))| τ ∈ [0,T], τ < 2π,x_RS(τ,T) ≥ 0}.

Далее рассмотрим управления типа CC, ведущие на B_CC (T ). Проинтегри-

руем уравнения динамики (2.1) при начальных условиях (2.2) для управле-

ния (3.1) при σ = 1 и получим систему

{

sx_T + 1 = (2 - cos(T - τ))cos τ - sin(T - τ)sin τ;

(3.3)

y_T = (2 - cos(T - τ))sin τ + sin(T - τ)cos τ.

Согласно [14, с. 211], для того чтобы (x_T , y_T ) ∈ B_CC (T ), требуется выполне-

ние s = sgn x_T при x_T = 0, т.е. по какую сторону точка (x_T , y_T ) лежит от

оси ординат, в противоположную ей сторону должна поворачивать машина

Дубинса в течение времени τ ≤ π/2. Если же x_T = 0, то направление перво-

го поворота произвольно, т.е. s = ±1. Подставляя s в первое равенство (3.3),

получим уравнение

(3.4)

|x_T

| = (2 - cos(T - τ))cosτ - sin(T - τ)sinτ - 1 ≥ 0,

которое при фиксированном T дает ограничение на время переключения τ.

По траектории типа CC можно попасть на границу множества достижи-

мости только при T < T^∗ = 2π + arccos(23/27) [14, с. 215]. Множество B_CC (t)

¾стягивается¿ в некоторую точку E^∗ в том смысле, что начиная с некото-

рого момента времени t, в произвольной ε-окрестности точки E^∗ содержатся

все точки из B_CC (t). В точку ¾стягивания¿ ведет траектория типа CC c τ =

= arccos(1/3) [14, с. 215]. Вычислить положение точки E^∗ можно, подставив

√

τ = arccos(1/3) и T = T ^∗ в уравнения (3.3), что даст E^∗ = (0,2

2/3).

Введем обозначения:

= (2 - cos(T - τ)) cos τ - sin(T - τ) sin τ - 1;

= (2 - cos(T - τ)) sin τ + sin(T - τ) cos τ.

Согласно [14, с. 214] при T > 2π границы внутренней полости состоят только

из точек B_CC (T ), поэтому точка с наименьшей ординатой из B_CC (T ) лежит

не ниже, чем T - 2π (иначе в точку с наименьшей ординатой приводила бы

траектория типа CS с τ = 2π). Теперь можно выписать явный вид для под-

множеств B_CC (T ) при T < T^∗:

{

B_LR(T) = (x_LR(τ,T),y_LR(τ,T))| τ ∈ [0,T],

}

τ ≤

,x_LR(τ,T) ≥ 0,y_LR(τ,T) ≥ T - 2π ;

{

B_RL(T) = (x_RL(τ,T),y_RL(τ,T))| τ ∈ [0,T],

}

τ ≤

,x_RL(τ,T) ≤ 0,y_RL(τ,T) ≥ T - 2π

В иных случаях полагаем B_CC (T ) = ∅. Иллюстрация эволюции границы мно-

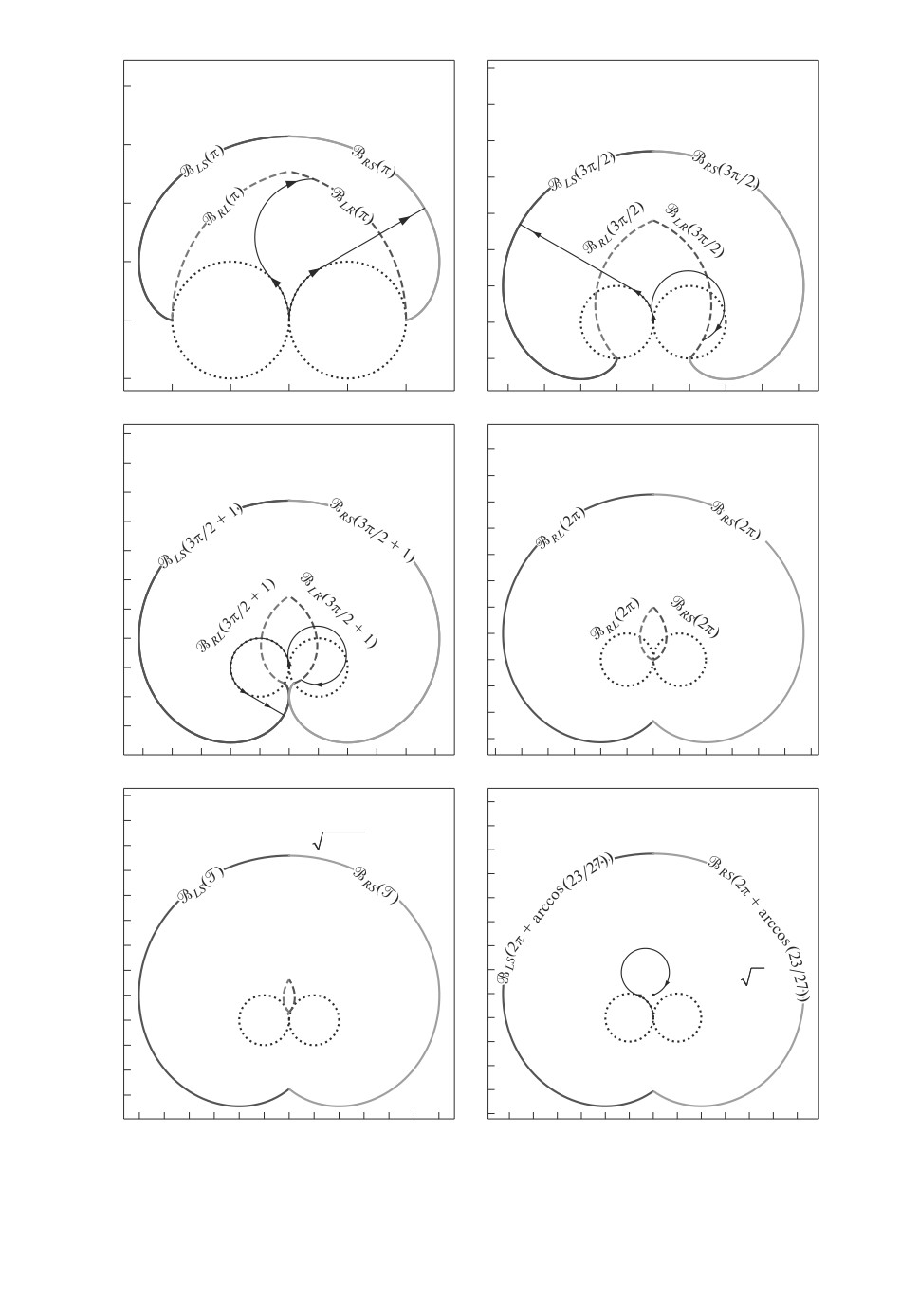
жества достижимости приведена на рис. 1.

Опишем множество точек B_G(T ) ⊂ B(T ), в которые машина Дубинса по-

падает в момент T по геодезической линии. Согласно [1, 3], если конечная

точка находится внутри кругов D_L, D_R, то геодезическая линия принадле-

жит классу CC, а если она лежит вне этих кругов, то классу CS. Учитывая

дополнительно, что все точки B_CS(t) лежат вне кругов D_L, D_R, получаем,

что

{

}

(3.5)

B_G(T) = B_CS(T) ∪

(x, y) ∈ B_CC(T )| (|x| - 1)² + y² < 1

T= 2p + arccos(23/27

)

c(t, T

) = 2(cos t - 1) + cos (T- t) - cos (

T- 2t) < 0

c(t, T) > 0

t = p/12

t = p/6

t = 2 arctg

5/27

t = p/3

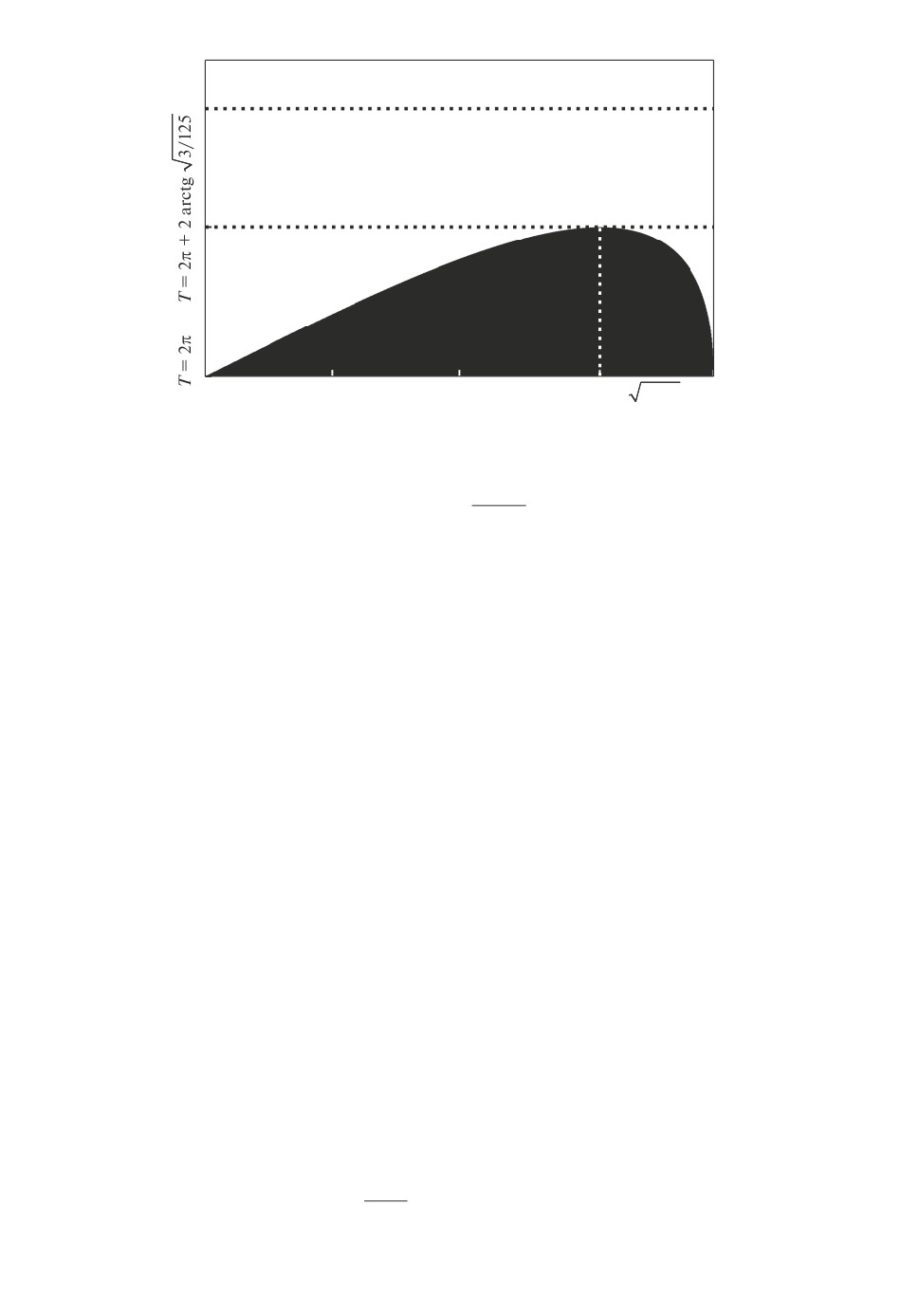
Рис. 2. Иллюстрация поведения неявно заданной функции χ(τ, T ) = 0. Об-

ласть, где χ(τ, T ) > 0, закрашена черным, а область, где χ(τ, T ) < 0, белым.

√

Лемма 2. Время T = 2(π + arctg

3/125) является минимальным вре-

менем, для которого при любых T ≥ T множество B_G(T) состоит только

из элементов множества B_CS(T).

Доказательство леммы 2. Согласно выражению (3.5) для BG(T )

нужно показать, что {(x, y) ∈ B_CC(T )| (|x| - 1)² + y² < 1} = ∅ для T ≥ T .

В силу симметрии рассмотрим только случай правой полуплоскости. Ра-

нее было отмечено, что τ ≤ π/2 для траекторий, ведущих на B_CC (T ). Если

τ > π/3, то вторая дуга траектории LR не пересечет круг D_R ни при каких T.

Значит всякая геодезическая линия, ведущая в D_R, имеет время переключе-

ния τ ≤ π/3. Подставим в

(|x_T | - 1)² + y^2T < 1

второе соотношение из (3.3) и соотношение (3.4). Получим

(3.6)

χ(τ, T )=

2(cos τ - 1) + cos(T - τ) - cos(T - 2τ) > 0.

Так как B_CC(T ) = ∅ при T ≥ T^∗, то нужно показать, что неравенство (3.6)

не справедливо ни при каких τ ∈ [0, π/3] и T ∈ [T , T^∗]. Функция χ(τ, T ) мо-

нотонно убывает по T при любом τ ∈ (0, π/3]. Проанализируем график неяв-

но заданной функции, определяемой уравнением χ(τ, T ) = 0 относительно T

(рис. 2). Эта неявная функции имеет единственный максимум на прямоуголь-

нике τ ∈ (0, π/3], T ∈ [2π, T^∗]. Положение этого максимума определяется ре-

шением системы уравнений

{

2(cos τ - 1) + cos(T - τ) = cos(T - 2τ);

-2sin τ + sin(T - τ) = 2sin(T - 2τ).

Ход решения этой системы на рассматриваемом прямоугольнике довольно

громоздкий. Непосредстве√ой подстановкой можно убедиться, что еe реше-

ние это пара τ = 2 arctg

5/27, T = T . Лемма доказана.

4. Решение задачи перехвата

Покажем, что оптимальная точка перехвата подвижной цели лежит на

границе B(t) множества достижимости R(t) за исключением одного случая.

Согласно [14, с. 208] множество R(t) замкнуто и ограничено для всех поло-

жительных t. Граница B(t) множества достижимости состоит из нескольких

гладких частей. Эти части непрерывно связаны между собой не более чем в

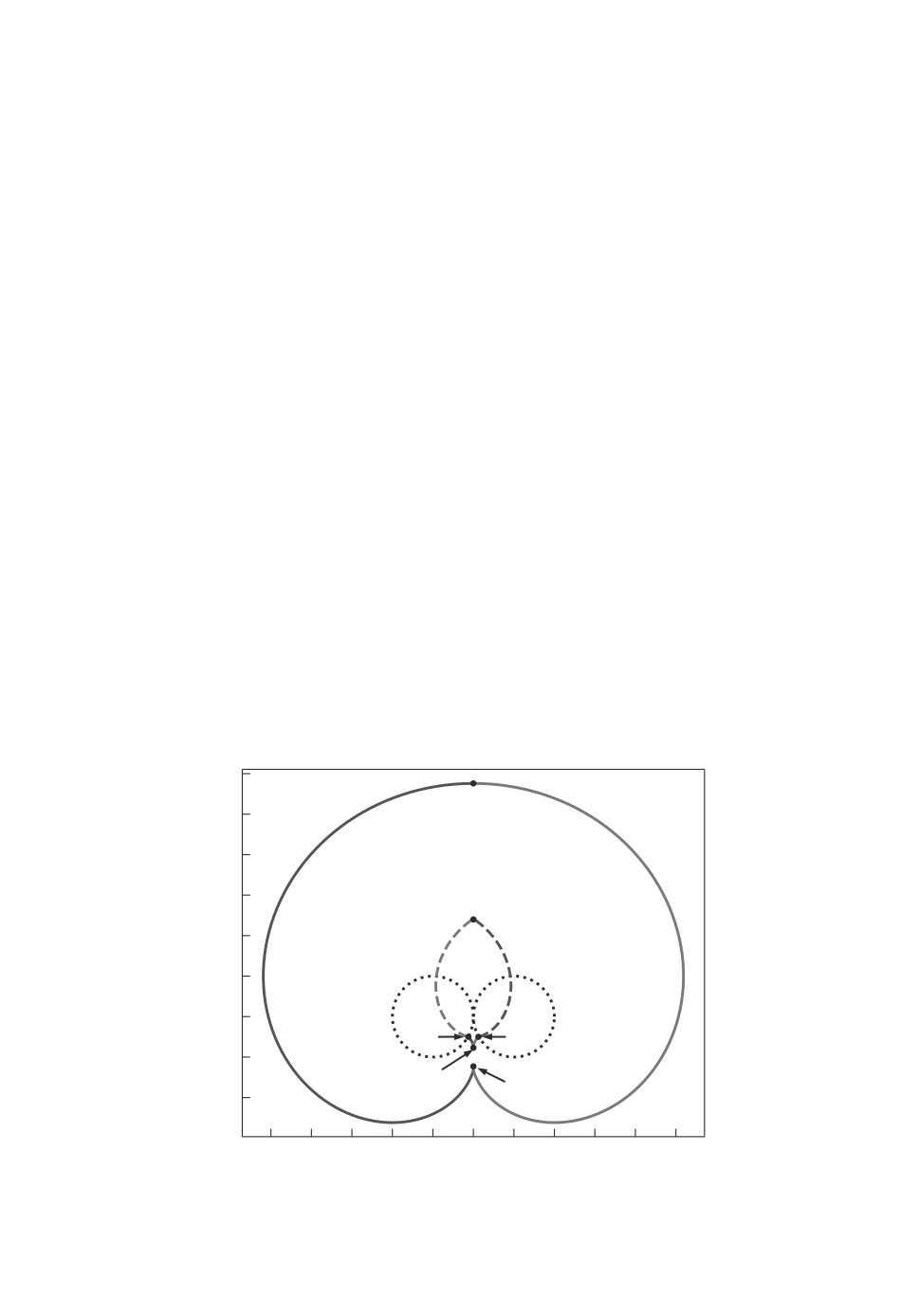
шести точках в каждый момент времени t (рис. 3). Для t ∈ (0,3π/2+ 1) таких

точек четыре: (a), (b), (c) и (d); при t = 3π/2 + 1 их пять: точка (e) совпадает

с точкой (f); для t ∈ (3π/2+1,2π) их шесть; для t ∈ [2π, T ^∗) их четыре: точки

(c), (d) и (e) совпадают при t = 2π; при t ≥ T^∗ их две: (a) и (f).

Многозначное отображение B называется полунепрерывным снизу в мо-

мент времени t₀, если для всякого ε > 0 и всякой точки P₀ ∈ B(t₀) суще-

ствует δ > 0, что для любого t : |t - t₀| < δ существует точка P ∈ B(t), что

∥P - P₀∥ < ε. Многозначное отображение B полунепрерывно сверху в мо-

мент времени t₀, если для всякого ε > 0 существует δ > 0, что для любо-

го t : |t - t₀| < δ и любой точки P ∈ B(t) существует точка P₀ ∈ B(t₀), что

∥P - P₀∥ < ε. Если многозначное отображение B полунепрерывно снизу и

сверху в точке t₀, то оно называется непрерывным в этой точке.

Лемма 3. Многозначное отображение B, задающее эволюцию границы

множества достижимости, является непрерывным в любой момент вре-

мени t > 0, кроме t = T^∗, где отображение B является полунепрерывным

снизу.

Доказательство леммы 3. Сначала покажем, что все точки B(t₀),

кроме (a)-(f), имеют конечную скорость движения на плоскости для всякого

t₀ > 0. Зафиксируем P₀ = (x₀,y₀) ∈ B(t₀) и рассмотрим два случая. В первом

(a)

(b)

(c)

(d)

-1

(e)

( f )

-2

-5

-4

-3

-2

-1

Рис. 3. Граница B(t) множества достижимости в момент t = 11π/6. В этот

момент на границе присутствуют все шесть точек сшивания гладких границ.

случае P₀ ∈ B_CS (t₀), причем точка P₀ не совпадает с точками (a), (c)-(f).

В соответствии с (3.2) имеет место система

{

x₀ = s₀(-(t₀ - τ₀)sin τ₀ + cos τ₀ - 1);

y₀ = (t₀ - τ₀)cos τ₀ + sinτ₀.

Берем частные производные по t₀ от первого и второго уравнения этой си-

стемы, возводим их в квадрат, суммируем и получаем уравнение

)₂

(∂x₀

(∂y₀)² = 1.

∂t₀

Во втором случае P₀ ∈ B_CC (t₀), причем точка P₀ не совпадает c точками

(b)-(d). В соответствии с (3.3) справедлива система

{

x₀ = s₀((2 - cos(t₀ - τ₀))cos τ₀ - sin(t₀ - τ₀)sin τ₀ - 1),

y₀ = (2 - cos(t₀ - τ₀))sin τ₀ + sin(t₀ - τ₀)cos τ₀.

Снова берем частные производные по t₀ от первого и второго уравнений этой

системы, возводим их в квадрат, суммируем и получаем уравнение

)₂

(∂x₀

(∂y₀)² = 1.

∂t₀

При единичной скорости всегда найдется δ = ε > 0 и точка P ∈ B(t), что при

|t - t₀| < δ имеет место ∥P - P₀∥ ≤ |t - t₀| < δ = ε.

Теперь пусть P₀ одна из точек (a)-(f). В силу того, что P₀ примыка-

ет к непрерывным линиям множества B(t₀), для любых t₀ найдется отлич-

ная от (a)-(f) точка P^′0 ∈ B(t₀) такая, что ∥P₀ - P^′0∥ < ε/2, а для P^′0, в связи

с доказанным выше, найдется P ∈ B(t), причем ∥P - P^′0∥ < ε/2. Пользуясь

неравенством треугольника, получим ∥P - P₀∥ < ε, что доказывает полуне-

прерывность снизу.

Так как B(t) состоит из непрерывных частей, то для любой точки P ∈ B(t)

найдется P^′ ∈ B(t), отличная от (a)-(f), причем ∥P - P^′∥ ≤ ε/2. Если t₀ = T^∗,

то выбрав δ = min(|T^∗ - t₀|, ε/2), для любого момента t : |t - t₀| < δ и любой

точки P ∈ B(t) найдется такая точка P₀ ∈ B(t₀), для которой выполняется

∥P - P₀∥ ≤ ∥P - P^′∥ + ∥P^′ - P₀∥ ≤ ε/2 + |t - t₀| < ε/2 + δ ≤ ε,

что доказывает полунепрерывность сверху для всех t₀ > 0, кроме t₀ = T^∗. В

момент t₀ = T^∗ пропадает множество B_CC (t₀), которое отделено от B_CS(t₀),

поэтому полунепрерывности сверху в этот момент нет. Лемма доказана.

Утверждение 1. Если оптимальный перехват цели возможен в мо-

мент времени T, то оптимальная точка перехвата лежит на B(T), кроме

√

случая, когда оптимальная точка перехвата E^∗ = (0, 2

2/3), а оптималь-

ное время перехвата T = T^∗.

Доказательство утверждения 1. Если E(T ) = E∗ и T = T∗, то

оптимальный перехват осуществляется по траектории типа RL или LR, но

происходит не на B(T ), так как в силу приведенного в разделе 3 описания

границы множества достижимости E^∗ ∈ B(T^∗). Пусть теперь E(T ) = E^∗ или

T = T ^∗. Предположим, что E(T) является внутренней точкой для R(T). То-

гда найдется шар O с центром в точке E(T ), который полностью лежит внут-

ри R(T ) и каждая точка границы такого шара удалена от B(T ) не менее чем

на ε > 0. В силу леммы 3 и ¾стягивания¿ B_CC (t) к E^∗ = E(T ) при t → T^∗

найдется такое δ > 0, что для всяких t ∈ (T - δ, T + δ) точки границы B(t) не

попадут в этот шар, поэтому O ⊂ R(t). В силу непрерывности E(t) можно вы-

брать δ настолько малым, чтобы выполнялось E(t) ∈ O. Значит E(t) ∈ R(t),

что противоречит тому, что T минимальное время перехвата, а следова-

тельно, E(T ) лежит на границе R(T ). Утверждение доказано.

Получим алгебраические уравнения для определения оптимального вре-

мени перехвата. Если оптимальный перехват осуществляется по траектории

типа CS, то в соответствии с (2.3) и (3.2) оптимальные τ и T определяются

следующей системой:

{

1 - |x_E(T)| = -(T - τ)sinτ + cosτ;

(4.1)

y_E(T) = (T - τ)cos τ + sin τ.

Возведем выражения (4.1) в квадрат и просуммируем их, тогда после нетруд-

ных преобразований и учета того, что T ≥ τ, получим

√

(4.2)

T -τ =

(1 - |x_E (T )|)² + y^2E

(T ) - 1.

Введем обозначения

√

1 - |x_E(T)| + y_E(T)

(1 - |x_E (T )|)² + y^2E(T ) - 1

(1 - |x_E(T )|)² + y^2E(T )

√

y_E(T) - (1 - |x_E(T)|)

(1 - |x_E (T )|)² + y^2E(T ) - 1

(1 - |x_E(T )|)² + y^2E(T )

тогда после подстановки (4.2) в (4.1), решая систему (4.1) относительно τ ∈

∈ [0, 2π), получим

{

arccos α_C (T ),

α_S(T) ≥ 0;

2π - arccos α_C (T ),

α_S(T) < 0.

Подставив значение τ = θ_CS (T ) в (4.2), получим уравнение для определения

оптимального времени перехвата. Таким образом, оптимальное время пере-

хвата T_CS[x_E , y_E] является наименьшим неотрицательным корнем следующе-

го уравнения относительно T

√

(4.3)

T - θ_CS(T) -

(1 - |x_E (T )|)² + y^2E

(T ) - 1 = 0.

Если данное уравнение не имеет неотрицательных корней, то будем полагать,

что T_CS[x_E , y_E ] = +∞. Для некоторых T в левой части выражения (4.3) мо-

гут возникать некорректные операции: деление на ноль, извлечение корня

из отрицательного числа и т.п. В таких случаях оптимальная поимка в мо-

мент T по траектории типа CS невозможна. Например, если предположить,

что оптимальная точка перехвата лежит внутри кругов D_L, D_R, то оптималь-

ный перехват не может быть осуществлен по траектории типа CS, так как

при вычислении левой части (4.3) возникнет корень из отрицательного числа,

поэтому в этом случае полагаем, что T_CS[x_E , y_E ] = +∞.

Теперь проведем аналогичные рассуждения для случая оптимального пе-

рехвата по траектории типа CC. В соответствии с (2.3) и (3.3) оптимальные

τ и T определяются системой

{

|x_E (T )| + 1 = (2 - cos(T - τ)) cos τ - sin(T - τ) sin τ,

(4.4)

y_E(T) = (2 - cos(T - τ))sin τ + sin(T - τ)cos τ.

Возведем выражения (4.4) в квадрат и просуммируем их, тогда после нетруд-

ных преобразований получим

5 - (1 + |x_E(T)|)² - y^2E(T)

def

(4.5)

cos(T - τ) =

= α(T ).

После подстановки (4.5) в (4.4), решая систему (4.4) относительно τ ∈ [0, π/2],

получим, вообще говоря, два решения:

√

(1 + |x_E (T )|)(2 - α(T )) ± y_E(T )

1 - α²(T)

= arccos

(1 + |x_E (T )|)² + y^2E(T )

Можно показать, что если T ≤ π, то τ = θ^+CC (T ), а если T ≥ π + arccos(1/3),

то τ = θ^-CC (T ).

Рассматривая отдельно случаи τ = θ^+CC (T ) и τ = θ^-CC (T ), после подстанов-

ки τ в (4.5) и обращения косинуса с учетом того, что T - τ ∈ [0, 2π], получим

два уравнения для определения оптимального времени перехвата:

T - θ^+CC(T) - arccosα(T) = 0,

(4.6)

T - θ^-CC(T) - 2π + arccosα(T) = 0.

Наименьшие неотрицательные корни этих двух уравнений будем обозначать

через T^+CC[x_E , y_E ], T^-CC [x_E, y_E ] соответственно. В случае отсутствия корней

будем полагать, что T^±CC [x_E , y_E] = +∞. Как и в случае траекторий типа CS,

при вычислении левой части какого-либо из уравнений (4.6) для некоторо-

го T могут возникать некорректные операции. Если некорректные операции

возникают при вычислении сразу двух выражений, то оптимальная поимка

в момент T по траектории типа CC невозможна. Если некорректные опера-

ции появляются при вычислении первого выражения, а второе выражение

при подстановке T превращается в тождество, то оптимальный перехват осу-

ществляется с моментом переключения θ^-CC (T ) и наоборот. Оптимальное вре-

мя перехвата определяется выбором наименьшего времени из двух времен:

T_CC[x_E,y_E] = min(T⁺

[x_E, y_E ], T_C

[x_E , y_E ]). Оптимальный момент переклю-

чения при известном T определяется следующим образом:

{

θ⁺

(T ),

T^+CC[x_E,y_E] ≤ T^-CC[x_E,y_E];

= CC

θ^-CC(T),

T^+CC[x_E,y_E] > T^-CC[x_E,y_E].

Если перехват невозможен, то уравнения (4.3), (4.6) не имеют неотри-

цательных решений. Если перехват возможен, то хотя бы одно из уравне-

ний (4.3), (4.6) имеет неотрицательное решение, так как машина Дубинса

вполне управляема в классах траекторий CS и CC.

Если оптимальная точка перехвата лежит на оси ординат, то начальный

знак управления может быть выбран произвольным (в силу симметрии за-

дачи). В соответствии с леммой 1, если оптимальной траекторией является

линия типа CS, то оптимальное управление выглядит так:



-sgn xE(TCS[xE,yE]), t < θCS(TCS[xE,yE]), xE(TCS[xE,yE]) = 0;



^def=

±1,

t < θ_CS(T_CS[x_E,y_E]), x_E(T_CS[x_E,y_E]) = 0;



0,

t ≥ θ_CS(T_CS[x_E,y_E]).

Если оптимальной траекторией является линия типа CC, то оптимальное

управление выглядит так:





sgn x_E (T_CC [x_E , y_E]), t < θ_CC (T_CC [x_E, y_E ]), x_E (T_CC [x_E , y_E]) = 0;





-sgn x_E(T_CC[x_E,y_E]), t ≥ θ_CC(T_CC[x_E,y_E]), x_E(T_CC[x_E,y_E]) = 0;

^def=

±1,

t < θ_CC(T_CC[x_E,y_E]), x_E(T_CC[x_E,y_E]) = 0;



∓1,

t ≥ θ_CC(T_CC[x_E,y_E]), x_E(T_CC[x_E,y_E]) = 0.

Выбор знака ± в приведенных выражениях может быть сделан произвольным

образом.

Пусть время перехвата цели, движение которой заранее известно, является

конечным. Тогда справедливо следующее утверждение.

Утверждение 2. Оптимальное управление в задаче перехвата по-

движной цели машиной Дубинса за кратчайшее время имеет вид

{

u^o

(t),

T_CS[x_E,y_E] ≤ T_CC[x_E,y_E],

= CS

u^oCC(t),

T_CS[x_E,y_E] > T_CC[x_E,y_E].

На основе описания B_G(t) и утверждения 1 нетрудно сформулировать ал-

гебраический критерий оптимальности перехвата по геодезической линии.

Для этого необходимо и достаточно потребовать, чтобы оптимальная точка

перехвата лежала на B_G(T ).

Утверждение 3. Оптимальная траектория перехвата является гео-

дезической линией в том и только в том случае, когда T_CS[x_E,y_E] ≤

≤ T_CC[x_E,y_E] или (|x_E(T_CC[x_E,y_E])| - 1)² + y^2E(T_CC[x_E,y_E]) < 1.

Теорема 5 из [26] является частным случаем этого утверждения. Действи-

тельно, если оптимальный перехват возможен и T_CS [x_E , y_E] ≤ T_CC[x_E , y_E ], то

он осуществляется по траектории типа CS и заканчивается вне кругов D_L

и D_R. При этом требование к траектории цели по ненахождению еe частей

внутри D_L и D_R отпадает.

5. Численные примеры

С помощью утверждения 2 и выражений (4.3), (4.6) можно построить оп-

тимальную траекторию перехвата подвижной цели. Опишем последователь-

ность действий, которая позволяет сделать подобное построение. На пер-

вом шаге нужно найти три минимальных неотрицательных корня уравне-

ний (4.3), (4.6). Если какое-либо уравнение не имеет корней, то считаем, что

его корень равен +∞. В конце первого шага имеем три значения T_CS[x_E , y_E],

v₂ = 1/5

j₂ = 3p/4

v₁ = 1/10

j₁ = p/3

E₄₀ = (1/2, 1/2)

v₄ = 1/2

E₂₀ = (3, 1)

j₄ = p

$_L

E₁₀ = (-1/2, 3/5)

$_R

$_L

E₃₀ = (3/2, -3/5)

E₅₀ = (-1/2, -1)

-1

v₃ = 3/10 j₃ = 11p/6

v₅ = 3/10 j₅ = p/12

-2

-1

-2

-1

$_L

$_R

v₆ = 3/2

j₆ = p/2

-1

v₇ = 3/2 j₇ = p/3

E₆₀ = (-1/2, -1)

E₇₀ = (0, -3/2)

-2

-1

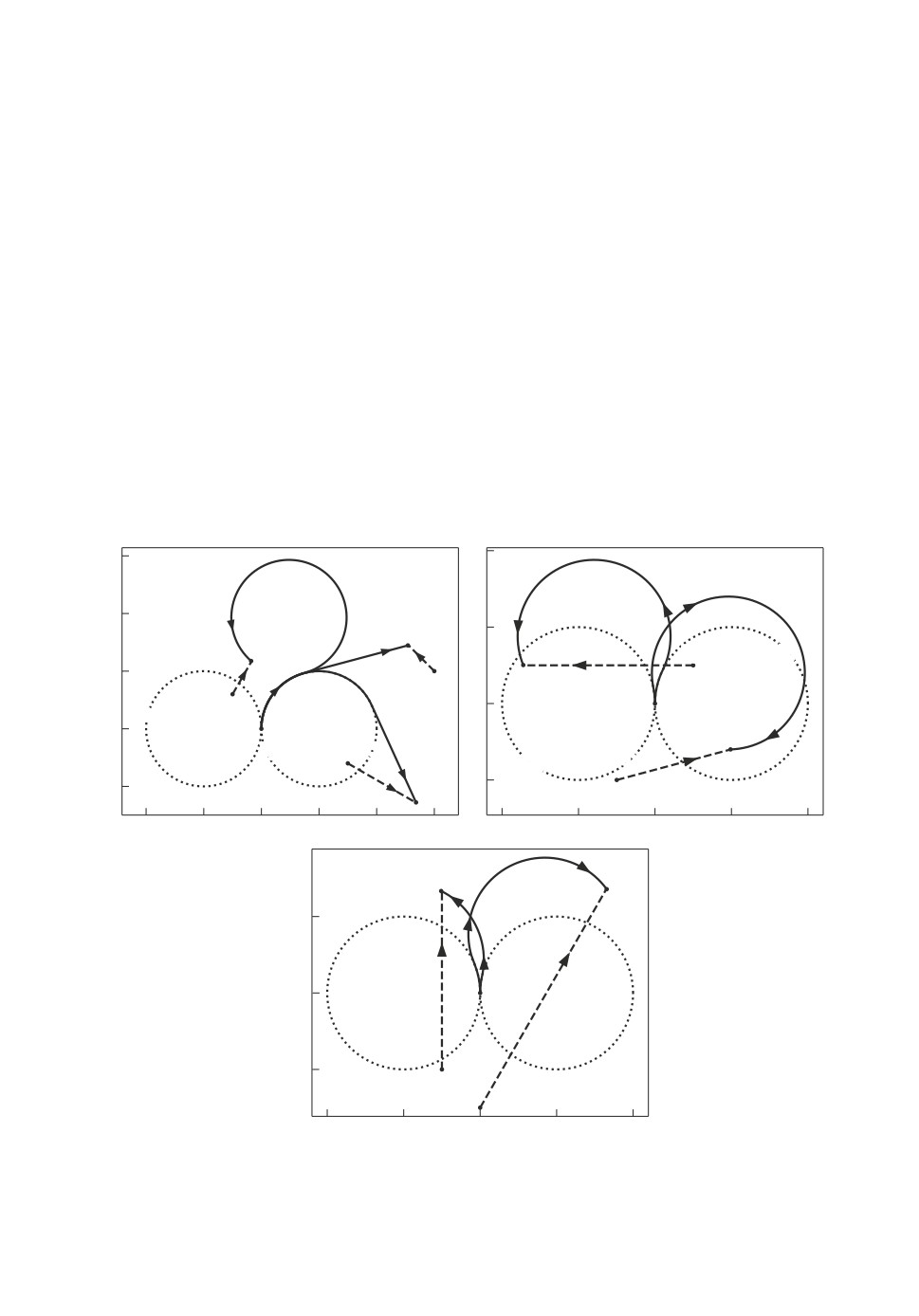
Рис. 4. Траектория оптимального перехвата (сплошная линия) при семи раз-

личных вариантах движения цели (пунктирная линия). E_i(t) = E_i0 + v_it, где

v_i = (v_i cosϕ_i, v_i sinϕ_i), i ∈ {1, 2, . . ., 7}.

T⁺

[x_E , y_E ], T_C

[x_E , y_E]. Если все три значения равны +∞, то перехват невоз-

можен. В противном случае трех вычисленных значений достаточно, чтобы

явно получить оптимальное управление при помощи утверждения 2.

Траектория движения цели может быть любой непрерывной линией. Для

простоты иллюстраций будем полагать, что цель движется по прямой с по-

стоянной скоростью. На рис. 4 изображено семь различных случаев перехва-

та. При i = 1 цель начинает свое движение из круга D_L с достаточно малой

скоростью, которая позволяет цели избежать встречи на множестве B_CS(t)

и отсрочить перехват до момента попадания на B_CC (T ). При i = 2 траекто-

рия цели не проходит через круги D_L, D_R, поэтому оптимальный перехват

осуществляется по траектории типа CS. При i = 3 цель начинает свое движе-

ние из D_R, а оптимальный перехват, как и в случае i = 2, осуществляется по

геодезической линии, так как выполнены условия утверждения 3. При i = 4

движение начинается из D_R, а оптимальный перехват происходит в D_L. Этот

случай примечателен тем, что траектория цели может пересекать оптималь-

ную траекторию машины до момента перехвата. При i = 5 движение цели на-

чинается вне кругов D_L, D_R, а оптимальный перехват происходит внутри D_R

по траектории класса CC. При i = 6 и i = 7 цель имеет скорость, которая

выше или равна скорости машины, но машина, несмотря на это, способна

перехватить цель.

Полученные примеры дополняют известные в литературе частные случаи

оптимального перехвата. Отметим, что случаи i ∈ {1, 2, 3, 6, 7} иллюстрируют

тот факт, что если оптимальная точка перехвата лежит вне кругов D_L, D_R,

то оптимальная траектория машины может быть как из класса CC (при

i ∈ {1,6,7}, например), так и из класса CS (при i ∈ {2,3}). Если же опти-

мальная точка перехвата лежит внутри кругов D_L, D_R, то оптимальная тра-

ектория машины принадлежит только классу CC.

6. Заключение

Для задачи перехвата подвижной цели машиной Дубинса за кратчайшее

время получены аналитические выражения (4.3), (4.6), позволяющие опреде-

лить минимальное время перехвата. С помощью леммы 3 показано, что мно-

гозначное отображение B, задающее эволюцию границы множества дости-

жимости, является непрерывным, кроме одного момента времени. Утверж-

дения 1, 2 позволяют определить положение оптимальной точки перехвата и

вид оптимального управления. Приведенные выражения позволяют решить

задачу наискорейшего перехвата при произвольной непрерывной и наперед

заданной траектории движения цели. Выражения (4.3), (4.6) могут быть

упрощены и оптимальное время перехвата может быть выражено явно, ес-

ли класс траекторий цели уже класса непрерывных линий (например, точка,

если цель покоится).

Утверждение 3 содержит в себе алгебраический критерий оптимальности

перехвата по геодезической линии. Лемма 2 определяет пороговое значение

времени перехвата для любого времени, больше которого оптимальные геоде-

зические траектории принадлежат только классу CS. Однако для некоторых

случаев движения цели оптимальный перехват не всегда проходит по геоде-

зической линии, что также проиллюстрировано численными примерами и

моделированием.

СПИСОК ЛИТЕРАТУРЫ

Марков А.А. Несколько примеров решения особого рода задач о наибольших и

наименьших величинах // Сообщения Харьк. мат. общества. Вторая серия. Т. I.

1889. С. 250-276.

Isaacs R. Differential games. N.Y.: Wiley, 1965.

Бердышев Ю.И. Синтез оптимального управления для одной системы 3-го по-

рядка // Вопросы анализа нелинейных систем автоматического управления.

1973. № 12. С. 91-101.

Coates S., Pachter M., Murphey R. Optimal Control of a Dubins Car with a Capture

Set and the Homicidal Chauffeur Differential Game // IFAC-PapersOnLine. 2017.

V. 50. No. 1. P. 5091-5096.

Pachter M., Coates S. The Classical Homicidal Chauffeur Game // Dyn. Games

Appl. 2019. V. 9. No. 3. P. 800-850.

Бердышев Ю.И. Синтез оптимального по быстродействию управления для одной

нелинейной системы четвертого порядка // ПММ. 1975. Т. 39. № 6. С. 985-994.

Berdyshev Iu.I. Time-optimal control synthesis for a fourth-order nonlinear system //

J. Appl. Math. Mech. 1975. V. 39. No. 6. P. 985-994.

Бердышев Ю.И. Нелинейные задачи последовательного управления и их прило-

жение: Монография. УрО РАН, Екатеринбург, 2015.

Clements J.C. Minimum-time turn trajectories to fly-to points // Optim. Control

Appl. Meth. 1990. V. 11. No. 1. P. 39-50.

Dubins L.E. On Curves of Minimal Length with a Constraint on Average Curvature,

and with Prescribed Initial and Terminal Positions and Tangents // Am. J. Math.

JSTOR. 1957. V. 79. No. 3. P. 497-516.

10.

Pecsvaradi T. Optimal horizontal guidance law for aircraft in the terminal area //

IEEE Trans. Autom. Control. 1972. V. 17. No. 6. P. 763-772.

11.

Bui X.N. et al. Shortest path synthesis for Dubins non-holonomic robot // Proc. Int.

Conf. on Robotics and Automation. San Diego, 1994. V. 1. P. 2-7.

12.

Бедин Д.А., Пацко В.С., Федотов А.А. и др. Восстановление траектории само-

лета по неточным измерениям // АиТ. 2010. № 2. С. 17-30.

Bedin D.A. et al. Restoration of aircraft trajectory from inaccurate measurements //

Autom. Remote Control. 2010. V. 71. No. 2. P. 185-197.

13.

Wu A., How J.P. Guaranteed infinite horizon avoidance of unpredictable, dynami-

cally constrained obstacles // Autonom. Robots. 2012. V. 32. No. 3. P. 227-242.

14.

Cockayne E.J., Hall G.W.C. Plane motion of a particle subject to curvature con-

straints // SIAM J. Control. 1975. V. 13. No. 1. P. 197-220.

15.

Boissonnat J., Bui X.N. Accessibility region for a car that only moves forwards along

optimal paths. Sophia-Antipolis, France, 1994. INRIA Tech. Rep. 2181.

16.

Пацко В.С., Пятко С.Г., Федотов А.А. Трехмерное множество достижимости

нелинейной управляемой системы // Известия РАН. Теория и системы управ-

ления. 2003. № 3. С. 8-16.

Patsko V.S., Pyatko S.G., Fedotov A.A. Three-dimensional reachability set for a

nonlinear control system // J. Comput. Syst. Sci. Int. 2003. V. 42. No. 3. P. 320-328.

17.

Пацко В.С., Федотов А.А. Аналитическое описание множества достижимости

для машины Дубинса // Тр. ИММ УрО РАН. 2020. Т. 26. № 1. С. 182-197.

Patsko V.S., Fedotov A.A. Analytic description of a reachable set for the Dubins

car // Trudy Inst. Mat. i Mekh. UrO RAN. 2020. V. 26. No. 1. P. 182-197.

18.

Рубинович Е.Я. Дифференциальная игра программного преследования с огра-

ничением на разворот преследователя // АиТ. 1978. №. 9. C. 38-44.

Rubinovich E.Ya. A differential game of programmed pursuit with a constraint on the

pursuant’s turnabout // Autom. Remote Control. 1979. V. 39. No. 9. P. 1292-1297.

19.

Guelman M., Shinar J. Optimal guidance law in the plane // J. Guid. Control Dyn.

1984. V. 7. No. 4. P. 471-476.

20.

Glizer V.Y. Optimal planar interception with fixed end conditions: Closed-form so-

lution // J. Optim. Theory Appl. 1996. V. 88. No. 3. P. 503-539.

21.

Cockayne E. Plane Pursuit with Curvature Constraints // SIAM J. Appl. Math.

1967. V. 15. No. 6. P. 1511-1516.

22.

Glizer V.Y., Shinar J. On the structure of a class of time-optimal trajectories //

Optim. Control Appl. Meth. 1993. V. 14. No. 4. P. 271-279.

23.

Бердышев Ю.И. О задачах последовательного обхода одним нелинейным объек-

том двух точек // Тр. ИММ УрО РАН. 2005. Т. 11. № 1. C. 43-52.

Berdyshev Yu.I. A problem of the sequential approach of a nonlinear object to two

moving points // Trudy Inst. Mat. i Mekh. UrO RAN. 2005. V. 11. No. 1. P. 43-52.

24.

Looker J.R. Minimum paths to interception of a moving target when constrained by

turning radius. Canberra, Australia: Defence Sci. Technol. Organisation, 2008.

25.

Meyer Y., Isaiah P., Shima T. On Dubins Paths to Intercept a Moving Target at a

Given Time // IFAC Proceedings Volumes. 2014. V. 47. No. 3. P. 2521-2526.

26.

Meyer Y., Isaiah P., Shima T. On Dubins Paths to Intercept a Moving Target //

Automatica. 2015. V. 53. P. 256-263.

27.

Gopalan A., Ratnoo A., Ghose D. Time-optimal guidance for lateral interception of

moving targets // J. Guid. Control Dyn. 2016. V. 39. No. 3. P. 510-525.

28.

Manyam S.G. et al. Optimal dubins paths to intercept a moving target on a circle //

Proc. Am. Control Conf. 2019. V. 2019-July. P. 828-834.

Статья представлена к публикации членом редколлегии Е.Я. Рубиновичем.

Поступила в редакцию 27.08.2020

После доработки 15.11.2020

Принята к публикации 08.12.2020