Автоматика и телемеханика, № 5, 2021
Управление в социально-экономических
системах
© 2021 г. Т.Ю. ПАШИНСКАЯ, канд. физ.-мат. наук (tatyana.obedko@mail.ru),
В.В. ДОМБРОВСКИЙ, д-р техн. наук (dombrovs.ef@tsu.ru)
(Национальный исследовательский Томский государственный университет)
ПРОГНОЗИРУЮЩЕЕ УПРАВЛЕНИЕ ИНВЕСТИЦИОННЫМ
ПОРТФЕЛЕМ НА ФИНАНСОВОМ РЫНКЕ
СО СКРЫТЫМ ПЕРЕКЛЮЧЕНИЕМ РЕЖИМОВ
И MS VAR МОДЕЛЬЮ ДОХОДНОСТЕЙ
Рассматривается задача управления инвестиционным портфелем на
финансовом рынке с переключением режимов с учетом ограничений на
объемы вложений и займов. Предполагается, что доходности рисковых
активов описываются векторной авторегрессионной моделью со скры-
тым переключением режимов (Markov Switching Vector Autoregression,
MS VAR). Для оценки параметров используется EM-алгоритм. Представ-
лены результаты численного моделирования с использованием реальных
данных российского фондового рынка.
Ключевые слова: инвестиционный портфель, прогнозирующее управле-
ние, векторная авторегрессионная модель с переключением режимов,
скрытая марковская цепь.
DOI: 10.31857/S0005231021050081
1. Введение
Задача управления инвестиционным портфелем (ИП) является одной из
ключевых в финансовой инженерии. Финансовые временные ряды представ-
ляют собой нестационарные динамические стохастические системы с высокой
волатильностью и скачкообразными изменениями. В связи с этим для описа-
ния динамики ИП широко используются модели с марковскими скачками.
Задаче управления ИП на финансовом рынке с марковским переключени-
ем режимов посвящены публикации [1-7], в которых предполагается, что цепь
Маркова является наблюдаемой. Однако на практике при управлении ре-
альным ИП состояние цепи, как правило, недоступно прямому наблюдению.
В [8, 9] рассматривается задача управления ИП на скачкообразном рынке со
скрытой сменой режимов цепи. В частности, публикация [8] посвящена задаче
управления по критерию “mean-variance”. Оценки параметров модели скры-
той цепи Маркова получены с использованием EM-алгоритма. Оптимизаци-
онная задача сводится к решению уравнений Гамильтона-Якоби-Беллмана.
В [9] рассматривается задача оптимизации ИП по критерию “mean-variance”
124
с учетом квадратичных транзакционных издержек и ограничений. Для ре-
шения задачи используется метод управления с прогнозирующей моделью
(Model Predictive Control).
Известные результаты по управлению ИП на рынке с переключением ре-
жимов ограничиваются рассмотрением модели экономического броуновского
движения со скачкообразно меняющимися параметрами, в основе которой
лежит предложение о независимости и одинаковой распределенности доход-
ностей рисковых активов. Однако на практике данное предположение, как
правило, не выполняется.
В данной статье рассматривается динамическая задача управления ИП на
финансовом рынке с переключением режимов с учетом явных ограничений
на объемы вложений и займов. Предполагается, что доходности рисковых
финансовых активов описываются векторной авторегрессионной моделью со
скрытым переключением режимов (Markov Switching Vector Autoregression
Model, MS VAR модель) [10, гл. 1, с. 10]. Задача управления ИП формули-
руется как динамическая задача слежения со скользящим горизонтом инве-
стирования за эталонным портфелем, имеющим заданную доходность [11].
Для оценки параметров MS VAR модели используется EM-алгоритм, пред-
ложенный в [10, гл. 6, с. 104]. Данная статья является обобщением результа-
тов, полученных авторами в [7], где предполагается, что состояние цепи Мар-
кова доступно прямому наблюдению. Представлены результаты численного
моделирования с использованием реальных данных российского фондового
рынка.
2. Описание модели и постановка задач управления
Рассмотрим ИП, состоящий из n видов рисковых финансовых активов и
одного безрискового финансового актива (банковский счет или надежные об-
лигации). Управление портфелем осуществляется путем перераспределения
капитала между различными видами инвестиций посредством банковского
счета. Капитал, помещенный в i-й рисковый актив в момент времени k, ра-
вен ui(k) (i = 1, 2, . . . , n), а в безрисковый - u0(k). Тогда общий объем вложе-
ний (капитал портфеля) в момент времени k равен:
∑
(2.1)
V (k) =
ui(k) + u0
(k).
i=1
Отметим, что если ui(k) < 0 (i = 1, n), то это означает участие в операции
“продажа без покрытия” на сумму |ui(k)|. В начальный момент времени весь
капитал помещен в безрисковый актив и заемные средства не используются:
ui(0) = 0 (i = 1,n), u0(0) = V (0).
Пусть ηi(k + 1) - ставка доходности i-го рискового актива за период вре-
мени [k, k + 1]. Это случайная ненаблюдаемая в момент времени k величина,
определяемая по формуле
(2.2)
ηi(k + 1) = (Zi(k + 1) - Zi(k)) /Zi
(k),
где Zi(k) - рыночная цена i-го рискового актива в момент времени k.
125
Отметим, что величина ui(k) (i = 1, n), полученная в момент времени k,
означает для инвестора необходимость совершения сделки на покупку или
на продажу актива i-го вида объемом |ui(k) - [1 + ηi(k)]ui(k - 1)|, где ηi(k) -
наблюдаемая в момент времени k величина.
В момент времени k + 1 капитал ИП станет равен:
∑
(2.3)
V (k + 1) =
[1 + ηi(k + 1)] ui(k) + [1 + r(k + 1)] u0
(k),
i=1
где r(k + 1) - доходность безрисковых вложений.
∑n
С учетом u0(k) = V (k) -
ui(k), уравнение (2.3) преобразуем к виду
i=1
∑
(2.4)
V (k + 1) = [1 + r(k + 1)] V (k) +
[ηi(k + 1) - r(k + 1)] ui
(k).
i=1
Будем полагать, что вектор доходностей рисковых активов η(k) =
= [η1(k), . . . , ηn(k)]T описывается уравнением
(2.5)
η(k + 1) = µ [θ(k + 1)] + y(k + 1),
где θ(k) = [δ(α(k), 1), . . . , δ(α(k), ν)]T , δ(α(k), j)
функция Кронекера
(j = 1, 2, . . . , ν); α(k)
однородная дискретная марковская цепь с конечным
множеством состояний {1, 2, . . . , ν}, матрицей переходных вероятностей
∑
P = [Pij] (i,j ∈{1,2,...,ν}), Pji = P{α(k +1) = j |α(k) = i},
Pji = 1,
j=1
∑ν
и начальным распределением pi = P {α(0) = i} (i = 1, ν),
pi = 1; µ[θ(k)] =
i=1
= [µ1[θ(k)], . . . , µn[θ(k)]]T - вектор ожидаемых доходностей (средних значе-
ний) рисковых активов; вектор y(k) ∈ Rn описывается векторной авторегрес-
сионной моделью порядка p без свободного члена, коэффициенты которой
зависят от состояния цепи Маркова θ(k) (MS VAR, Markov Switching Vector
Autoregression Model) [10, гл. 1, с. 13]:
y(k + 1) = γ1[θ(k + 1)]y(k) + . . . + γp[θ(k + 1)]y(k - p + 1) +
(2.6)
+ Σ[θ(k + 1)]w(k + 1).
Здесь w(k) ∈ Rn - вектор белых шумов с нулевым средним и матрицей кова-
{
}
риации E
w(k)wT(k)
= In, In - единичная матрица размерности n.
Параметры уравнений (2.5), (2.6) принимают одно из возможных значений
из заданного набора в зависимости от состояния цепи Маркова при α(k) = i:
µj[θ(k)] = µ(i)j (j = 1,n), Σ [θ(k)] = Σ(i), γj [θ(k)] = γ(i)j (j = 1,p).
Цепь Маркова θ(k) определяет режим рынка: рынок в состоянии высокой
или низкой волатильности и/или рынок в состоянии восходящего или нисхо-
дящего тренда.
126
Предполагается также, что доходность безрискового актива r[θ(k)] зависит
от состояния цепи Маркова θ(k) и принимает одно из возможных значений
{
}
r(i) ∈ R : i = 1,ν
Вектор θ(k) допускает представление в пространстве состояний [12, гл. 2,
с. 17]:
(2.7)
θ (k + 1) = Pθ(k) + υ(k + 1),
где {υ(k)} - последовательность мартингал-разностей.
Процесс, описываемый MS VAR моделью порядка p, может быть представ-
лен в виде процесса первого порядка MS VAR (1):
(2.8)
Y (k + 1) = γ[θ(k + 1)]Y (k) + σ[θ(k + 1)]W (k + 1),
[
]T
Y (k) =
yT(k),yT(k - 1),... ,yT(k + p - 1)
np×1,
[
]T
W (k) =
wT(k), 01×n, 01×n, . . . , 01×nnp×1,
∑
{
}
(2.9)
σ[θ(k)] =
θi(k)σ(i), σ(i) = diag Σ(i),0,... ,0
,
np×np
i=1
(i)
γ(i)1
γ(i)2
... γ(i)p-1 γ
p
∑
In
0
0
0
(2.10)
γ[θ(k)] =
θi(k)γ(i), γ(i) =
0
In ...
0
0
,
i=1
0
0
In
0
np×np
θi(k) (i = 1,ν) - компоненты вектора θ(k).
С учетом (2.5) и (2.8) уравнение (2.4) примет вид
(2.11)
V (k + 1) = A[θ(k + 1)]V (k) + B[Y (k + 1)]u(k) + D[θ(k + 1)]u(k),
где u(k) = [u1(k), . . . , un(k)]T ,
∑
(2.12)
A[θ(k + 1)] =
θi(k + 1)A(i), A(i) = 1 + r(i),
i=1
∑
[
]
(2.13) D[θ(k + 1)] =
θi(k + 1)D(i), D(i) =µ(i)
-r(i) ... µni) -r(i)
,
1
i=1
[
]
B [Y (k + 1)] =
y1(k + 1) y2(k + 1) ... yn(k + 1)
=
(2.14)
[
]
= Y T(k + 1)LT, L =
In,0n×n(p-1)
При управлении портфелем учитываются ограничения:
(2.15)
uimin(k) ≤ ui(k) ≤ uimax
(k) (i = 1, n),
∑
(2.16)
u0min(k) ≤ V (k) -
ui(k) ≤ u0max
(k).
i=1
127
Если uimin(k) < 0 (i = 1, n), то для рискового актива i-го вида допустимо
участие в операции “продажа без покрытия” на сумму не более |umini(k)|; ес-
ли umini(k) ≥ 0, то операции “продажа без покрытия” для рискового актива
i-го вида запрещены; umax0(k) ≥ 0 определяет максимальный размер капита-
ла, который можно вкладывать в безрисковый актив, umaxi(k) ≥ 0 (i = 1, n)
определяют максимальный объем капитала, который мжно вкладывать в
рисковый актив i-го вида; umin0(k) ≤ 0, величина
umin0(k)
определяет макси-
мальный размер займа безрискового актива. Отметим, что величины umini(k)
(i = 1, n), umaxi(k) (i = 0, n) на практике часто зависят от капитала ИП, что
можно учесть, положив umini(k) = γ′iV (k), umaxi(k) = γ′′iV (k), где γ′i, γ′′i - по-
стоянные коэффициенты.
Представим ограничения (2.15)-(2.16) в матричном виде
(2.17)
umin(k) ≤ S(k)u(k) ≤ umax
(k),
где
[
]T
umin(k) =
umin1(k),... ,uminn(k),umin0(k) - V (k)
,
umax(k) = [umax1(k),... ,umaxn(k),umax0(k) - V (k)]T,
[
]
S(k) =
In
-1n
,
−1n = [-1,... ,-1],
In - единичная матрица размерности n.
Будем определять стратегию управления ИП путем перераспределения ка-
питала между различными видами инвестиций так, чтобы капитал реального
портфеля с минимально возможными отклонениями (с минимально возмож-
ным риском) следовал капиталу заданного инвестором эталонного портфеля
с желаемой доходностью µ0, эволюция которого описывается уравнением
(2.18)
V0(k + 1) = [1 + µ0]V0(k), V0
(0) = V (0).
Для управления ИП используем стратегии управления с прогнозирующей
моделью. На каждом шаге k будем минимизировать квадратичный критерий
со скользящим горизонтом управления:
∑ {
[
]2
(2.19)
J (k + m | k) = E ρ1(k + i)
V (k + i | k) - V 0(k + i)
-
i=1
[
]
- ρ2(k + i)
V (k + i | k) - V 0(k + i)
+
}
+ uT(k + i - 1|k)R(k + i - 1)u(k + i - 1|k)V (k),Y (k),θ(k) ,
где m - горизонт прогноза; k - текущий момент времени; V (k + i | k) -
прогнозное значение капитала ИП согласно уравнению динамики (2.11),
u(k + i) = [u1(k + i), . . . , un(k + i)]T - вектор прогнозирующих управлений;
ρ1(k + i) ≥ 0, ρ2(k + i) ≥ 0 - весовые коэффициенты (скалярные величины);
R(k + i) > 0 - положительно определенная симметричная матрица размерно-
сти n.
128
Критерий (2.19) представляет собой линейную комбинацию квадратичной
части, минимизирующей среднеквадратическое отклонение капитала реаль-
ного портфеля от эталонной траектории, и линейной части, которая штра-
фует прогнозные значения капитала ИП, меньшие желаемого значения. Тре-
тье слагаемое неявно накладывает “штраф” за большие объемы вложений в
рисковые активы, а также гарантирует существование решения задачи опти-
мизации (см. замечание к теореме).
Критерий (2.19) может быть записан в эквивалентном виде:
∑ {
(2.20)
J (k + m | k) = E R1(k + i)V2
(k + i | k) -
i=1
- R2(k + i)V (k + i|k) +
}
+uT(k + i - 1|k)R(k + i - 1)u(k + i - 1|k)V (k),Y (k),θ(k) ,
где
R1(k + i) = ρ1(k + i), R2(k + i) = 2V0(k + i)ρ1(k + i) + ρ2(k + i).
Таким образом, имеем задачу управления ИП, динамика которого описы-
вается уравнением (2.11), по критерию (2.20) при ограничениях (2.17).
3. Алгоритм оценки скрытой цепи Маркова
На практике состояние цепи α(k) (или θ(k)) является скрытым. Наблюде-
нию доступен вектор доходностей η(k). Будем полагать, что доходности без-
рисковых активов r(i) и ожидаемые доходности рисковых активов µ(i)j извест-
ны (оцениваются отдельно). Для оценки состояния скрытой цепи Маркова и
параметров MS VAR(p) модели вида (2.6) будем использовать EM-алгоритм
[10, гл. 6, с. 104]. Альтернативным подходом к оценке MS VAR моделей явля-
ется метод “сэмплирования” Гиббса [10, гл. 8, с. 148]. Преимуществом метода
является его робастность по отношению к форме графика функции максиму-
ма правдоподобия. Однако он требует значительных вычислительных затрат.
В [13] предложен адаптивный EM-алгоритм (рекурсивная оценка максималь-
ного правдоподобия). Недостатком подхода является высокая чувствитель-
ность к адаптивной матрице, вычисление которой становится трудоемким
для моделей с большим количеством параметров. В частности, в [13] резуль-
таты ограничиваются моделью с восемью параметрами.
Предположим, что в модели (2.6) случайная составляющая w(k) под-
чиняется стандартно
{
}
раметрами являются β(i) = vec(γ(i)1, . . . , γpi)), Σ(i), i = 1, ν; ρ = vec(P ), θ(0) ,
vec(·) означает операцию векторизации матрицы. Обозначим через λ век-
тор, содержащий все неизвестные параметры модели. Обозначим через Yt =
{
}T
=
yT(t),yT(t - 1),... ,yT(1),yT(0),... ,yT(1 - p)
переменные, наблюдае-
мые до момента времени t включительно, Y ≡ YT - вся выборка наблюде-
ний, доступная на момент времени k, размера T . Обозначим через ηt вектор
129
условных плотностей процесса y(t):
(3.1)
ηt = f(y(t)|θ(t),Yt-1
)=
= [f (y(t) | θ(t) = e1, Yt-1) , . . . , f (y(t) | θ(t) = eν , Yt-1)]T ,
f (y(t)|θ(t) = ei,Yt-1) =
{
)T (
)-1 (
)}
1
1(
=
exp
-
y(t) - y(i)(t)
Σ(i)
y(t) - y(i)(t)
,
Σ(i)
1/2
2
(2π)n/2
y(i)(t) = γ(i)1y(t - 1) + γ(i)2y(t - 2) + ... + γ(i)py(t - p), i = 1,ν.
Пошагово EM-алгоритм имеет вид:
1. Инициализация. Задаются начальные значения параметров модели:
{
}
β(i),Σ(i)
,i = 1,ν;ρ,θ(0) = ξ1|0
2. E-шаг. Определяются отфильтрованные вероятности ξt|t = [ξ1,tt,
...,ξν,t|t]T по формуле (прямая рекурсия):
ηt ⊙ ξt|t-1
ηt ⊙ Pξt-1|t-1
ξt|t =
(
) =
(
), t = 1,T,
1ν = [1, . . . , 1]T .
1Tν
ηt ⊙ ξt|t-1
1Tν
ηt ⊙ Pξt-1|t-1
Определяются сглаженные вероятности по формуле (обратная рекурсия):
[
(
)]
ξT-j|T =
PT
ξT-j+1|T ⊘ ξT-j+1|T-j
⊙ ξT-j|T-j,j = 1,T - 1,
где ξT-j+1|T-j = P ξT-j|T-j. Рекурсия начинается с отфильтрованной вероят-
ности ξT|T . Символы ⊙, ⊘ означают поэлементное матричное умножение и
деление соответственно.
3. М-шаг. Оценки коэффициентов уравнения авторегрессии равны:
(
)
β(i) = (XTΞ(i)X)-1XTΞ(i)
⊗In y,
(3.2)
(
)-1 (
)T
i = 1,ν,
Σ(i) = T(i)
U(i)
Ξ(i)U(i),
(
)T
(
)-1
{(
)}
Υ(i)
= XTΞ(i)X
XTΞ(i)Y, Ξ(i) = diag
ξi,1|T ,... ,ξi,T|T
,
∑
(
)T
(
)T
T(i) =
ξi,t|T ,
U(i)
=Y -X Υ(i)
∈RT×n,
t=1
X = [Y-1,...,Y-p] ∈ RT×np, Y-i = [y(1 - j),...,y(T - j)]T ∈ RT×n,
[
]
y=
yT(1),... ,yT(T)
∈RTn×1.
130
Вероятности перехода равны
(
)
(3.3)
ρ=ξ(2) ⊘
1ν
⊗ξ(1) ,
∑
[(
)
(
)
(
)]
ξ(2) =
ξ(2)t|T,
ξ(2)t|T = vec(P) ⊙
ξt+1|T
⊘
ξt+1|k
⊗
ξt|t
,
t=1
(
)
ξ(1) =
1Tν ⊗ Iν
ξ(2)
символ ⊗ означает прямое произведение матриц.
Оценка начального распределения состояния цепи Маркова равна ξ0 =
=ξ1|T.
4. Шаги 2-3 повторяются до момента выполнения условий сходимости [10,
гл. 6, с. 111].
4. Синтез адаптивных стратегий управления ИП
Решение задачи управления ИП с динамикой (2.11) по критерию (2.20)
при ограничениях (2.17) в условиях скрытой цепи Маркова дается следующей
теоремой.
Теорема. Пусть капитал ИП описывается уравнением (2.11) при огра-
ничениях (2.17). Состояние скрытой цепи Маркова и оценки параметров
MS VAR модели (2.6) производятся EM-алгоритмом. Тогда стратегия про-
гнозирующего управления u(k + i | k) (i = 0, 1, . . . , m - 1) со скользящим го-
ризонтом m, минимизирующая критерий (2.20), на каждом шаге k опреде-
ляется уравнением
[
]
u(k) =
In
0n . . . 0n
U (k),
где In - единичная матрица размерности n, 0n - нулевая матрица размер-
ности n; U(k) = [uT(k |k),... ,uT(k + m - 1|k)]T - последовательность про-
гнозирующих управлений, которая определяется из решения задачи квадра-
тичного программирования с критерием
(4.1)
J (k + m | k) = [2V (k)G(k) - F (k)] U(k) + UT
(k)H(k)U(k)
при ограничениях
(4.2)
Umin(k) ≤ S(k)U(k) ≤ Umax
(k), S(k) = diag {S(k), 0 . . . , 0} ,
где
[
]T
Umin(k) =
uTmin(k),... ,uTmin(k + m - 1)
,
[
]T
Umax(k) =
uTmax(k),... ,uTmax(k + m - 1)
;
131
H(k) = {Htf (k)}, G(t) = {Gt(k)}, F (t) = {Ft(k)} (t, f = 1, m) - блочные мат-
рицы, блоки которых удовлетворяют уравнениям
∑
(
)T
(4.3)
Htt(k) = R(k + t - 1) +
D(it)
Q(it)(k)D(it) +
it=1
∑ ν∑
(
[
]
)T
[
]
+ ...
B γ(it)... γ(i1)Y (k)
+ 2D(it)
Q(i1,...,it)(k)B γ(it)... γ(i1)Y (k)
+
i1=1
it=1
∑
∑ ν∑
[
]
[
]T
+
LT γ(it) . . . γ(ij+1)σ(ij) Q(ij,...,it)(k) γ(it) . . . γ(ij+1)σ(ij)
L,
j=1 ij=1
it=1
∑ ν∑
(
)T
(4.4)
Htf(k) =
D(it)
A(it+1) . . . A(if )Q(it,...,if )(k)D(if ) +
it=1
if =1
∑ ν∑
(
)T
[
]
+ ...
D(it)
A(it+1) ... A(if )Q(i1,...,if )(k)B γ(if ) ... γ(i1)Y (k)
+
i1=1
if =1
∑ ν∑
[
]
(
+ ... BT γ(it) ... γ(i1)Y (k) A(it+1) ... A(if)Q(i1,...,if)(k) D(if) +
i1=1
if =1
[
])
+ B γ(if) ...γ(i1)Y (k)
+
∑
∑ ν∑
[
]
+
LT γ(it) ... γ(ij+1)σ(ij) A(it+1) ...
j=1 ij=1
if =1
[
]T
. . . A(if)Q(ij,...,if)(k) γ(if) . . . γ(ij+1)σ(ij)
L,t,f = 1,m,f > t,
(4.5)
Htf(k) = (Hft(k))T
,
f < t,
∑ ν∑
(
(4.6)
Gt(k) =
A(i1) ... A(it)Q(i1,...,it)(k) D(it) +
i1=1
it=1[
])
+ B γ(it) ... γ(i1)Y (k)
,
∑
(4.7)
Ft(k) =
Q(it)2(k)D(it) +
it=1
∑ ν∑
[
]
+ ... Q(i1,...,it)2(k)B γ(it) ...γ(i1)Y (k) ,
t = 1,m.
i1=1
it=1
132
Матрицы Q(it)(k), Q(it ,...,is)(k), Q(it)2(k), Q(it,...,is)2(k) определяются уравне-
ниями
(4.8)
Q(it)(k) = eitPtθ(k)R1
(k + t) +
∑(
)2
A(it+1)
Q(it,it+1)(k), t = 1,m - 1,
it+1=1
(4.9)
Q(it,...,is)(k) = Θ(it,...,is)(k)R1
(k + s) +
∑(
)2
A(is+1)
Q(it,...,is+1)(k),
t = 1,m - 2,s > t,
is+1=1
∑
(4.10)
Q(it)2(k) = eitPtθ(k)R2(k + t) +
Q(it,it+1)2(k)A(it+1)
,
t = 1,m - 1,
it+1=1
(4.11)
Q(it,...,is)2(k) = Θ(it,...,is)(k)R2
(k + s) +
∑
+
Q(it,...,is+1)2(k)A(is+1), t = 1,m - 2, t < s < m,
is+1=1
с граничными условиями
(4.12)
Q(im)(k) = eim Pmθ(k)R1(k + m),Q(it,...,im)
(k) =
= Θ(it,...,im)(k)R1(k + m), t = 1,m - 1,
(4.13)
Q(im)2(k) = eim Pmθ(k)R2(k + m),Q(it,...,im)2
(k) =
= Θ(it,...,im)(k)R2(k + m), t = 1,m - 1,
где eit = [0, . . . , 0, 1, 0, . . . , 0]1×ν (it = 1, ν, t = 1, m),
(4.14)
(k + t | k), t = 1, m - 1, s > t,
Θ(it,...,is)(k) = Pis,is-1 Pis-1,is-2 . . . Pit+1,itθit
θit(k + t|k)
компонента вектора прогноза состояния цепи Маркова
θ(k + t | k) = Ptθ(k), θ(k) = θT|T (k) - отфильтрованные вероятности, опре-
деляемые уравнениями
ηt ⊙ Pθt-1|t-1
θt|t =
(
), t = 1,T;
1Tν
ηt ⊙ Pθt-1|t-1
[
(
)]
θT-j|T =
PT
θT-j+1|T ⊘ θT-j+1|T-j
⊙ θT-j|T-j, j = 1,T - 1,
где θT-j+1|T-j = P θT-j|T-j, ηt определяется выражением (3.1) при t = k,
оценки γ(it), σ(ij ), P определяются выражениями (3.2)-(3.3).
Доказательство теоремы приведено в Приложении.
133
Замечание. Условие R(k + i) > 0 гарантирует, что критерий (4.1) явля-
ется выпуклым, так как данный критерий получен посредством выпуклого
преобразования критерия (2.20). Следовательно, решение задачи квадратич-
ного программирования с критерием (4.1) существует и единственное, если
ограничения (4.2) совместны.
5. Численное моделирование
Приведем результаты численного моделирования с использованием реаль-
ных данных российского фондового рынка. Предложен адаптивный, реали-
зуемый на практике алгоритм оценки параметров скрытой цепи.
Рассматривался ИП, состоящий из банковского счета и обыкновенных ак-
ций: ПАО “Сбербанк России” (SBER), ПАО “Газпром” (GAZP), ПАО “ГМК
“Норильский никель” (GMKN), ПАО “ЛУКОЙЛ” (LKOH), ПАО “НК “Рос-
нефть” (ROSN). Период инвестирования: 02.08.2010 г.-23.08.2019 г. (T =
= 2282 торговых дня). Моделирование производилось по ценам закрытия;
данные взяты с www.finam.ru. Предполагалось, что в модели ИП (2.11) скры-
тая цепь Маркова может находиться в двух состояниях (ν = 2). Вектор y(k)
описывается MS VAR моделью порядка p = 1 вида (2.6). Проводились числен-
ные эксперименты с порядками авторегрессий от единицы до пяти, однако ре-
зультаты не показали улучшения качества слежения для высоких порядков.
Из-за значительного количества оцениваемых параметров на основе
EM-алгоритма была реализована упрощенная адаптивная процедура оцен-
ки. Параметры уравнений авторегрессии и матрица переходных вероятностей
оценивались по выборке объемом N = 600 наблюдений, предшествующих пе-
риоду инвестирования, и предполагались фиксированными на весь горизонт
инвестирования T . На каждом шаге k = 1, . . . , T для оценки состояния скры-
той цепи переоценивались только отфильтрованные и сглаженные вероятно-
сти по выборке объемом N наблюдений, предшествующих моменту времени k.
Количество итераций EM-алгоритма не превышало 200. Матрица переход-
ных вероятностей на начальном шаге (при k = 1) задавалась произвольно.
В качестве начальных значений вероятностей состояний ξ1|T использовались
эргодические вероятности: p1 = P12/(P12 + P21), p2 = 1 - p1. При k = 2, 3, . . .
для инициализации алгоритма использовались оценки вероятностей состоя-
ний, полученные на шаге k - 1.
Векторы ожидаемых доходностей рисковых активов в каждом состоянии
цепи {µ(1), µ(2)} на каждом k-м шаге оценивались адаптивно методом про-
стой скользящей средней с периодом l[θ(k)], зависящим от состояния цепи,
по формуле:
l[θ(k)]∑
1
(5.1)
µ[θ(k)] =
η(k - i + 1), l[θ(k)] ∈ {l(1), l(2)}, l(1) > l(2).
l[θ(k)]
i=1
Предполагалось, что в состоянии низкой волатильности на рынке наблю-
дается долгосрочный тренд, поэтому применялась скользящая средняя с
более длинным периодом: l(1) = 24, l(2) = 9. Доходность безрискового акти-
ва r[θ(k)] полагалась равной r(1) = 0,00001, r(2) = 0,00005. Капитал реаль-
ного ИП вычислялся по формуле (2.4), где ηi(k + 1) (i = 1, n), r(k + 1) -
134
20
15
1
10
5
2
0
500
1000
1500
2000
k
Рис. 1. Динамика капиталов эталонного ИП (линия 1) и управляемого ИП
(линия 2).
0,20
0,15
0,10
2
3
0,05
0
-0,05
1
-0,10
-0,15
0
500
1000
1500
2000
k
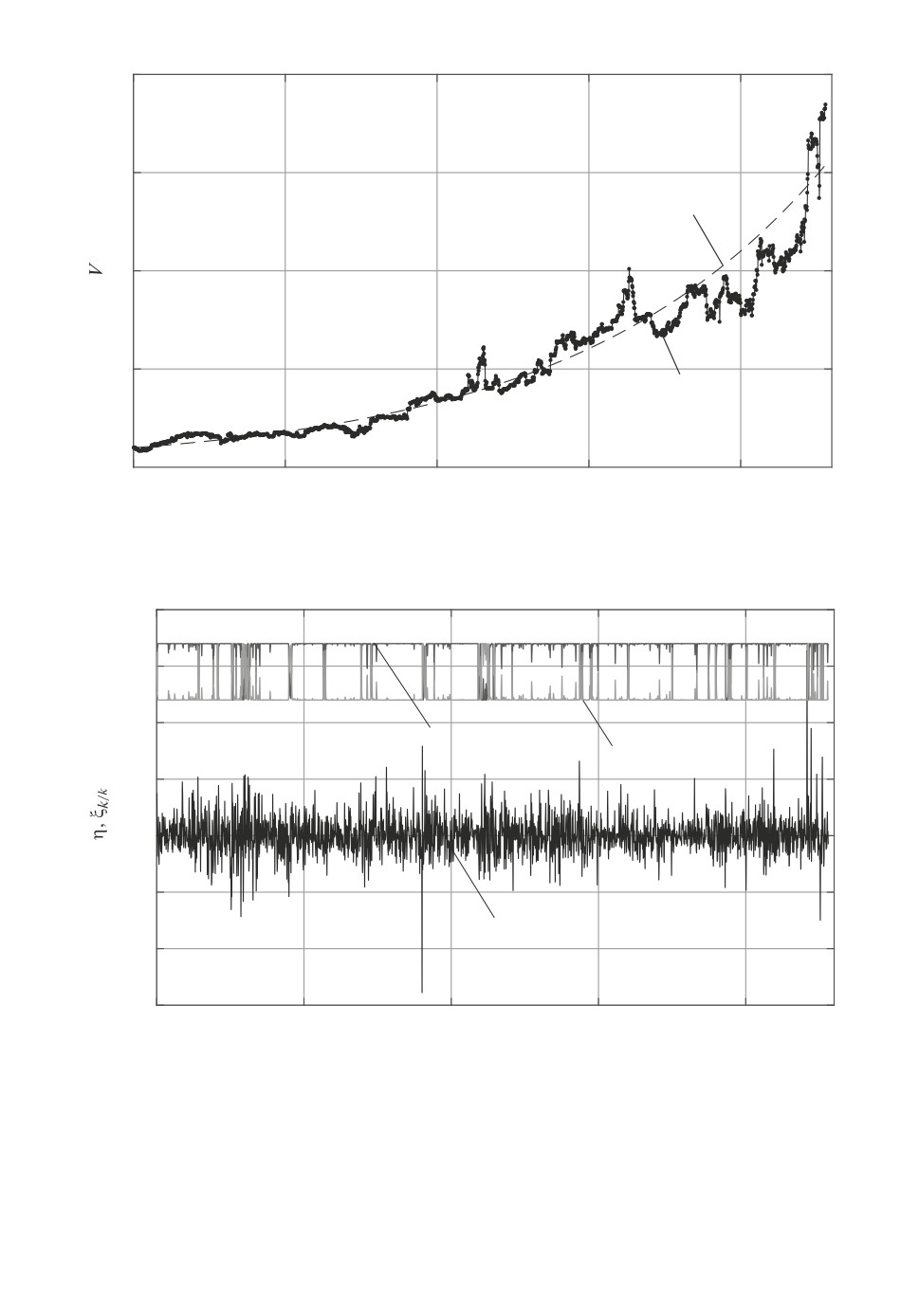
Рис. 2. Динамика доходности акции GAZP (линия 1) и сглаженные вероятно-
сти (линия 2 - состояние 1, линия 3 - состояние 2).
реальные доходности активов. Доходность эталонного ИП µ0 = 0,0012
(0,12 % в день). Весовые коэффициенты R(k + i) = diag{10-4, . . . , 10-4},
ρ1(k + i) = 1, ρ2(k + i) = 0,3 для всех k, i. Горизонт прогноза m = 10. При
135
управлении ИП учитывались ограничения в виде (2.15)-(2.16) с параметрами:
γ′i = 0 (i = 1,... ,5), γi = 3 (i = 0,... ,5). Задача квадратичного программиро-
вания решалась численно с использованием функции quadprog.m в MATLAB.
На рис. 1 показана динамика капиталов эталонного портфеля V0(k) и
управляемого портфеля V (k). Рисунок 2 иллюстрирует динамику доходно-
стей акции GAZP и оценки вероятностей состояний рыночного режима. Из
рис. 1 видно, что траектория капитала реального портфеля следует капиталу
эталонного портфеля.
6. Заключение
В статье решена задача управления ИП с прогнозирующей моделью на
финансовом рынке со скрытым переключением режимов и MS VAR моделью
доходностей с учетом ограничений на объемы вложений и займов. Для оценки
параметров скрытой цепи использовался EM-алгоритм. Проведено численное
моделирование стратегии управления на реальных данных с использованием
адаптивной процедуры оценки параметров скрытой цепи. Результаты демон-
стрируют эффективность предложенной стратегии управления.
ПРИЛОЖЕНИЕ
Доказательство теоремы. Алгоритм доказательства основан на ре-
зультатах, полученных в [7]. Используя сглаживающее свойство условного
математического ожидания, критерий (2.20) может быть представлен в виде
{
J (k + m | k) = E V2(k + 1 | k)R1(k + 1) - R2(k + 1)V (k + 1 | k) +
+ uT(k |k)R(k + 1)u(k |k) +
{
+ E V 2(k + 2|k)R1(k + 2) - R2(k + 2)V (k + 2|k) +
(Π.1)
+uT
(k + 1 | k)R(k + 2)u(k + 1 | k) +
{
+ ... + E V 2(k + m|k)R1(k + m) - R2(k + m)V (k + m|k) +
}
+ uT(k + m - 1|k)R(k + m)u(k + m - 1|k)|V (k + m - 1),θ(k + m - 1) ...
}
}
|V (k + 1),θ(k + 1) ... |V (k),θ(k)
Используя (2.8)-(2.10), (2.11)-(2.14) и (2.7), получим:
(Π.2)
V (k + m - t | k) =
∑
[
=
eim-t [Pθ(k+m-t-1)+υ(k+m-t)] A(im-t)V (k+m-t-1|k) +
im-t=1
(
[
]
+ B γ(im-t)Y (k + m - t - 1) + σ(im-t)W(k + m - t) +
)
]
+ D(im-t) u(k + m - t - 1|k) , t = 0,m - 1.
136
Последовательное вычисление математических ожиданий в (П.1) с учетом
(П.2) и с заменой параметров их оценками (3.1)-(3.3) приводит к выражению
∑
(
)2
∑
J (k + m | k) = V2(k)
A(i1)
Q(i1)(k) -
Q(i1)2(k)A(i1)V (k) +
(Π.3)
i1=1
i1=1
+ [2V (k)G(k) - F (k)]U(k) + UT(k)H(k)U(k),
матрицы G(k), F (k), H(k) имеют вид
(4.3)-(4.7), матрицы Q(it)(k),
Q(it,...,is)(k), Q(i1)2(k), Q(is,...,is)2(k) имеют вид (4.8)-(4.13). Очевидно, что за-
дача минимизации критерия (П.3) при ограничениях (2.17) эквивалентна за-
даче минимизации критерия (4.1), где удалены слагаемые, не зависящие от
управлений, при ограничениях (4.2). Теорема доказана.
СПИСОК ЛИТЕРАТУРЫ
1.
Costa O.L.V., Araujo M.V. A Generalized Multi-Period Portfolio Optimiza-
tion with Markov Switching Parameters // Automatica. 2008. V. 44. No. 10.
2.
Bäuerle N., Rieder U. Portfolio Optimization with Markov-Modulated Stock Prices
and Interest Rates // IEEE Trans. Autom. Control. 2004. V. 49. No. 3. P. 442-447.
3.
Sotomayor L.R., Cadenillas A. Explicit Solutions of Consumption-Investment
Problems in Financial Markets with Regime Switching // Math. Finance. 2009.
4.
Wu H. Mean-Variance Portfolio Selection with a Stochastic Cash Flow in a
Markov-switching Jump-Diffusion Market // J. Optim. Theory Appl. 2013. V. 158.
5.
Levy M., Kaplanski G. Portfolio Selection in Two-regime World // Eur. J. Oper.
6.
Dombrovskii V.V., Obyedko T.Yu., Samorodova M. Model Predictive Control of
Constrained Markovian Jump Nonlinear Stochastic Systems and Portfolio Opti-
mization under Market Frictions // Automatica. 2018. V. 87. No. 1. P. 61-68.
7.
Dombrovskii V., Pashinskaya T. Model Predictive Control Design for Constrained
Markov Jump Bilinear Stochastic Systems with an Application in Finance // Int.
J. Syst. Sci. 2020. V. 51. No. 16. P. 3269-3284.
8.
Ishijima H., Uchida M. Log Mean-Variance Portfolio Selection Under Regime
Switching // Asia-Pacific Financial Markets. 2011. V. 18. No. 2. P. 213-229.
9.
Nystrup P., Boyd S., Lindström E., Madsen H. Multi-Period Portfolio Selection
with Drawdown Control // Ann. Oper. Res. 2018. P. 1-27.
10.
Krolzig H.-M. Markov Switching Vector Autoregressions. Modelling, Statistical
Inference, and Application to Business Cycle Analysis. Berlin: Springer, 1997.
137
11. Dombrovskii V.V., Dombrovskii D.V., Lyashenko E.A. Investment Portfolio Opti-
mization with Transaction Costs and Constraints Using Model Predictive Control //
Proc. 8th Russian-Korean Int. Sympos. on Science and Technology. Tomsk: TPU.
12. Elliott R.J., Aggoun L., Moore J.B. Hidden Markov Models: Estimation and Con-
trol. Berlin, Heidelberg, N.Y.: Springer, 1995.
13. Holst U., Lindgren G., Holst J., Thuvesholmen M. Recursive Estimation in Switch-
ing Autoregressions with Markov Regime // J. Time Series Analysis. 1994. V. 15.
Статья представлена к публикации членом редколлегии А.В. Назиным.
Поступила в редакцию 31.10.2020
После доработки 08.12.2020
Принята к публикации 15.01.2021
138