Автоматика и телемеханика, № 6, 2021

Обзоры

(Томский государственный университет систем управления и радиоэлектроники)

МЕТОДЫ ПОВЫШЕНИЯ ЭФФЕКТИВНОСТИ РОЕВЫХ

АЛГОРИТМОВ ОПТИМИЗАЦИИ¹

Роевые алгоритмы относятся к классу популяционных метаэвристиче-

ских методов оптимизации. Несмотря на использование различных мета-

фор, большинство роевых алгоритмов имеют схожую структуру, в них

можно выделить такие общие компоненты, как инициализация популя-

ции решений, диверсификация и интенсификация решений. На основании

концепции общности был проведен анализ ключевых подходов, методов

и способов повышения эффективности роевых алгоритмов оптимизации.

В обзоре роевые алгоритмы оптимизации рассматриваются как совокуп-

ность операторов, без детального обсуждения каждого алгоритма, основ-

ное внимание сосредоточено на анализе ключевых компонентов алгорит-

мов. Основная идея повышения эффективности заключается в соблюде-

нии баланса между диверсификацией и интенсификацией. В этом контек-

сте рассмотрены механизмы поддержки популяционного разнообразия,

методы настройки и регулировки параметров роевых алгоритмов, подхо-

ды к гибридизации алгоритмов, обозначено несколько открытых проблем,

связанных с темой обзора.

Ключевые слова: оптимизация, метаэвристики, роевые алгоритмы, дивер-

сификация, интенсификация.

DOI: 10.31857/S0005231021060015

1. Введение

Многие сложные проблемы в области науки, техники, экономики и бизнеса

могут быть сформулированы как задачи оптимизации. Традиционные мето-

ды оптимизации, основанные на производных, доказали свою эффективность

в решении различных типов задач оптимизации. Однако применение этих ме-

тодов связано с рядом ограничений, таких как “застревание” в локальных оп-

тимумах, сильная зависимость от начальных условий, большая вычислитель-

ная сложность и неприменимость к конкретным классам целевых функций.

Это привело к необходимости разработки альтернативных методов, которые

могли бы преодолеть эти ограничения [1].

Поиск оптимальных решений NP-трудных задач часто выполняется с по-

мощью методов, получивших название “метаэвристики”. Прежде чем перейти

¹ Исследование выполнено при финансовой поддержке Российского фонда фундамен-

тальных исследований (проект № 19-17-50050).

к рассмотрению метаэвристик, дадим рабочее определение понятию эври-

стика это способ нахождения “достаточно хороших” решений без доказа-

тельства оптимальности найденных решений. Качество или эффективность

решения могут быть выражены через точность, стабильность, экономию па-

мяти или времени. Термин “мета” указывает на обобщенность и “методоло-

гию верхнего уровня”. Как правило, эвристики предназначены для решения

конкретных задач, в то время как метаэвристики независимы от решаемых

проблем. По мнению Шона Люка, автора известной книги “Основы метаэв-

ристик” [2], метаэвристика общее, но неудачное название стохастического

алгоритма оптимизации, который применяется в качестве последней надеж-

ды на пути к решению задачи оптимизации. Стохастическая оптимизация

большой класс алгоритмов и методов, использующих случайность для поиска

оптимального (субоптимального) решения сложных задач. Применяются ме-

таэвристики в том случае, когда 1) неизвестен способ поиска оптимального

решения; 2) недостаточно имеющейся априорной информации; 3) невозмо-

жен полный перебор; 4) можно проверить качество решения, т.е. неизвестна

аналитическая форма целевой функции f(x), но ее значение может быть вы-

числено для конкретного решения x.

Метаэвристики не используют вычисление производных целевой функции,

однако, в отличие от детерминированных методов оптимизации, метаэвристи-

ки позволяют находить за приемлемое время удовлетворительные решения

задач большой размерности. Широкому применению метаэвристик способ-

ствуют увеличение вычислительной мощности компьютеров и развитие па-

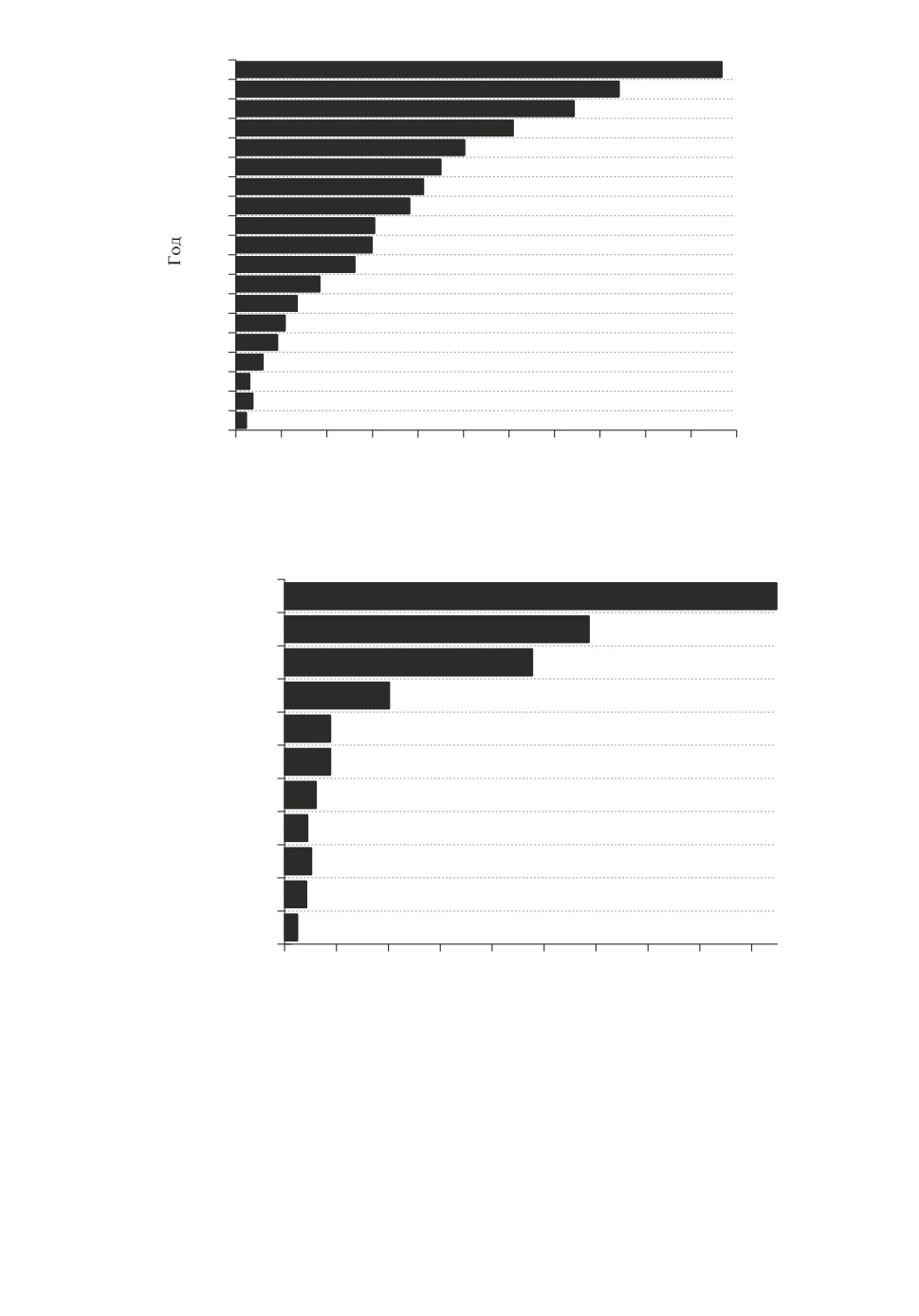
раллельных архитектур [3]. На рис. 1 приведено распределение количества

статей, индексируемых в базе данных Scopus, в которых упоминалось слово

“metaheuristic”, а на рис. 2 указано распределение статей по отраслям знаний.

Метаэвристические методы классифицируются по различным основани-

ям. Методы, формирующие последующее решение на основе единственного

предыдущего решения, относятся к траекторным методам, типичными пред-

ставителями которых являются алгоритм имитации отжига [4] и поиск с за-

претами [5]. Популяционные методы формируют решение на основе своего

предыдущего опыта и информации о лучших решениях в популяции. Траек-

торные методы в большей степени ориентированы на интенсификацию реше-

ний, тогда как базовая метаэвристика, основанная на популяциях, в большей

степени ориентирована на диверсификацию [3]. Популяционные методы раз-

делены на четыре класса [6]: эволюционные алгоритмы, основанные на про-

цессах эволюции; алгоритмы, имитирующие физические процессы; роевые

алгоритмы, основанные на поведенческих процессах социальных животных;

алгоритмы, имитирующие поведение человека.

Концепция отсутствия универсального алгоритма оптимизации, оформ-

ленная в виде “теоремы о бесплатных завтраках” [7], фактически констатиру-

ет отсутствие необходимости оценивать эффективность алгоритмов оптими-

зации в среднем для всех проблем. Теорема указывает на важность понима-

ния взаимосвязи между компонентами алгоритма оптимизации и спецификой

решаемой проблемы и побуждает специалистов к проведению новых иссле-

дований в области роевых алгоритмов. Эти исследования можно разделить

на три большие категории [8]. Первая категория связана с исследованием и

2019

2018

2017

2016

2015

2014

2013

2012

2011

2010

2009

2008

2007

2006

2005

2004

2003

2002

2001

200

400

600

800

1000 1200 1400 1600 1800 2000 2200

Количество статей

Рис. 1. Распределение количества статей, индексируемых в базе данных

Scopus, в которых упоминалось слово “metaheuristic”.

Computer Sci.

Engineering

Mathematics

Decision Sci.

Business

Energy

Physics & Astr.

Social Sci.

Materials Sci.

Environm. Sci.

Chemical Engin.

1000

2000

3000

4000

5000

6000

7000

8000

9000

Количество статей

Рис. 2. Распределение по отраслям знаний статей, в которых упомина-

лось слово “metaheuristic”.

модификацией роевого алгоритма для улучшения его сходимости, точности

решения, уменьшения времени выполнения. Вторая категория относится к

исследованию типов проблем, которые могут быть решены с помощью данно-

го алгоритма. Большинство роевых алгоритмов изначально предназначались

для решения однокритериальных задач безусловной оптимизации. После то-

го как алгоритм показал свою эффективность в решении указанных задач,

проводится его модификация для решения других типов задач, таких как

задачи одноцелевой оптимизации с ограничениями, задачи многоцелевой оп-

тимизации, задачи многоцелевой оптимизации с ограничениями, комбинатор-

ные задачи оптимизации и т.д. Третья категория связана с исследованиями

практических приложений алгоритмов.

Цель обзора связана с первой категорией исследований. Существующие об-

зоры, посвященные метаэвристической оптимизации, по большей части сосре-

доточены на эволюционных алгоритмах и в меньшей степени на роевых ал-

горитмах. Обзоры, за редким исключением, сосредоточены на рассмотрении

метафор, лежащих в основе метаэвристиеских алгоритмов, и не раскрывают

общего понимания механизмов генерации и модификации решений. В пред-

ставленном обзоре роевые алгоритмы оптимизации рассматриваются как со-

вокупность операторов, без детального обсуждения каждого алгоритма, ос-

новное внимание сосредоточено на анализе ключевых компонентов роевых

алгоритмов.

Статья организована следующим образом. В разделе 2 дается краткое опи-

сание основных понятий и терминологии роевых алгоритмов. Так как алго-

ритм роящихся частиц является прототипом для реализации многих после-

дующих роевых алгоритмов, его описанию посвящен раздел 3. Процедуры

инициализации рассматриваются в разделе 4. В разделе 5 приведены некото-

рые меры популяционного разнообразия, а механизмы поддержки разнообра-

зия в разделе 6. Проблемы настройки и регулировки значений параметров

рассматриваются в разделе 7. В разделе 8 дается краткое описание основных

подходов к гибридизации роевых алгоритмов. Открытые проблемы кратко

рассмотрены в разделе 9. В разделе 10 подведены итоги.

2. Основные понятия и терминология

Алгоритмы оптимизации ищут точку в пространстве поиска, в которой

значение целевой функции максимально или минимально в зависимости от

задачи оптимизации.

Рассмотрим задачу поиска минимального значения функции

min f(x), x_min ≤ x ≤ x_max,

x_min = (x_1,min,x_2,min,... ,x_D,min) , x_max = (x_1,max,x_2,max,... ,x_D,max),

x_min и x_max определяют пространство поиска, f : ℜ^D → ℜ целевая функ-

ция D-мерного векторного аргумента, которая оценивает решение x =

= (x₁, x₂, . . . , x_D).

Большинство традиционных методов оптимизации требуют выполнения

определенных условий, таких как выпуклость, непрерывность и т.д. Прини-

мая во внимание ограничения традиционных методов, исследователи предло-

жили использовать методы стохастической оптимизации, в частности роевые

алгоритмы.

Большинство роевых алгоритмов оптимизации основаны на метафоре при-

родных или техногенных процессов. Однако анализ работы метаэвристиче-

ского алгоритма должен быть выполнен с использованием общепринятой тер-

минологии в области оптимизации, а не на языке метафоры. Реальная цен-

ность использования таких метафор в алгоритмах оптимизации часто неясна

и вызывает ряд критических замечаний [9, 10]. Основное замечание связано

с отсутствием алгоритмических различий в так называемых новых метаэв-

ристиках по сравнению с ранее опубликованными. Автор публикации [11],

проведя строгий анализ гармонического поиска [12], приходит к выводу, что

эта метаэвристика является частным случаем хорошо известной эволюцион-

ной стратегии. В [13] показано, что оптимизация на основе черных дыр [14]

является упрощенной версией алгоритма роящихся частиц. Анализ алгорит-

ма под названием “интеллектуальные капли воды” [15] позволил авторам [10]

сделать вывод о том, что все основные алгоритмические компоненты этой

метаэвристики являются упрощениями или частными случаями алгоритма

муравьиной колонии. Другое важное критическое замечание связано с со-

мнением по поводу полезности использования некоторых метафор при раз-

работке алгоритмов оптимизации. Авторы публикаций [9, 10, 13] указывают

на то, что, хотя некоторые метафоры имеют хорошее математическое описа-

ние, созданные на их основе метаэвристики либо существенно модифицируют

указанные описания, либо вообще не соответствуют исходной метафоре. В [9]

утверждается, что в большинстве случаев метафоры совершенно не нужны

для описания алгоритма оптимизации, роль метафор часто преувеличивается

их авторами.

Роевые алгоритмы оптимизации могут рассматриваться как итеративные

процедуры поиска, где рой это множество взаимодействующих частиц, ко-

торые определяют потенциальное решение задачи оптимизации в D-мерном

пространстве. Итоговое решение может быть представлено либо отдельной

частицей (координаты частицы в пространстве поиска), либо группой частиц,

где каждая частица представляет собой часть решения. Существуют две ос-

новные схемы кодирования возможных решений: векторное и представление

в виде графа. В векторном типе представления каждое возможное решение

кодируется строкой значений:

(1)

x_i = (x_i1,x_i2,... ,x_iD

) i = 1,2,...,N,

где N размер популяции, D размерность пространства поиска.

Многие задачи комбинаторной оптимизации, например задача коммивоя-

жера, могут быть представлены в виде графа. В таком представлении части-

цы перемещаются от одного узла к другому, пока не пройдут все узлы, и не

будет найдено полное решение проблемы (путь, соединяющий все города).

Схемы кодирования во многом определяют способ формирования новых

вариантов решения. В большинстве роевых алгоритмов новые решения ге-

нерируются случайным образом или с использованием эвристики, которая

объединяет существующие решения для получения нового. Для векторного

представления типичный метод обновления выполняется на основе уравнения

(2)

x_i(t + 1) = x_i(t) + Δ_i

(t + 1),

где x_i(t)

текущее решение, x_i(t + 1) обновленное решение, Δ_i(t) мо-

дифицирующий вектор, t текущая итерация. Модифицирующий вектор

может быть сформирован так: 1) на основе градиента; 2) перестановкой от-

дельных частей нескольких решений; 3) внесением направленного возмуще-

ния, вычисленного как разность двух решений, умноженная на равномерно

распределенное случайное число; 4) внесением случайного возмущения, ос-

нованного на распределениях Гаусса, Коши, Леви.

В силу ограниченности объема статьи будет рассмотрен только векторный

тип представления решения.

Большинство роевых алгоритмов имеют сходную структуру, в которой

можно выделить ключевые компоненты и функции:

1) инициализация задание значений параметрам алгоритма, формиро-

вание начальной популяции;

2) диверсификация (глобальный поиск) генерация новых решений или

исследование всего пространства поиска, когда модифицирующий вектор мо-

жет принимать большие значения, обеспечивая разнообразие решений и не

позволяя застрять в локальном оптимуме;

3) интенсификация (локальный поиск) улучшение ранее найденных ре-

шений, выполняемое на ограниченном пространстве поиска, в этом случае

модифицирующий вектор принимает малые значения.

Перечисленные выше компоненты реализуют вычислительные процедуры,

например диверсификация почти всегда выполняется путем рандомизации, а

интенсификация реализуется путем незначительного изменения лучших ре-

шений. Роевые алгоритмы можно классифицировать на две группы. В первую

группу входят алгоритмы, в которых явно присутствуют компоненты дивер-

сификации и интенсификации, например меметические алгоритмы [16], алго-

ритм на основе теории электромагнетизма [17], алгоритм ворон [18], прямой

алгоритм муравьиной колонии [19]. Ко второй группе относятся алгоритмы

с одним выражением, отвечающим как за диверсификацию, так и за интен-

сификацию, например алгоритм роящихся частиц [20], алгоритм “кукушкин

поиск” [21]. Для соблюдения баланса между диверсификацией и интенсифи-

кацией необходима мера измерения популяционного разнообразия, определив

которую, можно поддерживать баланс путем изменения параметров алгорит-

ма или гибридизации.

Типичным представителем алгоритмов с одним выражением является ал-

горитм роящихся частиц, являющийся прототипом для реализации многих

последующих алгоритмов и примером для иллюстрации методов повышения

эффективности. Далее приведено краткое описание этого алгоритма.

3. Стандартный алгоритм роящихся частиц

Алгоритм роящихся частиц имеет мало настраиваемых параметров,

небольшое требование к памяти, что делает его вычислительно эффектив-

ным. Алгоритм роящихся частиц [20] это стохастический метод поиска,

основанный на итеративном взаимодействии частиц, образующих рой. Пере-

мещение частицы в пространстве поиска определяют три фактора: инерция,

память, сотрудничество. Инерция подразумевает, что частица не может мгно-

венно изменить свое направление движения. Каждая частица имеет память

и хранит свою лучшую позицию в пространстве поиска. Известна частице и

лучшая позиция роя. Зная эти две позиции, частица динамически изменя-

ет скорость согласно ее собственному опыту и опыту полета других частиц.

Таким образом, движение каждой частицы задается ее лучшей позицией, ее

текущей скоростью, ускорением, заданным предыдущей позицией, и уско-

рением, заданным лучшей частицей в рое. Рой прекращает движение при

выполнении хотя бы одного из следующих условий: рой достиг состояния

равновесия, найдено оптимальное решение (ошибка меньше заданной), вы-

полнено заданное количество итераций. Пространство поиска множество

действительных чисел, рой состоит из N частиц-решений. Позиция i-й части-

цы определяется вектором (1). Лучшая позиция, которую занимала i-я части-

ца, определяется вектором p_i = (p_i1, p_i2, . . . , p_iD), модифицирующий вектор в

выражении (2) определяется скоростью частицы v_i = (v_i1, v_i2, . . . , v_iD). Ско-

рость и положение i-й частицы на итерации t + 1 определяют уравнения

x_i(t + 1) = x_i(t) + v_i(t + 1),

v_i(t + 1) = w · v_i(t) + c₁ · rand · (p_i(t) - x_i(t)) + c₂ · Rand · (p_g(t) - x_i(t)),

где i = 1, 2, . . . , N ; v_i(t) вектор скорости i-й частицы на итерации t; x_i(t)

координаты i-й частицы на итерации t; c₁, c₂ положительные коэффици-

енты ускорения; p_i(t) лучшая позиция i-й частицы на первых t итерациях;

p_g(t) глобально лучшая позиция частицы в рое на первых t итерациях (за-

дается индексом g); w эмпирический коэффициент инерции; rand, Rand

случайные числа из диапазона [0; 1].

Если коэффициенты ускорения и инерции не меняются в процессе рабо-

ты алгоритма, то для соблюдения баланса между диверсификацией и ин-

тенсификацией значения этих коэффициентов рекомендуется устанавливать

c₁ = c₂ = 1,419, а w = 0,721 [22].

Рой имеет своего рода топологию, описывающую взаимосвязи между ча-

стицами. Каждая частица имеет множество соседей. Соседями частицы мо-

жет быть весь рой или некоторое его подмножество. Две наиболее часто ис-

пользуемые топологии известны как gbest и lbest. Топология gbest является

полносвязной топологией, в отличие от lbest, в которой частица взаимодей-

ствует с ограниченным числом соседей. Алгоритм с топологией gbest быстро

сходится и имеет больше шансов застрять в локальных оптимумах. Алгоритм

с топологией lbest медленнее сходится, но более полно исследует пространство

поиска и, как правило, находит лучшее решение [3].

4. Инициализация

Если целевая функция имеет несколько локальных оптимумов, то тради-

ционные алгоритмы сходятся к одному из тех, положение которого определя-

ет процедура инициализации. Алгоритмы могут найти глобальный оптимум,

если начальные решения принадлежат области притяжения глобального оп-

тимума. Процедура инициализации играет важную роль и в роевых алгорит-

мах, где отсутствие разнообразия в популяции может привести к преждевре-

менной сходимости и попаданию в локальный оптимум. Таким образом, эф-

фективность методов оптимизации может быть повышена за счет разработки

методов генерации перспективных начальных решений. Однако на сегодняш-

ний день отсутствуют системные исследования процесса инициализации и то-

го, как начальные распределения решений могут влиять на эффективность

роевых алгоритмов при решении определенного класса проблем [1].

Процедура инициализации включает задание начального размера популя-

ции и собственно создание начальной популяции. Размер популяции влия-

ет на надежность и вычислительные затраты алгоритма. Небольшой размер

популяции может привести к быстрой сходимости к локальному оптимуму,

большой размер увеличит вычислительные затраты и может привести к мед-

ленной сходимости [23]. Размер популяции может быть увязан с размерно-

стью пространства поиска D. В [8] предлагается определять размер популя-

ции в алгоритме роящихся частиц как

[10 + 2√D],

где [·]

целая часть числа. Для задач большой размерности (D ≥ 50) в [24]

размер популяции в алгоритме “кукушкин поиск” предлагается устанавли-

вать равным D. Авторы [25] определяют размер популяции в модифициро-

ванном алгоритме искусственной пчелиной колонии как 5D, а в модифициро-

ванном алгоритме серого волка размер популяции задается равным 3D [26].

Однако чаще всего размер популяции выбирается экспериментальным путем.

Другим подходом к решению этой проблемы является введение адаптивного

метода формирования размера популяции, который делает роевый алгоритм

менее чувствительным к начальному выбору размера популяции.

Можно выделить несколько различных стратегий создания начальной по-

пуляции: стохастические методы, квазислучайные последовательности, ме-

тод оппозиционного обучения, многошаговый метод. Группу стохастических

методов можно разделить на две подгруппы: генераторы псевдослучайных

чисел и генераторы хаотических чисел. В роевых алгоритмах при отсутствии

априорных знаний генерация случайных чисел является распространенным

способом создания начальной популяции, которая может быть определена

как

(

)

x_i,j ∼ U

low_j; up_j

i = 1,2,...,N, j = 1,2,...,D,

где U представляет собой равномерное распределение, low_j, up_j нижнее и

верхнее значения j-й переменной.

Равномерное распределение начальных решений по пространству поис-

ка не является единственно возможным, наряду с равномерным использует-

ся распределение Леви, бета-распределение, нормальное распределение, лог-

нормальное распределение и др. [1]. Основным достоинством метода на осно-

ве псевдослучайных чисел является простота, поскольку средства генерации

псевдослучайных чисел присутствуют в каждом языке программирования, с

их помощью легко решается проблема инициализации начальной популяции.

Для создания стохастических начальных популяций используются хаоти-

ческие методы, для которых характерны эргодичность, случайность и ре-

гулярность [27]. Чтобы создать хаотическую популяцию, нужна хаотическая

карта. В очень общем виде одномерные хаотические карты работают следую-

щим образом [27]:

(

)

x^t+1i,j = f_m

x^ti,j

где x^ti,j

j-я переменная i-й частицы на итерации t, m определяемый

пользователем параметр. Обычно x^0i,j выбирается случайным образом, по-

следующие точки создаются путем многократного применения хаотической

карты. Наиболее часто применяются следующие хаотические карты: логисти-

ческое отображение (Logistic Map), синусоидальное отображение (Sinusoidal

iterator), отображение tent-map, гауссово отображение (Gauss Map).

Авторы [28] считают что, хотя метод генерации случайных чисел очень

прост с точки зрения программирования, он не очень эффективен, потому

что сгенерированные компьютером числа не покрывают равномерно про-

странство поиска. Квазислучайные последовательности относятся к детер-

минированным методам, генерирующим одну и ту же популяцию. Детерми-

нированные методы инициализации разработаны для обеспечения равномер-

ного распределения частиц на всем пространстве поиска. В последнее время

эти методы привлекают больше внимания, потому что в отсутствие предва-

рительных знаний о проблеме, однородность начальной популяции может по-

высить исследовательскую способность алгоритма на его ранних стадиях [27].

В квазислучайной последовательности разнообразие популяции, как прави-

ло, лучше, чем при псевдослучайной генерации. Для формирования началь-

ной популяции алгоритма роящихся частиц использовались квазислучайные

последовательности Ван-дер-Корпута [28] и Фора [29], а для инициализации

популяции алгоритма гравитационного поиска использовали генератор Собо-

ля [30].

Идея инициализации на основе оппозиционного обучения основана на про-

тивоположных отношениях между сущностями и заключается в одновре-

менном формировании как текущих решений, так и решений, противопо-

ложных текущим, используя для этого противоположные числа. В [31] да-

но определение противоположной точки в D-мерном пространстве. Пусть

z = (z₁,...,z_D)

точка в пространстве и z_j ∈ [a_j ; b_j ], j = 1, 2, . . . , D. Про-

тивоположность z определяется как ž = (ž₁, . . . , ž_D) как

(3)

žj = aj + bj - zj .

Одновременное использование случайного решения и его противоположно-

сти дает больше шансов найти оптимальное решение [31]. Можно предпо-

ложить, если текущие случайно сгенерированные решения далеки от оп-

тимального решения, то их противоположности будут ближе к этому ре-

шению. Приведенное выше определение противоположной точки называет-

ся противоположностью типа I, она определяется в соответствии с отно-

шением между точками в пространстве поиска без учета их функциональ-

ных значений. Противоположность типа II определяется с учетом функцио-

нального пространства задачи следующим образом [31]. Предположим, что

для функции f (x₁, x₂, . . . , x_D) предопределены или могут быть оценены y_min

и y_max. Пусть y = f (x₁,x₂,... ,x_D) ∈ ℜ и y ∈ [y_min;y_max]. Для каждой точки

x = (x₁,x₂,...,x_D) противоположная точка типа II x = (x₁, x₂,..., x_D) опре-

деляется как

(4)

x^II = {x| y = y_min + y_max

− y}.

Авторы [31] теоретически доказали, что в общем случае противоположные

числа с бóльшей вероятностью будут ближе к оптимальному решению, чем

чисто случайные; в [32] теоретические исследования были подтверждены экс-

периментально применительно к метаэвристике “дифференциальная эволю-

ция”. Применением инициализации на основе оппозиционного обучения улуч-

шены алгоритм роящихся частиц [33], алгоритм на основе стада криля [34],

алгоритм на основе электромагнетизма [17]. На первом этапе методы оппози-

ционного обучения генерируют набор точек, называемых исходной популяци-

ей. Исходная популяция может быть сгенерирована с использованием любого

метода инициализации, например генератором равномерно распределенных

чисел [32] или хаотической картой [35]. Затем используются некоторые про-

стые эвристические правила (например выражения 3 или 4) для создания

другой популяции такого же размера. Итоговая популяция формируется пу-

тем объединения обеих популяций на основе значений целевых функций вхо-

дящих в них решений.

Примером многошагового метода является центроидальная тесселяция

Вороного. С помощью этого метода можно разделить пространство поиска на

равные объемы, не используя целевую функцию. Врéменная популяция со-

здается с использованием генератора равномерно распределенных чисел или

более сложных методов. Затем с помощью множества случайно сгенерирован-

ных вспомогательных точек пространство поиска разделяется на несколько

областей. Эти области итеративно расширяются, пока не будут выполнены

некоторые критерии. Центры областей используются в качестве начальной

популяции [36]. Другим примером многошагового метода является подход к

поиску перспективных регионов, названный Smart Sampling [37], который ге-

нерирует начальные решения, оценивает их, используя целевую функцию,

и разделяет их на два класса

“хорошие” и “плохие”

на основе порога,

применяемого к значению целевой функции каждого решения. На размечен-

ной выборке начальных решений строится классификатор, который позво-

ляет проверять, является ли вновь сгенерированное решение хорошим без

использования целевой функции. Если новое решение классифицируется как

“хорошее”, оно может быть оценено целевой функцией. Подход Smart Sam-

pling эффективен только в том случае, если вычислительно затратным явля-

ется процесс определения значения целевой функции.

В [1] предложен метод инициализации на основе латинского гиперкуба,

суть которого заключается в разделении значений каждой координаты по-

иска на N равных интервалов, в каждый из которых попадает по одному

начальному решению. Такой метод позволяет избежать проблемы чрезмер-

ного скопления решений в одной точке пространства поиска. Исследования

показывают, что такой метод может обеспечить лучшее покрытие, чем рав-

номерное распределение [1].

Автор обзора [1] отмечает следующие проблемы рассмотренных методов

инициализации: стохастические методы просты и легко реализуемы, однако

они плохо масштабируемы; хаотические методы сильно зависят от началь-

ных условий; методы оппозиционного обучения генерируют популяцию удво-

енного размера, что приводит к удваиванию вычислительных затрат; метод

латинского гиперкуба очень эффективен при небольших размерностях про-

странства поиска, но он не дает явного преимущества при решении задач

высокой размерности [1]. Как не существует единственного эффективного

алгоритма оптимизации (“теорема о бесплатных завтраках” [7]), так не су-

ществует единственного эффективного алгоритма инициализации, в [1] на

примерах показано, что для разных задач следует использовать разные ал-

горитмы.

5. Меры популяционного разнообразия

Эффективность роевого алгоритма во многом определяет баланс между

фазами диверсификации и интенсификации. О том, в какой фазе находится

алгоритм в каждый момент выполнения, можно судить по значению попу-

ляционного разнообразия. Разнообразие определяется как расстояние между

решениями в пространстве поиска или как различие между значениями целе-

вых функций найденных решений. Недостаточное популяционное разнообра-

зие приводит к быстрой сходимости к потенциально неоптимальному реше-

нию. Для управления поиском решений необходимо иметь метрику для опре-

деления популяционного разнообразия. Метрики, основанные на расстоянии

Минковского, наиболее часто используются для определения разнообразия.

В [38] популяционное разнообразие определяется как

∑u∑

√

Div =

(x_ij(t) - x_j(t))²,

i=1

j=1

где x_j(t) среднее значение по j-му признаку на итерации t.

В [35, 39] разнообразие популяции алгоритма роящихся частиц и алгорит-

ма искусственной пчелиной колонии рассчитывается по формуле

∑ ∥x_i - x∥

i=1

Div =

N max

∥x_i - x_j∥

1≤i,j≤N

В [40] разнообразие популяции основано на норме L1:

∑∑

Div =

|x_ij (t) - x_j (t)| .

N ·D

i=1 j=1

По мнению авторов [41], медиана более эффективно указывает на центр

j-го измерения, поэтому в [41] среднее значение x_j(t) заменено на медиану.

В [42] разнообразие определяется через Евклидово расстояние относитель-

но лучшего решения в популяции

∑u∑

√

Div =

(x_ij (t) - p_jg(t))².

i=1

j=1

Разнообразие может быть определено как значение расстояния между луч-

шими решениями. В [43] это расстояние между всеми лучшими решениями,

найденными каждой из частиц,

∑

Div =

|p_i - p_j| .

N (N - 1)

i=1 j=i+1

В [44] разнообразие определяется как значение расстояния между текущим

и усредненным лучшим решением каждой частицы:

∑

Div =

|p_i - p_i| .

i=1

В качестве показателя преждевременной сходимости в [45] рассматрива-

ется разность целевых функций лучших решений на двух итерациях:

δ(t) = f (p_g(t - 1)) - f (p_g(t)) .

Констатируется преждевременная сходимость, если для заданного числа по-

следовательных итераций значение δ (t) меньше заданного порога.

Мера разнообразия, основанная на относительном расстоянии частиц до

глобально лучшей частицы, предложена в [45]:

∥x_i - p_g∥

Div = max

√

i=1,...,N

∑ (x_max,j - x_min,j

)²

j=1

Популяционное разнообразие может быть определено на основе индекса

квази-энтропии, который вычисляется по формулам [46]

∑

QE(t) = - P_i(t)log P_i(t),

i=1

f (p_i(t))

P_i(t) =

∑

f (p_i(t))

i=1

где f(p_i(t))

лучшее значение целевой функции i-й частицы на первых t

итерациях. Авторы [46] предполагают, что на ранних стадиях оптимизации

ни одна из частиц не находится в области глобального оптимального решения

и индекс QE изменяется незначительно. На более поздних стадиях, когда

все больше частиц попадают в область глобального оптимального решения,

индекс QE резко уменьшается и, когда он достигнет определенной доли от

начального значения, запускается локальный поиск.

Разнообразие в [44] определяется через распределение текущих скоростей

частиц

∑

Div =

|v_i - v_i| ,

i=1

где v_i, v_i текущее и среднее значения скорости i-й частицы соответственно.

Популяционное разнообразие может быть определено на основе значения

целевой функции. В [1] популяционное разнообразие определяется по форму-

ле

min (f_best , f_avg )

Div =

max (f_best , f_avg )

где f_best (t), f_worst (t), f_avg (t)

лучшее, худшее и среднее значения целевой

функции.

В [16, 47] проведено исследование метрик разнообразия при поиске опти-

мума различных математических функций. Для исследования были выбраны

метрики

{



}

fbest - f_avg



ξ = Div = min



,

f_best

{



}

 σ_f



ν = Div = min



,

f_avg



 f_avg -f_best



ψ = Div = 1 - 



,

f_worst - f_best

(5)

|f_best - f_avg |

χ = Div = 1 -

max |f_best - f_avg |_k

σ_f

ϕ = Div =

|f_worst - f_best |

где σ_f

стандартное отклонение от среднего значения целевой функции.

Недостатками метрики ξ являются слабая устойчивость и сильная зависи-

мость от области изменения целевой функции. Однако с ее помощью удает-

ся получить хороший результат для многомерных и сложных ландшафтов

целевых функций, которые имеют ограниченный диапазон изменчивости и

минимум у которых находится около нуля (например в инженерных задачах

для минимизации ошибки). Метрика ν зависит от стандартного отклонения

и, следовательно, от распределения значений целевой функции по всем эле-

ментам популяции. Эта метрика также как и ξ-метрика хорошо работает с

целевыми функциями, имеющими ограниченный диапазон изменчивости, но

она менее чувствительна к разбросам значений этих функций. В отличие от

ξ- и ν-метрик, ψ не зависит от диапазона изменения значений целевой функ-

ции. Эта метрика очень чувствительна к небольшим изменениям и поэтому

особенно подходит для ландшафтов целевых функций, содержащих плато и

области с небольшим градиентом. Метрика χ характеризует не только ме-

ру разнообразия, но и является оценкой лучшего результата по сравнению с

другими решениями. Метрика ϕ может рассматриваться как комбинация ν-

и ψ-метрик [16, 47].

Метрик разнообразия столько же, сколько проблем, т.е. метрики разно-

образия специфичны для конкретной проблемы [48]. Не существует “наилуч-

шей” метрики в целом, но есть “наиболее подходящая” метрика, зависящая не

только от ландшафта целевой функции, но и от алгоритма оптимизации [16].

Автор [16] утверждает, что эффективная метрика разнообразия для эволюци-

онной стратегии вряд ли будет эффективной для определения разнообразия

для дифференциальной эволюции; это соображение автор [16] рассматривает

как следствие теоремы об отсутствии бесплатных завтраков [7].

Разнообразие характеризует состояние популяции или распределение ча-

стиц. Большое значение Div означает, что поиск находится в состоянии ди-

версификации, малое значение свидетельствует о том, что поиск находится

в состоянии интенсификации [40]. С помощью измерения разнообразия рас-

считывается доля диверсификации и интенсификации на каждой итерации:

(

)

Div

X_dv =

Div_max

)

( |Div - Div_max|

X_it =

Div_max

Используя приведенные выше соотношения, можно поддерживать разнооб-

разие популяции на достаточном уровне, не допуская ранней сходимости ал-

горитма. Механизмы поддержки популяционного разнообразия рассмотрены

в разделе 6.

6. Механизмы поддержки популяционного разнообразия

Результаты поиска, выполняемого роевым алгоритмом, зависят от уста-

новленного или динамического баланса между двумя компонентами алго-

ритма: диверсификацией и интенсификацией. Успешно работающий компо-

нент диверсификации обеспечит поиск на всем пространстве поиска, однако

этот компонент может замедлить процесс сходимости алгоритма. Существу-

ют несколько основных механизмов поддержания разнообразия: 1) ре-ини-

циализация; 2) введение новых операторов: хаотических процедур и операто-

ров кроссовера и мутации; 3) разделение популяции на субпопуляции.

6.1. Ре-инициализация

Ре-инициализация частиц является эффективным способом поддержания

разнообразия, такой механизм способствует выходу частиц из локальных оп-

тимумов и дает алгоритму возможность находить “достаточно хорошее” ре-

шение. Различают случайную ре-инициализацию, когда повторно генериру-

ются большинство частиц, и элитную ре-инициализацию, когда сохраняются

решения с лучшей целевой функцией [44].

В [49] новое решение генерируется на основе предыдущего решения пу-

тем добавления в него шума. По количеству повторно инициализированных

решений определено три стратегии.

1. Количество ре-инициализированных решений уменьшается в процессе

поиска. Более половины решений ре-инициализируются в начале поиска, а за-

тем количество ре-инициализированных решений линейно уменьшается при

каждой ре-инициализации. Эта стратегия заключается в том, чтобы сначала

сосредоточиться на диверсификации, а в конце поиска на интенсификации.

2. Часть решений повторно инициализируется после заданного числа ите-

раций. Количество ре-инициализированных решений не меняется в процессе

поиска.

3. Количество ре-инициализированных решений увеличивается в процессе

поиска. Менее половины решений ре-инициализируются в начале поиска, и

число ре-инициализированных решений линейно увеличивается при каждой

ре-инициализации. Эта стратегия заключается в том, чтобы сначала сосре-

доточиться на интенсификации, а в конце поиска на диверсификации.

В [50] ре-инициализация выполняется следующим образом: через заданное

количество итераций в текущую популяцию из N решений добавляется еще N

случайно сгенерированных решений; из полученных 2N решений выбираются

N лучших; процесс повторяется заданное количество раз. В [51] предлагаются

две стратегии ре-инициализации алгоритма роящихся частиц. Первая страте-

гия предполагает повторную инициализацию отдельных частиц, чье лучшее

положение не улучшается после заданного числа итераций. Вторая страте-

гия подразумевает ре-инициализацию всей популяции, когда число лучших

частиц в рое, имеющих значение целевой функции, близкое к значению целе-

вой функции глобально лучшей частицы, превысит заданное пороговое значе-

ние. В [52] предлагается элитная схема ре-инициализации, когда случайным

образом генерируются все решения за исключением лучшего, полученного на

последней итерации, при условии, что после заданного числа итераций отно-

сительное улучшение значения целевой функции меньше порогового. В [45]

активируется процедура ре-инициализации, если подтверждается состояние

преждевременной сходимости или недостаточного популяционного разнооб-

разия. В этом случае каждое решение заменяется на его противоположность,

используя метод оппозиционного обучения.

6.2. Введение новых операторов

6.2.1. Эволюционные операторы

Операторы кроссовера и мутации, применяемые в эволюционных алгорит-

мах, все чаще применяются и в роевых алгоритмах для увеличения популя-

ционного разнообразия [34, 53-56]. Оператор мутации, вносящий возмущение

в решение z ∈ ℜ^D, может быть определен как

x`= x + Z,

где Z

вектор случайных чисел, распределенных по заданному закону.

Примерами являются операторы мутации на основе распределения Гаусса

Таблица 1. Описание операторов мутации

Схема

Оператор мутации

De/Best/1

x = p_g + F · (x_r1 - x_r2)

De/Best/2

x = p_g + F · (x_r1 - x_r2 + x_r3 - x_r4)

De/CurrToBest/1 x = x_i + K · (p_g - x_i) + F · (x_r1 - x_r2)

De/CurrToRand/1 x = x_i + K · (x_r3 - x_i) + F · (x_r1 - x_r2)

De/Rand/1

x = x_r1 + F · (x_r2 - x_r3)

De/Rand/2

x = x_r5 + F · (x_r1 - x_r2 + x_r3 - x_r4)

De/RandToBest/1 x = x_r3 + K · (p_g - x_r3) + F · (x_r1 - x_r2)

(

))

Z ∼N

µ,σ²

и Коши (Z ∼ C(x₀, γ)). Динамическая регулировка парамет-

ров σ² и γ в процессе выполнения роевого алгоритма позволяет изменять

баланс между диверсификацией и интенсификацией. Большие значения ука-

занных параметров могут привести к появлению сильно возмущенных ре-

шений, малые значения параметров способствуют выполнению локального

поиска.

Оператор мутации может быть основан не только на законах распределе-

ния. Популяционное разнообразие алгоритма роящихся частиц и гравитаци-

онного поиска в [57, 58] регулируется оператором мутации, построенным на

основе вейвлета Морле:

{x_ij(t + 1) + (x_max,j - x_ij (t + 1)) , σ > 0,

x_ij(t + 1) =

x_ij(t + 1) + (x_ij(t + 1) - x_min,j) , σ ≤ 0,

(

(^z

)

σ=

cos

√ae

где a масштабный коэффициент, z ∈ [-2,5a; 2,5a].

Авторы [59] вводят в алгоритм гравитационного поиска знаковую мута-

цию:

x_i(t + 1) = x_i(t) + s_i · Δ_i(t + 1),

{-1, rand < P

s_ij =

1, rand ≥ P_s,

где Δ_i модифицирующий вектор, вычисленный по оригинальной схеме гра-

витационного поиска, s_i вектор мутации, P_s вероятность мутации.

В роевых алгоритмах для увеличения популяционного разнообразия ча-

сто применяется оператор мутации, заимствованный из алгоритма диф-

ференциальной эволюции [60-63]. В табл. 1 приведены операторы мутации

[64], здесь p_g

лучшее решение в текущей популяции; F и K коэффи-

циенты масштабирования, действительные положительные числа; индексы

r₁,r₂,r₃,r₄,r₅ = 1,N

случайно сгенерированные целые числа, причем r₁ =

= r₂ = r₃ = r₄ = r₅ = i.

Оператор кроссовера на основе исходного списка решений генерирует но-

вые решения путем “смешивания” информации о решениях из исходного спис-

ка. Оператор кроссовера O(x_i, x_k, j) применяется для формирования нового

решения путем изменения j-го элемента x_ij и x_kj в выбранных решениях.

Новый элемент решения x_lj с использованием оператора арифметического

кроссовера вычисляется по формуле

x_lj = αx_ij + (1 - α)x_kj,

где α коэффициент масштабирования, случайно выбранный из некоторо-

го интервала. Элемент решения с применением геометрического кроссовера

определяется по формуле

x_lj = (x_ij · x_kj)^α , α ∈ [0,1] .

Случайный кроссовер формирует элемент решения по схеме

{x_ij, rand ≤ 0,5,

x_lj =

x_kj, rand > 0,5.

В [55] предложен оператор самоадаптирующегося кроссовера:

x_lj(t + 1) = x_ij(t) · (1 - Cr) + x_kj(t) · Cr,

f (x_i(t)) - f (p_g(t))

Cr = 0,8 + 0,2 ·

f (p_w(t)) - f (p_g(t))

где p_w и p_g худшее и лучшее решения в популяции соответственно.

В [65] приведена классификация операторов кроссовера, применяемых в

решении задач с непрерывно меняющимися параметрами, а также проведе-

но эмпирическое исследование 14 операторов кроссовера при решении задач

нахождения минимума математических функций. В [56] описан двухточеч-

ный полный кроссовер, в котором каждое из двух решений (оригинальное и

его противоположность, полученная методом оппозиционного обучения) де-

лится на три части двумя случайно выбранными точками. Новое решение

формируется путем обмена частями исходных решений. Итоговые решения

получаются после упорядочения по значению целевой функции шести новых

решений и двух исходных.

Изменяя частоту (вероятность) применения операторов кроссовера и му-

тации в роевом алгоритме, можно регулировать баланс диверсификация-

интенсификация.

6.2.2. Хаотические операторы

Существуют два способа включения хаоса в роевые алгоритмы оптими-

зации. Первый способ состоит в том, чтобы использовать последовательно-

сти, сгенерированные хаотическими системами, для замены случайных чи-

сел, используемых в оригинальном алгоритме. Другой способ заключается

во включении хаотического поиска в качестве локального поиска в ориги-

нальный алгоритм. Оба способа авторы [66] применяют в алгоритме гравита-

ционного поиска для повышения скорости сходимости и решения проблемы

выхода из локальных оптимумов. Двенадцать хаотических карт применяются

для настройки значений коэффициентов инерции (ω_n, ω_f ) в алгоритме стадо

криля [54]. Хаотические последовательности используются в качестве гене-

раторов псевдослучайных чисел в алгоритме искусственной пчелиной коло-

нии [67], алгоритме роящихся частиц [68], алгоритме кузнечика [53].

6.3. Разделение популяции на субпопуляции

Многопопуляционные методы за последние десять лет стали одними из

часто используемых методов оптимизации. Концепция этого метода следую-

щая: исходная популяция делится на несколько субпопуляций; над элемен-

тами субпопуляции выполняются некоторые эволюционные операции; взаи-

модействуя между собой, субпопуляции обмениваются элементами, дробятся,

поглощают друг друга, что способствует предотвращению преждевременной

сходимости и поддержанию популяционного разнообразия путем распределе-

ния элементов по всему пространству поиска. Многопопуляционные методы

сравнительно легко интегрируются в роевые алгоритмы оптимизации и часто

работают эффективнее, чем алгоритмы с одной популяцией [69].

Многопопуляционные алгоритмы можно классифицировать на два ти-

па: конкурирующие и кооперативные. Для алгоритмов конкурирующего ти-

па каждая субпопуляция ищет решения в области, выделенной только для

нее [70]. Кооперативные алгоритмы ведут поиск в одной и той же области,

взаимодействуя и обмениваясь информацией [71].

В [69] обозначены проблемы и решения, характерные для многопопуля-

ционных методов оптимизации. Первая проблема заключается в том, как

определить количество субпопуляций: большое их количество связано с вы-

сокими вычислительными затратами, малое количество может не привести к

желаемому эффекту. Указанная проблема решается двумя способами. Пер-

вый способ использовать фиксированное количество субпопуляций. По это-

му способу функционирует большинство многопопуляционных методов. Его

преимущество заключается в простоте реализации. Однако число субпопуля-

ций определяется эмпирически, и трудно получить единые и эффективные

правила для определения этого числа при решении различных практических

задач. Второй способ заключается в динамическом изменении числа субпо-

пуляций во время оптимизации. Выдвигается предположение, что на началь-

ных этапах требуется большое количество субпопуляций для увеличения по-

пуляционного разнообразия и распределения возможных решений по всему

пространству поиска. На поздних этапах небольшое количество субпопуля-

ций способствует уменьшению разнообразия, что может быстрее приблизить

решение к глобальному оптимуму.

Вторая проблема заключается в определении параметров коммуникации

(миграции) между субпопуляциями. К таким параметрам относятся: 1) коли-

чество решений, подлежащих обмену; 2) коммуникационная (миграционная)

политика, которая определяет, какие решения должны быть заменены реше-

ниями других субпопуляций; 3) частота коммуникаций; 4) топология комму-

никаций. Чаще других применяется коммуникационная политика, основан-

ная либо на жадном алгоритме, либо на случайном отборе, например элитар-

ная политика миграции предполагает замену худших решений в субпопуля-

ции лучшими решениями другой субпопуляции. Среди множества топологий

можно выделить иерархическую и случайную топологии, а также линейные

(цепочечные), кольцевые и решетчатые (клеточные) топологии, которые мо-

гут быть однонаправленными или двунаправленными.

Одной из широко применяемых многопопуляционных стратегий является

модель островов [72], в которой популяция делится на несколько субпопуля-

ций, называемых островами, эволюционирующие независимо друг от друга,

но периодически взаимодействующие друг с другом посредством миграций.

Схема взаимодействия, состоящая из последовательно происходящих процес-

сов миграции и эволюции, позволяет создать баланс между диверсификацией

и интенсификацией [18]. В [73] приводится динамическая островная модель,

в которой размер популяции фиксирован, но размер каждой субпопуляции

может меняться; топология задается полносвязным неориентированным гра-

фом. На каждой итерации алгоритма каждое решение мигрирует с исходного

острова на остров назначения в соответствии с заданными вероятностями и

динамически изменяющейся матрицей миграции, которая формируется с ис-

пользованием алгоритма QLearning [74]; вместо единственной миграционной

политики используется несколько миграционных политик.

В [18] предлагается иерархическая модель с 16 островами и четырьмя то-

пологиями миграции. Острова нижних уровней ответственны за глобальный

поиск, острова верхнего уровня выполняют локальный поиск. После каж-

дой итерации лучшее решение мигрирует в соседнюю субпопуляцию верхне-

го уровня. Миграция между субпопуляциями одного уровня поддерживается

путем замены лучшего решения текущей субпопуляции худшим решением

соседнего острова.

Коммуникации могут быть синхронными или асинхронными. В первом

случае все субпопуляции обновляют свои решения одновременно, тогда как

во втором случае решения обновляются по наступлению какого-либо собы-

тия. Обе модели имеют свои преимущества и недостатки. Синхронные ост-

ровные модели проще в реализации, тогда как асинхронные модели являются

более гибкими и эффективными [75]. Важным улучшением модели островов

является слабосвязанная модель с виртуальным хранилищем совместно ис-

пользуемых данных, получившая название “океан” [76]. “Океан” позволяет

легко реализовать гетерогенность и динамическое изменение числа островов,

уменьшить задержку на обмен решениями за счет того, что “океан” хранит

решения, которые были отправлены островом, но еще не приняты другим ост-

ровом, таким образом реализован асинхронный режим обмена решениями.

В изложенном авторами [77] подходе на островах независимо работают четы-

ре алгоритма: алгоритм пчелиной колонии для генерации правил нечеткого

классификатора, алгоритм пчелиной колонии для оптимизации параметров,

алгоритм адаптивной эволюционной стратегии и метод наименьших квад-

ратов. “Океан” реализует обмен только множеством лучших решений, нахо-

дящихся в нем. Моменты отправки и приема лучших решений из “океана”

выбирают сами алгоритмы, выполняющиеся на островах.

В клеточной топологии популяция делится на множество субпопуляций

малого размера, обычно состоящих только из одного решения. Коммуникации

происходят только в пределах небольшой окрестности, определенной вокруг

отдельного решения или малой субпопуляции. При такой топологии снижа-

ется риск преждевременной сходимости по причине медленного распростра-

нения информации от соседа к соседу [78]. В качестве топологий окрестности

в [79] рассматриваются три клеточные структуры кубическая, тригональ-

ная и гексагональная, интегрированные в алгоритм роящихся частиц. В [80]

описан алгоритм роящихся частиц с клеточно-структурированной популяци-

ей, частицы в которой распределены в двумерной сетке и взаимодействуют

со своими соседями в соответствии с заданной окрестностью; авторы иссле-

дуют шесть типов окрестности: две линейные (L5, L9) и четыре компактных

окрестности (C9, C25, C13, C21); для обработки краевых ячеек используется

тороидальная структура.

Третья проблема многопопуляционных методов как определить область

поиска каждой субпопуляции. Одним из решений этой проблемы является

кластеризация. Авторы [81] используют метод кластеризации для разделения

популяции в алгоритме гравитационного поиска. При инициализации размер

субпопуляции выбирается случайным образом из множества T = {5, 10, 25}.

После каждого цикла работы алгоритма размер субпопуляции изменяется

по результатам поиска. Если лучшее решение в субпопуляции не улучшает-

ся, из множества T случайным образом выбирается новое значение, в про-

тивном случае размер не меняется. В [82] предлагается многопопуляционный

алгоритм роящихся частиц, который использует метод иерархической класте-

ризации, позволяющий адаптивно корректировать количество необходимых

субпопуляций. Алгоритм кластеризации на основе нечетких c-средних в [83]

используется для адаптивного разделения популяции на кластеры в алго-

ритме роящихся частиц. Для каждого кластера вычисляется его адаптивная

ценность, полученная в результате конкурентного обучения. Кластеры ран-

жируются в соответствии с их ценностью. Кластеры с малой адаптивной цен-

ностью поглощаются соседними кластерами, имеющими бóльшую ценность.

Роевый алгоритм со структурированной популяцией имеет больше пара-

метров, чем его аналог с единой популяцией. Дополнительно введенные па-

раметры существенно влияют на работу алгоритма, поэтому настройка и ре-

гулировка этих параметров имеют важное значение для повышения эффек-

тивности алгоритма [75].

7. Настройка и регулировка значений параметров

Роевые алгоритмы характеризуются наличием стохастических компонен-

тов и свободных параметров, которые могут быть установлены пользовате-

лем. Основная проблема здесь в том, что нет никакой гарантии, что хорошо

настроенный алгоритм, хорошо работающий для одного типа проблем, может

хорошо работать для другого типа проблем. Эффективность роевых алгорит-

мов во многом зависит от значений параметров, задаваемых в начале работы

и изменяемых в процессе выполнения алгоритма. По сути, это две проблемы:

проблема автономной настройки и проблема регулировки значений парамет-

ров “на лету”. Процедура настройки параметров требует большого количества

прогонов алгоритма для анализа его эффективности на одном или несколь-

ких экземплярах проблем с различными настройками параметров. Процедура

эта является вычислительно затратной, что является основным недостатком

настройки параметров. Преимущество настройки параметров заключается в

ее универсальности, хороший метод настройки применим для задания пара-

метров многих различных метаэвристик. Недостатком регулировки парамет-

ров является ее узкая специализация, хорошо подобранные стратегии управ-

ления для одного алгоритма обычно не подходят для другого алгоритма [84].

7.1. Автономная настройка параметров

Автономная настройка параметров выполняется перед началом работы ал-

горитма. Цель состоит в том, чтобы априори найти лучшее сочетание значе-

ний параметров. Автономная настройка параметров является сложной про-

блемой из-за большого количества значений, которые может принимать каж-

дый параметр. При этом необходимо учитывать, что параметры некоторых

алгоритмов являются взаимозависимыми. Теоретический анализ, проведен-

ный авторами [85], показал, что для обеспечения стабильной работы алгорит-

ма роящихся частиц необходимо выполнение следующего соотношения между

параметрами алгоритма:

(

)

(c₁ + c₂) < 24

1-ω²

/(7 - 5ω) .

А в [86] условие сходимости алгоритма роящихся частиц определено как

1 > ω > ((c₁ + c₂)/2 - 1) ≥ 0.

На ранних этапах исследований метаэвристик настройка параметров осу-

ществлялась либо “вручную” путем проведения серий экспериментов с раз-

личными конфигурациями параметров и выбора среди них лучшей на основе

полученных результатов, либо “по аналогии” с применением настроек, пока-

завших хорошие результаты при решении подобных проблем [87].

В последние два десятилетия проблеме автоматической настройки пара-

метров стали уделять больше внимания [84, 87-91]. В [92] утверждается, что

при разработке и создании нового метаэвристического алгоритма только 10 %

времени тратится на разработку алгоритма, а 90 % времени уходит на тон-

кую настройку его параметров. Актуальность этой проблемы определяется

следующим [89]:

1) использование методов автоматической настройки параметров может

сократить затраты времени и позволит достичь лучших результатов по срав-

нению с ручными методами;

2) методы автоматической настройки могут помочь решить вопрос, пре-

восходит ли один алгоритм другой, потому что он принципиально лучше или

потому что его разработчики более успешно подобрали его параметры;

3) конечные пользователи часто не знают о влиянии настроек параметров

алгоритма на его эффективность, поэтому просто используют настройки по

умолчанию, однако конфигурация параметров по умолчанию может не рабо-

тать должным образом для конкретных проблемных ситуаций, с которыми

сталкивается пользователь;

4) автоматическая настройка параметров позволяет устранить необходи-

мость пользователю устанавливать связь между настраиваемыми парамет-

рами и решаемой проблемой.

Проблема настройки параметров может рассматриваться как проблема оп-

тимизации, часто называемая мета-оптимизацией. Здесь алгоритм настройки

является мета-оптимизатором, который ищет оптимальный (или по крайней

мере хорошо работающий) набор параметров для целевого (настраиваемо-

го) алгоритма. Сложность проблемы автоматической настройки обусловлена

стохастической природой целевого алгоритма и метрики его эффективности

[84, 90].

Конечной целью оптимизации является решение конкретных проблем, воз-

никающих в реальном мире, но чтобы не решать каждую конкретную задачу

отдельно и заново не начинать исследование с нуля, когда появляется новая

задача, можно предположить, что некоторые из задач имеют общую структу-

ру и могут рассматриваться как различные примеры общей проблемы. Этот

шаг абстракции является фундаментальным для формального развития оп-

тимизации и открывает путь к разработке алгоритмов и формальному ана-

лизу их свойств [88]. Если настройка алгоритма выполняется на одном при-

мере проблемы, показателем эффективности может быть среднее значение

показателя эффективности целевого алгоритма на нескольких прогонах. По-

казатель эффективности целевого алгоритма для множества примеров про-

блемы может быть определен как средняя эффективность алгоритма по дан-

ному множеству. Однако в некоторых случаях показатели эффективности

могут сильно различаться, тогда показатели нормализуют для каждого при-

мера [88]. Для нахождения оптимальной настройки параметров (или конфи-

гурации) обычно требуется большое количество прогонов целевого алгоритма

с разными конфигурациями на различных примерах. Таким образом, про-

блема настройки параметров является вычислительно дорогой и трудоемкой

задачей [84].

Существующие методы автоматической настройки работают по принци-

пу генерация-оценка, т.е. путем генерации различных конфигураций пара-

метров и их оценки с помощью метрик эффективности [90, 91]. В качестве

методов генерации часто используются методы планирования эксперимента

[92-94], а также кригинг модели [95] и метод прямого поиска на адаптивных

сетках [96]. Простым является метод повторной оценки параметров, который

оценивает каждую конфигурацию несколько раз и возвращает среднее значе-

ние [90]. В методе грубой силы сначала генерируется семейство конфигураций

параметров, как правило, с помощью методов планирования эксперимента,

затем оценивается эффективность каждой конфигурации. В этом методе за-

траты на тестирование низкоэффективных конфигураций равны затратам

на тестирование высокоэффективных конфигураций. Кроме того, здесь нет

критерия, который определяет, сколько прогонов каждой конфигурации на

каждом экземпляре должно быть выполнено для обработки стохастичности

целевого алгоритма [84]. Метод F-Race [88] поэтапно оценивает возможные

конфигурации на примерах проблемы. После каждого этапа с использова-

нием непараметрического теста Фридмана проверяется, есть ли статистиче-

ские значимые отличия в показателях эффективности среди конфигураций-

кандидатов. Если обнаружены значимые отличия, то после ранжирования

кандидатов худшие отбрасываются и не участвуют в оценке на следующем

этапе. Ранжирование в методе F-Race является еще и способом нормализации

показателей эффективности, определяемых для разных примеров проблемы.

В методе F-Race вычислительные ресурсы используются более эффективно,

чем в методе грубой силы. Однако если целевой алгоритм имеет большое

количество параметров и/или каждый параметр имеет большой диапазон

изменений, тогда для получения хорошего результата необходимо оценить

большое количество возможных конфигураций, что может стать практически

невыполнимой задачей с точки зрения выполненных вычислений. К достоин-

ствам методов F-Race и грубой силы относятся их понятность и простота

реализации, с помощью этих методов можно настраивать как числовые, так

и категориальные параметры [84].

Метод ParamILS [89] это один из самых современных методов автома-

тической настройки параметров, с его помощью можно настраивать как чис-

ловые, так и категориальные параметры. В этом методе новая конфигурация

параметров сравнивается с лучшей на текущий момент конфигурацией после-

довательности примеров проблемы. Если новая конфигурация хуже лучшей

конфигурации, она исключается, иначе она оценивается на следующем при-

мере и снова сравнивается с лучшей. Процесс продолжается до тех пор, пока

новая конфигурация не будет оценена на всех примерах последовательности

и будет определена новая лучшая конфигурация.

Перспективным подходом к решению проблемы настройки параметров яв-

ляется применение моделей поверхности отклика для описания зависимости

эффективности целевого алгоритма от настроек его параметров. Процедура

SPO [84] настраивает только числовые параметры и строит модель поверх-

ности отклика, называемую моделью Кригинга. Метод SMAC работает как

с числовыми, так и категориальными параметрами целевого алгоритма. Для

построения поверхности отклика здесь используется случайный лес. Экспе-

риментальное исследование показало, что с помощью SMAC удается полу-

чить лучшие результаты по сравнению с ParamILS. Метод SMAC особенно

хорош при решении задач настройки со многими категориальными парамет-

рами [84].

Подводя итог рассмотрения методов настройки параметров, можно утвер-

ждать, что эти методы выполняются до запуска настраиваемого алгоритма

и выполняют поиск значений параметров, которые останутся фиксированны-

ми во время выполнения алгоритма. Кроме того, процессы настройки обычно

включают несколько прогонов алгоритма, чтобы проанализировать его эф-

фективность на разных значениях параметров с учетом его стохастической

природы [97].

7.2. Регулировка значений параметров

Проблема регулировки значений параметров в роевых алгоритмах появи-

лась одновременно с самими этими алгоритмами. В [98] отмечается, что изме-

нение параметров в процессе выполнения алгоритма позволяет: искать реше-

ния, двигаясь в пространстве поиска большими шагами в начале работы ал-

горитма, и вести поиск оптимальных решений малыми шагами на последних

этапах; алгоритму приспосабливаться к изменяющемуся ландшафту целевой

функции; алгоритму накапливать информацию о целевой функции в процес-

се поиска и использовать эту информацию для повышения эффективности

на поздних этапах и освобождает пользователя от необходимости выполнения

этапа настройки значений параметров.

Методы регулировки значений параметров выполняются во время работы

роевого алгоритма и изменяют значения его параметров во время выполнения

алгоритма. Указанные методы могут быть разделены на две категории [99]:

детерминированные и адаптивные. Детерминированные методы работают без

обратной связи и следуют заранее установленному правилу при задании но-

вых значений параметров. Адаптивные методы изменяют значения парамет-

ров на основе информации, получаемой после очередной итерации работы

алгоритма.

Детерминированные методы регулировки значений параметров основаны

исключительно на количестве пройденных итераций. В качестве примера рас-

смотрим методы регулировки коэффициента инерции алгоритма роящихся

частиц, поскольку этот параметр в бóльшей степени ответственен за соблюде-

ние баланса между диверсификацией и интенсификацией. Несмотря на зна-

чительный объем исследований, многие стратегии изменения коэффициента

инерции не изучены ни аналитически, ни эмпирически [100]. В табл. 2 приве-

дены детерминированные методы регулировки коэффициента инерции; здесь

Таблица 2. Детерминированные методы изменения значения коэффициента

инерции

Метод

Выражение

Ссылка

Случайное изменение

ω (t) = 0,5 + r (t)/2

[101]

Линейное изменение

ω (t) = ω_max - (ω_max - ω_min) · (t/T )

[102]

ω(t) = ω_max - (ω_max - ω_min)(t/T )1/π2

[103]

ω (t) = ω · u^-t

[104]

ω (t) = (2/t)^0,3

[105]

Нелинейное изменение

ω (t) = exp(- exp((T - t)/T ))

[106]

ω (t) = ω_min + (ω_max - ω_min)e^-10t/T

[107]

ω(t) = ω_min + (ω_max - ω_min)e-16t/T2

ω(t) = ω_max + (ω_min - ω_max) · log₁₀(1 + 10t/T )

[108]

ω (t) = 0,5z(t) + 0,5r(t)

Хаотическое изменение

[109]

ω (t) = z(t)ω_min + (ω_max - ω_min) · (T - t)/T



((ωmin + ωmax)/2 + (ωmax - ωmin)/2) ×

Осциллирующее

ω(t) =

× cos(2πt(4k + 6)/3T), t < 3T/4,

[110]

изменение



ω_min иначе

Таблица 4. Стратегии регулировки значений параметров c₁ и c₂

Стратегии

Состояния

c₁

c₂

Стратегия 1 Диверсификация Увеличение

Уменьшение

Незначительное Незначительное

Стратегия 2 Интенсификация

увеличение

снижение

Незначительное

Стратегия 3 Сходимость

увеличение

Стратегия 4 Прыжок

Уменьшение

Увеличение

приняты обозначения: t текущая итерация; T максимальное число ите-

раций; r (t) ∈ [0, 1] равномерно распределенное случайное число; ω ∈ [0, 1],

u ∈ [1,0001;1,005]; z (t) значение хаотического логистического отображения

(Logistic Map).

Авторами [111] предложен детерминированный способ регулировки значе-

ний коэффициентов c₁ и c₂ алгоритма роящихся частиц:

c₁(t) = c_1i + (c_1f - c_1i) · t/T,

c₂(t) = c_2i + (c_2f - c_2i) · t/T,

где c_1i и c_2i

начальные значения коэффициентов, c_1f и c_2f

конечные

значения коэффициентов. В [111] рекомендовано использовать следующие

начальные значения этих коэффициентов: c_1i = c_2f = 2,5, c_2i = c_1f = 0,5.

Адаптивные методы динамически регулируют параметры роевых алгорит-

мов в процессе их работы. В качестве средств адаптации используются та-

кие характеристики, как средняя скорость, компактность роя, расстояние до

лучшей частицы в рое. В табл. 3 приведены адаптивные методы регулировки

коэффициента инерции.

Быстрая сходимость и уход из локальных оптимумов две наиболее важ-

ные цели в исследовании роевых алгоритмов. Для достижения этих целей в

[116] предложены четыре стратегии адаптивной регулировки коэффициентов

ускорения алгоритма роящихся частиц (табл. 4).

Оценка состояния популяции основана на вычислении суммарного расстоя-

ния между частицами роя

f = (d_g - d_min)/(d_max - d_min),

где d_min, d_max, d_g минимальное, максимальное суммарное расстояние и сум-

марное расстояние до лучшей частицы в рое. Значение f относительно велико

в состоянии диверсификации или прыжка и относительно мало в состоянии

интенсификации или сходимости.

Коэффициент инерции ω уравновешивает возможности глобального и ло-

кального поиска, в [116] значение ω адаптивно регулируется в соответствии

с выражением:

ω(f) = 1/(1 + 1,5 exp(-2,6f)).

Регулировка значений параметров c₁ и c₂ выполняется с помощью нечеткой

системы типа синглтон, на вход которой подается значение f.

В последнее время увеличивается количество исследований, связанных с

встраиванием хаоса в алгоритмы оптимизации. Использование хаоса усили-

вает диверсификационные и интенсификационные свойства алгоритмов оп-

тимизации [53]. Стадии диверсификации и интенсификации в роевых алго-

ритмах регулируются хаотическим изменением их параметров: шага полетов

Леви в алгоритме кукушкин поиск [117], гравитационных констант в грави-

тационном поиске [118], коэффициента c в алгоритме кузнечика [53], двух

коэффициентов γ и β в алгоритме светлячков [119], четырех параметров

в алгоритме летучих мышей [120].

Нечеткие системы достаточно часто используются для регулировки пара-

метров роевых алгоритмов. В [121] адаптивная нечеткая схема построена на

вычислении разности значений целевой функции лучших решений на двух

последних итерациях алгоритма роящихся частиц (df). Предлагаются сле-

дующие нечеткие правила регулировки значений параметров c₁ и c₂:

ЕСЛИ df маленькое, ТО c₁ большое, c₂ маленькое,

ЕСЛИ df среднее, ТО c₁ среднее, c₂ среднее,

ЕСЛИ df большое, ТО c₁ маленькое, c₂ большое.

Входная переменная df и выходные переменные c₁ и c₂ представлены тре-

мя нечеткими термами: маленькое, среднее, большое.

В [122] для модификации параметров c₁ и c₂ построены три нечеткие си-

стемы типа Мамдани с разными входными переменными, в качестве кото-

рых используются нормированные значения: а) популяционного разнообра-

зия, б) усредненной разности между значением целевой функций каждой ча-

стицы и значением целевой функции лучшей частицы, в) итерации. Все вход-

ные переменные представлены тремя равномерно распределенными на интер-

вале [0; 1] нечеткими термами с треугольными функциями принадлежности.

Выходные переменные (c₁ и c₂) представлены пятью равномерно распреде-

ленными на интервале [0,5; 2,5] нечеткими термами с треугольными функ-

циями принадлежности. Входными переменными для первой нечеткой систе-

мы являются итерации и разнообразие, для второй итерации и усреднен-

ная разность, для третьей итерации, разнообразие и усредненная разность.

Первые две системы имеют по девять нечетких правил, третья

27.

В модифицированном алгоритме роящихся частиц FAIPSO [123] коэффи-

циенты c₁ и c₂ корректируются c применением нечеткой системы, которая

имеет шесть входных переменных, содержащих информацию о расстояниях

между частицами, два выхода (c₁ и c₂) и десять нечетких правил. Компро-

мисс между диверсификацией и интенсификацией при решении задач опти-

мизации с использованием гравитационного алгоритма достигается измене-

нием значения ускорения, для этого авторы [124] применяют нечеткую си-

стему типа 2. Системы этого же типа используются в [125] для регулировки

параметров алгоритма летучих мышей, а в [126] для динамической адап-

тации параметров алгоритма пчелиной колонии.

Размер популяции параметр, присутствующий во всех роевых алгорит-

мах и влияющий на их эффективность. В [23] предложено адаптивное из-

менение размера популяции в зависимости от популяционного разнообразия;

максимальное количество итераций делится на равные периоды, каждый из

которых содержит равное количество итераций; в конце каждого периода вы-

числяется разнообразие популяции и в зависимости от его значения размер

популяции либо увеличивается, либо уменьшается.

Методы регулировки значений параметров включаются в исходный алго-

ритм, что приводит к увеличению вычислительной и временной сложности

алгоритма. Одним из вариантов решения этой проблемы является разработ-

ка роевых алгоритмов без параметров, но этот подход требует детального

изучения [6]. Существует еще ряд открытых вопросов, связанных с настрой-

кой и регулировкой параметров. Необходимо теоретическое обоснование су-

ществования зависимости эффективности роевого алгоритма от его парамет-

ров. Необходимы разработки схем адаптации параметров для сложных задач

оптимизации, таких как многоцелевая оптимизация, оптимизация с ограни-

чениями, крупномасштабная оптимизация, оптимизация в динамических и

неопределенных средах. Необходимы исследования применения методов ма-

шинного обучения для решения проблем настройки и регулировки парамет-

ров роевых алгоритмов, частично эта проблема рассматривается в разделе 8

обзора.

8. Гибридизация

Создатели метаэвристических алгоритмов сталкиваются с трудно разре-

шимой проблемой: как найти хороший баланс между диверсификацией и ин-

тенсификацией; в одном алгоритме практически невозможно сбалансировать

указанные компоненты [127]. Задачи оптимизации могут быть более эффек-

тивно решены путем гибридизации существующих алгоритмических струк-

тур. Основная цель гибридизации заключается в использовании уникальных

особенностей и преимуществ каждого алгоритма для достижения компромис-

са между диверсификацией и интенсификацией, а также для предотвращения

преждевременной сходимости путем использования сильных сторон каждого

из компонентов в соответствующем алгоритме. Однако создание эффектив-

ного гибридного алгоритма является сложным процессом, который требует

обширных знаний и большого опыта в создании систем оптимизации [128].

В [129] приведена следующая классификация гибридных алгоритмов:

1) портфельные алгоритмы это библиотека последовательно работаю-

щих алгоритмов поиска;

2) гиперэвристика это библиотека алгоритмов поиска, снабженная меха-

низмом координации, который выбирает и активирует различные алгоритмы

или генерирует специальные компоненты поиска;

3) меметические алгоритмы это структура, которая содержит основной

решатель и несколько алгоритмов локального поиска; 4) ансамбль алгорит-

мов алгоритмическая структура, в которую входят стратегии поиска и

общие компоненты решения проблем оптимизации.

Авторы [129] указывают на то, что классификация скорее отражает истори-

ческий путь гибридизации, чем выявляет алгоритмические различия в под-

ходах.

8.1. Меметические алгоритмы

Роевые алгоритмы показывают хорошие результаты на стадии диверси-

фикации, но существенно уступают традиционным методам на стадии интен-

сификации; при приближении к оптимуму метаэвристические методы усту-

пают градиентным. Комбинирование глобального поиска на уровне популя-

ции и локального поиска на уровне отдельного решения получило развитие

в области меметических алгоритмов [49]. Меметические алгоритмы класс

алгоритмов оптимизации, в структуру которых включены компоненты попу-

ляционных метаэвристик и процедуры локального поиска. Термин “мемети-

ческий алгоритм” вытекает из того факта, что процедура локального поиска

сродни мему, представляющему некоторую форму предметно-специфических

априорных знаний человека-эксперта о том, как можно улучшить решение.

В гибридных алгоритмах мемы воспринимаются как инструкции, правила,

стратегии, априорные знания [130].

Авторы [131] разделяют меметические алгоритмы на три основных класса:

1) алгоритмы с одним фиксированным мемом или локальным оператором

поиска, применяемым к решению, сформированному популяционной метаэв-

ристикой;

2) алгоритмы с пулом заданных локальных операторов поиска (мемов), ко-

торые конкурируют между собой; выбор мема может быть основан на различ-

ных критериях, таких как абсолютное значение целевой функции решений,

связанных с мемом, или улучшение значения целевой функции в результате

прошлых применений мема;

3) эволюционирующие мемы с априори неизвестным пулом мемов, которые

автоматически адаптируются к ландшафту целевой функции.

Процедура локального поиска, используемая в меметических алгоритмах,

имеет как детерминированный, так и стохастический характер. В качестве

детерминированных процедур часто используются алгоритмы Хука-Дживса

[132] и Нелдера-Мида [133], а также градиентные и квазиньютоновские мето-

ды [134]. Стохастические процедуры в меметических алгоритмах представле-

ны поиском с запретами [135], имитационным отжигом [6, 133], хаотическим

локальным поиском [136]. Глобальный и локальный поиск в гибриде, пред-

ложенном в [127], выполняется двумя операторами, основанными на полетах

Леви и поисковых выражениях алгоритма криля соответственно.

В большинстве меметических алгоритмов локальный поиск применяет-

ся только к текущему глобально лучшему решению по причине того, что

1) окрестность такого решения может быть наиболее перспективной для по-

иска глобального оптимума; 2) экономится время выполнения по сравнению

со схемами, которые применяют локальный поиск ко всем решениям.

В [137] предложены три схемы, комбинирующие алгоритм роящихся ча-

стиц с локальным поиском:

Схема 1. Локальный поиск применяется к глобально лучшему решению p_g;

Схема 2. Локальный поиск применяется к лучшему решению i-й части-

цы p_i при условии, что случайно сгенерированное число r < ε, где ε > 0

заданный порог;

Схема 3,а. Локальный поиск применяется как к глобально лучшему реше-

нию p_g, так и к некоторым случайно выбранным решениям p_i;

Схема 3,б. Локальный поиск применяется как к глобально лучшему реше-

нию p_g, так и к некоторым случайно выбранным решениям p_i, для которых

|p_g - p_i| > c(S), где A ∈ (0, 1) и (S) размер поискового пространства S.

Приведенные три схемы могут применяться либо на каждой итерации ал-

горитма, либо на некоторых итерациях. Существуют и другие схемы, напри-

мер применяющие локальный поиск ко всем частицам, однако такие схемы

являются вычислительно затратными, на практике локальный поиск должен

применяться только к небольшому количеству частиц (порядка 5 % от общего

числа) [137].

В [138] предложен алгоритм роящихся частиц с двумя адаптивными мето-

дами локального поиска. Первый метод выполняет случайное перемещение

от текущего решения, уменьшая на каждой итерации длину шага. Во втором

методе процедуру локального поиска можно рассматривать как итеративное

локальное движение частицы, когда поиск направляется лучшим решением

i-й частицы без учета глобально лучшего решения:

x_i(t + 1) = x_i(t) + w · v_i(t) + c₁ · rand · (p_i(t) - x_i(t)).

В [139] предложен меметический алгоритм на основе алгоритма искус-

ственной пчелиной колонии, методов Нелдера-Мида и случайного блужда-

ния. Для поддержания баланса диверсификация/интенсификация использу-

ется адаптивная схема:

{ если rand(0,1) > p(ψ), то использовать Метод Нелдера-Мида,

в противном случае использовать метод случайных блужданий.

Значения p(ψ) находятся из экспоненциального распределения

(ψ-µp)

2σp

p(ψ) = e

где ψ значение меры разнообразия (5), µ_p, σ_p среднее значение и стан-

дартное отклонение меры разнообразия соответственно.

Оптимальный баланс между глобальным и локальным поиском явно за-

висит от решаемой задачи оптимизации, применяемого меметического алго-

ритма и настроек его параметров. Поэтому невозможно разработать универ-

сальные принципы проектирования роевых алгоритмов, всегда приводящие

к лучшим решениям [140]. Существование таких универсальных принципов

противоречит теореме о бесплатных завтраках [7].

8.2. Ансамбли

Одним из подходов к повышению эффективности роевых алгоритмов яв-

ляется ансамблевая стратегия. В контексте проблемы оптимизации понятие

“ансамбль” связано с использованием нескольких операторов и стратегий по-

иска, субпопуляций, алгоритмов, значений параметров для решения задачи

оптимизации. Ансамбли могут быть разделены на низкоуровневые и высоко-

уровневые. В ансамбль низкого уровня объединены различные типы опера-

торов и стратегий поиска. Высокоуровневые ансамбли относятся к методам,

которые для данной задачи адаптивно выбирают лучший алгоритм оптими-

зации из набора алгоритмов-кандидатов [141].

В [22] предлагается ансамбль стратегий адаптивного изменения коэффи-

циента инерции в алгоритме роящихся частиц. Линейное или нелинейное

уменьшение значения коэффициента инерции для каждой частицы опреде-

ляется предысторией; если стратегия, выбранная на предыдущей итерации,

приводит к лучшему решению, тогда назначенная стратегия сохраняется, в

противном случае меняется. В [68] описан ансамбль из шести хаотических

карт для генерации псевдослучайных чисел, используемых для формирова-

ния вектора скорости в алгоритме роящихся частиц. В начале работы алго-

ритма каждой частице случайным образом назначается одна из шести карт;

если частица не улучшает свое положение в течение 20 итераций, ей назнача-

ется другая хаотическая карта. В [142] описан алгоритм роящихся частиц, в

котором скорости частицы вычисляются с помощью одного из четырех опе-

раторов, ответственных за сходимость, интенсификацию, диверсификацию и

“выпрыгивание” из локальных оптимумов. Выбор одного из четырех опера-

торов основан на предложенной авторами адаптивной стратегии.

В модифицированном алгоритме искусственной пчелиной колонии

MEABC используется ансамбль из трех стратегий поиска решений [143]:

1) стратегия, принятая в оригинальном алгоритме, когда новое решение

генерируется путем перемещения старого решения к случайно выбранному

из популяции решению;

2) стратегия ABC/best, повторяющая первую, в которую добавлена ин-

формация о лучшем решении в популяции;

3) модифицированная стратегия ABC/best/1, основанная на мутации

DE/best/1 [64].

Указанные стратегии динамически меняются в процессе поиска, соревнуясь

между собой при генерации нового решения, что позволяет сбалансировать

процессы диверсификации и интенсификации. Эффективность MEABC про-

верялась экспериментально на множестве тестовых функций. По сравнению

с оригинальным алгоритмом искусственной пчелиной колонии и двумя его

модификациями MEABC показал более высокую скорость сходимости и бо-

лее точные решения. Алгоритм MEABC оказался лучшим при сравнении с

пятью модификациями алгоритма роящихся частиц, равным по эффектив-

ности третьей модификации при решении сложных мультимодальных задач

и уступил этой модификации при поиске оптимума на нескольких математи-

ческих функциях. Однако авторы утверждают, что MEABC проще и требует

настройки меньшего количества параметров при одинаковой вычислительной

временной сложности [143].

К высокоуровневым методам относится ансамбль алгоритмов роящихся

частиц с самоадаптивным механизмом выбора лучшего алгоритма [144]. Ан-

самбль состоит из пяти разных алгоритмов роящихся частиц, каждый из

которых используется для выполнения определенных задач, а именно: обес-

печения высокой скорости сходимости, для предотвращения преждевремен-

ной сходимости, для поддержания популяционного разнообразия, для увели-

чения возможностей локального поиска, для поиска нескольких локальных

оптимумов при мультимодальной оптимизации. Выбор наиболее подходящего

алгоритма на текущей итерации выполняется на основе механизма самоадап-

тации.

Хотя за последнее десятилетие были достигнуты впечатляющие резуль-

таты в разработке и исследовании ансамблевых стратегий в оптимизации,

существует ряд открытых проблем, требующих решения, далее приведены

некоторые из них [141].

1. В настоящее время количество элементов, включенных в ансамбль, от-

носительно невелико, было бы полезно включить в ансамбль большее коли-

чество элементов с различными характеристиками. Однако пока неизвестно,

как реализовать крупномасштабный ансамбль, насколько он будет надежен

и эффективен.

2. Нерешенной проблемой остается определение характеристики алгорит-

мических компонентов, входящих в ансамбль. Необходимо разработать адек-

ватные метрики описания компонентов, а также методы формирования ан-

самбля на основе этих метрик.

3. Эффективность стратегии ансамбля обычно проверяется с помощью

эксперимента. Необходим теоретический анализ компонентов ансамбля и опи-

сание эффекта от каждого из них.

4. Наличие множества различных алгоритмических компонентов может

вызвать нестабильность ансамбля по причине случайности, присущей этим

компонентам. В реализацию ансамбля должны быть включены оценки изме-

нения целевой функции и популяционного разнообразия, а также механизмы

взаимодействия между различными компонентами.

8.3. Гиперэвристика

Эффективность метаэвристических алгоритмов зависит от решаемых за-

дач. В общем случае неизвестно, какой алгоритм лучше всего подходит для

данной задачи. Как следствие, выбор наиболее подходящей метаэвристики

для конкретной задачи обычно является непростой задачей. Альтернативой

экспертному поиску лучшего алгоритма для конкретной задачи оптимизации

является гиперэвристика, которая обеспечивает универсальный эвристиче-

ской подход к решению сложных задач оптимизации. Гиперэвристика ориен-

тирована не на решение конкретной задачи, а на поиск (мета)эвристики или

их последовательностей, которые будут решать конкретную задачу. Отличие

метаэвристики от гиперэвристики в том, что первая работает в пространстве

решений, а вторая в пространстве (мета)эвристик.

С точки зрения пространства поиска различают гиперэвристики, которые

либо выбирают, либо генерируют (мета)эвристики низкого уровня, исполь-

зующиеся в дальнейшем для решения конкретной задачи оптимизации. Ги-

перэвристику можно рассматривать как алгоритм обучения либо в режиме

офлайн, либо в режиме онлайн. Онлайн обучение проводится в процессе ре-

шения проблемы, офлайн обучение заключается в формировании правил из

множества обучающих примеров. Среди подходов, основанных на онлайн-

обучении, можно выделить подходы, основанные на обучении с подкрепле-

нием для выбора эвристики нижнего уровня, и подходы, которые применя-

ют метаэвристику для поиска эвристики, работающей в пространстве реше-

ний [145].

Гиперэвристика на основе выбора строится следующим образом [146]:

1) выбрать множество эвристик низкого уровня для решения задач опти-

мизации, причем, не обязательно, чтобы каждая из них была высокоэффек-

тивной при решении поставленной задачи, но их число должно быть доста-

точным большим, чтобы генерировать большое пространство поиска;

2) определить алгоритм высокого уровня, который может быть обучаю-

щим автоматом или метаэвристикой (эволюционный алгоритм, алгоритм му-

равьиной колонии, роевый алгоритм);

3) определить процедуру кодирования для поиска низкоуровневых эври-

стик.

Подавляющее большинство гиперэвристик разработаны для дискретных

пространств поиска. Далее приведены несколько гиперэвристик, работаю-

щих в непрерывных пространствах. Гиперэвристика DEWCO [147], исполь-

зуя на верхнем уровне алгоритм дифференциальной эволюции, формирует

оптимальную начальную популяцию алгоритма китов. В выборе участвуют

метод оппозиционного обучения и множество хаотических карт. Гиперэври-

стика H3AD [148] сочетает в себе два подхода: генерацию и выбор. В основе

генерации лежит база знаний, которая содержит примеры алгоритмов, со-

зданных для набора репрезентативных задач, вместе с описанием характер-

ных признаков этих задач. Решение новой задачи начинается с выбора из

базы знаний по представленным признакам наиболее похожей задачи и ал-

горитма, ранее сгенерированного для решения этой задачи. Гиперэвристика

H3AD применяется для определения адекватных конфигураций параметров

и компонентов алгоритма роящихся частиц. Для формирования компонентов

алгоритма используется генетическое программирование, которое определя-

ет такую процедуру, как, например, стратегия инициализации популяции.

Выбор алгоритма роящихся частиц выполняется с использованием метода

рассуждений по прецедентам.

В гиперэвристику HyperSPAM [129] включены три алгоритма решения за-

дач оптимизации в непрерывном пространстве поиска. Алгоритм эволюцион-

ной стратегии с ковариационной матрицей адаптации активируется в начале

процесса оптимизации в качестве компонента предварительной обработки.

Далее полученное решение подается на два других алгоритма поиска. Пер-

вый выполняет перемещения по осям, а второй использует матричную ортого-

нализацию для выполнения диагональных перемещений. Четыре адаптивные

стратегии используются для координации работы алгоритмов поиска. Первая

стратегия является простым случайным выбором, а остальные три применя-

ют механизм вознаграждения, основанный на успехах алгоритма поиска на

предыдущих итерациях.

9. Открытые проблемы

Хотя за последние десятилетия исследование роевых алгоритмов продви-

нулось далеко вперед, остается еще ряд открытых проблем. Часть этих про-

блем затронута в обзоре, но в большинстве своем решаются эти проблемы на

эмпирическом уровне. Далее рассмотрены некоторые актуальные проблемы

в исследовании роевых алгоритмов [141, 149].

1. Эффективность роевого алгоритма напрямую связана с установлением

оптимального баланса между диверсификацией и интенсификацией. Однако

ни один алгоритм не может претендовать на решение проблемы достижения

такого баланса. По сути, сам баланс является проблемой гипероптимизации,

потому что это оптимизация алгоритма оптимизации.

2. Отсутствие единой математической структуры для всестороннего из-

учения роевых алгоритмов, позволяющей анализировать сложность, устойчи-

вость, сходимость, соотношение точности решения и вычислительных затрат,

настройку и регулировку параметров. Разработка такой структуры потребует

междисциплинарного подхода для объединения различных математических,

стохастических и численных методов.

3. Отсутствие унифицированной тестовой среды с комплексным набором

метрик для сравнения результатов работы различных роевых алгоритмов.

Показателем эффективности работы алгоритма чаще всего является точ-

ность. Однако если не учитывать время работы, то точность не будет адек-

ватной оценкой работы алгоритма. Практика современного тестирования ис-

пользует набор математических функций с различными свойствами, однако

реальные задачи гораздо более разнообразны, они могут иметь много нели-

нейных ограничений, образованных несколькими изолированными областя-

ми. Таким образом, алгоритмы, хорошо работающие на тестовых функциях,

могут быть неэффективными при решении реальных задач.

4. Масштабируемость роевых алгоритмов. Открытой остается проблема,

как наилучшим образом изменить алгоритмы, хорошо работающие на зада-

чах небольшой размерности (с числом переменных от нескольких единиц до

нескольких сотен), для эффективного решения задач большой (больше ты-

сячи переменных) и очень большой размерности.

5. Проблемой отдаленного будущего является создание интеллектуальных

алгоритмов и систем, способных распознавать особенности решаемой задачи

и выбирать или проектировать подходящий алгоритм.

10. Заключение

В статье рассмотрены некоторые подходы к повышению эффективности

роевых алгоритмов оптимизации. Модульная структура роевых алгоритмов

позволяет изменять входящие в них компоненты. Для задания популяции на-

чальных решений используется метод инициализации или комбинация этих

методов. Новое решение формируется как операторами оригинального алго-

ритма, так и эволюционными или хаотическими операторами. Лучшие ре-

шения получены путем гибридизации роевых алгоритмов с использованием

различных стратегий. В разработке и исследовании роевых алгоритмов оп-

тимизации существует ряд нерешенных проблем, некоторые из них указаны

в обзоре.

К настоящему времени в литературе представлено большое количество ре-

зультатов исследований, невозможно охватить все соответствующие публика-

ции в пределах заданного объема статьи. В обзоре не рассмотрены критерии

остановки работы роевых алгоритмов [150], их квантовые модификации [151],

а также аппаратная реализация роевых алгоритмов на основе облаков, вы-

числительных кластеров и графических процессоров [152-154].

СПИСОК ЛИТЕРАТУРЫ

Li Q., Liu S.-Y., Yang X.-S. Influence of Initialization on the Performance of Meta-

heuristic Optimizers // Appl. Soft Comput. 2020. V. 91. 106193.

Luke S. Essentials of Metaheuristics [Электронный ресурс]. Режим доступа:

https://cs.gmu.edu/∼sean/book/metaheuristics/

Boussaid I., Lepagnot J., Siarry P. A Survey on Optimization Metaheuristics //

Inf. Sci. 2013. V. 237. P. 82-117.

Kirkpatrick S., Gelatt C.D., Vecchi M.P. Optimization by Simulated Annealing //

Science. 1983. V. 220. P. 671-680.

Glover F. Future Paths for Integer Programming and Links to Artificial Intelli-

gence // Comput. Oper. Res. 1986. V. 13. P. 533-549.

Nematollahi A.F., Rahiminejad A., Vahidi B. A Novel Meta-Heuristic Optimization

Method Based on Golden Ratio in Nature // Soft Comput. 2020. V. 24. P. 1117-

1151.

Wolpert D., Macready W. No Free Lunch Theorems for Optimization // IEEE

Trans. Evol. Comput. 1997. V. 1. P. 67-82.

Clerc M. From Theory to Practice in Particle Swarm Optimization / Handbook of

Swarm Intelligence. V. 8. Berlin: Springer, 2011. P. 3-36.

Sorensen K. Metaheuristics The Metaphor Exposed // Int. Trans. Oper. Res. 2015.

V. 22. No. 1. P. 3-18.

10.

Camacho-Villalon C.L., Dorigo M., Stützle T. The Intelligent Water Drops Algo-

rithm: Why It Cannot Be Considered a Novel Algorithm // Swarm Intell. 2019.

V. 13. P. 173-192.

11.

Weyland D. A Rigorous Analysis of the Harmony Search Algorithm: How The Re-

search Community Can Be Misled by a “Novel” Methodology // Int. J. Appl. Meta-

heuristic Computing. 2010. V. 1. P. 50-60.

12.

Geem Z.W., Kim J.H., Loganathan G.V. A New Heuristic Optimization Algorithm:

Harmony Search // Simulation. 2001. V. 76. P. 60-68.

13.

Piotrowski A.P., Napiorkowski J.J., Rowinski P.M. How Novel is the “Novel” Black

Hole Optimization Approach? // Inf. Sci. 2014. V. 267. P. 191-200.

14.

Hatamlou A. Black Hole: A New Heuristic Optimization Approach for Data Clus-

tering // Inf. Sci. 2013. V. 222. P. 175-184.

15.

Shah-Hosseini H. The Intelligent Water Drops Algorithm: A Nature-Inspired

Swarm-Based Optimization Algorithm // Int. J. Bio-Inspired Computation. 2009.

V. 1. No. 1/2. P. 71-79.

16.

Neri F. Diversity Management in Memetic Algorithms // Handbook of Memetic

Algorithms. 2012. SCI. V. 379. P. 153-165.

17.

Cuevas E., Oliva D., Zaldivar D., Perez-Cisneros M., Pajares G. Opposition-Based

Electromagnetism-Like for Global Optimization // Int. J. Innov. Comput. I. 2012.

V. 8. No. 12. P. 8181-8198.

18.

Turgut M.S., Turgut O.E., Eliiyi D.T. Island-based Crow Search Algorithm for

Solving Optimal Control Problems // Appl. Soft Comput. 2020. V. 90. 106170.

19.

Ходашинский И.А., Дудин П.А. Идентификация нечетких систем на основе

прямого алгоритма муравьиной колонии // Искусственный интеллект и при-

нятие решений. 2011. № 3. С. 26-33.

20.

Kennedy J., Ebenhart R. Particle Swarm Optimization // Proc. 1995 IEEE Int.

Conf. Neural Networks. Perth: IEEE Service Center, 1995. P. 1942-1948.

21.

Yang X.-S., Deb S. Engineering Optimisation by Cuckoo Search // Int. J. Math.

Modelling and Numerical Optimisation. 2010. V. 1. No. 4. P. 330-343.

22.

Shirazi M.Z., et al. Particle Swarm Optimization with Ensemble of Inertia Weight

Strategies // ICSI 2017. LNCS. V. 10385. Heidelberg: Springer, 2017. P. 140-147.

23.

Chen D.B., Zhao C.X. Particle Swarm Optimization with Adaptive Population Size

and Its Application // Appl. Soft Comput. 2009. V. 9. No. 1. P. 39-48.

24.

Chen L., Lu H., Li H., Wang G., Chen L. Dimension-by-Dimension Enhanced

Cuckoo Search Algorithm for Global Optimization // Soft Comput. 2019. V. 23.

P. 11297-11312.

25.

Singh A., Deep K. Artificial Bee Colony Algorithm with Improved Search Mecha-

nism // Soft Comput. 2019. V. 23. P. 12437-12460.

26.

Gupta S., Deep K. Cauchy Grey Wolf Optimiser for Continuous Optimisation Prob-

lems // J. Exp. Theor. Artif. Intell. 2018. V. 30. P. 1051-1075.

27.

Kazimipour B., Omidvar M.N., Li X., Qin A. A Novel Hybridization of Opposition-

Based Learning and Cooperative Co-Evolutionary for Large-Scale Optimization /

Proc. IEEE Congr. on Evolutionary Computation. Beijing, 2014. P. 2833-2840.

28.

Pant M., Thangaraj R., Abraha A. Low Discrepancy Initialized Particle Swarm

Optimization for Solving Constrained Optimization Problems // Fundamenta In-

formaticae. 2009. V. 95. P. 511-531.

29.

Brits R., Engelbrecht A.P., van den Bergh F. A Niching Particle Swarm Opti-

mizer // Proc. 4th Asia-Pacific Conf. Simulated Evol. Learning. 2002. P. 692-696.

30.

Altinoz O.T., Yilmaz A.E., Weber G. Improvement of the Gravitational Search

Algorithm by Means of Low-Discrepancy Sobol Quasi Random-Number Sequence

Based Initialization // Adv. Electr. Comp. Eng. 2014. V. 14. No. 3. P. 55-62.

31.

Mahdavi S., Rahnamayan S., Deb K. Opposition Based Learning: A Literature

Review // Swarm Evol. Comput. 2018. V. 39. P. 1-23.

32.

Rahnamayan S., Tizhoosh H.R., Salama M. Opposition-Based Differential Evolu-

tion // IEEE Trans. Evol. Comput. 2008. V. 12. No. 1. P. 64-79.

33.

Farooq M.U., Ahmad A., Hameed A. Opposition-Based Initialization and a Modified

Pattern for Inertia Weight (IW) in PSO // Proc. IEEE Int. Conf. Innov. Intel. Sys.

Appl (INISTA). 2017. Number: 17083603.

34.

Wang G.-G., Deb S., Gandomi A.H., Alavi A.H. Opposition-Based Krill Herd Al-

gorithm with Cauchy Mutation and Position Clamping // Neurocomputing. 2016.

V. 177. P. 147-157.

35.

Gao W.-f., Liu S.-y., Huang L.-l. Particle Swarm Optimization with Chaotic

Opposition-Based Population Initialization and Stochastic Search Technique //

Commun. Nonlinear Sci. Numer. Simulat. 2012. V. 17. P. 4316-4327.

36.

Kazimipour B., Li X., Qin A.K. A Review of Population Initialization Techniques

for Evolutionary Algorithms // Proc. IEEE Congr. Evol. Comput. Beijing, 2014.

P. 2585-2592.

37.

Melo V.V., Botazzo Delbem A.C. Investigating Smart Sampling as a Population

Initialization Method for Differential Evolution in Continuous Problems // Inf. Sci.

2012. V. 193. P. 36-53.

38.

Grobler J., Engelbrecht A.P. A Scalability Analysis of Particle Swarm Optimization

Roaming Behaviour // ICSI 2017. LNCS. V. 10385. Heidelberg: Springer, 2017.

P. 119-130.

39.

Gao W.-f., Liu S.-y., Huang L.-l. Enhancing Artificial Bee Colony Algorithm using

More Information-Based Search Equations // Inf. Sci. 2014. V. 270. P. 112-133.

40.

Cheng S., Shi Y., Qin Q. Experimental Study on Boundary Constraints Handling

in Particle Swarm Optimization: From Population Diversity Perspective // Int. J.

Swarm Intell. Res. 2011. V. 2. P. 43-69.

41.

Salleh M.N.M., et al. Exploration and Exploitation Measurement in Swarm-Based

Metaheuristic Algorithms: An Empirical Analysis / Recent Advances on Soft Com-

puting and Data Mining. Springer, 2018. P. 24-32.

42.

Chaudhary R., Banati H. Swarm Bat Algorithm with Improved Search (SBAIS) //

Soft Comput. 2019. V. 23. P. 11461-11491.

43.

Blackwell T., Kennedy J. Impact of Communication Topology in Particle Swarm

Optimization // IEEE Trans. Evol. Comput. 2019. V. 23. No. 4. P. 689-702.

44.

Cheng S., Shi Y., Qin Q. Promoting Diversity in Particle Swarm Optimization

to Solve Multimodal Problem // Neural Inf. Proc. LNCS, V. 7063. Heidelberg:

Springer, 2011. P. 228-237.

45.

Kaucic M. A Multi-Start Opposition-Based Particle Swarm Optimization Algo-

rithm with Adaptive Velocity for Bound Constrained Global Optimization // J.

Glob. Optim. 2013. V. 55. P. 165-188.

46.

Cao Y., et al. Comprehensive Learning Particle Swarm Optimization Algorithm

With Local Search for Multimodal Functions // IEEE Trans. Evol. Comput. 2019.

V. 23. No. 4. P. 718-731.

47.

Neri F., Tirronen V., Karkkainen T., Rossi T. Fitness Diversity Based Adaptation

in Multimeme Algorithms: A Comparative Study // IEEE Congr. Evol. Comput.

Singapore: IEEE, 2007. INSPEC Accession Number: 9889441.

48.

Ghannami A., Li J., Hawbani A., Alhusaini N. Diversity Metrics for Direct-Coded

Variable-Length Chromosome Shortest Path Problem Evolutionary Algorithms //

Computing. 2020.

49.

Cheng S., Shi Y., Qin Q., Zhang Q., Bai R. Population Diversity Maintenance in

Brain Storm Optimization Algorithm // J. Artif. Intell. Soft Comput. Res. 2014.

V. 4. No. 2. P. 83-97.

50.

Simon D., Omran M.G., Clerc M. Linearized Biogeography-Based Optimization

with Re-Initialization and Local Search // Inf. Sci. 2014. V. 267. P. 140-157.

51.

Kennedy D.D., Zhang H., Rangaiah G.P., Bonilla-Petriciolet A. Particle Swarm

Optimization with Re-Initialization Strategies for Continuous Global Optimiza-

tion / Global Optimization: Theory, Developments and Applications. Nova Science

Publishers, 2013. P. 1-42.

52.

Merrikh-Bayat F. The Runner-Root Algorithm: A metaheuristic for Solving Uni-

modal and Multimodal Optimization Problems Inspired by Runners and Roots of

Plants in Nature // Appl. Soft Comput. 2015. V. 33. P. 292-303.

53.

Saxena A. A Comprehensive Study of Chaos Embedded Bridging Mechanisms and

Crossover Operators for Grasshopper Optimisation Algorithm // Expert Syst. Appl.

2019. V. 132. P. 166-188.

54.

Wang G.-G., et. al. Chaotic krill herd algorithm // Inf. Sci. 2014. V. 274. P. 17-34.

55.

Wang G.-G., Deb S., Zhao X., Cui Z. A New Monarch Butterfly Optimization with

an Improved Crossover Operator // Oper. Res. Int. J. 2018. V. 18. P. 731-755.

56.

Zhou L., Ma M., Ding L., Tang W. Centroid Opposition with a Two-Point Full

Crossover for the Partially Attracted Firefly Algorithm // Soft Comput. 2019. V. 23.

P. 12241-12254.

57.

San P.P., Ling S.H., Nguyen H.T. Hybrid PSO-based Variable Translation Wavelet

Neural Network and Its Application to Hypoglycemia Detection System // Neural

Comput. Applic. 2013. V. 23. P. 2177-2184.

58.

Saha S.K., Kar R., Mandal D., Ghoshal S.P. Optimal IIR Filter Design using

Gravitational Search Algorithm with Wavelet Mutation // J. King Saud Univ.

Comput. Inf. Sci. 2015. V. 27. P. 25-39.

59.

Nobahari H., Nikusokhan M., Siarry P. A Multi-Objective Gravitational Search

Algorithm Based on Non-Dominated Sorting // Int. J. Swarm. Intell. Res. 2012.

V. 3. P. 32-49.

60.

Chen Y., et al. Dynamic Multi-Swarm Differential Learning Particle Swarm Opti-

mizer // Swarm Evol. Comput. 2018. V. 39. P. 209-221.

61.

Yazdani S., Hadavandi E. LMBO-DE: A Linearized Monarch Butterfiy Optimiza-

tion Algorithm Improved with Differential Evolution // Soft Comput. 2019. V. 23.

P. 8029-8043.

62.

Luo J., Liu Z. Novel Grey Wolf Optimization Based on Modified Differential Evolu-

tion for Numerical Function Optimization // Appl. Intell. 2020. V. 50. P. 468-486.

63.

Zou F., et al. Teaching-Learning-Based Optimization with Differential and Repul-

sion Learning for Global Optimization and Nonlinear Modeling // Soft Comput.

2018. V. 22. P. 7177-7205.

64.

Мех М.А., Ходашинский И.А. Сравнительный анализ применения методов

дифференциальной эволюции для оптимизации параметров нечетких класси-

фикаторов // Изв. РАН. Теория и системы управления. 2017. № 4. С. 65-75.

65.

Herrera F., Lozano M., Sanchez A.M. A Taxonomy for the Crossover Operator

for Real-Coded Genetic Algorithms: An Experimental Study // Int. J. Intell. Syst.

2003. V. 18. P. 309-338.

66.

Gao S., et al. Gravitational Search Algorithm Combined with Chaos for Uncon-

strained Numerical Optimization // Appl. Math. Comput. 2014. V. 231. P. 48-62.

67.

Metlicka M., Davendra D. Chaos Driven Discrete Artificial Bee Algorithm for Loca-

tion and Assignment Optimisation Problems // Swarm Evol. Comput. 2015. V. 25.

P. 15-28.

68.

Pluhacek M., Senkerik R., Davendra D. Chaos Particle Swarm Optimization with

Eensemble of Chaotic Systems // Swarm Evol. Comput. 2015. V. 25. P. 29-35.

69.

Ma H., et al. Multi-Population Techniques in Nature Inspired Optimization Algo-

rithms: A Comprehensive Survey // Swarm Evol. Comput. 2019. V. 44. P. 365-387.

70.

Blackwell T., Branke J. Multiswarms, Exclusion, and Anti-Convergence in Dynamic

Environments // IEEE Trans. Evol. Comput. 2006. V. 10. P. 459-472.

71.

Lung R.I., Dumitrescu D. Evolutionary Swarm Cooperative Optimization in Dy-

namic Environments // Nat. Comput. 2010. V. 9. P. 83-94.

72.

Corcoran A.L., Wainwright R.L. A Parallel Island Model Genetic Algorithm for the

Multiprocessor Scheduling Problem // Proc. ACM Symp. Appl. Comput. ACM.

1994. P. 483-487.

73.

Lardeux F., Maturana J., Rodriguez-Tello E., Saubion F. Migration Policies in Dy-

namic Island Models // Nat. Comput. 2019. V. 18. P. 163-179.

74.

Sutton R., Barto A. Reinforcement Learning: An Introduction. London: MIT Press,

1998.

75.

Gong Y.J., et al. Distributed Evolutionary Algorithms and Their Models: A Survey

of the State-of-the-Art // Appl. Soft Comput. 2015. V. 34. P. 286-300.

76.

Raidl G.R. A Unified View on Hybrid Metaheuristics // Proc. Hybrid Metaheuris-

tics, Third Int. Workshop. LNCS V. 4030. Heidelberg: Springer, 2006. P. 1-12.

77.

Ходашинский И.А., Горбунов И.В. Гибридный метод построения нечетких си-

стем на основе модели островов // Информатика и системы управления. 2014.

№ 3. С. 114-120.

78.

Lynn N., Ali M.Z., Suganthan P.N. Population Topologies for Particle Swarm Opti-

mization and Differential Evolution // Swarm Evol. Comput. 2018. V. 39. P. 24-35.

79.

Shi Y., Liu H., Gao L., Zhang G. Cellular Particle Swarm Optimization // Inf. Sci.

2011. V. 181. P. 4460-4493.

80.

Fang W., Sun J., Chen H., Wu X. A Decentralized Quantum-Inspired Particle

Swarm Optimization Algorithm with Cellular Structured Population // Inf. Sci.

2016. V. 330. P. 19-48.

81.

Huang L., Qin C. A Novel Modified Gravitational Search Algorithm for the Real

World Optimization Problem // Int. J. Mach. Learn. Cybern. 2019. V.

10.

P. 2993-3002.

82.

Li C., Yang S. A General Framework of Multipopulation Methods with Clustering

in Undetectable Dynamic Environments // IEEE Trans. Evol. Comput. 2012. V. 16.

P. 556-577.

83.

Xia L., Chu J., Geng Z. A Multiswarm Competitive Particle Swarm Algorithm for

Optimization Control of an Ethylene Cracking Furnace // Appl. Artif. Intell. 2014.

V. 28. P. 30-46.

84.

Huang C., Li Y., Yao X. A Survey of Automatic Parameter Tuning Methods for

Metaheuristics // IEEE Trans. Evol. Comput. 2020. V. 24. No. 2. P. 201-216.

85.

Poli R. Mean and Variance of the Sampling Distribution of Particle Swarm Op-

timizers during Stagnation // IEEE Trans. Evol. Comput. 2009. V. 13. No. 4.

P. 712-721.

86.

Sengupta S., Basak S., Peters R.A. Particle Swarm Optimization: A Survey of His-

torical and Recent Developments with Hybridization Perspectives // Mach. Learn.

Knowl. Extr. 2019. V. 1. P. 157-191.

87.

Calvet L., Juan A.A., Serrat C., Ries J. A Statistical Learning Based Approach for

Parameter Fine-Tuning of Metaheuristics // SORT - Stat. Oper. Res. Trans. 2016.

V. 40. P. 201-224.

88.

Birattari M. Tuning Metaheuristics: A Machine Learning Perspective // SCI. 2009.

V. 197.

89.

Hutter F., Hoos H.H., Leyton-Brown K., Stützle T. ParamILS: An Automatic Al-

gorithm Configuration Framework // J. Artif. Intell. Res. 2009. V. 36. P. 267-306.

90.

Yuan Z., de Oca M.M.A., Birattari M., Stützle T. Continuous Optimization Algo-

rithms for Tuning Real and Integer Parameters of Swarm Intelligence Algorithms //

Swarm Intell. 2012. V. 6. P. 49-75.

91.

Eiben A.E., Smit S.K. Evolutionary Algorithm Parameters and Methods to Tune

Them / Autonomous Search. Springer, 2012. P. 15-36.

92.

Adenso-Diaz B., Laguna M. Fine-tuning of Algorithms using Fractional Experimen-

tal Designs and Local Search // Oper. Res. 2006. V. 54. P. 99-114.

93.

Barbosa E.B.M., Senne E.L.F. Improving the Fine-Tuning of Metaheuristics: An

Approach Combining Design of Experiments and Racing Algorithms // J. Optim.

2017. V. 2017. P. 1-7.

94.

Fallahi M., Amiri S., Yaghini M. A Parameter Tuning Methodology for Meta-

heuristics Based on Design of Experiments // Int. J. Eng. Techn. Sci. 2014. V. 2.

P. 497-521.

95.

Huang D., Allen T.T., Notz W.I., Zeng N. Global Optimization of Stochastic Black-

Box Systems via Sequential Kriging Meta-Models // J. Glob. Optim. 2006. V. 34.

No. 3. P. 441-466.

96.

Audet C., Dennis J.E. Mesh Adaptive Direct Search Algorithms for Constrained

Optimization // SIAM J. Optim. 2006. V. 17. No. 1. P. 188-217.

97.

Montero E., Riff M.-C., Neveu B. A Beginner’s Guide to Tuning Methods // Appl.

Soft. Comput. 2014. V. 17. P. 39-51.

98.

Karafotias G., Hoogendoorn M., Eiben A.E. Parameter Control in Evolutionary

Algorithms: Trends and Challenges // IEEE Trans. Evol. Comput. 2015. V. 19.

No. 2. P. 167-187.

99.

Zhang J., Chen W.-N., Zhan Z.-H., Yu W.-J., Li Y.-L., Chen N., Zhou Q. A Survey

on Algorithm Adaptation in Evolutionary Computation // Front. Electr. Electron.

Eng. 2012. V. 7. No. 1. P. 16-31.

100.

Harrison K.R., Engelbrecht A.P., Ombuki-Berman B.M. Inertia Weight Control

Strategies for Particle Swarm Optimization // Swarm. Intell. 2016. V. 10. No. 4.

P. 267-305.

101.

Eberhart R.C., Shi Y. Tracking and Optimizing Dynamic Systems with Particle

Swarms // Proc. IEEE Congr. Evol. Comput. V. 1. Seoul, South Korea, 2001.

P. 94-100.

102.

Shi Y., Eberhart R.C. Empirical Study of Particle Swarm Optimization // Proc.

IEEE Congr. on Evol. Comput. 1999. V. 3. P. 1945-1950.

103.

Yang C., Gao W., Liu N., Song C. Low-Discrepancy Sequence Initialized Particle

Swarm Optimization Algorithm with High-Order Nonlinear Time-Varying Inertia

Weight // Appl. Soft Comput. 2015. V. 29. P. 386-394.

104.

Jiao B., Lian Z., Gu X. A Dynamic Inertia Weight Particle Swarm Optimization

Algorithm // Chaos Solitons Fractals. 2008. V. 37. No. 3. P. 698-705.

105.

Fan S.K.S., Chiu Y.Y. A Decreasing Inertia Weight Particle Swarm Optimizer //

Eng. Optim. 2007. V. 39. No. 2. P. 203-228.

106.

Chauhan P., Deep K., Pant M. Novel Inertia Weight Strategies for Particle Swarm

Optimization // Memetic Comput. 2013. V. 5. No. 3. P. 229-251.

107.

Chen G., Huang X., Jia J., Min Z. Natural Exponential Inertia Weight Strategy in

Particle Swarm Optimization // Proc. Sixth World Congr. Intelligent Control and

Automation. V. 1. IEEE. 2006. P. 3672-3675.

108.

Gao Y.-l., An X.-h., Liu J.-m. A Particle Swarm Optimization Algorithm With

Logarithm Decreasing Inertia Weight and Chaos Mutation // Int. Conf. Comput.

Intell. Security. V. 1. IEEE, 2008. P. 61-65.

109.

Feng Y., Teng G.F., Wang A.X., Yao Y.M. Chaotic Inertia Weight in Particle

Swarm Optimization // Proc. Second Int. Conf. Innovative Computing, Information

and Control. Kumamoto: IEEE, 2007. P. 475-479.

110.

Kentzoglanakis K., Poole M. Particle Swarm Optimization with an Oscillating

Inertia Weight // Proc. 11th Annual Conf. Genetic Evol. Comput. ACM, 2009.

P. 1749-1750.

111.

Ratnaweera A., Halgamuge S.K., Watson H.C. Self-Organizing Hierarchical Parti-

cle Swarm Optimizer with Time-Varying Acceleration Coefficients // IEEE Trans.

Evol. Comput. 2004. V. 8. P. 240-255.

112.

Tanweer M.R., Suresh S., Sundararajan N. Self Regulating Particle Swarm Opti-

mization Algorithm // Inf. Sci. 2015. V. 294. P. 182-202.

113.

Xu G. An Adaptive Parameter Tuning of Particle Swarm Optimization Algo-

rithm // Appl. Math. Comput. 2013. V. 219. P. 4560-4569.

114.

Adewumi A.O., Arasomwan A.M. An Improved Particle Swarm Optimiser Based on

Swarm Success Rate for Global Optimisation Problems // J. Exp. Theoret. Artif.

Intell. 2014. V. 28. P. 441-483.

115.

Yang X., Yuan J., Mao H. A Modified Particle Swarm Optimizer with Dynamic

Adaptation // Appl. Math. Comput. 2007. V. 189. P. 1205-1213.

116.

Zhan Z.-H., Zhang J., Li Y., Chung H.S.-H. Adaptive Particle Swarm Optimiza-

tion // IEEE Trans. Syst. Man Cyber. B. 2009. V. 39. P. 1362-1381.

117.

Huang L., Ding S., Yu S., Wang J., Lu K. Chaos-Enhanced Cuckoo Search Opti-

mization Algorithms for Global Optimization // Appl. Math. Model. 2016. V. 40.

P. 3860-3875.

118.

Mirjalili S., Gandomi A.H. Chaotic Gravitational Constants for the Gravitational

Search Algorithm // Appl. Soft Comput. 2017. V. 53. P. 407-419.

119.

Gandomi A., Yang X.-S., Talatahari S., Alavi A. Firefly Algorithm with Chaos //

Commun. Nonlinear Sci. Numer. Simulat. V. 18. 2013. P. 89-98.

120.

Gandomi A.H., Yang X.-S. Chaotic Bat Algorithm // J. Comput. Sci. 2014. V. 5.

P. 224-232.

121.

Juang Y.-T., Tung S.-L., Chiu H.-C. Adaptive Fuzzy Particle Swarm Optimiza-

tion for Global Optimization of Multimodal Functions // Inf. Sci. 2011. V. 181.

P. 4539-4549.

122.

Melin P., et al. Optimal Design of Fuzzy Classification Systems using PSO with

Dynamic Parameter Adaptation through Fuzzy Logic // Expert Syst. Appl. 2013.

V. 40. P. 3196-3206.

123.

Neshat M. FAIPSO: Fuzzy Adaptive Informed Particle Swarm Optimization //

Neural Comput. Applic. 2013. V. 23. P. 95-116.

124.

Gonzalez B., Melin P., Valdez F., Prado-Arechiga G. A Gravitational Search Algo-

rithm using Fuzzy Adaptation of Parameters for Optimization of Ensemble Neural

Networks in Medical Imaging // Proc. Inter. Conf. on Artif. Intell. Las Vegas:

CSREA Press, 2017. P. 54-59.

125.

Perez J., et al. Interval Type-2 Fuzzy Logic for Dynamic Parameter Adaptation in

the Bat Algorithm // Soft Comput. 2017. V. 21. P. 667-685.

126.

Amador-Angulo L., Castillo O. Statistical Analysis of Type-1 and Interval Type-2

Fuzzy Logic in Dynamic Parameter Adaptation of the BCO // Proc. 9th Conf.

Europ. Society for Fuzzy Logic and Technology. Atlantis Press, 2015. P. 776-783.

127.

Abdel-Basset M., Wang G.-G., Sangaiah A.K., Rushdy E. Krill Herd Algorithm

Based on Cuckoo Search for Solving Engineering Optimization Problems // Mul-

timed. Tools Appl. 2019. V. 78. P. 3861-3884.

128.

Galvez J., Cuevas E., Becerra H., Avalos O. A Hybrid Optimization Approach

Based on Clustering and Chaotic Sequences // Int. J. Mach. Learn. Cybern. 2020.

V. 11. P. 359-401.

129.

Caraffini F., Neri F., Epitropakis M. HyperSPAM: A Study on Hyper-Heuristic Co-

ordination Strategies in the Continuous Domain // Inf. Sci. 2019. V. 477. P. 186-202.

130.

Chen X., Ong Y.-S., Lim M.-H., Tan K.C. A Multi-Facet Survey on Memetic

Computation // IEEE Trans. Evol. Comput. 2011. V. 15. P. 591-607.

131.

Bartoccini U., Carpi A., Poggioni V., Santucci V. Memes Evolution in a Memetic

Variant of Particle Swarm Optimization // Mathematics. 2019. V. 7. 423.

132.

Duan Q., Liao T.W., Yi H.Z. A Comparative Study of Different Local Search

Application Strategies in Hybrid Metaheuristics // Appl. Soft Comput. 2013. V. 13.

P. 1464-1477.

133.

Lopez-Garcia M., Garcia-Rodenas R., Gonzalez A.G. Hybrid Meta-Heuristic Opti-

mization Algorithms for Time-Domain-Constrained Data Clustering // Appl. Soft

Comput. 2014. V. 23. P. 319-332.

134.

de Oca M.A.M, Cotta C., Neri F. Local Search // Handbook of Memetic Algo-

rithms. 2012. SCI. V. 379. P. 29-41.

135.

Lai X., Hao J.-K. A Tabu Search Based Memetic Algorithm for the Max-Mean

Dispersion Problem // Comput. Oper. Res. 2016. V. 72. P. 118-127.

136.

Yu Y., et al. CBSO: A Memetic Brain Storm Optimization with Chaotic Local

Search // Memetic Comput. 2018. V. 10. P. 353-367.

137.

Petalas Y.G., Parsopoulos K.E., Vrahatis M.N. Memetic Particle Swarm Optimiza-

tion // Ann. Oper. Res. 2007. V. 156. P. 99-127.

138.

Wang H., Moon I., Yang S., Wang D. A Memetic Particle Swarm Optimization Al-

gorithm for Multimodal Optimization Problems // Inf. Sci. 2012. V. 197. P. 38-52.

139.

Fister I., Fister I. Jr., Brest J., Zumer V. Memetic Artificial Bee Colony Algorithm

for Large-Scale Global Optimization // 2012 IEEE Congr. Evol. Comput. Brisbane:

IEEE, 2012. P. 1-8.

140.

Sudholt D. Parametrization and Balancing Local and Global Search // Handbook

of Memetic Algorithms. SCI. 2012. V. 379. P. 55-72.

141.

Wu G., Mallipeddi R., Suganthan P.N. Ensemble Strategies for Population-

Based Optimization Algorithms-A Survey // Swarm Evol. Comput. 2019. V. 44.

P. 695-711.

142.

Li C., Yang S., Nguyen T.T. A Self-Learning Particle Swarm Optimizer for Global

Optimization Problems // IEEE Trans. Syst. Man Cybern. Part B. 2012. V. 42.

P. 627-646.

143.

Wang H., et al. Multi-Strategy Ensemble Artificial Bee Colony Algorithm // Inf.

Sci. 2014. V. 279. P. 587-603.

144.

Lynn N., Suganthan P.N. Ensemble Particle Swarm Optimizer // Appl. Soft Com-

put. 2017. V. 55. P. 533-548.

145.

Pillay N., Qu R. Hyper-Heuristics: Theory and Applications. Cham: Springer, 2018.

146.

Del Ser J., et al. Bio-inspired Computation: Where We Stand and what’s Next //

Swarm Evol. Comput. 2019. V. 48. P. 220-250.

147.

Elaziz M.A., Mirjalili S. A Hyper-Heuristic for Improving the Initial Population of

Whale Optimization Algorithm // Knowl. Based Syst. 2019. V. 172. P. 42-63.

148.

Miranda P., Prudencio R., Pappa G. H3ad: A Hybrid Hyper-Heuristic for Algo-

rithm Design // Inf. Sci. 2017. V. 414. P. 340-354.

149.

Yang X.-S. Nature-Inspired Optimization Algorithms: Challenges and Open Prob-

lems // J. Comput. Sci. 2020. 101104.

150.

Bassimir B., Schmitt M., Wanka R. Self-Adaptive Potential-Based Stopping Cri-

teria for Particle Swarm Optimization with Forced Moves // Swarm. Intell. 2020.

V. 14. P. 285-311.