Автоматика и телемеханика, № 6, 2021

Стохастические системы

(Институт проблем управления им. В.А. Трапезникова РАН, Москва)

АНИЗОТРОПИЙНАЯ ФИЛЬТРАЦИЯ ДЛЯ ЛИНЕЙНЫХ

ДИСКРЕТНЫХ НЕСТАЦИОНАРНЫХ СИСТЕМ

С МУЛЬТИПЛИКАТИВНЫМИ ШУМАМИ

НА КОНЕЧНОМ ИНТЕРВАЛЕ ВРЕМЕНИ¹

Рассматривается задача анизотропийной фильтрации на конечном ин-

тервале времени для линейной дискретной нестационарной системы с

мультипликативными шумами. На вход системы поступает случайное воз-

мущение с неточно известным распределением, неопределенность в описа-

нии которого характеризуется ограничением анизотропийного функцио-

нала. Оценка выхода исходной системы производится с помощью выбран-

ного фильтра определенного вида по принципу минимизации критерия

качества в виде анизотропийной нормы системы в ошибках фильтрации.

На основании леммы об ограниченности анизотропийной нормы системы

в ошибках фильтрации выводятся соотношения на неизвестные матрицы

фильтра. В качестве частных случаев рассмотрены задачи анизотропий-

ной фильтрации для системы с отказом в измерениях, а также аналогич-

ная задача для системы с фильтром специального вида. Приведен числен-

ный пример использования полученного метода синтеза анизотропийного

фильтра.

Ключевые слова: анизотропия, анизотропийная норма, задача фильтра-

ции, системы с отказом в измерениях, мультипликативный шум, дискрет-

ная система.

DOI: 10.31857/S0005231021060027

1. Введение

Задача фильтрации состояния или выходного сигнала системы на основа-

нии доступных измерений является одной из фундаментальных задач теории

управления. Технические системы чаще всего имеют достаточно сложную

структуру, и поэтому точно измерить все их параметры не представляется

возможным. Кроме того, те измерения параметров объекта, которые можно

провести с помощью разнообразных технических средств, таких как датчи-

ки и сенсоры, чаще всего содержат в себе случайные или постоянные шумы,

которые могут сильно влиять на конечное значение измеряемой величины

и динамику системы в целом. Наличие подобных проблем и является пред-

посылкой появления целого класса задач обработки цифровых сигналов и

фильтрации.

¹ Работа выполнена при финансовой поддержке Российского фонда фундаментальных

исследований (проект № 19-31-90060).

Проблема обработки данных, приходящих с разнообразных технических

объектов, актуальна до сих пор, и наблюдается повышенный интерес к дан-

ному разделу теории управления. Универсального метода решения задачи

фильтрации для любой технической системы и любых внешних условий не

существует, поэтому при разработке новых методов используются определен-

ные допущения о виде модели рассматриваемого объекта, фильтра, о свой-

ствах шумов, входящих в измеряемый выходной сигнал систем или дейст-

вующих на нее извне, и т.д.

При постановке задачи фильтрации для исследуемого объекта вводится

некоторый критерий эффективности искомого фильтра, который чаще всего

представляется в форме квадратичного функционала от ошибки фильтрации.

Поэтому задача фильтрации часто сводится к задаче поиска фильтра, при

котором функционал качества системы с данным фильтром достигает свое-

го экстремального значения (оптимальная фильтрация), или к задаче поис-

ка фильтра, обеспечивающего ограниченность значения заданного критерия

некоторой величиной. Наиболее известными методами решения задач фильт-

рации являются методы H₂- и H_∞-теорий [1-3]. В самом простом случае

LQG/H₂-оптимальный фильтр, или фильтр Калмана, используется при допу-

щении, что входное возмущение системы является гауссовским белым шумом.

Также предполагается, что точно известны параметры модели исследуемого

объекта, т.е. матрицы линейной системы объекта являются детерминирован-

ными. Подобный фильтр обеспечивает минимальный след ковариационной

матрицы ошибки оценивания состояния системы и эффективен для систем с

указанными допущениями. Однако фильтр Калмана оказывается неэффек-

тивным с точки зрения подавления возмущений, если указанные допущения

не выполняются (к примеру, если входное возмущение не является белым

шумом или параметры объекта не точно известны). Если статистические или

иные свойства шумов точно не известны, то используется H_∞-фильтр. При

его использовании предполагается, что входное возмущение является квад-

ратично суммируемым или возмущением с ограниченной мощностью. При

построении H_∞-фильтра математически конструируется наихудшее внешнее

возмущение и решается стандартная задача фильтрации при данном возму-

щении, в виду чего в реальных ситуациях данный фильтр оказывается из-

лишне консервативным, а в некоторых случаях практической реализации

неоправданно энергозатратным.

Поскольку H₂- и H_∞-фильтры являются наиболее эффективными толь-

ко при выполнении условий задач, существует множество научных работ по

поиску методов синтеза фильтров, более устойчивых к возмущениям со ста-

тистическими характеристиками, отличными от характеристик гауссовско-

го белого шума, чем H₂-, и менее консервативных, чем H_∞. В 90-е годы с

целью обобщения H₂- и H_∞-теории И.Г. Владимировым была предложена

анизотропийная теория управления и фильтрации в [4-7]. Фундаментальны-

ми понятиями этой теории являются анизотропия случайного вектора, сред-

няя анизотропия (стационарной эргодической) последовательности случай-

ных векторов и анизотропийная норма системы. Понятие анизотропии слу-

чайного вектора было введено на основе таких понятий теории информации,

как энтропия и количество информации, и представляет собой меру отличия

распределения случайного вектора от нормального распределения с нулевым

математическим ожиданием и единичной ковариационной матрицей.

Для линейных нестационарных систем существует множество публикаций

на тему анизотропийного анализа и задачи анизотропийной фильтрации. В [7]

было показано, что для решения задачи оптимальной анизотропийной филь-

трации в случае линейной дискретной нестационарной системы на конечном

интервале времени необходимо решить разностное уравнение Риккати с до-

полнительным условием в виде алгебраического уравнения специального ви-

да. В [8] приведена формулировка леммы об ограниченности анизотропийной

нормы для линейных нестационарных систем. Эта лемма является основой

для многих работ по анизотропийной фильтрации для различных классов

нестационарных систем. Задача субоптимальной анизотропийной фильтра-

ции для линейных нестационарных систем с неслучайными матрицами была

решена в [9]. Также в [10] была решена задача субоптимальной фильтрации

для линейных систем с условием равенства размерностей векторов оценивае-

мого выхода и внешнего возмущения. Задача субоптимальной фильтрации

заключается в поиске фильтра, который обеспечивает ограниченность ани-

зотропийной нормы сверху заданным числом. Это число можно менять для

достижения требуемого уровня качества фильтрации. В отличие от задачи

оптимальной фильтрации, в субоптимальной фильтрации условия существо-

вания искомого фильтра выражены в виде линейных матричных неравенств,

решение которых проще с точки зрения программной реализации алгоритма

решения задачи.

С середины двадцатого столетия появилось немало научных работ на тему

задач управления и фильтрации для частного случая стохастических систем,

а именно систем, содержащих мультипликативные шумы. Преимущество опи-

сания стохастических систем подобным образом заключается в том, что они

достаточно эффективно аппроксимируют линейные дискретные системы со

случайными матрицами и для них проще найти подход к решению задач

анализа, управления и фильтрации. Также системы с мультипликативными

шумами часто используются для математического описания разнообразных

физических и финансовых процессов, технических объектов и т.д., как пока-

зано в [11-13]. Вследствие большого научного интереса к таким системам уже

существует множество статей на темы задач робастного управления [14], оце-

нивания состояния системы [15], линейного квадратичного управления [16] и

многие другие.

В [17] представлена лемма об ограниченности анизотропийной нормы си-

стемы с мультипликативными шумами. Эта лемма является основой метода

решения задачи анизотропийной фильтрации для систем с мультипликатив-

ными шумами, который представлен в данной статье. Помимо общего случая

задачи анизотропийной фильтрации для линейных дискретных нестационар-

ных систем с мультипликативными шумами, в статье рассмотрены частные

случаи построения фильтров и решения исходных задач в рамках сделанных

предположений.

2. Обозначения и предварительные сведения

Перед описанием класса рассматриваемых систем введем необходимые

обозначения. Пусть Rⁿ множество n-мерных векторов с элементами из R;

R^n×m множество (n × m)-мерных матриц с элементами из R; Lⁿ² множе-

ство Rⁿ-значных интегрируемых с квадратом случайных векторов; L^n×m2

множество R^n×m-значных интегрируемых с квадратом случайных матриц;

E(x) математическое ожидание случайной величины x. В выкладках ста-

тьи будут использоваться следующие матричные и векторные нормы:

√

1) ||x||₂ =

E (x^⊤x) норма случайного вектора x из Lⁿ²;

√

2) ||X||₂ =

tr(E(X^⊤X))

2-норма случайной матрицы X из L^n×m2;

√

3) ||X||_∞ =

max(λi(E(X⊤X)))

∞-норма случайной матрицы X

из L^n×m2, где λ_i(E(X^⊤X)) собственные значения матрицы E(X^⊤X).

4) Φ_M (X) блочно-диагональная матрица из M матриц X.

Для сокращения записи линейных матричных неравенств (ЛМН) будет

использоваться символ ∗ на месте элемента ЛМН, равного симметричному

ему элементу относительно главной диагонали под знаком транспонирования.

В следующих подразделах приведены основные понятия анизотропийной

теории, определение системы с мультипликативными шумами и лемма об

ограниченности анизотропийной нормы для таких систем.

2.1. Класс рассматриваемых систем

Рассмотрим линейную дискретную нестационарную систему F на ограни-

ченном интервале [0, N] следующего вида:

{ x(k + 1) = A(k)x(k) + B(k)w(k),

(2.1)

F :

z(k) = C(k)x(k) + D(k)w(k),

x(0) = 0, k ∈ [0, N],

где x(k) ∈ Lnx2 вектор состояния системы, w(k) ∈ L2w вектор входа си-

вектор выхода системы. Матрицы системы A(k), B(k),

стемы, z(k) ∈ Lpz2

C(k), D(k) являются случайными матрицами специального вида

∑

A(k) = ξ_1i(k)A_i(k) ∈ Lnx×nx2 , B(k) =

ξ_2i(k)B_i(k) ∈ Lnx×mw2,

i=0

∑

C(k) = ξ_3i(k)C_i(k) ∈ Lpz×nx2, D(k) =

ξ_4i(k)D_i(k) ∈ Lpz×mw2,

i=0

где ξ_ji(k), j = 1, 4, i = 1, M, k = 0, N являются независимыми в совокуп-

ности по i, j, k скалярными случайными величинами с нулевыми матема-

тическими ожиданиями и единичными дисперсиями. Случайные величины

ξ_j0(k), j = 1,4, k = 0,N обладают единичными математическими ожидания-

ми и дисперсиями. Следовательно, выполняются равенства EA(k) = A₀(k),

EB(k) = B₀(k), EC(k) = C₀(k), ED(k) = D₀(k).

Соотношение вход-выход системы (2.1) можно записать в следующей фор-

ме:

Z_0:N = F_0:NW_0:N,

где Z_0:N = (z^⊤(0), . . . , z^⊤(N))^⊤ последовательность выходных сигналов си-

стемы, W_0:N = (w^⊤(0), . . . , w^⊤(N))^⊤ последовательность входных сигналов

системы, Z_0:N ∈ Lpz(N+1)2, W_0:N ∈ Lmw(N+1)2. Для сокращения записи дальней-

ших выкладок введем обозначения l_z = p_z(N + 1), l_w = m_w(N + 1). Матрица

связи в Z_0:N = F_0:N W_0:N имеет вид F_0:N = block (f(k, κ)), где

0≤k,κ≤N



 C(k)T(k,κ + 1)B(κ), если k > κ,

(2.2)

f (k, κ) =

D(k), если k = κ,



0, если k < κ.

Матрица перехода T (k, κ) для k > κ удовлетворяет рекуррентной форму-

ле T (k, κ) = A(k - 1)T (k - 1, κ) = T (k, κ + 1)A(κ) при граничном условии

T (k, k) = Inx . Стоит отметить, что случайная матрица F_0:N и случайный

вектор W_0:N являются независимыми в силу независимости случайных ве-

личин ξ_ji(k). Нормой системы (2.1) будем считать норму соответствующей

матрицы F_0:N . Рассмотрим следующие виды нормы случайной матрицы F_0:N :

• H₂-норма системы F вида (2.1)

√

∥F ∥₂ ≜ tr(E[F^⊤0:N F_0:N ]) = ∥F_0:N ∥₂;

• H_∞-норма системы F вида (2.1).

Меру отклика системы T_zw на входной вектор W_0:N можно описать с помо-

щью среднеквадратичного коэффициента усиления, который определяется

по формуле

||Z_0:N ||₂

(2.3)

Q(F_0:N , W_0:N ) =

||W_0:N ||₂

С учетом независимости F_0:N и W_0:N среднеквадратичный коэффициент

усиления можно записать следующим образом:

√

tr(ΛΣ)

(2.4)

Q(F_0:N , W_0:N ) =

tr(Σ)

где Λ = E[F^⊤0:N F_0:N ] ∈ Rlw×lw , Σ = E[W_0:N W^⊤0:N ] ∈ Rlw×lw . Для системы F

H_∞-норма определяется как супремум среднеквадратичного коэффициен-

та усиления Q(F_0:N , W_0:N ) системы по всем последовательностям входных

векторов W_0:N ∈ Llw2 , т.е.

∥F ∥_∞ ≜ sup

Q(F_0:N , W_0:N ) = ∥F_0:N ∥_∞.

W_0:N ∈L^lw

Далее приведены понятия анизотропии случайного вектора и анизотро-

пийной нормы системы, с помощью которых можно отказаться от предпо-

ложения о наихудшем возмущении и таким образом устранить консерватив-

ность H_∞-метода.

2.2. Анизотропия случайного вектора

Впервые определение анизотропии случайного вектора введено И.Г. Вла-

димировым в [4]. Впоследствии, в [7] определение сформулировано следую-

щим образом

Определение 1. Анизотропией A(W) m-мерного случайного векто-

ра W называется неотрицательная величина, определенная по формуле

)

( 2πe

(2.5)

A(W ) = minD(f∥pm,λ) =

∥W ∥²

− h(W ),

λ>0

где D(f∥p_m,λ) относительная энтропия (расстояние Кульбака-Лейблера)

функции плотности распределения вероятности f вектора W относитель-

но функции плотности гауссовского распределения p_m,λ с нулевым мате-

матически∫ ожиданием и скалярной ковариационной матрицей λI_m, λ > 0;

h(W ) = - f(w) ln f(w)dw дифференциальная энтропия W .

R^m

2.3. Анизотропийная норма

На основании определений среднеквадратичного коэффициента усиления

Q(F_0:N , W_0:N ) и понятия анизотропии случайного вектора A(W_0:N ) приведем

определение анизотропийной нормы.

Определение 2. Анизотропийной нормой системы

(2.1), которая

определяется матрицей F_0:N на временном интервале k ∈ [0,N], называет-

ся неотрицательная величина следующего вида:

(2.6)

|||F |||_a = sup Q(F_0:N , W_0:N

W_0:N ∈Wa

где W_a = {W ∈ Llw2 : A (W ) ≤ a} множество lw-мерных случайных век-

торов с анизотропией, ограниченной сверху числом a ≥ 0.

В [7] показано, что супремум среднеквадратичного коэффициента усиле-

ния Q(F_0:N , W_0:N ) в (2.6) достигается при входном возмущении в виде слу-

чайного вектора, распределенного по нормальному закону с нулевым мате-

матическим ожиданием и ковариационной матрицей вида

Σ(q) = (I

- qΛ)^-1,

где q скалярный параметр, являющийся решением уравнения

mΣ(q)

ln det

trΣ(q)

[

)

на интервале q ∈

0; ||F_0:N ||^-2∞

Анизотропийная норма является неубывающей функцией при любом

a ≥ 0, удовлетворяющей неравенствам

√

∥F ∥₂/

l_w = lim

|||F |||_a ≤ |||F |||_a,

a→0+

|||F |||_a ≤ lim

|||F |||_a = ∥F ∥_∞.

a→+∞

Эффективное использование математического аппарата анизотропийной тео-

рии имеет смысл при выполнении строгого неравенства ∥F ∥₂/√lw < ∥F∥∞.

В [17] показано, что для вычисления анизотропийной нормы системы

с мультипликативными шумами необходимо решить разностное уравнение

Риккати в обратном времени на интервале k = 0 . . . N + 1 и разностное урав-

нение Ляпунова в прямом времени. Для решения задачи анизотропийной

фильтрации для систем с мультипликативными шумами, которое обеспечи-

вает ограниченность анизотропийной нормы системы в ошибках фильтрации,

запишем лемму об ограниченности анизотропийной нормы для данного клас-

са систем.

Лемма 1. Дана линейная дискретная нестационарная система F с

мультипликативными шумами вида (2.1) и задано максимальное значение

анизотропии a ≥ 0 входного сигнала. Тогда анизотропийная норма системы

|||F |||_a ограничена заданной константой γ ≥ 0 тогда и только тогда, когда

cуществуют значение параметра q ≥ 0 и решения разностных уравнений

Риккати R₁(k) ≻ 0, R₂(k) ≻ 0 такие, что

∑

(2.7)

R₁(k) = A^⊤i(k)R₁(k + 1)A_i(k) + q C^⊤i(k)C_i

(k),

i=0

(2.8)

R₂(k) =A^⊤0(k)R₂(k + 1)A₀(k) + L^⊤(k)S^-1

(k)L(k),

(

∑

(2.9)

S(k) = Imz - (qD^⊤i(k)D_i(k) + B^⊤i(k)R₁(k + 1)B_i

(k)) -

i=0

)_-1

- B⊤0 (k)R₂(k + 1)B₀(k)

≻ 0,

(

(2.10)

L(k) =S(k) B^⊤0(k)R₁(k + 1)A₀(k) + B^⊤0(k)R₂(k + 1)A₀

(k) +

)

+ qD⊤0 (k)C₀(k) ,

∑

(2.11)

ln det S(k) ≥ 2a + l_w ln(1 - qγ²

k=0

3. Постановка задачи фильтрации

Задана линейная дискретная нестационарная стохастическая система F

на конечном временном интервале

{ x(k + 1) = A(k)x(k) + B(k)w(k),

(3.1)

F :

z(k) = C_z(k)x(k) + D_z(k)w(k),

где x(k) является вектором состояния системы, w(k)

вектором входно-

го возмущения, а z(k) вектором оцениваемого выхода системы. В систе-

ме (3.1) вход w(k) является случайным процессом, удовлетворяющим усло-

вию w(k) ∈ Lmw2 , E[w(k)] = 0. Предполагается, что известна априорная ин-

формация о других статистических характеристиках входной последователь-

ности W = w(k), на основе которой можно ввести ограничение анизотропии

A(W ) ≤ a, где параметр a является известным положительным числом.

Целью работы является получение оценки выхода z(k) на основе измеря-

емого выхода y(k), описываемого следующим уравнением наблюдения:

(3.2)

y(k) = C_y(k)x(k) + D_y

(k)w(k).

Ниже приведена формулировка задачи анизотропийной фильтрации

Задача 1. Получить такую оценку выхода z(k) системы (3.1) на осно-

ве измеряемого выхода y(k) вида (3.2), что анизотропийная норма |||T_˜zw|||_a

системы в ошибках фильтрации T_˜zw будет ограничена сверху заданным чис-

лом γ > 0.

Выбрана следующая модель фильтра T_ˆzw:





x(k + 1) = W (k)x(k) + H(k)(y(k) - ŷ(k)),



z(k) = F (k)x(k) + G(k)(y(k) - ŷ(k)),

(3.3)

T_ˆzw :



ŷ(k) = Γ(k)x(k),



x(0) = 0, k = 0, N .

Матрицы фильтра (3.3) являются детерминированными матрицами, являю-

щимися решением задачи фильтрации.

Обозначим ошибку оценивания выхода как z(k) = z(k) - z(k). Переписав

систему (3.3) относительно ошибки оценивания z(k) и ошибки оценивания со-

стояния e(t) = x(k) - x(k), получим систему в ошибках фильтрации. Вывод

уравнений этой системы подробно разобран в следующем разделе. Перефор-

мулируем задачу анизотропийной фильтрации следующим образом:

Задача 2. Для заданных системы F вида (3.1), уровня анизотропии

a ≥ 0 входного возмущения W и верхней границы анизотропийной нормы

γ ≥ 0 найти фильтр вида (3.3) такой, чтобы для системы в ошибках филь-

трации выполнялось неравенство

(3.4)

|||T_˜zw|||_a

≤ γ.

4. Решение задачи фильтрации

В первую очередь, необходимо построить систему в ошибках фильтрации,

соответствующую исходной системе объекта (3.1) и выбранной модели филь-

тра (3.3). Подставив выражение (3.2) измеряемого выхода y(k) в модель (3.3),

получим



x(k + 1) = (W (k) - H(k)Γ(k))x(k) + H(k)C_y(k)x(k) +





+ H(k)D_y(k)w(k),

(4.1)



(k) = (F (k) - G(k)Γ(k))x(k) + G(k)C_y(k)x(k) +

z

+ G(k)D_y (k)w(k).

Для упрощения дальнейших выкладок вводим замену переменных

X(k) = W (k) - H(k)Γ(k), Y (k) = F (k) - G(k)Γ(k).

Далее запишем выражение для ошибки оценивания выхода z(k) системы (3.1)

(

)

z(k) =

C_z(k) - G(k)C_y(k)

x(k) +

(4.2)

(

)

D_z(k) - G(k)D_y(k)

w(k) - Y (k)x(k).

Для записи системы в ошибках фильтрации введем обозначение

(4.3)

e(k) = x(k) - x(k).

Из (3.1), (3.3) с учетом (4.3) получим динамику ошибки оценивания состоя-

ния:

(

)

(4.4)

e(k + 1) =

A(k) - X(k) - H(k)C_y(k)

x(k) +

(

)

+ X(k)e(k) +

B(k) - H(k)D_y (k)

w(k).

В итоге получим следующий вид системы в ошибках фильтрации T_zw:



(

)

e(k + 1) =

A(k) - X(k) - H(k)C_y(k)

x(k) +



(

)



+ X(k)e(k) +

B(k) - H(k)D_y (k)

w(k),

(4.5)

T_zw :

(

)



(k) =

C_z(k) - Y (k) - G(k)C_y(k)

x(k) +

z

(

)

D_z(k) - G(k)D_y(k)

w(k) + Y (k)e(k).

Для сокращенной записи системы (4.5) введем расширенный вектор состоя-

ния

( x(k))

(4.6)

x(k) =

e(k)

Запишем систему в ошибках фильтрации T_zw вида (4.5) в терминах расши-

ренного вектора состояния





x(k + 1) = A(k)x(k) + B(k)w(k),

(4.7)

T_zw :

z(k) = C(k)x(k) + D(k)w(k),



x(0) = 0, k = 0, N ,

где матрицы A(k), B(k), C(k), D(k) определяются следующим образом:

(

)

A(k)

nx×nx

(4.8)

A(k) =

A(k) - X(k) - H(k)C_y(k) X(k)

(

)

B(k)

(4.9)

B(k) =

B(k) - H(k)D_y(k)

(

)

(4.10)

C(k) =

C_z(k) - Y (k) - G(k)C_y(k) Y (k)

(4.11)

D(k) = D_z(k) - G(k)D_y

(k).

Для решения задачи анизотропийной фильтрации в данной работе необ-

ходимо, чтобы система в ошибках фильтрации (4.7) была системой с муль-

типликативными шумами. Следовательно, должны быть выполнены следую-

щие условия:

1) матрицы системы (4.7) A(k), B(k), C(k), D(k) являются независимыми

в совокупности,

2) матрицы системы (3.1) A(k), B(k), C_z(k), D_z(k), C_y(k), D_y(k) являются

независимыми в совокупности,

3) матрицы системы (4.7) A(k), B(k), C(k), D(k) удовлетворяют следую-

щим выражениям:

∑

(4.12)

A(k) = A₀(k) + ζ_1i(k)A_i(k), B(k) = B₀(k) +

ζ_2i(k)B_i

(k),

i=1

∑

(4.13)

C(k) = C₀(k) +

ζ_3i(k)C_i(k), D(k) = D₀(k) +

ζ_4i(k)D_i

(k).

i=1

Cлучайные величины ζ_ij(k), i = 1, 4, j = 1, M_i, k = 0, N, в выражениях

(4.12)-(4.13) обладают следующими свойствами:

E[ζ_ij(k)] = 0, E[ζ^2ij(k)] = 1.

Заметим, что в матрицы системы A(k), B(k), C(k), D(k) входят матрицы

C_y(k) и D_y(k), в общем случае являющиеся случайными. Поскольку матрицы

A(k), B(k), C(k), D(k) должны быть независимыми в совокупности, необхо-

димо выполнение следующего условия:

(4.14)

H(k)G^⊤

(k) = 0.

Это условие, к примеру, выполняется в следующих случаях:

1) H(k) = 0 или G(k) = 0;

(

)

(

)

2) H(k) =

H^′(k)

, G(k) =

G′(k)

где H^′(k) ненулевая часть неизвестной матрицы H(k), G^′(k) нену-

левая часть неизвестной матрицы G(k).

Частные случаи фильтра H(k) = 0 и G(k) = 0 будут рассмотрены в сле-

дующих разделах статьи. Пока предполагаем, что условие (4.14) выполняется

при H(k) = 0 и G(k) = 0.

Стоит отметить, что матрица Γ(k) влияет на динамику изменения перемен-

ной фильтра x(k) и на связь между оценкой выхода z(k) и переменной x(k).

В зависимости от значения этой матрицы оценка выхода z(k) может кор-

ректироваться на основе значения измеряемого выхода y(k) исходной систе-

мы или на основе “ошибки оценки” измеряемого выхода. Поскольку в об-

щем случае матрица C_y(k) может быть случайной, а все искомые матрицы

фильтра являются детерминированными, выражение ŷ(k) является, скорее,

прогнозом значения измеряемого выхода системы. Это выражение вводится

дополнительно к основной модели фильтра. Значение матрицы Γ(k) выби-

рается вручную вне процесса решения задачи. Частные случаи фильтра при

различных значениях матрицы Γ(k) будут рассмотрены в соответствующем

разделе.

4.1. Условия ограниченности анизотропийной нормы системы

в ошибках фильтрации

В данном разделе воспользуемся леммой 1 для системы (4.7) для сведения

исходной задачи субоптимальной анизотропийной фильтрации к задаче вы-

пуклой оптимизации с условиями в виде линейных матричных неравенств.

Объединим уравнения (2.7)-(2.10) в одно уравнение Риккати. Для этого вве-

дем замену переменных R(k) = R₁(k) + R₂(k):

∑

A^⊤i(k)R₁(k + 1)A_i(k) +

qC^⊤i(k)C_i(k) +

i=0

+ A⊤0 (k)R₂(k + 1)A₀(k) + L^⊤(k)S^-1(k)L(k) =

∑

= A^⊤i(k)R(k + 1)A_i(k) + qC^⊤i(k)C_i(k) +

i=0

+ A⊤0 (k)R(k + 1)A₀(k) + L^⊤(k)S^-1(k)L(k) -

∑

(4.15)

- A^⊤i(k)R₂(k + 1)A_i(k) - A^⊤0(k)R₁(k + 1)A₀

(k),

i=0

где матрицы S(k) и L(k) принимают следующий вид:

∑

(4.16)

S(k) = I - B^⊤0(k)R(k + 1)B₀(k) - qD^⊤i(k)D_i

(k) -

i=0

∑(

)

B^⊤i(k)(R(k + 1) - R₂(k + 1))B_i(k)

+ B⊤0 (k)R₁(k + 1)B₀(k),

i=0

(

)

(4.17)

L(k) = S(k) B^⊤0(k)R(k + 1)A₀(k) + qD^⊤0(k)C₀(k)

В итоге получаем матричное уравнение

∑

(4.18)

R(k) = A^⊤i(k)R(k + 1)A_i(k) + qC^⊤i(k)C_i

(k) +

i=0

+ A⊤0 (k)R(k + 1)A₀(k) + L^⊤(k)S^-1(k)L(k) + Q(k),

∑

(4.19)

S(k) = I - B^⊤(k)R(k + 1)B0(k) -

qD^⊤i(k)D_i

(k) -

i=0

∑(

)

B^⊤i(k)(R(k + 1) - R₂(k + 1))B_i(k)

i=0

+ B⊤0 (k)R₁(k + 1)B₀(k)

(

)

(4.20)

L(k) = S(k) B^⊤0(k)R(k + 1)A₀(k) + qD^⊤0(k)C₀(k) ,

где

∑

Q(k) = - A^⊤i(k)R₂(k + 1)A_i(k) - A^⊤0(k)R₁(k + 1)A₀(k).

i=0

Уравнение (4.18) не является разностным уравнением Риккати относи-

тельно новой переменной R(k) по причине наличия членов с матрицами R₁(k)

и R₂(k), которые содержатся в (4.18)-(4.20). Стоит отметить, что слагаемые

∑

-Q(k), (B^⊤i(k)R₂(k + 1)B_i(k)) и B^⊤0(k)R₁(k + 1)B₀(k) являются неотрица-

i=0

тельно определенными матрицами. Второе и третье слагаемые из перечис-

ленных содержатся под знаком обратной матрицы, а в данном случае спра-

ведливо следующее утверждение

Если A ≻ 0, X ≽ 0, то (A + X)^-1 ≼ A^-1.

Введем матрицу R ≻ 0, являющуюся решением матричного неравенства

вида

∑

(4.21)

R(k) ≻ A^⊤0(k)R(k + 1)A₀(k) + A^⊤i(k)R(k + 1)A_i

(k) +

i=1

∑

+ q C⊤i (k)C_i(k) + L^⊤(k)S^-1(k)L(k),

i=0

R(N + 1) = 0,

(

∑

(4.22)

S(k) = I

m_w

- q

D^⊤i(k)D_i

(k) +

i=0

))_-1

∑

+ B^⊤i(k)R(k + 1)B_i(k)

≻ 0,

i=0

(

)

(4.23)

L(k) = S(k) B^⊤0(k)R(k + 1)A₀(k) + qD^⊤0(k)C₀(k) ,

∑

(4.24)

ln det S^-1(k) ≥ 2a + l_w ln(1 - qγ²

k=0

Разность правых частей неравенства (4.21) и уравнения (4.18) является неот-

рицательно определенной матрицей. Поэтому в силу свойства монотонности

решения дискретного уравнения Риккати, описанного в [18, 19], решение R(k)

неравенства (4.21) удовлетворяет условию R(k) ≻ R(k) при всех k ∈ [0, N].

Таким образом, получена система матричных неравенств (4.21)-(4.23) с нера-

венством специального вида (4.24), которая в соответствии с изложенными

преобразованиями позволяет получить субоптимальное решение поставлен-

ной задачи.

Запишем теорему об условиях существования фильтра вида (3.3), который

обеспечивает ограниченность анизотропийной нормы системы вида (4.7).

Теорема 1. Задана линейная дискретная нестационарная система F

на конечном интервале времени с реализацией в пространстве состояний

(3.1) и выбраны вещественные числа γ ≥ 0, a ≥ 0. Фильтр T_zw с реализа-

цией в пространстве состояний (3.3), гарантирующий выполнение неравен-

ства |||T_˜zw|||_a ≤ γ для системы в ошибках фильтрации с реализацией в про-

странстве состояний (4.7), существует, если найдутся матрицы P(k) ≻ 0,

P(N + 1) = 0, W (k), H(k), F (k), G(k), Γ(k) и Ψ(k), при которых выполня-

ются неравенства





P(k)

∗







ηImw

∗









P(k + 1)A₀(k) P(k + 1)B₀(k)

P(k + 1)

∗







(4.25)





≻ 0,



P(k + 1)A^⊤(k)

∗











C₀(k)

D₀(k)

P(k + 1)

∗





C^⊤(k)





P(N)

∗







ηI

∗



m_w

(4.26)





≻ 0,





Ipz

∗

 C

0(N) D0(N)



C(N)





ηI

m_w

- Ψ(k)

∗







P(k + 1)B^⊤0(k) P(k + 1)

∗











(4.27)



∗



≻ 0,









(k + 1)B^⊤M (k)

P(k + 1)

∗

 P



D^⊤(k)

(

)

ηI

- Ψ(N)

∗

m_w

(4.28)

≻ 0,

D(N)

Ipz

∏

(4.29)

det Ψ(k) ≥ e^2a(η - γ²)mw (N+1),

k=0

P(k) ≻ 0, k = N - 1, . . . , 0.

Доказательство теоремы приведено в Приложении 1.

Стоит отметить, что в произведении матриц A_iP(k + 1), B^⊤iP(k + 1) мо-

гут содержаться нелинейные члены в виде произведений неизвестных матриц

фильтра W (k), H(k), F (k), G(k), Γ(k) и компонент матрицы P(k + 1). В за-

висимости от частных случаев задачи фильтрации вводятся дополнительные

замены переменных и к неравенствам (4.25)-(4.29) добавляются новые усло-

вия в соответствии с введенными заменами переменных. В частных случаях

задачи анизотропийной фильтрации это будет показано наглядно.

4.2. Частные случаи задачи фильтрации

В данном разделе рассмотрены частные случаи задачи анизотропийной

фильтрации для разных типов стохастических систем и разных конфигура-

ций фильтра.

4.2.1. Система с отказами в измерениях

Рассмотрим систему F вида (3.1)

{ x(k + 1) = A(k)x(k) + B(k)w(k),

(4.30)

F :

z(k) = C_z(k)x(k) + D_z(k)w(k),

y(k) = λ(k)C_y(k)x(k) + D_y(k)w(k),

где матрицы системы A(k), B(k), C_z(k), D_z(k), C_y(k), D_y(k) являются детер-

минированными матрицами соответствующих размерностей, λ(k) случай-

ная величина с распределением вероятностей Бернулли:

P (λ(k) = 1) = p, P (λ(k) = 0) = 1 - p.

Рассмотрим модель фильтра T_ˆzw вида (3.3) со следующей конфигурацией:



x(k + 1) = W (k)x(k) + H(k)(y(k) - ŷ(k)),





z(k) = C_z(k)x(k),

(4.31)

T_ˆzw :



ŷ(k) = pC_y(k)x(k),



x(0) = 0, k = 0, N .

Для системы (4.30) и фильтра (4.31) рассмотрим задачу анизотропийной

фильтрации. Необходимо найти матрицы W (k), H(k) фильтра, при которых

анизотропийная норма системы в ошибках фильтрации удовлетворяет нера-

венству |||T_˜zw|||_a для фиксированного a > 0. В первую очередь, запишем си-

стему в ошибках фильтрации T_˜zw по формуле (4.7)

{ X(k + 1) = A(k)X(k) + B(k)w(k),

(4.32)

T_˜zw :

z(k) = C(k)X(k) + D(k)w(k),

где

(4.33)

A(k) = A₀(k) + (λ(k) - p)A₁

(k),

(

)

A(k)

0nx×nx

A₀(k) =

A(k) - W (k) W (k) - pH(k)C_y(k)

(

)

0nx×nx

A₁(k) =

-H(k)C_y(k)

0nx×nx

(

)

B(k)

B(k) =

B(k) - H(k)D_y(k)

(

)

C(k) =

, D(k) = D_z(k).

0pz ×nx Cz^(k)

Далее запишем сформулированные в предыдущем разделе условия огра-

ниченности анизотропийной нормы в форме системы неравенств (4.25)-(4.29)

для системы в ошибках фильтрации вида (4.32)





P(k)

∗





ηImw

∗









(4.34)



P(k + 1)A₀(k)

P(k + 1)B₀(k) P(k + 1)

∗

∗≻ 0,

√









p(1 - p)P(k + 1)A^⊤1(k)

P(k + 1)

∗

C(k)

D(k)





P(N)

∗





(4.35)

ηI

∗

≻ 0,



m_w



C₀(N) D(N) Ipz





ηI

- Ψ(k)

∗

m_w





(4.36)

 P(k + 1)B^⊤

(k) P(k + 1)

∗

 ≻ 0,

D^⊤(k)

(

)

ηI

- Ψ(N)

∗

m_w

(4.37)

≻ 0,

D(N)

Ipz

∏

(4.38)

det Ψ(k) ≥ e^2a(η - γ²)mw (N+1),

k=0

P(k) ≻ 0, k = N - 1, . . . , 0.

Видно, что в матричных неравенствах (4.34), (4.36) есть произведе-

ния матриц P(k + 1)A₀(k), P(k + 1)A₁(k) и P(k + 1)B^⊤(k). Матрицы A₀(k),

A₁(k), B₀(k) удовлетворяют условиям (4.33). Следовательно, в P(k + 1)A₀(k),

P(k + 1)A₁(k) и P(k + 1)B^⊤(k) есть произведения неизвестных матриц

P(k + 1), W (k) и H(k). С целью устранения нелинейных членов в матрич-

ных неравенствах введем следующие замены переменных системы матрич-

ных неравенств:

(

)

nx×nx

0nx×py

(4.39)

X (k) =

W (k) H(k)

(4.40)

P(k + 1)A₀(k) = P(k + 1

A⁰⁰(k) + P(k + 1)X(k

A¹⁰

(k),

(

)

(

)

-Inx Inx

A 0nx×nx

A⁰⁰(k) =

A¹⁰(k) =

-pC_y

A 0nx×nx

0nx×nx

P(k + 1)A₁(k) = P(k + 1)X (k

A¹¹(k),

(

)

0nx×nx

A¹¹(k) =

-C_y

0py ×nx

P(k + 1)B(k) = P(k + 1

B⁰(k) + P(k + 1)X(k

B¹(k),

)

( B

( 0nx×mw^),

B⁰(k) =

B¹(k) =

-D_y

(4.41)

Q(k) = P(k + 1)X (k).

Применим замену переменных (4.39)-(4.41) к неравенствам (4.34)-(4.37) и

получим выражения следующего вида:





P(k)

∗



ηImw

∗

∗









(4.42)

P(k+1)A00(k)+Q(k)A10(k) P(k+1

B⁰(k)+Q(k

B¹(k) P(k+1)

∗

∗≻ 0,



√





p(1-p)Q(k)A11(k)

P(k+1)

∗

C(k)

D(k)









ηImw -Ψ(k)

∗

0mw ×mw









(4.43)

P(k + 1

B⁰(k) P(k+1)

∗

+

Q(k

B¹(k)

∗

≻0,

02nx×2nx

D(k)

0pz ×2nx Ipz

0pz ×mw

0pz×2nx

0pz×pz





P(N)

∗

≻0,

0mw×2nx ηI

m_w

C(N) D(N) I2pz

)

( ηImw - Ψ(N) ∗

≻ 0,

D(N)

Ipz

∏

det Ψ(k) ≥ e^2a(η - γ²)mw (N+1),

k=0

P(k) ≻ 0, k = N - 1, . . . , 0.

Вместо неизвестных матриц фильтра W (k), H(k) переменными системы

линейных матричных неравенств становятся матрицы X (k) и Q(k). Стоит

обратить внимание, что при решении неравенств (4.42)-(4.43) необходимо

учитывать условия (4.39)-(4.41), ограничивающие область значений матриц

X (k), Q(k). Численный пример решения задачи анизотропийной фильтрации

для системы с отказами представлен в разделе Пример.

4.2.2. Фильтр с H(k) = 0

Заданы система вида (3.1) и фильтр (3.3). Если матрица H(k) = 0, то с

учетом условия x(0) = x(0) = 0 получаем

x(k + 1) = W (k)x(k),

x(0) = 0 ⇒ x(k) ≡ 0.

Следовательно, оценка выхода системы z(k) имеет вид z(k) = G(k)y(k).

Имеем статический фильтр с одной неизвестной матрицей G(k).

Матрицы фильтра в терминах ошибок имеют следующий вид:

A(k) = A(k), B(k) = B(k),

(4.44)

C(k) = C_z(k) - G(k)C_y (k), D(k) = D_z(k) - G(k)D_y

(k).

Подставив (4.44) в (4.25)-(4.29), получим систему линейных матричных

неравенств относительно матриц P(k), Ψ(k) и матрицы фильтра G(k), для

которых не требуется дополнительных замен переменных.

4.2.3. Фильтр с G(k) = 0

Заданы система вида (3.1) и фильтр (3.3). Если G(k) = 0, то оценка выхода

системы z(k) имеет вид

(4.45)

z(k) = F (k)x(k).

Если исходная система (3.1) с учетом (4.45) является детерминирован-

ной, то можно принять F (k) = C_z(k). В противном случае можно принять

F (k) = E[C_z(k)]. Таким образом, задача анизотропийной фильтрации сводит-

ся к поиску матриц фильтра W (k), H(k). В зависимости от вида матриц A(k)

и B(k) будет необходимо ввести замену переменных для устранения произве-

дений компонент неизвестной матрицы P(k + 1) и искомых матриц фильтра

W (k), H(k).

4.2.4. Фильтр с Γ(k) = 0

Заданы система вида (3.1) и фильтр (3.3). Рассмотрим случай Γ(k) = 0.

Поскольку необходимо, чтобы система в ошибках фильтрации принадлежа-

ла классу систем с мультипликативными шумами, матрицы (4.8) должны

удовлетворять условиям (4.12)-(4.13). Поэтому запишем матрицу A(k) в сле-

дующем виде:

)

∑

( A₁₁(k) A₁₂(k)

A(k) =

= A₀(k) + ζ_1i(k)A_i(k),

A₂₁(k) A₂₂(k)

i=1

( Ai11(k) Ai12(k))

(4.46)

A_i(k) =

i = 0,M.

Ai21 (k) Ai22 (k)

Далее запишем условия для каждой компоненты матрицы (4.46) с учетом

выражений матриц системы в ошибках фильтрации вида (4.8):

∑

(4.47)

A(k) = A (k) +₀

λ_1i(k)A

(k),

i₁₁

i=1

∑

(4.48)

0 = A012(k) +

λ_1i(k)Ai12

(k),

i=1

∑

(4.49)

A(k) - W (k) - H(k)C_y (k) = A021 (k) + λ_1i(k)Ai21

(k),

i=1

∑

(4.50)

W (k) = A (k) +₀

λ_1i(k)A

(k).

i₂₂

i=1

Из равенства (4.47) видно, что A(k) является матрицей специального вида.

Из (4.50) и того факта, что матрица фильтра W (k) не может быть случайной,

следует, что у уравнения (4.50) нет решений. Следовательно, условием нали-

чия решения является равенство нулю всех матриц A (k) при случайных_i

величинах λ_1i(k). Предположим, что W (k) = A (k).₀

С учетом вышесказанного, перепишем (4.49) в следующем виде:

A011 (k) - W(k) = A (k),₀

∑

(4.51)

λ_1i(k)Ai11

(k) - H(k)C_y(k) =

λ_1i(k)A

(k).

i₂₁

i=1

В общем случае E[C_y(k)] = 0. Следовательно, равенство (4.49) является

уравнением относительно случайных величин с разными математическими

ожиданиями. Необходимо свести (4.49) к уравнению относительно случай-

ных величин с нулевыми математическими ожиданиями. Для этого проведем

следующие преобразования (4.51):

∑

λ_1i(k)Ai11 (k) - H(k)C_y(k) + H(k)E[C_y(k)] -

i=1

∑

(4.52)

-H(k)E[C_y(k)] =

λ_1i(k)Ai21

(k).

i=1

Видно, что слагаемые H(k)C_y(k) и H(k)E[C_y (k)] можно сгруппировать, полу-

чив при матрице H(k) случайную матрицу с нулевым математическим ожи-

данием. Перепишем (4.52) в виде

A021 (k) = A011 (k) - W(k) - H(k)E[C_y(k)],

∑

(4.53)

λ_1i(k)Ai21 (k) =

λ_1i(k)Ai11 (k) + H(k)(E[C_y(k)] - C_y

(k)).

i=1

Равенство (4.53) выполняется, если матрица C_y(k) имеет следующий вид:

∑

(4.54)

C_y(k) = Cy0(k) +

λ_1i(k)Cyi

(k),

i=1

где

Cy0 (k) = E[C_y(k)], H(k)Cyi (k) = Ai11 (k) - A (k)._i

Предположив, что все матрицы A_i(k), Cyi (k), i = 0, M известны, имеем

(

)

A0(k)

A(k) =

A₀(k) - W(k) - H(k)Cy0 (k) W(k)

(

)

∑

A_i(k)

(4.55)

λ_1i(k)

A_i(k) - H(k)Cyi (k)

i=1

Далее, в соответствии с условиями (4.8), (4.12) для матриц системы с муль-

типликативными шумами матрица B(k) должна удовлетворять выражению

∑

(4.56)

B(k) = B₀(k) + λ_2i(k)B_i

(k).

i=1

Предположим, что выполняются соотношения

∑

B(k) = B₀(k) + λ_2i(k)B_i(k),

i=1

∑

(4.57)

D_y(k) = Dy0 (k) + λ_2i(k)Dyi

(k),

i=1

H(k)Dyi (k) = B_1i - B_2i,

где все матрицы B_i(k), Dyi (k), i = 0, M известны. Таким образом, (4.56) с

учетом (4.57) имеет вид

(

)

(

)

∑

B_i(k)

0(k)

(4.58)

B(k) =

λ_2i(k)

B₀(k) - H(k)Dy0 (k)

B_i(k) - H(k)Dyi (k)

i=1

При выполнении (4.54), (4.55) и (4.58) система в ошибках фильтрации

является системой с мультипликативными шумами. Запишем теорему об

условиях ограниченности анизотропийной нормы этой системы для случая

Γ(k) = 0:

Теорема 2. Заданы линейная дискретная нестационарная система T_zw

с реализацией в пространстве состояний (4.7) и вещественные числа a > 0

и γ > 0. Тогда a-анизотропийная норма системы на интервале [0,N] удовле-

творяет неравенству |||T_zw|||_a ≤ γ, если существуют q = η^-1 > 0 и матри-

цы P(k), Ψ(k), Y(k), которые являются решением системы линейных мат-

ричных неравенств





P(k)

A^0⊤0P(k + 1) A⁰(k)P(k + 1) C(k)









∗ ηI B^0⊤0(k)P(k + 1)











∗

P(k + 1)

+











∗

Φ_M (P(k + 1))



∗





A^1⊤0Y(k) A¹(k)Y(k)









∗

B^1⊤0(k)Y(k)









(4.59)

≻ 0,



∗







 ∗ ∗

∗



∗





ηI - Ψ(k) B^0⊤0(k)P(k + 1) B⁰(k)P(k + 1)





(4.60)



∗

P(k + 1)

+

∗

Φ_M (P(k + 1))





B^1⊤0(k)Y(k) B¹(k)Y(k)





+ ∗

 ≻ 0,

∗





P(N)

C(N)





(4.61)



∗ ηI

 ≻ 0,

∗

[

]

ηI - Ψ(N)

(4.62)

≻ 0,

∏

(4.63)

det Ψ(k) ≥ e^2a(η - γ²)mw (N+1),

k=0

(

)

Y(k) =

Y₂₁

Y₂₂

Доказательство теоремы приведено в Приложении 2.

Аналогично рассмотренным выше частным случаям фильтров, при реше-

нии неравенств (4.59)-(4.63) необходимо учитывать вид неизвестной матри-

цы Y(k) в соответствии с заменой переменных (см. док-во теоремы в При-

ложении). Решив полученные неравенства относительно матриц P(k), Ψ(k)

и Y(k), используем обратную замену переменных и находим матрицы филь-

тра W (k) и H(k).

4.2.5. Фильтр с Γ(k) = 0

Заданы система вида (3.1) и фильтр (3.3). Рассмотрим случай Γ(k) = 0.

Матрицы системы и фильтра должны удовлетворять следующим условиям:

∑

(4.64)

A(k) = A011 (k) +

λ_1i(k)Ai11

(k),

i=1

∑

(4.65)

0 = A012(k) +

λ_1i(k)Ai12

(k),

i=1

∑

(4.66)

A(k) - W (k) + H(k)(Γ(k) - C_y(k)) = A (k) +₀

λ_1i(k)A

(k),

i₂₁

i=1

∑

(4.67)

W (k) - H(k)Γ(k) = A (k) +₀

λ_1i(k)A

(k),

i₂₂

i=1

∑

(4.68)

B(k) = B₀₁(k) + λ_2i(k)B_i1

(k).

i=1

Так же, как и в случае Γ(k) = 0, равенство (4.66) имеет место, если ма-

тематические ожидания случайных величин обеих сторон выражения (4.66)

равны. Предположив, что Γ(k) = E[C_y(k)], преобразуем (4.66)-(4.67) к сле-

дующему виду:

A021 (k) = A (k) - W(k),₀

∑

(4.69)

λ_1i(k)Ai21 (k) =

λ_1i(k)Ai11 (k) + H(k)(E[C_y(k)] - C_y

(k)).

i=1

Если условие (4.69) выполняется, то условия ограниченности анизотропий-

ной нормы системы в ошибках фильтрации (4.7) выводятся тем же образом,

как и в случае Γ(k) = 0. Применив аналогичные преобразования и замены

переменных, получим условия ограниченности анизотропийной нормы для

рассматриваемого частного случая фильтра:

Теорема 3. Заданы линейная дискретная нестационарная система T_zw

с мультипликативными шумами и реализацией в пространстве состояний

(4.7) и вещественные числа a ≥ 0, γ ≥ 0. Тогда a-анизотропийная норма си-

стемы на интервале k ∈ [0,N] удовлетворяет условию |||T_zw|||_a ≤ γ, если

существуют q = η^-1 > 0 и матрицы P(k), Ψ(k), Y(k), при которых выпол-

няются неравенства





P(k)

A^0⊤0P(k + 1) A⁰(k)P(k + 1) C(k)









∗ ηI B^0⊤0(k)P(k + 1)











∗

P(k + 1)

+







∗

Φ_M (P(k + 1))



∗





A^1⊤0Y(k) A¹(k)Y(k)









∗

B^1⊤0(k)Y(k)











∗

≻





 ∗ ∗

∗



∗





ηI - Ψ(k) B^0⊤0(k)P(k + 1) B⁰(k)P(k + 1)







∗

P(k + 1)

+

∗

Φ_M (P(k + 1))





B^1⊤0(k)Y(k) B¹(k)Y(k)





+ ∗

 ≻ 0,

∗





P(N)

C(N)



∗ ηI

≻0,

∗

[

]

ηI - Ψ(N)

≻ 0,

∏

det Ψ(k) ≥ e^2a(η - γ²)mw (N+1),

k=0

(

)

Y(k) =

Y₂₁

Y₂₂

Стоит отметить, что единственным отличием частных случаев фильтров

Γ(k) = 0 и Γ(k) =0 является компонента H(k)E[C_y(k)] в матрице A (k). Да-₀

же при отсутствии в фильтре слагаемых H(k)Γ(k) компонента H(k)E[C_y(k)]

все равно появляется для центрирования случайной матрицы C_y(k) и тем

самым обеспечения выполнения ограничений на матрицы системы с мульти-

пликативными шумами. В следующем разделе приведен численный пример

решения задачи анизотропийной фильтрации для системы с отказами в из-

мерениях.

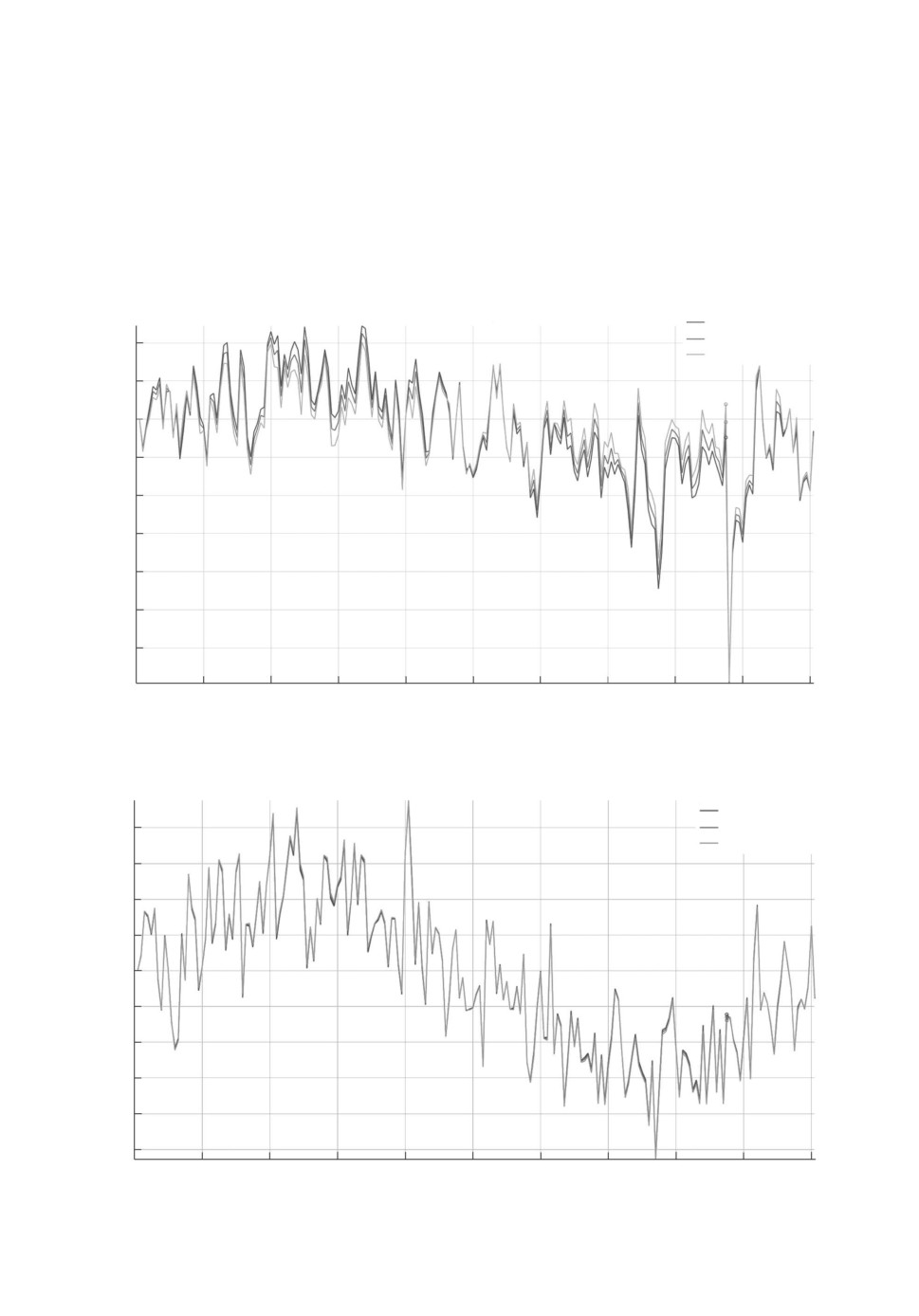
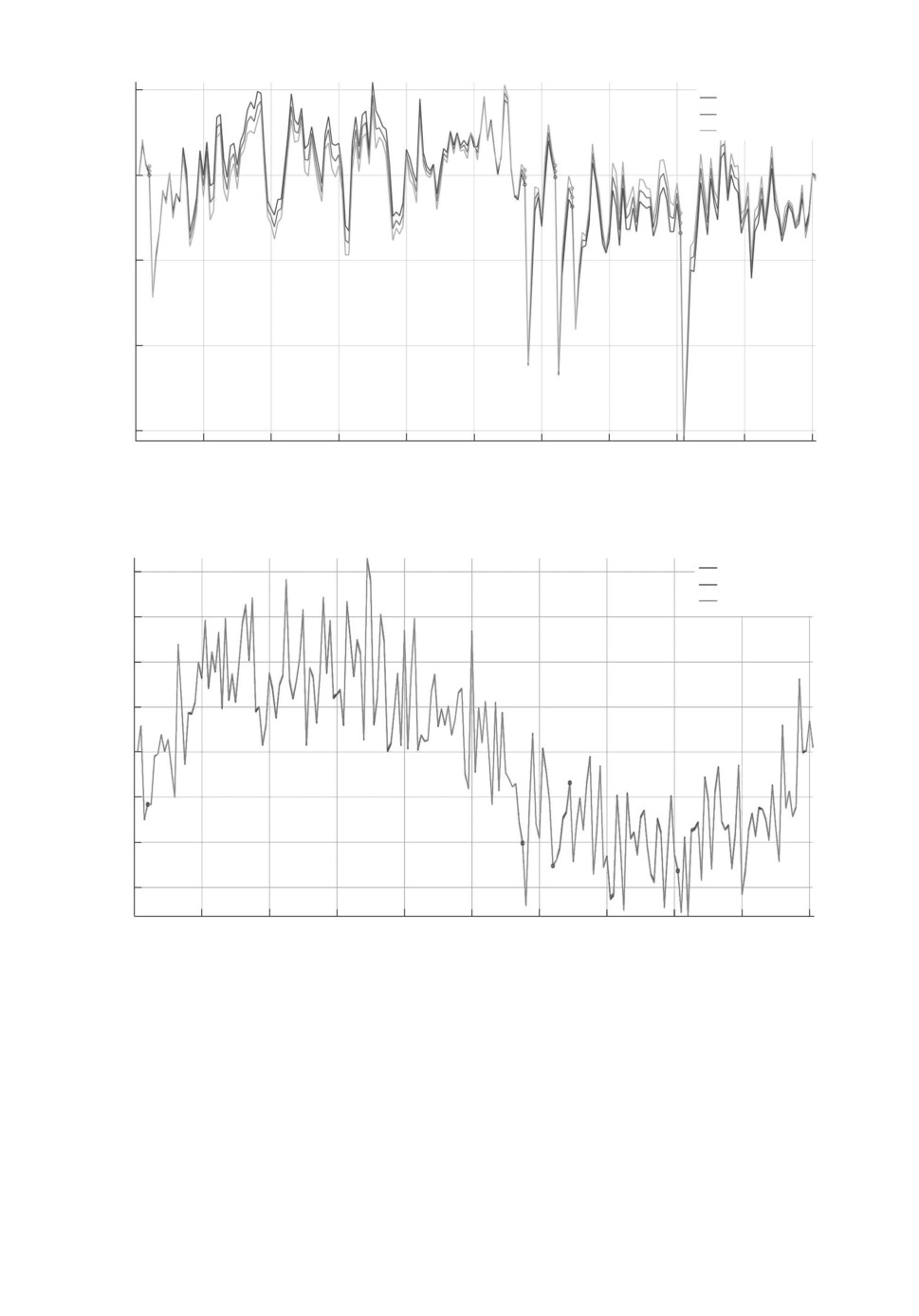
1-я компонента ошибки оценивания

e₁

0,5

H₂-фильтр

Аниз. фильтр

H_¥-фильтр

-0,5

-1,0

-1,5

100

120

140

160

180

200

Рис. 5. Ошибка оценивания e₁(t).

e₂

2-я компонента ошибки оценивания

0,4

H₂-фильтр

Аниз. фильтр

H_¥-фильтр

0,3

0,2

0,1

-0,1

-0,2

-0,3

100

120

140

160

180

200

Рис. 6. Ошибка оценивания e₂(t).

где σ(λ_k) среднеквадратичное отклонение случайной величины λ(k) при

матрице C_y, r(k)

синусоидальное задающее воздействие, подаваемое на

вход системы. По предложенному алгоритму для данной системы синтезиро-

ваны три a-анизотропийных фильтра при фиксированном параметре анизо-

тропии a и различных значениях вероятности отказа 1 - p. Каждый из этих

анизотропийных фильтров сравнивается с субоптимальным H₂-фильтром и

субоптимальным H_∞-фильтром, построенными для той же системы с соот-

ветствующими параметрами вероятности отказа.

1-я компонента оцениваемого выхода

z₁

z₁(t) без шумов

z₁(t) с шумом

H₂-фильтр

Аниз. фильтр

H_¥-фильтр

-1

-2

-3

100

120

140

160

180

200

Рис. 7. Оцениваемый выход z₁(t).

z₂

2-я компонента оцениваемого выхода

0,5

z₂(t) без шумов

z₂(t) с шумом

0,4

H₂-фильтр

Аниз. фильтр

0,3

H_¥-фильтр

0,2

0,1

-0,1

-0,2

-0,3

-0,4

-0,5

100

120

140

160

180

200

Рис. 8. Оцениваемый выход z₂(t).

В результате решения системы линейных матричных неравенств (4.39)-

(4.40) для системы (5.1) были получены последовательности значений мат-

риц фильтра W (k) и H(k). При решении системы линейных матричных нера-

венств использовались пакеты Yalmip Matlab toolbox и SeDuMi optimization

package.

Результаты моделирования представлены в виде графиков значений оце-

ниваемого выхода z(t) и ошибок оценивания выхода e(t) = z(t) - z(t) для трех

значений параметра p. Точками на графиках обозначены моменты отказа в

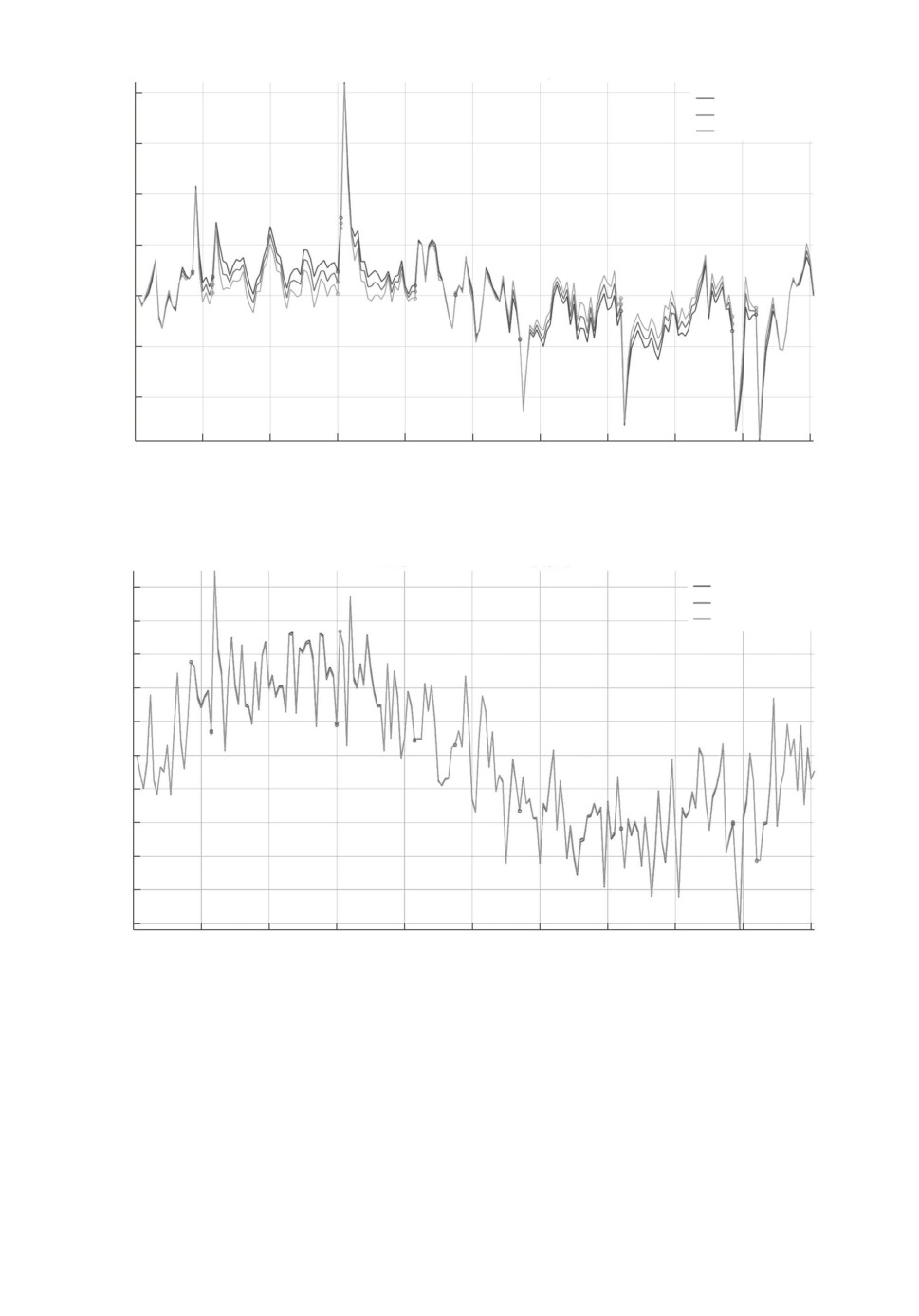
1-я компонента ошибки оценивания

e₁

2,0

H₂-фильтр

Аниз. фильтр

H_¥-фильтр

1,5

1,0

0,5

-0,5

-1,0

100

120

140

160

180

200

Рис. 9. Ошибка оценивания e₁(t).

e₂

2-я компонента ошибки оценивания

0,5

H₂-фильтр

Аниз. фильтр

0,4

H_¥-фильтр

0,3

0,2

0,1

-0,1

-0,2

-0,3

-0,4

-0,5

100

120

140

160

180

200

Рис. 10. Ошибка оценивания e₂(t).

измерениях, т.е. λ(k) = 0. Ниже приведены значения параметра вероятности

отказа, при которых производилось численное решение поставленной задачи

фильтрации:

• Вероятность отказа в измерениях 1 - p = 0,01. Графики ошибки филь-

трации и оцениваемого выхода представлены на рис. 1-4.

• Вероятность отказа в измерениях 1 - p = 0,03. Графики ошибки филь-

трации и оцениваемого выхода представлены на рис. 5-8.

z₁

1-я компонента оцениваемого выхода

z₁(t) без шумов

z₁(t) с шумом

H₂-фильтр

Аниз. фильтр

H_¥-фильтр

-1

-2

-3

-40

100

120

140

160

180

200

Рис. 11. Оцениваемый выход z₁(t).

2-я компонента оцениваемого выхода

z₂

z₂(t) без шумов

z₂(t) с шумом

0,4

H₂-фильтр

Аниз. фильтр

H_¥-фильтр

0,2

-0,2

-0,4

-0,6

100

120

140

160

180

200

Рис. 12. Оцениваемый выход z₂(t).

• Вероятность отказа в измерениях 1 - p = 0,05. Графики ошибки филь-

трации и оцениваемого выхода представлены на рис. 9-12.

На графиках видно, как при увеличении числа отказов в измерениях уве-

личивается ошибка оценивания выходов z(t) рассматриваемой системы. Но

после каждого отказа оценка постепенно сходится к реальному значению вы-

хода системы, т.е. ошибка оценивания продолжает колебаться около нуля.

Также видно, что субоптимальный анизотропийный фильтр эффективнее

H₂-субоптимального фильтра, но менее эффективен, чем H_∞-субоптималь-

ный фильтр, что обусловлено свойствами анизотропийной нормы. Однако,

как было сказано ранее, анизотропийный фильтр может менять свои свой-

ства в зависимости от параметра a, что позволяет решать задачу фильтрации

для конкретного случая входного возмущения менее энергозатратно с техни-

ческой точки зрения, чем с помощью H_∞-субоптимального фильтра.

6. Заключение

Решена задача анизотропийной фильтрации на конечном временном ин-

тервале для линейной дискретной нестационарной системы с мультиплика-

тивными шумами. Качество решения задачи фильтрации характеризуется

анизотропийной нормой системы в ошибках оценивания наблюдаемого выхо-

да исходной системы. На основании леммы об ограниченности анизотропий-

ной нормы системы с мультипликативными шумами выведены линейные мат-

ричные неравенства относительно неизвестных матриц искомого фильтра.

Рассмотрены частные случаи задачи анизотропийной фильтрации, включая

задачу фильтрации для системы с отказами в измерениях. Использование

предложенного метода решения задачи анизотропийной фильтрации проде-

монстрировано с помощью численного примера задачи для системы с отка-

зами в измерениях с различными значениями вероятности отказа.

ПРИЛОЖЕНИЕ 1

Доказательство теоремы

1. Приведем выражение (4.22) к виду

неравенства с учетом положительной определенности матрицы S(k):

Θ(k) ≻ 0 : Θ(k) ≻ S(k), Θ^-1(k) ≺ S^-1(k),

(Π.1.1)

Θ^-1(k) = Ψ(k) ≺ Imw -

(

)

∑

− q D⊤i (k)D_i(k) + B⊤i (k)R(k + 1)B_i(k)

i=0

Ψ^-1(k) ≻ S(k).

Применив (Π.1.1) к системе (4.21)-(4.24), получим систему неравенств сле-

дующего вида:

R(k) ≻ R(k),

R(N + 1) = 0,

(Π.1.2)

R(k) ≻ A^⊤0(k)R(k + 1)A₀

(k) +

∑

+ a_iA^⊤i(k)R(k +1)A_i(k)+q c_iC^⊤i(k)C_i(k) +

i=1

i=0

(

)

)⊤

+ B^⊤0 R(k +1)A0 +qD⊤0 C₀

Ψ^-1(k) B^⊤0 R(k +1)A₀ +qD^⊤

C0 ,

(

)

∑

(Π.1.3)

Ψ(k) ≺ I_m

- q D⊤i (k)D_i(k)+ B⊤i (k) R(k +1)B_i(k)

i=0

∑

(Π.1.4)

ln det Ψ(k) ≥ 2a + m_w(N + 1) ln(1 - qγ²

k=0

Заметим, что в неравенстве (Π.1.4) есть произведение двух переменных си-

стемы qγ². Для решения системы неравенств необходимо устранить данную

нелинейную компоненту с помощью преобразования самого выражения или

замены переменных. Следовательно, введем следующие новые переменные:

η = q^-1, Ψ = ηΨ,

(Π.1.5)

P(k) = ηR(k), P(N + 1) = ηR(N + 1).

Для компактности записи дальнейших выкладок с линейными матричны-

ми неравенствами введем обозначения

(

)

(

)

(Π.1.6)

A(k) =

A⊤1 ... A⊤M

B(k) =

B⊤1 ... B⊤M

(

)

(

)

(Π.1.7)

C(k) =

C^⊤1

... C^⊤M

D(k) =

D^⊤1

... D^⊤M

Для приведения неравенств (Π.1.2), (Π.1.3) к форме системы линейных

матричных неравенств (ЛМН) потребуется лемма Шура (в англоязычной ли-

тературе Schur complement lemma). Формулировку данной леммы можно

найти в [20].

Применим лемму Шура к системе неравенств Риккати (Π.1.2)-(Π.1.3) с

учетом замены переменных (Π.1.5) и обозначений (Π.1.6)-(Π.1.7):





P(k)

∗







ηImw

∗









A₀(k) B₀(k) P^-1(k + 1)

∗







(Π.1.8)





≻ 0,



A^⊤(k)

∗











P^-1(k + 1) ∗

 C0^(k)D0^(k)



C^⊤(k)





P(N)

∗





ηI

∗



m_w



(Π.1.9)





≻ 0,



C₀(N) D₀(N) Ipz

∗



C(N)





ηI

- Ψ(k)

∗

m_w







B^⊤0(k)

P^-1(k + 1)

∗











(Π.1.10)



∗



≻ 0,







⊤



(k)

P^-1(k + 1) ∗

 B



D^⊤(k)

(

)

ηI

- Ψ(N)

∗

m_w

(Π.1.11)

≻ 0,

D(N)

Ipz

∏

(Π.1.12)

det Ψ(k) ≥ e^2a(η - γ²)mw (N+1),

k=0

P(k) ≻ 0, k = N - 1, . . . , 0.

Для устранения обратных матриц в неравенствах (Π.1.8), (Π.1.10) сделаем

конгруэнтные преобразования неравенств с помощью блочно-диагональных

матриц вида

(

)

blockdiag

I2nx,Imw ,P(k + 1),... ,P(k + 1),Ipz(M)

(

)

blockdiag

I2nx,P(k + 1),... ,P(k + 1),Ipz(M)

Для упрощения записи преобразованных ЛМН введем обозначения

(

)

(Π.1.13)

A(k)P(k + 1) =

A^⊤1P(k + 1) ... A^⊤M P(k + 1)

(

)

(Π.1.14)

B(k)P(k + 1) =

B^⊤1P(k + 1) ... B^⊤M P(k + 1)

Применив обозначения (Π.1.13)-(Π.1.14) и необходимые конгруэнтные пре-

образования к неравенствам (Π.1.8)-(Π.1.12), получим искомые линейные

матричные неравенства (4.25)-(4.29).

ПРИЛОЖЕНИЕ 2

Доказательство теоремы 2. Запишем условия ограниченности ани-

зотропийной нормы для системы в ошибках фильтрации с учетом приведен-

ных выше выкладок:





P(k)

A^⊤0P(k + 1) A(k)P(k + 1) C(k)







∗ ηI B^⊤0(k)P(k + 1)









∗

P(k + 1)





≻





∗

Φ_M(P(k + 1))





∗





ηI - Ψ(k) B^⊤0(k)P(k + 1) B(k)P(k + 1)







∗

P(k + 1)

 ≻ 0,

∗

Φ_M (P(k + 1))





P(N)

C(N)







∗ ηI

 ≻ 0,

∗

[

]

ηI - Ψ(N)

≻ 0,

∏

det Ψ(k) ≥ e^2a(η - γ²)mw (N+1).

k=0

C учетом (4.55), (4.58) очевидно, что в неравенствах есть нелинейные

компоненты в виде произведений неизвестных матриц в произведениях

A_i(k)P(k + 1) и B^⊤i(k)P(k + 1).

Для устранения нелинейных членов в неравенствах используется следую-

щая замена переменных неравенств:

(

)

(Π.2.1)

X (k) =

Y(k) = X (k)P(k + 1).

W (k) H(k)

Применив замену переменных (Π.2.1) к системе неравенств (4.55), (4.58), по-

лучим

∑

(

)

(Π.2.2)

A(k) = A⁰⁰(k) + X (k)A¹⁰(k) + λ_1i(k)

A⁰ⁱ(k) + X(k)A¹ⁱ(k)

i=1

∑

(

)

(Π.2.3)

B(k) = B⁰⁰(k) + X (k)B¹⁰(k) +

λ_1i(k)

B⁰ⁱ(k) + X(k)B¹ⁱ(k)

i=1

где

)

(

)

( A₀(k)

-I I

(Π.2.4)

A⁰⁰(k) =

A¹⁰(k) =

A₀(k)

-Cy0(k)

)

(

)

( A_i(k)

(Π.2.5)

A⁰ⁱ(k) =

A¹ⁱ(k) =

A_i(k)

-Cyi(k)

)

(

)

( B₀(k)

(Π.2.6)

B⁰⁰(k) =

B¹⁰(k) =

B₀(k)

−Dy0

)

(

)

( Bi(k)

(Π.2.7)

B⁰ⁱ(k) =

B¹ⁱ(k) =

B_i(k)

−Dyi

Подставив (Π.2.1)-(Π.2.7) в матричные неравенства, устраняем нелиней-

ные компоненты из системы матричных неравенств. В итоге получаем иско-

мые линейные матричные неравенства (4.59)-(4.63).

СПИСОК ЛИТЕРАТУРЫ

1. Anderson B.D.O., Moore J.B. Optimal Filtering. New Jersey: Prentice Hall, 1979.

2. Hassibi B., Sayed A., Kailath T. Indefinite Quadratic Estimation and Control: A Uni-

fied Approach to H₂ and H_∞ Theories. Philadelphia: SIAM, 1999.

3. Simon D. Optimal State Estimation: Kalman, H_∞, and Nonlinear Approaches. New

Jersey: Wiley, 2006.

Vladimirov I.G., Kurdjukov A.P., Semyonov A.V. Anisotropy Of Signals And The

Entropy Of Linear Stationary Systems // Dokl. Math. 1995. V. 51. P. 388-390.

Vladimirov I.G., Kurdjukov A.P., Semyonov A.V. On Computing The Anisotropic

Norm Of Linear Discrete-Time-Invariant Systems // Proc. 13 IFAC World Congress.

1996. P. 179-184.

Vladimirov I.G., Diamond P., Kloeden P. Anisotropy-based robust performance

analysis of linear discrete time varying systems. CADSMAP Research Report 01-

01. The University of Queensland, Australia. 2001.

Vladimirov I.G., Diamond P. Robust Filtering in Finite Horizon Linear Discrete

Time Varying Systems by Minimum Anisotropic Norm Criterion. CADSMAP Res.

Report 01-05. 2001 [completed in 2001].

Maximov E.A., Kurdyukov A.P., Vladimirov I.G. Anisotropic Norm Bounded Real

Lemma for Linear Time-Varying System // Preprint 18th IFAC World Congr. Mi-

lano. 2011. P. 4701-4706.

Тимин В.Н., Курдюков А.П. Субоптимальная анизотропийная фильтрация на

конечном горизонте // АиТ. 2016. № 1. С. 5-29.

Timin V.N., Kurdyukov A.P. Suboptimal Anisotropic Filtering in a Finite Horizon //

Autom. Remote Control. 2016. V. 77. No. 1. P. 1-20.

10.

Yaesh I., Stoica A.-M. Linear Time-varying Anisotropic Filtering its Application to

Nonlinear Systems State Estimation // Proc. Eur. Control Conf. Strasbourg. 2014.

June 24-27. P. 975-980.

11.

Gershon E., Shaked U., Yaesh I. H_∞-control And Filtering Of Discrete-Time

Stochastic Systems With Multiplicative Noise

// Automatica. 2001. No.

37.

P. 409-417.

12.

Todorov E., Weiwei Li. Optimal Control Methods Suitable For Biomechanical Sys-

tems // Proceedings of the 25th Annual International Conference of the IEEE En-

gineering in Biology and Medicine Society. Mexico. 2003. P. 1758-1761.

13.

Todorov E. Stochastic Optimal Control And Estimation Methods Adapted To The

Noise Characteristics Of The Sensorimotor System // Neural Comput. 2005. No. 17.

P. 1084-1108.

14.

Semyonov A.V., Vladimirov I.G., Kurdyukov A.P. Stochastic approach to H-in-

finity optimization // Proc. 33rd IEEE Conf. Decision and Control. 1994. V. 3.

P. 2249-2250.

15.

Пакшин П.В. Оценивание состояния и синтез управления для дискретных ли-

нейных систем с аддитивными и мультипликативными шумами // АиТ. 1978.

№ 4. С. 75-85.

Pakshin P.V. State Estimation And Control Design For Digital Linear Systems With

Multiplicative Noises // Autom. Remote Control. 1978. V. 39. Is. 4. P. 526-636.

16.

Домбровский В.В., Ляшенко Е.А. Линейно-квадратичное управление дискрет-

ными системами со случайными параметрами и мультипликативными шумами

с применением к оптимизации инвестиционного портфеля // АиТ. 2003. № 10.

С. 50-65.

Dombrovskii V.V., Lyashenko E.A. A Linear Quadratic Control for Discrete Systems

with Random Parameters and Multiplicative Noise and Its Application to Investment

Portfolio Optimization // Autom. Remote Control. 2003. V. 64. Is. 10. P. 1558-1570.

17.

Belov I.R., Yurchenkov A.V., Kustov A.Yu. Anisotropy-Based Bounded Real Lemma

for Multiplicative Noise Systems: the Finite Horizon Case. 27th Mediterranean Con-

ference on Control and Automation. 2019.