Автоматика и телемеханика, № 6, 2021
© 2021 г. Ю.Е. ОБЖЕРИН, д-р техн. наук (objsev@mail.ru),
С.М. СИДОРОВ (xaevec@mail.ru),
М.М. НИКИТИН (m.nikitin.1979@gmail.com)
(Севастопольский государственный университет),
С.Г. ГЛЕЧ, канд. техн. наук (sergeyglech@gmail.com)
(Севастопольский экономико-гуманитарный институт (филиал)
Крымского федерального университета им. В.И. Вернадского)
СКРЫТАЯ МАРКОВСКАЯ МОДЕЛЬ НА ОСНОВЕ СУПЕРПОЗИЦИИ
ДВУХ ПРОЦЕССОВ ВОССТАНОВЛЕНИЯ1
В процессе функционирования системы, для которой построена полу-
марковская модель, не всегда возможно при изменении ее состояний полу-
чить всю информацию, содержащуюся в кодах состояний, а есть возмож-
ность получить некоторый сигнал (информацию), связанный с состоя-
ниями полумарковской модели. В этом случае состояния полумарковской
модели можно считать скрытыми (ненаблюдаемыми). В данной статье на
примере суперпозиции двух независимых процессов восстановления рас-
сматриваются подход к построению скрытой марковской модели на осно-
ве полумарковского процесса с фазовым пространством состояний общего
вида и использование такой модели для анализа функционирования мо-
делируемой системы на основе полученного вектора сигналов.
Ключевые слова: полумарковский процесс, полумарковская модель,
скрытая марковская модель, суперпозиция процессов восстановления,
вектор сигналов, оценка характеристик, прогнозирование состояний.
DOI: 10.31857/S0005231021060039
1. Введение
Полумарковские процессы широко используются для моделирования си-
стем различного назначения: технических [1-3], информационных [4-6], энер-
гетических [2, 7, 8], систем массового обслуживания [9-10], анализа финансо-
вых рисков [5, 11] и других.
В процессе функционирования системы, для которой построена полумар-
ковская модель, необходимо оценить, насколько построенная модель согласу-
ется с полученными в процессе функционирования системы данными, уточ-
нить ее, провести анализ функционирования системы и спрогнозировать ее
состояния на основе полученного вектора сигналов. Решить эти задачи поз-
воляют скрытые марковские модели [5, 12-15] и скрытые полумарковские
модели [16-19].
При построении полумарковской модели необходимо ввести фазовое про-
странство состояний системы. В ряде случаев достаточно использовать ко-
1 Работа выполнена при финансовой поддержке Российского фонда фундаментальных
исследований в рамках научного проекта № 18-01-00392а.
80
нечное или счетное множества состояний, которые отражают физические со-
стояния системы [2, 20]. Часто при построении полумарковской модели си-
стемы в фазовые состояния системы приходится вводить дополнительные
непрерывные компоненты, которые необходимы для корректного построения
модели [21-26]. Этими компонентами могут быть: время, прошедшее с начала
работы элемента системы; время, оставшееся до окончания восстановления
элемента системы; время, оставшееся до проведения контроля системы; вели-
чина оставшегося резерва времени и т.д. Отметим, что эти дополнительные
непрерывные компоненты содержат важную информацию о функционирова-
нии системы. В этом случае приходится использовать дискретно-непрерывное
фазовое пространство состояний, а для построения полумарковской модели
и анализа функционирования системы необходимо использовать теорию по-
лумарковских процессов с общим фазовым пространством состояний [21-25].
Важной составной частью полумарковского процесса является вложенная
цепь Маркова (ВЦМ), которая отвечает за переходы между состояниями си-
стемы. Фазовое пространство состояний ВЦМ совпадает с фазовым простран-
ством состояний полумарковского процесса. Второй важной составляющей
полумарковского процесса являются времена пребывания в состояниях на пе-
реходах. При построении полумарковских моделей ряда систем переходные
вероятности ВЦМ и функции распределения времен пребывания на перехо-
дах определяются общими параметрами. Так, для полумарковских моделей
надежности систем они определяются распределениями времен безотказной
работы и восстановления элементов системы.
При функционировании системы, для которой построена полумарковская
модель, не всегда удается при изменениях ее состояний полностью получить
информацию, содержащуюся в кодировке состояний, а есть возможность по-
лучить некоторый сигнал (информацию), связанный с состояниями ВЦМ (по-
лумарковского процесса). Например, в фазовом состоянии полумарковского
процесса для каждого элемента системы указано, находится он в рабочем
состоянии или на восстановлении, а при использовании системы можно по-
лучить сигнал только о числе работоспособных элементов. Для систем мас-
сового обслуживания, например, могут быть получены данные только о чис-
ле свободных приборов, а не о состоянии каждого прибора, содержащиеся
в фазовых состояниях. При функционировании системы бывает сложно или
невозможно получить значения дополнительных непрерывных компонент, ко-
торые, как было отмечено, несут важную информацию о функционировании
системы. В этих случаях состояния ВЦМ и полумарковской модели можно
считать скрытыми (ненаблюдаемыми). Поэтому возникает задача нахожде-
ния оценок характеристик и прогнозирования состояний ВЦМ и полумарков-
ской модели на основе полученного вектора сигналов. Как отмечено выше,
это можно сделать, используя аппарат теории скрытых марковских моделей.
В данной статье на примере суперпозиции двух независимых процессов
восстановления [21-23] рассматривается подход к построению скрытой мар-
ковской модели на основе полумарковского процесса с фазовым простран-
ством состояний общего вида, используя наличие у полумарковского процесса
ВЦМ. Результаты, содержащиеся в [12, 13], обобщаются на случай ненаблю-
даемой цепи Маркова с общим фазовым пространством состояний.
81
Скрытая марковская модель, построенная на основе суперпозиции двух
независимых процессов восстановления, используется для нахождения оце-
нок характеристик ВЦМ суперпозиции и сигналов на основе полученного
вектора сигналов.
Для ВЦМ находятся условные вероятности состояний на
2 ≤ k ≤ n,
(n + 1)-м и шагах при полученном векторе сигналов размера n. Для век-
тора сигналов получены условные вероятности значений вектора сигналов
на (n + 1)-м шаге, безусловные вероятности вектора сигналов и финальные
вероятности для значений вектора сигналов.
Для полноты изложения описана суперпозиция двух независимых процес-
сов восстановления, построенная в публикациях [21-23].
При реализации рассматриваемого подхода можно применять математи-
ческие пакеты, допускающие аналитические преобразования, используя при
этом рекуррентные формулы.
Эффективным методом решения проблемы размерности моделей явля-
ется алгоритм стационарного фазового укрупнения полумарковских систем
[21-23], разработанный В.С. Королюком и А.Ф. Турбиным. Используя этот
алгоритм, можно перейти к укрупненной полумарковской модели, вплоть до
полумарковской модели с конечным множеством состояний, а затем использо-
вать рассматриваемый подход к построению скрытой марковской модели [15].
2. Построение скрытой марковской модели
Построим скрытую марковскую модель на основе суперпозиции двух неза-
висимых процессов восстановления.
Дадим, обобщая результаты, содержащееся в [12, 13] определение скры-
той марковской модели, когда ненаблюдаемая цепь Маркова имеет фазовое
пространство состояний общего вида.
Пусть {Xn, n = 1, 2, 3, . . .} - однородная цепь Маркова, определенная в из-
меримом пространстве (E, F), с переходными вероятностями
P (x, B) = P (Xn+1 ∈ B|Xn = x), x ∈ E, B ∈ F,
и начальным распределением вероятностей
π(B) = P (X1 ∈ B), B ∈ F.
Жирными буквами x, e, y, z обозначаются элементы фазового простран-
ства состояний E.
Предположим, что множество сигналов J конечно:
J = {s1,s2,...,sm}.
Далее предположим, что когда цепь Маркова попадает в состояние x ∈ E,
то независимо от предыдущих состояний цепи Маркова и сигналов излуча-
ется сигнал s ∈ J с вероятностью
∑
(1)
R(s | x) = P (Sn = s | Xn = x), x ∈ E, s ∈ J,
R(s | x) = 1.
s∈J
82
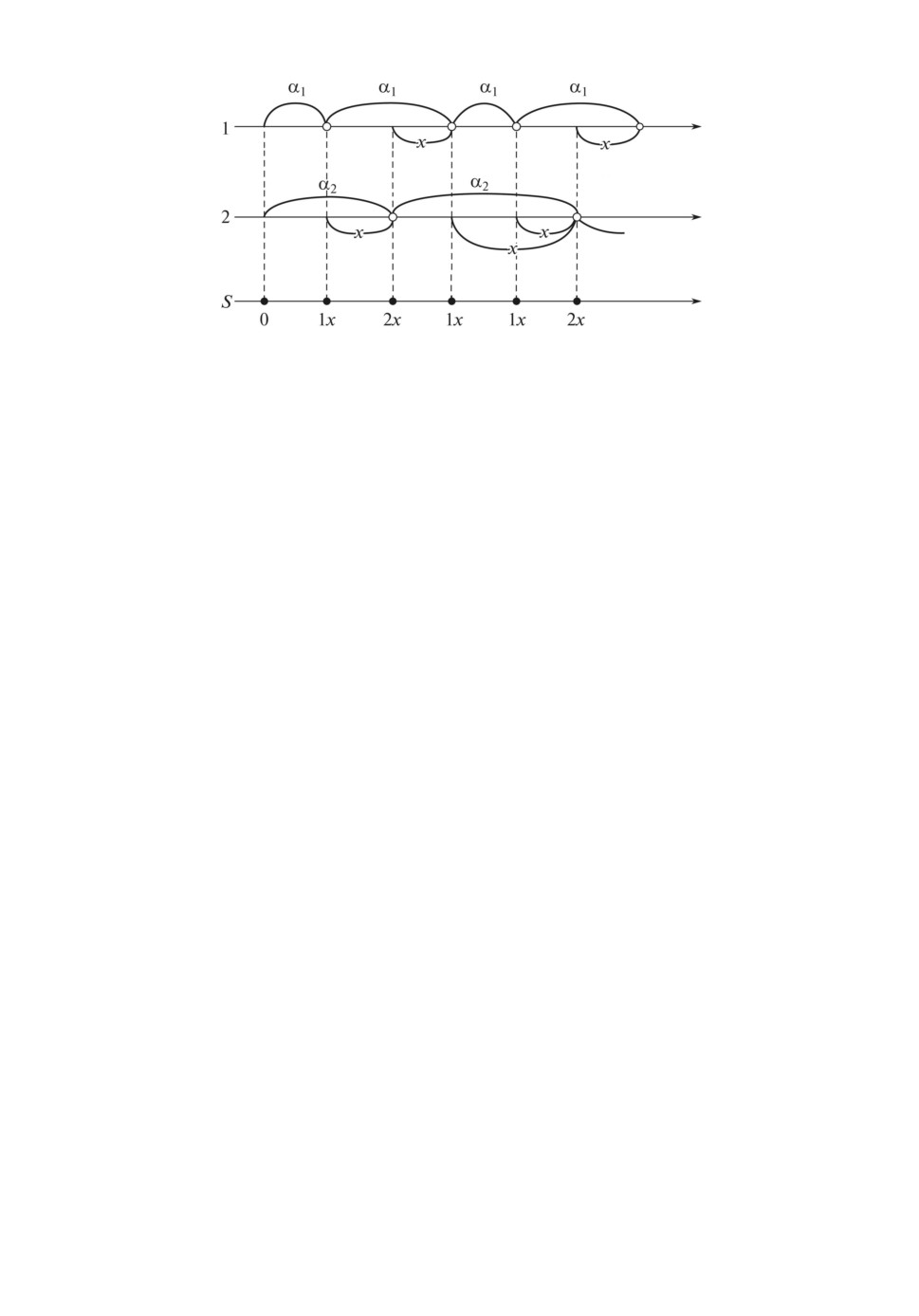
Рис. 1. Временная диаграмма функционирования системы.
Таким образом, если Sn представляет собой n-й сигнал, то
P (S1 = s | X1 = x) = R(s | x),
P (Sn = s | X1, S1, . . . , Xn-1, Sn-1, Xn = x) = R(s | x).
Модель такого типа, в которой последовательность сигналов S1, S2, . . . ,
...,Sn,... является наблюдаемой, в то время как цепь Маркова X1,X2,
...,Xn,... является ненаблюдаемой, называется скрытой марковской моде-
лью [5, 12, 13].
Опишем, следуя [21-23], суперпозицию двух независимых процессов вос-
становления, на основе которой строится скрытая марковская модель.
Рассмотрим систему S, состоящую из двух элементов, где функциони-
рование каждого элемента описывается процессом восстановления [21-23]
с временами восстановления α1 и α2, имеющими функции распределе-
ния G1(x) = P (α1 ≤ x), G2(x) = P (α2 ≤ x) и плотности распределения g1(x),
g2(x). Случайные величины α1 и α2 предполагаются независимыми, имею-
щими конечные математические ожидания.
Для описания функционирования системы S используется полумарков-
ский процесс ξ(t) со следующим дискретно-непрерывным фазовым простран-
ством состояний:
E = {0,1x,2x; x > 0}.
Кодировка состояний следующая:
• 0 - оба элемента восстановлены, начальное состояние;
• 1x - восстановился первый элемент; время, оставшееся до восстановле-
ния второго элемента, осталось равно x > 0;
• 2x - восстановился второй элемент; время, оставшееся до восстановления
первого элемента, осталось равно x > 0.
Временная диаграмма функционирования системы S представлена на
рис. 1.
83
Плотности вероятностей переходов ВЦМ имеют вид [21-23]:
∫∞
∫
∞
p1x0 = g2(x + t)g1(t)dt, x > 0, p2x0 = g1(x + t)g2(t)dt, x > 0;
0
0
p1y1x = g1(x - y),
0 < y < x,
p2y1x = g1(x + y), y > 0;
p1y2x = g2(x + y), y > 0,
p2y2x = g2(x - y),
0 < y < x.
Времена пребывания системы S в состояниях определяются следующим
образом:
θ0 = α1 ∧ α2, θ1x = α1 ∧ x, θ2x = α2 ∧ x,
∧ - знак минимума.
В [21] показано, что ВЦМ имеет стационарное распределение, плотности
которого определяются формулами:
(2)
ρ(1x) = ρ0 G2(x), ρ(2x) = ρ0 G1
(x),
1
где
Gi(x) = 1 - Gi(x), i = 1, 2, ρ0 =
, Mαi - математическое ожида-
Mα1+Mα2
ние случайной величины αi.
Перейдем к построению скрытой марковской модели, определенной на ос-
нове суперпозиции двух независимых процессов восстановления. Предполо-
жим, что при использовании системы S состояния ВЦМ 1x, 2x не наблюда-
ются (скрытые состояния), а наблюдается только номер элемента, который
восстановился на следующем переходе.
Следовательно, множество сигналов имеет вид
J = {1,2}.
Рассмотрим связь между состояниями ВЦМ и сигналами, т.е. определим
функцию R(s|x).
1. Состояние 0:
∫∞
P (Sn = 1 | Xn = 0) = P (α1 < α2) =
G2(t)g1(t)dt,
0
∫∞
P (Sn = 2 | Xn = 0) = P (α2 < α1) =
G1(t)g2(t)dt.
0
2. Состояния 1x:
P (Sn = 1 | Xn = 1x) = P (α1 < x) = G1(x),
P (Sn = 2 | Xn = 1x) = P (α1 > x) =G1(x).
3. Состояния 2x:
P (Sn = 1 | Xn = 2x) = P (α2 > x) =G2(x),
P (Sn = 2 | Xn = 2x) = P (α2 < x) = G2(x).
84
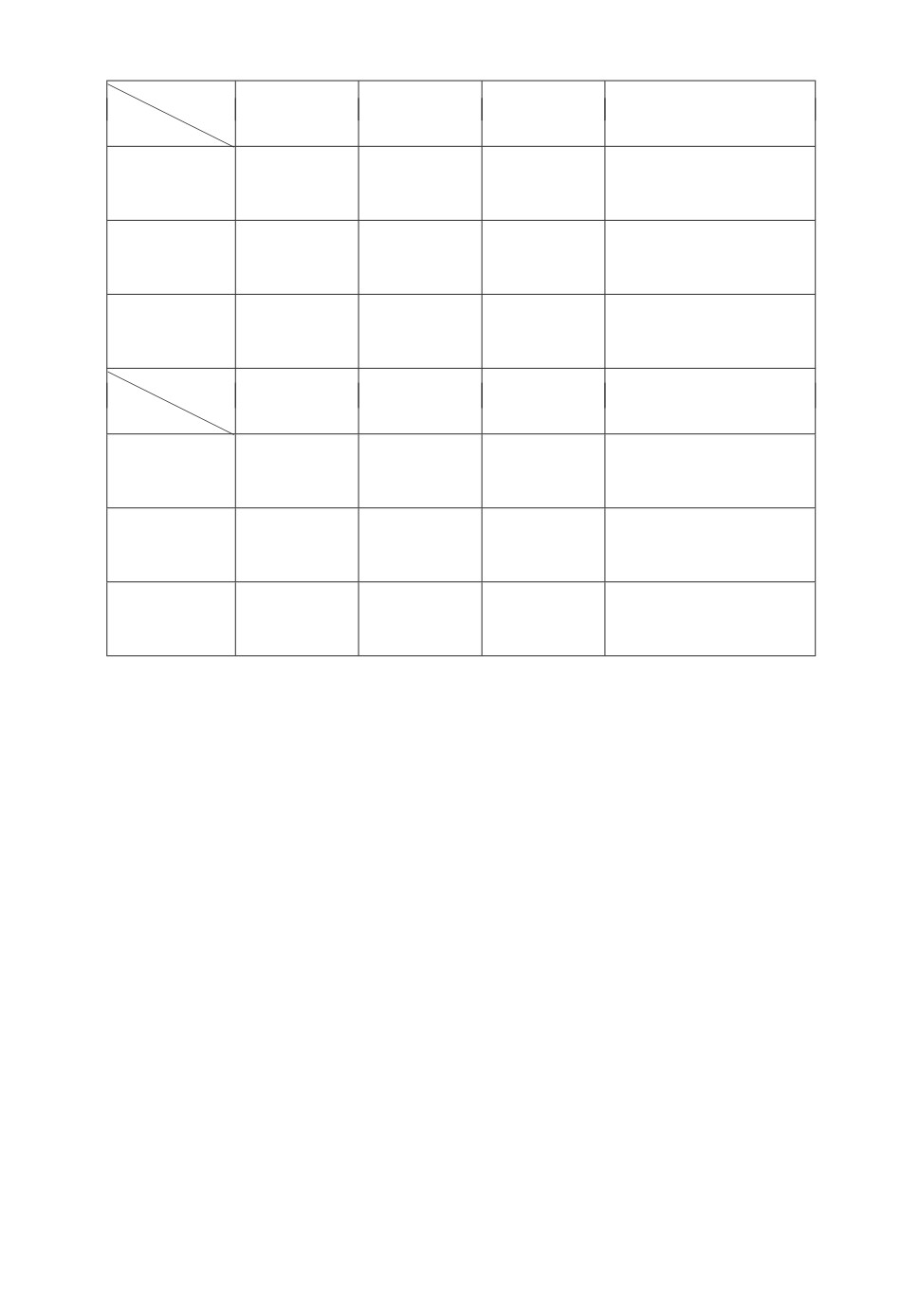
Таблица 1. Функция R(s | x) связи состояний ВЦМ с сигналами
Сигнал, s
s=1
s=2
Состояние, x
∫
∫
0
p1 =
G2(t)g1(t)dt
p2 =
G1(t)g2(t)dt
0
0
1x
G1(x)
G1(x)
2x
G2(x)
G2(x)
Функция R(s | x) связи состояний ВЦМ с сигналами представлена в
табл. 1.
3. Оценка характеристик на основе полученного вектора сигналов
Пусть
Sn = (S1,S2,... ,Sn) - случайный вектор первых n сигналов.
Для фиксированной последовательности сигналов sn = (s1, s2, . . . , sn) пусть
sk = (s1, s2, . . . , sk), k ≤ n. Требуется оценить характеристики ВЦМ и вектора
сигналов на основе полученного вектора сигналов sn.
I. Вначале определим условную вероятность ВЦМ в момент n при условии,
чт
Sn = sn, т.е. найдем условную вероятность
(
)
(3)
P
Xn ∈ B
Sn = sn
,
B ∈ F.
Для нахождения этой вероятности, следуя [12, 13], введем функции (пря-
мые переменные), которые играют важную роль в дальнейшем:
Fn(B) = P
Sn = sn,Xn ∈ B), B ∈ F,
или в дифференциальной форме
Fn(dx) = P
Sn = sn,Xn ∈ dx).
Имеем, что
Fn(dx) = P
Sn-1 = sn-1, Sn = sn, Xn ∈ dx) =
∫
= P
Sn-1 = sn-1, Xn-1 ∈ de, Xn ∈ dx, Sn = sn) =
E
∫
(
)
= Fn-1(de)P
Xn ∈ dx, Sn = sn
Sn-1 = sn-1, Xn-1 = e
=
E
∫
= Fn-1(de)P (Xn ∈ dx, Sn = sn |Xn-1 = e) =
E
∫
= Fn-1(de)P(e,dx)R(sn |x),
E
85
где использовалось, что
P (Xn ∈ dx, Sn = sn | Xn-1 = e) =
= P(Xn ∈ dx|Xn-1 = e)P(Sn = sn |Xn = x, Xn-1 = e) =
= P (Xn ∈ dx|Xn-1 = e)P(Sn = sn |Xn = x) = P(e,dx)R(sn |x).
Следовательно, для плотности fn(x) функции Fn(B) справедлива рекур-
рентная формула
∫
(4)
fn(x) = R(sn|x) fn-1(e)p(e, x)de,
E
где p(e, x) - плотность вероятности переходов P (e, B) ненаблюдаемой цепи
Маркова.
Найдем функции f1(x), f2(x), f3(x), f4(x).
1. F1(dx) = P (X1 ∈ dx, S1 = s1) = P (X1 ∈ dx)P (S1 = s1 | X1 = x) =
= π(dx)R(s1 |x), следовательно
(5)
f1(x) = π(x)R(s1
|x).
2. Применяя рекуррентную формулу (4), последовательно получаем:
∫
(6)
f2(x) = R(s2 |x) R(s1
| e)p(e, x)π(e)de,
E
∫
∫
(7)
f3(x) = R(s3 |x) R(s2 |e)p(e,x)de R(s1
|y)p(y,e)π(y)dy,
E
E
∫
∫
f4(x) = R(s4 |x) R(s3 |e)p(e,x)de R(s2 |z)p(z,e)dz ×
E
E
∫
× R(s1 |y)p(y,z)π(y)dy,
E
где π(x) - плотность начального распределения π(B).
Найдем функции F1(B), f2(x), f3(x) для построенной скрытой марковской
модели в случае вектора сигналов s3 = (s1, s2, s3).
Используя формулы (5)-(7), получаем
{ 0,
x = 0 ∈ B,
(8)
F1(B) =
R(s1 | 0), x = 0 ∈ B,
{ R(s1 |0)R(s2 |1E)ϕ1(x), x = 1x,
(9)
f2(x) =
R(s1 | 0)R(s2 | 2E)ϕ2(x), x = 2x,
86
где
∫∞
∫
∞
ϕ1(x) = g2(x + t)g1(t)dt, ϕ2(x) = g1(x + t)g2(t)dt,
0
0
∞
∫
R(s1 | 0)R(s3 | 1E) R(s2 | 2y)g2(y + x)ϕ2(y)dy +
∫
+ R(s2 |1y)g1(y - x)ϕ1(y)dy, x = 1x,
x
(10) f3(x) =
∞
∫
R(s1 | 0)R(s3 | 2E) R(s2 | 1y)g1(y + x)ϕ1(y)dy +
0
∞
∫
+ R(s2 |2y)g2(y - x)ϕ2(y)dy , x = 2x,
x
значения R(s | x) находятся из табл. 1.
Пусть полученный вектор сигналов s = (s1, s2, s3) имеет вид: s3 = (1, 2, 1),
s1 = 1, s2 = 2, s3 = 1. В этом случае, используя формулы (8)-(10) и табл. 1,
получаем, что функции F1(B), f2(x), f3(x) имеют вид:
{ 0, x = 0 ∈ B,
(11)
F1(B) =
p1, x = 0 ∈ B,
{ p1
F1(x)ϕ1(x), x = 1x,
(12)
f2(x) =
p1F2(x)ϕ2(x), x = 2x,
∞
∫
p1G1(x) G2(y)g2(y + x)ϕ2(y)dy +
0
∞
∫
+
G1(y)g1(y - x)ϕ1(y)dy , x = 1x,
∞
x
(13) f3(x) =
∫
p1 G2(x)
G1(y)g1(y + x)ϕ1(y)dy +
0
∞
∫
+
G1(y)g2(y - x)ϕ2(y)dy, x = 2x.
x
Аналогично можно найти вид функций F1(B), f2(x), f3(x) и для других
векторов s3 сигналов.
В качестве конкретного примера рассмотрим случай, когда случайные ве-
личины α1 и α2 имеют экспоненциальное распределение:
G1(x) = 1 - e-λ1x, g1(x) = λ1e-λ1x, G2(x) = 1 - e-λ2x, g2(x) = λ2e-λ2x.
87
Тогда
λ1λ2
λ1λ2
λ1
λ2
ϕ1(x) =
e-λ2x, ϕ2(x) =
e-λ1x, p1 =
,
p2 =
λ1 +λ2
λ1 +λ2
λ1 +λ2
λ1 +λ2
Используя формулы (11)-(13), найдем выражения функций F1(B), f2(x),
f3(x) для векторов сигналов s3 = (1,1,1), s3 = (1,2,1), s3 = (1,1,2), s3 =
= (1, 2, 2).
1. Для вектора s3 = (1, 1, 1):
{ 0, x = 0 ∈ B,
F1(B) =
p1, x = 0 ∈ B,
{
λ
2p1(1 - e-λ1x)e-λ2x, x = 1x,
f2(x) =
λ2p21e-(λ1+λ2)x,
x = 2x,
[
]
λ1
λ2
λ2p21(1 - e-λ1x)e-λ2x p1 -
e-λ1x +
, x = 1x,
2λ1 + λ2
λ1 + 2λ2
f3(x) =
[
]
λ1
λ2
λ2p21e-(λ1+λ2)x p1 -
e-λ1x +
e-λ2x ,
x = 2x.
2λ1 + λ2
λ1 + 2λ2
2. В случае вектора s3 = (1, 2, 1):
{
0, x = 0 ∈ B,
F1(B) =
p1, x = 0 ∈ B,
{
λ2p21e-(λ1+λ2)x, x = 1x,
f2(x) =
λ2p21(1 - e-λ2x)e-λ1x, x = 2x,
[
]
λ1
λ2
λ2p21(1 - e-λ1x)e-λ2x p2 +
e-λ1x -
, x = 1x,
2λ1 + λ2
λ1 + 2λ2
f3(x) =
[
]
λ1
λ2
λ2p21e-(λ1+λ2)x p2 +
e-λ1x -
e-λ2x , x = 2x.
2λ1 + λ2
λ1 + 2λ2
3. Если s3 = (1, 1, 2), то
{
0, x = 0 ∈ B,
F1(B) =
p1, x = 0 ∈ B,
{
λ
2p1(1 - e-λ1x)e-λ2x, x = 1x,
f2(x) =
λ2p21e-(λ1+λ2)x,
x = 2x,
(
)
λ1
λ2
p21
λ2e-(λ1+λ2)x p1 -
e-λ1x +
,
x = 1x,
2λ1 + λ2
λ1 + 2λ2
f3(x) =
(
)
λ1
λ2
p21
λ2(1 - e-λ2x)e-λ1x p1 -
+
e-λ2x
, x = 2x.
2λ1 + λ2
λ1 + 2λ2
88
4. Для вектора s3 = (1, 2, 2):
{
0, x = 0 ∈ B,
F1(B) =
p1, x = 0 ∈ B,
{
λ2p21e-(λ1+λ2)x,
x = 1x,
f2(x) =
λ2p21(1 - e-λ2x)e-λ1x, x = 2x,
(
)
λ1
λ2
p21
λ2e-(λ1+λ2)x p2 +
e-λ1x -
,
x=1x,
2λ1 + λ2
λ1 +2λ2
(14) f3(x) =
(
)
λ1
λ2
p21
λ2(1-e-λ2x)e-λ1x p2 +
-
e-λ2x
, x=2x.
2λ1 + λ2
λ1 +2λ2
Для остальных векторов сигналов s3 = (2, 2, 2), s3 = (2, 1, 2), s3 = (2, 2, 1),
s3 = (2,1,1) функции F1(B), f2(x), f3(x) могут быть определены с исполь-
зованием функций, найденных для ранее рассмотренных векторов сигналов.
Так, эти функции для вектора s3 = (2, 1, 2) могут быть получены из функций
для вектора s3 = (1, 2, 1) заменой λ1 на λ2, p1 на p2, состояний 1x и 2x на 2x
и 1x соответственно.
Используя функции Fn(B), fn(x), перейдем к нахождению вероятно-
сти (3):
∫
∫
∫
(15)
P
Sn = sn) = P
Sn = sn,Xn ∈ dx) = Fn(dx) = fn(x)dx.
E
E
E
Введем функцию
Hn(B) = P(Xn ∈ B
Sn = sn), B ∈ F,
или в дифференциальной форме
(
)
Hn(dx) = P
Xn ∈ dx
Sn = sn
Имеем, что
(
)
(
)
P
Xn ∈ dx
Sn = sn
Hn(dx) = P
Xn ∈ dx
Sn = sn
=
=
P
Sn = sn)
Fn(dx)
Fn(dx)
=
=
∫
Fn(E)
E
Fn(de)
Следовательно, плотность hn(x) функции Hn(B) определяется формулой:
1
1
(16)
hn(x) = cn · fn(x), cn =
=
∫
Fn(E)
fn(x)dx
E
89
h3(2x)
h3(1x)
II
0,05
0,009
0,008
0,04
0,007
III
0,006
0,03
0,005
0,004
I
I
0,02
0,003
0,002
0,01
II
III
0,001
0
20
40
60
80
100
0
20
40
60
80
100
x
x
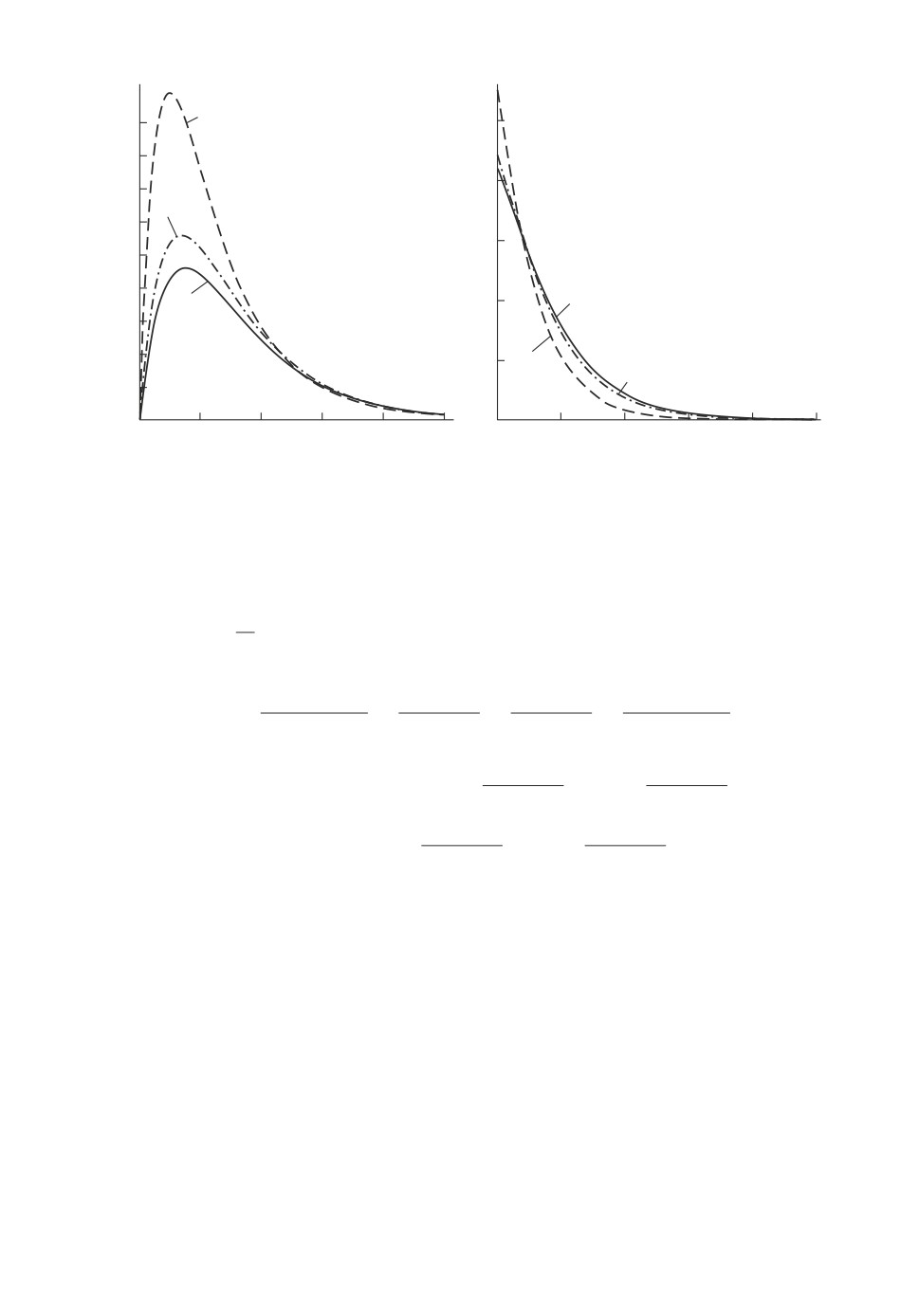
Рис. 2. Графики функций h3(1x), h3(2x).
В качестве примера, найдем P
S3 = s3) и функцию h3(x) для вектора сиг-
налов s3 = (1, 2, 1). Используя формулы (14)-(16), получаем
∫
∫
1
=P
S3 = s3) =
f3(1x)dx + f3(2x)dx =
c3
E1
E2
(17)
[
]
λ1p1
p1p2
p1p2 + 1
λ2
=λ2p2
+
+
-
,
1
(2λ1 + λ2)2
λ1 + 2λ2
2λ1 + λ2
(λ1 + 2λ2)2
[
]
λ1
λ2
c3 · λ2p21(1 - e-λ1x)e-λ2x p2 +
e-λ1x -
, x = 1x,
2λ1 + λ2
λ1 + 2λ2
h3(x) =
[
]
λ1
λ2
c3 · λ2p21e-(λ1+λ2)x p2 +
e-λ1x -
e-λ2x , x = 2x.
2λ1 + λ2
λ1 + 2λ2
Рассмотрим следующие наборы значений параметров λ1, λ2:
I. (λ2 = 0,025, λ2 = 0,05),
II. (λ2 = 0,05, λ2 = 0,05),
III. (λ2 = 0,025, λ2 = 0,0125).
Графики функций h3(1x), h3(2x) при значениях параметров I, II, III пред-
ставлены на рис. 2.
Введем следующие подмножества пространства состояний E:
E1 = {1x, x > 0}, E2 = {2x, x > 0}.
В табл. 2 приведены вероятности P
S3 = s3), P(X3 ∈E1|s3) и P(X3 ∈E2|s3)
при значениях параметров I, II, III для различных вариантов вектора сигна-
90
Таблица 2. Значения вероятностей P
S3 = s3), P(X3 ∈ E1|s3) и P(X3 ∈ E2|s3)
ss
s3 = (1, 1, 1)
s3 = (1, 2, 1)
s3 = (2, 1, 1)
s3 = (1, 1, 2)
λ1, λ2
0,04648
0,06463
0,09296
0,06463
λ1 = 0,025
0,48473
0,22445
0,48473
0,62559
λ2 = 0,05
0,51527
0,77555
0,51527
0,37441
0,13889
0,11111
0,13889
0,11111
λ1 = 0,05
0,65000
0,31250
0,65000
0,68750
λ2 = 0,05
0,35000
0,68750
0,35000
0,31250
0,31519
0,12926
0,15759
0,12926
λ1 = 0,025
0,88125
0,39557
0,88125
0,86052
λ2 = 0,0125
0,11875
0,60443
0,11875
0,13948
ss
s3 = (2, 2, 1)
s3 = (1, 2, 2)
s3 = (2, 1, 2)
s3 = (2, 2, 2)
λ1, λ2
λ1 = 0,025
0,12926
0,15759
0,12926
0,31519
λ2 = 0,05
0,22445
0,21347
0,62559
0,21347
0,77555
0,78653
0,37441
0,78653
λ1 = 0,05
0,11111
0,13889
0,11111
0,13889
λ2 = 0,05
0,31250
0,35000
0,68750
0,35000
0,68750
0,65000
0,31250
0,65000
λ1 = 0,025
0,06463
0,09296
0,06463
0,04648
λ2 = 0,0125
0,39557
0,67761
0,86052
0,67761
0,60443
0,32239
0,13948
0,32239
лов s3 = (s1, s2, s3). В ячейках табл. 2 эти вероятности расположены в том же
порядке сверху вниз.
II. Перейдем к нахождению условных вероятностей P (X4 ∈ B|s3),
P (S4 = s|s3).
Имеем, что
∫
P (X4 ∈ dx | s3) = P (X4 ∈ dx, X3 ∈ dy | s3) =
E
∫
= P(X3 ∈ dy | s3)P(X4 ∈ dx|X3 = y, s3) =
E ∫
= P(X3 ∈ dy | s3)P(X4 ∈ dx|X3 = y).
E
Таким образом,
∫
P (X4 ∈ dx | s3) = P (X3 ∈ dy | s3)P (X4 ∈ dx | X3 = y) =
E
(18)
∫
= P(X4 ∈ dx|X3 = y)H3(dy).
E
91
Таблица 3. Значения условных вероятностей
P (X4 ∈ E1|s3), P (X4 ∈ E2|s3)
P
P (X4 ∈ E1|s3) P (X4 ∈ E2|s3)
λ1, λ2
λ1 = 0,025
0,53895
0,46105
λ2 = 0,05
λ1 = 0,05
0,62500
0,37500
λ2 = 0,05
λ1 = 0,025
0,78677
0,21323
λ2 = 0,0125
Выражение для плотности p(X4 = x | s3) имеет вид:
∫
p(X4 = x | s3) = p(X3 = y | s3)p(X4 = x | X3 = y)dy =
E
(19)
∫
= p(X4 = x|X3 = y)h3(y)dy.
E
В качестве примера, найдем выражение для p(X4 = x | s3) в случае
s3 = (1,2,1):
p(X4 = x|s3) =
[ (
(
)
λ1e-λ1x
1
e-λ1x
c3λ2p1e-λ2x λ1
-
+
2λ1 + λ2
2λ1 + λ2
3λ1 + λ2
(
))
λ2p2
1
e-λ1x
+
-
+
λ1 + 2λ2
λ1 + λ2
2λ1 + λ2
((
)
)]
λ1
1
λ2
+λ2
+p2
-
,
2λ1 + λ2
λ1 + 2λ2
(λ1 + 2λ2)(λ1 + 3λ2)
x = 1x,
=
[ (
)
λ21
λ2p1p2
c3λ2p1e-λ1x λ1
+
+
(2λ1 + λ2)2(3λ1 + λ2)
(λ1 + 2λ2)(2λ1 + λ2)
((
)
)]
λ1
1
λ2e-λ2x
+λ2e-λ2x
+p2
-
,
2λ1 + λ2
λ1 + 2λ2
(λ1 + 2λ2)(λ1 + 3λ2)
x = 2x.
Значения условных вероятностей P (X4 ∈ E1|s3), P (X4 ∈ E2|s3) для век-
тора сигналов s3 = (1, 2, 1) при значениях параметров I, II, III приведены в
табл. 3.
92
Таблица 4. Значения условных вероятностей P (S4 = s | s3)
P
P (S4 = 1 | s3)
P (S4 = 2 | s3)
λ1, λ2
λ1 = 0,025
0,42159
0,57841
λ2 = 0,05
λ1 = 0,05
0,54167
0,45833
λ2 = 0,05
λ1 = 0,025
0,76997
0,23003
λ2 = 0,0125
Далее,
∫
P (S4 = s | s3) = P (S4 = s, X4 ∈ dx | s3) =
E
∫
= P(S4 = s|X4 = x, s3)P(X4 ∈ dx| s3) =
E
∫
∫
= P(S4 = s|X4 = x)P(X4 ∈ dx| s3) = R(s4 |x)P(X4 ∈ dx| s3).
E
E
Следовательно,
∫
(20)
P (S4 = s | s3) = p(X4x | s3)P (S4 = s | X4
= x)dx.
E
Условные вероятности P (S4 = s|s3) для вектора s3 = (1, 2, 1) при значени-
ях параметров I, II, III приведены в табл. 4.
III. Рассмотрим способы нахождения вероятности P
Sn = sn).
Вычисление вероятности P
Sn = sn) по формуле (15), основанное на ис-
пользовании функций Fn(B)(fn(x)), называется прямым подходом [12, 13].
Существует также обратный подход [12, 13] к вычислению вероятности
P
Sn = sn), основанный на использовании функций (обратные переменные)
Bk(x) [12, 13]:
(21)
Bk(x) = P(Sk+1 = sk+1, Sn = sn |Xk
=x), k = 1,n - 1, x ∈ E.
Найдем рекуррентное соотношение для функций Bk(x).
∫
Bk(x) = P(Sk+1 = sk+1,... ,Sn = sn,Xk+1 ∈ dy | Xk = x) =
E
∫
= P(Sk+1 = sk+1,...,Sn = sn |Xk = x,Xk+1 = y)P(Xk+1 ∈ dy |Xk = x) =
E
93
∫
=
P (Sk+1 = sk+1, . . . , Sn = sn | Xk+1 = y)P (Xk+1 ∈ dy | Xk = x) =
E∫
= P(Sk+1 = sk+1 |Xk+1 = y)P(Sk+2 = sk+2,... ,Sn = sn |Sk+1
=
E
= sk+1,Xk+1 = y)P(Xk+1 ∈ dy |Xk = x) =
∫
= R(sk+1 |y)P(Sk+2 = sk+2,... ,Sn = sn |Xk+1 = y)P(Xk+1 ∈ dy |Xk = x) =
E
∫
= R(sk+1 |y)Bk+1(y)P(Xk+1 ∈ dy |Xk = x) =
E
∫
= R(sk+1 |y)Bk+1(y)P(x,dy).
E
Следовательно,
∫
(22)
Bk(x) = Bk+1(y)R(sk+1
|y)P(x,dy), k = 1,n - 2.
E
Имеем, что
∫
Bn-1(x) = P(Sn = sn |Xn-1 = x) = P(Sn = sn,Xn ∈ dy |Xn-1 = x) =
E
∫
= P(Xn ∈ dy |Xn-1 = x)P(Sn = sn |Xn-1 = x,Xn = y) =
E
∫
∫
= P(Sn = sn |Xn = y)P(Xn ∈ dy |Xn-1 = x) = R(sn |y)P(x,dy).
E
E
Зная Bn-1(x), используя рекуррентное соотношение (22), можно последо-
вательно найти Bn-2(x), . . . , B1(x).
Выражения для функций B2(x), B1(x) для вектора сигналов s3 = (1, 2, 1)
имеют вид:
{ 1 - e-λ1x(p2 + λ1x), x = 1x,
B2(x) =
e-λ2x(p1 + λ2x),
x = 2x,
[
1
p2
λ1
λ2p1
-
-
+
λ1 + λ2
2λ1 + λ2
(2λ1 + λ2)2
]
B1(x) =
p1
λ2
p1
λ2
+
+
-
-
, x = 0,
λ1 + λ2
(λ1 + λ2)2
λ1 + 2λ2
(λ1 + 2λ2)2
0,
x = 1x,2x.
94
B2(1x)
B2(2x)
1,0
0,8
0,9
0,7
0,8
I
0,6
III
III
0,5
0,7
II
0,4
0,6
I
II
0,3
0,5
0,2
0,4
0,1
0,3
0
100
200
300
0
100
200
300
x
x
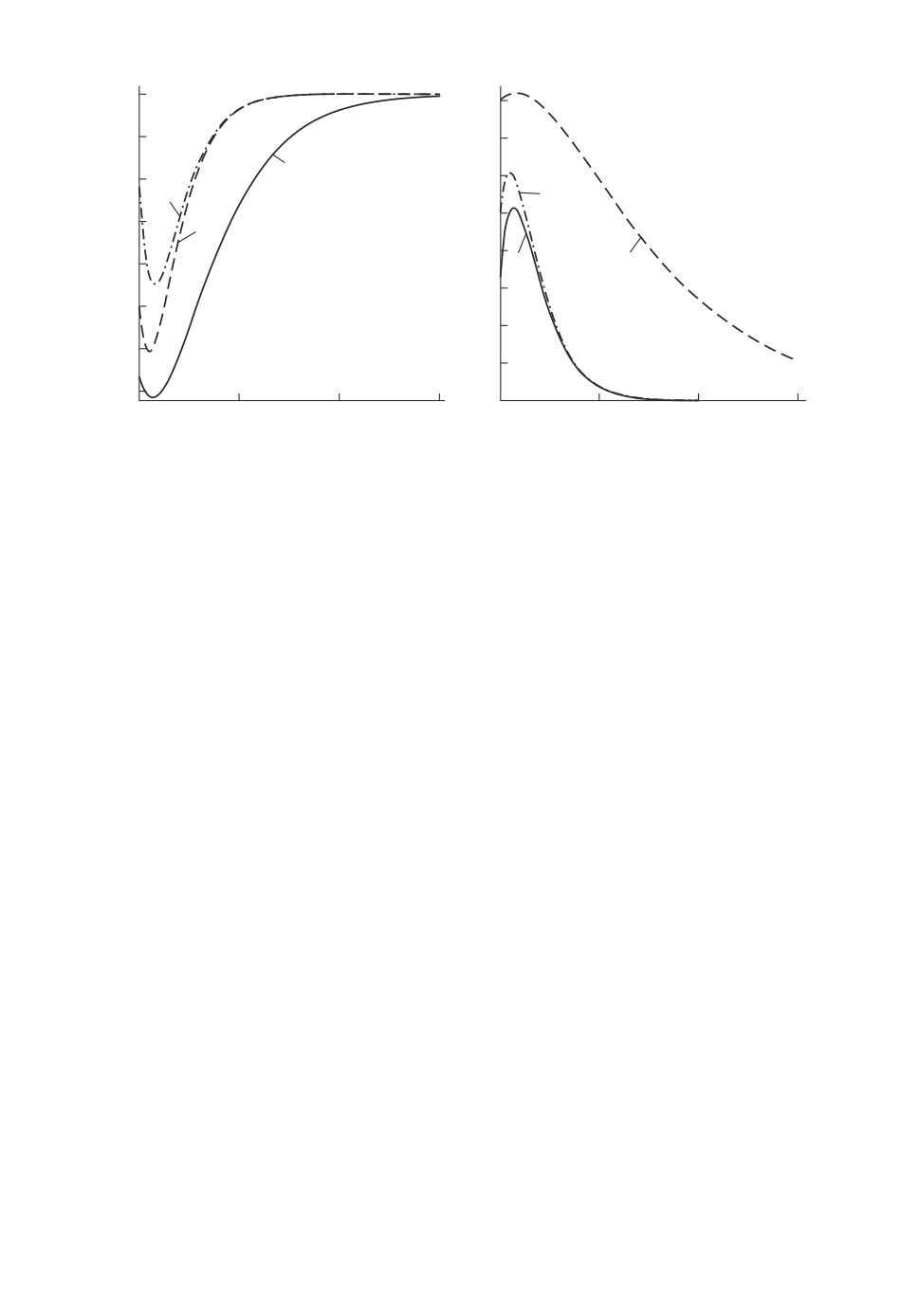
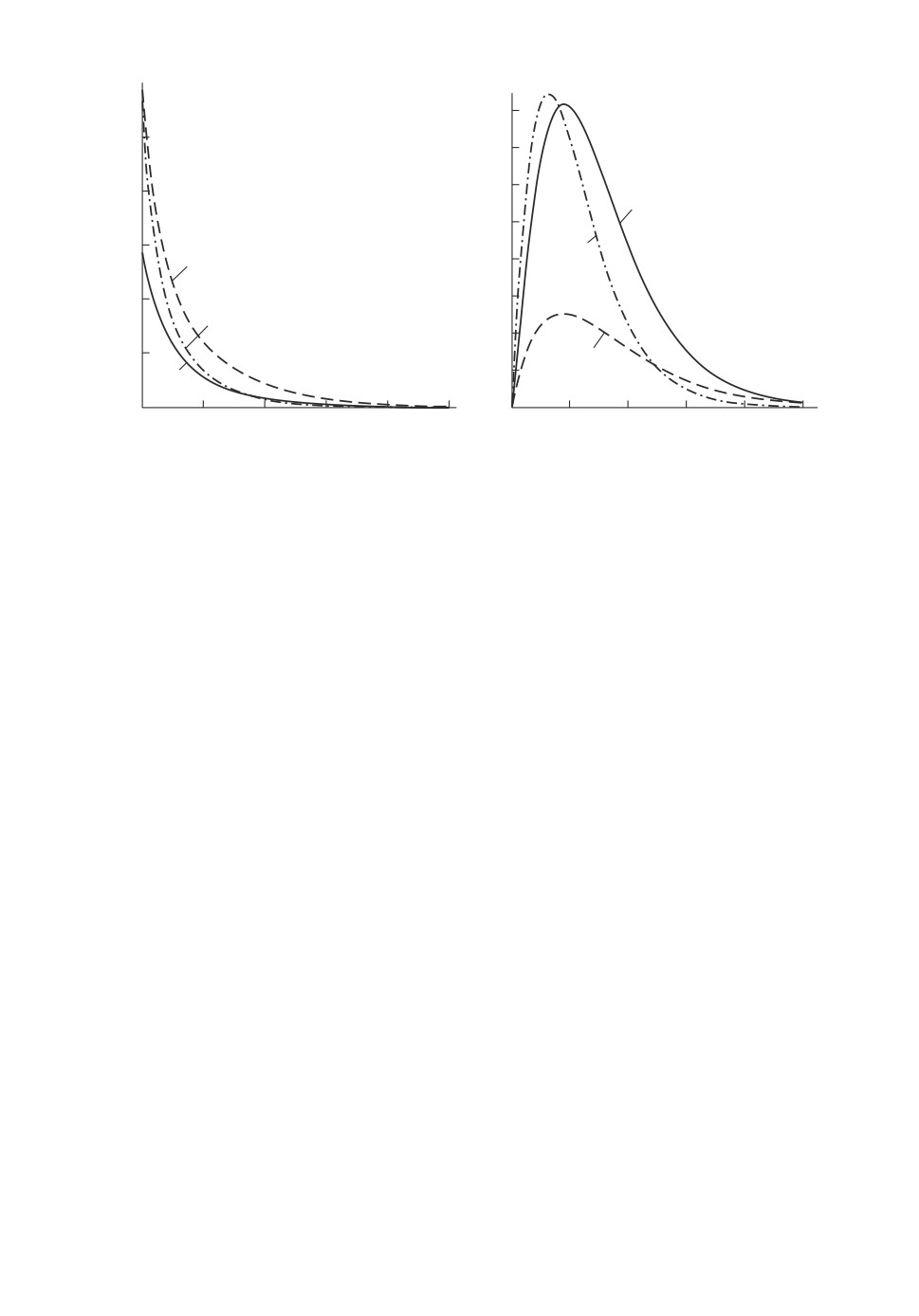
Рис. 3. Графики функций B2(1x), B2(2x).
Графики функций B2(1x), B2(2x) при значениях параметров I, II, III в
случае вектора сигналов s3 = (1, 2, 3) представлены на рис. 3.
Функция B1(x) позволяет найти вероятность P
Sn = sn).
∫
P
Sn = sn) = P(S1 = s1,... ,Sn = sn,X1 ∈ dx) =
E
∫
= P(X1 ∈ dx)P(S1 = s1,...,Sn = sn |X1 = x) =
E ∫
= P(S1 = s1,...,Sn = sn |X1 = x)π(dx) =
E
∫
= P(S1 = s1 |X1 = x)P(S2 = s2,...,Sn = sn |S1 = s1,X1 = x)π(dx) =
E
∫
= R(s1 |x)P(S2 = s2,... ,Sn = sn |X1 = x)π(dx) =
E
∫
= R(s1 |x)B1(x)π(dx).
E
Таким образом,
∫
(23)
P
Sn = sn) = R(s1 |x)B1
(x)π(dx).
E
Находя P
Sn = sn) по формуле (23) для вектора сигналов s3 = (1,2,1),
получаем выражение, совпадающее с (17).
95
q2(1x)
q2(2x)
0,016
0,05
0,014
0,012
0,04
I
0,010
0,03
II
III
0,008
0,02
0,006
III
0,004
0,01
II
0,002
I
0
20
40
60
80
100
0
20
40
60
80
100
x
x
Рис. 4. Графики функций q2(1x), q2(2x).
Еще один способ нахождения вероятности P
Sn = sn) состоит в комби-
нировании прямого и обратного подходов [5, 12, 13]. Предположим, что для
некоторого 1 ≤ k ≤ n - 1 можно найти обе функции Fk(B)(fk(x)) и Bk(x).
Тогда
P
Sn = sn,Xk ∈ dx) =
=P
Sk = sk,Xk ∈ dx)P(Sk+1 = sk+1,... ,Sn = sn
Sk = sk,Xk = x) =
=P
Sk = sk,Xk ∈ dx)P(Sk+1 = sk+1,... ,Sn = sn |Xk = x) = Fk(dx)Bk(x).
Следовательно,
∫
(24)
P
Sn = sn) = Bk(x)fk
(x)dx.
E
IV. Использование скрытой марковской модели позволяет на основе полу-
ченного вектора сигналов sn прогнозировать состояния цепи Маркова, кото-
рые ненаблюдаемы [12, 13].
Предположим, что получен вектор sn = (s1, s2, . . . , sn) первых n сигналов
и необходимо предсказать первые n состояний цепи Маркова, состояния ко-
торой ненаблюдаемы. Для этого, следуя [12, 13], при k ≤ n введем функции
(25)
Qk(B) = P(Xk ∈ B
Sn = sn),
B ∈ F,
или в дифференциальной форме
(26)
Qk(dx) = P(Xk ∈ dx
Sn = sn
),
x∈E.
96
Таблица 5. Значения вероятностей P (Xk = 0|s3), P (Xk ∈ E1|s3),
P (Xk ∈ E2|s3)
k
k=1
k=2
k=3
λ1, λ2
λ1 = 0,025
1
0
0
λ2 = 0,05
0
0,35817
0,22445
0
0,64183
0,77555
λ1 = 0,05
1
0
0
λ2 = 0,05
0
0,50000
0,31250
0
0,50000
0,68750
λ1 = 0,025
1
0
0
λ2 = 0,0125
0
0,64183
0,39557
0
0,35817
0,60443
Имеем, что
P
Sn = sn,Xk ∈ dx)
Fk(dx)Bk(x)
Qk(dx) = P(Xk ∈ dx
Sn = sn) =
=
∫
P
Sn = sn)
Bk(x)fk(x)dx
E
Следовательно, плотность qk(x) функции Qk(B) определяется формулой:
fk(x)Bk(x)
fk(x)Bk(x)
(27)
qk(x) =
=
∫
= cnfk(x)Bk
(x).
P
Sn = sn)
Bk(x)fk(x)dx
E
Графики функций q2(1x), q2(2x) для вектора сигналов s3 = (1, 2, 1) при
значениях параметров I, II, III представлены на рис. 4.
Знание функций qk(1x), qk(2x) позволяет найти прогноз состояний нена-
блюдаемой цепи Маркова на k-м шаге, в том числе и значений непрерывных
компонент, входящих в состав фазовых состояний системы.
В качестве примера, рассмотрим прогноз при k = 1, 2, 3 состояний ВЦМ
суперпозиции двух независимых процессов восстановления при значениях
параметров I, II, III в случае вектора s3 = (1, 2, 1). В табл. 5 при k = 1, 2, 3
приведены вероятности P (Xk = 0|s3), P (Xk ∈ E1|s3), P (Xk ∈ E2|s3), которые
расположены в ячейках табл. 5 сверху вниз.
V. Следуя публикации [17], найдем limn→∞ P (Sn = s|X1 = x).
Имеем, что
∫
P (Sn = s | X1 = x) = P (Sn = s, Xn ∈ dy | X1 = x) =
E
∫
= P(Xn ∈ dy |X1 = x)P(Sn = s|Xn = y,X1 = x) =
E
∫
∫
= P(Sn = s|Xn = y)P(Xn ∈ dy |X1 = x) = R(s|y)Pn(x,dy).
E
E
97
Таблица 6. Предельные вероятности lim
P (Sn = 1|X1
= x),
n→∞
lim
P (Sn = 2|X1 = x)
n→∞
lim
P (Sn = 1 | X1 = x) lim
P (Sn = 2 | X1 = x)
λ1, λ2
n→∞
n→∞
λ1 = 0,025
0,33333
0,66667
λ2 = 0,05
λ1 = 0,05
0,50000
0,50000
λ2 = 0,05
λ1 = 0,025
0,66667
0,33333
λ2 = 0,0125
Следовательно,
∫
∫
lim
P (Sn = s | X1 = x) = lim
R(s | y)Pn(x, dy) = R(s | y)ρ(dy),
n→∞
n→∞
E
E
где ρ(dy) - стационарное распределение ВЦМ {Xn, n = 1, 2, . . .}.
Таким образом,
∫
(28)
lim
P (Sn = s | X1 = x) =
R(s | y)ρ(dy), для любого x ∈ E.
n→∞
E
Найдем эти предельные вероятности для ВЦМ суперпозиции двух процес-
сов восстановления. Как отмечено выше, ВЦМ суперпозиции имеет стацио-
нарное распределение, определяемое формулой (2).
Применяя (2), (28) и табл. 1, получаем, что
∫
∫
lim
P (Sn = 1 | X1 = x) = R(1 | 1y)ρ(1dy) + R(1 | 2y)ρ(2dy) =
n→∞
E1
E2
∫
∞
∫
∞
= ρ0 G1(y) G2(y)dy +
G1(y)G2(y)dy =
0
0
∫∞
Mα2
=ρ0
G2(y)dy = ρ0Mα2 =
,
Mα1 + Mα2
0
∫
∫
lim
P (Sn = 2 | X1 = x) = R(2 | 1y)ρ(1dy) + R(2 | 2y)ρ(2dy) =
n→∞
E1
E2
Mα1
= ρ0Mα1 =
,
Mα1 + Mα2
а в случае экспоненциального распределения случайных величин α1 и α2 с
параметрами λ1 и λ2:
λ1
λ2
lim
P (Sn = 1|X1 = x) =
,
lim
P (Sn = 2|X1 = x) =
n→∞
λ1 + λ2
n→∞
λ1 + λ2
98
В табл. 6 приведены предельные вероятности для значений параметров I,
II, III.
Использование алгоритмов теории скрытых марковских моделей [5, 12, 13]
позволяет находить оценки и других характеристик ненаблюдаемой модели
и сигналов на основе полученного вектора сигналов.
4. Заключение
Большое число систем различного назначения допускает построение по-
лумарковской модели. При построении полумарковской модели приходится
строить достаточно сложное фазовое пространство состояний, отражающих
физические состояния системы и обеспечивающих корректность построения
полумарковской модели. Важной составной частью полумарковской модели
является вложенная цепь Маркова, отвечающая за переходы между состоя-
ниями системы. Фазовое пространство состояний полумарковской модели
совпадает с фазовым пространством состояний вложенной цепи Маркова.
В процессе функционирования системы, для которой построена полумар-
ковская модель, в ряде случаев при изменении состояний системы не удается
получить всю информацию, содержащуюся в кодах фазовых состояний по-
лумарковской модели, а удается получить только некоторую информацию
(сигнал), связанную с фазовыми состояниями. В этом случае фазовые со-
стояния вложенной цепи Маркова (полумарковской модели) можно считать
скрытыми, поэтому возникает задача оценки характеристик вложенной цепи
Маркова, полумарковской модели и сигналов на основе полученного вектора
сигналов. Решить эту задачу позволяют скрытые марковские модели.
В данной статье на примере суперпозиции двух независимых процессов
восстановления, построенной в работах В.С. Королюка и А.Ф. Турбина, рас-
сматривается подход к построению скрытой марковской модели на основе
полумарковского процесса с фазовым пространством состояний общего ви-
да. Обобщая на случай скрытой цепи Маркова с общим фазовым простран-
ством состояний результаты, известные для скрытых цепей Маркова с ко-
нечным множеством состояний, проводится оценка характеристик вложенной
цепи Маркова суперпозиции и сигналов на основе полученного вектора сиг-
налов. Для ВЦМ находятся условные вероятности состояний на 2 ≤ k ≤ n,
(n + 1)-м шагах на основе полученного вектора сигналов размера n. Для век-
тора сигналов получены условные вероятности значений вектора сигналов
на (n + 1)-м шаге, безусловные вероятности вектора сигналов и финальные
вероятности для значений вектора сигналов.
Рассматриваемый подход может быть использован для анализа функцио-
нирования систем различного назначения, допускающих построение полу-
марковской модели, в том числе и в случае конечного фазового пространства
состояний. При реализации рассматриваемого подхода можно применять ма-
тематические пакеты, используя при этом рекуррентные формулы.
Эффективным методом решения проблемы размерности моделей является
алгоритм стационарного фазового укрупнения полумарковских систем, раз-
работанный В.С. Королюком и А.Ф. Турбиным, который можно использо-
вать при построении скрытой марковской модели.
99
В дальнейшем предполагается использовать рассматриваемый подход для
анализа функционирования систем массового обслуживания, контроля, об-
служивания технических систем и анализа их надежности.
СПИСОК ЛИТЕРАТУРЫ
1.
Limnios N., Oprisan G. Semi-Markov Processes and Reliability. N.Y.: Springer Sci-
2.
Grabski F. Semi-Markov Processes: Applications in System Reliability and Mainte-
nance. Elsevier Science, 2014.
3.
Obzherin Yu.E., Boyko E.G. Semi-Markov Models: Control of Restorable Systems
with Latent Failures. London: Elsevier Academic Press, 2015.
4.
Jansen J., Limnios N. (Eds.) Semi-Markov Models and Applications. Netherlands:
5.
Kobayashi H., Mark B., Turin W. Probability, Random Processes, and Statisti-
cal Analysis: Applications to Communications. Signal Processing, Queueing The-
ory and Mathematical Finance. Cambridge: Cambridge University Press, 2011.
6.
Obzherin Y.E., Sidorov S.M., Nikitin M.M. Reliability of the information system
with intermediate storage devices // CCIS. 2018. V. 919. P. 432-444. http://doi-org-
443.webvpn.fjmu.edu.cn/10.1007/978-3-319-99447-5_37
7.
Limnios N., Nikulin M. Recent Advances in Reliability Theory: Methodology,
Practice, and Inference, еds. N. Limnios, M. Nikulin. New York: Springer Sci-
ence+Business Media, 2000.
8.
Руденко Ю.Н., Ушаков И.А. Надeжность систем энергетики, 2-е изд. Новоси-
бирск: Наука, 1989.
9.
Обжерин Ю.Е., Песчанский А.И. Об однолинейной системе обслуживания с
потерями и абсолютным приоритетом // АиТ. 1990. № 10. С. 107-115.
Obzherin Yu.E., Peschanskii A.I. On One-line Service System with Losses and Ab-
solute Priority // Autom. Remote Control. 1990. V. 51. No. 10. P. 1393-1400.
10.
Песчанский А.И. Стационарные характеристики ненадежной многоканальной
системы обслуживания с потерями и временным резервом // АиТ. 2019. № 4.
Peschansky A.I. Stationary Characteristics of an Unreliable Multi-Server Queueing
System with Losses and Time Redundancy // Autom. Remote Control. 2019. V. 80.
11.
Janssen J., Manca R. Semi-Markov Risk Models for Finance, Insurance and Relia-
bility. N.Y.: Springer Science & Business Media, 2007.
12.
Ross S.M. Introduction to Probability Models, Ninth Edition. USA: Elsevier Aca-
demic Press, 2006.
13.
Rabiner L.R. A Tutorial on Hidden Markov Models and Selected Applications
in Speech Recognition // Proc. IEEE
77.
1989. V. 189. No. 2. P. 257-286.
14.
Cappe’ O., Moulines E., Ryde’n T. Inference in Hidden Markov Models. N.Y.:
Springer Science+Business Media, 2005.
15.
Obzherin Y.E., Sidorov S.M., Nikitin M.M. Hidden Markov Model of Information
System with Component-Wise Storage Devices // Lecture Notes in Computer Science
(including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in
030-36614-8_27.
100
16. Yu S.-Z. Hidden Semi-Markov Models: Theory, Algorithms and Applications. Else-
vier Science, 2015.
17. Barbu V.S., Limnios N. Semi-Markov Chains and Hidden Semi-Markov Models to-
ward Applications: Their Use in Reliability and DNA Analysis. N.Y.: Springer, 2008.
18. Elliott R., Limnios N., Swishchuk A. Filtering hidden semi-Markov chains // Stat.
19. Van der Hoek J., Elliott R. Introduction to Hidden Semi-Markov Models. Cambridge:
Cambridge University Press, 2018.
20. Королюк В.С., Турбин А.Ф. Полумарковские процессы и их приложения. Киев:
Наук. думка, 1976.
21. Королюк В.С., Турбин А.Ф. Процессы марковского восстановления в задачах
надежности систем. Киев: Наук. думка, 1982.
22. Королюк В.С. Стохастические модели систем. Киев: Наук. думка, 1989.
23. Korolyuk V.S., Korolyuk V.V. Stochastic Models of Systems. Dordrecht: Springer
Science+Business Media, 1999.
24. Korolyuk V.S., Limnios N. Stochastic Systems in Merging Phase Space. World Sci-
entific, Imperial Coledge Press, 2005.
25. Корлат А.Н., Кузнецов В.Н., Новиков М.М., Турбин А.Ф. Полумарковские мо-
дели восстанавливаемых систем и систем массового обслуживания. Кишинев:
Штиица, 1991.
26. Obzherin Yu.E., Sidorov S.M. Semi-Markov Model and Phase-Merging Scheme of a
Multi-Component System with the Group Instantly Replenished Time Reserve //
Int. J. of Reliability, Quality and Safety Engineering, 2019. V. 26. No. 3. Art.
Статья представлена к публикации членом редколлегии А.В. Назиным.
Поступила в редакцию 20.06.2019
После доработки 13.01.2021
Принята к публикации 15.01.2021
101