Автоматика и телемеханика, № 6, 2021

Робастное, адаптивное и сетевое

управление

(Институт проблем управления им. В.А. Трапезникова РАН, Москва)

ОПТИМИЗАЦИЯ РАЗМЕЩЕНИЯ ПОЛЮСОВ

В ОДНОМЕРНОЙ СИСТЕМЕ УПРАВЛЕНИЯ

Рассматривается задача синтеза регулятора для линейного стационар-

ного объекта управления. Находится линейный регулятор, минимизи-

рующий некоторый критерий качества системы, например соотношение

выхода объекта и внешнего возмущения как H_∞ норму соответствую-

щей функции, при условии соблюдения требований к качеству системы:

радиус запасов устойчивости, соотношение сигнала управления и поме-

хи измерения выхода объекта, коэффициент демпфирования, быстро-

действие. Рассмотрены известные методы синтеза регулятора из пакета

MATLAB Robust Control Toolbox для решения такой задачи. Предложен

метод синтеза регулятора, использующий корни характеристического по-

линома замкнутой системы в качестве варьируемых переменных стан-

дартной процедуры оптимизации и стандартную процедуру размещения

полюсов для получения значений коэффициентов регулятора.

Ключевые слова: линейная система управления, робастная система, син-

тез регулятора, радиус запасов устойчивости, размещение полюсов,

H_∞ оптимизация, глобальная оптимизация.

DOI: 10.31857/S0005231021060040

1. Введение

Существует много методов синтеза регулятора для линейного стационар-

ного объекта управления [1-4]. Методы, разработанные для многомерных си-

стем, применимы и для рассматриваемых объектов с одним управляющим

входом и одним управляемым выходом. Одним из универсальных подходов

к синтезу регулятора с учетом нескольких целей и ограничений стал метод

H_∞ оптимизации [5, 6]. Так, например, классическое требование к запасам

устойчивости в этом методе выражается как ограничение или минимизация

H_∞ нормы функции чувствительности. Важно, что метод позволяет опти-

мизировать систему одновременно еще по нескольким H_∞ нормам функций:

чувствительности к помехе измерений, передаточной функции замкнутой си-

стемы относительно возмущения и другим [3, 5], а также учитывать допусти-

мую область полюсов замкнутой системы [6]. При этом регулятор, получае-

мый стандартным методом H_∞ оптимизации, который базируется на решении

системы линейных матричных неравенств, сформированных из обобщенной

102

оптимизируемой системы, имеет порядок больший или равный порядку моде-

ли объекта управления. Развитием метода H_∞ оптимизации, направленным

на простоту практического использования, стал подход к синтезу регулятора

с заданной структурой [7-9], где коэффициенты регулятора находятся как ре-

шение задачи негладкой оптимизации. При этом можно находить регулятор

заданного низкого порядка. Следует учитывать, что результат минимизации

целевой функции при выборе структуры регулятора низкого порядка будет

заведомо не лучше, чем при поиске регулятора стандартным методом H_∞ оп-

тимизации без ограничений структуры. И, кроме того, для некоторых объек-

тов может не существовать регулятора с порядком меньше порядка объекта

более чем на единицу, обеспечивающего хотя бы устойчивость системы.

Практическая задача поиска регулятора с заданной структурой делает

актуальным развитие и других подходов, таких как метод D-разбиения [10].

В публикации [11] решается задача построения регулятора методом D-раз-

биения с учетом ряда инженерных требований.

Необходимо заметить, что в большинстве методов используются некото-

рые весовые матрицы, весовые передаточные функции или другие парамет-

ры, характеризующие качество системы, выбор которых обычно не форма-

лизован и дает свободу проектировщику системы. Но если процедура син-

теза регулятора работает в системе самонастройки, когда модель объекта

получена в результате процедуры идентификации, и участие проектировщи-

ка не предусмотрено, то важно формулировать критерии синтеза так, чтобы

они позволяли получить практически работоспособную систему, удовлетво-

ряющую реальным требованиям к качеству. Так, в [12-15] решается задача

синтеза регулятора по инженерным критериям качества с использованием

метода H_∞ оптимизации. В [16, 17] для решения задачи синтеза регулято-

ра, удовлетворяющего требованиям к точности, быстродействию и радиусу

запасов устойчивости, применяется метод размещения полюсов и предложен

способ формирования желаемого характеристического полинома замкнутой

системы в соответствии с этими требованиями.

В настоящей статье рассматривается задача подавления внешних возму-

щений, т.е. минимизации H_∞ нормы функции чувствительности системы к

возмущению, при соблюдении ряда ограничений, обусловливающих робаст-

ность системы и качество переходных процессов. Предлагается новый подход

к решению этой задачи методом размещения полюсов, где желаемый харак-

теристический полином ищется с помощью процедуры глобальной оптими-

зации. При этом корни характеристического полинома замкнутой системы,

а не коэффициенты регулятора, являются варьируемыми переменными. Ме-

тод размещения полюсов позволяет найти регулятор, порядок которого на

единицу меньше порядка модели объекта. Возможно построение регулятора

более высокого порядка, но найти регулятор низкого порядка по сравнению с

порядком модели объекта этот метод не позволяет. В случае заданной струк-

туры регулятора можно редуцировать модель объекта до соответствующего

порядка.

Кроме того, для сравнения рассматриваются реализации решения постав-

ленной задачи с использованием стандартных процедур синтеза регулято-

103

ра методами H_∞ оптимизации из пакета MATLAB Robust Control Toolbox:

hinfsyn, h2hinfsyn и systune.

2. Постановка задачи

Рассмотрим управляемый объект со скалярными входами и выходом, опи-

сываемый линейным дифференциальным уравнением

(1)

y⁽ⁿ⁾ + a_n-1y^(n-1) + ... + a₁ y + a₀

=b_n-1u^(n-1) + ... + b₁ u + b₀u + g_n-1f^(n-1) + ... + g₁f˙ + g₀f,

где правый верхний индекс обозначает порядок производной по непрерыв-

ному времени t, y(t) ∈ R

управляемый и измеряемый выход объекта,

u(t) ∈ R вход управления, f(t) ∈ R неизмеряемое неизвестное возмуще-

ние, ограниченное по модулю, n ∈ N известный порядок объекта, a_i, b_i, g_i

(i = 0, . . . , n - 1) известные вещественные коэффициенты. Предполагается,

что все функции удовлетворяют условиям применения преобразования Ла-

пласа и начальные условия равны нулю. Тогда вместо уравнения (1) будем

использовать передаточные функции относительно управления и возмуще-

ния соответственно

b (s)

b_n-1s^n-1 + ... + b₀

(2)

P (s) =

a(s)

sⁿ + a_n-1s^n-1 + ... + a₀

g (s)

g_n-1s^n-1 + ... + g₀

(3)

P_f (s) =

a (s)

sⁿ + a_n-1s^n-1 + ... + a₀

где s - переменная преобразования Лапласа. Принимая s = jω, где частота

ω ∈ [0,∞), будем использовать частотные передаточные функции.

Некоторые коэффициенты a_i, b_i, g_i (i = 0, . . . , n - 1) могут быть равны ну-

лю, поэтому степени полиномов b (s) и g (s) могут быть меньше n - 1. Возмо-

жен случай, когда считается, что возмущение приложено вместе с управле-

нием, и тогда g (s) = b(s).

Рассмотрим систему, где объект управления (1) замкнут линейным регу-

лятором с передаточной функцией

d(s)

d_ms^m + d_m-1s^m-1 + ... + d₀

(4)

C (s) =

c(s)

c_ms^m + c_m-1s^m-1 + ... + c₀

где m - порядок регулятора, d_i, c_i (i = 0, . . . , m) - вещественные коэффици-

енты регулятора. Известно, что для любого управляемого объекта (1) суще-

ствует стабилизирующий регулятор степени m = n - 1, в то время как для

m < n - 1 такого регулятора может не существовать. Поэтому будем прини-

мать m ≥ n - 1 в зависимости от метода синтеза регулятора. Задача нахож-

дения регулятора порядка m < n - 1 в этой статье не рассматривается.

Структура системы управления представлена на рис. 1. Задача слежения

в этой статье не рассматривается, поэтому задающее воздействие r, присут-

ствующее на рис. 1, будем считать равным нулю. Кроме того, в структуру

104

Регулятор

Объект

Рис. 1. Структура системы управления.

добавлена помеха измерения ν, свойства которой не оговариваются, так как

действие помехи измерения в статье не рассматривается, но передаточная

функция относительно этого входа будет использоваться. При этом измеряе-

мый выход объекта y принимается равным сумме значений реального выхода

объекта η и помехи измерения ν.

Задача состоит в том, чтобы найти регулятор (4), обеспечивающий устой-

чивость и некоторое желаемое качество системы (2), (3), (4). Известно, что

система устойчива тогда и только тогда, когда отрицательны вещественные

части всех корней характеристического полинома замкнутой системы:

(5)

a(s)c(s) + b(s) d(s) .

Необходимо заметить, что уравнение (1) обычно является не абсолютно

точной моделью реального объекта управления, а упрощенной линеаризован-

ной моделью, причем коэффициенты определены неточно или могут менять-

ся со временем, т.е. реальная динамика объекта может быть нелинейная и

нестационарная. Поэтому при использовании модели (1) для синтеза регуля-

тора требование устойчивости системы необходимо сопровождать требовани-

ем робастности системы, т.е. сохранения устойчивости при отличии реальной

динамики объекта от исходной линейной модели. Один из критериев робаст-

ности это запасы устойчивости. Широко используемые запасы по фазе и по

амплитуде служат индикаторами удаленности амплитудно-фазовой частот-

ной характеристики (АФЧХ) разомкнутой системы P (jω) C(jω) от крити-

ческой точки (-1, j0) в соответствии с критерием устойчивости Найквиста.

Но так как эти запасы учитывают значения АФЧХ только на двух частотах,

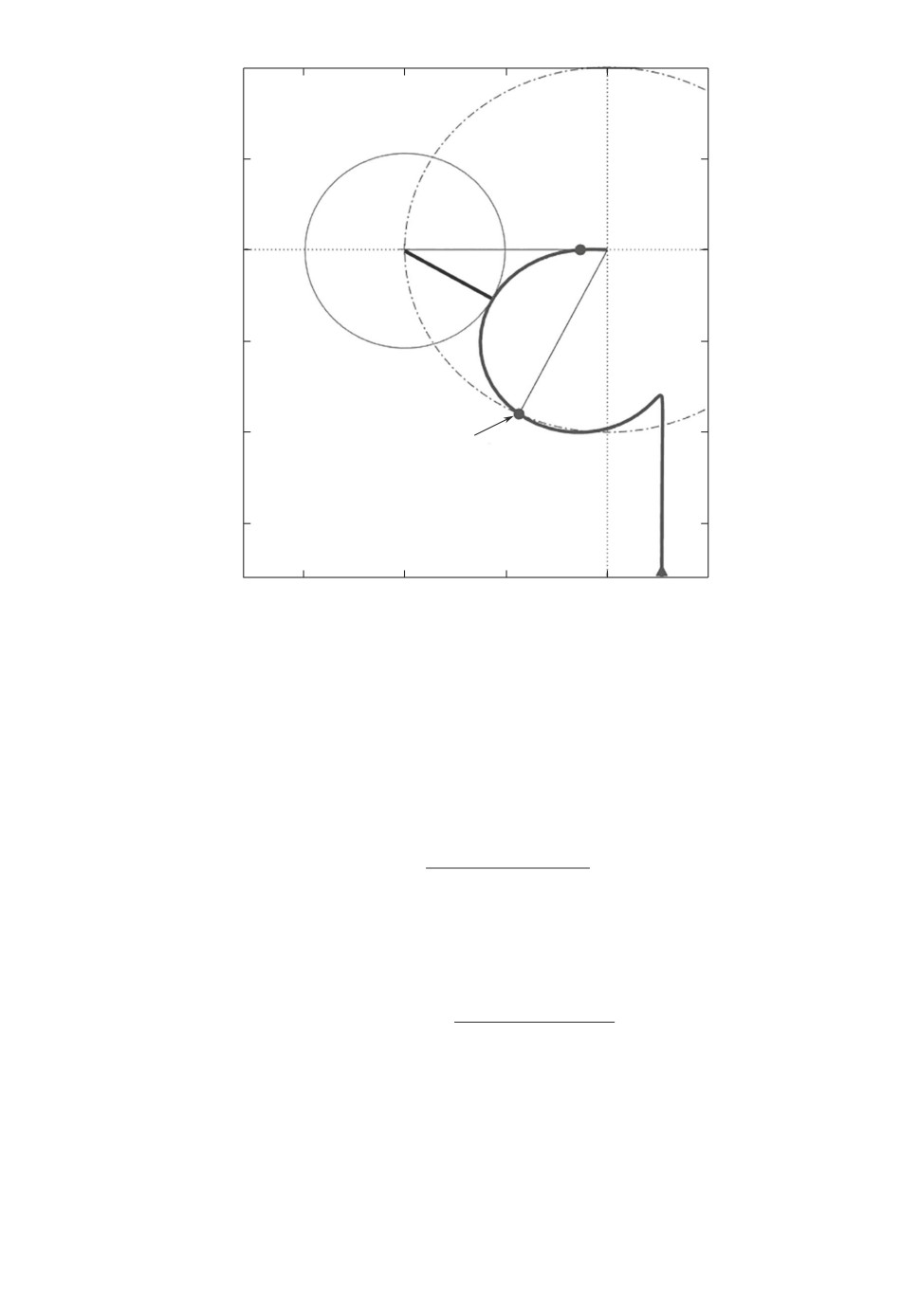
то вместо них все чаще используется значение радиуса запасов устойчивости

[2, 18, 19], который равен минимальному расстоянию АФЧХ разомкнутой си-

стемы от точки (-1, j0) для всех частот, т.е. минимальному значению модуля

функции возвратной разности:

(6)

R = inf

|1 + P (jω) C(jω)|

или обратному значению H_∞ нормы функции чувствительности S (jω) [2, 19]:

S (jω) =

1 + P (jω)C(jω)

(7)

∥S(jω)∥_∞

105

1,0

0,5

-1

-0,5

-1,0

Запас по фазе: 64,1 град

-1,5

-1,0

-0,5

0,5

Рис. 2. Годограф Найквиста разомкнутой системы и радиус запасов устойчивости.

Известно, что радиус запасов устойчивости не является достаточным кри-

терием робастности системы [19, 20]. В [2] отмечено, что для модели объекта,

представляющей сумму P (s) + Δ(s) исходной и неизвестной дополнительной

динамики, и для регулятора, обеспечивающего устойчивость исходной систе-

мы, система с дополнительной динамикой будет устойчива, если соблюдается

ограничение



1+P(jω)C(jω)

(8)

|Δ (jω)| <



.

C (jω)

В правой части неравенства (8) записан модуль функции, обратной к функ-

ции чувствительности к помехе, связывающей помеху измерения, добавлен-

ную к выходу объекта, и сигнал управления

C (jω)

(9)

C (jω) S (jω) =

1 + P (jω)C(jω)

т.е. значение ∥C (jω) S(jω)∥_∞ = sup_ω |C (jω) S(jω)| также является критери-

ем робастности системы, и чем оно меньше, тем большее значение |Δ (jω)| не

нарушит устойчивость системы. Кроме того, ограничение значения сигнала

управления, возникающего при наличии помехи измерения и описываемо-

го функцией чувствительности к помехе (9), необходимо для практической

реализации системы, чтобы помехи не приводили к скачкам управления до

предельных значений.

106

Таким образом, максимально допустимые значения

∥S(jω)∥_∞ и

∥C (jω) S(jω)∥_∞ должны задаваться при синтезе регулятора как строгие

ограничения, которые не должны превышаться. Значение радиуса запасов

устойчивости находится в диапазоне 0 < R ≤ 1, и требуемое значение R^∗

обычно выбирается от 0,5 до 0,7, что соответствует максимальному значе-

нию H_∞ нормы функции чувствительности в диапазоне 1,43 ≤ ∥S(jω)∥_∞ ≤ 2.

Необходимо учитывать, что, например, для неминимально-фазовых объек-

тов может существовать максимально возможное значение радиуса запасов

устойчивости меньше единицы, и тогда требуемое значение R^∗ должно

выбираться в пределах достижимого. Выбор требуемого значения N^∗

H_∞ нормы функции чувствительности к помехе ∥C (jω) S(jω)∥_∞ сложнее,

так как зависит от соотношения масштабов измеряемого выхода и сигнала

управления, а также их предельных значений и уровня помех.

Еще одно практическое ограничение коэффициент демпфирования, ко-

торый определяется соотношением вещественной и мнимой частей корней ха-

рактеристического полинома замкнутой системы. Его значение может быть

0 < ζ ≤ 1. Малая величина коэффициента демпфирования приводит к коле-

бательному характеру переходных процессов. Поэтому стандартное требова-

ние при синтезе регулятора это обеспечение коэффициента демпфирования

в пределах 0,7 ≤ ζ ≤ 1. Кроме того, желательно ограничивать и близость к

нулю вещественных частей корней характеристического полинома, так как их

слишком малое по модулю значение может приводить к недопустимо боль-

шому времени переходных процессов.

В рамках этих, а возможно, и других ограничений можно оптимизировать

остальные показатели качества. Одним из наиболее важных показателей ка-

чества системы управления является подавление внешних возмущений [21].

Передаточная функция замкнутой системы (2), (3), (4) относительно возму-

щения имеет вид

g (s) c (s)

(10)

Gyf (s) =

a(s)c(s) + b(s)d(s)

и минимизация H_∞ нормы этой функции

∥G_yf (jω)∥_∞ = sup |G_yf (jω)|

часто используется как цель оптимизации системы при синтезе регулято-

ра. Заметим, что если возмущение приложено вместе с управлением, т.е.

g (s) = b(s), то

P (jω)

(11)

Gyf (jω) =

= P (jω)S(jω),

1 + P (jω)C(jω)

что представляет собой функцию чувствительности к возмущению [2].

Итак, задачу синтеза регулятора можно сформулировать так.

Задача. Найти стабилизирующий регулятор (4) такой, что в системе

(2), (3), (4):

107

1) радиус запасов устойчивости (6) не меньше требуемого значения R^∗;

2) H_∞ норма функции чувствительности к помехе (9) не больше тре-

буемого значения N^∗;

3) коэффициент демпфирования не меньше требуемого значения ζ_min > 0;

4) вещественные части корней характеристического полинома не пре-

вышают требуемого значения (-β^∗) < 0;

5) H_∞ норма функции чувствительности к возмущению (10) будет ми-

нимальна при соблюдении перечисленных выше условий.

Следует внимательно подходить к выбору значений ограничений, так как

может не существовать удовлетворяющего им решения. В этом случае огра-

ничения должны быть пересмотрены.

3. Стандартные методы синтеза робастных регуляторов

3.1. H_∞ оптимальный регулятор

Стандартная процедура синтеза H_∞ оптимального регулятора (функция

hinfsyn из пакета MATLAB Robust Control Toolbox) не решает поставленную

в настоящей статье задачу полностью, так как в ней не предусмотрено вве-

дение ограничений на корни характеристического полинома. В процедурах,

рассмотренных далее, такая возможность есть, но для сравнения рассмотрим

и эту базовую процедуру, решая задачу без ограничений коэффициента демп-

фирования и близости к нулю вещественных частей корней характеристиче-

ского полинома. Для процедуры синтеза регулятора нужно сформировать

обобщенный объект управления [3]:

x (t) = Ax (t) + B₁w (t) + B₂u (t) ,

(12)

z (t) = C₁x (t) + D₁₁w (t) + D₁₂u (t) ,

y(t) = C₂x(t) + D₂₁w(t) + D₂₂u(t),

где x(t)

вектор состояния размерности n, w(t) и z(t) векторы входов

и выходов обобщенной системы, y(t) и u(t)

выход и вход объекта (1),

A, B₁, B₂, C₁, C₂, D₁₁, D₁₂, D₂₁, D₂₂ матрицы и векторы коэффици-

ентов соответствующих размерностей. Векторы входов и выходов обобщен-

ной системы выбираются так, чтобы минимизация H_∞ нормы передаточной

матрицы замкнутой системы, связывающей эти входы и выходы, решала по-

ставленную задачу. Кроме того, можно находить субоптимальное решение,

когда ищется регулятор, обеспечивающий значение H_∞ нормы передаточ-

ной матрицы замкнутой системы меньше заданного значения γ. В опциях

процедуры можно выбирать метод решения: 2-Риккати формула или метод

линейных матричных неравенств.

В [2] предлагается принять векторы выходов и входов обобщенной системы

как

[

]

[

]

(13)

-u

108

Тогда процедура будет минимизировать или ограничивать H_∞ норму систе-

мы

[

]

(14)

CG_yf CS

При этом в поставленной задаче нет требований к ∥CG_yf ∥_∞, которая появи-

лась в этой матрице, поэтому нужно будет проверять, что этот элемент не

повлиял на полученное решение. Вторая проблема состоит в том, что проце-

дура H_∞ оптимизации находит решение, которое обеспечивает значение всех

составляющих передаточной матрицы меньше заданного значения γ. Для

учета разных требований к передаточным функциям, связывающим разные

входы и выходы, можно использовать [2, 3] весовые передаточные функции.

Для решения поставленной Задачи будем использовать просто весовые коэф-

фициенты W₁ и W₂, тогда формируя векторы выходов и входов обобщенной

системы как

[

]

[

]

f /W₁

(15)

-W₂u

получим

[

]

1Gyf

(16)

W₁W₂CG_yf W₂CS

Принимая

(17)

γ=

W₂ =

R^∗

N^∗

и находя максимальное значение W₁, для которого существует решение про-

цедуры синтеза H_∞ оптимального регулятора, можно найти регулятор, обес-

печивающий минимальное значение ∥CG_yf ∥_∞ для заданных ограничений

∥S∥_∞ и ∥CS∥_∞. Если в результате получится неприемлемое значение ∥G_yf ∥_∞,

то необходимо пересмотреть требуемые значения R^∗ и N^∗, т.е. изменить це-

левое значение γ и весового коэффициента W₂. Надо также учитывать, что

если значения ∥S∥_∞, ∥W₁G_yf ∥_∞ и ∥W₂CS∥_∞ получились заметно меньше γ,

а ∥W₁W₂CG_yf ∥_∞ близка к заданному γ, то можно повторить процедуру, за-

давая большее значение γ, так как значение ∥W₁W₂CG_yf ∥_∞ в поставленной

задаче не ограничено.

3.2. H_∞ оптимальный регулятор с ограничением области

размещения полюсов

Функция h2hinfsyn из пакета MATLAB Robust Control Toolbox отлича-

ется от hinfsyn, во-первых, тем, что можно задавать допустимую область

размещения полюсов передаточной функции замкнутой системы [6]. Второе

отличие состоит в том, что можно определять два вектора выходов обобщен-

ной системы z_∞ и z₂. При этом формируются разные передаточные матрицы

109

замкнутой системы, для одной из которых минимизируется или ограничи-

вается H_∞ норма, а для другой H₂ норма, что повышает гибкость фор-

мирования целей и ограничений синтеза регулятора. Решение основано на

методе линейных матричных неравенств. Так как задача сформулирована

как требования к H_∞ нормам, то в этой статье не рассматривается возмож-

ность использования комбинированного H₂/H_∞ подхода и формирование

обобщенной системы может быть таким же, как описано в подразделе 3.1.

Возможность задавать область допустимого размещения полюсов позво-

ляет решать задачу со всеми ограничениями. Ограничения на область раз-

мещения полюсов формируются как линейное матричное неравенство вида

L + zQ + zQ^T < 0, где матрицы L и Q можно определить с помощью функ-

ции lmireg, которая позволяет задавать полуплоскость, круг, сектор, эллипс,

параболу, полосу и их пересечения. Для поставленной задачи нужно вместо

значения коэффициента демпфирования задавать внутренний угол θ^∗ секто-

ра. Значение θ^∗ = π/2 соответствует значению ζ_min = 0,707. Задавая значе-

ние (-β^∗) как границу левой полуплоскости и формируя пересечение этой

полуплоскости и сектора с углом θ^∗, получим область размещения полюсов,

соответствующую поставленной задаче.

Таким образом, функция h2hinfsyn предназначена для решения постав-

ленной и аналогичных задач. Следует помнить, что так же, как и в слу-

чае применения функции hinfsyn, рассмотренной выше, значение γ нужно

подбирать с учетом возможного влияния на полученный результат значе-

ния ∥W₁W₂CG_yf ∥_∞. Кроме того, нужно учитывать, что ищется регулятор с

порядком, равным порядку объекта. Полученный регулятор в пространстве

состояний можно преобразовать к виду (4) с m = n. На примере в разделе 5

будет показано, что поиск регулятора с m = n может не приводить к опти-

мальному решению, хотя, возможно, это проблемы конкретной программной

реализации алгоритма.

3.3. Синтез регулятора с фиксированной структурой

При задании структуры регулятора как передаточной функции вида (4) с

заданным порядком m или как, например, ПИД регулятора уже невозможно

свести задачу к решению системы линейных матричных неравенств, поэтому

в [7] предлагается искать коэффициенты регулятора заданной структуры как

решение задачи негладкой оптимизации. На основе этого подхода построены

процедуры hinfstruct, looptune [8] и systune [9] из пакета MATLAB Robust

Control Toolbox.

Рассмотрим функцию systune как наиболее универсальную. Для ее ис-

пользования не нужно формировать обобщенную матрицу передаточных

функций, норма которой должна минимизироваться, а критерии оптими-

зации можно формировать независимо друг от друга из широкого списка

целей (TuningGoal). Важно, что эти критерии можно разделить на две груп-

пы: минимизируемые цели оптимизации (Soft goals) и требуемые ограничения

(Hard goals). Для решения задачи можно использовать TuningGoal.Gain, где

вычисляется H_∞ норма передаточной функции от указанного входа к ука-

занному выходу, чтобы сформировать ∥G_yf ∥_∞, ∥S∥_∞ и ∥CS∥_∞, определив

110

H_∞ норму функции чувствительности к возмущению ∥G_yf ∥_∞ как миними-

зируемую цель, а H_∞ нормы функций чувствительности ∥S∥_∞ и чувстви-

тельности к помехе ∥CS∥_∞ как ограничения, а также добавить ограниче-

ния на корни характеристического полинома замкнутой системы, используя

TuningGoal.Poles.

Кроме того, в systune реализованы в качестве целей оптимизации ограни-

чения во временной области. Так, в TuningGoal.StepRejection можно задавать

требуемое время переходного процесса и использовать этот критерий как цель

оптимизации вместо ∥G_yf ∥_∞ или добавить его к требуемым ограничениям.

Следует отметить, что в методах, описанных в подразделах 3.1 и 3.2, по-

рядок регулятора m не задается и обычно находится регулятор с m = n,

причем если используются весовые передаточные функции, то порядок ре-

гулятора увеличивается в соответствии с их порядком. В функции systune

структура регулятора должна быть задана, и если ищется регулятор

вида (4), то для задания его структуры можно использовать команду

tunableTF(’Controller’, m, m), выбирая m = n - 1. В systune можно уста-

навливать и m < n - 1, но тогда нужно помнить, что стабилизирующего ре-

гулятора может не существовать, а если существует, то он оптимален только

в классе регуляторов выбранной структуры. Необходимо помнить, что про-

цедура основана на локальной оптимизации. Поэтому для получения лучше-

го решения, особенно в случае, когда не найдено решение, удовлетворяющее

заданным ограничениям, нужно при помощи команды systuneOptions уста-

новить значение параметра RandomStart больше единицы. Тогда процедура

оптимизации выполнится указанное число раз для различных случайных на-

боров начальных значений варьируемых коэффициентов регулятора.

Таким образом, возможности функции синтеза регулятора с фиксирован-

ной структурой systune полностью соответствуют поставленной задаче и поз-

воляют формулировать и решать широкий круг аналогичных задач, выбирая

различные ограничения и цели оптимизации в соответствии с требованиями

конкретной системы управления.

4. Оптимизация размещения полюсов замкнутой системы

Здесь предлагается новый подход к решению поставленной задачи, осно-

ванный на поиске при помощи процедуры оптимизации желаемых значений

полюсов замкнутой системы, обеспечивающих выполнение целей и ограни-

чений оптимизации, а не непосредственно коэффициентов регулятора, как в

подразделе 3.3.

Процедура размещения полюсов [22-24] основана на том, что для любо-

го заданного полинома δ(s) и известных полиномов a(s) и b(s) существует

единственное решение c(s) и d(s) уравнения

(18)

a(s)c(s) + b(s)d(s) = δ(s)

при условии deg(d(s)) < deg(a(s)) или deg(c(s)) < deg(b(s)). Кроме того,

решение будет удовлетворять условию причинности управления [22], т.е.

111

deg(d(s)) ≤ deg(c(s)) будет выполняться, если deg(δ(s)) ≥ 2deg(a(s)) - 1. Та-

ким образом, регулятор вида (4), принимая m = n - 1, можно получить как

решение уравнения (18), задавая желаемый характеристический полином

замкнутой системы δ(s) степени 2n - 1. При таких условиях можно, при-

равнивая коэффициенты при одинаковых степенях s левой и правой частей

уравнения (18), получить систему 2n линейных алгебраических уравнений

с 2n неизвестными и найти значения коэффициентов регулятора как ее ре-

шение:





c_n-1













δ_2n-1



c₀



(19)



=M^-1

···

,



d_n-1







δ₀

···

d₀

где квадратная матрица M размера 2n сформирована из левой части уравне-

ния (18), используя известные значения коэффициентов a_i, b_i(i = 0, . . . , n-1).

Таким образом, задавая полином δ (s) такой, что вещественные части всех

его корней отрицательны, получим стабилизирующий регулятор. При этом

остается проблема сформировать желаемый полином δ (s) так, чтобы решить

поставленную задачу. В [16, 17] решается похожая задача, но не рассматрива-

ется функция чувствительности к помехе и не утверждается оптимальность

подавления возмущения при заданном ограничении минимального радиуса

запасов устойчивости. В [25] для дискретной системы получены формулы

для выбора корней желаемого характеристического полинома, обеспечиваю-

щие заданный радиус запасов устойчивости и заданный уровень подавления

возмущения, но результаты получены только для объектов с вещественными

полюсами и носят достаточный характер.

В настоящей статье предлагается решать поставленную задачу, используя

процедуру оптимизации, в которой вектором переменных будут корни ха-

рактеристического полинома замкнутой системы. Задавая допустимый диа-

пазон значений корней, можно ограничивать коэффициент демпфирования

системы и длительность переходных процессов. Таким образом, в процедуре

оптимизации не проверяются условия устойчивости системы и ограничения

на область расположения полюсов, так как вектор переменных варьируется

только в пределах допустимой области.

В соответствии с постановкой задачи H_∞ норма функции чувствительно-

сти к возмущению (10) это цель оптимизации, а минимальное значение R^∗

радиуса запасов устойчивости (6) и максимальное значение N^∗ H_∞ нормы

функции чувствительности к помехе (9) - это ограничения. Главное отличие

предлагаемого подхода от процедуры синтеза оптимального регулятора для

заданных целей и ограничений, описанной в подразделе 3.3, состоит в том,

что вектор переменных оптимизации это корни характеристического поли-

нома замкнутой системы, а не коэффициенты регулятора. Хотя формально

это небольшое отличие, так как корни характеристического полинома одно-

значно определяют коэффициенты регулятора из уравнения (18), но факти-

112

-2

-4

-6

-8

-10

-8

-6

-4

-2

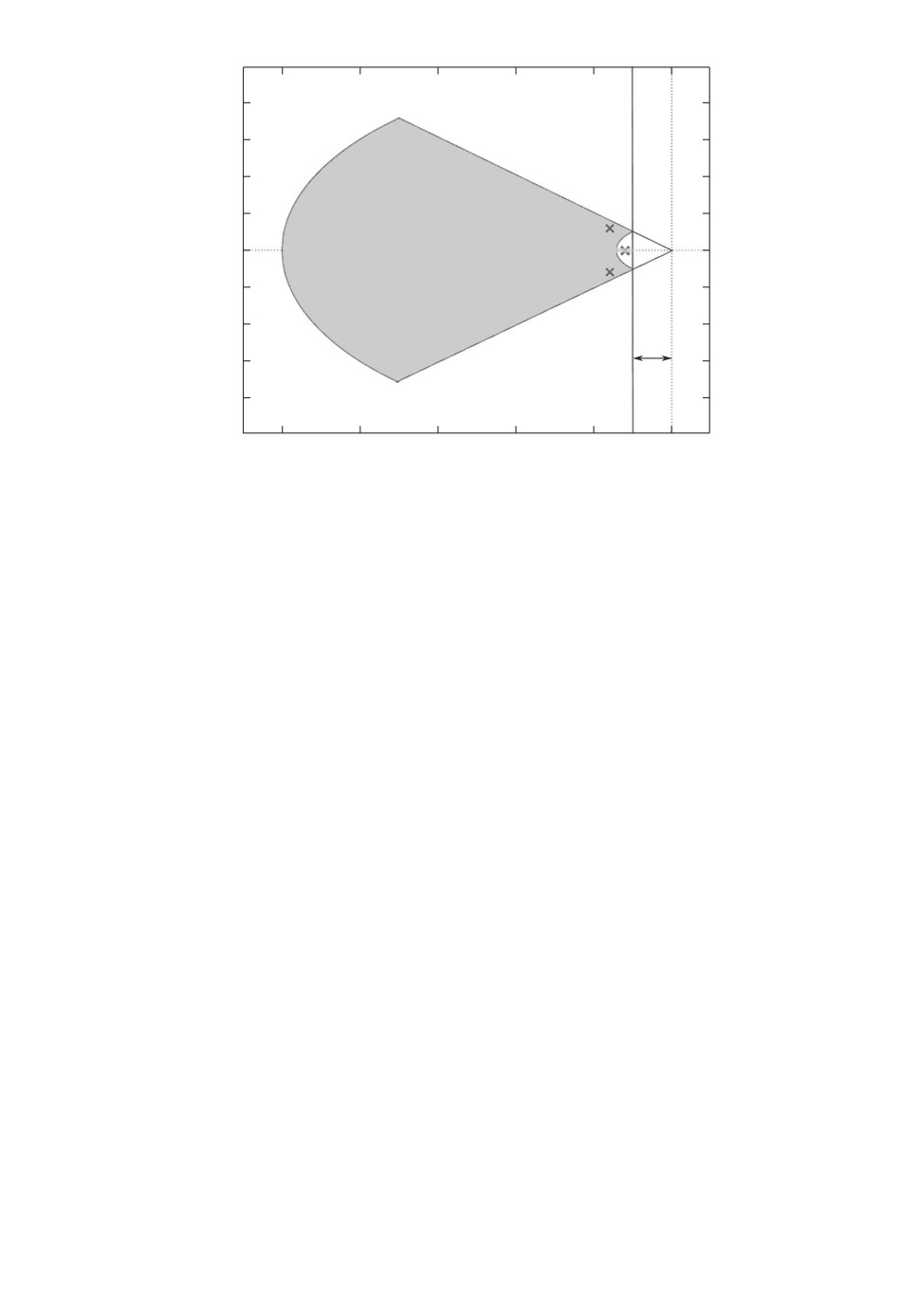
Рис. 3. Область допустимого расположения корней характеристического по-

линома.

чески оптимизация производится на другом множестве, что может приводить

к другому результату.

Для реализации предлагаемого подхода может быть использована стан-

дартная процедура глобальной оптимизации из пакета MATLAB Global Op-

timization Toolbox [26]. В этой процедуре вектор переменных это веществен-

ные числа. Поэтому зададим число 0 ≤ n₂ < n комплексно-сопряженных пар

корней полинома δ (s) и представим его в виде

∏

∏(

)

(20)

δ (s) =

(s + λ_i) ·

s² + 2ζ_iω_is + ω_i2

i=1

тогда вектор переменных будет [λ₁, . . . , λ2n-1-2n2 , ζ₁, . . . , ζn2 , ω₁, . . . , ωn2 ]. За-

давая границы ζ_min ≤ ζ_i ≤ 1, получим ограничение колебаний, а границы

λ_i ≤ -β^∗ и ω_i ≥ β^∗/ζ_min будут определять длительность переходных процес-

сов. Необходимо отметить, что для процедуры глобальной оптимизации гра-

ничные значения переменных должны быть заданы в любом случае, даже ес-

ли такие требования не сформулированы, т.е. ζ_min ≤ ζ_i ≤ 1, λ_min ≤ λ_i ≤ -β^∗,

β^∗/ζ_min ≤ ω_i ≤ ω_max, где можно принять ω_max = -λ_min. Задаваемые интерва-

лы должны быть замкнутыми, поэтому, например, вместо условия “больше

нуля” нужно использовать условие “больше или равно некоторому минималь-

ному приемлемому значению”. Вид области расположения корней характери-

стического полинома при таких ограничениях приведен на рис. 3.

Далее для процедуры глобальной оптимизации нужно сформировать две

функции, одна из которых функция цели вычисляет вещественное значе-

ние, которое должно минимизироваться, а вторая функция ограничений

вычисляет вектор значений, которые должны быть меньше заданных. В соот-

ветствии с поставленной задачей функция цели на каждом шаге процедуры

113

оптимизации для выбранного из допустимой области варианта вектора пере-

менных [λ₁, . . . , λ2n-1-2n2 , ζ₁, . . . , ζn2 , ω₁, . . . , ωn2 ] выполняет следующие опе-

рации:

1) формирует желаемый характеристический полином (20);

2) решая систему (19), находит коэффициенты регулятора;

3) вычисляет значение ∥G_yf (jω)∥_∞.

Далее функция ограничений вычисляет значения

∥S(jω)∥_∞ и

∥C (jω) S(jω)∥_∞ и сравнивает их с заданными значениями 1/R^∗ и N^∗.

Таким образом, такой поход решает поставленную задачу. Напомним, что

при заданных ограничениях решения может не существовать или результат

может оказаться неприемлемым, тогда нужно пересматривать ограничения.

Предлагается следовать следующим рекомендациям по выбору ограничений.

Минимальный радиус запасов устойчивости рекомендуется выбирать в диа-

пазоне 0,5 ≤ R^∗ ≤ 0,7, учитывая, что для систем, где такие значения недо-

стижимы, нужно предварительно определить максимально возможное зна-

чение R, например, используя описанную процедуру оптимизации, где зна-

чение ∥S(jω)∥_∞ выбрано в качестве минимизируемой цели, и тогда можно

принять R^∗ = 0,8R_max. Значение β^∗ нужно согласовывать со значениями ну-

лей объекта, так как при наличии устойчивых нулей они могут сокращаться

в замкнутой системе и быстродействие получится высоким, несмотря на на-

личие медленных полюсов замкнутой системы. С другой стороны, как пока-

зано в [20], большое значение β^∗ может приводить к отсутствию решения для

заданного R^∗, поэтому значение β^∗ нужно согласовывать и со значениями

полюсов объекта. Радиус запасов устойчивости должен иметь более высокий

приоритет, поэтому значение β^∗ лучше выбирать не желаемым, а минимально

допустимым, например равным минимальной собственной частоте объекта.

Таким образом, выбор некоторых ограничений легко формализовать, исхо-

дя из свойств объекта, определяемых его известной передаточной функцией.

А неформализованным остается только компромисс между желаемыми зна-

чениями H_∞ нормы функции чувствительности к помехе N^∗ и целевой функ-

ции. Можно рекомендовать увеличивать значение N^∗, если решение задачи не

существует при рекомендованных значениях остальных ограничений или по-

лученное значение ∥G_yf (jω)∥_∞ слишком большое. А если, наоборот, получено

решение с достаточно малыми значениями ∥G_yf (jω)∥_∞ и ∥C (jω) S(jω)∥_∞, то

можно повторить процедуру, увеличивая значение β^∗, если нужно повысить

быстродействие системы.

Следует отметить, что предлагаемый подход позволяет формулировать

и решать задачи с критериями, отличными от H_∞ норм. Например, если

требуется минимизировать или ограничить время переходного процесса, то в

качестве цели или ограничения оптимизации можно использовать результат

функции MATLAB

data = stepinfo(Gyf,’SettlingTimeThreshold’,0.05);

Objectve_Value = data.SettlingTime;

которая находит время установления моделированием реакции на ступенча-

тый вход замкнутой системы G_yf .

114

5. Пример

В качестве примера будем синтезировать регулятор для двухмассовой си-

стемы [1, 27], представляющей собой две тележки массами m₁ и m₂, соеди-

ненные пружиной с коэффициентом упругости k (рис. 4), трение не учиты-

вается, управление приложено к левой тележке, положение правой тележки

является измеряемым управляемым выходом, возмущение прикладывается к

правой тележке.

Модель такого объекта имеет вид

(

))

(m₂

m₂ + m₁

s⁴ +

s² +

m₁

m₂

(21)

)

s² +

m₁

Номинальные значения параметров предполагаются m₁ = m₂ = k = 1. Тогда

передаточные функции объекта будут

(22)

P (s) =

s² (s² + 2)

s² + 1

(23)

P_f (s) =

s² (s² + 2)

Ставится задача синтеза регулятора, обеспечивающего длительность пере-

ходного процесса на импульсное возмущение не более 15 с и устойчивость

системы при отклонении значения k от номинального в диапазоне 0,5 ≤

k ≤ 2,0 [27]. Используя рассмотренные методы, будем искать регулятор для

объекта (21) с номинальными значениями параметров и проверять устойчи-

вость системы с полученным регулятором для значений k = 0,5 и k = 2,0.

Если массы тележек не равны (например, m₂ = 2,0), то меняется структура

передаточной функции объекта

(24)

P_m (s) =

2s⁴ + 3s² + 0,5

поэтому проверим также устойчивость системы с таким объектом.

В качестве импульса будем использовать сигнал единичной амплитуды

и длительностью одна секунда. Зададим значения ограничений R^∗ = 0,6 и

N^∗ = 100 для всех рассматриваемых методов.

x₁

x₂

m₁

m₂

Рис. 4. Пример объекта управления.

115

5.1. Синтез регулятора методом H_∞ оптимизации

Для объекта (21) принимаем обобщенные входы и выходы вида (15). Тогда

получим обобщенную систему:





















x+





,

−1

-1 0 0

W₁

(25)











[

]

= 0 0 0 0

x+ 00-W2

ν

.

Для значений γ и W₂, полученных по формулам (17), при W₁ = 0,5 функция

hinfsyn с опцией LMI находит регулятор:

2170s³ + 354,3s² + 3506s + 1055

(26)

C₁ (s) =

s⁴ + 53,04s³ + 362,2s² + 1356s + 3032

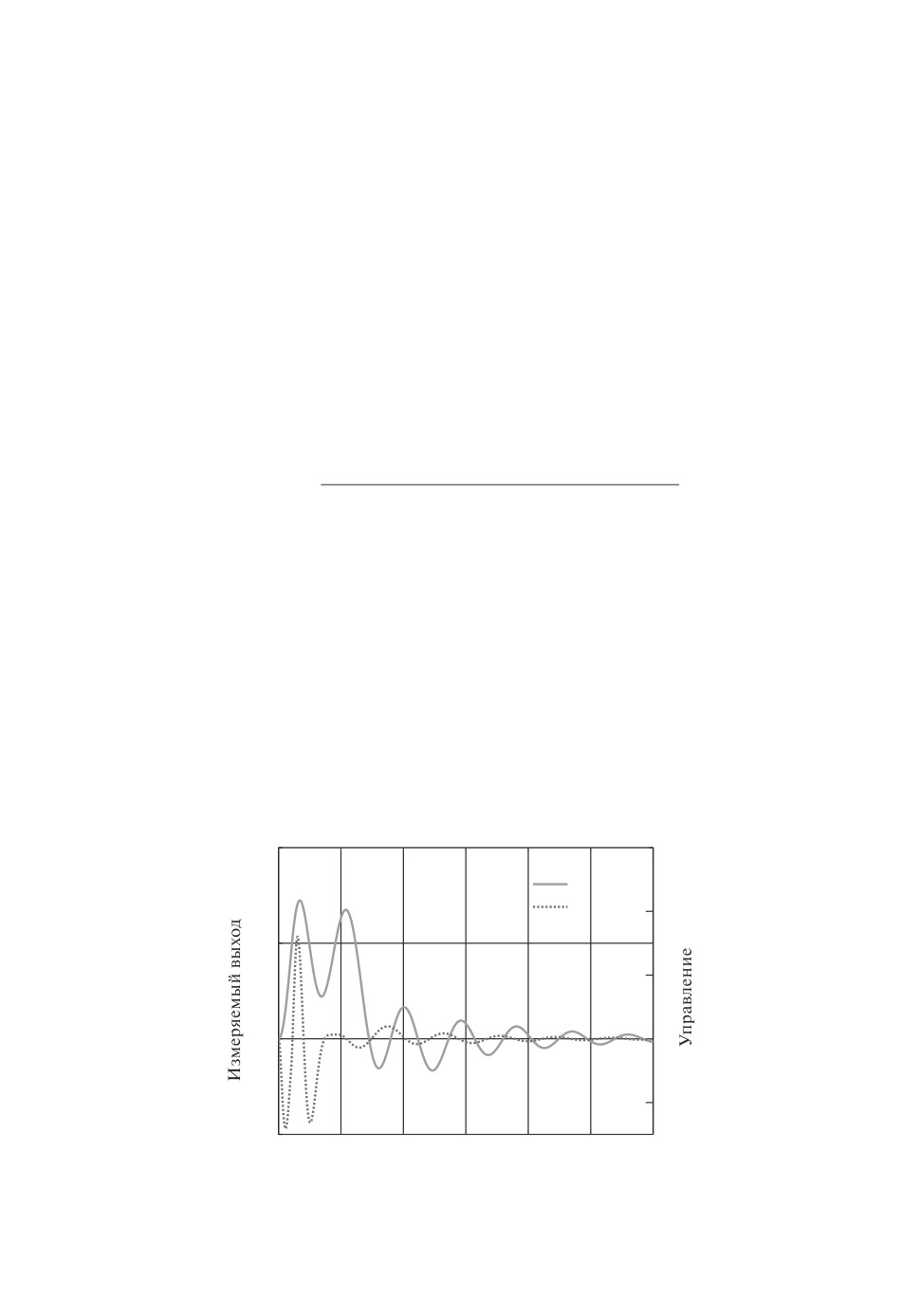
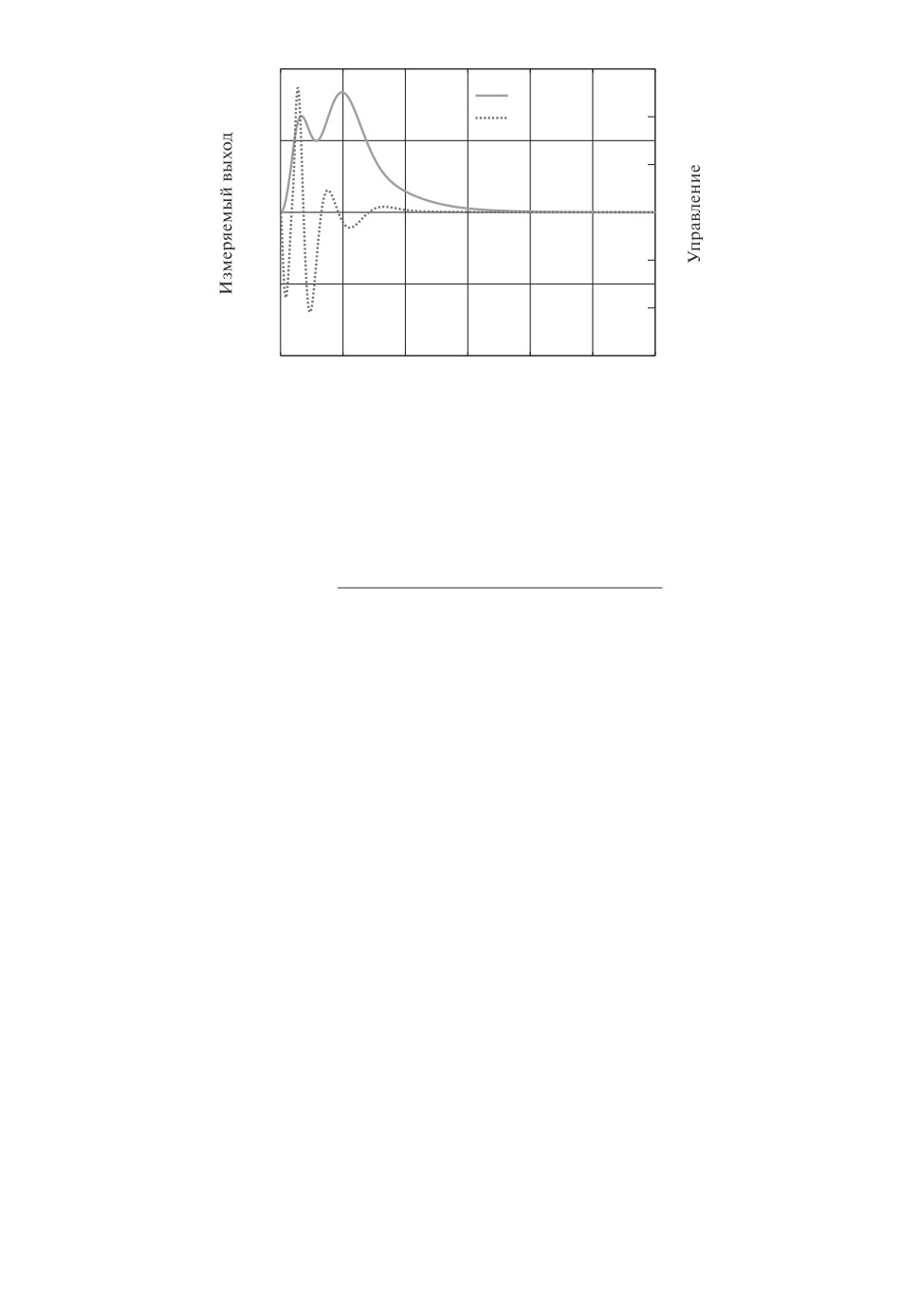
Переходный процесс системы с этим регулятором при воздействии возму-

щения f в виде импульса единичной амплитуды и длительностью одна се-

кунда показан на рис. 5. Этот регулятор обеспечивает значения R = 0,6577

и ∥CS∥_∞ = 47,27, что лучше требуемых значений. При этом ∥G_yf ∥_∞ = 2,87.

Тем не менее систему нельзя признать хорошей, так как переходный процесс

колебательный и не сходится за 15 с. Это обусловлено тем, что характеристи-

ческий полином замкнутой системы содержит корни (-0,117 ± j1, 4) с коэф-

фициентом демпфирования ζ = 0,083 (полюса замкнутой системы показаны

на рис. 6).

Кроме того, при значении коэффициента упругости k < 0,8, а также для

объекта (24) при m₂ = 2,0, k = 1,0 система становится неустойчивой. На этом

1,0

0,5

-1

-0,5

Время, с

Рис. 5. Импульсное возмущение с регулятором (26).

116

Коэффициент демпфирования 0,083

-1

-2

-3

-4

-5

-4

-3

-2

-1

Рис. 6. Полюса замкнутой системы с регулятором (26).

примере видно, что значение коэффициента демпфирования замкнутой си-

стемы также должно быть критерием робастности, так как хотя радиус за-

пасов устойчивости достаточно большой, система становится неустойчивой

даже при не очень большом изменении параметров объекта.

5.2. Синтез H_∞ оптимального регулятора с ограничением

области размещения полюсов

Попробуем получить регулятор для объекта (21) при тех же парамет-

рах и ограничениях, используя функцию h2hinfsyn. К обобщенной систе-

ме (25) добавим ограничение области размещения полюсов замкнутой систе-

мы: θ^∗ = π/2 (что соответствует значению ζ = 0,707) и β^∗ = 0,1. Функция не

находит решения при таких условиях и заданном значении γ = 1/R^∗. Поэто-

му проводим поиск оптимального регулятора, не задавая значения γ. Тогда

получаем регулятор

94,89s⁴ + 9,545 · 10⁶s³ - 4,591 · 10⁶s² + 4,907 · 10⁶s + 7,221 · 10

(27)

C₂ (s) =

s⁴ + 3,414 · 10⁴s³ + 5,376 · 10⁵s² + 3,23 · 10⁶s + 8,946 · 10⁶

который обеспечивает значения R = 0,523 и ∥CS∥_∞ = 279, что существенно

хуже требуемых, при этом значение ∥G_yf ∥_∞ = 12,38 тоже хуже, чем в си-

стеме с регулятором (26). Уменьшение значения весового коэффициента W₁

не приводит к получению регулятора, обеспечивающего заданное значение

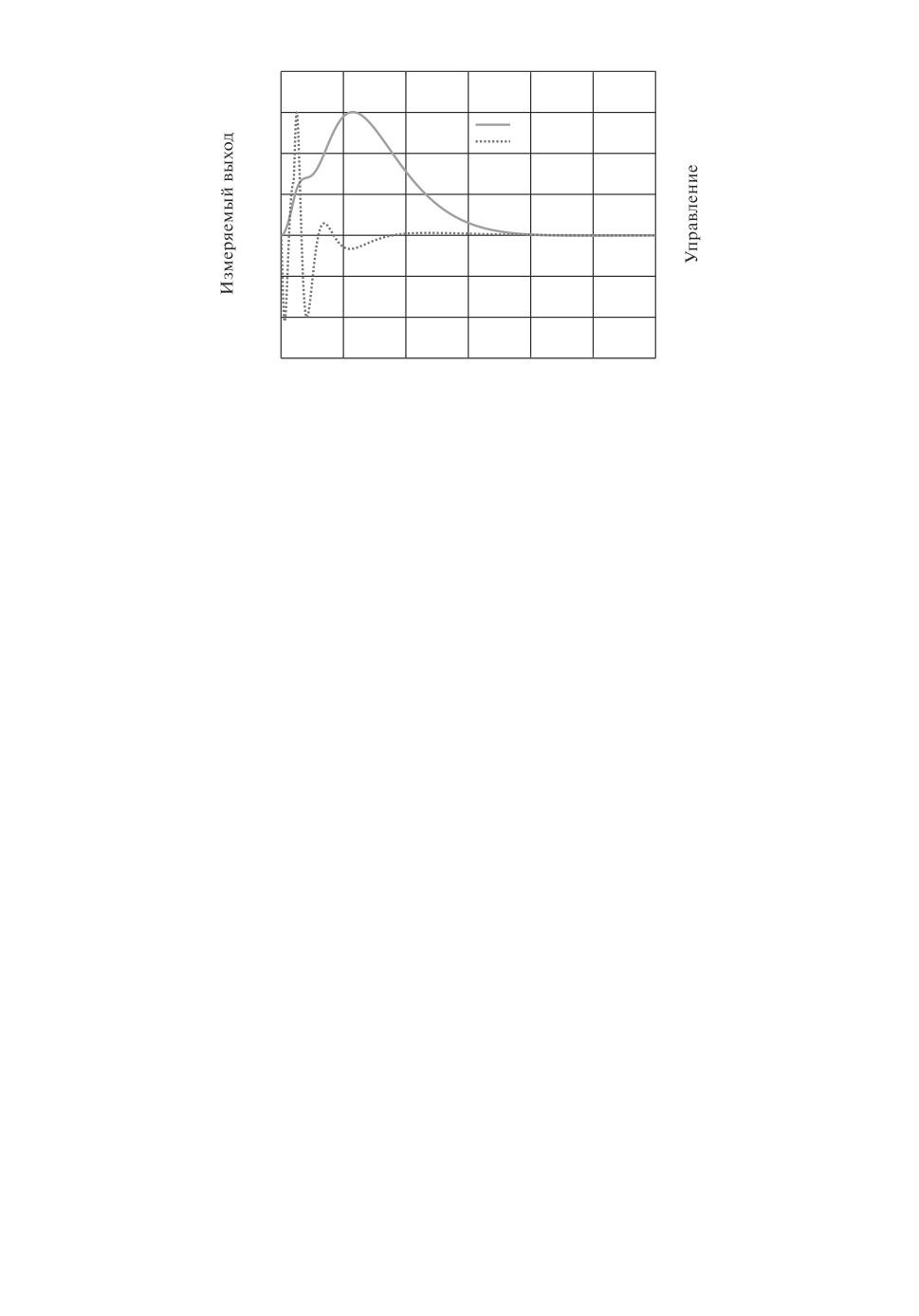
R^∗ = 0,6, поэтому проверяем работу регулятора (27). В переходном процессе

на рис. 7 уже нет колебаний на выходе, но амплитуды сигналов увеличились.

Кроме того, если посмотреть нули и полюса регулятора (27)

94,885(s + 1,006 · 10⁵)(s + 0,1278)(s² - 0,6088s + 0,5919)

C₂ (s) =

(s + 3,413 · 10⁴)(s + 8,027)(s² + 7,722s + 32,65)

117

2,0

1,5

1,0

0,5

-0,5

-1

-1,0

-2

-1,5

-3

Время, с

Рис. 7. Импульсное возмущение с регулятором (27).

то видно, что в регуляторе есть большие значения нуля и полюса, и скорее

всего регулятор 3-го порядка был бы лучше, чем получившийся регулятор

4-го порядка, в чем убедимся далее. Тем не менее длительность переходного

процесса получается около требуемых 15 с, и система с регулятором (27) оста-

ется устойчивой при значениях коэффициента упругости k = 0,5 и k = 2,0.

Для объекта (24) при m₂ = 2,0, k = 1,0 устойчивость системы сохраняется,

но процесс становится колебательным.

5.3. Синтез оптимального регулятора с фиксированной структурой

Для использования функции systune не нужно формировать обобщенную

систему, а нужно

1) объявить регулятор как некоторую структуру с настраиваемыми парамет-

рами, например при помощи команды

Controller3 = tunableTF(’Controller’, 3, 3),

которая задает структуру регулятора в виде (4) с m = 3;

2) сформировать командой feedback замкнутую систему с объектом, задан-

ным передаточной функцией (22), и регулятором Controller3;

3) сформировать цель оптимизации, например как TuningGoal.Gain для H_∞

нормы функции чувствительности к возмущению ∥G_yf (jω)∥_∞ с ограничи-

вающим профилем вида W₂ = 1/(s² + 1), который учитывает, что возму-

щение приложено не там, где управление;

4) установить ограничения в соответствии с задачей как:

• TuningGoal.Sensitivity для H_∞ нормы функции чувствительности

∥S(jω)∥_∞ с максимальным значением 1/R^∗;

• TuningGoal.Gain для H_∞ нормы функции чувствительности к помехе

∥C (jω) S(jω)∥_∞ с максимальным значением N^∗;

• TuningGoal.Poles для задания β^∗, минимального коэффициента демп-

фирования ζ_min и максимальной собственной частоты ω_max.

118

1,0

0,5

-1

-0,5

-2

-1,0

-3

Время, с

Рис. 8. Импульсное возмущение с регулятором (28).

Для значений R^∗ = 0,6, N^∗ = 100, β^∗ = 0,1, ζ_min = 0,7, ω_max = 100 получен

регулятор

99,99s³ - 15,87s² + 96,81s + 18,28

(28)

C₃ (s) =

s³ + 9,429s² + 42,74s + 96,99

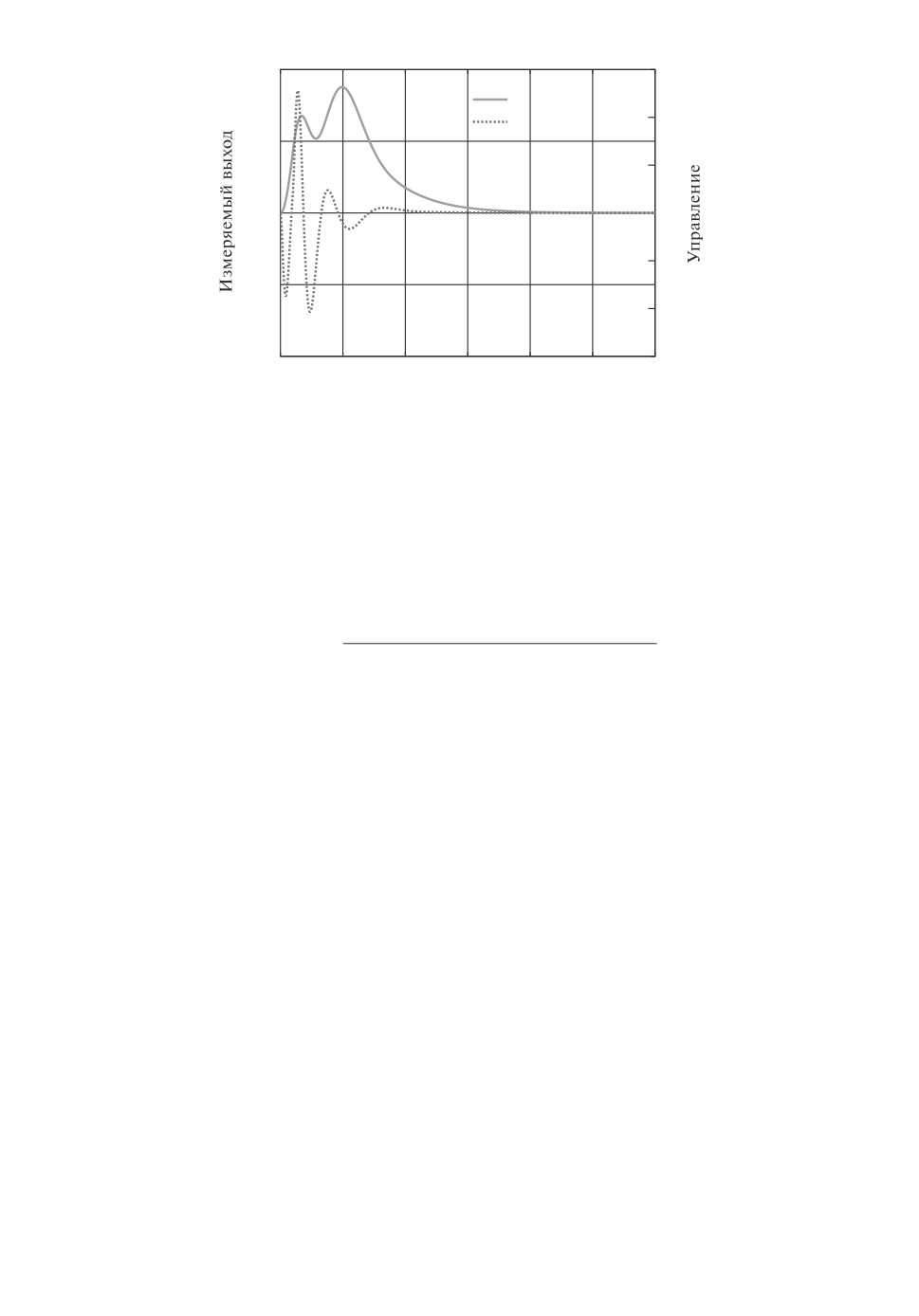
который обеспечивает все заданные ограничения и ∥G_yf ∥_∞ = 5,3. Переход-

ный процесс системы с этим регулятором показан на рис. 8 и длится ме-

нее 15 с. Система с регулятором (28) остается устойчивой при значениях

коэффициента упругости k = 0,55 и k = 2,0. При k < 0,55 устойчивость те-

ряется. Для объекта (24) при m₂ = 2,0, k = 1,0 устойчивость системы сохра-

няется. Если, например, найти регулятор для других ограничений: R^∗ = 0,606

и N^∗ = 70, то система будет устойчивой и при k = 0,5, но при номинальных

значениях длительность переходного процесса будет немного больше 15 с.

5.4. Синтез регулятора методом оптимизации размещения полюсов

В предлагаемом методе порядок регулятора (4) принимается m = n-1 = 3.

Желаемый характеристический полином замкнутой системы (20) порядка

2n - 1 = 7 может содержать до трех пар комплексно-сопряженных корней.

Для n₂ = 3 вектор переменных будет иметь вид [λ₁, ζ₁, ζ₂, ζ₃, ω₁, ω₂, ω₃]. Для

применения процедуры глобальной оптимизации к решению поставленной

задачи нужно определить:

• границы для каждого элемента вектора переменных, для чего будем ис-

пользовать область размещения полюсов замкнутой системы такой же, как

в подразделе 5.3: β^∗ = 0,1, ζ_min = 0,7, ω_max = 100, λ_min = -100;

• функцию цели оптимизации, которая для текущего вектора переменных,

определяющего коэффициенты желаемого характеристического полино-

ма (20), и соответственно коэффициенты регулятора как решение систе-

мы (19), вычисляет значение ∥G_yf (jω)∥_∞;

119

1,0

0,5

-1

-0,5

-2

-1,0

-3

Время, с

Рис. 9. Импульсное возмущение с регулятором (29).

• функцию ограничений, которая вычисляет значения

∥S(jω)∥_∞ и

∥C (jω) S(jω)∥_∞ и сравнивает их с заданными значениями 1/R^∗ и N^∗.

Для значений R^∗ = 0,6, N^∗ = 100 процедура глобальной оптимизации нахо-

дит регулятор

98,38s³ - 22,35s² + 86,06s + 14,8

(29)

C₄ (s) =

s³ + 10,15s² + 43,96s + 98,33

который обеспечивает все заданные ограничения и ∥G_yf ∥_∞ = 6,64. Видно,

что полученный регулятор (29) практически совпадает с регулятором (28),

полученным при помощи функции systune. Переходный процесс системы с

регулятором (29) показан на рис. 9, длится менее 15 с и также практически

не отличается от процесса на рис. 8.

Система с регулятором (29) остается устойчивой при значениях коэффи-

циента упругости k = 0,5 и k = 2,0, а также для объекта (24) при m₂ = 2,0,

k = 1,0, т.е. регулятор (29) обеспечивает устойчивость в заданных грани-

цах изменения параметров объекта в отличие от регулятора (28), найден-

ного функцией systune, который не обеспечивал устойчивость при k < 0,55.

Напомним, что регулятор (26), найденный с помощью функции hinfsyn, не

обеспечивал устойчивость системы уже при k < 0,8, а при помощи функции

h2hinfsyn не удалось найти регулятор, обеспечивающий заданные требова-

ния к радиусу запасов устойчивости и к H_∞ норме функции чувствительно-

сти к помехе.

6. Заключение

Классический метод H_∞ оптимизации, и особенно в версии с ограничением

области размещения полюсов, казалось бы, дает все возможности для поиска

оптимального регулятора, задавая необходимые для практической реализа-

ции ограничения. Но пример показывает, что не всегда полученные решения

120

будут действительно лучшими, в частности при прямом использовании реа-

лизации метода в пакете MATLAB Robust Control Toolbox. Следует учиты-

вать, что специалисты, имеющие опыт использования этого метода, могут

предложить дополнительные модификации подхода, существенно улучшаю-

щие результат. Тем не менее функция systune, основанная на процедуре оп-

тимизации системы с регулятором фиксированной структуры, оказывается

более гибкой при формировании целей и ограничений оптимизации, и в рас-

смотренном примере нашла решение, удовлетворяющее условиям поставлен-

ной задачи. При этом нужно учитывать, что решается невыпуклая задача

оптимизации и не гарантируется оптимальность найденного решения. Поэто-

му наличие альтернативных подходов может оказаться полезным.

Предложенный в разделе 4 метод оптимизации размещения полюсов мо-

жет предоставлять практически те же возможности и в рассмотренном при-

мере дает примерно такой же результат, как и метод синтеза регулятора

с фиксированной структурой, рассмотренный в подразделе 3.3. Так, регу-

ляторы (29) и (28), построенные при помощи этих методов, очень близки.

Отличие предлагаемого подхода в том, что варьируемые переменные про-

цедуры оптимизации это корни характеристического полинома замкну-

той системы, а не коэффициенты регулятора. В каких-то случаях это мо-

жет давать лучший результат, так как оптимизация производится на дру-

гом множестве варьируемых переменных. Использованная для реализации

предлагаемого подхода стандартная процедура глобальной оптимизации не

совсем подходит для решения задачи оптимизации размещения полюсов,

так как, во-первых, варьируемые переменные должны быть вещественны-

ми, а корни характеристического полинома могут быть как вещественными,

так и комплексно-сопряженными (хотя эта проблема решена заменой пары

комплексно-сопряженных корней на пару вещественных коэффициентов со-

ответствующего полинома второго порядка) и, во-вторых, процедура не учи-

тывает, что последовательность корней в векторе не имеет значения. Тем не

менее эта процедура может применяться для тестовых примеров.

СПИСОК ЛИТЕРАТУРЫ

1. Поляк Б.Т., Хлебников М.В., Рапопорт Л.Б. Математическая теория автома-

тического управления. М.: ЛЕНЛАНД, 2019.

Åström K.J., Murray R.M. Feedback Systems: an Introduction for Scientists and

Engineers. New Jersey: Princeton University Press, 2008.

3. Skogestad S., Postlethwaite I. Multivariable Feedback Control. Analysis and Design.

N.Y.: John Wiley and Sons, 2006.

4. Александров А.Г. Методы построения систем автоматического регулирования.

М.: Физматлит, 2008.

5. Gahinet P., Apkarian P. A Linear Matrix Inequality Approach to H_∞ Control //

Int. J. Robust Nonlinear Contr. 1994. V. 4. P. 421-448.

6. Chilali M., Gahinet P. H_∞ Design with Pole Placement Constraints: An LMI Ap-

proach // IEEE Trans. Autom. Control. 1996. V. 41. No. 3. P. 358-367.

7. Apkarian P., Noll D. Nonsmooth H_∞ Synthesis // IEEE Trans. Autom. Control.

2006. V. 51. No. 1. P. 71-86.

121

Gahinet P., Apkarian P. Decentralized and Fixed-Structure H_∞ Control in

MATLAB // Proc. IEEE Conf. on Decision and Control. 2011. P. 8205-8210.

Apkarian P., Gahinet P., Buhr C. Multi-Model, Multi-Objective Tuning of Fixed-

Structure Controllers // Proc. Eur. Control Conf. 2014. P. 856-861.

10.

Грязина Е.Н., Поляк Б.Т., Тремба А.А. Современное состояние метода D-раз-

биения // АиТ. 2008. № 12. С. 3-40.

Gryazina E.N., Polyak B.T., Tremba, A.A. D-decomposition Technique State-of-the-

art // Autom. Remote Control. 2008. V. 69. No. 12. P. 1991-2026.

11.

Щербаков П.С. Построение регуляторов заданной структуры при соблюдении

инженерных требований // Проблемы управления. 2009. № 5. С. 9-17.

Shcherbakov P.S. Fixed Order Controller Design Subject to Engineering Specifica-

tions // Autom. Remote Control. 2010. V. 71. No. 6. P. 1217-1229.

12.

Александров А.Г., Честнов В.Н. Синтез многомерных систем заданной точно-

сти. II. Применение процедур H_∞-оптимизации // АиТ. 1998. № 8. С. 124-138.

Alexandrov A.G., Chestnov V.N. Synthesis of Multivariable Systems of Prescribed

Accuracy. II. Use of Procedures of H-Infinity-Optimization // Autom. Remote Con-

trol. 1998. V. 59. No. 8. P. 1153-1164.

13.

Агафонов П.А., Честнов В.Н. Синтез регуляторов по заданному радиусу запа-

сов устойчивости с учетом внешних возмущений на основе H_∞-подхода // АиТ.

2004. № 10. С. 101-108.

Agafonov P.A., Chestnov V.N. Controllers of a Given Radius of Stability Margin:

Their Design by the H_∞-Approach with Regard for External Disturbances // Autom.

Remote Control. 2004. V. 65. No. 10. P. 1611-1617.

14.

Честнов В.Н. Синтез робастных H_∞-регуляторов многомерных систем по за-

данной степени устойчивости // АиТ. 2007. № 3. C. 199-205.

Chestnov V.N. Design of Robust H_∞-Controllers of Multivariable Systems Based on

the Given Stability Degree // Autom. Remote Control. 2007. V. 68. No. 3. P. 557-563.

15.

Честнов В.Н. Синтез многомерных систем по инженерным критериям качества

на основе H_∞-оптимизации // АиТ. 2019. № 10. С. 132-152.

Chestnov V.N. Synthesis of Multivariable Systems According to Engineering Quality

Criteria Based on H_∞-Optimization // Autom. Remote Control. 2019. V. 80. No. 10.

P. 1861-1877.

16.

Александров А.Г. Синтез регуляторов по показателям точности и быстродей-

ствию. I. Минимально-фазовые одномерные объекты // АиТ. 2015. № 5. С. 27-42.

Aleksandrov A.G. Controller Design in Precision and Speed. I. Minimal Phase One-

Dimensional Plants // Autom. Remote Control. 2015. V. 76. No. 5. P. 749-761.

17.

Александров А.Г. Синтез регуляторов по показателям точности и быстродей-

ствию. II. Неминимально-фазовые объекты // АиТ. 2017. № 6. С. 3-17.

Aleksandrov A.G. Design of Controllers by Indices of Precision and Speed. II.

Nonminimal-Phase Plants // Autom. Remote Control. 2017. V. 78. No. 6. P. 961-973.

18.

Александров А.Г. Критерии грубости нестационарных систем автоматического

регулирования // Аналитические методы синтеза регуляторов: Межвуз. научн.

сб. Саратов: Сарат. политехн. ин-т, 1980. С. 3-14.

19.

Честнов В.Н. Синтез регуляторов многомерных систем по заданному радиу-

су запасов устойчивости на базе процедуры оптимизации // АиТ. 1999. № 7.

С. 100-109.

Chestnov V.N. Synthesis of Controllers for Multivariate Systems with a Given Ra-

dius of Stability Margin by the H-Infinity-Optimization Method // Autom. Remote

Control. 1999. V. 60. No. 7. P. 986-993.

122

20. Alexandrov V.A., Chestnov V.N., Shatov D.V. Stability Margins for Minimum-Phase

SISO Plants: A Case Study // Proc. Eur. Control Conf. 2020. P. 2068-2073.

21. Поляк Б.Т., Хлебников М.В., Щербаков П.С. Управление линейными система-

ми при внешних возмущениях: Техника линейных матричных неравенств. М.:

ЛЕНАНД, 2014.

22. Острем К., Виттенмарк Б. Системы управления с ЭВМ. М.: Мир, 1987.

23. Гайдук А.Р. Теория и методы аналитического синтеза систем автоматического

управления (полиномиальный подход). М.: Физматлит, 2012.

24. Ким Д.П. Алгебраические методы синтеза систем автоматического управления.

М.: Физматлит, 2014.

25. Честнов В.Н., Александров В.А., Резков И.Г. Синтез одномерных дискретных

регуляторов по инженерным критериям качества на основе модального управ-

ления // Проблемы управления. 2019. № 6. С. 11-21.

Chestnov V.N., Alexandrov V.A., Rezkov I.G. Synthesis of Discrete Modal SISO

Controllers by Engineering Performance Indices // Autom. Remote Control. 2020.

V. 81. No. 6. P. 1107-1124.

26. Ugray Z., Lasdon L., Plummer J., Glover F., Kelly J., Marti R. Scatter Search and

Local NLP Solvers: A Multistart Framework for Global Optimization // INFORMS

J. Computing. 2007. V. 19. No. 3. P. 328-340.

27. Wie B., Bernstein D.S. A Benchmark Problem for Robust Control Design // Proc.

Amer. Control Conf. San Diego, CA, USA. 1990. P. 961-962.

Статья представлена к публикации членом редколлегии П.С. Щербаковым.

Поступила в редакцию 30.04.2020

После доработки 24.12.2020

Принята к публикации 15.01.2021

123