Автоматика и телемеханика, № 6, 2021

Интеллектуальные системы управления,

анализ данных

А.В. ПУПКОВ (andrewpupkov@gmail.com)

(Томский государственный университет)

ДОВЕРИТЕЛЬНОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ АВТОРЕГРЕССИИ

ПО ЗАШУМЛЕННЫМ ДАННЫМ¹

Рассматривается задача оценивания параметров процесса авторегрес-

сии по наблюдениям с аддитивным шумом. Разработан последовательный

метод построения доверительной области фиксированных размеров с за-

данным коэффициентом доверия для вектора неизвестных параметров

по конечной выборке. Получены формулы для длительности процедуры,

при которой достигается требуемое качество оценок неизвестных пара-

метров в случае гауссовских шумов. Построение доверительных оценок

параметров основано на использовании специальной последовательной

модификации классических оценок Юла-Уокера, позволяющей оценить

коэффициент доверия при малых и умеренных объемах выборки. Приво-

дятся результаты численного моделирования предлагаемых оценок и их

сравнение с оценками Юла-Уокера на примере доверительного оценива-

ния спектральной плотности.

Ключевые слова: идентификация авторегрессии по зашумленным наблю-

дениям, последовательные оценки Юла-Уокера, доверительное оценива-

ние, гарантированная точность.

DOI: 10.31857/S0005231021060052

1. Введение

Известно, что в теоретических и прикладных исследованиях, связанных с

задачами адаптивного управления и регулирования, фильтрации и прогнози-

рования, анализа спектров и обработки временных рядов, большое внимание

уделяется проблеме идентификации параметров динамических систем, опи-

сываемых стохастическими разностными и стохастическими дифференциаль-

ными уравнениями [1-3]. При этом для широкого круга используемых моде-

лей неизвестные параметры входят линейно в уравнения системы, а иден-

тификация параметров системы заключается в оценивании параметров де-

терминированной или стохастической регрессии [4-7]. Для идентификации

линейных динамических систем разработаны различные эффективные ме-

тоды: наименьших квадратов (МНК), максимального правдоподобия (МП),

¹ Работа выполнена при финансовой поддержке Российского научного фонда (проект

№ 17-11-01049).

124

стохастической аппроксимации и др. Теория оценивания параметров детер-

минированной регрессии разработана с исчерпывающей полнотой, позволяя

строить оптимальные оценки по имеющимся данным и контролировать их

точность в момент прекращения наблюдений динамической системы (см.,

например, [8]). Методы классической теории оценивания параметров стоха-

стической регрессии, типичным примером которой являются временные ряды

типа авторегрессии, позволили установить важные асимптотические свойства

оценок при неограниченной длительности наблюдений. При практическом ис-

пользовании оценок обычно исходят из того, что эти свойства сохраняются

при малых и умеренных объемах данных. В последние годы в теоретических и

прикладных исследованиях статистики случайных процессов возрастает роль

последовательных методов анализа, которые отличаются тем, что объем дан-

ных, используемых в оценках, не фиксируется заранее, а определяется специ-

альными правилами остановки наблюдений. Впервые целесообразность при-

менения последовательного анализа для процессов с зависимыми значениями

была установлена в публикациях [9, 10] в задаче оценивания коэффициента

сноса диффузионного процесса. Было доказано, что оценка максимального

правдоподобия, вычисленная в специальный (случайный) момент времени,

превосходит классическую оценку максимального правдоподобия: она явля-

ется несмещенной и гарантирует заданную среднеквадратическую точность.

В дальнейшем последовательный анализ стал успешно применяться в зада-

чах идентификации стохастических динамических систем с дискретным вре-

менем и более сложных моделей с непрерывным временем, позволяя улуч-

шить как асимптотические [11, 12], так и неасимптотические свойства [13-16]

классических оценок МНК и МП. Одним из важнейших результатов после-

довательных методов идентификации является построение точечных оценок

неизвестных параметров уравнений с гарантированной среднеквадратиче-

ской точностью в момент прекращения наблюдений. Последовательные оцен-

ки обычно строятся на основе классических оценок МНК и МП, используя

специальные правила прекращения наблюдений и проводя дополнительные

структурные изменения классических оценок. При этом конструкция после-

довательных оценок существенно зависит от числа неизвестных параметров:

она использует одну классическую оценку МНК, если число неизвестных па-

раметров не превышает размерности процесса, описывающего динамику си-

стемы [13, 14], и она включает целую серию базовых оценок (случайной дли-

ны) в случае, когда число неизвестных параметров больше, чем размерность

процесса [15, 16].

В данной статье рассматривается задача идентификации параметров авто-

регрессии по наблюдениям, искаженным аддитивным шумом. Такая модель

широко используется в задачах фильтрации и прогнозирования, при обра-

ботке сигналов в информационно-измерительных комплексах, анализе речи

и др. Проблеме идентификации параметров зашумленной авторегрессии по-

священо много публикаций [17-22] и др. Основные методы идентификации

можно разбить на две группы. К первой группе относятся методы, исполь-

зующие для описания зашумленной авторегрессии, модели авторегрессии и

скользящего среднего. Затем параметры оцениваются применением модифи-

цированных оценок Юла-Уокера, метода максимального правдоподобия или

125

метода рекуррентного прогноза ошибок. К другой группе методов относят

улучшенные методы МНК [21]. Теоретические исследования свойств оценок

носят асимптотический характер. Они позволили определить потенциальные

возможности построения авторегрессионных моделей в условиях, когда авто-

регрессионный процесс недоступен прямым наблюдениям. При этом вопросы

о точности оценок при малых и умеренных объемах данных остаются откры-

тыми.

Цель данной статьи разработать метод неасимптотического доверитель-

ного оценивания параметров зашумленной авторегрессии. Предполагается,

что шумы, задающие динамику процесса авторегрессии, и шумы в канале из-

мерений являются гауссовскими. Последовательная процедура идентифика-

ции строится на основе одной классической оценки Юла-Уокера, используя

специальные правила остановки наблюдений и дополнительную модифика-

цию структуры оценки с помощью весовых коэффициентов. Конструкция по-

следовательных оценок параметров зашумленной авторегрессии и ее анализ

существенно опираются на недавние результаты по последовательной иденти-

фикации гауссовской авторегрессии по прямым наблюдениям [23, 24]. Задача

неасимптотического доверительного оценивания линейных параметров в мно-

гомерных динамических системах с условно-гауссовскими шумами изучалась

в [25] в предположении, что число неизвестных параметров не превышает

размерности процесса, а сам процесс доступен прямому наблюдению. Другие

подходы к построению последовательных процедур идентификации динами-

ческих систем исследованы в [26, 27]. Отметим, что, помимо задач иденти-

фикации динамических систем, последовательные методы играют ключевую

роль в теории оптимальной остановки [28] и в задачах скорейшего оптималь-

ного обнаружения разладок [29].

2. Постановка задачи. Построение доверительной оценки

для авторегрессии первого порядка

Рассмотрим модель зашумленной авторегрессии AR(p) p-го порядка, опи-

сываемого уравнениями

(2.1)

x_k = θ₁x_k-1 + ··· + θ_px_k-p + ε_k,

(2.2)

y_k = x_k + η_k

k ≥ 1,

где {ε_k} и {η_k} независимые последовательности гауссовских случайных ве-

личин (шумы) с нулевыми средними Eε_k = Eη_k = 0 и дисперсиями Eε^2k = σ²

и Eη^2k = Δ². Параметры θ₁,... ,θ_p неизвестны, и их требуется оценить по на-

блюдениям процесса {y_k}. Предполагается, что вектор начальных значений

x₀,... ,x_1-p процесса AR(p) является случайным, не зависящим от процессов

{ε_k} и {η_k}.

Из (2.1), (2.2) получаем уравнение для наблюдаемого процесса

(2.3)

y_k = Y^Tk-1θ + ξ_k,

126

где Y_k = (y_k, . . . , y_k-p+1)^T, θ = (θ₁, . . . , θ_p)^T, ξ_k = ε_k + η_k - θ₁η_k-1 - . . .

··· - θ_pη_k-p;^T обозначает транспонирование. Поскольку оценка МНК для

вектора θ является смещенной, для оценивания θ часто используют оценку

Юла-Уокера, которая вычисляется по наблюдениям y_p, . . . , y_n по формуле

∑

(2.4)

θ(n) = G^-1

Y_k-p-1y_k, G_n =

Y_k-p-1Y^Tk-1.

k=2p+1

Подставляя y_k из (2.3) в (2.4), получаем уклонение оценки

∑

(2.5)

θ(n) - θ = G^-1nζ(n), ζ(n) =

Y_k-p-1ξ_k.

k=2p+1

Оценка (2.4) является нелинейной функцией от наблюдений, ее свойства

исследованы только при асимптотическом предположении, что объем выбор-

ки сколь угодно велик [2, 3]. Вопрос о качестве оценок (2.4) при малых и

умеренных объемах данных остается открытым.

Цель статьи получить решение задачи доверительного оценивания па-

раметров θ₁, . . . , θ_p в системе (2.1), (2.2) в неасимптотической постановке. На

основе оценки Юла-Уокера (2.4), используя подход последовательного ана-

лиза, построим доверительные оценки для θ = (θ₁, . . . , θ_p)^T, выбрав вместо

n специальное правило остановки наблюдений в зависимости от требуемой

точности оценки и проведя дополнительную модификацию структуры самой

оценки (2.4).

Отложив до раздела 3 построение последовательных оценок Юла-Уокера

и их анализ в общей модели (2.1), (2.2), рассмотрим сначала задачу оценива-

ния параметра θ в зашумленном процессе авторегрессии первого порядка

(2.6)

x_k = θx_k-1 + ε_k, y_k = x_k + η_k

k ≥ 1.

При этом из (2.4)-(2.6) получаем, что

∑

ζ(n)

(2.7)

θ(n) =

y_k-2y_k,

θ(n) - θ =

n ≥ 3,

∑

y_k-2yk-1 k=3

y_k-2y_k-1

k=3

∑

(2.8)

ζ(n) =

y_k-2ξ_k, ξ_k = η_k - θη_k-1 + ε_k.

k=3

Точечная последовательная оценка для θ строится в два этапа.

Этап 1. Представление процесса ζ(n) в виде суммы двух мартингалов.

Этап 2. Построение момента остановки наблюдений и выбор весовых ко-

эффициентов в модифицированной оценке Юла-Уокера.

127

Множество индексов суммирования в (2.8) T (n) = {3, 4, . . . , n} разобьем

на нечетные и четные: T (n) = T₁(n) ∪ T₂(n), где

(2.9)

T₁

(n) = {k = 2j + 1 : j = 1, 2, . . . ; k ≤ n},

T₂(n) = {k = 2(j + 1) : j = 1,2,... ;k ≤ n}.

Заметим, что количества индексов во множествах T₁(n) и T₂(n) опре-

деляются величинами d₁(n) = [(n - 1)/2], d₂(n) = [(n - 2)/2], n ≥ 3, где

[a] обозначает целую часть числа a. Далее запишем сумму (2.8) в виде

ζ(n) = ζ₁(n) + ζ₂(n), где

∑

(2.10)

ζ_i(n) =

χ{k∈Ti(n)}yk-2ξk

i = 1,2;

k=3

χ_A обозначает индикатор события A.

Обозначим через m₁(n) и m₂(n) максимальные индексы в T₁(n) и T₂(n),

т.е.

m₁(n) = max {2j + 1 : j = 1,2,... ;2j + 1 ≤ n},

m₂(n) = max {2(j + 1) : j = 1,2,... ;2(j + 1) ≤ n}.

Введем две фильтрации {

}n≥0 и {

}n≥0, где

F⁽ⁱ⁾⁰ = σ{x₀},

(2.11)

i = 1,2, n ≥ 1.

F⁽ⁱ⁾ⁿ = σ{x₀,ε₁,... ,ε_m

i (n),η1^,...,ηmi(n)^},

Первый этап завершается следующим результатом.

(

)

(

)

Лемма 1. Процессы ζ₁(n),Fn1)

и ζ₂(n),Fn2)

в разложении

n≥3

(2.10) являются мартингалами.

Доказательство леммы 1 приводится в Приложении.

Построим теперь последовательную оценку Юла-Уокера.

Пусть h > 0. Введем два момента остановки по нечетным и четным на-

блюдениям процесса y_k:







d₁(n)∑



τ₁(h) = inf

n≥3:

y^22j-1 ≥



Δ² + σ² 

j=1

(2.12)







d₂(n)∑



τ₂(h) = inf

n≥1:

y^22j ≥



Δ² + σ² 

j=1

Замечание 1. Известно (см., например, [11, 13]), что при построении

последовательных оценок параметра AR(1) по прямым наблюдениям момен-

ты остановки наблюдений определяются с помощью выборочной информа-

ции Фишера. В модели (2.6) с дополнительной аддитивной помехой моменты

128

τ₁(h) и τ₂(h) выбираются так, чтобы выборочные информации по Фишеру

∑d1(n)

∑d2(n)

y^22j-1 и

y^22j, содержащиеся отдельно в нечетных и четных на-

j=1

блюдениях, достигли заданного порога h/(Δ² + σ²).

Длительность наблюдений в последовательной процедуре оценивания θ

определим равенством

(2.13)

τ (h) = max (τ₁(h), τ₂

(h)) .

Кроме замены в оценке (2.7) n на τ(h), потребуется некоторая модифика-

ция самой оценки, используя специальные весовые коэффициенты. Сначала

найдем корректирующие множители α₁(h) и α₂(h), компенсирующие пере-

скоки в (2.12), из уравнений

d₁(τ₁(h))-1∑

y^22j-1 + α₁(h)y^22d

1(τ1(h))-1

Δ² + σ²

j=1

d₂(τ₂(h))-1∑

y^22j + α₂(h)y_2d

2(τ2(h)) =

Δ² + σ²

j=1

Заметим, что 0 < α_i(h) ≤ 1, i = 1, 2. Положим



если k = 2j - 1 и j < d₁(τ₁(h));

1,

β_1,k =

α₁(h), если k = 2d₁(τ₁(h)) - 1;



если k > 2d₁(τ₁(h)) - 1;



если k = 2j + 2 и j < d₂(τ₂(h));

1,

β_2,k =

α₂(h), если k = 2d₂(τ₂(h));



если k > 2d₂(τ₂(h)).

Построим точечную последовательную оценку Юла-Уокера в виде





τ (h)

-1 τ(h)_∑

∑√

(2.14)

τ (h) =

γ_ky_k-2y_k-1

√γ_ky_k-2y_k,

k=3

где весовые коэффициенты γ_k определяются по формуле



β1,k^{,еслиk∈T}1^(τ1^(h));

(2.15)

γ_k =

β_2,k, если k ∈ T₂(τ₂(h));



если k ∈ T (τ(h)).

Заметим, что весовые коэффициенты γ_k в оценке (2.14) равны единице

для наблюдений с нечетными номерами до момента остановки τ₁(h), а также

для наблюдений с четными номерами до момента τ₂(h); наблюдения в эти

129

моменты используются в суммах с корректирующими множителями α₁(h)

и α₂(h); остальные коэффициенты в обеих суммах равны нулю.

Покажем, что последовательная оценка (2.14) дает возможность решить

задачу доверительного оценивания параметра θ в зашумленной авторегрес-

сии AR(1) в неасимптотической постановке. Подставляя y_k из (2.6) в (2.14),

получаем

ζ(h)

τ (h) - θ =

;

s(h)

(2.16)

τ (h)

∑

s(h) =

√γ_ky_k-2y_k-1,

ζ(h) =

√γ_ky_k-2ξ_k.

k=3

Обозначим:

τ (h)

∑

ζ(h) = κ_θζ(h) =

√γ_ky_k-2

ξ_k,

k=3

(2.17)

√

Δ² + σ²

ξ_k = κ_θξ_k,

κ_θ =

Δ²(1 + θ²) + σ²

Подставляя в (2.17) весовые коэффициенты (2.15), получаем разложение

(2.18)

ζ(h)

ζ₁(h)

ζ₂

(h);

τ₁(h)∑

√

ζ₁(h) =

χ{k∈T1(τ₁(h))}

β_1,ky_k-2

ξ_k,

k=3

(2.19)

∑

√

ζ₂(h) =

β_2,ky_k-2

ξ_k.

χ{k∈T2(τ₂(h))}

k=3

Благодаря специальному выбору весовых коэффициентов (2.15) справед-

лив следующий результат.

Лемма 2. Пусть шумы {ε_k} и {η_k} в (2.6) являются гауссовскими, а

случайные величин

ζ₁(h)

ζ₂(h) определяются равенствами (2.19).

Тогда для любого h > 0 случайные величины h^-1/2

ζ₁(h) и h^-1/2ζ2(h) явля-

ются стандартными гауссовскими.

Доказательство леммы 2, основанное на теореме П.1, приводится в При-

ложении.

Построим доверительный интервал для θ с заданным коэффициентом до-

верия 0 < ρ < 1. Используя (2.16), (2.18), получаем неравенство

(

)

(2.20)

h^-1/2κ_∗|θτ(h) - θ|s(h) ≤ h^-1/2

ζ₁(h)| +

ζ₂(h)|

κ_∗ = min κ_θ.

|θ|≤L

130

Применяя лемму 2, находим оценку вероятности

(

)

ζ₁(h)|

|ζ2(h)|

P_θ

√

≥µ^∗

≤

(

)

(

)

∗

ζ₁(h)|

ζ₂(h)|

µ^∗

≤P_θ

√

≥

+P_θ

√

≥

(

)

(2.21)

(

∗

ζ₁(h)|

(µ^∗))

=2P_θ

√

≥

1-Φ

∫z

где Φ(z) = (2π)^-1/2

e-u2 du.

-∞

Из уравнения

4 (1 - Φ (µ^∗/2)) = 1 - ρ определяем µ^∗ = µ^∗(ρ) = 2Φ^-1×

× ((3 + ρ)/4) .

Используя неравенства (2.20), (2.21), приходим к следующему результату.

Теорема 1. Пусть шумы {ε_k} и {η_k} в (2.6) являются гауссовскими

и точечная последовательная оценкаθτ(h) определяется формулой (2.14).

Тогда для любых 0 < ρ < 1 и h > 0

{

}

|s(h)|

(2.22)

inf

P_θ κ_∗

√

|θτ(h)

- θ| < µ^∗

≥ ρ.

|θ|≤L

Неравенство (2.22) позволяет по заданным коэффициенту доверия ρ и па-

раметру h > 0 построить доверительный интервал для θ. При этом ширина

доверительного интервала зависит от уровней шумов σ² и Δ², а также от

статистики s(h).

Асимптотические свойства длительности последовательной процеду-

ры τ(h) и статистики s(h) при h → ∞ для устойчивого процесса авторе-

грессии (2.6) сформулируем в виде следующего утверждения.

Предложение 1. Пусть |θ| < 1, τ(h) и s(h) определяются равенства-

ми (2.13), (2.16). Тогда

τ (h)

2(1 - θ²)

(2.23)

lim

почти наверное (п.н.),

h→∞ h

(Δ² + σ²)((1 - θ²)Δ² + σ²)

s(h)

2σ²θ

(2.24)

lim

п.н.

h→∞ h

(Δ² + σ²)((1 - θ²)Δ² + σ²)

Утверждение предложения 1 следует из предложения 2, приведенного в раз-

деле 3.

3. Доверительное оценивание параметров AR(p)

по зашумленным наблюдениям

Рассмотрим теперь общую задачу неасимптотического оценивания пара-

метров θ₁, . . . , θ_p в модели (2.1), (2.2). На основе оценки Юла-Уокера (2.4)

131

построим последовательную процедуру, гарантирующую точность оценок в

момент прекращения наблюдений. При этом развивается подход, использо-

ванный в разделе 2. Во-первых, заметим, что шумовая часть ζ(n) в уклонении

оценки (2.5) не является мартингалом, как и в случае одного неизвестного па-

раметра.

На первом шаге покажем, что процесс ζ(n) допускает представление в виде

суммы мартингалов. Начнем с разбиения множества индексов суммирования

в (2.5):

⋃

T (n) = {2p + 1, 2p + 2, . . . , n} =

T_i(n),

i=1

(3.1)

T_i

(n) = {k = (p + 1)j + p + i - 1 : j = 1, 2, . . . ; k ≤ n}.

Обозначим через d_i(n) число элементов в множестве T_i(n):

d_i(n) = [(n - p - i + 1)/(p + 1)], если T_i = ∅, и

d_i(n) = 0, если T_i = ∅.

При этом максимальный номер t_i(n) в (3.1), если T_i(n) = ∅, есть t_i(n) =

= 3d_i(n) + i + 1.

{

}

Для каждого i = 1, p + 1 введем фильтрацию F⁽ⁱ⁾ = Fni)

, где

n≥0

F⁽ⁱ⁾⁰ = σ{x₀,x_-1,... ,x_-p+1}, если t_i(n) = 0,

(3.2)

F⁽ⁱ⁾ⁿ = σ{x₀,x_-1,... ,x_-p+1;ε₁,... ,ε_t

i(n),η1^,...,ηti(n)^},еслиti^(n)≥1.

Далее векторный процесс ζ(n) в (2.5) представим в виде

∑

(3.3)

ζ(n) =

ζ⁽ⁱ⁾(n), ζ⁽ⁱ⁾(n) =

χ{k∈Ti(n)}Yk-p-1ξk.

i=1

k=2p+1

Используя координаты p-мерного вектора ζ⁽ⁱ⁾(n), т.е.

∑

(3.4)

〈ζ⁽ⁱ⁾(n)〉_l =

χ{k∈Ti(n)}yk-p-lξk

l = 1,...,p,

k=2p+1

введем процессы

∑

(3.5)

M^(i)l(n) = κ_θ〈ζ⁽ⁱ⁾(n)〉_l =

χ{k∈Ti(n)}yk-p-

ξ_k;

k=2p+1

(

)_1/2

(3.6)

ξ_k = κ_θξ_k, κ_θ = (Δ² + σ²)^1/2/

σ² + Δ²(1 + θ²¹ + ··· + θ^2p)

Учитывая (2.3) и гауссовость шумов ε_k и η_k в (2.1), (2.2), отметим,

что случайная величин

ξ_k имеет гауссовское распределение с параметрами

(

)

0, Δ² + σ²

132

Следующие свойства процессов (3.5) играют ключевую роль при анализе

рассматриваемой процедуры в Приложении.

Лемма 3. Для каждого i = 1,p + 1 случайные процессы M^(i)l(n),

l = 1,p, являются квадратично-интегрируемыми мартингалами с условно-

гауссовскими приращениями, т.е.

(

)

Law

∆M^(i)l(n)|F⁽ⁱ⁾

= N(0,σ^2i,l(n - 1)),

n-1

причем

)

((

)₂

σ^2i,l(n - 1) = E_θ

∆M^(i)l(n)

|F⁽ⁱ⁾

n-1

= χ{n∈Ti(n)}(σ² + Δ²)yn-p-l.

Доказательство леммы 3 дано в Приложении.

На втором шаге построим последовательную модификацию оценки Юла-

Уокера. Сначала для каждого вектора ζ⁽ⁱ⁾(n) в разложении (3.3) введем p

моментов остановки, связанных с мартингалами (3.5). Пусть h > 0. Положим

τ⁽ⁱ⁾⁰(h) = 2p,









∑

τ^(i)l (h) = inf

n > τ(i)l-1 (h) :

χ{k∈Ti(n)} yk-p-l ≥



Δ² + σ² 

(3.7)

k=τ^(i)l-1(h)+1

l = 1,p.

Длительность наблюдений в последовательной процедуре определим по

формуле

(3.8)

τ (h) = max

τ^(i)p

(h).

1≤i≤p+1

Введенные моменты остановки (3.7) дают возможность контролировать

процесс накопления информации о неизвестных параметрах θ₁, . . . , θ_p. С их

помощью выберем весовые коэффициенты в последовательной оценке Юла-

Уокера. Во-первых, найдем корректирующие множители α^(i)l(h), 1 ≤ l ≤ p,

компенсирующие перескоки в (3.7), из уравнений

τ^(i)l(h)-1∑

y^2k-p-l + α^(i)l(h)y²

{k∈T_i(τ^(i)l(h))}

τ^(i)l(h)-p-l

Δ² + σ²

k=τ^(i)l-1+1

τ⁽ⁱ⁾⁰(h) = 2p.

Отметим, что моменты остановки τ⁽ⁱ⁾¹(h), . . . ,

p (h) для каждого i = 1, p + 1

образуют возрастающую последовательность, причем каждый из моментов

строится по квадратичной характеристике σ^2i,l(n - 1) своего мартингала (3.5).

133

Положим

{

если τ⁽ⁱ⁾

(h) < k < τ^(i)l(h),

l-1

(3.9)

β^(i)l,k(h) =

α⁽ⁱ⁾¹(h), если k = τ^(i)l(h),

и определим весовые коэффициенты γ_l,k равенствами

√

∑

]

(3.10)

γ_l,k =

µ⁽ⁱ⁾

β^(i)l,k,

µ^(i)k,l = χ_{k∈T

(k).

k,l

i(k)}χ^(τ(i)

(h),τ^(i)l(h)

l-1

i=1

Построение последовательной оценки Юла-Уокера завершим определе-

нием.

Определение 1. Для каждого h > 0 последовательный план оценива-

ния вектора параметров θ = (θ₁,... ,θ_p)^T в модели (2.1), (2.2) задается па-

рой (τ(h),θ^∗(h)), где τ(h)

длительность процедуры, определенная в (3.8),

θ^∗(h) = (θ^∗1(h),... ,θ^∗p(h))^T

вектор оценок, задаваемый формулами

(3.11)

θ^∗(h) = G^-1

(h)ϑ(h).

Здесь ϑ(h) = (ϑ₁(h), . . . , ϑ_p(h))^T

p-мерный вектор с координатами

τ (h)

∑

(3.12)

ϑ_l(h) =

γ_l,ky_k-p-ly_k

1 ≤ l ≤ p;

k=2p+1

G(h) матрица размера p × p с элементами

∑

(3.13)

〈G(h)〉_l,s =

γ_l,ky_k-p-ly_k-s.

k=2p+1

Отметим, что в отличие от оценки (2.4) последовательная оценка (3.11)

строится по выборке случайного объема. При этом длительность процеду-

ры τ(h) и весовые коэффициенты γ_l,k зависят от выбора значения парамет-

ра h, который позволяет контролировать точность оценивания. Используя

точечную оценку (3.11), получаем решение задачи доверительного оценива-

ния в неасимптотической постановке.

Теорема 2. Пусть шумы {ε_k} и {η_k} в уравнениях (2.1), (2.2) являются

гауссовскими, θ ∈ Θ ⊂ R^p и последовательный план оценивания вектора па-

раметров θ = (θ₁, . . . , θ_p)^T определяется формулами (3.8), (3.11). Тогда для

любого 0 < ρ < 1 и h > 0

(

)

κ_∗

inf

P_θ

√ ∥G(h)(θ^∗(h) - θ)∥ < µ^∗

≥ ρ,

θ∈Θ

где

κ_∗ = inf

κ_θ,

θ∈Θ

134

(p+ρ)

µ^∗ = (p + 1) Φ^-1

^p p+1

(3.14)

∫

Φ_p (a) =

(_p) z^p-1e-z2 dz, a ≥ 0.

2² -1Γ

Доказательство теоремы 2, приведенное в Приложении, опирается на

теорему П.2 о свойствах остановленных квадратично-интегрируемых мартин-

галов с условно-гауссовскими приращениями, установленных в [24]. Соглас-

но теореме 2 для построения доверительной области для вектора параметров

θ = (θ₁,...,θ_p)^T по заданному коэффициенту доверия ρ сначала находится

пороговое значение µ^∗ по формуле (3.14). Размеры доверительной области

для θ можно сократить, увеличивая параметр h, определяющий длительность

наблюдений в процедуре.

Предложение 2. Пусть AR(p) процесс

(2.1) устойчив, моменты

остановки τ(h) и матрица G(h) определяются равенствами (3.8) и (3.13).

Тогда

τ (h)

p(p + 1)

(3.15)

lim

п.н.,

h→∞ h

(Δ² + σ²) (〈F 〉₁₁ + Δ²)

G(h)

(p + 1)F (A^T)

lim

п.н.,

h→∞ h

(Δ² + σ²)(〈F 〉₁₁ + Δ²)

где

(

)

∑

θ₁

... θ_p

F =

A^jB(A^T)^j, B = ∥σ²δ_1,iδ_1,j∥, A =

I_p-1

j≥0

Доказательство предложения 2 приводится в Приложении.

Замечание 2. Из предложения 2 следует, что в случае устойчивого про-

цесса (2.1) диаметр доверительного эллипсоида, определяемый теоремой 2,

√

уменьшается с ростом h как const/

4. Численные результаты

Рассмотрим выборочные свойства построенных оценок и оценок Юла-

Уокера для параметра θ в модели (2.6) с гауссовским шумами {ε_k} и {η_k}

с Eε_k = Eη_k = 0, Eε^2k = 1 и Eη^2k = 0,01. Заметим, что при |θ| < 1 наблюдае-

мый процесс {y_k} имеет спектральную плотность [2]

(

)

σ² + Δ²

-2θ cos λ + 1 + θ²

(4.1)

f (λ) =

-π ≤ λ ≤ π,

2π (-2θ cos λ + 1 + θ²)

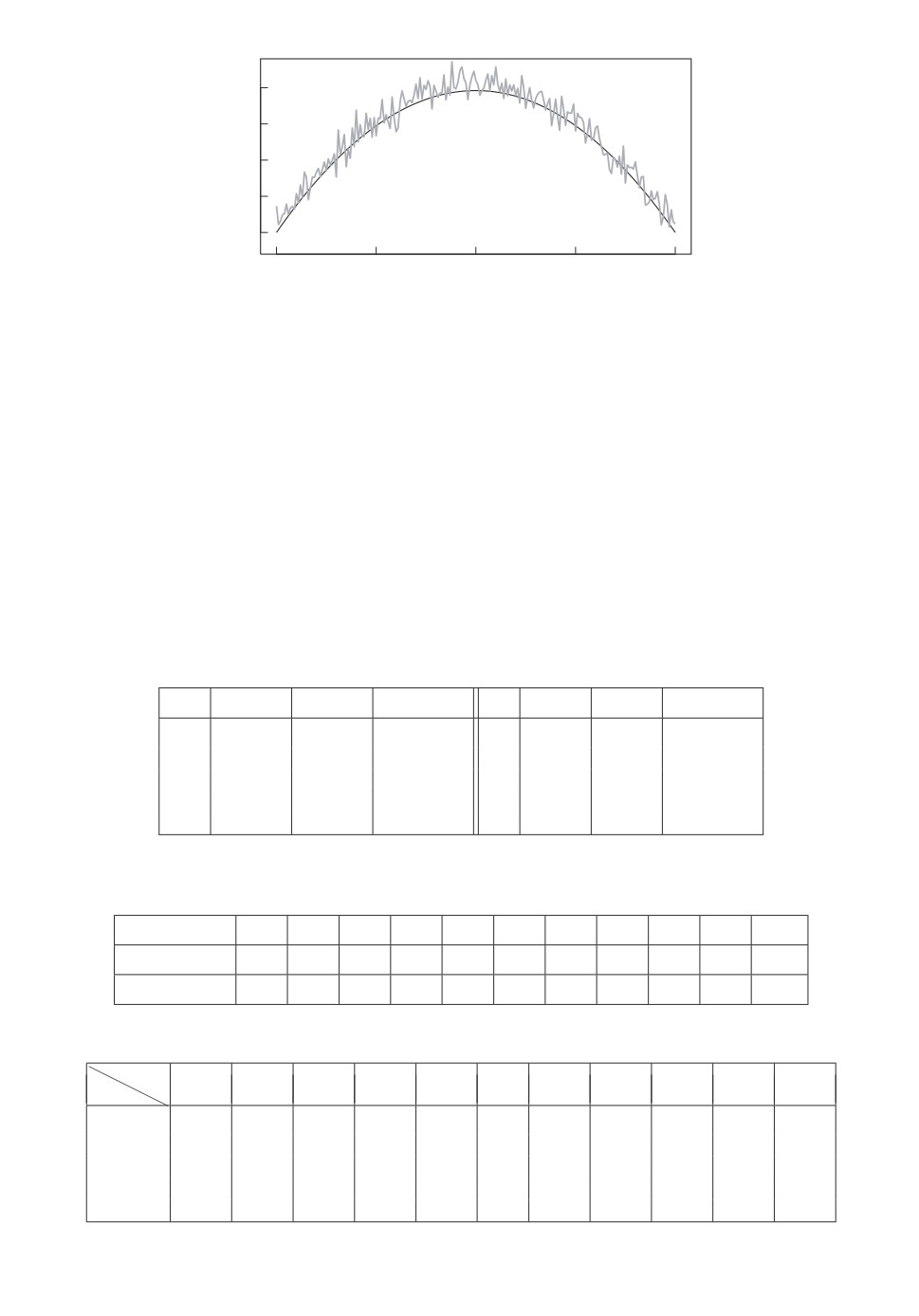
если {x_k} в (2.6) является стационарным. На рис. 1 для длительности τ(h)

предлагаемой последовательной процедуры (2.14) приводится выборочное по-

ведение отношения τ(h)/h в зависимости от параметра -1 < θ < 1 при h =

= 300.

135

2,0

1,5

1,0

0,5

-1,0

-0,5

0,5

1,0

Рис. 1. Выборочное поведение отношения τ(h)/h (серая линия) и асимптоти-

ческая кривая (2.23) (черная линия).

В табл. 1 представлены средние значения последовательных оценокθτ(h),

полученные с помощью процедуры (2.14) с h = 1000, а также средние значе-

ния классических оценок Юла-Уокера θ_n. Средние в обоих случаях вычис-

лялись по 1000 повторений каждой процедуры. При этом объем выборки для

оценок Юла-Уокера выбирался равным соответствующей средней длитель-

ности последовательной процедуры, указанной в столбце τ. Доверительный

интервал на основе последовательной оценки (2.14) строился с помощью тео-

ремы 1. При уровне доверия ρ = 0,9 и |θ| < 1, используя (2.22), получаем

Таблица 1. Усредненные оценки параметра AR(1) (h = 1000)

θ_n

τ (h)

–1,0

-1,0002

-0,9798

91,5450

0,3

0,2979

1832,2460

–0,8

-0,7969

-0,7976

736,0060

0,4

0,3985

0,3987

1693,9700

–0,6

-0,6005

-0,5974

1291,7620

0,6

0,5966

0,5992

1293,2380

–0,4

-0,3972

-0,3998

1690,6190

0,8

0,7984

0,7973

729,5970

–0,3

-0,2994

-0,2991

1829,6720

1,0

0,9993

0,9817

94,9450

Таблица 2. Выборочное поведение отношения |s(h)|/h и предела lim |s(h)|/h

в зависимости от θ (h = 300)

-1

-0,8

-0,6

-0,4

-0,2

0,2

0,4

0,6

0,8

lim |s(h)|/h

1,98

1,58

1,18

0,79

0,39

0,79

1,18

1,58

1,98

|s(h)|/h

1,74

1,48

1,25

0,66

0,54

0,10

0,34

0,82

1,26

1,65

1,81

Таблица 3. Усредненная ширина полуинтервала интервальной оценки (4.2)

-1

-0,8

-0,6

-0,4

-0,2

0,2

0,4

0,6

0,8

500

0,099

0,113

0,151

0,228

0,464

20,1

0,465

0,227

0,152

0,113

0,100

1000

0,068

0,080

0,106

0,161

0,326

13,5

0,330

0,160

0,106

0,080

0,068

2000

0,047

0,056

0,075

0,113

0,226

27,9

0,224

0,112

0,075

0,056

0,047

3000

0,038

0,046

0,061

0,092

0,185

69,6

0,183

0,092

0,061

0,046

0,038

5000

0,029

0,035

0,047

0,071

0,140

10,7

0,143

0,071

0,047

0,035

0,029

136

0,8

q = -0,5

q = 0,5

0,4

-3

-2

-1

Рис. 2. Доверительные области для оценки спектральной плотности (4.1).

доверительный интервал для θ

(

)

(4.2)

√

, θ_τ(h) + 3,94h

√

τ (h) - 3,94

|s(h)|

Здесь множитель |s(h)|/h выделен, учитывая равенство (2.24). В табл. 2 ука-

заны значения модуля асимптотической кривой (2.24) из предложения 1 для

различных значений θ, а также выборочное поведение этого отношения при

h = 300.

В та√. 3 приводятся выборочные средние для ширины полуинтервала

µ = 3,94

h/|s(h)| доверительного интервала (4.2), полученные по 100 повто-

рениям процедуры, для различных значений θ и h. Как видно из табл. 3,

качество доверительных последовательных оценок существенно зависит от

значений параметра θ, если параметр h, определяющий длительность на-

блюдений τ(h), остается постоянным. При значениях θ, близких к нулю, что

соответствует ослаблению авторегрессионного сигнала x_k, требуется значи-

тельно увеличивать порог h, чтобы сохранить приемлемую точность оцени-

вания θ. Это вполне объяснимо, если учесть в (4.2) асимптотическую зависи-

мость (2.24) от θ в предложении 1. При отсутствии условия отделимости |θ|

от нуля порог h, обеспечивающий приемлемое качество доверительного ин-

тервала (4.2), нельзя выбрать априорно, и его приходится подбирать эмпи-

рически, повторяя процедуру оценивания (2.14) для больших значений h.

На рис. 2 представлены доверительные области для оценки спектральной

плотности (4.1), полученные с помощью доверительных оценок для значе-

ний θ = -0,5 и θ = 0,5 при ρ = 0,9 и h = 5000.

5. Заключение

В разделах 2 и 3 предложены и исследованы последовательные процедуры

доверительного оценивания параметров гауссовской авторегрессии по наблю-

дениям с аддитивным гауссовским шумом. Последовательная оценка вектора

неизвестных параметров для авторегрессии любого порядка строится на ос-

нове одной классической оценки Юла-Уокера, вводя специальное правило

прекращения наблюдений и используя весовые коэффициенты в структуре

137

оценки. В теоремах 1 и 2 устанавливается, что предлагаемые последователь-

ные оценки Юла-Уокера дают решение задачи идентификации зашумленной

авторегрессии в неасимптотической постановке, позволяя определить дли-

тельность наблюдений в зависимости от требуемого качества оценивания.

В разделе 4 рассматривается численный пример доверительного оценивания

спектральной плотности зашумленной авторегрессии. Результаты могут ис-

пользоваться в задачах идентификации и управления.

Авторы выражают признательность анонимным рецензентам за конструк-

тивные замечания.

ПРИЛОЖЕНИЕ

Приведем теорему П.1 и теорему П.2 о свойствах остановленных мартин-

галов с условно-гауссовскими приращениями из публикаций [23] и [24], ис-

пользованных в разделах 2 и 3 при выборе весовых коэффициентов (2.15) и

(3.9), (3.10) в последовательных оценках Юла-Уокера (2.14) и (3.11), а также

при определении длительности процедуры. Дадим доказательства некоторых

технических результатов.

Теорема П.1. Пусть (M_k,F_k)_k≥0 квадратично интегрируемый мар-

тингал [23] такой, что

а) его квадратическая характеристика удовлетворяет условию

P_θ (〈M〉_∞ = +∞) = 1;

б) Law(∆M_k|F_k-1) = N (0, σ^2k-1), k = 1, 2, . . ., т.е. F_k-1 условное распре-

деление ∆M_k = M_k - M_k-1 является гауссовским с параметрами 0 и σ^2k-1 =

(

)

(∆M_k)²|F_k-1

Для каждого h определим момент остановки

{

}

∑

(Π.1)

τ = τ(h) = inf n > 0 :

σ^2k-1 ≥ h

inf{∅} = ∞,

k=1

и случайную величину

τ (h)

∑√

{ 1,

если 1 ≤ k < τ(h),

m(h) =

√

β_k(h)∆M_k, β_k(h) =

α(h), если k = τ(h);

h k=1

α(h) множитель, определяемый из уравнения

τ (h)-1∑

σ^2k-1 + α(h)σ^2τ(h)-1 = h.

k=1

Тогда для любого h > 0 величина m(h) является стандартной гауссов-

ской.

138

(

)

Доказательство леммы 1. Проверим, что

ζ₁(n),Fn1)

мар-

n≥3

тингал. Измеримость ζ₁(n) относительно

n следует из определений (2.10),

(

)

(2.11). Покажем, что E ζ₁(n + 1)|Fn1)

= ζⁿ¹⁾. Рассмотрим, например, случай

четного n. Пусть n = 2l, тогда

∑

ζ₁(2l + 1) =

χ{k∈T1(2l+1)}yk-2ξk.

k=3

Отсюда

(

)

(

)

∑

E ζ₁(2l + 1)|F⁽¹⁾

χ{k∈T1(2l+1)}yk-2ξk|F2l-

2l-1

k=3

∑

(

)

= χ{k∈T1(2l+1)}yk-2ξk + χ{(2l+1)∈T₁(2l+1)}y2l-1E ξ2l+1|F2l-

= ζ₁(2l).

k=3

Проверка мартингальности ζ₂(n) проводится аналогично.

Лемма 1 доказана.

Доказательство леммы 2. Покажем, что требуемый результат сле-

дует из теоремы П.1. Введем случайные процессы

∑

(Π.2)

M⁽¹⁾ⁿ =

χ{k∈T1(n)}yk-

ξ_k, M⁽²⁾ⁿ =

χ{k∈T2(n)}yk-

ξ_k

n ≥ 3.

k=3

(

)

(

)

Процессы

,Fn1)

,Fn2)

являются мартингалами, при-

n≥3

чем

)

((

)₂

E_θ

∆M⁽¹⁾ⁿ

|F⁽¹⁾

=y^2n-2E_θ

ξ²ⁿχ_{n∈T

n-1

1(n)},

(Π.3)

)

((

)₂

E_θ

∆M⁽²⁾ⁿ

|F⁽²⁾

=y^2n-2E_θ

ξ²ⁿχ_{n∈T

ξ²ⁿ = Δ² + σ².

n-1

2(n)};

Проверим эти свойства для

. По определению T₁(n) и T₂(n) в (2.9)

получаем

∑

M⁽¹⁾ⁿ =

ξ_n =

χ{k∈T1(n)}yk-

ξ_k + χ{n∈T1(n)}yn-

k=3

=M^(1)n-1 +χ_{n∈T

ξ_n.

1(n)}yn-

Отсюда ∆

=χ{n∈T1(n)}yn-

ξ_n. Поэтому

)

((

)₂

(

)

E_θ

∆M⁽¹⁾ⁿ

|F⁽¹⁾

ξ²ⁿ|F⁽¹⁾

n-1

=χ{n∈T1(n)}Eθ yn-

n-1

139

Заметим, что если n ∈ T₁(n), то F^(1)n-1 = F^(1)n-2. Если, например, n нечетно,

то число n - 1 четно. Следовательно, m₁(n) = n, m₁(n - 1) = m₁(n - 2). По

определению F^(1)n-1 = F^(1)n-2. Так как ξ²ⁿ не зависит от F^(1)n-2, то

)

((

)₂

(

)

E_θ

∆M⁽¹⁾ⁿ

|F⁽¹⁾

=y^2n-2E_θ

ξ²

n-1

χ{n∈T1(n)}

(

) (

)

Далее заметим, что мартингалы

,Fn1)

,Fn2)

, определяемые

равенствами (Π.2), и их квадратические характеристики (Π.3) удовлетворяют

условиям теоремы П.1. При этом момент остановки τ₁(h) в (2.12) совпадает

√

с (Π.1). В силу теоремы П.1 случайные величин

ζ₁(h)/

ζ₂(h)/

h явля-

ются стандартными гауссовскими. Лемма 2 доказана.

Доказательство предложения 2. Модель (2.1), (2.2) в векторной

форме записывается в виде

(Π.4)

X_k = AX_k-1 + ν_k, Y_k = X_k + ζ_k,

где X_k = (x_k, . . . , x_k-p+1)^T, ν_k = (ε_k, 0, . . . , 0)^T, ζ_k = (η_k, . . . , η_k-p+1)^T,

(

)

... θ_p

I_p-1

Для анализа τ(h) потребуется асимптотическое поведение суммы

∑

C⁽ⁱ⁾ⁿ =

χ{k∈Ti(n)}Yk-p-1

k-p-1

k=2p+1

Подставив Y_k из (Π.4), имеем разложение

(Π.5)

C⁽ⁱ⁾ⁿ = U⁽ⁱ⁾ⁿ + V⁽ⁱ⁾ⁿ + R⁽ⁱ⁾ⁿ;

∑

U⁽ⁱ⁾ⁿ =

χ{k∈Ti(n)}Xk-p-1Xk-p-1,

k=2p+1

∑

V(i)n =

χ{k∈Ti(n)}ζk-p-1ζk-p-1,

k=2p+1

∑

R⁽ⁱ⁾ⁿ =

χ{k∈Ti(n)}ζk-p-1Xk-p-1 +

χ{k∈Ti(n)}Xk-p-1ζk-p-1.

k=2p+1

Учитывая (3.1), получаем

d_i(n)∑

(Π.6)

U⁽ⁱ⁾ⁿ =

Z_jZ^Tj, Z_j = X_(p+1)j+i-2.

j=1

140

Последовательность {Z_j } удовлетворяет векторному уравнению авторе-

грессии

∑

Z_j = A^p+1Z_j-1 + w_j, w_j =

A^p+1-sν_{(p+1)(j-1)+i-2+s},

s=1

причем

∑

Ew_j = 0, Ew_jw^Tj = A^lB(A^T)^l =B, B = ∥σ²δ_1,iδ_1,j∥.

l=0

Поскольку процесс Z_j устойчив, то (см., например, [2])

∑

lim

Z_jZ^Tj

F п.н.;

n→∞ n

j=1

(Π.7)

∑

F = A^(p+1)j B(A^T)^(p+1)j =

A^jB(A^T)^j =: F.

j≥0

Из (Π.6) и (Π.7) с учетом (3.1) находим

n di(n)

(Π.8)

lim

= lim

п.н.

n→∞ n

n→∞ d_i(n) n

p+1

Далее непосредственно проверяется, что

Rⁿⁱ⁾

lim

I_p,

lim

п.н.

n→∞ n

p+1

n→∞ n

Отсюда и из (Π.5), (Π.8) получаем

(

)

lim

n^-1C⁽ⁱ⁾ⁿ = (p + 1)^-1

F +Δ²I_p

n→∞

Так как

∑

χ{k∈Ti(n)}yk-p-l = 〈Cⁿⁱ⁾〉ll,

k=2p+1

то

∑

(

)

(Π.9)

lim

〈F 〉₁₁ + Δ²

l = 1,p.

χ{k∈Ti(n)}yk-p-l =

n→∞ n

p+1

k=2p+1

Найдем теперь асимптотику для моментов остановки τ^(i)l(h). По определе-

нию τ⁽ⁱ⁾¹(h) в (3.7) имеем

τ⁽ⁱ⁾¹(h)-1∑

τ⁽ⁱ⁾¹(h)∑

(

χ^{

^)}y^2k-p-1 <

≤

χ^{(

^)}y^2k-p-1.

k∈Ti τ(i)1

k∈T_i τ⁽ⁱ⁾

Δ² + σ²

k=2p+1

141

Отсюда, используя (Π.9), получаем

(

)

lim

〈F 〉₁₁ + Δ²

p+1

^h→∞ (Δ² + σ²)τ⁽ⁱ⁾¹(h)

т.е.

(i)

τ₁

(h)

p+1

lim

h→∞ h

(Δ² + σ²) (〈F 〉₁₁ + Δ²)

Аналогично находим, что

(i)

τ_l

(h)

l(p + 1)

(Π.10)

lim

2 ≤ l ≤ p.

h→∞ h

(Δ² + σ²) (〈F 〉₁₁ + Δ²)

Принимая во внимание (3.8), получаем соотношение (3.15) для длительно-

сти последовательной процедуры. Далее рассмотрим асимптотическое пове-

дение матрицы G(h), определенной в (3.13). Для устойчивого процесса (2.1)

справедливо свойство [2]

∑

lim

Y_k-p-1Y^Tk-1 = F(A^T)^p.

n→∞ n

k=2p+1

Аналогично (Π.8) устанавливается, что матрица

∑

D⁽ⁱ⁾(n) =

χ{k∈Ti(n)}Yk-p-1

k-1

k=2p+1

удовлетворяет предельному соотношению

(Π.11)

lim

D⁽ⁱ⁾(n) =

F (A^T)^p.

n→∞ n

p+1

Далее, подставляя коэффициенты (3.10) в элемент матрицы (3.13) и учи-

тывая, что y_k-p-l = 〈Y_k-p-1〉_l, y_k-s = 〈Y_k-1〉_s, получаем

√

∑

τ^(i)l(h)∑

(Π.12)

〈G(h)〉_l,s =

χ{k∈Ti(k)}

〈Y_k-p-1Y^Tk-1〉_l,s.

l,k

i=1 k=τ^(i)l-1(h)+1

Учитывая определение коэффициентов (3.9), заметим, что внутренняя

сумма с точностью до одного слагаемого, отвечающего моменту τ^(i)l(h), сов-

падает с суммой

τ^(i)l(h)∑

〉_l,s =

χ{k∈Ti(k)}〈Yk-p-1

k-1

k=τ^(i)l-1(h)+1

(

= D⁽ⁱ⁾ τ^(i)l(h)

− D⁽ⁱ⁾ τ^(i)l-1(h)

l,s

142

Отсюда и из (Π.10), (Π.11) следует, что

τ^(i)l(h)∑

lim

〉_l,s =

χ{k∈Ti(k)}〈Yk-p-1

k-1

h→∞ h

k=τ^(i)l-1(h)+1



(



(i)

D⁽ⁱ⁾ τ^(i)l(h)

D⁽ⁱ⁾ τ^(i)l-1(h)

τl

(h)

l,s

τ^(i)l-1(h)

l,s



= lim



=

h→∞

τ^(i)l(h)

τ^(i)l-1(h)

^T)^p

F (A

l,s

(Δ² + σ²) (〈F 〉₁₁ + Δ²)

Используя это равенство в (Π.12), получаем

G(h)

(p + 1)F (A^T)

lim

h→∞ h

(Δ² + σ²)(〈F 〉₁₁ + Δ²)

Предложение 2 доказано.

Теорема П.2. Пусть заданы [24]:

1) вероятностное пространство (Ω, F, P) с фильтрацией (F)_k≥0;(

)

2) семейство M^(l),F

, l

= 1, p, квадратично интегрируемых мар-

k≥0

тингалов с квадратическими характеристиками {〈M^(l)〉_n}_n≥1, l = 1,p, та-

кими, ч(то

)

а) P

〈M^(l)〉_∞ = +∞

= 1, l = 1, p;

(

)

б) Law

∆M^(l)|Fk-1

= N(0,σ2l (k - 1)), k = 1,2,..., l = 1,p, т.е. F_k-1

условное распределение приращения ∆M^(l)k = M^(l)k - M^(l)k-1 является гауссов-

)

((

)₂

ским с параметрами 0 и σ^2l(k - 1) = E

∆M^(l)k

|F_k-1

Для каждого h > 0 определим момент остановки







∑



τ_l = τ_l(h) = inf

n > τ_l-1(h) :

σ^2l(k - 1) ≥ h

l = 1,p,





k=τ_l-1+1

τ₀ = τ₀(h) = 0, inf{∅} = +∞,

и случайные величины

∑

√

m_l(h) =

√

β_k(h,l)∆M^(l)k, l = 1,p;

h k=τ_l-1+1

{ 1,

если τ_l-1(h) < k < τ_l(h),

β_k(h,l) =

α_l(h), если k = τ_l(h);

143

α_l(h), l = 1,p,

корректирующие множители, определяемые из уравнений

∑

σ^2l(k - 1) + α_l(h)σ^2l(τ_l(h) - 1) = h.

k=τ_l-1+1

Тогда для любого h > 0 случайный вектор m(h) = (m₁(h), . . . , m_p(h))^T име-

ет стандартное нормальное распределение, т.е. m(h) ∼ N(0,I_p), где I_p

единичная матрица размерности p.

Доказательство леммы 3. Запишем (3.4) в виде

∑

M^(i)l(n) =

χ{k∈Ti(n)}yk-p-

ξ_k + χ{n∈Ti(n)}yn-p-

ξ_n =

k=2p+1

= M^(l)i(n - 1) + χ_{n∈T

ξ_n,

i(n)}yn-p-

т.е.

(Π.13)

∆M^(i)l(n) = χ_{n∈T

ξ_n.

i(n)}yn-p-

Отсюда имеем

)

((

)₂

σ^2i,l(n - 1) = E_θ

∆M^(i)l(n)

|F⁽ⁱ⁾

n-1

(Π.14)

(

)

ξ²ⁿ|F⁽ⁱ⁾

=χ{n∈Ti(n)}Eθ yn-p-

n-1

где F^(i)n-1

σ-алгебра, определенная в (3.2). Далее заметим, что если

n ∈ T_i(n), то t_i(n) = n, t_i(n - 1) = n - p - 1. Поэтому F^(i)n-1 = F^(i)n-p-1 и слу-

чайная величина y^2n-p-l измерима относительно F^(i)n-p-1, а

ξ_n не зависит

от F^(i)n-p-1. В силу (3.6) и гауссовост

ξ_n приращение (Π.13) имеет F^(i)n-1

условно-гауссовское распределение, причем, учитывая (Π.14), σ^2i,l(n - 1) =

= χ{n∈Ti(n)}(σ² + Δ²)y^n-p-l. Лемма 3 доказана.

Доказательство теоремы 2. Подставляя y_k из (2.1) в (3.12) и учи-

тывая (3.13), получаем

(

)

∑

(Π.15)

ϑ_l(h) =

γ_l,ky_k-p-l

y_k-sθ_s + ξ_k

k=2p+1

s=1





τ (h)

∑



γ_l,ky_k-p-ly_k-s θ_s +

γ_l,ky_k-p-lξ_k = 〈G(h)θ〉_l + ζ_l(n),

s=1

k=2p+1

где

∑

(Π.16)

ζ_l(h) =

γ_l,ky_k-p-lξ_k

1 ≤ l ≤ p.

k=2p+1

144

В векторной форме система уравнений (Π.15) имеет вид

(Π.17)

ϑ(h) = G(h)θ + ζ(h); ζ(h) = (ζ₁(h), . . . , ζ_p(h))^T.

Подставляя весовые коэффициенты (3.10) в (Π.16), получаем

∑

ζ_l (h) =

ζ^(i)l (h) ,

i=1

(Π.18)

√

τ^(i)l(h)∑

ζ^(i)l (h) =

β^(i)l,k (h) χ_{k∈T

i(k)} yk-p-l^ξk^.

k=τ^(i)l-1(h)+1

(

)_T

Введя векторы ζ⁽ⁱ⁾(h) = ζ⁽ⁱ⁾¹(h), . . . , ζ^pi)(h)

, i = 1,p + 1, имеем разложе-

ние

∑

ζ(h) =

ζ⁽ⁱ⁾(h).

i=1

Далее рассмотрим вектор

(

)_T

(Π.19)

m⁽ⁱ⁾(h) = m⁽ⁱ⁾¹(h),... ,m^(i)p(h)

:= κ_θh^-1/2ζ⁽ⁱ⁾

(h).

Учитывая (3.5), координаты этого вектора запишем в виде

√

τ^(i)l(h)∑

(Π.20)

m^(i)l(h) =

√

β^(i)l,k(h)∆M^(i)l

(k).

k=τ^(i)l-1(h)+1

Используя (Π.17), (Π.18), (Π.19), получаем

√

∑

(Π.21)

G(h) (θ^∗(h) - θ) =

m⁽ⁱ⁾

(h).

θ i=1

К векторам (Π.19) применима теорема П.2, поскольку мартингалы (3.5) и мо-

менты остановки (3.7) в (Π.20) удовлетворяют в силу леммы 3 всем условиям

этой теоремы. Согласно теореме П.2 все векторы (Π.19) имеют стандартное

p-мерное нормальное распределение N (0, I_p). Отсюда следует, что квадраты

норм этих векторов ∥m⁽ⁱ⁾(h)∥², i = 1, p + 1, имеют χ² распределение с p сте-

(

)

пенями свободы, т.е. P

∥m⁽ⁱ⁾(h)∥ > a

= 1 - Φ_p(a), где Φ_p(a) функция рас-

пределения, определенная в (3.14). Построим доверительную область для θ

по заданной доверительной вероятности. Из (Π.21) имеем неравенство

∑

κ_θ

(Π.22)

√ ∥G(h)(θ^∗(h) - θ)∥ ≤

∥m⁽ⁱ⁾

(h)∥.

i=1

145

Используя оценку

(_p+1

)

(

)

∑

(Π.23)

P_θ

∥m⁽ⁱ⁾(h)∥ > µ

≤ P_θ

∥m⁽ⁱ⁾(h)∥ >

p+1

i=1

(

)

(

))

= (p + 1) P_θ

∥m⁽¹⁾(h)∥ >

= (p + 1)

1-Φ_p

p+1

найдем µ по заданному ρ из уравнения (p + 1) (1 - Φ_p (µ/(p + 1))) = 1 - ρ.

Корень этого уравнения µ^∗ определяется формулой (3.14). Используя (Π.22),

(Π.23), получаем

(

)

κ_θ

P_θ

√ ∥G(h)(θ^∗(h) - θ)∥ ≤ µ^∗

≥ ρ.

Теорема 2 доказана.

СПИСОК ЛИТЕРАТУРЫ

Ljung L., Söderstrom T. Theory and Practice of recursive Identification. Cambridge,

Massachusetts: London The MIT Press, 1986.

Андерсон Т. Статистический анализ временных рядов. М.: Мир, 1976.

Brockwell P.J., Davis R.A. Time Series: Theory and Methods. N.Y.: Springer Sci-

ence+Business Media, 1991.

Васильев В.А., Добровидов А.В., Кошкин Г.М. Непараметрическое оценивание

функционалов от распределений стационарных последовательностей. М.: Наука,

2004.

Кашковский Д.В., Конев В.В. Последовательная идентификация линейной ди-

намической системы со случайными параметрами // АиТ. 2008. № 8. С. 82-95.

Kashkovskii D.V., Konev V.V. Successive Identification of the Random-parameter

Linear Dynamic Systems // Autom. Remote Control. 2008. V. 69. No. 8. P. 1344-

1356.

Konev V.V., Pergamenshchikov S.M. Robust Model Selection for a Semimartingale

Continuous Time Regression from Discrete Data // Stoch. Process. Their Appl. 2015.

V. 125. No. 1. P. 294-326.

Емельянова Т.В., Конев В.В. О последовательном оценивании параметров три-

гонометрической регрессии с непрерывным временем // АиТ. 2016. № 6. С. 61-80.

Emel’yanova T.V., Konev V.V. On Sequential Estimation of the Parameters of

Continuous-time Trigonometric Regression // Autom. Remote Control. 2016. V. 77.

No. 6. P. 992-1008.

Себер Дж. Линейный регрессионный анализ. М.: Мир, 1980.

Новиков А.А. Последовательное оценивание параметров диффузионных процес-

сов // Теория вероятн. и ее примен. 1971. Т. 16. № 2. С. 394-396.

10.

Липцер Р.Ш., Ширяев А.Н. Статистика случайных процессов. М.: Наука, 1974.

11.

Lai T.L., Siegmund D. Fixed Accuracy Estimation of an Autoregressive Parameter //

Ann. Statist. 1983. V. 11. P. 478-485.

12.

Galtchouk L., Konev V. On Asymptotic Normality of Sequential LS-estimate for

Unstable Autoregressive Process AR(2) // J. Multivariate Anal., Academic Press.

2010. V. 101. No. 10. P. 2616-2636.

146

13.

Борисов В.З., Конев В.В. О последовательном оценивании параметров дискрет-

ных процессов // АиТ. 1977. № 10. С. 58-64.

Borisov V.Z., Konev V.V. On Sequential Parameter Estimation in Discrete-time

Processes // Autom. Remote Control. 1977. V. 38. No. 10. P. 1475-1480.

14.

Воробейчиков С.Э., Конев В.В. О последовательной идентификации стохасти-

ческих систем // Изв. АН СССР. Техническая кибернетика. 1980. № 4. С. 91-98.

15.

Конев В.В., Пергаменщиков С.М. Последовательные планы идентификации па-

раметров динамических систем // АиТ. 1981. № 7. С. 84-92.

Konev V.V., Pergamenshchikov S.M. Sequential Plans of Parameter Identification in

Dynamic Systems // Autom. Remote Control. 1981. V. 42. No. 7. Part 1. P. 917-924.

16.

Васильев В.А., Конев В.В. Последовательное оценивание параметров динами-

ческих систем при неполном наблюдении // Изв. АН СССР. Техническая ки-

бернетика. 1982. № 6. С. 145-154.

17.

Xia Y., Zheng W.X. Novel Parameter Estimation of Autoregressive Signals in the

Presence of Noise // Automatica. 2015. V. 62. P. 98-105.

18.

Куликова М.В. Максимально правдоподобное оценивание линейных стохасти-

ческих систем в классе последовательных квадратно-корневых ортогональных

методов фильтрации // АиТ. 2011. № 4. С. 99-120.

Kulikova M.V. Maximum Likelihood Estimation of Linear Stochastic Systems in the

Class of Sequential Square-root Orthogonal Filtering Methods // Autom. Remote

Control. 2011. V. 72. No. 4. P. 766-786.

19.

Diversi R., Guidorzi R., Soverini U. Identification of Autoregressive Models in the

Presence of Additive Noise // Int. J. Adapt. Control Signal Process. 2008. V. 22.

No. 5. P. 465-481.

20.

Labarre D., Grivel E., Berthoumieu Y., Todini E., Najim M. Consistent Estimation

of Autoregressive Parameters from Noisy Observations Based on Two Interacting

Kalman Filters // Signal Processing. 2006. V. 86. No. 10. P. 2863-2876.

21.

Zheng W.X. Fast Identification of Autoregressive Signals from Noisy Observations //

IEEE Trans. Circuits and Systems-II: Express Briefs. 2005. V. 52. No. 1. P. 43-48.

22.

Pagano M. Estimation of Models of Autoregressive Signal Plus White Noise // Ann.

Stat. 1974. V. 2. No. 1. P. 99-108.

23.

Конев В.В. Об одном свойстве мартингалов с условно-гауссовскими прираще-

ниями и его применении в теории неасимптотических выводов // ДАН. 2016.

Т. 471. № 5. С. 523-527.

Konev V.V. On One Property of Martingales with Conditionally Gaussian Incre-

ments and Its Application in the Theory of Nonasymptotic Inference // Doklady

Mathematics. 2016. V. 471. No. 5. P. 523-527.

24.

Konev V., Nazarenko B. Sequential Fixed Accuracy Estimtion for Nonstationary

Autoregressive Processes // AISM. 2020. V. 72. No. 1. P. 235-264.

25.

Воробейчиков С.Э., Конев В.В. О доверительном последовательном оценивании

параметров стохастических динамических систем с условно-гауссовскими шума-

ми // АиТ. 2017. № 10. С. 90-108.

Vorobeichikov S.E., Konev V.V. On Sequential Confidence Estimation of Parameters

of Stochastic Dynamical Systems with Conditionally Gaussian Noises // Autom.

Remote Control. 2017. V. 78. No. 10. P. 1803-1818.

26.

Куржанский А.Б., Фурасов В.Д. Идентификация билинейных систем. Гаранти-

рованные псевдоэллипсоидальные оценки // АиТ. 2000. № 1. С. 41-53.

Kurzhanskii A.B., Furasov V.D. Identification of Bilinear Systems. Guaranteed Pseu-

doellipsoidal Estimates // Autom. Remote Control. 2000. V. 61. No. 1. P. 38-49.

147