Автоматика и телемеханика, № 6, 2021
© 2021 г. А.Ю. ПОПКОВ, канд. техн. наук (apopkov@isa.ru)
(Федеральный исследовательский центр “Информатика и управление” РАН,
Москва)
РАНДОМИЗИРОВАННОЕ МАШИННОЕ ОБУЧЕНИЕ НЕЛИНЕЙНЫХ
МОДЕЛЕЙ С ПРИМЕНЕНИЕМ К ПРОГНОЗИРОВАНИЮ
РАЗВИТИЯ ЭПИДЕМИЧЕСКОГО ПРОЦЕССА1
Развивается дискретный подход в теории рандомизированного машин-
ного обучения, ориентированный на применение к нелинейным моделям.
Формулируется задача энтропийного оценивания распределений вероят-
ностей и шумов измерений для дискретных нелинейных моделей. Рас-
сматриваются вопросы, связанные с применением таких моделей к зада-
чам прогнозирования, в частности проблеме генерации энтропийно-опти-
мальных распределений. Демонстрация предложенных методов прово-
дится на решении задачи прогнозирования общего количества инфици-
рованных SARS-CoV-2 в Германии в 2020 г.
Ключевые слова: рандомизированное машинное обучение, энтропия, эн-
тропийное оценивание, прогнозирование, рандомизированное прогнозиро-
вание, COVID-19, SARS-CoV-2.
DOI: 10.31857/S0005231021060064
1. Введение
Большое количество различных процессов, наблюдаемых в разных обла-
стях человеческой деятельности, природе и т.п., не могут быть эффективно
описаны линейными математическими моделями. В этой связи разработка
и развитие общих подходов нелинейного моделирования являются актуаль-
ными задачами. Однако необходимо отметить, что разработка и примене-
ние нелинейных моделей для конкретных задач сопряжены с определенными
трудностями, связанными как с их обучением с использованием реальных
данных, так и с выбором структуры модели.
Машинное обучение как раздел прикладной науки интегрирует в себе
большое количество методов и подходов, накопленных в различных научных
дисциплинах [1, 2], большой вклад в которые был сделан в таких направле-
ниях, как теория вероятностей и математическая статистика [3, 4]. Методы
машинного обучения успешно применяются к различным задачам, в част-
ности к задачам классификации и регрессии, которые относятся к задачам
обучения с учителем [1], основной особенностью которых является идея на-
стройки (обучения) параметров требуемой модели с использованием реаль-
ных данных. Настроенную (обученную) модель предполагается использовать
1 Работа выполнена при поддержке Российского фонда фундаментальных исследований
(проект № 20-07-00683).
149
для прогнозирования, т.е. получать от нее ответ, предъявляя ей входные дан-
ные, не участвующие ранее в обучении.
Этот подход является эффективным и известен, по крайней мере, с
1960-х гг. [5-8]. Однако большинство подходов, разработанных в данной об-
ласти, ориентировано на использование линейных моделей. В частности, од-
ним из эффективных подходов к решению задач классификации является
линейная классификация, состоящая в поиске линейной разделяющей гипер-
плоскости и применяемая, например, в широко используемом методе опорных
векторов [9]. Задачи восстановления регрессии давно и широко применяются
в эконометрике [3], и также большинство из них в этой области ориентировано
на восстановление линейной регрессии. Основные причины такого положения
состоят в основном в том, что, во-первых, линейные модели легче исследо-
вать и интерпретировать, во-вторых, численные и аналитические решения
линейных задач возможно получать либо абсолютно точно (аналитически),
либо с высокой точностью численно и, в-третьих, многие практические зада-
чи часто можно свести к линейным постановкам, а следовательно, получать
более качественное их решение с учетом отмеченных ранее свойств.
В то же время в некоторых прикладных задачах классификации и ре-
грессии проявляются различные нелинейные эффекты, которые необходимо
каким-то образом решать. Эффективным подходом к этой проблеме являет-
ся, например, ядерный подход, состоящий в нелинейном переходе в простран-
ство высокой размерности с последующим применением в нем уже линейного
метода для решения задачи классификации или регрессии [1]. Этот подход де-
монстрирует свою эффективность во многих прикладных задачах и приводит
к появлению различных ¾ядерных¿ версий известных линейных методов. Тем
не менее часто вопрос о выборе модели (точнее, ядерной функции) продолжа-
ет возникать при применении этих методов на практике. Кроме этого, всякий
переход в пространство высокой размерности при отсутствии большого ко-
личества данных в этом пространстве неизбежно приводит к нежелательным
эффектам таким, например, как переобучение, а также ряду других.
Другим подходом борьбы с нелинейными эффектами предлагают методы,
в которых не выделяется модель в явном виде, например методы, основанные
на деревьях решений [10], нейросетевые модели [1, 11, 12] и ряд других.
Таким образом, с одной стороны, наблюдается ситуация, когда в практи-
ческих задачах анализа данных явным образом наблюдается наличие “нели-
нейности”, требующей применения нелинейных моделей, с другой стороны,
существующие методы, части используемые на практике, недостаточно раз-
виты для эффективного решения задачи в нелинейном случае и требуют пе-
реформулирования или какой-либо адаптации задачи к их применению.
В настоящей работе предлагается универсальный подход к работе с нели-
нейными моделями в задачах анализа данных, в частности в задачах обуче-
ния регрессионных моделей. Этот подход основан на теории рандомизирован-
ного машинного обучения [13], основная идея которой состоит в искусствен-
ной рандомизации параметров модели, что позволяет перейти от модели с
детерминированными параметрами к модели со случайными параметрами и
определять в результате обучения не их точечные оценки, а их распреде-
150
ления. Распределения определяются таким образом, чтобы они доставляли
максимум энтропийному функционалу при условии баланса со средним вы-
ходом модели.
Основным достоинством предлагаемого подхода является независимость
от реальных характеристик используемых данных. Для корректного приме-
нения метода не требуется подтверждения или предположения о нормально-
сти данных (или иных их вероятностных свойствах), а полученные в резуль-
тате обучения распределения вычислены в условиях максимальной энтро-
пии, таким образом отражая наиболее “плохой” сценарий развития исследуе-
мого процесса, соответствующий его максимальной неопределенности. Дан-
ные свойства метода энтропийного оценивания восходят к работам Больц-
мана [14], Джейнса [15, 16], Шеннона [17]. Еще одной важной особенностью
метода является получение энтропийно-оптимальных распределений шумов,
содержащихся в данных, вместе с оптимальными распределениями парамет-
ров. Это свойство существенно отличает метод от классических подходов,
в которых делаются различные предположения о характеристиках шумов и
данных.
Оценки характеристик модели используются для прогнозирования моде-
лируемого процесса. Стандартный подход к прогнозированию состоит в при-
менении модели с точечными оценками параметров, полученных оцениванием
по реальным данным, для неизвестных (“будущих”) точек данных [18-20].
С учетом того, что подобрать модель точно под данные не представляет-
ся возможным, вводится предположение о стохастической природе данных,
точнее о том, что механизм порождения наблюдаемых данных, который неиз-
вестен, содержит стохастическую компоненту. Следствием этого предположе-
ния становится то, что в наблюдаемых данных есть как детерминированная,
так и стохастическая компонента, вероятностные характеристики которой
неизвестны. Фактически, на моделирование этой стохастической компонен-
ты и направлен весь разработанный к настоящему времени математический
аппарат, применяемый в данной области. Существенную часть этого подхо-
да составляет предположение о нормальности случайных компонент данных,
из которого становится возможным установить свойства получаемых оценок
параметров моделей.
Например, известный и широко применяемый метод максимума правдопо-
добия основан на идее максимизации распределения параметров модели при
условии наблюдаемых данных: необходимо определить такие значения пара-
метров, при которых будет достигаться максимум функции правдоподобия
данных. Это означает, что вероятность того, что при найденных значениях
параметров будут наблюдаться существующие данные, максимальна. Пред-
положение о нормальности (или о наличии другого известного закона распре-
деления) случайных компонент данных является основой этого метода, без
этого предположения будет невозможно получить функцию правдоподобия в
аналитическом виде [3].
Для вычисления оценок, максимизирующих правдоподобие, часто приме-
няется метод наименьших квадратов (МНК), однако получаемые им оценки
соответствуют оценкам максимального правдоподобия только для линейных
151
моделей. В нелинейном случае определение свойств этих оценок связано с
существенными трудностями.
Предположение о нормальности стохастических компонент моделей, а зна-
чит и данных, с которыми ассоциирована модель, очевидно, не всегда явля-
ется вполне корректным, так как не всегда удается выяснить или доказать
требуемые факты о вероятностных характеристиках данных по имеющимся
в наличии данным.
Энтропийно-оптимальные распределения, полученные на этапе обучения
модели, могут быть использованы для прогнозирования несколькими спосо-
бами, в частности, они могут быть сгенерированы для получения ансамбля
выходов модели с последующим его анализом.
Работа посвящена развитию метода энтропийно-рандомизированного об-
учения и прогнозирования для нелинейным моделей с дискретными парамет-
рами. Переход от непрерывных к дискретным моделям позволяет преодолеть
трудности использования непрерывных моделей в условиях большого коли-
чества переменных, которые приводят к проблеме вычисления многомерных
интегралов, произвести которое точно (аналитически) невозможно, а числен-
ное решение сопряжено с существенными вычислительными трудностями.
Предлагаемый в работе подход демонстрируется на примере задачи про-
гнозирования общего количества инфицированных в результате развития
эпидемии COVID-19 в Германии. Проводится сравнение предлагаемого под-
хода с нелинейным методом наименьших квадратов [18, 21].
2. Нелинейная дискретная рандомизированная модель
Рассмотрим объект c n скалярными входами xi, i = 1, n и выходом ŷ,
преобразование которых описывается в общем случае нелинейной функцией
(2.1)
ŷ = Φ(x,a),
где x = (x1, . . . , xn)
вектор входов, a = (a1, . . . , ad)
вектор параметров
модели.
Выход модели измеряется с некоторым шумом ξ, действующим аддитивно
на выход, приводя к модели следующего вида:
(2.2)
v = ŷ+ ξ = Φ(x,a) + ξ.
Предположим, что значения каждого параметра сосредоточены на интер-
вале Ak = [a-k, a+k], k = 1, d, и выход модели измеряется с шумом ξj , значения
которого сосредоточены на интервале Ξj = [ξ-j, ξ+j] для каждого заданного
входа xj , j = 1, m.
Параметры ak реализуются дискретной случайной величиной с M значе-
ниями на интервале Ak, приводя к следующим распределениям:
(2.3)
akℓ ∈ Ak, pkℓ
∈ [0, 1], k = 1, d, ℓ = 1, M,
где akℓ значения случайной величины, а pkℓ вероятности их реализации.
152
Шумы измерений выхода реализуются дискретной случайной величи-
ной ξj с L значениями на интервале Ξj для каждого входа xj . Измерения
выхода производятся независимо друг от друга, таким образом при m изме-
рениях приводя к следующим распределениям:
(2.4)
ξjh ∈ Ξj, qjh
∈ [0, 1], j = 1, m, h = 1, L,
где ξjh значения случайной величины, а qjh вероятности их реализации.
С учетом m измерений получаем итоговый вид модели (2.2):
(2.5)
v = ŷ + ξ = Φ(xj
,a) + ξ, j = 1,m,
где v = (v1, . . . , vm) вектор измеренного выхода модели, ξ = (ξ1, . . . , ξm)
вектор шумов, ŷ = (y1, . . . , ym) вектор выхода модели.
Распределения параметров и шумов измерений модели подлежат оцени-
ванию с использованием реальных данных об измерениях выхода объекта,
модель которого описывается (2.5).
3. Обучение модели с использованием реальных данных
Рандомизированное машинное обучение базируется на принципах энтро-
пийного оценивания параметров модели и шумов измерений ее выхода.
Энтропийно-оптимальные распределения отражают наиболее неопределен-
ную ситуацию, что в условиях полного отсутствия информации о реальных
характеристиках является единственным доступным в этих условиях реше-
нием [13, 22, 23].
Для вычисления оптимальных распределений требуется решить задачу
условной максимизации энтропии распределений параметров и шумов изме-
рений при условиях нормировки соответствующих распределений и выполне-
нии условий на баланс среднего выхода модели с измерением выхода объекта.
Задача формулируется следующим образом:
∑∑
∑∑
(3.1)
H(P, Q) = -
pkℓ ln pkℓ -
qjh ln qjh → max,
P,Q
k=1 ℓ=1
j=1 h=1
где P и Q распределения параметров и шумов (2.3) и (2.4), при условиях:
∑
∑
(3.2)
pkℓ = 1,
qjh
= 1, k = 1, d, j = 1, m,
ℓ=1
h=1
(3.3)
E[v] = E[Φ(xj
,a) + ξ] = y,
где y = (y1, . . . , ym)
вектор измерений выхода объекта (реальные данные
выхода).
153
Условие (3.3) определяет баланс среднего выхода модели с реальными дан-
ными выхода:
E[vj] = E[Φ(xj , a) + ξj ] = E[Φ(xj , a)] + E[ξj ] =
∑
∑
=
Φ(xj, a1ℓ1 , . . . , adℓd )p1ℓ1 · · · pdℓd +
ξjhqjh =
ℓk=1
h=1
k=1,d
∑
(3.4)
= Φ(xj) + ξjhqjh = yj.
h=1
Сумма в выражении дляΦ содержит Md членов, суммирование осуществ-
ляется для всех комбинаций значений случайных величин akℓ. Решение за-
дачи (3.1)-(3.3), подробно рассмотренное в Приложении, дает энтропийно-
оптимальные распределения параметров и шумов измерений, что и является
конечной целью обучения модели с использованием реальных данных.
4. Рандомизированное прогнозирование
В результате обучения модель оказывается снабжена энтропийно-опти-
мальными оценками распределений параметров и измерительных шумов,
формируя таким образом рандомизированную предсказательную модель
(РПМ). Такая модель определяет специальную методику прогнозирования
рандомизированное прогнозирование, элементы которого применялись для
некоторых прикладных задач [24-26].
Рандомизированное прогнозирование базируется на генерации энтро-
пийно-оптимальных распределений параметров (Π.4) и измерительных шу-
мов (Π.5) с последующим построением ансамбля выхода модели для новых,
не известных при обучении, входов модели.
Рассмотрим набор входов РПМ, для которых требуется построить прогноз,
который может быть представлен в виде блочного вектора или матрицы,
столбцами которой являются указанные входы:
x11
... x1s
X = {x1,...,xs} =
.
xn1
... xns
Пусть имеется выборка параметров из распределения P объема S. Тогда
ансамбль выхода модели для одного входа x формируется согласно (2.1) и
имеет вид
Y = {ŷi = Φ(x,ai)}, i = 1,S,
где ai реализация параметров с распределением P . Ансамбль содержит S
траекторий.
154
Теперь для каждого входа xj , j = 1, s и каждой реализации параметров ai,
i = 1,S рассмотрим выборку шумов из распределения q объема U и сформи-
руем итоговый ансамбль выхода модели согласно (2.2):
V = {vj = Φ(xj,ai) + ξj}, i = 1,S, j = 1,s,
где ξj = (ξj1, . . . , ξjU ) вектор реализаций шумов для j-го входа, vj вектор
измеренного выхода модели для j-го входа.
Таким образом, при прогнозировании для каждого входа и каждой реа-
лизации параметров модели, генерируется шум в количестве U реализаций.
В итоге ансамбль V состоит из W = SU траекторий, которые все вместе могут
быть представлены блочным вектором или матрицей со строками, соответ-
ствующими прогнозируемому выходу модели для каждого входа
v11
... v1s
V = [v1,...,vW] =
.
vW1
... vWs
Для построения итоговой прогнозной траектории моделируемого процесса
по ансамблю V могут быть вычислены средняя и медианные траектории, об-
ласть стандартного отклонения, а также другие выборочные вероятностные
характеристики.
Как видно из выражений ансамблей, для их формирования необходимо
иметь распределение шума для каждого входа. Распределения, полученные
при обучении, не могут быть напрямую использованы для произвольного
количества прогнозных входов, так как получены из известных на этом этапе
данных, а количество и характеристики данных при прогнозировании заранее
не известны. Выходов из этой ситуации может быть несколько.
Первый состоит в применении в качестве прогнозного распределения шу-
ма q распределения, определяемого выражением (Π.5) для среднего значения
параметра λ (множителей Лагранжа).
Второй подход состоит в использовании в качестве прогнозного распре-
деление шума для одного из входов, используемых при обучении, например
последнего, если постановка задачи допускает порядок входов в наборе. Идея
этого способа состоит в следующем: если исходить из того, что измерения в
каждой точке последовательно расположенных данных производятся одним
“устройством”, то логично ожидать некоторой стабилизации характеристик
этого измерительного устройства, которое достигается к последнему измере-
нию из последовательности.
Третий подход основан на том предположении, что в результате энтропий-
ного оценивания одновременно и параметров, и шумов можно рассматривать
чистый выход модели без шума. Таким образом, можно говорить, что эн-
тропийное оценивание осуществляет фильтрацию. В этом случае применение
модели должно осуществляться в чистом виде, без шума.
Важной проблемой в применении энтропийно-рандомизированного подхо-
да к прогнозированию является генерация оптимальных распределений пара-
метров и шумов измерений, полученных при оценивании (обучении) модели.
155
w*
a
w*
б
1,00
1,00
0,75
0,75
0,50
0,50
0,25
0,25
0
0
-0,10 -0,05
0
0,05
0,10
-0,10 -0,06 -0,02 0,02 0,06
0,10
x
x
Рис. 1. Дискретное и кусочно-постоянное непрерывное распределение.
Для решения этой проблемы можно предложить два основных подхода, ис-
пользующих генератор равномерно распределенных случайных чисел.
Первый подход состоит в генерации дискретного распределения. Для это-
го применяется стандартный подход, состоящий в случайном выборе значе-
ния случайной величины и затем соответствующей ему вероятности. В этом
случае, очевидно, реализации, сделанные таким образом, будут представлять
собой набор значений соответствующей случайной величины, многие из ко-
торых будут повторяться.
Второй подход основан на идее представления дискретного распределе-
ния в качестве кусочно-постоянной аппроксимации некоторого непрерывного
распределения на соответствующем интервале. Для этого интервал значений
соответствующей случайной величины разбивается на L + 1 подынтервалов
(где L
количество значений дискретной случайной величины), левые и
правые границы конечных подынтервалов соответствуют левым и правым
границам интервала распределения. Внутри каждого подынтервала генера-
ция происходит равномерно. В результате реализации такого подхода можно
получить существенно больше различных значений соответствующих случай-
ных величин. Пример построения непрерывных распределений для случай-
ной величины w∗(ξ), где ξ ∈ [-0,1, 0,1] и L = 5, представлен на рис. 1.
5. Прогнозирование роста числа инфицированных COVID-19 в Германии
Предлагаемый в работе подход применяется для моделирования динамики
развития эпидемии COVID-19 в Германии на основе данных Университета
Джонcа Хопкинса [27] начиная с сорокового дня эпидемии (8 марта 2020 г.),
когда впервые общее количество инфицированных превысило 1000 человек.
Данные о развитии эпидемии (см. рис. 2) свидетельствуют о том, что сна-
чала инфекция активно распространяется в популяции и наблюдается ее экс-
поненциальный рост. Далее наблюдается снижение числа зараженных, ве-
роятно, вследствие ограничительных мер или увеличения количества иммун-
ных членов популяции. При этом, как и в большинстве живых систем при рас-
смотрении их на относительно коротком промежутке времени, можно предпо-
ложить, что объем популяции не меняется (например, можно пренебречь ми-
грацией, воспроизводством и смертностью), а значит, существует ограниче-
156
200 000
150 000
100 000
50 000
0
0
25
50
75
100
125
150
175
День
Рис. 2. Общее количество инфицированных в Германии по дням начиная с
8.03.2020.
ние на количество инфицированных. Динамика инфицированных членов по-
пуляции N в такой системе может быть описана следующим уравнением [28]:
(
)
dN
N
(5.1)
= λN
1-
,
dt
K
где λ скорость роста инфицированных, N количество инфицированных,
K объем популяции. Решением этого уравнения является кривая Ферхюль-
ста [29, 30]
K
K-N0
(5.2)
N (t) =
,
B=
,
1+Be-λt
N0
где N0
количество инфицированных в популяции в начальный момент вре-
мени [30].
Модель вида (5.2) активно использовалась в начале 2020 г. для предсказа-
ния общего количества заболевших [31-37] и показала свою эффективность
на начальном этапе развития эпидемии. В этой связи представляется обос-
нованным использовать аналогичную модель для применения энтропийно-
рандомизированного подхода к прогнозированию общего количества инфи-
цированных. В качестве такой модели будем использовать трехпараметри-
ческую логистическую модель роста (Logistic Growth Model, LGM), которая
определяет преобразование скалярного входа x в выход ŷ с использованием
логистической нелинейной функции
a3
(5.3)
ŷ = Φ(x,a) =
,
1 + a1e-a2x
где a = (a1, a2, a3)
вектор параметров модели. Данная модель является
обобщением модели (5.2) и рассматривается здесь как абстрактная модель
с параметрами без использования дополнительных связей между ними.
157
В контексте рассматриваемой задачи входом является порядковый номер
(или индекс) дня, а выходом накопленное (общее) количество инфициро-
ванных. Вход и выход являются целыми, однако в вычислениях целые числа
преобразуются в числа с плавающей точкой.
Рандомизированная модель, выход которой искажен аддитивным шумом,
а параметры и шумы реализуются дискретными случайными величинами со
значениями из соответствующих интервалов, имеет вид
v = ŷ+ ξ = Φ(x,a) + ξ,
akℓ ∈ Ak, pkℓ ∈ [0,1], k = 1,d, ℓ = 1,M,
ξjh ∈ Ξj, qjh ∈ [0,1], j = 1,m, h = 1,L,
где akℓ, ξjh значения случайных величин, реализующих параметры и шумы,
а pkℓ, qjh вероятности их реализации, m количество точек данных, d = 3.
Для обучения (оценивания) предсказательной модели использовались дан-
ные за несколько дней (интервал обучения Test) начиная с 8 марта 2020 г.
(40-й день эпидемии в Германии), когда впервые было зафиксировано общее
количество инфицированных свыше 1000 человек.
Прогнозирование производится на следующие за интервалом оценивания
дни вплоть до 120-го дня эпидемии (интервал прогнозирования Tpred).
Полученные рандомизированные прогнозы сравнивались с подгонкой кри-
вой по модели (5.3) с помощью нелинейного метода наименьших квадра-
тов, реализованного функцией curve_fit библиотеки scipy на платформе
Python 3.7.
После оценивания модели проводилась ее реализация на интервале оце-
нивания (тестирование) и на интервале прогнозирования с вычислением сле-
дующих метрик качества для истинных (реальных, true) значений y и пред-
сказанных (модельных, predicted) значений ŷ:
1) коэффициент детерминации R2, определяемый формулой
n (yi - ŷi)2
R2(y, ŷ) = 1 -i=1n
,
∑ (yi - y)2
i=1
где y среднее значение по реальным данным позволяет оценить ка-
чество приближения кривой (goodness of fit (GoF)) и предсказательную
способность модели через долю объясненной дисперсии. Максимум это-
го индикатора равен 1, чем его значение ближе к единице, тем выше
качество модели;
2) средне-квадратичная ошибка (Mean Squared Error (MSE)), определяе-
мая формулой
∑
1
MSE(y, ŷ) =
(yi - ŷi)2,
n
i=1
показывает ожидаемую (среднюю) квадратичную ошибку;
158
3) Norm Error (NE), определяемую формулой
n (yi - ŷi)2
∥y - ŷ∥
NE(y, ŷ) =
= i=1n
;
∥y∥ + ∥ŷ∥
∑
∑
y2i
+
ŷ2
i
i=1
i=1
4) Rooted Norm Error (RNE), определяемую формулой
√
∑
√
(yi - ŷi)2
∥y - ŷ∥
i=1
RNE(y, ŷ) =
√
√
=
√
√
∥y∥ +
∥ŷ∥
∑
∑
y2i
+
ŷ2
i
i=1
i=1
Согласно теории метода энтропийного оценивания определяемые в резуль-
тате оценивания распределения параметров и шумов являются интерваль-
ными. Таким образом, для применения метода необходимо задать эти ин-
тервалы. В данной работе интервалы для параметров задавались на основе
оптимальных значений, полученных при оценивании методом наименьших
квадратов. Границы интервалов устанавливались в пределах 20% от этих
значений.
В экспериментах использовались данные, масштабированные на отрезок
[0, 1] на интервале оценивания.
Оценивание, тестирование и прогнозирование производилось для несколь-
ких конфигураций:
• без шума;
• с шумом в пределах 10%;
• с шумом в пределах 30%.
При прогнозировании использовалось распределение шума, полученное
для последней точки на интервале оценивания. Тестирование модели про-
водилось в конфигурации, соответствующей прогнозированию.
На рисунках изображены следующие результаты моделирования (траек-
тории):
• метод наименьших квадратов (пунктирная линия с меткой ols);
• реальные данные (пунктирная линия с меткой real);
• рандомизированное прогнозирование со средними по распределению
значениями параметров модели (линия с меткой mean_params);
• рандомизированное прогнозирование со средним по ансамблю (линия с
меткой mean);
• рандомизированное прогнозирование с медианой по ансамблю (линия с
меткой med).
Светло-серым цветом отмечены траектории, составляющие полученный
ансамбль, темно-серым цветом область стандартного отклонения по ан-
самблю. Все эксперименты производились для выборки из распределения
параметров модели объемом 1000 и выборки из распределениям шумов объ-
емом 100 для каждого значения параметра. Генерация распределений шума
159
avg
175 000
mean
med
150 000
ols
real
125 000
100 000
75 000
50 000
25 000
0
40
48
60
71
84
96
108
120
Day
Рис. 3. Прогнозирование без шума (NN) для Test = [40, 70] и Tpred = [71, 120].
175 000
avg
mean
150 000
med
ols
125 000
real
100 000
75 000
50 000
25 000
0
40
48
60
71
84
96
108
120
Day
Рис. 4. Прогнозирование с шумом в пределах 10% (N1) для Test = [40, 70] и
Tpred = [71, 120].
avg
175 000
mean
150 000
med
ols
125 000
real
100 000
75 000
50 000
25 000
0
40
48
60
71
84
96
108
120
Day
Рис. 5. Прогнозирование с шумом в пределах 30% (N3) для Test = [40, 70] и
Tpred = [71, 120].
160
P1*
P2*
P3*
1,0
0,8
0,6
0,4
0,2
0
Рис. 6. Энтропийно-оптимальное распределение параметров P∗.
*
*
*
*
*
*
*
*
1,0
0,8
0,6
0,4
0,2
0
q*
*
*
*
*
*
*
*
9
1,0
0,8
0,6
0,4
0,2
0
*
*
*
*
*
*
*
*
1,0
0,8
0,6
0,4
0,2
0
*
*
*
*
*
*
*
1,0
0,8
0,6
0,4
0,2
0
Рис. 7. Энтропийно-оптимальные распределения шумов Q∗.
проводилась для каждой точки соответствующего интервала (тестирования
и прогнозирования). Таким образом, полученный ансамбль состоял из 105
траекторий. Вертикальная красная пунктирная линия нанесена в точке на-
чала интервала прогнозирования. Эксперименты проводились на платформе
Python 3.7 в среде Windows 10.
На рис. 3-5 приведены результаты реализации рандомизированной пред-
сказательной модели на интервалах Test = [40, 70] и Tpred = [71, 120] для трех
вариантов прогнозирования: без шума (NN), с шумом 10% (N1) и с шу-
мом 30% (N3).
На рис. 6-7 изображены энтропийно-оптимальные распределения пара-
метров и шумов, полученные в результате обучения модели на интервале
T = [40,70] с шумом 30%.
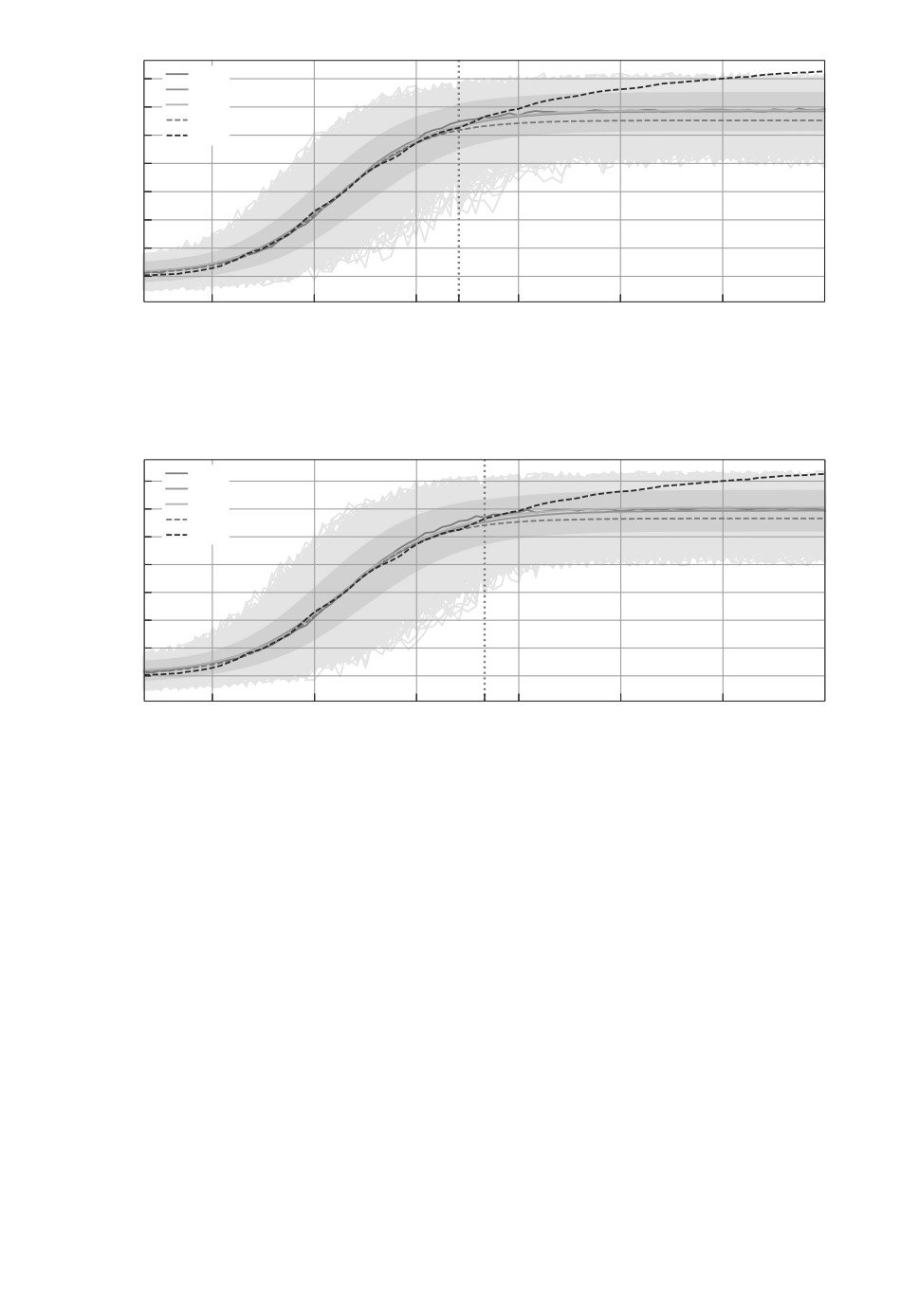
На рис. 8-9 приведены результаты реализации рандомизированной пред-
сказательной модели на интервалах Test = [40, 76], Test = [40, 79] и соответ-
ствующих интервалах прогнозирования.
Важно отметить, что на 77-й день произошел небольшой рост количества
заболевших, что видно на графике. Однако при обучении модели этих данных
161
avg
175 000
mean
150 000
med
ols
125 000
real
100 000
75 000
50 000
25 000
0
40
48
60
72
77
84
96
108
120
Day
Рис. 8. Прогнозирование с шумом в пределах 30% (N3) для Test = [40, 76] и
Tpred = [77, 120].
avg
175 000
mean
150 000
med
ols
125 000
real
100 000
75 000
50 000
25 000
0
40
48
60
72
77
84
96
108
120
Day
Рис. 9. Прогнозирование с шумом в пределах 30% (N3) для Test = [40, 79] и
Tpred = [80, 120].
еще не было. На 79-й день по-прежнему происходил рост количества заболев-
ших, который начался ранее, но в этом случае уже была возможность учесть
эти данные при обучении. На графиках видно, что во всех случаях рандоми-
зированная модель предоставляет более реалистичный прогноз по сравнению
с классической моделью.
Оценки параметров, полученные методом наименьших квадратов, и ин-
тервалы параметров рандомизированной модели указаны в табл. 1-2. В кон-
фигурациях с шумом интервалы шумов задаются как Ξj = [-0,1, 0,1] для N1
и Ξj = [-0,3,0,3] для N3 соответственно.
Значения показателей качества моделирования при тестировании на трех
разных интервалах для варианта модели с шумом 30% указаны в табл. 3.
Анализируя полученные результаты, можно отметить, что стандартная
методика прогнозирования, связанная с использованием подгонки кривой под
данные методом наименьших квадратов, хоть и обладает определенной эф-
162
Таблица 1. Оценки параметров, полученные методом
наименьших квадратов
Ttest
a1
a2
a3
[40, 70]
297749
0,2065
1,1448
[40, 76]
1086539
0,1856
1,0624
[40, 79]
83517
0,1803
1,0278
Таблица 2. Конфигурации параметров рандомизированной модели
Tpred
A1
A2
A3
[40, 70]
[238199, 357299]
[0,1652, 0,2478]
[0,9158, 1,3738]
[40, 76]
[86923, 130384]
[0,1485, 0,2227]
[0,8499, 1,2749]
[40, 79]
[66813, 100220]
[0,1443, 0,2164]
[0,8223, 1,2334]
Таблица 3. Метрики качества на интервале оценивания
R2
MSE
NE
RNE
Ttest = [40, 70]
ols
0,9984
0,0002
0,0004
0,0135
mean_params
0,9899
0,0011
0,0022
0,0335
mean
0,9997
0,0000
0,0001
0,0058
med
0,9980
0,0002
0,0004
0,0149
Ttest = [40, 76]
ols
0,9982
0,0002
0,0004
0,0139
mean_params
0,9903
0,0012
0,0020
0,0314
mean
0,9994
0,0001
0,0001
0,0078
med
0,9985
0,0002
0,0003
0,0127
Ttest = [40, 79]
ols
0,9982
0,0002
0,0004
0,0133
mean_params
0,9903
0,0012
0,0019
0,0306
mean
0,9997
0,0000
0,0001
0,0054
med
0,9986
0,0002
0,0003
0,0119
фективностью, не всегда способна качественно решить задачу построения
корректного прогноза.
Из-за специфики рассматриваемой здесь эпидемии COVID-19 во всем мире
наблюдается существенное искажение данных, связанных с ней. В этой связи
представляется актуальной задача прогнозирования количества инфициро-
ванных с некоторым превышением. Из полученных результатов видно, что
прогнозирование с помощью логистической модели, оцененной с использова-
нием тех данных, которые были на момент прогноза, существенно недооце-
нивает реальные данные. В то же время прогнозы, получаемые с использова-
нием предлагаемого в работе подхода, показывают превышение прогнозных
значений по сравнению с МНК. Необходимо также отметить, что использо-
вание шума в модели, который оценивается поточечно и потом используется
при прогнозировании, позволяет построить более реалистичный прогноз.
163
6. Заключение
В работе развит метод рандомизированного машинного обучения и про-
гнозирования, основанный на использовании дискретных случайных вели-
чин, что приводит к задачам, более адаптированным к численному реше-
нию с использованием современной вычислительной техники. Демонстрация
предложенного метода проведена на задаче прогнозирования общего количе-
ства инфицированных COVID-19 в Германии. Полученные результаты сви-
детельствуют о работоспособности и эффективности метода и его числен-
ной реализации, что определяется меньшей ошибкой при прогнозировании
по сравнению со стандартной методикой, основанной на методе наименьших
квадратов. Необходимо также отметить, что построенная рандомизирован-
ная модель показала хороший результат на интервале обучения, однако на
интервале прогноза погрешность по сравнению с реальными данными соста-
вила существенную величину. Это связано, по всей видимости, с тем, что
логистическая модель эффективна для прогноза не на всех этапах разви-
тия эпидемии, в частности, для обеспечения приемлемого уровня качества
прогноза необходимо наличие признаков замедления эпидемии на интерва-
ле обучения, а также наличие реального затухания эпидемии на интервале
прогноза. При проведении экспериментов для обучения использовались дан-
ные на этапе начала и активного развития эпидемии, что объясняет большую
ошибку при прогнозировании.
ПРИЛОЖЕНИЕ
Рассмотрим решение задачи (3.1)-(3.3), которое осуществляется методом
множителей Лагранжа. Функция Лагранжа будет иметь вид
L(P, Q, α, β, λ) = -H(P, Q)+
(
)
(
)
∑
∑
∑
∑
+ αk
pkℓ - 1
+ βj
qjh - 1
+
k=1
ℓ=1
j=1
h=1
(
)
∑
∑
+ λj
Φ(xj ) +
ξjhqjh - yj
j=1
h=1
Для поиска экстремума функции Лагранжа вычислим производные по
прямым переменным P и Q:
∑
∂L
∂L
∂Φj
=
= ln pkℓ + 1 + αk +
λj
,
∂P
∂pkℓ
∂pkℓ
j=1
∑
∂L
∂L
=
= ln qjh + 1 + βj +
λjξjh,
∂Q
∂q
jh
j=1
k = 1,d, j = 1,m, ℓ = 1,M, h = 1,L,
164
гдеΦj =Φ(xj ) и производная среднего значения модели по pkℓ определяется
выражением
∑
∏
∂Φ
j
(Π.1)
=
Φ(xj , a1ℓ1 , . . . , adℓd )
prℓr .
∂pkℓ
ℓs=1
r=k
s=1,d
Сумма в выражении для производной
∂Φ содержит M(d - 1) членов.
∂pkℓ
Приравнивая к нулю производные функции Лагранжа по прямым пере-
менным, получим выражения оптимальных распределений вероятностей па-
раметров и шумов от множителей Лагранжа:
∑
∂Φj
p∗kℓ(α,λ) = exp -1 - αk -
λj
,
∂pkℓ
j=1
q∗jh(β,λ) = exp (-1 - βj - λjξjh) .
Преобразуем эти выражения следующим образом:
∑
∂Φj
(Π.2)
p∗kℓ(α,λ) = exp (- (1 + αk)) exp -
λj
,
∂pkℓ
j=1
(Π.3)
q∗jh(β,λ) = exp (- (1 + βj)) exp (-λjξjh
),
и, подставляя их в условия нормировки (3.2), получим выражения:
(
)
∑
∂Φj
exp (1 + αk) = exp
-
λj
,
∂pkℓ
ℓ=1
exp (1 + βj ) = exp (-λjξjh) .
Подставим эти выражения обратно в (Π.2)-(Π.3), исключив таким образом
множители α и β, получим финальные выражения энтропийно-оптимальных
распределений параметров и шумов, зависящих от множителей λ:
(
)
∑
∂Φj
exp
-
λ
j∂p
kℓ
j=1
(Π.4)
p∗kℓ(λ) =
(
), k = 1,d, ℓ = 1,M,
∑
∑
∂Φj
exp
-
λ
j∂pkℓ
ℓ=1
j=1
exp (-λj ξjh)
(Π.5)
q∗jh(λ) =
,
j = 1,m, h = 1,L.
∑
exp (-λj ξjh)
h=1
165
Множители λ определяются решением системы уравнений, получающихся
подстановкой выражений (Π.4)-(Π.5) в балансовые соотношения (3.3):
∑
∏
∑
(Π.6)
Φ(xj , a1ℓ1 , . . . , adℓd )
p∗ (λ) +sℓ
ξjhq∗jh(λ) = yj
,
j = 1,m.
s
ℓk=1
ℓs=1
h=1
k=1,d
s=1,d
Таким образом, решив систему (Π.6), получим энтропийно-оптимальные
распределения параметров и шумов измерений, что и является конечной це-
лью обучения модели с использованием реальных данных.
Необходимо отметить, что для решения этой системы на практике необхо-
димо привлекать какой-нибудь численный метод, так как ее решение анали-
тически сопряжено с существенными трудностями.
Вычисление левой части системы потребует вычисления среднего значе-
ния случайной функцииΦ, а также ее производной по распределению P ,
определяемых выражениями (3.4) и (Π.1). Cуммирования в этих выражени-
ях должны производиться по всем комбинациям индексов, таким образом
количество операций суммирования растет как степень от количества пара-
метров d.
СПИСОК ЛИТЕРАТУРЫ
1.
Bishop C.M. Pattern Recognition and Machine Learning. Springer, Series: Informa-
tion Theory and Statistics, 2006.
2.
Hastie T., Tibshirani R., Friedman J. The Elements of Statistical Learning. Springer,
2001.
3.
Айвазян С.А., Мхитарян В.С. Прикладная статистика и основы эконометрики.
М.: Юнити, 1998.
4.
Мерков А.Б. Распознавание образов. Введение в методы статистического обуче-
ния. М.: URSS, 2010.
5.
Аркадьев А.Г., Браверман Э.М. Обучение машины распознаванию образов.
М.: Наука, 1964.
6.
Цыпкин Я.З. Основы теории обучающихся систем. М.: Наука, 1970.
7.
Вапник В.Н., Червоненкис А.Я. Восстановление зависимостей по эмпирическим
данным, М.: Наука, 1979.
8.
Вапник В.Н. Червоненкис А.Я. Теория распознавания образов. М.: Наука, 1974.
9.
Cristianini N., Shawe-Taylor J. An introduction to support vector machines, 2000.
10.
Breiman J.H., Friedman R., Olshen A., Stone C.J. Classification and regression
trees. 1984.
11.
Rosenblatt F. The perceptron, a perceiving and recognizing automaton Project Para.
Cornell Aeronautical Laboratory, 1957.
12.
Rumelhart D.E., Williams R.J., Hinton G. Learning representations by back-
propagating errors // Nature. 1986. V. 323. No. 6088. P. 533-538.
13.
Попков Ю.С., Попков А.Ю., Дубнов Ю.А. Рандомизированное машинное обу-
чение при ограниченных наборах данных: от эмпирической вероятности к эн-
тропийной рандомизации. М.: ЛЕНАНД, 2019.
166
14.
Больцман Л. О связи между вторым началом механической теории теплоты
и теорией вероятностей в теоремах о тепловом равновесии / Больцман Л.Э.
Избранные труды. под ред. Шлак Л.С. Классики науки. М.: Наука, 1984.
15.
Jaynes E.T. Information theory and statistical mechanics // Physical review. 1957.
V. 106. No. 4. P. 620-630.
16.
Jaynes E.T. Probability theory: the logic of science. Cambridge university press,
2003.
17.
Shannon C.E. Communication theory of secrecy systems // Bell Labs Technical J.
1949. V. 28. No. 4. P. 656-715.
18.
Diebold F. Elements of Forecasting. Thomson, South-Western, Ohio, US, 4th edition,
2007.
19.
Gneiting T., Katzfuss M. Probabilistic forecasting // Annual Review of Statistics
and Its Application, 2014. No. 1. P. 125-151.
20.
Hong T., Fan S. Probabilistic electric load forecasting: A tutorial review // Int. J.
Forecasting. 2016. V. 32. No. 3. P. 914-938.
21.
Айвазян С.А., Мхитарян В.С. Прикладная статистика. Классификация и сни-
жение размерности. М.: Финансы и статистика, 1989.
22.
Golan A., Judge G., Miller D. Maximum Entropy Econometrics: Robust Estimation
with Limited Data. N.Y.: John Wiley & Sons, 1996.
23.
Golan A. et al. Information and Entropy Econometrics A Review and Synthesis //
Foundations and Trends in Economet. 2008. V. 2. No. 1-2. P. 1-145.
24.
Popkov Y.S., Volkovich Z., Dubnov Y.A., Avros R., Ravve E. Entropy 2-soft classi-
fication of objects // Entropy. 2017. V. 19. No. 4. P. 178.
25.
Попков Ю.С., Попков А.Ю., Дубнов Y.A. Элементы рандомизированного про-
гнозирования и его применение для предсказания суточной электрической на-
грузки энергетической системы // АиТ. 2020. № 7. C. 148-172.
Popkov Y.S., Popkov A.Y., Dubnov Y.A. Elements of Randomized Forecasting and
Its Application to Daily Electrical Load Prediction in a Regional Power System //
Autom. Remote Control. 2020. V. 81. P. 1286-1306.
26.
Popkov Y.S., Popkov A.Y., Dubnov Y.A., Solomatine D. Entropy-randomized fore-
casting of stochastic dynamic regression models // Mathematics. 2020. V. 8. No. 7.
P. 1119.
27.
Dong E., Du H., Gardner L. An interactive web-based dashboard to track covid-19
in real time // The Lancet Infectious Diseases. 2020. V. 20. No. 5. P. 533-534.
28.
van den Driessche P. Mathematical Epidemiology. In F. Brauer, P. van den Driessche
978-3-540-78911-6.
29.
Verhulst P.-F. Notice sur la loi que la population suit dans son accroissement //
Corresp. Math. Phys., 1893. No. 10. P. 113-126.
30.
Singer H.M. The COVID-19 pandemic: growth patterns, power law scaling, and
saturation // Physical Biology. 2020. Vol. 17. No. 5. P. 055001. https://doi.org/
10.1088/1478-3975/ab9bf5
31.
Kumar J., Hembram K.P.S.S. Epidemiological study of novel coronavirus
32.
Yang W., Zhang D., Peng L., Zhuge C., Hong L. Rational evaluation of various
epidemic models based on the COVID-19 data of China // ArXiv. 2020.
167
33. Tatrai D., Varallyay Z. COVID-19 epidemic outcome predictions based on logistic
2003.14160
34. Morais A.F. Logistic approximations used to describe new outbreaks in the 2020
35. Shen C.Y. Logistic growth modelling of COVID-19 proliferation in China and its
international implications // Int. J. Infectious Diseases. 2020. Vol. 96. P. 582-589.
36. Wang P., Zheng X., Li J., Zhu B. Prediction of epidemic trends in COVID-19 with
logistic model and machine learning technics // Chaos Solitons & Fractals. 2020.
37. Chen D.-G., Chen X., Chen J. K. Reconstructing and forecasting the COVID-19
epidemic in the United States using a 5-parameter logistic growth model // Global
s41256-020-00152-5
Статья представлена к публикации членом редколлегии А.И. Михальским.
Поступила в редакцию 15.10.2020
После доработки 12.01.2020
Принята к публикации 15.01.2021
168