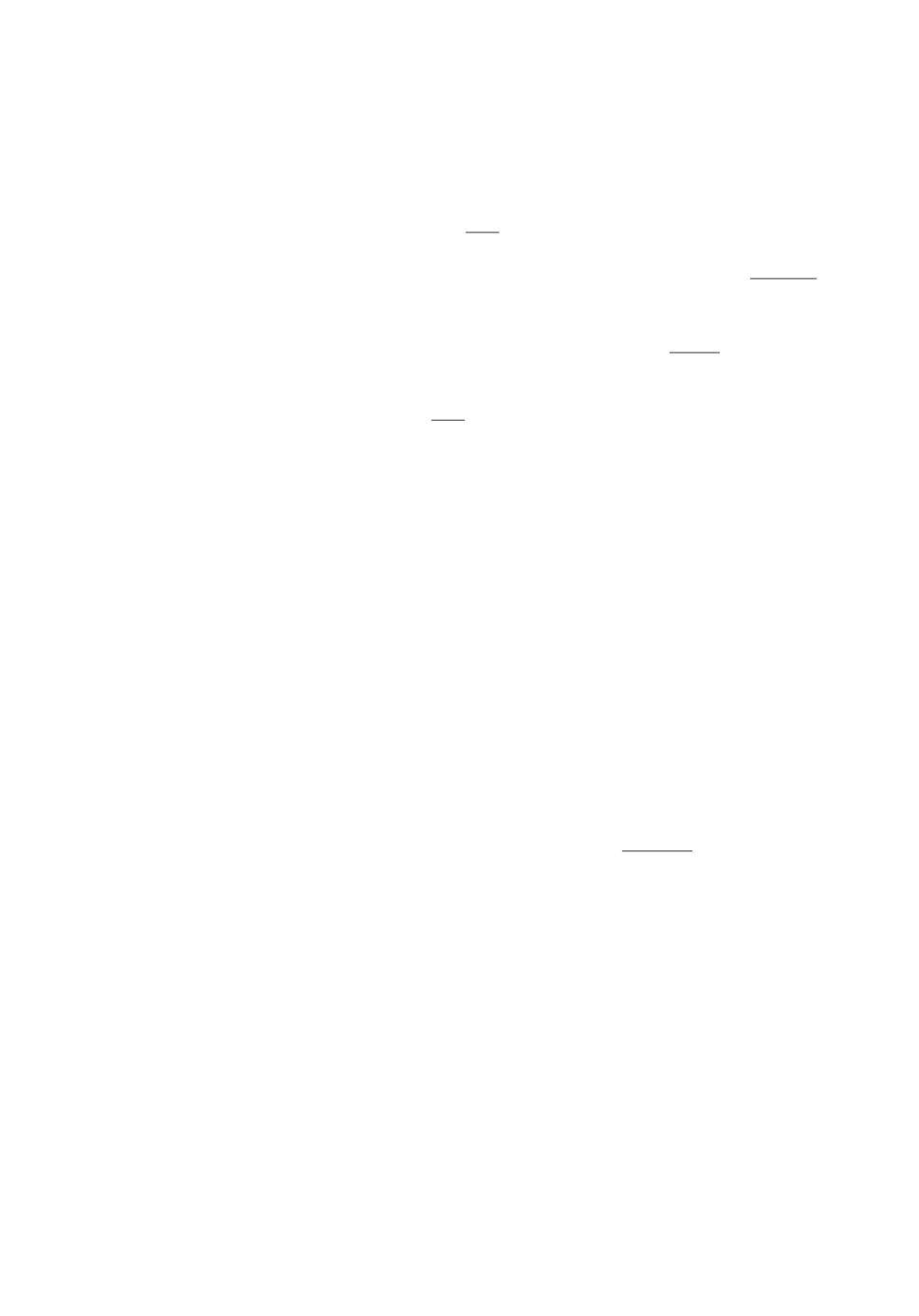Автоматика и телемеханика, № 7, 2021

Линейные системы

С.А. КРАСНОВА, д-р техн. наук (skrasnova@list.ru),

В.А. УТКИН, д-р. техн. наук (viktorutkin013@gmail.com)

(Институт проблем управления им. В.А. Трапезникова РАН, Москва)

КАСКАДНЫЙ СИНТЕЗ ДИФФЕРЕНЦИАТОРОВ

С КУСОЧНО-ЛИНЕЙНЫМИ КОРРЕКТИРУЮЩИМИ

ВОЗДЕЙСТВИЯМИ¹

На основе теории наблюдателей состояния динамических объектов,

функционирующих в условиях неопределенности, для сигнала, поступаю-

щего в реальном времени (например, задающего воздействия в системе

слежения), предложен метод восстановления его производных высокого

порядка, не требующий ни численного дифференцирования, ни наличия

аналитического описания данного сигнала. Динамический дифференциа-

тор строится как реплика виртуальной канонической модели с неизвест-

ным, но ограниченным входом. Использование ограниченных корректи-

рующих воздействий и специальной структуры дифференциатора позво-

ляет уменьшить выбросы получаемых оценок в начале переходного про-

цесса по сравнению с линейным дифференциатором с большими коэф-

фициентами. В качестве приложения рассмотрена задача отслеживания

центром масс беспилотного летательного аппарата пространственной тра-

ектории, приведены результаты моделирования.

Ключевые слова: динамический дифференциатор, наблюдатель состоя-

ния, неопределенный вход, каскадный синтез, слежение, БПЛА.

DOI: 10.31857/S0005231021070035

1. Введение

Во многих практических задачах возникает необходимость в дифферен-

цировании сигналов. Например, для функционирования следящих систем с

автоматическим управлением, как правило, требуется текущая информация

не только о задающих воздействиях, но и об их производных до n-го поряд-

ка включительно, где n относительный порядок одноканальной системы

(или максимальный элемент вектора относительного порядка многоканаль-

ной системы) [1, 2]. В некоторых системах слежения можно обойтись без непо-

средственной генерации производных задающих воздействий и полагать их,

как и внешние возмущения, неизвестными ограниченными функциями вре-

мени. Тогда при определенных условиях можно использовать для синтеза

выходное отображение и комплексный подход к задаче наблюдения неизме-

ряемых сигналов. В этом случае наблюдатель строится как реплика системы

“вход-выход”, записанной относительно ошибки слежения, и по ее измерени-

ям оцениваются смешанные переменные (линейные комбинации функций от

¹ Работа выполнена при частичной финансовой поддержке Российского фонда фунда-

ментальных исследований (проект 20-01-00363А).

переменных состояния, внешних возмущающих воздействий и задающих сиг-

налов, а также их производных), по которым формируется обратная связь

[3-5]. Для подавления внешних возмущений в рамках этого подхода могут

использоваться глубокие обратные связи, скользящие режимы или их до-

предельные аналоги в наблюдателе смешанных переменных с последующим

синтезом комбинированной обратной связи по получаемым оценкам. Другая

альтернатива связана с использованием указанных методов непосредственно

в законе управления, когда производные задающих и возмущающих воздей-

ствий неизвестны и не подлежат оцениванию [6, 7]. При этом возмущение

непосредственно действует на регулируемую переменную и не может быть

полностью подавлено из-за физических ограничений на управление, что при-

водит к бóльшей ошибке слежения, чем в первом случае. Таким образом,

для создания высокоточных систем слежения в общем случае необходима те-

кущая информация о производных задающих воздействий до n-го порядка

включительно.

Для объектов управления с однотипными режимами работы и простым

контуром движения, описываемым одним аналитическим выражением, эта

проблема решается с помощью составления динамического генератора задаю-

щих воздействий или аналитического описания желаемой траектории, что да-

ет информацию о производных целевых сигналов требуемого порядка. Одна-

ко в системах управления автономными движущимися объектами на плоско-

сти или в пространстве полное аналитическое описание сложной траектории,

которая представлена разными функциями на разных временных интерва-

лах, является достаточно трудоемким процессом, требующим привлечения

теории графов, сплайновой интерполяции и других методов [8-12]. С другой

стороны, численное дифференцирование задающих воздействий приводит к

нежелательному возбуждению помех и появлению запаздывания, причем по-

грешности увеличиваются с ростом порядка производной, получаемой чис-

ленными методами [13].

В данной статье представлен метод получения информации о производных

задающих воздействий по их текущим значениям, основанный на теории на-

блюдателей состояния объектов управления при действии внешних возмуще-

ний. Эти алгоритмы, реализуемые в вычислительной среде в реальном вре-

мени, не требуют ни численного дифференцирования данных сигналов, ни

их аналитического описания. Суть заключается в построении виртуального

(т.е. реально не существующего) генератора задающего воздействия в виде

динамической модели с неизвестным входом и последующим синтезом на-

блюдателя состояния этого генератора с использованием в корректирующих

воздействиях наблюдателя реального задающего воздействия, поступающе-

го из автономного источника. Особенности построения указанного наблюда-

теля: при его синтезе реализуется метод разделения движений с помощью

непрерывных, ограниченных по модулю корректирующих воздействий, что

позволяет избежать больших выбросов в получаемых оценках; наблюдатель

не имеет собственной динамики, что также способствует снижению выбро-

сов и упрощает процедуру синтеза параметров корректирующих воздействий

[14-16].

Отметим, что и целевые сигналы, и возмущения являются внешними воз-

действиями для объекта управления. Но в задачах получения оценок произ-

водных задающих воздействий и внешних возмущений есть принципиальные

отличия. Во-первых, в отличие от внешних возмущений целевые сигналы не

действуют непосредственно на объект управления, а поступают в контрол-

лер, где используются для формирования управления. Во-вторых, обычно

задающие воздействия полагаются известными, что позволяет построить ав-

тономный наблюдатель для оценивания их производных, который не зависит

от процессов, протекающих в объекте управления. Внешние возмущения, как

правило, неизвестны и оцениваются по их воздействию на объект управления

с использованием для построения наблюдателя возмущений модели объекта

управления [15, 16]. В случае когда наблюдатель возмущений строится на

основе виртуальной динамической модели возмущений, он функционирует

совместно с объектом управления, сигналы которого используются для кор-

рекции такого наблюдателя [17]. В-третьих, задача получения оценок произ-

водных задающих воздействий, как показано в данной статье, всегда имеет

решение и не зависит от постановки задачи управления. В то же время за-

дача получения оценок возмущений и их производных не всегда разрешима,

в частности, когда для измерения доступны только выходы объекта управ-

ления, как правило, удается получить оценки только смешанных сигналов

(комбинации переменных состояния объекта управления и внешних возму-

щений) [3-5].

Статья организована следующим образом. В разделе 2 для восстановления

n производных сигнала, поступающего в реальном времени, предложен диф-

ференциатор в виде наблюдателя состояния, построенного на основе вирту-

альной канонической модели (n + 1)-го порядка с неизвестным ограниченным

входом. Выходом такой модели полагается данный сигнал, его текущие значе-

ния известны, аналитическое описание отсутствует, предполагается, что его

производные до (n + 1)-го порядка ограничены известными константами на

рассматриваемом интервале времени. В результате целенаправленного синте-

за переменные наблюдателя с заданной точностью воспроизводят неизвест-

ные производные данного сигнала. В публикации [18] рассматривалась ана-

логичная постановка для гладких сигналов из класса алгебраических поли-

номов любых конечных степеней с непрерывными производными. Настройка

наблюдателя стандартно выполнялась с помощью линейных глубоких обрат-

ных связей. В данной статье, во-первых, класс допустимых сигналов расши-

ряется за счет кусочно-дифференцируемых составных функций, производные

которых имеют точки разрыва первого рода в моменты изменения вида функ-

ций. Во-вторых, для настройки наблюдателя используются ограниченные,

непрерывные, но негладкие кусочно-линейные корректирующие воздействия

[3, 4, 16], которые являются гибридом линейных и разрывных управлений и

имеют по два настраиваемых параметра: полку (амплитуду) и угол наклона

(большой коэффициент). Они привносят в замкнутую систему положитель-

ные свойства обоих методов и исключают их недостатки. Идея заключается

в том, чтобы выбором амплитуд последовательно, по каскадному принципу

обеспечить попадание за конечное время аргументов корректирующих воз-

действий в линейные зоны, границы которых и соответственно точность оце-

нивания определяются выбором больших коэффициентов. Заметим, что в от-

личие от обычных линейных наблюдателей [18] в данном подходе настройка

больших коэффициентов осуществляется на основе неравенств и не требует

составления эталонных характеристических полиномов. В-третьих, помимо

стандартного наблюдателя, который строится как реплика объектов оцени-

вания, в данной статье рассматривается также наблюдатель без собственных

движений [14-16]. При этом в системе относительно ошибок наблюдения оце-

ниваемые сигналы присутствуют в явном виде, что существенно упрощает

процедуру настройки параметров корректирующих воздействий по сравне-

нию с базовыми алгоритмами [3, 4].

В разделе 3 разработанный метод восстановления производных применя-

ется в системе управления движением центра масс беспилотного летательного

аппарата (БПЛА). Демонстрируется также возможность оценивания внеш-

них возмущений, действующих на объект [15, 16], с помощью наблюдателя

с кусочно-линейной коррекцией, построенного как реплика модели объекта

управления. Приводятся результаты численного моделирования.

2. Синтез динамических дифференциаторов в виде наблюдателей состояния

Представим два способа построения дифференциаторов задающего сигна-

ла для выходной переменной следящей одноканальной системы. Без ограни-

чения общности данные методы могут быть использованы в многоканальных

системах, где для каждой компоненты вектора задающих воздействий стро-

ится свой дифференциатор соответствующего порядка, а также могут найти

применение в других прикладных задачах, требующих получения производ-

ных сигналов, аналитическое описание которых неизвестно.

2.1. Постановка задачи

Рассмотрим случай управляемого объекта с одним входом и одним вы-

ходом y₁(t) ∈ Y ⊂ R, t ≥ 0, где Y

открытая рабочая область изменения

регулируемой переменной. Предположим, что для данного объекта в рамках

тех или иных методов синтезирован закон управления, обеспечивающий от-

слеживание выходной переменной заданного сигнала, который зависит и от

производных задающего воздействия до n-го порядка включительно. Задаю-

щее воздействие поступает в систему управления в реальном времени в виде

непрерывного детерминированного сигнала g₁(t), его аналитическое описание

как функции времени не известно. Задающий сигнал является допустимым

для отработки, т.е. g₁(t) ∈ G₁ ⊂ Y , t ≥ 0, и его производные до (n + 1)-го по-

рядка включительно ограничены



(2.1)

g⁽

(t)≤Gi+1

i = 1,n + 1, t ≥ 0,

где G_i+1

известные положительные константы, отвечающие проектным

ограничениям конкретного объекта управления.

Ставится задача оценивания с заданной точностью производных задаю-

щего сигнала до n-го порядка включительно с помощью динамического на-

блюдателя состояния, который выполняет функции дифференциатора. В ка-

честве основы для построения наблюдателя введем динамическую модель

(n + 1)-го порядка, имеющую канонический вид

(2.2)

ġ_i = g_i+1

i = 1,n + 1.

Выходом системы (2.2) полагается измеряемый сигнал g₁(t); переменными

состояния являются задающий сигнал и его производные g⁽ⁱ⁾¹(t) = g_i+1(t)

до n-го порядка включительно; вход g⁽ⁿ⁺¹⁾¹(t) = g_n+2(t)

производная

(n + 1)-го порядка является неизвестной ограниченной функцией времени.

В силу канонической структуры система (2.2) является наблюдаемой отно-

сительно выхода, что является предпосылкой решения задачи оценивания ее

состояния.

Естественно предположить, что g₁(t) как функция времени является

непрерывной и кусочно-дифференцируемой, т.е. допускается, что на разных

временных интервалах она описывается разными аналитическими выраже-

ниями. Как следствие, ее производные в общем случае являются ку-

сочно-непрерывными, ограниченными на интервалах и имеют конечное число

точек разрыва первого рода, в которых форма сигнала меняется и в которых

ограничения (2.1) следует понимать как односторонние. Применительно к

модели (2.2) это означает, что входной виртуальный сигнал g_n+2(t) являет-

ся неизвестной кусочно-непрерывной ограниченной функцией, которая имеет

различный вид на различных временных интервалах.

Таким образом, динамическая модель (2.2) порождает достаточно широ-

кий класс функций g₁(t), а именно множество решений канонической систе-

мы (n + 1)-го порядка с произвольным входом g_n+2(t). Допускаемые точки

конечного разрыва производных можно трактовать как моменты изменения

скачком начальных условий в системе (2.2).

Обратим внимание, что в рассматриваемой постановке модель (2.2) яв-

ляется виртуальной и не используется в контуре обратной связи в качестве

генератора задающего сигнала, она служит для определения структуры и

размерности наблюдателя производных данного сигнала. В других поста-

новках входной сигнал g_n+2(t) может зависеть от вектора состояния модели

(2.2), а также и от внешних по отношению к модели (2.2) сигналов, в част-

ности от вектора состояния модели объекта управления. В этом смысле (2.2)

является обобщением и расширением динамических моделей, используемых

для имитации и генерации внешних воздействий в виде экзогенных систем с

неизвестными начальными условиями [1, 17]. В [19] рассматривался генера-

тор заданий с неопределенными параметрами. В робастной постановке зада-

ча наблюдения его состояний дополнялась решением задачи идентификации

неизвестных параметров с привлечением методов теории систем с разрывны-

ми управлениями, функционирующих в скользящем режиме.

2.2. Наблюдатель производных стандартной структуры

В данном подразделе для системы (2.2) вводится стандартный наблюда-

тель состояния. Рассматриваются частные случаи, при которых можно по-

лучить асимптотические оценки производных с помощью обычной линей-

ной коррекции. Мотивируется использование в общем случае наблюдателя

с кусочно-линейными корректирующими воздействиями.

Стандартный наблюдатель состояния строится как реплика объекта, пе-

ременные которого подлежат оцениванию, т.е. в данном случае повторяет

структуру виртуальной модели (2.2) и имеет вид

(2.3)

Ż_i = z_i+1 + v_i, i = 1,n;

Ż_n+1 = v_n+1,

где z = (z₁, . . . , z_n+1)^T∈Rⁿ⁺¹- вектор состояний наблюдателя, v_i (i = 1, n + 1) -

корректирующие воздействия, которые формируются на основе измере-

ний g₁(t) и переменных наблюдателя так, чтобы обеспечить стабилизацию

системы относительно ошибок наблюдения ε_i = g_i - z_i, i = 1, n+1, которая в

силу (2.2), (2.3) имеет вид:

(2.4)

ε_i = ε_i+1 - v_i, i = 1,n,

ε_n+1 = g_n+2 - v_n+1.

Особенность системы (2.4) заключается в наличии неизвестного ограни-

ченного сигнала g⁽ⁿ⁺¹⁾(t) = g_n+2(t), который трактуется как внешнее возму-

щение. Сначала выделим частные случаи, при которых возможна асимпто-

тическая стабилизация системы (2.4).

Если функция g_n+2(t) известна, то с использованием этой информа-

ции последние уравнения систем (2.3) и (2.4) примут соответственно вид:

Ż_n+1 = g_n+2 + v_n+1, ε_n+1 = -v_n+1. Тогда применение обычной линейной кор-

рекции

(2.5)

v₁ = a₁ε₁, v₂ = a₂ε₁, ... , v_n+1 = a_n+1ε₁,

параметры которой являются коэффициентами гурвицева полинома λⁿ⁺¹+

+a₁λⁿ + a₂λ^n-1 + ... + a_nλ + a_n+1, обеспечит асимптотическую сходимость

в нуль ошибок наблюдения и, следовательно, асимптотическую сходимость

переменных наблюдателя к неизмеряемым производным:

(2.6)

lim

ε_i(t) = 0 ⇒ lim

z_i(t) = g_i

(t), t = 1, n + 1.

t→+∞

Если есть основание полагать, что задающий сигнал описывается алгеб-

раическим полиномом с максимальной степенью n = n, то тогда g⁽ⁿ⁺¹⁾¹(t) ≡ 0,

внешнее возмущение в системе (2.4) отсутствует и линейная коррекция (2.5)

также обеспечит асимптотическое оценивание производных (2.6). Если из-

вестно, что максимальная степень полиномов 1 ≤ n < n, то тогда все произ-

водные начиная с (n + 1)-й тождественно равны нулю. Соответственно по-

рядок наблюдателя (2.3) следует понизить на n - n. Если n < n < ∞, то,

наоборот, можно повысить порядок наблюдателя на n - n, чтобы обеспе-

чить асимптотические оценки (2.6). При этом попутно полученная избыточ-

ная информация о (n + 1)-й производной и выше не используется в законе

управления.

В общем случае, когда о “внешнем возмущении” g_n+2(t) предполага-

ется только его ограниченность по модулю (2.1), для его подавления с

необходимостью требуется применять методы теории скользящих режимов

[6, 14, 15, 19, 20] или линейных систем с глубокими обратными связями. В по-

следнем случае линейная коррекция (2.5) дополняется большим коэффици-

ентом l > 1 [21] следующим образом:

(2.7)

v₁ = a₁lε₁, v₂ = a₂l²ε₁, ... , v_n+1 = a_n+1lⁿ⁺¹ε₁,

что обеспечивает в замкнутой системе (2.4), (2.7) стабилизацию ошибок на-

блюдения с заданной точностью. Известным недостатком линейных наблю-

дателей с большими коэффициентами является большое перерегулирование

в начале переходных процессов [5, 18, 21-23], что приводит к перерегулиро-

ванию и в объекте управления, обратная связь в котором формируется по

сигналам наблюдателя.

Чтобы избежать указанной проблемы, в данной статье используется дру-

гой метод подавления возмущений

каскадный синтез наблюдателей с

кусочно-линейными, всюду ограниченными корректирующими воздействия-

ми [3, 4, 16] вида

[

p₁sign(ε₁),

|ε₁| > 1/l₁,

(2.8)

v₁ = p₁sat(l₁ε₁) =

p₁l₁ε₁,

|ε₁| ≤ 1/l₁;

[

p_i sign(v_i-1),

|v_i-1| > 1/l_i,

v_i = p_isat(l_iv_i-1) =

p_il_iv_i-1,

|v_i-1| ≤ 1/l_i, i = 2, n + 1.

Каждое корректирующее воздействие (2.8) имеет по два настраиваемых

параметра: p_i > 0

амплитуду, которая отвечает за скорость оценива-

ния, и l_i > 0

угол наклона, который играет роль большого коэффи-

циента и отвечает за точность оценивания. Будем говорить, что если

|ε₁| ≤ 1/l₁, |vi-1| ≤ 1/li, i = 2,n + 1, то соответствующие корректирующие

воздействия v_i, i = 1, n + 1, (2.8) находятся в “линейной зоне”.

В [3] в рамках синтеза одноканальной системы слежения при действии

внешних возмущений наблюдатель, аналогичный (2.3), (2.8), применялся

для оценивания смешанных переменных (функций от переменных состояния,

внешних воздействий и их производных) по измерениям ошибки слежения.

Были получены иерархические системы неравенств для выбора параметров

кусочно-линейных корректирующих воздействий, при которых за заданное

время T > 0 с заданной точностью δ > 0 обеспечивается оценивание неизме-

ряемых сигналов канонической системы, аналогичной (2.1)-(2.2). Соответ-

ственно в терминах решаемой задачи использование этого подхода обеспечит

(2.9)

|ε_i(t)| = |g_i(t) - z_i(t)| ≤ δ, i = 1, n + 1,

|g_n+2(t) - v_n+1

(t)| ≤ δ, t ≥ T.

Первая группа неравенств (2.9) означает, что переменные наблюдателя (2.3)

служат оценками соответствующих производных задающего сигнала, послед-

нее неравенство (2.9) показывает, что корректирующее воздействие послед-

него уравнения может служить оценкой неизвестного входа. Как следствие,

для оценивания n производных можно использовать наблюдатель, порядок

которого по сравнению с (2.3) понижен на единицу, при этом n-я производная

будет трактоваться как возмущение, а ее оценкой будет служить корректи-

рующее воздействие v_n(t) [3].

Замечание. Для простоты изложения в оценках (2.9) и далее области

сходимости различных ошибок наблюдения, имеющих различные единицы

измерения, будем единообразно обозначать δ и придавать им одинаковые чис-

ловые значения δ > 0, но в соответствующих единицах измерения по умол-

чанию.

Основное преимущество наблюдателя (2.3), (2.8) по сравнению с наблюда-

телем с глубокими обратными связями заключается в том, что корректирую-

щие воздействия (2.8) всюду ограничены, следовательно, будут существенно

ограничены всплески оценочных сигналов в начале всех переходных процес-

сов, которые порождаются сменой формы выходного кусочно-дифференци-

руемого сигнала. Результаты моделирования показали [23], что всплески оце-

ночных сигналов производных, полученные с помощью линейного наблюда-

теля с большими коэффициентами, каждый раз увеличиваются на порядок с

ростом порядка производной (что обусловлено иерархией большого коэффи-

циента (2.7)), в отличие от оценочных сигналов наблюдателя с кусочно-ли-

нейными корректирующими воздействиями, которые заведомо ограничены

амплитудами корректирующих воздействий. Таким образом, применение на-

блюдателя (2.3), (2.8) существенно расширяет класс допустимых функций,

оценочные сигналы производных которых могут быть непосредственно ис-

пользованы в практических приложениях без дополнительных ограничений.

К преимуществам наблюдателя (2.3), (2.8) можно также отнести каскад-

ную процедуру настройки на основе иерархии неравенств, не требующую со-

ставления эталонных характеристических полиномов (в отличие от (2.5)).

Заметим, что в указанных выше частных случаях применение корректирую-

щих воздействий (2.8) не только обеспечит асимптотические оценки (2.6), но

и даст возможность последовательно управлять темпами сходимости каждой

переменной замкнутой системы. Однако для настройки амплитуд и в част-

ных, и в общем случаях требуется определять области изменения ошибок

наблюдения в процессе регулирования [3, 4], что усложняет вычислительный

аспект, а также приводит к завышенным расчетным оценкам для выбора

параметров. Соответствующая процедура будет продемонстрирована в под-

разделе 3.4 на примере оценивания производных задающих сигналов БПЛА.

В подразделе 2.3 представлен основной результат. Для снятия указан-

ной проблемы предложена другая структура наблюдателя производных с

кусочно-линейными корректирующими воздействиями, который обеспечива-

ет такое же качество оценивания (2.9), как и наблюдатель (2.3), (2.8), но име-

ет более простую первичную настройку благодаря исключению из анализа

собственных движений ошибок наблюдения.

2.3. Наблюдатель производных без собственных движений

В данном подразделе представлен основной результат. Для системы (2.2)

вводится наблюдатель состояния специальной структуры без собственных

движений. Выделяются особенности каскадного синтеза кусочно-линейных

корректирующих воздействий, при котором реализуется разделение движе-

ний в пространстве ошибок наблюдения. Формализуются особенности оце-

нивания кусочно-непрерывных сигналов, с учетом которых формулируется

теорема о существовании решения задачи оценивания производных предло-

женным методом.

На основе модели (2.2) построим наблюдатель-дифференциатор специаль-

ного вида

(2.10)

Ż_i = v_i

i = 1,n + 1,

что приведет к системе относительно ошибок наблюдения

(2.11)

ε_i = g_i+1 - v_i

i = 1,n + 1,

и следующему виду кусочно-линейных корректирующих воздействий:

[

p₁sign(ε₁),

|ε₁| > 1/l₁,

(2.12)

v₁ = p₁sat(l₁ε₁) =

p₁l₁ε₁,

|ε₁| ≤ 1/l₁;

[

p_isign(v_i-1 - z_i),

|v_i-1 - z_i| > 1/l_i,

v_i = p_isat(l_i(v_i-1 - z_i)) =

p_il_i(v_i-1 - z_i),

|v_i-1 - z_i| ≤ 1/l_i, i = 2, n + 1.

Отметим, что в отличие от стандартного наблюдателя (2.3), приводящего

к системе (2.4), в системе (2.11)-(2.12) асимптотическая сходимость ошибок

наблюдения (2.6) может быть обеспечена только тогда, когда все n + 1 про-

изводных затухают со временем. Но даже в этом частном случае с помощью

обычной линейной коррекции (2.5) невозможно обеспечить асимптотическую

стабилизацию нейтральной системы (2.11) из-за наличия неустранимых ну-

левых собственных значений. Таким образом, синтез наблюдателя (2.10) тре-

бует применения специальных подходов, основанных на методе разделения

движений ошибок наблюдения в замкнутой системе.

В силу структуры системы (2.11) сигналы, на основе которых формиру-

ются корректирующие воздействия v_i, i = 2, n + 1, (2.12), можно представить

в виде

(2.13)

v_i-1 - z_i = g_i - ε_i-1 - z_i = ε_i - ε_i-1

i = 2,n + 1,

что совпадает с детализацией соответствующих корректирующих воздей-

ствий (2.8) системы (2.4), а именно

(2.14)

v_i-1 = ε_i - ε_i-1

i = 2,n + 1.

Отличие состоит в том, что в системе (2.11) оцениваемые сигналы присут-

ствуют в явном виде и области их изменения априори известны (2.1), что

позволяет достаточно просто обеспечить стабилизацию с заданной точностью

ошибок наблюдения.

Согласно идеологии метода разделения движений, реализуемой при кас-

кадном синтезе наблюдателя с кусочно-линейной коррекцией [3, 4, 15, 16], в

замкнутой системе (2.11)-(2.12) с учетом (2.13) выбором амплитуд p_i > 0,

i = 1,n + 1, требуется последовательно обеспечить сходимость аргументов

корректирующих воздействий в линейные зоны:

|ε₁(t)| ≤ 1/l₁, t ≥ t₁ ≥ 0 ⇒ |v₁(t) - z₂(t)| = |ε₂(t) - ε₁(t)| ≤ 1/l₂,

(2.15)

t ≥ t₂ > t₁ ⇒ |ε₃(t) - ε₂(t)| ≤ 1/l₃,

t ≥ t₃ > t₂ ⇒ ... ⇒ |ε_n+1(t) - ε_n(t)| ≤ 1/l_n+1, t ≥ t_n+1 > t_n.

Особенность каскадного синтеза заключается в том, что только в первом

уравнении системы (2.11)-(2.12) равенство знаков регулируемой переменной

и ее корректирующего воздействия имеет место на протяжении всего про-

цесса: sign(ε₁(t)) = sign(v₁(t)), t ≥ 0. Для остальных уравнений совпадения

знаков sign(ε_i(t)) = sign(v_i(t)), i = 2, n + 1, гарантируются только вне обла-

стей (2.15) при достаточном затухании производных ошибок наблюдения в

предыдущих уравнениях.

Грубой (первичной) настройкой дифференциатора будем называть проце-

дуру, в которой время оценивания T > 0 априори не устанавливается. Выбо-

ром параметров корректирующих воздействий (2.12) обеспечивается последо-

вательная сходимость ошибок наблюдения в заданные окрестности нуля, при

этом не учитываются: скорости сходимости в линейные зоны (2.15) и затуха-

ния производных ошибок наблюдения, а также ошибки уравнений статики,

т.е. полагается, что ε_i(t) ≈ 0, t > t_i, i = 1, n.

В этих допущениях на основе (2.15) и достаточных условий сходимости

имеем первичные нижние оценки для выбора параметров кусочно-линейной

коррекции (2.12), обеспечивающих первую группу неравенств (2.9):

ε_i ε_i = ε_i(g_i+1 - p_isign(ε_i)) ≤ |ε_i|(G_i+1 - p_i) < 0 ⇒ p_i > G_i+1,

(2.16)

|ε_i| ≤ 1/l_i < δ ⇒ l_i > 1/δ, i = 1, n + 1.

Заметим, что второе неравенство (2.16) можно использовать и для первич-

ной настройки больших коэффициентов базового наблюдателя (2.3), (2.8) в

силу (2.14). Однако и грубая (p_i > |ε_i+1(t, p_i+1)|, i = 1, n; p_n+1 > G_n+2 [3]), и

тонкая (т.е. с обеспечением заданного времени сходимости с учетом быстрых

движений) настройки его амплитуд уже не являются автономными, как в

первом выражении (2.16), а основаны на иерархии неравенств (как будет по-

казано в подразделе 3.4, выбор допустимой величины p_i, i = n, 1, зависит от

принятого значения p_i+1). Преимущество дифференциатора (2.10), (2.12) по

сравнению с наблюдателем (2.3), (2.8) заключается в том, что независимый

выбор его амплитуд сохранится и при тонкой настройке с учетом заданно-

го времени сходимости (см. Приложение). Кроме того, диапазоны изменения

оценочных сигналов (2.1), как правило, меньше расчетных максимальных

значений соответствующих ошибок наблюдения в начале переходного про-

цесса, что позволит обеспечить заданное время оценивания с меньшими ам-

плитудами и, как следствие, уменьшить перерегулирование.

Отметим, что порядок дифференциатора (2.10) также может быть пони-

жен на единицу, если использовать корректирующее воздействие последнего

уравнения в качестве оценочного сигнала для n-й производной (аналогич-

но второму неравенству (2.9)). Более того, корректирующие воздействия при

выполнении уравнений статики могут служить оценками не только входного

сигнала, но и всех остальных производных:

ε_i = g_i+1 - v_i ≈ 0 ⇒ v_i(t) ≈ g_i+1(t), i = 1,n + 1.

Однако на практике в качестве оценочных сигналов производных до n-го по-

рядка рекомендуется использовать соответствующие переменные дифферен-

циатора: z_i(t) ≈ g_i(t), i = 1, n + 1, t ≥ T . Причина заключается в том, что

при каждой смене формы задающего сигнала корректирующие воздействия

v_i(t) ≤ p_i, i = 2,n + 1, могут выходить на предельные значения (в отличие от

переменных наблюдателя, которые в общем случае этих пиков не достигают),

что приведет к большей ошибке оценивания и негладкости оценочных сигна-

лов в начале переходных процессов. По указанным причинам для оценивания

1 < n незатухающих производных целесообразно использовать полноразмер-

ный дифференциатор (2.10), (2.12) порядка n + 1, и далее будем рассматри-

вать его тонкую настройку без соблюдения точности оценивания входного

сигнала (т.е. без требования выполнения последнего неравенства (2.9)). При

необходимости получения оценки ненулевой производной порядка n + 1 ре-

комендуется использовать дифференциатор порядка n + 2.

Что касается установки начальных условий в дифференциаторе (2.10), то с

учетом измерений g₁(t) и для сокращения времени оценивания целесообразно

принять

z₁(0) = g₁(0) ⇒ ε₁(0) = 0, z_i(0) = 0 ⇒ ε_i(0) = g_i(0),

|ε_i(0)| ≤ G_i, i = 2, n + 1.

Соответствующие оценки начальных условий ошибок наблюдения являются

опорными при тонкой настройке дифференциатора гладкого сигнала с непре-

рывными производными, которая в рамках используемого подхода обеспечит

|g₁(t) - z₁(t)| ≤ δ, t ≥ 0;

|g_i(t) - z_i(t)| ≤ δ, i = 2, n + 1, t ≥ T.

Теперь формализуем особенности процесса оценивания кусочно-диффе-

ренцируемых функций, удовлетворяющих (2.1). Наложим следующее условие

на формирование задающего сигнала. Пусть минимальный интервал време-

ни, на котором g₁(t) является n + 1 раз дифференцируемой функцией, равен

τ_min ≤ τ_j - τ_j-1, j = 1,2,..., где [τ_j-1;τ_j)

текущий интервал времени, на

котором сигнал является гладким. В точках τ₁, τ₂, . . .: 0 = τ₀ < τ₁ < τ₂ < . . .

его производные могут иметь конечные разрывы, которые трактуются как

переустановка скачком начальных условий в виртуальной модели (2.2). Каж-

дая следующая переустановка допускается не раньше, чем через τ_min. Соот-

ветственно при настройке параметров дифференциатора следует положить

T ≪ τ_min, тогда ошибки наблюдения будут находиться в заданной окрестно-

сти нуля в интервалах

|ε_i(t)| ≤ δ, τ_j-1 + T ≤ t < τ_min ≤ τ_j, j = 1, 2, . . . , i = 2, n + 1;

(2.17)

|ε₁(t)| ≤ δ, t ≥ 0.

Максимальные величины скачков производных |g_i(τ_j + 0) - g_i(τ_j - 0)| ≤ 2G_i,

i = 2,n + 1, с учетом z_i(τ_j - 0) ≈ g_i(τ_j - 0) можно принять в качестве кон-

сервативных расчетных оценок начальных условий системы (2.11) для всех

интервалов:

(2.18)

|ε₁(τ_j-1)| ≤ δ,

|ε_i(τ_j-1)| ≤ 2G_i

i = 2,n + 1, j = 1,2,...

Данные оценки позволяют не учитывать особые точки τ₁, τ₂, . . . и выполнить

тонкую настройку параметров корректирующих воздействий (2.12), рассмат-

ривая только наименьший интервал t ∈ [0; τ_min), где g₁(t) является гладкой

функцией с непрерывными производными. Параметры, выбранные исходя из

расчетных начальных условий (2.18), а также выполнение T ≪ τ_min обеспечат

нахождение ошибок наблюдения в заданной окрестности нуля в указанное

время (2.17). В сделанных предположениях имеет место следующая теорема.

Теорема. Если в системе (2.11)-(2.12) условия (2.1) выполняются, то

тогда для любых начальных условий ε_i(0), i = 1,n + 1, и сколь угодно ма-

лых δ, T > 0 найдутся такие положительные действительные числа p^∗i, l^∗i,

что при любых p_i, l_i: p_i > p^∗i, l_i > l^∗i, i = 1, n + 1, выполняются неравенства

(2.19)

|ε_i(t)| = |z_i(t) - g_i

(t)| ≤ δ, i = 1, n + 1, t ≥ T.

В Приложении приведено конструктивное доказательство теоремы, в ходе

которого получены неравенства (П.8), (П.13) для выбора параметров (2.12) с

учетом быстрых движений, обеспечивающие (2.19).

Заметим, что априори моменты времени τ₁, τ₂, . . . и τ_min > 0 неизвестны.

Если длина текущего интервала окажется меньше принятого при настройке

времени оценивания T > τ_j - τ_j-1, то тогда на этом интервале заданная точ-

ность оценивания (2.17) в общем случае достигнута не будет, можно только

гарантировать ограниченность ошибок оценивания:

|ε_i(τ_j )| ≤ 2G_i + (G_i+1 + p_i)(τ_j - τ_j-1), i = 2, n + 1.

3. Синтез системы управления БПЛА без использования

генераторов внешних воздействий

В данном разделе представленные методы построения дифференциато-

ров применяются в системе управления беспилотным летательным аппара-

том (БПЛА) для оценивания производных задающих сигналов и внешних

возмущений.

3.1. Модель объекта управления. Постановка задач

Рассматривается математическая модель пространственного движения

центра масс (материальной точки) БПЛА в траекторной системе координат,

представленная в нормальной форме [12, 22]

x₁ = x₂,

(3.1)

x₂ = ag + η + B(θ,Ψ)u,

где x₁ = (x₁₁, x₁₂, x₁₃)^T ∈ R³

вектор пространственных координат центра

масс (выходные регулируемые переменные) с элементами x₁₁ := L про-

дольная дальность, x₁₂ := H высота, x₁₃ := Z боковое смещение; x₂ =

= (x₂₁, x₂₂, x₂₃)^T ∈ R³ вектор скорости пространственных координат с эле-

ментами

(3.2)

x₂₁ := V cos θ cos Ψ, x₂₂ := V sin θ, x₂₃

:= -V cos θ sin Ψ,

где V путевая скорость, θ угол наклона траектории, Ψ путевой угол;

g ускорение свободного падения, a = (0; -1; , 0)^T ; u = (u₁, u₂, u₃)^T ∈ R³

вектор управления, элементы которого u₁ = gn_x, u₂ = gn_y cos γ, u₃ = gn_y sin γ

выражены через продольную n_x и поперечную n_y перегрузки, а также угол

крена γ вектора перегрузки, |γ(t)| < π; η(t) вектор внешних детерминиро-

ванных возмущений;





cos θ cos Ψ

-sin θ cos Ψ sin Ψ

B =  sinθ

cos θ

,detB≡1,B-1 = B^T.

− cos θ sin Ψ sin θ sin Ψ cos Ψ

Рассматривается проблема синтеза обратной связи, обеспечивающей от-

слеживания выходными переменными x₁(t) заданных сигналов g₁(t) =

= (g₁₁, g₁₂, g₁₃)^T в следующих предположениях:

прямым измерениям доступны пространственные координаты x₁(t), а

также V (t), θ(t), Ψ(t), через которые пересчитываются элементы вектора ско-

рости x₂(t) (3.2);

генераторы внешних воздействий в системе управления отсутствуют,

сигналы g₁(t) поступают в нее в реальном времени из независимого источ-

ника, их аналитический вид неизвестен, но предполагается, что задающие

воздействия корректны и могут быть отработаны конкретным БПЛА;

элементы векторов η(t), ġ₁(t) = g₂(t), g₁(t) = g₃(t),

g₁ (t) = g₄(t) являют-

ся неизвестными функциями времени, нормы векторов ограничены известны-

ми константами:



(3.3)

|η(t)| ≤ H,

g⁽

(t)≤Gj

t ≥ 0, j = 1,3,

здесь и далее под обозначением |∗| следует понимать евклидову норму век-

тора.

Ставится задача синтеза динамической обратной связи, обеспечивающей

стабилизацию ошибок слежения e₁(t) = x₁(t) - g₁(t), которая включает ре-

шение следующих подзадач:

1) синтез базового (т.е. в предположении, что все внешние сигналы из-

вестные) закона комбинированного управления, обеспечивающего экспонен-

циальную сходимость в нуль ошибки слежения с заданной скоростью:

(3.4)

|e₁(t)|

O(exp(-k₁t)) ⇔ lim

e₁(t) = 0, k₁

= const > 0;

t→+∞

2) синтез наблюдателя внешних возмущений, построенный как реплика

редуцированной модели объекта управления (3.1), с получением оценок

(3.5)

|η(t) - v₀

(t)| ≤ δ, t ≥ T > 0,

где v₀ ∈ R³ корректирующие воздействия наблюдателя возмущений;

3) синтез наблюдателя производных задающих воздействий, построенный

как реплика виртуальной канонической модели (2.2), с получением оценок

(3.6)

|g_i(t) - z_i

(t)| ≤ δ, t ≥ T > 0, i = 2, 3,

где z_i ∈ R³ переменные состояния наблюдателя производных.

Как будет показано далее, данные наблюдатели функционируют и настраи-

ваются автономно друг от друга, поэтому имеется возможность реализовать

процесс оценивания внешних сигналов за заданное время T > 0 с одинаковой

точностью δ > 0 (см. замечание). Как следствие, использование оценочных

сигналов в базовом законе управления обеспечит экспоненциальную сходи-

мость ошибок слежения с заданной скоростью в некоторую окрестность нуля

(3.7)

|e₁(t)| ≤δ+ O(exp(-k₁

t)), t > T.

Приведем последовательно решение указанных подзадач.

3.2. Синтез базового закона управления

Модель объекта управления (3.1) представлена в блочно-канонической

форме “вход-выход” и является управляемой. Для синтеза базового закона

управления целесообразно использовать блочный подход [4-7, 22], который в

отличие от стандартных методов позволяет непосредственно установить за-

данную скорость стабилизации ошибок слежения (3.4) на этапе синтеза.

Согласно идеологии блочного принципа запишем первое уравнение систе-

мы (3.1) относительно ошибки слежения ė₁ = x₂ - g₂, где переменная x₂ трак-

туется как фиктивное управление и выбирается в виде x₂ = -k₁e₁ + g₂, где

k₁ = const > 0 заданный коэффициент усиления (3.4). Задача синтеза за-

ключается в выборе истинного управления, обеспечивающего стабилизацию

невязки между реальным и выбранным фиктивным управлением:

(3.8)

e₂ = x₂ - g₂ + k₁e₁, e₂ = (e₂₁,e₂₂,e₂₃)^T.

Относительно ошибки слежения и невязки (3.8) получим следующую си-

стему:

ė₁ = -k₁e₁ + e₂,

(3.9)

ė₂ = q(x₂,g₂,g₃,η) + B(θ,Ψ)u,

где

(3.10)

q(x₂, g₂, g₃, η) = ag - g₃ + k₁ ė₁ + η = ag - g₃ + k₁(x₂ - g₂

)+η.

В предположении, что не только все внутренние, но и внешние сигналы

известны, в терминах системы (3.7) сформируем закон комбинированного

управления с линейной стабилизирующей составляющей

(3.11)

u = -B^T(θ,Ψ)(k₂e₂ + q(x₂,g₂,g₃,η)), k₂

= const > 0

и получим замкнутую линейную виртуальную систему (3.7), (3.9) вида

ė₁ = -k₁e₁ + e₂,

ė₂ = -k₂e₂.

При k₂ ≥ k₁ переменные этой системы стремятся к нулю с заданной скоро-

стью

|e₂(t)|

O(exp(-k₂t)) ⇒ |e₁(t)|

O(exp(-k₁t)) ⇔ lim

x₁(t) = g₁(t),

t→+∞

поставленная задача (3.4) выполняется.

При реализации закона управления (3.11) по оценочным сигналам внеш-

них воздействий (3.5), (3.6) с учетом (3.8), (3.10) имеем

u = -B(θ,Ψ)^T(k₂(x₂ - z₂ + k₁(x₁ - g₁)) + ag - z₃ + k₁(x₂ - z₂) + v₀) =

(3.12)

= -B^T(θ,Ψ)(k₂e₂ + q(x₂,g₂,g₃

,η) + ϕ(t)),

где ϕ(t)

суммарный сигнал ошибок оценивания, |ϕ(t)| ≤ δ(k₂ + k₁ + 2),

t > T, с учетом которого замкнутая виртуальная система (3.9), (3.12) при-

нимает вид

ė₁ = -k₁e₁ + e₂,

ė₂ = -k₂e₂ + ϕ(t),

а ее переменные при t > T последовательно сходятся в указанные окрестности

нуля:

δ(k₂ + k₁ + 2)

|e₂(t)| ≤

+ O(exp(-k₂t)) ⇒

k₂

δ(k₂ + k₁ + 2)

⇒ |e₁(t)| ≤

+ O(exp(-k₁t)).

k₂k₂

Для решения задачи слежения с заданной точностью (3.7) потребуется

обеспечить при решении задач наблюдения (3.5), (3.6) следующую точность

оценивания:

δ(k₂ + k₁ + 2)

(3.13)

≤δ⇒δ≤δk2k²

k₂k₂

k₂ + k₁ + 2

3.3. Синтез наблюдателя возмущений

Используем возможности наблюдателей с кусочно-линейными корректи-

рующими воздействиями восстанавливать при определенных условиях внеш-

ние ограниченные сигналы (входы) без наличия их динамической модели (см.

второе неравенство (2.9)) и будем оценивать внешние возмущения по их воз-

действию на объект в процессе управления. В качестве основы для наблюда-

теля возмущений примем второе уравнение исходной системы (3.1)

x₂ = ag + η + B(θ,Ψ)u,

где все параметры и сигналы, кроме η(t), известны. Наблюдатель-дифферен-

циатор строится как реплика этой системы с использованием всех известных

сигналов в виде

(3.14)

Ż₀ = ag + B(θ,Ψ)u + v₀, z₀, v₀ ∈ R³,

что приведет к следующей системе относительно ошибок наблюдения ε₀ =

=x₂ -z₀ ∈R³ :

(3.15)

ε₀ = η - v₀.

Для решения поставленной задачи (3.5) используем кусочно-линейные

корректирующие воздействия

[

p sign(ε_0j),

|ε_0j | > 1/l;

(3.16)

v_0j = p sat(lε_0j) =

plε_0j,

|ε_0j | ≤ 1/l, j = 1, 3,

с одинаковыми (для простоты изложения) параметрами p, l = const > 0.

Установим в наблюдателе (3.14) следующие начальные условия

z₀(0) = x₂(0) ⇒ ε₀(0) =0,

что сразу обеспечит нахождение ошибки наблюдения в линейной зоне.

Чтобы обеспечить |ε₀(t)| ≤ 1/l на протяжении всего процесса при t ≥ 0, вы-

берем амплитуду корректирующих воздействий на основе достаточных усло-

вий сходимости в линейную зону, аналогичных первому выражению (2.16).

В силу (3.3) имеем:

(3.17)

ε^T0 ε₀ = ε₀(η - psign(ε₀)) ≤ |ε₀

| (H - p) < 0 ⇒ p > H.

Аналогично второму неравенству (2.16) получим первичную оценку для вы-

бора второго параметра, обеспечивающего заданную точность стабилизации

ошибки наблюдения:

|ε₀(t)| ≤ 1/l < δ ⇒ l > 1/δ.

Более детально: в линейной зоне система (3.15)-(3.16) имеет вид ε₀ = η -

-plε₀, тогда

(3.18)

ε^T0 ε₀ = ε^T0 (η - plε₀) ≤ |ε₀

| (H - plδ) < 0 ⇒ l > H/(pδ).

С учетом (3.17) нижняя оценка (3.18) меньше, чем первичная. Однако основ-

ная цель построения наблюдателя (3.14) обеспечить заданную точность

оценивания внешнего возмущения (3.5). С этой целью оценим решение систе-

мы (3.15), (3.16) на интервале [0; T ]:

|η(t)|

|ε₀(T )| ≤

(1 + e^-plT ) ≤

e^-plT ⇒ pl |ε₀(T)| ≤ H + He^-plT .

Из данного выражения с учетом v₀(t) = plε₀(t) следует, что при t ≥ T кор-

ректирующее воздействие сходится к оцениваемому сигналу с заданной точ-

ностью, если

|η₂(t) - v₀(t)| ≤ δ ⇔ He^-plT ≤ δ ⇒ l >

В итоге имеем нижнюю оценку для выбора большого коэффициента, при

котором обеспечивается стабилизация ошибок наблюдения и их производных

за заданное время

}

(3.19)

max

;

что в совокупности с (3.18) и решает поставленную задачу (3.5). Заметим, что

для получения менее консервативных оценок следует рассматривать систему

(3.15)-(3.16) покомпонентно.

3.4. Синтез наблюдателя производных задающих воздействий

Основой для построения наблюдателя производных задающих воздей-

ствий является виртуальная модель (2.2), которая в данном случае имеет

три блока третьей размерности:

ġ₁ = g₂,

ġ₂ = g₃,

ġ₃ = g₄(t),

где g₁(t) ∈ R³ измеряемый выход, g_i ∈ R³, i = 2, 4, неизвестные ограни-

ченные сигналы (3.3). Для получения оценок первых g₂(t) и вторых g₃(t)

производных задающих сигналов с заданными показателями (3.6) исполь-

зуем стандартный наблюдатель с целью продемонстрировать процедуру его

настройки [3]. Выражения (2.3), (2.4), (2.8) в данном случае принимают вид:

(3.20)

Ż₁ = z₂ + v₁,

Ż₂ = z₃ + v₂,

Ż₃ = v₃, z_i ∈ R³,

ε₁ = ε₂ - v₁,

ε₂ = ε₃ - v₂,

ε₃ = g₄(t) - v₃,

(3.21)

ε_i = g_i - z_i = (ε_i1,ε_i2,ε_i3)^T;

[

p₁sign(ε_1j),

|ε_1j | > 1/l₁;

v_1j = p₁sat(l₁ε_1j) =

p₁l₁ε_1j,

|ε_1j | ≤ 1/l₁, p₁, l₁ = const > 0;



(3.22)

p_isign(v_i-1,j),

|v_i-1,j| > 1/l_i;

v_ij = p_jsat(l_jε_ij) = p_il_iv_i-1,j,

|v_i-1,j| ≤ 1/l_i, p_i, l_i = const > 0,

i = 2,3, j = 1,3.

Установим в наблюдателе начальные условия z₁(0) = g₁(0), z_i(0) =0,

i = 2,3. Допуская смену формы непрерывных задающих сигналов g₁(t) в про-

цессе управления, для настройки параметров принимаются оценки началь-

ных условий системы (3.21), аналогичные (2.18):

(3.23)

|ε₁(0)| ≤ δ,

|ε_i(0)| ≤ 2G_i

i = 2,3.

Разделим интервал оценивания на отрезки 0<t1 <t2 <t3 <t4 =T и

формализуем желаемое поведение переменных виртуальной системы (3.21)-

(3.22), обеспечивающее решение поставленной задачи (3.6)):

1) |ε₁(t)| ≤ 1/l₁ ≤ δ, t ≥ 0;

2) |ε₂(t) - v₁(t)| ≤ Δ₂ < δ ⇔ v₁(t) = ε₂(t) - α₂(t),

|α₂(t)| ≤ Δ₂, t ≥ t₁;

3) |v₁(t)| ≤ 1/l₂ ⇔ |ε₂(t)| ≤ Δ₂ + 1/l₂ ≤ δ, t ≥ t₂;

(3.24)

4) |ε₃(t) - v₂(t)| ≤ Δ₃ < δ ⇔ v₂(t) = ε₃(t) - α₃(t),

|α₃(t)| ≤ Δ₃, t ≥ t₃;

5) |v₂(t)| ≤ 1/l₃ ⇔ |ε₃(t)| ≤ Δ₃ + 1/l₃ ≤ δ, t ≥ t₄.

Нечетные неравенства в (3.24), которые означают попадание (и нахож-

дение) в линейные зоны аргументов соответствующих корректирующих воз-

действий (3.22), обеспечиваются выбором амплитуд p_j , j = 1, 3. Вне линейных

зон система (3.21), (3.22) представима в виде:

ε₁ = ε₂ -p₁sign(ε₁),

ε₂ = ε₃ -p₂sign(ε₂ -α₂),

ε₃ = g₄(t)-p₃sign(ε₃ -α₃).

Достаточные условия для выбора амплитуд, аналогичные (2.16), в данном

случае имеют вид:

ε^Ti ε_i = ε^Ti(ε_i+1 - p_isign(ε_i)) ≤ |ε_i| (|ε_i+1| - p_i) < 0 ⇒ p_i > |ε_i+1|,

(3.25)

i = 1,3, ε₄ := g₄.

Учитывая, что сходимость ошибок наблюдения ε_i(t), i = 2, 3, в указанные

области (3.24) гарантируется только при t > t_2i-3 (3.24), определим области

их изменения с учетом (3.23):

|ε₂(t)| ≤ E₂ = 2G₂ + (E₃ + p₂)t₁,

|ε₃(t)| ≤ E₃ = 2G₃ + (G₄ + p₃)t₃, t ≥ 0.

С учетом (3.25) и данных оценок получим неравенства для последовательного

(снизу вверх) выбора амплитуд, которые обеспечивают на интервалах [t₃; t₄],

[t₁; t₂] сходимость ошибок наблюдения ε₃(t), ε₂(t) соответственно в указанные

области нуля (3.24), а также выполнение первого неравенства (3.24):

E₃ - δ

2G₃ + (G₄ + p₃)t₃ - δ

p₃ > G₄ +

=G₄ +

⇒

t₄ - t₃

2G₃ + G₄t₄ - δ

t₄

⇒p₃ >

t₂ < t₃ <

;

t₄ - 2t₃

(3.26)

E₂ - δ

2G₂ + (E₃ + p₂)t₁ - δ

p₂ > E₃ +

=E₃ +

⇒p₂ >

t₂ - t₁

2G₂ + E₃t₂ - δ

2G₂ + (2G₃ + (G₄ + p₃)t₃)t₂ - δ

t₂

0<t₁ <

;

t₂ - 2t₁

p₁ > E₂ = 2G₂ + (E₃ + p₂)t₁.

В неравенствах (3.26) продемонстрирована указанная в разделе 2 зависи-

мость выбора амплитуд в верхних уравнениях от принятых значений ампли-

туд в нижних уравнениях.

В линейных зонах в указанных интервалах система (3.21), (3.22) предста-

вима в виде:

ε₁ = ε₂ - p₁l₁ε₁, t ≥ 0;

(3.27)

ε₂ = ε₃ - p₂l₂(ε₂ - α₂), t ≥ t₂;

ε₃ = g₄(t) - p₃l₃(ε₃ - α₃), t ≥ t₄.

Из достаточных условий устойчивости аналогично (3.18) получим нера-

венства для выбора больших коэффициентов наблюдателя, обеспечивающих

заданную точность стабилизации ошибок наблюдения (3.21):

ε^T1 ε₁ ≤ |ε₁|(E₂ - p₁l₁|ε₁|) < 0 ⇒ l₁ > E₂/(p₁δ),

ε^T2 ε₂ ≤ |ε₂|(E₃ - p₂l₂(|ε₂| - Δ₂)) < 0 ⇒ l₂ > E₃/(p₂(δ - Δ₂)),

ε^T3 ε₃ ≤ |ε₃|(G₄ - p₃l₃(|ε₃| - Δ₃)) < 0 ⇒ l₃ > G₄/(p₃(δ - Δ₃)).

Для оценок больших коэффициентов, обеспечивающих выполнение чет-

ных неравенств (3.24) (т.е. стабилизацию производных ошибок наблюдения

ε₁(t),

˙ε₂(t)), оценим решения первого и второго уравнения системы (3.27) на

интервалах [0; t₁], [t₂; t₃] соответственно:

E₂

p₁ - E₂

|ε₁(t₁)| ≤

e-p1l¹t¹ ⇒ |ε₂(t) - v₁(t)| ≤ Δ₂ ⇔

p₁l₁

p₁ - E₂

⇔ (p₁ - E₂)e-p1l¹t¹ ≤ Δ₂ ⇒ l₁ >

;

t₁p₁

Δ₂

E₃

p₂ - E₃

|ε₂(t₃)| ≤

+Δ₂ +

e-p2l²(t3-t2) ⇒

|ε₃(t) - v₂(t)| ≤ Δ₃ ⇔

p₂l₂

p₂ - E₃

⇔ (p₂ - E₃)e-p2l²(t3-t2) ≤ Δ₃ ⇒ l₂ >

(t₃ - t₂)p₂

Δ₃

С учетом данных оценок приведем последовательность действий при на-

стройке параметров наблюдателя (3.21), (3.22), обеспечивающих (3.24) и, сле-

довательно, цель наблюдения (3.6):

1) исходя из заданного времени оценивания T > 0, с учетом t₁ < t₂/2,

t₃ < t₄/2 зафиксировать моменты времени 0 < t₁ < t₂ < t₃ < t₄ = T;

2) выбрать значения амплитуд p_i, i = 3, 1, на основе нижних оценок (3.26);

3) принять значение 0 < Δ₃ < δ и на основе нижней оценки выбрать

G₄

(3.28)

l₃ >

;

p₃(δ - Δ₃)

4) принять значение 0 < Δ₂ < δ и на основе нижней оценки выбрать

{

}

E₃

p₂ - E₃

(3.29)

l₂ >

max

;

p₂

δ-Δ₂

t₃ - t₂

Δ₃

5) на основе нижней оценки выбрать

}

{E₂

p₁ - E₂

(3.30)

l₁ >

max

;

p₁

t₁

Δ₂

3.5. Результаты моделирования

Для численного моделирования разработанных алгоритмов (которое про-

водилось в среде MATLAB-Simulink с методом интегрирования Эйлера с по-

стоянным шагом 0,001) были использованы параметры микро БПЛА весом

до 5 кг, поднимающегося на высоту до 5 км. Электрический двигатель может

обеспечить ему скорость до 95 км/ч (26 м/c), в воздухе способен находиться

до одного часа. Подобные летательные аппараты выполняют разведыватель-

ные функции и предоставляют информацию о текущей обстановке.

Для системы (3.1) с начальными условиями x₁(0) = (0; 100; 1)^T метров при

действии внешних возмущений

η₁(t) = 0,2sin(t), η₂(t) = 0,24sin(t), η₁(t) = 0,9cos(t)

ставилась задача вывода центра масс БПЛА на пространственную траекто-

рию:

(3.31)

g₁₁(t) = 3sin(πt/3), g₁₂(t) = t+100, g₁₃

(t) = 3 cos(πt/3), t = [0; 3) с;

g₁₁(t) = t² - 9, g₁₂(t) = t + 100, g₁₃(t) = t - 6, t ≥ 3 с.

В законе управления (3.11) были приняты следующие коэффициенты уси-

ления: k₁ = diag(64; 66; 65), k₂ = diag(67; 66; 65).

Для наблюдателя возмущений (3.14) на основе (3.18)-(3.19) были приняты

следующие параметры корректирующих воздействий (3.16): p = 4, l = 180.

Для наблюдателя производных задающих сигналов (3.20) на основе (3.26),

(3.28)-(3.30) были приняты следующие параметры корректирующих воздей-

ствий (3.22): p₁ = 13, l₁ = 100; p₂ = 8, l₂ = 100; p₃ = 4, l₃ = 100.

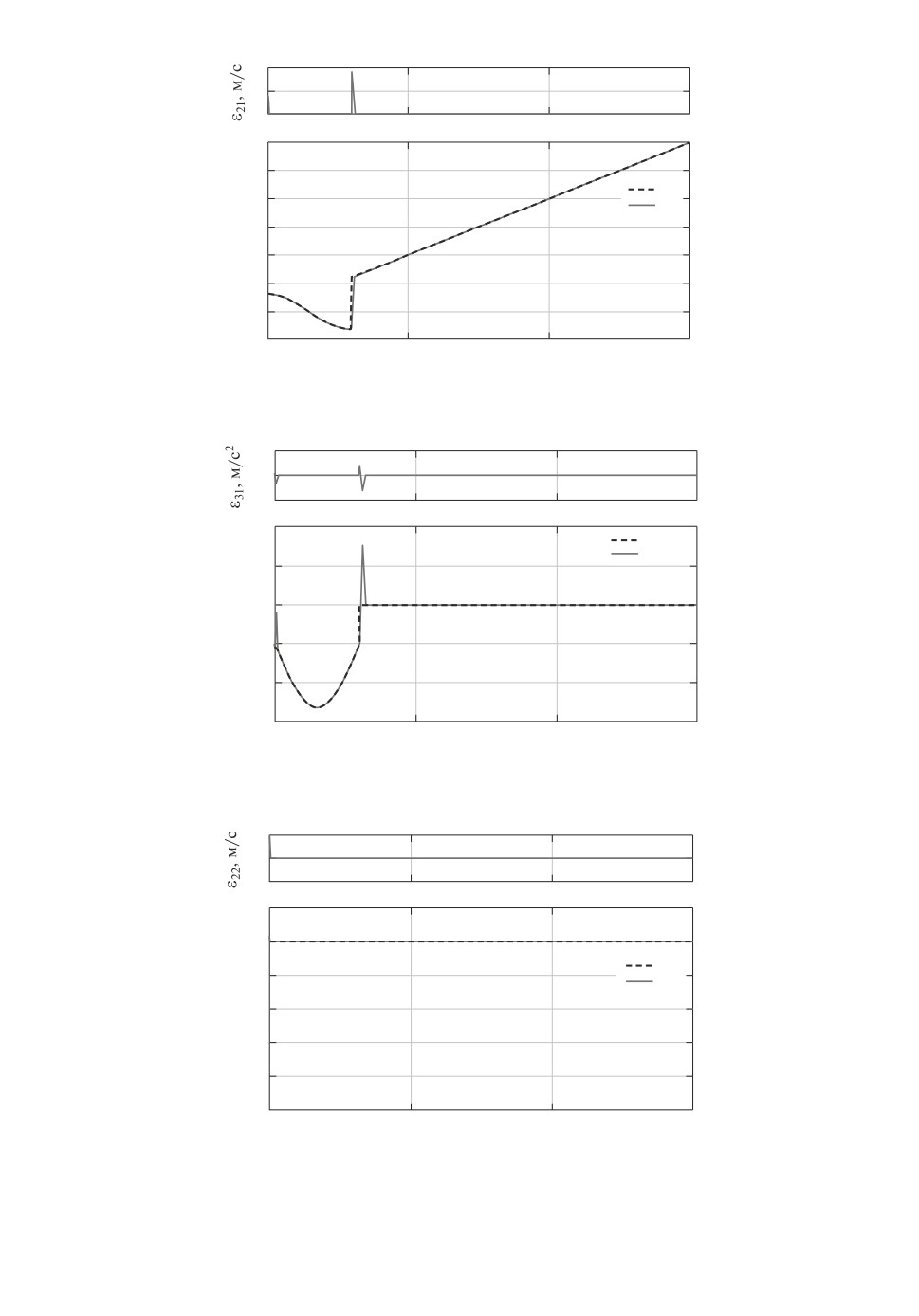
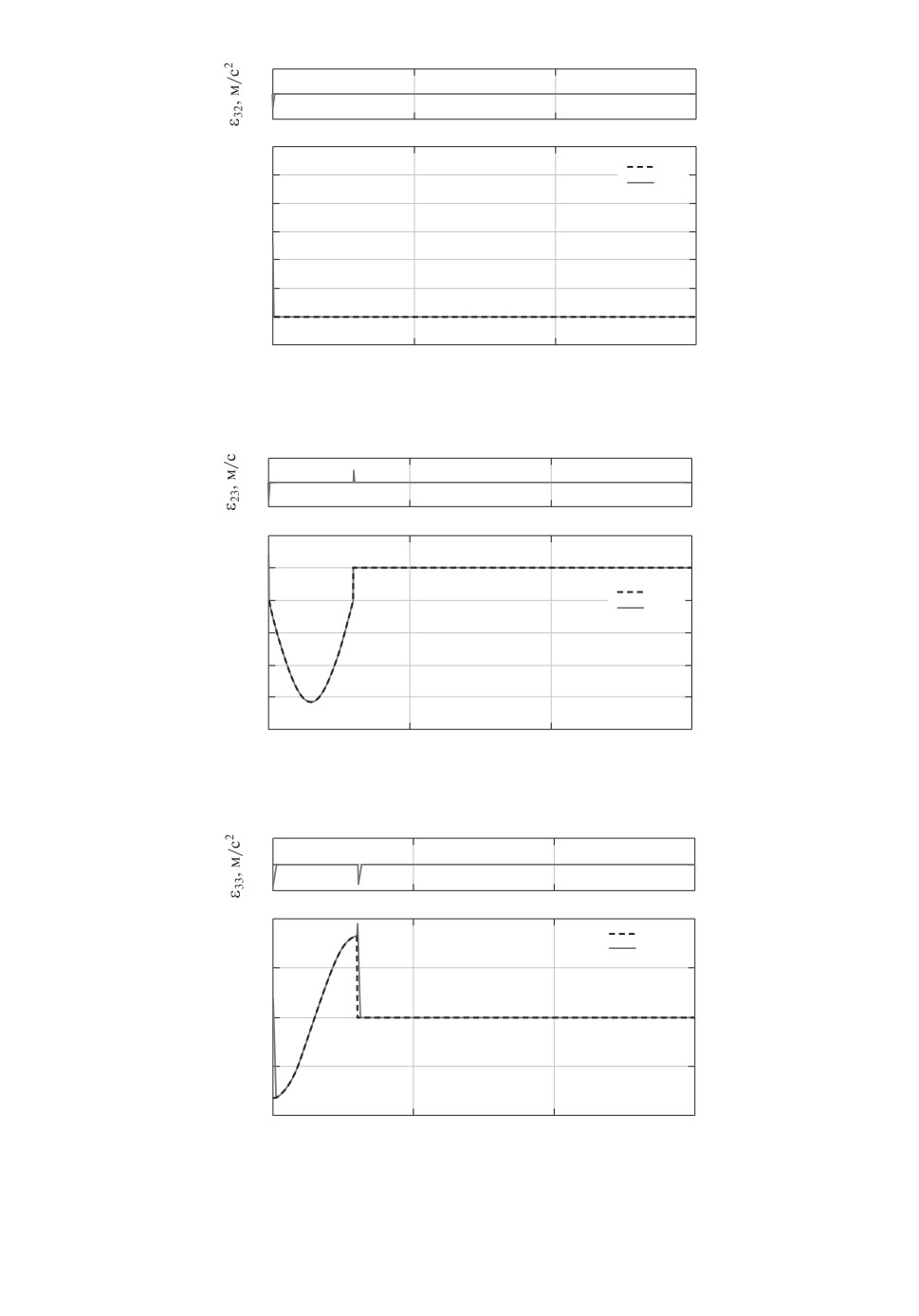
На рис. 1-6 показаны графики первых g_2i(t) и вторых g_3i(t) производ-

ных задающих воздействий и их оценок z_2i(t), z_3i(t), полученных с помощью

дифференциатора (3.20), а также ошибок наблюдения ε_2i(t) метров в секунду,

ε_3i(t) метров за секунду в квадрате, i = 1,2,3.

Как видно из рис. 1-2 и 5-6, в момент t = 3 с при смене формы задающих

сигналов g₁₁(t), g₁₃(t), приводящей к точкам конечного разрыва производ-

ных, имеют место небольшие всплески оценочных сигналов, ошибки наблю-

дения в установившемся режиме составляют |ε_2i| ≤ 10^-7 метров в секунду,

|ε_3i| ≤ 5 · 10^-5 метров за секунду в квадрате.

Заметим, что результаты моделирования дифференциатора (2.10), (2.12)

с выходом (3.31) практически не отличаются от представленных на рис. 1-6.

При использовании наблюдателя (2.3) с глубокой обратной связью (2.7), обес-

печивающего такую же точность оценивания, всплески оценочных сигналов

вторых производных оказались на порядок больше [23].

Следует отметить, что на практике задающие воздействия должны быть

допустимыми для конкретного объекта управления (2.1), в частности, доста-

точно гладкими, что обеспечивается на этапе планировании траекторий. С це-

лью продемонстрировать работоспособность дифференциатора производных

кусочно-дифференцируемых функций рассмотрена нештатная ситуация с ис-

пользованием непрерывных, но негладких задающих воздействий (3.31). Учи-

тывая, что в законах управления (3.11), (3.12) используется линейная стаби-

u₁

u₂

u₃

-1

-2

-3

-4

-⁴0

t, с

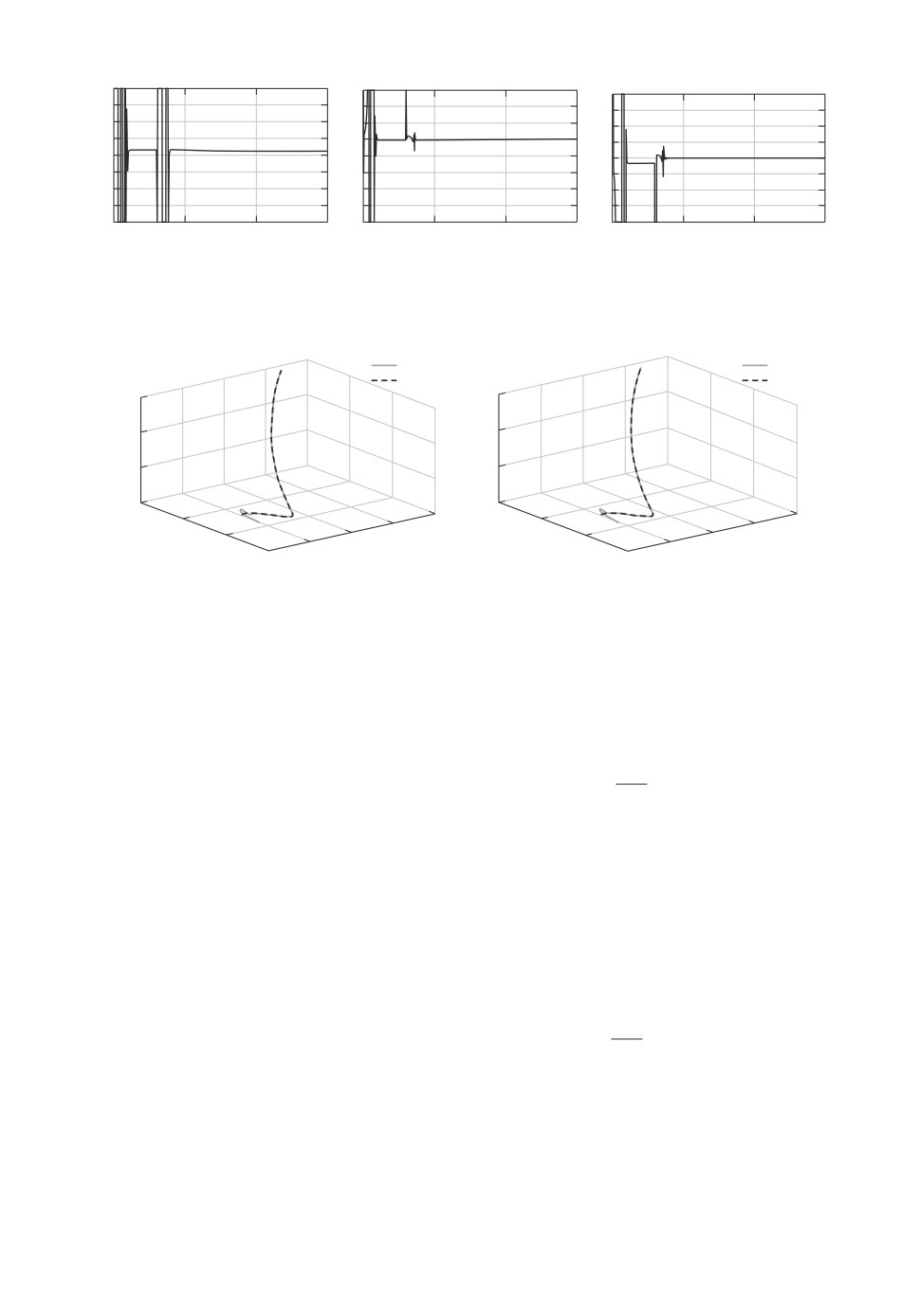
Рис. 7. Графики управлений для системы с динамической обратной связью.

x₁

H, м

g₁

H, м

g₁

115

110

105

100

300

200

100

Z, м

-5 -1000

L, м

Рис. 8. Пространственные графики заданной траектории g₁(t) и изображаю-

щей точки x₁(t): эталонной системы (а); системы с динамической обратной

связью (б).

лизирующая составляющая, для снижения перегрузок в начале переходных

процессов при моделировании управляющие воздействия были ограничены:

(3.32)

U_i = 4sat(u_i),

U_i = 4sat(u_i

i = 1,3.

Графики управлений с указанными ограничениями для системы с динамиче-

ской обратной связью представлены на рис. 7.

На рис. 8,а показан эталонный процесс отслеживания центром масс x₁(t)

заданной пространственной траекторией g₁(t) с базовым законом управления

(3.11), (3.32) в предположении, что все внешние сигналы и их производные

известны. На рис. 8,б показан график изображающей точки замкнутой си-

стемы (3.1) с динамической обратной связью (3.12), (3.32) с наблюдателями

возмущений (3.14) и производных заданий (3.20).

В таблице для ошибок слежения e_1i = x_1i - g_1i, i = 1, 3, эталонной системы

и системы с динамической обратной связью на интервалах t ∈ [0; 3)/t ≥ 3 c

представлены: величина перерегулирования e_1max,i ≥ |e_1i(t)|; время регули-

рования t_i: |e_1i(t)| ≤ 0,01 м, t ≥ t_i, а также точность в установившемся режи-

ме Δ_i ≥ |e_1i(t)| при t → 3 - 0/t ≥ 10 с. Показатели системы с наблюдателями

практически не отличаются от показателей эталонной системы, что подтвер-

ждает эффективность разработанных алгоритмов оценивания внешних сиг-

налов.

Таблица. Показатели регулирования ошибок слежения

Сигнал

Эталонная система (3.1), (3.11) t ∈ [0; 3)/t ≥ 3 с

e_1max,i, м

t_i, c

Δ_i, м

e₁₁ = x₁₁ - g₁₁

0,35/0,7

0,97/3,83

6 · 10^-4/8 · 10^-4

e₁₂ = x₁₂ - g₁₂

0,3/0,083

0,84/3,77

3, 5 · 10^-4/3, 2 · 10^-5

e₁₃ = x₁₃ - g₁₃

0,6/0,095

0,97/3,77

3, 15 · 10^-4/3, 1 · 10^-5

Система (3.1) с динамической обратной связью

Сигнал

(3.12), (3.14), (3.20) t ∈ [0; 3)/t ≥ 3 с

e_1max,i, м

t_i, c

Δ_i, м

e₁₁ = x₁₁ - g₁₁

0,36/0,78

1/3,837

6 · 10^-4/8 · 10^-4

e₁₂ = x₁₂ - g₁₂

0,35/0,084

0,85/3,79

3, 5 · 10^-4/3, 2 · 10^-5

e₁₃ = x₁₃ - g₁₃

0,6/0,092

1/3,79

3, 6 · 10^-4/3, 1 · 10^-5

4. Заключение

Использование теории наблюдателей состояния на основе виртуальных мо-

делей является конструктивной альтернативой по отношению к численному

дифференцированию сигналов. При этом пространство состояний замкну-

той системы расширяется только за счет порядка наблюдателей и не требует

построения реальных динамических генераторов внешних воздействий и за-

дающих сигналов. Предложенный подход, с одной стороны, обобщает случай,

когда дифференцируемый сигнал порождается известной динамической мо-

делью, до робастной постановки. С другой стороны, введение виртуальной

динамической модели и получение оценок ее вектора состояния на основе

теории робастных наблюдателей позволяют исключить или по крайней ме-

ре не учитывать динамику такого дифференциатора при синтезе обратной

связи, что является важным преимуществом по сравнению с использованием

устройств непосредственного дифференцирования.

Предложенный подход апробирован на примере синтеза системы управ-

ления беспилотным летательным аппаратом пространственной траектории,

заданной в виде вектора целевых сигналов для путевых координат. Предла-

гаемый подход к получению информации о производных задающего сигна-

ла обобщает случаи, когда траектория движения задается и когда задание

формируется в текущий момент времени (последнее актуально, например, в

задачах преследования, наведения и т.п.). Результаты моделирования под-

тверждают эффективность использования предложенного подхода.

ПРИЛОЖЕНИЕ

Доказательство теоремы. Учитывая специфику решаемой задачи,

без ограничения общности примем в системе (2.11) начальные условия в виде

(2.18), а именно:

(Π.1)

|ε₁(0)| ≤ δ,

|ε_i(0)| ≤ 2G_i,

2G_i

≫ δ, i = 2, n + 1.

Разделим отрезок времени [0; T ] на 2n отрезков с помощью точек 0 =

= t₀ < t₁ < t₂ < ... < t_2n-1 < t_2n = T и формализуем во времени желаемое

поведение ошибок наблюдения и их производных, обеспечивающих выполне-

ние (2.19):

|ε₁(t)| ≤ δ, t ≥ t₀, | ε₁(t)| ≤ Δ_1,1, t ≥ t₁, |ε₁(t)| ≤ Δ_1,2, t ≥ t₂,

...,|ε⁽ⁿ⁾¹(t)| ≤ Δ_1,n, t ≥ t_n,

|ε₂(t)| ≤ δ, t ≥ t₂, | ε₂(t)| ≤ Δ_2,1, t ≥ t₃, |ε₂(t)| ≤ Δ_2,2, t ≥ t₄,

...,|ε^(n-1)2(t)| ≤ Δ_2,n-1, t ≥ t_n+1,

|ε₃(t)| ≤ δ, t ≥ t₄, | ε₃(t)| ≤ Δ_3,1, t ≥ t₅, |ε₃(t)| ≤ Δ_3,2, t ≥ t₆,

...,|ε^(n-2)3(t)| ≤ Δ_3,n-2, t ≥ t_n+2,

(Π.2)

|ε_n-1(t)| ≤ δ, t ≥ t_2(n-1)-2, | ε_n-1(t)| ≤ Δ_n-1,1, t ≥ t_2(n-1)-1,

|ε_n-1(t)| ≤ Δ_n-1,2, t ≥ t_2(n-1);

|ε_n(t)| ≤ δ, t ≥ t_2n-2, | ε_n(t)| ≤ Δ_n,1, t ≥ t_2n-1;

Δ_i,j < δ, i = 1,n, j = 1,n + 1 - i;

|ε_n+1(t)| ≤ δ, t ≥ t_2n.

C учетом (2.13), (2.15) конкретизируем первые неравенства в строках

(П.2), предполагая, что на предыдущих интервалах указанные соотношения

были выполнены:

|ε₁(t)| ≤ 1/l₁ ≤ δ, t ≥ t₀;

(Π.3)

|v_i-1(t) - z_i(t)| = |ε_i(t) - ε_i-1(t)| ≤ 1/l_i ⇔ |ε_i(t)| ≤ 1/l_i + Δ_i-1,1 ≤ δ,

t ≥ t_2i-2, i = 2,n + 1.

Сходимость аргументов корректирующих воздействий в линейные зоны (П.3)

обеспечивается выбором амплитуд p_i > 0, а размеры линейных зон и выпол-

нение остальных, вспомогательных неравенств (П.2) выбором больших ко-

эффициентов l_i > 0, i = 1, n + 1.

Как было отмечено, в системе (2.11)-(2.12) по построению |ε₁(0)| ≤ δ и

sign(v₁(t)) = sign(ε₁(t)), t ≥ 0, требуется обеспечить первое неравенство (П.3)

выбором p₁ > 0, который совпадает с первичной настройкой (первое неравен-

ство (2.16)), а именно

(Π.4)

ε₁ ε₁ = ε₁(g₂ - p₁sign(ε₁)) ≤ |ε₁|(G₂ - p₁) < 0 ⇒ p₁ > G₂.

В остальных уравнениях системы (2.11) совпадение знаков sign(v_i(t)) =

= sign(ε_i(t)), i = 2,n + 1, может не иметь места при 0 ≤ t ≤ t_2(i-1)-1 и гаран-

тируется только при t > t_2(i-1)-1 вне окрестности |ε_i| ≤ Δ_i-1,1. Это означает,

что в общем случае значения ε_i(t) растут по модулю на интервале [0; t_2(i-1)-1],

нужно обеспечить их сходимость в области (П.3) за время t_2(i-1) - t_2(i-1)-1

выбором p_i, i = 2, n + 1. Детализируем первичную настройку амплитуд с уче-

том начальных условий (П.1) и заданного времени сходимости:



ε

i(t2(i-1)-1)

p_i ≥

+G_i+1,

t_2(i-1) - t_2(i-1)-1



ε_i(t_2(i-1)-1)≤2Gi + (Gi+1 + pi)t2(i-1)-1,

i = 2,n + 1,t ≥ 0.

Отсюда имеем

2G_i + (G_i+1 + p_i)t_2(i-1)-1

(Π.5)

p_i ≥

+G_i+1 ⇒

t_2(i-1) - t_2(i-1)-1

2G_i + G_i+1t_2(i-1)

⇒p_i ≥

i = 2,n + 1,

t_2(i-1) - 2t_2(i-1)-1

где 2t_2(i-1)-1 < t_2(i-1). Положим, например, все нечетные временные интерва-

лы одинаковыми Δt = t_2i-1 - t_2i-2 > 0, i = 1, n, а для четных установим Δt =

= t_2(i-1) - 2t_2(i-1)-1, i = 2,n + 1, тогда

(Π.6)

t_2(i-1) - t_2(i-1)-1 = (3 · 2^i-2

− 1)Δt, i = 2, n + 1,

откуда имеем верхнюю оценку для выбора Δt > 0:

t_2n = 3(1 + 2 + 2² + 2³ + ... + 2^n-1)Δt ≤ T ⇒ 0 < Δt ≤

(Π.7)

3(2ⁿ - 1)

С учетом (П.4)-(П.7) имеем нижние оценки для выбора амплитуд, обеспе-

чивающих сходимость аргументов корректирующих воздействий в линейные

зоны (П.3) за заданное время:

2G_i + G_i+13(2^i-1 - 1)Δt

2G_i

p^∗1 = G₂, p^∗i =

+ 3(2^i-1 - 1)G_i+1,

(Π.8)

Δt

i = 2,n + 1.

Еще раз отметим, что в отличие от (3.26) в дифференциаторе (2.10), (2.12)

амплитуды выбираются независимо друг от друга.

Для настройки больших коэффициентов рассмотрим уравнения системы

(2.11)-(2.12) с учетом (2.13) в линейных зонах, куда они попадают в указан-

ные интервалы времени:

ε₁ = g₂ - p₁l₁ε₁,

|ε₁| ≤ 1/l₁, t ≥ 0,

(Π.9)

ε_i = g_i+1 - p_il_i(ε_i - ε_i-1),

|ε_i - ε_i-1| ≤ 1/l_i, t ≥ t_2i-2, i = 2, n + 1.

Из достаточных условий сходимости ε_i ε_i < 0 найдем нижние оценки для

выбора l_i > 0, i = 1, n + 1, обеспечивающих заданную точность оценивания

(2.19), а также установим точность, которую надо обеспечить при стабилиза-

ции первых производных ошибок оценивания, разделив заданную величину δ

на две части, например пополам:

G₂

|ε₁(t)| ≤ δ(t ≥ 0) ⇒ l₁ ≥

;

p₁δ

Gi+1

2G_i+1

|ε_i(t)| ≤

+|ε_i-1|

≤ δ(t ≥ t_2i-2) ⇒ l_i ≥

(Π.10)

p_il_i

| {z }

p_iδ

| {z }

δ/2

|ε_i-1| ≤ Δ_i-1,1 =

i = 2,n + 1.

Далее для обеспечения стабилизации с заданной точностью за заданное

время производных ошибок наблюдения (П.2) рассмотрим итерационную

процедуру, состоящую из n шагов, где n максимальный порядок учиты-

ваемых производных.

Шаг 1. Выбором l_i, i = 1,n, нужно также обеспечить сходимость первых

производных ошибок наблюдения ε_i(t) в установленные области (П.10) за вре-

мя t_2i-1 - t_2i-2 = Δt (П.2) из начальных условий | ε_i(t_2i-2)| = G_i+1 + p_i (П.9).

С этой целью оценим на указанных интервалах решения вспомогательной

системы

(Π.11)

ε₁ = g₃ - p₁l₁ ε₁;

εi = gi+2 - pili( εi - εi-1

i = 2,n,

и установим точность, которую надо обеспечить при стабилизации вторых

производных ошибок оценивания, разделив величины Δ_i,1 = δ/2 на части,

например указанным образом:

G₃

|ε₁(t)| ≤ (G₂ + p₁)e-p1l¹Δt

≤Δ_1,1 =

(t ≥ t₁) ⇒

}

p₁l₁

|{z}

δ/4

}

{ 4G₃

4(G₂ + p₁)

⇒l₁ ≥

max

;

p₁

Δt

Gi+2

(Π.12)

| ε_i(t)| ≤ (G_i+1 + p_i)e-pilⁱΔt

+|ε_i-1|

≤Δ_i,1 =

(t ≥ t_2i-1) ⇒

}

p_il_i

| {z }

δ/8

δ/4

δ/8

}

{ 8G_i+2

8(G_i+1 + p_i)

⇒l_i ≥

max

;

p_i

Δt

|ε_i-1| ≤ Δ_i-1,2 =

i = 2,n.

Шаг 2. Выбором l_i, i = 1,n - 1, нужно также обеспечить сходимость

вторых производных ошибок наблюдения

εi(t) в установленные области

(П.12) за время t_2i - t_2i-1 = (3 · 2^i-1 - 1)Δt (П.2), (П.6) из начальных условий

|ε_i(t_2i-1)| = G_i+2 + p_i (П.11). С этой целью оценим на указанных интервалах

решения вспомогательной системы

ε_i-1), i = 2,n - 1,

а также установим точность, которую надо обеспечить при стабилизации тре-

тьих производных ошибок оценивания, разделив величины Δ_i,2 = δ/4, напри-

мер, аналогично (П.12):

G₄

|ε₁(t)| ≤ (G₃ + p₁)e-p1l¹2Δt

≤

(t ≥ t₂) ⇒

}

p₁l₁

|{z}

δ/8

}

{ 8G₄

8(G₃ + p₁)

⇒l₁ ≥

max

;

p₁

2Δt



Gi+3

|ε_i(t)| ≤ (G_i+2 + p_i)e-pilⁱ(3·2i-1-1)Δt

ε_i-1

≤Δ_i,2 =

(t ≥ t_2i) ⇒

}

p_il_i

| {z }

δ/16

δ/8

δ/16

}

{ 16G_i+3

16(G_i+2 + p_i)

⇒l_i ≥

max

;

p_i

(3 · 2^i-1 - 1)Δt



ε_i-1≤Δi-1,3 =δ

i = 2,n - 1,

и т.д. На каждом шаге количество рассматриваемых больших коэффициен-

тов и размерность вспомогательных систем понижаются на единицу. Таким

образом, на последнем n-м шаге выбором l₁ нужно обеспечить сходимость

ε⁽ⁿ⁾¹(t) в область, установленную на предыдущем шаге, например, указанным

выше образом Δ_1,n = δ/2ⁿ за время t_n - t_n-1 (П.2) из начальных условий

|ε⁽ⁿ⁾¹(t_n-1)| = G_n+1 + p₁. Оценка решения вспомогательного уравнения

ε⁽ⁿ⁺¹⁾¹ = g_n+2 - p₁l₁ε⁽ⁿ⁾¹

дает следующий результат:



Gn+2

ε⁽

(t)

 ≤ (G_n+1 + p₁)e-p1l¹(tn-tn-1)Δt

≤

⇒

}

p₁l₁

| {z }

δ/2n+1

}

{2ⁿ⁺¹G_n+2

2n+1(G_n+1 + p₁)

⇒l₁ ≥

max

;

p₁

(t_n - t_n-1)Δt

Здесь если n нечетное число, то t_n - t_n-1 = Δt, если четное, то t_n - t_n-1 =

= (3 · 2^n/2-1 - 1)Δt.

Учитывая, что логарифмическая функция очень медленно возрастает,

множитель при Δt, определяющий длину четного интервала (П.6), есть нату-

ральное число и 1/Δt > 1/((3 · 2^i-1 - 1)Δt), можно упростить конечный ре-

зультат, полагая этот множитель равным единице в формулах, полученных

на четных шагах.

Неравенства для выбора больших коэффициентов (П.10) и типа (П.12), по-

лученные на разных шагах процедуры, должны выполняться одновременно.

С учетом указанного упрощения объединим их и получим итоговые ниж-

ние оценки, при которых поставленная задача (2.19) обеспечивается с учетом

быстрых движений и погрешностей уравнений статики:

}

2G_n+2

{2G_n+1

8G_n+2

8(G_n+1 + p_n)

(Π.13) l^∗n+1 =

l^∗n =

max

;

p_n+1δ

p_n

Δt

{ 2G_n

8G_n+1

16G_n+2

8(G_n + p_n-1)

l^∗n-1 =

max

;

p_n-1

Δt

}

16(G_n+1 + p_n-1)

Δt

{ 2G₄

2³G₅

2⁴G₆

2nG_n+2

l^∗3 =

max

;

;...;

;

p₃

}

2³(G₄ +p₃)

2⁴(G₅ +p₃)

2n(G_n+1 + p₃)

;

;...;

Δt

{ 2G₃

2³G₄

2⁴G₅

2n+1G_n+2

l^∗2 =

max

;

;...;

;

p₂

}

2³(G₃ +p₂)

2⁴(G₄ +p₂)

2n+1(G_n+1 + p₂)

;

;...;

Δt

{G₂

2²G₃

2³G₄

2n+1G_n+2

l^∗1 =

max

;

; ...;

;

p₁

}

2²(G₂ +p₁)

2³(G₃ +p₁)

2n+1(G_n+1 + p₁)

;

;...;

Δt

Таким образом, существуют такие p^∗i (П.8) и l^∗i (П.13), что для любых

p_i, l_i: p_i > p^∗i, l_i > l^∗i, i = 1,n + 1, неравенства (2.19) будут выполнены. Теоре-

ма доказана.

Следует отметить, что оценки для выбора больших коэффициентов (П.13),

полученные из достаточных условий, могут оказаться достаточно консерва-

тивными, особенно для систем (2.11) большой размерности. При практиче-

ском применении данной процедуры рекомендуется опираться на заданные

значения G_i, i = 2, n + 2, δ > 0, T > 0 и при необходимости снижения расчет-

ных оценок:

учитывать множители при Δt в формулах, полученных на четных шагах

процедуры;

использовать другой способ разделения Δ_i,j (i = 1, n, j = 1, n + 1 - i) на

части, отводя меньшую долю при оценке затухающих собственных движений

производных.

Обратим внимание, что введенный прием с разделением на части областей

сходимости производных ошибок наблюдения позволил сделать независимым

друг от друга выбор больших коэффициентов (П.13). Можно использовать

другую, связную процедуру настройки, в ходе которой последовательно (сни-

зу вверх) из достаточных условий фиксируются значения l^∗i, i = n + 1, 1,

с учетом которых области сходимости старших производных определяются

по остаточному принципу. Такая процедура будет более трудоемкой, но мо-

жет привести к менее консервативным расчетным оценкам.

СПИСОК ЛИТЕРАТУРЫ

Wonham W.M. Linear Multivariable Control: a Geometric Approach. N.Y.: Springer-

Verlar, 1979.

Фомичев В.В., Высоцкий А.О. Алгоритм построения каскадного асимптотиче-

ского наблюдателя для системы с максимальным относительным порядком //

ДУ. 2019. Т. 55. № 4. С. 567-573.

Fomichev V.V., Vysotskii A.O. Algorithm for Designing a Cascade Asymptotic Ob-

server for a System of Maximal Relative Order // Differ. Equations. 2019. V. 55.

No. 4. P. 553-560.

Краснов Д.В., Уткин А.В. Синтез многофункциональной системы слежения в

условиях неопределенности // УБС. 2017. Вып. 69. С. 29-49.

Krasnov D.V., Utkin A.V. Synthesis of a Multifunctional Tracking System in Con-

ditions of Uncertainty // Autom. Remote Control. 2019. V. 80. No. 9. P. 1704-1716.

Краснова С.А., Уткин В.А., Уткин А.В. Блочный подход к анализу и синтезу

инвариантных нелинейных систем слежения // АиТ. 2017. № 12. С. 26-53.

Krasnova S.A., Utkin V.A., Utkin A.V. Block Approach to Analysis and Design of

the Invariant Nonlinear Tracking Systems // Autom. Remote Control. 2017. V. 78.

No. 12. P. 2120-2140.

Антипов А.С., Краснов Д.В., Уткин А.В. Декомпозиционный синтез системы

управления электромеханическими объектами в условиях неполной информа-

ции // ПММ. 2019. Т. 83. Вып. 4. С. 530-548.

Antipov A.S., Krasnov D.V., Utkin A.V. Decomposition Synthesis of the Control

System of Electromechanical Objects in Conditions of Incomplete Information //

Mechanics of Solids. 2019. V. 54. No. 5. P. 47-60.

Уткин В.А. Инвариантность и автономность в системах с разделяемыми дви-

жениями // АиТ. 2001. № 11. С. 73-94.

Utkin V.A. Invariance and Independence in Systems with Separable Motion // Au-

tom. Remote Control. 2001. V. 62. No. 11. P. 1825-1843.

Kochetkov S.A., Krasnova S.A., Antipov A.S. Cascade Synthesis of Electromechan-

ical Tracking Systems with Respect to Restrictions on State Variables // IFAC-

PapersOnLine. 2017. V. 50. No. 1. P. 1042-1047.

LaValle S.M. Planning Algorithms. Cambridge University Press, 2006.

De Filippis L., Guglieri G., Quagliotti F. Path Planning Strategies for UAVS in 3D

Environments // J. of Intelligent and Robotic Systems. 2012. V. 65. No. 1. P. 247-264.

10.

Гилимьянов Р.Ф., Рапопорт Л.Б. Метод деформации пути в задачах планиро-

вания движения роботов при наличии препятствий // ПУ. 2012. № 1. С. 70-76.

Gilimyanov R.F., Rapoport L.B. Path Deformation Method for Robot Motion Plan-

ning Problems in the Presence of Obstacles // Autom. Remote Control. 2013. V. 74.

No. 12. P. 2163-2172.

11.

Kamyar K., Taheri E. Aircraft Optimal Terrain/Threat-Based Trajectory Planning

and Control // J. of Guidance, Control, and Dynamics. 2014. V. 37. No. 2. P. 466-483.

12.

Ткачев С.Б., Крищенко А.П., Канатников А.Н. Автоматическая генерация

сложных пространственных траекторий БПЛА и синтез управлений // Мате-

матика и математическое моделирование. МГТУ им. Н.Э. Баумана. Электрон.

журн. 2015. № 01. С. 1-17.

Tkachev S.B., Krishenko A.P., Kanatnikov A.N. Automatic Generation of Com-

plex Spatial Trajectories of the UAV and Synthesis of Control // Mathematics and

Mathematical Modelling of the Bauman MSTU. 2015. No. 01. P. 1-17.

13.

Емельянов С.В., Афанасьев А.П. Дифференцирование сигнала в системах ав-

томатического регулирования // АиТ. 2015. № 12. С. 27-42.

Emel’yanov S.V., Afanas’ev A.P. Signal Differentiation in Automatic Control Sys-

tems // Autom. Remote Control. 2015. V. 76. No. 12. P. 2110-2123.

14.

Utkin V.A., Krasnova S.A. Improving the Accuracy of the Estimated Signalsin the

State and Disturbance Observer // Proc. of the Twelfth Int. Conf. “Management

of large-scale system development” (MLSD). 1-3 October, 2019. Moscow, Russia,

V.A. Trapeznikov Institute of Control Sciences. IEEE Xplore, 2019. 4 p.

15.

Краснова С.А., Кузнецов С.И. Оценивание на скользящих режимах неконтро-

лируемых возмущений в нелинейных системах // АиТ. 2005. № 10. С. 54-69.

Krasnova S.A., Kuznetsov S.I. Incontrollable Perturbations on Nonlinear Dynamic

Systems: Estimation on Moving Modes // Autom. Remote Control. 2005. V. 66.

No. 10. Р. 1580-1593.

16.

Краснова С.А. Оценивание внешних возмущений на основе виртуальных дина-

мических моделей // УБС. 2018. Вып. 76. С. 6-25.

Krasnova S.A. Estimating the Derivatives of External Perturbations Based on Vir-

tual Dynamic Models // Autom. Remote Control. 2020. V. 81. No. 5. P. 897-910.

17.

Никифоров В.О. Наблюдатели внешних детерминированных возмущений. Ч. 2.

Объекты с неизвестными параметрами // АиТ. 2004. № 11. С. 40-48.

Nikiforov V.O. Observers of External Deterministic Disturbances. P. II. Objects with

Unknown Parameters // Autom. Remote Control. 2004. V. 65. No. 11. P. 1724-1732.

18.

Дылевский А.В., Лозгачев Г.И. Применение метода пространства состояний для

синтеза дифференциаторов // АиТ. 1999. № 9. С. 13-20.

Dylevskii A.V., Lozgachev G.I. State Space Approach to the Design of Differentia-

tors // Autom. Remote Control. 1999. V. 60. No. 9. P. 1222-1229.

19.

Уткин В.А., Уткин А.В. Задача слежения в линейных системах с параметри-

ческими неопределенностями при неустойчивой нулевой динамике // АиТ. 2014.

№ 9. С. 62-81.

Utkin V.A., Utkin A.V. Problem of Tracking in Linear Systems with Parametric Un-

certainties under Unstable Zero Dynamics // Autom. Remote Control. 2014. V. 75.

No. 9. P. 1577-1592.

20.

Levant A. Higher-Order Sliding Modes, Differentiation and Output-Feedback Con-

trol // Int. J. Control. 2003. V. 76. No. 9. P. 924-941.

21.

Khalil H.K., Praly L. High-Gain Observers in Nonlinear Feedback Control // Int. J.

Robust and Nonlinear Control. 2014. V. 24. No. 6. P. 993-1015.

22.

Кокунько Ю.Г., Краснов Д.В., Уткин А.В. Два метода синтеза наблюдателей

состояния и возмущений для беспилотного летательного аппарата // ПУ. 2020.

№ 1. С. 3-16.

23.

Кокунько Ю.Г., Антипов А.С., Краснова С.А. Наблюдатели состояния как сред-

ство оценивания производных детерминированных сигналов // Матер. XXXII

конф. памяти выдающегося конструктора гироскопических приборов Н.Н. Ост-

рякова, 13-я Мультиконференция по проблемам управления (МКПУ-2020),

Санкт-Петербург, 6-8 октября 2020 г. СПб.: АО “Концерн “ЦНИИ “Электро-

прибор”, 2020. С. 312-315.

Статья представлена к публикации членом редколлегии П.В. Пакшиным.

Поступила в редакцию 09.08.2020

После доработки 20.01.2021

Принята к публикации 16.03.2021