Автоматика и телемеханика, № 7, 2021

Нелинейные системы

(Институт проблем управления им. В.А. Трапезникова РАН),

Е.Ю. ЗЫБИН, д-р техн. наук (zybin@mail.ru),

В.В. КОСЬЯНЧУК, д-р техн. наук (kos.vl.v@gmail.com),

Н.И. СЕЛЬВЕСЮК, д-р техн. наук (nis@gosniias.ru)

(ФГУП Государственный научно-исследовательский институт

авиационных систем),

А.А. ТРЕМБА, канд. физ.-мат. наук (atremba@ipu.ru),

М.В. ХЛЕБНИКОВ, д-р физ.-мат. наук (khlebnik@ipu.ru)

(Институт проблем управления им. В.А. Трапезникова РАН)

ОПТИМИЗАЦИЯ ВЫСОТНО-СКОРОСТНОГО ПРОФИЛЯ

КРЕЙСЕРСКОГО ПОЛЕТА ВОЗДУШНОГО СУДНА

ПРИ ФИКСИРОВАННОМ ВРЕМЕНИ ПРИБЫТИЯ¹

Рассматривается задача минимизации расхода топлива дозвуковых

пассажирских и транспортных самолетов на этапе крейсерского полета.

Для формирования высотно-скоростного профиля полета сформулирова-

на задача оптимизации и предложено ее решение методом покоординат-

ного спуска с учетом ограничений, совмещенного с использованием набо-

ра вспомогательных точек-кандидатов. Вычисление расхода топлива как

целевой функции оптимизации реализовано через численное моделирова-

ние с фиксированным шагом переходных процессов скорости и высоты и

упрощенный расчет значений секундного расхода по статическим урав-

нениям на участках полета с постоянной скоростью и высотой.

Ключевые слова: оптимизация, воздушное судно, расход топлива, крей-

серский полет, моделирование полета, высотно-скоростной профиль.

DOI: 10.31857/S0005231021070047

1. Введение

Задача оптимизации маневрирования воздушных судов была и остается

актуальной, требуя новых подходов и решений с развитием авиации и воз-

можностей вычислительных систем [1, 2]. Проблема снижения расхода топли-

ва обусловлена не только экономическими критериями, но и необходимостью

сокращения выбросов CO₂. В настоящей работе рассматривается задача фор-

мирования высотно-скоростного профиля полета воздушного судна, обеспе-

чивающего снижение расхода топлива в рамках уже совершающегося полета,

когда задано время прибытия в конечную точку. При этом предполагается,

что оптимизация профиля скорости и высоты периодически обновляется в

процессе полета с учетом фактического местоположения воздушного судна

и параметров полета. Поэтому важен вопрос разработки процедуры оптими-

зации с невысокой вычислительной сложностью для получения результата

расчетов за несколько минут с учетом ограниченных вычислительных ресур-

сов на борту воздушного судна.

¹ Исследование выполнено при поддержке Российского научного фонда (проект № 21-

71-30005).

Сложность вычисления целевой функции оптимизации состоит в том, что

секундный расход топлива зависит в том числе от массы воздушного судна, а

масса, в свою очередь, постоянно уменьшается на величину расхода топлива.

Поэтому для получения значения целевой функции необходимо промодели-

ровать расход на всем оптимизируемом этапе полета.

В [3] рассмотрен выбор оптимальной скорости при полете на постоянной

высоте как решение задачи оптимального управления (вариационной зада-

чи). Получено аналитическое решение, при этом использована упрощенная

модель расхода топлива, а также не учитываются ветровые условия. Изме-

нение скорости для такого режима непрерывное.

Альтернативным подходом является разбиение траектории полета на ин-

тервалы и оптимизация скоростного профиля на этих интервалах (на по-

стоянной высоте). В [4] сделана попытка найти точное решение задачи об

оптимальной скорости на каждом из участков с учетом продольного ветрово-

го воздействия. Для решения необходимо использовать явный вид функции

расхода топлива, зависящей от скорости и массы, и ее особенность в виде

выпуклости. Оптимальный профиль скоростей является решением системы

уравнений и находится с помощью метода Ньютона. Существенной особен-

ностью этого подхода является то, что задача с фиксированным временем

полета заменяется задачей оптимизации по критерию “прямой цены полета”

(direct operation cost), учитывающей как расход топлива, так и задержку по

времени прибытия в конечную точку.

В [5] выполнена оптимизация профиля скорости и высоты по критерию

“прямой цены полета” для случая, когда скорости и высоты являются дис-

кретными, тем самым задача сводится к задаче смешанного целочисленно-

нелинейного программирования, которая решалась стандартными методами

среды Matlab. При этом число сегментов траектории выбиралось малым

(до трех), что позволяло осуществлять прямой перебор вариантов.

Все три подхода являются многообещающими с точки зрения дальнейшей

работы над оптимизацией полного профиля полета, но для их реализации

требуется уточнение аналитической модели полета, которая должна учиты-

вать как адекватную модель расхода топлива, так и динамику изменения

скорости и высоты полета.

Вопрос модели полета, с одной стороны, позволяющей с достаточной точ-

ностью оценить расход топлива, а с другой стороны, достаточно простой,

чтобы на ее основе можно было строить расчет целевой функции процеду-

ры оптимизации, остается актуальным [6]. В [7] рассмотрена задача миними-

зации расхода топлива дальнемагистрального самолета. Для моделирования

полета использована упрощенная система дифференциальных уравнений, где

тяга и угол атаки вычисляются по статическим уравнениям. Сделан вывод,

что маневрирование по скорости не дает заметного снижения расхода топли-

ва, а оптимизация высоты полета эффективна при дальности полета более

5000 км. При этом не рассматривается быстродействие используемых алго-

ритмов для применения в функции самолетовождения, реализуемой вычис-

лительной системой на борту воздушного судна.

Таким образом, задача формирования высотно-скоростного профиля по-

лета, обеспечивающего минимальный расход топлива на этапе крейсерского

полета, исследована недостаточно. Для оценки расхода топлива обычно ис-

пользуются статические уравнения или приближенные аппроксимации рас-

хода в зависимости от массы воздушного судна, скорости и высоты полета.

Такой подход не учитывает характер расхода топлива при переходных про-

цессах, возникающих при изменении скорости или высоты полета.

В настоящей работе предлагается комбинированный подход, когда пере-

ходные процессы при изменении скорости или высоты полета моделируются

системой дифференциальных уравнений, описывающей динамику полета, а

расход топлива на участках с постоянной скоростью и высотой полета вычис-

ляется по статическим уравнениям.

Для задач невыпуклой оптимизации с ограничениями (таких, как рассмат-

риваемая задача) можно применять разные подходы, например градиентный

или покоординатный спуск с проекцией на множество ограничений, метод

доверительной области, случайный поиск и т.п. Часто применяются приемы

глобальной оптимизации, использующие множественные начальные точки и

рандомизацию поиска, а также эвристики типа генетических алгоритмов, так

как невыпуклые задачи часто многоэкстремальные. Часть методов использу-

ют оценки градиента функции, которые требуют многократного вычисления

самой функции, тем самым общее время выполнения алгоритма замедляет-

ся в число раз, кратное числу варьируемых компонент. В безградиентных

методах чаще всего используется случайный поиск, что приводит к непред-

сказуемым результатам. В рассматриваемой задаче такие подходы признаны

нецелесообразными из-за недетерминированности результата и с учетом, что

вычислительная сложность это один из основных критериев выбора метода

оптимизации для реализации в бортовой вычислительной системе при огра-

ниченном времени выполнения. Поэтому предлагается использовать детер-

минированный безградиентный поисковый метод оптимизации [8] с учетом

ограничений.

Статья организована следующим образом: в разделе 2 сделана постановка

задачи и сформулирована задача оптимизации расхода топлива; в разделе 3

рассмотрена динамическая модель движения центра масс воздушного судна;

в разделе 4 приведены статические уравнения, по которым можно получить

секундный расход топлива из текущих значений высоты и скорости полета

и массы воздушного судна, считая их постоянными; в разделе 5 предложен

алгоритм расчета расхода топлива на этапе крейсерского полета; в разде-

ле 6 предлагается алгоритм оптимизации, решающий поставленную задачу;

в разделе 7 предложенные алгоритмы проверяются на примере среднемаги-

стрального пассажирского самолета; в разделе 8 приведены заключительные

выводы.

2. Постановка задачи

Рассматривается крейсерский полет без учета маневрирования по курсу.

Предполагается, что заданы

1) расстояние R, которое должно быть пройдено на этапе крейсерского

полета;

2) время t_s, отведенное для прохождения этого расстояния;

3) интервал допустимых скоростей крейсерского полета [V_min, V_max];

4) разрешенные значения эшелонов высоты {h₁, . . . , h_K };

5) значения скорости V₀ и высоты h₀ в начале этапа крейсерского полета,

а также высоты h_N+1, на которую необходимо выйти в конце этапа крейсер-

ского полета;

6) масса воздушного судна в начале этапа крейсерского полета m₀;

7) параметры воздушного судна.

Задача состоит в том, чтобы определить требуемые скорость и высоту по-

лета в каждый момент времени, которые передаются в бортовую систему

управления, такие что суммарный расход топлива на этапе крейсерского по-

лета будет минимальным для заданных расстояния, времени, других исход-

ных данных и ограничений крейсерского полета. При определении высоты

полета необходимо учитывать, что 1) высота должна быть равна одному из

заданных допустимых значений, соответствующих эшелонам полета, 2) зада-

ется некоторое минимальное время нахождения в одном эшелоне, т.е. смена

эшелонов может производиться не чаще, чем через некоторое заданное вре-

мя. При этом требуемые скорость и высота полета будут определяться для

некоторого количества участков, на которых эти значения остаются постоян-

ными. Это означает, что требуемые скорость и высота полета не будут функ-

циями времени с разными значениями в каждый момент, а будут кусочно-

постоянными функциями. Количество участков по скорости и по высоте, на

которые разбивается весь этап крейсерского полета, должно быть задано.

Таким образом, можно сформулировать решаемую задачу.

Задача. Определить для этапа крейсерского полета требуемую скорость

на каждом участке по скорости и требуемую высоту полета на каждом участ-

ке по высоте, минимизирующие суммарный расход топлива на всем этапе

крейсерского полета при заданных времени и расстоянии полета, высотах в

начале и в конце этапа крейсерского полета, массе и скорости в начале эта-

па крейсерского полета, ограничениях на допустимые минимальную и мак-

симальную скорость и минимальное допустимое время между изменениями

требуемой высоты, допустимые дискретные значения высоты полета, соот-

ветствующие эшелонам полета.

Чтобы сформулировать эту задачу как задачу оптимизации, необходимо

выделить вектор варьируемых переменных, ограничения на эти переменные,

целевую функцию и функции ограничений. Для скоростного профиля зада-

дим число n участков равного размера r = R/n, для каждого из которых

нужно выбрать скорость V_i ∈ [V_min, V_max], i = 1, . . . , n, так чтобы выполня-

лось условие прибытия в заданное время t_s:

∑

(1)

=t_s.

i=1

Предлагается использовать в качестве варьируемых переменных не ско-

рости V_i, а периоды времени x_i = r/V_i, так как в этом случае вместо (1)

получаем линейную функцию ограничения

[

]

∑

(2)

x_i = t_s, x_i ∈

V_max

min

i=1

Пусть для высотного профиля задано число N участков с различной вы-

сотой полета. Тогда следующая группа варьируемых переменных это вы-

сота полета на каждом из N участков x_i ∈ {h₁, . . . , h_K }, i = n + 1, . . . , n + N,

где K число разрешенных эшелонов высоты.

Для каждого участка различной высоты необходимо определить его дли-

тельность. Высота полета не может меняться слишком часто, т.е. число N

выбирается в пределах от 1 до 5 в зависимости от расстояния, которое долж-

но быть пройдено на этапе крейсерского полета. Поэтому дополнительная

группа варьируемых переменных это время полета для каждого участка

высоты x_i ≥ t_hmin, i = n + N + 1, . . . , n + 2N, где t_hmin минимальное до-

пустимое время между изменениями требуемой высоты. Тем самым участки

для каждой высоты не имеют фиксированную длину, как для скорости, а

время полета на каждом эшелоне может варьироваться. При этом должно

выполняться условие

∑

(3)

x_i = t_s - t_e,

i=n+N+1

где t_e

время, зарезервированное для выхода на заданную высоту в конце

крейсерского полета.

Таким образом, задача оптимизации состоит в том, чтобы найти вектор

x = [x₁,... ,x_n,x_n+1,...,x_n+N,x_n+N+1,... ,x_n+2N],

минимизирующий целевую функцию

∫ts

(4)

q_s = q_c

(t)dt,

где q_c секундный расход топлива, при соблюдении ограничений (2) и (3).

3. Динамическая модель

Динамика движения центра масс воздушного судна определяется дейст-

вующими силами тяги двигателей, лобового сопротивления, подъемной силы

и силы тяжести [9] с учетом того, что масса не постоянна, а уменьшается за

счет расхода топлива [6] и может быть описана уравнениями

(5)

mV = T cos(α + ϕ) -1cxρSV2 - mg sin Θ + V qc,

(6)

mVΘ = T sin(α + ϕ) +1cyρSV2

− mg cosΘ,

(7)

= V sinΘ,

(8)

L=VcosΘ+Vw,

(9)

m= -q_c,

(10)

α = θ - Θ,

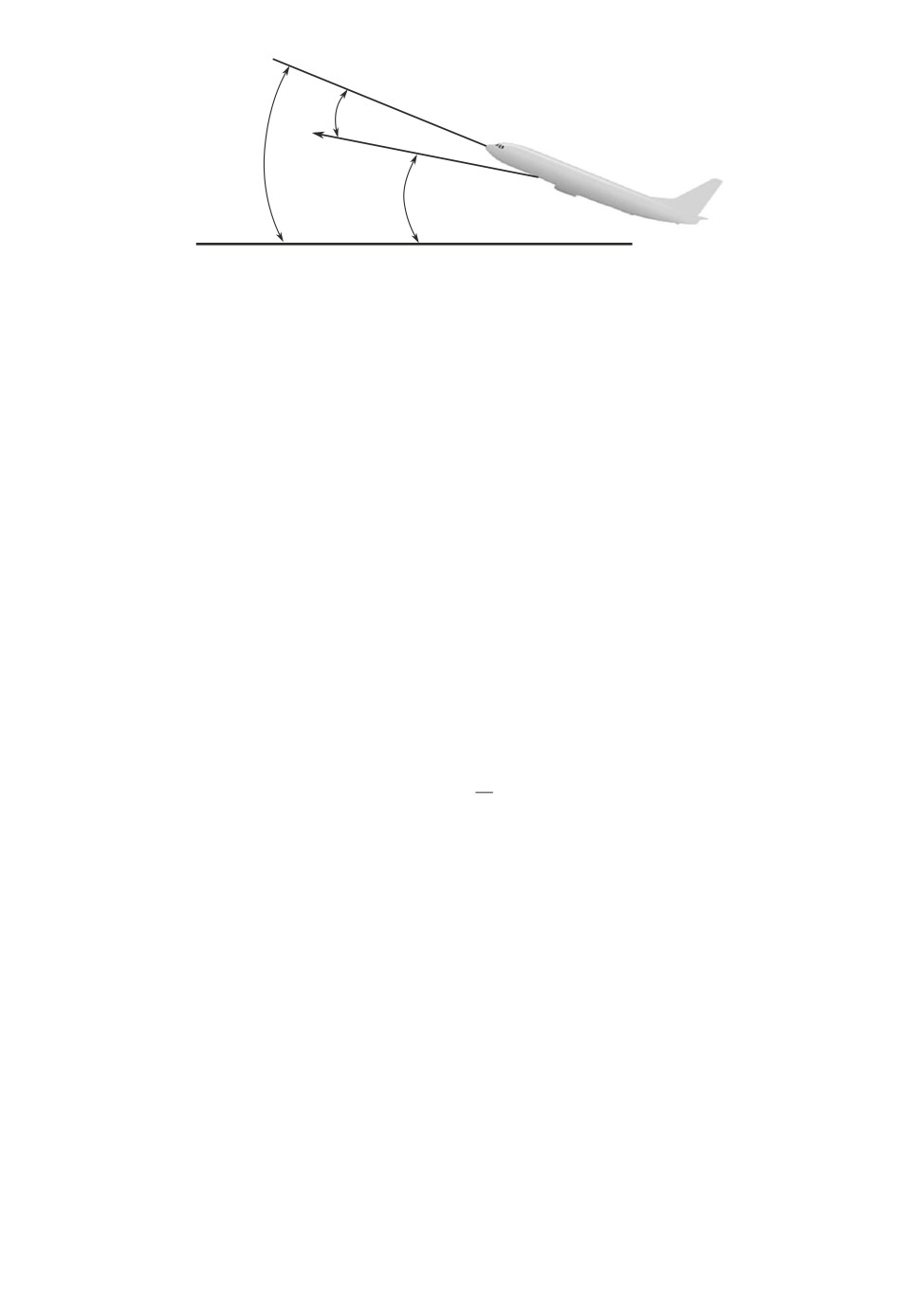
Рис. 1. Взаимосвязь угла атаки и тангажа.

где переменные состояния m масса воздушного судна (кг), V

воздуш-

ная скорость (м/с), Θ угол наклона траектории (рад), h высота поле-

та (м), L пройденное расстояние (м); известные для исследуемой модели

воздушного судна константы ϕ угол установки двигателей (рад) и S

площадь крыла (м²), ускорение свободного падения будем считать констан-

той g = 9,80665 м/с², плотность воздуха ρ (кг/м³) определяем из стандартной

атмосферы [10] в зависимости от высоты h, α угол атаки (рад) (его соотно-

шение с углами наклона траектории и тангажа показано на рис. 1), c_x и c_y

аэродинамические коэффициенты лобового сопротивления и подъемной си-

лы, q_c

секундный расход топлива (кг/с), V_w известная или прогнози-

руемая скорость попутной/встречной составляющей ветра (м/с), значения T

суммарной тяги двигателей (Н) и тангажа θ (рад) определяются работой ре-

гуляторов скорости и высоты бортовой системы управления.

Для исследуемой модели воздушного судна должны быть известны ап-

проксимирующие формулы зависимости аэродинамических коэффициентов

от числа Маха и угла атаки c_x(M, α) и c_y(M, α) или заданы таблицы для

интерполяции. Число Маха находим как

M =

где a скорость звука, определяемая из стандартной атмосферы в зависи-

мости от высоты h. Кроме того, аэродинамические коэффициенты зависят

от значения числа Рейнольдса, но так как в работе рассматривается толь-

ко крейсерский полет, то в подразумеваемом диапазоне высот влияние этого

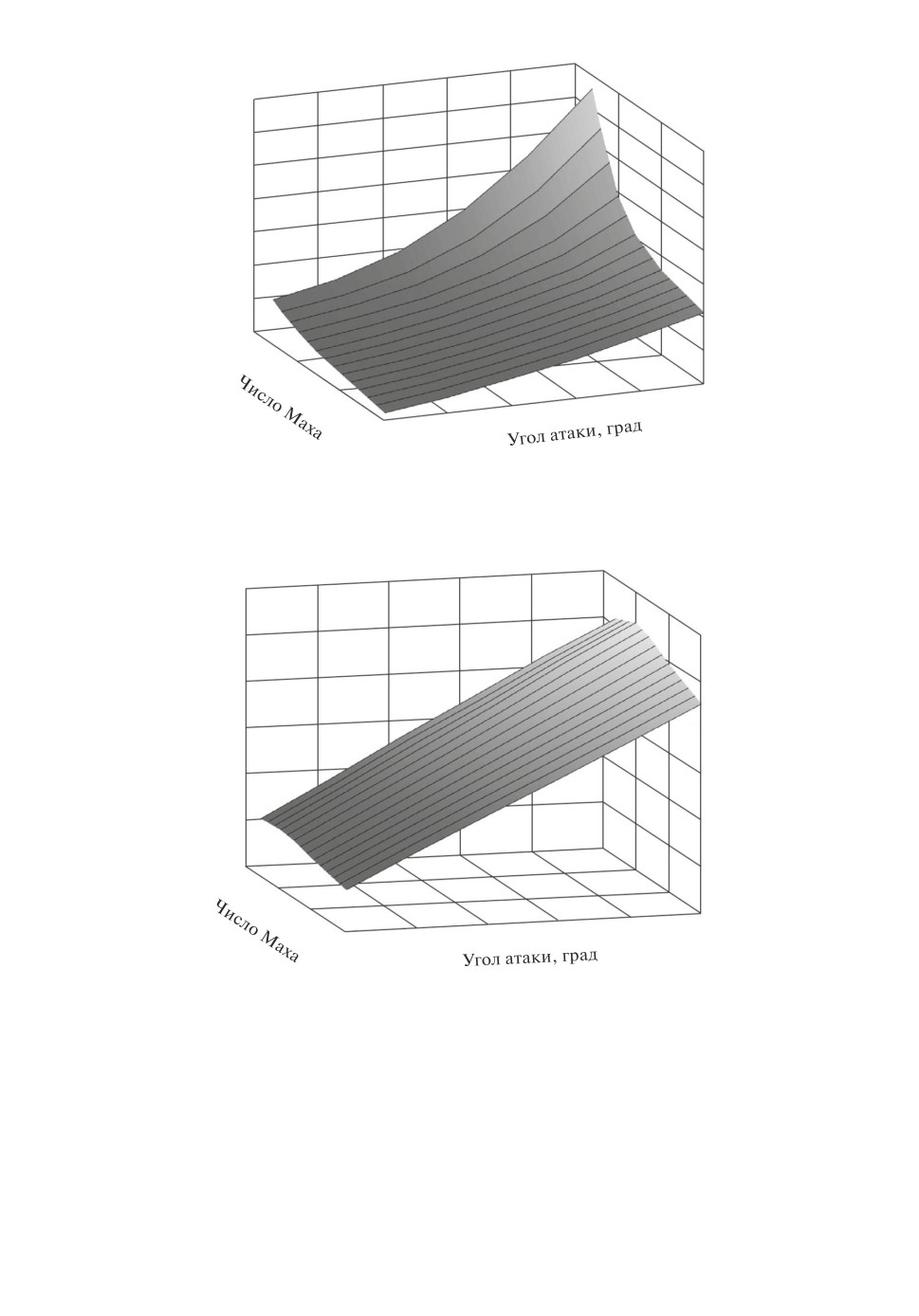
значения несущественно и им пренебрегаем. Типовые зависимости c_x(M, α)

и c_y(M,α) для диапазона значений M и α в режиме крейсерского полета

показаны на рис. 2 и рис. 3.

Секундный расход топлива можно выразить как

(11)

q_c

= η(M,T,h)T,

где η(M, T, h) удельный расход топлива (кг/с/Н) известная для двига-

телей исследуемой модели воздушного судна функция от числа Маха, тяги,

высоты полета и, возможно, других параметров [11].

ПИД-регулятор скорости формирует сигнал управления как функцию

уставки и измеренного значения воздушной скорости. Коэффициенты регуля-

тора должны быть известны. Следует учитывать, что существует некоторая

С_x

0,060

0,055

0,050

0,045

0,040

0,035

0,030

0,025

0,85

0,80

3,0

0,75

2,5

2,0

1,5

1,0

0,70 0,5

Рис. 2. Зависимость аэродинамического коэффициента лобового сопротивле-

ния c_x от числа Маха и угла атаки (градусы).

С_y

0,8

0,7

0,6

0,5

0,4

0,3

0,2

0,85

0,80

0,75

3,0

2,0

2,5

0,70 0,5

1,0

1,5

Рис. 3. Зависимость аэродинамического коэффициента подъемной силы c_y от

числа Маха и угла атаки (градусы).

динамика тяги в зависимости от этого сигнала управления, и модель этой ди-

намики также должна быть известна. В этой работе для моделирования дина-

мики двигателей используется дифференциальное уравнение первого поряд-

ка. Аналогично работа регулятора высоты моделируется как ПИ-регулятор

с известными коэффициентами, а инерционность тангажа к сигналу управ-

ления рулем высоты моделируется дифференциальным уравнением первого

порядка. Кроме того, в регуляторе высоты предусмотрено ограничение угла

наклона траектории.

Таким образом, система уравнений (1)-(10), дополненная формулами рас-

чета c_x(M, α), c_y(M, α) и η(M, T, h), уравнениями регуляторов скорости и

высоты и уравнениями динамики тяги и тангажа, позволяет моделировать

крейсерский полет для заданных уставок скорости и высоты, определяющих

высотно-скоростной профиль полета. Начальные условия должны быть за-

данными в соответствии с параметрами полета в начале этапа крейсерского

полета.

В рассматриваемой задаче предполагается, что время t_s, отведенное на

крейсерский полет, задано (и скорость выбирается так, что за это время будет

преодолено планируемое расстояние крейсерского полета). Поэтому, модели-

руя полет в течение времени t_s, можно получить суммарный расход топлива

на этапе крейсерского полета как разность заданной массы воздушного судна

в начале этапа крейсерского полета и массы, полученной в конце моделиро-

вания.

4. Статическая модель

При решении задачи оптимизации целевая функция (4) вычисляется для

каждого варианта варьируемых переменных, использованного в процедуре

поиска минимального значения целевой функции. Поэтому время, необходи-

мое для вычисления значения целевой функции, должно быть достаточно

малым, и даже за счет некоторой потери точности расчета значения целевой

функции нужно искать пути сокращения вычислений.

Статическая модель позволяет получить значение секундного расхода топ-

лива для текущих значений скорости и высоты полета и массы воздушного

судна. Так как существуют участки полета, когда скорость и высоту можно

принять постоянными значениями, а при моделировании без учета возмуще-

ний весь этап крейсерского полета, кроме участков переходного процесса

между сформированными уставками скорости и высоты, то тогда

(12)

= 0,

Θ=0,Θ=0,

= 0.

Для этих условий из уравнения (5), приняв q_c = η₀T , где η₀ прибли-

зительное среднее значение удельного расхода топлива, получаем формулу

расчета тяги

c_xρSV

(13)

T =

(

cos(α + ϕ) + V η₀

Для использования формулы (13) необходимо определить значение c_x(M, α),

т.е. нужно еще найти значение угла атаки α. Для этого запишем уравнение (6)

при условиях (12):

(14)

T sin(α + ϕ) +

c_yρSV²

− mg = 0.

Так как в режиме крейсерского полета угол α + ϕ мал, то часто первым

слагаемым в этом уравнении пренебрегают, и тогда можно получить значение

2mg

(15)

c_y =

ρSV²

Приблизительное значение

α определяется из известной зависимости

c_y(M,α). В настоящей работе предлагается определять значение угла ата-

ки α более точно. Для этого подставим в (14) вместо T выражение (13), где

пренебрегаем малым слагаемым V η₀:

(16)

tg(α + ϕ)c_xρSV² + c_yρSV²

− 2mg = 0.

Для малых значений угла α + ϕ можно принять tg(α + ϕ) ≈ α + ϕ и из (16)

получить

2mg

(17)

(α + ϕ)c_x(M, α) + c_y(M, α) -

= 0.

ρSV²

Здесь важно помнить, что использование приблизительных статических

уравнений предполагается для сокращения времени вычислений. Поэтому

для того, чтобы получение значения α как решение уравнения (17) не стало

вычислительно сложной задачей, необходимо получить линейные аппрокси-

мации

(18)

c_x(M,α) = k_x1(M,α)α + k_x0

(M, α),

(19)

c_y(M,α) = k_y1(M)α + k_y0

(M).

На рис. 3 видно, что зависимость c_y(M, α) практически линейна относи-

тельно α, и будем считать, что коэффициенты в линейной аппроксимации (19)

зависят только от числа Маха M, которое при рассмотрении статических

уравнений является известным значением для заданных воздушной скорости

и высоты полета. На рис. 2 видно, что зависимость c_x(M, α) нелинейна отно-

сительно α, поэтому коэффициенты в линейной аппроксимации (18) зависят и

от угла атаки α. Будем использовать оценку α, полученную из уравнений (15)

и (19) для вычисления значений коэффициентов k_x1(M, α) и k_x0(M, α).

Таким образом, подставив (18) и (19) в (17), получим квадратное уравне-

ние с неизвестным α, из которого легко находится его значение. Выбирается

большее из двух решений квадратного уравнения с учетом, что значение уг-

ла атаки в рассматриваемых режимах должно быть положительным. Теперь

можно посчитать тягу по формуле (13) и найти текущее значение расхода

топлива (11).

Следует заметить, что в (17) использовано текущее значение массы m, ко-

торое постоянно уменьшается в соответствии с расходом топлива. Поэтому

для получения расхода топлива на участке с постоянными скоростью и высо-

той полета нужно выбрать некоторый шаг времени, на котором изменением

массы можно пренебречь, и с этим шагом повторять расчет секундного рас-

хода топлива по формулам (11) и (13), обновляя значение массы на каждом

шаге с учетом расхода топлива и интегрируя расход. В рассматриваемом в

разделе 7 примере расход топлива на участках без переходных процессов со-

ставляет не более 0,72 кг/с, и при выборе шага в 60 с изменение общей массы

за один шаг будет менее 0,07 %, а изменение расхода топлива менее 0,04 %, что

можно считать верхней оценкой возможной ошибки расчета расхода. Ошибка

по сравнению с моделированием этого примера методом Рунге-Кутты четвер-

того порядка практически оказалась в несколько раз меньше.

5. Алгоритм расчета расхода топлива

Предлагается вычислять значение суммарного расхода топлива на этапе

крейсерского полета (4), используя для участков с постоянными скоростью и

высотой полета формулы (11) и (13), где значение массы будет уменьшаться

на величину расхода топлива с шагом вычислений таким, на котором массу

можно считать постоянной с достаточной степенью точности. То есть вы-

брав шаг моделирования Δ_st, принимаем длительность участка с постоянны-

ми скоростью и высотой полета равным

t_k = lΔ_st + Δ,

где l

натуральное число, Δ < Δ_st, и вычисляем расход топлива на этом

участке как сумму

∑

q_k =

qc_i Δst + qcl+1 Δ,

i=1

где qci полученные значения секундного расхода топлива на каждом шаге.

Для переходных процессов при изменении скорости или высоты полета

предлагается находить расход топлива, моделируя полет по уравнениям (5)-

(11), формулам расчета c_x(M, α), c_y(M, α) и η(M, T, h) и формулам регулято-

ров скорости и высоты, учитывая инерционность тяги и тангажа и используя

простейший численный метод Эйлера первого порядка с шагом одна секунда.

Использование этого метода для рассматриваемого в разделе 7 примера дает

ошибку значения расхода топлива по сравнению с моделированием методом

Рунге-Кутты четвертого порядка всего 0,004 % при повышении быстродей-

ствия в 3 раза.

Следует учитывать, что если принимать уставку скорости на каждом из

n участков равной

(20)

V_i =

i = 1,...,n,

x_i

то в результате моделирования пройденное расстояние может отличаться от

заданного, так как в начале каждого участка во время переходного процесса

от скорости V_i-1 к скорости V_i реальная скорость еще не равна значению V_i.

Поэтому для соблюдения условия, что необходимо преодолеть заданное рас-

стояние за заданное время, уставка скорости на участке рассчитывается как

r-t_vV_i-1

(21)

V_i =

i = 1,...,n,

x_i - t_v

где t_v примерное усредненное значение, подбираемое экспериментально, со-

ответствующее половине времени основной части переходного процесса, где

скорость принимается как среднеарифметическое от скоростей предыдуще-

го и текущего участков. Это позволяет скомпенсировать ошибку в итоговом

пройденном расстоянии. В рассматриваемом в разделе 7 примере t_v = 11 с.

При больших участках постоянной скорости, например, для r = 500 000 м и

x_i = 2200 с разница значений, полученных по формуле (20) или (21), соста-

вит примерно 0,02 % при изменении скорости на 10 м/с и еще меньше при

меньшем изменении. Такой разницей можно пренебречь. Но если значения r

и x_i будут в 10 раз меньше, то ошибка вырастет в 10 раз и будет уже не-

приемлемой.

Кроме того, во время переходного процесса по высоте горизонтальная ско-

рость должна учитывать угол наклона траектории. Поэтому уставка скорости

на участке рассчитывается следующим образом:

r-t_vV_i-1

(22)

V_i =

i = 1,...,n,

x_i - t_v - t_hi(1 - cos Θ_max)

где Θ_max максимально разрешенный угол наклона траектории в режиме

крейсерского полета, t_hi общее время переходных процессов по высоте на

i-м участке по скорости (если их нет на этом участке, то t_hi = 0, и тогда (22)

совпадает с (21)), которое находится как сумма длительностей переходных

процессов по высоте, каждую из которых определяем как

|x_j - x_j-1|

V_i sin Θ_max

где x_j

значение высоты. Такой расчет требуемой скорости носит оценоч-

ный характер, что может приводить к тому, что за заданное время при най-

денных значениях скоростей пройденное расстояние будет отличаться от за-

данного. Так, в примере раздела 7 при моделировании профиля полета дли-

тельностью 6 ч, показанного на рис. 7, расстояние полета получилось рав-

ным 5 000 031 м при заданном значении 5 000 000 м, т.е. ошибка составила

менее 0,001 %. Практически требуемая точность моделирования расхода топ-

лива составляет 0,05 %. При этом нужно учитывать, что задача найти оп-

тимальный высотно-скоростной профиль полета, а не значение расхода, т.е.

важно, чтобы разные исходные данные моделирования не приводили к суще-

ственно разным ошибкам и таким образом влияли на полученный результат,

а расхождение моделируемого и реального расхода топлива может быть более

существенным.

6. Алгоритм оптимизации

Целевая функция расхода топлива моделируется нелинейными дифферен-

циальными и алгебраическими уравнениями, поэтому ее градиент аналити-

чески недоступен, а его численная оценка по непрерывным переменным тре-

бует n + N дополнительных вычислений функций, что неприемлемо с точки

зрения замедления алгоритма. Более того, функция невыпуклая и много-

экстремальная, что затрудняет применение ряда алгоритмов (ускоренных и

проксимальных), а также исключает гарантии нахождения глобального ми-

нимума методами оптимизации, не использующими переборный подход. По-

этому применяются эвристические и частично переборные алгоритмы, схо-

дящиеся к локальному минимуму. Постановка задачи усложняется введени-

ем дискретных переменных (эшелоны высоты). Их полный перебор требует

K^N вычислений целевой функции и представляется нереализуемым даже для

небольшого числа переменных N (число участков полета на постоянной вы-

соте) и доступных эшелонов K.

Обе сложности удалось преодолеть с помощью гибридного метода опти-

мизации, требующего небольшое количество вычислений целевой функции и

одновременно учитывающего “разумный” перебор дискретных величин. Реа-

лизованный метод схож с методом покоординатного спуска [8, 12]. Метод от-

личается тем, что для соблюдения ограничений на каждом шаге может изме-

няться не одна, а несколько компонент вектора переменных. Кроме того, ис-

пользуется набор вспомогательных точек-кандидатов, что позволяет успешно

решать проблему попадания в локальный минимум, в отличие от метода ло-

кальных вариаций [12]. Выбор точек-кандидатов детерминирован в отличие

от метода роя частиц [13]. Алгоритм выполняется с фиксированным парамет-

ром шага, поэтому нужно учитывать, что это минимум на множестве варьи-

руемых переменных, зависящем от выбранного параметра шага. При выпол-

нении алгоритма генерируется последовательность точек {x⁽ⁱ⁾, i = 1, 2, . . .},

образующих релаксирующую, убывающую последовательность

q_s(x⁽ⁱ⁺¹⁾) ≤ q_s(x⁽ⁱ⁾).

Вектор переменных x = [x¹, x², x³] состоит из трех групп: x¹ время на

каждый из n участков различной скорости, x² высота из множества раз-

решенных эшелонов для каждого из N участков различной высоты, x³

время на каждый из N участков различной высоты. При изменении компо-

ненты в первой или третьей группах необходимо соблюдать ограничения (2)

или (3) соответственно. Например, при увеличении выбранной компоненты

“соседние” с ней или все остальные компоненты группы уменьшаются так,

чтобы выполнялись ограничения (2) и (3). По существу подзадача выбо-

ра точек-кандидатов состоит в подборе нескольких “соседних” по отноше-

нию к текущей точек, удовлетворяющих ограничениям. Изменение основной

выбранной компоненты характеризуется внутренним параметром алгоритма,

играющим роль длины шага. В группе варьируемых переменных x² (высо-

та полета на каждом из N участков x_i ∈ {h₁, . . . , h_K }, i = n + 1, . . . , n + N) в

качестве точек-кандидатов берутся все возможные варианты, т.е. все K эше-

лонов.

Алгоритм оптимизации.

Шаг 1. Выбрать начальную точку

x⁽⁰⁾ = [x^1,(0), x^2,(0), x^3,(0)],

удовлетворяющую всем ограничениям. Инициировать общий счетчик итера-

ций k = 0, внутренние счетчики для каждой группы переменных k¹ = k² =

= k³ = 1 и счетчик неэффективных шагов k^bad = 0.

Шаг 2. Выбрать группу переменных j = mod(k, 3) + 1.

Шаг 3. В группе переменных x^j выбрать основную изменяемую компонен-

ту и увеличить ее счетчик.

Шаг 4. Сформировать набор точек-кандидатов X = {x^a, x^b, . . .} на основе

выбранной группы и изменяемой компоненты. Число кандидатов зависит от

группы.

Шаг 5. Вычислить целевую функцию во всех точках-кандидатах и выбрать

среди них минимальное значение и соответствующую точку

x^cand = arg minqs(x).

x∈X

Шаг 6. Если значение функции удалось улучшить, т.е.

q_s(x^cand) < q_s(x^(k)),

то изменить текущую точку x^(k+1) ← x^cand и сбросить счетчик неэффектив-

ных шагов k^bad ← 0. В противном случае сохранить точку x^(k+1) ← x^(k) и

увеличить счетчик неэффективных шагов k^bad ← k^bad + 1.

Шаг 7. Если счетчик неэффективных шагов меньше числа переменных

k^bad < n + 2N, то перейти к Шагу 2. Иначе

Завершить алгоритм: Вернуть в качестве решения текущую точку x^(k).

7. Пример

Предложенные алгоритмы оптимизации и расчета целевой функции реа-

лизованы в среде Matlab. Проверка их работоспособности проведена на сле-

дующем примере. Рассмотрим среднемагистральный пассажирский самолет

МС-21-300 с площадью крыла S = 113 м² и следующими исходными данными

крейсерского полета, представленными в табл. 1.

Проверим сначала эффективность варьирования скорости на постоянной

высоте. Пусть для скорости задано n = 10 участков (тогда r = R/n = 500 км),

а высоту считаем постоянной: N = 1, K = 1, h₀ = h₁ = h_N+1 = 9144 м. Про-

цедурой оптимизации найдены значения скоростей:

V = [235,33,

235,45,

235,58,

235,7,

234,96, . . .

227,37,

227,48,

227,59,

228,64] м/с.

Таблица 1. Исходные данные

Расстояние крейсерского полета

5 000000 м (5000 км)

Время крейсерского полета

t_s

21600 c (6 ч)

Минимальная скорость

V_min

210 м/с

Максимальная скорость

V_max

250 м/с

Начальная скорость

V₀

R/t_s = 231,48 м/с

Начальная высота

h₀

9144 м (30 000 футов)

Конечная высота

h_N+1

9144 м (30 000 футов)

Разрешенный угол наклона траектории Θ_max

1 градус

Масса в начале крейсерского полета

m₀

75000 кг

236

n = 1

n = 10

234

n = 20

232

230

228

226

0,5

1,0

1,5

2,0

2,5

Время, с

´10⁴

Рис. 4. Скорость при моделировании найденного профиля.

0,85

n = 1

0,80

n = 10

n = 20

0,75

0,70

0,65

0,60

0,55

0,50

0,5

1,0

1,5

2,0

2,5

Время, с

´10⁴

Рис. 5. Расход топлива при моделировании найденного профиля скорости.

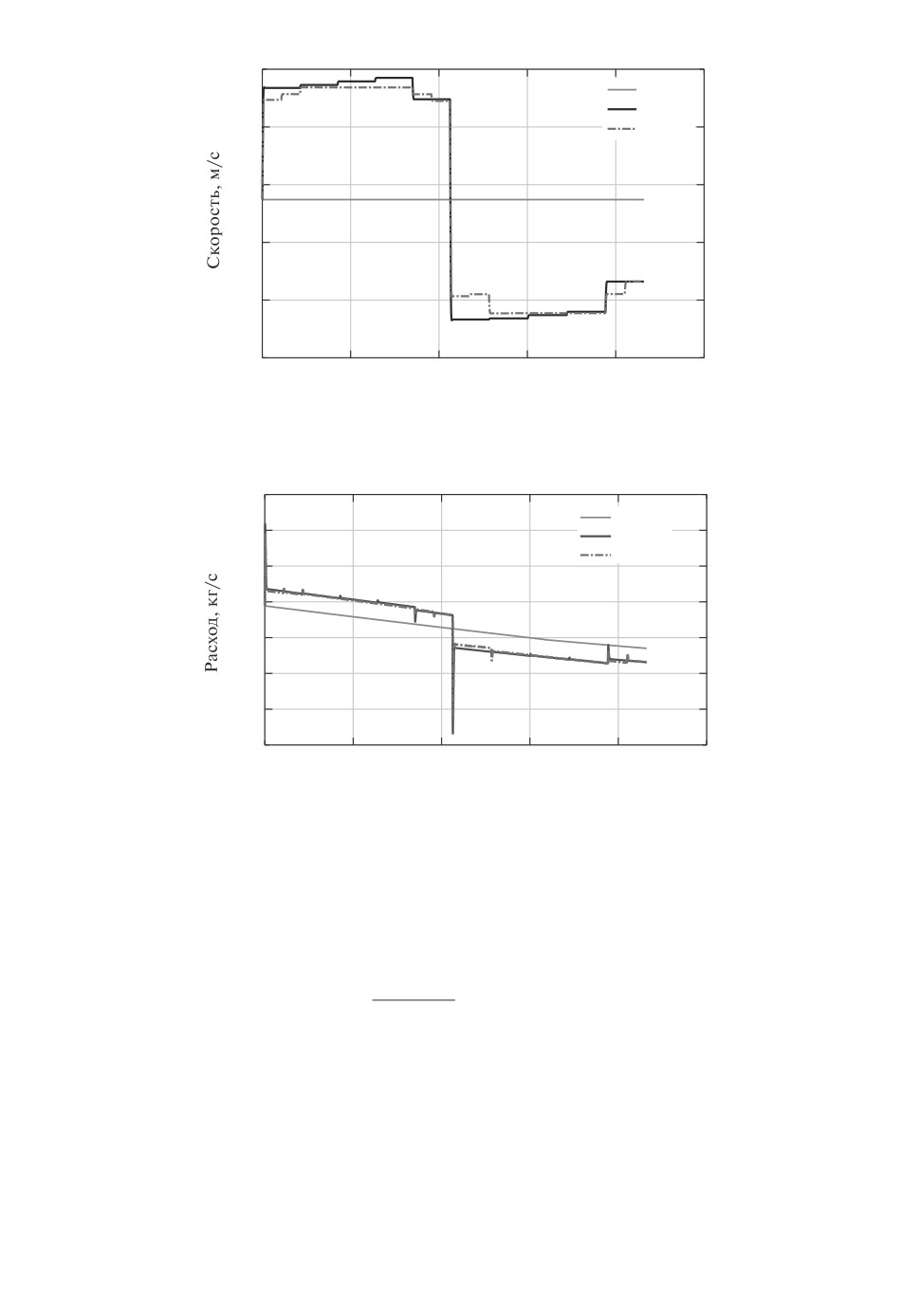
Расход топлива составил 14 293 кг. Если менять скорость чаще и принять

n = 20, то получим такой же расход топлива с точностью до 0,2 кг. То есть

повышение вариативности скорости не дает дополнительной экономии. При

моделировании полета с постоянной скоростью

5 000000

V =

= 231,481 м/с

21600

расход топлива составил 14 314 кг. Маневрирование по скорости дало эко-

номию всего 21 кг. Графики моделирования скорости и секундного расхода

топлива для этих трех вариантов показаны на рис. 4 и 5.

При оптимизации высоты и скорости для n = 10, N = 4, K = 6, h₀ =

= h_N+1 = 9144 м и разрешенных значениях эшелонов высоты

{h₁, . . . , h_K } = {9144,

9753,6,

10363,2,

10972,8,

11582,4,

12192} м =

= {30 000,

32000,

34000,

36000,

38000,

40000} футов

Таблица 2. Зависимость расхода топлива от высоты полета

Высота, м

9144

11582,4

12192

Расход, кг

14314

12893

13016

значениях длительности каждого из четырех участков высоты:

x³ = [5082,4, 5224,2,

5204,1,

5189,3] с.

Графики моделирования скорости и высоты показаны на рис. 6, график

секундного расхода топлива на рис. 7. При моделировании полета с по-

стоянной скоростью V = 231,481 м/с и на постоянной высоте 11582,4 м рас-

ход топлива составил 12 893 кг. Маневрирование дало более заметную эконо-

мию 55 кг. Заметим, что даже если не менять высоту на этапе крейсерского

полета (N = 1), важен выбор высоты полета в зависимости от массы. Для

рассматриваемого примера при m₀ = 75 000 кг при полете с постоянной ско-

ростью V = 231,481 м/с и на постоянной высоте расход на разных высотах

приведен в табл. 2.

Заметим, что в полученных значениях расхода топлива учтены набор вы-

соты от начальной высоты крейсерского полета и снижение к высоте, требуе-

мой в конце этапа крейсерского полета.

8. Заключение

Полученные результаты моделирования подтверждают результаты дру-

гих исследований, что при решении задачи минимизации расхода топлива

при условии заданных расстоянии и времени крейсерского полета маневри-

рование по скорости и высоте не дает существенной экономии топлива. Так, в

рассмотренном примере маневрирование только по скорости дало снижение

расхода на 0,15 %, а при маневрировании по скорости и высоте на 0,4 %.

Тем не менее важен расчет экономичной высоты полета при заданной массе

воздушного судна, так как правильный выбор эшелона дает существенную

экономию топлива. Кроме того, разработанные алгоритмы позволяют учи-

тывать прогнозные значения скорости ветра. При этом оптимальное форми-

рование высотно-скоростного профиля полета может давать более заметное

снижение расхода. Таким образом, дальнейшее развитие работы предпола-

гает исследование оптимизации расхода топлива с использованием данных о

скорости ветра.

Авторы выражают признательность Борису Теодоровичу Поляку и Нико-

лаю Владимировичу Куланову за ценные советы при подготовке работы.

СПИСОК ЛИТЕРАТУРЫ

1. Русол В.А. Оптимизация маневрирования воздушных судов. М.: Транспорт,

1986.

2. Скрипниченко С.Ю. Оптимизация режимов полета по экономическим критери-

ям. 2-е изд., перераб. и доп. М.: Машиностроение, 1988.

3. Franco A., Rivas D., Valenzuela A. Minimum-Fuel Cruise at Constant Altitude With

Fixed Arrival Time // J. Guidance, Control, Dynam. 2010. V. 33. No. 1. P. 280-285.

4. Saucier A., Maazoun W., Soumis F. Optimal Speed-Profile Determination for Air-

craft Trajectories // Aerosp. Sci. Technol. 2017. V. 67. P. 327-342.

5. Valenzuela A., Rivas D. Optimization of Aircraft Cruise Procedures Using Discrete

Trajectory Patterns // J. Aircraft. 2014. V. 51. Iss. 5. P. 1632-1640.

6. Григоров П.Ю., Куланов Н.В. Применение концепции обратных задач динамики

в задачах вертикальной навигации // Известия РАН. Теория и системы управ-

ления. 2016. № 3. С. 130-140.

7. Губарева Е.А., Мозжорина Т.Ю. Оптимизация программы полета дозвукового

пассажирского самолета на участке крейсерского полета // Инженерный жур-

нал: наука и инновации. 2014. Вып. 12(36).

8. Поляк Б.Т. Введение в оптимизацию. 2-е изд., испр. и доп. М.: ЛЕНАНД, 2014.

9. Hull D.G. Fundamentals of Airplane Flight Mechanics. Berlin: Springer-Verlag, 2007.

10. ГОСТ 4401-81. Атмосфера стандартная. Параметры. М.: Изд-во стандартов,

2004.

11. Bartel M., Trevor M.Y. Simplified Thrust and Fuel Consumption Models for Modern

Two-Shaft Turbofan Engines // J. Aircraft. 2008. V. 45. Iss. 4. P. 1450-1456.

12. Васильев Ф.П. Методы оптимизации. М.: Факториал Пресс, 2002.

13. Kennedy J., Eberhart R. Particle Swarm Optimization // Proc. 1995 IEEE Int. Conf.

Neural Networks. 1995. Vol. 4. P. 1942-1948.

Статья представлена к публикации членом редколлегии А.А. Галяевым.

Поступила в редакцию 23.11.2020

После доработки 05.02.2021

Принята к публикации 16.03.2021