Автоматика и телемеханика, № 7, 2021
© 2021 г. Я.Г. САПУНКОВ, канд. физ.-мат. наук (iptmuran@san.ru),
А.В. МОЛОДЕНКОВ, д-р техн. наук (molalexei@yandex.ru)
(Институт проблем точной механики и управления РАН, Саратов)
АНАЛИТИЧЕСКОЕ РЕШЕНИЕ ЗАДАЧИ ОПТИМАЛЬНОГО
В СМЫСЛЕ КОМБИНИРОВАННОГО ФУНКЦИОНАЛА РАЗВОРОТА
ОСЕСИММЕТРИЧНОГО КОСМИЧЕСКОГО АППАРАТА1
В кватернионной постановке рассматривается задача оптимального
управления пространственной переориентацией космического аппарата
как твердого тела с одной осью симметрии без ограничения на функ-
цию управления. В качестве критерия оптимальности используется ком-
бинированный функционал, который объединяет время и энергию, за-
траченные на разворот космического аппарата. На основании принципа
максимума Л.С. Понтрягина для этой задачи получены новые аналитиче-
ские решения в классах конических и обобщенных конических движений.
Приводятся численные примеры.
Ключевые слова: оптимальное управление, космический аппарат, осесим-
метричное твердое тело, аналитическое решение.
DOI: 10.31857/S0005231021070059
1. Введение
Построение управления угловым движением космического аппарата (КА)
как твердого тела в традиционной постановке включает задачи программно-
го углового движения (разворота), программного управления и построения
управления, стабилизирующего программу углового движения в малом. За-
дача построения программного углового движения и программного управле-
ния во многих случаях решается с помощью методов теории оптимального
управления. Точное аналитическое решение этой задачи для наиболее ча-
сто используемых функционалов оптимизации при произвольных граничных
условиях по угловому положению и угловой скорости КА не найдено даже в
случае сферической симметрии КА, не говоря уже о его произвольной дина-
мической конфигурации. Известны лишь некоторые частные случаи решения
задачи (например, [1-13]); в общем случае приходится рассчитывать только
на приближенные численные методы. Между тем аналитическое решение за-
дачи оптимального разворота КА (твердого тела) в замкнутой форме имеет
не только теоретический, но и большой практический интерес, так как поз-
воляет использовать на борту КА готовые законы программного управления
и изменения оптимальной траектории.
В статье (разделы 2-6) в традиционной постановке рассматривается зада-
ча оптимального разворота КА как твердого тела с одной осью симметрии
1 Работа выполнена при финансовой поддержке Российского фонда фундаментальных
исследований (проект № 19-01-00205).
86
при произвольных граничных условиях по угловому положению и угловой
скорости КА без ограничения на управление. В качестве критерия оптималь-
ности используется комбинированный функционал, который объединяет вре-
мя и энергию, затраченные на переориентацию КА. С помощью замен пере-
менных исходная задача упрощается (в отношении динамических уравнений
Эйлера) до задачи оптимального разворота твердого тела со сферическим
распределением масс, содержащей одно дополнительное скалярное диффе-
ренциальное уравнение. С использованием кватернионов на основании прин-
ципа максимума Л.С. Понтрягина получено точное аналитическое решение
этой задачи в классе конических движений. Представлено явное выражение
для оптимального управления и постоянного по модулю оптимального векто-
ра угловой скорости КА. Траектория движения осесимметричного КА пред-
ставляет собой регулярную прецессию (в этом отличие предлагаемого реше-
ния от [4]). Векторы начального и конечного значений угловой скорости КА
должны принадлежать конической поверхности, порождаемой произвольно
заданными постоянными условиями задачи. В разделах 7, 8 статьи получе-
но аналитическое решение модифицированной задачи оптимального в смысле
комбинированного функционала разворота КА при произвольных граничных
условиях по угловому положению и угловой скорости КА. В классе обоб-
щенных конических движений произведена модификация традиционной за-
дачи оптимального разворота, которая позволила получить аналитические
решения для уравнений движения, содержащие произвольные постоянные и
две произвольные скалярные функции (параметры обобщенного конического
движения). Относительно этих функций и их производных формулируется
и решается оптимизационная задача, в которой в качестве управлений вы-
ступают вторые производные от этих двух функций. Полученное аналити-
ческое решение модифицированной задачи может рассматриваться как при-
ближенное (квазиоптимальное) решение традиционной задачи оптимального
разворота КА. Следует отметить, что для случаев аналитической разрешимо-
сти традиционной задачи оптимального разворота при сферической симмет-
рии КА, когда наложены ограничения на краевые условия задачи плоский
эйлеров разворот, коническое движение, решения традиционной и моди-
фицированной задач полностью совпадают [8-11]. В разделе 9 приводятся:
численный пример решения задачи оптимальной переориентации КА с одной
осью симметрии в классе конических движений (в виде регулярной прецес-
сии); примеры, показывающие близость решений традиционной и модифици-
рованной задач оптимального разворота КА при произвольных граничных
условиях.
Статья продолжает исследования, начатые в [11-13]. Отметим, что в
[12, 13] были получены аналитические решения традиционной и модифици-
рованной задач оптимальных по быстродействию и в смысле минимума энер-
гетических затрат разворотов осесимметричного КА в классах конических и
обобщенных конических движений. В [11] найдено аналитическое решение
задачи оптимального в смысле комбинированного функционала разворота
сферически-симметричного твердого тела.
87
2. Постановка задачи
Движение КА как твердого тела с одной осью симметрии вокруг центра
масс описывается дифференциальными уравнениями [1]:
(2.1)
2L
=L◦w,
I1w˙1 = M1,
(2.2)
I2w˙2 = M2 - (I1 - I2) w1w3,
I2w˙3 = M3 + (I1 - I2) w1w2.
Здесь фазовыми координатами являются L(t) нормированный кватернион
поворота КА:
L(t) = l0(t) + l1(t)i1 + l2(t)i2 + l3(t)i3 = [l0(t), l1(t), l2(t), l3(t)]T ,
∥L∥ = l20 + l21 + l22 + l23 = 1,
где i1, i2, i3 - орты гиперкомплексного пространства (мнимые единицы Га-
мильтона), которые можно идентифицировать с ортами i1, i2, i3 жестко свя-
занного с КА трехмерного векторного пространства, и w(t) - вектор угловой
скорости КА:
w(t) = w1(t)i1 + w2(t)i2 + w3(t)i3 = [w1(t), w2(t), w3(t)]T,
причем символ “◦” означает кватернионное умножение, а управление век-
тор M(t) действующего на КА внешнего момента
M(t) = M1(t)i1 + M2(t)i2 + M3(t)i3 = [M1(t), M2(t), M3(t)]T.
Фазовые координаты и управление подчинены требованиям задачи понтря-
гинского типа (L(t), w(t) - непрерывные функции, M(t) - кусочно-непрерыв-
ная функция). В динамических уравнениях Эйлера (2.2) для КА с одной осью
симметрии (направленной в данном случае вдоль орта i1 связанной с КА си-
стемы координат) I1, I2 - главные центральные моменты инерции твердого
тела, I1, I2 = const > 0.
Заданы произвольные граничные условия по угловому положению
(2.3)
L(0) = L0, L(T ) = LT
и у гловой скорости КА
(2.4)
w(0) = w0, w(T ) = wT .
Требуется определить оптимальное управление Mопт(t) системой (2.1),
(2.2) при условиях (2.3)-(2.4), доставляющее минимум функционалу
∫T
(
)
(2.5)
J =
1 + aM2
dt,
0
где a = const > 0, время Т не задано. Функционал (2.5) представляет собой
комбинацию двух критериев с размерным весовым множителем a: времени и
энергии, затраченных на разворот КА.
88
3. Переход к безразмерным переменным
Перейдем от размерных переменных в задаче к безразмерным по форму-
лам
((
)∕
)1/2
Iмасш =
I21 + 2I22
3
,
Iбезразk = Ik/Iмасш, k = 1,2;
wбезраз = (Iмасш)1/2 a1/4w, tбезраз = (Iмасш)-1/2 a-1/4t,
Mбезраз = a1/2M, Jбезраз = (Iмасш)-1/2 a-1/4J,
при этом вид выражений (2.1)-(2.4) не изменится, а функционал (2.5) примет
вид
∫T
(
)
(3.1)
J =
1+M2
dt.
0
Далее будем иметь в виду постановку задачи (2.1)-(2.4), (3.1) в безразмер-
ных переменных, и верхние индексы у них будут опущены. Таким образом,
безразмерная задача явно не зависит от параметра а. Зависимость возникнет
лишь при обратном переходе к размерным переменным.
4. Замены переменных в задаче с осевой симметрией КА
С целью упрощения (в отношении динамических уравнений Эйлера) за-
дачи (2.1)-(2.4), (3.1) осуществим замены переменных, сводящие исходную
задачу к задаче оптимального разворота КА со сферическим распределе-
нием масс, содержащей одно дополнительное скалярное дифференциальное
уравнение. Для этого перепишем уравнения (2.2) в виде
w1 = m1,
w2 = b1m2 - bw1w3,
w3 = b1m3 - bw1w2,
где
m1 = M1/I1, m2 = M2/I1, m3 = M3/I1, b = (I1 - I2)/I2, b1 = I1/I2.
Заменим переменные w1, w2, w3 на новые ω1, ω2, ω3:
w1
b-11
0
0
ω1
(4.1)
w2
=0
cos(θ(t))
-sin(θ(t))
ω2
.
w3
ω3
0
sin(θ(t)) cos(θ(t))
Тогда получим для уравнений Эйлера (2.2) в кватернионной записи
(4.2)
ω=B◦b1
m ◦ B,
(4.3)
B(t) = exp {i1
θ(t)/2} ,
89
где “∼” - сопряжение кватерниона, “exp { . }” - кватернионная экспонента,
вектор m = [m1, m2, m3]T,
∫t
(4.4)
θ(t) = b2 ω1
(τ) dτ,
0
b2 = bb-11 = 1 - I2/I1 = 1 - b-11.
Отметим, что |B(t)| = 1, ∀t.
Кватернионное уравнение углового движения КА (2.1) при этом запишется
так:
(
)
(4.5)
2L=L◦B◦
b-11ω1i1 + ω2i2 + ω3i3
◦B,
где кватернион B определяется (3.3).
С учетом начального условия по угловой скорости КА (1.5) уравнение (3.2)
можно переписать следующим образом:
(4.6)
ω
β◦b1
m◦β,
τ
∫ t
∫
(4.7)
β(t) = exp
i1b2
m1(ξ)dξ + w01dτ/2
0
0
Нелинейное выражение, стоящее в правой части (4.5) и зависящее только
от переменных mk(t), k = 1, 3, примем за новое управление u(t):
(4.8)
u
β◦b1
m◦β,
где β определяется (4.7). Отметим, что u1(t) = b1m1(t), и поэтому в замене
переменных (4.8) всегда можно совершить обратный ход: по новой векторной
переменной u(t) (когда она будет известна) восстановить управление m(t)
задачи (2.1)-(2.4), (3.1).
Модуль вектора нового управления связан с модулем вектора управляю-
щего момента КА так:
|u| =
β◦b1m◦β=b1
β |m| |β| = b1 |m| = b1 |M| /I1 = |M| /I2
Исходя из (3.5), осуществим еще одну замену переменных:
(4.9)
L=Λ◦B
,
где Λ = Λ(t) - новая кватернионная переменная, описывающая угловое по-
ложение КА, при этом, так как
∥B(t)∥ = |B(t)|2 = 1, ∀t,
то
∥L(t)∥ = ∥Λ(t)∥ = 1, ∀t.
90
С учетом всех указанных выше замен переменных задача оптимального
разворота КА (2.1)-(2.4), (3.1) примет вид
(4.10)
2Λ
=Λ◦ω,
(4.11)
ω= u,
(4.12)
θ=b2ω1,
(4.13)
θ (0) = 0,
(4.14)
ω (0) = ω0 = b1w01 i1 + w02 i2 + w03 i3, Λ (0) = Λ0 = L0,
ω (T ) = ωT = B (θ(T )) ◦ (b1wT1 i1 + wT2 i2 + wT3 i3) ◦ B (θ(T )) ,
(4.15)
Λ(T) = ΛT = LT ◦ B(θ(T)),
∫T
(
)
(4.16)
J =
1+I22u2
dt → min,
0
где w01 , w02 , w03 , wT1 , wT2 , wT3 компоненты вектора
w(t) = [w1(t), w2(t), w3(t)]T
в начальный и конечный моменты времени соответственно, а кватернион
B (θ(T )) определяется по формуле (4.3).
Согласно (4.9), (4.15) задачу (4.10)-(4.16) можно переформулировать так:
в восьмимерном фазовом пространстве Λ × ω × θ управляемую систему
(4.10)-(4.12) необходимо оптимально в смысле функционала (4.16) переве-
сти из начального состояния (3.14) на многообразие, которое определяется
соотношениями
vect( Λ ◦B (θ) ◦LT ) = 0,
(4.17)
ω - B (θ) ◦ (b1wT1i1 + wT2i2 + wT3i3) ◦ B(θ) = 0,
где “vect ( . )” обозначает векторную часть кватерниона.
Из этой задачи найдем оптимальные управление uопт и траекторию Λопт,
ωопт. Как видно, векторное дифференциальное уравнение (4.11) имеет струк-
туру, соответствующую динамическим уравнениям Эйлера для сферически-
симметричного твердого тела. Это существенно облегчает исследование за-
дачи.
Далее будем рассматривать задачу (4.10)-(4.16) ((4.17)).
5. Применение принципа максимума
Выполним процедуру принципа максимума Л.С. Понтрягина [1, 14]. Вве-
дем вспомогательные функции Ψ(t) (кватернион) и ϕ(t) (вектор), со-
ответствующие фазовым координатам Λ(t) и ω(t). Составим функцию
Гамильтона-Понтрягина
(
)
(5.1)
H = -ψ∗
1+I22u2
+ (Ψ,Λ ◦ ω) /2 + (ϕ,u) + b2ω1
ρ,
где постоянная ψ∗ ≥ 0, а “( . , . )” означает скалярное произведение векторов.
91
Будем рассматривать невырожденные решения краевой задачи принципа
максимума, для которых ψ∗ > 0. В силу однородности функции Гамильтона-
Понтрягина Н [14] в (5.1) положим ψ∗I22 = 1.
Сопряженная система:
2Ψ=Ψ◦ω,
ρ = 0,
(5.2)
(
)∕
ϕ = -vect
Λ◦Ψ
2-b2ρi1.
Как видно, уравнения для переменных Ψ и Λ совпадают с точностью до
константы. Используя это и введя обозначение [1]
(5.3)
p = vect(Λ ◦ Ψ) = Λ ◦ cv
◦ Λ,
где cv - произвольная векторная постоянная, сопряженную систему запишем
так:
{
p = Λ ◦ cv ◦ Λ, ρ = ρ0 = const,
(5.4)
ϕ = -p/2 - b2ρ0 i1.
Следует отметить, что применение этого приема [1], основанного на само-
сопряженности дифференциальной кватернионной системы уравнений (4.10)
(замена кватернионной сопряженной переменной Ψ на векторную перемен-
ную p (5.3)), позволяет понизить размерность краевой задачи, получаемой
после применения принципа максимума, на четыре единицы.
Условие максимума функции Гамильтона-Понтрягина (5.1) дает следую-
щую структуру оптимального управления:
(5.5)
uопт
= ϕ/2.
Как видно, вектор-функция управления в задаче носит непрерывный харак-
тер.
Из (4.11), (4.12), (5.4), (5.5) имеем:
(5.6)
p = [p,ω],
(5.7)
p = -4ω + 2b2ρ0i1,
где “[ . , . ]” означает векторное произведение.
Подставляя (5.7) в (5.6), получим
(5.8)
ω= [ω - b2ρ0i1
/2, ω].
Таким образом, оптимальная угловая скорость твердого тела на всем ин-
тервале времени движения удовлетворяет векторному дифференциальному
уравнению третьего порядка (5.8). Решение поставленной задачи оптималь-
ного управления сводится тем самым к решению краевой задачи (4.11), (5.8),
(4.13)-(4.16).
92
Из постановки задачи видно, что конечные значения фазовых координат
Λ(t), ω(t) не являются фиксированными величинами, а принадлежат мно-
гообразию, определяемому выражениями (4.5), (4.15), (4.16). Поэтому для
фазовых координат Λ(t), ω(t) θ(t) и сопряженных переменных Ψ(t), ϕ(t), ρ0
в момент времени t = T выполняются условия трансверсальности
(5.9)
scal(Λ
◦ Ψ(t)) = 0,
где “scal ( . )” обозначает скалярную часть кватерниона, и
(5.10)
ρ0 + p1 (T)/2 + ϕ2 (T) ω3 (T) - ϕ3 (T)ω2
(T) = 0,
полное построение которых приведено в [12,13].
Относительно условия (5.9) отметим, что оно выполняется автоматиче-
ски при переходе к вектору сопряженных переменных p (5.3). Условие (5.10)
вытекает из первого интеграла задачи (4.11)-(4.17), (5.2)-(5.8), который спра-
ведлив для оптимального управления и оптимальной траектории и получа-
ется на основе выражений (4.12), (5.4)-(5.6). Покажем это.
Из (4.12), (5.5) следует, что [ ω, ϕ] = 0, ∀t ∈ [0, T ]. Тогда с учетом выраже-
ния для ϕ˙ (5.4) и p (5.6) можем записать
ω•2ϕ3 - ω•3ϕ2 + ω2ϕ•3 - ω3ϕ•2 = p•1/2
или
(5.11)
p1(t)/2 + ω3(t)ϕ2(t) - ω2(t)ϕ3(t) = const = ρ0
,
∀t ∈ [0, T].
Это выражение и есть первый интеграл задачи (4.11)-(4.17), (5.2)-(5.8).
Отметим, что функция Гамильтона-Понтрягина (5.1) для оптимального
процесса управления может быть представлена в виде
(5.12)
H = -I-22 + ω 2 - (2ω + b2ρ0i1, ω) + b2ω1ρ0
= 0, t ∈ [0, T ].
6. Аналитическое решение задачи оптимального разворота КА
в классе конических движений
Будем искать решение уравнений (4.11), (5.8) в классе конических движе-
ний. Для этого оптимальную угловую скорость КА представим в виде
(6.1)
ω(t) = i1γ + α eδ ◦ (i2 sin Ωt + i3 cos Ωt) ◦ eδ,
где α, δ, γ, Ω - неопределенные постоянные, а eδ = exp{i1δ/2}.
Последовательно дифференцируя (6.1) три раза по переменной t, получим:
(6.2)
ω= αΩeδ ◦ (i2 cosΩt - i3 sinΩt) ◦ eδ,
(6.3)
ω = -αΩ2eδ ◦ (i2 sinΩt + i3 cosΩt) ◦ eδ,
(6.4)
ω= -αΩ3eδ ◦ (i2 cos Ωt - i3 sin Ωt) ◦ eδ.
93
Подставляя (6.1)-(6.4) в (5.8) и учитывая выражения (4.12), (5.5), (5.11), убе-
димся в выполнении равенства в (5.8); при этом
(6.5)
γ = Ω - b2α2/((1 + b2)Ω), ρ0 = 2α2Ω/(1 + b2
).
Отметим, что
ω= [ω - b2ρ0i1/2, ω] = ((ω - b2ρ0i1/2) ◦ ω - ω ◦ (ω - b2ρ0i1/2))/2.
Траектория движения КА при угловой скорости (5.1) из (3.10) находится
явно и имеет вид регулярной прецессии
(6.6)
Λ(t) = Λ0 ◦ eδ ◦ exp{(i3α + i1(γ - Ω))t/2} ◦ exp{i1
(Ωt + δ)/2}.
Вектор оптимального управления u определяется из формул (4.11), (6.2).
Подставляя в выражение для функции Гамильтона-Понтрягина (5.12)
формулы (6.1)-(6.4), получим дополнительное условие
(6.7)
α2Ω2 = I-22
/3.
Возвращаясь к исходным безразмерным переменным задачи (2.1)-(2.4),
(3.1), запишем окончательные выражения для вектора оптимальной угловой
скорости
(6.8)
w(t) = i1b-11γ + α(i2 sin((Ω - b2γ)t + δ) + i3 cos((Ω - b2
γ)t + δ)),
кватерниона оптимальной траектории
(6.9)
L(t) = L0 ◦ eδ ◦ exp{(i3α + i1
(γ - Ω))t/2} ◦
◦ exp{i1((b2γ + Ω)t + δ))/2}
и в ектора оптимального управляющего момента КА
(6.10)
M(t) = I2αΩ (i2 cos((Ω - b2γ)t + δ) - i3 sin((Ω - b2
γ)t + δ)) ,
где γ определяется первым из выражений (6.5).
При t = 0 из (6.7) имеем
(6.11)
w(0) = i1b-11(Ω - b2α2/((1 + b2)Ω)) + α(i2 sin δ + i3
cos δ).
При t = T из (6.7), (6.8), (2.3) имеем:
(6.12)
w(T ) = i1b-11(Ω - b2α2/((1 + b2)Ω)) + α(i2 sin((Ω - b2
γ)T + δ)) +
+ i3 cos((Ω - b2γ)T + δ)),
(
(6.13)
vect
eδ ◦ exp{(i3α - i1b2α2/((1 + b2)Ω))T/2} ◦
◦ exp{i1(ΩT(1 + b2) - b22α2T/((1 + b2)Ω)) + δ)/2} ◦ LT ◦ L0) = 0.
94
В выражения (6.10)-(6.12) входят три произвольные постоянные α, δ, Ω и
неизвестное время переориентации Т. Определяя их из условия (6.7) и си-
стемы трех нелинейных алгебраических уравнений (6.13), удовлетворим гра-
ничные условия по угловому положению КА (2.3) (α, δ, Ω, T будут зависеть
от компонент кватернионов L0, LT и главных центральных моментов инер-
ции КА (твердого тела) I1, I2). Из-за недостаточного количества произволь-
ных постоянных в решении задачи на величины w0, wT (2.4) налагаются
требования вида (6.11), (6.12).
Таким образом, в случаях, когда на граничные условия по угловой скоро-
сти КА наложены ограничения вида (6.11), (6.12) (это означает, что вектор
угловой скорости w(t) на всем интервале времени движения принадлежит
некоторой конической поверхности, определяемой в пространстве заданны-
ми постоянными задачи I1, I2, L0, LT ), траектория углового движения осе-
симметричного КА находится в классе конических движений и определяется
явными аналитическими выражениями (6.8), (6.9), управляющий момент КА
определяется (6.10).
Оптимальное значение функционала качества в безразмерных переменных
(3.1) составляет величину
∫T
(6.14)
J =
(1 + M2)dt = (1 + I22α2Ω2
)T = 4T/3.
0
Из выражений (4.4), (4.6), (4.9), (4.10), (5.3), (5.5), (5.7), (6.5), (6.8) и (6.9)
можно найти сопряженные переменные. Тем самым, задача при существую-
щих ограничениях решена полностью.
Приведем алгоритм решения задачи оптимального разворота осесиммет-
ричного КА (2.1)-(2.4), (3.1) в безразмерных переменных в классе конических
движений:
Шаг 1. По заданным кватернионам L0, LT (2.3), главным центральным
моментам инерции КА (твердого тела) I1, I2 и формулам (6.7), (6.13) опре-
деляются величины α, δ, Ω и времени переориентации Т.
Шаг 2. Используя α, δ, Ω, I1, I2, Т, по формуле (6.11)
wвыч0 = i1(Ω - b2α2/((1 + b2)Ω))I2/I1 + α(i2 sinδ + i3 cos δ)
и формуле (6.12)
wвычT = i1(Ω - b2α2/((1 + b2)Ω))I2/I1 + α(i2 sin((Ω - b2γ)T + δ)) +
+ i3 cos((Ω - b2γ)T + δ)), b2 = 1 - I2/I1
вычисляются значения векторов wвыч0, wвыч0.
Шаг 3. Полученные значения wвыч0, wвычT сравниваются с заданными в
(2.4) величинами w0, wT .
Шаг 4. Если равенство на шаге 3 алгоритма выполняется, то оптималь-
ное решение задачи находится в классе конических движений; при этом угло-
вая скорость КА, траектория его углового движения, вектор управляющего
95
момента и значение функционала оптимизации вычисляются по формулам
(6.8)-(6.10), (6.14) и шагу 1 алгоритма.
Шаг 5. Сопряженные переменные задачи находятся по формулам (4.4),
(4.6), (4.9), (4.10), (5.3), (5.5), (5.7), (6.5), (6.8) и (6.9).
7. Модифицированная задача оптимального разворота твердого тела
Движение КА по-прежнему описывается соотношениями (2.1)-(2.4), (3.1)
при этом начальное и конечное значения по угловому положению и угловой
скорости КА произвольны. Далее будем рассматривать приведенную задачу
(4.10)-(4.17).
Одной из основных проблем при построении аналитического решения в
задаче оптимального разворота твердого тела (КА) является разрешимость
классической задачи Дарбу аналитического определения Λ(t) из уравнения
(4.10) при известных Λ0, ω(t).
Для кватернионного дифференциального уравнения (4.10) при условии,
что вектор угловой скорости ω(t) задается выражением
(7.1)
ω(t) = i1 f˙(t) sin g(t) + i2 f˙(t) cos g(t) + i3
ġ(t),
в котором f(t) и g(t) - произвольные функции времени, известно решение [15],
удовлетворяющее начальному условию (4.16)
Λ(t) = Λ0 ◦ exp{-i3g(0)/2} ◦ exp{-i2f(0)/2} ◦ exp{i2f(t)/2} ◦
(7.2)
◦ exp{i3g(t)/2}.
Формулы (7.1), (7.2) включают в себя все известные точные аналитические
решения традиционной задачи оптимального разворота КА при его сфериче-
ской симметрии, когда вектор угловой скорости на всем интервале времени
движения КА постоянен по направлению или описывает в пространстве кру-
говой конус [1-3, 5, 6, 8-11].
Заметим [15], что задачу Дарбу с произвольно заданным вектором угло-
вой скорости ω(t) с помощью замен переменных можно свести к решению
уравнения типа (4.10) с угловой скоростью
ω∗(t) = -(i1f˙(t)sin g(t) + i2f˙(t)cos g(t) + i3 ġ(t)),
отличающейся от (7.1) только знаком. При этом явное аналитическое решение
этой задачи, как и при произвольном векторе ω(t), не известно.
Выражение (7.1) и решение (7.2) можно обобщить, добавив поворот на
постоянный угол вокруг некоторой оси. Такой поворот задается с помощью
кватерниона K, ∥K∥ = 1. Тогда вектор ω и кватернион Λ будут определяться
соотношениями
(7.3)
ω = K ◦ (i1f˙(t)sing(t) + i2f˙(t)cosg(t) + i3
ġ(t)) ◦ K,
Λ = Λ0 ◦ K ◦ exp{-i3g(0)/2} ◦ exp{i2(f(t) - f(0))/2} ◦
(7.4)
◦ exp{i3g(t)/2} ◦ K.
96
Будем рассматривать вторые производные от функций f и g в качестве
управляющих параметров. Тогда если ввести обозначения
˙
(7.5)
f
=f1,
ġ=g1,
то можно составить систему дифференциальных уравнений, описывающих
управляемую систему:
˙
˙
(7.6)
f
=f1,
ġ=g1,
f
1 = ν1,
ġ1 = v2,
где f, f1, g, g1 - фазовые координаты, v1, v2 - управляющие параметры. Огра-
ничимся случаем, когда кватернион K представляется в виде произведения
(7.7)
K = K2 ◦ K1, K1 = exp{i1α1/2}, K2 = exp{i2α2
/2},
где α1, α2 - некоторые постоянные. Отметим, что кватернионы K1 и K2 опре-
деляют поворот вектора ω (7.1) вокруг осей i1, i2. Поворот вокруг оси i3 уже
включен в формулу (7.3), если учесть, что в функцию g(t) входит аддитивная
постоянная. Сопряженный кватернионK будет представляться так:
̂
̂
̂
̂
̂
(7.8)
E=
E1 ◦
E2,
E1 = exp{-i1α1/2},
E2 = exp{-i2α2
/2}.
Условия того, что выражения для ω, Λ (6.3), (6.4) удовлетворяют граничным
условиям (4.14), (4.15) ((4.17)) с учетом (7.7), (7.8), запишутся как
K ◦ (i1f1(0)sing(0) + i2f1(0)cosg(0) + i3g1(0)) ◦ K -
(7.9)
- b1w01i1 + w02i2 + w03i3 = 0,
K ◦ (i1f1(T)sing(T) + i2f1(T)cosg(T) + i3g1(T)) ◦ K -
(7.10)
- B (θ(T)) ◦ (b1wT1i1 + wT2i2 + wT3i3) ◦ B(θ(T)) = 0,
vect(L0 ◦K ◦ exp{-i3g(0)/2} ◦ exp{i2(f(T ) - f(0))/2} ◦
(7.11)
◦ exp{i3g(T)/2} ◦ K ◦ B(θ(T)) ◦ LT ) = 0.
С учетом (7.7), компоненты вектора ω (7.3) имеют в явной форме вид
ω1 = f1 sin g cos α2 - g1 sinα2,
(7.12)
ω2 = f1(sin g sin α1 sin α2 + cos g cos α1) + g1 sinα1 cos α2,
ω3 = f1(sin g cos α1 sin α2 - cos g sin α1) + g1 cos α1 cos α2.
Компоненты вектора управления u, который согласно (5.11) является произ-
водной по времени от вектора ω, определяется по формулам
u1 = ω1 = (v1 sin g + f1g1 cos g)cos α2 - v2 sinα2,
u2 = ω2 = v1(sin g sin α1 sin α2 + cos g cos α1) +
(7.13)
+ f1g1(cos g sinα1 sin α2 - sing cos α1) + v2 sin α1 cos α2,
u3 = ω3 = v1(sin g cos α1 sin α2 - cosg sin α1) +
+ f1g1(cos g cos α1 sin α2 + sin g sin α1) + v2 cos α1 cos α2.
97
Тогда для управляемой системы (7.6) можно сформулировать следующую
задачу оптимального управления, решение которой можно рассматривать
(с учетом замен переменных раздела 4) как приближенное (квазиоптималь-
ное) решение задачи (4.10)-(4.16) ((2.1)-(2.4), (3.1)): требуется найти опти-
мальные управления ν1(t), ν2(t), которые переводят управляемую систему
(7.6) из начального состояния
(7.14)
f = f(0), f1 = f1(0), g = g(0), g1 = g1
(0)
в конечное состояние
(7.15)
f = f(T), f1 = f1(T), g = g(T), g1 = g1
(T ),
удовлетворяющие соотношениям (7.9)-(7.11), в которых α1, α2 выступают
как параметры, подлежащие определению, и доставляют минимум комбини-
рованному функционалу, где время Т не задано,
∫T
(7.16)
J =
(1 + ν21 + ν22
)dt.
0
Такую задачу оптимального управления будем называть модифицирован-
ной задачей оптимального разворота осесимметричного КА.
8. Решение задачи с помощью принципа максимума
Функция Гамильтона-Понтрягина для поставленной задачи оптимального
управления имеет вид
(8.1)
H = -(1 + ν21 + ν22) + ψ1f1 + ψ2g1 + ψ3ν1 + ψ4ν2,
где ψ1, ψ2, ψ3, ψ4 - сопряженные переменные, удовлетворяющие системе
уравнений:
(8.2)
dψ1/dt = 0, dψ2/dt = 0, dψ3/dt = -ψ1, dψ4/dt = -ψ2.
Общее решение уравнений (8.2), содержащее произвольные постоянные
c1,... ,c4, имеет вид
(8.3)
ψ1 = c1, ψ2 = c2, ψ3 = -c1t + c3, ψ1 = -c2t + c4.
Из условия максимума для функции Гамильтона-Понтрягина (8.1) опре-
деляется оптимальное управление
(8.4)
ν1 = ψ3/2 = (-c1t + c3)/2, ν2 = ψ4/2 = (-c2t + c4
)/2.
После подстановки (8.4) в систему уравнений (7.6) находится общее реше-
ние для фазовых координат, содержащее восемь произвольных постоянных
c1,... ,c8:
f = -c1t3/12 + c3t2/4 + c5t + c7, g = -c2t3/12 + c4t2/4 + c6t + c8,
(8.5)
f1 = -c1t2/4 + c3t/2 + c5, g1 = -c1t2/4 + c4t/2 + c6.
98
Так как в поставленной задаче оптимального управления конечный мо-
мент времени Т не задается, то функция Гамильтона-Понтрягина (8.1) при
t = T должна обращаться в нуль
H = -(1 + ν21(T) + ν22(T)) + c1f1(T) + c2g1(T) +
(8.6)
+ ψ3(T)ν1(T) + ψ4(T)ν2(T) = 0.
Для системы уравнений (7.6), (8.2) функция Н является первым интегра-
лом. По этой причине условие (8.6) выполняется для всех t ∈ [0, T ].
В связи с тем, что c7 входит в функцию f как аддитивная постоянная, из фор-
мулы (7.4) видно, что эта постоянная не оказывает влияние; поэтому c7 можно
положить равной нулю. Таким образом, для определения десяти неизвестных
постоянных задачи c1, . . . , c6, c8, T и α1, α2 служат девять уравнений систе-
мы (7.9)-(7.11) и условие (8.6). Если формулы (8.5) подставить в (7.3), (7.4),
то будут получены аналитические выражения для определения законов из-
менения оптимальной угловой скорости и оптимальной траектории твердого
тела. Эти выражения определят оптимальный в смысле минимума комбини-
рованного функционала (7.16) разворот твердого тела в классе обобщенных
конических движений. Далее по формулам (4.1), (4.4), (4.10) вычисляются
вектор безразмерной угловой скорости w и кватернион ориентации КА L. По
формулам (7.13) определяются компоненты вектора u. Из выражений (4.2),
(4.4), (4.7), (4.8) следует, что безразмерный управляющий момент M выра-
жается через вектор u так
(8.7)
M=I2B
(θ) ◦ u ◦ B(θ).
Формула (8.7) определяет аналитическое решение для управляющего момен-
та, соответствующего решению модифицированной задачи. Модифицирован-
ная задача оптимального разворота КА тем самым решена полностью. Полу-
ченные таким способом кватернион L и векторы w, M можно рассматривать
как приближенное решение традиционной задачи оптимального разворота
осесимметричного КА (твердого тела).
Следует отметить, что при сферической симметрии КА (I1 = I2 = I3)
квадрат модуля безразмерного управляющего момента традиционной задачи
выражается через управляющие параметры и фазовые координаты модифи-
цированной задачи следующим образом:
(8.8)
M2 = v21 + f21g21 + v22.
Если в задаче оптимального разворота сферически-симметричного КА векто-
ры граничных условий по угловой скорости ω0, ωT положить параллельными
vect(Λ0 ◦ ΛT ) (плоский эйлеров разворот КА), то решения задач в традици-
онной и модифицированной постановках полностью совпадут. То же самое
можно сказать и о случае, когда решение традиционной задачи оптимально-
го разворота сферически-симметричного КА получено в классе конических
движений [11]. В этих случаях слагаемое f21g21 в (8.8) обращается в нуль и
функционал (7.16) полностью переходит в функционал (3.1) традиционной
задачи.
99
9. Численные примеры
В данном разделе на примере осесимметричного КА “Спейс Шаттл” [16]
приводятся результаты численных решений задачи оптимального разворота
в традиционной и модифицированной постановке для нескольких вариантов
граничных условий по угловому положению и угловой скорости КА. Ниже
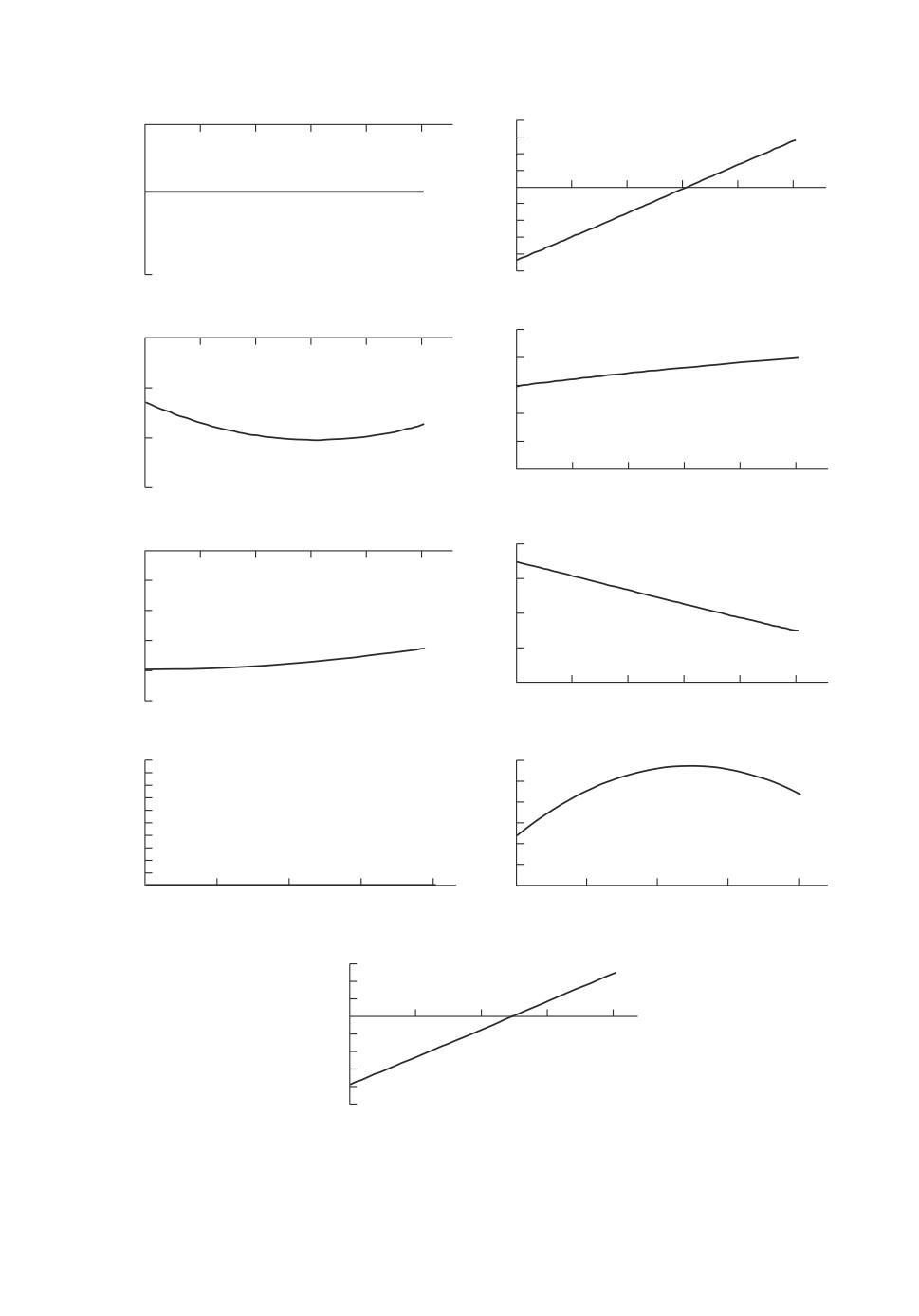
на рисунках представлены графики изменения во времени компонент угло-
вой скорости wi(t), i = 1, 3, векторной части кватерниона ориентации Li(t),
i = 1,3 и компонент вектора управляющего момента Mi(t), i = 1,3 КА.
На рис. 1 приведены результаты решения задачи в традиционной поста-
новке в классе конических движений по формулам раздела 6.
Расчеты проводились для значений:
I1 = 3400648 кг · м2, I2 = 21041672 кг · м2, I3 = I2 = 21041672 кг · м2
или I1 = 0,1967, I2 = 1,2168, I3 = I2 (безразмерные моменты инерции);
L0 = [0,79505, 0,29814, -0,39752, 0,34783]T,
(9.1)
LT = [0,84434, 0,39846, -0,3260, 0,14848]T,
w0 = [-0,02249, -0,21699, -0,61494]T,
wT = [-0,02249, -0,14018, -0,63685]T,
где граничные условия по угловой скорости КА удовлетворяют ограничениям
раздела 6.
Вначале по формулам (6.7), (6.13), находились величины α, δ, Ω, T (α =
= 0,65210, δ = 3,48082, Ω = -0,72761, T = 0,74469), затем по формулам (6.8)-
(6.10) определялись векторы w, M и кватернион L.
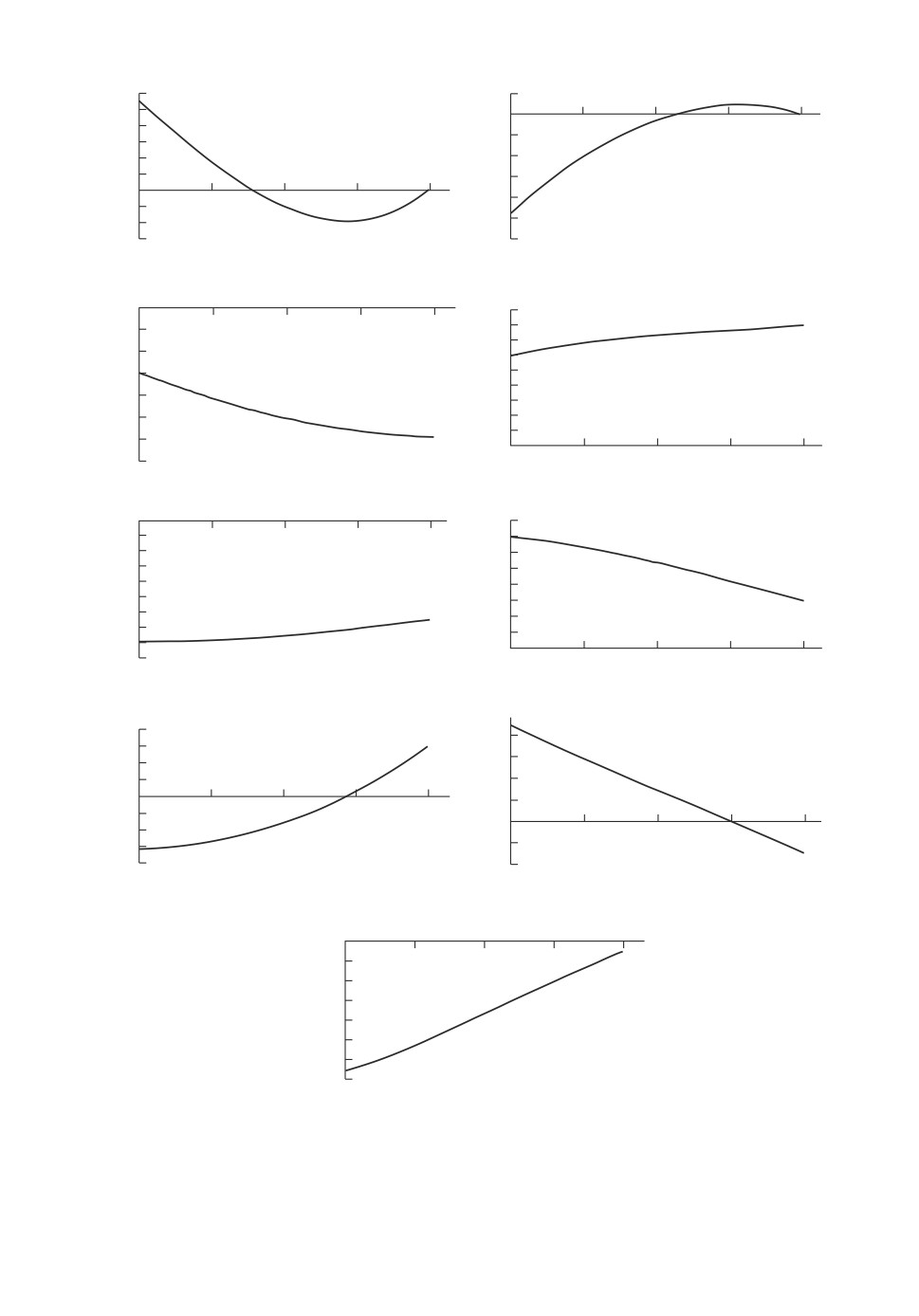
На рис. 2 приведены результаты решения модифицированной задачи оп-
тимального разворота КА при произвольно выбранных граничных условиях
по угловому положению и угловой скорости КА по формулам разделов 7, 8.
Расчеты проводились для значений угловой скорости:
(9.2)
w0 = [0,27388, -0,23883, -0,3]T, wT = [0, 0, -0,59]T;
граничные условия по угловому положению КА задавались (9.1)
Значения постоянных α1, α2, c1, . . . , c6, c8, входящих в аналитическое ре-
шение задачи, таковы:
α1 = -1,22190, α2 = -0,89091, C1 = -0,44648, c2 = -3,82943,
c3 = -0,63861, c4 = -2,71375, c5 = -0,37172,
c6 = 0,28961, c8 = -0,20978.
С граничными условиями (9.1), (9.2) при помощи универсальной програм-
мы численного решения, описанной в [17], также решалась задача оптималь-
ного разворота КА в традиционной постановке (2.1)-(2.4), (3.1) в безразмер-
ных переменных. Графики решения двух задач практически совпали. Для
примера в табл. 1 приведем значения компонент вектора M(t) на концах и в
100
T = 0,7447
w1(t)
w2(t)
0
0,15
0,30
0,45
0,60
0,74
0,2
0,1
0
0,15
0,30
0,45
0,60
0,74
-0,1
-0,2
-0,05
w3(t)
L1(t)
0
0,15
0,30
0,45
0,60
0,74
0,5
0,4
-0,60
0,3
0,2
-0,65
0,1
-0,70
0
0,15
0,30
0,45
0,60
0,74
L2(t)
L3(t)
0
0,15
0,30
0,45
0,60
0,74
0,4
-0,1
0,3
-0,2
0,2
-0,3
0,1
-0,4
-0,5
0
0,15
0,30
0,45
0,60
0,74
M1(t) = 0
M2(t)
1,0
0,58
0,8
0,57
0,56
0,6
0,55
0,4
0,54
0,2
0,53
0
0,52
0,19
0,37
0,56
0,74
0
0,19
0,37
0,56
0,74
M3(t)
0,15
0,10
0,05
0
0,19
0,37
0,56
0,74
-0,05
-0,10
-0,15
-0,20
-0,25
Рис. 1. Результаты решения традиционной задачи (коническое движение).
101
T = 0,9850
w1(t)
w2(t)
0,3
0
0,2
0,25
0,50
0,75
0,1
-0,1
0
-0,2
0,25
0,50
0,75
-0,1
-0,3
w3(t)
L1(t)
0,25
0,50
0,75
0
0,4
-0,1
-0,2
0,3
-0,3
0,2
-0,4
-0,5
0,1
-0,6
0
-0,7
0,25
0,50
0,75
L2(t)
L3(t)
0,25
0,50
0,75
0
0,4
-0,1
0,3
-0,2
0,2
-0,3
0,1
-0,4
0
0,25
0,50
0,75
M1(t) = 0
M2(t)
0,2
0,8
0,6
0,1
0,4
0
0,2
0,25
0,50
0,75
0
-0,1
0,25
0,50
0,75
-0,2
-0,2
-0,4
M3(t)
0
0,25
0,50
0,75
-0,1
-0,2
-0,3
-0,4
-0,5
-0,6
-0,7
Рис. 2. Результаты решения модифицированной задачи при произвольных
граничных условиях.
102
T = 1,8713
w1(t)
w2(t)
0
0,25
0,75
1,25
1,75
0,020
0,016
-0,01
0,012
0,008
-0,02
0,004
-0,03
0
0,25
0,75
1,25
1,75
w3(t)
L1(t)
0
0,25
0,75
1,25
1,75
0,4
-0,1
0,3
-0,2
0,2
-0,3
0,1
-0,4
0
0,25
0,75
1,25
1,75
L2(t)
L3(t)
0
0,25
0,75
1,25
1,75
0,4
-0,1
0,3
-0,2
0,2
-0,3
0,1
-0,4
0
0,25
0,75
1,25
1,75
M1(t) = 0
M2(t)
0,08
0,008
0,004
0,04
0
0
0,25
0,75
1,25
1,75
0,25
0,75
1,25
1,75
-0,004
-0,04
-0,008
-0,08
M3(t)
1,5
1,0
0,5
0
0,25
0,75
1,25
1,75
-0,5
-1,0
-1,5
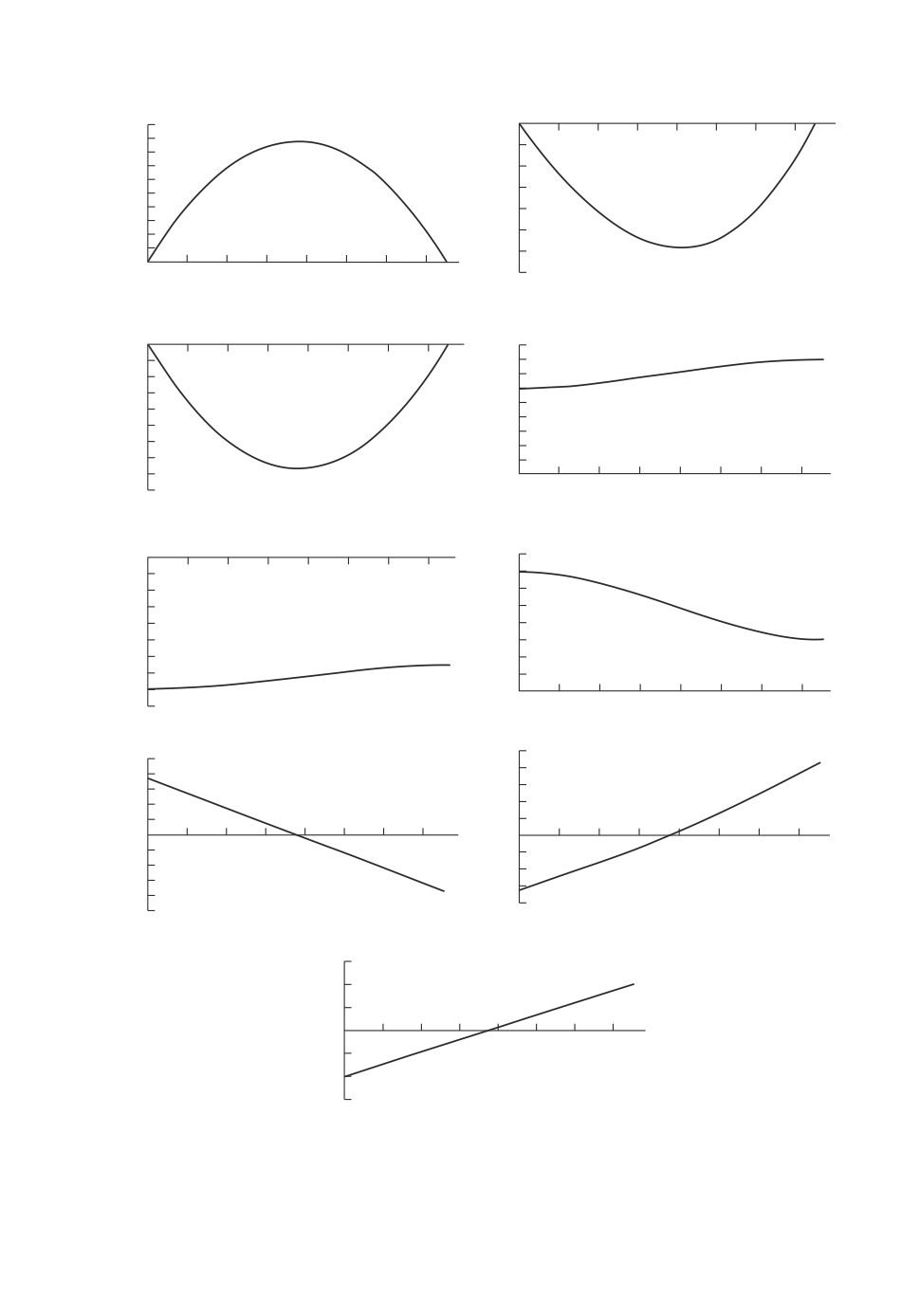
Рис. 3. Результаты решения модифицированной задачи при развороте из по-
ложения покоя в положение покоя.
103
Таблица 1
t
Mтрадиц1
Mтрадиц2
Mтрадиц3
t
Mмодиф1
Mмодиф2
Mмодиф3
0
-0,1574
0,8887
-0,6587
0
-0,2123
0,8856
-0,7918
0,4925
-0,0792
0,2893
-0,3699
0,4840
-0,0521
0,3001
-0,3691
T = 0,9850
0,1460
-0,2898
-0,0539
T = 0,9679
0,0881
-0,3024
0,0072
Таблица 2
t
Mтрадиц1
Mтрадиц2
Mтрадиц3
t
Mмодиф1
Mмодиф2
Mмодиф3
0
0,0074
-0,0655
-0,9978
0
0,0091
-0,0907
-1,2121
0,9356
0,0000
-0,0003
0,0000
0,8486
-0,0002
0,0076
-0,0006
T = 1,8713
-0,0074
0,0850
0,9963
T = 1,6972
-0,0086
0,0925
1,2121
промежуточных точках интервала времени движения КА [0, T ] в этих двух
решениях.
Значение функционала (3.1) для традиционной задачи в рассматриваемом
примере составляет 1,35662. Значение того же функционала вычисленного
на основе решения модифицированной задачи составляет J = 1,35928. Дру-
гими словами, в рассматриваемом примере расхождение между величинами
функционала (3.1) для традиционной и модифицированной задачи составля-
ет менее 0,00266. Таким образом, построено управление, которое сообщает
функционалу значение, близкое к оптимальному для традиционной задачи.
Из таблицы видно, что построенные управляющие моменты для этих двух
задач близки друг к другу.
На рис. 3 приведены результаты решения модифицированной задачи оп-
тимального разворота КА “Спейс Шаттл” в важном с практической точки
зрения случае разворота из положения покоя в положение покоя. По форму-
лам разделов 7, 8 расчеты проводились для граничных условий по угловому
положению (9.1) и угловой скорости КА
(9.3)
w0 = wT = [0, 0, 0]T.
Значения постоянных α1, α2, c1, . . . , c6, c8, входящих в аналитическое реше-
ние задачи, таковы:
α1 = -1,47437, α2 = -0,55315, c1 = -2,35673, c2 = 0,01373,
c3 = -1,99997, c4 = 0,01165, c5 = 0,0, c6 = 0,0, c8 = -0,05078.
Также с граничными условиями (9.1), (9.3) численно решалась задача оп-
тимального разворота КА в традиционной постановке (2.1)-(2.4), (3.1). Гра-
фики решения двух задач практически совпали. Для примера в табл. 2 при-
ведены значения компонент вектора M(t) на концах и в середине интервала
времени движения КА [0, T ] в этих двух решениях.
Величина функционала (3.1) для традиционной задачи в рассматриваемом
примере составляет 2,49504. Значение того же функционала, вычисленного
на основе решения модифицированной задачи, составляет J = 2,53333. Таким
образом, расхождение между величинами функционала (2.6) для традицион-
ной и модифицированной задач составляет 0,03826.
104
Следует отметить, что кватернион ориентации КА L(t) может быть дву-
значным [1], т.е. L и -L соответствуют одному и тому же угловому положе-
нию КА в пространстве.
10. Заключение
Представленное в статье аналитическое решение традиционной задачи оп-
тимального разворота осесимметричного КА (твердого тела) в классе кониче-
ских движений (в виде регулярной прецессии) может найти свое применение
при построении систем управления КА, как и известное аналитическое реше-
ние задачи оптимального разворота сферически-симметричного КА, полу-
ченное в классе плоских эйлеровых разворотов. Решение модифицированной
задачи оптимального разворота осесимметричного КА можно использовать
для этих же целей как аналитическое приближенное (квазиоптимальное) ре-
шение задачи оптимального управления при произвольных граничных усло-
виях. Также отметим, что аналитическое решение модифицированной задачи
оптимального разворота осесимметричного КА при произвольных граничных
условиях, полученное на основе решения приведенной задачи (4.10)-(4.16),
оказалось существенно точнее, чем решение [18] (применительно к осевой
симметрии КА), где квазиоптимальный управляющий момент КА строился
на основе обратной задачи динамики КА по результатам решения модифи-
цированной задачи без приведения с помощью замен переменных системы
уравнений Эйлера для осесимметричного твердого тела к такой же системе
для тела со сферической динамической симметрией.
СПИСОК ЛИТЕРАТУРЫ
1. Бранец В.Н., Шмыглевский И.П. Применение кватернионов в задачах ориента-
ции твердого тела. М.: Наука, 1973.
2. Scrivener S.L., Thompson R.C. Survey of Time-Optimal Attitude Maneuvers //
J. Guidance, Control Dynam. 1994. V. 17. No. 2. Р. 225-233.
3. Петров Б.Н., Боднер В.А., Алексеев К.Б. Аналитическое решение задачи управ-
ления пространственным поворотным маневром // ДАН СССР. 1970. Т. 192. № 6.
С. 1235-1238.
4. Бранец В.Н., Черток М.Б., Казначеев Ю.В. Оптимальный разворот твердого
тела с одной осью симметрии // Космич. исслед. 1984. Т. 22. Вып. 3. С. 352-360.
5. Сиротин А.Н. Оптимальное управление переориентацией симметричного твер-
дого тела из положения покоя в положение покоя // Изв. АН СССР. МТТ. 1989.
№ 1. 36-47.
6. Челноков Ю.Н. Кватернионное решение кинематических задач управления ори-
ентацией твердого тела: уравнения движения, постановка задач, программное
движение и управление // Изв. РАН. МТТ. 1993. № 4. С. 7-14.
7. Levskii M.V. Pontryagin’s Maximum Principle in Optimal Control Problems of Ori-
entation of a Spacecraft // J. Comput. Sci. Int. 2008. V. 47. No. 6. P. 974-986.
8. Molodenkov A.V., Sapunkov Ya.G. A New Class of Analytic Solutions in the Optimal
Turn Problem for a Spherically Symmetric Body // Mechan. Solid. 2012. V. 47. No. 2.
P. 167-177.
105
9.
Molodenkov A.V., Sapunkov Ya.G. Analytical Solution of the Optimal Slew Problem
of a Spherically Symmetric Spacecraft in the Class of Conical Motion // J. Comput.
Sci. Int. 2013. V. 52. No. 3. P. 491-501.
10.
Molodenkov A.V., Sapunkov Ya.G. Analytical Solution of the Time-Optimal Slew
Problem of a Spherically Symmetric Spacecraft in the Class of Conical Motion //
J. Comput. Sci. Int. 2014. V. 53. No. 2. P. 159-171.
11.
Molodenkov A.V., Sapunkov Ya.G. Analytical Solution of the Optimal Attitude Ma-
neuver Problem with a Combined Objective Functional for a Rigid Body in the Class
of Conical Motions // Mechan. Solid. 2016. Vol. 51. No. 2. P. 135-147.
12.
Molodenkov A.V., Sapunkov Ya.G. Analytical Solution of the Optimal Slew Problem
for an Axisymmetric Spacecraft in the Class of Conical Motions // J. Comput. Sci.
Int. 2016. V. 55. No. 6. P. 969-985.
13.
Molodenkov A.V., Sapunkov Ya.G. Analytical Solution of the Minimum Time Slew
Maneuver Problem for an Axially Symmetric Spacecraft in the Class of Conical
Motions // J. Comput. Sci. Int. 2018. V. 57. No. 2. P. 302-318.
14.
Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Матема-
тическая теория оптимальных процессов. М.: Наука, 1961.
15.
Molodenkov A.V. On the solution of the Darboux problem // Mechan. Solid. 2007.
V. 42. No. 2. P. 167-176.
16.
Li. F., Bainum P.M. Numerical Approach for Solving Rigid Spacecraft Minimum
Time Attitude Maneuvers // J. Comput. Sci. Int. 1990. V. 13. No. 1. P. 38-45.
17.
Сапунков Я.Г., Молоденков А.В. Численное решение задачи оптимальной пе-
реориентации вращающегося космического аппарата // Мехатроника, автома-
тизация, управление. 2008. № 6. С. 66-70.
18.
Molodenkov A.V., Sapunkov Ya.G. Analytical Approximate Solution of the Problem
of a Spacecraft’s Optimal Turn with Arbitrary Boundary Conditions // J. Comput.
Sci. Int. 2015. V. 54. No. 3. P. 458-468.
Статья представлена к публикации членом редколлегии Е.Я. Рубиновичем.
Поступила в редакцию 07.07.2019
После доработки 24.02.2021
Принята к публикации 16.03.2021
106