Автоматика и телемеханика, № 8, 2021

(Институт науки данных и цифровых технологий Вильнюсского университета,

Вильнюс, Литва),

Н.М. МАРКОВИЧ, д-р физ.-мат. наук (nat.markovich@gmail.com)

(Институт проблем управления им. В.А. Трапезникова РАН, Москва)

ОЦЕНКА ПАРАМЕТРОВ В СУЖЕННОМ РАСПРЕДЕЛЕНИИ ПАРЕТО¹

Статья посвящена задаче оценивания параметров суженного распре-

деления Парето. Методом моментов получены новые оценки, зависящие

от дополнительного параметра. Доказано, что совместное асимптотиче-

ское распределение полученных оценок является гауссовским. Предло-

жена процедура, позволяющая выбрать дополнительный параметр опти-

мально. Проводится сравнение новых оценок с соответствующими оценка-

ми максимального правдоподобия. В качестве примера приведено приме-

нение новых оценок к данным заболеваемости КОВИД-19. Предлагается

новый алгоритм генератора случайных величин с суженным распределе-

нием Парето.

Ключевые слова: суженное распределение Парето, оценивание парамет-

ров, оценки методом моментов, оценки максимального правдоподобия,

заболеваемость Ковид-19.

DOI: 10.31857/S0005231021080043

1. Введение

Случайная величина (сл.в.) X называется распределенной по (экспонен-

циально) суженному распределению Парето, если она имеет кумулятивную

функцию распределения (ф.р.)

)_β

⁽a

^{a-x^}

(1)

Fa,β,θ(x) = 1 -

exp

x ≥ a,

где a > 0 - минимальное значение сл.в. X, β > 0 - параметр формы и θ ≥ a -

параметр верхнего среза. Плотность распределения вероятностей этого рас-

пределения имеет вид

)_β

⁽β

)(a

^{a-x^}

f_a,β,θ(x) =

exp

x ≥ a.

Суженное распределение Парето, также известное как модифицированное

распределение Гутенберга-Рихера, было впервые предложено В. Парето в [1].

В [2] было отмечено следующее свойство суженного распределения Паре-

то. Пусть сл.в. χ₁ имеет распределение Парето с ф.р. F_a,β (x) = 1 - (a/x)^β ,

¹ Работа выполнена при частичной финансовой поддержке второго автора грантом Рос-

сийского фонда фундаментальных исследований, проект № 19-01-00090.

x ≥ a, а χ₂ - сл.в., имеющая экспоненциальное распределение с ф.р. F_θ(x) =

= 1 - exp{-x/θ}, x ≥ 0, причем χ₁ и χ₂ - независимые сл.в. Тогда сл.в.

(2)

X = min{χ₁,χ₂

+ a}

имеет ф.р. F_a,β,θ(x), x ≥ a. Этот факт используется при моделировании

суженного распределения Парето, см. [2-4].

Следующее определение основано на нарушении условия Крамера для рас-

пределений с тяжелыми хвостами.

Определение 1

[5]. Ф.р. F называется имеющей тяжелый хвост

(справа), если

∫

(3)

e^tx

F (dx) = ∞

−∞

для всех t > 0. Если F не удовлетворяет условию (3), то называется имею-

щей легкий хвост.

Например, ф.р. Парето F_a,β(x), x ≥ a имеет тяжелый хвост, а ф.р. экспонен-

циального закона — легкий хвост. Ф.р. F_a,β,θ(x), x ≥ a имеет легкий хвост.

Действительно, в этом случае для 0 < t < 1/θ имеем

(

⁾⁽a(1 - tθ))β

IEe^tX =

+β

a(1 - tθ)

{

} (

)

a(1 - tθ)

× exp at +

-β,

∫_∞

где Γ(-β, x) =

t-β-1e^-tdt - неполная гамма-функция. Здесь и далее

IE обозначает математическое ожидание. Напомним, что при x > 0 послед-

ний интеграл сходится для всех вещественных β.

Суженное распределение Парето используется для моделирования магни-

туды землетрясений в сейсмологии [3, 4], а также размеров лесных пожа-

ров [6, 7]. В [8] было найдено, что суженное распределение Парето хоро-

шо описывает размеры деревьев. В [9] поддерживается идея, что финансо-

вые данные следуют этому распределению, см. [9]. В настоящей работе, по-

видимому впервые, суженное распределение Парето применяется к данным

КОВИД-19, относящимся к разным странам.

Обозначим через (X₁, . . . , X_n) случайную выборку, где X₁, . . . , X_n - неза-

висимые копии сл.в. X с ф.р. F_a,β,θ(x), x ≥ a.

Оценки максимального правдоподобия (МП

βn1) иλn1) параметров β и

λ = a/θ являются решением следующих уравнений:

∑

(4)

) = 1,

((

)

i=1 1 -λn1)

X_n/â_n

- 1 -bn (X_i/â_n)

)

(X¯

λ(1)

β(1)n +

ⁿ -1

= 1,

â_n

где

(5)

â_n = min{X₁,... ,X_n

)

∑

⁽X_i

bn =1

â_n

i=1

∑

X_n =1

X_i.

i=1

Нелинейное уравнение (4) может быть решено только численно. Это можно

сделать, например, методом Ньютона-Рафсона с начальной точкойXn - â_n,

см. [2, 4].

Обозначим

(

)

s₁₁(β,λ) = IE

(β + λχ)²

(

)

s₂₂(β,λ) = IE

(β + λχ)²

(

)

s₁₂(β,λ) = IE

(β + λχ)²

где сл.в. χ имеет ф.р. F1,β,1/λ. В следующей теореме собраны известные ре-

зультаты о совместной асимптотической нормальност

βn1) иλn1). В част-

ности, случай, когда a известно, обсуждался в [3]. В случае неизвестного a

приведенный далее результат является прямым следствием теоремы 2.4.(б) и

леммы 2.6.(а) в [9].

Теорема 1. Предположим, что (X₁,...,X_n) - выборка из распределения

с ф.р. F_a,β,a/λ. Предположим, что параметр a известен или оценивается по

формуле (5). Тогда

)

√n

β(1)n - β,λ(1)n - λ

→ (ξ₁, ξ₂) , n → ∞,

→ обозначает сходимость по рас(ре)елению. Здесь((ξ),ξ2) - гаус-

совский вектор с IE (ξ₁) = IE(ξ₂) = 0, IE

ξ²¹

= S²¹(β,λ), IE

ξ²²

= S²²(β,λ) и

IE (ξ₁ξ₂) = S₁₂(β, λ), где

s₁₁(β,λ)

S²¹(β,λ) =

s₁₁(β,λ)s₂₂(β,λ) - s²¹²(β,λ)

s₂₂(β,λ)

S²²(β,λ) =

s₁₁(β,λ)s₂₂(β,λ) - s²¹²(β,λ)

s₁₂(β,λ)

S₁₂(β,λ) = -

s₁₁(β,λ)s₂₂(β,λ) - s²¹²(β,λ)

Оценки М

βn1) иλn1) имеют несколько недостатков. Во-первых, как от-

мечено выше, решение уравнения (4) может быть получено лишь численно.

Более того, оно в основном зависит лишь от нескольких самых больших на-

блюдений выборки, см. [4]. Во-вторых, в статистической практике часто ис-

пользуются усеченные слева выборки, а для таких выборок оценка МП для

параметра θ = a/λ является существенно смещенной, см. подробнее [4]. По-

этому нужны оценки параметров β и λ, построенные другими методами.

Целью работы являются предложение новых оценок параметров суженно-

го распределения Парето, их теоретическое исследование и применение этого

распределения для моделирования данных заболеваемости КОВИД-19.

Содержание статьи следующее. В разделе 2 вводятся оценки параметров

β и λ суженного распределения Парето с помощью метода моментов. Приво-

дится главный результат, в котором утверждается, что предлагаемые оцен-

ки для β и λ имеют совместное асимптотически нормальное распределение.

В разделе 3 обсуждается моделирование сл.в. с суженным распределением

Парето. В разделе 4 нововведенные оценки сравниваются с оценками, по-

лученными методом МП. Раздел 5 содержит приложение к данным заболе-

ваемости КОВИД-19. В разделе 6 сформулированы выводы. Доказательства

содержатся в Приложении.

2. Оценивание параметров суженного распределения Парето

методом моментов

Напомним, что однопараметрическое преобразование Бокса-Кокса с пара-

метром r ∈ R определяется следующим образом:

{

ln(x),

r = 0,

h_r(x) =

(x^r - 1)/r, r = 0.

Обозначим

(6)

ν_r = IE(h_r

(X/a)) ,

где X - сл.в. с ф.р. F_a,β,a/λ. Нетрудно убедиться, что

(7)

ν_r = λ^β-re^λ

Γ(r - β, λ), r ∈ R.

Неполная гамма-функция удовлетворяет свойству

(8)

Γ (r - β + 1, λ) = λ^r-βe^-λ

+ (r - β)Γ (r - β, λ) ,

см., например, [10]. Комбинируя (7) и (8), получим

(9)

Λ_r

(β, λ) = 0,

где Λ_r(β, λ) = λνr+1 - (r - β)ν_r - 1. Система уравнений Λ_r(β, λ) = 0,

Λr+1(β,λ) = 0 может быть представлена как

^{ λνr+1 + βν_r = 1 + rν_r,

λνr+2 + βνr+1 = 1 + (1 + r)νr+1.

По теореме 4 из [11] неравенство ν2r+1 - ν_rνr+2 < 0 выполнено для всех r ∈ R,

β > 0 и λ > 0. Поэтому последняя система уравнений относительно β и λ

имеет единственное решение

g⁽¹⁾ (νr+1,νr+2)

g⁽²⁾ (ν_r,νr+1)

(10)

β =r-

λ=

g⁽³⁾ (ν_r,νr+1,νr+2)

где

(11)

g⁽¹⁾(x₂,x₃) = x₂ - x₃ + x²²,

(12)

g⁽²⁾(x₁,x₂) = x₁ - x₂ + x₁x₂,

(13)

g⁽³⁾(x₁,x₂,x₃) = x₁x₃ - x²², (x₁,x₂,x₃) ∈ R³.

Заменив ν_r, νr+1, νr+2 в (10) их выборочными аналогами ν_n,r, νn,r+1, νn,r+2,

где

)

∑

⁽X_i

νn,r =

h_r

â_n

i=1

а (X₁, . . . , X_n) - случайная выборка с ф.р. F_a,β,a/λ, введем новое семейство

оценок для пары параметров (β, λ):

g⁽¹⁾ (νn,r+1, νn,r+2)

(14)

β(2)n,r = r -

g⁽³⁾ (ν_n,r, νn,r+1, νn,r+2)

g⁽²⁾ (ν_n,r, νn,r+1)

λ(2)

(15)

n,r

g⁽³⁾ (ν_n,r, νn,r+1, νn,r+2)

Предложенные оценк

βⁿ

,r иλn

,r зависят от параметра Бокса-Кокса r. Оп-

тимальный выбор этого параметра получен в разделе 4.

Перед формулировкой главного результата введем обозначения:

c0,r = λνr+3 - 2νr+2 - 1, c1,r = 1 - 2λνr+2, c2,r := λνr+1,

c3,r = -λνr+2 + νr+1 + 1, c4,r = 2λνr+1 + ν_r - 1, c5,r = -λν_r.

Пусть Y_t, t ∈ R - гауссовский процесс со средним 0 и ковариационной функ-

цией

(16)

ρ_s,t = IE (Y_sY_t) = Cov (h_s(χ),h_t

(χ)) ,

где сл.в. χ та же, что и в теореме 1. В случае st = 0 ковариации ρ_s,t могут

быть представлены следующим образом:

νs+t - ν_t

νs+t - ν_s

(17)

ρ_s,t =

-ν_sν_t.

Ковариации ρ0,t, t ∈ R могут быть выражены в терминах G-функции Мейера

(см. определение в [12]).

Теорема 2. Предположим, что X₁,...,X_n - случайная выборка из рас-

пределения с ф.р. F_a,β,a/λ и r ∈ R. Тогда

)

(18)

√n

β(2)n,r - β,λ(2)n,r - λ

→ (η1,r, η2,r

n → ∞,

(

)

где (η1,r, η2,r) - гауссовский вектор со средними ноль, дисперсиями IE

η21,r

(

)

= σ21,r(β,λ), IE

η22,r

= σ22,r(β,λ) и ковариацией IE(η1,rη2,r) = σ12,r(β,λ), где

∑

(19)

σ21,r(β,λ) =

(

)₂

c_i,rc_j,rρr+i,r+j,

ν_rνr+2 - ν²

r+1

i,j=0

∑

(20)

σ22,r(β,λ) =

(

)₂

ci+3,rcj+3,rρr+i,r+j,

ν_rνr+2 - ν²

r+1

i,j=0

∑

(21)

σ12,r(β,λ) :=

(

)₂

c_i,rcj+3,rρr+i,r+j.

ν_rνr+2 - ν²

r+1

i,j=0

Если параметр a известен, то может быть применена очевидная модификация

оцено

βⁿ

,r иλn

,r, для которых соотношение (18) остается верным.

Рассмотрим оценивание параметра срезки θ, когда другие параметры a

и β известны. Комбинируя θ = a/λ и (9), получим

aνr+1

θ=

1 + (r - β)ν_r

Заменяя ν_r и νr+1 на ν_n,r и νn,r+1 соответственно, получаем оценку

aνn,r+1

θn,r =

1 + (r - β)ν_n,r

Заметим, что оценкаθn,1 совпадает с оценкой параметра θ, введенной в [4].

Обобщим теорему 1 из [4].

Теорема 3. Предположим, что X₁,...,X_n - случайная выборка из рас-

пределения с ф.р. F_a,β,θ, где a и β - известные параметры. Пусть r ∈ R.

Тогда

(

)

(22)

→ N

0, σ2r

n → ∞,

где

)

((θ(r - β))2

2θ(r - β)

(23)

σ2r =

ρ_r,r +

ρr,r+1 + ρr+1,r+1

ν²

r+1

а ρ_s,r определено по (16).

3. Моделирование случайных величин с

суженным распределением Парето

Для моделирования сл.в. с непрерывной ф.р. в ряде случаев можно ис-

пользовать метод обратной функции: если F непрерывная и строго монотон-

но возрастающая ф.р., а F^← - обратная к ней функция, то сл.в. F^←(U), где U

равномерно распределеннaя на (0, 1) сл.в., имеет ф.р. F , см. теорему 2.1 в [13].

Например, сл.в. F^←a,β (U), где F^←a,β (y) = a(1 - y)-1/β , 0 < y < 1, распределена

по закону Парето F_a,β (x), x ≥ a, а сл.в

F^←a,θ(U), где

F^←a,θ(y) = a - θ ln(1 - y),

0<y<1,имеет ф.р

Fa,θ(x) = Fθ(x - a), x ≥ a.

В [2] отмечено, что сл.в. с суженным распределением Парето и заданными

параметрами a, β, θ можно смоделировать, взяв за основу (2). А именно, сл.в.

{

}

min F^←a,β (1 - U₁)

F^←a,θ(1 - U₂)

имеет ф.р. F_a,β,θ(x), где U₁ и U₂ - независимые равномерно распределенные на

(0, 1) сл.в. Неверное применение этого метода содержится в [14], где утверж-

дается, что сл.в.

{

}

V =min F^←a,β(1-U)

F^←a,θ(1 - U)

где U - равномерно распределенная на (0, 1) сл.в., имеет ф.р. F_a,β,θ(x). Пе-

ред получением распределения сл.в. V напомним, что для x ≥ -1/e функция

Ламберта W (x) определена как решение уравнения

W (x) exp{W (x)} = x.

Для x - 1/e ≤ x < 0 существует два возможных вещественных значения

функции W (x) (см. рис. 1 в [15]). Обычно ветвь, удовлетворяющая W (x) ≥

≥ -1, обозначается как W₀(x), а ветвь, удовлетворяющая W(x) ≤ -1, — как

W-1(x).

Предложение 1. Пусть c = a/(βθ). Если c ≥ 1, то сл.в. V имеет ф.р.

Fa,θ(x), x ≥ a. Если 0 < c < 1, то для x ≥ a

^{ F

(24)

P (V ≤ x) =^a,β (x),x<-(a/c)W-1 (-cexp{-c}),˜

Fa,θ(x), x ≥ -(a/c)W-1 (-c exp{-c}).

Заметим, что ф.р. P (V ≤ x), x ≥ a может быть переписана следующим

образом. Для любого c > 0

{

}

P (V ≤ x) = max F_a,β (x)

Fa,θ (x)

x ≥ a.

(

)

Очевидно, что P (V > x) /

Fa,θ(x)

→ 1 при x → ∞. Отсюда следует, что

{

}

max F_a,β(x)

Fa,θ (x) , x ≥ a можно рассматривать как еще один способ суже-

ния распределения Парето э{споненциальн

}

вание параметров ф.р. max F_a,β (x)

Fa,θ (x) , x ≥ a рассматриваться не бу-

дет.

В [9] моделирование сл.в. с распределением суженное Парето осуществ-

ляется с помощью метода исключения. Подробно этот метод изложен в [13].

Заметим, что функция, обратная к ф.р. F_a,β,θ(x), x ≥ a, выражается как

(

)

(25)

F^←a,β,θ(y) =

W₀

ce^c(1 - y)-1/β

0 < y < 1,

где c та же, что и в Предложении 1. Поэтому применение теоремы 2.1 из [13]

позволяет моделировать сл.в. с распределением суженного Парето с помощью

метода обратной функции.

Предложение 2. Если U - равномерно распределенная сл.в. на интер-

вале (0, 1), то F^←a,β,θ(1 - U) имеет ф.р. F_a,β,θ.

4. Сравнение п(р оценок )араметров методом м(симума п)авдоподобия

β(1)n,λ(1)

и методом моментов

β(2)n,r,λ(2)

n,r

Напомним, что обобщенная дисперсия гауссовского вектора (η1,r, η2,r),

определенного в теореме 3, - это определитель его ковариационной матри-

цы:

(26)

GV_r(β, λ) = σ21,r(β, λ)σ22,r (β, λ) - σ212,r

(β, λ).

Обобщенная дисперсия GV_r(β, λ) характеризуeт степень случайного разбро-

са. Выберем GV_r(β, λ) в качестве асимптотической меры эффективности оце-

(

)

нок

βⁿ

,r,λn,r

. GV_r(β, λ) зависит от параметра Бокса-Кокса r. Естественно

выбрать такое r, которое бы минимизировало GV_r(β, λ). Однако GV_r(β, λ)

имеет сложную форму, а именно, при r + i = 0, i = 0, 1, . . . , 4, имеем

GV_r(β, λ) =

(27)

λ²(d1,r(β,λ) + d2,r(β,λ)Γ(2r - β,λ) + d3,r(β,λ)Γ²(2r - β,λ))

(λ2r + d4,r(β, λ)Γ(r - β, λ) + d5,r(β, λ)Γ²(r - β, λ))²

где

d1,r(β,λ) = - λ4r(2β + 2βr + 2λr - 2r - 1),

d2,r(β,λ) = - 2e^λλβ+2r(-β² - βλ + 2βr² + 2λr²

- 4r² - β²r - 2βλr + 3βr - λ²r - 2r),

(

)

d3,r(β,λ) = e2λλ2β(2r - β)

β + 4r² + 2r

d4,r(β,λ) = - e^λλβ+r(β + λ - r + 1),

d5,r(β,λ) = - e2λλ2β(r - β).

Поэтому в статье ее минимизация по r произведена численно, с использо-

ванием метода главных осей. Точку глобального минимума r^∗ на R будем

называть оптимальным выбором параметра r. Контурный график (со значе-

ниями изолиний) r^∗ как функции от β и λ представлен на рис. 1.

1,0

0,8

0,6

0,4

0,2

0,5

0,4

0,2

0,4

0,6

0,8

1,0

1,2

1,4

Рис. 1. Контурный график функции r^∗(β, λ).

(

)

Асимптотическую относительную эффективность (АОЭ) для

β(2)n,r∗,λ(2)n,r∗

(

)

в отношении

βn1),λn1)

определим как отношение обобщенных дисперсий

для гауссовских векторов (η1,r, η2,r) и (ξ₁, ξ₂), определенных в теоремах 2 и 1

соответственно:

(β, λ)

σ21,r∗(β,λ)σ22,r∗ (β,λ) - σ212,r∗

ARE(β, λ) =

β > 0, 0 < λ < 1.

S²¹(β,λ)S²²(β,λ) - S²¹²(β,λ)

Аналогично определим АОЭ дл

β(2)n,r∗ в отношении

βn1) иλ(2)n,r∗ в отноше-

нииλn1):

σ21,r∗

(β, λ)

σ22,r∗(β,λ)

ARE₁(β, λ) =

ARE₂(β, λ) =

β > 0, 0 < λ < 1.

S²¹(β,λ)

S²²(β,λ)

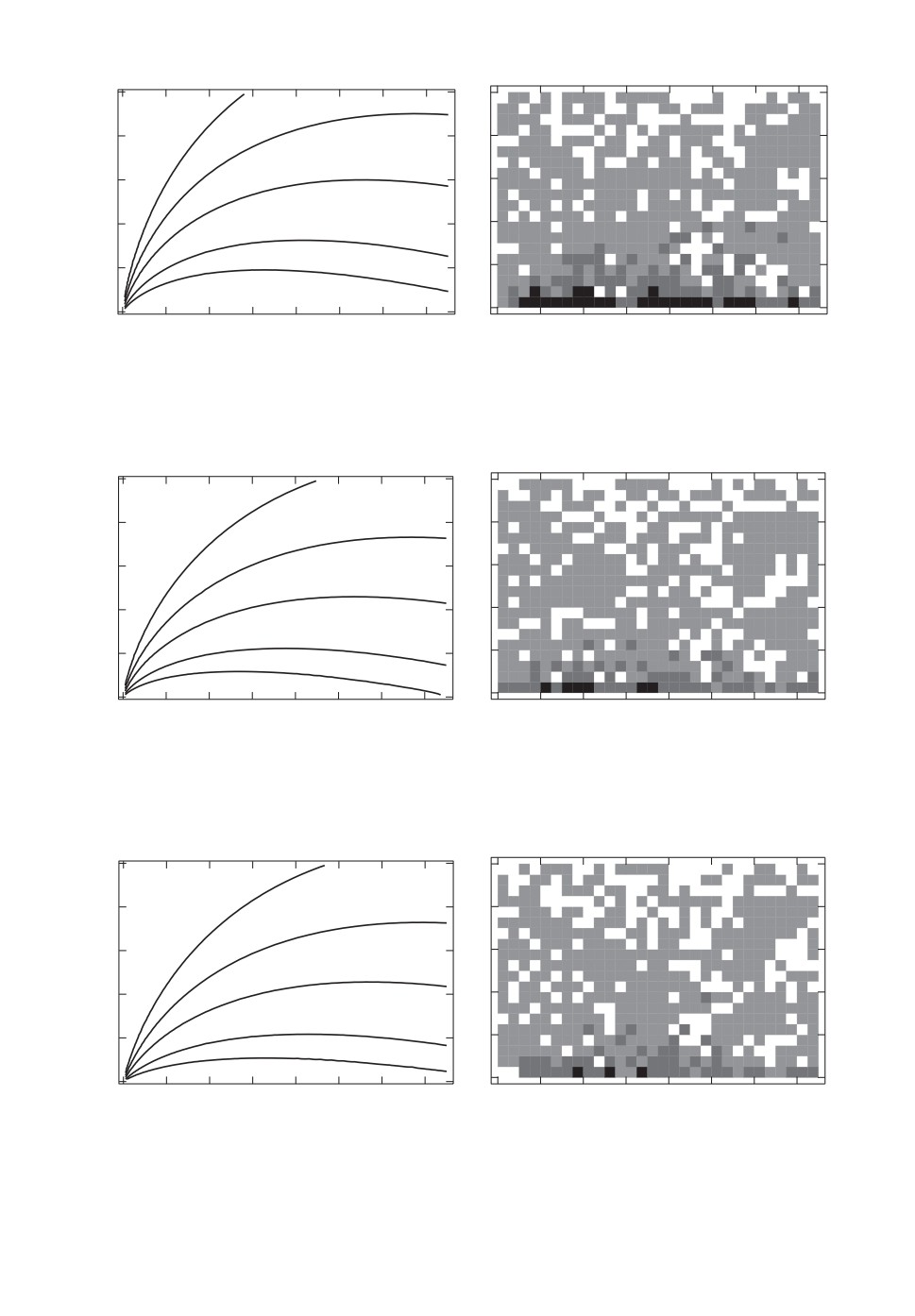
Контурный график на рис. 2 (слева) показывает, что ARE(β, λ) близка к 1

почти во всем прямоугольнике (β, λ) ∈ (0, 1, 5] × (0, 1). Теоретическое доми-

(

)

нирование оценок

βn1),λn1)

более значимо в области, где величины λ малы.

Это замечание справедливо для ARE_i(β, λ), i ∈ {1, 2}, см. рис. 3 (слева) и

рис. 4 (слева) соответственно.

Далее с помощью численного моделирования продемонстрируем качество

работы предложе(ных оце)ок.(Во врем)моделирования делается сравнение

между оценками

βn1),λn1)

βⁿ

,r,λn,r

, используя выборки среднего и ма-

лого обьема n из распределения (1). Во всем моделировании предполагается,

что параметр a = 1 неизвестен и оценивается, используя â_n.

1,0

1,0005

1,001

0,8

0,6

1,002

0,6

0,4

1,005

0,2

1,01

0,2

0,4

0,6

0,8

1,0

1,2

1,4

0,2

0,4

0,6

0,8

1,0

1,2

1,4

Рис. 2. Контурный график ARE(β, λ) (слева) и график

RE (β_i,j , λ_i,j ),

0 ≤ i ≤ 29, 0 ≤ j ≤ 19 (справа).

1,0

0,8

1,0005

1,001

0,6

1,002

0,4

1,005

0,2

1,01

0,2

0,4

0,6

0,8

1,0

1,2

1,4

0,2

0,4

0,6

0,8

1,0

1,2

1,4

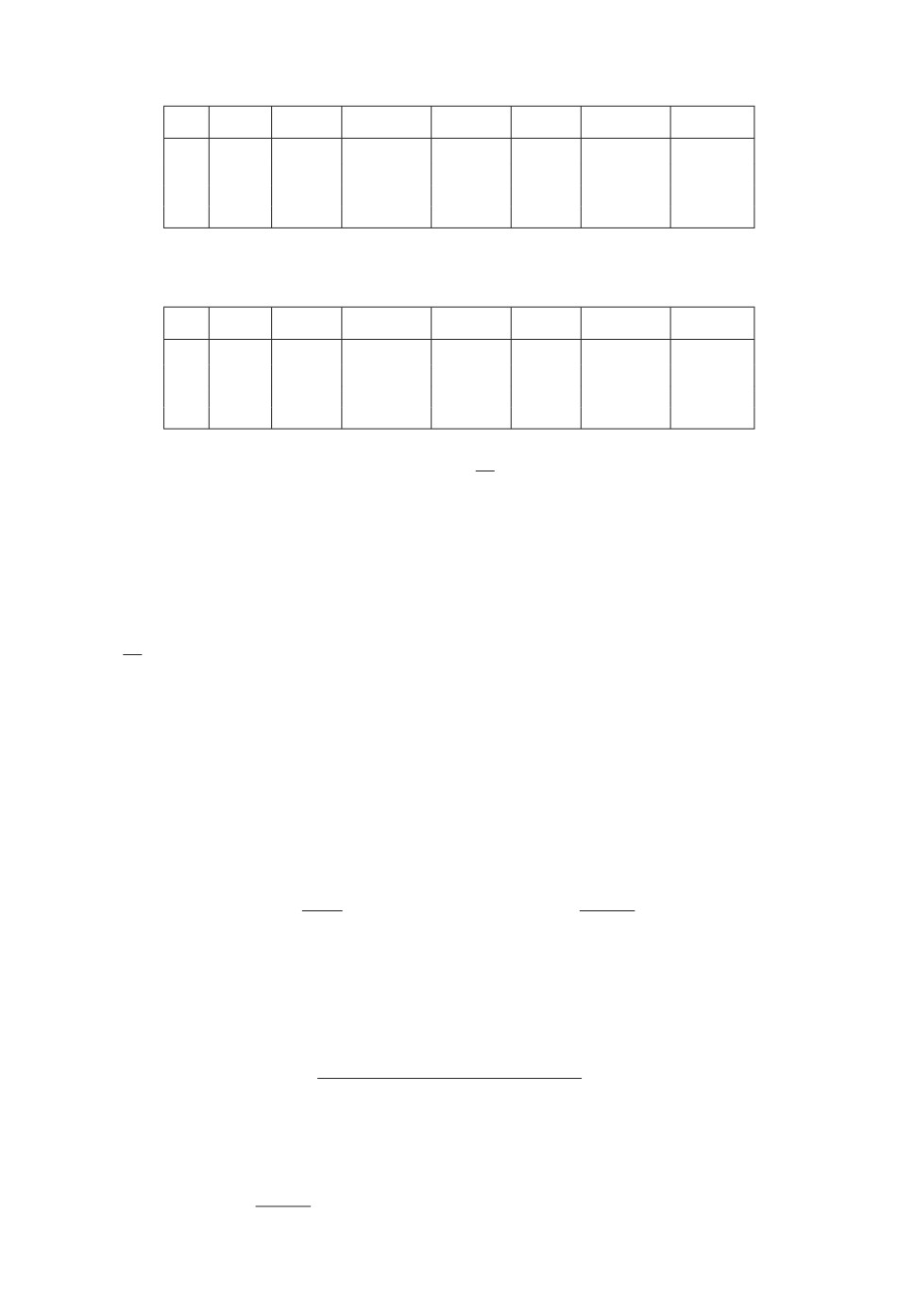
Рис. 3. Контурный график ARE₁(β, λ) (слева) и график

RE₁ (β_i,j , λ_i,j ),

0 ≤ i ≤ 29, 0 ≤ j ≤ 19 (справа).

1,0

0,8

1,0005

1,001

0,6

1,002

0,4

1,005

0,2

1,01

0,2

0,4

0,6

0,8

1,0

1,2

1,4

0,2

0,4

0,6

0,8

1,0

1,2

1,4

Рис. 4. Контурный график ARE₂(β, λ) (слева) и график

RE₂ (β_i,j , λ_i,j ),

0 ≤ i ≤ 29, 0 ≤ j ≤ 19 (справа).

Для практических целей, чтобы выбрать параметр r оптимально, доста-

точно минимизировать GV_r(β, λ) (см. (27)) по параметру r ∈ (-1, 0). Так как

оптимальный выбор r^∗ зависит от неизвестных параметров β и λ, предла-

гается следующая итерационная процедура. Если выполнена k-я итерация

оценивания оптимального выбора r^∗, во время которой вычислено его при-

ближение r^∗k, то (k + 1)-ю итерацию выполняем следующим образом:

1) вычислить оценк

β(2)n,r∗

и λ(2)n,r∗ по формулам (14) и (15) соответственно;

{ k

(

)}

2) вычислить r∗k+1 = argmin r ∈ (-1, 0) : GV_r

β(2)n,r∗,λ(2)n,r∗

по формуле (27);

3) проверить критерий останова |r∗k+1 - r^∗k| ≤ ϵ, и если он не выполнен, то

увеличить k на единицу и перейти к шагу 1.

После выполнения критерия останова, значение r∗k+1 принимается за r^∗ и со-

ответственно принимаетс

β(2)n,r∗

и λ(2)n,r∗ =λ(2)n,r∗

. Чтобы избежать

k+1

большого числа итераций, используется еще одно ограничение. А именно, ес-

ли |r∗k+1 - r^∗k| > ϵ для всех 0 ≤ k ≤ 9, то r^∗ = r∗10

β(2)n,r∗

иλ(2)n,r∗ =λ(2)n,r∗ .

В моделировании использовалось начальное приближение r∗0 = -1/2 и точ-

ность ϵ = 0,001. Заметим, что шаг 2 предлагаемой процедуры может быть

выполнен комбинированием функций “Last” и “FindMinimum” в “Wolfram

Mathematica 10”.

В первой части моделирования прямоугольник (0, 3/2] × (0, 1) разделяется

на квадраты

s_i,j = {(i/20,(i + 1)/20] × (j/20,(j + 1)/20], 0 ≤ i ≤ 29, 0 ≤ j ≤ 19} .

В качестве истинных значений параметров β и λ взяты координаты

2i + 1

2j + 1

β_i,j =

λ_i,j =

центра квадрата s_i,j и сгенерированы N = 750 реализаций случайной выбор-

ки из распределения (1) размером n = 2500 наблюдений.

(

)

(

)

(

)

Пусть

βn1,k),λn1,k)

βn2,k),λn2,k)

∗

,λn,r∗

обозначают оценки

параметров (β, λ), вычисленные по k-й реализации. Рассмотрим следующие

эмпирические моменты:

∑(

)_j

m_i,j =

β(i,k)n

i = 1,2, j = 1,2,

k=1

∑(

)_j

λ(i,k)

M_i,j =

i = 1,2, j = 1,2,

k=1

∑

μ_i =

β(i,k)nλ(i,k)n, i = 1,2.

k=1

Выборочные аналоги характеристик ARE(β, λ), ARE₁(β, λ) и ARE₂(β, λ) име-

ют вид

(

)(

)

m2,2 - (m2,1)2

M2,2 - (M2,1)2

- (μ₂ - m2,1M2,1)

RE (β_i,j , λ_i,j ) =

(

)(

)

m1,2 - (m1,1)2

M1,2 - (M1,1)2

- (μ₁ - m1,1M2,1

)²

m2,2 - (m2,1)

M2,2 - (M2,1)²

RE₁ (β_i,j , λ_i,j ) =

RE₂ (β_i,j , λ_i,j) =

m1,2 - (m1,1)²

M1,2 - (M1,1)²

График

RE (β_i,j, λ_i,j ), 0 ≤ i ≤ 29, 0 ≤ j ≤ 19 представлен на рис. 2 (справа),

где квадрат s_i,j окрашен следующим образом:

⎧

⎪

черный,

RE (β_i,j, λ_i,j ) ≥ 1, 03,

⎪

⎨

темно-серый,

1, 01 ≤

RE (β_i,j, λ_i,j ) < 1, 03,

⎪

серый,

1≤

RE (β_i,j, λ_i,j ) < 1, 01,

⎪

⎩

белый,

RE (β_i,j, λ_i,j ) < 1.

Та же цветовая схема используется для получения графиков

RE₁ (β_i,j , λ_i,j)

RE₂ (β_i,j, λ_i,j ), см. рис. 3 (справа) и рис. 4 (справа) соответственно.

Вторая часть моделирования посвящена выборкам малого объема. Истин-

ные значения (β, λ) выбраны следующими: β_i = i/20, λ_i = cβ_i, 1 ≤ i ≤ 29, где

(

)

делированы N = 1500 раз. Из каждой выборки X(k)1, . . . , X(k)

, 1≤k≤N

110

сформированы три выборки объемом n = 100:

(

)

a) неусеченная выборка X(k)1, . . . , X(k)

;

100

б) выборка с усечененными пятью наименьшими наблюдениями₍

)

X(k)6,105,... ,X(k)

, где X(k)1,n ≤ . . . ≤ Xⁿ

105,105

,n - вариационный ряд выбор-

(

)

ки X(k)1, . . . , Xnk)

;

в) выборка с усечененными десятью наименьшими наблюдениями₍

)

X(k)11,110,... ,X(k)

110,110

В качестве эффективности оценивания параметров для неусеченных выборок

рассмотрены отношения средних квадратов отклонения от истинных значе-

ний параметров:

m2,2 - 2β_im2,1 + β2i

ψ₁(c,β_i) =

m1,2 - 2β_im1,1 + β²

M2,2 - 2cβ_iM2,1 + c²β2i

Ψ₁(c,β_i) =

M1,2 - 2cβ_iM1,1 + c²β²

Пусть ψ₂(c, β_i), ψ₃(c, β_i) и Ψ₂(c, β_i), Ψ₃(c, β_i) обозначают аналоги эмпириче-

ских характеристик ψ₁(c, β_i) и Ψ₁(c, β_i), вычисленные по усеченным слева

выборкам. Численные результаты представлены на рис. 5-7.

1,1

1,15

1,0

0,2

0,4

0,6

0,8

1,0

1,2

1,4

1,10

0,9

1,05

0,8

0,2

0,4

0,6

0,8

1,0

1,2

1,4

0,7

Рис. 5. Графики ψ_j (1/96, β_i), j = 1, 2, 3 (слева) и Ψ_j (1/96, β_i), j = 1, 2, 3

(справа), 1 ≤ i ≤ 29 (j = 1 - черная ломаная, j = 2 - темно-серая лома-

ная, j = 3 - серая ломаная).

1,14

1,05

1,12

1,00

1,10

0,2

0,4

0,6

0,8

1,0

1,2

1,4

1,08

0,95

1,06

0,90

1,04

0,85

1,02

0,80

0,2

0,4

0,6

0,8

1,0

1,2

1,4

Рис. 6. Графики ψ_j (1/24, β_i), j = 1, 2, 3 (слева) и Ψ_j (1/24, β_i), j = 1, 2, 3

(справа), 1 ≤ i ≤ 29 (j = 1 - черная ломаная, j = 2 - темно-серая лома-

ная, j = 3 - серая ломаная).

1,05

1,10

1,00

1,08

0,2

0,4

0,6

0,8

1,0

1,2

1,4

0,95

1,06

1,04

0,90

1,02

0,85

0,2

0,4

0,6

0,8

1,0

1,2

1,4

0,80

Рис. 7. Графики ψ_j (1/6, β_i), j = 1, 2, 3 (слева) и Ψ_j(1/6, β_i), j = 1, 2, 3

(справа), 1 ≤ i ≤ 29 (j = 1 - черная ломаная, j = 2 - темно-серая лома-

ная, j = 3 - серая ломаная).

На основе полученных результатов моделирования можно сделать следую-

щие выводы.

1) Из сравнения контурного графика ARE(β, λ) и графика

RE(s_i,j , λ_i,j),

0 ≤ i ≤ 29, 0 ≤ j ≤ 19 на рис. 2 следует, что результаты моделирования

на рис. 2 (справа) в целом соответствуют теоретическим результатам

на рис. 2 (слева). Во-первых, значения ARE(β, λ) не превышают 1,01

в прямоугольнике (β, λ) ∈ (0, 1,5] × (0, 2, 1), и это отражено на графике

RE(s_i,j, λ_i,j). Более того, достаточное количество белых квадратов в пря-

моугольнике на рис. 2 (справа) (β, λ) ∈ (0, 1, 5] × (0, 2, 1) указывает, что

(

)

предложенные оценки

βⁿ

,r,θn,r

могут быть полезны для практических

приложений. Во-вторых, результаты моделирования на рис. 2 (справа) до-

статочно хорошо отражают доминирование оценок МП при малых значе-

ниях λ. По существу, графики на рис. 3, 4 ничем не отличаются от графи-

ков на рис. 2.

2) Поскольку ψ₁(c, β_i) > 1 для всех β_i, 1 ≤ i ≤ 29 и c = 1/96, 1/24, 1/6, то

оценк

βn1) доминирует над оценко

β(2)n,r∗ во всех исследованных точках

(β_i, λ_i), 1 ≤ i ≤ 29. Нужно отметить, что доминирование оценк

βn1) со-

храняется при оценивании параметра β по усеченным слева выборкам, см.

графики ломаных ψ_j (c, β_i), j = 2, 3 на рис. 5-7 (слева). Усечение выборок

не отражается на относительных статистиках ψ_j (c, β_i), j = 2, 3, т.е. значе-

ния ψ₁, ψ₂ и ψ₃ при фиксированых c и β_i практически не различаются.

3) Сравнение оценокλn1) иλ(2)n,r∗ при неусеченных выборках зависит от значе-

ния параметра c. При c = 1/6 ни одна из оценокλn1) иλ(2)n,r∗ не превосходит

другой, см. график ломаной Ψ₁(1/6, β_i), 1 ≤ i ≤ 29 на рис. 7 (справа). При

β_i ∈ [1,3/2) значения ломаной Ψ₁(1/96,β_i) осциллируют вокруг единицы,

но при β_i ∈ (0, 1) оценкаλn1) имеет преимущество, см. рис. 5 (справа). Ана-

логичный вывод может быть сделан и в отношении оценокλn1) иλ(2)n,r∗ при

c = 1/24. При усечении наблюдении слева оценка λ(2)n,r∗ превосходит оцен-

куλn1), см. графики ломаных Ψ₂ и Ψ₃ на рис. 5-7 (справа). Исходя из

результатов моделирования, представленных в табл. 1, можно заключить,

что в основном превосходство оценкиλ(2)n,r∗ создается за счет лучшего эм-

пирического среднеквадратического отклонения. В этой таблице через

BI₁ = M1,1 - λ, bi₁ = M2,1 - λ,

RD₁ = M1,2 - (M1,1)² , rd₁ = M2,2 - (M2,1)²

обозначены эмпирические смещения и среднеквадратические отклонения

оценокλn1) иλ(2)n,r∗ при неусеченных выборках. При усеченных выборках

используются те же обозначения, но с нижними индексами 2 и 3 соответ-

ственно.

4) Приводимые в табл. 1 значения BI₁ позволяют судить о смещении оцен-

киλn1) при неусеченных выборках. Результаты моделирования не проти-

воречат полученному в [4] выводу, что оценка МП (как и оценкаλ(2)n,r∗ )

Таблица 1. Эмпирические характеристики

0,05

0,75

1,45

0,05

0,75

1,45

0,05

0,75

1,45

100 · λ

5/6

75/6

145/6

5/24

75/24

145/24

5/96

75/96

145/96

100 · BI₁

0,01

0,55

5,25

0,04

0,70

5,12

0,18

1,50

7,79

100 · bi₁

0,01

0,57

5,34

0,04

0,73

5,13

0,18

1,51

7,72

100 · BI₂

0,13

0,63

5,32

0,04

0,91

5,26

1,40

2,40

8,58

100 · bi₂

0,13

0,63

5,35

0,03

0.94

5,27

1,36

2,28

8,46

100 · BI₃

0,42

0,70

5,30

1,32

1,17

5,44

3,21

3,26

8,41

100 · bi₃

0,41

0,68

5,30

1,27

1,16

0,56

3,11

2,98

9,04

100 · RD₁

0,01

1,16

8,87

0,06

2,23

11,45

0,24

6,15

23,23

100 · rd₁

0,01

1,17

8,81

0,06

2,24

11,40

0,24

6,15

23,73

100 · RD₂

0,11

1,32

9,30

0,39

2,45

11,98

0,97

6,76

24,30

100 · rd₂

0,10

1,19

8,88

0,35

2,34

11,30

0,87

6,58

23,62

100 · RD₃

0,34

1,43

9,31

0,94

2,71

12,50

1,73

7,28

25,04

100 · rd₃

0,30

1,23

8,35

0,85

2,46

11,60

1,54

6,88

23,87

оказывается существенно смещенной вправо. Усечение слева приводит к

смещению обoих оценок параметра λ вправо, а увеличение среднеквадра-

тических отклонений зависит от параметра c.

5. Применение к данным КОВИД-19

В статье исследовались данные, связанные с заболеванием коронавирусной

инфекцией КОВИД-19 по дням (см. https://www.kaggle.com/allen-institute-

for-ai/CORD-19-research-challenge). Анализируется число выздоровевших ин-

дивидуумов по дням путем предварительного усечения слева с разным уров-

нем. Анализ основан на данных, собранных до 22 июня 2020 г., т.е. на первой

волне пандемии. Применим суженное распределение Парето как модель рас-

пределения числа выздоровевших индивидуумов для двух соседних стран

восточной Азии: Японии и Южной Кореи. Средняя плотность населения в

Японии 338 человек, а в Южной Корее 496 человек на 1 кв. км. Эти страны

сопоставимы по индексу развития и занимают 19 и 22 места в мировом списке

стран соответственно.

Оценки параметров (по методам МП и моментов) суженного распределе-

ния Парето представлены в табл. 2 и 3, где для полноты анализа приведены

и оценки параметра верхнего усечения θ. Параметр a считается известным

и равным выбранному уровню усечения слева. В табл. 2 и 3 n(a) обозначает

объем усеченной слева выборки.

Получив различающиеся оценки максимального правдоподобия и по мето-

ду моментов для β, λ (или θ) для одной какой-то страны, трудно решить, яв-

ляется ли эта разница статистически значимой. Поэтому применим несколь-

ко тестов согласия. Пусть F_n - эмпирическая ф.р. выборки X₁, . . . , X_n, а

X1,n < X2,n < ··· < X_m,n - ее порядковые статистики. Пуст

β и λ обознача-

ют оценки параметров β и λ.

Тест Колмогорова-Смирнова (KS) определяет наибольшее расстояние

между F_n и ф.р. суженного распределения Парето Fa,ˆβ,a/ˆλ:



K_n =

√n sup

F_n(x) - Fa,ˆβ,a/ˆλ(x)

.

x≥a

Таблица 2. Оценка параметров суженного распределения Парето

на японских данных

a n(a)

βn1)

λ⁽¹⁾

θ(1)

βⁿ

λ⁽²⁾

θ(2)

,r∗

n,r∗

0,108

0,01952

256.02

0,108

0,01743

286,83

0,177

0,03324

300,82

0,171

0,03092

323,38

0,234

0,04417

339,56

0,220

0,04253

352,62

0,279

0,05367

372,63

0,256

0,05333

375,00

Таблица 3. Оценка параметров суженного распределения Парето

на южнокорейских данных

λ⁽¹⁾

θ(1)

λ⁽²⁾

θ(2)

a n(a)

βn1)

βⁿ

,r∗

n,r∗

102

0,077

0,03978

125,66

0,074

0,03778

132,49

0,220

0,06000

166,65

0,218

0,05674

176,22

0,292

0,07913

189,55

0,291

0,07522

199,39

0,428

0,08430

237,24

0,437

0,07842

255,01

Статистика теста KS имеет вид K_n =

√mmax{K^-m,K+m}, где

{

}

K+m = max

Fn (Xi,n) - F_a,

(X_i,n)

β,a/λ

1≤i≤m

{

}

K^-m = max

(X_i,n) - F_n (Xi-1,n)

Fa,β,a/λ

2≤i≤m

Статистика

K_n для теста Койпера (K) имеет представление в виде

K_n =

√m (K^-m + K+m). Статистика для теста Крамера-фон Мизеса-Смирнова

(CvMS) использует квадратичную меру близости между F_n(x) и Fa,ˆβ,a/ˆλ:

∫∞

(

)₂

ω2n = n

Fn(x) - F_a,

dFa,ˆβ,a/ˆλ(x).

β,a/λ(x)

Практическое вычисление статистики теста CvMS удобно производить по

формуле

(

)₂

∑

2i - 1

ω2n =

(X_i,n) -

Fa,β,a/λ

12m

i=1

Статистика для теста Андерсона-Дарлинга (AD) использует взвешенную

квадратичную меру близости между F_n(x) и Fa,ˆβ,a/ˆλ:

(

)₂

∫∞

Fn(x) - Fa,β,a/λ(x)

A2n = n

(

)

dFa,ˆβ,a/ˆλ(x).

1 - Fa,ˆβ,a/ˆλ(x) Fa,ˆβ,a/ˆλ(x)

Практическое вычисление статистики теста AD производится по формуле

∑

(

)

(

))

2i - 1⁽

A2n = -m -

ln Fa,ˆβ,a/ˆλ (X_i,n)

+ ln

1 - Fa,ˆβ,a/ˆλ (Xm+1-i,n)

i=1

100

Таблица 4. p-значения для тестов KS, K, CvMS и AD

Япония

CvMS

a F₁

F₂

F₁

F₂

F₁

F₂

F₁

F₂

0,040

0,129

0,015

0,042

0,070

0,161

0,001

0,002

0,130

0,281

0,030

0,049

0,152

0,235

0,002

0,003

0,220

0,406

0,039

0,051

0,214

0,278

0,080

0,094

0,294

0,408

0,048

0,059

0,254

0,305

0,090

0,098

Южная Корея

CvMS

a F₁

F₂

F₁

F₂

F₁

F₂

F₁

F₂

0,284

0,531

0,062

0,128

0,136

0,278

0,042

0,072

0,533

0,625

0,165

0,239

0,577

0,701

0,512

0,631

0,690

0,782

0,324

0,422

0,726

0,802

0,170

0,187

0,728

0,792

0,585

0,634

0,829

0,860

0,232

0,242

При нулевой гипотезе, что выборка соответствует распределению Fa,ˆβ,a/ˆλ,

статистики K_n,

K_n, ω2n и A2n убывают с увеличением числа наблюдений до

бесконечности. С помощью процедур, входящих в “Wolfram Mathematica 10”,

нетрудно посчитать p-значения для приведенных выше статистических те-

стов. Таблица 4 содержит p-значения для тестов KS, K, CvMS и AD, где

p-значения выше уровня значимости α = 0,05 показаны жирным шрифтом.

При этом нулевая гипотеза не отвергается. В табл. 4 F₁ и F₂ обозначают

ф.р. F

и F

соответственно. Напомним, что F

βn1),a/λn1)

βⁿ

,r∗,a/λn

,r∗

βn1),a/λn1)

обозначает модель с параметрами, оцененными методом максимума правдо-

подобия, а F

- предложенным в статье методом моментов.

βⁿ

,r∗,a/λn,

r∗

По результатам анализа можно сделать следующие выводы.

1) Идентифицировать параметрическую модель по малой выборке объ-

емом около 100 наблюдений (см. n(a) в табл. 2, 3) чрезвычайно сложно,

так как можно подобрать множество моделей, одинаково хорошо описы-

вающих выборочные данные с позиций нескольких критериев согласия.

2) Сравнивая соответствующие p-значения для моделей F₁ и F₂ в табл. 4,

заметим, что для всех примененных тестов p-значения для модели F₂

выше, чем для модели F₁. Это указывает на то, что модель с новыми

оценками параметров (β, λ) лучше описывает анализируемые данные,

чем модель F₁.

3) Приведенные в табл. 4 p-значения растут вместе с уровнем усечения a.

Отсюда следует вывод, что наблюдения (как для Япония, так и для

Южной Кореи) из нижней части вариационого ряда хуже описываются

суженным распределением Парето.

4) Из табл. 4 следует, что суженное распределение Парето лучше описыва-

ет число выздоровевших от КОВИД-19 индивидуумов в Южной Корее,

чем в Японии. Это отражается в оценках параметров β и λ (при со-

ответствующем уровне усечения), которые различаются 1,5-2 раза, см.

табл. 2 и 3.

101

6. Заключение

В статье применяется метод моментов для получения семейства новых

оценок для параметров суженного распределения Парето. Доказано, что сов-

местное асимптотическое распределение новых оценок является гауссовским.

Предложена процедура оптимального выбора дополнительного параметра.

Теоретическое сравнение показало, что при неусеченных выборках пара но-

вовведенных оценок незначительно уступает в качестве соответствующeй па-

ре оценок максимального правдоподобия. Как показало компьютерное мо-

делирование, оценки максимума правдоподобия теряют превосходство при

некоторых истинных значениях параметров β и λ, см. рис. 2-4.

Новым в работе является также предложение генератора случайных чи-

сел, распределенных по суженному распределению Парето.

Часто в задачах статистического анализа данных используется усечение

наблюдений слева. Эмпирические исследования статистических свойств оце-

нок по выборкам, содержащим усеченные слева наблюдения, показали, что

из оценокλn1) иλn,r∗ более предпочтительным является использование ново-

введеной оценкиλn,r∗. Что касается оцено

βn1)

βn,r∗, то усечение данных

воздействует на их эффективность примерно одинаково.

Компьютерное моделирование выявило, что как при усеченных слева, так

и при неусеченных данных смещение оценокλn1) иλn,r∗ вносит значитель-

ный вклад в их отклонения средних квадратов. Устранение (или сокращение)

смещения обсуж(аемых )енок(тесно св )ано с исследованием асимптотики

λ⁽¹⁾

λ⁽²⁾

матожиданий IE

- λ и IE

n,r∗ - λ при n → ∞. Эту проблему авторы

статьи намерены решить в дальнейшем.

ПРИЛОЖЕНИЕ 1

Лемма 1. Пусть (X₁,...,X_n) - выборка сл.в. из распределения F_a,β,a/λ и

r ∈ R. Тогда

(Π.1)

√nh_r (a/â_n)→

0, n → ∞.

Доказательство. Утверждение леммы следует из соотношения

(Π.2)

→ -

n → ∞,

λ+β

где Z

- экспоненциально распределенная сл.в. с ф.р. P (Z ≤ x) = 1-

- exp{-x}, x ≥ 0.

Для любого r ∈ R функция h_r(x) строго возрастает на [1, ∞). Используя

это свойство, можно проверить тождество

{ (

)

X₁

⁽X_n)}

h_r (a/â_n) = - min h_-r

,...,h_-r

Положим

{

+∞, r ≤ 0,

L_r =

1/r, r > 0.

102

Имеем P(h_-r(X₁/a) ≤ x) = F1,β,1/λ(h^←-r(x)), x ∈ [1, L_r). Используя

(25),

(

)

нетрудно убедиться, что функция h_-r F←1,β,1/λ(y) , 0 ≤ y ≤ 1 является обоб-

щенной обратной к ф.р. F1,β,1/λ(h^←-r(x)), x ∈ [1, L_r). Согласно теореме 8.3.6(ii)

в [16] соотношение

(

)

{

(_X

)

(_X

)}

min

h_-r

,...,h_-r

− h_-r F←1,β,1/λ(0)

(

)

(

)

→ Z, n → ∞

h_-r F←1,β,1/λ(1/n)

- h_-r F←1,β,1/λ(0)

(

)

будет доказано, если показать, что h_-r F←1,β,1/λ(0) конечно, и верно

(

)

))

F1,β,1/λ h^←

h_-r F←1,β,1/λ

(0)

+ ϵx

−r

(Π.3)

lim

(

)

)) = x

ϵ→0+

F1,β,1/λ h^←

h_-r F←1,β,1/λ(0)

+ϵ

−r

для всех x > 0.

Сочетая (25) и тождество W₀ (xe^x) = x, которое выполнено для x ≥ -1,₍₎

выводим h_-r F←1,β,1/λ(0)

= h-r (1) = 0. Применяя правило Лопиталя, полу-

чаем, что левая часть (Π.3) равна

f1,β,1/λ

(exp {ϵx})

x lim

exp {ϵ(x - 1)} = x

ϵ→0+ f1,β,1/λ (exp {ϵ})

при r = 0, и

(

)

(

)

-1-1/r

f1,β,1/λ

(1 - rϵx)-1/r

rϵ(1 - x)

x lim

(

)

ϵ→0+

1-rϵ

f1,β,1/λ

(1 - rϵ)-1/r

при r = 0.

Чтобы завершить доказательство соотношения (Π.2), остается доказать,₍₎

что h_-r F←1,β,1/λ(n-1)

∼ (λ + β)-1n-1, n → ∞. Напомним, что

dW₀(t)

W₀(t)

t = 0,

t (1 + W₀(t))

см., например, (3.2) в [15]. Применив правило Лопиталя еще раз, получим

(

)

(

)_r

h_-r F←1,β,1/λ

(n-1)

F←1,β,1/λ(t)

lim

= lim

(

) =

n→∞

n-1

λ+β

t→0 β(1 - t) 1 + (λ/β)F←1,β,1/λ(t)

103

Лемма 2. Пусть выполнены условия леммы 1. Тогда

(Π.4)

→ (Y_r, Yr+1, Yr+2)

при n → ∞.

Доказательство. По теореме Крамера-Вольда (см. теорему 29.4 в [17]),

достаточно показать, что для любого вектора констант (c₀, c₁, c₂) ∈ R³

√

∑

→ c_kYr+k, n → ∞.

k=0

Заметим, что

)

∑ ((Xi)

ζ_i =

c_k hr+k

-νr+k

i = 1,2,...

k=0

являются независимыми одинаково распределенными случайными величина-

∑₂

ми с IE (ζ_i) = 0 и Var (ζ_i) =

c_ic_jρr+i,r+j. Используя центральную пре-

i,j=0

дельную теорему Линдеберга-Леви (см., например, теорему 27.1 в [17]), за-

ключаем, что

∑

(Π.5)

→ c_kYr+k

n → ∞.

i=1

k=0

Ввиду декомпозиции

∑

c_k (νn,r+k - νr+k) = T_n +

ζ_i,

√n

k=0

i=1

где

( (

)

∑∑

X_i

⁽X_i))

T_n =

c_k hr+k

-hr+k

i=1 k=0

остается доказать, что

→ 0, n → ∞,

заметив, что соотношение

) (

)

⁽X₁

X₁

h_r

-h_r

â_n

^{ h0 (a/â_n),

r = 0,

rh_r (a/â_n){h_r (X₁/a) - ν_r} + (rν_r + 1) h_r (a/â_n) , r = 0,

вытекает из (Π.1) и (Π.5).

104

Доказательство теоремы 2. Применяя теорему Крамера-Вольда

еще раз, достаточно доказать, что для любого вектора констант (c₀, c₁) ∈ R²

)

√ ((

(Π.6)

n c

β(2)n,r + c₁λ⁽²⁾

- (c₀β + c₁λ)

→c₀η1,r + c₁η2,r

n → ∞.

n,r

Положим

c₁g⁽²⁾(x₁,x₂) - c₀g⁽¹⁾(x₂,x₃)

g(x₁, x₂, x₃) = c₀r +

g⁽³⁾(x₁,x₂,x₃)

где функции g⁽¹⁾, g⁽²⁾ и g⁽³⁾ те же, что и в (11)-(13). Используя (10) и (14)-(15),

получаем, что

(

)

c₀

β(2)n,r + c₁λ⁽²⁾

n,r

- (c₀β + c₁λ) = g (ν_n,r, νn,r+1, νn,r+2) - g (ν_r,νr+1,νr+2).

Пусть g^′ℓ(x₁, x₂, x₃) обозначает частную производную g относительно x_ℓ. Мож-

но проверить, что

(

)

(

)

νr+2

νr+1 + ν2r+1 - νr+2

νr+1

νr+2 - νr+1 - ν2r+1

g′1 (ν_r,νr+1,νr+2) = c₀

(

)₂

+c₁

(

)₂

ν_rνr+2 - ν2r+1

ν_rνr+2 - ν²

r+1

2νr+1νr+2 - ν2r+1 - ν_rνr+2 - 2ν_rνr+1νr+2

g′2 (ν_r,νr+1,νr+2) = c₀

(

)₂

ν_rνr+2 - ν²

r+1

ν_rνr+1 - ν2r+1 + ν_rν2r+1 - ν_rνr+2 + ν2rνr+2

+c₁

(

)₂

ν_rνr+2 - ν²

r+1

νr+1 (ν_r - νr+1 + ν_rνr+1)

ν_r (νr+1 - ν_r - ν_rνr+1)

g′3 (ν_r,νr+1,νr+2) = c₀

(

)₂

+c₁

(

)₂

ν_rνr+2 - ν2r+1

ν_rνr+2 - ν²

r+1

Используя дельта-метод (см., например, теорему 3.1 в [18]), находим, что

√

n (g (ν_n,r, νn,r+1, νn,r+2) - g (ν_r, νr+1, νr+2)) сходится по распределению к

сл.в., имеющей нормальное распределение с математическим ожиданием 0

и дисперсией

⎛

⎞

ρ_r,r

ρr,r+1

ρr,r+2

G^⎝ ρr,r+1 ρr+1,r+1 ρr+1,r+2

⎠GT =

ρr,r+2

ρr+1,r+2

ρr+2,r+2

= c²⁰σ211,r(β,λ) + 2c₀c₁σ12,r(β,λ) + c²¹σ222,r(β,λ),

где σ211,r(β, λ), σ12,r(β, λ), σ222,r(β, λ) даны в (19)-(21), а

(

)

g′1 (ν_r,νr+1,νr+2) g′2 (ν_r,νr+1,νr+2) g′3 (ν_r,νr+1,νr+2)

Остается заметить, что сл.в. c₀η1,r + c₁η2,r распределена по нормальному за-

кону со средним 0 и дисперсией c²⁰σ211,r(β, λ) + 2c₀c₁σ12,r(β, λ) + c²¹σ222,r(β, λ).

105

Доказательство теоремы 3 опущено, так как оно аналогично доказатель-

ству теоремы 2.

Доказательство предложения 1. Положим J(y) = F^←a,β (1- y)

F^←a,θ(1-y),

0 < y ≤ 1. Имеем

(

)

dJ(y)

y1/β

Отсюда немедленно следует, что для c ≥ 1 функция J(y) строго возрастает

на (0, 1). Это вместе с J(1) = 0 дает J(y) > 0 для 0 < y < 1. Таким образом,

=F˜^←a,θ(1 - U) или, что эквивалентно, сл.в. V имеет

смещенную экспоненциальную ф.р. F_θ(x - a), x ≥ a.

Пусть 0 < c < 1. Уравнение J(y) = 0 может быть переписано как

{

}

(Π.7)

−cy-1/β exp

-cy-1/β

= -cexp{-c}.

Поскольку -1/e < -c exp{-c} < 0 для любого 0 < c < 1, уравнение (Π.7) име-

ет два корня:

(

)_-β

(

)_-β

y₀ =

- (1/c)W-1 (-c exp{-c})

и y₁ =

- (1/c)W₀ (-c exp{-c})

Применяя тождество W₀ (-c exp{-c}) = -c, получим y₁ = 1. Используя стро-

гое неубывание W-1(x), -1/e < x < 0, можно проверить, что J(y) > 0 выпол-

нено для 0 < y < y₀ и J(y) < 0 для y₀ < y < 1. Тогда для x ≥ a имеем

P(V ≤ x) =

(

)

(

)

F^←a,θ(1 - U) ≤ x, 0 < U < y₀

F^←a,β(1 - U) ≤ x, y₀ ≤ U < 1

(

)

=P 0<U <y₀, 1

Fa,θ(x) ≤ U < 1 + P(max{y0,1 - Fa,β(x)} ≤ U < 1).

Доказательство предложения 1 можно завершить, заметив, чт

F^←a,θ(1 - y₀) =

= F^←a,β(1 - y₀) = -(a/c)W-1 (-cexp{-c}) и используя

{

(

)

F^←a,θ(1 - y₀),

P 0<U <y₀, 1

Fa,θ(x) ≤ U < 1

y₀ - 1

Fa,θ(x), x

F^←a,θ(1 - y₀),

^{ Fa,β(x), x <

(1 - y₀),

a,β

P (max {y₀, 1 - F_a,β (x)} ≤ U < 1) =

1 - y₀, x ≥ F^←a,β(1 - y₀).

СПИСОК ЛИТЕРАТУРЫ

1. Pareto V. The New Theories of Economics // J. of Political Economy. 1897. V. 5.

No. 4. P. 485-502.

2. Vere-Jones D., Robinson R., Yang W.Z. Remarks on the accelerated moment release

model: problems of model formulation, simulation and estimation // Geophys. J. Int.

2001. V. 144. P. 517-531.

106

Kagan Y.Y. Seismic moment distribution revisited: I. Statistical results // Geophys.

J. Int. 2002. V. 148. P. 520-541.

Kagan Y.Y., Schoenberg F. Estimation of the upper cutoff parameter for the tapered

Pareto distribution // J. Appl. Probab. 2001. V. 38A. P. 158-175.

Foss S., Korshunov D., Zachary S. An Introduction to Heavy-Tailed and

Subexponential Distributions. New York: Springer, 2011.

Cumming S.G. A parametric model of the fire-size distribution // Canad. J. Forest

Res. 2001. V. 31. No. 8. P. 1297-1303.

Schoenberg F.P., Peng R., Woods J. On the distribution of wildfire sizes //

Environmetrics. 2003. V. 14. P. 583-592.

Swetnam T.L., Falk D.A., Lynch A.M., Yool S.R. Estimating individual tree mid-

and understory rank-size distributions from airborne laser scanning in semi-arid

forests // Forest Ecology and Management. 2014. V. 330. P. 271-282.

Meerschaert M.M., Roy P., Shao Q. Parameter estimation for tempered power law

distributions // Communications in Statistics — Theory and Methods. 2012. V. 41.

P. 1839-1856.

10.

Jameson G.J.O. The incomplete gamma functions // Math. Gazette. 2016. V. 100.

P. 298-306.

11.

Baricz

Á., Ismail M.E.H. Turán Type Inequalities for Tricomi Confluent

Hypergeometric Functions // Constructive Approximation. 2013. V. 37. P. 195-221.

12.

Beals R., Szmigielski J. Meijer G-Functions: A Gentle Introduction // Notices of the

American Mathematical Society. 2013. V. 60. P. 866-872.

13.

Devroye L. Non-Uniform Random Variate Generation. New York: Springer-Verlag,

1986.

14.

Geist E.L., Parsons T. Undersampling power-law size distributions: effect on the

assessment of extreme natural hazards // Nat. Hazards. 2014. V. 72. P. 565-595.

15.

Corless R.M., Gonner G.H., Hare D.E., Jeffrey D.J., Knuth D.E. On the Lambert

W Function // Advances in Computational Mathematics. 1996. V. 5. P. 329-359.

16.

Arnold B.C., Balakrishnan N., Nagaraja H.N. A first course in order statistics. New

York: Wiley, 1992.

17.

Bilingsley P. Probability and Measure. New York: Wiley, 1995.

18.

Van der Vaart A.W. Asymptotic Statistics. Cambridge: Cambridge University Press,

2000.

Статья представлена к публикации членом редколлегии А.И. Михальским.

Поступила в редакцию 19.11.2020

После доработки 26.02.2021

Принята к публикации 16.03.2021

107