Автоматика и телемеханика, № 8, 2021
Робастное, адаптивное и сетевое
управление
© 2021 г. В.Ф. СОКОЛОВ, д-р физ.-мат. наук (sokolov@ipm.komisc.ru)
(Коми научный центр УрО РАН, Сыктывкар)
АДАПТИВНОЕ ОПТИМАЛЬНОЕ СЛЕЖЕНИЕ
ДЛЯ ДИСКРЕТНОГО МИНИМАЛЬНО-ФАЗОВОГО ОБЪЕКТА
С НЕОПРЕДЕЛЕННОСТЬЮ В КАНАЛЕ ВЫХОДА
Рассматриваются задачи адаптивного оптимального слежения для ми-
нимально-фазового объекта с дискретным временем, неопределенностью
в канале выхода и ограниченным внешним возмущением. Коэффициен-
ты уравнения линейной стационарной номинальной модели, коэффици-
ент усиления неопределенности и верхняя граница внешнего возмущения
предполагаются неизвестными, а показателем качества служит наихуд-
шая асимптотическая ошибка слежения. Показано, что постановка оп-
тимальной задачи зависит от априорной информации об ограниченном
задающем сигнале. Решение задач базируется на полиэдральном оцени-
вании всех неизвестных параметров и использовании показателя качества
задачи слежения как идентификационного критерия для вычисления те-
кущих оптимальных оценок. Работоспособность и эффективность предло-
женных алгоритмов управления иллюстрируются результатами числен-
ного моделирования.
Ключевые слова: адаптивное робастное управление, оптимальное управ-
ление, ограниченное возмущение, верификация модели.
DOI: 10.31857/S0005231021080055
1. Введение
Первоначальный период бурного развития теории робастного управления
пришелся на 1980-90-е годы. При этом основной поток публикаций относился
к H∞-постановке задачи, имеющей классические частотные и статистические
интерпретации [1, 2]. Предметом теории робастного управления являются си-
стемы с неопределенностью, под которой понимается не внешнее возмущение
или помеха измерений, а неточность самой модели (немоделируемая дина-
мика, малые нелинейности или нестационарность). В начале 1992 г. вышел
первый спецвыпуск одного из ведущих журналов по теории автоматического
управления IEEE TAC [3], посвященный ставшей сверхактуальной проблеме
идентификации для робастного управления. Три основные проблемы были
таковы: 1) теория робастного управления была детерминированной, а теория
идентификации — в основном стохастической; 2) как вычислять номиналь-
ную модель по данным измерений; 3) как определить доли неопределенности
108
и внешнего возмущения в суммарном возмущении. Эти важнейшие пробле-
мы обсуждались ведущими мировыми экспертами на семинаре по иденти-
фикации систем и робастному управлению [4], на котором специалисты по
идентификации призывали к разработке стохастической теории робастно-
го управления, а специалисты по робастному управлению — к разработке
теории идентификации без привлечения априорных статистических гипотез.
Проблемы идентификации для робастного управления остаются актуальны-
ми до настоящего времени, о чем свидетельствуют, в частности, последующие
регулярные спецвыпуски ведущих мировых журналов [5-7]. Однако до на-
стоящего времени в публикациях по этому направлению задачи оценивания
номинальной модели и квантификации неопределенности и внешнего возму-
щения рассматриваются в стохастической офлайн постановке и вне контекста
задач управления и поэтому не могут быть применены в задачах адаптивного
управления, где указанные оценивание и квантификация должны осуществ-
ляться в онлайн режиме (ограничимся ссылками [8, 9] на публикации двух
ведущих мировых экспертов Л. Льюнга и Г. Гудвина и соавт.).
Многие практические задачи управления формулируются в терминах до-
пусков на отклонения выхода системы управления от задающего сигнала.
Таким задачам соответствует ℓ1-теория робастного управления, основы кото-
рой были заложены в [10, 11]. Сигнальным пространством в ℓ1-теории в слу-
чае дискретного времени является пространство ограниченных вещественных
последовательностей ℓ∞, внешнее возмущение предполагается ограниченным
и качество управления оценивается в терминах супремум нормы этого про-
странства. Оказалось, что в этой теории можно получить более продвинутые
по сравнению с H∞-теорией результаты по анализу робастной устойчивости,
оценке качества и синтезу оптимального управления [11-14], что открывает
возможности ставить и решать задачи адаптивного робастного управления в
оптимальной постановке. Решению одной из таких задач в рамках ℓ1-теории
робастного управления посвящена настоящая работа.
Системы с ограниченным внешним возмущением породили множественное
оценивание неизвестных параметров, характеризующих номинальную модель
управляемого объекта. Для моделей, аффинных относительно оцениваемых
параметров, из предположения об ограниченности внешнего возмущения из-
вестной константой следует, что множество параметров, согласованных с дан-
ными измерений на некотором промежутке времени, является ограниченным
многоугольником в пространстве параметров. Сложность описания этих мно-
гоугольников растет с ростом объема данных измерений, и сотни статей по
идентификации таких моделей начиная с 1970-х и до настоящего времени, в
том числе некоторые статьи в недавнем спецвыпуске [7], посвящены построе-
нию более простых для вычислений верхних или нижних аппроксимаций этих
многоугольников. В зарубежной литературе это направление в идентифика-
ции систем получило названия set-membership approach и unknown but bounded
disturbance. Как и в случае H∞-теории, при наличии неопределенности зада-
чи квантификации неопределенности и внешнего возмущения в рамках это-
го подхода, как правило, рассматриваются при фиксированной номинальной
модели, в офлайн постановке и вне контекста задачи управления. А под опти-
мальной идентификацией может подразумеваться, например, офлайн вычис-
ление модели с минимальной верхней границей неопределенности при фикси-
109
рованной априорной верхней границе внешнего возмущения (или наоборот),
как, например, в [15] для систем с ограниченным внешним возмущением или
в [16] — в H∞-постановке.
Настоящая работа посвящена решению задачи синтеза адаптивного опти-
мального слежения для минимально-фазового объекта с неопределенностью
в канале выхода и с ограниченным внешним возмущением. Показателем каче-
ства служит наихудшая по возмущениям асимптотическая ошибка слежения.
Коэффициенты уравнения линейной стационарной минимально-фазовой но-
минальной модели, коэффициент усиления неопределенности и верхняя гра-
ница внешнего возмущения предполагаются неизвестными и оцениваются в
режиме онлайн. Для построения адаптивного оптимального управления ис-
пользуется метод рекуррентных целевых неравенств [17], дополненный двумя
ключевыми идеями: 1) выбора показателя качества задачи управления как
идентификационного критерия и 2) использования множественных оценок
неизвестных параметров. Это подход был первоначально предложен для за-
дачи адаптивной оптимальной стабилизации в [18, 19] для систем только с
ограниченным возмущением и был обобщен на робастные системы в [20, 21].
Для рассматриваемой системы с неопределенностью только в канале выхода
показатель качества задачи слежения является дробно-рациональной функ-
цией нормы внешнего возмущения и коэффициента усиления неопределен-
ности, благодаря чему вычисление текущих оптимальных оценок сводится к
задаче линейного программирования, для которой имеется современное эф-
фективное программное обеспечение. Это позволяет довести общий метод
синтеза адаптивного оптимального робастного управления [20, 21] до числен-
ной реализации в более общей и существенно более сложной задаче слежения
и помимо алгоритма полиэдрального оценивания, сохраняющего почти пол-
ную информацию о всех оцениваемых параметрах, предложить новый, менее
затратный для вычислений, алгоритм с заранее выбираемым числом сохра-
няемых в памяти регулятора информационных неравенств. Приведенные в
статье результаты моделирования на примере модели с девятью оцениваемы-
ми параметрами иллюстрируют эффективность обоих алгоритмов.
Подчеркнем важные особенности рассматриваемой задачи.
1) Все неизвестные параметры в рассматриваемой задаче неидентифици-
руемы и решение рассматриваемой оптимальной задачи на базе других иден-
тификационных критериев недостижимо (см. раздел 3.1).
2) Показатель качества в виде наихудшей асимптотической ошибки сле-
жения зависит от верхнего предела модуля задающего сигнала. Поэтому в
условиях неидентифицируемости неизвестных параметров постановка опти-
мальной задачи зависит от априорной информации о задающем сигнале. Эта
зависимость ранее не обсуждалась в работах по идентификации для робаст-
ного управления даже в офлайн постановке.
Обозначения:
|ϕ| - евклидова норма вектора ϕ ∈ Rn, dim ϕ := n - размерность ϕ;
ℓ∞ - нормированное пространство ограниченных вещественных последова-
тельностей x = (x0, x1, x2, . . .) с нормой ∥x∥ = supt |xt|;
∥x∥ss = lim supt→+∞ |xt|;
110
∑+∞
∥G∥ =
|gk| - индуцированная норма линейной стационарной системы
k=0
∑+∞
G : ℓ∞ → ℓ∞ с устойчивой передаточной функцией G(λ) =
gkλk.
k=0
2. Постановка задачи
Пусть управляемый объект описывается моделью с дискретным временем
(2.1)
a(q-1)yt+1 = b(q-1)ut + vt+1
,
t = 0,1,2,... ,
где yt, ut, vt ∈ R - соответственно измеряемый выход объекта, управление
и суммарное возмущение в момент времени t, q-1 - оператор сдвига назад
(q-1xt := xt-1) и
a(λ) = 1 + a1λ + . . . + anλn, b(λ) = b1 + b2λ + . . . + bmλm-1.
Априорная информация об объекте состоит из предположений:
П.1. Неизвестный вектор-столбец коэффициентов модели принадлежит из-
вестному ограниченному многограннику Ξ,
{
}
ξ := (a1, . . . , an, b1, . . . , bm)⊤ ∈ Ξ =
ξ |
ξ≥p
⊂Rn+m,
P ∈Rl×(n+m), p∈Rl,
и для любого ξ ∈ Ξ b1 = 0, корни полинома b(λ) лежат вне замкнутого единич-
ного круга {z ∈ C | |z| ≤ 1} (такие полиномы называются устойчивыми, а со-
ответствующие им модели - минимально-фазовыми) и sup ∥(a(λ)∥∥1/b(λ)∥ ≤
ξ∈Ξ
≤ Cu < +∞ с известной верхней границей Cu.
П.2. Неизвестное суммарное возмущение v удовлетворяет ограничению
(2.2)
|vt| ≤ δw + δypt, pt = max
|ys
|
∀t,
t-μ≤s<t
где δw ≥ 0 и δy ≥ 0 неизвестны и δy ≤δy < 1 с известной верхней границейδy.
В терминах ℓ1-теории робастного управления число δw характеризует
ℓ∞-норму неизвестного ограниченного внешнего возмущения в объекте
управления, а число δy - коэффициент усиления неизвестной неопределен-
ности в канале выхода, описываемой в виде линейного нестационарного или
нелинейного строго причинного оператора на пространстве выходов y. Па-
мять μ в ограничении на неопределенность выбирается конструктором исхо-
дя из априорной информации об объекте управления и может быть выбрана
сколь угодно большой, но не бесконечной, без ущерба для гарантируемого
качества управления. Ограниченность памяти неопределенности по выходу
обеспечивает независимость асимптотического качества замкнутой системы
управления от начальных данных [13], что необходимо для синтеза адаптив-
ного управления.
Введем обозначение
θ := (ξ⊤, δy, δw)⊤
для вектора всех неизвестных конструктору параметров модели (2.1).
111
Пусть y∗ = (y∗1, y∗2, . . .) - ограниченный задающий сигнал задачи слежения
и в момент времени t известно значение y∗t+1. Показателем качества управ-
ления будет служить наихудшая по всем допустимым предположением П.2
возмущениям v асимптотическая ошибка слежения
Jμ(θ,y∗) := sup
∥y - y∗∥ss = sup lim sup |yt - y∗t|.
v
v
t→+∞
Из уравнения (2.1) следует, что для модели с известным вектором коэф-
фициентов ξ и любыми начальными значениями y-n+1, . . . , y0, u-m+1, . . . , u0
регулятор
(2.3)
b(q-1)ut = (a(q-1) - 1)yt+1 + y∗t+1
обеспечивает равенство
yt+1 - y∗t+1 = vt+1
и, следовательно, является оптимальным для показателя качества Jμ(θ, y∗)
в силу непредсказуемости возмущения vt+1.
Для формулировки теоремы об оценке показателя качества Jμ(θ, y∗) при
использовании оптимального регулятора (2.3) понадобится следующее опре-
деление.
Определение 1. Будем говорить, что последовательность |y∗t| равно-
мерно часто попадает в окрестности своего верхнего предела, если для лю-
бого ε > 0 существуют число N и подпоследовательность {tj }∞j=1 последо-
вательности натуральных чисел такие, что
∀j ( tj+1 - tj ≤ N
∧ |y∗t
| ≥ ∥y∗∥ss - ε ).
j
Теорема 1. Для модели
(2.1) с известным вектором коэффициен-
тов ξ, удовлетворяющей предположениям П.1, П.2 и замкнутой регулято-
ром (2.3),
δw + δy∥y∗∥ss
Jμ(θ,y∗) ≤ J(θ,y∗) :=
,
1-δy
и
Jμ(θ,y∗) ↗ J(θ,y∗) (μ → +∞),
если последовательность |y∗| равномерно часто попадает в окрестности
своего верхнего предела (знак ↗ обозначает монотонную сходимость сни-
зу).
Теорема 1 следует из теорем 3 и 8 [13], примененных к замкнутой си-
стеме (2.1), (2.3). Отметим, что условие 0 ≤ δy < 1 является необходимым и
достаточным условием робастной стабилизируемости модели (2.1) в классе
линейных стационарных регуляторов при μ → +∞ (см. детали в [11]).
Формула для показателя качества J(θ, y∗) в теореме 1 позволяет сформу-
лировать следующую задачу адаптивного субоптимального робастного сле-
жения.
112
Задача 1. Пусть объект управления удовлетворяет уравнению модели
(2.1) с неизвестным вектором параметров θ и известно значение ∥y∗∥ss.
Требуется построить причинную обратную связь, гарантирующую с задан-
ной точностью неравенство
∥yt - y∗t∥ss ≤ J(θ, y∗).
Значение ∥y∗∥ss доступно, например, в случае постоянного или периоди-
ческого задающего сигнала y∗, но в общем случае может быть неизвестным.
Если известна некоторая верхняя оценка Y∗ неизвестного (и заведомо не
идентифицируемого) значения ∥y∗∥ss, то задача синтеза адаптивного опти-
мального робастного слежения формулируется в виде
Задача 2. Пусть объект управления удовлетворяет уравнению модели
(2.1) с неизвестным вектором параметров θ и известна верхняя граница Y∗
неизвестного значения ∥y∗∥ss. Требуется построить причинную обратную
связь, гарантирующую с заданной точностью неравенство
∗
δw + δyY
∥yt - y∗t∥ss ≤ J2(θ, Y∗) :=
1-δy
Если неизвестна и верхняя граница Y∗, то задача синтеза адаптивного
оптимального робастного слежения формулируется в виде
Задача 3. Пусть объект управления удовлетворяет уравнению модели
(2.1) с неизвестным вектором параметров θ и информация о задающем сиг-
нале y∗ заключается в его ограниченности. Требуется построить причин-
ную обратную связь, гарантирующую с заданной точностью неравенство
δw + δy∥y∗∥
∥yt - y∗t∥ss ≤ J3(θ, y∗) :=
1-δy
Далее будет описано решение задачи 1. Решение задач 2 и 3 аналогично
(см. замечание 3 в разделе 3.2).
Специфика, нетрадиционность и сложность сформулированных задач за-
ключаются в их оптимальной постановке в условиях неидентифицируемости
не только вектора коэффициентов ξ, но и коэффициента усиления неопре-
деленности δy и нормы внешнего возмущения δw. Необходимость оценивания
параметров δy и δw для решения сформулированных задач становится понят-
ной из следующего вопроса. Предположим, что неизвестный объект управ-
ляется оптимальным регулятором, но конструктору это не известно. Как при
априорных предположениях П.1, П.2 конструктор, измеряя выход объекта,
может судить об оптимальности регулятора, если параметры δy и δw не из-
вестны?
Ответ на этот частный вопрос кроется в понимании используемого подхода
к синтезу адаптивного оптимального управления (см. раздел 3.1), вытекаю-
щего из того, что при априорных предположениях П.1, П.2 исчезает поня-
тие “истинного” вектора коэффициентов ξ номинальной модели. Эти пред-
положения соответствует принципу неопределенности, сформулированному
Р.Е. Калманом в [22, с. 30]:
113
“(2.1) П р и н ц и п н е о п р е д е л е н н о с т и . Неточные (недо-
стоверные) данные → неединственная (недостоверная) система.”
Этот принцип выдвинут как альтернатива стандартной статистической
априорной гипотезе [22, с. 31]:
“(i) Вся неопределенность порождается жестко фиксированным аб-
страктным вероятностным механизмом (зачастую очень простого
вида).
(ii) Все данные получены путем независимого выбора из фиксированной
стационарной генеральной совокупности, управляемой абстрактным ве-
роятностным механизмом.”
3. Синтез адаптивного управления
В этом разделе описано решение всех поставленных задач. Для их реше-
ния используется идентификационный подход, согласно которому по данным
измерений вычисляются оценки неизвестного вектора коэффициентов ξ и в
каждый момент времени применяется оптимальный регулятор (2.3), соответ-
ствующий текущей оценке.
3.1. Выбор идентификационного критерия в оптимальной задаче
в условиях неидентифицируемости объекта
Вся новая информация о векторе ξ, получаемая в момент времени t + 1
после измерения выхода yt+1, заключается в неравенстве
(3.1)
a(q-1)yt+1 - b(q-1)ut≤δw + δypt+1,
вытекающем из уравнения модели (2.1) и ограничения на суммарное воз-
мущение (2.2). Каждое неравенство (3.1) состоит из пары линейных нера-
венств относительно вектора параметров θ. Для каждого конкретного век-
тора θ только одно из этих двух линейных неравенств может нарушаться, и
для краткости будем называть его неравенством (3.1), соответствующим
вектору θ. Метод рекуррентных целевых неравенств синтеза адаптивного
управления базируется на следующем простом утверждении.
Утверждение 1. Если для некоторой оценки
θ=
ξ⊤,δy,δw)⊤,
ξ ∈ Ξ,
0≤δy ≤δy,
0≤δw,
неравенства (3.1), соответствующие этому вектору, выполняются при
θ
всех достаточно больших t, то модель (2.1) с вектором параметров
удовлетворяет априорным предположениям П.1, П.2 при всех достаточно
больших t.
Полная информация о неизвестном векторе θ к моменту времени t имеет
вид
{
}
(3.2)
θ ∈ Θmaxt :=
θ∈Θ0
|â(q-1)yk+1 - b(q-1)uk| ≤ δw + δypk+1 ∀k < t
,
114
где
{
}
θ
Θ0 :=
ξ ∈ Ξ, 0 ≤ δy ≤ δy,δw ≥ 0
— априорное множество допустимых неизвестных параметров. Множество
Θmaxt в любой момент времени t включает те и только те оценкиθ из апри-
орного множества Θ0, которые согласованы с уравнением модели (2.1), апри-
орными предположениями П.1, П.2 и с измерениями на промежутке [0, t],
и является полиэдром (многогранником) в пространстве оценокθ. С ростом
времени полиэдры Θmaxt убывают по включению ввиду добавления новых
неравенств.
Утверждение 2. При любом управлении объектом (2.1) на любом про-
межутке [0,t], для любог
ξ ∈ Ξ и любого δy ≥ 0
(3.3)
θ=
ξ⊤,δy,δw)⊤ ∈ Θmaxt
при всех достаточно большихδw.
Утверждение 2 очевидно следует из неограниченного роста правой части
неравенств (3.1) при неограниченном возрастании δw и представляет собой
строгое математическое утверждение о неидентифицируемости неизвестно-
го вектора параметров θ при априорных предположениях П.1, П.2. Если пы-
таться решать задачу 1 с помощью какого-либо алгоритма оценивания, обес-
печивающего сходимость оценок к некоторому предельному значению θ∞, и
использования оптимального регулятора для вычисляемых оценок, то зада-
ча 1 будет решена, если вектор θ∞ будет удовлетворять неравенствам (3.1)
при всех достаточно больших t и
(3.4)
J (θ∞, y∗) ≤ J(θ, y∗
).
Поскольку вектор параметров θ управляемой модели неизвестен и никакой
вектор коэффициентов (от которого и зависит выбор регулятора
ξ ∈ Ξ не
может быть сфальсифицирован данными измерений в силу включения (3.3),
т.е. может оказаться вектором коэффициентов ξ управляемой модели, клю-
чевое неравенство (3.4) диктует выбор текущих оптимальных оценок в виде
(3.5)
θoptt = argmin
J(θ, y∗
).
θ∈Θmax
t
Таким образом, использование показателя качества J задачи управления как
идентификационного критерия диктуется постановкой задачи адаптивного
оптимального управления, если решение ищется с помощью сходящихся оце-
нок.
3.2. Синтез на основе полиэдрального оценивания
Прямое применение оптимального оценивания (3.5) невозможно ввиду
потенциально не ограниченного роста числа неравенств в описании множе-
ственных оценок Θmaxt и сложности оценки качества нелинейной замкнутой
115
системы с оценками (3.5). Ограниченность числа изменений множественных
оценок и сходимость векторных оценок θt за конечное время можно обеспе-
чить за счет введения мертвой зоны при обновлении множественных оценок.
Платой за введение мертвой зоны будет решение только субоптимальной за-
дачи, т.е решение оптимальной задачи с заданной точностью.
Перейдем к описанию рекуррентного алгоритма оценивания и основанного
на нем адаптивного субоптимального управления. Выберем параметр мерт-
вой зоны ε > 0. В каждый момент времени t вычисляются полиэдральная
оценка Θt и векторная оценка
θt = (ξ⊤t,δy,t,δw,t)⊤
неизвестного вектора θ. Начальной полиэдральной оценкой служит априор-
ное множество Θ0, а начальной векторной оценкой - вектор θ0 = (ξ⊤0, 0, 0)⊤ с
любым ξ0 ∈ Ξ. После измерения выхода yt+1 в момент t + 1 положим
ϕt := (-yt, -yt-1, . . . , -yt-n+1, ut, . . . , ut-m+1)⊤, ηt+1 := sign(yt+1 - ϕtξt),
pt+1 = max
|ys|, ψt+1 := (ηt+1ϕ⊤t, pt+1, 1)⊤, ζt+1 := ηt+1yt+1.
t-μ≤s<t+1
В этих обозначениях неравенство (3.1), соответствующее вектору θt, эквива-
лентно неравенству
(3.6)
ψ⊤t+1θt ≥ ζt+1.
Положим
(3.7)
θt+1 := θt, Θt+1 := Θt, если ψ⊤t+1θt ≥ ζt+1 - ε|ψt+1
|.
В противном случае положим
{
}
θ
(3.8)
Θt+1 := Θt ∩ Ωt+1, Ωt+1 :=
ψ⊤t+1θ≥ζt+1 ,
(3.9)
θt+1 := argmin J(θ,y∗
).
θ∈Θt+1
Формулы (3.7) и (3.8) имеют простую геометрическую интерпретацию.
Каждое множество Θt описывается системой линейных неравенств, состоя-
щей из нескольких неравенств из описания априорного множества Θ0 и из
нескольких неравенств ψ⊤s+1 θ ≥ ζs+1, т.е. неравенств (3.1), соответствующих
некоторым предыдущим оценкам θs, s < t. Неравенство в определении полу-
пространства Ωt+1 является линейным неравенством (3.1), соответствующим
текущей оценке θt. Благодаря введению мертвой зоны обновление Θt соглас-
но (3.8) производится только в том случае, когда расстояние от вектора θt
до полупространства Ωt+1 больше параметра мертвой зоны ε. Обновленная
оценка θt+1 согласно (3.9) является оптимальной относительно идентифика-
ционного критерия J(θ, y∗) на полиэдре Θt+1.
116
Перед формулировкой теоремы о качестве адаптивного управления на ос-
нове описанного алгоритма оценивания заметим, что уравнение оптимально-
го регулятора (2.3), соответствующего вектору ξt оценок неизвестных коэф-
фициентов ξ, благодаря введению обозначения ϕt можно кратко записать в
виде уравнения
(3.10)
ϕ⊤tξt = y∗t+1
относительно компоненты ut фазового вектора ϕt. Таким образом, управле-
ние ut будет вычисляться из уравнения (3.10), которое будем называть адап-
тивным регулятором.
Теорема 2. Пусть объект управления удовлетворяет уравнению (2.1)
и априорным предположениям П.1, П.2 с неизвестным вектором пара-
метров θ = (ξ⊤,δy,δw)⊤. Пусть объект управляется адаптивным регуля-
тором (3.10) и используется алгоритм оценивания (3.7)-(3.9) с параметром
мертвой зоны ε ≤ (1 -δy)/(2(2 + Cu)). Тогда при любых начальных данных
в замкнутой системе управления (2.1), (3.10) полиэдральные оценки Θt и
векторные оценки θt не изменяются при всех достаточно больших t и
(3.11)
∥yt - y∗t∥ss ≤ J(θ∞, y∗) + Kθ∞ ε ≤ J(θ, y∗
) + Kε,
где θ∞ = (ξ⊤∞, δy,∞, δw,∞) - финальное значение оценок θt и
1+(2+∥a∞(λ)/b∞(λ)∥)∥y∗∥ss+(δw,∞+δy,∞∥y∗∥ss)(2+∥(a∞(λ)-1)/b∞(λ)∥)
Kθ∞ =
,
(1 - δy,∞ - ε(2 + ∥(a∞(λ) - 1)/b∞(λ)∥))2
4(1 + 2∥y∗∥ss + Cu + (δw,∞ +δy∥y∗∥ss)(2 + Cu))
(3.12)
K =
(1 -δy)2
Доказательство теоремы 2. Докажем, что при каждом изменении
оценки θt расстояние от θt до полупространства Ωt+1 больше ε. Действитель-
но, θt изменяется только если
ψ⊤t+1θt < ζt+1 - ε|ψt+1|.
Поскольку ψ⊤t+1 θ ≥ ζt+1 для любогоθ ∈ Ωt+1, то
|ψt+1||θ - θt| ≥ |ψ⊤t+1(θ - θt)| > ε|ψt+1|
и, следовательно, |θ - θt| > ε для любогоθ ∈ Ωt+1. Из этого следует, что после
изменения оценки Θt на оценку Θt+1 ⊂ Ωt+1 монотонно убывающая по вклю-
чению последовательность оценок Θt не будет в дальнейшем пересекаться с
ε-окрестностью точки θt ∈ Θt, при этом не попадающие в будущие оценки Θs,
s > t, ε/2-окрестности оценок θt не пересекаются. Тогда число возможных из-
менений оценок Θt и θt будет заведомо конечным, если оценки θt принимают
значения только в ограниченном множестве. Для доказательства ограничен-
ности оценок θt заметим, что θ ∈ Ωt при всех t и поэтому θ ∈ Θt при всех t.
Тогда из (3.9) следует J(θt, y∗) ≤ J(θ, y∗) при всех t, и все оценки θt лежат
117
{
}
в ограниченном множестве
θ | J(θ,y∗) ≤ J(θ,y∗) . Ввиду конечного числа
изменений оценок θt
(3.13)
∃ t∗ ∀t ≥ t∗ θt = θ∞ = (ξ⊤∞,δy,∞,δw,∞) ∧ ψ⊤t+1θ∞ ≥ ζt+1 - ε|ψt+1
|.
Неравенства (3.13) гарантируют, что при всех t ≥ t∗ и μ ≥ max(n, m)
a∞(q-1)yt+1 - b∞(q-1)ut≤δw,∞ + δy,∞pt+1 + ε|ψt+1| ≤
(
)
(3.14)
δw,∞ + δy,∞pt+1 + ε
|ytt-n+1| + |utt-m+1| + pt+1 + 1
≤
δw,∞ + ε + (δy,∞ + 2ε)pt+1 + ε
utt-m+1
.
Неравенства (3.14) позволяет рассматривать выход y для всех t ≥ t∗ как вы-
ход модели (2.1) с параметрами ξ∞, δy,∞ + 2ε, δw,∞ + ε вместо ξ, δy, δw со-
ответственно и с дополнительной неопределенностью в канале управления,
соответствующей слагаемому ε|utt-m+1| с коэффициентом усиления ε. Тогда
по теореме 8 [13]
δw,∞ + ε + (δy,∞ + 2ε + ε∥a∞(λ)/b∞(λ)∥)∥y∗∥ss
(3.15)
∥yt - y∗t∥ss ≤
1 - (δy,∞ + 2ε) - ε∥(a∞(λ) - 1)/b∞(λ)∥
Из определения (3.9) оптимальных оценок θt и включений θ ∈ Θt при всех t
следует ключевое неравенство
(3.16)
J (θ∞, y∗) ≤ J(θ, y∗
).
Для сравнения верхней оценки (3.15) и J(θ∞, y∗) и вычисления постоян-
ной Kθ∞ в (3.11) достаточно воспользоваться неравенством
C1 + ε1
C1
C2ε1 + C1ε2
ε1 + C1ε2
-
=
≤
C2 - ε2
C2
C2(C2 - ε2)
(C2 - ε2)2
с параметрами
C1 = δw,∞ + δy,∞∥y∗∥ss, ε1 = ε(1 + (2 + ∥a∞(λ)/b∞(λ)∥)∥y∗∥ss),
C2 = 1 - δy,∞ ≤ 1, ε2 = ε(2 + ∥(a∞(λ) - 1)/b∞(λ)∥).
Формула для постоянной K из неравенства (3.11) следует из формулы
для Kθ∞ после применения неравенств
∥a∞(λ)/b∞(λ)∥ ≤ Cu,
∥(a∞(λ) - 1)/b∞(λ)∥ ≤ Cu,
ε(2 + Cu) ≤ (1 -δy)/2.
Наконец, из неравенств Kθ∞ ≤ K и (3.16) следует справедливость правого
неравенства в (3.11). Теорема доказана.
118
Замечание 1. Последнее неравенство в (3.11) гарантирует решение за-
дачи 1 с неизвестной верхней оценкой J(θ, y∗) + Kε. Оно же позволяет оце-
нивать эту неизвестную верхнюю оценку снизу. Действительно, вычисляе-
мые в каждый момент времени текущие оптимальные значения показателя
качества J(θt, y∗), не сфальсифицированные данными измерений на проме-
жутке [0, t], сходятся снизу за конечное, но неизвестное, время к предельно-
му значению J(θ∞, y∗). Более того, если на некотором достаточно длинном
интервале времени оценка θt не изменяется, то оценка J(θt, y∗) + Kθt ε ста-
новится верной верхней оценкой ошибки слежения, поскольку для оценки θt
выполнено уравнение модели, при этом вычисление постоянной Kθt - отно-
сительно простая задача. Если при этом вычисленное значение Kθt ε хуже
желаемой точности, значение параметра мертвой зоны ε можно уменьшить.
Замечание 2. Из способа доказательства конечности числа возможных
изменений оценок Θt и θt за счет исключения шаров радиуса ε/2 следует
грубая оценка числа возможных коррекций оценок порядка (1/ε)n+m, соот-
ветствующая методу перебора по сетке размером порядка ε. Эта оценка пред-
ставляется излишне грубой по двум причинам. Во-первых, алгоритм оценива-
ния (3.7)-(3.9) осуществляет целенаправленный перебор оценок θt в порядке
возрастания согласованного с измерениями показателя качества J(θt, y∗) и,
во-вторых, накопление информации о неизвестных параметрах идет наиболее
эффективно, при этом из полиэдральных оценок исключаются не просто ша-
ры, а “максимальные” не согласованные с измерениями области в простран-
стве оценокθ. Результаты моделирования подтверждают излишнюю грубость
указанной выше экспоненциальной по размерности dim ξ оценки, однако по-
лучение более адекватной алгоритму (3.7)-(3.9) верхней оценки числа воз-
можных коррекций Θt и θt является открытой математической задачей.
Замечание 3. Решение задачи 2 обеспечивается тем же алгоритмом оце-
нивания, что и решение задачи 1, после замены показателя качества J(θ, y∗)
в (3.9) показателем качества J2(θ, Y ∗). Для решения задачи 3 показатель ка-
чества J(θ, y∗) в (3.9) следует заменить показателем качества
δw +δySt+1
J3(θ,y∗) =
,
St+1 := sup |y∗k|,
1-δy
k≤t+1
где St+1 вычисляется рекуррентно: St+1 = max(St, |y∗t+1|). Последователь-
ность St монотонно снизу сходится к ∥y∗∥, что гарантирует справедливость
аналогичного (3.16) ключевого неравенства для показателя качества J3(θ, y∗).
3.3. Синтез на основе полиэдрального оценивания
фиксированной сложности
Показатели качества во всех сформулированных в разделе 2 задачах явля-
ются дробно-линейными функциями вектора θ и, следовательно, их поверхно-
сти уровня — гиперплоскости в пространстве оцениваемых параметров. Это
обстоятельство открывает возможность использования полиэдральных оце-
нок с фиксированным числом линейных неравенств.
Алгоритм полиэдрального оценивания c N неравенствами. Выберем число
N ≥ n + m + 2 = dimθ линейных неравенств (3.6), используемых для описа-
119
ния полиэдральных оценок ΘNt , и параметр мертвой зоны ε > 0. В качестве
начальной оценки θ0 выберем любую из вершин априорного полиэдра Θ0 ви-
да θ0 = (ξ⊤0, 0, 0)⊤. При этом ξ0 будет одной из вершин априорного множества
коэффициентов Ξ и
J (θ0, y∗) = 0 = min J(θ, y∗).
θ∈Θ0
В качестве начальной полиэдральной оценки ΘN0 возьмем Rn+m+2, т.е. описа-
ние ΘN0 не содержит ни одного неравенства (3.6). Пусть θt - векторная оценка
и ΘNt - полиэдральная оценка неизвестного вектора θ в момент t. После из-
мерения выхода yt+1 в момент t + 1 положим
(3.17)
θt+1 := θt, ΘNt+1 := ΘNt, если ψ⊤t+1θt ≥ ζt+1 - ε|ψt+1
|.
В противном случае положим
{
}
θ
(3.18)
θt+1 :=
argmin J(θ, y∗), Ωt+1 :=
ψ⊤t+1θ≥ζt+1
,
θ∈Θ0∩ΘNt ∩Ωt+1
где θt+1 - вершина полиэдра Θ0 ∩ ΘNt ∩ Ωt+1, являющаяся решением задачи
дробно-линейного программирования (3.18). Множественная оценка Θt об-
новляется по правилу
(3.19)
ΘNt+1 = ΘNt ∩ Ωt+1,
если число неравенств в описании ΘNt строго меньше N. Если же число нера-
венств достигло значения N, то новое неравенство (3.6) включается в описа-
ние ΘNt+1 вместо любого из неравенств в описании ΘNt , на границе которого
не лежит θt+1. В вырожденном случае, когда вершина θt+1 оказалась на гра-
нице более n + m + 2 неравенств из описания Θ0 ∩ ΘNt ∩ Ωt+1, оценка θt+1
пересчитывается по формуле (3.18) с заменой неравенства, задающего по-
лупространство Ωt+1, на ослабленное неравенство ψ⊤t+1 θ ≥ ζt+1 - ε1|ψt+1| со
сколь угодно малым ε1 > 0 для устранения вырожденного случая.
Таким образом, число неравенств в описании ΘNt увеличивается на еди-
ницу в некоторые начальные моменты времени и не изменяется, достигнув
значения N. Отметим, что вычисление оценок θt+1 согласно (3.18) - задача
дробно-линейного программирования в Rn+m+2 с не более l + 3 + N + 1 ли-
нейных ограничений (l + 3 - число неравенств в описании априорного множе-
ства Θ0). Известно (см., например, [23]), что любая задача дробно-линейного
программирования стандартным образом сводится к задаче линейного про-
граммирования посредством добавления одной вещественной переменной, од-
ного линейного неравенства и одного линейного равенства.
Теорема 3. Пусть объект управления удовлетворяет уравнению (2.1)
и априорным предположениям П.1, П.2 с неизвестным вектором парамет-
ров θ = (ξ⊤,δy,δw)⊤. Пусть объект управляется адаптивным регулятором
(3.10) с использованием алгоритма полиэдрального оценивания c N нера-
венствами и ε ≤ (1 -δy)/(2(2 + Cu)). Тогда при любых начальных данных в
замкнутой системе:
120
1) последовательность J(θt, y∗) возрастающая и
(3.20)
J (θt, y∗) = min
J(θ, y∗) ≤ J(θ, y∗
)
∀ t;
θ∈Θ0∩ΘN
t
2) если оценки ΘNt и θt не изменяются при всех достаточно больших t, то
справедливы неравенства (3.11).
Доказательство теоремы 3. Доказательство монотонности последо-
вательности J(θt, y∗) проведем индукцией по времени t. На начальном про-
межутке времени, пока количество неравенств в оценках ΘNt не достигло N,
полиэдральные оценки ΘNt убывают по включению, и возрастание после-
довательности J(θt, y∗) и равенство в (3.20) прямо следуют из (3.18) и ра-
венств Θt+1 = Θt ∩ Ωs+1. Докажем индукционный переход. Пусть возраста-
ние J(θt, y∗) имеет место до момента t включительно, справедливо равенство
в (3.20) и количество линейных неравенств в описании ΘNt равно N. В мо-
мент времени t + 1 после вычисления оценки θt+1 согласно формуле (3.18)
неравенство
J (θt+1, y∗) ≥ J(θt, y∗)
следует из включения Θ0 ∩ ΘNt ∩ Ωt+1 ⊂ ΘNt и равенства (3.20), справедливо-
го в силу индукционного предположения. Покажем, что после изменения ΘNt
на ΘNt+1
(3.21)
min
J(θ, y∗) =
min
J(θ, y∗) = J(θt+1, y∗)
θ∈Θ0∩ΘNt+1
θ∈Θ0∩ΘNt ∩Ωt+1
несмотря на замену одного из неравенств полиэдра ΘNt на неравенство,
описывающее Ωt+1. Правое равенство в (3.21) является определением θt+1
в (3.18). Пусть Ct+1
- конус с вершиной θt+1, определенный системой
n + m + 2 неравенств из описания Θ0 ∩ ΘNt ∩ Ωt+1, на границе которых ле-
жит θt+1. Тогда Θ0 ∩ ΘNt+1 ⊂ Ct+1, так как в описание Θ0 ∩ ΘNt+1 заведомо вхо-
дят неравенства, задающие конус Ct+1. Из включенийθ ∈ Θ0 ∩ ΘNt ∩ Ωt+1⊂
⊂Θ0 ∩ ΘNt+1 ⊂ Ct+1 следует
J (θt+1, y∗) =
min
J(θ, y∗) ≥ min
J(θ, y∗) ≥ min J(θ, y∗).
θ∈Θ0∩ΘNt ∩Ωt+1
θ∈Θ0∩ΘNt+1
θ∈Ct+1
Теперь для доказательства (3.21) достаточно показать, что
(3.22)
min J(θ, y∗) = J(θt+1, y∗
).
θ∈Ct+1
Это равенство следует из того, что линии уровня дробно-линейного показа-
теля качества J(θ, y∗) - гиперплоскости в Rn+m+2:
J(θ, y∗) = C
⇔
δw +δy(∥y∗∥ss + C) = C.
121
В малой окрестности θt+1 векторы из полиэдра Θ0 ∩ ΘNt ∩ Ωt+1 описываются
только неравенствами из описания конуса Ct+1 и лежат в полупространстве
{
}
θ | J(θ,y∗) ≥ J(θt+1,y∗)
Из этого следует, что конус Ct с вершиной θt+1 весь лежит в этом полупро-
странстве и, следовательно, справедливо равенство (3.22).
Доказательство второго утверждения теоремы аналогично доказательству
неравенств (3.11) в теореме 2. Теорема 3 доказана.
Замечание 4. Формально множественными оценками неизвестного век-
тора параметров θ следовало бы называть полиэдры Θ0 ∩ ΘNt , поскольку
argminˆθ∈ΘN J(θ, y∗) может оказаться вне априорного полиэдра Θ0. Однако
t
при достаточно разнообразных возмущениях такое случается на относитель-
но коротком начальном этапе настройки оценок θt, когда δyt = 0 или δwt = 0,
и с некоторого момента полиэдры ΘNt фактически оказываются множествен-
ными оценками θ. Алгоритм полиэдрального оценивания с N неравенствами
приведен выше в той форме, в какой он применялся при численном модели-
ровании, описанном в разделе 4, при этом при добавлении нового неравенства
(3.6) в оценку ΘNt+1 из описания ΘNt удалялось неравенство, граница которого
наиболее удалена от новой оценки θt+1.
Замечание 5. Второе утверждение теоремы 3 базируется на предполо-
жении о сходимости оценок за конечное время. В [24] была доказана конеч-
ная сходимость конусного алгоритма оценивания (соответствующего случаю
N = dimθ) для размерностей 2 и 3. Этот результат остается справедливым
при любом числе запоминаемых неравенств. Доказательство конечной сходи-
мости для размерностей выше трех остается открытой проблемой.
4. Моделирование
Для численного моделирования выбрана неустойчивая и минимально-
фазовая модель (2.1) с полюсами, т.е. корнями a(λ), равными 0,8, 0,9 и 0,8 ±
± 0,4 i, с нулями, т.е. корнями b(λ), равными 1,1 и 1,2 и с коэффициентом
b1 = 2. Этим параметрам соответствует (с точностью 10-4) вектор коэффи-
циентов
ξ = (-4,3611, 7,3611, -5,7292, 1,7361, 2, -3,4848, 1,5152)⊤.
Таким образом, размерность вектора оцениваемых параметров θ равна 9.
Суммарное возмущение v моделируется в виде
(4.1)
vt = wt + 0,5κt pt,
где wt, κt - последовательности независимых равномерно распределенных на
отрезке [-1, 1] случайных величин, так что δy = 0,5, δw = 1. Память неопреде-
ленности μ = 10, параметр мертвой зоны ε = 0,001. Априорные ограничения
на вектор θ имеют вид
(-9, 3, -10, -3, 0,1, -8, -3) ≤ ξ⊤ ≤ (3, 15, 2, 9, 10, 4, 9),
122
a
15
10
5
0
5
10
15
100
500
700
1000
t
б
12
10
8
6
4
2
0
20
100
200
300
400
500
700
800
900
1000
t
Рис. 1. Алгоритм (3.9): графики ошибки слежения (a) и J(θt, y∗) (б ).
где неравенство понимается покомпонентно, т.е. вектор ξ лежит в кубе
в
Rn+m со стороной 12 и
b1 ≥ 0,1,
0,8 ≥ δy ≥ 0, δw ≥ 0,
b1 - b3 ≥ 0,01, b1 - b2 + b3 ≥ 0,01, b1 + b2 + b3 ≥ 0,01.
Неравенства в нижней строке эквивалентны условию минимально-фазовости
модели, если в правых частях этих неравенств вместо 0,01 поставить нули. За-
мена нуля числом 0,01 в правых частях неравенств нижней строки дает необ-
ходимый отступ от границы множества минимально-фазовых моделей. На-
чальные значения y1, y2, y3, y4 - случайные из отрезка [-1, 1], u1, u2, u3, u4 -
нули.
Для иллюстрации поведения адаптивной системы при наихудших возму-
щениях внешнее возмущение и неопределенность на промежутке [500, 700]
имеют максимальную амплитуду,
vt+1 = (δw + δypt+1)sign(ξ⊤tϕt),
123
a
15
10
5
0
5
10
15
100
500
700
1000
t
б
15
10
5
0
0
100
200
300
400
500
700
800
900
1000
t
Рис. 2. Алгоритм (3.18): графики ошибки слежения (a) и J(θt, y∗) (б ).
максимизируя абсолютную величину выхода. Задающий сигнал y∗t =
= 10 sin(0,001 t) - периодический и ∥y∗t∥ss = 10. Пунктирные линии на гра-
фиках ошибки слежения соответствуют неизвестным конструктору адаптив-
ной системы оптимальным асимптотическим границам для ошибки слежения
±J(θ,y∗) = ±12.
Графики ошибки слежения и значений J(θt, y∗) для алгоритмов оценива-
ния (3.9) и (3.18) приводятся соответственно на рис. 1 и 2 для одинаковых
реализаций случайных начальных данных и wt и κt из (4.1). Использован-
ное при моделировании число запоминаемых неравенств N = 2 dim θ = 18 в
алгоритме оценивания (3.18) соответствует полиэдрам ΘNt , в каждом из ко-
торых вершинами являются текущая оценка θt и ее девять смежных вершин.
Число коррекций оценок для алгоритмов (3.9) и (3.18) в многочисленных
экспериментах находилось в основном в промежутках 50-70 и 60-80 коррек-
ций соответственно. Время счета в экспериментах на ноутбуке с процессором
4xIntelCore i5-7200U CPU@2,50GHz варьировалось от 1,5 до 3 сек.
124
10
5
0
5
10
100
300
500
700
1000
t
80
60
40
20
0
20
40
6
20
40
60
80
100
t
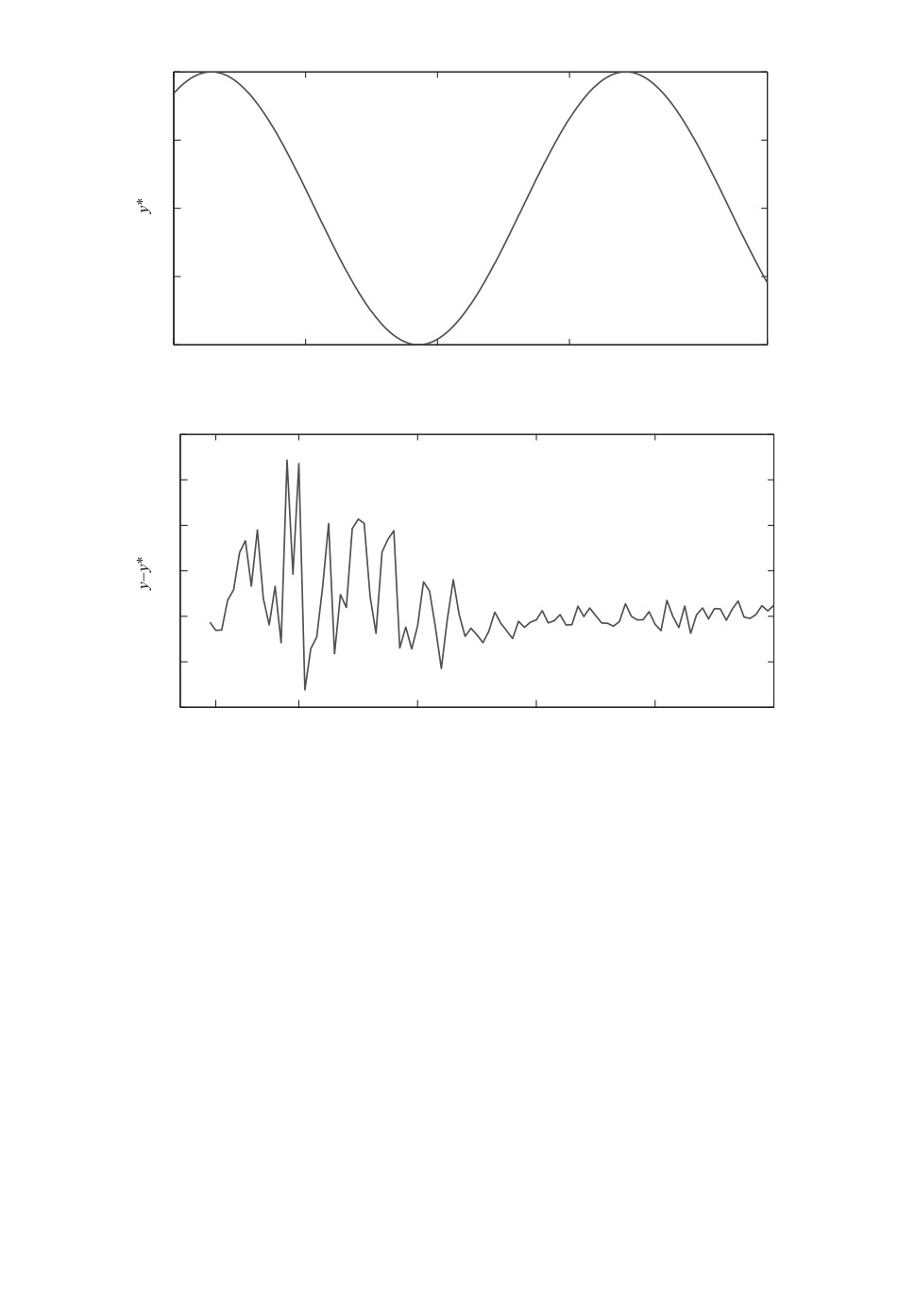
Рис. 3. График задающего сигнала y∗ и график ошибки слежения на началь-
ном промежутке [0, 100] для алгоритм (3.18).
На графиках рис. 1,б и 2,б иллюстрируется онлайн верификация текущих
оценок. В каждый момент времени t вычисляемое значение J(θt, y∗) явля-
ется, с точностью Kθt ε, верхней оценкой ошибки слежения, согласованной с
данными измерений. При этом гарантируется справедливость этой верхней
оценки, если текущая оценка θt не изменяется. Например, последней обнов-
ленной оценке алгоритма (3.9)
(
θ765 =
- 4,5459, 7,6979, -6,0380, 1,8589, 2,0574,
)⊤
- 3,6490, 1,6233, 0,3448, 3,4526
неизвестного вектора
(
θ=
- 4,3611, 7,3611, -5,7292, 1,7361, 2,0000,
)⊤
- 3,4848, 1,5152, 0,5000, 1,0000
125
соответствует J(θ765, y∗) = 10.5314 < 12 = J(θ, y∗), а последней оценке алго-
ритма (3.18)
(
θ798
- 6,1669, 11,3053, -9,1758, 3,0296, 2,7700,
)⊤
- 5,3721, 2,6408, 0,3120, 3,9614
соответствует меньшее значение J(θ798, y∗) = 10,2939, поскольку в алгорит-
ме (3.18) задействовано меньшее число целевых неравенств. Заметим, что,
несмотря на заметное различие последних оценок алгоритмов (3.9) и (3.18),
эти оценки согласованы с измерениями на финальных промежутках длиной
более 200 тактов и иллюстрируют принцип неопределенности Р.Е. Калмана.
На рис. 3 представлены графики задающего сигнала y∗ и переходного про-
цесса для алгоритма (3.18). График задающего сигнала позволяет наглядно
увидеть, как в приведенных численных экспериментах значения периодиче-
ского сигнала y∗ проявляются в виде “пульсации” ошибки слежения в уста-
новившемся режиме.
В целом результаты моделирования показали высокую эффективность
обоих алгоритмов оценивания в задаче адаптивного оптимального слежения с
9 оцениваемыми параметрами. Алгоритм оценивания (3.18) с фиксированным
числом неравенств представляется перспективным и для задач с бóльшим
числом оцениваемых параметров.
5. Заключение
Р.Е. Калман завершил свою работу [22] словами:
“Проблема шума, безусловно, является центральной проблемой всей
прикладной математики. Она должна быть разрешена при помощи ма-
тематики, а не априорной гипотезы”.
Настоящая работа посвящена проблеме оптимального управления в усло-
виях шума и соответствует процитированному в разделе 2 принципу неопре-
деленности. Для минимально-фазового объекта с неизвестным вектором ко-
эффициентов, неопределенностью в канале выхода с неизвестным коэффици-
ентом усиления и ограниченным внешним возмущением с неизвестной верх-
ней границей впервые решена задача адаптивного оптимального робастного
слежения. Показана зависимость постановки оптимальной задачи от априор-
ной информации о задающем сигнале. Решение задачи получено при мини-
мальных априорных предположениях в рамках детерминированной теории
робастного управления в ℓ1-постановке, не требует использования тестовых
или пробных сигналов и реализует максимальные возможности обратной свя-
зи. Главное достоинство предложенных алгоритмов оценивания заключает-
ся в обеспечении асимптотической субоптимальности адаптивного управле-
ния. Важнейшим, помимо оптимальности, достоинством используемого под-
хода является онлайн верификация не только текущей оценки модели, но
и априорных предположений об управляемом объекте, неопределенности и
внешнем возмущении. Такая верификация не доступна другим методам син-
теза адаптивного управления, в том числе в стохастических постановках. Ре-
зультаты численного моделирования показали эффективность предложенных
126
алгоритмов, и эти алгоритмы представляются перспективными для практи-
ческих приложений.
СПИСОК ЛИТЕРАТУРЫ
1.
Zhou K., Doyle J.C., Glover K. Robust and Optimal Control. Upper Saddle River,
New Jersey. Prentice-Hall, 1996.
2.
Поляк Б.Т., Щербаков П.С. Робастная устойчивость и управление. М.: Наука,
2002.
3.
Kosut R., Goodwin G., Polis M. (Eds.) Special issue on system identification for
robust control design // IEEE Transactions Automatic Control. 1992. V. 37. No. 7.
4.
Smith R.S., Dahleh M. (Eds.) The Modeling of Uncertainty in Control Systems
(Lecture Notes in Control and Information Sciences). V. 192. London, U.K.: Springer-
Verlag, 1994.
5.
Ljung L., Vicino A. (Eds.) Special Issue on System Identification // IEEE
Transactions on Automatic Control. 2005. V. 50. No. 10.
6.
Soderstrom T., Van Den Hof P., Wahlberg B., Weiland S. (Eds.) Special Issue on
Data-Based Modelling and System Identification // Automatica. 2005. V. 41. No. 3.
7.
Regruto D., Dabbene F. (Eds.) Special Issue on Relaxation Methods in Identification
and Estimation Problems // IEEE Transactions on Automatic Control. 2014. V. 59.
No. 11.
8.
Ljung L., Goodwin G., Agüero J.C., Chen T. Model Error Modeling and Stochastic
Embedding // IFAC-PapersOnLine. 2015. V. 48. No. 28. P. 75-79.
9.
Delgado R.A., Goodwin G.C., Carvajal R., Agüero J.C. A novel approach to model
error modelling using the expectation-maximization algorithm // In IEEE 51st
Conference on Decision and Control (CDC). 2012. P. 7327-7332.
10.
Khammash M., Pearson J.B. Performance robustness of discrete-time systems with
structured uncertainty // IEEE Trans. Automat. Control. 1991. V. AC-36. No. 4.
P. 398-412.
11.
Khammash M.H. Robust steady-state tracking // IEEE Trans. Automat. Control.
1995 V. 40. No. 11. P. 1872-1880.
12.
Khammash M.H. Robust Performance: Unknown Disturbances and Known Fixed
Inputs // IEEE Transactions on Automatic Control. 1997. V. 42. P. 1730-1P734.
13.
Соколов В.Ф. Асимптотическое робастное качество дискретной системы слеже-
ния в ℓ1-метрике // АиТ. 1999. № 1. С. 101-112.
Sokolov V.F. Asymptotic Robust Performance of the Discrete Tracking System in
the ℓ1-metric // Autom. Remote Control. 1999. V. 60. No. 1. Part 2. P. 82-91.
14.
Sokolov V.F. ℓ1 robust performance of discrete-time systems with structured
uncertainty // Syst. Control Lett. 2001. V. 42(5). P. 363-377.
15.
Smith R. Model Validation and Parameter Identification for Systems in H∞ and ℓ1 //
Proc. American Control Conf. 1992. P. 2852-2856.
16.
Bianchi F., Sánchez-Penã R. Robust identification/invalidation in an LPV
framework // Int. J. Robust Nonlinear Control. 2010. V. 20. P. 301-312.
17.
Фомин В.Н., Фрадков А.Л., Якубович В.А. Адаптивное управление динамиче-
скими объектами. М.: Наука. 1981.
18.
Sokolov V.F. Adaptive suboptimal control of a linear system with bounded
disturbances // Syst. Control Lett. 1985. V. 6. P. 93-98.
127
19. Соколов В.Ф. Адаптивное субоптимальное управление в случае ограниченной
помехи // АиТ. 1985. № 9. С. 78-86.
Sokolov V.F. Adaptive Suboptimal Control in the Case of Constrained Noise //
Autom. Remote Control. 1985. V. 46. P. 1. P. 1131-1139.
20. Соколов В.Ф. Адаптивное робастное управление дискретным скалярным объек-
том в ℓ1-постановке // АиТ. 1998. № 3. С. 107-131.
Sokolov V.F. Adaptive Robust Control of a Discrete Scalar Object in the ℓ1-state-
ment // Autom. Remote Control. 1998. V. 59. No. 3. P. 2. P. 392-411.
21. Sokolov V.F. Adaptive ℓ1 robust control for SISO system // Systems Control Lett.
2001. V. 42. P. 379-393.
22. Калман Р.Е. Идентификация систем с шумами // Успехи математических наук.
1985. Т. 40. Вып. 4(244). С. 27-41.
23. Boyd S., Vandenberghe L. Convex optimization. N.Y. Cambridge University Press.
2004.
24. Соколов В.Ф. Адаптивное минимаксное управление на основе рекуррентного ли-
нейного программирования // АиТ. 1993. № 12. С. 127-139.
Sokolov V.F. Adaptive Minimax Control Based on Recursive Linear Programming //
Autom. Remote Control. 1993. V. 54. No. 12. P. 1835-1845.
Статья представлена к публикации членом редколлегии Е.Я. Рубиновичем.
Поступила в редакцию 25.11.2019
После доработки 24.09.2020
Принята к публикации 15.01.2021
128