Автоматика и телемеханика, № 8, 2021

(Российский университет транспорта, Москва),

В.В. САПОЖНИКОВ, д-р техн. наук (port.at.pgups@gmail.com),

Вл.В. САПОЖНИКОВ, д-р техн. наук (at.pgups@gmail.com)

(Петербургский государственный университет путей сообщения

Императора Александра I, Санкт-Петербург)

ОТКАЗОУСТОЙЧИВЫЕ СТРУКТУРЫ ЦИФРОВЫХ УСТРОЙСТВ

НА ОСНОВЕ ЛОГИЧЕСКОГО ДОПОЛНЕНИЯ

Предложены новые отказоустойчивые структуры, имеющие в своем со-

ставе только один комплект исходного устройства, в отличие от извест-

ных структур с двойной и тройной модульной избыточностью. Для вы-

бора корректируемых функций в новых структурах используется блок

фиксации искаженных сигналов, строящийся на основе метода логиче-

ского дополнения с контролем вычислений по паритету. Приведена обоб-

щенная структура с коррекцией сигналов на основе логического дополне-

ния, позволяющая получать наиболее простые отказоустойчивые цифро-

вые устройства. Даны алгоритмы синтеза блоков фиксации искаженных

сигналов, а также примеры их применения.

Ключевые слова: комбинационное устройство автоматики, отказоустой-

чивая структура, структура с тройной модульной избыточностью, струк-

тура с двойной модульной избыточностью с контролем вычислений, кор-

рекция ошибок с контролем по коду паритета, метод логического допол-

нения.

DOI: 10.31857/S0005231021080079

1. Введение

При построении систем автоматики широко применяются методы обна-

ружения и коррекции ошибок в вычисленных значениях рабочих функций

блоков и компонентов [1-4]. Использование схем коррекции требует внесения

значительной избыточности, что определяется необходимостью сравнения ре-

зультатов вычислений сразу от нескольких устройств. Например, широко из-

вестна мажоритарная схема коррекции, имеющая три идентичных вычисли-

тельных блока [5-11], а также ее модификации [12-14]. Коррекция сигналов

может проводиться на различных уровнях архитектуры управляющей систе-

мы, в том числе на уровне памяти, арифметико-логических составляющих

и т.д.

В [15, 16] рассмотрены отказоустойчивые структуры для устройств комби-

национной логики, основанные на использовании известного метода логиче-

ского дополнения [17-19]. Данный метод подразумевает преобразование зна-

чений рабочих функций в значения специальных контролепригодных функ-

ций с использованием каскада сумматоров по модулю два (элементов XOR)

по правилу:

(1)

h_i = f_i ⊕ g_i

i = 1,m,

где f_i — i-я рабочая функция, g_i — функция дополнения, h_i — контролепри-

годная функция.

140

Метод логического дополнения эффективно применяется при организации

самопроверяемых схем встроенного контроля комбинационных устройств ав-

томатики по признакам принадлежности формируемых функций к функци-

ям специального вида (например, принадлежности формируемых кодовых

слов на выходах каскада преобразующих сумматоров избыточному равно-

мерному коду [20-22], принадлежности функций h_i классу самодвойственных

функций [23, 24] или же и тому и другому свойству [25, 26]).

Исследования показывают, что эффективным является использование ме-

тода логического дополнения при организации отказоустойчивых структур

цифровых устройств. Таким образом, цель статьи - показать принципиаль-

ную возможность синтеза отказоустойчивых устройств с меньшей структур-

ной избыточностью, чем при использовании традиционной структуры с трой-

ной модульной избыточностью, на основе использования схем встроенного

контроля и логического дополнения для фиксации искажаемых сигналов

на выходах объекта диагностирования, а также привести отказоустойчивые

структуры для синтеза таких устройств. Рассмотрим их подробнее.

2. Отказоустойчивые структуры на основе

двойной модульной избыточности

Наиболее распространенной отказоустойчивой структурой является

структура, основанная на принципе тройной модульной избыточности

(TMR-структура) с мажоритарной коррекцией сигналов [27]. Тройная из-

быточность структуры необходима для наделения ее свойством нечувстви-

тельности к проявлениям неисправностей в исходном устройстве в виде ис-

кажений сигналов на его выходах. Использование ее на практике приводит

к существенному увеличению сложности технической реализации конечного

устройства. Кроме того, приведенная структура имеет недостаток, связанный

с невозможностью идентификации неверно функционирующего устройства

без введения дополнительных устройств контроля.

При разработке структуры с мажоритарным принципом коррекции мо-

жет возникнуть несколько случаев. Первый случай — когда исходное устрой-

ство F (x) дается разработчику в неизменяемом виде, а его задача состоит в

разработке отказоустойчивой системы, при этом разработчик может пользо-

ваться точными копиями данного устройства. Второй случай — когда имеет-

ся возможность оптимизации двух дополнительных копий устройства F (x)

в процессе разработки отказоустойчивой системы. Третий случай — когда

возможна оптимизация самого устройства F (x) и его копий. Очевидно, что

из трех вариантов наименьшую структурную избыточность будет давать по-

следний. Для типовых отказоустойчивых структур, таким образом, имеет

смысл введение понятия структуры с минимальной избыточностью — та-

кой структуры, которая будет для выбранного варианта внесения избыточ-

ности давать наименьшую сложность технической реализации.

Для создания отказоустойчивой структуры может быть применена струк-

турная схема, включающая в себя вместо трех копий исходного объекта толь-

ко две. При этом один из комплектов (или даже оба) снабжается схемой кон-

троля по какому-либо диагностическому признаку. Известны варианты реа-

лизации подобных схем при нахождении обоих комплектов под нагрузкой и

141

Блок коррекции

f₁

d₁

f₂

d₂

f₂

Входы

c₁

F(x)

fm1

dm1

fm1

m 2

f_m

cm1

c_m

P(x)

a₁

e₁

a₂

e₂

F *(x)

am1

em1

a_m

e_m

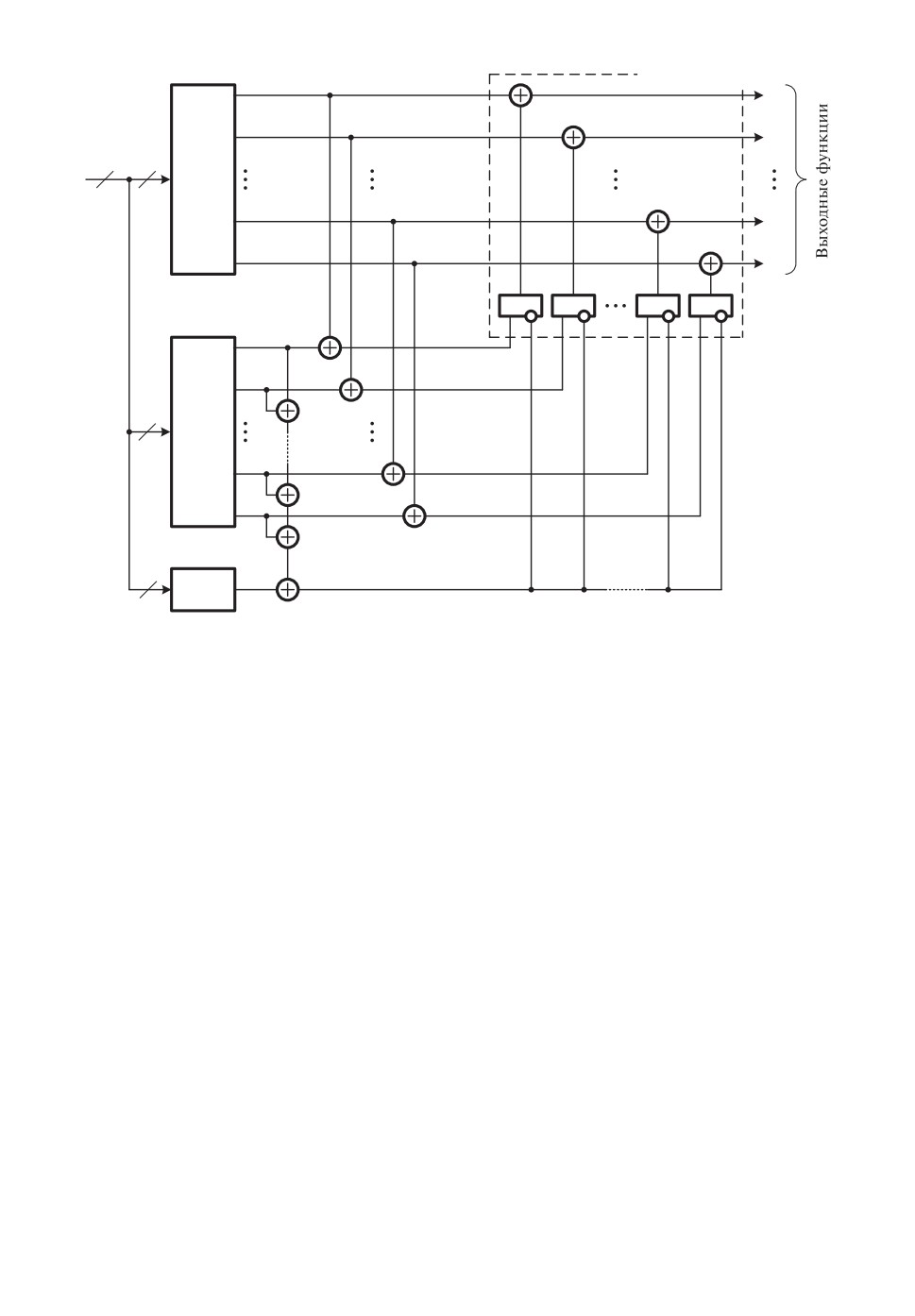
Рис. 1. Структура на основе дублирования с контролем основного комплекта.

нахождении одного комплекта под нагрузкой, а второго — в горячем резер-

ве [27]. Для случая отказоустойчивых комбинационных схем целесообразно

использовать вариант с постоянно нагруженными комплектами F (x) и F^∗(x)

с контролем вычислений одного из них. На рис. 1 и 2 приведены такие струк-

туры. В первом случае контролируются вычисления основным комплектом,

а во втором — дополнительным.

Если отходить от известного принципа тройной модульной избыточности

при реализации отказоустойчивого устройства, то необходимо решать сле-

дующие задачи.

Первая и основная задача состоит в необходимости восстановления

правильных значений искаженных выходных функций основного устрой-

ства F (x). В структуре с двойной модульной избыточностью для решения

этой задачи используется блок коррекции сигналов, включающий в себя

m элементов сложения по модулю два (XOR) d₁, d₂, . . . , dm-1, d_m, выходы

которых фактически являются и выходами всего устройства, а входы - с вы-

ходами основного блока F (x) и с выходами элементов логического умно-

жения (AND). Последние непосредственно формируют логические сигналы,

восстанавливающие правильные значения искаженных значений сигналов на

выходах основного блока. Ошибки в вычислениях, возникающие в результате

неисправностей элементов блока коррекции сигналов, не исправляются, так-

же как и выходных мажоритарных элементов, используемых в структурах с

тройной модульной избыточностью [27].

142

Блок коррекции

f₁

d₁

f₂

d₂

f₂

Входы

F(x)

fm1

dm1

fm1

f_m

d_m

e₁

e₂

em1

e_m

a₁

f₁

f₂

a₂

c₁

F *(x)

fm1

am1

cm2

f_m

a_m

cm1

c_m

P(x)

Рис. 2. Структура на основе дублирования с контролем дополнительного ком-

плекта.

Вторая задача заключается в необходимости определения тех выходов ос-

новного блока F (x), на которых в результате неисправностей элементов в

его структуре реализуются ошибочные функции. С этой целью в структу-

ры рис. 1 и 2 вводится второй блок F^∗(x) как копия основного блока F (x)

и элементы сложения по модулю два a₁, a₂, . . . , am-1, a_m, на которых срав-

ниваются сигналы с одноименных выходов блоков F (x) и F^∗(x). Активные

сигналы, возникающие на выходах этих элементов, свидетельствуют о нали-

чии неисправностей в одном из блоков.

Коррекция логических сигналов в блоке коррекции должна осуществлять-

ся только в том случае, если неисправным является основной блок F (x).

Фиксация факта отказа этого блока является третьей задачей. В структу-

ре рис. 1 она решается путем контроля исправности основного блока F (x)

при помощи схемы паритета (блок P (x) и элементы сложения по модулю два

c₁,c₂,... ,cm-1,c_m) [28], а в структуре рис. 2 - путем контроля исправности

дополнительного блока F^∗(x) по тому же принципу. Выходная функция f_i

в схеме рис. 1 корректируется только в том случае, когда z = 1 (блок F (x)

неисправен). В схеме рис. 2 выходная функция f_i корректируется только в

том случае, когда функция z = 0 (блок F^∗(x) исправен) и на выходе элемента

сложения по модулю два a_i присутствует сигнал 1.

Представленные на рис. 1 и 2 структуры во многих случаях позволяют

синтезировать более простые отказоустойчивые дискретные устройства, чем

143

по структурной схеме с тройной модульной избыточностью. Следует отме-

тить, что при построении структур, приведенных на рис. 1 и 2, также как и

в схеме с тройной избыточностью, возможны варианты с оптимизацией вто-

рого устройства F (x), а также обоих устройств, что еще больше уменьшит

сложность технической реализации системы «дублирование с коррекцией».

В последнем случае будет получена структура дублирования с минималь-

ной избыточностью.

Покажем, что принципиально возможно построение таких отказоустой-

чивых структур, которые в своем составе содержат только одно исходное

устройство F (x), что позволяет для определенных схем уменьшить сложность

технической реализации по сравнению со структурами с тройной и двойной

модульной избыточностью, имеющими минимальную избыточность.

3. Отказоустойчивые структуры на основе логического дополнения

Известные способы реализации отказоустойчивых структур на основе

двойной и тройной модульной избыточности обладают двумя существенны-

ми недостатками. Во-первых, при их построении для конкретного устрой-

ства F (x) возможна только единственная реализация (если не учитывать

все варианты с оптимизацией структур копий исходного объекта и допол-

нительных блоков и элементов). А во-вторых, не учитываются особенности

самого блока F (x), состав его функциональных элементов и конфигурации

связей, в конечном итоге влияющих на характеристики булевых функций

f₁,f₂,... ,fm-1,f_m. Учесть указанные недостатки можно путем использова-

ния принципа логического дополнения в процессе синтеза отказоустойчиво-

го цифрового устройства [18], являющегося развитием описанного в [28] ме-

тода контроля функционирования устройств по паритету. Как показано в

[19-22] на примере синтеза схем встроенного контроля возможна реализация

нескольких вариантов структур с различной сложностью, среди которых мо-

жет быть выбран наилучший по заданному критерию (например, по крите-

рию минимальных показателей сложности технической реализации).

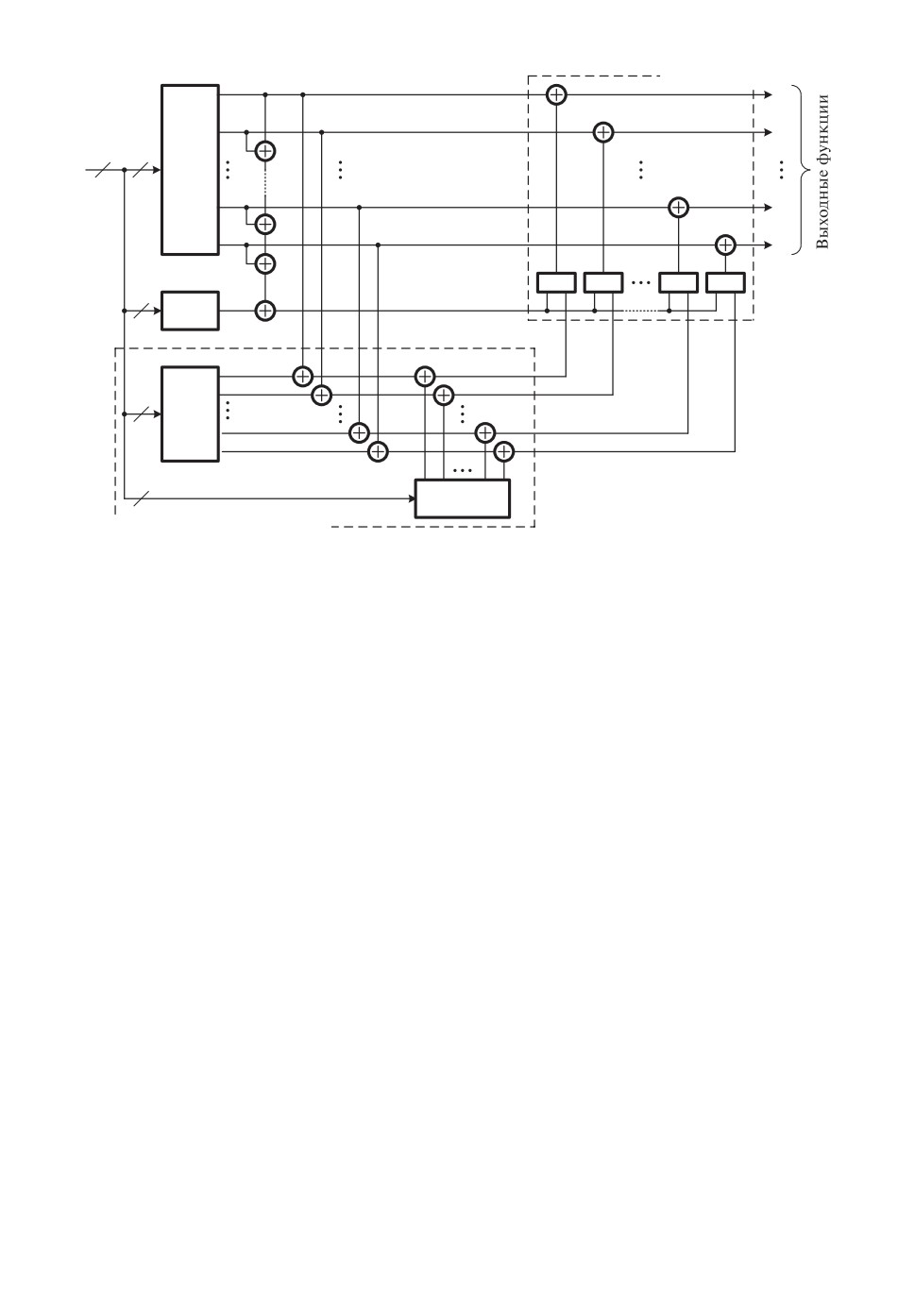
На рис. 3 и 4 приведены две новые отказоустойчивые структуры, при по-

строении которых используется принцип логического дополнения. В данных

структурах используются блок фиксации искаженных сигналов (ФИС), схема

контроля по паритету и аналогичный блок коррекции сигналов (КС), исполь-

зующийся и в представленных на рис. 1 и 2 структурах с двойной модульной

избыточностью.

Принципиально по-новому в представленных структурах решается зада-

ча выявления тех выходов блока F (x), на которых имеет место искажение

правильного сигнала. Для этого в обеих структурах используется блок ФИС.

В структуру блока ФИС для схемы, приведенной на рис. 3, входит блок

логического дополнения G(x), на выходах которого вычисляются специаль-

ные функции дополнения g₁, g₂, . . . , gm-1, g_m. Последние сравниваются с од-

ноименными функциями выходов блока F (x) при помощи элементов сло-

жения по модулю два a₁, a₂, . . . , am-1, a_m, на выходах которых вычисля-

ются функции сравнения q₁, q₂, . . . , qm-1, q_m. Блок ФИС включает в себя

также блок коррекции функций сравнения R(x), вычисляющий функции

r₁,r₂,... ,rm-1,r_m, которые выбираются с таким расчетом, чтобы на выхо-

144

Блок коррекции

f₁

d₁

f₁

f₂

d₂

c₁

F(x)

fm1

dm1

fm1

f_m

d_m

cm 2

cm1

c_m

P(x)

g₁

q₁

e₁

g₂

a₁

q₂

b₁

e₂

a₂

G(x)

b₂

gm1

qm1

em1

g_m

am1

q_m

bm1

b_m

e_m

a_m

rm1

r_m

R(x)

Блок фиксации искаженных

сигналов

Рис. 3. Структура на основе логического дополнения с контролем основного

комплекта.

де блока ФИС в исправной структуре были реализованы функции

e₁ = f₁ ⊕ g₁ ⊕ r₁ = 0;

e₂ = f₂ ⊕ g₂ ⊕ r₂ = 0;

(2)

e_m = f_m ⊕ g_m ⊕ r_m = 0.

Если в результате неисправности в блоке F (x) искажается значение функ-

ции f_i, то, как следует из (2), e_i = 1, и активизируются вход и выход со-

ответствующего элемента логического умножения (при этом на выходе схе-

мы паритета сигнал z = 1). Осуществляется исправление неверного значения

функции f_i.

Задача установления факта возникновения неисправности в основном бло-

ке F (x) решается в структуре, приведенной на рис. 1, при помощи схемы па-

ритета (блок P (x) и элементы сложения по модулю два c₁, c₂, . . . , cm-1, c_m),

которая контролирует значения сигналов непосредственно на выходах основ-

ного блока (аналогично представленной на рис. 1 схеме с двойной модуль-

ной избыточностью). Неисправности элементов схемы паритета, при которых

устанавливается значение функции z = 1 в структуре рис. 3, не приводят к

искажению правильных значений функций f₁, f₂, . . . , fm-1, f_m, так как в это

время блок ФИС исправен и все функции e_i = 0. И, наоборот, неисправно-

сти элементов блока ФИС, которые вызывают появление значений функций

e_i = 1, также не приводят к изменению указанных функций, так как в этом

случае сигнал z = 0.

145

Блок коррекции

f₁

d₁

f₂

d₂

Входы

F(x)

fm1

dm1

fm1

f_m

d_m

g₁

q₁

a₁

b₁

e₁

g₂

q₂

a₂

e₂

G(x)

c₁

gm1

qm1

em1

am1

bm1

g_m

m 2

q_m

b_m

e_m

a_m

m 1

c_m

P(x)

r₁

r₂

m 1 rm

R(x)

Блок фиксации искаженных

сигналов

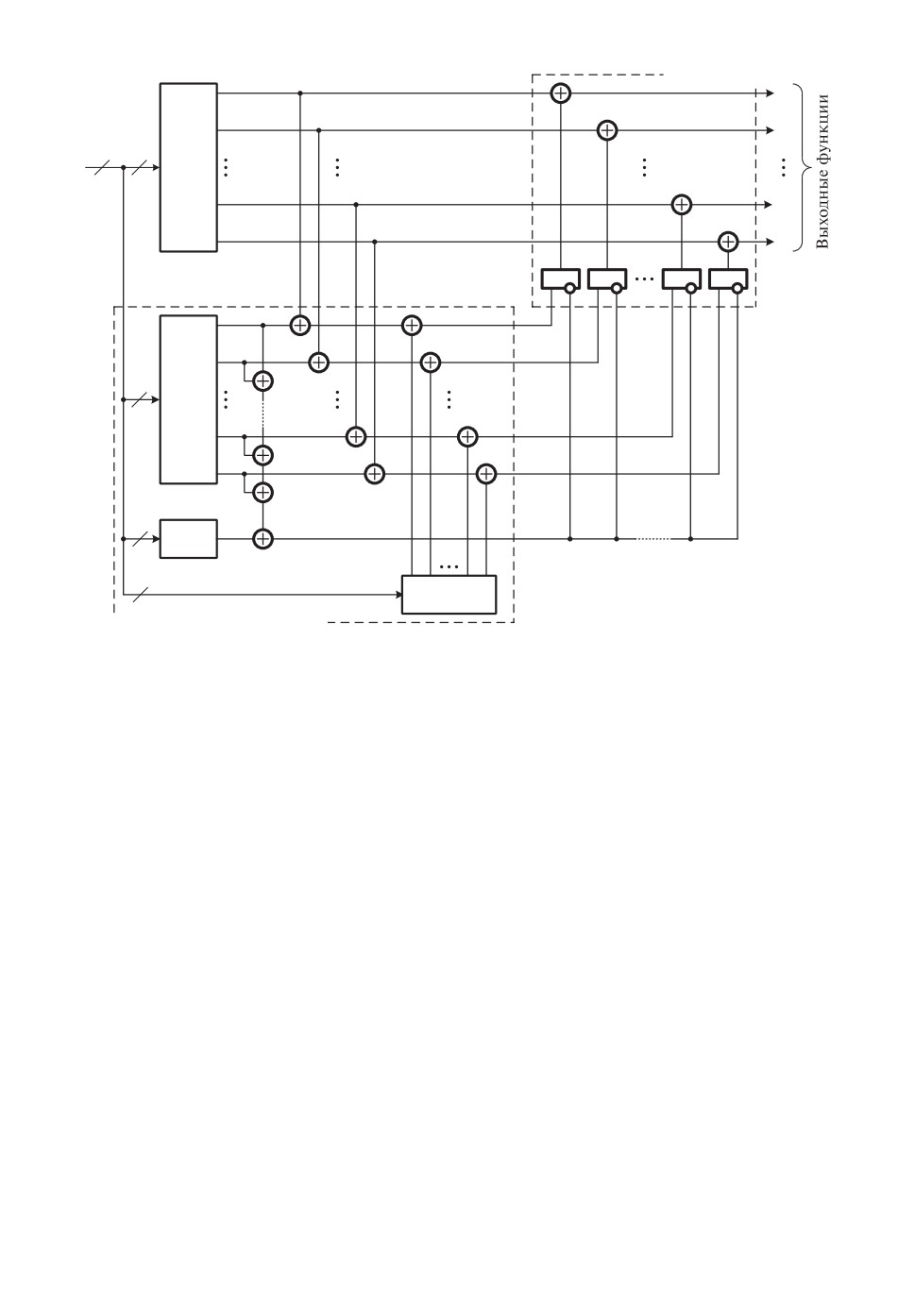
Рис. 4. Структура на основе логического дополнения с контролем блока до-

полнения.

В отличие от структуры, приведенной на рис. 3, в структуре, изображен-

ной на рис. 4, не контролируются вычисления в блоке основной логики F (x).

В ней контролируются вычисления в самом блоке ФИС. С этой целью блок

логического дополнения G(x) дополняется схемой контроля по паритету (ана-

логично схеме контроля вычислений в блоке основной логики). При возник-

новении неисправности в блоке G(x) или в каком-либо из элементов сложения

по модулю два и блока P (x) фиксируется значение сигнала z = 1. Этот сиг-

нал поступает на входы элементов AND блока коррекции сигналов и инвер-

тируется, что исключает ложную коррекцию сигналов. Это справедливо при

условии, что одновременно возможно возникновение неисправности только в

одном из блоков структуры.

Так как блок логического дополнения G(x) может быть реализован боль-

шим числом способов, в структуре, приведенной на рис. 4, возможно умень-

шение сложности блока паритета P (x) по сравнению с аналогичным блоком

в схеме, изображенной на рис. 3.

При синтезе блока ФИС необходимо определить функции g₁, g₂,

...,gm-1,g_m и r₁,r₂,...,rm-1,r_m. Из (2) следует, что g_i = f_i ⊕ r_i. Каждая

функция r_i может быть выбрана произвольным образом независимо от то-

го, какими являются функции f_i и g_i. От выбранного варианта функции r_i

зависит сложность реализации функции g_i. При этом никакой зависимости

146

между функциями g_i и r_i с различными индексами i не существует. По этой

причине задача получения структуры блока ФИС с наименьшей сложностью

может быть решена следующим образом. Для каждой пары функций (g_i, r_i)

путем подбора функции r_i находится вариант с наименьшей сложностью обе-

их функций. Затем блоки G(x) и R(x) описываются наборами соответствую-

щих функций и осуществляется оптимизация структуры каждого блока в

отдельности (возможна и совместная оптимизация обоих блоков).

При реализации структур рис. 3 и 4 для любого блока F (x) существует

большое число вариантов выбора набора функций {r₁, r₂, . . . , rm-1, r_m}, при

которых достигается свойство отказоустойчивости. Поэтому возможен выбор

варианта, при котором обеспечивается минимальная сложность блока ФИС.

Особым вариантом набора функций {r₁, r₂, . . . , rm-1, r_m} является вари-

ант, в котором каждая функция приравнивается к какой-либо (любой) вход-

ной переменной x₁, x₂, . . . , xt-1, x_t. В этом случае реализация блока R(x) не

требует аппаратных затрат (он фактически является коммутатором входных

сигналов).

Элементы блока коррекции сигналов следует реализовать в виде высоко-

надежных устройств с резервированием внутренних компонентов [27]. Отме-

тим также, что обе структуры могут быть дополнены элементом, на выходе

которого реализуется функция v = z ∨ e₁ ∨ e₂ ∨ . . . ∨ e_m и формируется сиг-

нал о наличии неисправности в схеме контроля и/или блока ФИС при ис-

правном основном блоке F (x).

Корректирующая способность всех рассмотренных выше структур

(рис. 1-4) ограничивается тем, что при помощи паритета обнаруживаются

только те неисправности в блоке F (x), которые искажают значения сигналов

на нечетном числе выходов блока, что следует из свойств функции пари-

тета [29]. Для улучшения корректирующей способности могут быть исполь-

зованы различные подходы. Например, может быть выбран способ контроля

вычислений, при котором возможна идентификация большего числа ошибок,

чем в схеме контроля по паритету. Такой эффект достигается при использова-

нии равномерных блочных кодов, например классических кодов с суммирова-

нием (кодов Бергера) и их модификаций [30, 31]. Другим способом является

модификация внутренней структуры блока F (x), если это допустимо, либо

же контроль отдельных групп независимых выходов на основе отдельных

подсхем паритета [32-35].

Рассмотрим пример синтеза блока ФИС для структуры рис. 3 (для струк-

туры рис. 4 задача решается аналогично) для комбинационного устройства

автоматики, заданного следующими функциями:

⎧

f₁ = x₁x₃x₄ ∨ x₁x₂ x₄ ∨ x₁x₂x₄ ∨ x₁x₂x₃ ∨ x₁x₃x₄;

⎪

⎨

f₂ = x₁x₂x₃ ∨ x₁x₃x₄ ∨ x₁x₂ x₄ ∨ x₁x₂x₃ ∨ x₁ x₂ x₃ ∨ x₁x₂x₃x₄;

(3)

f₃ = x₃x₄ ∨ x₁x₂x₄ ∨ x₂x₃ x₄ ∨ x₁ x₂ x₄;

⎪

f₄ = x₁x₂x₃ ∨ x₁x₂x₄ ∨ x₂x₃ x₄ ∨ x₁ x₂x₃ ∨ x₁ x₂x₄;

⎩

f₅ = x₁ x₂ x₄ ∨ x₁x₂x₃ ∨ x₁x₂x₃ ∨ x₁x₂x₃x₄.

Рассмотрим решение поставленной задачи пошагово, приведя один из воз-

можных алгоритмов [15, 16].

147

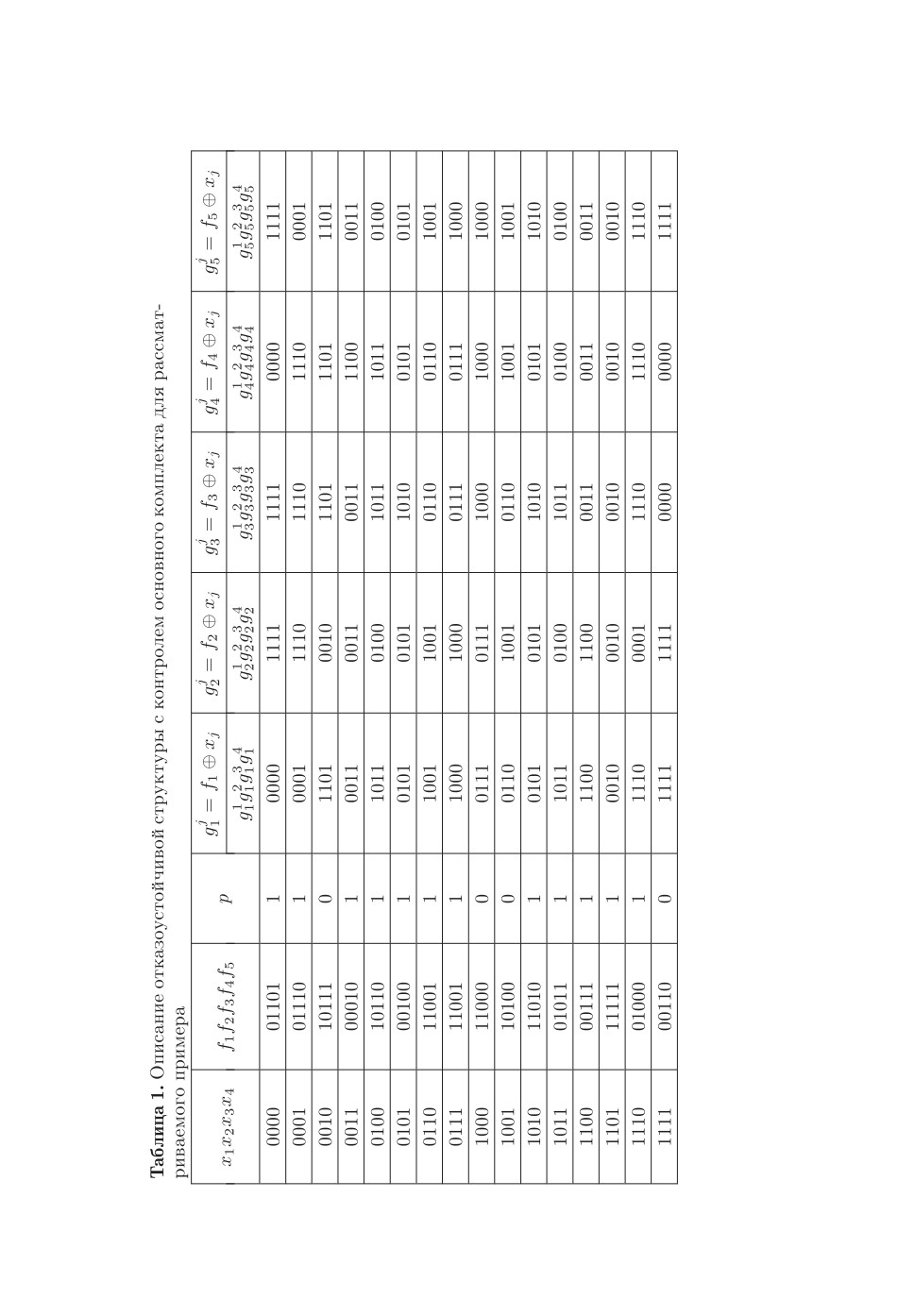
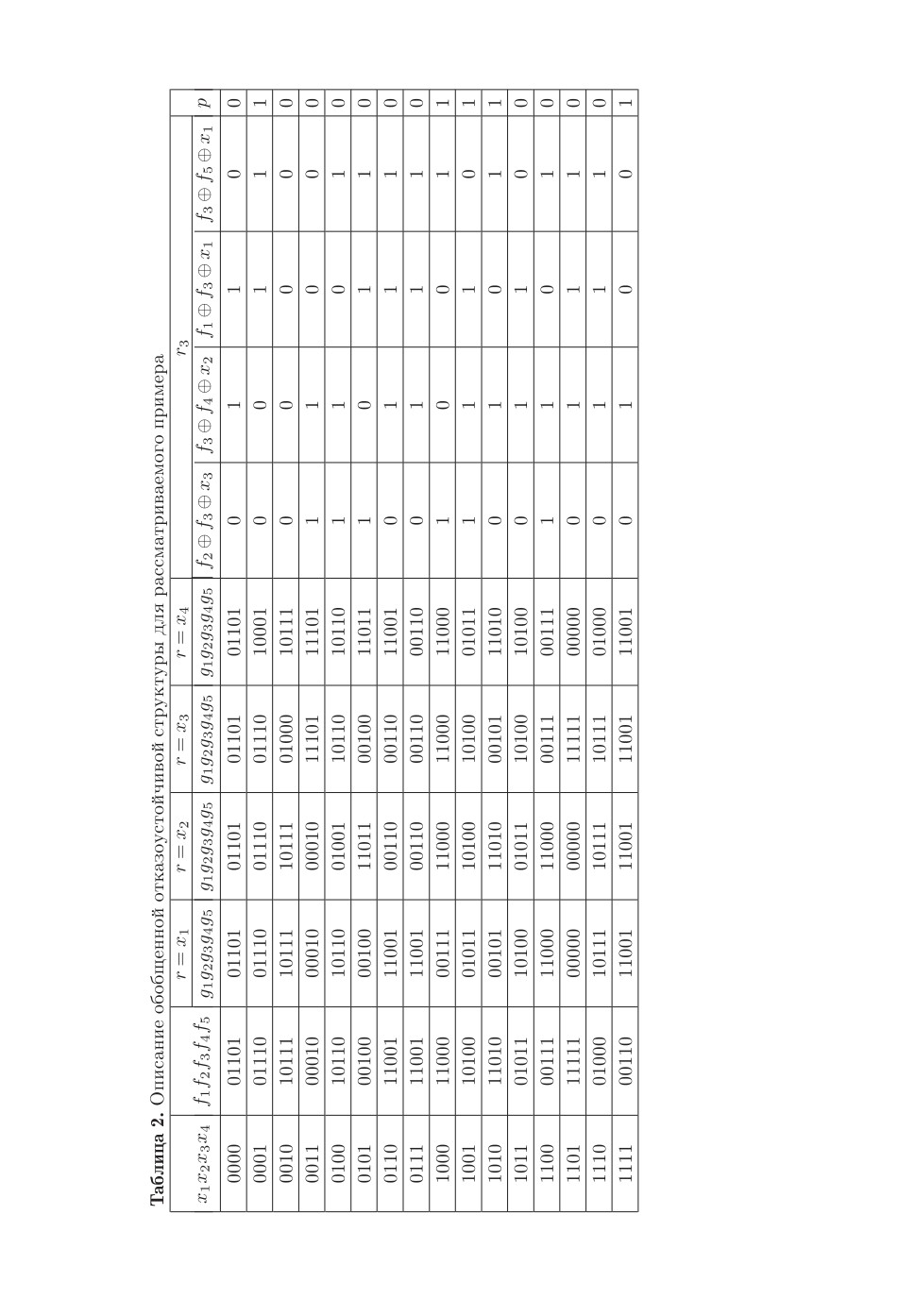
Шаг 1. Для каждой из функций f_i (i ∈ {1,...,m}) определим функции

коррекции {r₁, r₂, . . . , rm-1, r_m}. Будем для этого использовать наиболее про-

стой вариант — осуществим поиск переменной x_j , которая позволяет по-

лучить наиболее простое с точки зрения технической реализации выраже-

ние для функции g^ji = f_i ⊕ x_j . Еще раз подчеркнем, что в качестве функций

{r₁, r₂, . . . , rm-1, r_m} могут использоваться произвольные функции, что так-

же может дать эффект в уменьшении сложности реализации блока ФИС.

Для каждого выхода f_i (i ∈ {1, . . . , m}) существует по четыре варианта фор-

мирования функций коррекции сигналов (см. табл. 1). Минимизируя функ-

ции (в данном случае использована двухуровневая оптимизация по методу

Карно [27]) и выбирая наиболее простые из них, получаем систему функций

алгебры логики, описывающую блок G(x):

g¹¹ = x₁x₃x₄ ∨ x₁x₃x₄ ∨ x₂x₄ ∨ x₂x₃;

g³² = x₁ x₂ ∨ x₁x₂x₄ ∨ x₂ x₃ x₄;

g¹³ = x₁ x₃ ∨ x₂ x₄ ∨ x₁x₂x₃ ∨ x₁x₃x₄;

g²⁴ = x₁x₄ ∨ x₁x₃ ∨ x₂x₃ ∨ x₃x₄;

g¹⁵ = x₂ x₄ ∨ x₂x₃ ∨ x₁x₂ x₃.

Сложность реализации каждой функции блока G(x) можно оценить

по числу входов логических элементов без учета внутренних инверсий:

L(g¹¹) = 14, L(g³²) = 11, L(g¹³) = 14, L(g²⁴) = 12, L(g¹⁵) = 10.

Шаг 2. Блок G(x) реализуется путем оптимизации полученных подсхем

для реализации каждой из функций g_i.

Шаг 3. Определяется функция паритета p. Минимизация данной функции

дает возможность синтеза блока P (x):

p=x₁x₃ ∨x₁x₄ ∨x₂x₄ ∨x₂x₃ ∨x₁x₂x₃.

Сложность блока P (x) определяется величиной L (p) = 16.

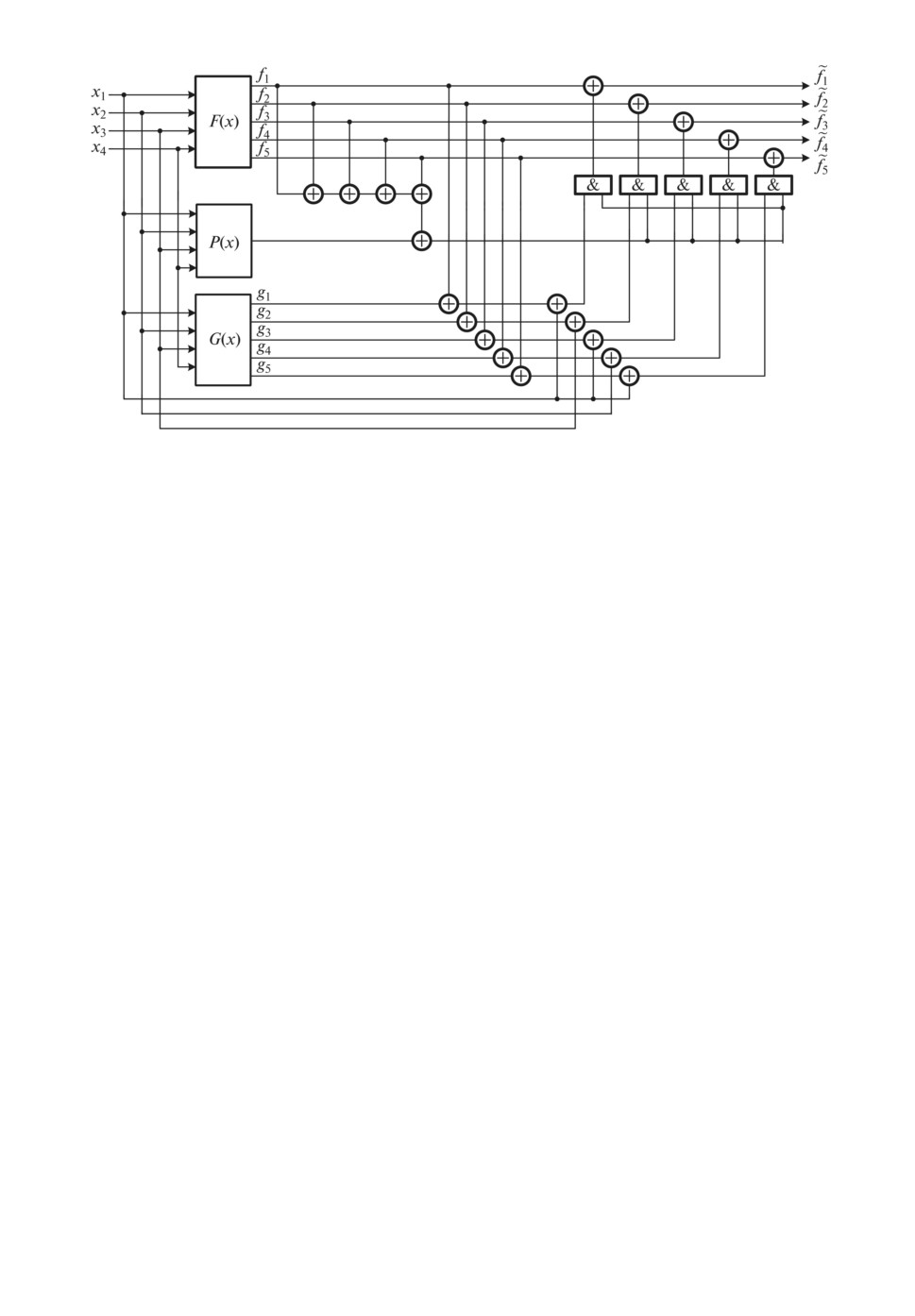
Полученное устройство изображено на рис. 5.

Учитывая сложности реализации элементов сложения по модулю два и

логического умножения, входящих в схему паритета и блока ФИС (L_XOR = 6

и L_AND = 2), получим значение сложности технической реализации отказо-

устойчивой структуры на основе логического дополнения с контролем основ-

ного комплекта:

L_BC = LF(x) + LG(x) + LP(x) + 4 · 5L_XOR + 5L_AND =

= 97 + (14 + 11 + 14 + 12 + 10) + 16 + 20 · 6 + 5 · 2 = 97 + 61 + 16 + 120 + 10 = 304.

Для сравнения, сложность системы дублирования с контролем основного

комплекта определяется величиной:

L_D = 2LF(x) +LP(x) +3·5·L_XOR +5L_AND = 2·97+16+15·6+5·2 = 310.

Сложность структуры с тройной модульной избыточностью (с учетом то-

го, что сложность мажоритарных элементов коррекции оценивается величи-

ной L≥2 = 9) равна:

L_TMR = 3LF(x) + 5L≥2 = 3 · 97 + 5 · 9 = 336.

149

Рис. 5. Отказоустойчивое устройство для рассматриваемого примера, реали-

зованное по структуре логического дополнения с контролем основного ком-

плекта.

Данный пример показывает возможности построения более простых отка-

зоустойчивых цифровых устройств по сравнению с известными методами с

двойной и тройной модульной избыточностью.

4. Обобщенная отказоустойчивая структура

на основе логического дополнения

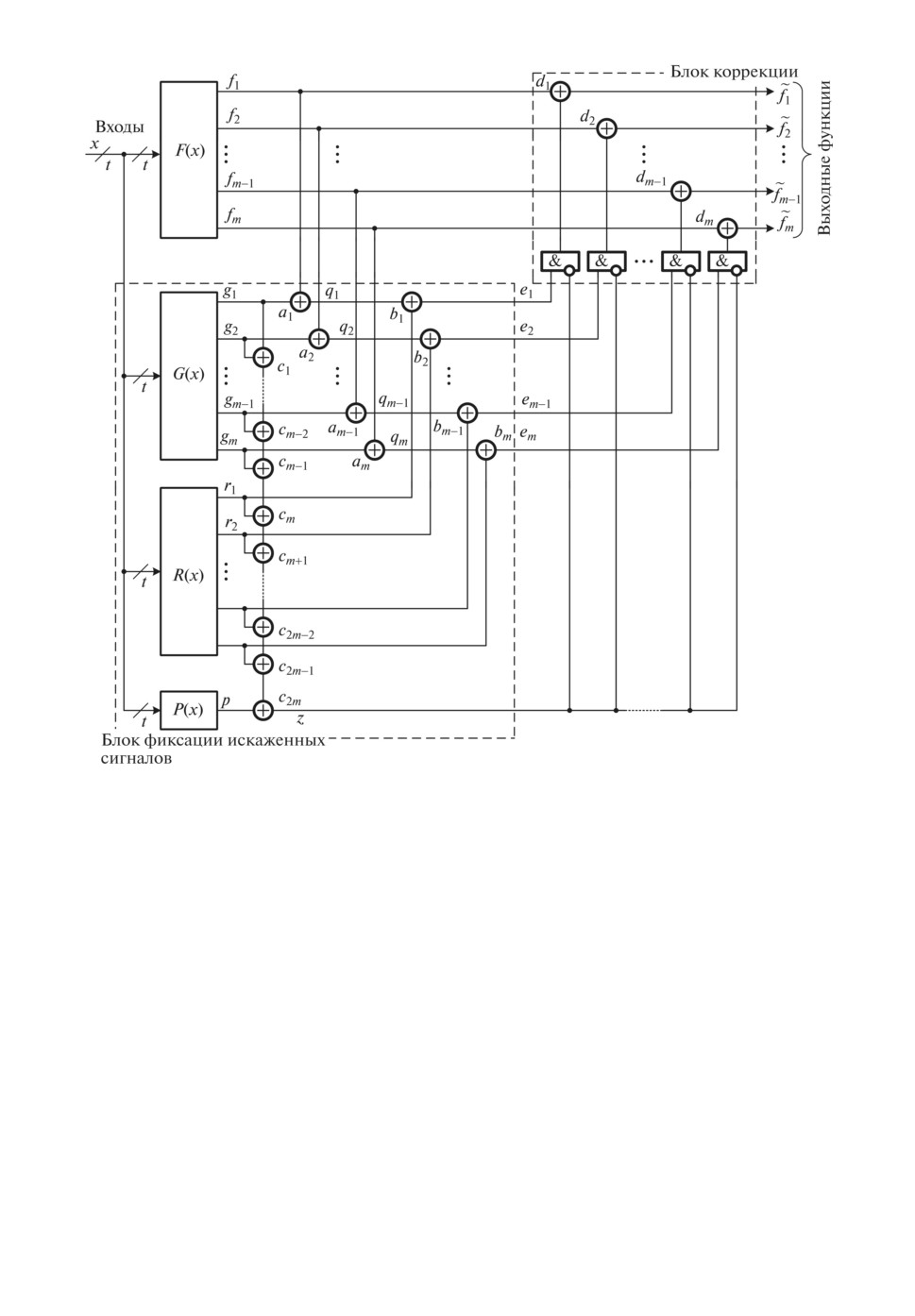
На рис. 6 приведена обобщенная отказоустойчивая структура, в которой

контролируется не только работа блока дополнения, но и блока вычисления

функций коррекции сигналов. Данная структура реализует более общую мо-

дель, чем рассмотренные ранее структуры на основе логического дополнения.

В ней устройство F (x) является исходным объектом, вычисляющим си-

стему рабочих функций f₁, f₂, . . . , fm-1, f_m от t входных переменных. Для

контроля правильности вычислений функций f₁, f₂, . . . , fm-1, f_m использован

блок ФИС, в котором выделены блоки G(x), R(x) и P (x), а также каскады

сумматоров по модулю два (элементов XOR). Блоки G(x) и R(x) представ-

ляют собой блоки логического дополнения и коррекции сигналов. Блок P (x)

предназначен для формирования значения решающей функции ошибки и в

данном случае формирует значение функции контроля по паритету кодово-

го вектора, образованного на выходах g₁, g₂, . . . , gm-1, g_m и r₁, r₂, . . . , rm-1, r_m

обоих блоков G(x) и R(x):

(4)

p=g₁ ⊕g₂ ⊕...⊕gm-1 ⊕g_m ⊕r₁ ⊕r₂ ⊕...⊕rm-1 ⊕r_m.

Значения функций g₁, g₂, . . . , gm-1, g_m, вычисляемых блоком G(x), и функ-

ций r₁, r₂, . . . , rm-1, r_m, вычисляемых блоком R(x), подбираются на этапе про-

ектирования структуры таким образом, чтобы при штатной работе (в отсут-

ствие неисправностей) значения функции активации коррекции (функции z)

были равными 0. Неисправности в блоке F (x) искажают значения функций

на выходах элементов a₁, a₂, . . . , am-1, a_m в блоке ФИС. Поскольку речь идет

150

Рис. 6. Обобщенная отказоустойчивая структура.

о случае, когда одновременно возможно возникновение неисправности только

в одном из блоков, функция z = 0, происходит коррекция сигналов. Коррек-

ции не произойдет в том случае, если функция z = 1 - в этом случае будет

зафиксирована неисправность в одном из блоков G(x) или R(x) или в одном

из элементов сложения по модулю два. Коррекция сигналов производится

только при наличии неисправностей в исходном устройстве F (x).

Элементы блоков ФИС и коррекции сигналов являются стандартными,

за исключением блоков G(x) и R(x). Задача построения отказоустойчивой

структуры состоит как раз в синтезе этих блоков. Рассмотрим ее решение на

примере реализации отказоустойчивого устройства для блока F (x), заданно-

го функциями (3).

Шаг 1. Для каждой из функций f_i (i ∈ {1,...,m}) определяется слож-

ность ее реализации (будем также использовать в качестве показателя слож-

ности реализации число входов внутренних логических элементов при реа-

лизации по дизъюнктивной форме без учета инверсий [27]): L(f₁) = 20,

L(f₂) = 25, L(f₃) = 15, L(f₄) = 20, L(f₅) = 17.

151

Шаг 2. Устанавливается равенство r₁ = r₂ = ... = r_m = r. А переменной r

последовательно придаются значения отдельных переменных и рассчитыва-

ются функции g_i: g_i = f_i ⊕ x_j. После этого определяется сложность реализа-

ции каждой функции g_i. В рассматриваемом примере для каждой функции g_i

получаем 4 реализации соответственно четырем входным переменным (см.

табл. 2).

Шаг 3. Для каждой функции g_i выбирается реализация с наименьшей

сложностью и соответствующая ей функция r_i:

g¹¹ = f₁ ⊕ x₁ = x₂x₄ ∨ x₂x₃ ∨ x₁x₃x₄ ∨ x₁x₃x₄,

(

)

g¹¹

= 14,

g³² = f₂ ⊕ x₃ = x₁ x₂ ∨ x₁x₂x₄ ∨ x₂ x₃ x₄,

(

)

g³²

= 11,

g²³ = f₃ ⊕ x₂ = x₂x₃x₄ ∨ x₁x₂x₃ ∨ x₁ x₂ ∨ x₂ x₃x₄,

(

)

g²³

= 15,

g²⁴ = f₄ ⊕ x₂ = x₁x₄ ∨ x₃x₄ ∨ x₁x₂x₃,

(

)

g²⁴

= 10,

g¹⁵ = f₅ ⊕ x₁ = x₂x₃ ∨ x₃x₄ ∨ x₁x₂ x₃ ∨ x₁ x₂ x₄,

(

)

g¹⁵

= 14.

Шаг 4. Для каждого выхода определяется значение разности C_i = L(f_i)-

-L(g_i) - L(XOR), характеризующей эффект от применения дополнения по

данному выходу:

C₁ = 2, C₂ = 10, C₃ = -4, C₄ = 6, C₅ = -1.

Шаг 5. Выходы ранжируются в порядке уменьшения эффекта: f₂, f₄, f₁,

f₅, f₃.

Шаг 6. Рассматривается возможность улучшения эффекта для «плохих»

выходов.

В приведенном примере рассмотрим выход f₃. Выход f₃ рассматриваем в

сочетании с «хорошими» выходами, например в сочетании f₃ - f₂.

Установим равенство f₃ = f₂. Тогда в блоке G(x) не требуется подсхема

для реализации функции g₃, но в блоке R(x) появляется подсхема для реа-

лизации функции r₂.

Если g₃ = g₂, то f₃ ⊕ r₃ = f₂ ⊕ r₂. Так как в данном случае r₂ = x₃, то

получим f₃ ⊕ r₃ = f₂ ⊕ x₃, тогда r₃ = f₃ ⊕ f₂ ⊕ x₃.

В данном случае получаем, что r₃ = x₁x₂x₃ ∨ x₁x₂ x₃ ∨ x₁x₃ x₄ ∨ x₁ x₂x₃x₄.

Так как L (r₃) = 17 > L (g₃) = 15, то рассмотренное преобразование неце-

лесообразно.

Улучшение дает рассмотрение пары f₃ - f₅:

r₃ = f₃ ⊕ f₅ ⊕ x₁,

r₃ = x₁x₄ ∨ x₁x₂ ∨ x₁ x₃x₄ ∨ x₂x₃x₄,

L (r₃) = 14 < L (g₃) = 15.

153

f₁

x₁

f₂

x₂

f₃

F(x)

f₃

x₃

f₄

x₄

f₅

g₁

g₂

r₃

G(x)

g₄

g₅

r₃

R(x)

P(x)

Рис. 7. Отказоустойчивое устройство для рассматриваемого примера, реали-

зованное по обобщенной структуре на основе логического дополнения.

Шаг 7. Получаем выражение для функции паритета, реализуемой блоком

P (x):

p=x₁x₂x₄ ∨x₂x₃x₄ ∨x₁x₂x₃x₄,

LP(x) = 13.

На рис. 7 приведена отказоустойчивая структура для рассматриваемого

примера. Сложность ее реализации вычисляется из значений сложности ком-

понентов:

L_GeneralBC = LF(x) + LG(x) + LP(x) + LR(x) + 4 · 5L_XOR + 5L_AND =

= 97 + (14 + 11 + 10 + 14) + 13 + 14 + 20 · 6 + 5 · 2 =

= 97 + 49 + 13 + 14 + 120 + 10 = 303.

Полученная величина сложности улучшена по сравнению с рассмотрен-

ным ранее примером на одну условную единицу. Для других примеров воз-

можно получение еще более простых структур по обобщенной структуре на

основе логического дополнения.

В отличие от способа синтеза блока ФИС, описанного в предыдущем раз-

деле, представленный способ позволяет увеличить число вариантов с допол-

нительными функциями, равными переменной. За счет максимального упро-

щения блока R(x) и возможностей выбора функций логического дополнения,

вычисляемых блоком G(x), может быть достигнуто существенное уменьше-

154

ние сложности технической реализации схемы коррекции по сравнению с тра-

диционными методами.

5. Заключение

Предложенные в работе отказоустойчивые структуры на основе принципа

логического дополнения позволяют на практике получать более простые от-

казоустойчивые цифровые устройства. Эксперименты с контрольными ком-

бинационными схемами показывают, что на практике можно добиться суще-

ственного уменьшения сложности технической реализации отказоустойчиво-

го устройства путем применения новых структур в сравнении с известными

структурами с двойной и тройной модульной избыточностью. Например, в

[15, 16] показано, что возможно упрощение структур до 25-30% по сравнению

со структурами с двойной модульной избыточностью и до 40-45% по срав-

нению со структурой на основе тройной модульной избыточности. При этом

возможно достижение высоких показателей коррекции сигналов без измене-

ния структур исходных объектов. К примеру, для комбинационных устройств

применение структуры на основе логического дополнения с контролем вычис-

лений исходного объекта по паритету в эксперименте для двадцати двух ком-

бинационных устройств получено среднее значение вероятности коррекции

p_c = 0,95421. Повышение обнаруживающей способности метода возможно за

счет использования схем контроля по другим принципам, например по моди-

фицированным кодам с суммированием [36, 37], либо же путем применения

специальных схемотехнических способов обнаружения ошибок на выходах

объектов диагностирования [32-35].

Следует отметить две особенности предложенных структур. Первая за-

ключается в том, что по сравнению со структурами с двойной модульной

избыточностью в новых структурах за счет использования двух каскадов

сумматоров по модулю два a₁, a₂, . . . , am-1, a_m и b₁, b₂, . . . , bm-1, b_m увеличе-

но время прохождения сигналов и таким образом снижено быстродействие

структуры. Тем не менее задержка несущественна, и путь прохождения сиг-

нала увеличивается незначительно. Увеличение времени срабатывания мож-

но считать некоторой ценой за снижение аппаратных затрат на реализацию

предложенной структуры. Вторая особенность связана с процедурами поис-

ка значений функций логического дополнения g₁, g₂, . . . , gm-1, g_m и выбора

функций коррекции r₁, r₂, . . . , rm-1, r_m. Требуется анализ Q = tm (t и m -

число входов и число выходов блока F (x) соответственно) различных спосо-

бов вычисления функций логического дополнения на 2^t входных комбинаци-

ях. Число Q существенно зависит от числа входов и выходов устройства F (x),

что определяет ограничения на применение предложенных алгоритмов полу-

чения функций дополнения и выбора функций коррекции. Для современ-

ной вычислительной техники полный алгоритм вычисления реализуется за

разумное время при числе входных переменных, не превышающих значе-

ний 30÷35 (это связано и с возможностями автоматической минимизации

функций алгебры логики). При большем числе входов можно использовать

упрощенный алгоритм вычисления функций дополнения, рассмотренный в

статье.

Использование логического дополнения - перспективный подход к реали-

зации отказоустойчивых цифровых устройств.

155

СПИСОК ЛИТЕРАТУРЫ

Согомонян Е.С., Слабаков Е.В. Самопроверяемые устройства и отказоустойчи-

вые системы. М.: Радио и связь, 1989.

Fujiwara E. Code Design for Dependable Systems: Theory and Practical

Applications. John Wiley & Sons, 2006.

Gavrilov S.V., Gurov S.I., Zhukova T.D., et. al. Methods to Increase Fault Tolerance

of Combinational Integrated Microcircuits by Redundancy Coding // Computational

Mathematics and Modeling. 2017. Vol. 28. No. 3. P. 400-406.

https://doi.org/10.1007/s10598-017-9372-3

Сапожников В.В., Сапожников Вл.В., Ефанов Д.В. Коды Хэмминга в системах

функционального контроля логических устройств. СПб.: Наука, 2018.

Гаврилов М.А., Остиану В.М., Потехин А.И. Надежность дискретных си-

стем // Итоги науки и техники. Серия «Теория вероятностей. Математическая

статистика. Теоретическая кибернетика». 1969, 1970. C. 7-104.

Каравай М.Ф., Согомонян Е.С. Анализ надежностных характеристик самопро-

веряемых избыточных структур // АиТ. 1979. № 8. С. 105-119.

Karavai M.F., Sogomonyan E.S. Analysis of Reliability Characteristics of Self-

Checkable Redundant Structures // Autom. Remote Control. 1980. V. 40. No. 8.

P. 1186-1197.

Matsumoto K., Uehara M., Mori H. Evaluating the Fault Tolerance of Stateful

TMR // 13th International Conference on Network-Based Information Systems,

14-16 September 2010, Takayama, Japan. P. 332-336.

https://doi.org/10.1109/NBiS.2010.86

Borecký J., Kohlik M., Vit P., Kubátová H. Enhanced Duplication Method

with TMR-Like Masking Abilities // Euromicro Conference on Digital System Design

(DSD), 31 August - 2 September 2016, Limassol, Cyprus. P. 690-693.

https://doi.org/10.1109/DSD.2016.91

Krcma M., Kotasek Z., Lojda J. Triple Modular Redundancy Used in Field

Programmable Neural Networks // Proceedings of 15th IEEE East-West Design &

Test Symposium (EWDTS’2017), Novi Sad, Serbia, September 29-October 2, 2017.

P. 372-377. https://doi.org/10.1109/EWDTS.2017.8110128

10.

Sogomonyan E.S. Self-Correction Fault-Tolerant Systems. - Preprint, October 2018.

11.

Dug M., Krstic M., Jokic D. Implementation and Analysis of Methods for Error

Detection and Correction on FPGA // IFAC-PapersOnLine. 2018. V. 51. I. 6.

P. 348-353.

12.

Харченко В.С. Модели и свойства многоальтернативных отказоустойчивых си-

стем // АиТ. 1992. № 12. С. 140-147.

Kharchenko V.S. Models and Properties of Multialternative Fault-Tolerant

Systems // Autom. Remote Control. 1993. V. 53. No. 12. P. 1944-1950.

13.

Лысенко И.В., Харченко В.С. Оценка живучести многоярусных мажоритарно-

резервированных систем, функционирующих в условиях неблагоприятных воз-

действий импульсной природы // АиТ. 1997. № 2. С. 209-218.

Lysenko I.V. Kharchenko V.S. Potential Vitality of Multi-Layered Majorant-

Reserved Systems Subject to Adverse Impulse Effects // Autom. Remote Control.

1997. V. 58. No. 2. P. 320-327.

14.

Скляр В.В., Харченко В.С. Отказоустойчивые компьютерные системы управле-

ния с версионно-пороговой адаптацией: способы адаптации, оценка надежности,

выбор архитектур // АиТ. 2002. № 6. С. 131-145.

156

Sklyar V.V., Kharchenko V.S. Fault-Tolerant Computer-Aided Control Systems with

Multiversion-Threshold Adaptation: Adaptation Methods, Reliability Estimation,

and Choice of an Architecture // Autom. Remote Control. 2002. V. 63. No. 6.

P. 991-1003. https://doi.org/10.1023/A:1016130108770

15.

Сапожников В.В., Сапожников Вл.В., Ефанов Д.В. Схема коррекции сигна-

лов для комбинационных устройств автоматики на основе логического дополне-

ния с контролем вычислений по паритету // Информатика. 2020. Том 17. № 2.

С. 71-85. https://doi.org/10.37661/1816-0301-2020-17-2-71-85

16.

Сапожников В.В., Сапожников Вл.В., Ефанов Д.В. Отказоустойчивая струк-

тура на основе логического дополнения с контролем вычислений по паритету //

Автоматика на транспорте. 2020. Т. 6. № 3. С. 377-403.

https://doi.org/10.20295/2412-9186-2020-6-3-377-403

17.

Lala P.K. Self-Checking and Fault-Tolerant Digital Design. - San Francisco: Morgan

Kaufmann Publishers, 2001.

18.

Гессель М., Морозов А.В., Сапожников В.В., Сапожников Вл.В. Контроль

комбинационных схем методом логического дополнения // АиТ. 2005. № 8.

С. 161-172.

Goessel M., Morozov A.V., Sapozhnikov V.V., Sapozhnikov Vl.V. Checking Combi-

national Circuits by the Method of Logic Complement // Autom. Remote Control.

2005. V. 66. No. 8. P. 1336-1346. https://doi.org/10.1007/s10513-005-0174-2

19.

Göessel M., Ocheretny V., Sogomonyan E., Marienfeld D. New Methods of

Concurrent Checking: Edition 1. Dordrecht: Springer Science+Business Media B.V.,

2008.

20.

Das D.K., Roy S.S., Dmitiriev A., Morozov A., Gössel M. Constraint Don’t Cares

for Optimizing Designs for Concurrent Checking by 1-out-of-3 Codes // Proceedings

of the 10th International Workshops on Boolean Problems, Freiberg, Germany,

September, 2012. P. 33-40.

21.

Сапожников В.В., Сапожников Вл.В., Ефанов Д.В. Построение самопроверяе-

мых структур систем функционального контроля на основе равновесного кода

«2 из 4» // Проблемы управления. 2017. № 1. С. 57-64.

22.

Ефанов Д.В., Сапожников В.В., Сапожников Вл.В., Пивоваров Д.В. Синтез

самопроверяемых схем встроенного контроля на основе метода логического до-

полнения до равновесного кода «2 из 4» // Информатика. 2018. Том 15. № 4.

С. 71-85.

23.

Saposhnikov Vl.V., Dmitriev A., Goessel M., Saposhnikov V.V. Self-Dual Parity

Checking - a New Method for on Line Testing // Proceedings of 14^th IEEE VLSI

Test Symposium, USA, Princeton, 1996. P. 162-168.

24.

Сапожников В.В., Сапожников Вл.В., Гёссель М. Самодвойственные дискрет-

ные устройства. СПб: Энергоатомиздат (Санкт-Петербургское отделение), 2001.

25.

Efanov D., Sapozhnikov V., Sapozhnikov Vl., Osadchy G., Pivovarov D. Self-

Dual Complement Method up to Constant-Weight Codes for Arrangement of

Combinational Logical Circuits Concurrent Error-Detection Systems // Proceedings

of 17th IEEE East-West Design & Test Symposium (EWDTS’2019), Batumi,

Georgia, September 13-16, 2019. P. 136-143.

https://doi.org/10.1109/EWDTS.2019.8884398

26.

Ефанов Д.В., Сапожников В.В., Сапожников Вл.В., Пивоваров Д.В. Метод

функционального контроля комбинационных логических устройств на основе

самодвойственного дополнения до равновесных кодов // Электронное модели-

рование. 2020. Т. 42. № 3. С. 27-52. https://doi.org/10.15407/emodel.42.03.027

27.

Сапожников В.В., Сапожников Вл.В., Ефанов Д.В. Основы теории надежности

и технической диагностики. СПб.: Изд-во «Лань», 2019.

157

28.

Аксёнова Г.П. Метод синтеза схем встроенного контроля для автоматов с памя-

тью // АиТ. 1973. № 2. С. 109-116.

Aksjonova G.P. Method of Synthesizing Built-In Monitoring Arrangements for

Automata with Memory // Autom. Remote Control. 1973. V. 34. No. 2. P. 267-273.

29.

Аксёнова Г.П. Необходимые и достаточные условия построения полностью про-

веряемых схем свертки по модулю 2 // АиТ. 1979. № 9. С. 126-135.

Aksjonova G.P. Necessary and Sufficient Conditions for Design of Completely

Checkable Modulo 2 Convolution Circuits // Autom. Remote Control. 1980. V. 40.

No. 9. P. 1362-1369.

30.

Сапожников В.В., Сапожников Вл.В., Ефанов Д.В. Коды с суммированием для

систем технического диагностирования. Т. 1: Классические коды Бергера и их

модификации. М.: Наука, 2020.

31.

Сапожников В.В., Сапожников Вл.В., Ефанов Д.В. Коды с суммированием для

систем технического диагностирования. Т. 2: Взвешенные коды с суммировани-

ем. М.: Наука, 2021.

32.

Sogomonyan E.S., Gössel M. Design of Self-Testing and On-Line Fault Detection

Combinational Circuits with Weakly Independent Outputs // J. Electron. Testing:

Theory Appl. 1993. V. 4. No. 4. P. 267-281. https://doi.org/10.1007/BF00971975

33.

Busaba F.Y., Lala P.K. Self-Checking Combinational Circuit Design for Single and

Unidirectional Multibit Errors // J. Electron. Testing: Theory Appl. 1994. V. 5.

No. 5. P. 19-28. https://doi.org/10.1007/BF00971960

34.

Morosow A, Saposhnikov V.V., Saposhnikov Vl.V., Goessel M. Self-Checking

Combinational Circuits with Unidirectionally Independent Outputs // VLSI Design.

1998. V. 5. No. 4. P. 333-345. https://doi.org/10.1155/1998/20389

35.

Matrosova A., Levin I., Ostanin S. Survivable Self-Checking Sequential Circuits //

Proceedings of 2001 IEEE International Symposium on Defect and Fault Tolerance

in VLSI Systems (DFT’2001), USA, CA, San Francisco, October 24-26, 2001.

P. 395-402.

36.

Sapozhnikov V., Sapozhnikov Vl., Efanov D. Typical Signal Correction Structures

Based on Duplication with the Integrated Control Circuit // Proceedings of 18th

IEEE East-West Design & Test Symposium (EWDTS’2020), Varna, Bulgaria,

September 4-7, 2020. P. 78-87. https://doi.org/10.1109/EWDTS50664.2020.9224649

37.

Efanov D.V., Sapozhnikov V.V., Sapozhnikov Vl.V. Typical Structure of a Duplicate

Error Correction Scheme with Code Control with Summation of Weighted

Transitions // Electronic Modeling. 2020. V. 42. No. 5. P. 38-50.

https://doi.org/10.15407/emodel.42.05.038

Статья представлена к публикации членом редколлегии М.Ф. Караваем.

Поступила в редакцию 19.12.2020

После доработки 09.04.2021

Принята к публикации 29.04.2021

158