Автоматика и телемеханика, № 9, 2021
© 2021 г. Б.Т. ПОЛЯК, д-р техн. наук (boris@ipu.ru),
М.В. ХЛЕБНИКОВ, д-р физ.-мат. наук (khlebnik@ipu.ru)
(Институт проблем управления им. В.А. Трапезникова РАН, Москва)
СИНТЕЗ СТАТИЧЕСКОГО РЕГУЛЯТОРА
ДЛЯ ПОДАВЛЕНИЯ ВНЕШНИХ ВОЗМУЩЕНИЙ
КАК ЗАДАЧА ОПТИМИЗАЦИИ1
В последнее время стал очень популярным подход к линейным систе-
мам управления с точки зрения оптимизации. Например, в классической
задаче о линейно-квадратичном регуляторе можно рассматривать мат-
рицу линейной обратной связи как переменную и сводить проблему к
минимизации показателя качества по этой переменной. Для этого можно
применять градиентный метод и получать обоснование сходимости. Та-
кой подход был успешно применен для ряда задач, включая оптимизацию
обратной связи по выходу. В настоящей статье такой подход впервые при-
меняется к задаче подавления ограниченных внешних возмущений. Вы-
писан градиентный метод для отыскания статической обратной связи по
состоянию или выходу и дано его обоснование. Рассмотрен ряд примеров,
включающих в себя простой и двойной маятники.
Ключевые слова: линейные системы, внешние возмущения, обратная
связь по выходу, обратная связь по состоянию, оптимизация, градиент-
ный метод, метод Ньютона, сходимость.
DOI: 10.31857/S0005231021090038
1. Введение
Задача о подавлении ограниченных внешних возмущений (peak-to-peak gain
minimization) формулируется следующим образом. Рассмотрим линейную
стационарную динамическую систему в непрерывном времени
x = Ax + Bu + Dw, x(0) = x0,
(1)
y = C1x,
z = C2x + B1u,
где A ∈ Rn×n, B ∈ Rn×p, B1 ∈ Rr×p, D ∈ Rn×m, C1 ∈ Rl×n, C2 ∈ Rr×n, с со-
стоянием x(t) ∈ Rn, измеряемым выходом y(t) ∈ Rl, регулируемым выходом
z(t) ∈ Rr, управлением u(t) ∈ Rp и измеримым по t внешним возмущением
w(t) ∈ Rm, ограниченным в каждый момент времени:
|w(t)| ≤ 1 для всех t ≥ 0.
1 Исследование выполнено при поддержке Российского научного фонда, проект № 21-
71-30005.
86
Никаких других ограничений на возмущение w(t) не накладывается; так,
оно не предполагается ни случайным, ни гармоническим. Задача заключается
в выборе стабилизирующего управления в форме обратной связи по состоя-
нию (если оно доступно) u = Kx или по выходу u = Ky, чтобы уменьшить
“пик” выхода z(t), т.е. величину max |z(t)|. Точное решение такой задачи за-
t
труднительно, однако возможна минимизация верхней грани этой величины,
формулируемой с помощью понятия инвариантного эллипсоида. Такой под-
ход впервые был применен в монографии С. Бойда и соавт. [1] и развит в пуб-
ликациях [2-4]. Подробное изложение этой техники можно найти в книге [5].
При этом задача управления по состоянию с помощью замен переменных сво-
дится к параметрической задаче полуопределенного программирования, т.е. к
задаче выпуклой оптимизации при ограничениях в форме линейных матрич-
ных неравенств при наличии скалярного параметра. Для таких задач суще-
ствуют удобные численные методы решения [6, 7]. В задаче управления по
выходу такое сведение невозможно (впрочем, можно применять не статиче-
ский, а динамический регулятор, и тогда задача записывается как выпуклая,
см. [5]). Авторы настоящей статьи, однако, задаются управлением в форме
статической обратной связи в силу простоты таких регуляторов; для таких
задач требуются новые методы решения.
В связи с этим напомним о новых подходах для классической проблемы
линейно-квадратичного регулирования. Ее можно рассматривать как задачу
оптимизации, где переменной является матрица обратной связи, а миними-
зируется интегральный квадратичный показатель качества переходного про-
цесса. Градиент такой функции (для управления по состоянию) выписан еще
в основополагающей работе Калмана [8], а для обратной связи по выходу
в статье Левина и Атанса [9]. С тех пор неоднократно применялись итера-
тивные методы оптимизации градиентного типа (см., например, обзор [10]),
однако обоснование подобных методов появилось лишь недавно, в [11-15].
В настоящей статье аналогичный подход впервые применяется к задачам с
внешними возмущениями.
Структура статьи следующая. В разделе 2 мы напоминаем технику инва-
риантных эллипсоидов и приводим формулировку задачи анализа (нахожде-
ния минимального инвариантного эллипсоида для замкнутой системы). При
этом предлагается новый эффективный алгоритм однопараметрической оп-
тимизации. В разделе 3 задача синтеза регулятора, оптимально подавляю-
щего помехи, записывается как задача невыпуклой матричной оптимизации.
Раздел 4 посвящен исследованию возникающей функции, вычислению ее гра-
диента, формулировке и обоснованию итеративного алгоритма оптимизации.
Раздел 5 содержит описания результатов вычислений для нескольких приме-
ров. В заключении обсуждаются возможные обобщения полученных резуль-
татов.
Всюду далее | · | евклидова норма вектора, ∥ · ∥ спектральная нор-
ма матрицы, ∥ · ∥F
фробениусова норма матрицы,⊤ символ транспо-
нирования, tr след матрицы, 〈·, ·〉 скалярное произведение Фробениуса
для матриц, I единичная матрица соответствующей размерности, λi(A)
87
собственные значения матрицы A, а σ(A) = - maxRe (λi(A)) > 0
степень
i
устойчивости гурвицевой матрицы A. Все матричные неравенства понимают-
ся в смысле знакоопределенности матриц.
2. Метод инвариантных эллипсоидов и задача анализа
2.1. Формулировка задачи и алгоритм оптимизации
Для дальнейшего изложения напомним концепцию метода инвариантных
эллипсоидов. Рассмотрим линейную стационарную динамическую систему в
непрерывном времени
x = Ax + Dw, x(0) = x0,
(2)
z = Cx,
где A ∈ Rn×n, D ∈ Rn×l, C ∈ Rn×n, с состоянием x(t) ∈ Rn, выходом z(t) ∈ Rn
и измеримым по t внешним возмущением w(t) ∈ Rl, ограниченным в каждый
момент времени:
(3)
|w(t)| ≤ 1 для всех t ≥ 0.
Никаких других ограничений на возмущение w(t) не накладывается; так, оно
не предполагается ни случайным, ни гармоническим. Будем полагать, что си-
стема (2) устойчива (т.е. матрица A гурвицева), пара A, D управляема, C
матрица полного ранга. Заметим, что наложены более жесткие требования
к постановке задачи, чем обычно [3, 5, 16]: предполагается, что размерности
выхода и состояния совпадают, а матрица C невырожденная. Это пред-
положение можно было бы ослабить, но цель авторов сейчас получить
наиболее простые и наглядные результаты.
Определение 1. Эллипсоид с центром в начале координат
{
}
(4)
Ex = x ∈ Rn : x⊤P-1x ≤ 1
,
P ≻ 0,
называется инвариантным для динамической системы (2), (3), если из усло-
вия x(0) ∈ Ex следует x(t) ∈ Ex для всех моментов времени t ≥ 0.
Иными словами, любая траектория системы, исходящая из точки, лежа-
щей в эллипсоиде Ex, при всех допустимых внешних возмущениях, действую-
щих на систему, в любой момент времени будет находиться в этом эллипсоиде.
Инвариантный эллипсоид обладает следующим свойством:
x(t) ---→
Ex при x(0) ∈ Ex
t→∞
(при этом, возможно, x(t) ∈ Ex при t ≥ T для некоторого T > 0), т.е. траекто-
рия системы, исходящая из точки вне эллипсоида Ex, стремится к эллипсои-
ду Ex с течением времени. Таким образом, инвариантный эллипсоид является
также и притягивающим.
88
Соответственно, если начальное состояние системы принадлежит инвари-
антному эллипсоиду, имеем равномерную оценку поведения траекторий си-
стемы в любой момент времени траектории принадлежат этому эллипсоиду
при любых допустимых внешних возмущениях; если же начальные условия
произвольны, имеем асимптотическую оценку поведения траекторий систе-
мы: при любых допустимых внешних возмущениях траектории будут стре-
миться к этому эллипсоиду с течением времени.
Инвариантные эллипсоиды можно рассматривать как характеристику
влияния внешних возмущений на траектории динамической системы. А имен-
но в рамках задачи анализа проблема состоит в оценке степени влияния внеш-
них возмущений на вектор выхода системы. В этой связи естественно интере-
соваться минимальными в том или ином смысле эллипсоидами, содержащими
выход системы.
Нетрудно видеть, что если Ex инвариантный эллипсоид (4) с матрицей P ,
то выход системы (2) при x0 ∈ Ex принадлежит эллипсоиду
{
}
(5)
Ez = z ∈ Rn : z⊤(CPC⊤)-1z ≤ 1
Эллипсоид (5) будем называть ограничивающим (по выходу). Часто в
качестве критерия его минимальности рассматривается линейная функция
f (P ) = tr CP C⊤, значение которой равно сумме квадратов полуосей ограни-
чивающего эллипсоида. Нетрудно видеть, что справедлива оценка
|z(t)|2 ≤ tr CP C⊤.
Таким образом, получаем верхнюю оценку выхода при ограниченной помехе,
ее и будем минимизировать.
В [1] был установлен результат, дающий критерий инвариантности эллип-
соида в терминах линейных матричных неравенств. Несколько уточняя этот
критерий (см. [5]), приходим к следующей одномерной оптимизационной за-
даче при наличии матричных ограничений типа равенств.
Теорема 1. Пусть матрица A гурвицева, σ = -maxRe (λi(A)) > 0, па-
i
ра (A, D) управляема, матрица C квадратная невырожденная, а матрица
P (α) ≻ 0, 0 < α < 2σ, удовлетворяет уравнению Ляпунова
(
)
(
)⊤
α
α
1
(6)
A+
I P +P A+
I
+
DD⊤
= 0.
2
2
α
Тогда задача об оптимальном ограничивающем эллипсоиде сводится к ми-
нимизации одномерной функции
f (α) = tr CP (α)C⊤
на интервале 0 < α < 2σ и если α∗ точка минимума и x(0) удовлетво-
ряет условию x⊤(0)P-1(α∗)x(0) ≤ 1, то гарантируется оценка
|z(t)|2 ≤ f(α∗),
0 ≤ t < ∞.
89
Поскольку уравнение (6) нелинейно по совокупности переменных P и α,
то в литературе по этой проблематике (см. [4] и др.) поиск минимального
ограничивающего эллипсоида предлагалось проводить на одномерной сетке
по параметру α; при этом вместо матричного уравнения (6) рассматривалось
соответствующее матричное неравенство Ляпунова. В статье предлагается
более эффективный способ оптимизации, основанный на свойствах миними-
зируемой функции и на явном виде ее производных. Сформулируем эти свой-
ства.
Лемма 1. Пусть матрица A гурвицева, 0 < α < 2σ, пара (A,D) управ-
ляема, а матрица C такова, что C⊤C ≻ 0. Тогда функция f(α) = tr CP C⊤,
где P = P (α) удовлетворяет (6), обладает следующими свойствами:
а) функция f(α) определена, положительна и сильно выпукла на интер-
вале 0 < α < 2σ, а ее значения стремятся к бесконечности на концах ин-
тервала, причем существует c > 0 такое, что
c
f (α) ≥
,
0 < α < 2σ;
α(2σ - α)
б) производная функции f(α) имеет вид
(
)
1
(7)
f′(α) = tr Y P -
DD⊤
,
α2
где Y
решение уравнения Ляпунова
(
)⊤
(
)
α
α
(8)
A+
I
Y +Y A+
I
+C⊤C = 0;
2
2
в) вторая производная функции f(α) определяется формулой
(
)
1
(9)
f′′(α) = 2tr Y X +
DD⊤
,
α3
где X решение уравнения Ляпунова
(
)
(
)⊤
α
α
1
(10)
A+
I X+X A+
I
+P -
DD⊤
= 0,
2
2
α2
причем f′′(α∗) > 0 и f′′(α) монотонно возрастает слева и справа от α∗.
Доказательства этого и последующих утверждений приведены в Прило-
жении. Заметим, что для вычисления функции f(α) и двух ее производных
достаточно решить три уравнения Ляпунова.
Указанные свойства функции позволяют применить метод Ньютона для
ее минимизации. Задаемся начальным приближением 0 < α0 < 2σ, например
α0 = σ, и применяем итерационный процесс
f′(αj)
(11)
αj+1 = αj -
f′′(αj)
Следующая теорема 2 гарантирует глобальную сходимость алгоритма.
90
Теорема 2. В методе (11) справедливы оценки
f′′(α0)
|αj - α∗| ≤
|α0 - α∗|,
|αj+1 - α∗| ≤ c|αj - α∗|2,
2j f′′(α∗)
где c > 0 некоторая константа (она может быть выписана явно).
Этот результат следует из утверждений леммы 1 и по существу является
небольшой модификацией теорем 3.3 и 3.5 публикации [17], поэтому опускаем
его доказательство. Таким образом, первая оценка гарантирует глобальную
сходимость метода (быстрее, чем геометрическая прогрессия с коэффици-
ентом 1/2), а вторая квадратичную сходимость в окрестности решения.
Реально требуется не более 3-4 итераций для получения решения с большой
точностью (если только начальная точка не слишком близка к границам ин-
тервала).
Таким образом, авторы располагают быстрым алгоритмом для оптимиза-
ции по параметру α.
3. Задача синтеза
3.1. Формулировка задачи оптимизации
Перейдем к задаче синтеза и рассмотрим линейную непрерывную систему
управления
x = Ax + Bu + Dw, x(0) = x0,
(12)
y = C1x,
z = C2x,
где A ∈ Rn×n, B ∈ Rn×p, D ∈ Rn×n, C1 ∈ Rl×n, C2 ∈ Rn×n, с состоянием
x(t) ∈ Rn, наблюдаемым выходом y(t) ∈ Rl, регулируемым выходом z(t) ∈ Rn,
управлением u(t) ∈ Rp и внешним возмущением w(t) ∈ Rn, удовлетворяющим
ограничению (3); матрицы D и C2 квадратные невырожденные. Отметим,
что вновь рассматривается не самая общая постановка задачи по сравнению
с (2): размерности x, w и z совпадают, матрицы D, C2 невырожденные, а в
выходе z отсутствует управление (смысл последнего отличия будет пояснен
далее).
Целью является нахождение регулятора K в форме статической линейной
обратной связи по выходу
(13)
u=Ky, K ∈Rp×l,
который стабилизирует замкнутую систему и подавляет воздействие внеш-
них возмущений w, минимизируя размер ограничивающего эллипсоида для
выхода z. В качестве критерия оптимальности рассмотрим величину
(14)
tr C2P C⊤2 + ρ∥K∥2F .
91
Первая компонента (14) определяет размер ограничивающего эллипсои-
да по критерию следа, а вторая представляет штраф за величину управле-
ния (при этом коэффициент ρ > 0 регулирует его важность). Наличие второй
компоненты позволяет избежать появления больших значений матрицы ре-
гулятора: в частности, если управление и возмущение “приложены в одной
точке” (т.е. матрицы B и D совпадают), то за счет больших величин K линей-
ный выход системы может быть сделан сколь угодно малым. Обычно штраф
за управление вводится путем добавления члена с управлением в регулируе-
мый выход (см. выражение B1u в (1)); авторам статьи удобнее использовать
форму показателя качества (14).
В целом вид целевой функции (14) аналогичен критерию оптимальности в
задаче о линейно-квадратичном регуляторе, где также присутствуют члены,
отвечающие за величину отклонения траектории и за величину управления;
разница лишь в том, что там эти члены имеют вид интегралов, а не макси-
мальных значений.
Таким образом, задача о синтезе регулятора, подавляющего внешние воз-
мущения, свелась к следующей матричной оптимизационной задаче:
min f(K, α), f(K, α) = tr C2P C⊤2 + ρ∥K∥2F
при ограничении
(
)
(
)⊤
α
α
1
(15)
AK +
I P +P AK +
I
+
DD⊤ = 0, AK = A + BKC1,
2
2
α
относительно матричных переменных P = P⊤ ∈ Rn×n, K ∈ Rp×n и скалярно-
го параметра α > 0. Запись f(K, α) подчеркивает, что при заданных K и α
матрица P находится из уравнения Ляпунова (15); тем самым независимыми
переменными являются K и α. Однако минимизацию по α можно произ-
водить достаточно эффективно, см. подраздел 2.1; нужно лишь матрицу A
заменить на AK . Поэтому будем интересоваться функцией
(16)
f (K) = min
f (K, α);
α
ее минимизацией и займемся. Предварительно исследуем свойства этой функ-
ции.
3.2. Свойства функции f(K)
В дальнейшем делаем следующее предположение.
Предположение. Известен стабилизирующий регулятор K0, т.е.
такой, что матрица A + BK0C1 гурвицева.
Это предположение существенно, поскольку проблема существования ста-
билизирующего статического регулятора по выходу является нерешенной.
Перейдем к описанию свойств функции f(K).
Лемма 2. Функция f(K) определена и положительна на множестве S
стабилизирующих регуляторов.
92
Действительно, если матрица AK = A + BKC1 гурвицева, то σ(AK ) > 0 и
для 0 < α < 2σ(AK ) решение P ≻ 0 уравнения Ляпунова (15) существует. Тем
самым определена функция f(K, α) > 0; при этом f(K) > 0 в силу леммы 1.
Множество ее определения S может быть невыпуклым и несвязным, причем
его границы могут быть негладкими, см. примеры далее.
Лемма 3. На множестве S стабилизирующих регуляторов функция
f (K) коэрцитивна (т.е. стремится к бесконечности на границе области),
причем справедливы следующие оценки:
λmin(DD⊤)λmin(C2C⊤2)
(17)
f (K) ≥
,
4σ2(AK )
f (K) ≥ ρ∥K∥2.
Введем в рассмотрение множество уровня
S0 = {K ∈ S : f(K) ≤ f(K0)}.
Из леммы 3 вытекает очевидное следствие 1.
Следствие 1. Для любого регулятора K0∈S множество S0 ограничено.
C другой стороны, у функции f(K) на множестве S0 существует точка
минимума (как у непрерывной функции на компактном множестве), но мно-
жество S0 не имеет общих точек с границей S в силу (17). Впоследствии
будет показано, что f(K) дифференцируема на S0. Следовательно, справед-
ливо следствие 2.
Следствие 2. Существует точка минимума K∗ на множестве S, и в
ней градиент обращается в нуль.
Перейдем к свойствам функции f(K, α).
Лемма 4. Функция f(K,α) определена на множестве стабилизирую-
щих обратных связей K и для 0 < α < 2σ(AK ). На этом допустимом мно-
жестве она дифференцируема, причем градиент дается выражениями
(
)
(18)
∇Kf(K,α) = 2 ρK + B⊤Y PC⊤
,
1
(
)
1
(19)
∇αf(K,α) = tr Y P -
DD⊤ ,
α2
где матрица Y является решением уравнения Ляпунова
(
)⊤
(
)
α
α
(20)
AK +
I
Y +Y AK +
I
+C⊤2C2
= 0.
2
2
Минимум f(K,α) достигается во внутренней точке допустимого мно-
жества и определяется условиями
∇Kf(K,α) = 0,
∇αf(K,α) = 0.
93
При этом f(K, α) как функция от α строго выпукла на 0 < α < 2σ(AK ) и
достигает минимума во внутренней точке этого интервала (см. подраз-
дел 2.1).
Свойства гессиана функции f(K, α) представлены следующим утвержде-
нием.
Лемма 5. Функция f(K,α) дважды дифференцируема по K, причем дей-
ствие гессиана функции на произвольную матрицу2 E ∈ Rp×l дается выра-
жением
1
(21)
∇2Kf(K)[E,E] = ρ〈E,E〉 + 2〈B⊤Y P′C⊤1,E〉,
2
где P′
решение уравнения Ляпунова
(
)
(
)⊤
α
α
(22)
AK +
I P′ +P′ AK +
I
+ BEC1P + P(BEC1)⊤
= 0.
2
2
Градиент функции f(K, α) по K не является липшицевым на множестве S
стабилизирующих регуляторов, однако он обладает этим свойством на его
подмножестве S0. Соответствующий результат представлен далее.
Лемма 6. На множестве S0 градиент функции f(K,α) по K липшицев
с константой
f2(K0)
(23) L = ρ + 8√n∥B∥F ∥C1∥
×
λmin(C⊤2C2)λ2min(DD⊤)
)
(
√
)2 (f2(K0)
× ∥A∥ +
f (K0)∥B∥∥C1∥
+ ∥B∥2∥C1∥2
λ2min(C⊤2C2)
Полученные свойства минимизируемой функции и ее производных позво-
ляют построить метод минимизации и обосновать его сходимость.
3.3. Алгоритм оптимизации
Ограничение в оптимизационной задаче (15) невыпукло по совокупности
переменных P и K. В случае управления по состоянию (т.е. при C1 = I) за-
дачу можно свести к эквивалентной линейной, введя вспомогательную мат-
ричную переменную и исключив матрицу регулятора K (подробнее см. [4]).
Однако в случае управления по выходу такой подход неприменим. Отметим
еще, что даже в случае управления по состоянию минимизирумая функция
не является выпуклой.
Авторы предлагают итеративный подход к решению этой задачи; в его
основе лежит применение градиентного метода по переменной K и миними-
зации по α, описанной в подразделе 2.1. Приведем принципиальную схему
алгоритма.
2 Понимаемое в смысле второй производной по направлению.
94
Алгоритм 1 для минимизации f(K,α):
1) Задаемся параметрами ε > 0, γ > 0, 0 < τ < 1 и начальным стабилизи-
рующим приближением K0. Вычисляем величину α0 = σ(A + BK0C1).
2) На j-й итерации заданы Kj , αj. Вычисляем Aj = A + BKjC1, решаем
уравнение (20) и находим Y , вычисляем градиент Hj = ∇K f(Kj, αj ) из
уравнения (18). Если ∥Hj ∥ ≤ ε, то Kj принимаем за приближенное ре-
шение.
3) Делаем шаг градиентного метода
Kj+1 = Kj - γjHj.
Длину шага γj > 0 подбираем дроблением γ до выполнения условий:
а. Kj+1
стабилизирующий регулятор;
б. f(Kj+1) ≤ f(Kj ) - τγj ∥Hj∥2.
4) Для полученного Kj+1 решаем задачу минимизации f(Kj+1, α) по α
(см. раздел 2), получаем αj+1. Переходим к п. 2.
Предлагаемый метод сходится в следующем смысле.
Теорема 3. В алгоритме 1 на каждой итерации реализуется лишь ко-
нечное число дроблений γj, функция f(Kj) монотонно убывает и градиент
стремится к нулю
lim
∥Hj∥ = 0
j→∞
со скоростью геометрической прогрессии.
Доказательство (в Приложении) использует обычную схему анализа гра-
диентного метода для безусловной минимизации функций с липшицевым гра-
диентом [18], при этом способ подбора шага в алгоритме гарантирует, что
величины Kj остаются в области S0, для которой лемма 6 обеспечивает лип-
шицевость градиента. Естественно, что трудно рассчитывать на сходимость
к глобальному минимуму, поскольку область определения f(K) может быть
даже несвязной. Однако, по-видимому, для задачи управления по состоянию
(C1 = I) можно гарантировать и глобальную сходимость к единственной точ-
ке минимума подобно тому, как это удается доказать для задачи о линейно-
квадратичном регуляторе [15].
Заметим еще, что способ выбора шага в алгоритме 1 отнюдь не является
самым быстрым с вычислительной точки зрения. Например, весьма перспек-
тивным является способ, аналогичный предложенному в [15] и основанный
на использовании вторых производных. При этом пробный шаг выбирается
по формуле
2
∥Hj∥
(24)
γj =
,
∇2Kf(K)[Hj,Hj]
где вычисление выражения в знаменателе делается с помощью формулы (21),
после чего он корректируется так же, как в алгоритме 1. Отметим, что ис-
пользование вторых производных требует всего лишь решения еще одного
уравнения Ляпунова, т.е. не сильно усложняет вычисления.
95
Смысл формулы (24) в том, что это один шаг метода Ньютона для мини-
мизации одномерной функции φ(γ) = f(Kj - γHj ). Свойства такого метода
описаны в [15]; как правило, он (назовем его в нашем контексте Алгорит-
мом 2 ) дает заметно более быструю сходимость, чем алгоритм 1; это под-
тверждается приводимыми далее примерами.
4. Примеры
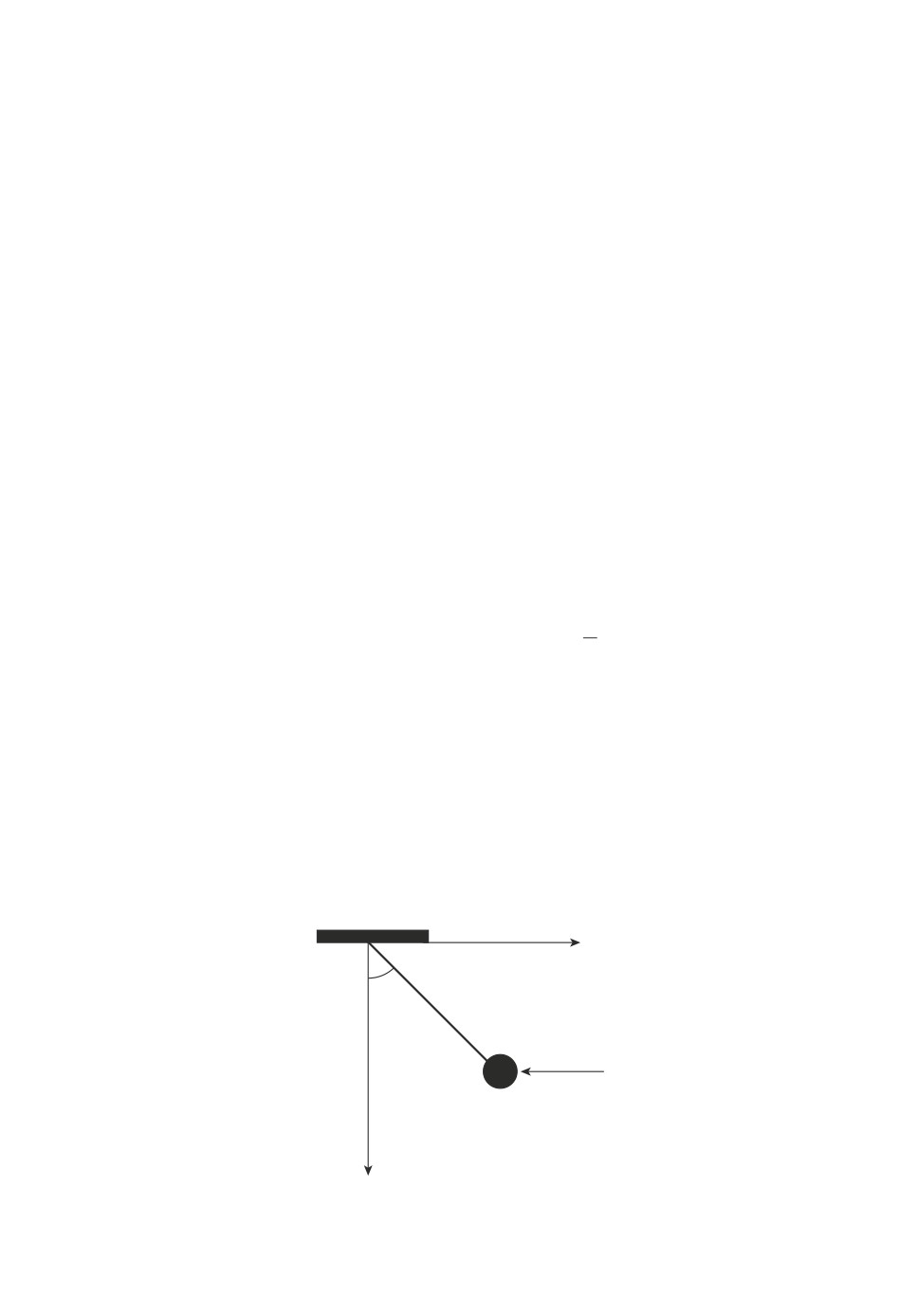
Пример 1. Рассмотрим математический маятник (рис. 1), движущийся
в вязкой среде, на который действует ограниченное внешнее возмущение.
Полагая параметры единичными, приходим к линеаризованной системе
x1 = x2,
x2 = -x1 - x2 + w,
|w| ≤ 1,
или в матричной форме
(
)
0
1
(0)
A=
,
D=
−1 -1
1
Рассматривая в качестве выхода состояние системы (C = I), приходим к за-
даче
1
min tr P при AP + P A⊤ + αP +
DD⊤ = 0
α
относительно P = P⊤ ∈ R2×2 и 0 < α < -2 max Re λ(A) = 1.
Зная первую (7) и вторую (9) производные минимизируемой функции,
с помощью метода Ньютона находим оптимальное значение α∗ = 0,4618 и
соответствующую матрицу
(
)
2,4461
-0,5649
P∗
=
-0,5649
2,1422
эллипса, содержащего траектории системы; при этом tr P∗ = 4,5883.
x
j
l
w
m
y
Рис. 1. Математический маятник из примера 1.
96
a
б
60
4,615
1
2
50
4,610
40
4,605
30
4,600
20
4,595
10
4,590
0
0,1 0,2 0,3 0,4 0,5
0,6 0,7 0,8 0,9
1,0
0,46
0,47
0,48
0,49
0,50
a
a
Рис. 2. Оптимизационная процедура в примере 1.
На рис. 2,а показан график функции f(α) = tr P (α), а на рис. 2,б ди-
намика оптимизационной процедуры (линия 1 соответствует функции f(α),
а линия 2 собственно оптимизационной процедуре). По существу, уже пер-
вая итерация дает решение с достаточной точностью.
Пример 2. Рассмотрим математический маятник, на который воздей-
ствует ограниченное внешнее возмущение, для компенсации которого к нему
приложено управляющее воздействие:
x1 = x2,
x2 = -x1 + u + w,
|w| ≤ 1.
При этом измеряемым выходом служит все состояние системы (т.е. y = x).
Отметим, что в данном примере (и ряде следующих) не выполнено одно из
предположений теоремы 3: здесь размерность возмущений меньше числа со-
стояний, однако алгоритм оптимизации применим и работает.
В результате имеем
(
)
(
)
0
1
0
)
A=
,
B=D=
,
C1 = I, K =
(k1 k2
−1 0
1
Для
)
C2 =
(1
0
,
ρ = 1,
решая на двумерной сетке по k1 и k2 уравнение Ляпунова (15) и вычисляя
min
tr C2P (α)C⊤2, численным образом находим функцию
α
f (k1, k2) = C2P (K)C⊤2 + ∥K∥2.
Ее линии уровня показаны на рис. 3. В данном случае линии уровня гладкие
и выпуклые.
97
1
-0,5
2
-1,0
-1,5
-2,0
-2,5
-3,0
-3,5
-4,0
-3,5
-3,0
-2,5
-2,0
-1,5
-1,0
-0,5
k1
Рис. 3. Линии уровня и оптимизационная процедура в примере 2.
Для начального регулятора
(
)
K0 =
-3 -3
вычисления в соответствии с алгоритмом 1 доставляют на 119-й итерации
регулятор
)
K∗ =
(-0,7224 -1,2205
,
при котором f(K∗) = 2,9377 (линия 1 на рис. 3). Алгоритм 2 требует всего
лишь 7 итераций и приводит к регулятору
(
)
K∗ =
-0,6477
-1,2038
,
для которого f(K∗) = 2.8670 (линия 2 на рис. 3).
Пример 3. Рассмотрим систему с матрицами
0
1
0
0
A=
0
0
1, B=D=
0,
−1 -1 a
1
(
)
C1 =
5
2
1
,
C2 = I, ρ = 1.
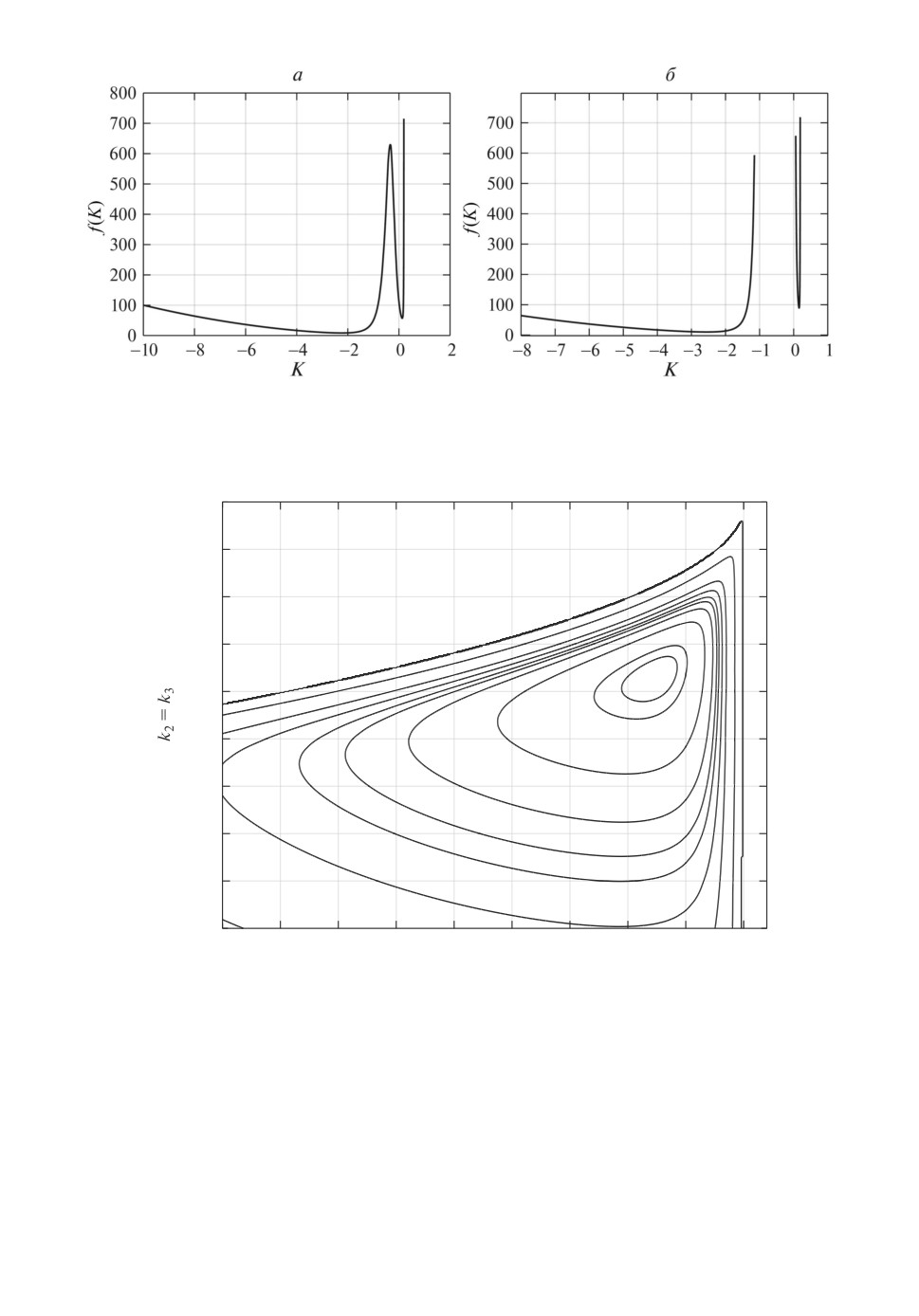
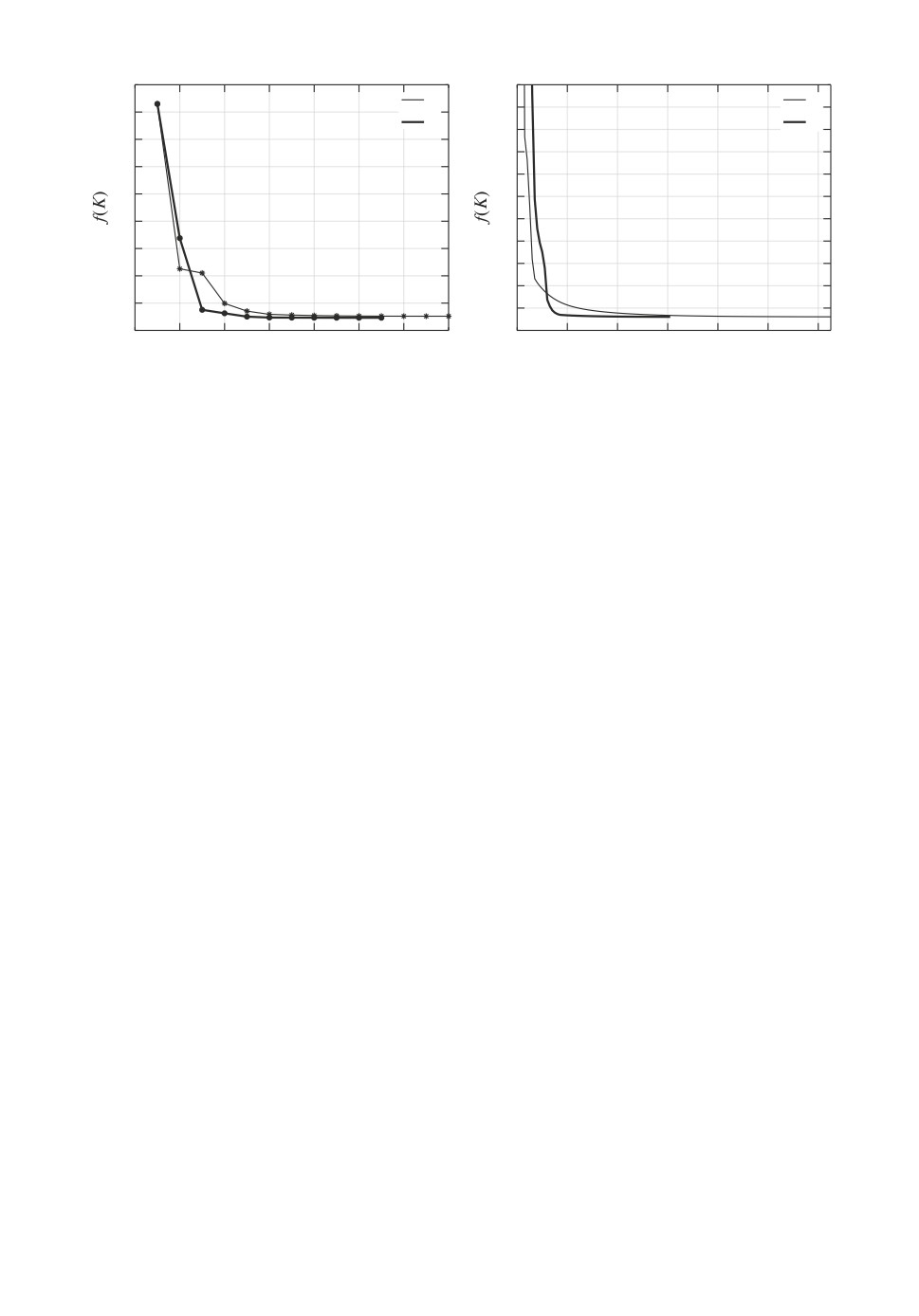
При a = -1,4 функция
(
)
f (k) = tr C2P (k)C⊤
2
+k2
98
Рис. 4. Графики целевой функции в примере 3.
0
-0,5
-1,0
-1,5
-2,0
-2,5
-3,0
-3,5
-4,0
-4,5
-4,0
-3,5
-3,0
-2,5
-2,0
-1,5
-1,0
-0,5
0
k1
Рис. 5. Линии уровня в примере 4.
имеет два локальных минимума (см. рис. 4,a), а при a = -1 ее область опре-
деления несвязна (см. рис. 4,б). Ясно, что отыскивать глобальный минимум
в такой задаче очень трудно.
Заметим, что в данном примере используется управление по выходу, тогда
как в предыдущем управление по состоянию.
99
x1
x2
k
u
w
m1
m2
Рис. 6. Двухмассовая система из примера 5.
Пример 4. Для системы с матрицами
0
1
0
0
A = 0 0 1,B=D= 0,C1 = C2 = I, ρ = 1,
0
0
0
1
(
)
сечение области определения функции f(K) = tr
C2P(K)C⊤2
+ ∥K∥2F плос-
костью k2 = k3 невыпукло, см. рис. 5. Более того, сама область S негладкая,
а области уровня S0 гладкие.
Пример 5. Рассмотрим задачу управления двухмассовой системой из
двух твердых тел с массами m1 и m2, соединенных пружиной с коэффициен-
том упругости k, скользящих без трения вдоль неподвижного горизонтально-
го стержня (см. рис. 6); к левому телу приложено управление u, а к правому
внешнее возмущение |w| ≤ 1. Эта задача часто используется как тестовая для
различных методов синтеза регуляторов, чему способствуют ее реальное про-
исхождение и разумная размерность модели.
Обозначим через x1, v1 координату и скорость левого тела, а через x2, v2
правого тела. Тогда
(
)⊤
x=
x1
x2
v1
v2
есть вектор фазового состояния рассматриваемой динамической системы,
полностью описывающий ее поведение.
Непрерывная модель колебаний системы описывается уравнениями
x1 = v1,
x2 = v2,
k
k
1
v1 = -
x1 +
x2 +
u,
m1
m2
m1
k
k
1
v2 =
x1 -
x2 +
w.
m2
m2
m2
При единичных параметрах системы (k = m1 = m2 = 1) приходим к системе
с матрицами
0
0
1
0
0
0
0
0
0
1
0
0
A=
B=
D=
-1
1
0
0,
1,
0.
1
-1 0 0
0
1
100
a
б
60
70
1
1
55
65
2
2
60
50
55
45
50
40
45
35
40
35
30
30
25
25
20
20
15
15
0
2
4
6
8
10
12
14
0
20
40
60
80
100
120
Niter
Niter
Рис. 7. Оптимизационная процедура в примере 5.
Пусть измерению доступно все состояние системы (C1 = I), а в качестве ми-
нимизируемого выхода возьмем координаты левого и правого тела:
)
(1 0 0
0
C2 =
0
1
0
0
Пусть также ρ = 1.
Сначала в качестве начальной точки выберем некоторый начальный ста-
билизирующий регулятор
(
)
K0 =
-1 0 -1 0
и соответствующее ему допустимое начальное значение параметра
α0 = σ(A + BK0C1).
Критерием остановки процесса будет служить уменьшение целевой функции
на некотором шаге менее, чем на 0,001.
На рис. 7,a линия 1 соответствует динамике изменения критерия f(K) =
= tr C2P C⊤2 + ∥K∥2F в соответствии с алгоритмом 1. Процесс завершился на-
хождением регулятора
(
)
K∗ =
-1,3800
-0,0836
-1,5482
-0,8047
,
при этом f(K∗) = 17,5974.
Линия 2 на рис. 7,a соответствует вычислениям по алгоритму 2. Получен
регулятор
)
K∗ =
(-1,0921 -0,1720
-1,4263
-0,5916
При этом значение целевой функции f(K∗) = 17,3148 улучшилась менее, чем
на 2%, однако число итераций сократилось.
101
x
j1
l1
u
m1
j2
l2
w
m2
y
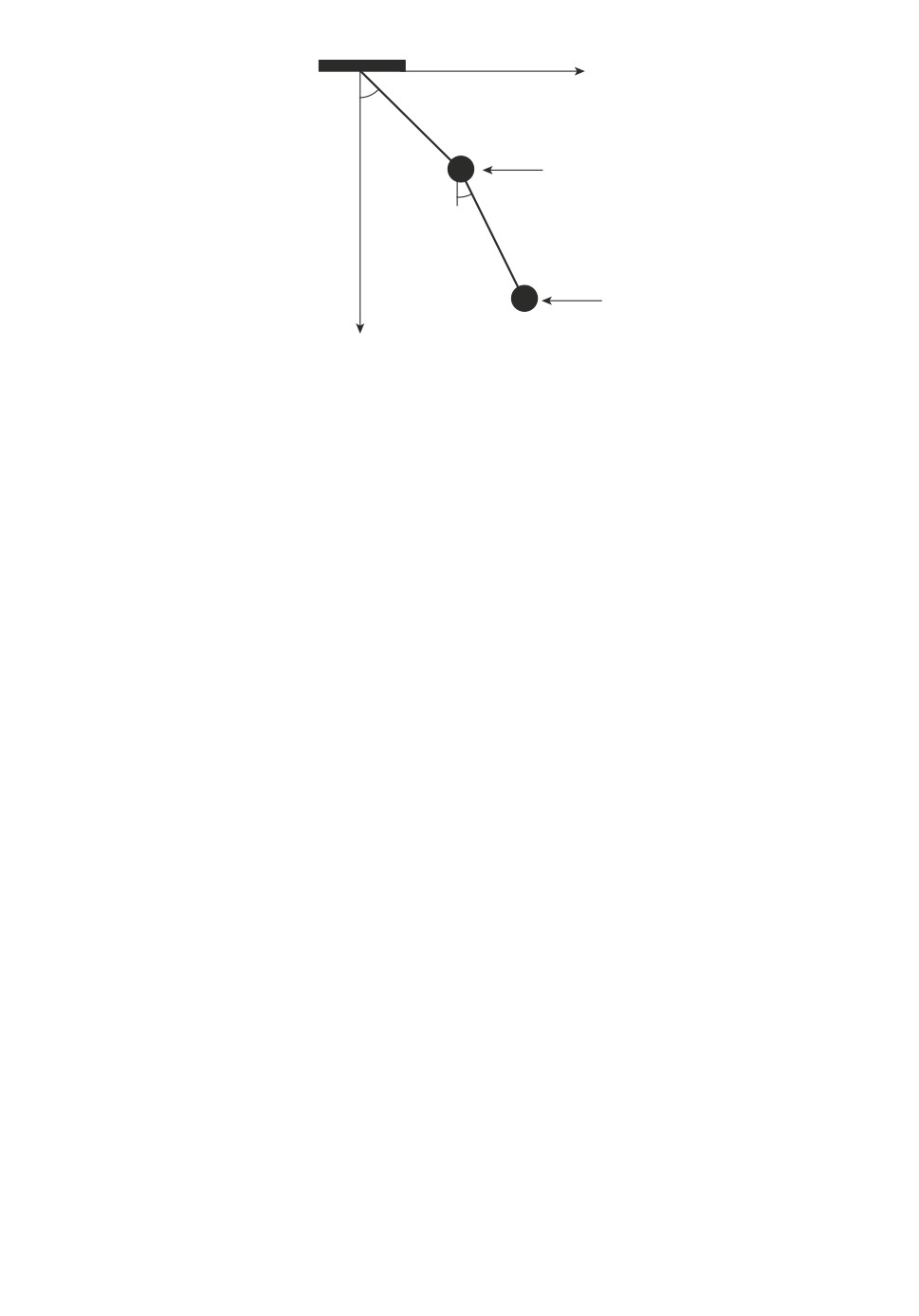
Рис. 8. Двойной математический маятник из примера 6.
Далее, для начального регулятора
(
)
K0 =
-2 0 -3 1
итерационный процесс на порядок более длителен; его динамика показана на
рис. 7,б. Линией 1 показан расчет в соответствии с алгоритмом 1; на 125-й ите-
рации процесс завершился нахождением регулятора
)
K∗ =
(-1,6245 -0,0794
-1,5570
-0,9869
;
при этом f(K∗) = 18,0417.
Линия 2 на рис. 7,б соответствует алгоритму 2. Процесс завершается быст-
рее (61 итерация) и доставляет регулятор
(
)
K∗ =
-1,6234
-0,0793
-1,5565
-0,9843
;
при этом значение целевой функции f(K∗) = 18,0367 практически не изме-
нилось.
Таким образом, здесь из разных начальных точек получаем очень близкие
оптимальные регуляторы и близкое значение критерия.
Пример 6. Рассмотрим двойной математический маятник, состоящий из
двух невесомых стержней длины l1 и l2, на концах которых укреплены гру-
зики массами m1 и m2. Система движется в вязкой среде с коэффициентом
сопротивления γ, в вертикальной плоскости xy, и положение маятника опре-
деляется углами ϕ1 и ϕ2 отклонения стержней от вертикали, см. рис. 8.
На “нижнее” тело воздействует ограниченное внешнее возмущение |w| ≤ 1,
для компенсации которого к “верхнему” телу приложено управляющее воз-
действие u.
Вводя переменные
ϕ3 =ϕ˙1, ϕ4 =ϕ˙2,
102
приходим к линеаризованной системе
ϕ1 = ϕ3,
ϕ2 = ϕ4,
(
)
m2
g
m2 g
γ
1
ϕ3 = -
1+
ϕ1 +
ϕ2 -
ϕ3 +
u,
m1
l1
m1 l1
m1
m1
(
)
(
)
m2
g
m2
g
γ
1
ϕ4 =
1+
ϕ1 -
1+
ϕ2 -
ϕ4 +
w.
m1
l2
m1
l2
m2
m2
При
m1 = m2 = 1, l1 = l2 = g, γ =
0,2
матрицы системы имеют вид
0
0
1
0
0
0
0
0
0
1
0
0
A=
,
B=
,
D=
-2
1
-0,2
0
1
0
2
-2
0
-0,2
0
1
В качестве наблюдаемого выхода выберем
)
(ϕ
1
y=
,
ϕ2
т.е.
)
(1 0 0
0
C1 =
,
0
1
0
0
а в качестве регулируемого выхода вектор
(
)
ϕ1
z=
,
ϕ2
т.е.
(
)
0
0
1
0
C2 =
0
0
0
1
Положим также ρ = 1.
Поскольку разомкнутая система устойчива, в качестве начального при-
ближения для регулятора выберем
)
K0 =
(0
0
103
a
б
55
38
1
1
37
2
2
50
36
35
45
34
40
33
32
35
31
30
30
29
28
25
0
1
2
3
4
5
6
7
8
9
10
0
2
4
6
8
10
12
14
16
Niter
Niter
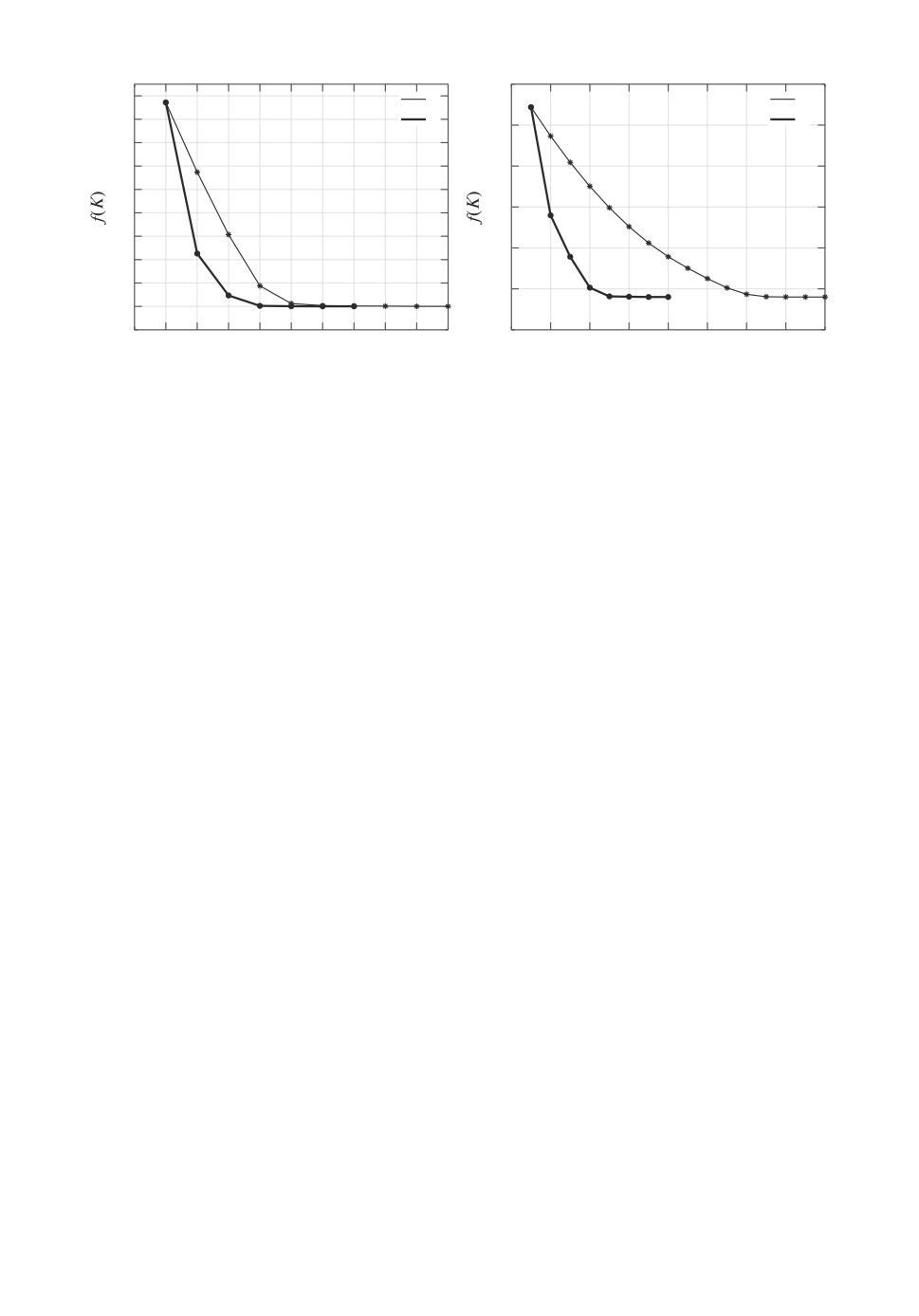
Рис. 9. Оптимизационная процедура в примере 6.
При расчете по алгоритму
1
динамика изменения критерия f(K) =
= tr C2P C⊤2 + ∥K∥2F показана линией 1 на рис. 9,а. Процесс завершился на
10-м шаге нахождением стабилизирующего регулятора по выходу
(
)
K∗ =
0,0088
-0,8657
;
при этом f(K∗) = 29,0021. При выборе шага по алгоритму 2 (линия 2 на
рис. 9,а) процесс завершается на 7-м шаге и доставляет регулятор
(
)
K∗ =
0,0083
-0,8680
;
при этом значение целевой функции f(K∗) = 29,0029 практически не изме-
нилось.
Теперь в качестве начального выберем регулятор
(
)
K0 =
-1 1
При выборе шага в соответствии с алгоритмом 1 процесс (линия 1 на рис. 9,б)
завершается на 16-й итерации и доставляет стабилизирующий регулятор по
выходу
)
K∗ =
(0,0086 -0,8697
,
при этом целевая функция f(K∗) = 29,0040. При выборе шага по алгоритму 2
(линия 2 на рис. 9,б) процесс вновь завершается раньше на 8-й итерации
и дает регулятор
(
)
K∗ =
0,0165
-0,8711
,
при этом значение целевой функции f(K∗) = 29,0071 вновь практически не
изменилось.
104
5. Обсуждение
1. Рассмотрены проблемы подавления внешних возмущений при достаточ-
но жестких ограничениях: предполагалось, что размерность возмущений и
регулируемых выходов совпадает с числом состояний. Это было сделано для
того, чтобы получить строгое доказательство сходимости предлагаемого ал-
горитма (теорема 3). Однако метод применим и в более общей ситуации.
В частности, рассмотренные примеры демонстрируют, что метод работает
и достаточно эффективен и при отсутствии таких ограничений. Его обосно-
вание представляет важную задачу.
2. Второй открытой проблемой является обоснование глобальной сходимо-
сти метода к единственной точке минимума в случае управления по состоя-
нию (т.е. когда измеряемый выход y совпадает с x). Можно ожидать, что в
этом случае минимизируемая функция удовлетворяет условию градиентного
доминирования подобно ситуации с линейно-квадратичным регулятором [15].
3. В статье рассмотрена задача управления по выходу. Возможно обоб-
щение на более широкий класс задач (в [10] аналогичные задачи названы
параметрическими LQR); именно управление имеет вид
∑
u = kiCix,
i=1
где ki параметры управления. К такому классу управлений относятся, на-
пример, ПИД-регуляторы.
4. Возможны заметно более быстрые методы минимизации первого поряд-
ка, чем градиентный метод (алгоритм 1). В частности, формула (24) дает ос-
нову для применения метода сопряженных градиентов подобно тому, как это
сделано в [15]. Подробная проверка более эффективных методов на задачах
большой размерности предполагается в будущем; в данной статье авторам
важна принципиальная возможность нового подхода к задачам подавления
возмущений.
5. В статье рассмотрена лишь задача синтеза статического регулятора.
Для динамических регуляторов в принципе возможен аналогичный подход
матрицы, задающие динамический регулятор, можно рассматривать как пе-
ременные и вести по ним оптимизацию. Однако развитие такого подхода тре-
бует серьезного обоснования.
6. Заключение
Предложен новый подход к задаче синтеза регулятора, оптимально подав-
ляющего ограниченные внешние возмущения. Он основан на сведении про-
блемы к задаче матричной оптимизации, где переменной является матрица
обратной связи (по состоянию или по выходу). Далее эта задача решается
градиентным методом; его сходимость теоретически обосновывается для ря-
да важных частных случаев. Многочисленные примеры демонстрируют эф-
фективность предлагаемого алгоритма.
105
Представляет интерес обобщение данного подхода на новые классы задач,
в частности на параметрические регуляторы типа ПИД-регуляторов, где пе-
ременными являются коэффициенты этих регуляторов, а также на случай
динамических регуляторов.
Авторы считают своим приятным долгом выразить благодарность
А.А. Трембе и анонимному рецензенту за интерес к статье, критические за-
мечания и предложения.
ПРИЛОЖЕНИЕ
Лемма П.1. Пусть X и Y решения двойственных уравнений Ляпуно-
ва с гурвицевой матрицей A:
A⊤X + XA + W = 0
и
AY + Y A⊤ + V = 0.
Тогда
tr (XV ) = tr (Y W ).
Доказательство леммы П.1. В самом деле, прямым вычислением
имеем
(
)
tr (XV ) = tr X(-AY - Y A⊤)
=
= -tr(XAY ) - tr(XY A⊤) =
= -tr(XAY )⊤ - tr(A⊤XY )⊤ =
(
)
= tr Y (-A⊤X - XA)
= tr (Y W ).
Лемма П.1 доказана.
Следующая лемма содержит некоторые хорошо известные результаты
(см., например, [19]), необходимые для дальнейшего изложения.
Лемма П.2.
1. Для матриц A и B соответствующих размерностей справедливы со-
отношения
∥AB∥F ≤ ∥A∥F ∥B∥,
| tr AB| ≤ ∥A∥F ∥B∥F ,
∥A∥ ≤ ∥A∥F ,
1
AB + B⊤A⊤ ≤ εAA⊤ +
B⊤B для любого ε > 0.
ε
106
2. Для неотрицательно определенных матриц A и B справедливы соот-
ношения
0 ≤ λmin(A)λmax(B) ≤ λmin(A)trB ≤ trAB ≤ λmax(A)trB ≤ trAtrB.
Лемма П.3. Для решения P уравнения Ляпунова
AP + P A⊤ + Q = 0
с гурвицевой матрицей A и Q ≻ 0 справедливы оценки:
λmin(Q)
λmin(Q)
(Π.1)
λmax(P) ≥
,
λmin(P) ≥
,
2σ
2∥A∥
где σ = - maxRe λi(A).
i
Если же Q = DD⊤ и пара (A, D) управляема, то
2
∥u∗D∥
(Π.2)
λmax(P) ≥
> 0,
2σ
где
u∗A = λu∗, Reλ = -σ,
∥u∥ = 1,
т.е. u левый собственный вектор матрицы A, отвечающий собственно-
му значению λ матрицы A с наибольшей вещественной частью. Вектор u
и число λ могут быть комплексными; здесь u∗ означает комплексное сопря-
жение и транспонирование.
Доказательство леммы П.3. Оценки (Π.1) хорошо известны, см.,
например, [20]. Докажем справедливость оценки (Π.2). Явное решение урав-
нения Ляпунова для гурвицевой матрицы имеет вид
+∞
P = eAtDD⊤eA⊤tdt.
0
Умножая это равенство справа на u и слева на u∗ и учитывая, что u∗eAt =
= eλtu∗, eA⊤tu = eλ∗tu, получаем, что
+∞
λmax(P) ≥ u∗Pu = u∗eAtDD⊤eA⊤tudt =
0
+∞
= e(λ+λ∗)tu∗DD⊤udt =∥u∗D∥2,
2σ
0
причем ∥u∗D∥ > 0 в силу управляемости пары (A, D), см., например, [5, тео-
рема Д.1.5]. Лемма П.3 доказана.
107
Доказательство леммы 1.
а. Уравнение (6) представимо в виде
(
)
(
)⊤
α
α
1
A+
I P +P A+
I
=-
DD⊤
2
2
α
и согласно [5, лемма 1.2.3] имеет единственное решение тогда и только тогда,
когда матрица A +α2 I гурвицева: Re λi(A +α2 I) < 0, т.е. при 0 < α < 2σ.
Оценим величину f(α) = tr CP (α)C⊤, используя лемму П.3 с очевидными
заменами:
∥u∗D∥2λmin(C⊤C)
f (α) = tr CP (α)C⊤ ≥ λmin(C⊤C)λmax (P (α)) ≥
,
α(2σ - α)
где u имеет тот же смысл, что и в лемме П.3, а величина ∥u∗D∥2 положи-
тельна в силу предположения об управляемости пары (A, D) (а тем самым и
пары (A +α2 I, D)).
Покажем теперь, что функция f(α) = tr CP (α)C⊤ строго выпукла на ин-
тервале (0, 2σ). В соответствии с [5, лемма 1.2.3] решение уравнения (6) пред-
ставимо в явном виде как
+∞
∫
eαt
P (α) = e(A+2 I)t 1
DD⊤e(A+2I)⊤tdt =
eAtDD⊤eA⊤t
|
{z
}dt.
α
α
|{z}
0
0
h(t)
g(α,t)
Но g(α, t) > 0, h(t) ≻ 0 при α > 0, поэтому на интервале (0, 2σ) имеем
+∞
P (α) = g(α, t)h(t)dt ≻ 0, f(α) = tr P (α)C⊤2C2 > 0.
0
Прямым вычислением получаем
(
αt
)e
eαt
1
g′′(α,t) =
(αt - 1)2 + 1
≥
=
g(α, t)
α3
α3
α2
(здесь дифференцирование производится по α), так что
+∞
1
1
f′′(α) =
g′′(α,t)h(t)dt ≥
f (α) ≥
f (α∗) > 0.
α2
4σ2
0
Таким образом, вторая производная функции f(α) положительна и стре-
мится к бесконечности на концах интервала (0, 2σ).
Аналогичным образом прямым вычислением четвертой производной по-
лучаем
(
αt
)e
6
6
g(IV)(α,t) =
(αt - 2)2α2t2 + 2(2αt - 3)2 + 6
≥
eαt =
g(α, t),
α5
α5
α4
108
таким образом,
6
f(IV)(α) ≥
f (α) > 0,
α4
т.е. вторая производная f′′(α) сама является выпуклой и растет на границах
интервала.
б. Выведем теперь формулу для производной функции f(α). В уравне-
нии (6) решение P является функцией от α. Продифференцируем это урав-
нение; под P′ будем понимать производную по α:
1
AP′ + P′A⊤ + αP′ + P -
DD⊤ = 0.
α2
Сравнивая уравнения для P′ и Y и применяя лемму П.1, получаем желаемую
формулу
(
)
1
f′(α) = tr CP′C⊤ = tr Y P -
DD⊤ .
α2
в. Аналогично получим выражение для второй производной f(α). Диффе-
ренцируя уравнение для P′ по α, получаем
2
AP′′ + P′′A⊤ + αP′′ + 2P′ +
DD⊤ = 0.
α3
Вновь применяя лемму П.1 к этому уравнению и уравнению (10) (и имея в
виду, что X = P′), получаем
(
)
1
f′′(α) = tr CP′′C⊤ = 2tr Y X +
DD⊤
α3
Лемма 1 доказана.
Доказательство леммы 3. Рассмотрим последовательность стабили-
зирующих регуляторов {Kj }⊆S такую, что Kj → K ∈ ∂S, т.е. σ(A+BKC1) =
= 0. Это означает, что для любого ε > 0 найдется число N = N(ε) такое, что
неравенство
|σ(A + BKjC1) - σ(A + BKC1)| = σ(A + BKjC1) < ε
справедливо для всех j ≥ N(ε).
Пусть Pj решение уравнения Ляпунова (15), ассоциированного с регу-
лятором Kj :
(
)
(
)⊤
αj
αj
1
AKj +
I Pj +Pj AKj +
I
+
DD⊤ = 0,
2
2
αj
а Yj решение двойственного к нему уравнения Ляпунова
(
)⊤
(
)
αj
αj
AKj +
I
Yj + Yj AKj +
I
+ C2C⊤2 = 0.
2
2
109
Тогда
(
)
(
)
(
)
1
f (Kj) = tr C2Pj C⊤
2
+ ρ∥Kj ∥2F ≥ tr Pj C2C⊤
2
= tr Yj
DD⊤
≥
αj
1
1
λmin(C2C⊤2)
≥
λmin(Yj)∥D∥2F ≥
αj
αj 2∥A + BKjC +αj2I∥∥D∥F ≥
λmin(C2C⊤2)
≥
4σ(A + BKjC1)∥A + BKjC +αj2I∥∥D∥F ≥
λmin(C2C⊤2)
≥
∥D∥2F
-−-→ +∞,
4ε(∥A + BKjC∥ + ε)
ε→0
поскольку
(
)
αj
0 < αj < 2σ(A + BKjC1) и σ A + BKjC1 +
I
≤ σ(A + BKjC1).
2
C другой стороны,
f (Kj ) = tr (C2Pj C⊤2) + ρ∥Kj ∥2F ≥ ρ∥Kj ∥2F ≥ ρ∥Kj ∥2 -------→ +∞.
∥Kj ∥→+∞
Лемма 3 доказана.
Доказательство леммы 4. Система (12), замкнутая обратной свя-
зью (13), принимает замкнутый вид
x = (A + BKC1)x + Dw,
(Π.3)
z = C2x.
Применяя к системе (Π.3) теорему 1, приходим к задаче
min f(K, α), f(K, α) = tr C2P C⊤2 + ρ∥K∥2F
при ограничении в виде уравнения Ляпунова относительно матрицы P инва-
риантного эллипсоида:
(A + BKC1)P + P (A + BKC1)⊤ + αP +1DD⊤ = 0.
α
Дифференцирование по α делается так же, как и выше, с заменой A на AK =
= A + BKC1. Для дифференцирования по K дадим ему приращение ΔK и
обозначим соответствующее приращение P через ΔP :
(A + B(K + ΔK)C1) (P + ΔP ) + (P + ΔP )(A + B(K + ΔK)C1)⊤+
1
+ α(P + ΔP ) +
DD⊤ = 0
α
или, после линеаризации и вычитания этого и предыдущего уравнений,
(
)
(
)⊤
α
α
(Π.4)
A+BKC1 +
I ΔP + ΔP A + BKC1 +
I
+
2
2
+ BΔKC1P + P(BΔKC1)⊤ = 0.
110
Вычислим приращение функционала f(K), линеаризуя соответствующие
величины:
Δf(K) = tr C2ΔPC⊤2 + ρtr K⊤ΔK + ρtr (ΔK)⊤K =
= tr C⊤2C2ΔP + 2ρ tr K⊤ΔK.
Рассмотрим уравнение Ляпунова (20), двойственное к (Π.4). По лемме П.1
из уравнений (Π.4) и (20) имеем
Δf(K) = tr 2C1PY BΔK + 2ρtr K⊤ΔK = 〈2(ρK + B⊤Y PC⊤1),ΔK〉.
Таким образом,
∇Kf(K,α) = 2(ρK + B⊤Y PC⊤1).
Лемма 4 доказана.
Доказательство леммы 5. Вычислим
∇2Kf(K)[E,E] = 〈∇2Kf(K)[E],E〉,
взяв производную по направлению E ∈ Rp×l от ∇K f(K)[E] = 〈∇K f(K), E〉.
Линеаризуя соответствующие величины, вычислим приращение функцио-
нала ∇K f(K)[E] по направлению E:
(
)
Δ∇Kf(K)[E] = 2 ρK + ρδE + B⊤(Y + ΔY )(P + ΔP)C⊤
1
-
(
)
- 2 ρK + B⊤Y PC⊤
=
1
(
)
= 2 ρK + ρδE + B⊤(Y + δY ′(K)[E])(P + δP′(K)[E])C⊤
-
1
(
)
(
)
(
)
- 2 ρK + B⊤Y PC⊤
= 2δ ρE + B⊤
Y P′(K)[E] + Y ′(K)[E]P
C⊤
,
1
1
где
ΔP = P(K + δE) - P(K) = δP′(K)[E],
ΔY = Y (K + δE) - Y (K) = δY′(K)[E].
Таким образом, обозначая P′ = P′(K)[E] и Y′ = Y′(K)[E], имеем
1
∇2Kf(K)[E,E] = 〈ρE + B⊤(Y P′ + Y′P)C⊤1,E〉.
2
Далее, P = P (K) есть решение уравнения (15); запишем его в прираще-
ниях по направлению E:
(A + B(K + δE)C1) (P + δP′) + (P + δP′)(A + B(K + δE)C1)⊤+
1
+ α(P + δP′) +
DD⊤ = 0,
α
111
или
(A + BKC1)(P + δP′) + (P + δP′)(A + BKC1)⊤+
(
)
1
+ α(P + δP′) + δ BEC1P + P (BEC1)⊤
+
DD⊤ = 0.
α
Вычитая из полученного соотношения уравнение (6), приходим к уравне-
нию (22).
Далее, Y = Y (K) есть решение уравнения Ляпунова (20); запишем его в
приращениях по направлению E:
(A + B(K + δE)C1)⊤(Y + δY′) + (Y + δY′) (A + B(K + δE)C1) +
+ α(Y + δY ′) + C⊤2 C2 = 0,
или
(A + BKC1)⊤(Y + δY′) + (Y + δY′)(A + BKC1)+
(
)
+ α(Y + δY ′) + δ (BEC1)⊤Y +YBEC1
+ C⊤2 C2 = 0.
Вычитая из полученного соотношения уравнение (8), имеем
(
)
(
)
α
⊤
α
(Π.5) A + BKC1 +
I
Y′ +Y′ A+BKC1 +
I
+
2
2
+ (BEC1)⊤Y + Y BEC1 = 0.
Из (22) и (Π.5) имеем соотношение
tr P′Y BEC1 = tr Y′BEC1P,
так что
1
∇2Kf(K)[E,E] = ρ〈E,E〉 + 〈B⊤(Y P′ + Y′P)C⊤1,E〉 =
2
= ρ〈E, E〉 + 2〈B⊤Y P′C⊤1 , E〉.
Лемма 5 доказана.
Следствие П.1. Для действия гессиана функции f(K) на матрицу E ∈
∈ Rp×l, такую что ∥E∥F = 1, справедлива оценка
1
sup
|∇2K f(K)[E, E]| ≤ ρ + 2∥P′∥F ∥Y ∥∥B∥F ∥C1∥.
2
∥E∥F =1
Доказательство следствия П.1. Согласно (21)
1
sup
|∇2K f(K)[E, E]| ≤ sup ρ〈E, E〉 + 2 sup
|〈B⊤Y P′C⊤1, E〉| =
2
∥E∥F =1
∥E∥F =1
∥E∥F =1
= ρ sup
∥E∥2F + 2 sup
|〈P′, Y BEC1〉| ≤ ρ + 2∥P′∥F sup
∥Y BEC1∥F ≤
∥E∥F =1
∥E∥F =1
∥E∥F =1
≤ ρ + 2∥P′∥F∥Y ∥∥B∥F∥C1∥,
112
поскольку с учетом леммы П.2
∥Y BEC1∥F ≤ ∥Y ∥∥B∥F ∥E∥F ∥C1∥.
Следствие П.1 доказано.
Доказательство леммы 6. Согласно следствию П.1 достаточно оце-
нить сверху величину
ρ + 2∥P′∥F∥Y ∥∥B∥F∥C1∥.
Имеем оценку для ∥Y ∥:
1
1
1
1
λmin(DD⊤)∥Y ∥ ≤
λmin(DD⊤)tr Y ≤
tr Y DD⊤ = tr Y
DD⊤ =
α
α
α
α
= tr P C⊤2C2 = tr C2P C⊤2 = f(K) - ρ∥K∥2F ≤ f(K) ≤ f(K0),
откуда
α
(Π.6)
∥Y ∥ ≤
f (K0
).
λmin(DD⊤)
Оценка для α устанавливается следующим образом:
α < 2σ(A + BKC1) ≤ 2∥A + BKC1∥ ≤
≤ 2(∥A∥ + ∥B∥∥K∥∥C1∥) ≤ 2(∥A∥ + ∥B∥∥K∥F ∥C1∥) ≤
√
√
≤ 2(∥A∥ + ∥B∥
f (K)∥C1∥) ≤ 2(∥A∥ +
f (K0)∥B∥∥C1∥),
так что
√
∥A∥ +
f (K0)∥B∥∥C1∥
∥Y ∥ ≤ 2
f (K0).
λmin(DD⊤)
Теперь оценим сверху ∥P ∥:
λmin(C⊤2C2)∥P∥ ≤ tr (C2PC⊤2) = f(K) - ρ∥K∥2F ≤ f(K) ≤ f(K0),
откуда
f (K0)
∥P ∥ ≤
λmin(C⊤2C2)
Наконец, оценим сверху ∥P′∥F . С учетом леммы П.2 заметим, что
(
)
λmax BEC1P + P(BEC1)⊤
=
= ∥BEC1P + P (BEC1)⊤∥ ≤ ∥P2 + BEC1(BEC1)⊤∥ ≤
f2(K0)
1
≤ ∥P ∥2 + ∥B∥2∥C1∥2∥E∥2F ≤
+ ∥B∥2∥C1∥2 = ξ
λmin(DD⊤)
λ2min(C⊤2C2)
α
при
(
)
α
f2(K0)
ξ=
+ ∥B∥2∥C1∥2
λmin(DD⊤) λ2min(C⊤2C2)
113
Поэтому для решения P′ уравнения Ляпунова (22) справедлива оценка
(
)
α
f2(K0)
f (K0)
P′ ≼ ξP ≼
+ ∥B∥2∥C1∥2
I ≼
λmin(DD⊤) λ2min(C⊤2C2)
λmin(C⊤2C2)
√
(
)
∥A∥ +
f (K0)∥B∥∥C1∥
f2(K0)
≼ 2f(K0)
+ ∥B∥2∥C1∥2 I,
λmin(DD⊤)λmin(C⊤2C2) λ2min(C⊤2C2)
откуда
∥P′∥F ≤ 2√nf(K0) ×
√
(
)
(Π.7)
∥A∥ +
f (K0)∥B∥∥C1∥
f2(K0)
×
+ ∥B∥2∥C1∥2
λmin(DD⊤)λmin(C⊤2C2) λ2min(C⊤2C2
)
C учетом оценок (Π.6) и (Π.7) приходим к величине (23). Лемма 6 доказана.
Доказательство теоремы 3. Прежде всего, алгоритм 1 определен
корректно в начальной точке, так как K0 является стабилизирующим регу-
лятором в силу предположения. Далее, при достаточно малых γj в алгоритме
происходит монотонное уменьшение f(K) (движение по антиградиенту), т.е.
Kj остаются в области S0 и тем самым можно применять результаты леммы 6
о липшицевости градиента.
Таким образом, применимы результаты о сходимости градиентного метода
для безусловной минимизации [18]. В частности, условие б на шаге 3 алго-
ритма 1 будет выполнено после конечного числа дроблений, а в градиентном
методе будет иметь место сходимость по градиенту с линейной скоростью.
Теорема 3 доказана.
СПИСОК ЛИТЕРАТУРЫ
1. Boyd S., El Ghaoui L., Feron E., et al. Linear Matrix Inequalities in System and
Control Theory. Philadelphia: SIAM, 1994.
2. Abedor J., Nagpal K., Poolla K. A Linear Matrix Inequality Approach to Peak-to-
Peak Gain Minimization // Int. J. Robust Nonlinear Control. 1996. V. 6. No. 9-10.
P. 899-927.
3. Назин С.А., Поляк Б.Т., Топунов М.В. Подавление ограниченных внешних воз-
мущений с помощью метода инвариантных эллипсоидов // АиТ. 2007. № 3.
С. 106-125.
Nazin S.A., Polyak B.T., Topunov M.V. Rejection of Bounded Exogenous Distur-
bances by the Method of Invariant Ellipsoids // Autom. Remote Control. 2007.
V. 68. No. 3. P. 467-486.
4. Хлебников М.В., Поляк Б.Т., Кунцевич В.М. Оптимизация линейных систем
при ограниченных внешних возмущениях (техника инвариантных эллипсои-
дов) // АиТ. 2011. № 11. С. 9-59.
Khlebnikov M.V., Polyak B.T., Kuntsevich V.M. Optimization of Linear Systems
Subject to Bounded Exogenous Disturbances: The Invariant Ellipsoid Technique //
Autom. Remote Control. 2011. V. 72. No. 11. P. 2227-2275.
114
5.
Поляк Б.Т., Хлебников М.В., Щербаков П.С. Управление линейными система-
ми при внешних возмущениях: Техника линейных матричных неравенств. М.:
ЛЕНАНД, 2014.
6.
Grant M., Boyd S. CVX: Matlab Software for Disciplined Convex Programming,
7.
Баландин Д.В., Коган М.М. Синтез законов управления на основе линейных
матричных неравенств. М.: Физматлит, 2007.
8.
Kalman R.E. Contributions to the Theory of Optimal Control // Boletin de la So-
ciedad Matematica Mexicana. 1960. V. 5. No. 1. P. 102-119.
9.
Levine W., Athans M. On the Determination of the Optimal Constant Output Feed-
back Gains for Linear Multivariable Systems // IEEE Trans. Automat. Control.
1970. V. 15. No. 1. P. 44-48.
10.
Mäkilä P.M., Toivonen H.T. Computational Methods for Parametric LQ Problems -
A Survey // IEEE Trans. Automat. Control. 1987. V. 32. No. 8. P. 658-671.
11.
Fazel M., Ge R., Kakade S., Mesbahi M. Global Convergence of Policy Gradient
Methods for the Linear Quadratic Regulator // Proc. 35th Int. Conf. Machine Learn-
ing. Stockholm, Sweden, July 10-15, 2018. V. 80. P. 1467-1476.
12.
Mohammadi H., Zare A., Soltanolkotabi M., Jovanović M.R. Global Exponential
Convergence of Gradient Methods Over the Nonconvex Landscape of the Linear
Quadratic Regulator // Proc. 2019 IEEE 58th Conf. Decision Control. Nice, France,
December 11-13, 2019. P. 7474-7479.
13.
Zhang K., Hu B., Basar T. Policy Optimization for H2 Linear Control with H∞
Robustness Guarantee: Implicit Regularization and Global Convergence // arXiv:
1910.09496, 2020.
14.
Bu J., Mesbahi A., Fazel M., Mesbahi M. LQR through the Lens of First Order
Methods: Discrete-Time Case // arXiv:1907.08921, 2019.
15.
Fatkhullin I., Polyak B. Optimizing Static Linear Feedback: Gradient Method //
SIAM J. on Control and Optimization (in press), arXiv:2004.09875, 2020.
16.
Поляк Б.Т., Хлебников М.В., Щербаков П.С. Линейные матричные неравенства
в системах управления с неопределенностью // АиТ. 2021. № 1. С. 3-54.
Polyak B.T., Khlebnikov M.V., Shcherbakov P.S. Linear Matrix Inequalities in Con-
trol Systems with Uncertainty // Autom. Remote Control. 2021. V. 82. No. 1.
P. 1-40.
17.
Nesterov Y., Protasov V.Y. Computing Closest Stable Non-Negative Matrices //
SIAM J. Matrix Anal. Appl. 2020. V. 41. Iss. 1. P. 1-28.
18.
Поляк Б.Т. Введение в оптимизацию. 2-е изд. М.: УРСС, 2014.
19.
Хорн Р., Джонсон Ч. Матричный анализ. М.: Мир, 1989.
20.
Lee C.-H. New Results for the Bounds of the Solution for the Continuous Riccati
and Lyapunov Equations // IEEE Trans. Automat. Control. 1997. V. 42. No. 1.
P. 118-123.
Статья представлена к публикации членом редколлегии Л.Б. Рапопортом.
Поступила в редакцию 25.01.2021
После доработки 16.04.2021
Принята к публикации 29.04.2021
115