Автоматика и телемеханика, № 9, 2021

Стохастические системы

(Сочинский институт Российского университета дружбы народов),

Ю.Г. МАРТЫШЕНКО, канд. физ.-мат. наук (j-mart@mail.ru)

(Российский государственный университет нефти и газа, Москва)

К ЗАДАЧЕ ЧАСТИЧНОЙ УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ

ДИСКРЕТНЫХ СТОХАСТИЧЕСКИХ СИСТЕМ

Рассматривается система нелинейных дискретных уравнений, подвер-

женных воздействию дискретного случайного процесса типа “белого” шу-

ма. Предполагается, что система допускает “частичное” (по некоторой ча-

сти переменных состояния) нулевое положение равновесия. Ставится за-

дача частичной устойчивости по вероятности: устойчивости данного по-

ложения равновесия не по всем, а только по отношению к части опре-

деляющих его переменных. Для решения применяется дискретно-стоха-

стический вариант метода функций Ляпунова при соответствующей кон-

кретизации требований к функции Ляпунова. С целью расширения воз-

можностей используемого метода предлагается проводить корректировку

области, в которой строится вспомогательная функция Ляпунова; это до-

стигается посредством введения дополнительной (векторной, вообще го-

воря) вспомогательной функции. Получены условия частичной устойчи-

вости и асимптотической устойчивости по вероятности указанного вида.

Приводится пример, показывающий особенности предложенного подхода.

Ключевые слова: система нелинейных дискретных (конечно-разностных)

стохастических уравнений, частичная устойчивость, метод функций Ля-

пунова.

DOI: 10.31857/S000523102109004X

1. Введение

Задачи устойчивости относятся к основным задачам качественного анали-

за и синтеза нелинейных динамических систем, подверженных воздействию

случайных возмущений и изменениям структуры. Как и в случае детермини-

рованных систем, для их решения используется метод функций Ляпунова.

Существенное влияние на развитие стохастического варианта метода

функций Ляпунова оказала идея И.Я. Каца и Н.Н. Красовского [1] использо-

вания усредненной производной функции Ляпунова, для вычисления которой

достаточно знать лишь правые части системы и вероятностные характеристи-

ки воздействующего на систему случайного процесса. Данный подход, пред-

ложенный для систем дифференциальных уравнений, правая часть которых

содержит однородную марковскую цепь с конечным числом состояний, в зна-

чительной степени предопределил многие последующие исследования: систем

116

стохастических дифференциальных уравнений в форме Ито [2, 3], а также

более общих классов стохастических систем со случайными параметрами и

(или) структурой [4, 5].

Отдельное направление исследований связано с анализом устойчивости

дискретных (конечно-разностных) систем, подверженных воздействию слу-

чайных факторов. Повышенный интерес к дискретным системам связан с

использованием цифровых систем управления, проблемами финансовой ма-

тематики, динамики биоценозов, а также с задачами численного решения

систем стохастических дифференциальных уравнений. На этом пути разра-

ботан [2, 6-13] соответствующий дискретно-стохастический вариант метода

функций Ляпунова применительно к обладающей большой общностью за-

даче устойчивости по отношению ко всем переменным нулевого положения

равновесия. Рассмотрена также [14] задача устойчивости компактных мно-

жеств в фазовом пространстве системы. Усредненная производная (или диф-

ференциальный производящий оператор [2, 3, 5]) заменяется в данных слу-

чаях усредненной конечной разностью функции Ляпунова [6].

Начиная с публикаций В.В. Румянцева [15, 16] в теории устойчивости де-

терминированных систем, а затем и стохастических систем с непрерывной ди-

намикой рассматриваются задачи частичной устойчивости (см. обзор [17]):

устойчивости по отношению к части переменных нулевого положения рав-

новесия, а также устойчивости по всем и по части переменных “частично-

го” (нулевого) положения равновесия. С формально-математической точки

зрения задача устойчивости по всем переменным “частичного” положения

равновесия относится к задаче устойчивости некомпактных (замкнутых, но

неограниченных) множеств, в то время как задачи устойчивости по части пе-

ременных имеют самостоятельное значение и не сводятся, вообще говоря, к

каким-либо задачам устойчивости множеств. Дело в том, что устойчивость

по отношению к части переменных не предполагает близости траекторий, со-

ответствующих возмущенным движениям и невозмущенному движению (по-

ложению равновесия) системы.

Содержательно указанные задачи частичной устойчивости естественным

образом возникают в приложениях как исходя из требования нормального

функционирования, так и при оценке возможностей проектируемой системы.

Они также могут рассматриваться и как вспомогательные задачи при анализе

устойчивости по всем переменным выделенных положений равновесия. Кро-

ме того, возникают соответствующие задачи частичной стабилизации нели-

нейных управляемых систем, активно рассматриваемые в последние годы.

Однако для систем стохастических дискретных уравнений задачи частичной

устойчивости и стабилизации практически не изучались.

В данной статье рассматривается система нелинейных дискретных (ко-

нечно-разностных) уравнений общего вида, подверженных воздействию дис-

кретного случайного процесса типа “белого” шума. Предполагается, что си-

стема допускает “частичное” (по некоторой части переменных состояния)

нулевое положение равновесия. Дается постановка задачи устойчивости по

вероятности этого положения равновесия; устойчивость рассматривается по

117

отношению к части определяющих его фазовых переменных. Анализируется

возможность решения поставленной задачи на основе метода функций Ляпу-

нова.

2. Определения. Постановка задачи

Рассмотрим линейное конечномерное пространство векторов x с евклидо-

вой нормой ∥x∥. Введем разбиение вектора x на две части: x = (y^T, z^T)^T

(T обозначает транспонирование). Обозначим через Z₊ = {k = 0, 1, 2, . . . }

множество целых неотрицательных чисел.

Пусть дана конечномерная нелинейная система стохастических дискрет-

ных (конечно-разностных) уравнений [2, 6-14]

x(k + 1) = X(k, x(k), ξ(k)),

в которой: k ∈ Z₊ - дискретное время; x(k) - последовательность значений

фазового вектора, определяющих состояние системы; ξ(k) - последователь-

ность независимых случайных векторов, заданных на вероятностном про-

странстве (Ω, F , P), с одинаковыми законами распределения для каждого

k ∈ Z₊. Здесь Ω - пространство элементарных событий {ω} с заданными на

нем σ-алгеброй F измеримых множеств с фильтрацией F_k и вероятностной

мерой P: F → [0, 1].

С учетом сделанного разбиения x = (y^T,z^T)^T представим рассматривае-

мую систему в виде двух групп уравнений

(1)

y(k + 1) = Y(k, y(k), z(k), ξ(k)), z(k + 1) = Z(k, y(k), z(k), ξ(k)).

Если имеет место условие

Y(k, 0, z(k), ξ(k)) ≡ 0,

то множество M = {x(k) : y(k) = 0} является “частичным” положением рав-

новесия системы (1).

Допустим также, что вектор-функция X = (Y^T, Z^T)^T, определяющая пра-

вую часть системы (1), при каждом k ∈ Z₊ непрерывна по x, ξ в обла-

сти ∥x∥ < ∞. Начальное значение x₀ фазового вектора будем считать де-

терминированным. Тогда (см., например, [9, 11]) для всех k₀ ≥ 0, x₀ су-

ществует единственный случайный многомерный марковский процесс, со-

гласованный с потоком σ-алгебр F_k и являющийся в пространстве {x, ξ}

случайной вектор-функцией {x(k) = x(k; k₀, x₀), ξ(k)}, реализации {x(k, ω) =

= x(k, ω; k₀, x₀), ξ(k, ω)} которой удовлетворяют системе (1). Данный случай-

ный процесс и соответствующий ему набор реализаций случайной вектор-

функции при всех k ≥ k₀ определяют решение системы (1), удовлетворяю-

щее начальным условиям x₀ = x(k₀; k₀, x₀), а также соответствующий этому

решению набор выборочных траекторий системы (1). Марковское свойство

решений системы (1) используется далее при обосновании условий частич-

ной устойчивости по вероятности.

118

При сделанных предположениях

“частичное” положение равновесия

y(k) = 0 системы (1) является инвариантным множеством этой системы.

Предположение X(k, 0, ξ(k)) ≡ 0 о существовании “полного” положения рав-

новесия x(k) = 0 не является необходимым и даже может противоречить

смыслу решаемых задач.

Следуя подходу теории частичной устойчивости, будем анализировать

устойчивость “частичного” положения равновесия y(k) = 0 не по всем опре-

деляющим его переменным, а только по отношению к их некоторой наперед

заданной части. Для этого предположим, что y = (y^T1, y₂)^T, причем вектор y₁

включает те компоненты вектора y, устойчивость по отношению к которым

рассматривается.

В данном случае входящие в вектор z переменные являются “неконтроли-

руемыми”, хотя они существенно влияют на динамику y₁-переменных. Для

расширения функциональных возможностей рассматриваемых далее поня-

тий y₁-устойчивости “частичного” положения равновесия y(k) = 0 введем

произвольным образом разбиение z = (z^T1, z^T2)^T вектора z на две группы пе-

ременных.

Обозначим через D_δ область значений x₀ таких, что ∥y₀∥ < δ, ∥z₁₀∥ ≤ L,

∥z₂₀∥ < ∞; область D_Δ получается заменой δ на Δ.

Определение. “Частичное” положение равновесия y(k) = 0 систе-

мы (1) при больших значениях z₁₀ в целом по z₂₀ (for a large values of z₁₀

and on the whole with respect to z₂₀):

1) y₁-устойчиво по вероятности, если для каждого k₀ ∈ Z₊ и для любых

сколь угодно малых чисел ε > 0, γ > 0, а также для любого наперед задан-

ного числа L > 0 найдется число δ(ε,γ,L,k₀) > 0 такое, что для всех k ≥ k₀

и x₀ ∈ D_δ имеет место соотношение

{

}

(2)

P sup ||y₁(k;k₀,x₀)|| > ε

< γ;

k≥k₀

2) равномерно y₁-устойчиво, если δ = δ(ε, γ, L);

3) асимптотически y₁-устойчиво, если оно равномерно y₁-устойчиво по

вероятности и, кроме того, для каждого k₀ ∈ Z₊ и для любого наперед за-

данного числа L > 0 найдется число Δ(L) > 0 такое, что для всех k ≥ k₀ и

x₀ ∈ D_Δ имеет место предельное соотношение

{

}

lim

P lim

||y₁(k; k₀, x₀)|| = 0

= 1.

||y₀||→0

k→+∞

Замечание 1. Можно показать (см., например, [5]), что если x₀ - слу-

чайная величина (не зависящая от ξ(k)), а включения x₀ ∈ D_δ и x₀ ∈ D_Δ

выполняются почти наверное (с вероятностью единица), то получаем опре-

деления, эквивалентные введенным определениям частичной устойчивости.

Замечание 2. Наиболее близкими к введенным являются понятия ча-

стичной устойчивости: по всем [18, 19] и по отношению к части перемен-

119

ных [20] “частичного” положения равновесия стохастических систем диффе-

ренциальных уравнений в форме Ито. Предположения “в целом по z₀” или

“при больших значениях z₀” характерны для определений устойчивости (как

по всем, так и по части переменных) “частичного” положения равновесия

y(k) = 0 системы (1), но приводят к различным требованиям к функциям

Ляпунова. За счет разделения вектора z₀ на две части возникают “проме-

жуточные” понятия y₁-устойчивости в смысле введенных определений 1-3.

При этом надлежащий выбор разбиения z = (z^T1, z^T2)^T зависит от структуры

системы (1) и является результатом поиска компромисса между содержатель-

ным смыслом понятия y₁-устойчивости “частичного” положения равновесия

y(k) = 0 и соответствующими требованиями к функциям Ляпунова. Кроме

того, введенные понятия устойчивости возникают при переходе (посредством

обозначений w = k, r = k - k₀) от системы (1) к стационарной дискретной

системе

x(r + 1) = X(x(r), w(r), ξ(r)), w(r + 1) = w(r) + 1,

когда требования равномерности (неравномерности) по k₀ в задачах y₁-устой-

чивости при больших значениях z₀ или в целом по z₀ “частичного” положения

равновесия y(k) = 0 заменяются требованиями “в целом по w₀” (“при боль-

ших значениях w₀”).

3. Условия частичной устойчивости

В контексте метода функций Ляпунова будем рассматривать однознач-

ные непрерывные по x при каждом k ∈ Z₊ скалярные функции V = V (k, x),

V (k, 0) ≡ 0, определенные в области

(3)

∥y₁∥ < h,

∥y₂

∥ + ∥z∥ < ∞.

Аналогом производных этих функций в силу исследуемой системы (1) яв-

ляются их усредненные разности (приращения), вычисляемые по формуле

[6, 9]

LV (k,x) = E[V (k + 1,X(k,x(k),ξ(k)))|x(k) = x] - V (k,x),

где оператор E[V (k + 1, X(k, x(k), ξ(k)))|x(k) = x] определяет условное

математическое ожидание при x(k) = x случайной величины V (k + 1,

X(k, x(k)ξ(k))), порожденной набором реализаций {x(k, ω), ξ(k, ω)} процес-

са {x(k), ξ(k)}, являющегося решением системы (1).

Также для формулировки условий частичной устойчивости дополнительно

будут использоваться следующие вспомогательные функции.

1) Скалярные функции V^∗(k, y, z₁), V^∗(y, z₁), необходимые для конкрети-

зации (в соответствии с постановкой задачи) требований к V -функции Ляпу-

нова, и вспомогательная векторная функция µ(k, x), µ(k, 0) ≡ 0, посредством

которой корректируется область, где строится основная V -функция Ляпуно-

ва. Эти функции при каждом k ∈ Z₊ непрерывны по x в области (3).

120

2) Непрерывные монотонно возрастающие по r > 0 скалярные функции

a_i(r), a_i(0) = 0 (i = 1,2,3) (функции типа Хана [16]), определяющие стан-

дартные требования к основной V -функции Ляпунова.

Введение, наряду с основной V -функцией Ляпунова, дополнительной вспо-

могательной µ(k, x)-функции мотивируется следующим обстоятельством.

При исследовании y₁-устойчивости по вероятности “частичного” положения

равновесия y(k) = 0 системы (1) в общем случае имеет место зависимость

V -функций Ляпунова не только от k, y₁, но и от y₂, z. В такой ситуации

анализ поставленной задачи y₁-устойчивости в обычно рассматриваемой об-

ласти

(4)

∥y₁∥ < h₁ < h,

∥y₂

∥ + ∥z∥ < ∞

не всегда дает возможность выявить желаемые свойства V -функции Ляпуно-

ва или наделить ее этими свойствами. Причина в требовании ∥y₂∥ + ∥z∥ < ∞,

которое существенно затрудняет возможность получения необходимых оце-

нок для V -функции Ляпунова и ее усредненной конечной разности.

Указанное требование представляет, по сути, расчет на “наихудший” слу-

чай изменения переменных y₂, z, и его можно заменить более “мягким” тре-

бованием

(5)

∥y₁∥ + ∥µ(k, x)∥ < h₁ < h,

∥y₂

∥ + ∥z∥ < ∞,

если иметь в виду “расширенную” (y₁, µ)-устойчивость “частичного” положе-

ния равновесия y = 0 системы (1). В данном случае µ-функция не являет-

ся изначально заданной и подбирается в процессе решения исходной задачи

y₁-устойчивости, причем расширение понятия y₁-устойчивости может проис-

ходить за счет зависимости µ-функции не только от k, y, но и от z.

Поэтому выбор подходящей V -функции Ляпунова не только возможно,

но и целесообразно согласовывать с выбором области (k, x)-пространства, в

которой эта функция рассматривается. Указанного согласования можно до-

биться введением, наряду с основной V -функцией Ляпунова, дополнительной

(векторной, вообще говоря) вспомогательной µ(k, x)-функции для корректи-

ровки области, в которой строится основная V -функция Ляпунова.

Теорема 1. Пусть для системы (1), наряду с основной скалярной

V -функцией Ляпунова, можно указать дополнительную векторную функ-

цию µ(k, x), µ(k, 0) ≡ 0, для которых при каждом k ∈ Z₊ и достаточно ма-

лом h₁ > 0 в области (5) выполняются условия:

(6)

V (k, x) ≥ a₁(∥y₁

∥ + ∥µ(k,x)∥),

(7)

V (k, x) ≤ V ^∗(k, y, z₁), V ^∗(k, 0, z₁

) ≡ 0,

(8)

LV (k,x) = E[V (k + 1,X(k,x(k),ξ(k))|x(k) = x] - V (k,x) ≤ 0.

Тогда “частичное” положение равновесия y(k) = 0 системы (1) y₁-устой-

чиво по вероятности при больших значениях z₁₀ в целом по z₂₀.

121

Если условия (7) заменить условиями

(9)

V (k, x) ≤ V ^∗(y, z₁), V ^∗(0, z₁

) ≡ 0,

то “частичное” положение равновесия y(k) = 0 системы (1) равномерно

y₁-устойчиво по вероятности при больших значениях z₁₀ в целом по z₂₀.

Доказательства теоремы 1 и последующей теоремы 2 вынесены в Прило-

жение.

В рамках рассматриваемого подхода можно сформулировать также и усло-

вия асимптотической y₁-устойчивости по вероятности при больших значе-

ниях z₁₀ в целом по z₂₀ “частичного” положения равновесия y(k) = 0 систе-

мы (1). Приведем один из вариантов таких условий.

Теорема 2. Пусть для системы (1), наряду с основной скалярной

V -функцией Ляпунова, можно указать дополнительную векторную функ-

цию µ(x), µ(0) ≡ 0, для которых при каждом k ∈ Z₊ и достаточно малом

h₁ > 0 в области (5) выполняются условия:

(10)

a₁(∥y₁∥ + ∥µ(x)∥) ≤ V (k,x) ≤ a₂(∥y₁

∥ + ∥µ(x)∥),

(11)

LV (k,x) ≤ -a₃(∥y₁

∥ + ∥µ(x)∥),

а также условия (9).

Тогда “частичное” положение равновесия y(k) = 0 системы (1) асимпто-

тически y₁-устойчиво по вероятности при больших значениях z₁₀ в целом

по z₂₀.

Замечание 3. Вспомогательная V -функция Ляпунова и ее усредненная

разность (приращение) LV (k, x) в силу системы (1) в теоремах 1, 2 при каж-

дом k ∈ Z₊ являются, вообще говоря, знакопеременными функциями в обла-

сти (4). Наряду с основной V -функцией Ляпунова дополнительная вспомога-

тельная µ-функция вводится для наиболее рациональной замены области (4)

областью (5).

Условия (7) являются “промежуточными” между менее ограничитель-

ным условием V (k, 0, z) ≡ 0 и более ограничительными условиями V (k, x) ≤

≤ V ^∗(k,y), V ^∗(k,0) ≡ 0, при выполнении которых “частичное” положение

равновесия y(k) = 0 системы (1) соответственно y₁-устойчиво по вероятности

при больших значениях z₀ или y₁-устойчиво по вероятности в целом по z₀.

Замечание 4. В рамках предложенного подхода нелинейные V -функции

Ляпунова могут быть построены как знакоопределенные квадратичные фор-

мы (или формы более высокого порядка) V (k, x) ≡ V^∗(k, y₁, µ(k, x)) пере-

менных y₁, µ. При этом выбор µ-функций должен быть согласован с усло-

виями (7), (9): допустимы, например, вспомогательные µ-функции вида µ =

= µ(y₂, z₁), µ(0, z₁) ≡ 0.

Eсли от исходной системы (1) можно отделить подсистему вида

(

)

y₁(k + 1) = Y₁ k,y₁(k),µ(k),ξ(k) ,

(

)

µ(k + 1) = Y^∗1 k, y₁(k), µ(k), ξ(k) ,

122

то построение V -функции Ляпунова можно провести, используя числен-

ный метод [11] применительно к задаче устойчивости по всем переменным

(по y₁, µ) нулевого положения равновесия этой подсистемы.

Замечание 5. Если система (1) допускает “полное” положение равнове-

сия x(k) = 0, то в случае µ(k, x) ≡ 0, ξ(k) ≡ 0, ∥x₀∥ < δ при выполнении усло-

вий (6), (8) имеем дискретный вариант классической теоремы В.В. Румянцева

[15] об устойчивости по отношению к части переменных. В случае ξ(k) ≡ 0

теорема 1 переходит в дискретные варианты [21, 22] соответствующих теорем

из [23, 24].

Замечание 6. Устойчивость по части переменных “в среднем” нулевого

положения равновесия систем дискретных стохастических уравнений изуча-

лась в [25, 26] на основе выделения “усеченных” подсистем [25], а также путем

построения вспомогательных систем [26]. Возможности использования мето-

да функций Ляпунова анализировались для решения задач частичной устой-

чивости (стабилизации) систем стохастических дифференциальных уравне-

ний [27-31], в том числе для систем со случайной структурой [32-34]; для

квазилинейных систем стохастических дифференциальных уравнений на мо-

дельном примере дано сравнение задач оптимальной стабилизации по всем и

по части переменных [35].

4. Пример

Пусть дискретная система (1) состоит из уравнений

y₁(k + 1) = [a + αξ₁(k)]y₁(k) + ly₂(k)z₁(k),

(12)

y₂(k + 1) = [b + dy₁(k)]y₂

(k),

z₁(k + 1) = [c + ey₁(k)]z₁(k), z₂(k + 1) = Z₂(k,x(k)),

где ξ₁(k) - последовательность независимых случайных величин c одинако-

вым стандартным нормальным распределением при каждом k ∈ Z₊; функ-

ция Z₂ произвольна и удовлетворяет только общим требованиям к систе-

ме (1); a, b, c, d, e, l, α - постоянные параметры.

Система (12) допускает “частичное” положение равновесия

(13)

y₁(k) = y₂

(k) = 0.

Наряду с основной функцией Ляпунова

(14)

V (x) = y²¹ + 2y²²z²¹

также рассмотрим вспомогательную функцию µ₁ = y₂z₁.

Для V -функции Ляпунова в области (5) выполняются условия (9) и (10),

а ее усредненная разность (приращение) LV (x) в силу системы (12) при всех

123

k ∈ Z₊ определяется следующим образом:

[(

)₂

LV (x) = E ay₁(k) + ly₂(k)z₁(k) + αy₁(k)ξ₁(k)

]

+ 2y²²(k)z²¹(k)(b + dy₁(k))²(c + ey₁(k))²|x(k) = x - y21 - 2y22z21 =

= a²y²¹ + 2aly₁y₂z₁ + l²y²²z²¹ + α²y²¹ + 2b²c²y²²z²¹ +

+ r₁y₁y²²z²¹ + r₂y²¹y²²z²¹ + r₃y³¹y²²z²¹ + 2d²e²y⁴¹y²²z²¹ - y²¹ - 2y²²z²¹ =

= (a² + α² - 1)y²¹ + 2aly₁µ₁ + (l² + 2b²c² - 2)µ²¹ + r₁y₁µ²¹ +

+ r₂y²¹µ²¹ + r₃y³¹µ²¹ + 2d²e²y⁴¹µ²¹,

r₁ = bcr₀, r₂ = 2(b²e² + 4bcde + c²d²), r₃ = der₀, r₀ = 4(be + cd);

вычисление условного математического ожидания проведено с учетом соот-

ношений E[ξ₁(k)] = 0, E[ξ²¹(k)] = 1, определяющих стандартное нормальное

распределение случайных величин ξ₁(k).

При выполнении неравенств

(15)

a² + α² < 1, (a² + α² - 1)(l² + 2b²c² - 2) > a²l²

для каждого k ∈ Z₊ при достаточно малом h₁ > 0 в области (5) (но не в обла-

сти (4)) при любых значениях параметров d, e имеет место оценка LV (x) ≤

≤ -β(y²¹ + µ²¹), β = const > 0. Это значит, что для V -функции Ляпунова (14)

в области (5) помимо условий (9), (10) также выполняется условие (11).

Hа основании теоремы 2 заключаем, что при выполнении условий (15) “ча-

стичное” положение pавновесия (13) системы (12) при больших значениях z₁₀

в целом по z₂₀ асимптотически y₁-устойчиво по вероятности.

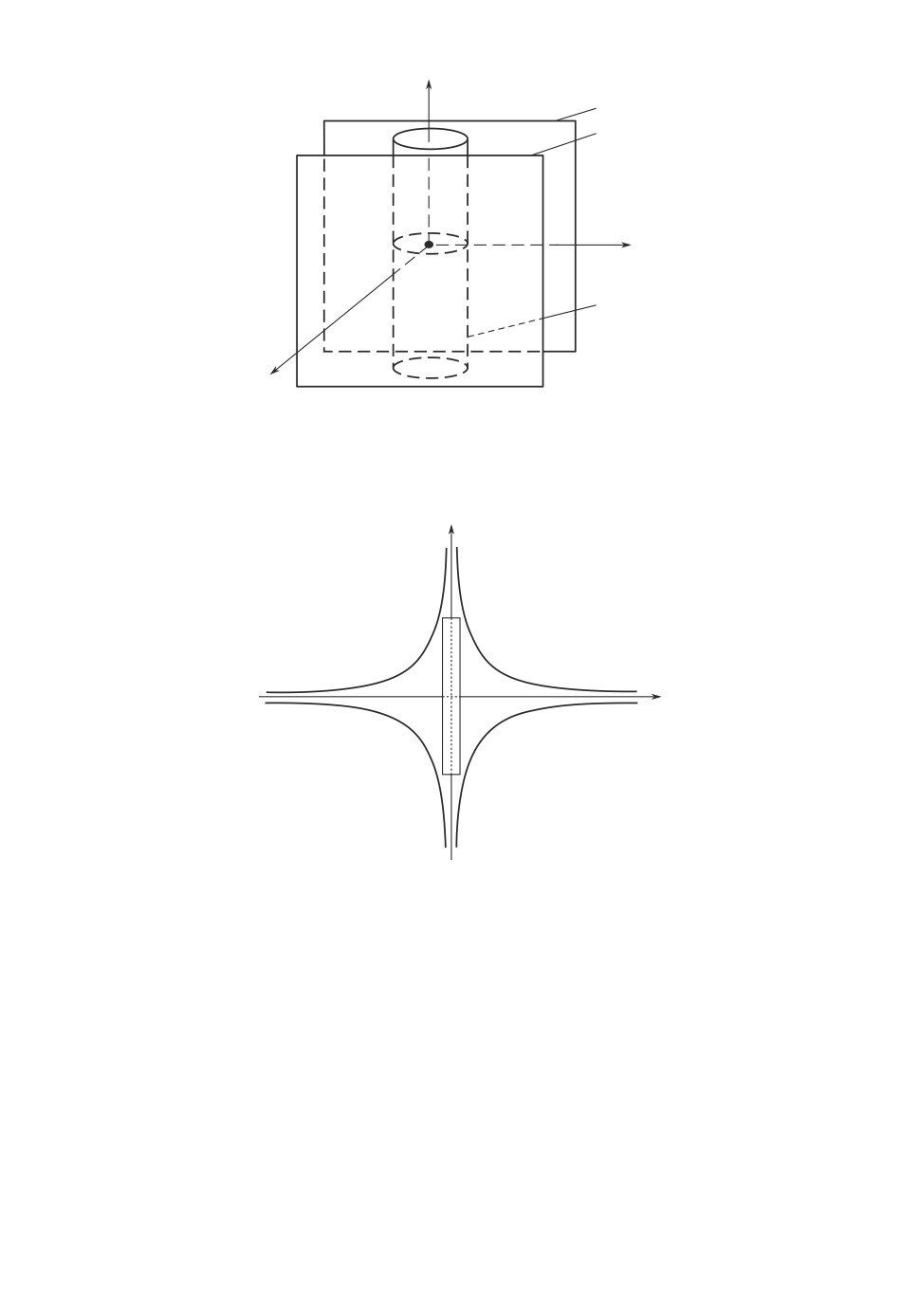
Поясним геометрически данное свойство частичной устойчивости приме-

нительно к введенным в разделе 2 определениям 2, 3. Для каждого k₀ ∈ Z₊ и

для любых сколь угодно малых чисел ε > 0 (ε < h₁), γ > 0, а также для лю-

бого наперед заданного числа L > 0 в трехмерном пространстве Oy₁y₂z₁ гра-

ница допустимой области x₀ ∈ D_δ начальных возмущений является цилин-

дром ∥y₀∥ = δ высоты 2L, расположенном между двумя плоскостями y₁ = ±ε

(рис. 1); при этом δ = δ(ε, γ, L). Если решения системы (12) начинаются при

k = k₀ внутри этого δ-цилиндра (при произвольном значении z₂₀), то соот-

ветствующие указанным решениям выборочные траектории в пространстве

Oy₁y₂z₁ будут с вероятностью, не меньшей 1 - γ, оставаться при всех k ≥ k₀

между указанными двумя ε-плоскостями.

Также можно указать число Δ = Δ(γ, L, h₁) > 0 такое, что

{

}

P sup |y₁(k;k₀,x₀)| ≥ h₁

< γ,

k≥k₀

(16)

{

}

P lim

y₁(k;k₀,x₀) = 0

≥1-γ

k→+∞

124

z₁

y₁ = -e

y₁ = e

y₂

|| y₀|| = d

y₁

Рис. 1. Области допустимых начальных и текущих отклонений от инвариант-

ного множества y₁(k) = y₂(k) = 0.

z₁

y₂

Рис. 2. Области допустимых начальных и текущих отклонений (в проекции

на плоскости Oy₂z₁.

для всех k ≥ k₀ и x₀ ∈ D_Δ. Если решения системы (12) начинаются при k = k₀

внутри Δ-цилиндра ∥y₀∥ = Δ высоты 2L (при произвольном значении z₂₀),

то соответствующие этим решениям выборочные траектории в пространстве

Oy₁y₂z₁ будут с вероятностью, не меньшей 1 - γ, не только оставаться при

всех k ≥ k₀ между ε-плоскостями, но и при k → ∞ будут сходиться к плоско-

сти y₁ = 0.

Однако в рамках рассматриваемого подхода, основанного на перехо-

де от области (4) к области (5), имеет место “расширенная” равномерная

(y₁, µ₁)-устойчивость “частичного” положения равновесия (13) системы (12),

обеспечивающая правомерность такого перехода. Поэтому δ-цилиндр распо-

125

Таблица

k ξ₁(k) y₁(k)

y₂(k)

z₁(k)

ξ₁(k)

y₁(k)

y₂(k)

z₁(k)

0,1

0,15

0,16

0,4333

-1

0,1167

0,16

0,4333

0,1443

0,2640

0,2094

0,1665

0,2587

0,1950

0,1275

0,4340

0,1000

0,1891

0,4311

0,0975

0,1072

0,7063

0,0461

0,1366

0,7282

0,0509

0,0861

1,1352

0,0203

-1

0,0599

1,1918

0,0239

0,0661

1,8005

0,0085

-1

0,0385

1,8590

0,0094

0,0484

2,8198

0,0034

0,0496

2,8601

0,0035

0,0338

4,3662

0,0013

0,0348

4,4320

0,0013

0,0226

6,6969

0,0005

0,0233

6,8022

0,0005

0,0145

10,197

0,00017

0,0227

10,362

0,00017

0,0009

79,001

7,6 × 10^-7

-1

0,0007

82,073

9,1 × 10^-7

0,000048

600,69

3,2 × 10^-9

-1

0,000017

623,28

3,7 × 10^-9

ложен в области D^∗ пространства Oy₁y₂z₁, ограниченной поверхностью y²¹ +

+y²²z²¹ = ε². (На рис. 2 расположение δ-цилиндра показано в проекции на

плоскость Oy₂z₁; соответствующий прямоугольник со сторонами длины 2δ

и 2L находится в области, границами которой являются ветви гипербол y₂z₁ =

= ±ε.) Если решения системы (12) начинаются при k = k₀ внутри δ-цилиндра

(при произвольном значении z₂₀), то соответствующие указанным решениям

выборочные траектории в пространстве Oy₁y₂z₁ будут с вероятностью, не

меньшей 1 - γ, оставаться при всех k ≥ k₀ в области D^∗.

Анализ структуры системы (12) позволяет дополнить сделанные выво-

ды: при выполнении условий (15) выборочные траектории в пространстве

Oy₁y₂z₁, соответствующие решениям системы (12), начинающимся внут-

ри Δ-цилиндра ∥y₀∥ = Δ высоты 2L (при произвольном значении z₂₀), с

вероятностью, не меньшей 1 - γ,

“фокусируются” при k → ∞ или вдоль

оси Oy₂, или вдоль оси Oz₁. Действительно, в силу имеющей место “рас-

ширенной” асимптотической (y₁, µ₁)-устойчивости “частичного” положения

равновесия (13) системы (12) второе и третье уравнения этой нелинейной

системы можно представить в виде линейных рекуррентных уравнений

y₂ (k + 1) = [b + dy₁ (k; k₀,x₀)]y₂(k),

z₁ (k + 1) = [c + ey₁ (k;k₀,x₀)]z₁(k),

причем для компоненты y₁(k; k₀, x₀) любого решения системы (12), начавше-

гося внутри Δ-цилиндра высоты 2L, выполнены соотношения (16). Поэтому

при выполнении условий (15) для этих решений системы (12) при k → ∞

с вероятностью, не меньшей 1 - γ, имеют место соотношения |y₂(k)| → ∞ и

|z₁(k)| → 0 (при |b| > 1, |c| < 1) или соотношения |y₂(k)| → 0 и |z₁(k)| → ∞

(при |b| < 1, |c| > 1).

Для численной конкретизации сделанных выводов в левой части табли-

цы для “невозмущенного” случая ξ₁(k) ≡ 0 приводятся результаты вычисле-

126

ний по рекуррентным соотношениям (12) на отрезке k ∈ [0, 20] при y₁(0) =

= y₂(0) = 0,1 и z₁(0) = 1, а также при значениях параметров a = 1/2, b = 3/2,

c = 1/3, d = e = l = 1. При случайном воздействии ξ₁(k) выборочные траек-

тории группируются около “невозмущенной” траектории, фокусирующейся

при k → ∞ вдоль оси Oy₂. Для оценки влияния случайного воздействия на

динамику системы (12) в правой части таблицы при α = 1/3 и тех же значе-

ниях параметров приводятся результаты вычислений в случае, когда допу-

стимая реализация ξ₁(k) на отрезке k ∈ [0, 20] определяется последователь-

ностью {0, -1, 1, 1, 0, -1, -1, 1, 0, 0, 1, 1, -1, 0, 0, -1, 1, 0, -1, 1, -1}.

5. Заключение

Для нелинейной системы стохастических дискретных (конечно-разност-

ных) уравнений, подверженных действию дискретного случайного процесса

типа “белого” шума, дана поставка задачи устойчивости (асимптотической

устойчивости) по части переменных “частичного” нулевого положения рав-

новесия. Начальные значения “неконтролируемых” переменных, не опреде-

ляющих рассматриваемое “частичное” положение равновесия, предполагают-

ся большими (ограниченными по норме любым наперед заданным числом)

по одной их части и произвольными по другой.

Приводятся достаточные условия разрешимости этой задачи в контек-

сте дискретно-стохастического варианта метода функций Ляпунова в со-

ответствующей модификации. Наряду с основной V -функцией Ляпунова

рассматривается дополнительная (векторная, вообще говоря) вспомогатель-

ная µ-функция для корректировки области, в которой строится основная

V -функция Ляпунова. Целесообразность такого подхода заключается в том,

что в результате основная V -функция Ляпунова, а также ее усредненная

разность (приращение) в силу рассматриваемой системы могут быть знако-

переменными.

ПРИЛОЖЕНИЕ

Доказательство теоремы 1. I. Пусть при каждом k ∈ Z₊ и доста-

точно малом h₁ > 0 в области (5) выполняются условия (6)-(8).

Возьмем произвольное число ε (0 < ε < h₁), рассмотрим произвольный мо-

мент времени k₀, а также начальную точку x₀ из области

{

}

D_ε =

∥y₀∥ < ε, ∥z₁₀∥ ≤ L, ∥z₂₀∥ < ∞

Рассмотрим случайный процесс x(k; t₀, x₀) (k ≥ k₀), являющийся решени-

ем системы (1), и обозначим через τ_ε “целочисленный” момент первого выхода

этого процесса из области ∥y₁∥ ≤ ε. Если некоторые траектории ни за какое

конечное время не выходят из области ∥y₁∥ ≤ ε, то для них τ_ε считаем рав-

ным ∞. Положим

τ (k) = min(τ_ε, k); τ(k₀) = k₀.

127

Имеют место равенства

(

)

V τ(k),x(τ(k);k₀,x₀)

- V (k₀,x₀) =

(

)

(

)

= V τ(k),x(τ(k);k₀,x₀)

- V τ(k - 1),x(τ(k - 1);k₀,x₀)

(

)

(

)

+ V τ(k - 1),x(τ(k - 1);k₀,x₀)

- V τ(k - 2),x(τ(k - 2);k₀,x₀)

(

)

+ V τ(k₀ + 1),x(τ(k₀ + 1);k₀,x₀)

- V (k₀,x₀) =

∑

(

)

= ΔV τ(s),x(τ(s);k₀,x₀) ;

s=k₀

(

)

ΔV τ(s),x(τ(s);k₀,x₀)

(

)

(

)

= V τ(s + 1),x(τ(s + 1);k₀,x₀)

- V τ(s),x(τ(s);k₀,x₀)

Из этих равенств следует, что для последовательности v(k) случай-

ных величин v(k) = V (τ(k), x(τ(k); k₀, x₀)), порожденных реализациями

{x(k, ω), ξ(k, ω)} случайного процесса

{x(k), ξ(k)}, определяемого систе-

мой (1), имеют место “усредненные” соотношения

[

(

)

]

τ (k), x(τ(k); k₀, x₀)

- V (k₀,x₀)

(

)

= EV

τ (k), x(τ(k); k₀, x₀)

- V (k₀,x₀) =

∑

(

)

= EΔV

τ (s), x(τ(s); k₀, x₀)

s=k₀

Учитывая равенства (полученные с учетом правила вычисления повтор-

ного математического ожидания)

[

(

)]

ΔV

τ (s), x(τ(s); k₀, x₀)

[

(

)

(

))]

τ (s + 1), X

τ (s), x(τ(s); k₀, x₀), ξ(τ(s))

-V

τ (s), x(τ(s); k₀, x₀)

{

[

(

)

)]}

τ (s + 1), X

τ (s), x(τ(s), ξ(τ(s))|x(τ(s)))

= x(τ(s); k₀, x₀)

[

(

)]

−E

τ (s), x(τ(s); k₀, x₀)

{

[

(

)

)]

τ (s + 1), X

τ (s), x(τ(s), ξ(τ(s)))

|x(τ(s)) = x(τ(s); k₀, x₀)

}

[

]

− V (τ(s),x(τ(s);k₀,x₀))

LV (τ(s),x(τ(s);k₀,x₀))

приходим к соотношению (дискретный вариант формулы Дынкина) [9]

(

)

τ (k), x(τ(k); k₀, x₀)

- V (k₀,x₀) =

∑

[

(

)]

= E

τ (s), x(τ(s); k₀, x₀)

s=k₀

128

В результате на основании условия (8) получаем неравенство

(

)

(Π.1)

τ (k), x(τ(k); k₀, x₀)

≤ V (k₀,x₀

) < ∞.

Если справедливо неравенство k > τ_ε (в этом случае имеем τ(k) = τ_ε), то

выполняются соотношения ∥y₁(τ(k); k₀, x₀)∥ = ∥y₁(τ_ε; k₀, x₀)∥ ≥ ε. Если же

справедливо неравенство k < τ_ε (в этом случае имеем τ(k) = k), то на ос-

новании неравенства Чебышева-Маркова и оценки (П.1) находим

[

]

[

]

∥y₁(k; k₀, x₀)∥ > ε

≤ a^-11(ε)E

a₁(||y₁(k;k₀,x₀)||)

≤

[

]

≤ a^-11(ε)E

a₁(||y₁(k;k₀,x₀)|| + ||µ(k,x(k;k₀,x₀))||)

≤

(Π.2)

[

(

)]

≤ a^-11(ε)E

k,x(k;k₀,x₀)

[

(

)]

= a^-11(ε)E

τ (k), x(τ(k); k₀, x₀)

≤ a^-11(ε)V (k₀,x₀).

Поскольку при каждом k ∈ Z₊ функция Ляпунова V (k, x) непрерывна,

V (t, 0) ≡ 0, а также выполняются условия (7), то для всех k₀ ≥ 0 и для любого

заданного числа L > 0 предельное соотношение

(Π.3)

lim V (k₀, x₀

)=0

||y₀||→0

выполняется при ∥z₁₀∥ ≤ L равномерно по ∥z₂₀∥ < ∞.

Поэтому для всех k₀ ≥ 0 и для любого заданного числа L > 0 на основании

неравенств (П.2), (П.3) имеем предельное соотношение

[

]

lim P sup ||y₁(k; t₀, x₀)|| > ε

= 0,

||y₀||→0

k>k₀

выполняющееся при ∥z₁₀∥ ≤ L равномерно по ∥z₂₀∥ < ∞.

В результате для каждого k₀ ≤ 0 и для любых сколь угодно малых чисел

ε > 0, γ > 0, а также для любого наперед заданного числа L > 0 найдется

число δ(ε, γ, L, k₀) > 0 такое, что неравенство (2) имеет место для всех k ≥ k₀

и x₀ ∈ D_δ. Следовательно, при больших значениях z₁₀ в целом по z₂₀ “ча-

стичное” положение равновесия y(k) = 0 системы (1) y₁-устойчиво по веро-

ятности.

II. Если вместо условий (7) выполняются условия (9), то для любого задан-

ного числа L > 0 предельное соотношение (П.3) выполняется при ∥z₁₀∥ ≤ L

равномерно не только по ∥z₂₀∥ < ∞, но и по k₀ ≥ 0. В результате для каж-

дого k₀ ≥ 0 и для любых сколь угодно малых чисел ε > 0, γ > 0, а также

для любого наперед заданного числа L > 0 найдется независимое от k₀ чис-

ло δ(ε, γ, L) > 0 такое, что неравенство (2) имеет место для всех k ≥ k₀ и

x₀ ∈ D_δ. Следовательно, при больших значениях z₁₀ в целом по z₂₀ “частич-

ное” положение равновесия y(k) = 0 системы (1) равномерно y₁-устойчиво

по вероятности. Теорема 1 доказана.

129

Доказательство теоремы 2. При выполнении условий теоремы “ча-

стичное” положение равновесия y(k) = 0 системы (1) равномерно y₁-устой-

чиво по вероятности при больших значениях z₁₀ в целом по z₂₀.

На основании неравенства (П.1) последовательность v(k) случайных ве-

личин v(k) = V (τ(k), x(τ(k); k₀, x₀)), порожденных реализациями {x(k, ω),

ξ(k, ω)} случайного процесса {x(k), ξ(k)}, определяемого системой (1), об-

разует неотрицательный супермартингал, являющийся аналогом монотонно

убывающей последовательности в детерминированном случае. Поэтому на

основании неравенства (П.1) для каждой начальной точки x₀ из области D_ε

с вероятностью единица имеет место предельное соотношение [36]

v(k) = V (τ(k), x(τ(k); k₀, x₀)) → v_∗, k → ∞.

Используя известную схему [2, 3, 9] анализа, можно показать, что равен-

ство v_∗ = 0 выполняется с вероятностью единица. Действительно, применяя

операцию математического ожидания и переходя к пределу в обеих частях

неравенства (11), с вероятностью единица получаем

E[a₃(||y₁(τ(k); k₀, x₀)||)] → 0, k → ∞.

Поэтому в силу условий (10), (11) и леммы Фату справедливо равен-

ство E[a₃(a^-12(v_∗))] = 0, которое означает, что v_∗ = 0. Но в случае v_∗ = 0 при

∥y₀∥ → 0 имеет место предельное соотношение

{

}

P lim

||y₁(k; k₀, x₀)|| = 0

k→+∞

и, следовательно, “частичное” положение равновесия y(k) = 0 системы (1)

асимптотически y₁-устойчиво по вероятности при больших значениях z₁₀ в

целом по z₂₀. Теорема 2 доказана.

СПИСОК ЛИТЕРАТУРЫ

1. Кац И.Я., Красовский Н.Н. Об устойчивости систем со случайными параметра-

ми // Прикл. матем. и механика. 1960. Т. 24. Вып. 5. С. 809-823.

2. Кушнер Г.Дж. Стохастическая устойчивость и управление. М.: Мир, 1969.

3. Хасьминский Р.З. Устойчивость систем дифференциальных уравнений при слу-

чайных возмущениях их параметров. М.: Наука, 1969.

4. Kats I.Ya., Martynyuk A.A. Stability and Stabilization of Nonlinear Systems with

Random Structure. London: Taylor & Francis, 2002.

5. Mao X.R., Yuan C.G. Stochastic Differential Equations with Markovian Swit-ching.

London: Imperial College Press, 2006.

6. Ахметкалиев T. О связи между устойчивостью стохастических систем разност-

ных и дифференциальных систем // Дифференц. уравнения. 1965. Т. 1. № 8.

С. 1016-1026.

7. Халанай А., Векслер Д. Качественная теория импульсных систем. М.: Мир, 1971.

130

Константинов В.М. Об устойчивости стохастических разностных систем //

Пробл. передачи информ. 1970. Т. 6. Вып. 1. С. 81-86.

Пакшин П.В. Дискретные системы со случайными параметрами и структурой.

М.: Физматлит, 1994.

10.

Ажмяков В.В., Пятницкий Е.С. Нелокальный синтез систем стабилизации дис-

кретных стохастических объектов управления // АиТ. 1994. № 2. С. 68-78.

Azhmyakov V.V., Pyatnitskiy E.S. Nonlocal Synthesis of Systems for Stabilization

of Discrete Stochastic Controllable Objects // Autom. Remote Control. 1994. V. 55.

No. 2. P. 202-210.

11.

Барабанов И.Н. Построение функций Ляпунова для дискретных систем со слу-

чайными параметрами // АиТ. 1995. № 11. С. 31-41.

Barabanov I.N. Construction of Lyapunov Functions for Discrete Systems with

Stochastic Parameters // Autom. Remote Control. 1995. V. 56. No. 11. P. 1529-

1537.

12.

Jian X.S., Tian S.P., Zhang T.L., Zhang W.H. Stability and Stabilization of Non-

linear Discrete-Time Stochastic Systems // Int. J. Robust Nonlinear Control. 2019.

V. 29. No. 18. P. 6419-6437.

13.

Qin Y., Cao M., Anderson B.D.O. Lyapunov Criterion for Stochastic Systems and

its Applications in Distributed Computation // IEEE Trans. Autom. Control. 2020.

V. 65. No. 2. P. 546-560.

14.

Teel A.R., Hespanha J.P., Subbaraman A. Equivalent Characterizations of Input-to-

State Stability for Stochastic Discrete-Time Systems // IEEE Trans. Autom. Con-

trol. 2014. V. 59. No. 2. P. 516-522.

15.

Румянцев В.В. Об устойчивости движения по отношению к части переменных //

Вестн. МГУ. Сер. Матем., Механика, Физика, Астрономия, Химия. 1957. № 4.

C. 9-16.

16.

Румянцев В.В., Озиранер А.С. Устойчивость и стабилизация движения по от-

ношению к части переменных. М.: Наука, 1987.

17.

Воротников В.И. Частичная устойчивость и управление: состояние проблемы и

перспективы развития // АиТ. 2005. № 4. С. 3-59.

Vorotnikov V.I. Partial Stability and Control: the State of the Art and Developing

Prospects // Autom. Remote Control. 2005. V. 66. No. 4. P. 511-561.

18.

Rajpurohit T., Haddad W.M. Stochastic Finite-Time Partial Stability, Partial-State

Stabilization, and Finite-Time Optimal Feedback Control // Math. Control, Signals,

Syst. 2017. V. 29. No. 2. art. 10.

19.

Rajpurohit T., Haddad W.M. Partial-State Stabilization and Optimal Feedback Con-

trol for Stochastic Dynamical Systems // J. Dynam. Syst., Measurement, and Con-

trol. 2017. V. 139. No. 9. P. DS-15-1602.

20.

Воротников В.И., Мартышенко Ю.Г. К задаче частичной устойчивости по ве-

роятности нелинейных стохастических систем // АиТ. 2019. № 5. С. 86-98.

Vorotnikov V.I., Martyshenko Y.G. On the Partial Stability in Probability of Non-

linear Stochastic Systems // Autom. Remote Control. 2019. V. 80. No. 5. P. 856-866.

21.

Воротников В.И., Мартышенко Ю.Г. К задаче частичной устойчивости нели-

нейных дискретных систем // Мехатроника. Автоматизация. Управление. 2017.

Т. 18. № 6. С. 371-375.

22.

Ram

ırez-Llanos E., Mart´ınez S. Distributed and Robust Fair Optimization Applied

to Virus Diffusion Control // IEEE Trans. Network Sci. Engineer. 2017. V. 4. No. 1.

P. 41-54.

131

23.

Воротников В.И. Об устойчивости и устойчивости по части переменных “ча-

стичных” положений равновесия нелинейных динамических систем // Докл.

РАН. 2003. Т. 389. № 3. С. 332-337.

24.

Воротников В.И., Мартышенко Ю.Г. К теории частичной устойчивости нели-

нейных динамических систем // Изв. РАН. Теория и системы управления. 2010.

Т. 51. Вып. 5. С. 23-31.

25.

Юдаев Г.С. Об устойчивости стохастических разностных систем // Изв. Вузов.

Матем. 1979. № 8. С. 74-78.

26.

Phillis Y.A. y-Stability and Stabilization in the Mean of Discrete-Time Sto-chastic

Systems // Int. J. Control. 1984. V. 40. No. 1. P. 149-160.

27.

Шаров В.Ф. Устойчивость и стабилизация стохастических систем по отношению

к части переменных // АиТ. 1978. № 11. С. 63-71.

Sharov V.F. Stability and Stabilization of Stochastic Systems vis-a-vis Some of the

Variables // Autom. Remote Control. 1978. V. 39. No. 11. P. 1629-1636.

28.

Vorotnikov V.I. Partial Stability and Control. Boston: Birkhauser, 1998.

29.

Ignatyev O. Partial Asymptotic Stability in Probability of Stochastic Differential

Equations // Statist. Probab. Lett. 2009. V. 79. No. 5. P. 597-601.

30.

Zuyev A., Vasylieva I. Partial Stabilization of Stochastic Systems with Application

to Rotating Rigid Bodies // IFAC-PapersOnLine. 2019. V. 52. No. 16. P. 162-167.

31.

Sultanov O. Capture into Parametric Autoresonance in the Presence of Noise //

Commun. Nonlinear Sci. Numer. Simul. 2019. V. 75. P. 14-21.

32.

Kao Y., Wang C., Zha F., Cao H. Stability in Mean of Partial Variables for Stochas-

tic Reaction-Diffusion Systems with Markovian Switching // J. Franklin Institute.

2014. V. 351. No. 1. P. 500-512.

33.

Socha L., Zhu Q.X. Exponential Stability with Respect to Part of the Variab-les for

a Class of Nonlinear Stochastic Systems with Markovian Switching // Math. Comp.

Simul. 2019. V. 155. P. 2-14.

34.

Socha L. Stability and Positivity with Respect to Part of the Variables for Positive

Markovian Jump Systems // Bull. Polish Acad. Sci.: Tech. Sci. 2019. V. 67. No. 4.

P. 769-775.

35.

Хрусталев М.М., Онегин Е.Е. Необходимые и достаточные условия в задаче

оптимальной стабилизации квазилинейных стохастических систем // АиТ. 2019.

№ 7. С. 89-104.

Khrustalev M.M., Onegin E.E. Necessary and Sufficient Conditions for Optimal Sta-

bilization of Quasi-Linear Stochastic Systems // Autom. Remote Control. 2019.

V. 80. No. 7. P. 1252-1264.

36.

Дуб Дж.Л. Вероятностные процессы. М.: ИЛ, 1956.

Статья представлена к публикации членом редколлегии П.В. Пакшиным.

Поступила в редакцию 05.10.2020

После доработки 20.02.2021

Принята к публикации 16.03.2021

132