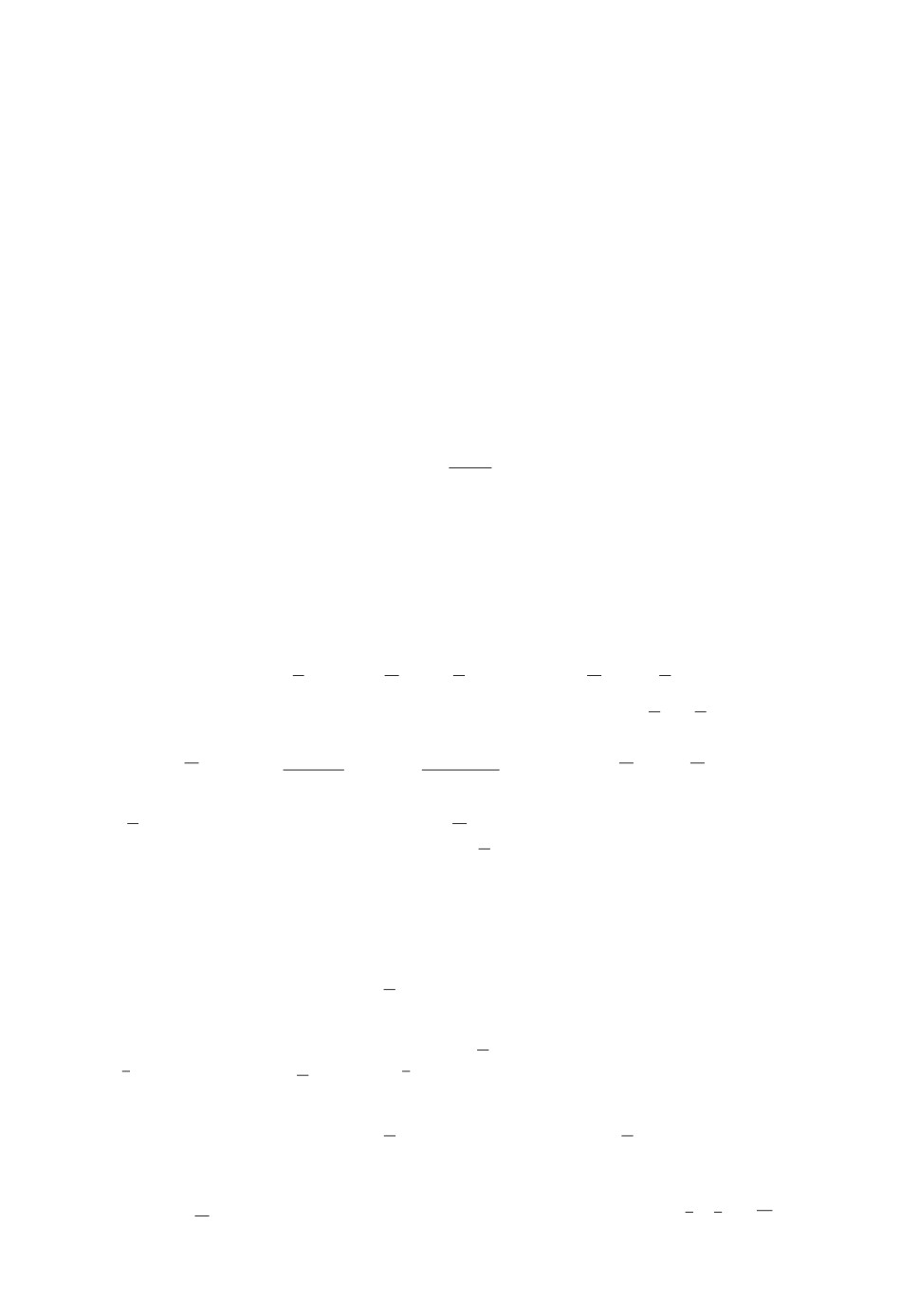Автоматика и телемеханика, № 1, 2022

Линейные системы

К.А. ЛАСТОЧКИН (lastconst@yandex.ru)

(Институт проблем управления им. В.А. Трапезникова РАН, Москва),

В.А. ПЕТРОВ, канд. техн. наук (petrov.va@misis.ru)

(Старооскольский технологический институт им. А.А. Угарова (филиал)

ФГАОУ ВО “Национальный исследовательский технологический

университет “МИСиС”, Старый Оскол)

НОРМАЛИЗАЦИЯ ВОЗБУЖДЕНИЯ РЕГРЕССОРА В ПРОЦЕДУРЕ

ДИНАМИЧЕСКОГО РАСШИРЕНИЯ И СМЕШИВАНИЯ¹

Предложен подход к нормализации возбуждения регрессора контура

идентификации, построенного на основе процедуры динамического рас-

ширения и смешивания. Применение этого подхода позволяет при посто-

янном значении коэффициента усиления контура оценки иметь одина-

ковую верхнюю границу параметрической ошибки идентификации для

скалярных регрессоров с различной степенью возбуждения, что является

существенным преимуществом для практики. Выполнено сравнение раз-

работанного подхода с известным методом амплитудной нормализации

регрессора и показано, что классический метод нормализации не обла-

дает указанным свойством. В качестве валидации полученных теорети-

ческих выводов приводятся результаты сравнительного математического

моделирования классического градиентного контура оценки, контуров с

амплитудной нормализацией регрессора и с предложенной нормализаци-

ей возбуждения регрессора.

Ключевые слова: идентификация, градиентный метод, параметрическая

ошибка, коэффициент усиления контура оценки, степень возбуждения,

нормализация.

DOI: 10.31857/S0005231022010020

1. Введение

Методы классической теории идентификации динамических объектов [1]

получили широкое распространение в инженерной практике специалистов по

автоматизации технологических процессов различных отраслей промышлен-

ности и, как правило, используются в процессе пусконаладочных работ для

получения математической модели технологического агрегата. Полученная

модель в дальнейшем обычно используется для расчета параметров промыш-

ленных ПИ и ПИД регуляторов. При этом точность модели является крити-

чески важным показателем, поскольку от нее напрямую зависит и точность

¹ Работа выполнена при частичной финансовой поддержке Российского фонда фунда-

ментальных исследований (проект № 18-47-310003 р_а).

параметров регуляторов, а значит, и экономические показатели технологиче-

ского агрегата, зависящие от качества управления.

Классические методы теории идентификации, к которым прежде всего

относятся рекурсивный метод наименьших квадратов и метод градиентно-

го спуска, обеспечивают точную идентификацию параметров модели толь-

ко при выполнении условия незатухающего возбуждения регрессора [2]. На

практике это требует инжекции высокочастотного тестового сигнала в управ-

ляющий вход технологического агрегата [3]. Использование метода инжек-

ции не всегда возможно в условиях реального промышленного производства.

Поэтому для ослабления условия незатухающего возбуждения за последние

несколько лет в публикациях были предложены новые методы [4-9], позво-

ляющие так или иначе улучшить точность идентификации параметров мо-

дели и, следовательно, степень ее соответствия реальному промышленному

агрегату. Главным достижением этих методов можно считать новые конту-

ры оценки со сходимостью за конечное время [4-6] и различные алгоритмы

фильтрации и предобработки регрессора [7-10], позволяющие исключить ин-

жекцию тестовых сигналов и точно идентифицировать параметры модели в

режиме работы технологического агрегата, близком к нормальному. В целом

с некоторыми оговорками можно считать, что проблема точной идентифика-

ции стационарных параметров динамических объектов является развитой с

ясными направлениями дальнейших исследований и перспективными прак-

тическими приложениями [11, 12] в промышленности.

Среди актуальных направлений исследований необходимо отметить пере-

нос полученных результатов на регрессионные уравнения с нелинейной пара-

метризацией [13] и интервально заданными и нестационарными параметрами

[6, 9,14].

Другой, менее проработанной проблемой как классических, так и совре-

менных контуров идентификации является задача выбора коэффициента уси-

ления γ закона оценки [15].

Для контуров оценки, обеспечивающих сходимость оценок параметров мо-

дели за конечное время [4-6], данная проблема состоит в необходимости вы-

бора коэффициента γ исходя из удовлетворения специальных условий.

Для классического градиентного контура оценки, а также для контуров

оценки градиентного типа, построенных с использованием процедур пред-

обработки регрессора [7-10], данную проблему можно условно разделить на

технический и теоретический уровни.

На техническом уровне проблема заключается в невозможности числен-

ного решения средствами современной промышленной микроконтроллерной

техники “жесткого” дифференциального уравнения контура оценки, получае-

мого при большом значении коэффициента усиления [15].

На теоретическом уровне упомянутая проблема состоит в: а) прямой за-

висимости от коэффициента усиления скорости сходимости оценок парамет-

ров модели и обратной зависимости точности получаемых оценок при нали-

чии возмущений, б) необходимости использования различных коэффициен-

тов усиления в зависимости от степени возбуждения регрессора [1].

В данной статье остановимся подробней на п. (б) теоретического уров-

ня проблемы выбора коэффициента усиления законов оценки градиентного

типа.

Основная трудность выбора коэффициента усиления как для базового гра-

диентного контура оценки, так и для его усовершенствованных путем пред-

обработки регрессора аналогов [7-10] заключается в зависимости между ве-

личиной верхней оценки ошибки идентификации и произведением коэффи-

циента усиления контура оценки γ на степень возбуждения регрессора α.

Здесь отметим, что для стандартного градиентного контура оценки зависи-

мость ошибки идентификации от γα получена при некоторых допущениях

[16], а для большинства современных контуров оценки с предобработкой ре-

грессора эта зависимость имеет место без допущений.

Степень возбуждения регрессора α в общем виде определяется длиной ин-

тервала возбуждения T и амплитудой регрессора A, поэтому упомянутая за-

висимость означает различную верхнюю оценку ошибки идентификации для

регрессоров с различной степенью возбуждения. Другими словами, при выбо-

ре стационарного коэффициента усиления γ для одних регрессоров парамет-

рическая ошибка может быть чрезвычайно большой, а для других напротив

чрезвычайно малой. С точки зрения практики применения современных ме-

тодов теории идентификации в промышленности весьма желательным было

бы иметь одинаковую верхнюю оценку параметрической ошибки для регрес-

соров с различной степенью возбуждения α.

Для этого в публикациях были предложены: 1) метод масштабирова-

ния [17], позволяющий, изменяя коэффициент усиления контура оценки γ в

зависимости от косвенной оценки степени возбуждения регрессора α, поддер-

живать приближенно одинаковую верхнюю оценку параметрической ошибки;

2) рекурсивный метод наименьших квадратов с экспоненциальным забывани-

ем [14, 15, 17], который в пределе обеспечивает зависимость верхней оценки

параметрической ошибки только от коэффициента экспоненциального забы-

вания. Метод масштабирования требует ручного выбора целого ряда пара-

метров масштабирования, а рекурсивный метод наименьших квадратов обес-

печивает необходимое свойство пропорциональности верхней оценки парамет-

рической ошибки и коэффициента забывания только в предельном случае и

только в контурах оценки с регрессорами определенного вида.

Метод масштабирования и рекурсивный метод наименьших квадратов с

экспоненциальным забыванием основаны на общей идее поддержания соот-

ношения γα постоянным путем динамической коррекции коэффициента уси-

ления γ в зависимости от оценки степени возбуждения регрессора α. Однако,

по мнению авторов настоящей статьи, такой подход, в конечном итоге, неиз-

бежно приводит или к новому контуру настройки с новыми параметрами,

требующими ручной настройки, или к различного рода эвристикам.

Поэтому в данной работе для получения одинаковой верхней оценки па-

раметрической ошибки для регрессоров с различной степенью возбуждения

предлагается не настраивать коэффициент усиления γ, а разработать проце-

дуру нормирования возбуждения регрессора, позволяющую получить зави-

симость параметрической ошибки не от произведения γα, а от нового про-

изведения γΔ, в котором Δ - величина, в отличие от α, не зависящая от

амплитуды A регрессора.

Предлагаемый подход позволит использовать стационарный коэффициент

усиления оценки γ и при этом иметь одинаковую верхнюю оценку парамет-

рической ошибки для различных исходных регрессоров.

Построить контур идентификации, обладающий указанными свойствами,

в статье предлагается, дополнив один из методов предобработки регрессора,

а именно процедуру динамического расширения и смешивания [10].

2. Формальное описание проблемы и постановка задачи

Рассматривается задача идентификации параметров класса линейных

объектов:

b(p)

(2.1)

y (t) =

u(t),

a (p)

где p = d/dt оператор дифференцирования, y выходная переменная, u

∑_n-1

∑m

управляющее воздействие, b (p) =

b_ipⁱ и a(p) = pⁿ +

a_ipⁱ

поли-

i=0

номы с квазистационарными (bi ≈ 0, ˙a_i ≈ 0) неизвестными параметрами.

Модель (2.1) известным методом [15] может быть представлена в виде ли-

нейной регрессии:

z (t) = θ^Tω (t) + η = y (t) + ψ^Tω₂ (t) +η,

θ := [b_m, b_m-1, . . . , b₀, a_n-1, a_n-2, . . . , a₀]^T , η := ρeΨct,

(2.2)

[

]_T

α_m (p)

α_n-1 (p)

[

]

ω (t) :=

u (t)

y (t)

ω^T1 (t) ω^T2 (t)

^T,

Ψ(p)

Ψ (p)

где z ∈ R

измеримая функция, ω ∈ R^m+n+1

измеримый регрессор,

вектор неизвестных параметров, η ∈ R

экспоненциально затухаю-

щее возмущение, вызванное несоответствием начальных условий в (2.1) и

[

]_T

(2.2), α_i (p) :=

pⁱ,p^i-1,... ,1

оператор дифференцирования, Ψ (p) = pⁿ +

+ψ^Tαn-1 (p) устойчивый полином с ψ = [ψ_n-1,ψ_n-2,... ,ψ₀]^T, Ψ_c мат-

рица, соответствующая полиному Ψ (p).

Относительно возмущения η в статье принимается следующее предполо-

жение.

Предположение 1. Возмущение η = 0 ∀t ≥ 0 или существует извест-

ное t₀ → 0, такое что η = 0 ∀t ≥ t₀.

Замечание 1. В предположении 1 предполагается или полное отсутствие

в регрессии (2.2) возмущения η, или обеспечение для η достаточно быстрой

сходимости к нулю путем выбора характеристического полинома Ψ (p).

В дальнейших рассуждениях также будем предполагать выполнение для

[

]

регрессора ω условия конечного возбуждения на интервале

t_s; t_s + T

Определение 1. Регрессор ω возбуждается конечно (ω ∈ FE) на ин-

[

]

тервале

t_s; t_s + T

, если существуют t_s ≥ t₀ ≥ 0, T > 0 и α > 0 такие, что

верно неравенство

∫

(2.3)

ω (τ) ω^T

(τ) dτ ≥ αI,

где α - степень возбуждения, I - единичная матрица.

Учитывая предположение 1, применим к регрессии (2.2) процедуру дина-

мического расширения и смешивания [10]. Для этого ∀t ≥ t₀ введем операто-

ры запаздывания в количестве m + n:

(2.4)

);

i ∈ {1,2,...,m + n},

(.)fi(t)^:=[Hi^{(.)](t)=(.)(t-d}i

где d_i - параметр, определяющий временнóе запаздывание i-го оператора

(2.4).

Пропуская через (2.4) функцию z и регрессор ω, сформируем ∀t ≥ t₀ рас-

ширенное уравнение регрессии

z_f (t) = ω_f (t) θ,

[

]_T

z_f (t) : =

z (t) zf1 (t) . . . zfn+m (t)

;

(2.5)

[

]_T

ω_f (t) := ω (t) ωf1 (t) ... ω

f_n+m

(t)

Домножив уравнение (2.5) слева на присоединенную матрицу алгебраиче-

ских дополнений adj {ω_f (t)} матрицы расширенного регрессора ω_f (t), а так-

же пользуясь равенством adj {ω_f (t)} ω_f (t) = det {ω_f (t)} I, получим ∀t ≥ t₀

уравнение:

z (t) = ω (t) θ,

(2.6)

z (t) : = adj {ω_f (t)} z_f (t) ; ω (t) : = det {ω_f (t)} ,

где z ∈ R^m+n+1, ω ∈ R.

Относительно параметров d_i принимается предположение 2.

Предположение 2. Параметры d_i выбраны так, что если ω ∈ FE на

[

]

интервале

t_s; t_s + T

, то ω ∈ FE на интервале [t_s; t_s + T ], поэтому существу-

ют t_s ≥ t₀ > t_s, T > 0 и α > 0 такие, что для ω верно неравенство

∫

(2.7)

ω²

(τ) dτ ≥ α,

где α - степень возбуждения скалярного регрессора, t₀ - момент времени

неравенства нулю выхода оператора (2.4) с максимальным значением пара-

метра d_i.

Замечание 2. Предположение 2 необходимо, поскольку при неудачном

выборе параметров d_i, матрица ω_f (t) может являться вырожденной ∀t [18].

Ослабить предположение 1 возможно, использовав вместо операторов запаз-

дывания (2.4) устойчивые минимально-фазовые динамические фильтры или

применив для генерации скаляризованной регрессии (2.6) вместо базовой про-

цедуры DREM ее модифицированный аналог [19] или процедуру MREM [20].

В силу принятых предположений, уравнение стандартного градиентного

контура оценки параметров регрессии (2.6) имеет вид

(

)

(2.8)

θ_i (t) =

θ_i (t) = -γω

θiω - z

= -γω²θ_i

(t) .

Получим решение скалярного дифференциального уравнения (2.8):

∫

-γ

ω²(τ)dτ

(2.9)

θi (t) = e^t0

θi (t0).

С учетом предположения 1 из (2.9) получим выражение для ошибки

θi (ts + T ) на интервале [ts; ts + T ]:

∫

-γ

(2.10)

θi (ts + T ) = e^ts

ω²dτ θ_i (t_s) ≤ e^-γα θ_i (t_s

Как следует из (2.10), параметрическая ошибка

θi (ts + T ) ограничена

сверху выражением, зависящим от произведения γα. С точки зрения прак-

тики применения контура оценки (2.8) полезно поддерживать одинаковую

точность идентификации, а значит, иметь для различных регрессоров оди-

наковую верхнюю границу (2.10) на параметрическую ошибку. Однако, как

следует из (2.7), параметр α меняется от регрессора к регрессору и определя-

ется длиной интервала возбуждения T и амплитудой регрессора A. Поэтому

для поддержания одинакового соотношения γα при изменении параметров A

и T в контуре оценки (2.8) требуется коррекция коэффициента γ. В против-

ном случае при постоянном γ для регрессоров с α → 0, но α > 0 возможны

значения параметрической ошибки, такие чтоθi (t_s + T ) →θi (t_s), а для ре-

грессоров с α → ∞, наоборот,θi (t_s + T ) → 0.

В этой статье ограничимся решением задачи поддержания одинаковой

верхней границы (2.10) параметрической ошибки (2.8) для класса регрессо-

ров c различными амплитудами A, но возбуждаемыми конечно на интервалах

одинаковой длинны T.

Определение 2. Регрессоры ω_j возбуждены конечно на одинаковом ин-

тервале времени [t_s; t_s + T], если существуют t_s ≥ t₀ > t_s, T > 0 и α_j > 0

такие, что верны неравенства

∫

(2.11)

ω^2j (τ) dτ ≥ α_j,

где α_j - степень возбуждения j-го регрессора.

Замечание 3. В частности, классу (2.11) принадлежат регрессоры, по-

лученные процедурой (2.2)-(2.6) при управляющих воздействиях различной

амплитуды (например, u = 1, u = 10, u = 100).

На частном численном примере продемонстрируем необходимость коррек-

ции коэффициента усиления γ для регрессоров из класса (2.11).

Пример 1. Пусть t_s = 0 c, T = 10 c, тогда при ω = Ae^-1t в (2.10) соответ-

ственно имеем:

∫

-γA²

e^-2tdτ

(2.12)

(0) .

θi (10) = e

θi (0) ≈ e-γA20,5 θi

Откуда, устремив A к нулю при зафиксированном γ, получаемθi (10) →θi (0),

что означает: 1) разную верхнюю границу на параметрическую ошибку для

регрессоров из класса (2.11); 2) необходимость перевыбора коэффициента γ

при изменении амплитуды A регрессора для поддержания одинаковой верх-

ней границы параметрической ошибки.

Обойти необходимость перевыбора коэффициента γ можно было бы, имея

для регрессоров из класса (2.11) вместо регрессора ω в уравнениях контура

оценки (2.8)-(2.10) некоторый нормированный регрессор ϕ =^ωf(ω) , такой что

верно неравенство

∫

(2.13)

ϕ²

(τ) dτ ≥ Δ > 0.

Тогда перевыбор коэффициента γ не требуется, а для всех регрессоров

класса (2.11) обеспечивается одинаковая верхняя граница параметрической

ошибки.

Таким образом, цель настоящей статьи разработка функции нормали-

зации f (ω), позволяющей для регрессоров из класса (2.11) получить одина-

ковую верхнюю границу параметрической ошибки без перевыбора коэффи-

циента γ.

Замечание 4. В примере 1 экспоненциально затухающий регрессор был

использован исключительно для наглядности, а продемонстрированная про-

блема характерна для всех регрессоров c различными амплитудами, но воз-

буждаемыми конечно на интервалах одинаковой длины T.

3. Основной результат

Определим нормирующую функцию для регрессора ω в виде

(3.1)

f (ω) : = sat (ω) ,

где sat (ω) - функция насыщения:

{

sgn (ω) ω_min, ecли

|ω| ≤ ω_min,

(3.2)

sat (ω) =

ω иначе.

Разделим регрессию (2.6) на нормирующую функцию (3.1):

Υ = ϕθ,

{

(3.3)

|ω| ω^-1min, если

|ω| ≤ ω_min,

Υ:=

;

ϕ:=

f (ω)

1 иначе,

где ϕ - нормированный скалярный регрессор.

Замечание 5. На данном этапе работы необходимо кратко отметить воз-

можность аналитического вычисления из регрессии (3.3) оценки неизвестных

параметров за конечное время. На основании определения регрессора ϕ в

(3.3) неизвестные параметры θ при отсутствии шумов измерения w могут

быть найдены за конечное время t_k с помощью процедуры:

θ = Υ(t_k),

(3.4)

если ϕ (t) = 1, то t_k = t.

Однако поскольку на практике в регрессии (3.3) неизбежно присутству-

ют шумовые составляющие w (t_k), то ϕ(t_k) = 1 может означать равенство

Υ (t_k) = θ + w (t_k), в котором в конкретный момент времени t_k может слу-

читься так, что w (t_k) > θ. Тогда оценка (3.3), полученная за конечное время,

является недостаточно точной. В то же время применение градиентного кон-

тура идентификации для регрессии Υ (t) = ϕ (t) θ + w (t) позволяет получить

оценку параметров не по одной точке t = t_k, а следовательно, уменьшить

влияние на качество оценки возмущений в каждый конкретный момент вре-

мени t_k [15].

Утверждение 1. Нормированный регрессор ϕ ∈ [0; 1].

Утверждение 2. Если для регрессора ω выполняется условие конечного

возбуждения (2.7) на интервале [t_s; t_s + T ], то для нормированного регрес-

сора ϕ на интервале [t_s; t_s + T]:

1) при |ω| ≤ ω_min выполняется неравенство

∫

(3.5)

αω^-2min ≤

ϕ²

(τ)dτ ≤ T;

2) при |ω| > ω_min выполняется неравенство

∫

(3.6)

0<Δ≤ ϕ²

(τ) dτ = T,

где Δ ∈ (0; T ] - одинаковая величина ∀ωj, для которых на интервале

[t_s; t_s + T ] верно |ω_j| > ω_min.

Доказательства утверждений 1 и 2 приведены в Приложении.

Градиентный контур оценки, построенный по нормированной регрессии

(3.3), имеет вид:

(3.7)

θ_i (t) = -γϕ²

θi

(t).

Получим решение дифференциального уравнения

(3.7) на интервале

[t_s; t_s + T ]:

∫

-γ

ϕ²(τ)dτ

(3.8)

θi (ts + T ) = e^ts

θi (ts).

Для решения (3.8), пользуясь утверждением 2, могут быть получены два

важных следствия.

Следствие 1. Для всех ω_j, для которых на всем интервале [t_s; t_s + T]

верно |ω_j| ≤ ω_min, параметрическая ошибкаθi (t_s + T ) ограничена в соответ-

ствии c выражением:

(3.9)

e^-γT θ_i (t_s) ≤θi (t_s + T) ≤ e-γαjωminθi (t_s

Следствие 2. Для всех ω_j, для которых на всем интервале [t_s; t_s + T]

верно |ω_j| > ω_min, параметрическая ошибкаθi (t_s + T ) ограничена в соответ-

ствии c выражением:

(3.10)

θi (ts + T ) = e^-γT θi (ts) ≤ e^-γΔ θi (ts).

В следствиях 1 и 2 рассмотрены ситуации, когда на всем интервале воз-

буждения [t_s; t_s + T ] выполняется либо условие |ω_j| > ω_min, либо условие

|ω_j| ≤ ω_min. На практике такие ситуации обычно периодически чередуются

на интервале возбуждения [t_s; t_s + T ], поэтому рассмотрим ситуацию, ко-

гда для ω_j на интервале [t_s; t_s + T ] хотя бы раз было выполнено условие

|ω_j| > ω_min. Для этого введем утверждение 3.

У т в е р ж д е н и е 3. Пусть ω_j ∈ FE на интервале

[t_s; t_s + T ] и

для ω_j существуют моменты времени t_j ∈ (0; T ) и T_j ∈ (t_j ; T ) такие, что

∀t ∈ [t_s + t_j; t_s + T_j] верно неравенство |ω_j| > ω_min.

Тогда:

1. Для нормированного регрессора ϕ верно

∫

(3.11)

0<Δ_min ≤

ϕ²

(τ)dτ ≤ T,

где Δ_min - одинаковая величина ∀ω_j, соответствующих постановке утвер-

ждения 3.

2. Для всех ω_j, соответствующих постановке утверждения 3, парамет-

рическая ошибкаθi (t_s + T) ограничена сверху в соответствии с выражени-

ем

(3.12)

θi (ts + T ) ≤ e-γΔmin θi (ts).

Доказательство утверждения 3 и определение величины Δ_min приводятся

в Приложении.

Таким образом, из утверждения 3 следует, что выбор параметра ω_min

из условия выполнения неравенства |ω_j| > ω_min хотя бы раз на интервале

[t_s; t_s + T ] является необходимым и достаточным для ограниченности пара-

метрической ошибкиθi (t_s + T ) сверху одинаковой величиной для различных

регрессоров ω_j, что позволяет в контуре оценки (3.7) использовать одинако-

вое значение коэффициента усиления γ.

Замечание 6. Выбор величины ω_min из класса (2.11) позволяет выде-

лить некоторый подкласс регрессоров, для которых хотя бы раз на интер-

вале возбуждения [t_s; t_s + T ] выполняется |ω_j| > ω_min, и поэтому существует

одинаковая верхняя оценка параметрической ошибки. Для регрессоров ω_j , не

входящих в этот подкласс, т.е. таких, для которых на всем интервале возбуж-

дения [t_s; t_s + T ]

|ω_j| ≤ ω_min будет осуществлена нормализация регрессора,

но не нормализация его возбуждения (3.5). Поэтому на практике величи-

ну ω_min необходимо выбирать, исходя из априорных данных о минимально

возможном регрессоре ω_j и максимальной амплитуде шумов измерения. При

неудачном выборе параметра ω_min, так что |ω_j| ≤ ω_min ∀t ∈ [t_s; t_s + T ], пред-

ложенная нормализация при ω_min < 1 позволяет (3.9) увеличить в ω^-2min раз

исходную степень возбуждения регрессора, что свидетельствует о преимуще-

стве выбора значений параметра ω_min из условия ω_min < 1.

Продемонстрируем описанные свойства нормированного контура оценки

(3.7) на примере 2.

Пример 2. Пусть t_s = t_j = 0 с, T = 10 с, ω_min = 10^-2. Рассмотрим для

примера регрессоры: ω₁ = e^-1t и ω₂ = 10e^-1t. Чтобы воспользоваться выво-

дами утверждения 3, сначала определим моменты времени T_j для каждого

регрессора:

(

)

0,01

ln (0,01)

(3.13)

T₁ =

≈ 4,61; T₂

≈ 6,91.

-1

Откуда, учитывая ω_min = 10^-2, можем получить функциональное описа-

ние регрессоров ϕ₁ и ϕ₂ на соответствующих интервалах (см. таблицу).

Таблица

ϕ₁

ϕ₂

[0; 4,61]

[0; 6,91]

[4,61; 10]

|ω| ω^-1min = e^-1(t-4,61)

[6,91; 10]

|ω| ω^-1min = e^-1(t-6,91)

Пользуясь полученным описанием регрессоров ϕ₁ и ϕ₂, вычислим значение

интеграла в (3.8):

∫

ϕ²¹ (τ) dτ ≈

1²dτ + e^-2(t-4,61)dτ ≈ 5,11 ≥ Δ_min,

4,61

(3.14)

∫

ϕ²² (τ)dτ ≈

1²dτ + e^-2(t-6,91)dτ ≈ 7,409 ≥ Δ_min.

6,91

Зная моменты времени T_j , в соответствии с (П.7) для ϕ₁ и ϕ₂ можем вы-

брать общую Δ_min из интервала (0; 4,61]. Тогда параметрическая ошибка на

интервале [0; 10] для регрессоров ϕ₁ и ϕ₂ имеет вид:

θϕ¹i (10) ≈ e^-γ5,11 θi (ts) ≤ e-γΔmin θi (0) ,

(3.15)

θϕ²i (10) ≈ e^-γ7,409 θi (ts) ≤ e-γΔmin θi (0) .

Как следует из (3.14) и (3.15), для параметрических ошибок, полученных

контуром (3.7) с различными регрессорами, существует одинаковая оценка

сверху, значение которой может быть отрегулировано с помощью выбора еди-

ного коэффициента усиления γ.

4. Сравнение с нормализованным градиентным законом оценки

Сравним разработанный контур оценки с уже известным градиентным

контуром с классической нормализацией регрессора [15]. Уравнение гради-

ентного контура оценки с классической нормализацией имеет вид

ω²

(4.1)

θ_i = -γ

θi.

1+ω²

При выполнении условия (2.7) для нормированного регрессора будет вер-

ным неравенство

∫

ω² (τ)

(4.2)

0<α_n ≤

dτ < T,

1 + ω2 (τ)

где α_n < α - степень возбуждения нормированного регрессора.

Как следует из (4.2), степень возбуждения α_n нормированного регрессо-

ра в законе оценки (4.1) строго меньше степени возбуждения исходного α и

строго ограничена сверху величиной T для любого регрессора.

Однако в сравнении с предложенной в этой статье нормализацией воз-

буждения регрессора, во-первых, верхняя оценка возбуждения в (4.2) только

строгая, во-вторых, в предложенном контуре оценки (3.7) в самом плохом

случае (3.5) возможно не уменьшить, а увеличить степень возбуждения пу-

тем выбора ω_min < 1.

С учетом (4.2) верхняя оценка на решение дифференциального уравне-

ния (4.1) на интервале [t_s; t_s + T ] имеет вид

(4.3)

θi (ts + T ) ≤ e-γαn θi (ts).

Из (4.3) по аналогии с (2.10) следует, что для контура оценки с классиче-

ской нормализацией (4.1) также требуется перевыбор коэффициента усиле-

ния γ с целью поддержания соотношения γα_n постоянным для регрессоров

с различной степенью возбуждения α_n, в то время как в разработанном кон-

туре оценки (3.7) этого не требуется.

5. Численный пример

В среде Matlab/Simulink сравним разработанный контур оценки (3.7) с

нормализацией возбуждения регрессора с градиентным контуром (2.8) и гра-

диентным контуром с нормализованным регрессором (4.1). Моделирование

будем проводить, используя численное интегрирование методом Эйлера c по-

стоянным шагом дискретизации τ_s = 10^-2 с.

В качестве объекта, параметры которого необходимо идентифицировать,

выберем следующее звено:

b₁p + b₀

2p + 1

(5.1)

y (t) =

u(t) =

u(t).

p² + a₁p + a₀

p² + 1p + 2

Параметры фильтров (2.2), величины задержек (2.4), а также пара-

метр ω_min зададим следующим образом:

(5.2)

ψ₁ = 20; ψ₀ = 100; d₁ = 0,2; d₂ = 0,4; d₃ = 0,6; ω_min = 10^-12.

Значения задержек были определены в соответствии с рекомендациями,

данными в [18], а величина параметра ω_min была выбрана в соответствии с

замечанием 6.

1,0

0,8

0,6

0,4

0,2

0,5

1,0

1,5

2,0

2,5

3,0

3,5

t, c

Рис. 1. Сравнение нормализованных регрессоров ϕ при различных u (сплош-

ная линия u = 1, штриховая линия u = 10, штрихпунктирная линия

u = 100).

||q||-(2.8)

3,5

3,0

2,5

2,0

1,5

1,0

0,5

1,0

1,5

2,0

2,5

3,0

3,5

t, c

||q||-(3.7)

3,2

3,0

2,8

2,6

2,4

0,5

1,0

1,5

2,0

2,5

3,0

3,5 t, c

||q||-(4.1)

3,5

3,0

2,5

2,0

1,5

1,0

0,5

1,0

1,5

2,0

2,5

3,0

3,5 t, c

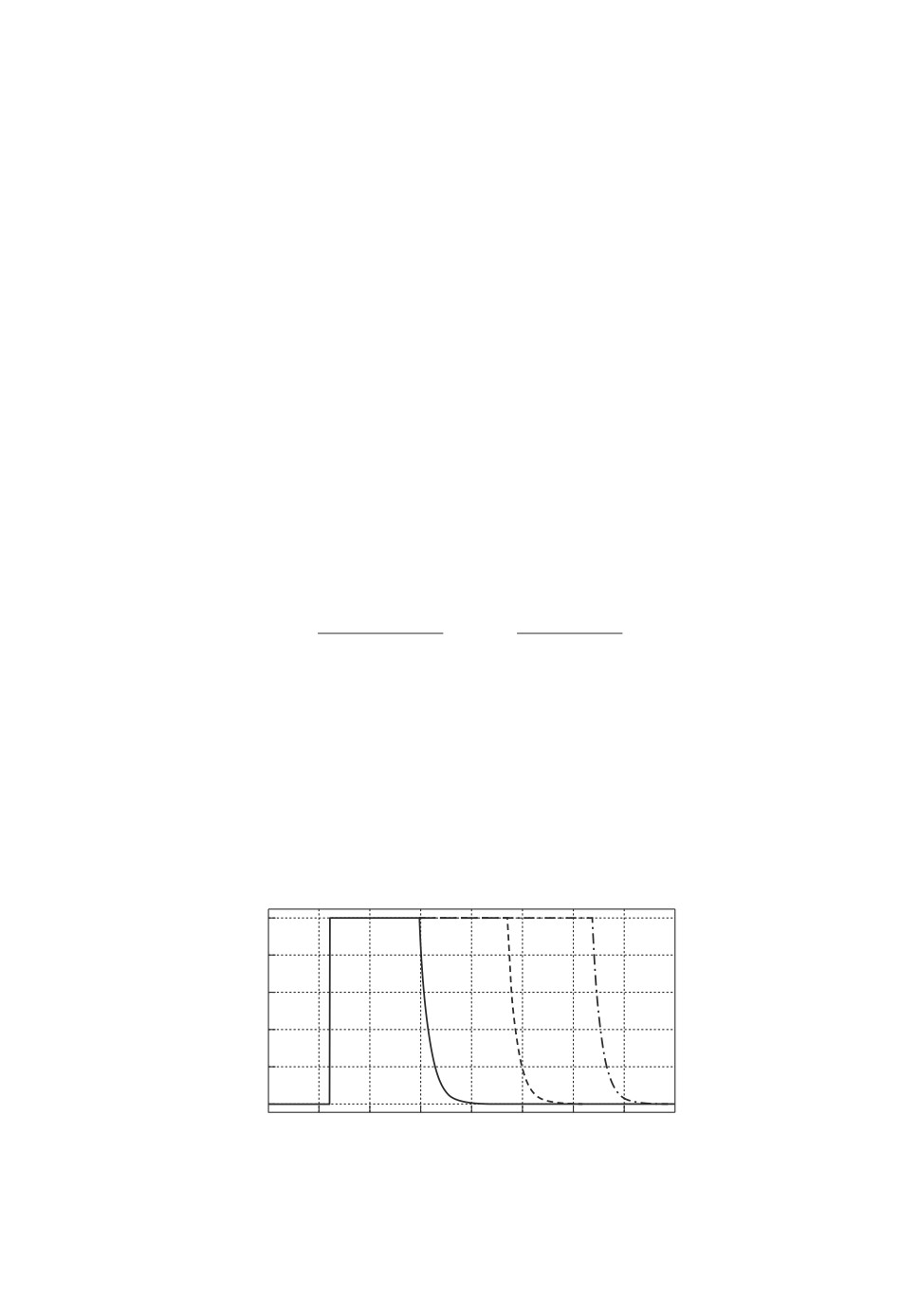
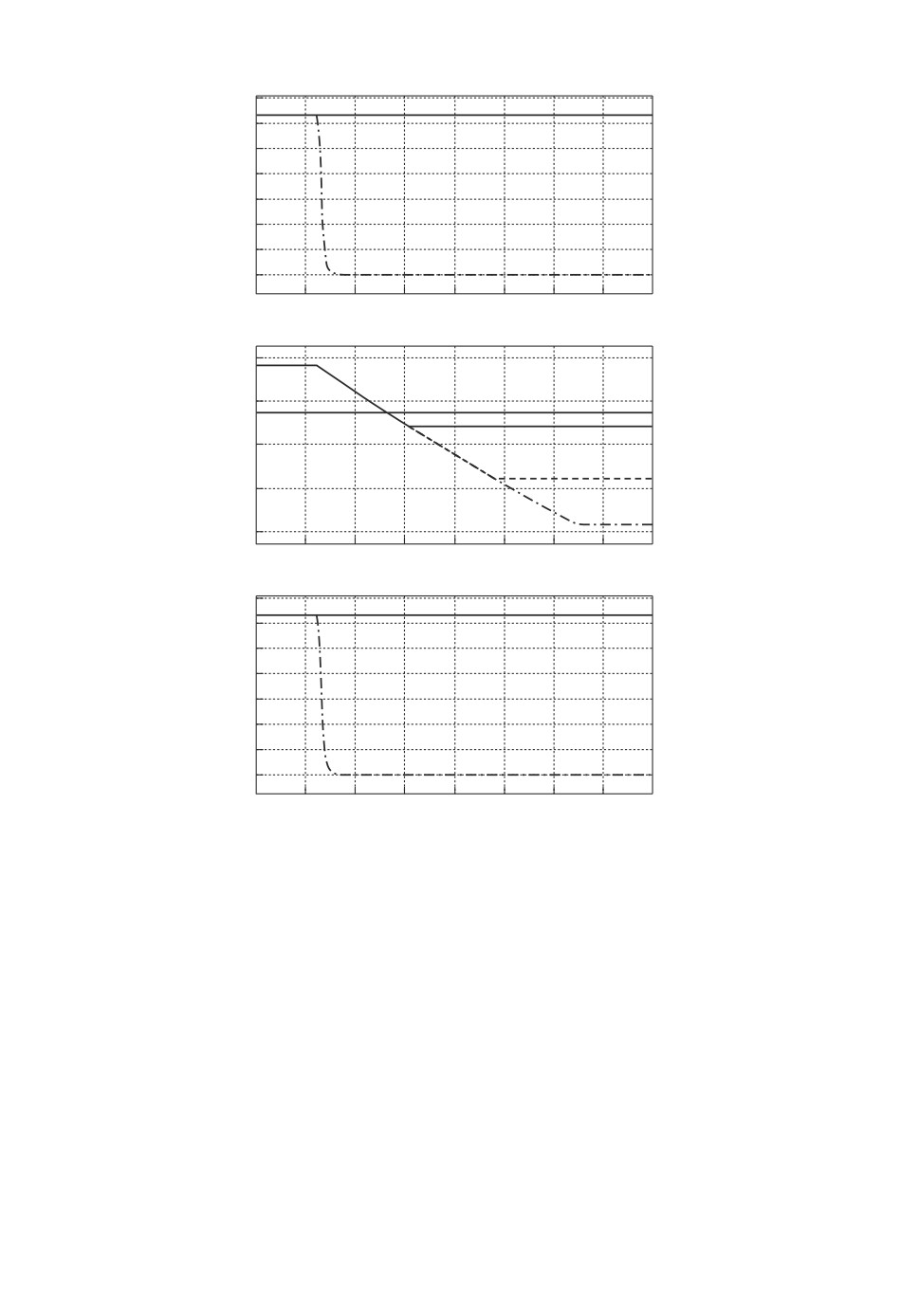
Рис. 2. Нормы параметрических ошибок контуров оценки (2.8), (3.7) и (4.1)

(сплошная линия u = 1, штриховая линия u = 10, штрихпунктирная ли-

ния u = 100, UB Ultimate Bound (верхняя граница)).

В качестве сигнала управления u на вход объекта (2.1) в соответствии с

замечанием 1 будем подавать постоянные сигналы различной амплитуды:

(5.3)

u = 1; u = 10; u = 100.

Начальную параметрическую ошибку примемθ(0) = -θ, а коэффициенты

усиления моделируемых контуров оценки выберем следующим образом:

(5.4)

γ = 10⁴; γ_NE = 0,1; γ_NR = 10⁴,

где γ, γ_NE , γ_NR - коэффициенты усиления контуров оценки (2.8), (3.7) и (4.1)

соответственно.

На рис. 1 приведено сравнение нормализованных регрессоров ϕ, получен-

ных из регрессора ω при сигналах управления различной амплитуды (5.3).

||q||-(g~NE = 1)

3,5

3,0

2,5

2,0

1,5

1,0

0,5

1,0

1,5

2,0

2,5

3,0

3,5

t, c

||q||-(g_NE = 10)

3,5

3,0

10^-3

2,5

2,0

1,5

1,0

0,5

t, c

0,5

1,0

1,5

2,0

2,5

3,0

3,5

t, c

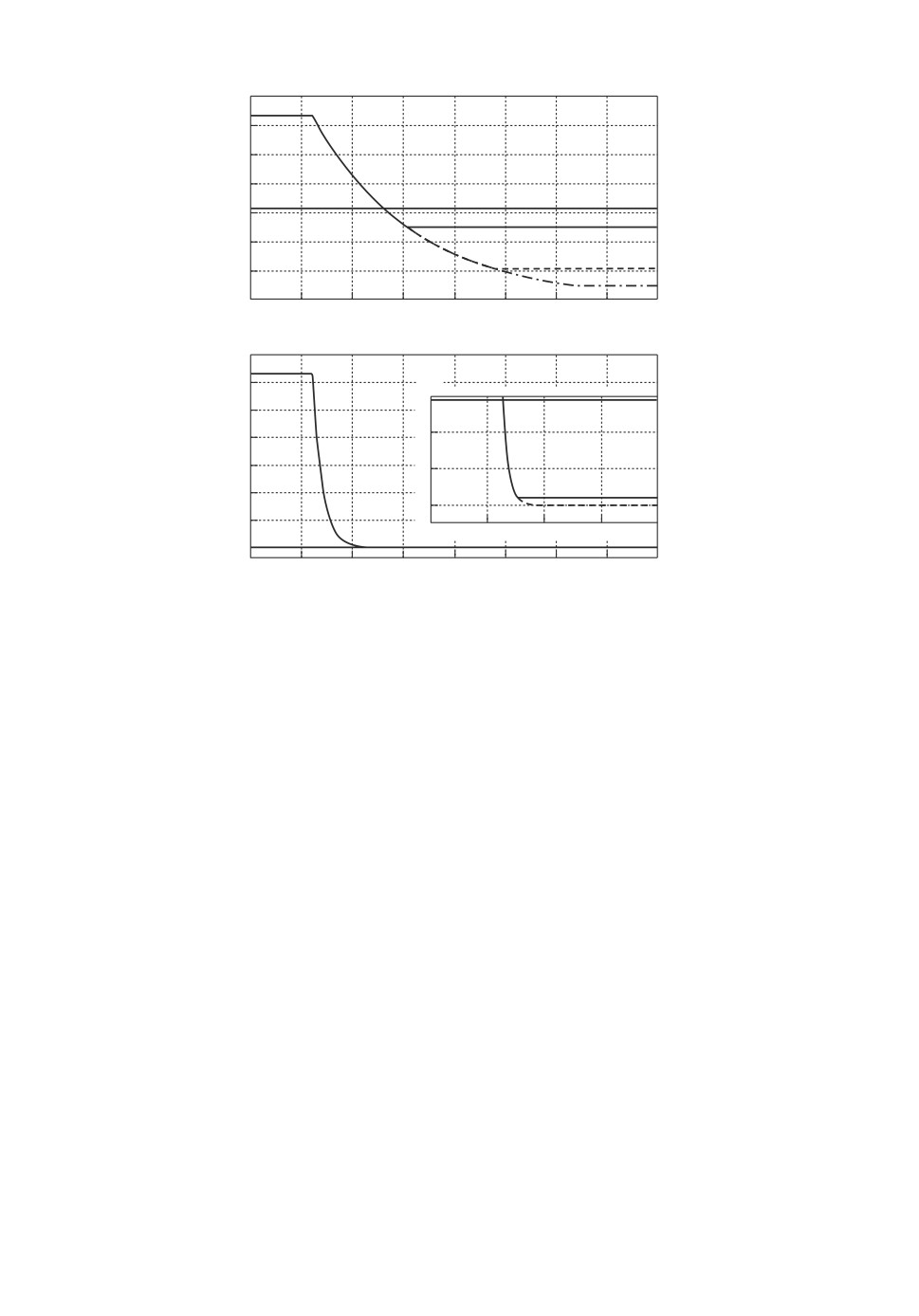
Рис. 3. Нормы параметрической ошибки контура (3.7) при различных γ

(сплошная линия u = 1, штриховая линия u = 10, штрихпунктирная ли-

ния u = 100, UB Ultimate Bound (верхняя граница)).

Приведенные на рис. 1 переходные процессы подтверждают выводы, сде-

ланные в утверждениях, и в терминах утверждения 3 позволяют определить

величину Δ_min ∈ (0; 0,88].



На рис. 2 приведено сравнение переходных процессов по

θ,полученных

при применении контуров оценки (2.8), (3.7) и (4.1). На графике нормы пара-

метрической ошибки разработанного контура оценки (3.7) также приводится

верхняя оценка (UB), рассчитанная по формуле (3.12) при Δ_min = 0,7 и t_s =

= 0 с.

Как следует из рис. 2, разработанный контур оценки, в отличие от (2.8)

и (4.1), позволяет не допускать ситуаций, когда для одних регрессоров



θ(t → ∞)→

θ(t₀), а для других

θ(t → ∞)→ 0, что и является

основным результатом статьи.

Далее промоделируем разработанный контур оценки (3.7) при различных

управляющих воздействиях (5.3) и различных значениях коэффициента уси-

ления γ.

Результаты данного эксперимента показывают, что выбор коэффициен-

та γ в (3.7) позволяет корректировать верхнюю оценку параметрической

шибки и ри том н допускать сиуаций, кога для одних регрессоров

θ(t → ∞)

→

θ(t₀)

, а для других

θ(t → ∞)

→ 0.

6. Заключение

Для идентификации параметров линейных динамических объектов в раз-

личных режимах работы без перевыбора коэффициента усиления контура

оценки в исследовании была разработана процедура нормализации возбуж-

дения регрессора. Предложенная процедура может оказаться полезной при

оффлайн идентификации интервальных моделей промышленных объектов

управления, функционирующих по технологическим ступеням уставок.

Так как в данной статье влияние шумов измерения на полученные ре-

зультаты было отмечено кратко (см. замечание 3 и 4), то в дальнейших ра-

ботах планируется более подробно исследовать свойства разработанной нор-

мализации в условиях их наличия. Также в следующих работах планиру-

ется использование предложенного подхода для нормализации возбуждения

интегрально-растущего регрессора в процедуре [21].

ПРИЛОЖЕНИЕ

Доказательство утверждения 1. При |ω| > ω_min регрессор ϕ = 1

по определению в (3.3). В противном случае |ω| ω^-1min ≤ 1, откуда следует при-

надлежность ϕ отрезку [0; 1], что и требовалось доказать.

Доказательство утверждения 2. Для доказательства утвержде-

ния выпишем из (3.3) выражение для регрессора ϕ:

(Π.1)

ϕ=

f (ω)

Выражая из (П.1) ω² и подставляя полученное выражение в определение

(2.11), имеем:

∫

(Π.2)

ω² (τ) dτ =

f² (ω (τ))ϕ²

(τ)dτ ≥ α.

Откуда при |ω| ≤ ω_min с учетом (3.1) и (3.2) непосредственно следует ниж-

няя оценка в (3.5). Также, пользуясь теоремой об оценке определенного ин-

теграла и учитывая ϕ ∈ [0; 1], из (П.2) имеем верхнюю оценку в (3.5).

В случае |ω| > ω_min из (П.1) можем получить:

∫

ω²

(τ)

(Π.3)

dτ =

ϕ²

(τ) dτ.

f² (ω (τ))

Пользуясь формулой Лейбница и учитывая ϕ = 1 при |ω| > ω_min, из (П.3)

нетрудно получить равенство:

∫

ω²

(τ)

(Π.4)

dτ =

ϕ²

(τ) dτ = T.

f² (ω (τ))

Так как T > 0 по условию конечного возбуждения, то в (П.4) всегда су-

ществует некоторое 0 < Δ ≤ T такое, что верно неравенство (3.6). Поскольку

T одинакова для всех регрессоров класса (2.11), то величина Δ также может

быть принята одинаковой ∀ω_j, для которых верно |ω_j| > ω_min, что завершает

доказательство утверждения 2.

Доказательство утверждения 3. Условие конечного возбужде-

ния для регрессора ϕ может быть записано в эквивалентном виде:

∫

ϕ² (τ)dτ =

ϕ² (τ)dτ +

ϕ² (τ)dτ ≥

ts+tj

ts+Tj

(Π.5)

∫

≥

ϕ² (τ)dτ.

ts+tj

В силу |ω_j| > ω_min на интервале [t_s+t_j; t_s + T_j ], по доказанному в утвер-

ждении 2, для нижней оценки в (П.5) имеем:

∫

(Π.6)

ϕ² (τ)dτ = T_j - t_j.

ts+tj

Поскольку по условию утверждения t_j ∈ (0; T ), а T_j ∈ (t_j; T ), то существует

момент времени Δ_min, такой, что:

(Π.7)

0 < Δ_min ≤ min{Tj - tj} ≤ Tj - tj

<T.

j≥0

Учитывая неравенства (П.5), (П.6) и (П.7), имеем нижнюю оценку в (3.11).

Для получения верхней оценки в (3.11) запишем с учетом утверждения 2

оценку сверху на первое и третье слагаемое в равенстве (П.5):

∫

ϕ² (τ)dτ ≤ t_j;

(Π.8)

∫

ϕ² (τ) dτ ≤ T - T_j.

ts+Tj

Складывая верхние оценки (П.6) и (П.8), имеем верхнюю оценку в (3.11),

что вместе с полученной нижней оценкой в (П.5) позволяет записать нера-

венство (3.11) в полном виде. С помощью оценки (3.11) нетрудно получить

оценку (3.12) на решение (3.8), что завершает доказательство утверждения 3.

СПИСОК ЛИТЕРАТУРЫ

Льюнг Л. Идентификация систем. Теория для пользователя. М.: Наука, 1991.

Narendra K.S., Annaswamy A.M. Persistent Excitation in Adaptive Systems // Int.

J. Control. 1987. V. 45. No. 1. P. 127-160.

Holtz J. Sensorless Control of Induction Machines - With or without Signal Injec-

tion? // IEEE Trans. Industr. Electronics. 2006. V. 53. No. 1. P. 7-30.

Wang J., Efimov D., Aranovskiy S., Bobtsov A. Fixed-time Estimation of Parameters

for Non-persistent Excitation // Eur. J. Control. 2020. V. 55. P. 24-32.

Wang J., Efimov D., Bobtsov A. On Robust Parameter Estimation in Finite-time

without Persistence of Excitation // IEEE Trans. Automat. Control. 2019. V. 65.

No. 4. P. 1731-1738.

Ortega R., Bobtsov A., Nikolaev N. Parameter Identification with Finite-Convergence

Time Alertness Preservation // IEEE Control Syst. Lett. 2021. P. 1-6.

Chowdhary G., Mühlegg M., Johnson E. Exponential Parameter and Tracking Error

Convergence Guarantees for Adaptive Controllers without Persistency of Excita-

tion // Int. J. Control. 2014. V. 87. No. 8. P. 1583-1603.

Cho N., Shin H., Kim Y., Tsourdos A. Composite Model Reference Adaptive Con-

trol with Parameter Convergence under Finite Excitation // IEEE Trans. Automat.

Control. 2017. V. 63. No. 3. P. 811-818.

Lee H.I., Shin H.S., Tsourdos A. Concurrent Learning Adaptive Control with Direc-

tional Forgetting // IEEE Trans. Automat. Control. 2019. V. 64. No. 12. P. 5164-

5170.

10.

Aranovskiy S., Bobtsov A., Ortega R., Pyrkin A. Performance Enhancement of Pa-

rameter Estimators via Dynamic Regressor Extension and Mixing // IEEE Trans.

Automat. Control. 2016. V. 62. No. 7. P. 3546-3550.

11.

Bobtsov A., Pyrkin A., Ortega R., Vedyakov A. A State Observer for Sensorless

Control of Magnetic Levitation Systems // Automatica. 2018. V. 97. P. 263-270.

12.

Ortega R., Bobtsov A., Nikolaev N., Schiffer J., Dochain D. Generalized Parameter

Estimation-based Observers: Application to Power Systems and Chemical-biological

Reactors // arXiv preprint arXiv:2003.10952. 2020. P. 1-13.

13.

Ortega R., Gromov V., Nuno E., Pyrkin A., Romero J. Parameter Estimation of

Nonlinearly Parameterized Regressions without Overparameterization: Application

to Adaptive Control // Automatica. 2021. V. 127. P. 109544.

14.

Glushchenko A., Petrov V., Lastochkin K. Regression Filtration with Resetting to

Provide Exponential Convergence of MRAC for Plants with Jump Change of Un-

known Parameters // arXiv preprint arXiv:2102.10359. 2021. P. 1-12.

15.

Ioannou P., Sun J. Robust Adaptive Control. N.Y.: Dover, 2013.

16.

Sastry S., Bodson M. Adaptive Control - Stability, Convergence, and Robustness.

N.J.: Prentice Hall, 1989.

17.

Schatz S.P., Yucelen T., Gruenwal B., Holzapfe F. Application of a Novel Scalabil-

ity Notion in Adaptive Control to Various Adaptive Control Frameworks // AIAA

Guidance, Navigation, and Control Conf. 2015. P. 1-17.

18.

Aranovskiy S., Belov A., Ortega R., Barabanov N., Bobtsov A. Parameter Identifi-

cation of Linear Time-invariant Systems Using Dynamic Regressor Extension and

Mixing // Int. J. Adaptive Control Signal Process. 2019. V. 33. No. 6. P. 1016-1030.