Автоматика и телемеханика, № 1, 2022

Нелинейные системы

С.А. КРАСНОВА, д-р техн. наук (skrasnova@list.ru),

В.А. УТКИН, д-р техн. наук (viktorutkin013@gmail.com)

(Институт проблем управления им. В.А. Трапезникова РАН, Москва)

СИНТЕЗ ИНВАРИАНТНЫХ НЕЛИНЕЙНЫХ ОДНОКАНАЛЬНЫХ

СИСТЕМ СЛЕЖЕНИЯ С СИГМОИДАЛЬНЫМИ ОБРАТНЫМИ

СВЯЗЯМИ С ОБЕСПЕЧЕНИЕМ ЗАДАННОЙ ТОЧНОСТИ СЛЕЖЕНИЯ¹

Для нелинейных одноканальных объектов управления, математиче-

ская модель которых представима в треугольной форме вход - выход,

рассматривается задача слежения в условиях внешних и параметриче-

ских возмущений. В рамках блочного подхода разработана декомпози-

ционная процедура синтеза нелинейной обратной связи, обеспечивающая

отслеживание выходной переменной целевого сигнала с заданной точно-

стью за заданное время. Формализован новый тип сигмоидальных ло-

кальных связей из класса гладких и всюду ограниченных S-образных

функций, обеспечивающих инвариантность по отношению к неконтроли-

руемым ограниченным возмущениям, не принадлежащим пространству

управления, без предположений об их гладкости. Приведены результа-

ты моделирования разработанных алгоритмов для системы управления

перевернутым маятником.

Ключевые слова: нелинейная SISO система, слежение, декомпозиция, ин-

вариантность, сигма-функция, перевернутый маятник.

DOI: 10.31857/S0005231022010032

1. Введение

Базовой проблемой теории автоматического управления является задача

слежения, при решении которой нужно обеспечить в замкнутой системе от-

работку выходными переменными целевых допустимых сигналов с заданны-

ми показателями переходных и установившихся процессов. Основные усилия

специалистов направлены на решение этой задачи применительно к объек-

там, функционирующим при действий внешних неконтролируемых возмуще-

ний. Наиболее разработанным является случай, когда аффинные внешние

возмущения действуют в пространстве управления, т.е. условия согласования

(англ. “matching conditions”) выполнены [1]. По отношению к согласованным

возмущениям можно обеспечить инвариантность всего вектора состояния как

¹ Работа выполнена при частичной финансовой поддержке Российского фонда фунда-

ментальных исследований (проект № 20-01-00363А).

с помощью динамической, так и статической обратной связи. В первом слу-

чае предварительно нужно получить оценки внешних возмущений с помощью

динамического компенсатора или наблюдателя возмущений (см., например,

[1-6]) и компенсировать их действие с помощью комбинированного управле-

ния. Во втором случае для подавления внешних ограниченных возмущений

используются “силовые” методы: глубокие обратные связи или разрывные

управления с организацией скользящего режима [7-9].

Наибольшую сложность представляют объекты с несогласованными воз-

мущениями, которые нельзя непосредственно компенсировать или подавить

с помощью истинного управления. В задаче слежения к таким возмущени-

ям относятся также производные целевых сигналов. Поэтому задача обеспе-

чения инвариантности по отношению к возмущениям ставится только для

регулируемых выходов (ошибок слежения), а остальные переменные вы-

нуждены отрабатывать соответствующие внешние воздействия. Для синтеза

следящей системы в предположении о гладкости внешних и параметриче-

ских возмущений используют генераторы задающих и возмущающих воздей-

ствий, наблюдатели возмущений, регрессоры и идентификаторы параметров

[1, 10-12]. При этом динамический порядок замкнутой системы увеличивает-

ся в несколько раз по сравнению с размерностью модели объекта управления.

Кроме того, построение адекватных динамических моделей внешних воздей-

ствий достаточно проблематично, если они меняются в процессе эксплуатации

или недостаточно гладкие. Примером могут служить ударные нагрузки и си-

лы сухого трения при управлении электромеханическими объектами [13-15].

В частном случае, когда негладкое возмущение отделено от истинного управ-

ления одним интегратором, можно подавить его с помощью “вихревого” ста-

тического управления с непрерывной и разрывной составляющими. Результат

достигается за счет организации в системе колебательного переходного про-

цесса, при котором часть переменных состояния автоматически компенсирует

влияние неизвестных слагаемых [16].

В общем случае для обеспечения инвариантности ошибок слежения по от-

ношению к несогласованным возмущениям, которые не подлежат дифферен-

цированию, целесообразно использовать локальные связи специального вида

и блочный принцип управления как методологическую основу для их реа-

лизации. При решении задачи слежения в рамках блочного подхода [17-22]

уравнения внешней динамики приводятся к блочной форме вход-выход с аф-

финным вхождением фиктивных и истинных управлений. Она состоит из

элементарных блоков, в каждом из которых размерность управляемых пере-

менных равна рангу матрицы перед фиктивными управлениями, в качестве

которых используются переменные следующего блока. Последовательно фор-

мируемые стабилизирующие локальные связи в каждом блоке в итоге обеспе-

чиваются выбором истинного управления. Внешние возмущения при блочной

организации являются согласованными с фиктивными управлениями. Как

было отмечено, классическими методами подавления внешних и параметри-

ческих ограниченных возмущений, действующих в пространстве управления,

являются: 1) непрерывные линейные обратные связи с большими коэффици-

ентами усиления; 2) ограниченные по модулю разрывные управления с ор-

ганизаций скользящих режимов. При этом только управления первого типа

(в силу гладкости) можно использовать для формирования локальных свя-

зей. Применению глубоких обратных связей на практике препятствует из-

вестная проблема всплесков в начале переходных процессов [23-24], на ве-

личину которых в практических приложениях накладываются ограничения.

Гибридом линейного и разрывного управлений является кусочно-линейное

управление с насыщением в виде sat-функции [25-26], которое сочетает в себе

положительные свойства обоих методов, но свободно от их недостатков. С по-

мощью ограниченного и непрерывного sat-управления в замкнутой системе

обеспечиваются свойства, близкие к свойствам систем с разрывными управле-

ниями, функционирующим в скользящем режиме. Негладкость sat-функции

не является препятствием для ее использования в истинном управлении и

в корректирующих воздействиях наблюдателей состояния [5, 18], но сужает

возможности ее применения для синтеза фиктивных управлений в практиче-

ских задачах.

Для универсального формирования инвариантных локальных связей

требуются гладкие аналоги sat-функции

трансцендентные S-образные

функции (арктангенс, гиперболический тангенс, логистическая функция и

т.п.). Конструктивным инструментом для анализа и синтеза нелинейного

управления представляется нечетный гиперболический тангенс th(x) = 1-

-2/(exp(2x) + 1), он зависит от экспоненты, его производные всюду огра-

ничены и рекурсивно выражаются через первообразную. В данной работе

используется более удобная для построений модификация гиперболического

тангенса сигма-функция σ(x) = -th(-x/2).

Заметим, что с помощью сигма-функций можно с любой точностью ап-

проксимировать любую ограниченную функцию с конечным числом разры-

вов. Это свойство используется в задачах нейросетевого обучения, где сиг-

моиды служат функциями активации нейронов: из набора сигмоидов фор-

мируется нейронный слой, выходом которого является их линейная комби-

нация. Вычисление параметров нейронной сети (весовых коэффициентов и

смещений) происходит в процессе обучения по заранее известной обучающей

выборке (англ. “data set”) с целью минимизации функции потерь, в каче-

стве которой выступает среднеквадратическая ошибка между целевыми зна-

чениями обучающей выборки и выходом нейронной сети. После завершения

процесса обучения нейронная сеть применяется к новым данным и позволя-

ет прогнозировать целевые значения на основе настроенных при обучении

параметров [27].

В данной работе сигма-функции используются непосредственно в контуре

обратной связи в качестве фиктивных и истинных управлений. Параметры

регулятора выбираются на этапе синтеза исходя из наихудших допустимых

значений параметров объекта управления и границ изменения внешних воз-

действий. В процессе регулирования сигмоидальные фиктивные и истинные

управления за конечное время сходятся к согласованным с ними неизвестным

сигналам и повторяют их форму с наперед заданной точностью. При этом

автоматически реализуется механизм компенсации возмущений, в том чис-

ле не принадлежащих пространству истинного управления, что и обеспечи-

вает инвариантность выходных переменных. Таким образом, предлагаемый

метод принципиально отличается от способа использования сигмоидальных

функций в задачах нейросетевого управления, где параметры регулятора на-

страиваются по заранее известной обучающей выборке, при формировании

которой требуется предусмотреть все возможные модификации регулируемо-

го процесса [28].

Апробация сигмоидальных обратных связей в задачах наблюдения [3, 17],

а также в задачах управления применительно к различным мехатронным

объектам [15, 29-32] показала несомненное преимущество этого подхода

по сравнению с линейной обратной связью с большими коэффициентами.

К недостаткам метода можно отнести более сложную вычислительную реали-

зацию, но с учетом постоянно наращиваемой мощности современных управ-

ляющих микропроцессоров это не является серьезным препятствием для его

использования в системах управления современными и перспективными тех-

ническими объектами.

В данной работе блочный принцип управления с сигмоидальными обрат-

ными связями формализован для решения задачи слежения применитель-

но к нелинейным одноканальным системам треугольного вида произволь-

ной размерности, функционирующих в условиях параметрических и внешних

несогласованных возмущений (без предположений об их гладкости). Обратим

внимание, что динамические генераторы внешних воздействий в построения

не вводятся; в оценивании параметрических и внешних возмущений нет необ-

ходимости. Задача рассматривается в детерминированной постановке: пола-

гается, что весь вектор состояния объекта управления измеряется, шумы в

измерениях отсутствуют.

Работа имеет следующую структуру. В разделе 2 приводятся базовые све-

дения о сигма-функции и ее применении для синтеза инвариантной элемен-

тарной системы; описывается математическая модель объекта управления,

формулируется постановка задачи слежения. В разделе 3 представлен основ-

ной результат: формализованы достаточные условия и разработана декомпо-

зиционная процедура синтеза параметров сигмоидальных обратных связей

на основе иерархических неравенств, обеспечивающих стабилизацию ошибки

слежения с заданной точностью за заданное время. В разделе 4 приведены

результаты численного моделирования разработанных алгоритмов для систе-

мы управления перевернутым маятником.

2. Описание проблемы

2.1. Особенности сигмоидальной обратной связи

Рассмотрим гладкую и ограниченную сигма-функцию

σ(kx) =

- 1, k = const > 0,

1 + exp(-kx)

1,00

0,90

0,57

-0,57

-0,90

-1,00

-3/k

-1,3/k

1,3/k

3/k

0,50k

0,34k

0,10k

-3/k

-1,3/k

1,3/k

3/k

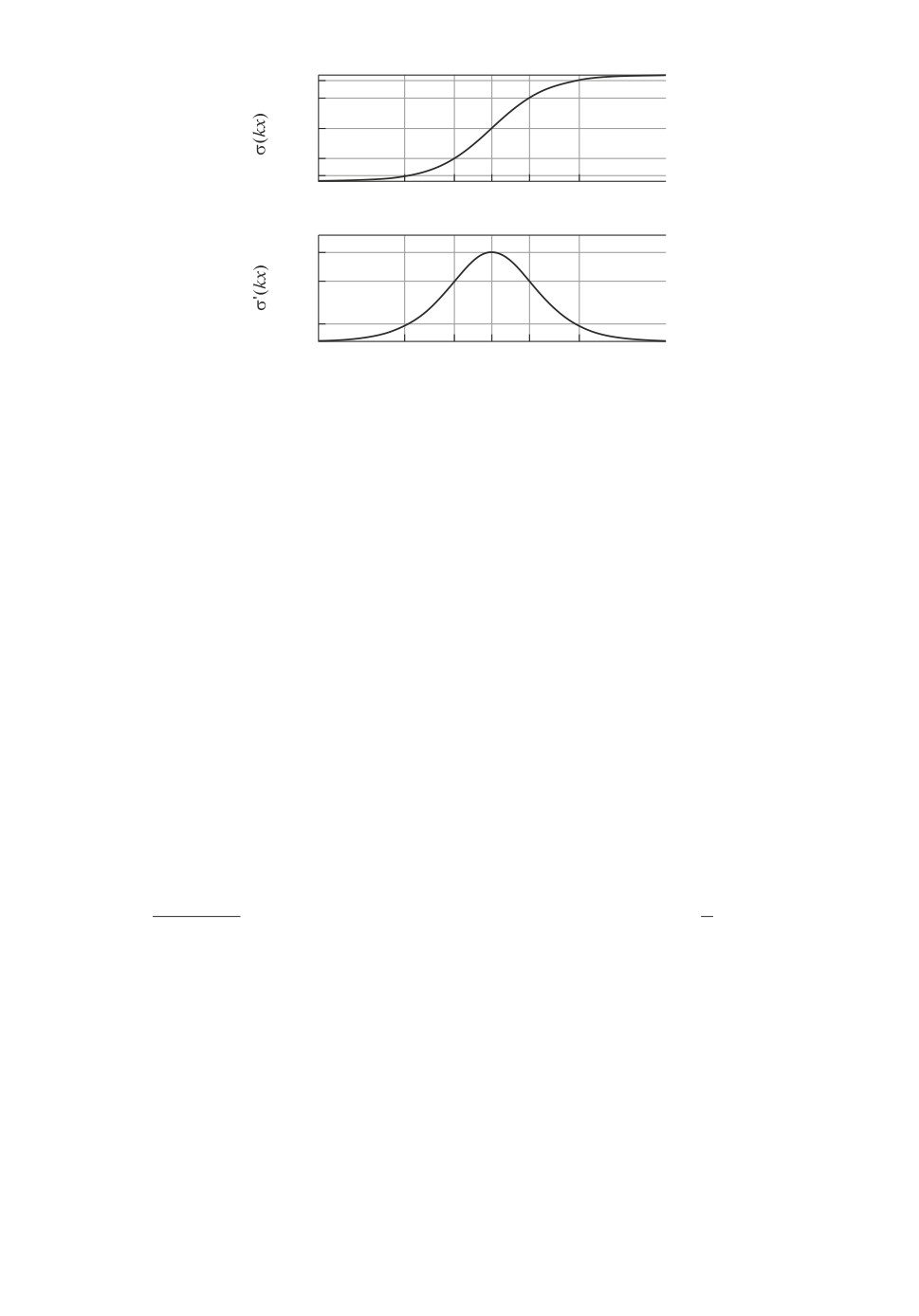
Рис. 1. Графики сигма-функции (сверху) и ее производной (снизу).

которая определена на всей числовой оси и имеет следующие свойства:

σ(-kx) = -σ(kx), σ(kx) ∼

kx/2, σ(kx)

∼ sign(x).

x→0

k→+∞

В аргументе специально выделен множитель k, который в дальнейших по-

строениях играет роль большого коэффициента усиления в малой окрестно-

сти нуля. Производная сигма-функции имеет рекурсивный вид:

σ^′(kx) = k(1 - σ²(kx))/2 > 0, x ∈ R, σ^′(-kx) = σ^′(kx).

Для упрощения анализа нелинейной сигма-функции установим ее анало-

гию с кусочно-линейной sat-функцией. Рассмотрим некоторую окрестность

нуля с радиусом Δ > 0. Для сигма-функции и ее производной в указанных

интервалах справедливы следующие оценки:

σ(kΔ) < |σ(kx)| < 1,

0 < σ^′(kx) < σ^′(kΔ),

|x| > Δ;

(2.1)

σ(kΔ) |x|

≤ |σ(kx)| ≤ σ(kΔ), σ^′(kΔ) ≤ σ^′(kx) ≤ σ^′(0) =

|x| ≤ Δ.

Неравенства (2.1) демонстрируют, что при |x| > Δ сигма-функция близка к

постоянной, а при |x| ≤ Δ

к линейной функции (см. рис. 1). Для фор-

мализации абсцисс указанного разделения введем параметр c = const > 0:

|x| = Δ = c/k, который целесообразно выбирать из интервала

(2.2)

kΔ = c ∈ [1,3; 3],

где: ±1,3

абсциссы точек перегиба первой производной σ^′′′(±1,3) = 0,

при этом σ(±1,3) ≈ ± 0,57, σ^′(±1,3) ≈ 0,34k; ± 3 абсциссы вершин сигма-

функции, в которых ее кривизна достигает максимума, при этом σ(±3) ≈

≈ ± 0,9, σ^′(±0,9) ≈ 0,095k [17].

Поясним идею использования сигмоидальной обратной связи и выбора ее

параметров в задаче обеспечения инвариантности на примере элементарной

возмущенной системы

(2.3)

x = f(t) + u,

где x ∈ R - измеряемая переменная состояния, f(t) - внешнее возмущение, ко-

торое описывается детерминированной, неизвестной, но ограниченной функ-

цией времени, требование гладкости к ней не предъявляется, достаточно, что-

бы она была кусочно-непрерывная. Переменную системы (2.3) можно трак-

товать как ошибку слежения, тогда f(t) аддитивно включает производную

задающего воздействия.

Ставится задача стабилизации системы (2.3) с помощью статической об-

ратной связи. Управляющее воздействие u сформируем в виде сигма-функ-

ции

(2.4)

u = -mσ(kx)

с постоянной амплитудой m = const > 0.

Лемма. Если в системе (2.3), (2.4) внешнее возмущение ограничено из-

вестной константой |f(t)| ≤ F = const > 0, t ≥ 0, то тогда для любых сколь

угодно малых Δ > 0, T > 0 и любого начального условия x(0) найдутся та-

кие положительные действительные числаk и m, что при любых k ≥k,

m ≥ m выполнится неравенство

(2.5)

|x(t)| ≤ Δ, t ≥ T.

Доказательство леммы. Заданное Δ > 0 (2.5) и коэффициент k свя-

жем параметрически (2.2), что сводит проблему выбора k к выбору c из ука-

занного диапазона.

Формализуем для замкнутой системы (2.3), (2.4) достаточные условия

устойчивости: введем функцию Ляпунова V = x²/2 и оценим ее производ-

ную. Вне области |x| ≤ Δ с учетом (2.1)-(2.2) имеем:

(2.6)

= x(f(t) - mσ(kx)) ≤ |x| (F - mσ(c)).

Из (2.6) следует, что неравенство

≤ |x| (F - mσ(c)) < 0 справедливо, если

(2.7)

m>m^∗

= F/σ(c).

Выполнение (2.7) обеспечивает |x(t)| ≤ Δ без учета времени сходимости,

которое зависит от начального условия. В частном случае |x(0)| ≤ Δ нера-

венство |x(t)| ≤ Δ обеспечивается при (2.7) и t ≥ 0, т.е. цель управления (2.5)

достигается.

В общем случае |x(0)| > Δ для гарантированного достижения переменной

состояния заданной области за заданное время T > 0 повысим нижнюю

границу для выбора амплитуды (2.7). С учетом оценки решения системы (2.3)

на интервале t ∈ [0; T ]

|x(t)| ≤ |x(0)| + (F - mσ(c))T ≤ Δ, t ≥ T

получим

(

)

|x(0)| - Δ

(2.8)

m≥ m=

>m^∗

|x(0)| > Δ.

σ(c)

Таким образом, принятое значение c (2.2) определяет m (2.8) иk

(2.9)

k≥k

= c/Δ,

отвечающие цели управления (2.5) при любом x(0). Выбор амплитуды m

управления (2.4) на основе неравенства (2.8) гарантирует попадание пере-

менной состояния системы (2.3) из любого начального условия в окрестность

нуля за заданное время (и чем больше m, тем быстрее). Если переменная

изначально находится в этой области, то гарантированно не покинет ее в

процессе регулирования. Выбор большого коэффициента k на основе (2.9)

обеспечивает заданный радиус этой окрестности (и чем больше k, тем мень-

ше радиус). Лемма доказана.

Замечание 1. В процессе доказательства леммы 1 формализованы до-

статочные условия (2.8), (2.9), гарантирующие выполнение целевых показа-

телей (2.5). Однако предельный радиус окрестности нуля, достигаемой пе-

ременной x(t) в стационарном режиме, будет несколько меньше заданного

Δ > 0. Действительно, при t ≥ T для замкнутой системы (2.3), (2.4) оценка

производной функции Ляпунова (2.6) в силу (2.1) имеет вид

= x(f(t) - mσ(kx)) ≤ |x|(F - mσ(c)|x|/Δ).

НеравенствоV < 0 справедливо вне области

(2.10)

|x| ≤ Δ

< Δ,

mσ(c)

к которой асимптотически стремится x(t) и которая в силу (2.8) меньше за-

данной (2.5). Ее радиус сокращается с ростом амплитуды m.

Тем не менее на практике целесообразно выбирать k и m как можно ближе

к базовым значениям k (2.9) и m (2.8) в целях экономии ресурса управления.

Рассмотрим вопрос о выборе параметра c из указанного диапазона (2.2).

Принимая во внимание последующее использование сигма-функций для син-

теза локальных связей в многомерных системах, в качестве критерия выбора

примем минимум базовой оценки модуля скорости управления. Для замкну-

той системы (2.3) имеют место следующие выражения:

u(t) = -mk(1 - σ²(kx)) x/2;

0 < 1 - σ²(kx) ≤ 1, x ∈ R;

| x(t)| < F + m < 2m, t ≥ 0.

Отсюда с учетом (2.8), (2.9) следует базовая оценка скорости изменения

управления:

(

)₂

|x(0)| - Δ

(2.11)

| u(t)| < m²k, t ≥ 0, m²k ≥ m²(c)k(c) =

σ²(c)Δ

Из (2.11) при фиксированных значениях Δ, |x(0)|, T, F имеем целевое

условие:

(2.12)

y(c) =

→ min, c > 0.

σ²(c)

Исследуем на экстремумы функцию (2.12). Ее производная имеет вид

(1 + e^c)(e^2c - 4ce^c - 1)

y^′ =

(e^c - 1)³

из уравнения y^′ = 0 ⇒ e^2c - 4ce^c - 1 = 0 численно находим стационарную

точку c ≈ 2,17. На интервале c ∈ (0; 2,17) функция убывает (y^′ < 0), на интер-

вале c ∈ (2,17; +∞) возрастает (y^′ > 0), следовательно, c ≈ 2,17 ∈ [1,3; 3]

точка минимума. Для удобства расчетов положим

(2.13)

c= 2,2; σ(c) ≈ 0,8;

≈ 1,25.

σ(c)

В принятой точке y(2,2) ≈ 3,43322, что практически не отличается от мини-

мального значения функции y(2, 17) ≈ 3,43299. Тогда с учетом (2.13) оценки

(2.1) примут следующий вид:

(2.14)

0,8 < |σ(kx)| < 1,

0<σ^′

(kx) < 0,18k,

|x| > c/k,

c= 2,2;

0,8k |x|

= 0,36k |x| ≤ |σ(kx)| ≤ 0,8,

0,18k ≤ σ^′(kx) ≤ σ^′(0) =

|x| ≤ c/k.

Замечание 2. В элементарной возмущенной системе (2.3) с помощью

сигмоидального управления обеспечивается монотонный переходный про-

цесс и |x(t)| ≤ x = max{|x(0)| , Δ}, t ≥ 0, что позволяет расширить класс

рассматриваемых элементарных систем за счет систем вида

(2.15)

x = f₁(x) + f₂

(t) + b(x, t)u,

где значения f₁(x) точно не известны, требование ограниченности на всей

области определения к данной функции не предъявляется, достаточно вы-

полнения условия |f₁(x)| ≤ F₁ = const > 0 при |x| ≤ x + ε, где ε > 0 любая

малая величина; f₂(t) неизвестное ограниченное возмущение |f₂(t)| ≤ F₂ =

= const > 0 при t ≥ 0. Достаточное условие управляемости системы (2.15)

в сделанных предположениях: b(x, t)

знакопостоянная функция, т.е.

b(x, t) = 0 при |x| ≤ x + ε, t ≥ 0, допускается ее параметрическая неопреде-

ленность, но в указанных интервалах известны ее знак sign(b(x, t)) = const

и границы изменения 0 < b_min ≤ |b(x, t)| ≤ b_max. Ко всем функциям системы

(2.15) не предъявляется требование гладкости, достаточно, чтобы они были

кусочно-непрерывными с конечным числом точек разрыва первого рода.

Обозначим: f(x, t) = f₁(x) + f₂(t), |f(x, t)| ≤ F = F₁ + F₂ при |x| ≤ x + ε,

t ≥ 0. Управление

u = -sign(b)mσ(kx)

приводит к замкнутой системе

(2.16)

x = f(x,t) - |b(x,t)|mσ(kx).

Зафиксируем большой коэффициент на основе (2.9) с учетом (2.13):

2,2

(2.17)

k≥k=c

Для замкнутой системы (2.15) при Δ < |x| < x + ε аналогично (2.6), (2.7) име-

ем:

= x(f - |b| mσ(kx)) ≤ |x|(F - b_minmσ(c)) = |x|(F - 0,8b_minm),

(2.18)

0,8b_minm > F ⇔ m > 1,25F/b_min ⇒V < 0.

Если |x(0)| ≤ Δ, то выполнение (2.17), (2.18) обеспечит |x(t)| ≤ Δ при t ≥ 0.

В общем случае Δ < |x(0)| < x + ε переменная состояния не выйдет из обла-

сти |x(t)| ≤ x, t ≥ 0, а цель управления (2.5) будет достигнута, если анало-

гично (2.8) амплитуда принята на основе неравенства

)

(|x(0)| - Δ

1, 25

( |x(0)| - Δ

m≥ m=

(2.19)

b_minσ(c)

b_min

|x(0)| > Δ.

Приведенные построения далее распространяются на неэлементарные управ-

ляемые системы.

2.2. Описание модели объекта управления. Постановка задачи

В качестве объекта управления рассматривается нелинейная одноканаль-

ная система, функционирующая при действии внешних несогласованных воз-

мущений, математическая модель которой представима в треугольной (по

составу аргументов функций ее подсистем) форме вход-выход:

x_i = f_i(x₁,... ,x_i,t) + b_i(x₁,... ,x_i,t)x_i+1, i = 1,n - 1,

(2.20)

x_n = f_n(x₁,... ,x_n,t) + b_i(x₁,... ,x_n,t)u,

где x = col(x₁, . . . , x_n) ∈ X ⊂ Rⁿ - измеряемый вектор состояния, X - откры-

тая ограниченная область изменения переменных состояния, определяемая

физикой процесса, границы области допустимых начальных значений пере-

менных x(0) ∈ X заранее известны; x₁ ∈ X₁ ⊂ R - регулируемая переменная

(выход), u ∈ R - управляющее воздействие (вход); f_i(x₁, . . . , x_i, t) - функции

от указанных переменных вектора состояния и внешних возмущений, кото-

рые в общем случае полагаются неизвестными функциями времени, ограни-

ченными по модулю:

(2.21)

|f_i(x₁(t),... ,x_i(t),t)| ≤ F_i

= const > 0, x(t) ∈ X, t ≥ 0, i = 1, n,

характер вхождения параметрических и сигнальных возмущений не принци-

пиален, так как задача их индивидуального оценивания и компенсации не

ставится.

Замечание 3. Константы F_i, i = 1,n (2.21) нужно знать заранее, поэто-

му самый простой вариант предполагать, что функции f_i(x₁, . . . , x_i, t) огра-

ничены по всем указанным аргументам. Конечно, это сильно сужает класс

допустимых систем, из рассмотрения сразу выпадают линейные системы. От-

метим, что предлагаемая далее процедура синтеза всюду ограниченных об-

ратных связей является удобным аналитическим инструментом для обеспече-

ния в процессе регулирования заданных ограничений на переменные состоя-

ния и управления [15]. В данной работе эта проблема не рассматривается. Тем

не менее если функции f_i(x₁, . . . , x_i, t) не ограничены всюду по x₁, . . . , x_i, то

имеется принципиальная возможность априори для худшего расчетного слу-

чая оценить область изменения переменных состояния X и соответствующие

значения F_i, i = 1, n при x(t) ∈ X (см. замечание 2).

Система (2.20) является управляемой, а именно, b_i(x₁(t), . . . , x_i(t), t) = 0,

x(t) ∈ X, t ≥ 0, i = 1, n [20]. Данные функции могут содержать различ-

ные неопределенности, но при этом известными считаются их знаки

sign(b_i(x₁(t), . . . , x_i(t), t)) = const, t ≥ 0 и диапазоны изменения

0 < b_i,min ≤ |b_i(x₁(t),...,x_i(t), t)| ≤ b_i,max,

(2.22)

x(t) ∈ X, t ≥ 0, i = 1, n.

Требование гладкости к функциям f_i(t), b_i(t), i = 1, n (2.20) не предъявля-

ется, достаточно, чтобы они были кусочно-непрерывными с конечным числом

точек разрыва первого рода.

Модель (2.20) без ограничения общности можно рассматривать как одну

из подсистем уравнений внешней динамики многоканальной системы [1, 33].

Под такое описание попадает представительный класс динамических объек-

тов управления, например теплообменные и электромеханические системы

[9, 12-15, 19, 25, 26, 29-32, 34, 35]. Модели ряда других объектов можно пред-

ставить в виде связного набора подсистем типа (2.20) с помощью невырож-

денных замен переменных без задействования в преобразованиях внешних

возмущений.

Для объекта управления (2.20) ставится задача синтеза закона управле-

ния в форме статической обратной связи, обеспечивающего отслеживание

выходной переменной x₁(t) заданного допустимого сигнала g(t), который по-

ступает в систему управления в реальном времени из внешнего источника, его

аналитическое описание отсутствует, известны только его текущие значения,

области изменения начальных условий и первой производной:

(2.23)

g(t) ∈ G ⊆ X₁,

|ġ(t)| ≤ G₁

t ≥ 0.

В сделанных предположениях задача слежения, а именно стабилизация ошиб-

ки слежения e₁(t) = x₁(t) - g(t), может быть решена только с некоторой точ-

ностью. Пусть заданы точность стабилизации Δ₁ > 0 и время t₁ > 0 ее до-

стижения. Цель управления обеспечить в замкнутой системе

(2.24)

|e₁(t)| ≤ Δ₁, t ≥ t₁.

В следующем разделе получены достаточные условия решения поставлен-

ной задачи (2.24) в рамках блочного подхода с использованием сигмоидаль-

ных обратных связей.

3. Декомпозиционная процедура синтеза сигмоидальных обратных связей

с обеспечением заданной точности стабилизации ошибки слежения

Система (2.20) имеет структуру блочной формы управляемости [20-22].

Согласно идеологии блочного принципа управления каждое уравнение си-

стемы (2.20) трактуется как элементарный блок, аналогичный (2.15), отно-

сительно фиктивного или истинного управления. В i-м блоке (i = 1, n - 1)

в качестве фиктивного управления выступает переменная следующего бло-

ка x_i+1. Таким образом, неопределенности f_i(x₁, . . . , x_i, t), i = 1, n - 1, кото-

рые не согласованы с истинным управлением, находятся в пространстве со-

ответствующих фиктивных управлений. Чтобы избежать большого перере-

гулирования, характерного для линейных обратных связей с большими ко-

эффициентами, которые стандартно используются для подавления неопреде-

ленностей [22-24, 30], стабилизирующие фиктивные управления предлагается

выбрать в виде гладких и ограниченных сигма-функций:

x^∗i = -sign(b_i-1)m_i-1σ(k_i-1e_i-1), k_i-1, m_i-1

(3.1)

= const > 0, i = 2, n,

где e₁ - ошибка слежения, e_i-1 (i = 3, n + 1) - невязки между переменными x_i

и выбранными фиктивными управлениями (3.1):

e₁ = x₁ - g,

(3.2)

e_i = x_i - x^∗i = x_i + sign(b_i-1)m_i-1σ(k_i-1e_i-1), i = 2, n.

В замкнутой системе с помощью истинного управления, которое также

для единообразия принимается в виде сигма-функции

(3.3)

u = -sign(b_n)m_nσ(k_ne_n), k_n,m_n

= const > 0,

требуется обеспечить стабилизацию невязок (3.2), в том числе ошибки сле-

жения e₁, что отвечает цели управления (2.24).

Перепишем замкнутую систему (2.20), (3.3) относительно невязок (3.2):

ė₁ = - |b₁|m₁σ(k₁e₁) + f₁ - ġ + b₁e₂;

(3.4)

ė_i = - |b_i| m_iσ(k_ie_i) + f_i + Λ_i-1 + b_ie_i+1, i = 2,n - 1;

ė_n = - |b_n|m_nσ(k_ne_n) + f_n + Λ_n-1,

где слагаемые

k_i(1 - σ²(k_ie_i))

(3.5)

Λ_i = sign(b_i)m_i

ė_i

i = 1,n - 1

являются производными соответствующих фиктивных управлений (3.1), ко-

торые возникают при переходе к новому координатному базису (3.2).

Для настройки параметров сигмоидальных обратных связей в системе

(3.4) используем блочный подход, в котором реализуется принцип декомпози-

ции [34, 35]. Задача сводится к последовательному решению элементарных за-

дач синтеза в подсистемах (блоках), аналогичных (2.16). Отличие заключает-

ся в том, что только последняя, n-я подсистема регулируется непосредствен-

но истинным управлением, а в остальных в качестве фиктивных управлений

выступают переменные следующего блока. Как следствие, в общем случае

ненулевых начальных значений невязок только в последнем блоке гаранти-

руется монотонный переходный процесс. Формализуем достаточные условия

стабилизации системы (3.4).

Теорема. Если в системе (3.4) выполняются условия (2.21)-(2.23), то

тогда для любых начальных условий x(0) ∈ X и любых, сколь угодно малых

Δ₁ > 0, t₁ > 0 найдутся такие действительные числаki > 0, i = 1,n, 0 <

< m_i < m_i, i = 1,n - 1, m_n > 0, что при любых k_i ≥ ki, m_i: m_i < m_i ≤ m_i,

m_n ≥ m_n неравенство (2.24) выполнится.

В Приложении приведено конструктивное доказательство теоремы, в ходе

которого получена декомпозиционная процедура выбора параметров фиктив-

ных и истинного управлений на основе неравенств, обеспечивающая решение

поставленной задачи (2.24). Заметим, что на стадии проектирования следя-

щей системы в полученные оценки для выбора амплитуд вместо конкретных

значений |x_i(0)|, i = 1, n, |g(0)| (2.23) следует подставлять граничные значе-

ния областей допустимых начальных условий соответствующих переменных

состояния.

Для упрощения вычислительной реализации в качестве истинного управ-

ления вместо (3.3) можно также использовать всюду ограниченную, но

негладкую sat-функцию [25, 26].

Замечание 4. Для управления механическими системами часто исполь-

зуют электрические безынерционные исполнительные устройства, построен-

ные на базе силовых электронных элементов, которые могут функциониро-

вать исключительно в ключевом режиме. В этом случае вместе с сигмоидаль-

ными локальными связями (3.2) естественно вместо непрерывного управле-

ния (3.3) использовать закон разрывного управления:

(3.6)

u = -sign(b_n)m_nsign(e_n

Разрывное управление (3.6) имеет один настраиваемый параметр амплиту-

ду, которая выбирается на основе неравенства, аналогичного (Π.22), а именно:

)

( |x_n(0)| + m^∗n-1

(3.7)

m_n ≥ m_n =

+ F_n + k^∗n-1(m^∗n-1)²b_n-1,max

b_n,min

t^∗n

При выполнении (3.7) в замкнутой системе (2.20), (3.2), (3.6) за конечное вре-

мя 0 < t^∗n < 0,2b_n-1,mint^∗n-1/b_n-1,max < t₁ возникнет скользящий режим [7-9].

В теории на поверхности e_n = 0 в виртуальном пространстве невязок

(e₁, . . . , e_n) ∈ Rⁿ, а в реальности из-за различного рода неидеальностей дви-

жение изображающей точки происходит в пограничном слое поверхности пе-

реключения |e_n(t)| ≤ Δ_n, t ≥ t^∗n, ширина которого пропорциональна ампли-

туде разрывного управления. При этом неравенства (Π.1), а следовательно,

и цель управления (2.24) обеспечиваются.

Необходимо отметить, что параметры обратной связи в предложенной

процедуре определяются на основе неравенств, составленных для худшего

расчетного случая, что не требует перенастройки регулятора при измене-

нии внутренних и внешних факторов в допустимых пределах. Кроме то-

го, показана принципиальная возможность в рамках предложенного подхо-

да обеспечить любую, сколь угодно малую ошибку слежения с любым, до-

статочно малым перерегулированием (Π.11) за любое, сколь угодно малое

время при любых начальных условиях. Но эти построения имеют больше

теоретическую значимость, поскольку уменьшение показателей цели управ-

ления (2.24), (Π.11) обернется ростом параметров регулятора. Это может

привести к избыточным величинам фиктивных и истинных управлений в

переходном процессе, недопустимым в реальных системах автоматического

управления.

Замечание 5. При использовании разработанной в доказательстве тео-

ремы процедуры настройки в практических приложениях рекомендуется

фиксировать коэффициенты обратной связи как можно ближе к нижним

базовым границам. Учитывая консервативность полученных оценок, мож-

но несколько завышать целевые показатели (2.24) при выполнении расчетов,

так как реально в установившемся режиме будет достигаться меньшая ошиб-

ка слежения (2.10) и/или меньшее время регулирования (см. раздел 4).

Обратим внимание, что в силу организации локальных обратных связей

(3.1) в замкнутой системе (2.20), (3.6) переменные состояния x_i(t), i = 2, n

будут “отслеживать” ограниченные сигмоидальные сигналы, при этом мак-

симальные отклонения фиктивных управлений от “задающих воздействий”

ограничены (Π.6), а точность слежения будет зависеть от задаваемой точ-

ности стабилизации невязок (3.2) (“ошибок слежения”). Этот факт является

предпосылкой для использования данного подхода при решении задачи сле-

жения в условиях проектных ограничений на переменные состояния и управ-

ления.

4. Результаты моделирования

Для иллюстрации разработанного метода рассмотрим задачу синтеза сле-

дящей системы для перевернутого математического маятника. За точку от-

x₁

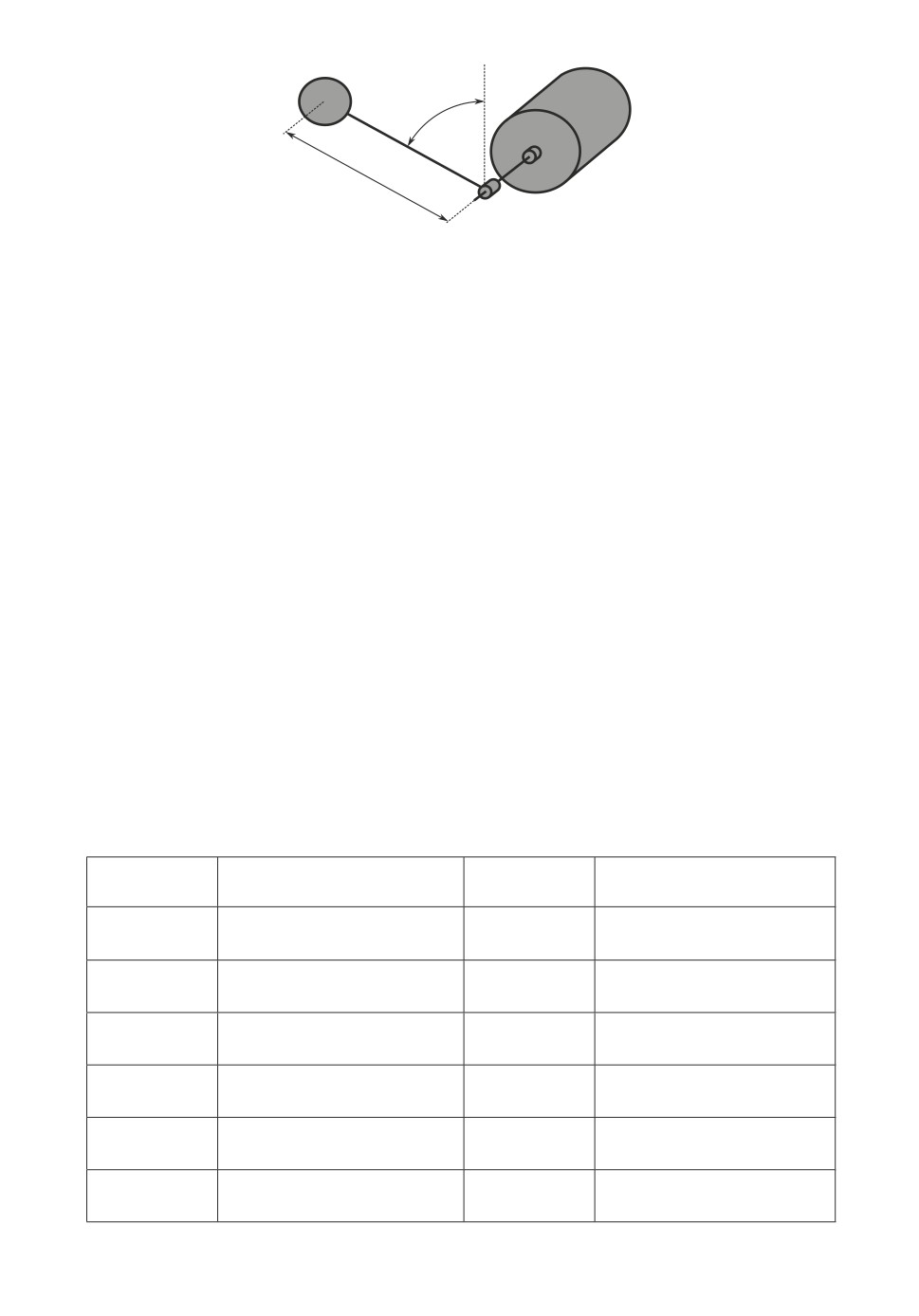
Рис. 2. Схема перевернутого маятника.

счета принято верхнее вертикальное положение x₁ = 0, которое является

неустойчивым (см. рис. 2).

Математическая модель с учетом редуцированной динамики двигателя по-

стоянного тока (ДПТ) аналогична (2.20) и имеет третий порядок:

x₁ = x₂,

(4.1)

x₂ = a₂₁ sin x₁ - a₂₂x₂ + b₂x₃ + η(t),

x₃ = -a₃₂x₂ - a₃₃x₃ + b₃u,

где a_ij, b_i - положительные конструктивные коэффициенты

a₂₁ = g/l, a₂₂ = κ/l, b₂ = k_a/( ml²),

(4.2)

a₃₂ = c/L, a₃₃ = R/L, b₃ = 1/L,

которые не определены и могут изменяться в известных диапазонах. Описа-

ние переменных состояния x = col(x₁, x₂, x₃) системы (4.1), которые подлежат

прямым измерениям, и параметров (4.2) приведено в табл. 1.

В системе (4.1) регулируемой (выходной) переменной является угловое по-

ложение маятника x₁(t), для которого ставилась задача отслеживания задан-

ного сигнала g(t) (2.23). Для обеспечения (2.24) применялся разработанный

метод с формированием сигмоидальных локальных связей и синтеза разрыв-

Таблица 1. Описание переменных состояния и параметров объекта управления

Описание,

Обозначение

единица измерения

x₁(t)

угловое положение маят-

длина маятника, [м]

ника, [-π; π] [рад]

x₂(t)

угловая скорость маятни-

коэффициент вязкого

ка, [-2; 2] [рад/с]

трения, [H · c/м²]

x₃(t)

ток якоря ДПТ, [-4; 4] [А]

коэффициент противо-

ЭДС ДПТ, [В · с/рад]

η(t)

неконтролируемое возму-

сопротивление якоря

щение, [H · м]

ДПТ, [Ом]

g = 9,81

ускорение свободного па-

индуктивность якоря

дения, [м/c²]

ДПТ, [Гн]

масса маятника, [кг]

k_a

коэффициент пропор-

циональности, [H · м/А]

Таблица 2. Параметры объекта управления, принятые при моделировании

Диапазон

Вид или значение

изменения

Эксперимент 1 Эксперимент 2 Эксперимент 3 Эксперимент 4

0,25t, t ∈ [(k - 1)T, kT ),

η(t)

[-0,5; 0,5]

0,5 cos t

0,3 sin t

k = 1,2,..., T = 2

[-0,5; 0,5]

g(t)

0,2 sin t

0,5| sin t|

0,25 sin 2t

|ġ(t)| ≤ 0,5

[0,18; 0,25]

0,18

0,25

0,07 |cos(t/2)| + 0,18

[0,2; 0,3]

0,2

0,3

0,25

0,23

[2; 4]

3,8

[0,27; 0,33]

0,27

0,33

0,3

0,28

[4,15; 4,2]

4,15

4,2

4,18

4,1

[0,012; 0,013]

0,012

0,013

0,012

k_a

[1,68; 1,75]

1,68

1,75

1,7

1,69

ного управления, аналогично (3.1), (3.6) соответственно, где n = 3, u - напря-

жение питания якорной цепи ДПТ, [B].

В табл. 2 приведены рассматриваемые диапазоны изменения внешних воз-

действий, параметров объекта, а также конкретные функции и значения, при-

нятые при моделировании.

По данным табл. 2 были рассчитаны допустимые диапазоны для коэффи-

циентов (4.2):

a₂₁ ∈ [32,70;49,05], a₂₂ ∈ [6,67;20], b₂ ∈ [74,67;243,06],

a₃₂ ∈ [20,76;27,5], a₃₃ ∈ [319,23;350], b₃ ∈ [76,92;83,34].

На их основе, а также с учетом заданных (завышенных, см. замечание 5)

показателей (2.24)

(4.3)

Δ₁ = 0,1 [рад], t₁

= 5 [с]

и принятых E₁ = 2,05 (Π.11), Δ₂ = 0,64, Δ₃ = 0,05 (Π.1) для худшего расчет-

ного случая на основе неравенств (Π.2), (Π.16), (Π.21), (Π.22) были выбраны

следующие коэффициенты обратной связи:

(4.4)

m₁ = 1,96, k₁ = 22; m₂ = 3,54, k₂ = 3,44; m₃

= 190.

Моделирование проводилось в среде MATLAB-Simulink, для численного

интегрирования системы (4.1) использовался метод Эйлера с постоянным

шагом 10^-5. Как показано в табл. 2, в первых двух экспериментах были при-

няты граничные значения параметров объекта из допустимых диапазонов

(в первом наименьшие, во втором наибольшие). В третьем и четвертом

экспериментах масса маятника полагалась переменной негладкой величиной,

задающее воздействие негладким (в третьем) и гладким (в четвертом),

параметры приняты в виде промежуточных значений из допустимых диа-

пазонов. Все четыре эксперимента проводились при одинаковых коэффици-

ентах обратной связи (4.4) и одинаковых начальных условиях x₁(0) = π/3,

x₂(0) = 0,64, x₃(0) = 0,5.

1,2

1,0

x₁

0,8

0,6

0,4

0,2

-0,2

t, c

Рис. 3. Графики g(t), x₁(t) (эксперимент 1).

1,2

1,0

0,8

0,6

0,4

0,2

-0,2

t, c

Рис. 4. График e₁(t) (эксперимент 2).

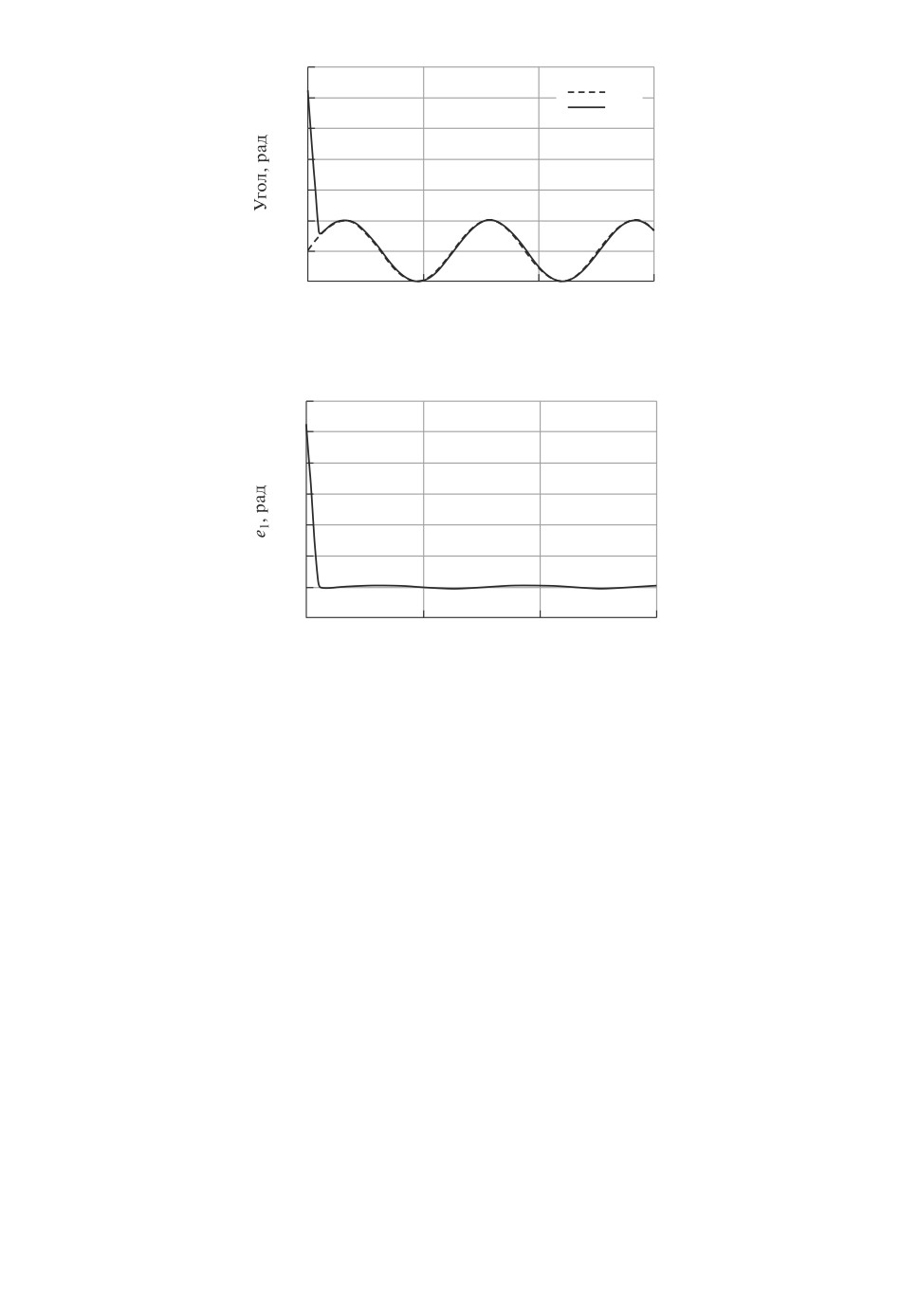
На рис. 3 для эксперимента 1 представлены графики задающего воздей-

ствия g(t) и регулируемой переменной x₁(t), ее поведение во втором экспери-

менте практически не отличается от показанного на рис. 3. На рис. 4 пред-

ставлен график ошибки слежения e₁(t) = x₁(t) - g(t) [рад] для эксперимен-

та 2. На рис. 5-6 для экспериментов 3 и 4 приведены графики задающего

воздействия g(t) и регулируемой переменной x₁(t) (снизу), а также ошибки

слежения e₁(t) = x₁(t) - g(t) [рад] (сверху).

В табл. 3 для всех экспериментов представлены показатели регулирования

ошибки слежения e₁(t): время регулирования t_∗: |e₁(t)| ≤ 0,1, t ≥ t_∗; величина

перерегулирования e_1,max ≥ |e₁(t)|, t ≥ 0; точность δ₁ ≥ |e₁(t)|, достигаемая

при t ≥ 5 [c].

Таким образом, из рис. 3-6 и табл. 3 следует, что цель управления дости-

гается во всех случаях, все показатели не превышают заданных значений.

Следует отметить, что в силу выбора параметров регулятора из достаточных

условий, радиусы областей сходимости ошибок слежения в установившемся

режиме оказались примерно в 4-10 раз меньше заданного, а время регулиро-

вания в 10-12 раз меньше заданного (4.3).

Конечно, высокоточные системы слежения потребуют индивидуальной на-

стройки каждого рабочего режима в условиях полной определенности пара-

1,0

0,5

1,0

x₁

0,5

t, c

Рис. 5. Графики g(t), x₁(t), e₁(t) = x₁(t) - g(t) (эксперимент 3).

1,0

0,5

1,0

x₁

0,5

t, c

Рис. 6. Графики g(t), x₁(t), e₁(t) = x₁(t) - g(t) (эксперимент 4).

метров объекта управления и внешних воздействий. Для системы (4.1), функ-

ционирующей в условиях неопределенности, можно обеспечить лучшие, чем

указанные в табл. 3, показатели регулирования путем увеличения коэффи-

циентов обратной связи (4.4). Предельные значения зависят от проектных

ограничений на переменные состояния и управления конкретного объекта

управления.

Таблица 3. Значения показателей качества регулирования

Требования Эксперимент Эксперимент Эксперимент Эксперимент

Показатель

(не более)

t_∗, c

0,4532

0,4714

0,4067

0,4138

e_1,max, рад

2,05

1,0474

1,0477

1,0473

1,0472

δ₁, рад

0,1

0,0093

0,0096

0,0242

0,0240

5. Заключение

Предложен метод синтеза сигмоидальных обратных связей, который прин-

ципиально отличается от способа использования сигмоидов в задачах нейро-

сетевого обучения. Цель исследований заключалась в синтезе системы сле-

жения для нелинейного объекта одноканального управления при воздействии

параметрических и внешних возмущений без предположений об их гладкости,

о которых известны только границы диапазонов их изменения. Поставленная

цель была достигнута за счет распространения блочного подхода на форми-

рование нелинейных, всюду ограниченных сигмоидальных локальных связей,

обеспечивающих ε-инвариантность по отношению к возмущениям, не согла-

сованным с истинным управлением. Результаты моделирования подтвердили

эффективность разработанных алгоритмов.

Представленный материал является установочным для дальнейшего прак-

тикоориентированного решения задачи слежения с учетом проектных огра-

ничений на переменные состояния и управление. Эта проблема, а также рас-

пространение данного метода на многоканальные системы, представимые в

блочной форме управляемости с блоками разной размерности, составит пред-

мет дальнейших исследований авторов.

ПРИЛОЖЕНИЕ

Доказательство теоремы. Согласно идеологии блочного подхода в

замкнутой системе (3.4) нужно обеспечить следующую последовательность

сходимости невязок:

|e_n(t)| ≤ Δ_n (t ≥ t_n > 0) ⇒ |e_n-1(t)| ≤

(Π.1)

≤ Δn-1 (t ≥ t_n-1 > t_n) ⇒ ... ⇒ |e₁(t)| ≤ Δ1 (t ≥ t₁ > t₂),

где Δ₁ > 0, t₁ > 0 заданы (2.24), Δ_i > 0, i = 2, n назначаются произвольно,

зависимости t_i от начальных значений невязок и принятых Δ_i > 0 устанав-

ливаются в процессе доказательства.

Из леммы следует существованиеki > 0, i = 1, n таких, что для лю-

бых k_i ≥ki, i = 1, n гарантируются желаемые радиусы Δ_i > 0, i = 1, n (Π.1)

окрестностей нуля, в которые невязки сойдутся в указанные моменты време-

ни (Π.1). С учетом (2.13) аналогично (2.17) зафиксируем значения больших

коэффициентов k_i на основе неравенств:

(Π.2)

k^∗i ≥ki = 2,2/Δ_i

i = 1,n.

Сходимость невязок в установленные области за указанное время (Π.1) обес-

печивается с помощью выбора m_i, i = 1, n.

Стабилизация системы (3.4) осуществляется “снизу вверх” (Π.1). Доста-

точные условия для выбора амплитуд, аналогичные (2.18), справедливы при

выполнении указанных условий:

0,8b_1,minm₁ > F₁ + G₁ + b_1,minΔ₂,

|e₂| ≤ Δ₂;

(Π.3)

0,8b_i,minm_i > F_i + |Λ_i-1| + b_i,minΔ_i+1,

|e_i+1| ≤ Δ_i+1, i = 2,n - 1;

0,8b_n,minm_n > F_n + |Λ_n-1| .

Выполнение (Π.2)-(Π.3) обеспечивает последовательную стабилизацию

невязок с заданной точностью без учета времени сходимости, которое за-

висит от начальных условий. В частном случае |e_i(0)| ≤ Δ_i, i = 1, n выполне-

ние (Π.2)-(Π.3) обеспечит |e_i(t)| ≤ Δ_i, i = 1, n при t ≥ 0, т.е. цель управления

(2.24) достигается. Заметим, что если |e_i(0)| ≤ Δ_i, i = n, j + 1, |e_j(0)| > Δ_j, то

переходный процесс невязки e_j(t) будет монотонным; в частности, при j = 1

у ошибки слежения e₁(t) переходный процесс будет без перерегулирования.

В общем случае |e_i(0)| > Δ_i, i = 1, n в рамках данных построений моно-

тонный переходный процесс гарантируется только для e_n(t). Пока перемен-

ные нижних блоков системы (3.4) не достигнут установленных окрестностей

нуля (Π.1), переменные верхних блоков растут по модулю и достигают мак-

симального значения не позже, чем в следующие моменты времени:

|e_n(t)| ≤ |e_n(0)| = e_n,max,

(Π.4)

|e_i(t)| ≤ |e_i(t_i+1)| = e_i,max, i = n - 1, 1, t ≥ 0.

В силу построений (3.2) оценим начальные значения невязок:

|e₁(0)| ≤ |x₁(0)| + |g(0)| ,

(Π.5)

|e_i(0)| ≤ |x_i(0)| + m_i-1σ(k_i-1 |e_i-1(0)|) ≤ |x_i(0)| + m_i-1, i = 2, n.

Принимая во внимание (3.4), (Π.3), (Π.5) и учитывая, что собственные дви-

жения в замкнутой системе (3.4) устойчивые, составим оценки максимальных

значений (Π.4):

e_1,max = |e₁(0)| + b_1,max(e_2,max - Δ₂)t₂;

(Π.6)

e_i,max = |x_i(0)| + m_i-1 + b_i,max(e_i+1,max - Δ_i+1)t_i+1, i = 2,n - 1;

e_n,max = |x_n(0)| + m_n-1.

Для обеспечения заданного времени сходимости требуется увеличить ниж-

ние границы для выбора амплитуд (Π.3). Предварительно дадим оценки про-

изводных фиктивных управлений (3.5). Они отличаются на разных интер-

валах и зависят от соответствующих оценок производных сигма-функций и

производных соответствующих невязок (3.4). Для производных невязок e_i(t),

i = 1,n - 1 с учетом (Π.3) справедливы оценки:

t ∈ [0;t₂) : |ė₁(t)| ≤

≤F₁ +G₁ +b_1,maxΔ₂

+b_1,max(e_2,max - Δ₂) + b_1,maxm₁ <

}

<0,8b_1,minm₁

< 2b_1,maxm₁ + b_1,max(e_2,max - Δ₂),

t ≥ t₂ : |ė₁(t)| ≤ F₁ + G₁ + b_1,maxΔ₂ + b_1,maxm₁ < 2b_1,maxm₁;

(Π.7)

t ∈ [0;t_i+1) : |ė_i(t)| =

= F_i + |Λ_i-1| + b_i,maxΔ_i+1

+b_i,max(e_i+1,max - Δ_i+1) + b_i,maxm_i <

}

<0,8b_i,minm_i

< 2b_i,maxm_i + b_i,max(e_i+1max - Δ_i),

t ≥ t_i+1 : |ė_i(t)| = F_i + |Λ_i-1| + b_i,maxΔ_i+1 + b_i,maxm_i <

< 2b_i,maxm_i, i = 2, n - 1.

Для производной сигма-функции в силу (2.14) на указанных интервалах

имеем:

|e_i(t)| > c/k_i, t ∈ [0;t_i) : 0 < 0,5k_i(1 - σ²(k_ie_i)) < 0,18k_i,

(Π.8)

|e_i(t)| ≤ c/k_i, t ≥ t_i : 0,18k_i ≤ 0,5k_i(1-σ²(k_ie_i)) ≤ 0,5k_i, i = 1,n-1.

Объединяя (Π.7)-(Π.8), получим оценки производных фиктивных управле-

ний (3.5) на указанных интервалах:

k_i(1 - σ²(k_ie_i))

|Λ_i| = m_i

|ė_i| ≤



0,36k_im²ⁱb_i,max + 0,18k_im_ib_i,max(e_i+1,max - Δ_i+1), t ∈ [0; t_i+1);



≤

 0,36kimⁱbi,max, t ∈ [ti+1; ti);

k_im²ⁱb_i,max, t ≥ t_i; i = 1,n - 1.

Для того чтобы единообразно принять в качестве оценки

(Π.9)

|Λ_i| ≤ k_im²ⁱb_i,max

t ≥ 0; i = 1,n - 1,

нужно обеспечить

0,18k_im_ib_i,max(e_i+1,max - Δ_i+1) ≤ 0,64k_im²ⁱb_i,max ⇒ e_i+1,max - Δ_i+1 ≤ 3,5m_i,

i = 1,n - 1.

С этой целью введем ограничения на пиковые значений невязок, несколько

снизив предельные оценки для удобства расчетов:

(Π.10)

e_i,max ≤ 3m_i-1 + Δ_i

i = 2,n.

Для единообразия введем ограничение для перерегулирования по ошибке

слежения:

(Π.11)

|e₁(0)| < e_1,max ≤ E₁.

В частном случае |e₁(0)| < Δ₁ выполнение e_1,max ≤ E₁ = Δ₁ обеспечит |e₁(t)| ≤

≤ Δ₁, t ≥ 0.

С учетом (Π.10)-(Π.11) неравенства (Π.6) примут вид

e_1,max = |e₁(0)| + 3b_1,maxm₁t₂ ≤ E₁;

(Π.12) e_i,max = |x_i(0)| + m_i-1 + 3b_i,maxm_it_i+1 ≤ 3m_i-1 + Δ_i, i = 2, n - 1;

e_n,max = |x_n(0)| + m_n-1 ≤ 3m_n-1 + Δ_n,

откуда следуют дополнительные условия, которые надо учитывать при вы-

боре t_i, i = n, 2 (0 < t_n < t_n-1 < . . . < t₂ < t₁) и амплитуд фиктивных управ-

лений:

(Π.13)

E₁ - |e₁(0)|

2m_i-1 + Δ_i - |x_i(0)|

0<m₁ ≤

0<m_i ≤

i = 2, n - 1;

3b_1,maxt₂

3b_i,maxt_i+1

|x_i+1(0)| - Δ_i+1

(Π.14)

m_i >

i = 1, n - 1.

Заметим, что по построениям (Π.3) m_i-1 > Δ_i, i = 2, n, при этом Δ_i > 0

могут быть приняты как меньше, так и больше величин |x_i(0)|, требования

малости к ним не предъявляются. Для упрощения расчетов можно изначаль-

но зафиксировать Δ_i = |x_i(0)|, i = 2, n, что снимает необходимость проверки

выполнения условий (Π.14).

В общем случае Δ_i < |x_i(0)|, i = 2, n неравенства нижней границы выбора

амплитуд m_i, i = 1, n - 1 будут содержать две базовые компоненты. С помо-

щью первой компоненты m_i1, а также m_n аналогично (2.19) обеспечивает-

ся сходимость невязок e₁(t), e₂(t), . . . , e_n(t) на интервалах [t₂; t₁], [t₃; t₂], . . . ,

[0; t_n] соответственно из пиковых значений (Π.6), (Π.12) в заданные области

(Π.1) за заданное время (2.24); а с помощью второй m_i2 ограничения (Π.14).

При этом в отличие от амплитуды истинного управления m_n, которая выби-

рается только на основе нижней оценки, для выбора амплитуд фиктивных

управлений имеются ограничения сверху (Π.13).

Формализуем пошаговую процедуру последовательного “сверху вниз” вы-

бора амплитуд сигмоидальных управлений и допустимых моментов време-

ни t_i, i = 2, n при заданных Δ₁, t₁, назначенных E₁ (Π.11), Δ_i > 0, i = 2, n и

принятых на их основе k^∗i, i = 1, n (Π.2). В процессе процедуры допускается

варьирование свободных параметров.

Шаг 1. С учетом (Π.12) первое неравенство (Π.3) примет вид:

|e₁(0)| + 3b_1,maxm₁t₂ - Δ₁

0,8b_1,minm₁ ≥

+F₁ +G₁ +b_1,minΔ₂ ⇒

t₁ - t₂

|e₁(0)| - Δ₁ + (F₁ + G₁ + b_1,minΔ₂)(t₁ - t₂)

⇒m₁₁ ≥

0,8b_1,mint₁ - (0,8b_1,min + 3b_1,max)t₂

откуда следует ограничение на выбор 0 < t₂ < t₁:

b_1,min

(Π.15)

0,8b_1,mint₁ - (0,8b_1,min + 3b_1,max)t₂ > 0 ⇒ t₂ < 0,2

t₁.

b_1,max

Выбираем t^∗2 > 0 на основе (Π.15) и подставляем его в двойное неравенство

(Π.16)

max{m₁₁; m₁₂} < m₁ < m₁,

где

|e₁(0)| - Δ₁ + (F₁ + G₁ + b_1,minΔ₂)(t₁ - t^∗2)

m₁₁ =

0,8b_1,mint₁ - (0,8b_1,min + 3b_1,max)t^∗

(Π.17)

|x₂(0)| - Δ₂

E₁ - |e₁(0)|

m₁₂ =

m₁ =

3b_1,maxt∗

Если (Π.16) выполняется, то тогда фиксируем t^∗2, m^∗1 ∈ ( m₁; m₁] и переходим

на второй шаг. При невыполнении (Π.3) следует варьировать произвольные

параметры. Это можно сделать двумя способами.

Первый способ . Если требуется обеспечить принятое E₁ (Π.11), то то-

гда варьируем Δ₂ и/или t₂. Если при изначально принятом

0<t^∗2 <

< 0,2b_1,mint₁/b_1,max имеет место m₁₂ > m₁₁ (Π.17), то путем увеличения Δ₂

(вплоть до Δ₂ = |x₂(0)|) нужно обеспечить m₁₁ > m₁₂. Если при новом Δ^∗2

неравенство (Π.16) не выполняется или изначально m₁₁ > m₁₂, то тогда сни-

жаем t^∗2. Критическое значение t₂ > 0 : m₁₁(t₂) = m₁(t₂) существует и равно

√

p²¹² - 4p₁₁p₁₃ - p₁₂

t₂ =

2p₁₁

где

p₁₁ = -3b_1,max(F₁ + G₁ + b_1,minΔ₂),

p₁₂ = 0,8b_1,min (E₁ - |e₁(0)|) + 3b_1,max(E₁ - Δ₁ + (F₁ + G₁ + b_1,minΔ₂)t₁),

p₁₃ = -0,8b_1,min (E₁ - |e₁(0)|)t₁.

Из предельного соотношения

|e₁(0)| - Δ₁ + (F₁ + G₁ + b_1,minΔ₂)t₁

lim

m₁₁(t₂) =

t₂→+0

0,8b_1,mint₁

(Π.18)

E₁ - |e₁(0)|

= const < lim

= +∞

t₂→+0

3b_1,maxt₂

следует, что m₁ можно сделать сколь угодно большим и при любом t^∗2 > 0 :

0 < t^∗2 < t₂ неравенство (Π.16) будет выполнено.

Таким образом, путем снижения t₂ можно обеспечить любое, достаточ-

но малое перерегулирование по ошибке слежения (Π.11). Однако это может

привести к существенному росту нижних границ для выбора амплитуд в сле-

дующих блоках.

Второй способ . Если отказаться от принятого E₁ (Π.11) и увеличить его

значение:

E₁ >E = |e₁(0)| + 3b_1,maxm^∗1t^∗2,

где

E - минимально возможное перерегулирование ошибки слежения при

изначально принятом 0 < t^∗2 < 0,2b_1,mint₁/b_1,max, то тогда можно произвольно

увеличить верхнюю границу m₁ для выбора амплитуды (Π.16).

Допустимые значения t^∗2, m^∗1, Δ^∗2 и k^∗2(Δ^∗2) фиксируются, переходим на

второй шаг.

Шаг i (i = 2,n - 1). Соответствующее номеру шага неравенство (Π.1), а

именно |e_i(t)| ≤ Δ_i (t ≥ t_i > t_i+1), обеспечивается путем выбора m_i. С учетом

(Π.9), (Π.12) i-е неравенство (Π.3) примет вид

|x_i(0)| + m^∗i-1 + 3b_i,maxm_it_i+1 - Δ^∗i

(Π.19)

0,8b_i,minm_i ≥

t^∗i - t_i+1

+ F_i + k^∗i-1(m^∗i-1)²b_i-1,max + b_i,minΔ_i+1 ⇒

)

|x_i(0)| + m^∗i-1 - Δ^∗i + (F_i + k^∗i-1(m^∗i-1)²b_i-1,max + b_i,minΔ_i+1)(t^∗i - t_i+1

m_i1 ≥

0,8b_i,mint^∗i - (0,8b_i,min + 3b_i,max)t_i+1

откуда следует ограничение на выбор 0 < t_i+1 < t^∗i, аналогичное (Π.15):

b_i,min

(Π.20)

0,8b_i,mint^∗i - (0,8b_i,min + 3b_i,max)t_i+1 > 0 ⇒ t_i+1 < 0,2

t^∗i.

b_i,max

Выбираем t^∗i+1 > 0 на основе (Π.20) и подставляем его в двойное неравен-

ство

(Π.21)

max{m_i1; m_i2} < m_i < m_i,

где m_i1(t^∗i+1) (Π.19),

|x_i+1(0)| - Δ_i+1

2m^∗i-1 + Δ^∗i - |x_i(0)|

m_i2 =

m_i =

3b_i,maxt^∗

i+1

Если (Π.21) выполняется, то тогда фиксируем t^∗i+1, m^∗i ∈ ( m_i; m_i] и пе-

реходим на следующий шаг. При невыполнении (Π.21) следует варьиро-

вать произвольные параметры Δ_i+1 и/или t_i+1. Если изначально m_i2 > m_i1,

то путем увеличения Δ_i+1 (вплоть до Δ_i+1 = |x_i+1(0)|) нужно обеспе-

чить m_i1 > m_i2. Если при новом Δ^∗i+1 неравенство (Π.21) не выполняется

или изначально m_i1 > m_i2, то тогда снижаем t^∗i+1. Критическое значение

ti+1 > 0 : mi1(ti+1) =mi(ti+1) существует и равно

√

p²ⁱ² - 4p_i1p_i3 - p_i2

ti+1 =

2p_i1

где

(

)

p_i1 = - 3b_i,max

Fi + k^i-1(m^i-1)²bi-1,max + bi,minΔi+1

(

)

p_i2 = 3b_i,max

3m^∗i-1 + (F_i + k^∗i-1(m^∗i-1)²b_i-1,max + b_i,minΔ_i+1)t^∗i

(

)

+ 0,8b_i,min

2m^∗i-1 + Δ^∗i - |x_i(0)|

(

)

p_i3 = - 0,8b_i,min

2m^∗i-1 + Δ^∗i - |x_i(0)|

t^∗i,

i = 2,n - 1.

Из предельного соотношения, аналогичного (Π.18), а именно

lim

m_i1(t_i+1) =

ti+1→+0

|x_i(0)| + m^∗i-1 - Δ^∗i + (F_i + k^∗i-1(m^∗i-1)²b_i-1,max + b_i,minΔ_i+1)t^∗i

= const <

0,8b_i,mint^∗

(0)|

2m^∗i-1 + Δ^∗i - |x_i

< lim

= +∞,

ti+1→+0

3b_i,maxt_i+1

следует, что при любом t^∗i+1 > 0 : 0 < t^∗i+1 < t_i+1 неравенство (Π.3) будет вы-

полнено.

Заметим, что на i-м шаге (в отличие от первого) обеспечить выполнение

(Π.21) можно только указанным способом. Увеличение верхней границы m_i

путем увеличения m^∗i-1 приведет также к росту нижней границы m_i(m_i1),

причем более быстрыми темпами.

Допустимые значения t^∗i+1, m^∗i, Δ^∗i+1 и k^∗i+1(Δ^∗i+1) фиксируются, переходим

на следующий шаг.

Шаг n (последний). С учетом (Π.9), (Π.12) третье неравенство (Π.3) при-

мет вид, аналогичный (2.19):

)

1,25

(Π.22)

m_n ≥ m_n =

( |x_n(0)| + m^∗n-1 - Δ^∗n + F_n + k∗n-1(m∗n-1)2b_n-1,max

b_n,min

t^∗n

На основе (Π.22) фиксируем m^∗n. Процедура настройки амплитуд законче-

на.

Таким образом, существуют такиеki > 0, i = 1, n (Π.2), 0 < m_i < m_i, i =

= 1, n - 1 (Π.16)-(Π.17), (Π.21) и

m_n > 0 (Π.22), что для любых k_i ≥ki,

m_i : mi < mi ≤ mi, ∀mn ≥ mn в замкнутой системе (3.4) переменные по-

следовательно сходятся в указанные области за указанное время (Π.1), что и

обеспечивает цель управления (2.24). Теорема доказана.

СПИСОК ЛИТЕРАТУРЫ

Wonham W.M. Linear Multivariable control: a geometric approach. N.Y.: Springer-

Verlar, 1979.

Никифоров В.О. Адаптивное и робастное управление с компенсацией возмуще-

ний. СПб.: Наука, 2003.

Краснова С.А., Уткин А.В. Сигма-функция в задачах синтеза наблюдателей

состояний и возмущений // ПУ. № 5. 2015. С. 27-36.

Krasnova S.A., Utkin A.V. Sigma Function in Observer Design for States and Per-

turbations // Autom. Remote Control. 2016. V. 77. No. 9. P. 1676-1688.

Маликов А.И. Синтез наблюдателей состояния и неизвестных входов для нели-

нейных липшицевых систем с неопределенными возмущениями // АиТ. 2018.

№ 3. С. 21-43.

Malikov A.I. Synthesis of State Unknown Input Observers for Nonlinear Lipschitz

Systems with Uncertain Disturbances // Autom. Remote Control. 2018. Vol. 79.

No. 3. P. 406-424.

Краснова С.А. Оценивание внешних возмущений на основе виртуальных дина-

мических моделей // УБС. 2018. Вып. 76. С. 6-25.

Krasnova S.A. Estimating the Derivatives of External Perturbations Based on Vir-

tual Dynamic Models // Autom. Remote Control. 2020. V. 81. No. 5. P. 897-910.

Андриевский Б.Р., Фуртат И.Б. Наблюдатели возмущений: методы и приложе-

ния. Часть 1. Методы // АиТ. 2020. № 9. С. 3-61.

Andrievsky B.R., Furtat I.B. Disturbance Observers: Methods and Applications. I.

Methods // Autom. Remote Control. 2020. Vol. 81. No. 9. P. 1563-1610.

Емельянов С.В., Коровин С.К. Новые типы обратной связи. М.: Наука. Физмат-

лит, 1997.

Edwards С., Spurgeon S. Sliding mode control: theory and applications. Taylor &

Francis Ltd, 1998.

Utkin V.I., Guldner J., Shi J. Sliding Mode Control in Electromechanical Systems.

N.Y.: CRC Press, 2009.

10.

Уткин В.А., Уткин А.В. Задача слежения в линейных системах с параметри-

ческими неопределенностями при неустойчивой нулевой динамике // АиТ. 2014.

№ 9. С. 62-81.

Utkin V.A., Utkin A.V. Problem of Tracking in Linear Systems with Parametric Un-

certainties under Unstable Zero Dynamics // Autom. Remote Control. 2014. V. 75.

No. 9. P. 1577-1592.

11.

Krstic M., Kanellakopoulos I., Kokotovic P. Nonlinear and adaptive control design.

N.Y.: Wiley, 1995.

12.

Ebrahim A., Murphy G.V. Adaptive backstepping controller design of an inverted

pendulum // Proc. Thirty-Seventh Southeastern Symposium on System Theory.

2005. P. 172-174.

13.

Feng H., Qiao W., Yin C., Yu H., Cao D. Identification and compensation of non-

linear friction for a electro-hydraulic system // Mechanism and Machine Theory.

2019. V. 141. P. 1-13.

14.

Hidalgo M., Garcia C. Friction compensation in control valves: Nonlinear control

and usual approaches // Control Engineering Practice. 2018. V. 58. P. 42-53.

15.

Антипов А.С., Краснова С.А. Блочный синтез системы слежения для двухро-

торной электромеханической системы при ограничениях на переменные состоя-

ния // ПММ. 2021. Т. 85. № 1. С. 3-20.

Antipov A.S., Krasnova S.A. Block-Based Synthesis of a Tracking System for a Twin-

Rotor Electromechanical System with Constraints on State Variables // Mech. Solids.

2021. V. 56. No. 7. Р. 43-56.

16.

Кочетков С.А., Уткин В.А. Обеспечение инвариантности за счет создания ко-

лебательных режимов // ДАН. 2013. Т. 452. № 6. С. 1-6.

Kochetkov S.A., Utkin V.A. Providing the invariance property on the basis on oscil-

lation modes // Doklady Mathematics. 2013. Vol. 88. No. 2. Р. 618-623.

17.

Краснова С.А., Мысик Н.С. Каскадный синтез наблюдателя состояния с нели-

нейными корректирующими воздействиями // АиТ. 2014. № 2. С. 106-128.

Krasnova S.A., Mysik N.S. Cascade Synthesis of a State Observer with Nonlinear

Correction Influences // Autom. Remote Control. 2014. V. 75. No. 2. P. 263-280.

18.

Краснова С.А., Уткин В.А., Уткин А.В. Блочный подход к анализу и синтезу

инвариантных нелинейных систем слежения // АиТ. 2017. № 12. С. 26-53.

Krasnova S.A., Utkin V.A., Utkin A.V. Block Approach to Analysis and Design of

the Invariant Nonlinear Tracking Systems // Autom. Remote Control. 2017. V. 78.

No. 12. P. 2120-2140.

19.

Антипов А.С., Краснов Д.В., Уткин А.В. Декомпозиционный синтез системы

управления электромеханическими объектами в условиях неполной информа-

ции // Прикладная математика и механика. 2019. Т. 83. Вып. 4. С. 530-548.

Antipov A.S., Krasnov D.V., Utkin A.V. Decomposition Synthesis of the Control

System of Electromechanical Objects in Conditions of Incomplete Information //

Mech. Solids. 2019. V. 54. No. 5. P. 47-60.

20.

Лукьянов А.Г. Блочный метод синтеза нелинейных систем на скользящих ре-

жимах // АиТ. 1998. № 7. С. 14-34.

Luk’yanov A.G. A block method of synthesis of nonlinear systems at sliding modes //

Autom. Remote Control. 1998. V. 59. No. 7. Part 1. P. 916-933.

21.

Краснова С.А., Сиротина Т.Г., Уткин В.А. Структурный подход к робастному

управлению // АиТ. 2011. № 8. С. 65-95.

Krasnova S.A., Sirotina T.G., Utkin V.A. A structural approach to robust control //

Autom. Remote Control. 2011. Vol. 72. No. 8. P. 1639-1666.

22.

Уткин В.А. Инвариантность и автономность в системах с разделяемыми дви-

жениями // АиТ. 2001. № 11. С. 73-94.

Utkin V.A. Invariance and Independence in Systems with Separable Motion // Au-

tom. Remote Control. 2001. V. 62. No. 11. P. 1825-1843.

23.

Tsypkin Y., Polyak B. High-Gain Robust Control // European J. Control. 1999.

Vol. 5. P. 3-9.

24.

Поляк Б.Т., Тремба А.А., Хлебников М.В., Щербаков П.С., Смирнов Г.В. Боль-

шие отклонения в линейных системах при ненулевых начальных условиях //

АиТ. 2015. № 6. С. 18-41.

Polyak B.T., Tremba A.A., Khlebnikov M.V., Shcherbakov P.S., Smirnov G.V. Large

Deviations in Linear Control Systems with Nonzero Initial Conditions // Autom.

Remote Control. 2015. Vol. 76. No. 6. С. 957-976.

25.

Slotine J.Е., Li W. Applied Nonlinear Control. New Jersey: Prentice-Hall, 1991.

26.

Пестерев А.В. Оценка области притяжения нулевого решения для аффинных

систем с ограниченным управлением // АиТ. 2017. № 4. С. 3-20.

Pesterev A.V. Attraction domain estimate for single-input affine systems with con-

strained control // Autom. Remote Control. 2017. V. 78. No. 4. P. 581-594.

27.

Бенджио И., Гудфеллоу Я., Курвилль А. Глубокое обучение. М.: ДМК-Пресс,

2018.

Goodfellow I., Bengio Y., Courville A. Deep Learning. The MIT Press, 2016.

28.

Шумихин А.Г., Бояршинова А.С. Идентификация сложного объекта управле-

ния по частотным характеристикам, полученным экспериментально на его ней-

росетевой динамической модели // АиТ. 2015. № 4. С. 125-132.

Shumikhin A.G., Boyarshinova A.S. Identification of a complex control object with

frequency characteristics obtain whith its dynamic neural network model // Autom.

Remote Control. 2015. V. 76. No 4. P. 650-657.

29.

Краснова С.А., Антипов А.С. Иерархический синтез сигмоидальных обобщен-

ных моментов манипулятора в условиях неопределенности // ПУ. 2016. № 4.

С. 10-21.

Krasnova S.A., Antipov A.S. Hierarchical Design of Sigmoidal Generalized Moments

of Manipulator under Uncertainty // Autom. Remote Control. 2018. Vol. 79. No. 3.

P. 554-570.

30.

Kochetkov S.A., Krasnova S.A., Antipov A.S. Cascade Synthesis of Electromechan-

ical Tracking Systems with Respect to Restrictions on State Variables // IFAC-

PapersOnLine. 2017. V. 50. No. 1. P. 1042-1047.

31.

Антипов А.С., Краснова С.А. Система стабилизации положения тележки кра-

на с использованием сигмоидальной функции // Мехатроника, автоматизация,

управление. 2019. Т. 20. № 10. С. 609-614.

Antipov A.S., Krasnova S.A. Sistema stabilizatsii polozheniya telezhki krana s is-

pol’zovaniyem sigmoidal’noy funktsii (Stabilization System of Convey-Crane Posi-

tion Via Sigmoidal Function) // Mekhatronika, avtomatizatsiya, upravleniye. 2019.

V. 20. No. 10. P. 41-54. (In Russian)

32. Kokunko Yu., Krasnova S. Synthesis of a tracking system with restrictions on UAV

state variables // Mathematics in Engineering, Science and Aerospace (MESA). 2019.

Vol. 10. No. 4. Р. 695-705.

33. Фомичев В.В., Краев А.В., Роговский А.И. Об уравнения нулевой динамики

некоторых аффинных нелинейных систем // ДУ. 2018. Т. 54. № 12. С. 1695-1709.

Fomichev V.V., Kraev A.V., Rogovskii A.I. On the zero dynamics equations of

some nonlinear systems affine in control // Differ. Equations. 2018. V. 54. No. 12.

P. 1654-1668.

34. Живанович М.М., Лазаревич М.П. Применение принципа декомпозиции для

стабилизации с заданной точностью номинального движения механической си-

стемы // АиТ. 2012. № 12. С. 65-88.

Živanović, M.M., Lazarević, M.P. Using the decomposition principle to stabilize the

nominal motion of a mechanical system with given accuracy // Autom. Remote

Control. 2012. Vol. 73. No. 12. P. 2001-2020.

35. Юркевич В.Д. Синтез многоканальной системы управления роботами-манипу-

ляторами на основе метода разделения движений // Автометрия. 2016. Т. 52.

№ 2. С. 107-114.

Yurkevich V.D. Multi-channel control system design for a robot manipulator based

on the time-scale method // Optoelectronics, Instrumentation and Data Processing.

2016. V. 52. No. 2. P. 196-202.

Статья представлена к публикации членом редколлегии П.В. Пакшиным.

Поступила в редакцию 04.03.2021

После доработки 02.08.2021

Принята к публикации 29.08.2021