Автоматика и телемеханика, № 1, 2022
Нелинейные системы
© 2022 г. В.П. ИВАНОВ, д-р техн. наук (vladguc@ipu.ru),
Д.Д. ТАБАЛИН (corovan@mail.ru)
(Институт проблем управления им. В.А. Трапезникова РАН, Москва)
ОБ ОДНОМ МЕТОДЕ ДЕТЕРМИНИРОВАННОГО ТЕРМИНАЛЬНОГО
УПРАВЛЕНИЯ С ПРЕДИКТИВНЫМ ПРОГНОЗИРОВАНИЕМ
НЕВЯЗОК КРАЕВЫХ УСЛОВИЙ1
Рассматривается формулировка задачи синтеза терминального управ-
ления с разделением координат состояния объекта на два типа: медленно
меняющиеся координаты, участвующие в краевых условиях, и координа-
ты контура стабилизации. Получено обобщение теоремы о производной
невязок краевых условий. На ее основе производится дискретизация си-
стемы. Выводится критерий наличия возможности приведения получен-
ной системы к линейной путем замены управления. Полученный резуль-
тат используется для построения управления с прогнозирующими моде-
лями. Произведено численное моделирование полученного алгоритма для
задачи вывода центра масс ступени ракеты-носителя на заданную орбиту
на безатмосферном участке.
Ключевые слова: терминальное управление, управление с прогнозирую-
щими моделями, управление тангажом ракеты-носителя.
DOI: 10.31857/S0005231022010056
1. Введение
Задачи терминального управления возникают во многих областях техни-
ки. В ракетодинамике примерами таких задач являются выведение на око-
лоземную орбиту, расходование топлива до его полной выработки из баков,
сближение космических аппаратов и др. В указанных примерах задача управ-
ления заключается в приведении объекта в заданные конечные состояния при
известных начальных условиях. Конечные условия могут определяться в ви-
де значений координат состояния объекта, а также и более сложным образом,
например в виде функций от координат состояния.
Современная концепция терминального управления объектами ра-
кето-космической техники в наиболее полном объеме сформулирована в [1].
Принципиальным элементом способа терминального управления является
прогнозирование конечного состояния объекта в виде заданных краевых усло-
вий.
1 Работа выполнена при финансовой поддержке Российского фонда фундаментальных
исследований (проект № 20-08-00073 A).
77
Принципы методов прогнозирования в области ракетодинамики рассмат-
ривались уже в [2, 3]. Для обзора подхода в области управления линейными
системами, см., например, [4]. Применение современных методов управления
с прогнозирующей моделью к нелинейным системам подробно рассматрива-
ется в [5]. Общая идея метода состоит в том, что задается прогнозирующая
модель объекта, для которой находится оптимальное управление в текущий
и последующие моменты времени. При этом на реализацию идет только те-
кущее управление, а в следующий момент времени процедура оптимизации
повторяется. В публикации [6] для заданного управления в модели прогно-
зирования определяется производная прогнозируемых значений координат
по времени. Методы синтеза алгоритмов управления развивались также в
направлении применения оптимизации в реальном времени [7] и придания
робастности замкнутой системе [8].
В приведенных выше примерах терминальное управление формулируется
как часть общей задачи управления объектом путем выделения в объекте
сравнительно медленно протекающих физических процессов, определяющих
движение к заданной цели. При этом общее управление декомпозируется на
терминальное управление и задачу стабилизации объекта относительно дви-
жения к заданной цели. В качестве примера можно привести стабилизацию
углового положения ракеты-носителя относительно программы угла тангажа
при управлении выведением. Отметим, что управление непосредственно воз-
действует на ту динамическую часть объекта, которая относится к контуру
стабилизации. Синтез терминального управления, как правило, рассматри-
вается независимо от контура стабилизации. При этом координаты объекта,
формируемые на выходе контура стабилизации, принимаются в качестве тер-
минального управления.
В данной статье задача синтеза терминального управления рассматрива-
ется при условии декомпозиции общей задачи с учетом формального опи-
сания динамики объекта в целом, включая контур стабилизации. Суть та-
кого подхода состоит не в том, чтобы учитывать погрешности работы это-
го контура. Целью такого рассмотрения является учет динамики переход-
ных процессов реакции контура стабилизации на управляющее воздействие.
В этом случае идея прогнозирования конечного состояния объекта реализу-
ется для всего динамического тракта системы: от места непосредственного
воздействия управления до значений невязок краевых условий. В результате
может быть получено дифференциальное уравнение, определяющее в явном
виде зависимость невязок от управления.
Полученное дифференциальное уравнение дискретизируется. Для рас-
смотренного уравнения выводится критерий, при котором это уравнение с
точностью до невырожденной замены управления сводится к линейному. Это
используется для обобщения результатов для линейных систем, в частности
для алгоритма терминального управления в случае отсутствия ограничений
на управление. Затем данный алгоритм используется в качестве эвристики
для решения задачи управления с учетом ограничений. Производится числен-
ное моделирование полученных алгоритмов для задачи управления центром
78
масс ступени ракеты-носителя на безатмосферном участке путем изменения
программы угла тангажа.
Элементы описанного подхода докладывались на [9] и были отмечены
в [10].
2. Постановка задачи
Рассматривается динамическая система
dx1
= f1(x1(t),x2(t),t),
dt
(1)
dx2
= f2(x2(t),u(t),t),
dt
x(t0) = x0,
где x1 ∈ Rn1 , x2 ∈ Rn2 , x0 ∈ X0 ⊂ Rn1+n2 , u ∈ U ⊂ Rm, t ∈ [t0, T ], u управ-
ление, значения которого принадлежат множеству U.
Здесь предполагается, что решение (1) для любых начальных условий су-
ществует и единственно (например, при выполнении условий одной из соот-
ветствующих теорем в [11, гл. 1]). Это же предположение используется для
всех рассматриваемых в статье систем и не будет в дальнейшем оговаривать-
ся отдельно.
Ставится задача терминального управления перевода системы в состоя-
ние x, удовлетворяющее краевым (граничным) условиям ψ в момент време-
ни T :
ψ(x1) : ψj (xj (T )) = 0, j ∈ L ⊂ 1, l,
l
число краевых условий. Предполагается, что краевые условия наклады-
ваются только на координаты x1, а граничные условия представляют собой
вектор условий для отдельных x1j . Функция ψ предполагается дифференци-
руемой.
Момент времени T > t0 либо является фиксированным, либо определяется
первым моментом выполнения p-го краевого условия ψp(x1p) = 0.
Координаты x2 объекта формируются на выходе стабилизирующего кон-
тура системы управления. В данном случае работа контура рассматрива-
ется только в части переходных процессов реакции на изменение управ-
ляющего воздействия. Предполагается, что переходный процесс завершается
на интервале, существенно меньшем, чем интервал терминального управле-
ния. Ограничением общности является независимость динамики координат
состояния x2 от координат объекта x1.
Задачу синтеза терминального управления объектом (1) будем рассмат-
ривать в классе систем с прогнозирующей моделью. Данный класс систем
рассматривался в [1]. Общий обзор метода представлен, например, в [4, 5].
79
3. Теорема о производной прогнозируемой невязки
Рассмотрим динамическую систему общего вида:
dx
= f(x(t),u(t),t),
(2)
dt
x(t0) = x0.
Краевые условия могут накладыватся на все координаты xi.
Определение 1. Назовем прогнозирующей моделью для системы (2) в
момент времени t при управлении û(t) систему вида
dx
=
f(x(τ), û(τ),τ),
(3)
dτ
x(t) = x(t).
Обозначим интеграл системы (3), записанной в момент времени t с на-
чальными условиями x(t) через x(τ|t, x(t)). Это обозначение подчеркивает,
что x(τ|t, x(t)) зависит от момента прогнозирования и начальных условий
прогноза. В дальнейшем изложении будем писать просто x(τ|t), опуская x и
подразумевая, что x(t) совпадает с состоянием системы (2) в момент време-
ни t, или просто x(τ), опуская t и x(t), когда момент прогнозирования t ясен
из контекста.
Определение 2. Прогнозируемой невязкой краевых условий (в силу
прогнозирующей модели) будем называть
z(t) ≡ ψ(x(T |t)),
где момент времени T вычисляется для системы (3) так же, как и для
исходной системы (2), т.е. либо фиксирован, либо определяется первым мо-
ментом выполнения краевого условия ψp.
Замечание 1. В определениях 1 и 2 dim x = dimx. Аналогичные опреде-
ления можно сформулировать для dim x = dim x путем выбора координат x,
участвующих в начальных/краевых условиях.
Замечание 2. Прогнозируемая невязка краевых условий определена не
всегда, в частности при выбранном û(t) условие ψp(xp) = 0 может никогда
не выполняться. В дальнейшем рассматриваются только те прогнозирующие
модели, для которых прогнозируемая невязка краевых условий существует.
Это одно из ограничений области применения рассматриваемых методов
требуется знать û, для которого прогнозируемая невязка существует.
Справедлива теорема 1.
Теорема 1. Пусть ψ, x(T|t), T
дифференцируемы (по x, {x,t} и t
соответсвтенно), тогда
80
)
dz(t)
∂ψ
[∂x(T)(
(4)
=
f (x(t), u(t), t)
f (x(t), û(t), t)
+
dt
∂x(T)
∂x(t)
]
dT
+
f(x(T), û(T),T)
dt
Доказательство теоремы 1 (и следствий из нее) приведено в Приложении.
Замечание 3. Теорема 1 не является новой. Аналог теоремы 1 исполь-
зовался в [6] для решения задачи нетерминального типа.
Замечание 4. Для доказательства дифференцируемости x(T|t) может
использоваться, например, теорема Люстерника, см., например, [12]. В част-
ности, достаточно существования непрерывной сюръективно
f ′.
Следствие 1. Пусть верны условия теоремы 1 и T = const, тогда
)
dz(t)
∂ψ
∂x(T)(
=
f (x(t), u(t), t)
f (x(t), û(t), t)
dt
∂x(T) ∂x(t)
Прогнозируемая невязка зависит от разностиddt (x(t) - x(t)), т.е. от ошиб-
ки прогнозирующей модели, вызванной отличием f о
f.
Для T, соответствующего ψp(xp(T )) = 0, при выполнении некоторых до-
полнительных условий возможно явно вычислитьdTdt .
Следствие 2. Пусть верны условия теоремы 1, T определяется первым
моментом выполнения ψp(xp(T )) = 0 и дополнительно
dψp
fp(x(T), û(T)) = 0,
(xp(T)) = 0.
dxp
Тогда
[
](
)
dz(t)
∂ψ
∂x(T)
(5)
=
-C(x(T)) f(x(t),u(t),t)
f (x(t), û(t), t) ,
dt
∂x(T)
∂x(t)
где
f(x(T), x(T),T) ∂xp(T)
(6)
C(x(T)) =
fp(x(T), x(T),T) ∂x(t)
Замечание 5. Условие зависимости ψp только от xp существенно. Для
других координат x данное требование можно опустить.
Рассмотрим систему (1) с прогнозирующей моделью
dx1
= f1(x1(τ), x2(τ),τ),
dτ
(7)
dx2
= 0,
dτ
x(t) = x(t).
81
Прогнозирующую модель (7) можно рассматривать как движение объекта с
фиксированным значением x2.
После применения теоремы 1 получим
]
dz(t)
∂ψ
[∂x1(T)
dT
=
f2(x(t),u(t),t) +
f1(x1(T), x2(T),T)
dt
∂x1(T)
∂x2(t)
dt
Для T = const:
dz(t)
∂ψ
∂x1(T)
(8)
=
f2(x2
(t), u(t), t).
dt
∂x1(T) ∂x2(t)
Использование декомпозиции (1) и прогнозирующей модели (7) позволяет
получить более простой вид уравнения (4).
4. Дискретизация уравнения для прогнозируемой невязки.
Неограниченное управление при сведении задачи к линейной
∂z
Введем обозначение
. Под
∂z будем понимать матрицу, на которую в
∂x2
∂x2
выражении дляdzdt домножается f2. В данных обозначениях (8) примет вид
dz
∂z
(9)
=
(x(t), t)f2(x2
(t), u(t)).
dt
∂x2
Проинтегрируем (9) на малом интервале [t; t + δt] :
∫
∂z
z(t + δt) = z(t) +
(x(τ), τ)f2(x2(τ), u(τ), τ)dτ =
∂x2
t
∂z
= z(t) +
(x(t), t)Δx2 + o(δt).
∂x2
При малых δt переходим к дискретной системе
∂z
(10)
z(ti+1) = z(ti) +
(x(ti), ti)Δx2(ti
).
∂x2
Рассмотрим случай, когда отсутствуют ограничения на возможные значе-
ния Δx2. Будем искать решение терминальной задачи:
(11)
{Δx2(ti)} : z(tk
) = 0.
Запишем (10) для z(tk) :
∂z
(12)
z(tk) = z(tk-1) +
(x(tk-1), tk-1)Δx2(tk-1
).
∂x2
Пусть Qk-1 матрица размерности m × n, где n = dim z, m ∈ N. Справед-
лива следующая теорема.
82
Теорема 2. Решение задачи
{Δx2(t1), Δx2(t2), . . . , Δx2(tk-2), Q} :
Qk-1z(tk-1) = 0,
∂z
Qk-1
(x(tk-1), tk-1) = 0,
∂x2
(13)
Qk-1
rank ∂z⊺
=dimz,
(x(tk-1), tk-1)
∂x2
⊺
∂z
{Δx2(tk-1)} :
(x(tk-1), tk-1)z(tk) = 0
∂x2
является решением задачи (11). При этом матрицу Qk-1 (если она суще-
ствует) можно выбрать в виде
⊺
∂z
( ∂z⊺ ∂z)-1 ∂z
(14)
Qk-1 ≡ K(x(tk-1),tk-1) = E -
,
∂x2
∂x2
∂x2
∂x2
где
∂z
∂z
=
(x(tk-1), tk-1).
∂x2
∂x2
Доказательство теоремы 2 приведено в Приложении. Управление Δx2 при
этом можно выбирать в виде линейной обратной связи:
⊺
( ∂z⊺ ∂z)-1 ∂z
(15)
Δx2(tk-1) = -
z(tk-1
),
∂x2
∂x2
∂x2
z(tk) при данном управлении примет значение
(
)
⊺
∂z
( ∂z⊺ ∂z)-1 ∂z
(16)
z(tk) = E -
= K(x(tk-1))z(tk-1
).
∂x2
∂x2
∂x2
∂x2
В выражении (16) K линейный оператор относительно z(tk-1).
∂z
⊺ ∂z
Замечание 6. Данные выражения предполагают, что матрица
∂x2
∂x2
∂z
обратима. Если
⊺ ∂z = 0, то воспользуемся результатами из [13]. Управ-
∂x2
∂x2
ление Δx2 можно выбрать в виде
∑
〈z(tk-1), ei〉 ∂z⊺
(17)
Δx2(tk-1) = -
ei,
λi
∂x2
i=1
∑
(18)
K =E- eie⊺i,
i=1
∂z
∂z
где ei
ортонормированные собственные векторы оператора
⊺, соот-
∂x2 ∂x2
ветствующие собственным значениям λi > 0. Заметим, что (17) также линей-
но относительно z(tk-1).
83
Замечание 7. Полученное управление (17) также является решением
задачи минимизации квадрата невязки z(tk) при фиксированном z(tk-1).
В дальнейшем будем пользоваться записью (16).
∂z
В случае
⊺ ∂z = 0 управление не оказывает влияния в момент време-
∂x2
∂x2
ни tk-1 и z(tk) = z(tk-1). Их можно исключить из рассмотрения.
Предположим, что
(19)
K(x(tj ), tj ) ≡ K(tj
),
т.е. линейный оператор K зависит только от времени tk-1, а не от всего век-
тора состояния. Обозначим через zk-1
zk-1(t) = K(tk-1)z(t).
Новая невязка zk-1 представляет собой значение z(tk) при управле-
нии (17). Для zk-1 справедливы равенства:
zk-1(tk-1) = K(tk-1)z(tk-1) =
(
)
∂z
= K(tk-1) z(tk-2) +
(x(tk-2), tk-2)Δx2(tk-2)
,
∂x2
∂zk-1
(20)
zk-1(tk-1) = zk-1(tk-2) +
(x(tk-2), tk-2)Δx2(tk-2
).
∂x2
Так как (20) имеет вид (12), то для невязки zk-1(tk-1) можно искать реше-
ние задачи, аналогичной (11). В результате найдем zk-2(t). Процедура может
быть продолжена для моментов времени, предшествующих tk-1, если усло-
вие на K продолжает выполняться. Управление при этом находится исходя
из выражений типа (15). Заметим, что в будущие моменты времени управ-
ление будет зависеть от, вообще говоря, неизвестных координат объекта, а в
текущий момент времени зависит только от текущих координат.
Выясним, для каких систем выполняется (19). Ответ на этот вопрос дает
теорема 3.
Теорема 3. Для системы
(10) K(x(tk-1), tk-1) = K(tk-1) тогда и
только тогда, когда система невырожденной заменой входов сводится к
линейной:
∂z
∂z
∃Ptk-1 (x,y) ∀x,xs :
(x, tk-1) =
(xs, tk-1)Ptk-1 (xs, x),
∂x2
∂x2
где матрицы Ptk-1 (x, y) ∈ RdimΔx2×dimΔx2 образуют группу:
∀x : Ptk-1 (x,x) = I,
∀x,y : Ptk-1 (x,y)Ptk-1 (y,x) = I,
∀x,y,z : Ptk-1 (y,x)Ptk-1 (z,y) = Ptk-1 (z,x).
84
Заменой Δx′2(tk-1) = Ptk-1 (xs, x(tk-1))Δx2(tk-1) уравнение (10) будет приве-
дено к линейному виду
∂z
z(tk) = z(tk-1) +
(xs, tk-1)Δx′2(tk-1).
∂x2
Доказательство теоремы 3 приведено в Приложении. Замены данного типа
производятся для всех будущих и текущего моментов времени.
Для определения управления можно применять рекуррентные выражения
для K и z :
(21)
z(tk) = zj-1(tj-1) = K(tj-1)z(tj-1
)
∀j ∈ 2,k,
K(tk) = E,(
)
)-1
⊺
(22)
∂z
( ∂z
∂z
∂z⊺
K(tj-1) = E - K(tj)
K(tj)
K(tj ) K(tj ),
∂x2
∂x2
∂x2
∂x2
где
∂z
∂z
=
(xs, tj ).
∂x2
∂x2
Эти выражения проверяются непосредственно. В них учтено, что оператор K
есть симметричный ортогональный проектор. Следовательно, в явном виде
замену входов P можно не находить.
Из того что управления находятся из условий
⊺
∂z
∂z⊺
(xs, ti)K(ti)zi(ti) =
(xs, ti)z(tk) = 0
∀i ∈ p,k - 1,
∂x2
∂x2
имеет следствие 3.
Следствие 3. Управляемость системы
(10) на интервале tk-p, . . . ,
tk-1 в случае удовлетворения системой условия (19) в моменты времени
tk-p+1,... ,tk эквивалентна полноте ранга матрицы
[
]
∂z
∂z
∂z
(xs, tk)
(xs, tk-1) . . .
(xs, tk-p)
∂x2
∂x2
∂x2
для произвольных xs. Управление, решающее терминальную задачу (11), при
этом можно выбирать исходя из (15).
Обобщением результата публикации [14] служит теорема 4.
Теорема 4. Пусть управление u в задаче (1) импульсное в моменты tj
без ограничений на размер и направление импульса Δx2. Пусть выполнено
условие (19), где K определяется рекурсивно по формуле (22).
Тогда существует управление из r ≤ dim(z) импульсов, минимизирующее
z⊺(T)z(T).
85
Следствие 4. Пусть выполнены условия теоремы 4. Тогда ядро опе-
ратора K(tj ) есть управляемое подпространство невязок, если управление
ведется начиная с момента времени tj . Если K(tj) = 0, то система полно-
стью управляема.
Замечание 8. Существенна линейность оператора K. Для ограничен-
ных импульсов аналогично определенный оператор K перестанет быть ли-
нейным.
5. Эвристический алгоритм управления
Воспользуемся теоремой 4 как эвристикой для построения управления с
учетом ограничений. В основу возьмем метод управления с прогнозирующи-
ми моделями.
Запишем выражение типа (10) для z(T ) через текущее и будущее управ-
ление:
∑
∂z
∂z
(23)
z(T ) = z(tc) +
(x(tc), tc)Δx2(tc) +
(x(ti), ti)Δx2(ti
),
∂x2
∂x2
i=c+1
где tc есть текущий момент времени в дискретизированной системе. В выра-
жении (23) отдельно выделены члены для текущего и будущих управлений.
Будем приближать сумму в (23) суммой импульсов в моменты времени
{tp}, p ∈ 1, I :
∑
∑
∂z
∂z
(24)
(x(ti), ti)Δx2(ti) ≈
(x(tp), tp)Δx2(tp
).
∂x
2
∂x2
i=c+1
p=1
Обозначив прогнозируемое будущее изменение невязки через Δf z, полу-
чим
∂z
(25)
z(T ) - Δf z =
(x(tc), tc)Δx2(tc
).
∂x2
Текущий же импульс можно найти, обрезав полученный импульс.
В следующий момент дискретизации процедуру следует повторить для
нахождения нового управления.
Замечание 9. Важно, чтобы будущие импульсы не могли целиком све-
сти невязку в 0 иначе текущее управление не будет выбрано.
В данной статье для модельной задачи (26) с управлением по тангажу
было численно промоделировано с одним будущим управлением в момент
времени t1 = (1 - α)t + αT . Коэффициент α был подобран в процессе моде-
лирования.
86
6. Модельная задача управления
Упрощенная модель ступени ракеты-носителя на безатмосферном участке
взята из [1, c. 74-75]:
Wβ
x=
cos(ν),
m0 + m1 + m2
Wβ
(26)
ÿ=
sin(ν) - g,
m0 + m1 + m2
m= -β,
ν = u,
где x, y горизонтальная и вертикальная координаты,
m масса топлива,
m0
масса ступени,
β секундный расход топлива,
W скорость истечения топлива,
g ускорение силы притяжения,
ν угол тангажа.
Координаты x, y и их производные x, y являются координатами x1 в де-
композиции (1), m, ν принадлежат x2.
Управление ограничено:
(27)
νmin ≤ ν(t) ≤ νmax.
Данная система рассматривается при фиксированном моменте времени T
и фиксированном β(t) случай управления только тангажом через произ-
водную.
Требуется достижение заданной высоты при нулевой вертикальной скоро-
сти:
{
y(T ) = yk,
(28)
y(T ) = 0.
Фиксируем ν, β. Известно [1, c. 304-305], что
x(T ) = S cos(ν),
dx
(T ) = L cos(ν),
dτ
(29)
ŷ(T ) = S sin(ν),
dŷ
(T ) = L sin(ν),
dτ
87
где
tM ≡ T - t,
m+m0
τf ≡
,
β
τ
f
(30)
L ≡ W ln
,
τf - tM
J≡τfL-WtM,
S ≡ LtM - J,
τf есть время “полного сгорания” ступени.
Заметим, что согласно (8) достаточно дифференцировать только по на-
чальным условиям, на которые прямо влияет управление.
Матрица частных производных для краевых условий (28) будет иметь вид
[S(t)cos ν]
(31)
L(t) cos ν
Очевидно, что замена управления
Δν
Δν′ =
cos ν
сводит уравнение к линейному.
7. Результаты моделирования
В рамках статьи было произведено численное моделирование системы (26).
Параметры, использованные при моделировании:
t0 = 0, T = 388,
m0 = 24142, m(t0) = 64930,
vx(t0) = 2905, vy(t0) = 1677,
π
θ(t0) =
,
θmaxspeed = 0,01,
6
β(t) = 167,15,
W = 3537, g = 9,8,
где -θmaxspeed ≤ ν ≤ θmaxspeed.
Частота дискретизации одна секунда. Считается, что в момент дискре-
тизации все необходимые вычисления производятся мгновенно.
При этом вместо импульсного управления использовалось кусочно-непре-
рывное, постоянное между точками дискретизации. В последние 10 с симу-
ляции управление фиксируется. Это производится, чтобы избежать вырож-
дения управления вследствие приближения обращаемых в алгоритме матриц
к вырожденным.
88
×105
4,5
4,0
3,5
3,0
2,5
2,0
1,5
1,0
0
50
100
150
200
250
300
350
400
Секунды
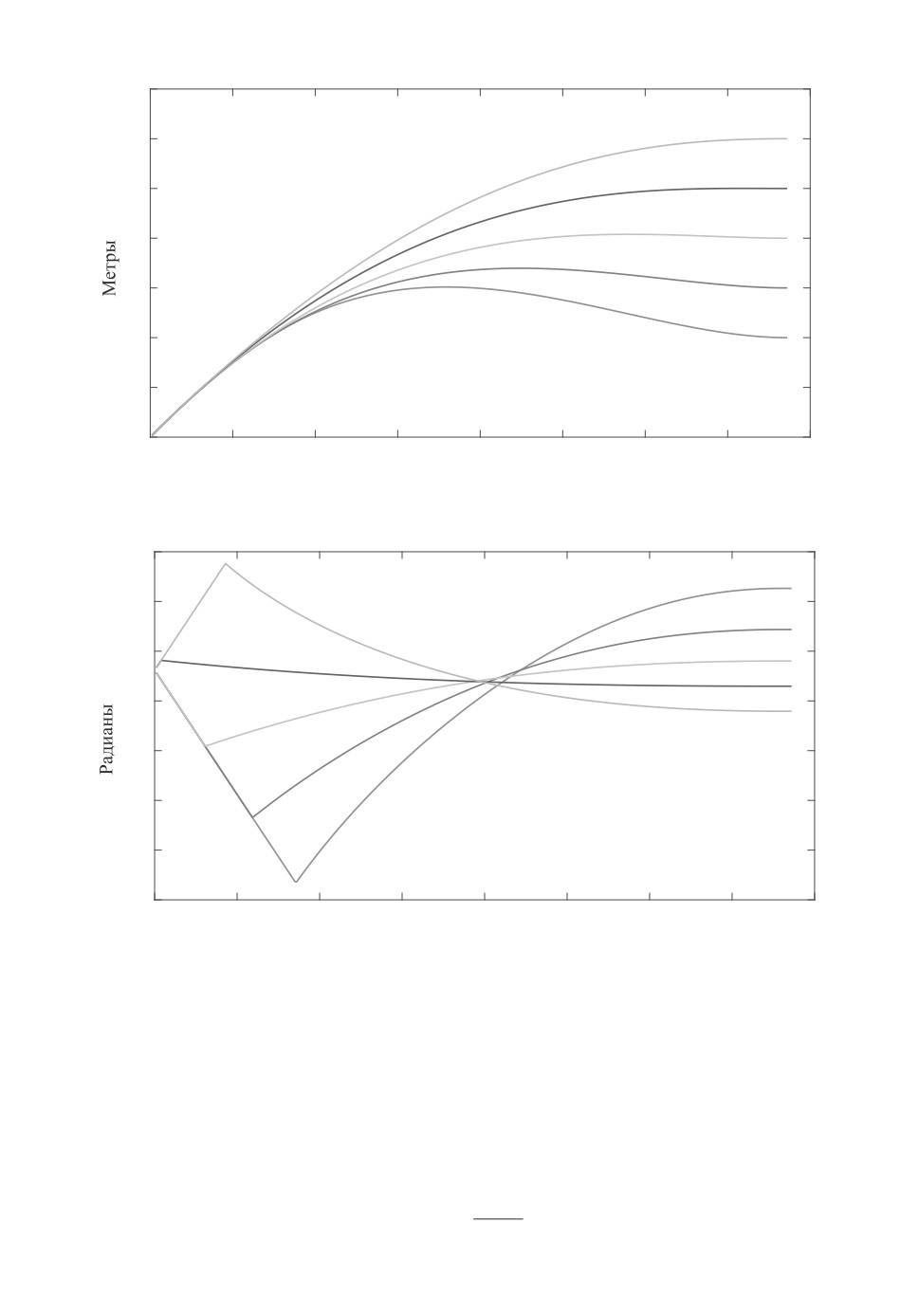
Рис.
1. Зависимость высоты от времени полета.
1,0
0,8
0,6
0,4
0,2
0
-0,2
-0,4
0
50
100
150
200
250
300
350
400
Секунды
Рис. 2. Зависимость угла тангажа от времени полета.
Способность предложенного алгоритма обеспечивать подъем на различ-
ные высоты демонстрируется на рис. 1, где изображены траектории подъема
на высоты 200
400 км c шагом 50 км. Соответствующие управления изобра-
жены на рис. 2.
Будущий момент времени один, в каждый момент дискретизации вычис-
ляемый по формуле
T -t
tI = t +
4
89
Результаты моделирования
Высота, км
200
250
300
350
400
vx(T), м/c
6634,2
6829,6
6927,9
6948,6
6885,4
z⊺(T)z(T)
0,0030
8,5e-04
1,1e-04
6,5e-06
2,9e-04
Перенабор высоты в процессе управления объясняется высокой начальной
вертикальной скоростью.
Конечные значения квадрата невязки и энергетические характеристики
(горизонтальной скорости) представлены в таблице.
8. Заключение
При терминальном управлении объектами ракето-космической техники,
например при управлении вектором тяги в задаче выведения на околоземную
орбиту, в общем движении объекта выделяются два класса взаимосвязанных
процессов с существенно различающимися динамическими характеристика-
ми. Первый класс процессов характеризуется уравнениями с медленно из-
меняющимися координатами состояния, на которые накладываются краевые
условия. Ко второму классу относятся сравнительно быстро изменяющие-
ся координаты, которые негативно влияют на динамику объекта. При этом
управление непосредственно воздействует на производные этих координат.
При рассмотрении общих уравнений движения объекта получено обобще-
ние теоремы о производной прогнозируемой невязки краевых условий (тео-
рема 1 и ее следствия). Проведена дискретизация уравнения путем интегри-
рования дифференциальных уравнений для производных невязок на малом
интервале затухания реакции объекта на изменение управления. Разностные
уравнения непосредственно связывают невязку с импульсами управляющих
воздействий.
Сформулирована задача синтеза импульсного терминального управления
из условий нулевой невязки и минимизации квадратичного критерия. Раз-
вита процедура синтеза и получены алгоритмы импульсного терминального
управления для систем, сводящихся к линейным. Работоспособность предло-
женных алгоритмов была продемонстрирована на модельной задаче терми-
нального управления тангажем ступени ракеты-носителя на безатмосферном
участке.
ПРИЛОЖЕНИЕ
Доказательство теоремы 1.
По формуле полной производной
dx(T)
dx(T|t,x(t))
∂x(T) dx(t)
∂x(T)
∂x(T) dT
(Π.1)
:=
=
+
+
dt
dt
∂x(t) dt
∂t
∂T dt
90
Частные производные будут иметь вид
∂x(T)
=
f(x(T), û(T),T),
∂T
∫
T
∂x(T)
∂
(Π.2)
=E+
f
(x(τ), û(τ),τ)dτ,
∂x(t)
∂x(t)
t
∫
T
∂x(T)
∂
=
f(x(τ), û(τ),τ)dτ.
∂t
∂t
t
Воспользуемся формулой Ньютона Лейбница:
T
∫
f(x(τ), û(τ),τ)dτ = x(T) - x(s).
s
Дифференцируя по s внутри одного прогноза (помня, что внутри одного про-
гноза T = const), получим
T
∫
d
(Π.3)
f(x(τ), û(τ),τ)dτ = -f
(x(s), û(s),s).
ds
s
∫T
Распишемd
f(x(τ), û(τ),τ)dτ через формулу полной производной
ds s
T
T
∫
∫
d
∂
f(x(τ), û(τ),τ)dτ =
f(x(τ), û(τ),τ)dτ dx(s)
+
ds
∂x(s)
ds
s
s
T
∫
∂
+
f(x(τ), û(τ),τ)dτ.
∂s
s
∫T
Выразив∂
f(x(τ), û(τ))dτ и воспользовавшись (Π.3), получим
∂s s
T
∫
∂
f(x(τ), û(τ),τ)dτ =
∂s
s
(Π.4)
T
∫
∂
= -E +
f(x(τ),û(τ),τ)dτ
f(x(s), û(s),s).
∂x(s)
s
Заметим, что (Π.4) верна для любого s из интервала [t; T ], в частности для
s = t, и соответственно x(s)|s=t = x(t) = x(t) :
T
T
∫
∫
∂
∂
f(x(τ), û(τ),τ)dτ = -E +
f(x(τ),û(τ),τ)dτ
f(x(t), û(t),t).
∂t
∂x(t)
t
t
91
Подставим результат в (Π.1), воспользовавшись (Π.2):
)
dx(T|t)
∂x(T)(
dT
(Π.5)
=
f (x(t), u(t), t)
f (x(t), û(t), t)
+
f
(x(T), û(T)).
dt
∂x(t)
dt
Формула (4) получается из (Π.5) дифференцированием сложной функции
ψ(x(T|t)). Теорема 1 доказана.
Доказательство следствия 2.
(
)
dzp(T |t)
dψp
[∂xp(T)
(Π.6)
=
f (x(t), u(t), t)
f (x(t), û(t), t)
+
dt
dxp(T )
∂x(t)
]
dT
+
fp(x(T), û(T),T) ,
dt
полная из условия зависимости p-го краевого условия
где производна
xp(T)
только от p-й координаты. Также заметим, что эта производная является
числом.
По условию определения T : ψp(xp(T )) = 0, следовательно,
dzp(T |t)
(Π.7)
= 0.
dt
Объединив (Π.6), (Π.7) и сократив наdxpdp(xp(T))=0,получим
)
∂xp(T)(
dT
f (x(t), u(t), t)
f (x(t), û(t), t)
+
fp(x(T), û(T),T) = 0.
∂x(t)
dt
Выразим производную T пр
fp(x(T), û(T),T) = 0 :
)
dT
1
∂xp(T)(
(Π.8)
=-
f (x(t), u(t), t)
f (x(t), û(t), t)
dt
fp(x(T), û(T),T)
∂x(t)
Подстановка (Π.8) в (4) приводит к (5). Следствие 2 доказано.
Доказательство теоремы 2.
Пусть найдены {Δx2(t1), Δx2(t2), . . . , Δx2(tk-2), Δx2(tk-1), Q}, удовлетво-
ряющие условиям (13). Рассмотрим
(
)
∂z
Qk-1z(tk) = Qk-1 z(tk-1) +
Δx2(tk-1)
= 0.
∂x2
Следовательно,
Qk-1
0
[
]
0
∂z⊺z(tk) =
∂z⊺
=
0
z(tk)
∂x2
∂x2
92
]
[Q
k-1
Так как матрица
∂z
⊺ имеет полный ранг, то z(tk) = 0. Управление Δx2
∂x2
находится из равенства
⊺
⊺
∂z
∂z
∂z⊺ ∂z
z(tk) = 0 =
z(tk-1) +
Δx2.
∂x2
∂x2
∂x2
∂x2
Проверим, что если существует Qk-1, удовлетворяющее условиям (2), то
этим условиям также удовлетворяет K, определенное по (18). Рассмотрим
(
)(
)⊺
K ∂z∂x
K ∂z
:
2
∂x2
)
(
)
(
)⊺ (
∑
∑
∂z
∂z
∂z
∂z⊺
K
K
= E-
eie⊺
E-
eie⊺
=
i
i
∂x2
∂x2
∂x2 ∂x
2
i=0
i=0
(
)
⊺
∑
∑
∂z
∂z
∂z⊺
∂z
∂z⊺
=
−
eie⊺ ∂z
= E-
eie⊺
=
i
∂x2 ∂x2
i ∂x2 ∂x2
∂x2 ∂x2
i=0
i=0
(
)
⊺
∑
∑
∂z
∂z
∂z
∂z⊺
=
E-
eie⊺
=
-
λieie⊺i.
i
∂x2 ∂x2
∂x2 ∂x
2
i=0
i=0
∑l
Для любой матрицы A верно AA⊺ =
λieie⊺i. Следовательно, K∂z
= 0.
i=0
∂x2
Покажем, что K удовлетворяет ранговому условию. Так как K ортого-
нальна
∂z , то
∂x2
([
])
)
K
( ∂z
( ∂z)≥n.
rank
∂z
⊺
= rank (K) + rank
= n - l + rank
∂x2
∂x2
∂x2
Условие Kz(tk) = 0 следует из того, что управление Δx2 минимизирует
квадрат невязки. Теорема 2 доказана.
Доказательство теоремы 3.
Пусть K(x(tk-1), tk-1) = K(tk-1). Заметим, что
∂z
ker K(tk-1) = Im
(x(tk-1), tk-1).
∂x2
∂z
Следовательно, образ
(x(tk-1), tk-1) не зависит от x(tk-1). Фиксируем
∂x2
∂z
xs,x. Выберем Ptk-1 (xs,x), отображающее векторы ядра
(x, tk-1) в векто-
∂x2
ры ядра∂z∂x
(xs, tk-1) и производящее аналогичное отображение для векторов
2
из прообраза, т.е.
∂z
∂z
(x, tk-1) =
(xs, tk-1)Ptk-1 (xs, x).
∂x2
∂x2
При x = xs можно выбрать Ptk-1 (x, x) = I. Если определено Ptk-1 (x, y), то
Ptk-1 (y,x) можно определить как обратную к ней матрицу. Если определены
Ptk-1 (y,x),Ptk-1 (z,y), то можно определить Ptk-1 (x,z) = Ptk-1 (y,x)Ptk-1 (z,y).
Достаточность проверяется непосредственно. Теорема 3 доказана.
93
СПИСОК ЛИТЕРАТУРЫ
1.
Сихарулидзе Ю.Г. Баллистика и наведение летательных аппаратов. М.: Бином.
Лаборатория знаний, 2011.
2.
Haeussermann W. Description and Performance of the Saturn Launch Vehicle’s Nav-
igation, Guidance, and Control System // 3rd Int. IFAC Conf. on Automatic Control
in Space. Toulouse. France. 1970. V. 3. P. 275-312.
3.
Петров Б.Н., Портнов-Соколов Ю.П., Андриенко А.Я., Иванов В.П. Бортовые
терминальные системы управления. М.: Машиностроение, 1983.
4.
Веремей Е.И., Еремеев В.В. Введение в задачи управления на основе предска-
заний // Всероссийская науч. конф. “Проектирование научных и инженерных
приложений в среде MATLAB”. М.: 2004. C. 98-115.
5.
Grüne L., Pannek J. Nonlinear model predictive control. Theory and Algorithms.
Springer, 2011.
6.
Гулько Ф.Б., Новосельцева Ж.А. Применение методов прогнозирования в зада-
чах синтеза систем автоматического управления // VIII Всесоюзное совещание
по проблемам управления. М.: 1980. Т. 1. C. 32-34.
7.
Klaučo M., Kalúz M., Kvasnica M. Real-time Implementation Of an Explicit MPC-
based Reference Governor for Control of a Magnetic Levitation System // Control
Engineering Practice. 2017. V. 60. No. 3. P. 99-105.
8.
Langson W., Chryssochoos I., Rakovic S.V., Mayne D.Q. Robust Model Predictive
Control Using Tubes // Automatica. 2004. V. 40. No. 1. P. 125-133.
9.
Табалин Д.Д. Детерминированный синтез алгоритмов терминального управле-
ния с прогнозированием невязок краевых условий // Тезисы на международ-
ном научном форуме “Ломоносов”. П. математика. С. “Вычислительная матема-
тика и кибернетика”. Матер. Международного молодежного научного форума
“ЛОМОНОСОВ-2020”.
10.
Табалин Д.Д. О терминальной задаче с прогнозированием невязок краевых
условий // Хроника доклада на семинаре по проблемам нелинейной динамики
и управления при Московском государственном университете им. М.В. Ломоно-
сова. Журн. Дифференциальные уравнения. 2020. Т. 56. № 8. С. 1138-1139.
11.
Coddington E.A., Levinson N. Theory Of Ordinary Differential equations. N.Y.:
McGraw-Hill Book Company, 1955.
12.
Дмитрук А.В., Милютин А.А., Осмоловский Н.П. Теорема Люстерника и тео-
рия экстремума // Успехи математических наук. 1980. Т. 35. № 6 (216).
13.
Balakrishnan A.V. An Operator Theoretic Formulation of a Class of Control Prob-
lems and a Steepest Descent Method of Solution // J.S.I.A.M. Control. Ser. A. Publ.
1963. V. 1. No. 2. P. 109-127.
14.
Красовский Н.Н. Об одной задаче оптимального регулирования // Прикл. ма-
тематика и механика. 1957. Т. 21. № 5. C. 670-677.
Статья представлена к публикации членом редколлегии В.М. Глумовым.
Поступила в редакцию 26.05.2021
После доработки 08.10.2021
Принята к публикации 15.10.2021
94