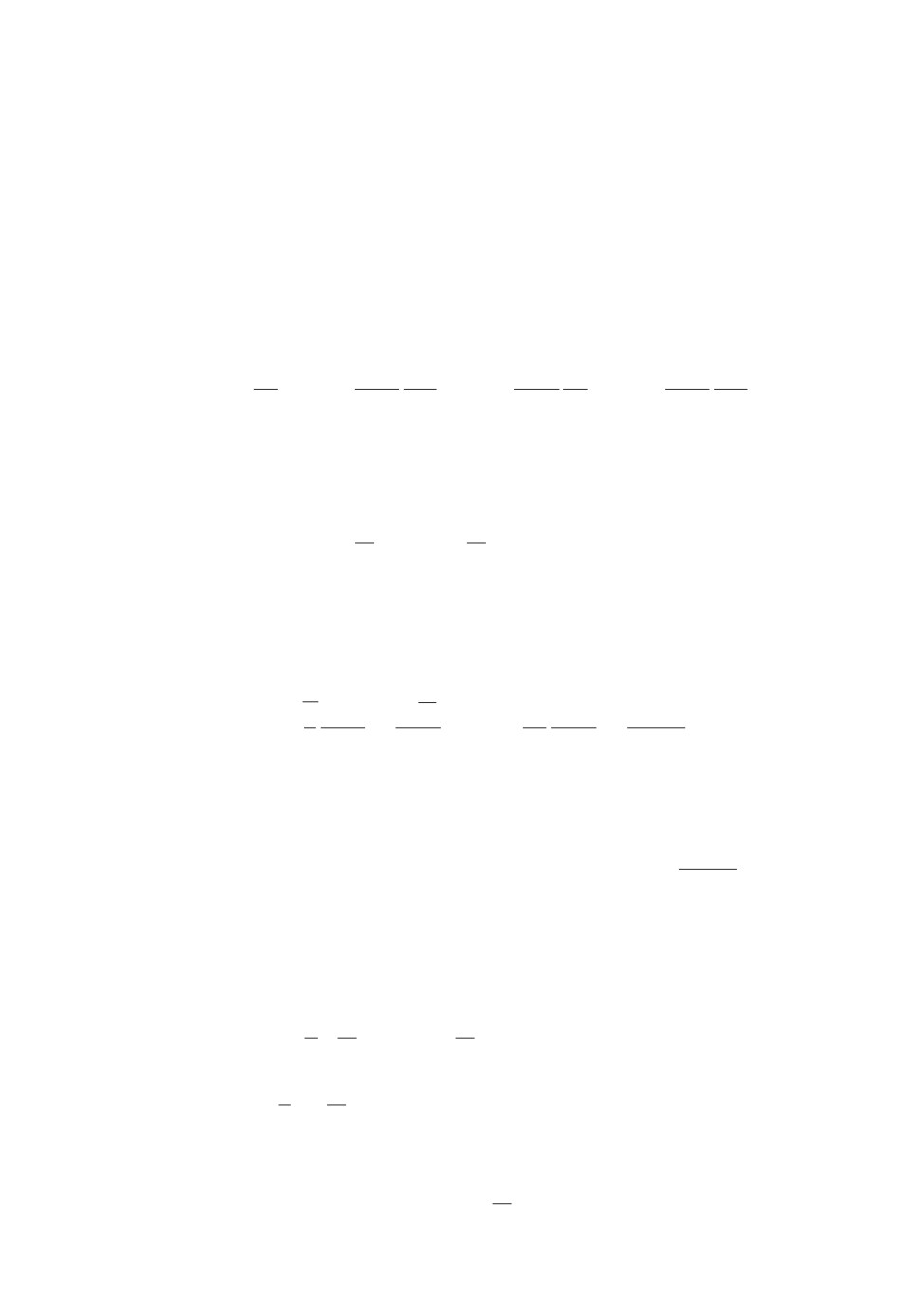Автоматика и телемеханика, № 1, 2022

Нелинейные системы

Ю.В. МОРОЗОВ, канд. физ.-мат. наук (tot1983@inbox.ru)

(Институт проблем управления им. В.А. Трапезникова РАН, Москва)

СТАБИЛИЗАЦИЯ ТЕЛЕЖКИ С ОБРАТНЫМ МАЯТНИКОМ

Рассматривается задача стабилизации движущейся вдоль прямой те-

лежки с установленным на ней перевернутым маятником. Цель управ-

ления стабилизировать тележку в заданной целевой точке так, чтобы

при этом маятник находился в верхнем вертикальном положении. Ос-

новная трудность, связанная с решением данной задачи, заключается в

том, что две подсистемы (тележка и маятник) должны быть стабилизиро-

ваны одновременно с помощью одного управления. Предлагается новый

закон управления, основанный на введении эталонной системы второго

порядка, траектория движения которой принимается в качестве целевой

для тележки с маятником. С помощью расширения эталонной системы

до 4-го порядка и введения алгебраического условия, связывающего две

системы, находится целевая траектория в четырехмерном фазовом про-

странстве исходной системы и строится закон управления, обеспечиваю-

щий асимптотическое стремление траектории замкнутой системы к це-

левой. Полученный в работе закон управления применим к системам с

произвольным соотношением масс маятника и тележки, так как замкну-

тая система не зависит от массовых характеристик системы. Найдена об-

ласть значений параметров системы, при которых линеаризованная си-

стема устойчива. Изложение иллюстрируется численными примерами, де-

монстрирующими эффективность предлагаемого управления.

Ключевые слова: стабилизация, тележка с обратным маятником, локаль-

ная устойчивость.

DOI: 10.31857/S0005231022010068

1. Введение

Тележка с обратным маятником

классический пример нелинейной

неустойчивой системы. Модель рассматривалась во множестве работ по тео-

рии управления и использовалась как тестовый пример при апробации новых

идей и подходов, разработанных для стабилизации неминимально фазовых

аффинных систем, в частности систем, описывающих движение велосипеда,

моноцикла, сигвея и т.п. В линейном приближении задача подробно обсуж-

далась в книге Ю. Неймарка [1]. Большинство обсуждаемых в литературе

нелинейных законов управления основаны на представлении системы в виде

совокупности двух связанных подсистем с разнотемповой динамикой: подси-

стемы с быстрой динамикой (маятник) и подсистемы с медленной динамикой

(тележка). При этом можно выделить три различных подхода, используемых

почти во всех работах по этой тематике.

Первый подход [2] основан на оптимальной стабилизации маятника по

быстродействию, при этом стабилизация тележки в нужной точке достигает-

ся введением силы вязкого трения, которая не позволяет тележке разгонять-

ся. Если эта сила равна нулю, как в рассматриваемом в настоящей статье

случае, стабилизация тележки вообще не гарантируется, несмотря на стаби-

лизацию маятника. Дальнейшее развитие этого подхода можно найти в [3].

Идея второго подхода [4] заключается в выделении “многообразия внут-

реннего равновесия” (internal equilibrium manifold). Ищется такой закон

управления, который приводит систему в малую окрестность многообразия и

обеспечивает ее движение в этой окрестности. Предположение о более быст-

рой динамике маятника по сравнению с динамикой тележки позволяет за-

давать многообразие с помощью алгебраического уравнения, связывающе-

го отклонение маятника с позицией и скоростью тележки. Похожий прием

в упрощенном виде применялся позднее в [5, 6]. В [5] ставится задача гло-

бальной оптимизации при ограниченном ресурсе управления и предлагается

комбинированный закон управления, когда при больших начальных отклоне-

ниях для попадания в область, где стабилизация может быть гарантирована,

применяется раскачивание маятника. В [6] указанный подход обобщается на

случай, когда параметры системы известны неточно, и предлагается робаст-

ный вариант закона управления.

Разработанный Тилом третий подход [7] применим к достаточно широкому

классу нелинейных систем, представимых в блочном виде, где одна из под-

систем асимптотически устойчива при нулевой динамике второй подсистемы

(feedforward form), и основан на применении теоремы о малом параметре уси-

ления [7]. Основная идея данного подхода применительно к рассматриваемой

системе заключается в том, что если есть глобальный закон управления ма-

ятником, то всегда можно построить локальный закон управления тележкой.

На этих же идеях основаны работы [8, 9]. Основной недостаток данного под-

хода заключается в том, что стабилизация достигается только для достаточно

узкой локальной области по переменным, отвечающим за позицию тележки.

С другой стороны, если, наоборот, потребовать глобальную стабилизацию те-

лежки, будет сужена гарантированная область устойчивости по переменным,

отвечающим за положение маятника.

Множество законов управления, предложенных для рассматриваемой си-

стемы, не исчерпывается непрерывными законами. Так, в [10] для стабили-

зация системы применяется разрывный закон управления на скользящих ре-

жимах. Автор приводит исходную систему с помощью обратимой нелинейной

замены переменных к регулярной форме, содержащей управление только в

последнем уравнении. В результате синтезируется закон управления для но-

вой системы, содержащий как непрерывную (отвечающую за компенсацию

внутренней динамики маятника), так и разрывную компоненты (гарантиру-

ет выход и скольжение системы по нелинейной поверхности в 4-х мерном

фазовом пространстве для некоторого множества начальных условий).

Основной недостаток всех вышеперечисленных работ отсутствие кон-

структивного метода выбора параметров в законе управления, гарантирую-

щих хотя бы локальную стабилизацию. Как правило, авторы ограничиваются

достаточно общими утверждениями о существовании таких параметров.

В настоящей работе предлагается новый гладкий нелинейный закон управ-

ления, основанный на введении более простой, эталонной, системы второго

порядка. Эталонная система стабилизируется в целевой точке с помощью

аналитически заданного ограниченного управления, обеспечивающего желае-

мые характеристики переходного процесса. Траектория эталонной системы

принимается в качестве целевой для тележки с маятником, и ищется такое

управление, которое обеспечит движение тележки по траектории, асимпто-

тически приближающейся к целевой траектории. Синтезированный в работе

закон управления применим к системам с произвольным соотношением масс

маятника и тележки, так как замкнутая система не зависит от массовых

характеристик системы. Проведен исчерпывающий анализ линеаризованной

замкнутой системы и определена область значений параметров закона управ-

ления, гарантирующих локальную стабилизируемость системы.

2. Постановка задачи

Рассматривается задача стабилизации движущейся без проскальзывания

колес вдоль прямой тележки массы M с установленным на ней переверну-

тым маятником массы m. Для простоты будем считать маятник математи-

ческим и пренебрежем трением. Координату центра тележки обозначим че-

рез x, а угловое отклонение маятника от вертикальной оси через φ (рис. 1).

Будем считать положительным угол, отсчитываемый от верхнего положения

маятника в направлении по часовой стрелке. Уравнения движения системы

хорошо известны (например, [5, 10]):

(1)

µx+m

φ cos φ - mlφ2

sin φ = U,

(2)

mlxcos φ + ml² φ

− mgl sin φ = 0.

Здесь µ = M + m, l - длина подвеса маятника и U - действующая на тележ-

ку управляющая сила. Будем считать, что в начальный момент отклонение

Рис. 1. Тележка с обратным маятником.

маятника ограничено прямым углом, т.е. |φ(0)| < π/2. Случай большего от-

клонения сводится к рассматриваемому предварительным применением спе-

циального закона управления, позволяющего перевести маятник из произ-

вольного начального положения в указанную область (например, с помощью

раскачивания, как в [5] в случае ограниченного управления).

Цель управления стабилизировать тележку в заданной целевой точке

на линии так, чтобы при этом маятник находился в верхнем вертикальном

положении. Без потери общности будем считать, что целевая точка совпада-

ет с началом координат. Основная трудность, связанная с данной задачей,

заключается в том, что две подсистемы (тележка и маятник) должны быть

стабилизированы одновременно с помощью одного управления.

Рассмотрим также более простую задачу стабилизации в начале координат

тележки массы µ = M + m без маятника, которую будем называть эталон-

ной системой, с помощью заданной управляющей силы U₁(w,w˙) (будем ис-

пользовать обозначение w для координаты центра тележки, чтобы отличать

эталонную систему от исходной):

(3)

µw=U₁

(w,w˙ ), w(0) = x(0),

w(0) = x(0).

Относительно функции U₁(w,w˙ ) предполагаем, что она дважды непрерывно

дифференцируема и удовлетворяет условиям U₁(0, 0) = 0 и ∂U₁/∂w(0, 0) < 0,

∂U₁/∂w˙(0,0) < 0. Будем также полагать, что управление U₁ и скорость эта-

лонной системы ограничены:

|U₁(w,w˙ )| ≤ U_max,

∀w,w˙,

w(t)| ≤ V_max ∀t ≥ 0.

Конкретный вид функции U₁ обсуждается в конце статьи в разделе 5. В на-

стоящий момент достаточно знать, что она удовлетворяет сформулирован-

ным выше условиям, из которых, в частности, следует, что начало координат

является положением устойчивого равновесия системы (3), в окрестности ко-

торого функция U₁(w,w˙ ) аппроксимируется линейной функцией.

Цель введения эталонной системы определить для тележки с маятни-

ком некоторую “желаемую” (целевую) траекторию, которая задается неявно

управлением U₁, и свести задачу к нахождению такого управления U, кото-

рое обеспечит движение тележки в начало координат по траектории, асимп-

тотически приближающейся к желаемой. Максимальная скорость системы

и управляющая сила на практике всегда ограничены. В настоящей рабо-

те ограничения на управление и скорость при синтезе закона управления

не вводились, однако учитывались при планировании траектории: введение

ограничений при стабилизации эталонной системы позволяет получить “ра-

зумную” целевую траекторию, которая может быть реализована (за исклю-

чением, быть может, некоторого начального участка) исходной системой с за-

данными ограниченным управлением и скоростью. Параметры U_max и V_max

будут также использованы при приведении уравнений движения системы к

безразмерной форме.

3. Безразмерная модель

Перейдем к безразмерным переменным. В отличие от большинства посвя-

щенных решению данной задачи работ, где в качестве масштаба времени при-

нимается период колебаний маятника (см., например, [4, 5, 7, 8]), в настоящей

работе в качестве масштаба берется величина l/V_max, и безразмерные пере-

менные вводятся как

(4)

t=tVmax/l,

x = x/l,

= φ.

Производные по времени в размерных и безразмерных переменных связаны

формулами

V^2max d²x

V^2max d²φ

φ=Vmax^dφ

(5)

x=V_max

φ=

dt²

l²

dt²

Подставляя эти выражения в уравнения (1), (2) и деля первое уравнение на

µV^2max/l, а второе на mV^2max, получаем уравнения системы в безразмерном

виде:

(6)

x+mφ co

φ-

φ²

φ=U

(7)

xcosφ+

φ-ω²

sin φ = 0,

где ω₀ - безразмерная круговая частота маятника иŨ - безразмерное управ-

ление,

√g l

√gl

Ũ=Ugl

ω₀ =

≡

l V_max

V_max

µg V^2max

µV^2max

Уравнение эталонной системы (3) и ограничения при переходе к безраз-

мерной записи принимают вид:

w= Ũ₁,

w(t)| ≤ 1,

|Ũ1( w,w˜)| ≤Ũmax,

Ũ_max =Umaxl .

µV^2max

Далее в статье все уравнения приводятся в безразмерном виде и, чтобы из-

бежать громоздкости, тильду над символами опускаем.

Разрешая систему (6), (7) относительно старших производных, получим

[

]

(8)

φ² sin φ -mω20 sin φcos φ + U ,

[

]

(9)

φ=

φ² sin φ cos φ + ω²⁰ sin φ - cos φ · U ,

где

(10)

γ ≡ γ(φ) = 1 -

cos²

φ.

4. Синтез стабилизирующего управления

4.1. Замена переменных

Сделаем замену переменных в φ-подсистеме и запишем уравнения (8)-(9)

в виде системы уравнений первого порядка. Для этого введем новые пере-

менные состояния

x₁ = x, x₂ = x, x₃ = ω²⁰ tan φ, x₄ = ω²⁰φ˙/cos² φ

и обозначение X = [x₁, . . . , x₄]. В новых переменных (для компактности за-

писи здесь и далее будем применять смешанные обозначения, т.е. наряду с

новыми переменными в правых частях уравнений использовать старые) си-

стема (8)-(9) принимает вид

x₁ = x₂,

[

]

x₂ =

φ² sin φ -mω20 sin φcos φ + U ,

(11)

x₃ = x₄,

x₄ = f_φ(φ,φ) + g_φ(φ)U,

где, с учетом формулы x₄ = ω²⁰

φ + 2 φ2 tanφ)/cos2 φ,

[

)]

φ² tan(φ)(

ω²⁰

f_φ(φ,φ) =ω0

x₃ +

2γ -

cos² φ

g_φ(φ) = -

γ cos φ

cos φ

γ cos φ

4.2. Идея подхода

Так как исходная система имеет четвертый порядок, запишем уравнения

эталонной системы также в виде системы четвертого порядка:

(12)

w₁ = w₂,

w₂ = w₃,

w₃ = w₄,

w₄ =Ü1,

где w₁ и w₂ - координата и скорость, w₃ и w₄ - зависимые переменные,

(13)

w₃ = U₁(w₁,w₂), w₄ =U1(w₁,w₂

U₁

и Ü₁ - производные по времени функции U₁ в силу системы (3). Ре-

шение системы (12) будет решением (3) только при фиксированных началь-

ных условиях для третьей и четвертой переменных, а именно при w₃(0) =

= U₁(w₁(0),w₂(0)) и w₄(0) =U1(w₁(0),w₂(0)).

Наряду с (12) рассмотрим еще одну систему (будем называть ее возму-

щенной эталонной системой):

(14)

w₁ = w₂,

w₂ = w₃,

w₃ = w₄,

w₄ =Ü1 + β₁δ₁ + β₂δ₂,

где β₁, β₂ > 0 и

δ₁ = U₁(w₁,w₂) - w₃, δ₂ =U1(w₁,w₂) - w₄.

100

Здесь w₃ и w₄ - независимые переменные, которые могут принимать произ-

вольные начальные значения. Решение системы (14) с начальными условиями

w_i(0) = x_i(0), i = 1,2,3,4, будем называть целевой траекторией для исход-

ной системы.

Будем искать такое управление U в исходной системе, при котором пра-

вые части четвертых уравнений исходной и эталонной систем совпадают при

подстановке x_i вместо w_i:

f_φ(φ,φ) + g_φ(φ)U =Ü1(x₁,x₂) + β₁δ₁ + β₂δ₂.

Подставляя правые части выражений для функций f_φ и g_φ в левую часть

уравнения, находим:

(

)

φ2

[

]

tan(φ)

(15) U = x₃ +

2γ -

cos² φ -

γ cos φ

Ü₁(x₁,x₂)+β₁δ₁ +β₂δ₂ ,

cos φ

ω²

где

(16)

δ₁ = U₁(x₁,x₂) - x₃, δ₂ =U1(x₁,x₂) - x₄.

Подставляя найденное управление U в (11), получаем уравнения замкнутой

системы в виде

x₁ = x₂,

2 φ2 tan(φ)

x₂ = x₃ +

cos φ

U₁ + β₁δ₁ + β₂δ₂),

(17)

cos φ

ω²

x₃ = x₄,

x₄ =Ü1 + β₁δ₁ + β₂δ₂,

отличающиеся от уравнений возмущенной эталонной системы только правой

частью второго уравнения. Из вида правой части (17) следует, что поведение

системы, замкнутой управлением (15), не зависит от массовых характеристик

системы и определяется одним параметром ω₀ и выбранной функцией U₁.

Обратная связь (15) получена с помощью эвристических соображений, так

что предыдущие рассуждения не являются доказательством устойчивости

замкнутой системы (17). В следующем разделе докажем, что функция U₁ и

параметры β₁ и β₂ могут быть выбраны так, чтобы система (17) была ло-

кально устойчива, и найдем область значений параметров, гарантирующих

устойчивость линеаризованной системы.

4.3. Локальная устойчивость замкнутой системы

Для доказательства локальной устойчивости линеаризуем систему (17) в

малой окрестности начала координат четырехмерного пространства состоя-

ний. Согласно предположению функция U₁(x₁, x₂) линейна в окрестности ну-

ля: U₁(x₁, x₂) = α₁x₁ + α₂x₂ + o(x₁, x₂), откуда следует, что матрица линеари-

зованной системы зависит от пяти параметров: ω₀, α₁, α₂, β₁ и β₂. Ограничим

101

выбор коэффициентов α₁ и α₂ условием α²¹ ≥ 4α₂, при выполнении которого

начало координат в пространстве переменных x₁, x₂ будет положением рав-

новесия типа узел, что, в свою очередь, обеспечит монотонное приближение

эталонной системы к целевой точки. Далее, чтобы уменьшить количество па-

раметров, ограничимся случаем вырожденного узла, взяв функцию U₁(x₁, x₂)

вида

(18)

U₁ = -λ²x₁ - 2λx₂ + o(x₁,x₂

Аналогично будем выбирать β₁ и β₂ из однопараметрического семейства ко-

эффициентов: β₁ = ρ² и β₂ = 2ρ, ρ > 0, сведя, таким образом, количество па-

раметров до трех: ω₀, λ и ρ.

Дифференцируя (18) в силу системы (3), получим

∂o

U₁ = -λ² x₁ - 2λ x₂ +∂o

x₁ +

x₂ =

∂x₁

∂x₂

(

)

∂o

= 2λ³x₁ + 3λ²x₂ - λ²

x₁ +

- 2λ

x₂ + o(x₁,x₂).

∂x₂

∂x₁

∂x₂

Так как (по определению функции o(x₁, x₂)) ∂o/∂x_i → 0 при x_i → 0, i = 1, 2,

получаем

U₁ = 2λ³x₁ + 3λ²x₂ + o(x₁,x₂).

Аналогично дифференцируя второй раз в силу системы, находим

Ü₁ = -3λ⁴x₁ - 4λ³x₂ + o(x₁,x₂).

Отсюда правая часть четвертого уравнения принимает в окрестности на-

чала координат вид

Ü₁ + β₁δ₁ + β₂δ₂ ≈ W₁x₁ + W₂x₂ - β₁x₃ - β₂x₄,

где

∂Ü1

∂U₁

∂U˙₁

W₁ =

+β₁

+β₂

= -λ²(β₁ - 2β₂λ + 3λ²),

∂x₁

∂Ü1

∂U₁

∂U˙₁

W₂ =

+β₁

+β₂

= -λ(2β₁ - 3β₂λ + 4λ²).

∂x₂

Введем обозначения

(19)

ξ = ρ/λ, s = (λ/ω₀)².

Оставляя линейные члены в (17) и пренебрегая членами более высокого по-

рядка, после несложных преобразований получим зависящую от двух пара-

метров линеаризованную систему









sλ²c₁(ξ) sλc₂(ξ)

1 + sξ²

2sξ/λ





(20)

= AX, A =



,





−λ⁴c₁(ξ) -λ3c2(ξ)

-λ²ξ²

-2λξ

102

где

(21)

c₁(ξ) = (ξ - 3)(ξ - 1), c₂

(ξ) = 2(ξ - 2)(ξ - 1).

Пусть ν - собственное значение матрицы A. Нормируя его на λ, ν = λν,

получаем характеристический полином линеаризованной системы в виде



-λν



sλ²c₁

sλc₂ - λν

1 + sξ²

2sξ/λ



P (ν) = det(A - νI) =



=

-λν



-λ⁴c₁

-λ³c₂

-λ²ξ²

-2λξ - λν



sλc₂ - λν

1 + sξ²

2sξ/λ



-

-λν



-λ³c₂

-λ²ξ²

-2λξ - λν



sλ²c₁

1 + sξ²

2sξ/λ



=

-λν



-λ⁴c₁

-λ²ξ²

-2λξ - λν

[

]

(22)

=λ⁴

ν⁴ + ν³(2ξ - sc₂(ξ)) + ν²(ξ² - sc₁(ξ)) + νc₂(ξ) + c₁(ξ)

Отметим, что устойчивость характеристического полинома, а следователь-

но, и линеаризованной системы, зависит только от двух параметров s и ξ,

определенных формулой (19), а так как s и ξ не зависят ни от масс маят-

ника и тележки, ни от их отношения, то и область устойчивости не зависит

от массовых характеристик исходной системы. Анализ устойчивости поли-

нома, результат которого сформулирован в следующей теореме, приведен в

Приложении.

Теорема. Линеаризованная система (20) устойчива при любых s и ξ,

принадлежащих области

Ω = {3 < ξ < ∞,0 < s < s_max(ξ)},

где

ξ²(ξ - 2)² + 4(ξ - 1)

(23)

s_max(ξ) =

ξ(ξ - 1)(ξ - 2)(ξ² - 3ξ + 3)

Из теоремы следует, что найдется окрестность нуля в 4-мерном простран-

стве такая, что система (17) (система (11), замкнутая обратной связью (15))

устойчива при любом принадлежащем ей начальном векторе X(0).

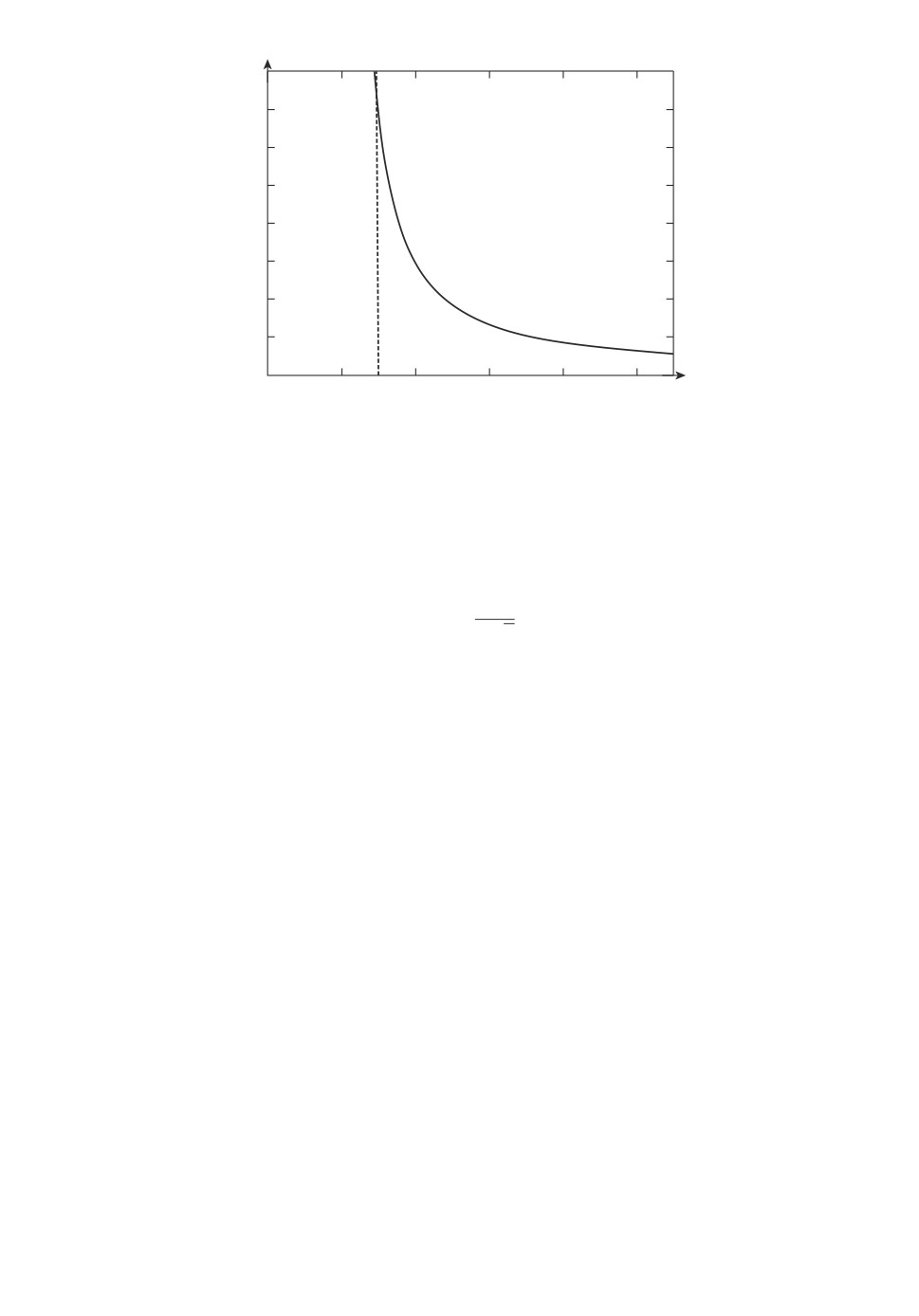
Легко видеть, что s_max(ξ) - монотонно убывающая функция при ξ > 3.

Кривая s_max(ξ) изображена на рис. 2. Здесь Ω - внутренность области,

ограниченной кривой s_max(ξ), горизонтальной осью и вертикальной пря-

мой ξ = 3. Подставляя ξ = 3 в правую часть формулы для s_max(ξ), нахо-

дим верхнюю границу значений s, при которых возможна стабилизация:

max_ξ s_max(ξ) = 25/18. Отсюда получаем ограничение на выбор желаемой экс-

поненциальной скорости убывания отклонения λ:

103

1,4

1,2

1,0

0,8

0,6

0,4

0,2

Рис. 2. Область устойчивости линеаризованной системы в пространстве пара-

метров s и ξ, определенных формулой (19).

Следствие 1. Система (11) может быть локально стабилизирована

с помощью обратной связи (15), если λ принадлежит интервалу 0 < λ <

< λ_max, где

5ω₀

(24)

λ_max =

√ .

Из рис. 2 видно, чем больше значение λ, тем меньше диапазон значений ξ

(а значит, и β₁, β₂), при которых линеаризованная система устойчива.

Следствие 2. Для любых параметров исходной системы (6), (7) и за-

данной скорости λ убывания отклонения из интервала 0 < λ < λ_max суще-

ствует ξ_max(λ) такое, что обратная связь (15) с коэффициентами β₁ = λ²ξ²

и β₂ = 2λξ, где ξ ∈ (3,ξ_max(λ)), локально стабилизирует рассматриваемую

систему.

5. Управление эталонной системой

Для стабилизации эталонной системы предлагается применять обратную

связь в виде вложенных сигмоидов, позволяющую одновременно удовлетво-

рить фазовые ограничения и ограничения на управление (например, [11, 12]):

(25)

U₁(w,w˙) = -k₄σ₂(k₃(w˙ + k₂σ₁(k₁

w))),

где σ₁ и σ₂ - сигмоиды. Напомним, что сигмоидой называется гладкая моно-

тонно возрастающая функция, меняющаяся от -1 до +1. В семейство функ-

ций класса сигмоид входят такие функции, как арктангенс, гиперболический

тангенс, функция ошибок и многие другие подобного вида. Нетрудно прове-

рить, что функция (25) удовлетворяет всем требованиям, сформулированным

в разделе 2 при k₂ = V_max и k₄ = U_max, или в безразмерной записи (см. раз-

дел 3) при k₂ = 1 и k₄ =Ũmax. С помощью двух оставшиеся коэффициентов

104

k₁ и k₃ можно регулировать форму кривой и ее наклон в окрестности нуля,

который, в свою очередь, определяет скорость экспоненциального убывания

отклонения вблизи нуля, а также оптимизировать некоторый критерий каче-

ства управления, как, например, в [12]. Легко проверить, что если положить

k₁ = λ/2, k₃ = 2λ

U_max,

то нулевая точка будет положением равновесия эталонной системы типа вы-

рожденный узел (см. раздел 4.3) с экспоненциальной скоростью убывания

отклонения вблизи нуля λ.

6. Численные примеры

Прежде чем представить результаты численных экспериментов, опишем,

как выбрать параметры закона управления для физической (размерной) си-

стемы. Здесь и далее, чтобы различать размерные и безразмерные парамет-

ры, будем помечать последние тильдой. Для реализации описанного выше

подхода, кроме физических параметров системы и ограничений на скорость

и управление в эталонной системе, требуется выбрать конкретные сигмои-

дальные функции σ₁ и σ₂. В приведенных здесь численных экспериментах,

результаты которых обсуждаются ниже, в качестве обоих сигмоид использо-

валась функция арктангенса:

σ_i = (2/π)arctan(x), i = 1,2.

Заметим, что вид сигмоиды влияет на поведение системы вдали от положения

равновесия, в то время как локальная устойчивость зависит только от коэф-

фициентов k_i в формуле (25). Коэффициенты k₁ и k₃ выбираются так, чтобы

обеспечить желаемую экспоненциальную скорость λ приближения к целевой

точке, которая должна принадлежать интервалу (0, λ_max). Связь размерно-

го λ(λ_max) и безразмерногоλ(λmax) легко определить, рассматривая линеа-

ризацию в окрестности нуля функции U₁(x, x), заданной выражением (25), в

размерной и безразмерной записи. С помощью формул (4), (5), связывающих

размерные и безразмерные переменные и их производные по времени, легко

находим: λ =λV_max/l. Отсюда размерные λ_max и ω₀ связаны тем же соотно-

шением (24), что и безразмерные величины, а значит, чем больше круговая

√

частота маятника ω₀ =

g/l, тем больше максимально возможная экспонен-

циальная скорость приближения к целевой точке λ_max, при которой локаль-

ная стабилизация уже невозможна.

По заданным физическим параметрам исходной (1), (2) и эталонной (3)

систем и заданому λ определяется безразмерный параметр s = (λ/ω₀)², вы-

бирается значение ξ из диапазона (3, ξ_max(λ)) и строится обратная связь по

формуле (15) с коэффициентами β₁ = λ²ξ² и β₂ = 2λξ. Умножая полученное

управление на масштабирующий множитель µV^2max/l, получаем управление в

исходной размерной системе (1), (2). Как установлено в разделе 4.2, замкну-

тая система (17) не зависит от массовых характеристик исходной системы.

105

1,0

0,5

-0,5

-1,0

-1,5

-2,0

-2,5

-3,0

-3,5

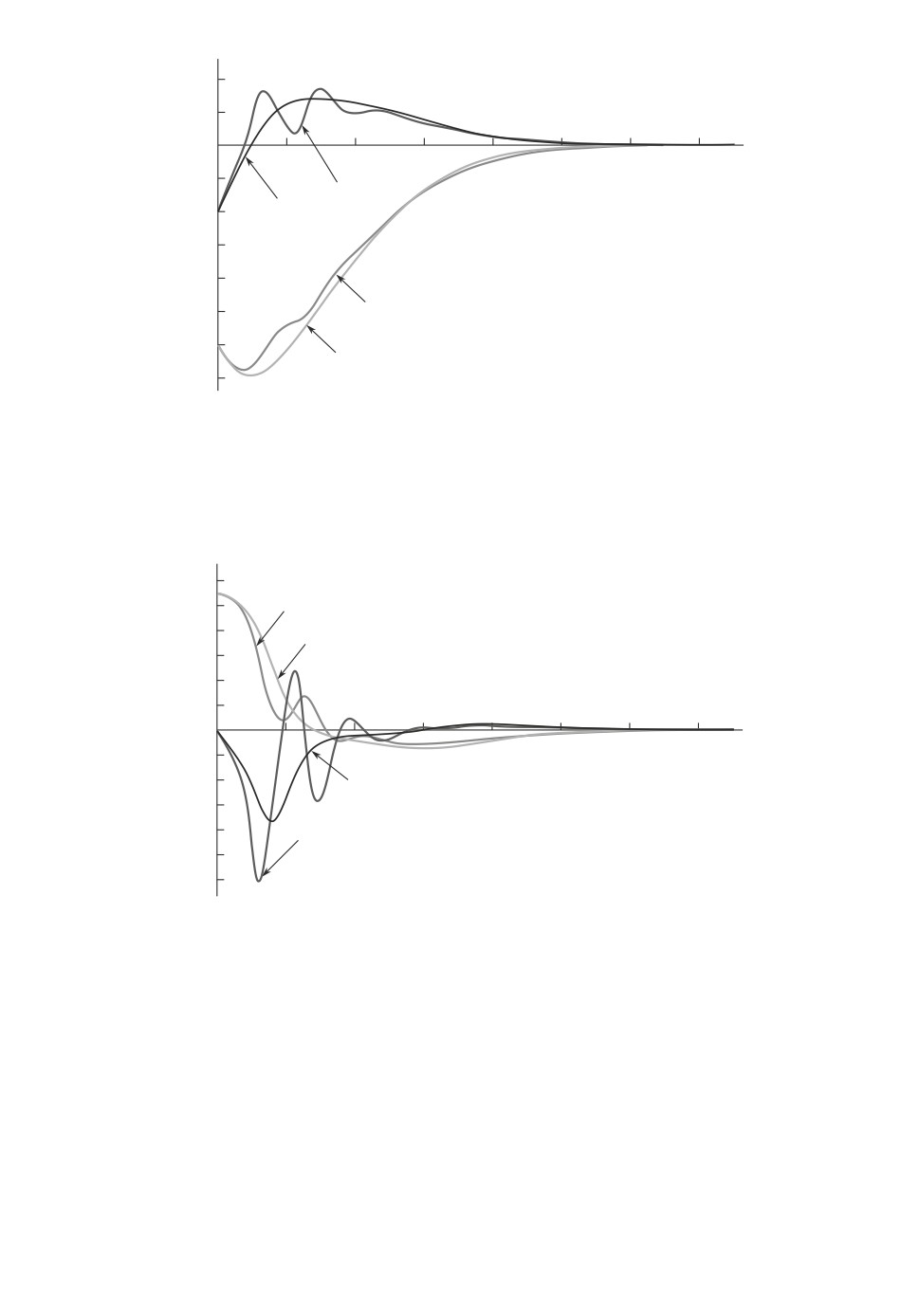
Рис. 3. Стабилизация системы с начальным состоянием x(0) = -3,0,

x(0) = -1,0, φ(0) = 0,5,

φ(0) = 0 при ξ = 4, 0. Зависимость от времени

расстояния до целевой точки (кривые 1 и 3) и скорости тележки

(кривые 2 и 4) для тележки с маятником и возмущенной эталонной

системы соответственно.

1,2

1,0

0,8

0,6

0,4

0,2

-0,2

-0,4

-0,6

-0,8

-1,0

-1,2

Рис. 4. Стабилизация системы с начальным состоянием x(0) = -3,0,

x(0) = -1,0, φ(0) = 0,5,

φ(0) = 0 при ξ = 4,0. Зависимость от времени

переменных x₃ (кривая 1), x₄ (кривая 2) (тележка с маятником) и

w₃ (кривая 3), w₄ (кривая 4) (возмущенная эталонная система).

По этой причине не имеет смысла рассматривать системы с разными отноше-

ниями масс маятника и тележки, так как для таких систем отличаться будут

только графики управлений.

Экспериментально установлено, что область притяжения замкнутой систе-

мы (область начальных значений в четырехмерном пространстве состояний)

зависит от значения ξ ∈ (3, ξ_max(λ)) и сложно устроена. Область притяже-

ния уменьшается при увеличении ξ, стягиваясь в точку, когда ξ → ξ_max(λ).

106

1,8

1,6

1,4

1,2

1,0

0,8

0,6

0,4

0,2

-0,2

-0,4

-0,6

Рис. 5. Стабилизация системы с начальным состоянием x(0) = -3,0,

x(0) = -1,0, φ(0) = 0,5,

φ(0) = 0 при ξ = 4,0. Зависимость от времени

управления U (кривая 1) тележкой с маятником и управления U₁

(кривая 2) возмущенной эталонной системой.

При уменьшении же ξ область притяжения растет, расширяясь предположи-

тельно до всего пространства R⁴ вблизи нижней границы интервала ξ = 3.

Установление зависимости области притяжения от параметра ξ является пер-

востепенной задачей будущих исследований.

Полученный закон управления апробировался в численных экспериментах

для различных параметров и начальных условий. Представленные ниже ре-

зультаты получены для безразмерной системы со следующими параметрами:

m/µ = 1/3, ω²⁰ = 2 иŨmax = 2. Управление U₁ в эталонной системе определено

формулой (25) с коэффициентами k₁ = 0,5π/2, k₂ = 1, k₃ = 4k₁

U_max = π/2

и k₄ = 2. Такие значения коэффициентов соответствуют единичной скоро-

сти экспоненциального убывания отклонения:λ = 1, при этом s = 0,5. Под-

ставляя s = 0,5 вместо s_max в левую часть формулы (23) и решая чис-

ленно получившееся уравнение относительно ξ, находим верхнюю границу

ξ_max(0,5) ≈ 4,315 диапазона устойчивости линеаризованной системы.

Серия численных экспериментов с различными значениями параметра ξ

и различными начальными условиями подтвердила приведенные выкладки:

для любых значений ξ, принадлежащих интервалу (3, 4,315), нашлось мно-

жество начальных значений переменных, при которых стабилизировалась ис-

ходная нелинейная система, в то время как для всех тестируемых значений ξ

за пределами указанного диапазона система не стабилизировалась.

Приведенные в данном разделе графики показывают результаты двух чис-

ленных примеров. В первом примере (рис. 3-5) ξ = 4,0, x(0) = -3,0, x(0) =

= -1,0, φ(0) = 0,5 rad,φ(0) = 0. На рис. 3 показаны графики отклонения от

целевой точки (кривая 1) и скорости (кривая 2) тележки; кривые 3 и 4 по-

казывают для сравнения графики отклонения и скорости эталонной системы

(целевая траектория). На рис. 4 показана зависимость от времени третьей

107

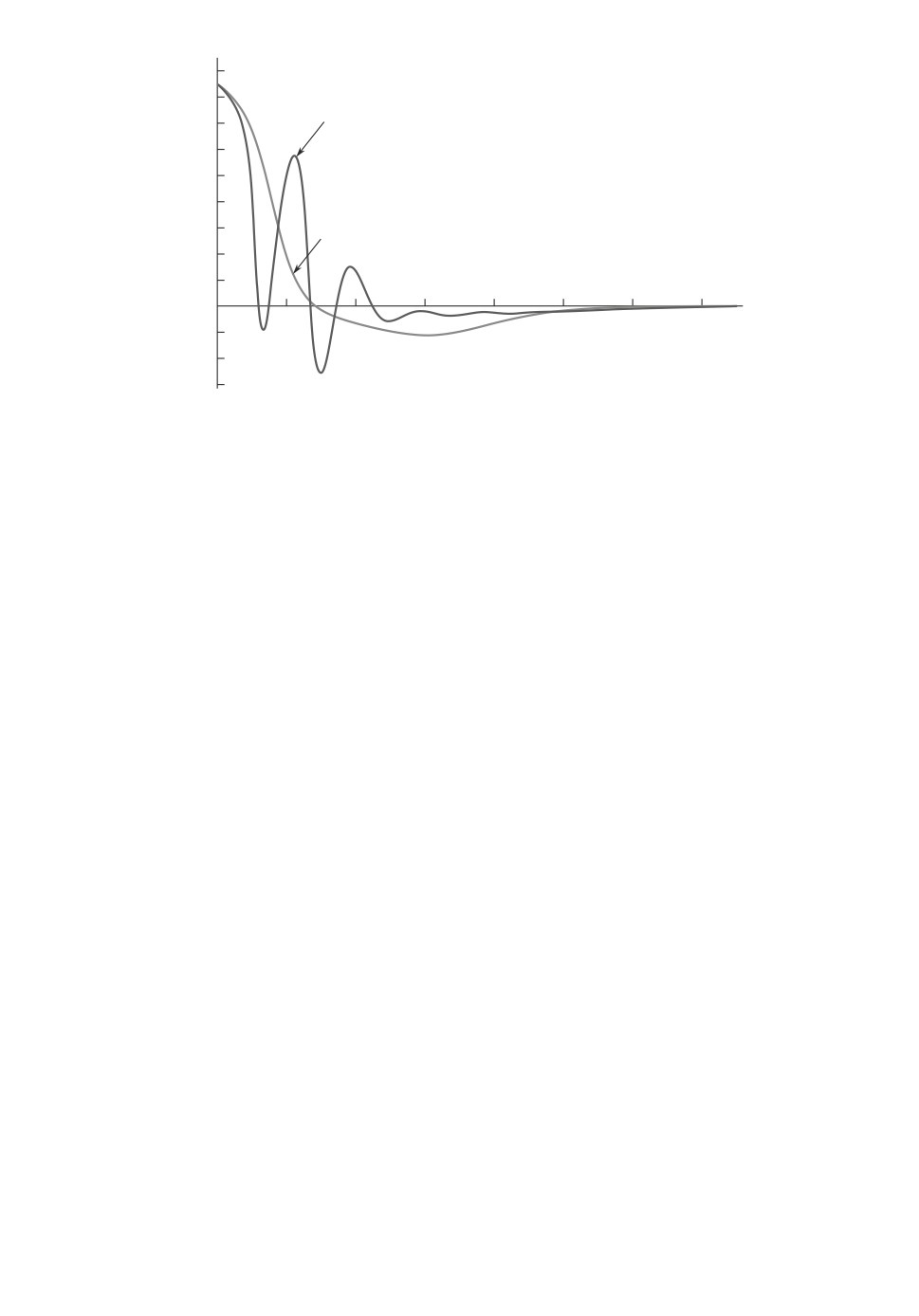
-1

Рис. 6. Стабилизация системы с начальным состоянием x(0) = x(0) = 0,

φ(0) = 1,0,

φ(0) = 0 при ξ = 3,5. Зависимость от времени расстояния до

целевой точки (кривые 1 и 3) и скорости тележки (кривые 2 и 4) для

тележки с маятником и возмущенной эталонной системы соответствен-

но.

-1

-2

-3

-4

-5

-6

Рис. 7. Стабилизация системы с начальным состоянием x(0) = x(0) = 0, φ(0) =

= 1,0,

φ(0) = 0 при ξ = 3,5. Зависимость от времени переменных x₃ (кривая 1),

x₄ (кривая 2) (тележка с маятником) и w₃ (кривая 3), w₄ (кривая 4)) (возму-

щенная эталонная система).

(кривая 1) и четвертой (кривая 2) переменных, x₃ и x₄ = x₃; графики соот-

ветствующих переменных w₃ и w₄ эталонной системы показаны кривыми 3

и 4 соответственно. На рис. 5 показано, как меняются во времени управле-

ния U (кривая 1) в исходной системе и U₁ (кривая 2) в эталонной системе

при следовании по целевой траектории.

108

-2

-4

Рис. 8. Стабилизация системы с начальным состоянием x(0) = x(0) = 0, φ(0) =

= 1,0,

φ(0) = 0 при ξ = 3,5. Зависимость от времени управления U (кривая 1)

тележкой с маятником и управления U₁ (кривая 2) возмущенной эталонной

системой.

Во втором примере тележка изначально находилась в целевой точке с нуле-

вой скоростью (x(0) = x(0) = 0) и отклоненным на большой угол маятником

(φ(0) = 1 rad,φ(0) = 0), ξ = 3,5. На рис. 6-8 показаны те же характеристики,

что и в первом примере. Для компенсации большого начального отклонения

маятника в начальный момент времени потребовалась большая управляю-

щая сила (кривая 1 на рис. 8, которая привела к значительному отклонению

тележки от целевой точки (кривая 1 на рис. 6).

7. Заключение

Рассмотрена задача стабилизации движущейся вдоль прямой тележки с

установленным на ней обратным маятником. Предложен новый закон управ-

ления, основанный на введении эталонной системы второго порядка, траекто-

рия движения которой принимается в качестве целевой для тележки с маят-

ником. Проведен исчерпывающий анализ линеаризованной замкнутой систе-

мы, определена область значений параметров закона управления, гаранти-

рующих локальную стабилизируемость системы, и предложен конструктив-

ный метод их выбора.

Численные эксперименты показали, что для заданной системы и заданной

скорости убывания отклонения λ (т.е. при фиксированном параметре s) об-

ласть притяжения мала для больших значений параметра ξ (вблизи верхней

границы) и увеличивается с его уменьшением. Вблизи верхней границы до-

пустимых значений параметра ξ при достаточно небольших отклонениях от

положения равновесия в системе возникают незатухающие колебания. Вбли-

зи нижней границы ξ = 3 область притяжения настолько велика (возможно

расширяется до всего пространства R⁴), что при любых тестируемых началь-

ных значениях замкнутая система была устойчива.

109

Область притяжения нелинейной системы с устойчивой матрицей линеа-

ризованной системы может быть оценена с помощью квадратичной функции

Ляпунова линеаризованной системы, матрица которой находится решением

известного линейного матричного неравенства. Результаты численных экспе-

риментов, однако, показывают, что область притяжения исследуемой систе-

мы устроена довольно сложно, поэтому любая ее аппроксимация с помощью

эллипсоида в 4-мерном пространстве, на взгляд авторов, будет крайне консер-

вативной. Менее консервативные оценки можно надеяться получить только с

помощью неэллипсоидальных областей. Получение такого рода оценок явля-

ется достаточно сложной задачей, над решением которой авторы в настоящее

время работают. Предполагается, в частности, попробовать применить для

этой цели некоторые из известных из литературы численных методов (см.,

например, [13-15]).

ПРИЛОЖЕНИЕ

Доказательство теоремы. Для нахождения области устойчиво-

сти характеристического полинома (22) можно воспользоваться критериями

Рауса-Гурвица или Льенара-Шипара [16]. Согласно второму критерию, для

того чтобы полином был устойчивым, необходимо и достаточно, чтобы были

положительными все коэффициенты полинома и нечетные главные миноры

матрицы Гурвица. Найдем область в пространстве параметров ξ и s, в кото-

рой эти условия выполнены.

Коэффициент при старшем члене ν⁴ всегда положителен: a₄ = 1. Осталь-

ные коэффициенты с учетом (21) имеют вид

a₀ = λ⁴(ξ - 3)(ξ - 1), a₁ = 2λ⁴(ξ - 2)(ξ - 1),

a₂ = λ⁴[ξ² - (ξ - 3)(ξ - 1)s], a₃ = 2λ⁴[ξ - (ξ - 2)(ξ - 1)s].

Свободный член a₀ и коэффициент a₁ оба положительны, когда 0 < ξ < 1 или

ξ > 3. Коэффициенты a₂ и a₃ положительны в этих интервалах при условии

(Π.1)

s < s₃(ξ) =

(ξ - 2)(ξ - 1)

Минор первого порядка Δ₁ = a₁ > 0. Подставляя коэффициенты харак-

теристического полинома в формулу для Δ₃ = a₁(a₂a₃ - a₁) - a₀a²³, после

несложных преобразований получим

[(

)

(

)

]

Δ₃ = 4λ⁶(ξ - 1)

ξ⁴ - 4ξ³ + 8ξ² - 8ξ + 4

-ξ

ξ⁴ - 6ξ³ + 14ξ² - 15ξ + 6

{[

]

}

= 4λ⁶(ξ - 1)

ξ²(ξ - 2)² + 4(ξ - 1)²

- ξ(ξ - 1)(ξ - 2)(ξ² - 3ξ + 3)s

Введем обозначение

ξ²(ξ - 2)² + 4(ξ - 1)

(Π.2)

s_max(ξ) =

ξ(ξ - 1)(ξ - 2)(ξ² - 3ξ + 3)

110

и найдем разность правых частей (Π.2) и (Π.1):

Δ_s = s_max(ξ) - s₃(ξ) =

ξ²(ξ - 2)² + 4(ξ - 1)² - ξ²(ξ² - 3ξ + 3)

ξ(ξ - 1)(ξ - 2)(ξ² - 3ξ + 3)

2-ξ

ξ(ξ² - 3ξ + 3)

В интервале 0 < ξ < 1 имеем Δ₃ > 0 только тогда, когда s > s_max. Так как

s_max > s₃ в этом интервале, неравенства s > s_max и (Π.1) несовместны. Таким

образом, в интервале 0 < ξ < 1 характеристический полином неустойчив.

В интервале ξ > 3 при s < s_max имеем Δ₃ > 0. Так как в этом интервале

s_max < s₃, справедливо неравенство (Π.1). Таким образом, все условия кри-

терия Льенара-Шипара выполнены. Теорема доказана.

СПИСОК ЛИТЕРАТУРЫ

Неймарк Ю.И. Математическое моделирование как наука и искусство. Нижний

Новгород: Изд-во Нижегород. ун-та, 2010.

Martynenko Y.G., Formal’skii A.M. Controlled pendulum on a movable base //

Mechanics of Solids. 2013. Т. 48. № 1. С. 6-18.

Формальский А.М. Управление движением неустойчивых объектов. М.: Физ-

матлит, 2014.

Getz N.H., Hedrick J.K. An Internal Equilibrium Manifold Method of Tracking for

Nonlinear Nonminimum Phase Systems // ACC Proc. 1995. P. 1-5.

Srinivasan B., Huguenin P., Bonvin D. Global stabilization of an inverted pendu-

lum - Control strategy and experimental verification // Automatica. 2009. V. 45.

P. 265-269.

Lee J., Mukherjee R., Khalil H.K. Output feedback stabilization of inverted pendu-

lum on a cart in the presence of uncertainties // Automatica. 2015. V. 54. No. 4.

P. 146-157.

Teel A.R. A nonlinear small gain theorem for the analysis of control systems with

saturation // Trans. Autom. Contr. IEEE, 1996. V. 41. No. 9. P. 1256-1270.

Gordillo F., Aracil J. A new controller for the inverted pendulum on a cart // Int.

J. Robust Nonlinear Control. 2008. No. 18. P. 1607-1621.

Magni L., Scattolini R., Aström K.J. Global stabilization of the inverted pendulum

using model predictive control // IFAC Proc. V. 35. Iss. 1. 2002. P. 141-146.

10.

Utkin V., Guldner J., Shi J. Sliding mode control in electromechanical systems. 2nd

ed. CRC Press, 2009.

11.

Matrosov I.V., Morozov Yu.V., Pesterev A.V. Control of the robot-wheel with a pen-

dulum // Proc. of the 15th International Conference on Stability and Oscillations of

Nonlinear Control Systems (Pyatnitskiy’s Conference) (STAB), IEEE. 2020. P. 1-4.

12.

Pesterev A.V., Morozov Yu.V., Matrosov I.V. On Optimal Selection of Coefficients

of a Controller in the Point Stabilization Problem for a Robot-wheel// Commun.

Comput. Inform. Sci. (CCIS). 2020. V. 1340. P. 236-249.

111