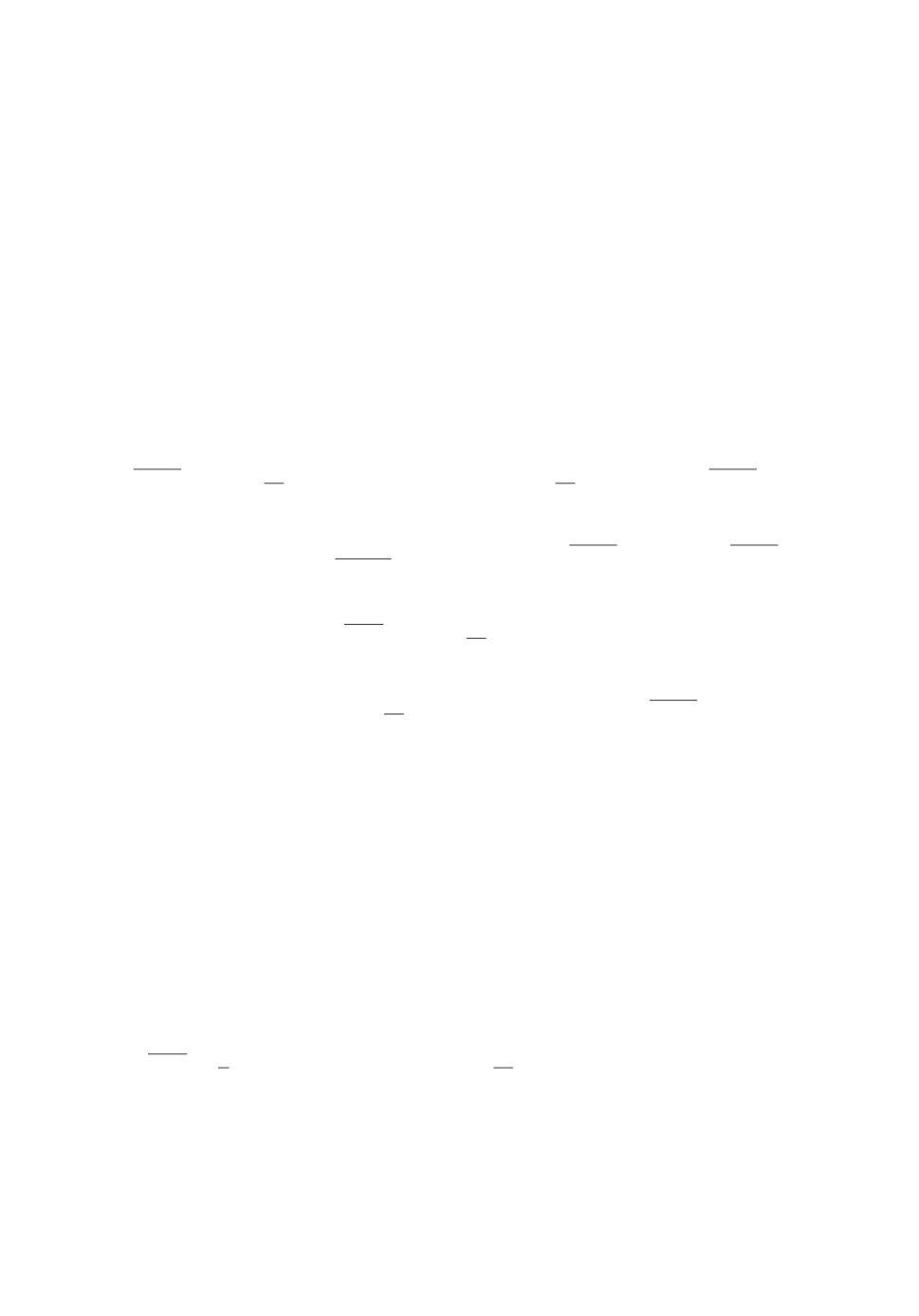Автоматика и телемеханика, № 1, 2022

Стохастические системы

И.А. БЛАТОВ, д-р физ.-мат. наук (blatow@mail.ru)

(Поволжский государственный университет телекоммуникаций

и информатики, Самара),

Е.В. КИТАЕВА, канд. физ.-мат. наук (el_kitaeva@mail.ru)

(Самарский национальный исследовательский университет

им. акад. С.П. Королева)

ОБ ОЦЕНКАХ СРЕДНЕЙ ДЛИНЫ ОЧЕРЕДИ

ДЛЯ ОДНОКАНАЛЬНЫХ СИСТЕМ МАССОВОГО ОБСЛУЖИВАНИЯ

ЧЕРЕЗ СТАТИСТИЧЕСКИЕ БЕЗУСЛОВНЫЕ МОМЕНТЫ

ВТОРОГО ПОРЯДКА МОДИФИЦИРОВАННОГО ВХОДНОГО ПОТОКА

Рассматривается математическая модель простейшей одноканальной

системы массового обслуживания (СМО) с детерминированным временем

обслуживания в случае входящего потока с произвольной корреляцией.

Для данной СМО получены различные обобщения формулы Хинчина-

Полячека средней длины очереди. Предложена интервальная модель вхо-

дящего потока, в рамках которой получено выражение средней длины

очереди через статистические безусловные моменты второго порядка. Все

результаты были получены при весьма общих предположениях эргодич-

ности и стационарности. Приводятся результаты численных эксперимен-

тов, подтверждающие теоретические выводы.

Ключевые слова: система массового обслуживания, коррелированный

входной поток, средняя длина очереди, формула Хинчина-Полячека.

DOI: 10.31857/S000523102201007X

1. Введение

В мультисервисных сетях с пакетной коммутацией поток пакетов суще-

ственно отличается от пуассоновского, поскольку такие потоки формируются

множеством источников запросов на предоставление услуг, существенно от-

личающихся между собой. Это приводит к тому, что для потоков в мульти-

сервисных сетях характерна неравномерность поступления заявок и пакетов.

Пакеты группируются в “пачки” в одних промежутках времени и практи-

чески отсутствуют в других промежутках. Случайный процесс поступления

заявок (пакетов) в систему характеризуется законом распределения, устанав-

ливающим связь между значениями случайной величины и вероятностями

появления указанных значений. В большинстве случаев такой поток характе-

ризуется функцией распределения временных интервалов между соседними

заявками, а процесс их обработки характеризуется функцией распределения

113

вероятностей интервалов времени обслуживания. В подавляющем числе пуб-

ликаций по теории массового обслуживания указанные случайные величины

считаются некоррелированными и взаимно независимыми. Однако указан-

ные допущения для анализа пакетного трафика мультисервисных сетей со-

вершенно недопустимы. В ряде публикаций [1-9], а также в публикациях ав-

торов этой статьи [10-13] предпринимались попытки учета корреляционных

свойств потоков, образующих очереди. Имеется много публикаций, посвящен-

ных различным частным случаям СМО при наличии корреляции входных

данных (см. обзор [14]).

В задачах управления СМО важной характеристикой является средняя

длина очереди. Обобщения формулы Хинчина-Полячека средней длины оче-

реди для некоторых конкретных СМО рассматривались в [15, 16]. Однако

авторам неизвестны работы, в которых разрабатываются общие подходы ана-

лиза СМО при наличии произвольных коррелированных входных потоков.

Одним из перспективных, на взгляд авторов, направлений изучения пакет-

ного трафика является разрабатываемый нами Интервальный метод [17, 18],

позволяющий заменить анализ интервалов времени между соседними заявка-

ми и интервалов времени обработки заявок, анализом одной случайной вели-

чины числом заявок, поступающих в течение последовательных интерва-

лов времени обработки каждой из заявок. Авторами показано, что дисперсия

и корреляционные свойства указанной случайной величины, при заданной за-

грузке, полностью характеризуют размер очереди в системах массового об-

служивания [18].

В настоящей статье для одноканальной системы с коррелированным вхо-

дящим потоком и постоянным временем обработки заявок при весьма общих

предположениях стационарности и эргодичности получены формулы средней

длины очереди, обобщающие формулу Хинчина-Полячека. При этом приме-

нение модели, основанной на интервальном методе, позволило получить фор-

мулу, выражающую оценку средней длины очереди через безусловные выбо-

рочные ковариации входящего потока. Результаты численных экспериментов

подтверждают теоретические выводы.

2. Постановка задачи

Введем терминологию и обозначения. Анализируются стационарные по-

токи заявок (пакетов). Весь промежуток времени анализа разбивается на

равные интервалы τ_i одинаковой длины τ. Считается, что интервал време-

ни обработки каждой из заявок постоянный и равен τ. Число заявок на

i-м интервале обозначаем через m_i(τ). Пусть ρ = λτ коэффициент загруз-

ки, где λ - средняя интенсивность заявок. Предполагается, что ρ ∈ (0, 1).

Величины m(τ) = λτ = ρ и D_m(τ) = [m_i(τ) - m(τ)]² - математическое ожи-

дание и дисперсия чисел заявок, поступающих в течение интервала вре-

мени τ соответственно. Через q_i(τ) обозначим количество заявок, стоя-

щих в очереди в конце i-го интервала обработки (длину очереди). Че-

рез µqi-1m_i (τ) = K[qi-1(τ), mi(τ)] обозначим ковариацию случайных величин

114

q_i-1(τ) и m_i(τ). Для предположений, которые будем делать по ходу статьи,

будем использовать обозначения A1, A2, . . .

Для любой одноприборной СМО справедливо рекуррентное соотноше-

ние, устанавливающее связь между поступающими и обработанными заяв-

ками [19],

(1)

q_i(τ) = q_i-1(τ) + m_i(τ) - δ_i

(τ),

где

{

0, если q_i-1(τ) = m_i(τ) = 0,

δ_i(τ) =

1 в противном случае.

В случае пуассоновского потока заявок с постоянным временем обслу-

живания для средней длины очереди (математического ожидания) известна

формула Хинчина-Полячека [19], которая имеет вид

(2)

q(τ) =

2(1 - ρ)

В [20] получено обобщение формулы (2) на случай произвольных корре-

лированных потоков:

D_m(τ) + 2µqi-1m_i (τ)

(3)

q(τ) =

2(1 - ρ)

В частном случае пуассоновского потока µqi-1m_i (τ) = 0, Dm(τ) = ρ и форму-

ла (3) принимает вид (2). Доказательство формулы (3) приводится в разде-

ле 4. Из доказательства следует, что формула (3) справедлива для любых

стационарных в широком смысле потоков с конечным математическим ожи-

данием и дисперсией, для которых процесс q_i(τ) обладает такими же свой-

ствами, т.е. и для МАР-потока, управляемого эргодической марковской це-

пью.

Задача настоящей статьи получение формул, в которых средняя длина

очереди выражается через корреляционные свойства входящего потока m_i(τ)

при весьма общих предположениях.

3. Предположения и определения

В [12] формула (3) была преобразована к более удобному для применения

виду. Приведем некоторые понятия из [12], поскольку они необходимы для

решения задач данной статьи.

Введем понятие цикла обслуживания. Циклом обслуживания Z_k =

⋃j_k+N_k-1

I_j будем называть совокупность смежных интервалов обработ-

j=j_k

ки I_j, на которых q_j > 0 везде, кроме последнего интервала, на котором оче-

редь обнуляется после обработки последней заявки, а слева от данного цикла

115

тоже находится хотя бы один такой интервал. Здесь N_k обозначает количе-

ство смежных интервалов длину k-го цикла.

Замечание 1. Понятие цикла обслуживания отличается от введенного

Л. Клейнроком [21] понятия периода занятости, поскольку период занято-

сти предполагает наличие слева и справа как минимум одного интервала, на

котором m_i(τ) = δ_i(τ) = 0. Поэтому период занятости Клейнрока может со-

держать несколько циклов Z_k. Целесообразность введения данного понятия

обоснована в [12].

Сделаем следующее п р е д п о л о ж е н и е.

А1. Гипотеза эргодичности и взаимной стационарности. Предположим,

что все рассматриваемые процессы обладают свойствами эргодичности,

стационарности и взаимной стационарности в широком смысле. В част-

ности, для любой реализации случайного процесса m_i(τ) существуют соот-

ветствующие пределы и

∑

∑(

)₂

m(τ) = lim

m_i(τ), D_m(τ) = lim

m_i(τ) - m(τ)

N→∞ N

i=1

∑

(

)(

)

(4)

µmi-jm_i (τ) = lim

m_k-j(τ) - m(τ) m_k(τ) - m(τ)

N→∞ N - j

k=j+1

∑

q(τ) = lim

q_i(τ),

N→∞ N

i=1

∑

[

]

(5)

µqi-1m_i (τ) = lim

q_i-k-1(τ) m_i-k(τ) - m(τ)

N→∞

k=1

4. Основные результаты

Формулы для средней длины очереди, полученные в [12], были записаны

для конкретной фиксированной реализации случайного процесса m_i(τ). Од-

нако представляет интерес преобразование формулы (3) к выражению, зави-

сящему от корреляционных свойств входящего потока m_i. Получим соответ-

ствующие результаты. Пусть m_i(τ) произвольная реализация случайного

процесса {m_i}.

Теорема 1. Справедлива формула

∑

(6)

q(τ) =

(D_m(τ) - ρ(1 - ρ)) + lim

m_i(τ)

(m_j

(τ) - 1).

N→∞

Zs⊂[1,N]

j=js

Эта и последующие теоремы будут доказаны в разделе 5.

Второе слагаемое в (6) при естественных дополнительных предположени-

ях есть весовая сумма условных выборочных ковариаций (см. далее) элемен-

тов входящего потока. Покажем это.

116

Пусть A_k(τ) = {δ_s = 1, s = i - k, i - k + 1, . . . , i} - случайное событие, со-

стоящее в том, что случайно выбранная пара (m_i-k(τ), m_i(τ)), k + 1 ≤ i ≤ N,

принадлежит одному циклу обработки Z_s ⊂ [1, N]. Пусть N_k(N) - число та-

ких пар. Обозначим через

∑

µ(k, N) =

m_i(τ)

(m_i-k(τ) - 1),

N_k(N)

i∈Zs⊂[1,N]

k:i-k∈Zs

(7)

N_k(N)

P (A_k(τ)) =

N-k

условную выборочную ковариацию случайных величин (m_i-k(τ), m_i(τ)) при

условии A_k(τ) и выборочную вероятность события A_k(τ) соответственно.

Теорема 2. Справедлива формула

∑

N-k

(8)

q(τ) =

(D_m(τ) - ρ(1 - ρ)) + lim

µ(k, N)P (A_k

(τ)).

N→∞

k=1

Теорема 2 непосредственно вытекает из (6), (7). Теорема 2 доказана.

Формулы (8) содержат условные корреляции и вероятности P (A_k(τ)), вы-

числение которых затруднительно. Получим формулу, содержащую только

безусловные моменты второго порядка нового случайного процесса, тесно

связанного с исходным.

Произведем замену переменной интервалов τ_i, на которых рассматривает-

ся поступление заявок, на другую переменную θ_i, которая представляет со-

бой интервал между двумя соседними заявками, покидающими очередь. Чис-

ло заявок, поступивших на указанных интервалах, обозначим через m_i(θ).

Это и есть новый случайный процесс, который рассмотрим.

Замечание 2. Каждая реализация случайного процесса m_i(θ) совпада-

ет с соответствующей реализацией исходного случайного процесса m_i(τ), из

которой удалены все участки покоя, на которых m_i(τ) = δ_i(τ) = 0, т.е. остают-

ся только примыкающие друг к другу циклы обслуживания. Таким образом,

между реализациями потоков m_i(θ) и m_i(τ) существует взаимно однозначное

соответствие.

Определение 1. Процесс m_i(θ) будем называть интервальным пред-

ставлением процесса m_i(τ).

A2. Гипотеза A1 для процесса m_i(θ). Предположим, что для нового слу-

чайного процесса также справедлива гипотеза A1.

Пусть N рассматриваемое число членов m₁(τ), . . . , m_N (τ) реализации

процесса m_i(τ), а M = M(N) число членов соответствующей реализации

процесса m_i(θ), полученных из m₁(τ), . . . , m_N (τ) удалением нулевых членов,

принадлежащих участкам покоя.

Пусть

∑

(9)

ν_m(k,θ,M) =

m_i(θ)(m_i-k

(θ) - 1)

M-k

i=k+1

117

безусловная выборочная ковариация числа заявок нового случайного про-

цесса.

Теорема 3. Пусть справедливы предположения А1-А2. Тогда имеет

место формула

∑

M -k

(10)

q(τ) =

(D_m(τ) - ρ(1 - ρ)) + ρ lim

ν_m

(k, θ, M).

M→∞

k=1

В формуле (10) присутствует дисперсия исходного случайного процес-

са m_i(τ). Обозначим через D_m(θ) дисперсию процесса m_i(θ).

Теорема 4. Пусть справедливы предположения А1-А2. Тогда имеет

место формула

(

)

M-1

M -k

(11)

q(τ) =

D_m(θ) + 2 lim

ν_m(k, θ, M)

M→∞

k=1

Формула (11) выражает среднюю длину очереди через безусловные мо-

менты второго порядка случайного процесса m_i(θ).

Замечание 3. Если предположить, что теоретические ковариации

(12)

ν_m(k,θ) = lim

ν_m

(k, θ, M)

M→∞

∑_∞

достаточно быстро убывают так, что ряд

ν_m(k,θ) сходится, а сходи-

k=1

мость в (12) достаточно быстрая, т.е. выполнены условия перестановки пре-

дельных переходов в (11), то формула (11) принимает вид

(

)

∑

(13)

q(τ) =

D_m(θ) + 2 ν_m(k,θ)

k=1

Однако формула (13) для рассматриваемых нами потоков оказывается

непригодной, в отличие от формулы (11), которая всегда верна при выполне-

нии условий стационарности и эргодичности. Это связано с медленным убы-

ванием выборочных ковариаций в (11) и медленной сходимостью в (12).

5. Доказательства теорем

Доказательство формулы (3). Возведем в квадрат уравнение ба-

ланса (1). Учитывая, что δ²ⁱ(τ) = δ_i(τ), q_i-1(τ)δ_i(τ) = q_i-1(τ), (τ)m_i(τ)δ_i(τ) =

= m_i, получим

(q_i(τ))² = (q_i-1(τ))² + (m_i(τ))² + δ_i(τ) +

+ 2q_i-1(τ)m_i(τ) - 2q_i-1(τ) - 2m_i(τ).

118

Вычислим математическое ожидание от обеих частей последнего равен-

ства. Учитывая, что m_i(τ) = δ_i(τ) = ρ, а в силу стационарности (q_i(τ))² =

= (q_i-1(τ))², получим

0 = (m_i(τ))² + ρ + 2q_i-1(τ)m_i(τ) - 2q_i-1(τ) - 2ρ,

или же

q(τ) =

((m_i(τ))² - ρ) + q_i-1(τ)m_i(τ),

или же

(14)

q(τ) =

(D_m(τ) - ρ(1 - ρ)) + q_i-1(τ)m_i

(τ).

Подставляя в (14) q_i-1(τ)m_i(τ) = µqi-1m_i (τ) + m(τ) · q(τ) = µq_i-1m_i (τ) + ρq(τ)

и выражая q(τ), получаем (3).

Доказательство теоремы 1. Из (14) следует, что для доказатель-

ства (6) достаточно установить равенство

∑

(15)

q_i-1(τ)m_i(τ) = lim

m_i(τ)

(m_j

(τ) - 1).

N→∞

Zs⊂[1,N]

j=js

Докажем (15). Отметим важное свойство цикла обслуживания.

Лемма 1. Для любого цикла обслуживания

∑

(m_j (τ) - δ_j ) =

(m_j (τ) - 1) = 0.

j=j_k

Доказательство леммы 1 вытекает из того, что окончание цикла

обслуживания означает обработку всех заявок, которые поступили на всех

интервалах, входящих в данный цикл обслуживания.

Последовательно применяя равенство (1) к значениям очереди в правой

части (1), находим, что

∑

q_i-1(τ) = q_i-(N+1)(τ) +

(m_i-j (τ) - δ_i-j(τ)).

j=1

Отсюда имеем (здесь и далее с точностью до бесконечно малой при N → ∞)

∑

q_i-1(τ)m_i(τ) =

i=1





∑

(16)

m_i(τ)

(m_i-j (τ) - δ_i-j (τ)) + q_i-(N+1)(τ) .

i=1

j=1

119

В силу леммы 1 отсюда имеем

q_i-1(τ)m_i(τ) =





∑

m_i(τ)

(m_j (τ) - 1) + q_i-(N+1)(τ) +

i=1

j∈Z_l∩[i-N,i-1]:Z_l∩{i-N}=∅





∑

m_i(τ)

(m_j(τ) - 1) .

i=1

j∈Z_l∩[i-N,i-1]:Z_l∩{i-1}=∅

Но в силу леммы 1 первая сумма в последнем равенстве равна нулю, так как

∑

(m_j(τ) - 1) =

j∈Z_l∩[i-N,i-1]:Z_l∩{i-N}=∅

∑

(m_j (τ) - 1) = -q_i-(N+1)(τ).

j∈Z_l\[i-N,i-1]:Z_l∩{i-N}=∅

Поэтому имеем





∑

q_i-1(τ)m_i(τ) =

m_i(τ)

(m_j (τ) - 1) =

i=1

j∈Z_l∩[i-N,i-1]:Z_l∩{i-1}=∅

∑

= lim

m_i(τ)

(m_j(τ) - 1).

N→∞

Zs⊂[1,N]

j=js

Тем самым формула (15), а значит, и формула (6) доказаны. Теорема 1 до-

казана.

Доказательство теоремы 3. Сначала установим вспомогательное

утверждение.

Лемма 2. Для процесса m_i(θ) справедлива формула

(17)

m_i

(θ) = 1,

M (N)

(18)

lim

= ρ.

N→∞ N

Доказательство леммы 2. Вычисляя математическое ожидание от

обеих частей формулы (1), в силу стационарности находим, что

(19)

δ(τ) = m(τ) = ρ.

Поскольку m_i(θ) получается из m_i(τ) удалением участков покоя, на которых

m_i(τ) = δ_i(τ) = 0, то для соответствующего процесса δ_i(θ) будем иметь

(20)

δ(θ) = m(θ).

120

Но на участках обработки δ_i(θ) = 1, откуда

(21)

δ(θ) = 1.

Из (20), (21) следует (17). Формула (18) следует из (19), (21) и того, что

∑_N

∑_M

δ_i(τ) =

δ_i(θ).

i=1

Лемма 2 доказана.

Преобразуем сумму безусловных ковариаций (9) из (10).

Имеем

∑

ν_m(k,θ,M) =

m_i(θ)(m_i-k(θ) - 1),

M -k

i=k+1

∑

M-k

ν_m(k,θ,M) =

m_i(θ)(m_i-k(θ) - 1) =

k=1

k=1 i=k+1

∑

(22)

m_i(θ) (m_i-k

(θ) - 1).

i=1

k=1

Из (22), определения процесса m_i(θ), циклов обработки и замечания 2 сле-

дует, что

∑

(23)

m_i(θ) (m_i-k(θ) - 1) =

m_i(τ)

(m_j

(τ) - 1),

i=1

k=1

Zs⊂[1,N]

j=js

поскольку эти суммы состоят из одних и тех же слагаемых.

Далее заметим, что в силу леммы 2 и (23)

∑

lim

m_i(θ) (m_i-k(θ) - 1) =

M→∞

i=1

k=1

(24)

∑

lim

m_i(τ)

(m_j (τ) - 1).

N→∞

Zs⊂[1,N]

j=js

Из (6), (22) и (24) получаем (10). Теорема 3 доказана.

Доказательство теоремы 4. Очевидно, что D_m(θ) = D_δ=1(τ). По-

этому в силу (10), (11) достаточно доказать формулу

(25)

D_m(τ) = D_δ=1

(τ)ρ + ρ(1 - ρ).

Для краткости будем опускать аргумент τ. Имеем в силу леммы 2

M (D_δ(m)) = D_δ=0(m)P (δ = 0) + D_δ=1(m)P (δ = 1) =

= D_δ=1(m)P(δ = 1) = D_δ=1(m)ρ,D(M_δ(m)) = (M_δ=0(m) - ρ)²P(δ = 0) +

+ (M_δ=1(m) - ρ)²P (δ = 1) = (0 - ρ)²(1 - ρ) + (1 - ρ)²ρ = ρ(1 - ρ).

Отсюда, используя известную формулу D_m = D(m) = M(D_δ(m)) + D(M_δ(m)),

получаем (25). Теорема 4 доказана.

121

6. Результаты численных экспериментов

6.1. Анализируемые потоки

Справедливость полученных результатов иллюстрируется результатами

численных экспериментов на основе формулы (11) для реализации видео-

трафика на фоне пуассоновского потока [19] той же интенсивности. Кро-

ме того, приводим результаты аналогичных расчетов для одной из моде-

лей заявок, управляемых цепью Маркова (МАР-поток). МАР-поток обра-

зовывался последовательным во времени переключением двух пуассонов-

ских потоков заявок с параметрами интенсивности λ₁ = 1000 и λ₂ = 10. При

этом в соответствии с определением МАР-потока в обозначениях [22] пере-

ходные вероятности, определяющие МАР-поток, задавались следующим об-

разом: P (λ_i → λ_i, 1) = 0,9 при i = 1, 2; P (λ_i → λ_j, 1) = 0,1; P (λ_i → λ_j , 0) = 0

при i = j. Всего для МАР-потока и пуассоновского потока было сгенерирова-

но по 100 тысяч временных отсчетов, а поток телетрафика содержал 16 910 от-

счетов. Отсчетом называем момент времени, в который в систему поступает

заявка.

Все результаты были также проверены и подтверждены с помощью фор-

мулы (3) на основе оценок входящего в нее корреляционного члена согласно

гипотезе A1, а также с помощью сравнения с оценками среднего значения оче-

реди, вычисленных их непосредственным усреднением (см. подраздел 6.2).

Результаты приведены в табличной и графической формах. Приведем гра-

фические иллюстрации. Численные результаты в виде таблиц приводятся в

подразделе 6.2. В табл. 1, 3, 4 приведены данные для потоков, полученных

имитационным моделированием, а в табл. 2 - результаты реального видео-

трафика. Файл моментов прихода пакетов видеотрафика, анализируемого

на рисунках и в табл. 2, получен экспериментально с помощью открытой

программной системы WireSark на реальной сети. Все результаты анализа,

приведенные на рисунках, получены с экранов разработанной авторами про-

граммной системы АМС, подробное описание которой дано в [18]. Файл мо-

ментов прихода пакетов МАР-потока заявок, показанный на рис. 5, был сге-

нерирован специально разработанной программой, а затем проанализирован

с помощью системы АМС и с помощью отдельной программы имитационного

моделирования. Результаты моделирования представлены в табл. 2.

Поскольку численные результаты получены для конечных значений N, то

в данном подразделе речь идет об оценках соответствующих характеристик.

Сохраним за ними прежние обозначения предельных значений, обозначая

через D_m(ρ), q(ρ) оценки дисперсии и средней длины очереди соответственно.

В мультисервисных сетях связи (МСС) с пакетной коммутацией поток па-

кетов существенно отличается от пуассоновского и носит явно выраженный

пачечный характер.

На рис. 1 представлена реализация видеотрафика (узкие пачки) на фоне

пуассоновского потока одинаковой интенсивности (серый фон). На рис. 2

показан фрагмент указанной реализации в увеличенном масштабе времени.

Каждая тонкая вертикальная полоска соответствует числу пакетов, посту-

122

mt(

36,84

33,56

30,29

27,01

23,74

20,46

17,19

13,92

10,64

,37

4,09

0,82

12 285 24 57

36 855 49 140 61 242 7

3 109 85 894 98 27

-2,48

t, c

Рис. 1. Поток видеотрафика и пуассоновский поток.

mt(

11317

11606 12254 12623 12991 13360 137

14097

14465

t, c

Рис. 2. Поток видеотрафика и пуассоновский поток в увеличенном масштабе

времени.

пающих в течение интервала времени обработки одного пакета. Из графиков

следует, что для видеопотока имеются интервалы, в течение которых посту-

пают десятки пакетов, в то время как пуассоновский поток содержит на ука-

занных интервалах один или два пакета. Это и объясняет наличие больших

очередей при передаче потоков видеотрафика.

На рис. 3 представлены зависимости оценок среднего размера очереди при

различных значениях коэффициента загрузки ρ (верхний график видео-

трафик, нижний график пуассоновский поток). Из рис. 3 видно, что при

одинаковых значениях коэффициента загрузки ρ оценка среднего размера

очереди у пуассоновского потока во много раз меньше, чем у потока видео-

трафика.

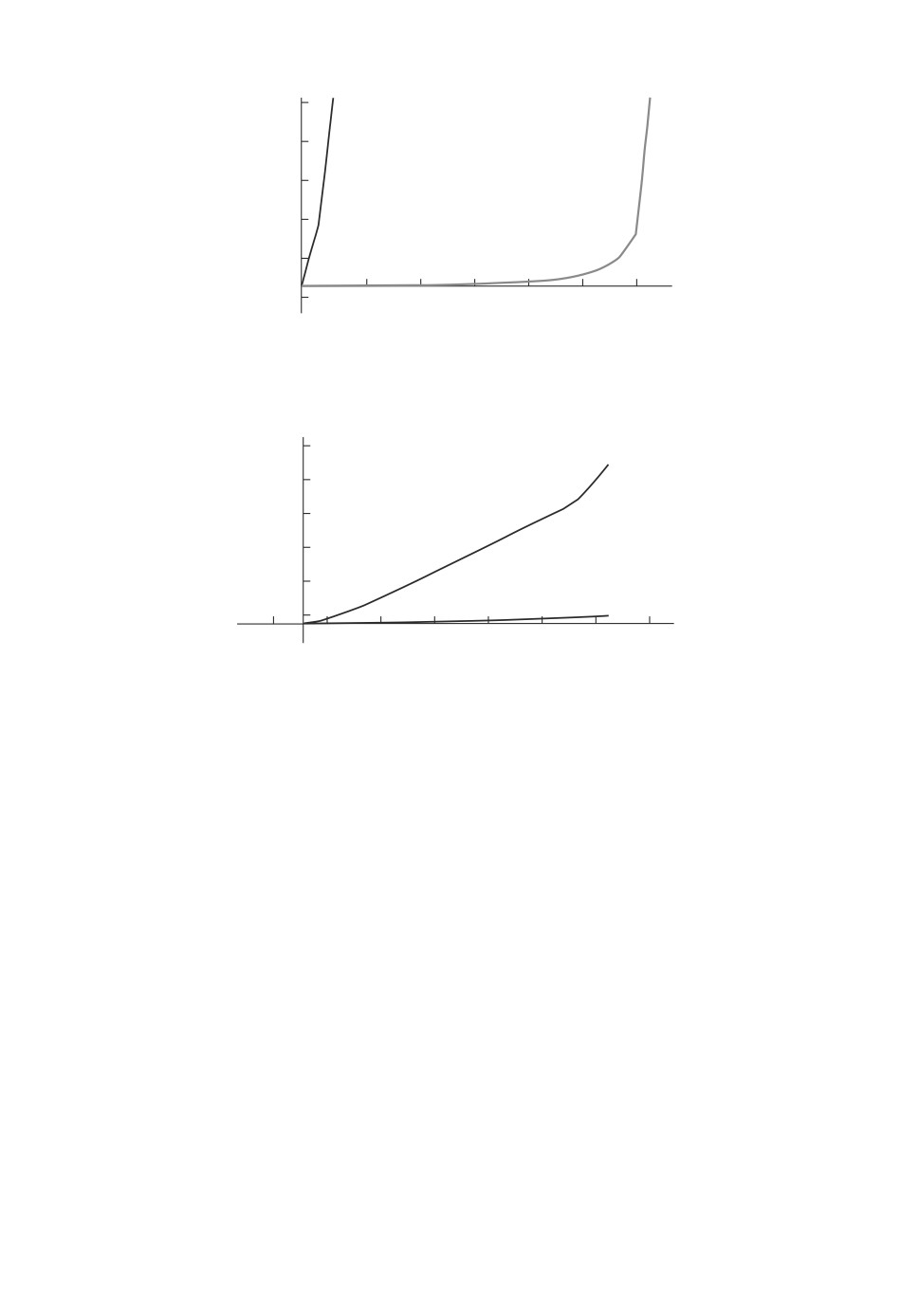
На рис. 4 для рассматриваемого видеотрафика показаны зависимости оце-

нок дисперсии (нижняя кривая) и оценок среднего размера очереди (верх-

123

---

q(r)

,536

21,800

16,063

10,326

4,589

-1,147

0,153

0,306

0,460

0,613

0,766

0,919 r

Рис. 3. Зависимости оценок среднего размера очереди при различных значе-

ниях коэффициента загрузки ρ.

Dm(

770,876

627,457

484,038

340,619

197,201

53,781

-0,129

0,047

0,222

0,398

0,573

0,749

0,924

1,100 r

Рис. 4. Зависимости оценок дисперсии и среднего размера очереди видеотра-

фика, при различных значениях коэффициента загрузки ρ.

няя кривая), при различных значениях коэффициента загрузки (ρ), полу-

ченные в результате имитационного моделирования. Значение оценки дис-

персии D_m(τ)(0, 5) = 10,6 в то время, когда оценка размера очереди превы-

шает 250 пакетов. Корреляционная составляющая в десятки раз превышает

значение дисперсии, и не учитывать ее нельзя.

Разница впечатляет, поскольку при постоянном времени обработки и коэф-

фициенте загрузки, равном 0,5, оценка среднего значения очереди для пуас-

соновского потока составляет лишь 0,25 пакета. Для пачечного потока ви-

деотрафика составляющая, обусловленная оценкой дисперсии D_m(τ)(ρ), ока-

зывается существенно меньше, чем составляющая, обусловленная наличием

корреляционных связей.

Наконец, приведем результаты расчетов для МАР-потока.

На рис. 5 показан поток, представляющий число заявок, поступающих в

течение каждого из интервалов времени τ = 2,72 · 10^-2, которые соответству-

ют коэффициенту загрузки ρ = λτ = 0,5.

Поток носит пачечный характер, и интервалы, в течение которых посту-

пает более 20 заявок, чередуются с интервалами, содержащими не более двух

заявок.

124

mt(

41,525

34,110

26,695

19,280

11,864

4,449

-113,269

-26,139

60,991

148,121

235,251 322,382 409,512 496,642

t, c

Рис. 5. Поток заявок, поступающих в течение интервалов времени, соответ-

ствующих коэффициенту загрузки ρ = 0,5.

---

q(r), Dm

(

14,173

10,933

,694

4,454

1,215

-0,103

0,037

0,178

0,318

0,459

0,599

0,740

0,880 r

Рис. 6. Зависимости оценок дисперсии и среднего размера очереди для рас-

сматриваемого потока при различных значениях коэффициента загрузки ρ.

Несмотря на высокую пачечность, в отличие от видеотрафика, представ-

ленного на рис. 3, здесь оценки среднего значения длины очереди имеют

небольшие размеры q(0, 5) = 5,21 заявок при коэффициенте загрузки (ρ), рав-

ном 0,5. На рис. 6 для рассматриваемого потока показаны зависимости оценок

среднего размера очереди (верхний график) и дисперсии (нижний график),

при различных значениях коэффициента загрузки (ρ). Из рис. 6 видно, что

в отличие от видеотрафика (рис. 4), при малых загрузках оценка размера

очереди близка к значению оценок дисперсии, а влияние корреляционной со-

ставляющей соизмеримо с влиянием дисперсии.

6.2. Численные результаты

В разделах статьи 1-5 ρ предполагалось фиксированным. Здесь иссле-

дуется зависимость величин от ρ. Поэтому далее используем обозначения,

которые связаны с предыдущими следующим образом: D_m(τ) = D_m(τ)(ρ),

D_m(θ) = D_m(θ)(ρ), q(τ) = q_cov(ρ) - значение средней длины очереди, вычис-

∑_M-1M-k

ляемое по формуле (11). Через cov_m(θ)(ρ) = 2

ν_m(k,θ,M) обозначе-

k=1

125

Таблица 1. Пуассоновский поток

0,1

0,2

0,3

0,5

0,7

0,9

D_m(θ)(ρ)

9,71 · 10^-2

1,98 · 10^-1

2,98 · 10^-1

4,96 · 10^-1

7,00 · 10^-1

9,00 · 10^-1

cov_m(θ)(ρ)

5,42 · 10^-3

2,39 · 10^-2

6,27 · 10^-2

2,47 · 10^-1

8,28 · 10^-1

3,94

q_cov(ρ)

5,40 · 10^-3

2,46 · 10^-2

6,37 · 10^-2

2,48 · 10^-1

8,25 · 10^-1

3,96

q_exact(ρ)

5,40 · 10^-3

2,46 · 10^-2

6,37 · 10^-2

2,48 · 10^-1

8,25 · 10^-1

3,96

D_m(τ)(ρ)

9,97 · 10^-2

1,99 · 10^-1

2,99 · 10^-1

4,98 · 10^-1

7,00 · 10^-1

8,99 · 10^-1

Таблица 2. Поток видеотрафика

0,1

0,2

0,3

0,5

0,7

0,9

D_m(θ)(ρ)

6,57

1,04 · 10¹

1,40 · 10¹

2,08 · 10¹

2,76 · 10¹

3,49 · 10¹

cov_m(θ)(ρ)

7,16 · 10²

8,72 · 10²

9,46 · 10²

1,01 · 10³

1,06 · 10³

3,04 · 10³

q_cov(ρ)

3,62 · 10¹

8,81 · 10¹

1,44 · 10²

2,58 · 10²

3,82 · 10²

1,38 · 10³

q_exact(ρ)

3,62 · 10¹

8,81 · 10¹

1,44 · 10²

2,58 · 10²

3,82 · 10²

1,38 · 10³

D_m(τ)(ρ)

0,75

2,24

4,42 · 10¹

1,07 · 10¹

1,95 · 10¹

3,15 · 10¹

Таблица 3. МАР поток

0,1

0,2

0,3

0,5

0,7

0,9

D_m(θ)(ρ)

2,19

3,81

5,07

6,77

7,87

8,67

cov_m(θ)(ρ)

3,1

3,98

4,61

7,03

1,33 · 10¹

4,99 · 10¹

q_cov(ρ)

4,68 · 10^-1

1,19 · 10^-1

2,17

5,30

1,22 · 10¹

4,84 · 10¹

q_exact(ρ)

4,68 · 10^-1

1,19 · 10^-1

2,17

5,30

1,22 · 10¹

4,84 · 10¹

D_m(τ)(ρ)

3,08 · 10^-1

9,23 · 10^-1

1,73

3,53

5,71

7,88

Таблица 4. Зависимость оценки среднего значения очереди

от размера выборки для МАР-потока

N\ρ

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

10000

0,55

1,40

2,49

3,89

5,83

8,51

12,2

19,6

34,0

20000

0,51

1,33

2,41

3,79

5,74

8,62

13,0

20,9

40,7

30000

0,5

1,28

2,35

3,70

5,65

8,44

12,6

20,7

41,6

40000

0,50

1,29

2,34

3,70

5,66

8,50

12,9

21,1

45,8

50000

0,49

1,26

2,29

3,62

5,52

8,26

12,6

20,5

45,8

60000

0,48

1,25

2,26

3,57

5,43

8,08

12,2

20,2

49,2

70000

0,48

1,22

2,22

3,51

5,38

8,08

12,3

20,5

48,3

80000

0,47

1,21

2,20

3,50

5,35

8,06

12,3

29,4

48,0

90000

0,47

1,20

2,19

3,48

5,32

8,01

12,3

20,4

48,5

100000

0,47

1,19

2,17

3,45

5,30

7,99

12,2

20,3

48,4

126

на оценка корреляционной составляющей длины очереди в (11). Кроме того,

∑_N

q_exact(ρ) =¹

q_i(τ), где q_i(τ) последовательно вычисляются по форму-

N i=1

лам (1). Графические результаты полностью согласуются с численными и

были получены на их основе.

Отметим, что в табл. 1 для интервального представления m_i(θ) пуассо-

новского потока m_i(τ) присутствует корреляционная составляющая, которая

может быть не меньше дисперсионной. Это связано с тем, что пуассоновский

поток при переходе от m_i(τ) к m_i(θ) подвергается изменениям (за счет удале-

ния многих нулевых элементов) и, возможно, становится коррелированным,

а также с тем, что выборочные ковариации медленно сходятся к теоретиче-

ским (см. замечание 3). Из табл. 2 видно, что корреляционная составляющая

сильно преобладает над дисперсионной и определяет длину очереди. В случае

МАР-потока (табл. 3) видно, что корреляционная составляющая преобладает,

но не так сильно, как для потока видеотрафика.

Наконец, в табл. 4 представлена зависимость оценки среднего размера оче-

реди МАР-потока от объема выборки. Видно, что при больших значениях N

оценка среднего значения очереди стабилизируется с точностью до десятых

и сотых, что согласуется с теоремами 1-4.

7. Заключение

Таким образом, можно сделать следующие выводы.

1. В статье для однолинейной системы массового обслуживания с ожи-

данием, неограниченным бункером, детерминированным обслуживанием и

коррелированным входящим потоком получена формула (11), выражающая

среднюю длину очереди через безусловные статистические моменты первого

и второго порядков потока, тесно связанного с исходным потоком.

2. Теоретическое значение формулы (11) состоит в том, что для одно-

канальных систем с детерминированным временем обслуживания впервые

получена точная зависимость средней длины очереди от корреляционных

свойств входящего потока в предположениях только стационарности в ши-

роком смысле и эргодичности этого потока.

3. Непосредственное практическое применение формулы (11) для вычис-

ления средней длины очереди нецелесообразно, так как оно более затратно,

чем непосредственное наблюдение очереди по выборке. Однако формулы (11)

и (12) стимулируют изучение интервальных представлений m_i(θ) входящих

потоков, их моделирование и аппроксимацию потоками, для которых авто-

корреляционная функция может быть точно или приближенно определена

параметрами, задающими поток. Это, например, гауссовы потоки. Решение

этих задач требует дополнительных исследований.

4. Результаты имитационного моделирования подтверждают справедли-

вость полученного авторами обобщения (11) формулы Хинчина-Поллачека

для СМО со стационарными коррелированными потоками.

5. Реальные потоки пакетов видеотрафика в телекоммуникационных се-

тях имеют высокую степень корреляции, которая и обусловливает наличие

127

большого размера очереди. Влияние корреляционной составляющей на раз-

мер очереди в десятки раз превосходит влияние дисперсии числа заявок на

интервалах обслуживания. Анализ примера потока пакетов реального ви-

деотрафика показал, что определяющее влияние на размер очереди в нем

оказывает корреляционная составляющая потока.

6. Анализ примера одного из потоков, образуемых с помощью случайно-

го независимого переключения двух пуассоновских потоков с различными

параметрами интенсивности, показал, что, несмотря на высокую пачечность

результирующего потока, его дисперсия и корреляционные свойства оказы-

вают сопоставимое влияние на средний размер очереди. Следовательно, в

первом случае причиной возникновения большой очереди является большая

корреляционная составляющая, в то время как во втором случае причинами

возникновения очереди являются дисперсия и корреляционная составляющая

в сопоставимых пропорциях.

СПИСОК ЛИТЕРАТУРЫ

Leland W.E., Taqqu Murad S., Willinger W., Wilson D.V. On the Self-Similar Na-

ture of Ethernet Traffic // J. IEEE/ACM Transact. Networking, 1994. V. 2. No. 1.

P. 1-15.

Neuts M.F. Versatile Markovian Point Process // J. Appl. Probab., 1979. V. 16.

No. 4. P. 764-779.

Ramaswami V. The N/G/1 Queue and Its Detailed Analysis // Advances Appl.

Probab. 1980. V. 12. No. 1. P. 222-261.

Jagerman D.L., Balcioglu B., Altiok T., Melamed B. Mean Waiting Time Approxi-

mations in the G/G/1 Queue // Queueing Systems. 2004. V. 46. P. 481-506.

Balcioglu B., Jagerman D.L., Altiok T. Approximate Mean Waiting Time in a

GI/D/1 Queue with Autocorrelated Time to Failures // IEEE Transactions. 2007.

V. 39. No. 10. P. 985-996.

Карташевский И.В., Сапрыкин А.В. Обработка коррелированного трафика в

узле сети типа G/G/1 // Радиотехника. 2017. № 10. С. 119-125.

Карташевский И.В. Модель трафика для программно-конфигурируемых се-

тей // Радиотехника. 2016. № 6. С. 124-129.

Цыбаков Б.С. Модель телетрафика на основе самоподобного случайного процес-

са // Радиотехника. 1999. № 5. C. 24-31.

Шелухин О.И., Тенякшев А.М., Осин А.В. Фрактальные процессы в телеком-

муникациях / Под ред. О.И. Шелухина. Радиотехника, 2003.

10.

Лихтциндер Б.Я. Корреляционные связи в пачечных потоках систем массового

обслуживания // Телекоммуникации. Наука и технологии. 2015. № 9. С. 8-12.

11.

Лихтциндер Б.Я. Корреляционные свойства длин очередей в системах массо-

вого обслуживания с потоками общего вида // Инфокоммуникационные техно-

логии. 2015. Т. 13. № 3. С. 276-280.

12.

Блатов И.А., Лихтциндер Б.Я. Об оценке длин очередей в СМО с произволь-

ной корреляцией // Сб. тр. Информационные технологии и нанотехнологии

(ИТНТ-2018). Самара: Самарский национальный исследовательский универси-

тет им. акад. С.П. Королева, 2018. С. 1607-1616.

128

13.

Лихтциндер Б.Я. О некоторых обобщениях формулы Хинчина-Полячека //

Инфокоммуникационные технологии. 2007. Т. 5. № 4. С. 253-258.

14.

Вишневский В.М., Дудин А.Н. Системы массового обслуживания с коррелиро-

ванными входными потоками и их применение для моделирования телекомму-

никационных сетей // АиT. 2017. № 8. С. 3-59.

Vishnevskii V.M., Dudin A.N. Queueing Systems with Correlated Arrival Flows and

Their Applications to Modeling Telecommunication Networks // Autom. Remote

Control. 2017. V. 78. No. 8. P. 1361-1403.

15.

Шульга Ю.Н. Обобщение формулы Полячека-Хинчина для объемных стохасти-

ческих сетей // АиT. 1989. № 3. С. 84-98.

Shul’ga Yu.N. Extension of the Polaczek - Khinchin Formula to 3d Stochastic Net-

works // Autom. Remote Control. 1989. V. 50. No. 3. P. 355-365.

16.

Jain G., Sigman K. A Pollaczeek-Khinchine Formula for M/G/1 Queues with Dis-

asters // J. Appl. Prob. 1996. V. 33. P. 1191-1200.

17.

Лихтциндер Б.Я. Интервальный метод анализа мультисервисного трафика се-

тей доступа // Электросвязь. 2015. № 12. С. 52-54.

18.

Лихтциндер Б.Я. Трафик мультисервисных сетей доступа (интервальный ана-

лиз и проектирование). М.: Горячая линия - Телеком, 2018.

19.

Вентцель Е.С. Исследование операций. Задачи, принципы, методология. М.:

Наука, 1988.

20.

Лихтциндер Б.Я. Интервальный метод анализа трафика мультисервисных се-

тей доступа. Самара ПГУТИ, 2015.

21.

Клейнрок Л. Теория массового обслуживания. М.: Машиностроение, 1979.

22.

Горцев А.М., Нежельская Л.А. О связи МС-потоков и МАР-потоков событий //

Вестн. ТГУ. Управление, вычислительная техника и информатика. 2010. Т. 13.

№ 4. С. 50-60.

Статья представлена к публикации членом редколлегии В.М. Вишневским.

Поступила в редакцию 15.09.2019

После доработки 25.08.2021

Принята к публикации 29.08.2021

129