Автоматика и телемеханика, № 1, 2022

Управление в технических системах

(kamil_aydazade@rambler.ru)

(Институт систем управления НАН Азербайджана, Баку;

Институт математики и механики НАН Азербайджана, Баку),

В.М. АБДУЛЛАЕВ, д-р физ.-мат. наук (vaqif_ab@rambler.ru)

(Азербайджанский государственный университет нефти и промышленности, Баку;

Институт систем управления НАН Азербайджана, Баку)

УПРАВЛЕНИЕ ПРОЦЕССОМ НАГРЕВА СТЕРЖНЯ С

ИСПОЛЬЗОВАНИЕМ ТЕКУЩЕЙ И ПРЕДЫДУЩЕЙ ПО ВРЕМЕНИ

ОБРАТНОЙ СВЯЗИ

На примере процесса нагрева стержня в печи исследуется задача син-

теза управления объектами с распределенными параметрами с обратной

связью. Для формирования значений управляющих воздействий предла-

гается использовать их линейную зависимость от значений состояния в

точках замера как в текущий, так и в предыдущий моменты времени.

Неизвестные коэффициенты, участвующие в этой зависимости управле-

ния от замеренных значений состояния, являются параметрами обратной

связи. Они определяются минимизацией целевого функционала с исполь-

зованием численных методов оптимизации первого порядка. Для этого

получены формулы градиента целевого функционала по параметрам об-

ратной связи. Приводятся результаты численных экспериментов.

Ключевые слова: система с распределенными параметрами, процесс на-

грева, обратная связь, коэффициент усиления, точка контроля, градиент

функционала, параметры обратной связи.

DOI: 10.31857/S0005231022010081

1. Введение

В работе на примере задачи управления нагревом стержня в печи с об-

ратной связью предлагается подход к синтезу управляющих воздействий, ис-

пользующий результаты замера состояния процесса в заданных точках кон-

троля не только в текущий момент времени t, но и в момент t - τ , где τ -

некоторый заданный параметр. Предложена формула линейной зависимо-

сти текущего значения управляющего воздействия от замеренных значений

в точках замера, включающая неизвестные постоянные параметры обратной

связи. В результате задача синтеза управления редуцируется в задачу па-

раметрического оптимального управления распределенной системой с запаз-

дывающим аргументом по определению оптимальных значений параметров

130

обратной связи, участвующих в формулах зависимости значений управлений

от замеренных значений состояний в точках контроля.

Отметим, что в отличие от задач синтеза управления объектами с сосредо-

точенными параметрами, описываемых системами обыкновенных дифферен-

циальных уравнений [1-4], эти задачи для объектов с распределенными пара-

метрами исследованы существенно меньше. Это было связано, во-первых, со

сложностью как исследования самих краевых задач для систем дифференци-

альных уравнений с частными производными, так и численного их решения.

Во-вторых, имелись сложности технического и технологического характера,

связанные с оперативностью, точностью проводимых замеров и обработки

их результатов, в-третьих, отсутствие достаточно эффективных математиче-

ских методов и мощных вычислительных средств для своевременного приня-

тия решения по определению текущих значений управляющих воздействий.

В 60-70-е годы прошлого века в связи с развитием вычислительных

средств и математического аппарата эти работы существенно активизиро-

вались как в теоретическом направлении, так и для практических приложен-

ный. Здесь следует отметить работы [5-11], которыми были предложены раз-

личные подходы к построению систем управления с обратной связью. В ра-

ботах [5, 12, 13] описаны системы управления реальными технологическими

процессами, техническими объектами с распределенными параметрами.

Предлагаемый в данной работе подход, развивающий работы [10, 11] на

случай использования текущих и предыдущих во времени результатов за-

меров, может быть использован для объектов, у которых нет возможности

оперативного замера значений всего вектора состояния или точность замеров

не достаточно высока. Например, при нагреве стержня замер температуры

в его отдельных точках не позволяет судить о текущей динамике (скорости)

процесса нагрева, а измерительная техника, позволяющая это сделать, пока

отсутствует или недостаточно точна.

2. Постановка задачи

Рассматривается задача регулирования температуры стержня длиной l в

печи, состояние которого описывается начально-краевой задачей:

(2.1)

u_t(x,t) = a²u_xx(x,t) + µ₁ [ϑ(t) - u(x,t)] , (x,t) ∈ Ω = (0,l) × (t₀

,T],

(2.2)

u(x, t) = u⁰(x, t; ϕ), ϕ = const, ϕ ∈ Φ ⊂ R^m, x ∈ [0, l], t ≤ t₀,

(2.3)

u_x(0,t) = -µ₂ [ϑ(t) - u(0,t)] , t ≥ t₀,

(2.4)

u_x(l,t) = µ₂ [ϑ(t) - u(l,t)] , t ≥ t₀.

Здесь u(x, t) - температура стержня в точке x ∈ [0, l] в момент времени t;

T - длительность процесса управления; u⁰(x,t;ϕ) - параметрически задан-

ная непрерывная функция, определяющая температуру стержня при t ≤ 0.

Точное значение m-мерного скалярного вектора параметров ϕ не задано, но

известно, что его значения принадлежат заданному компактному множеству

131

Φ ⊂ R^m с заданной функцией плотности ρ_Φ(ϕ) такой, что

∫

ρ_Φ(ϕ) ≥ 0, ϕ ∈ Φ,

ρ_Φ(ϕ)dϕ = 1.

Заданные коэффициенты µ₁, µ₂ характеризуют процесс теплопередачи меж-

ду печью и стержнем. Поддержание температуры самой печи осуществляется

управляемым внешним источником тепла, создающего в печи температуру,

определяемую кусочно-непрерывной функцией ϑ(t), удовлетворяющей техно-

логическому ограничению:

{

}

(2.5)

ϑ(t) ∈ V =

ϑ:ϑ≤ϑ

t ∈ [t₀

,T],

значения ϑ, ϑ заданы.

Рассматриваемая задача управления процессом (2.1)-(2.4) заключается в

определении допустимой управляющей функции ϑ(t), приводящей состояние

стержня к заданному состоянию, определяемой непрерывной функцией U(x)

при условии, что в момент времени t₀ на стержне имеются точки x ∈ [0, l],

состояние u(x, t₀) в которых по каким-либо причинам вышло из требуемого

по технологическим соображениям диапазона температуры на стержне:

(2.6)

u ≤ u(x,t₀

) ≤ u.

Предельные значения температуры стержня u, u считаются заданными и

определяются из технологических требований.

Управление ϑ(t) должно доставлять минимум некоторому заданному

функционалу, например следующему:

∫

J_T (ϑ) =

µ(x) [u(x, t; ϑ, ϕ) - U(x)]² dxdtdϕ +

Φ T-ΔT 0

(2.7)

∫T

+α

[ϑ(t) - V_α(t)]² dt.

t₀

Здесь функция u(x, t; ϑ, ϕ) является решением начально-краевой задачи

(2.1)-(2.3) при заданных допустимых управлении ϑ(t) ∈ V , t ∈ [t₀, T ] и на-

чальном условии u⁰(x, 0; ϕ), ϕ ∈ Φ; µ(x) ≥ 0 - заданная весовая функция;

[T - ΔT, T ] заданный отрезок времени, в течение которого оценивается сте-

пень устойчивости достижения заданного желаемого распределения темпе-

ратуры на стержне; параметры α, V_α(t) введены для регуляризации целевого

функционала задачи.

Функционал (1.7) определяет качество управления множеством (пучком)

функций u(x, t; ϑ, ϕ), являющихся решением дифференциального уравнения

(1.1) и удовлетворяющих краевым условиям (2.3), (2.4), с начальными усло-

виями u⁰(x, t₀; ϕ) при значениях параметра ϕ из заданного множества Φ.

132

Как видно из целевого функционала (2.7), в задаче требуется не только

достичь желаемого распределения температуры U(x) на стержне в заданный

момент времени T - ΔT , но и поддерживать его в течение заданного отрез-

ка времени [T - ΔT, T ]. Такое свойство качества управления требуется, как

правило, в системах оптимального (финитного) регулирования [5].

Пусть в N_c точках ξ_j стержня непрерывно во времени производятся заме-

ры температуры, u_i(t) = u(ξ_i, t), i = 1, . . . , L, используемые для формирова-

ния текущего значения управления ϑ(t).

В качестве зависимости управления ϑ(t) от замеренных значений исполь-

зуем следующую формулу:

∑

(2.8)

ϑ(t) =

[k_1i (u(ξ_i, t) - U(ξ_i)) + k_2i (u(ξ_i, t - τ) - U(ξ_i))] , t ∈ [t₀

,T].

i=1

Здесь постоянные k_1i, k_2i, i = 1, . . . , L, являются оптимизируемыми пара-

метрами обратной связи, определяющими текущие значения управления в

процесса нагрева.

Как видно из (2.8), в формировании управляющего воздействия участву-

ют не только текущие значения температуры в точках замера, но и значе-

ния температуры в этих точках в предыдущий момент времени, а именно

при t - τ. Значение τ задано, и оно назначается в зависимости от точности

проведения замеров и динамики (скорости) протекания процесса: для быст-

ро протекающих процессов τ необходимо назначать малым, а для медленно

протекающих процессов τ выбирается таким, чтобы за промежуток времени

(t - τ, t) изменение состояния процесса существенно превышало как точность

проводимых замеров, так и решения краевой задачи (1.1)-(2.4). Из практи-

ческих соображений предполагается выполнение условия τ < ΔT .

Оптимизируемые параметры k_1i, k_2i, i = 1, . . . , L, как и в задачах синтеза

управления в системах c сосредоточенными параметрами, будем называть

коэффициентами усиления.

Введя обозначение для заданной функции U(x) U_i = U(ξ_i), зависимость

(2.8) запишем так:

∑

(2.9)

ϑ(t; K) =

(k_1i (u(ξ_i,t) - U_i) + k_2i (u(ξ_i,t - τ) - U_i)), t ∈ [t₀

,T],

i=1

и будем еe использовать в дальнейшем.

Здесь использовано обозначение для оптимизируемых параметров обрат-

ной связи K = (k₁, k₂) ∈ R^2L, k₁ = (k₁₁, k₁₂, . . . , k_1L), k₂ = (k₂₁, k₂₂, . . . , k_2L).

Управление с обратной связью ϑ(t), определенное формулой (2.9), в силу

свойства решения дифференциальных уравнений с запаздывающим по вре-

мени аргументом, является не только непрерывным при всех t ∈ [t₀, t₀ + τ],

но, более того, его гладкость улучшается во времени [13].

Рассмотрим также случай, когда имеется возможность осуществлять за-

меры температуры только в заданные дискретные моменты времени t_j+1 =

133

= t₀ + jΔt, j = 0,1,... ,N_t - 1, t₀ = t₀, Δt = (T - t₀)/N_t. Значение Δt опре-

деляется технологическими особенностями как самого процесса нагрева, так

и возможностями проведения замеров.

Для управления ϑ(t) в этом случае используем следующую, аналогичную

(1.8), зависимость от замеренных в дискретные моменты времени значений

состояния:

∑

ϑ(t; K) =

(k_1i (u(ξ_i, t_j) - U_i) + k_2i (u(ξ_i, t_j - τ) - U_i)) ,

(2.10)

i=1

t ∈ [t_j,t_j + Δt), j = 0,1,...,N_t - 1.

Значение запаздывания τ должно выбираться, естественно, кратным зна-

чению Δt, т.е. τ = σΔt, σ = 1, 2, . . . , и удовлетворять тем же требованиям,

что и при непрерывной обратной связи.

Управление ϑ(t), определяемое зависимостью (2.10) при дискретной об-

ратной связи, непрерывно на интервалах (t_j, t_j+1), а в моменты времени t_j

проведения замеров состояния процесса может претерпевать конечные скач-

ки. Состояние самого процесса нагрева в эти моменты времени изменяется

непрерывно.

Для случая непрерывной обратной связи подставим зависимость (1.9) в

дифференциальное уравнение (2.1) и в краевые условия (2.3), (2.4), получим

уравнение

u_t(x,t) = a²u_xx(x,t) +

∑

(2.11)

+µ₁

[k_1i (u(ξ_i, t) - U_i) + k_2i (u(ξ_i, t - τ) - U_i)] -

i=1

- µ₁u(x,t), (x,t) ∈ Ω,

и краевые условия

u_x(0,t) = µ₂u(0,t) -

(2.12)

∑

-µ₂

[k_1i (u(ξ_i, t) - U_i) + k_2i (u(ξ_i, t - τ) - U_i)] , t ≥ t₀,

i=1

u_x(l,t) = -µ₂u(l,t) +

(2.13)

∑

+µ₂

[k_1i (u(ξ_i, t) - U_i) + k_2i (u(ξ_i, t - τ) - U_i)] , t ≥ t₀.

i=1

Дифференциальное уравнение (2.11) характеризуется следующими осо-

бенностями: во-первых, оно является уравнением с запаздывающим аргумен-

том по времени в фазовой переменной [14]; во-вторых, оно является точечно

нагруженным по временной переменной [15-18]. В-третьих, краевые условия

(2.12), (2.13) имеют запаздывание во времени и являются нелокальными, так

134

как в них участвуют значения искомой функции в промежуточных точках.

Такие условия называют также неразделенными [11, 19]. Работы, в которых

рассматривались начально-краевые задачи одновременно с такими особенно-

стями, авторам не встречались. Использование имеющихся результатов, от-

дельных для каждой из особенностей (метод шагов во времени для систем с

запаздыванием [15] и метод сдвига для нелокальных нагруженных уравнений

[17, 18]), не представляет каких-либо проблем для исследования и численного

решения полученной начально-краевой задачи (2.11)-(2.13). Схема решения

этих задач будет изложена в разделе 4 при описании результатов компьютер-

ных экспериментов на примере иллюстративной задачи.

В случае дискретной во времени обратной связи (2.10) в промежутках

между замерами дифференциальное уравнение (1.1) имеет вид

u_t(x,t) = a²u_xx(x,t) +

∑

(2.14)

+µ₁

[k_1i (u(ξ_i, t_j ) - U_i) + k_2i (u(ξ_i, t_j - τ) - U_i)] - µ₁u(x, t),

i=1

t ∈ [t_j,t_j + Δt), j = 0,1,...,N_t - 1,

а в моменты времени замеров t_j, j = 1,...,N_t - 1 выполняется условие непре-

рывности процесса

(2.15)

u(x, t⁺ⁱ) = u(x, t^-i), x ∈ [0, l], i = 1, . . . , N_t

− 1.

Здесь использованы обозначения:

u(x, t⁺ⁱ) = u(x, t_j + 0), u(x, t^-i) = u(x, t_j - 0).

Краевые условия в этом случае будут иметь вид:

u_x(0,t) = µ₂u(0,t) -

∑

(2.16)

-µ₂

[k_1i (u(ξ_i, t_j ) - U_i) + k_2i (u(ξ_i, t_j - τ) - U_i)] ,

i=1

t ∈ [t_j,t_j + Δt), j = 0,1,...,N_t - 1,

u_x(l,t) = -µ₂u(l,t) +

∑

(2.17)

=µ₂

[k_1i (u(ξ_i, t_j ) - U_i) + k_2i (u(ξ_i, t_j - τ) - U_i)] ,

i=1

t ∈ [t_j,t_j + Δt), j = 0,1,...,N_t - 1.

Ограничение (2.5) на управляющее воздействие, учитывая зависимость

(2.9) и условия на состояние температуры при протекании процесса регули-

рования (2.6), несложно привести к следующим ограничениям на параметры

обратной связи:

∑

(2.18)

(k_1i + k_2i) (u - U_i) ≤ϑ,

i=1

135

∑

(2.19)

(k_1i + k_2i) (u - U_i

) ≥ ϑ.

i=1

Ясно, что ограничения (2.18), (2.19) являются линейными по K.

Целевой функционал (2.7) на случай управления с обратной связью запи-

шем в виде

∫

(2.20)

J_T (K) = I(K;ϕ)ρ_Φ

(ϕ)dϕ,

∫T

∫



₂



(2.21)

I(K; ϕ) =

µ(x) [u(x, t; K, ϕ) - U(x)]² dxdt + αK -K



R^2L

T-ΔT 0

где α,

K_α ∈ R^2L - параметры регуляризации функционала.

Таким образом, задача оптимального управления процессом нагрева как с

непрерывной, так и дискретной обратной связью заключается в определении

таких параметров обратной связи K ∈ R^2L, удовлетворяющих ограничениям

(2.18) при непрерывной и (2.19) при дискретной обратной связи, при кото-

рых совместно с решением соответствующих начально-краевых задач (2.11)-

(2.13), (2.2) и (2.14), (2.2)-(2.4) функционал (2.20), (2.21) принимает мини-

мальное значение.

Исследуемая далее полученная задача относится к параметрическим зада-

чам оптимального управления, поскольку непосредственно оптимизируемым

является конечномерной вектор K ∈ R^2L. Специфическими особенностями

дифференциальных уравнений, как указывалось выше, являются наличие

запаздывания во времени у фазовой переменной и точечная нагруженность

по пространственной переменной. Специфика задачи заключается и в целе-

вом функционале (2.20), (2.21), оценивающем на некотором конечном проме-

жутке времени [T - ΔT, T ] поведение множества решений начально-краевой

задачи (пучка-траекторий), параметры ϕ начальных условий u⁰(x, t₀; ϕ) кото-

рых принадлежат множеству Φ. Отметим еще одну важную специфическую

особенность полученной задачи. Несмотря на то что исходная задача опти-

мального управления без обратной связи (2.1)-(2.7) является, как несложно

проверить, выпуклой, задачи как с непрерывной, так и с дискретной обрат-

ной связью являются невыпуклыми. Это видно из зависимостей (2.9), (2.10),

в которых участвуют произведения оптимизируемых параметров K и зави-

сящих от них, в общем случае нелинейно, значений фазовой переменной в

точках замера u(ξ_i, t), i = 1, . . . , L. Эта особенность важна и требует привле-

чения к ее численному решению каких-либо подходов к отысканию глобаль-

ного оптимума. Одним из таких подходов является применение известных

эффективных методов локальной оптимизации с использованием различных

начальных точек поиска для оптимизируемого вектора K ∈ R^2L (метод муль-

тистарта). В следующем разделе будет изложен предлагаемый подход и по-

лучены необходимые формулы для применения эффективных локальных ме-

тодов оптимизации первого порядка.

136

3. Подход к численному решению задачи синтеза управления

Для численного решения полученной задачи параметрического оптималь-

ного управления (2.11), (2.2), (2.12), (2.13), (2.18)-(2.21) с учетом линейности

ограничений (2.18), (2.19) на оптимизируемые параметры, а следовательно,

выпуклости допустимой области параметров K предлагается использовать

метод проекции градиента [20, 21].

(3.1)

K^s+1 = P_{(2.17),(2.18)} (K^s - γ_s grad_K J_T (K^s

)) ,

(

)

(3.2)

γ_s = arg minJ_T

P_{(2.18),(2.19)}(K^s - γgrad_K J_T (K^s))

s = 0,1,...

γ≥0

Здесь grad_K J_T (K) - 2L-мерной вектор компонент градиента целевого функ-

ционала (2.20), (2.21); γ_s - величина шага одномерной оптимизации по на-

правлению градиента на s-й итерации, определяемой, например, методом зо-

лотого сечения; K⁰ - некоторое начальные значение вектора параметров об-

ратной связи (в случае, если оно не удовлетворяет ограничениям (2.18), (2.19),

необходимо его предварительно спроектировать на допустимую область). Для

построения оператора проектирования P_{(2.18),(2.19)}(K) произвольного вектора

K ∈ R^2L на допустимую область, определяемую линейными неравенствами

(2.18), (2.19), имеются известные конструктивные формулы [13, 20, 21].

Как было отмечено выше, полученная задача параметрического оптималь-

ного управления может быть многоэкстремальной по оптимизируемым пара-

метрам K, а метод (3.1), (3.2) позволяет отыскивать лишь ближайшую к точ-

ке K⁰ ∈ R^2L точку локального минимума целевого функционала. Поэтому в

приведенных расчетах использовался метод “мультистарта”, заключающийся

в многократном применении итерационной процедуры (3.1), (3.2) для различ-

ных допустимых начальных точек K⁰. При этом за решение принимается тот

вектор локального минимума K^∗, которому соответствует меньшее значение

целевого функционала.

Ясно, что для реализации процедуры (3.1), (3.2) важную роль имеет век-

тор градиента целевого функционала grad_K J_T (K). Далее в теореме показа-

на дифференцируемость целевого функционала J_T (K) и приведены формулы

для компонент его градиента.

Теорема 1. При принятых допущениях на функции и параметры зада-

чи (2.1)-(2.4), (2.7) функционал (2.20), (2.21) задачи управления (2.11), (2.2),

(2.12), (2.13), (2.18)-(2.21) с обратной связью (2.9) дифференцируем по допу-

стимым значениям параметров обратной связи K, а компоненты градиен-

та определяются формулами







∫

gradk1i J_T (K) =



-a2

µ₂ (ψ(0,t) + ψ(l,t)) - µ₁ ψ(x,t)dx ×

Φ t0

(3.3)



(

)

× (u(ξ_i,t) - U_i) dt + 2 k_1i -k1i

ρΦ(ϕ)dϕ, t₀ ≤ t ≤ T,

137







∫

grad

J_T (K) =



-a²µ2(ψ(0,t+τ)+ψ(l,t+ τ))-µ1 ψ(x,t+τ)dx×

k_2i

Φ t0



(

)

(3.4)

× (u(ξ_i, t) - U_i) dt + 2 k_2i -k2i

ρΦ(ϕ)dϕ,

-τ ≤ t ≤ T - τ,

где u(x, t; ϕ) - решение начально-краевой задачи (2.11)-(213), (2.2); ψ(x, t) -

решение следующей сопряженной начально-краевой задачи при каждом за-

данном допустимом значения параметра ϕ:

(3.5)

ψ_t(x,t) = -a²ψ_xx(x,t) + αψ(x,t), t₀

≤ t ≤ T - ΔT,

ψ_t(x,t) = -a²ψ_xx(x,t) + αψ(x,t) + 2µ(x)(u(x,t;y,ϕ) - U(x)) ,

(3.6)

T - ΔT < t ≤ T,

(3.7)

ψ(x, T ) = 0,

0≤x≤l,

(3.8)

ψ_x(0,t) = µ₂ψ(0,t), t₀

≤t≤T,

(3.9)

ψ_x(l,t) = -µ₂ψ(l,t), t₀

≤t≤T,

∫l

µ₁k_1i

ψ_x(ξ⁺ⁱ,t) = ψ_x(ξ^-i,t) + µ₂k_1i (ψ(0,t) + ψ(l,t)) +

ψ(x, t)dx,

(3.10)

a²

t₀ ≤ t ≤ T,

ψ_x(ξ⁺ⁱ,t + τ) = ψ_x(ξ^-i,t + τ) + µ₂k_2i (ψ(0,t + τ) + ψ(l,t + τ)) +

∫

(3.11)

µ₁k_2i

ψ(x, t + τ)dx, t₀ ≤ t ≤ T - τ,

a²

(3.12)

ψ(ξ⁺ⁱ, t) = ψ(ξ^-i, t), t₀

≤t≤T.

В случае дискретной по времени обратной связи в виде зависимости (2.10)

имеет место следующая

Теорема 2. При принятых допущениях на функции и параметры,

участвующие в задаче (2.1)-(2.4), (2.7), функционал (2.20), (2.21) задачи

управления (2.14)-(2.17), (2.2) при дискретной обратной связи (2.8) диффе-

ренцируем по параметром обратной связи K при их допустимых значениях,

компоненты градиента целевого функционала определяются формулами







tj∫+Δt

∫

∑



-a2

gradk1i J_T (K) =



µ2 (ψ(0, t) + ψ(l, t)) - µ1

ψ(x, t)dx ×

Φ j=0



(

)

× (u(ξ_i,t) - U_i)dt + 2 k_1i - k1i

 ρΦ(ϕ)dϕ,

tj ≤ t ≤tj + Δt,

138

gradk2i J_T (K) =







∫

∑





-a²µ2(ψ(0,t + τ) + ψ(l,t + τ)) - µ1

ψ(x, t + τ)dx ×

Φ j=0



(

)

× (u(ξ_i, t) - U_i) dt + 2 k_2i -k2i

 ρΦ(ϕ)dϕ,

tj - τ ≤ t ≤tj + Δt - τ,

а функция ψ(x, t) при каждом заданном допустимом значении парамет-

ра ϕ и соответствующей функции u(x, t; ϕ)решения начально-краевой за-

дачи (2.14)-(2.17), (2.2) определяется решением сопряженной начально-

краевой задачи:

ψ_t(x,t) = -a²ψ_xx(x,t) + αψ(x,t),

tj ≤ t ≤tj + Δt - τ, j = 0, 1, . . . , Nt - 1,

ψ_t(x,t) = -a²ψ_xx(x,t) + αψ(x,t) + 2µ(x)(u(x,t;y,ϕ) - U(x)) ,

tj + Δt - τ < t ≤tj + Δt,

ψ(x, T ) = 0,

0≤x≤l,

ψ_x(0,t) = µ₂ψ(0,t),

tj ≤ t ≤tj + Δt, j = 0, 1, . . . , Nt - 1,

ψ_x(l,t) = -µ₂ψ(l,t),

tj ≤ t ≤tj + Δt, j = 0, 1, . . . , Nt - 1,

в точках ξ_i, i = 1,... ,L, при t_j ≤ t ≤ t_j + Δt должна удовлетворять усло-

виям

∫

∑

ψ_x(ξ^-i,t_j) = ψ_x(ξ⁺ⁱ,t_j) - µ₂k_1i

(ψ(0, τ) + ψ(l, τ)) dτ,

k=1 t_k-1

i = 1,...,L, j = 1,...,N_t - 1,

ψ(ξ⁺ⁱ, t) = ψ(ξ^-i, t), i = 1, . . . , L,

∫

∑

ψ_x(ξ⁺ⁱ,t_j + τ) = ψ_x(ξ^-i,t_j + τ) + µ₂k_2i

(ψ(0,t + τ) + ψ(l,t + τ)) dt,

k=1 t_k-1

tj ≤ t ≤tj + Δt - τ, i = 1, . . . , L, j = 1, . . . , Nt - 1,

а в точках t_j, j = 0,1,...,N_t - 1, при x ∈ [0,l] удовлетворять условиям

∫

∑

ψ(ξ_i, t^-j) = ψ(ξ_i, t^+j) -

k_i

ψ(x, t)dxdt,

a²

ν=1

tj-1

ξν

i = 1,...,L, j = 0,1,...,N_t - 1.

139

Сформируем необходимые условия оптимальности параметров обратной

связи K в вариационной форме.

Теорема 3. Для оптимальности параметров обратной связи K^∗ ∈ R^2L

в задаче синтеза (2.11)-(2.13), (2.20), (2.21) с непрерывной обратной связью

(2.9) необходимо выполнение условия

(grad_KJ_T (K^∗), K - K^∗) ≥ 0

для произвольного допустимого вектора K ∈ R^2L, удовлетворяющего усло-

виям (2.18), (2.19), где градиент целевого функционала (2.20), (2.21) опреде-

ляется формулами (3.3)-(3.12).

Аналогичную теорему можно сформировать для случая дискретной об-

ратной связи (2.10).

4. Результаты компьютерных экспериментов

Приведем результаты численных экспериментов, полученные при решении

задачи (2.1)-(2.7), для следующих функций и значений параметров, участ-

вующих в постановке задачи:

t₀ = 0, T = 2, a = 1, µ₁ = µ₂ = 1, µ(x) = 1,

l = 1, u⁰(x,t;ϕ) = ϕ, x ∈ [0,1], Φ = {55,60,65},

ϑ = 10,

ϑ = 1000, ΔT = 1, U(x) = 85, x ∈ [0,1].

При проведении экспериментов время запаздывания τ, число L точек

непрерывного во времени контроля и места их размещения принимали раз-

личные значения. В приводимых далее результатах были использованы сле-

дующие значения параметров: τ = 0,05, L = 2, ξ₁ = 0,3, ξ₂ = 0,6.

Для реализации итерационной процедуры (3.1), (3.2) использовались по-

лученные выше формулы для компонентов градиента (3.3), (3.4).

Для решения прямой (2.11)-(2.13) и сопряженной (3.5)-(3.12) начально-

краевых задач при заданных текущих значениях параметров обратной свя-

зи K и начальном условии ϕ ∈ Φ использовалась неявная схема метода се-

ток с шагами дискретизации по x и t, соответственно равными h_x = 0,01,

h_t = 0,01 [22]. Для учета запаздывания τ использовался метод шагов [14].

К нелокальным краевым условиям (2.12), (2.13) прямой задачи и (3.8)-(3.12)

сопряженной задачи после дискретизации применялась схема сдвига условий,

описанная в [18] основанная на идее метода прогонки [23].

С учетом возможности многоэкстремальности функционала (2.20), (2.21)

в качестве начальной точки для итерационной процедуры (3.1), (3.2) исполь-

зовались разные точки, в частности приведенные в табл. 1. В этой же таблице

приведены соответствующие этим точкам значения целевого функционала.

В табл. 2 приведены полученные с применением процедуры (3.1), (3.2)

оптимальные значения параметров обратной связи. Отметим, что при даль-

нейших итерациях процедуры (3.1) оптимизируемые параметры и значение

140

Таблица 1. Начальные значения оптимизируемых параметров k⁰¹¹,k⁰¹²,k⁰²¹,k⁰²²

и соответствующие значения функционала

k⁰¹¹

k⁰¹²

k⁰²¹

k⁰²²

J^0T (K)

6,0000

9,0000

7,0000

8,0000

4514,7446001

0,5000

0,9000

0,3000

0,6000

4440,8716378

Таблица 2. Полученные значения параметров обратной связи (2.9)

и целевого функционала

N T χ k^(∗)11

k^(∗)12

k^(∗)21

k^(∗)22

J^(∗)T(K)

0% -0,54691

1,51775

1,36562

1,42903

0,00000042134

1% -0,54655

1,50549

1,37056

1,42836

0,00000063847

3% -0,53125

1,51231

1,37452

1,44927

0,00000095917

0% -0,54693

1,51773

1,36560

1,42901

0,00000041473

1% -0,54827

1,51537

1,36314

1,42821

0,00000052774

3% -0,54949

1,50465

1,35546

1,41236

0,0000091645

0,86006

1,31130

0,65608

1,00734

0,00000042441

0,84875

1,30618

0,65785

1,00908

0,00000053893

0,85589

1,30355

0,65777

1,00626

0,00000061959

0,86004

1,31128

0,65606

1,00732

0,00000041806

0,85746

1,31135

0,64758

1,00563

0,00000062639

0,86481

1,31407

0,66105

1,00586

0,00000724320

функционала практически не изменялись. В этой же таблице приведены

значения параметров обратной связи, полученные процедурой оптимизации

(3.1), (3.2) при условии, что замеры фазового состояния в точках контроля ξ_i,

i = 1,2 проводятся не точно, а с погрешностью χ%. Замеренные значения с

погрешностью определялись по формуле

u(t) = u(ξ_i, t) = u(ξ_i, t)(1 + χs(t)), t ∈ [t₀, T ],

где случайные значения s(t) при каждом t ∈ [t₀, T ] имеют равномерное рас-

пределение на отрезке [-1; 1] и стандартной программой Randomize.

Как видно из таблицы, параметры обратной связи достаточно устойчивы

к погрешностям проводимых замеров.

Для сравнения предлагаемого подхода к синтезу управления проводились

эксперименты с решением задачи синтеза управления с обратной связью без

использования предыдущих по времени результатов замеров в виде [10]:

∑

(4.1)

ϑ(t; K) =

k_ij(u(ξ_i,t) - U_i), t ∈ [t₀

,T].

i=1

141

Таблица 3. Начальные значения параметров обратной связи (4.1)

и соответствующие значения целевого функционала

k⁰¹¹

k⁰¹²

J^0T (K)

6,0000

9,0000

4068,59998

0,5000

0,9000

4188,42555

Таблица 4. Полученные значения параметров обратной связи (4.1)

и целевого функционала

k^(∗)11

k^(∗)12

J^(∗)T(K)

0,75542

2,98977

0,24977233550

0,75533

2,98965

0,24982552763

0,75512

2,98936

0,25005961886

0,53942

2,74553

0,23500497418

0,53891

2,74491

0,23519332257

0,53877

2,74476

0,23525947935

1,64570

2,21322

0,24976508234

1,64565

2,21315

0,24985018452

1,64522

2,21257

0,24996574232

1,43147

1,96693

0,23500821019

1,43110

1,96645

0,23522688761

1,43026

1,96523

0,23564519287

Как видно, в (4.1) для формирования текущего значения управления ϑ(t)

не используется информация о фазовом состоянии в предыдущие моменты

времени.

В табл. 3 проведены значения начальных значений параметров обратной

связи из (4.1), использованные для итерационной процедуры (3.1), (3.2), и

соответствующие значения целевого функционала.

В табл. 4 аналогично табл. 2 приведены полученные оптимальные значе-

ния параметров обратной связи в виде (4.1) при различных уровнях погреш-

ностей χ проводимых замеров.

Введем функционал



∫

1_/2

Φ(t; K, ϕ) =

[u(x, t; K, ϕ) - U(x)]² dx

характеризующий состояние процесса нагрева всего стержня в интегральном

смысле, при параметрах обратной связи K и начальном условии u(x, t₀) = ϕ.

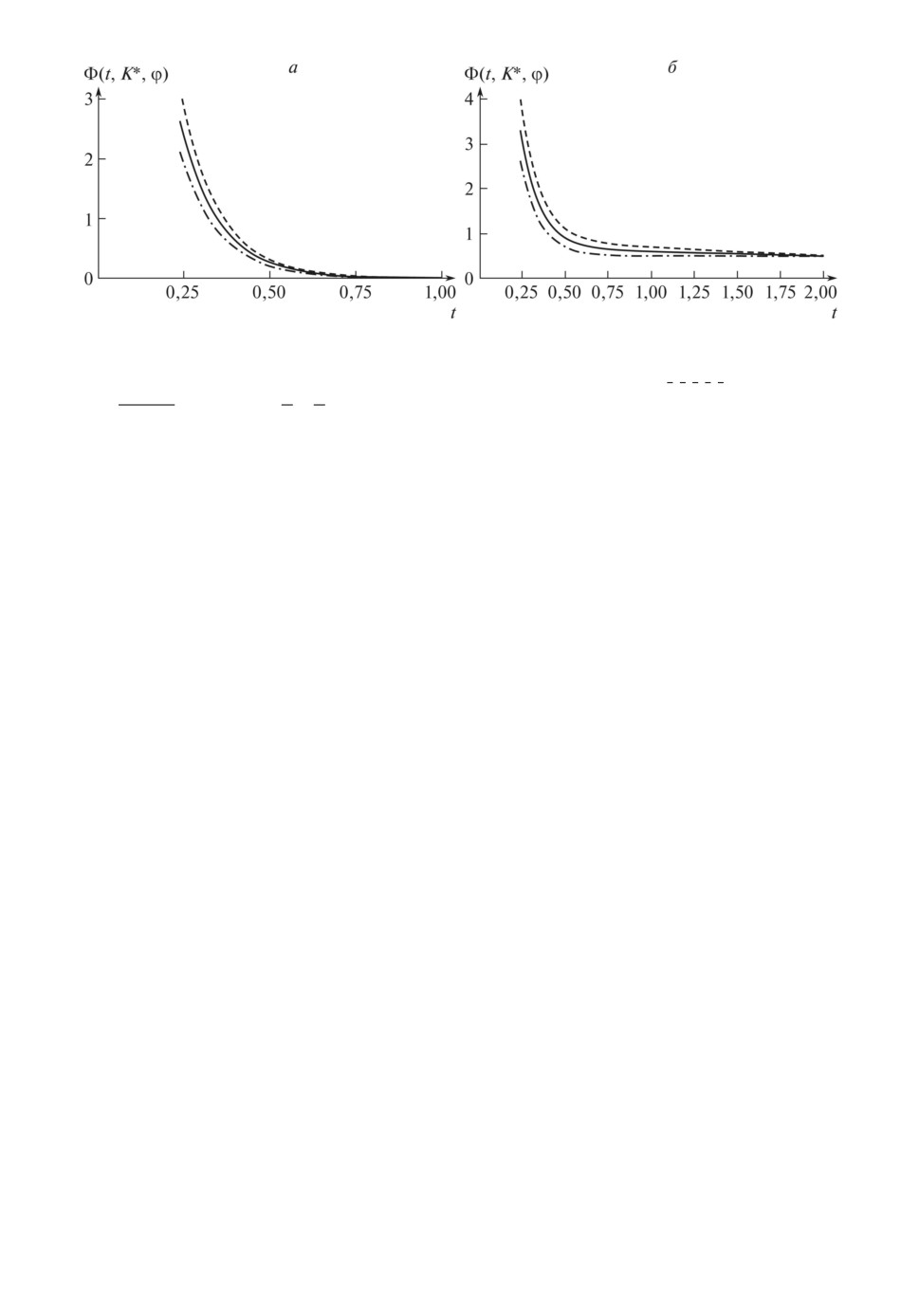
На рисунке приведены графики функции Φ(t; K^∗, ϕ) при оптимальных

значениях параметров K^∗, полученные из первой начальной точки K⁰ (пер-

142

Графики функционала Φ(t; K^∗, ϕ). а для обратной связи вида (1.9); б для

обратной связи вида (3.1) для начальных условий: ϕ = 550 (

), ϕ = 60⁰

(

), ϕ = 65⁰

(

·).

вая строка табл. 1), с состояниями в начальный момент времени u(x, t₀) = 55⁰,

u(x, t₀) = 60⁰, u(x, t₀) = 65⁰. На рисунке а использованы приведенные в пер-

вой строке табл. 2 полученные оптимальные значения параметров обратной

связи в виде (2.9). На рисунке б использованы приведенные в первой стро-

ке табл. 4 полученные оптимальные значения параметров обратной связи в

виде (4.1).

В случае обратной связи вида (2.9), как видно из рисунка а, графики функ-

ций Φ(t; K^∗, ϕ) при t ≥ 0,75 для разных начальных условий устанавливаются

достаточно близко к U(x) = 85, а из рисунка б следует, что установление при

обратной связи вида (4.1) начинает наблюдаться только при t ≥ 1,5.

5. Заключение

На примере процесса нагрева стержня предложен подход к синтезу управ-

ления в системах с распределенными параметрами. Для формирования те-

кущего управления предлагается использовать информацию о состоянии в

точках замера не только в текущий, но и в некоторый предыдущий момент

времени.

Применение такого подхода может быть обусловлено невозможностью про-

ведения замера всех компонентов состояния объекта или объекта в целом.

В работе задача синтеза параметров обратной связи приведена к задаче па-

раметрического оптимального управления, в котором процесс описывается

дифференциальным уравнением с запаздывающими по времени аргумента-

ми.

Получены формулы градиента целевого функционала по параметрам об-

ратной связи, сформулированы необходимые условия оптимальности. Приве-

дены численные эксперименты.

Предложенный подход к синтезу управления в системах с распределенны-

ми параметрами несложно распространить на другие процессы, описываемые

другими видами начально-краевых задач.

143

ПРИЛОЖЕНИЕ

Доказательство теоремы 1. Из взаимной независимости возмож-

ных начальных условий u⁰(x, t; ϕ) при различных параметрах ϕ имеет место

∫

(Π.1)

grad_KJ_T (K) = grad_K I(K; ϕ)ρ_Φ(ϕ)dϕ = grad_KI(K; ϕ)ρ_Φ

(ϕ)dϕ.

Поэтому сначала займемся исследованием дифференцируемости функцио-

нала I(K; ϕ) и получением формул для компонент его градиента по пара-

метрам обратной связи K при каком-либо заданном допустимом параметре

ϕ ∈ Φ.

Для доказательства теоремы воспользуемся известным методом прираще-

ния оптимизируемых параметров и оценки соответствующего приращения

функционала [20].

Пусть вектор параметров обратной связи K = (k₁, k₂), которому соответ-

ствует решение u(x, t) нагруженной краевой задачи (2.11)-(2.13), получил

приращение

K= K + ΔK = (k₁ + Δk₁,k₂ + Δk₂) и этому вектору соответ-

ствует решение краевой задачи ũ(x, t) = u(x, t) + Δu(x, t).

Из (2.11)-(2.13), (2.2) следует, что Δu(x, t) является решением краевой

задачи

∑

Δu_t(x,t) = a²Δu_xx(x,t) + µ₁

[k_1iΔu(ξ_i,t) + k_2iΔu(ξ_i,t - τ)]+

i=1

(Π.2)

∑

+µ₁

(u(ξ_i, t) - U_i) Δk_1i + µ₁

(u(ξ_i, t - τ) - U_i) Δk_2i -

i=1

− µ₁Δu(x,t), (x,t) ∈ Ω = (0,l) × (t₀,T],

∑

Δu_t(0,t) = µ₂Δu(0,t) - µ₂

[k_1iΔu(ξ_i, t) + k_2iΔu(ξ_i, t - τ)] -

i=1

(Π.3)

∑

-µ₂

[(u(ξ_i, t) - U_i) Δk_1i + (u(ξ_i, t - τ) - U_i) Δk_2i] , t ∈ [t₀, T ] ,

i=1

∑

Δu_t(l,t) = -µ₂Δu(l,t) + µ₂

[k_1iΔu(ξ_i, t) + k_2iΔu(ξ_i, t - τ)] +

i=1

(Π.4)

∑

+µ₂

[(u(ξ_i, t) - U_i) Δk_1i + (u(ξ_i, t - τ) - U_i) Δk_2i] , t ∈ [t₀, T ] ,

i=1

(Π.5)

Δu(x, 0) = 0, x ∈ [0, l].

Пользуясь известными результатами об устойчивости дифференциальных

уравнений с запаздывающей во времени фазовой переменной и нагружен-

144

ных нелокальных краевых задач, можно показать справедливость оценки

∥Δu(x, t)∥L2(Ω)^{≤α∥ΔK∥}R2L^{,гдеα>0независитотK[20].}

Для приращения функционала (2.19) несложно непосредственно получить

представление:

ΔI(K;ϕ) = I(K + ΔK;ϕ) - I(K;ϕ) =

∫T

∫

µ(x) [u(x, t; K, ϕ) - U(x)] Δu(x, t)dxdt +

T-ΔT 0

(Π.6)

∑[

]

σ₁(k_1i -k1i)Δk_1i + σ₂(k_2i -k2i)Δk_2i

i=1

(

)

+ R ∥Δu∥L2

,∥ΔK∥_R2L

(Ω)

(

)

где остаточный член R

∥Δu∥L2(Ω)^,∥ΔK∥R2L^{включаетслагаемыевторого}

порядка малости относительно ∥ΔK∥_R2L и ∥Δu∥L2(Ω)^{.Изэтойоценкиприра-}

щения функционала следует и его дифференцируемость [20].

Получим формулы для компонентов градиента целевого функционала по

параметрам обратной связи. Пусть функция ψ(x, t) некоторая пока про-

извольная непрерывная всюду в Ω, дважды дифференцируемая по x при

x ∈ (ξ_i,ξ_i+1), i = 0,1,...,L, ξ₀ = 0, ξ_L+1 = l, дифференцируемая по t при

t ∈ (t₀,T). Умножим (П.2) на ψ(x,t), проинтегрируем результат по прямо-

угольнику Ω. С учетом принятых предположений и условий (П.3)-(П.5) бу-

дем иметь:

∫

∑

ψ(x, t)Δu_t(x, t)dxdt - a2

ψ(x, t)Δu_xx(x, t)dtdx -

i=0

t₀

ξ_i t0

[

∫T

∫

∑

(Π.7)

ψ(x, t) µ₁

[k_1iΔu(ξ_i, t) + k_2iΔu(ξ_i

,t - τ)]+

i=1

t₀

]

∑

+µ₁

[(u(ξ_i, t) - U_i) Δk_1i + (u(ξ_i, t - τ) - U_i) Δk_1i] - µ₁Δu(x, t) dxdt = 0.

i=1

Используя интегрирование по частям отдельно для первого и второго чле-

нов (П.7) и, учитывая (П.3)-(П.5) , имеем:

∫

ψ(x, t)Δu_t(x, t)dxdt =

t₀

(Π.8)

∫^l

∫

= ψ(x,T)Δu(x,T)dx -

ψ_t(x,t)Δu(x,t)dxdt,

t₀

145

∫

∑

(Π.9)

a²

ψ(x, t)Δu_xx

(x, t)dtdx =

i=0

ξ_i t0

∫T

=a²

[(ψ_x(0, t) - µ₂ψ(0, t))Δu(0, t) - (ψ_x(l, t) + µ₂ψ(l, t))Δu(l, t)] dt +

t₀

∫

∑

[

]

+a²

ψ_x(ξ^-i,t) - ψ_x(ξ⁺ⁱ,t) + µ₂k_1i (ψ(0,t) + ψ(l,t))

Δu(ξ_i, t)dt +

i=1 t₀

∫

∑

[

]

+a²

ψ_x(ξ^-i,t + τ) - ψ_x(ξ⁺ⁱ,t + τ) + µ₂k_2i (ψ(0,t + τ) + ψ(l,t + τ))

i=1 t₀

∫

∑

[

]

×Δu(ξ_i,t)dt + a²

(ψ(ξ⁺ⁱ, t) - ψ(ξ^-i, t))Δu_x(ξ_i, t)

dt +

i=1

t₀

∫

∑

+a²

µ₂Δk_1i

(ψ(0, t) + ψ(l, t)) (u(ξ_i, t) - U_i) dt +

i=1

t₀

∫

∑

+a²

µ₂Δk_2i

(ψ(0, t + τ) + ψ(l, t + τ)) (u(ξ_i, t) - U_i) dt +

i=1

t₀

∫T

∫

+a²

ψ_xx(x,t)Δu(x,t)dxdt.

t₀

Используя (П.6)-(П.9), для приращения функционала будем иметь:

∫l

(Π.10)

ΔI(K;ϕ) =

ψ(x, T )Δu(x, T )dx -

∫T

[

]

-a²

(ψ_x(0, t) - µ₂ψ(0, t))Δu(0, t) - (ψ_x(l, t) + µ₂ψ(l, t))Δu(l, t) dt +

t₀

∫

[

]

- ψ_t(x,t) - a²ψ_xx(x,t) + αψ(x,t) Δu(x,t)dxdt +

t₀

∫T

∫

[

- ψ_t(x,t) - a²ψ_xx(x,t) + αψ(x,t) +

T-ΔT 0

]

+ 2µ(x)(u(x, t; K, ϕ) - U(x)) Δu(x, t)dxdt +

146



∫

-a²

ψ_x(ξ^-i, t) - ψ_x(ξ⁺ⁱ, t) + µ₂k_1i(ψ(0, t) + ψ(l, t)) +

i=1 t₀



∫

µ₁k_1i

ψ(x, t)dx Δu(ξ_i, t)dt -

a²



∫

∑

-a²

ψx(ξ^-i,t + τ) - ψ_x(ξ⁺ⁱ,t + τ) + µ₂k_2i (ψ(0,t + τ) + ψ(l,t + τ)) +

i=1 t₀



∫

µ₁k_2i

ψ(x, t + τ)dx Δu(ξ_i, t)dt +

a²

∫

∑

[

]

+a²

(ψ(ξ⁺ⁱ, t) - ψ(ξ^-i, t))Δu_x(ξ_i, t)

dt +

i=1

t₀







∫T

∫

∑

-a²

Δk_1i

µ₂ (ψ(0, t) + ψ(l, t)) +µ1

ψ(x, t)dx ×



a²

i=1

t₀



(

)

× (u(ξ_i, t) - U_i) dt -

k_1i -k1i

a²









∫

∑

-a²

Δk_2i

µ2 (ψ(0,t + τ) + ψ(l,t + τ)) +µ1

ψ(x, t + τ)dx ×



a²

i=1

t₀



(

) (

)

× (u(ξ_i,t) - U_i)dt -

k_2i -k

+ R ∥Δu∥L2(Ω) ^,∥ΔK∥R2L

a²



В силу произвольности функции ψ(x, t) потребуем, чтобы она почти всюду

являлась решением начально-краевой задачи (3.5)-(3.12).

Учитывая, что компоненты градиента функционала определяются линей-

ной частью приращения функционала при приращениях соответствующих

аргументов, получаем:





∫T

∫

grad I(K; ϕ) =_k

-a2

µ₂ (ψ(0,t) + ψ(l,t)) - µ₁ ψ(x,t)dx ×

t₀

(

)

× (u(ξ_i,t) - U_i) dt + 2 k_1i - k1i ,

i = 1,...,L, t₀ ≤ t ≤ T,

147





∫

grad

I(K; ϕ) =

-a²µ2(ψ(0,t+τ)+ψ(l,t+τ))-µ1 ψ(x,t+τ)dx ×

k_2i

t₀

(

)

× (u(ξ_i, t) - U_i) dt + 2 k_2i -k2i ,

i = 1,...,L,

-τ ≤ t ≤ T - τ.

Учитывая (П.1), получим приводимые в теореме выражения для искомых

компонент градиента функционала.

Доказательство теоремы 2 проводится аналогично вышеприведенному с

той разницей, что всюду в проводимых выкладках интегрирование по ин-

тервалу t ∈ [0, T ] заменяется интегрированием по отдельным интервалам t ∈

∈ [t_i, t_i+1), i = 0, 1, . . . , N_t - 1.

СПИСОК ЛИТЕРАТУРЫ

Егоров А.И. Основы теории управления. М.: Физматлит, 2004.

Mitkowski W., Bauer W., Zagórowska M. Discrete-Time Feedback Stabilization //

Archives of Control Sciences. 2017. V. 27. No. 1. P. 309-321.

Брайсон А., Хо Ю-ши. Прикладная теория оптимального управления. М.: Мир,

1972.

Поляк Б.Т., Щербаков П.С. Робастная устойчивость и управление. М.: Наука,

2001.

Бутковский А.Г. Методы управления системами с распределенными парамет-

рами. М.: Наука, 1984.

Aida-zade K.R., Abdullayev V.M. Control Synthesis for Temperature Maintaining

Process in a Heat Supply Problem // Cybern. Syst. Analysis. 2020. V. 56. No. 3.

P. 380-391.

Поляк Б.Т., Хлебников М.В., Рапопорт Л.Б. Математическая теория автома-

тического управления. М.: Ленанд, 2019.

Afifi L., Lasri K., Joundi M., Amimi N. Feedback Controls for Exact Remediability

in Disturbed Dynamical Systems // IMA J. Math. Control Inform. 2018. V. 35.

No. 1. P. 411-425.

Coron J.M., Wang Zh. Output Feedback Stabilization for a Scalar Conservation Law

with a Nonlocal Velocity // SIAM J. Math. Anal. 2012. V. 45. No. 5. P. 2646-2665.

10.

Айда-заде К.Р., Абдуллаев В.М. Оптимизация размещения точек контроля при

синтезе управления процессом нагрева // АиТ. 2017. Т. 78. № 9. С. 49-66.

Aida-zade K.R., Abdullayev V.M. Optimizing Placement of the Ccontrol Points at

Synthesis of the Heating Process Control // Autom. Remote Control. 2017. V. 78.

No. 9. P. 1585-1599.

11.

Айда-заде К.Р., Абдуллаев В.М. Об одном подходе к синтезу управления про-

цессами с распределенными параметрами // АиТ. 2012. № 9. С. 3-19.

Aida-zade K.R., Abdullaev V.M. On an Approach to Designing Control of the

Distributed-Parameter Processes // Autom. Remote Control. 2012. V. 73. No. 2.

P. 1443-1455.

12.

Сиразетдинов Т.К. Оптимизация систем с распределенными параметрами. М.:

Наука, 1977.

13.

Ray W.H. Advanced Process Control. McGraw-Hill Book Company. 1981.

148

14. Эльсгольц Л.Э., Норкин С.Б. Введение в теорию дифференциальных уравнений

с отклоняющимся аргументом. М.: Наука, 1971.

15. Нахушев А.М. Нагруженные уравнения и их применение. М.: Наука, 2012.

16. Алиханов А.А., Березков А.М., Шхануков-Лафишев М.Х. Краевые задачи для

некоторых классов нагруженных дифференциальных уравнений и разностные

методы их численной реализации // Журн. вычисл. матем. и матем. физ. 2008.

Т. 48. № 9. С. 1619-1628.

17. Abdullayev V.M., Aida-zade K.R. Finite-Difference Methods for Solving Loaded

Parabolic Equation // Comput. Math. Math. Phys. 2016. V. 56. No. 1. P. 93-105.

18. Абдуллаев В.М., Айда-заде К.Р. О численном решении нагруженных систем

обыкновенных дифференциальных уравнений // Журн. вычисл. матем. и ма-

тем. физ. 2004. Т. 44. № 9. С. 1585-1595.

19. Abdullayev V.M., Aida-zade K.R. Optimization of Loading Places and Load Re-

sponse Functions for Stationary Systems // Comput. Math. Math. Phys. 2017. V. 57.

No. 4. P. 634-644.

20. Васильев Ф.П. Методы оптимизации. М.: Факториал Пресс, 2008.

21. Поляк Б.Т. Введение в оптимизацию. М.: Ленанд, 2014.

22. Самарский А.А., Николаев Е.С. Методы решения сеточных уравнений. М.: Нау-

ка, 1978.

23. Абрамов А.А. О переносе граничных условий для систем линейных обыкновен-

ных дифференциальных уравнений (вариант метода прогонки) // Журн. вы-

числ. матем. и матем. физ. 1961. Т. 1. № 3. С. 542-545.

Статья представлена к публикации членом редколлегии М.В. Хлебниковым.

Поступила в редакцию 30.07.2021

После доработки 25.08.2021

Принята к публикации 29.08.2021

149