Автоматика и телемеханика, № 1, 2022

Оптимизация, системный анализ

и исследование операций

(Московский физико-технический институт),

В.В. СТРИЖОВ, д-р физ.-мат. наук (strijov@phystech.edu)

(Московский физико-технический институт;

Вычислительный центр им. А.А. Дородницына ФИЦ ИУ РАН, Москва)

ВЕРОЯТНОСТНАЯ ИНТЕРПРЕТАЦИЯ ЗАДАЧИ ДИСТИЛЛЯЦИИ¹

Статья посвящена методам понижения сложности аппроксимирующих

моделей. Предлагается вероятностное обоснование методов дистилляции

и привилегированного обучения. Приведены общие выводы для произ-

вольной параметрической функции с наперед заданной структурой. По-

казано теоретическое обоснование для частных случаев: линейной и логи-

стической регрессии. Проводится анализ рассмотренных моделей в вычис-

лительном эксперименте на синтетических выборках и реальных данных.

В качестве реальных данных рассматриваются выборки FashionMNIST и

Twitter Sentiment Analysis.

Ключевые слова: выбор модели, байесовский вывод, дистилляция модели,

привилегированное обучение.

DOI: 10.31857/S0005231022010093

1. Введение

Увеличение точности аппроксимации в задачах машинного обучения уве-

личивает сложность моделей и снижает их интерпретируемость. Примерами

являются трансформеры [1], BERT [2], ResNet [3] и ансамбли этих моделей.

При построении модели оптимизируются два критерия: сложность и точ-

ность аппроксимации модели. Сложность определяет время, которое модель

требует для принятия решения, и интерпретируемость модели. Модель мень-

шей сложности является более предпочтительной [4]. С учетом снижения

сложности требуется сохранить приемлемой точность аппроксимации. В дан-

ной статье рассматривается метод дистилляции модели, предназначенный

¹ Настоящая статья содержит результаты проекта Математические методы интеллекту-

ального анализа больших данных, выполняемого в рамках реализации Программы Центра

компетенций Национальной технологической инициативы “Центр хранения и анализа боль-

ших данных”, поддерживаемого Министерством науки и высшего образования Российской

Федерации по Договору МГУ им. М.В. Ломоносова с Фондом поддержки проектов На-

циональной технологической инициативы от 11.12.2018 № 13/1251/2018. Работа выполнена

при поддержке Российского фонда фундаментальных исследований (проекты 19-07-01155,

19-07-00875, 19-07-00885).

150

для снижения сложности при сохранении точности моделей. Этот метод стро-

ит новые модели на основе ранее обученных моделей.

Определение 1. Дистилляция модели снижение ее сложности пу-

тем выбора из множества более простых моделей с использованием отве-

тов более сложной модели.

Основным подходом дистилляции модели учителя в модель ученика является

метод, основанный на использовании ответов модели учителя при оптимиза-

ции модели ученика [5-10]. В первых публикациях по генерации псевдоме-

ток предлагается пополнить множество объектов редких классов с помощью

предобученной модели [6]. Это искусственно увеличивает объем обучающей

выборки. В [5] предложен метод, в рамках которого моделью учителя ге-

нерируются новые метки объектов. Эти метки соответствуют вероятностям

классов с некоторым параметром температуры, который позволяет увеличи-

вать или уменьшать дисперсию в полученных ответах учителя. В [5] проведен

ряд экспериментов по дистилляции моделей для разных задач машинного

обучения: эксперимент на выборке MNIST [11], в котором нейросеть избы-

точной сложности была дистиллирована в нейросеть меньшей сложности, и

эксперимент по распознаванию речи, в котором ансамбль моделей был ди-

стиллирован в одну модель. Также в [5] был проведен эксперимент по обу-

чению экспертных моделей на основе одной большой модели. В [8] предло-

жено добавить к новым вероятностным меткам, введенным Дж. Хинтоном,

метки классов, которые соответствуют предсказанному классу модели учи-

теля. Различные подходы к дистилляции рассматривают значение на про-

межуточных слоях модели учителя [12-14]. В [12, 14] обучение происходит

при помощи введения дополнительных матриц, которые выравнивают раз-

меры промежуточных слоев модели учителя и ученика. В [13] предложен

метод передачи селективности нейронов, основанный на минимизации мак-

симального среднего отклонения между выходами всех слоев модели учителя

и ученика.

Определение 2. Привилегированная информация множество при-

знаков, которые доступны только в момент выбора модели, но не в момент

тестирования.

В [15] В.Н. Вапником введено понятие привилегированной информации. В [7]

метод дистилляции [5] используется вместе с привилегированным обучени-

ем [15]. В предложенном методе на первом этапе обучается модель учителя

в пространстве привилегированной информации, после чего обучается модель

ученика в исходном признаковом пространстве, используя дистилляцию [5].

Для обучения строится функция ошибки специального вида. Эта функция

состоит из нескольких слагаемых, включая ошибки учителя, ученика и регу-

ляризирующие элементы. Первые варианты подобной функции ошибки были

предложены А.Г. Ивахненко [16].

Определение 3. Учитель

фиксируемая модель, ответы которой

используются при выборе модели ученика.

151

Определение 4. Ученик модель, которая выбирается согласно за-

данному критерию.

Данная статья посвящена вероятностной интерпретации методов дистил-

ляции, предложенных Дж. Хинтоном [5] и В.Н. Вапником [15]. В рамках веро-

ятностного подхода предлагаются анализ и обобщение функции ошибки [5, 7].

Рассматриваются задачи классификации и регрессии в [16]. В ходе вычисли-

тельного эксперимента обучается модель ученика с использованием модели

учителя и без использования модели учителя. Рассмотрены выборки задач

классификации изображений FashionMNIST [17] и классификации текстов

Twitter Sentiment Analysis [18]. Выборка FashionMNIST включена в экспери-

мент вместо выборки MNIST, так как последняя имеет приемлемое качество

аппроксимации даже для линейного классификатора. Вычислительный экс-

перимент рассматривает различные модели: линейную модель, полносвязную

нейронную сеть, сверточную нейронную сеть [19], модель Bi-LSTM [20] и мо-

дель BERT [2].

2. Постановка задачи обучения с учителем

Заданы множество объектов Ω и множество целевых переменных Y. Мно-

жество Y = {1, . . . , K} для задачи классификации, где K число классов,

множество Y = R для задачи регрессии. Для каждого объекта из ω_i ∈ Ω зада-

(

)

на целевая переменная y_i = y

ω_i

. Множество целевых переменных для всех

объектов обозначим Y. Для множества Ω задано отображение в признаковое

пространство Rⁿ:

ϕ:Ω→Rⁿ,

|Ω| = m,

где n размерность признакового пространства, а m число объектов в

множестве Ω. Отображение ϕ отображает объект ω_i ∈ Ω в соответствующий

ему вектор признаков x_i = ϕ(ω_i). Пусть для объектов Ω^∗ ⊂ Ω задана приви-

легированная информация

ϕ∗ : Ω^∗ → Rn∗ ,

|Ω^∗| = m^∗,

где m^∗ ≤ m число объектов с привилегированной информацией, n^∗ число

признаков в пространстве привилегированной информации. Отображение ϕ^∗

отображает объект ω_i ∈ Ω^∗ в соответствующий ему вектор признаков x^∗i =

= ϕ^∗(ω_i).

Множество индексов объектов, для которых известна привилегированная

информация, обозначим

{

I =

1 ≤ i ≤ m| для i-го объекта задана

}

привилегированная информация ,

а множество индексов объектов, для которых неизвестна привилегированная

информация, обозначимI = {1, . . . , m} \ I.

152

Пусть на множестве привилегированных признаков задана функция учи-

теля

(

)

x^∗

:Rn∗ →Y^∗,

где для задачи регрессии Y^∗ = R¹, а для задачи классификации Y^∗ является

единичным симплексом S_K в пространстве размерности K. Модель учителя f

(

)

ставит объекты X^∗ в соответствие объектам S, т.е. f

x^∗i

=s_i.

(

)

Требуется выбрать модель ученика g

из множества

{

}

(1)

G = g|g : Rⁿ → Y^∗ .

Например, для задачи классификации множество G обобщенно-линейные

модели

{

}

(

)

(

)

G_lin,cl

= g|g

W,x

= softmax

W∈R^n×K .

3. Постановка задачи Хинтона и Вапника

Рассмотрим описание метода, предложенного в публикациях [5, 7], в кото-

рых предполагается, что для всех данных доступна привилегированная ин-

формация I = {1, 2, . . . , m}. В [5] решается задача классификации:

D = {(x_i,y_i)}mi=1 ,

x_i ∈ Rⁿ, y_i ∈ Y = {1,... ,K},

где y_i класс объекта. Обозначим через y_i вектор вероятности класса объ-

екта x_i.

В постановке Хинтона рассматривается параметрическое семейство функ-

ций:

{

}

(

)

(2)

G_cl

= g|g = softmax

z:Rⁿ →RK ,

где z дифференцируемая параметрическая функция заданной структуры,

T параметр температуры. В качестве модели учителя f рассматривается

функция из множества F_cl:

{

}

(

)

(3)

F_cl

= f|f = softmax

v:Rⁿ →R^K ,

где v

дифференцируемая параметрическая функция, модель заданной

структуры, T параметр температуры. Свойства параметра температуры T :

1) при T → 0 получаем вектор, в котором один из классов имеет высокую

вероятность;

2) при T → ∞ получаем равновероятные классы.

153

Функция потерь L, в которой учитывается перенос информации от модели

учителя f к модели ученика g, имеет вид:

∑

(

)

∑

(

)



L_st

y^ki log g

x_i

T=1

i=1

k=1

}

исходная функция потерь

(4)

∑∑

(

)

(

)



x_i

log g

x_i

T=T₀

i=1 k=1|

}

слагаемое дистилляции



где ·

обозначает, что параметр температуры T в предыдущей функции

T=t

равняется t.

Получаем оптимизационную задачу

(

)

(5)

ĝ = arg min L_st

g∈G_cl

Публикация [7] обобщает метод, предложенный в [5]. Решение задачи оп-

тимизации (5) зависит только от вектора ответов модели учителя f. Следо-

вательно, признаковые пространства учителя и ученика могут различаться.

В этом случае получаем постановку задачи:

D = {(x_i,x^∗i,y_i)}mi=1 ,

x_i ∈ Rⁿ, x^∗i ∈ Rn∗, y_i ∈ {1,... ,K},

где x_i

информация, доступная на этапах обучения и контроля, а x^∗i

информация, доступная только на этапе обучения. Модель учителя принад-

лежит множеству моделей F^∗cl:

{

}

(

)

(6)

F^∗cl

= f|f = softmax

v^∗

x^∗

v^∗ : Rn∗ → R^K

где v^∗ дифференцируемая параметрическая функция заданной структуры,

T параметр температуры. Множество моделей F^∗cl отличается от множества

моделей F_cl из выражения (3). В множестве F_cl модели используют простран-

ство исходных признаков, а в множестве F^∗cl модели используют пространство

привилегированных признаков. Функция потерь (4) в случае модели учите-

ля f ∈ F^∗cl переписывается в виде:

(

)

∑∑

(

)

∑∑

(

)

(

)



(7)

L_st

y^ki log g

x_i

x^∗i

log g

x_i

T=1

T=T₀

i=1 k=1

Требуется построить модель, которая использует привилегированную ин-

формацию x^∗i при обучении. Для этого рассмотрим двухэтапную модель обу-

чения, предложенную в [7]:

1) выбираем оптимальную модель учителя f ∈ F^∗cl;

154

2) выбираем оптимальную модель ученика g ∈ G_cl, используя дистилля-

цию [5].

Модель ученика минимизирует (7). Модель учителя минимизирует кросс-

энтропийную функцию ошибки

(

)

∑∑

(

)

L_th

y^ki log f

x^∗i

i=1 k=1

4. Постановка задачи: вероятностный подход

4.1. Метод максимального правдоподобия

(

)

Задано распределение целевой переменной p

y_i|x_i,g

. Для поиска ĝ вос-

пользуемся методом максимального правдоподобия. В качестве ĝ выбирается

функция, которая максимизирует правдоподобие модели:

∏

(

)

(8)

ĝ = argmax p

y_i|x_i,g

g∈G

i=1

где множество G задается в (1).

4.2. Подход дистилляции модели учителя в модель ученика

Рассмотрим вероятностную постановку, в которой выполнены ограниче-

ния:

(

)

1) задано распределение целевой переменной p

y_i|x_i,g

;

2) задано совместное распределение целевой переменной и ответов модели

(

)

учителя p

y_i,s_i|x_i,g

;

3) для всех ω ∈ Ω^∗ элементы y(ω) и s(ω) являются зависимыми величинами,

так как ответы учителя должны коррелировать с истинными ответами;

4) если |Ω^∗| = 0, то решение должно соответствовать решению (8).

Рассмотрим совместное правдоподобие истинных меток и меток учителя:

(

)

∏

(

)∏

(

)

(9)

Y,S|X,g,I

= p

y_i|x_i,g

y_i,s_i|x_i,g

i∈I

(

)

Перепишем p

y_i,s_i|x_i,g

по формуле условной вероятности:

(

)

(

)

(

)

(10)

y_i,s_i|x_i,g

y_i|x_i,g

s_i|y_i,x_i,g

Подставляя выражения (10) в (9), получим

(

)

∏

(

)∏

(

)∏

(

)

Y,S|X,g,I

= p

y_i|x_i,g

s_i|y_i,x_i,g

i∈I

155

x_i

y_i

Cat

s_i

Рис. 1. Вероятностная модель в формате плоских нотаций.

x_i

Cat

dot

softmax

y_i

s_i

Рис. 2. Вероятностная модель, используемая в синтетическом эксперименте.

Заметим, что y_i и s_i зависимы только через переменную x_i, тогда

(

)

(

)

s_i|y_i,x_i,g

s_i|x_i,g

. Получаем совместное правдоподобие

(

)

∏

(

)∏

(

)∏

(

)

(11)

Y,S|X,g,I

= p

y_i|x_i,g

s_i|x_i,g

i∈I

Используя (11), получаем оптимизационную задачу для поиска ĝ

∏

(

)∏

(

)∏

(

)

(12)

ĝ = argmax

y_i|x_i,g

s_i|x_i,g

g∈G

i∈I

Для удобства будем минимизировать логарифм выражения. Тогда из (12)

получаем, что

∑

(

)

∑

(

)

ĝ = argmax

log p

y_i|x_i,g

+ (1 - λ) log p

y_i|x_i,g

g∈G

i∈I

(13)

∑

(

)

+ λ logp

s_i|x_i,g

i∈I

где параметр λ ∈ [0, 1] введен для взвешивания ошибок на истинных ответах

и ошибок ответов учителя.

156

На рис. 1 показан вид вероятностной модели в графовой нотации для про-

извольной функции g. Для каждой реализации g соответствующий блок тре-

бует уточнения. На рис. 2 показана более подробная реализация в случае,

когда g линейная модель.

5. Обучение с учителем для задачи классификации и регрессии

5.1. Случай классификации

Для задачи многоклассовой классификации рассматриваются вероятност-

ные п р е д п о л о ж е н и я:

1) рассматривается функция учителя f ∈ F^∗cl (6);

2) рассматривается функция ученика g ∈ G_cl (2);

3) для истинных меток рассматривается категориальное распределение

(

)

(

))

(

)

y|x, g

= Cat

, где g

задает вероятность каждого класса;

4) для меток учителя введем плотность распределения

(

)

∏

(

(14)

s|x, g

=C g_k

)_sk ,

k=1

где g^k

вероятность класса k, которую предсказывает модель ученика,

а s^k вероятность класса k, которую предсказывает модель учителя.

Теорема 1. Пусть вероятность каждого класса отделима от нуля и

единицы, т.е. для всех k выполняется условие

(

)

1>1-ε>g_k

> ε > 0.

Тогда при

K/2

∏

(

)

( )

C = (-1)^K K

g_k

log g_k

2K(K-1)/2

k=1

(

)

функция p

s|x, g

, определенная в (14), является плотностью распределе-

ния.

Доказательство. Во-первых, покажем, что для произвольного векто-

(

)

ра ответов s ∈ S_K выполняется p

s|x, g

≥ 0. Заметим, что для всех k выпол-

няется

(

)

log g_k

< 0,

тогда

K/2

∏

( )(

( ))

C =

g_k

- log g_k

> 0.

2K(K-1)/2

| {z }|

}

k=1

>ε

157

(

)

(

)

Так как g_k

> 0 и C > 0, получаем, что p

s|x, g

≥ 0. Во-вторых, покажем,

что интеграл по всему пространству ответов S_K является конечным:

∫

(

)

∏

(

∏

(

)_sk

)s^k

(15)

s|x, g

ds =

g_k

ds =

g_k

ds =

k=1

S_K

√

∫

∏

r^K-1

(

)_r

√

g_k

dr =

(K - 1)!

2K-1

k=1 0

√

∫

∏

(

)_r

√

r^K-1g_k

dr =

(K - 1)!

2K-1

k=1

}

∫

∏

(

))

=D^K

r^K-1 exp

r log g_k

dr =

k=1 0

∏

(

)(

(

)

(

)))

= (-D)^K log g_k

-Γ

K,- log g_k

k=1

∏

(

)(

(

)

(

))

(

))

= (-D)^K (K - 1)!^K log g_k

1-g_k

exp_K-1

- log g_k

+g_k

k=1

(

√ )K

∏

(

)(

(

)

(

))

(

))

log g_k

1-g_k

exp_K-1

- log g_k

+g_k

< ∞,

2K(K-1)/2

k=1

(

)

(

))

где Γ

является гамма-функцией, Γ

K,- log g_k

является неполной

(

)

гамма функцией, exp_n

является суммой Тейлора из первых n слагаемых.

(

)

(

)

В рамках приближенных расчетов будем считать, что exp_n

≈ exp

, то-

гда с учетом (15) получаем

∫

(

)

(

)

∏

(

)

(

)

(16)

g,x

= p

s|x, g

g_k

log g_k

2K(K-1)/2

k=1

S_K

Полученное выражение (16) заканчивает доказательство теоремы 1.

Из теоремы 1 следует, что плотность, введенная для меток учителя, яв-

ляется плотностью распределения. Поэтому можно воспользоваться выра-

жением (13). Используя предположения 1-4 и подставляя в (13), получаем

158

оптимизационную задачу:

∑∑

(

)



ĝ = argmax

y^ki log g_k

x_i

T=1

g∈G

i∈I k=1

∑∑

(

)

∑∑

(

)



(17)

+ (1 - λ)

y^ki log g_k

x_i

+λ

s_i,k log g_k

x_i

T=1

T=T₀

i∈I k=1

(

)

∑∑

(

)



+λ

log g_k

x_i



+ log log

(

)

T=T₀

g_k

x_i

i∈I k=1

Проанализировав выражение (17), получаем, что первые три слагаемых

совпадают со слагаемыми в выражении (4) при I = {1, . . . , m} и λ =¹² , а

четвертое слагаемое является некоторым регуляризатором, который получен

из вида распределения. Анализируя первые три слагаемых в выражении (17)

при T₀ = 1, получаем сумму кросс-энтропий между двумя распределениями

для каждого объекта:

1) первое распределение это выпуклая комбинация с весами 1 - λ и λ рас-

(

)

пределения, задаваемого метками объектов Cat

, и распределения, за-

(

)

даваемого моделью учителя Cat

;

2) второе распределение

это распределение, задаваемое моделью учени-

(

))

ка Cat

Следовательно, модель ученика восстанавливает плотность не исходных

меток, а новую плотность, которая является выпуклой комбинацией плотно-

сти исходных меток и меток учителя.

5.2. Случай регрессии

Для задачи регрессии рассматриваются вероятностные предположения:

1) рассматривается функция учителя f ∈ F^∗rg,

{

}

(

)

F^∗rg = f|f = v^∗

x^∗

v^∗ : Rn∗ → R ,

где v^∗ дифференцируемая параметрическая функция;

2) рассматривается функция ученика g ∈ G_rg,

{

}

(

)

G_rg

= g|g = z

z:Rⁿ →RK ,

где z дифференцируемая параметрическая функция;

3) истинные метки имеют нормальное распределение

(

)

(

)

y|x, g

y|g

,σ

;

4) метки учителя имеют распределение

(

)

(

)

s|x, g

s|g

,σ_s

159

Используя предположения 1-4 и подставляя в (13), получаем оптимизацион-

ную задачу:

∑

(

))₂

ĝ = argmin

σ²

y_i - g

x_i

g∈G

i∈I

(18)

∑

(

))

(

))

+ (1 - λ) σ²

y_i - g

x_i

² +λ σ^2s

s_i - g

x_i

².

i∈I

Выражение (18) записано с точностью до аддитивной константы относитель-

но g.

Теорема 2. Пусть множество G описывает класс линейных функций

(

)

вида g

= w^Tx. Тогда решение оптимизационной задачи (18) эквивалент-

но решению задачи линейной регрессии:

(

)

(19)

y^′′ = Xw + ε,

ε∼N

0, Σ

(

)

где Σ^-1 = diag

σ^′

и y^′′ имеют вид:

{

σ², если i ∈ I,

σ^′i =

(1 - λ) σ² + λσ^2s, иначе,

(20)

y^′′ = Σy^′,

{

σ²yi, если i ∈ I,

y^′i =

(1 - λ) σ²y_i + λσ^2ss_i, иначе.

Доказательство. Обозначим a_J = [a_i|i ∈ J]^T, где a произвольный

вектор, а J произвольное непустое индексное множество. Подвектор век-

тора ответов y, для элементов которого доступна привилегированная ин-

формация, обозначим y_I = [y_i|i ∈ I]^T. Аналогично обозначим матрицу X_I =

= [x_i|i ∈ I]^T.

(

)

В случае линейной модели g

= w^Tx выражение (18) принимает вид:

ŵ = arg min

σ² (y¯I - X¯Iw)^T (y¯I - X¯Iw)+

w∈W

+ σ2 (1 - λ)(y_I - X_Iw)T (y_I - X_Iw) + σ^2sλ(s_I - X_Iw)T (s_I - X_Iw).

Раскроем скобки и сгруппируем:

(

)

ŵ = arg min

σ²

w^TX^¯IXIw - 2y^¯IXIw +

w∈W

(

)

(

)

+ (1 - λ) σ² w^TX^TIX_I w - 2y^TIX_I w

+ λσ²

w^TX^TIX_Iw - 2s^TIX_Iw .

Продифференцируем выражение, приравняем к нулю и сгруппируем элемен-

ты:

(

)

σ²X^¯IXI + (1 - λ) σ²X^IXI + λσ^sX^IXI w =

(21)

= 2σ²X^¯IyI + 2 (1 - λ) σ²X^IyI + 2λσ^sX^IsI .

160

Воспользуемся равенствами:

σ²X^¯IX¯I + (1 - λ)σ²X^IXI + λσ^sX^IXI = X^TΣ^-1X,

(22)

2σ²X^¯IyI + 2 (1 - λ) σ²X^IyI + 2λσ^sX^IsI = 2Xy^′,

где Σ и y^′ из условия задачи (20).

Подставляя (22) в (21), получаем:

(

)_-1

w=2 X^TΣ^-1X

XΣ^-1y^′′,

что соответствует решению задачи (19). Теорема 2 доказана.

Теорема 2 показывает, что обучение с учителем для задачи регрессии мож-

но свести к задаче оптимизации в линейной регрессии.

6. Вычислительный эксперимент

Проводится вычислительный эксперимент для анализа моделей, которые

получены путем дистилляции модели учителя в модель ученика. Как пока-

зано в теореме 2, задачу регрессии с учителем можно свести к задаче ре-

грессии без учителя, поэтому в эксперименте рассматривается только случай

классификации. Во всех частях вычислительного эксперимента для поиска

оптимальных параметров нейросетей использовался градиентный метод оп-

тимизации Adam [21].

6.1. Выборка FashionMNIST

Эксперимент проводился для задачи классификации для выборки Fashion-

MNIST [17]. В качестве модели учителя f рассматривается нейросеть с двумя

сверточными слоями и с тремя полносвязными слоями, в качестве функции

активации рассматривается ReLu. Модель учителя содержит

30 тысяч обу-

чаемых параметров. В качестве модели ученика рассматривается модель ло-

гистической регрессии для многоклассовой классификации. Модель ученика

содержит 7850 обучаемых параметров.

Студент без учителя

0,54

Студент без учителя

0,6

Студент с учителем

0,52

0,50

0,5

0,48

0,46

0,4

0,44

100

Итерации

Рис. 3. Зависимость кросс-энтропии между истинными метками и предска-

занными учеником вероятностями классов: а на обучающей выборке; б

на тестовой выборке.

161

На рис. 3 показан график зависимости кросс-энтропии между истинными

метками объектов и вероятностями, которые предсказывает модель ученика.

На графике сравнивается модель, которая обучалась без учителя (в задаче

оптимизации (17) присутствует только первое слагаемое) с моделью, которая

была получена путем дистилляции модели нейросети в линейную модель. Из

графика видно, что обе модели начинают переобучаться после 30-й итерации.

Но модель, которая получена путем дистилляции, переобучается не так быст-

ро: ошибка на тестовой выборке растет медленнее, а на обучающей выборке

падает также медленнее.

В таблице показано, что для выборки FashionMnist итоговые модели уче-

ника с учителем и без учителя сравнимы по точности и кросс-энтропийной

ошибке, если учитывать дисперсию этих величин.

6.2. Синтетический эксперимент

Проанализируем модель на синтетической выборке. Выборка построена

следующим образом:

[

(

)]

[

(

)]

w_jk|0,1

x_ij|0,1

n×K

m×n

[

(

)]

S = softmax(XW), y =

Cat

y_i|s_i

где функция softmax берется построчно. Строки матрицы S будем рассмат-

ривать как предсказание учителя, т.е. учитель знает истинные вероятности

каждого класса. На рис. 2 показана вероятностная модель в графовой но-

тации. В эксперименте число признаков n = 10, число классов K = 3, для

обучения было сгенерировано m_train = 1000 и m_test = 100 объектов.

На рис. 4 показано распределение по классам для 20 объектов из обучаю-

щей выборки. Каждому столбцу на графике соответствует объект, а каждой

строке соответствует вероятность класса. Видно, что для каждого рассмот-

ренного объекта вероятности разных классов близки. Получается, что если

в качестве истинных меток взять класс с максимальной вероятностью, то

выборка будет сильно зашумленной и модель будет описывать эти данные

некорректно.

Построим в качестве ученика линейную модель, которая минимизирует

кросс-энтропийную (первое слагаемое в формуле (17)). Представление данной

модели в виде графовой модели показано на рис. 2.

На рис. 5 показано распределение вероятностей классов, которое предска-

зала модель. Видно, что полученное распределение не соответствует истин-

ному, так как модель сосредотачивает всю вероятность в одном классе.

Рассмотрим модель, которая учитывает информацию об истинных распре-

делениях на классах для каждого объекта. Для этого будем минимизировать

первые три слагаемых в формуле (17) при T₀ = 1 и λ = 0,75. В качестве меток

учителя s_i,k использовались истинные вероятности для каждого класса дан-

ного объекта. На рис. 6 показано распределение, которое дала модель. В дан-

ном случае видно, что распределения являются сглаженными. Концентрации

всей вероятности в одном классе не наблюдается.

162

1,0

0,8

0,6

0,4

0,2

Рис. 4. Истинное распределение объектов по классам.

1,0

0,8

0,6

0,4

0,2

Рис. 5. Распределение, предсказанное моделью без использования информа-

ции об истинном распределении на классах.

1,0

0,8

0,6

0,4

0,2

Рис. 6. Распределение, предсказанное моделью с использованием информации

об истинном распределении на классах.

Заметим, что в данном примере предполагается, что модель учителя учи-

тывает не только метки классов, но и распределение на метках классов, в то

время как в выборке {X, y} имеются только точечные оценки в виде меток.

В данном примере используются истинные распределения в качестве пред-

сказаний учителя, но их можно заменить предсказаниями модели учителя,

которая предсказывает не только сами метки, но и их распределение для

каждого объекта.

На рис. 7 показана зависимость вероятности верного класса от температу-

ры T и параметра доверия λ для одного из объектов из тестовой выборки. На

рис. 7 видно, что изменение температуры T влечет изменение концентрации

вероятностной меры. При уменьшении параметра температуры и приближе-

нии его к нулю наблюдаем, что вероятность одного из классов приближается

к единице, а остальных классов к нулю. С другой стороны, при увеличении

параметра температуры вероятности классов сглаживаются и распределение

классов для каждого объекта становится близким к равномерному.

В таблице в колонке “Кросс-энтропийная ошибка с реальными вероятно-

стями” показано сравнение кросс-энтропии в случае, если в качестве истин-

163

0,30

0,9

0,25

0,20 0,25

0,25

0,8

0,15

0,20

0,50

0,7

0,10

0,15

1,00

0,6

1,00

0,05

0,10

0,5

0,05

0,25

0,50

0,25

0,50

0,25

0,50

0,200

0,25

0,180

0,9

0,150

0,20

0,50

0,8

0,50

0,120

0,50

0,15

0,100

0,7

0,075

0,10

1,00

0,050

1,00

0,05

0,6

0,025

0,25

0,50

0,25

0,50

0,25

0,50

0,25

0,34

0,25

0,65

0,33

0,20

0,60

0,32

0,50

0,31

0,50

0,55

0,15

0,30

0,50

0,29

0,10

1,00

0,28

1,00

0,45

0,27

0,05

0,40

0,25

0,50

0,25

Рис. 7. Иллюстрация распределения вероятности предсказания классов при

различных значениях λ и T .

ных вероятностей меток рассмотреть не onehot-кодированные вероятности

классов, а истинные вероятности:

(

)

∑∑

(

)

L_real

s^ki log g_k

x_i

i=1 k=1

где g модель ученика. Видно, что модель с учителем лучше аппроксими-

рует истинные вероятности классов. Также в таблице представлено среднее

значение разницы максимальной вероятности с минимальной вероятностью

для каждого объекта:

(

)

(

)

∑

(

)

(

)

L_maxmin

maxgk

x_i

- mingk

x_i

i=1

Видно, что модель учителя имеет меньшую разницу между вероятностями

классов, т.е. вероятности классов не концентрируются в одном классе.

6.3. Выборка Twitter Sentiment Analysis

Проводится эксперимент на выборке Twitter Sentiment Analysis. Данная

выборка содержит короткие сообщения, для которых требуется предсказать

эмоциональный окрас: содержит твит позитивный окрас или негативный. Вы-

борка разделена на 1,18 млн твитов для обучения и 0,35 млн твитов для

164

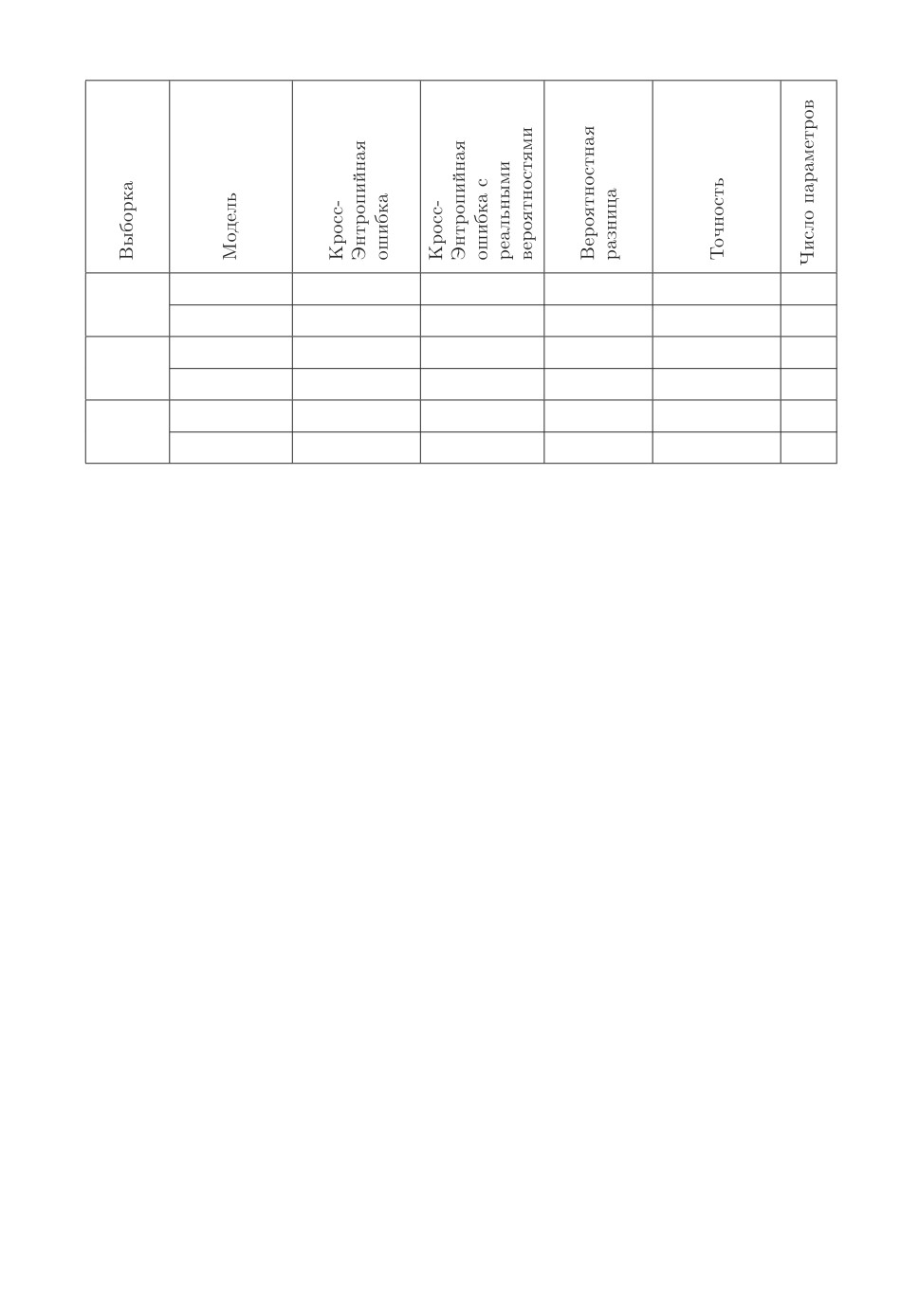
Таблица. Сводная таблица результатов вычислительного эксперимента

с учителем

0,453 ± 0,003

0,84 ± 0,13

0,842 ± 0,002

7850

Fashion-

Mnist без учителя 0,461 ± 0,005

0,86 ± 0,18

0,841 ± 0,002

7850

с учителем

0,618 ± 0,001

1,17 ± 0,05

0,45 ± 0,20

0,828 ± 0,002

Systetic

без учителя

0,422 ± 0,002

2,64 ± 0,02

0,75 ± 0,22

0,831 ± 0,001

с учителем

0,489 ± 0,003

0,79 ± 0,17

0,764 ± 0,005

1538

Twiter

без учителя

0,501 ± 0,006

0,83 ± 0,22

0,747 ± 0,004

1538

тестирования. В твитах была выполнена предобработка: все твиты были пе-

реведены в нижний регистр, все никнеймы вида “@andrey” были заменены на

токен “name”, все цифры были заменены на токен “number”.

Результаты данной части эксперимента показаны в таблице. В качестве

модели учителя использовалась модель Bi-LSTM с линейным слоем на вы-

ходе. В качестве векторного представления токенов обучалась матрица па-

раметров. В ней каждая строка соответствует токену из обучающей выбор-

ки. Суммарное число обучаемых параметров модели учителя составляет бо-

лее 30 млн. Обученная модель учителя имеет точность предсказания 0,835.

В качестве модели ученика рассматривается линейная модель с 1538 пара-

метрами, где в качестве векторного представления предложения рассматри-

вается выход предобученной модели BERT с размерностью векторного про-

странства 768. Признаковое описание модели учителя и модели ученика раз-

личаются. Модель учителя в качестве признакового описания рассматрива-

ет исходные слова в предложении. Модель ученика в качестве признакового

описания использует готовое векторное представление предложения, которое

получено при помощи модели BERT.

В таблице показано качество модели ученика с использованием предска-

зания модели учителя и без него. В рамках данных результатов качество

модели ученика с дистилляцией выше, чем модели ученика без дистилляции,

но разница находится в пределах погрешности, что не позволяет говорить о

значительных улучшениях качества.

Программное обеспечение для проведения экспериментов и проверки ре-

зультатов находится в [22].

7. Заключение

В данной статье проанализирована задача обучения модели ученика с по-

мощью модели учителя. Исследован метод дистилляции и привилегированно-

165

го обучения. Предложено вероятностное обоснование дистилляции. Введены

вероятностные предположения, описывающие дистилляцию моделей. В рам-

ках данных вероятностных предположений проанализированы модели для

задачи классификации и регрессии. Результат анализа сформулирован в ви-

де теорем 1 и 2.

Теорема 2 показала, что обучение линейной регрессии с учителем эквива-

лентно замене обучающей выборки и вероятностных предположений о рас-

пределении истинных ответов. Для задачи классификации ответы учителя

дают дополнительную информацию в виде распределения классов для каж-

дого объекта из обучающей выборки. Данная информация не может быть

представлена в виде задачи классификации. Требуется ввести распределе-

ние, которое представлено в теореме 1.

В вычислительном эксперименте сравниваются модели ученика, которые

обучены с использованием модели учителя и без него. В таблице показаны ре-

зультаты вычислительного эксперимента для разных выборок. Показано, что

точность аппроксимации выборки учеником улучшается при использовании

модели учителя. Задача регрессии не приведена в вычислительном экспери-

менте, так как в теореме 2 была показана ее эквивалентность задаче линейной

регрессии. Для задачи классификации проведен вычислительный экспери-

мент. Из вычислительного эксперимента видно, что дистилляция влияет на

распределение классов в рамках одного объекта. Вероятности классов для

каждого объекта являются более разреженными, а не концентрируются в од-

ном классе. Данное свойство хорошо видно в синтетической выборке, так как

она генерировалась с максимальной дисперсией в вероятностях классов.

Основным результатом данной статьи является вероятностная интерпре-

тация задачи дистилляции. Рассмотрен частный случай, когда признаковые

описания модели учителя и ученика совпадают. В рамках вычислительно-

го эксперимента проведен анализ ответов модели ученика с использованием

модели учителя и без нее. Из результатов эксперимента видно, что модель

ученика наследует распределение вероятностей по классам от модели учи-

теля. Когда модель учителя адекватно описывает данные, описание данных

моделью ученика также улучшается, что показано в вычислительном экспе-

рименте на синтетических данных.

В дальнейшем предполагается обобщить метод максимального правдопо-

добия для дистилляции моделей с помощью байесовского подхода выбора

моделей машинного обучения. Также в рамках байесовского подхода плани-

руется развить методы повышения качества не только для задачи классифи-

кации, но и для задачи регрессии.

СПИСОК ЛИТЕРАТУРЫ

1. Vaswani A., Gomez A., Jones L., Kaiser L., Parmar N., Polosukhin I., Shazeer N.,

Uszkoreit J. Attention Is All You Need // Advances in Neural Information Processing

Syst. 2017. V. 5. P. 6000-6010.

2. Devlin J., Chang M., Lee K., Toutanova K. BERT: Pre-training of Deep Bidirec-

tional Transformers for Language Understanding // Proc. 2019 Conf. North Amer-

166

ican Chapter of the Association for Computational Linguistics: Human Language

Technologies. Minnesota. 2019. V. 1. P. 4171-4186.

He K., Ren S., Sun J., Zhang X. Deep Residual Learning for Image Recognition //

Proc. IEEE Conf. on Computer Vision and Pattern Recognition. Las Vegas. 2016.

P. 770-778.

Бахтеев О.Ю., Стрижов В.В. Выбор моделей глубокого обучения субопти-

мальной сложности // АиТ. 2018. № 8. С. 129-147.

Bakhteev O.Yu., Strijov V.V. Deep Learning Model Selection of Suboptimal Com-

plexity // Automat. Remote Control. 2018. V. 79. P. 1474-1488.

Hinton G., Dean J., Vinyals O. Distilling the Knowledge in a Neural Network //

NIPS Deep Learning and Representation Learning Workshop. 2015.

Bucilu C., Caruana R., Mizil A. Model compression // Proc. ACM SIGKDD Conf.

on Knowledge Discovery and Data mining. Philadelphia. 2006. P. 535-541.

Lopez-Paz D., Bottou L., Scholkopf B., Vapnik V. Unifying Distillation and Privi-

leged Information // Int. Conf. on Learning Representations. Puerto Rico. 2016.

Tang Z., Wang D., Zhang Z. Recurrent neural network training with dark knowledge

transfer // Proc. IEEE Conf. on Acoustics, Speech and Signal Processing. Shanghai.

2016. V. 2. P. 5900-5904.

Darrell T., Hoffman J., Saenko K., Tzeng E. Simultaneous deep transfer across

domains and tasks // Proc. IEEE Conf. on Computer Vision. Santiago. 2015. V. 2.

P. 4068-4076.

10.

Ahn S., Dai Z., Damianou A., Hu S., Lawrence N. Variational information distilla-

tion for knowledge transfer // Proc. IEEE Conf. on Computer Vision and Pattern

Recognition. Long Beach. 2019. P. 9163-9171.

11.

Burges C., Cortes C., LeCun Y. The MNIST dataset of handwritten digits. 1998.

http://yann.lecun.com/exdb/mnist/index.html.

12.

Che Z., Chen Y., Guoping H., Liu W., Wang T., Ziqing Y. TextBrewer: An Open-

Source Knowledge Distillation Toolkit for Natural Language Processing // Proc. 58th

Annual Meeting of the Association for Computational Linguistics: System Demon-

strations. Online. 2020.

13.

Huang Z., Naiyan W. Like What You Like: Knowledge Distill via Neuron Selectivity

Transfer // arXiv:1707.01219. 2017.

14.

Fu T., Lei Z., Liao S., Mei T., Wang S., Wang X. Exclusivity-Consistency Regu-

larized Knowledge Distillation for Face Recognition // Lect. Notes in Computer Sci.

2020. V. 1 P. 23-69.

15.

Vapnik V., Izmailov R. Learning Using Privileged Information: Similarity Control

and Knowledge Transfer // J. of Machine Learning Research. 2015. V. 16. P. 2023-

2049.

16.

Ivakhnenko A., Madala H. Inductive Learning Algorithms for Complex Systems Mod-

eling. Boca Raton: CRC Press Inc. 1994.

17.

Rasul K., Vollgraf R., Xiao H. Fashion-MNIST: a Novel Image Dataset for Bench-

marking Machine Learning Algorithms // arXiv preprint arXiv:1708.07747. 2017.

18.

Kozareva Z., Nakov P., Ritter A., Rosenthal S., Stoyanov V., Wilson T. SemEval-

2013 Task 2: Sentiment Analysis in Twitter // Proc. Seventh Int. Workshop on

Semantic Evaluation (SemEval 2013). Atlanta. 2013. P. 312-320.

19.

Boser B., Denker J., Henderson D., Howard R., Hubbard W., Jackel L., LeCun Y.

Backpropagation Applied to Handwritten Zip Code Recognition // Neural Compu-

tation. 1989. V. 1. No. 4. P. 541-551.

167