Автоматика и телемеханика, № 10, 2022
© 2022 г. А.И. БАЗАРОВА (bazarova.ai@phystech.edu),
А.В. ГРАБОВОЙ (grabovoy.av@phystech.edu)
(Московский физико-технический институт),
В.В. СТРИЖОВ, д-р физ.-мат. наук (strijov@phystech.edu)
(Вычислительный центр им. А.А. Дородницына ФИЦ ИУ РАН, Москва)
АНАЛИЗ СВОЙСТВ ВЕРОЯТНОСТНЫХ МОДЕЛЕЙ
В ЗАДАЧАХ ОБУЧЕНИЯ С ЭКСПЕРТОМ1
Работа посвящена построению интерпретируемых моделей машинного
обучения. Решается задача аппроксимации набора фигур на контурном
изображении. Вводятся предположения, что фигуры являются кривыми
второго порядка. При аппроксимации фигур используются информация о
типе, расположении и форме кривых, а также о множестве их возможных
преобразований. Такая информация называется экспертной, а метод ма-
шинного обучения, основанный на экспертной информации, называется
обучение с экспертом. Предполагается, что набор фигур аппроксимиру-
ется набором локальных моделей. Каждая локальная модель, основанная
на экспертной информации, аппроксимирует одну фигуру на контурном
изображении. Для построения моделей предлагается отображать кривые
второго порядка в пространство признаков, в котором каждая локаль-
ная модель является линейной. Таким образом, кривые второго порядка
аппроксимируются набором линейных моделей. В вычислительном экс-
перименте рассматривается задача аппроксимации радужной оболочки
глаза на контурном изображении.
Ключевые слова: смесь экспертов, экспертное обучение, линейные модели,
интерпретируемые модели.
DOI: 10.31857/S0005231022100051, EDN: AKCUFQ
1. Введение
Современные решения задачи классификации изображений на основе се-
тей глубокого обучения ResNet, VGG, Intercept [1] представляют собой плохо
интерпретируемые модели [2]. В [3, 4] показано, что сети глубокого обучения
являются не устойчивыми даже к небольшому шуму в данных [5].
В данной работе предлагается метод обучения с экспертом. Метод предпо-
лагает использование экспертной информации для повышения качества ап-
проксимации, а также для получения интерпретируемых моделей машинно-
го обучения. Предметные знания экспертов о данных называются эксперт-
ная информация. Предполагается, что использование экспертной информа-
ции позволяет аппроксимировать выборку простыми интерпретируемыми мо-
1 Исследование выполнено при финансовой поддержке Российского фонда фундамен-
тальных исследований в рамках научных проектов 20-37-90050, 19-07-01155 и проекта На-
циональной технологической инициативы 13/1251/2018.
47
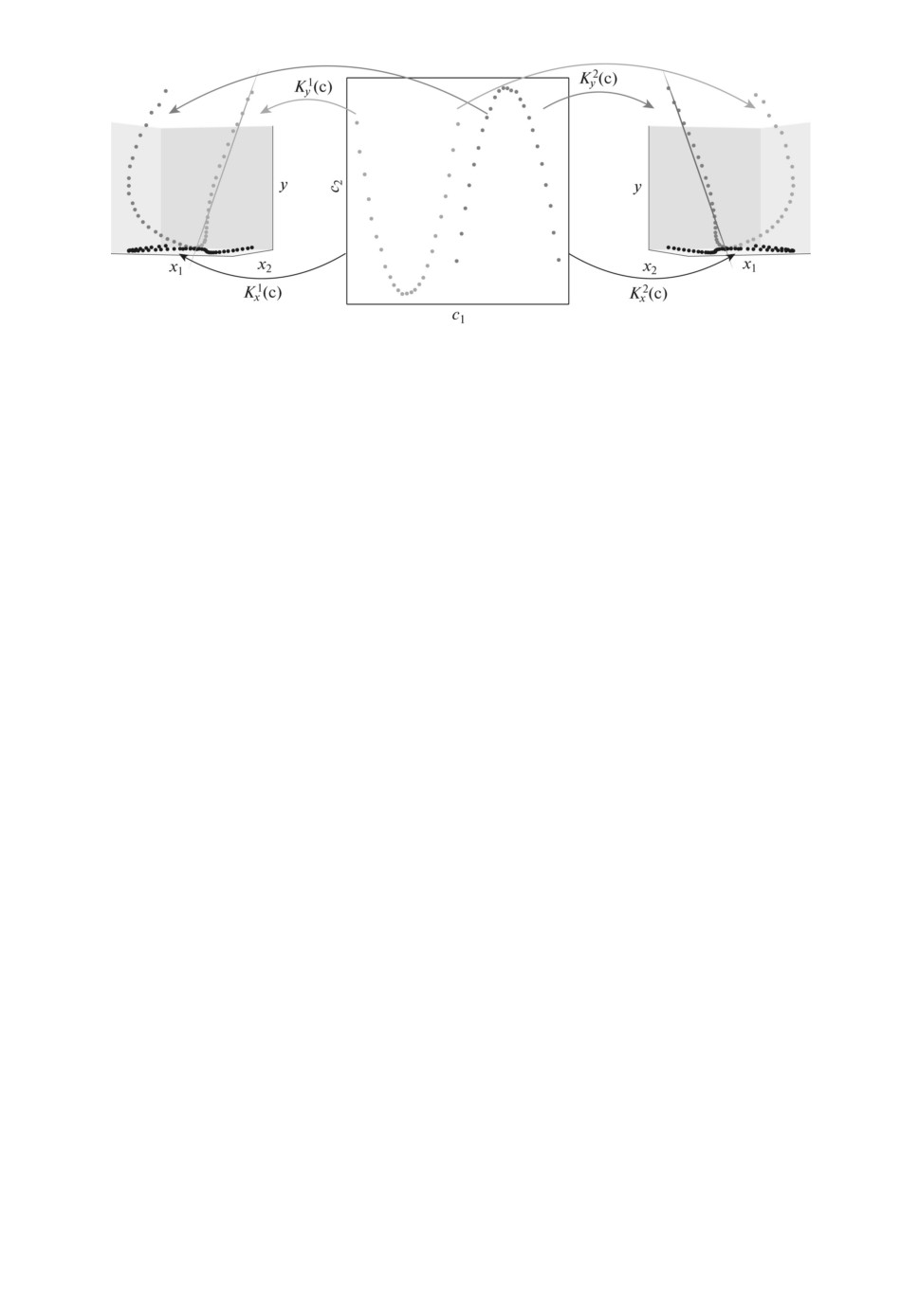
Рис. 1. Визуализация экспертной информации в случае с двумя экспертами.
Слева направо: экспертная информация первого эксперта; исходные данные;
экспертная информация второго эксперта.
делями, такими как линейные модели. Метод машинного обучения, учиты-
вающий экспертные знания при построении моделей, называется обучение с
экспертом. В данной работе решается задача аппроксимации кривых вто-
рого порядка на контурном изображении. В работе анализируются кривые
второго порядка, так как они описываются линейными моделями. Парамет-
ры кривых второго порядка необходимо восстановить в задаче распознавания
радужной оболочки глаза [6-8], в задаче описания трека частицы в адронном
коллайдере [9]. Экспертная информация о кривой второго порядка отобража-
ет точки на плоскости в новое признаковое описание объекта. Каждая кри-
вая аппроксимируется одной линейной моделью. Модель, аппроксимирующая
кривую, называется локальной моделью. Для аппроксимации всего контурно-
го изображения требуется аппроксимация нескольких кривых второго поряд-
ка с использованием локальных моделей. Вводятся следующие ограничения
на изображения: а) изображение состоит только из кривых второго порядка;
б) изображение аппроксимируется небольшим числом кривых второго поряд-
ка; в) известно число и тип кривых на изображении.
На рис. 1 показан пример кривых второго порядка, а также экспертная
информация о кривых. Рассматривается пример двух кривых, которые зада-
ются своим цветом. На центральном изображении показаны точки, лежащие
на кривых, а на рисунках справа и слева представлены экспертные признако-
вые описания рассмотренных кривых. В каждом из экспертных признаковых
описаний получаем, что одна из кривых аппроксимируется линейной моде-
лью, а вторая яв(я)тся (ш)мом(о)носи(е)ьно построенной линейной модели.
Отображение K1x
c
,K2x
c
,K1y
c
,K2y
c
описываeтся на основе экспертной
информации. На рис. 1 слева показана экспертная информация о первом экс-
перте. С использованием этой информации первая кривая аппроксимируется
линейной моделью, а вторая кривая представляет собой шум. На рис. 1 справа
показана экспертная информация второго эксперта. С использованием этой
информации вторая кривая аппроксимируется линейной моделью, а первая
кривая представляет собой шум.
48
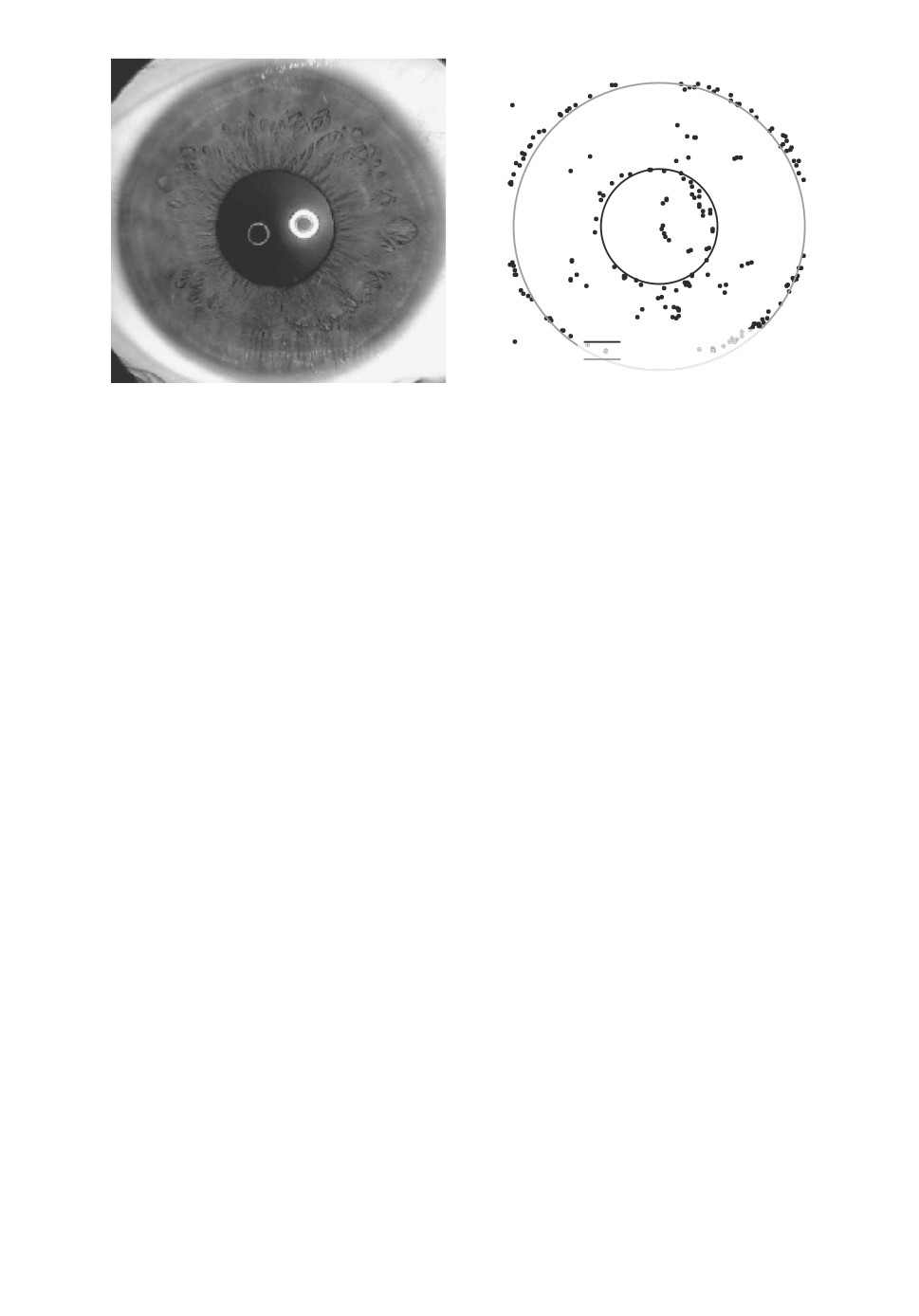
Внутренняя окружность
Внешняя окружность
Рис. 2. Пример изображения радужной оболочки глаза и его контурное пред-
ставление. Слева: изображение радужной оболочки глаза. Справа: контурное
изображение радужной оболочки и аппроксимирующие заданное изображение
окружности.
При аппроксимации нескольких кривых на одном контурном изображе-
нии строится мультимодель. Примером мультимоделей является случайный
лес [10], бустинг деревьев [11], смесь экспертов [12]. В данной работе в ка-
честве мультимодели рассматривается смесь экспертов. Смесь экспертов
это мультимодель, которая линейно взвешивает локальные модели, аппрок-
симирующие часть выборки. Значения весовых коэффициентов зависят от
объекта, для которого делается прогноз. Для решения задачи используется
вариационный EM-алгоритм [13-16]. Смесь экспертов имеет множество при-
менений в ряде приложений. В [17] решается задача классификации текстов.
В [18-24] смесь экспертов используется для прогнозирования временных ря-
дов, для распознавания речи, распознавания повседневной деятельности че-
ловека и прогнозирования стоимости ценных бумаг. В [14] рассматривалась
смесь экспертов для решения задачи распознавания рукописных цифр на
изображениях.
В качестве примера рассматривается задача аппроксимации изображения
радужной оболочки глаза. На рис. 2 показан пример изображения, которое
необходимо аппроксимировать. В данной работе рассматривается обработан-
ное изображение в виде контурного изображения.
Для задачи аппроксимации радужной оболочки используется экспертная
информация: радужная оболочка глаза аппроксимируется двумя концентри-
ческими окружностями. Экспертная информация используется для построе-
ния описания признаков точек плоскости, а также для построения регуляри-
затора в функции оптимизации. Часть функции ошибок для оптимизации,
использующая экспертную информацию, называется регуляризатором. Та-
ким образом, информация о том, что изображение является окружностями,
задается видом признакового описания, а информация о том, что окружности
концентрические, задается с помощью специального регуляризатора.
49
Вычислительный эксперимент анализирует качество аппроксимации кон-
турного изображения в зависимости от экспертной информации и уровня
шума в синтетически сформированных данных. Проведен анализ качества
аппроксимации радужной оболочки в зависимости от объема экспертной ин-
формации, которая использовалась для построения модели. Каждое аппрок-
симированное изображение представляет собой отдельный набор точек, ко-
торые необходимо аппроксимировать.
2. Постановка задачи восстановления параметров
кривых второго порядка на изображении
Задано бинарное изображение
M ∈ {0,1}m1×m2,
где 1 соответствует черной точке изображения, а 0 соответствует белой точке
фона. С использованием изображения M строится выборка C, элементами
которой являются координаты (xi, yi) черных точек:
C∈RN×2.
Каждый эксперт предполагает, что изображение состоит из кривой второго
порядка Ω. Пусть для множества точек C ∈ RN×2, образующих кривую Ω,
задана экспертная информация о фигуре E(Ω). Множество E(Ω) состоит из
ожидаемого экспертом образа Ω и множества его допустимых преобразова-
ний. На основе экспертного описания введем отображения в задачу аппрок-
симации:
(
)
(
)
(1)
Kx
E(Ω)
:R2 →Rn, Ky
E(Ω)
:R2
→ R,
где Kx отображение объектов в признаковое описание объектов, n число
признаков, а Ky отображение в целевую переменную для аппроксимации.
Применяя отображения Kx, Ky для выборки C поэлементно, получаем:
(
)
(
)
(2)
Kx
E(Ω
, c) = x, Ky
E(Ω), c
= y,
где c = (xi, yi) точка из множества точек C.
Применяя отображения (2) к исходному множеству точек C, получаем
выборку
(3)
D = {(x,y) | ∀c ∈ C x = Kx(c), y = Ky
(c)} .
Получаем, что исходная задача аппроксимации кривой Ω сводится к ап-
проксимации выборки D. В работе предполагается, что выборка D аппрок-
симируется линейной моделью:
g(x, w) = xTw,
где w вектор параметров для аппроксимации.
50
Для нахождения оптимального вектора параметров ŵ решается оптими-
зационная задача
∑
ŵ = arg min
∥g(x, w) - y∥22.
w∈Rn
(x,y)∈D
Задача аппроксимации исходной кривой Ω сводится к решению задачи
линейной регрессии, т.е. к нахождению компонент вектора ŵ.
В случае, когда на изображении K кривых второго порядка Ω1, . . . , ΩK ,
где для каждой задана экспертная информация Ek = E(Ωk), k ∈ {1, . . . , K}
получаем задачу построения мультимодели, которая называется смесью K
экспертов.
Определение 1. Назовем мультимодель f смесью K экспертов
∑
∑
f = πk(x,V)gk(wk), πk(x,V) : Rn×|V| → [0, 1],
πk(x,V) = 1,
k=1
k=1
где gk
локальная модель, называемая экспертом. Вектор x признако-
вое описание объекта, πk
шлюзовая функция, вектор wk параметры
локальной модели, V являются параметрами шлюзовой функции.
Для каждой кри(о) втор(го по)ядка(Ω) зада(ы от)бражения (1). Вве-
дем обозначения: Kkx
c
=Kx
Ωk,c
иKky
c
=Ky
Ωk,c
. Используя локаль-
ные линейные модели gk, строим мультимодель f, описывающую кривые
Ω1,... ,ΩK на изображении M:
∑
∑
(
(4)
f =
πk(c,V)gk(Kkx
c), wk
),
c∈C k=1
где πk( шлюзовая ф(нкция. В работе рассматривается случай, когда x =
= K1x
c) = . . . = KKx
c). В этом случае выражение (4) переписывается в
виде
∑
∑
f =
πk(x,V)gk(x,wk),
c∈C k=1
где шлюзовая функция πk имеет вид
∑
πk(x,V) : Rn×|V| → [0, 1],
πk(x,V) = 1,
k=1
где V параметры функции шлюза, а gk локальная модель.
51
В работе рассматривается следующий вид шлюзовой функции:
(
)
π(x, V) = softmax
VT1σ(VT2x)
,
где V = {V1, V2} параметры шлюзовой функции, V1 ∈ Rp×k, V2 ∈ Rn×p.
Для нахождения оптимальных параметров мультимодели решается опти-
мизационная задача
∑
∑
(
)
(5)
L=
πk(x,V)(y - wTkx)2 + R
V,W,E(Ω)
→ min,
V,W
(x,y)∈D k=1
(
)
где W = [w1, . . . , wk] параметры локальных моделей, R
V,W,E(Ω)
параметры регуляризации, основанные на экспертной информации.
3. Построение признакового описания фигур
Единое пространство для кривых второго порядка. Произвольная
кривая второго порядка, главная ось которой не параллельна оси ординат,
задается уравнением
x2 = B′xy + C′y2 + D′x + E′y + F′,
где на коэффициенты B′, C′ накладываются ограничения, зависящие от типа
кривой. Выражение (2) для кривой второго порядка принимает вид
(
)
[
]
(
)
Kx
ci
=
xiyi,y2i,xi,yi,1
,
Ky
ci
=x2i,
откуда получаем задачу линейной регрессии для восстановления параметров
B′,C′,D′,E′,F′ по заданой выборке.
Окружность. В качестве частного случая кривой второго порядка рас-
смотривается окружность. Пусть (x0, y0) центр окружности, которую тре-
буется восстановить на бинарном изображении M, а r ее радиус. Элементы
выборки (xi, yi) ∈ C представляют собой геометрическое место точек, кото-
рое аппроксимируется уравнением окружности:
(
)
(2x0)xi + (2y0)yi +
r2 - x20 - y20
=x2i +y2i.
Тогда выражение (2) принимает следующий вид:
Kx(ci) = [xi,yi,1] = x, Ky(ci) = x2i + y2i = y.
Получаем задачу линейной регрессии
(3). Компоненты вектора w =
= [w0, w1, w2]T восстанавливают параметры окружности:
√
w0
w1
x0 =
,
y0 =
,
r= w3 +x20 +y20.
2
2
52
4. Композиция фигур
Для построения композиции фигур используется уравнение (5), которое
принимает вид
∑
∑
(
(
)
(
L=
πk(c,V) Kky
c
-wTkKkx
c))2 + R(V,W,E(Ω)) → min,
V,W
c∈C k=1
где Kkx, Kky
экспертное представление k-го эксперта. Предполагая, что
все кривы( )на изображ(н)и описы(а)ются одним(п)изнаковым описани-
ем x = K1x
c
=...=KKx
c
,x=K1y
c
=···=KKy
c
, получаем оптимиза-
ционную задачу:
∑
∑
(
)2
(
)
(6)
L=
πk(x,V) y - wTkx
+R
V,W,E(Ω)
→ min,
V,W
(x,y)∈D k=1
где регуляризатор R учитывает дополнительные ограничения параметров ло-
кальных моделей. Для решения задачи оптимизации (6) используется EM-ал-
горитм, описанный в [16].
5. Вычислительный эксперимент
Проведен вычислительный эксперимент по анализу качества аппрокси-
мации кривых второго порядка на изображении. Эксперимент разделен
на несколько частей. Первая часть описывает эксперимент с несколькими
окружностями на изображении. Во второй части анализируется сходимость
метода в зависимости от уровня шума в данных и от заданной экспертной
информации. В третьей части проводится эксперимент по аппроксимации ра-
дужной оболочки глаза.
5.1. Эксперимент по восстановлению параметров окружности
В этой части эксперимента анализируется аппроксимация нескольких кри-
вых второго порядка предложенной мультимоделью. Аппроксимируется сге-
нерированная синтетическая выборка. Выборка состоит из трех произволь-
ных непересекающихся окружностей. К окружностям добавлен шум. Шум
добавлялся к каждой точке окружности в отдельности, а также в выборку
добавлялись случайные точки, не относящиеся к окружности.
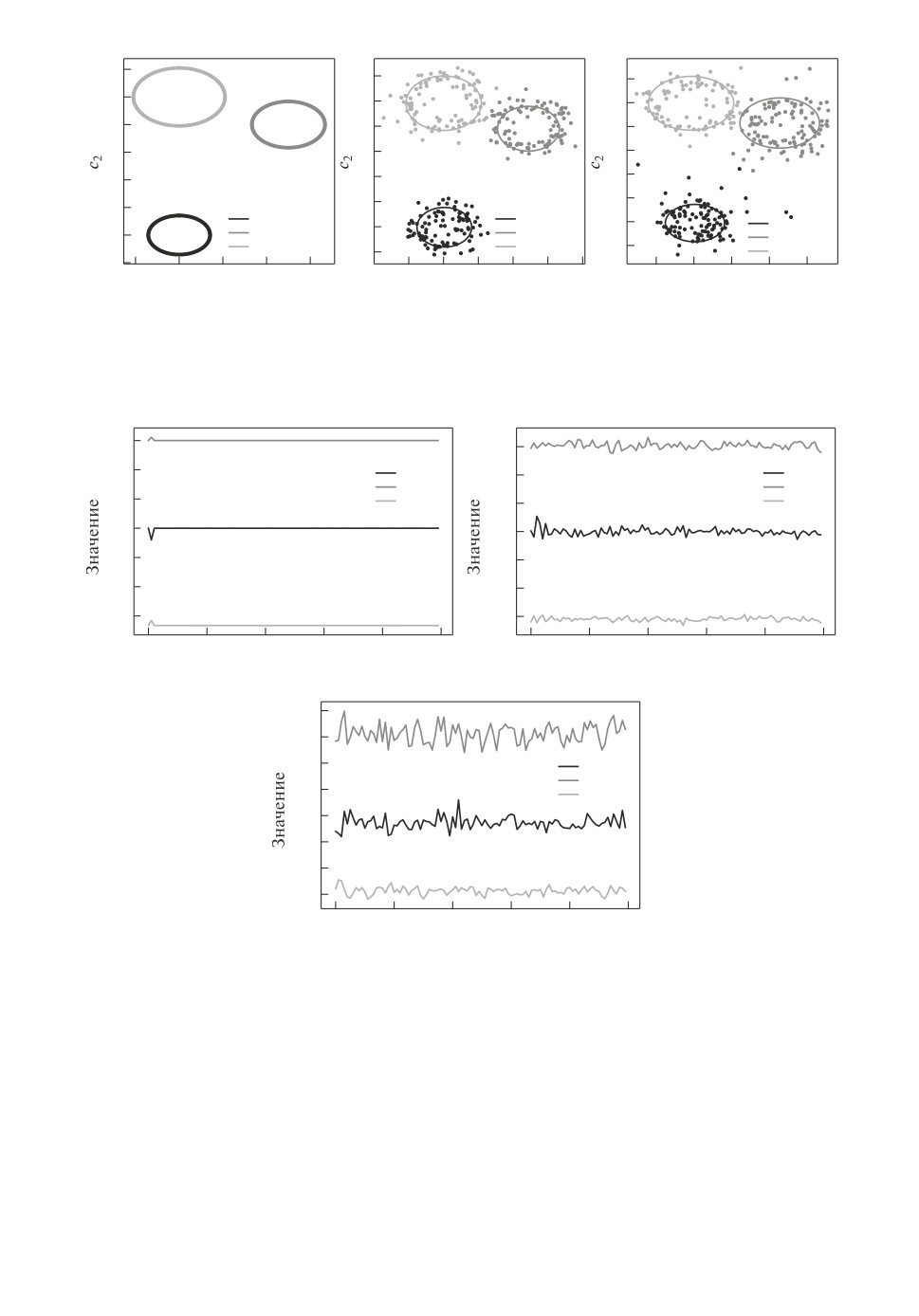
На рис. 3 показан результат построения ансамбля локальных аппроксими-
рующих моделей. Каждая локальная модель аппроксимирует одну окруж-
ность. Видно, что при добавлении шума качество аппроксимации падает.
На рис. 4 показан график зависимости радиуса окружностей r и их цен-
тров (x0, y0) от номера итерации.
5.2. Анализ качества аппроксимации
для выборки с разным уровнем шума
В этой части эксперимента анализируется качество аппроксимации S в
зависимости от уровня шума β в данных и от параметра априорных рас-
53
6
6
6
5
5
5
4
4
4
3
3
3
2
2
2
1
1
1
Модель 0
Модель 0
0
Модель 0
Модель 1
0
Модель 1
0
Модель 1
Модель 2
Модель 2
-1
-1
Модель 2
-1
-1
0
1
2
3
-1
0
1
2
3
4
-1
0
1
2
3
c1
c1
c1
Рис. 3. Мультимодель в зависимости от уровня шума в выборке. Слева напра-
во: окружности без шума; шум в радиусе круга; шум в радиусе круга, шум по
всему изображению.
4,0
4,0
3,5
w0
w0
3,5
w1
w1
3,0
w2
3,0
w2
2,5
2,5
2,0
2,0
1,5
1,5
1,0
1,0
0
20
40
60
80
100
0
20
40
60
80
100
Итерация
Итерация
4,5
4,0
3,5
w0
w1
3,0
w2
2,5
2,0
1,5
1,0
0
20
40
60
80
100
Итерация
Рис. 4. Зависимость параметров r, x0 и y0 от номера итерации в зависимости от
уровня шума в выборке. Слева направо: окружности без шума; шум в радиусе
круга; шум в радиусе круга, шум по всему изображению.
пределений γ. Выборка сгенерирована в таком виде: сначала случайным об-
разом выбираются два вектора параметров wtrue1 и wtrue2 коэффициенты
двух парабол. Векторы wtrue1 и wtrue2 исполь(уют)ся для генерации точек xi
и yi с добавлением нормального шума ε ∼ N
0, β
. При обучении мультимо-
(
)
дели учитывается априорное распределение параметров w1 ∼ N
wtrue1,γI
,
(
)
w2 ∼ N
wtrue2,γI
54
S
10
8
6
4
2
0
1,0
0,8
0,6
0,5
0,4
0,3
0,4
g
0,2
0,2
0
0,1
0
b
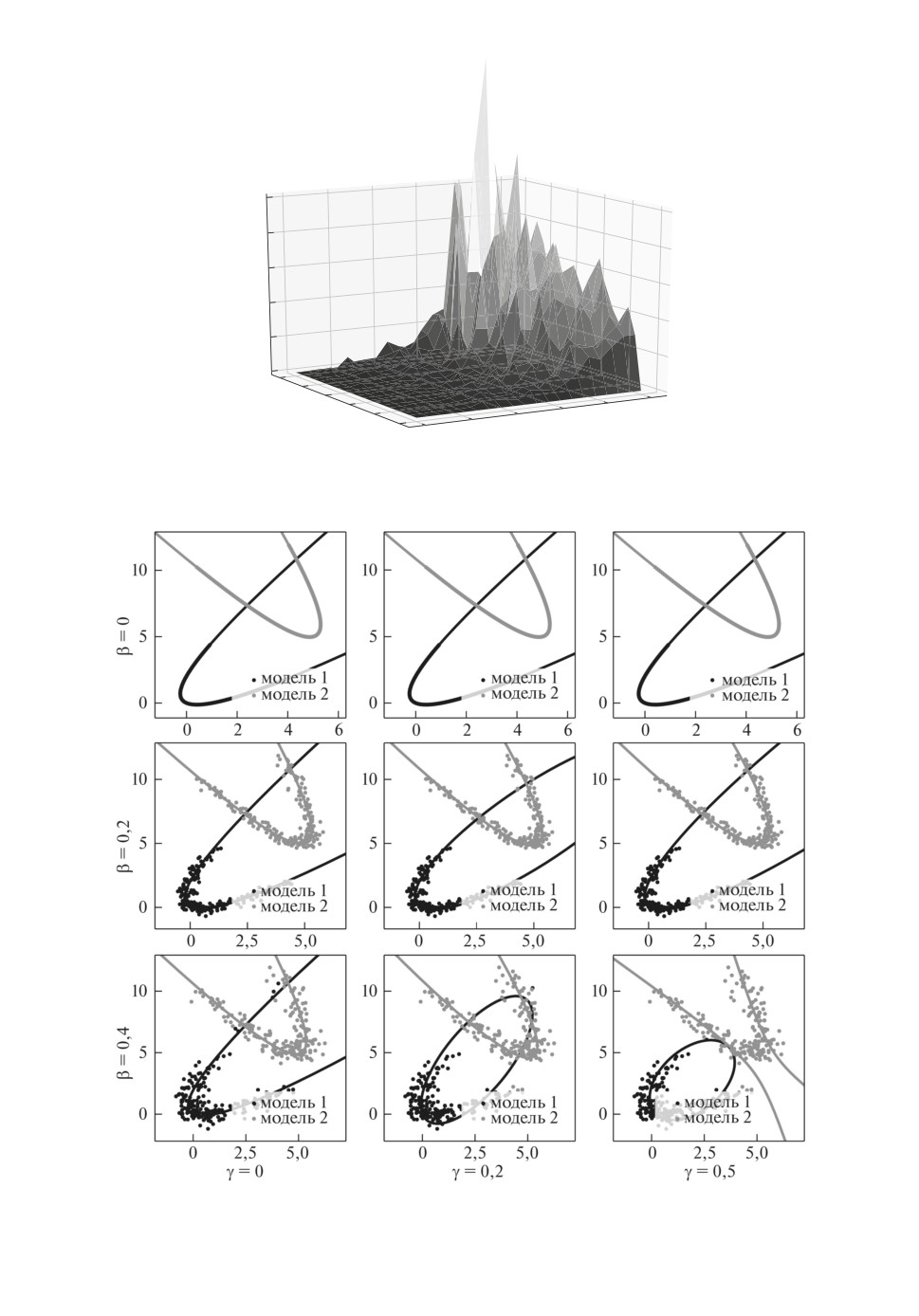
Рис. 5. Зависимость моделей от уровня шума β в данных, а также от
дисперсии априорного распределения γ.
Рис. 6. Результат аппроксимации данных с разным уровнем шума β
и по дисперсии априорного распределения γ.
55
Рассматривается критерий качества:
S = ||wpred1 - wtrue1||22 + ||wpred2 - wtrue2||22,
где wpred1
аппроксимация вектора параметров первой локальной модели,
аwpred2
аппроксимация вектора параметров второй локальной модели.
На рис. 5 показана зависимость критерия качества S от уровня шума β и
параметра априорного распределения γ. Из графика видно, что при малом
уровне шума β качество аппроксимации не зависит от параметра γ, а при
увеличении шума β качество аппроксимации S уменьшается.
На рис. 6 показан пример работы алгоритма с разными параметрами β
и γ. Видно, что в отсутствие шума β обе локальные модели аппроксимируют
выборку корректно. С ростом уровня шума качество аппроксимации падает:
при β = 0,2 с ростом γ первая локальная модель из параболы преобразовыва-
ется в эллипс; для β = 0,4 с ростом γ первая локальная модель из параболы
преобразовывается в эллипс, а вторая модель из параболы в гиперболу.
5.3. Аппроксимация радужки глаза
Анализ качества аппроксимации проводится для задачи аппроксимации
радужной оболочки глаза на изображении. Радужная оболочка глаза состо-
ит из двух концентрических окружностей, поэтому рассматривается муль-
тимодель, состоящая из двух экспертов: каждый эксперт аппроксимирует
одну из окружностей. В вычислительном эксперименте сравнивается каче-
ство аппроксимации окружносте( в случае з)адания разных регуляризато-
ров R0, R1, R2. Регуляризатор R0
V,W,E(Ω)
= 0, что соответствует отсут-
ствию регуляризатора. Регуляризатор
(
)
∑
R1
V,W,E(Ω)
=- wTkwk
k=1
способствует околонулевым параметрам локальных моделей. Регуляризатор
∑
∑
∑(
)2
(
)
R2
V,W,E(Ω)
=- wTkwk +
wjk - w′j
k
k=1
k=1 k′=1 j=1
способствует совпадению центров окружностей и близким к нулю параметрам
локальных моделей.
Рисунок 7 показывает результат аппроксимации радужной оболочки глаза
после 10 итераций. Видно, что при отсутствии регуляризатора одна из окруж-
ностей находится некорректно. В случае задания регуляризатора R1 модель
аппроксимирует обе окружности, но окружности неконцентричны. В случае
задания регуляризатора R2 получаем концентрические окружности на изоб-
ражении.
На рис. 8-10 показан процесс сходимости мультимоделей в случае указа-
ния разных регуляризаторов R0, R1, R2. Видно, что модели с регуляризато-
ром типа R1 и R2 аппроксимируют обе окружности, а мультимодель с регу-
ляризатором R0 аппроксимирует только большую окружность.
56
2,0
2,0
2,0
1,5
1,5
1,5
1,0
1,0
1,0
0,5
0,5
0,5
модель 0
модель 1
0
0
0
-0,5
-0,5
-0,5
-1,0
-1,0
-1,0
модель 0
модель 0
-1,5
модель 1
-1,5
модель 1
-1,5
-2
-1
0
1
-2
-1
0
1
-2
-1
0
1
Рис. 7. Визуализация аппроксимации радужной оболочки. Слева направо: ес-
ли указан регуляризатор R0; если указан регуляризатор R1; если указан ре-
гуляризатор R2.
2
1
1
1
0
0
0
0
-1
-1
-1
-2
0
-2
0
-2
0
-2
0
1 итерация
3 итерации
5 итераций
10 итераций
Рис. 8. Визуализация мультимодели в случае регуляризатора R0.
2
1
1
1
0
0
0
0
-1
-1
-1
-2
0
-2
0
-2
0
-2
0
1 итерация
3 итерации
5 итераций
10 итераций
Рис. 9. Визуализация мультимодели в случае регуляризатора R1.
2
2
1
1
0
0
0
0
-1
-1
-2
0
-2
0
-2
0
-2
0
1 итерация
3 итерации
5 итераций
10 итераций
Рис. 10. Визуализация мультимодели в случае регуляризатора R2.
57
6. Заключение
В статье предлагается метод построения интерпретируемых моделей ма-
шинного обучения на основе экспертной информации. В качестве задачи рас-
сматривается задача аппроксимации кривых второго порядка: параболы, ги-
перболы, эллипса. Аппроксимация кривых второго порядка применяется в
задаче об аппроксимации радужной оболочки.
Проведен эксперимент, в ходе которого анализируется качество аппрокси-
мации кривых второго порядка в зависимости от начального уровня шума в
данных, а также в зависимости от регуляризатора функции ошибки. В ходе
эксперимента показано, что с увеличением уровня шума в исходных данных
точность аппроксимации снижается: при большом шуме форма аппроксими-
руемой фигуры меняется с параболы на гиперболу. Проведен вычислитель-
ный эксперимент по аппроксимации радужной оболочки глаза двумя концен-
трическими окружностями. Эксперимент показывает, что регуляризация на
основе экспертной информации улучшает качество аппроксимации.
СПИСОК ЛИТЕРАТУРЫ
1.
He K., Ren S., Sun J., Zhang X. Deep Residual Learning for Image Recognition //
Proc. IEEE Conf. on Computer Vision and Pattern Recognition. Las Vegas. 2016.
P. 770-778.
2.
Ribeiro M., Singh S., Guestrin C. Why Should I Trust You?: Explaining the Predic-
tions of Any Classifier // Proc. of the 22nd ACM SIGKDD International Conference
on Knowledge Discovery and Data Mining. 2016. P. 1135-1144.
3.
Han X., Yao M., Debayan D., Hui L., Ji-Liang T., Anil J. Adversarial Attacks and
Defenses in Images, Graphs and Text: A Review // Int. J. Automat. Comput. 2020.
V. 17. P. 151-178.
4.
Akhtar N., Mian A. Threat of Adversarial Attacks on Deep Learning in Computer
Vision: A Survey // IEEE Access. 2018. V. 6. P. 14410-14430.
5.
Grabovoy A., Strijov V. Probabilistic Interpretation of the Distillation Problem //
Autom. Remote Control. 2022. V. 83. P. 123-137.
6.
Matveev I. Detection of iris in image by interrelated maxima of brightness gradient
projections // Appl. Comput. Math. 2010. V. 9. P. 252-257.
7.
Matveev I., Simonenko I. Detecting precise iris boundaries by circular shortest path
method // Pattern Recognition and Image Analysis. 2014. V. 24. P. 304-309.
8.
Bowyer K., Hollingsworth K., Flynn P. A Survey of Iris Biometrics Research: 2008-
2010 // Handbook of iris recognition. 2010. P. 15-54.
9.
Salamani D., Gadatsch S., Golling T., Stewart G., Ghosh A., Rousseau D., Hasib A.,
Schaarschmidt J. Deep Generative Models for Fast Shower Simulation in ATLAS //
IEEE 14th International Conference on e-Science. 2018. P. 348-348.
10.
Chen Xi., Ishwaran H. Random Forests for Genomic Data Analysis // Genomics.
2012. V. 6. P. 323-329.
11.
Chen T., Guestrin C. XGBoost: A Scalable Tree Boosting System // Proc. of the
22nd ACM SIGKDD International Conference on Knowledge Discovery and Data
Mining. 2016. P. 785-794.
12.
Yuksel S., Wilson J., Gader P. Twenty Years of Mixture of Experts // IEEE Trans-
actions on Neural Networks and Learning Systems. 2012. V. 8. P. 1177-1193.
58
13.
Dempster A., Laird N., Rubin D. Maximum Likelihood from Incomplete Data via the
EM Algorithm // Journal of the Royal Statistical Society. Series B (Methodological).
1977. V. 39. P. 1-38.
14.
Ebrahimpour R., Moradian R., Esmkhani A., Jafarlou F. Recognition of Persian
handwritten digits using characterization loci and mixture of experts // J. Digital
Content Technol. Appl. 2009. P. 42-46.
15.
Peng F., Jacobs R., Tanner M. Bayesian inference in mixtures-of-experts and hi-
erarchical mixtures-of-experts models with an application to speech recognition //
J. Amer. Stat. Assoc. 1996. V. 91. P. 953-960.
16.
Grabovoy A., Strijov V. Prior Distribution Selection for a Mixture of Experts //
Comput. Math. and Math. Phys. 2021. P. 1140-1152.
17.
Estabrooks A., Japkowicz N. A mixture-of-experts framework for text classification //
Proc. Workshop Comput. Natural Lang. Learn., Assoc. Comput. Linguist. 2001.
P. 1-8.
18.
Cheung Y., Leung W., Xu L. Application of mixture of experts model to financial
time series forecasting // Proc. Int. Conf. Neural Netw. Signal Process. 1995. P. 1-4.
19.
Weigend A., Shi S. Predicting daily probability distributions of S&P500 returns //
J. Forecast. 2000. V. 19. P. 375-392.
20.
Cao L. Support vector machines experts for time series forecasting // Neurocomput-
ing. 2003. V. 51. P. 321-339.
21.
Mossavat S., Amft O., Vries B., Petkov P., Kleijn W. A Bayesian hierarchical mix-
ture of experts approach to estimate speech quality // Proc. 2nd Int. Workshop
Qual. Multimedia Exper. 2010. P. 200-205.
22.
Sminchisescu C., Kanaujia A., Metaxas D. Discriminative density propagation for
visual tracking // IEEE Trans. Pattern Anal. Mach. Intell. 2007. V. 29. P. 2030-2044.
23.
Tuerk A. The state based mixture of experts HMM with applications to the recog-
nition of spontaneous speech // Ph.D. thesis, University of Cambridge. 2001.
24.
Yumlu M., Gurgen F., Okay N. Financial time series prediction using mixture of
experts // Proc. 18th Int. Symp. Comput. Inf. Sci. 2003. P. 553-560.
Статья представлена к публикации членом редколлегии А.А. Лазаревым.
Поступила в редакцию 31.01.2022
После доработки 25.06.2022
Принята к публикации 29.06.2022
59