Автоматика и телемеханика, № 10, 2022

(Московский физико-технический институт

(государственный университет)),

О.Ю. БАХТЕЕВ, канд. физ.-мат. наук (bakhteev@phystech.edu),

В.В. СТРИЖОВ, д-р физ.-мат. наук (strijov@gmail.com)

(Вычислительный центр имени А.А. Дородницына

Федерального исследовательского центра

¾Информатика и управление¿ РАН, Москва)

ГРАДИЕНТНЫЕ МЕТОДЫ ОПТИМИЗАЦИИ

МЕТАПАРАМЕТРОВ В ЗАДАЧЕ ДИСТИЛЛЯЦИИ ЗНАНИЙ¹

В работе исследуется задача дистилляции моделей глубокого обуче-

ния. Дистилляция знаний это задача оптимизации метапараметров, в

которой происходит перенос информации модели более сложной структу-

ры, называемой моделью-учителем, в модель более простой структуры,

называемой моделью-учеником. В работе предлагается обобщение зада-

чи дистилляции на случай оптимизации метапараметров градиентными

методами. Метапараметрами являются параметры оптимизационной за-

дачи дистилляции. В качестве функции потерь для такой задачи высту-

пает сумма слагаемого классификации и кросс-энтропии между ответами

модели-ученика и модели-учителя. Назначение оптимальных метапара-

метров в функции потерь дистилляции является вычислительно сложной

задачей. Исследуются свойства оптимизационной задачи с целью предска-

зания траектории обновления метапараметров. Проводится анализ тра-

ектории градиентной оптимизации метапараметров и предсказывается

их значение с помощью линейных функций. Предложенный подход про-

иллюстрирован с помощью вычислительного эксперимента на выборках

CIFAR-10 и Fashion-MNIST, а также на синтетических данных.

Ключевые слова: машинное обучение, дистилляция знаний, оптимизация

метапараметров, градиентная оптимизация, назначение метапараметров.

DOI: 10.31857/S0005231022100075, EDN: AKGKQX

1. Введение

В работе рассматривается задача дистилляции моделей глубокого обуче-

ния. Оптимизация модели глубокого обучения является вычислительно слож-

ной задачей [12]. В работе исследуется частный случай задачи оптимизации,

называемый дистилляцией знаний. Он позволяет использовать одновременно

обучающую выборку и информацию, содержащуюся в предобученных моде-

лях. Дистилляцией знаний [5] назовем задачу оптимизации параметров моде-

ли, в которой учитывается не только информация, содержащаяся в исходной

¹ Работа выполнена при поддержке Научной академической стипендии имени К.В. Ру-

дакова.

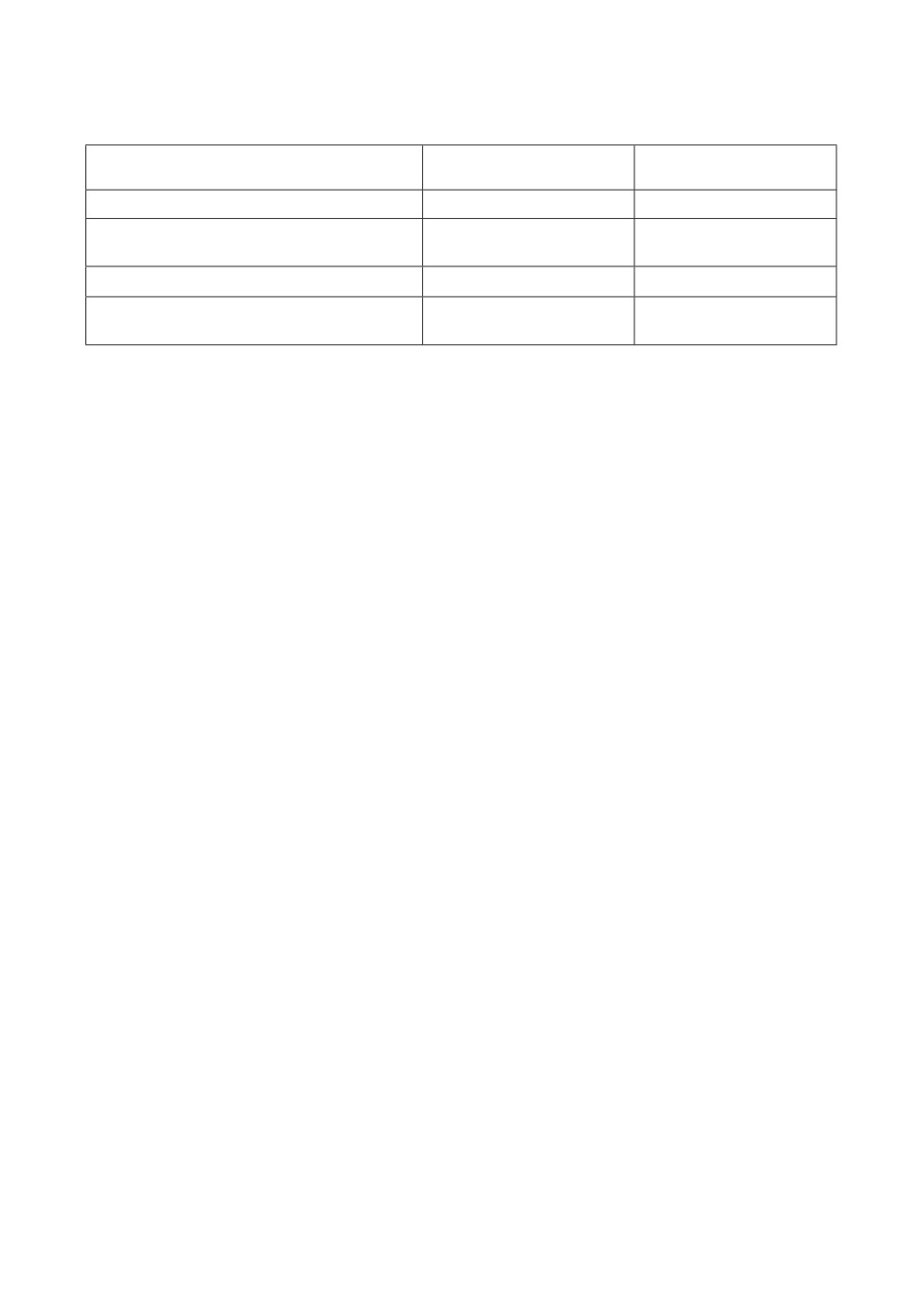
Таблица 1. Сложность различных методов оптимизации метапараметров и ги-

перпараметров. Здесь |w| является числом параметров модели, |λ| числом ме-

тапараметров, r это количество запусков стохастических методов оптимизации,

s сложность порождения из вероятностных моделей

Тип метода

Метод

Сложность

оптимизации

Случайный поиск [2]

Стохастический

O(r · |w|)

Основанный на вероятностных

Стохастический

O (r · (|w| + s))

моделях [3]

Жадный градиентный [8]

Градиентный

O(|w| · |λ|)

Жадный градиентный

Градиентный

O(|w| + |λ|)

с разностной аппроксимацией [7]

выборке, но также и информация, содержащаяся в модели-учителе. Модель-

учитель имеет высокую сложность. В ней содержится информация о выборке,

а также о распределениях параметров модели, перенос которых будет осу-

ществлен. Модель более простой структуры, называемая моделью-учеником,

оптимизируется путем переноса знаний модели-учителя.

Исследуется процедура оптимизации метапараметров в задаче дистилля-

ции знаний. Метапараметрами являются параметры оптимизационной зада-

чи. Корректное назначение метапараметров может существенно повлиять на

качество итоговой модели [11]. В отличие от [9, 11], в данной работе учи-

тывается различие между гиперпараметрами, вероятностными параметрами

априорного распределения [4] и метапараметрами. Несмотря на количество

методов оптимизации метапараметров и гиперпараметров, использующихся

в глубоком обучении, таких как случайный поиск [2] или модели, основанные

на использовании вероятностных моделей [3], во многих подходах предлага-

ется последовательно порождать случайное значение метапараметров и оце-

нивать качество модели, обученной при данных значениях гиперпараметров.

Данный подход может не подойти в случае обучения моделей, требующих зна-

чительных временных затрат для обучения. В табл. 1 содержатся сложности

различных подходов к оптимизации метапараметров. Видно, что в случае,

если оптимизация параметров занимает значительное время, подходы, тре-

бующие несколько запусков оптимизации, являются неэффективными.

Предлагается рассматривать задачу оптимизации метапараметров как

двухуровневую задачу оптимизации. На первом уровне оптимизируются па-

раметры модели, на втором метапараметры [1, 8, 9]. Жадный градиентный

метод для решения двухуровневой задачи описан в [8]. В [1] проанализиро-

ваны различные градиентные методы и случайный поиск. В данной работе

анализируется подход к оптимизации и предсказанию метапараметров, полу-

ченных после применения градиентных методов. Из табл. 1 можно увидеть,

что для больших задач предпочтительны градиентные методы оптимизации

метапараметров. Тем не менее, даже с применением жадного алгоритма оп-

тимизации метапараметров с разностной аппроксимацией, оптимизация ме-

тапараметров становится значительно требовательнее к вычислительным ре-

сурсам, что было продемонстрировано в [7]. Для уменьшения затрат на оп-

тимизацию в настоящей работе проводится анализ траектории оптимизации

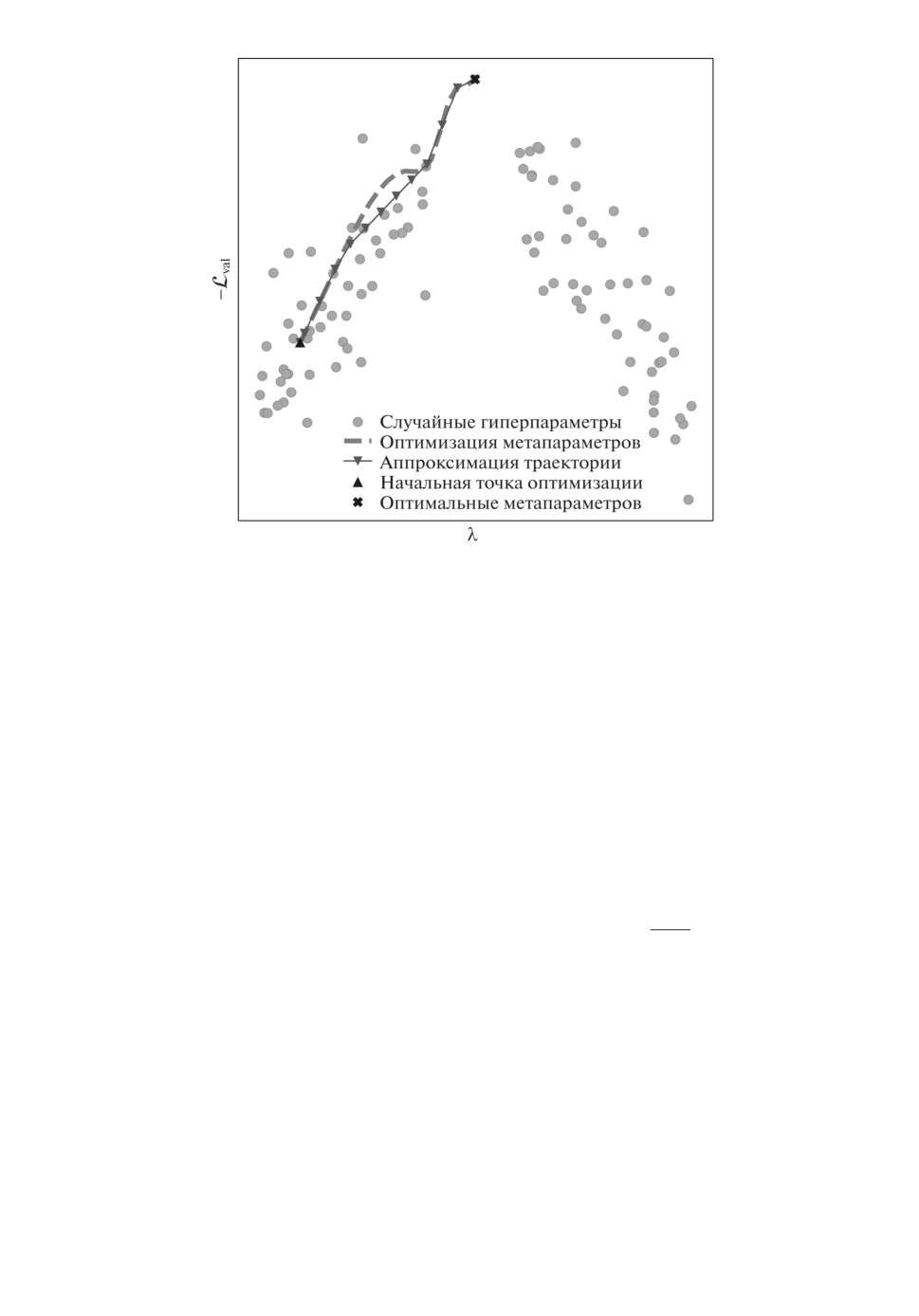
Рис. 1. Схема работы предложенного метода: вместо непосредственной опти-

мизации значений метапараметра λ предлагается аппроксимировать траекто-

рию оптимизации с помощью линейных моделей для достижения минимума

функции потерь на валидационной части выборки L_val. Случайные метапара-

метры не являются точками минимума функции L_val и доставляют субопти-

мальное качество модели.

метапараметров и предсказывается ее значение с помощью линейных моде-

лей. Этот метод проиллюстрирован на рис. 1. Данный метод оценивается и

сравнивается с другими методами оптимизации метапараметров на выборках

изображений CIFAR-10 [6], Fashion-MNIST [14] и синтетической выборке.

2. Постановка задачи

Решается задача классификации вида

D = {(x_i,y_i)}^mi=1, x_i ∈ Rⁿ, y_i ∈ Y = {e_k|k = 1,K},

где e_k k-й столбец единичной матрицы, y_i вектор с единицей на месте

класса x_i.

Разделим выборку на два подмножества D: D = D_train ⊔ D_val. Подмноже-

ство D_train будем использовать для оптимизации параметров модели, а под-

множество D_val для оптимизации метапараметров.

Рассмотрим модель-учителя f(x), которая была обучена на выборке

D_train. Оптимизируем модель-ученика g(x,w), w ∈ R^s путем переноса зна-

ний модели-учителя. Определим данную задачу формально.

Определение 1. Пусть функция D : R^s → R₊ задает расстояние

между моделями g и f. Назовем D-дистилляцией модели-ученика такую

задачу оптимизации параметров модели-ученика, которая минимизирует

функцию D.

Определим функцию потерь L_train, которая учитывает перенос знаний от

модели f к модели g:

∑

eg(x,w)k

L_train(w,λ) = -λ₁

y_k log

∑

(x,y)∈D_train k=1

eg(x,w)j

j=1

}

слагаемое классификации

∑

∑ e^f(x)k^/T

eg(x,w)k/T

- (1 - λ₁)

log

∑

(x,y)∈D_train k=1

e^f(x)j^/T

∑ eg(x,w)j /T

j=1

}

слагаемое дистилляции

где y_k это k-я компонента вектора ответов, T параметр температуры в

задаче дистилляции. Температура T имеет следующие свойства:











eg(x,w)k/T

1) если T → 0, то получаем единичный вектор

;



∑



 e^g(x,w)j^/T



j=1

k=1

2) если T → ∞, то получаем вектор с равными вероятностями.

Покажем, что оптимизация L_train является D-дистилляцией при λ₁ = 0.

Предложение 1. Если λ₁ = 0, то оптимизация функции потерь (1),

является D-дистилляцией с D = D_KL (σ (f(x)/T ) , σ (g(x, w)/T )), где σ

это функция softmax

∑_K

, D_KL дивергенция Кульбака-Лейблера.

j=1

e^xj

Доказательство. При λ₁ = 0 имеем:

∑

∑ e^f(x)k^/T

eg(x,w)k/T

(1) L_train(w, λ) =

log

∑

(x,y)∈D_train k=1

e^f(x)j^/T

e^g(x,w)j^/T

j=1

= DKL (σ(f(x)/T),σ(g(x,w)/T)) - C.

Получаем, что L_train(w, λ) равняется D_KL (σ(f(x)/T ), σ(g(x, w)/T )) с точ-

ностью до константы C, не влияющей на оптимизацию. Константа является

энтропией от σ(f(x)/T ). Функция D_KL (σ (f/T ) , σ (g/T )) определяет расстоя-

ние между логитами модели f и модели g. Получаем, что определение D-ди-

стилляции выполняется.

Определим множество метапараметров λ как вектор, компонентами кото-

рого являются коэффициент λ₁ перед слагаемыми в L_train и температура T :

λ = [λ₁,T].

Определим двухуровневую задачу

(2)

λ= arg min

L_val

(ŵ,λ),

λ∈R²

(3)

ŵ = arg min

L_train

(w, λ),

w∈R^s

где L_val это функция потерь на валидации:

∑

eg(x,w)k/Tval

L_val(w,λ) = -

y^k log

∑

(x,y)∈D_val k=1

e^g(x,w)j^/Tval

j=1

метапараметр T_val определяет температуру в валидационной функции потерь.

Его значение выбрано вручную и не является предметом оптимизации.

3. Градиентная оптимизация метапараметров

Одним из методов оптимизации метапараметров является использование

градиентных методов. Ниже приведены схема их применения и подход к оп-

тимизации траектории метапараметров.

Определение 2. Определим оператор оптимизации как алгоритм U,

который выбирает вектор параметров модели w^′, используя значения пара-

метров на предыдущем шаге w.

Оптимизируем параметры w, используя η шагов оптимизации:

ŵ = U ◦ U ◦ ··· ◦ U(w₀,λ) = U^η(w₀,λ),

где w₀

начальное значение вектора параметров w, λ множество метапа-

раметров.

Переформулируем оптимизационную задачу, используя определение опе-

ратора U:

(

)

λ= arg min

L_val

U^η(w₀,λ)

λ∈R²

Решим оптимизационную задачу (2) и (3) с помощью оператора градиент-

ного спуска:

U (w, λ) = w - γ∇L_train(w, λ),

где γ длина шага градиентного спуска. Для оптимизации метапараметров

используется жадный градиентный метод, который зависит только от зна-

чения параметров w на предыдущем шаге. На каждой итерации получим

следующее значение метапараметров:

(4)

λ^′ = λ - γ_λ∇_λL_val(U(w,λ),λ) = λ - γ_λ∇_λL_val(w - γ∇L_train

(w, λ), λ).

Рис. 2. Схема оптимизации метапараметров.

В данной работе используется численная разностная аппроксимация для

данной процедуры оптимизации [7]:

dL_val(w^′, λ)

= ∇_λL_val(w^′,λ) - γ∇^2λ,w′L_val(w^′,λ)∇_w′L_val(w^′,λ),

dλ

∇_λL_val(w⁺,λ) - ∇_λL_val(w^-,λ)

∇^2λ,w′L_val(w^′,λ)∇_w′ L_val(w^′,λ) ≈

2ε

∇_λL_val(w⁺,λ) - ∇_λL_val(w^-,λ)

λ^′ ≈ λ - γ_λ∇_λL_val(w^′,λ) + γ

2ε

где w^′ = w - γ∇L_train(w, λ), w^± = w^′ ± ε∇_w′ L_val(w^′, λ), ε некоторая за-

данная константа.

Для дальнейшего уменьшения стоимости оптимизации предлагается

аппроксимировать траекторию оптимизации метапараметров. Траектория

предсказывается с помощью линейных моделей, которые используются пе-

риодически после заданного числа итераций e₁. После этого линейная модель

используется для предсказания метапараметров на протяжении e₂ итераций:

(

)

(5)

λ^′ = λ + c^⊤

где c это вектор параметров линейной модели, оптимизированный с помо-

щью метода наименьших квадратов, z число итераций оптимизации.

Диаграмма на рис. 2 описывает полученный метод оптимизации. Пара-

метры модели оптимизируются на первом уровне двухуровневой оптимиза-

ционной задачи с помощью подмножества D_train и функции потерь L_train.

Метапараметры оптимизируются на втором уровне с помощью подмноже-

ства D_val и функции потерь L_val. На протяжении e₁ итераций метапарамет-

ры оптимизируются с помощью метода стохастического градиентного спуска.

На протяжении e₂ итераций предсказываются с помощью линейных моделей.

Алгоритм 1. Оптимизация метапараметров

Require: число e₁ итераций с использованием градиентной оптимизации

Require: число e₂ итераций с предсказанием λ линейными моделями

1: while нет сходимости do

Оптимизация λ и w на протяжении e₁ итераций, решая двухуровневую

задачу

traj =траектория (∇λ) изменяется во время оптимизации;

Положим z = [1, . . . , e₁]^T

Оптимизация c с помощью МНК:

ĉ = arg min

||traj - z · c₁ + c₂||²²

c∈R²

Оптимизация w и предсказание λ на протяжении e₂ итераций с помо-

щью линейной модели с параметрами c.

7: end while

Алгоритм для предложенного метода

Следующая теорема доказывает корректность предложенной аппроксима-

ции для простого случая: когда параметры w модели g достигли оптимума

задачи (3), гессиан H = ∇^2wL_train является единичной матрицей, и оптими-

зация метапараметров ведется в области, в которой градиент метапарамет-

ров можно аппроксимировать константой. Отметим, что в общем случае дан-

ные условия при оптимизации моделей глубокого обучения не выполняются.

В [8, 13] было показано, что использование методов нормализации проме-

жуточных представлений выборки под действием нелинейных функций, вхо-

дящих в модель глубокого обучения, приближает гессиан функции потерь к

единичному. Анализ качества градиентной оптимизации метапараметров для

случая, когда параметры модели не достигли оптимума, приведен в [11].

Теорема 1. Если функция L_train(w,λ) является гладкой и выпуклой, и

ее гессиан H = ∇^2wL_train является единичной матрицей, H = I, а также

если параметры w равны w^∗, где w^∗ точка локального минимума для те-

кущего значения λ, тогда жадный алгоритм (4) находит оптимальное ре-

шение двухуровневой задачи. Если существует область D ∈ R² в простран-

стве метапараметров, такая что градиент метапараметров может быть

аппроксимирован константой, то оптимизация является линейной по ме-

тапараметрам.

Доказательство. В работе [11] была выведена формула для ∇_λL_val =

= ∇_λL_val(U(w,λ)) в случае, если L_train(w,λ) является гладкой и выпуклой,

и найдена w^∗ точка локального минимума для текущего значения λ:

∇_λL_val(λ) = ∇_λL_val - (∇^2w,λL_train)^⊤(∇^2wL_train)^-1∇_wL_val.

Эта формула упрощается исключением первого слагаемого, так как функ-

ция L_val явно не зависит от метапараметров:

∇_λL_val(λ) = -(∇^2w,λL_train)^⊤(∇^2wL_train)^-1∇_wL_val.

Если ∇^2wL_train равен единичной матрице, то жадный алгоритм дает опти-

мум двухуровневой задачи в том случае, если его шаг выражается следующей

формулой [8]:

λ_t+1 = λ_t + η₁(∇^2w,λL_train)^⊤∇_wL_val.

Также заменим ∇^2wL_train на единичную матрицу.

Вернемся к упрощенной формуле градиента:

∇_λL_val(λ) = -(∇^2w,λL_train)^⊤∇_wL_val.

Предположим, что существует область D, в которой ∇_λL_val(λ) равен кон-

стантному вектору

(

)

a₁

∇_λL_val(λ) ≈

a₂

Тогда в D шаг оптимизации можно представить в виде

(

)

a₁

λ_t+1 = λ_t - γ_λ

a₂

и имеет вид, аналогичный (5).

4. Вычислительный эксперимент

Целью эксперимента являются оценка качества предложенного мето-

да дистилляции и анализ полученных моделей и их метапараметров. Ме-

тод оценивался на синтетической выборке, а также выборках CIFAR-10 и

Fashion-MNIST. На выборке CIFAR-10 было проведено два вида эксперимен-

тов: на всей выборке, |D_train| = 50 000, и на уменьшенной обучающей выборке,

|D_train| = 12 800.

Были проанализированы следующие методы оптимизации метапарамет-

ров:

1) оптимизация без дистилляции;

2) оптимизация со случайной инициализацией метапараметров. Метапара-

метры порождаются из равномерного распределения

λ₁ ∼ U(0;1), T ∼ U(0,1,10).

3) оптимизация с “наивным” назначением метапараметров:

λ₁ = 0,5, T = 1;

4) градиентная оптимизация;

5) предложенный метод с e₁ = e₂ = 10.

6) оптимизация с помощью вероятностной модели. Для данного типа оп-

тимизации использовалась библиотека hyperopt [3], в которой реализована

оптимизация с помощью метода парзеновского окна. Для этого метода про-

водилось 5 запусков перед итоговым предсказанием метапараметров.

Для методов 1-3 использовалась вся обучающая выборка D. Для ме-

тодов 4-6 выборка разбивалась на обучение, валидацию, контроль D =

=D_train ⊔D_val ⊔D_test.

0,6

0,8

0,7

0,5

0,6

0,4

Без дистилляции

Наивный подбор метапараметров

Случайные метапараметры

0,5

Градиентная оптимизация

0,3

Градиентная оптимизация

Предложенный метод

Hyperopt

0,4

0,2

500

1000

1500

Номер итерации

Размер эпохи

Рис. 3. Точность модели на выборках: a - синтетической, б - уменьшенной

CIFAR-10. Здесь и далее точки незначительно смещены относительно оси абс-

цисс для лучшей читаемости графиков.

В качестве внешнего критерия качества была использована метрика

accuracy:

∑

accuracy =

[g(x_i,w) = y_i].

i=1

Для всех экспериментов порождение начальных значений метапараметров

происходило следующим образом:

λ₁ ∼ U(0,1), log₁₀ T ∼ U(-1,1).

Для каждого эксперимента проводилось 10 запусков, затем результаты

усреднялись. Код эксперимента доступен в [15].

Итоговые результаты представлены в табл. 2. Зависимость точности от

номера итерации на синтетической выборке и уменьшенной версии CIFAR-10

изображена на рис. 3.

Таблица 2. Результаты эксперимента. Числа в скобках являются максимальным

полученным значением точности в конкретном эксперименте

Синтетическая

Метод

Fashion-MNIST

Уменьшенный CIFAR-10

выборка

CIFAR-10

Без дистилля-

0,63 (0,63)

0,87 (0,88)

0,55 (0,56)

0,65 (0,66)

ции

Наивные мета-

0,63 (0,63)

0,87 (0,88)

0,55 (0,56)

0,66 (0,67)

параметры

Случайные ме-

0,64 (0,72)

0,79 (0,88)

0,54 (0.57)

0.64

(0.67)

тапараметры

Градиентная

0.77 (0,78)

0,88 (0,89)

0,57 (0,61)

0,70 (0,72)

оптимизация

Hyperopt

0,77 (0,78)

0,87 (0,88)

0,55 (0,58)

0,65 (0,69)

Предложенный

0,76 (0,78)

0,88 (0,89)

0,57

0,70 (0,72)

метод

4.1. Эксперимент на синтетической выборке

Для оценки полученного метода был проведен эксперимент на синтетиче-

ской выборке:

D = {(x_i,y_i)}^mi=1, x_ij ∈ N(0,1), j = 1,2, x_i3 = [sign(x_i1) + sign(x_i2) > 0],

y_i = sign(x_i1 · x_i2 + δ),

где δ ∈ N (0, 0,5) это шум. Размер выборки модели-ученика значительно

меньше размера выборки модели-учителя и D_train. Для корректной демон-

страции предложенного метода в этом эксперименте выборка была поделена

на 3 части: обучающая выборка для модели-учителя, состоящая из 200 объ-

ектов; обучающая выборка для модели-ученика, состоящая из 15 объектов; и

валидационная выборка, которая также является тестовой, D_val = D_test. Она

также состоит из 200 объектов. Визуализация выборки изображена на рис. 4.

Модель-учитель была обучена на протяжении 20 000 итераций методом стоха-

стического градиентного спуска с длиной шага, равной 10^-2. Для ее обучения

было использовано модифицированное признаковое пространство:

x_i3 = [sign(x_i1) + sign(x_i2) + 0,1 > 0].

Данная модификация не позволяет модели-учителю безошибочно предска-

зывать обучающую выборку. В данном случае, для обучения модели-учени-

ка предпочтительно использование только слагаемого дистилляции, λ₁ = 0.

Обучение модели-ученика происходило на протяжении 2000 итераций мето-

дом стохастического градиентного спуска с длиной шага, равной 1,0 и T_val =

= 0,1.

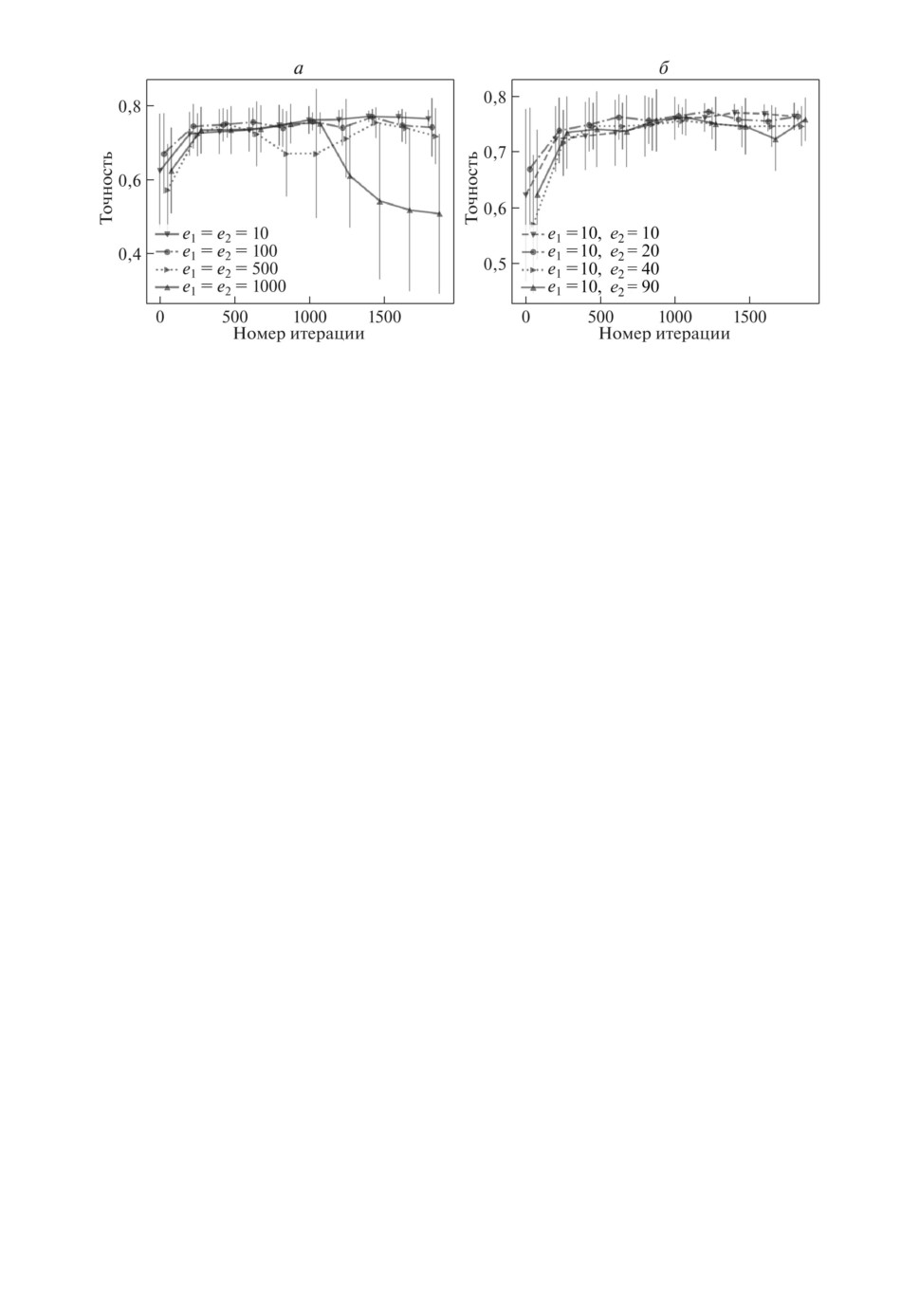
Была проведена серия экспериментов для определения наилучших значе-

ний e₁ и e₂. На рис. 5,а приведен график точности для различных e₁ с e₂

равным 10. На рис. 5,б изображена точность для различных значений e₂.

Можно заметить, что с возрастанием e₁ и e₂ качество аппроксимации траек-

тории обновления метапараметров уменьшается.

На рис. 3,а изображена точность модели для различных методов. Наи-

лучшие результаты были получены для оптимизированных значений ме-

тапараметров и предложенного метода. Можно заметить, что предложен-

ный метод хорошо аппроксимирует оптимизацию метапараметров в данном

эксперименте.

y = 0

y = 1

-1

y = 0

-2

y = 1

-3

-2

-1

-3

-2

-1

-3

-2

-1

x₁

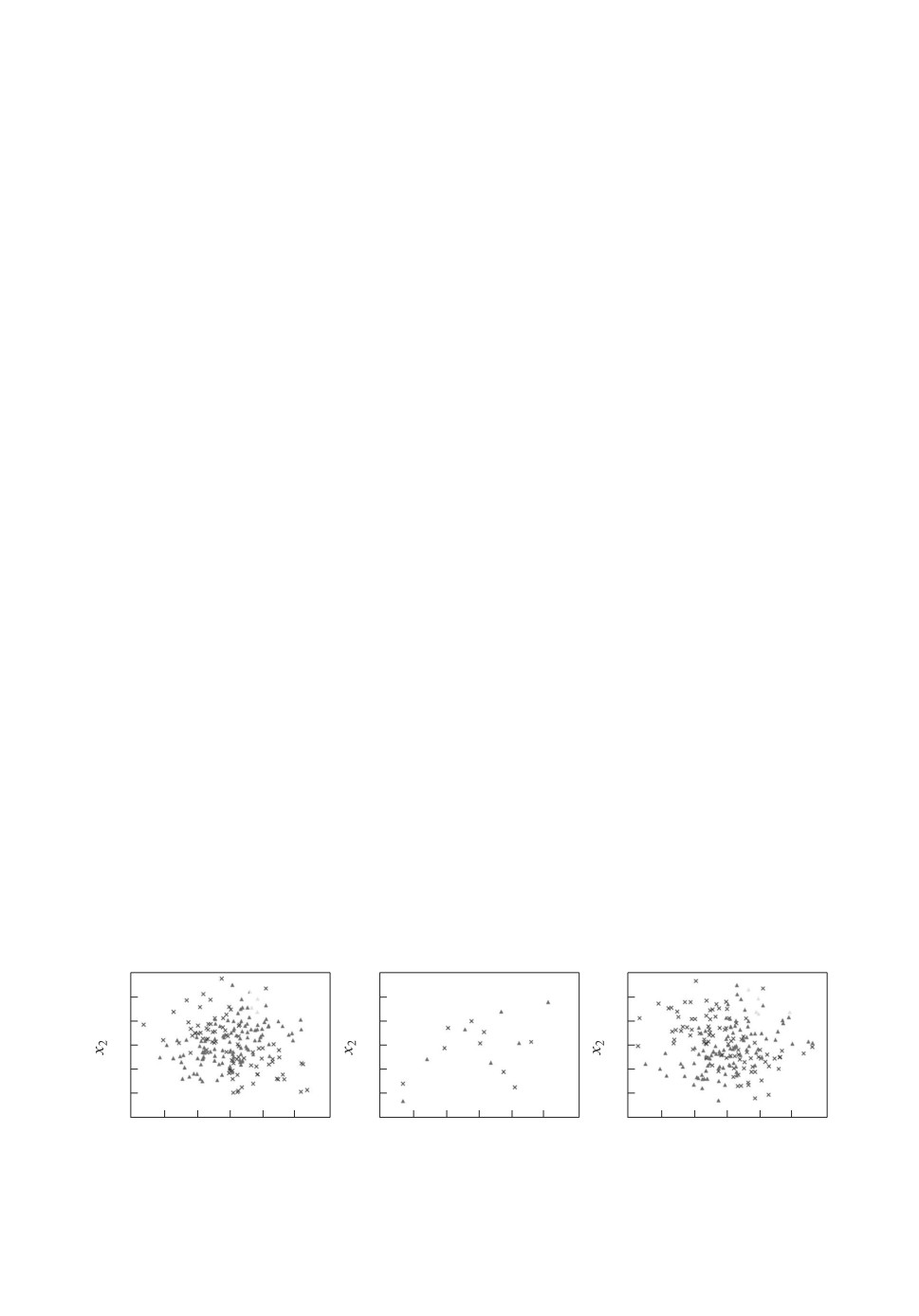
Рис. 4. Визуализация выборки для a - модели-учителя; б - модели-ученика;

в - тестовой выборки.

Рис. 5. Точность модели со значениями e₁ и e₂: a - e₁ = e₂; б - подбор e₂ при

e₁ = 10.

4.2. Эксперименты на выборках CIFAR-10 и Fashion-MNIST

Обе выборки были разделены в пропорции 9:1 для обучения и валидации.

Для оптимизации параметров модели был использован метод стохастическо-

го градиентного спуска с начальной длиной шага, равной 1,0. Длина шага

умножалась на 0,5 каждые 10 эпох. Значение T_val задано равным 1,0.

Для эксперимента на выборке CIFAR-10 была использована предобучен-

ная модель ResNet из [10] в качестве модели-учителя. В качестве модели-

ученика была использована модель CNN с тремя сверточными слоями и дву-

мя полносвязными слоями.

Для экспериментов на уменьшенной выборке длина шага для оптимизации

метапараметров была равна 0,25 и модель обучалась 50 эпох. Для экспери-

мента на полной выборке была использована дина шага, равная 0,1. Модель

обучалась 100 эпох.

Для эксперимента на выборке Fashion-MNIST использовались архитекту-

ры модели-ученика и модели-учителя, аналогичные архитектурам в экспери-

менте на выборке CIFAR-10. Для оптимизации метапараметров была исполь-

зована длина шага, равная 0,1, и модель обучалась 50 эпох.

Из результатов в табл. 2 видно, что предложенный метод и градиентные

методы дают высокое значение точности. Однако недостаток градиентных

методов заключается в ¾застревании¿ в точках локального минимума, из-за

чего дисперсия результатов получается гораздо выше, чем у остальных ме-

тодов. Этот эффект можно заметить на рис. 3 и в табл. 2.

5. Заключение

Была исследована задача оптимизации параметров модели глубокого обу-

чения. Было предложено обобщение методов дистилляции, заключающееся

в градиентной оптимизации метапараметров. На первом уровне оптимизиру-

ются параметры модели, на втором метапараметры, задающие вид опти-

мизационной задачи. Был предложен метод, уменьшающий вычислительную

сложность оптимизации метапараметров для градиентной оптимизации. Бы-

ли исследованы свойства оптимизационной задачи и методы предсказания

траектории оптимизации метапараметров модели. Под метапараметрами мо-

дели понимаются параметры оптимизационной задачи дистилляции. Предло-

женное обобщение позволило производить дистилляцию модели с лучшими

эксплуатационными характеристиками и за меньшее число итераций оптими-

зации. Данный подход был проиллюстрирован с помощью вычислительного

эксперимента на выборках CIFAR-10 и Fashion-MNIST, и на синтетической

выборке. Вычислительный эксперимент показал эффективность градиентной

оптимизации для задачи выбора метарапараметров функции потерь дистил-

ляции. Проанализирована возможность аппроксимировать траекторию опти-

мизации метапараметров локально-линейной моделью. Планируются даль-

нейшее исследование оптимизационной задачи и анализ качества аппрокси-

мации траектории оптимизации метапараметров более сложными прогности-

ческими моделями.

СПИСОК ЛИТЕРАТУРЫ

Bakhteev O.Y., Strijov V.V. Comprehensive analysis of gradient-based hyperparam-

eter optimization algorithms // Ann. Oper. Res. 2020. Vol. 289. No. 1. P. 51-65.

Bergstra J., Bengio Y. Random search for hyper-parameter optimization // MA-

CHINE LEARNING RES. 2012. Vol. 13. No. 2.

Bergstra J., Yamins D., Cox D. Making a science of model search: Hyperparame-

ter optimization in hundreds of dimensions for vision architectures // International

conference on machine learning. 2013. P. 115-123.

Bishop C.M. Pattern recognition and machine learning (information science and

statistics). 2006.

Hinton G.E., Vinyals O., Dean J. Distilling the knowledge in a neural network //

CoRR. 2015. Vol. abs/1503.02531. URL: http://arxiv.org/abs/1503.02531.

Krizhevsky A., et al. Learning multiple layers of features from tiny images, 2009.

Liu H., Simonyan K., Yang Y. Darts: Differentiable architecture search // arXiv

preprint arXiv:1806.09055, 2018.

Luketina J., Berglund M., Greff K., Raiko T. Scalable gradient-based tuning of con-

tinuous regularization hyperparameters // CoRR. 2015. Vol. abs/1511.06727.

URL: http://arxiv.org/abs/1511.06727.

Maclaurin D., Duvenaud D., Adams R.P. Gradient-based hyperparameter optimiza-

tion through reversible learning // CoRR. 2015. Vol. abs/1502.03492.

URL: http://arxiv.org/abs/1502.03492.

10.

Passalis N., Tzelepi M., Tefas A. Heterogeneous knowledge distillation using infor-

mation flow modeling // Proceedings of the IEEE Conference on Computer Vision

and Pattern Recognition. 2020.

11.

Pedregosa F. Hyperparameter optimization with approximate gradient // CoRR,

2016. Vol. abs/1602.02355. URL: http://arxiv.org/abs/1602.02355.

12.

Rasley J., Rajbhandari S., Ruwase O., He Y. Deepspeed: System optimizations en-

able training deep learning models with over 100 billion parameters // Proceedings of

the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data

Mining. 2020. P. 3505-3506.