Автоматика и телемеханика, № 10, 2022

А.С. АНИКИН, канд.физ.-мат. наук (anikin@icc.ru),

Т.С. ЗАРОДНЮК, канд. техн. наук (tz@icc.ru),

П.С. СОРОКОВИКОВ (sorokovikov.p.s@gmail.com)

(Институт динамики систем и теории управления

им. В.М. Матросова СО РАН, Иркутск)

МОДИФИКАЦИЯ АЛГОРИТМА ДОВЕРИТЕЛЬНОГО БРУСА,

ОСНОВАННОГО НА АППРОКСИМАЦИИ ГЛАВНОЙ

ДИАГОНАЛИ МАТРИЦЫ ГЕССЕ, ДЛЯ РЕШЕНИЯ

ЗАДАЧ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ¹

В работе предложен подход к исследованию стандартной задачи опти-

мального управления, основанный на использовании редукции к конечно-

мерной задаче оптимизации с последующим использованием аппроксима-

ции главной диагонали гессиана. Приведены результаты вычислительных

экспериментов по решению вспомогательных задач оптимизации сепара-

бельных, квазисепарабельных функций и функций Розенброка-Скокова.

Ключевые слова: алгоритм доверительного бруса, квазисепарабельная

функция, матрица Гессе, задача оптимального управления.

DOI: 10.31857/S0005231022100117, EDN: ALGZQW

1. Введение

Задачи оптимального управления (ЗОУ) возникли из стремления учесть

ограничения на управляющие воздействия и фазовые координаты объек-

тов, динамика которых описывается системами обыкновенных дифферен-

циальных уравнений. Эта область исследований, подобно другим направле-

ниям теории экстремальных задач, возникла в связи с запросом со сторо-

ны приложений: появление постановок задач автоматического регулирова-

ния с ограничениями на управления (А.А. Фельдбаум [15], Д.В. Бушау [3]),

которые уже не укладывались в теорию вариационного исчисления. Хотя

первые подобные постановки точечно возникали и ранее (например, задача

Р. Годдарда (1919 г.) о подъеме ракеты на заданную высоту с минимальны-

ми затратами топлива), активное развитие этого направления традиционно

связывают с появлением фундаментальных принципов теории оптимального

управления: принципа максимума [14] и метода динамического программиро-

вания [7]. Сейчас теория оптимального управления активно развивается как

в связи с наличием трудных и интересных математических постановок, так и

с обилием приложений, в том числе и в таких областях, как космонавигация,

¹ Работа выполнена за счет субсидии Минобрнауки России в рамках проекта ¾Теория

и методы исследования эволюционных уравнений и управляемых систем с их приложе-

ниями¿ (№121041300060-4).

122

робототехника, динамика полета, экономика, биология, медицина, ядерная

энергетика, нанофизика и других.

Несмотря на активные исследования этой области стандартная ЗОУ с па-

раллелепипедными ограничениями на управление по-прежнему довольно ча-

сто возникает на практике и может характеризоваться наличием особенно-

стей, требующих использования специализированных подходов к их рассмот-

рению.

2. Задачи оптимального управления:

стандартная постановка

Разбиение переменных на фазовые и ограниченное управление, при на-

личии связывающих их дифференциальных уравнений стандартная мо-

дель для процесса, развивающегося по законам природы, но испытывающе-

го управляющие воздействия, стремящиеся сделать его в некотором смысле

оптимальным. Наличие параллелепипедных ограничений на управления воз-

никает естественным образом в силу ограниченности имеющихся ресурсов

и присутствует в стандартной постановке задачи оптимального управления.

Управляемая динамическая система с начальными условиями описывается

дифференциальными уравнениями в нормальной фоме Коши:

(1)

x = f(x(t),u(t),t), x(t₀) = x⁰, t ∈ [t₀,t₁

где t независимая переменная (время), x(t) вектор фазовых координат

размерности n, x = dx/dt производная фазовой траектории, u(t) r-вектор

управляющих воздействий, x⁰ вектор начального состояния системы. До-

пустимые управления это вектор-функции, определенные на временном

отрезке T и удовлетворяющие ограничениям:

(2)

u(t) ∈ U = {u(t) ∈ Rⁿ

: u ≤ u(t) ≤ u}.

Задача состоит в поиске допустимого управления u^∗(t), доставляющего ми-

нимум терминальному функционалу, зависящему от траектории системы (1)

в конечный момент времени t₁

(3)

I(u) = ϕ(x(t₁

)) → min .

Допустимый процесс (u, x), u = u(t) ∈ U, на котором функционал минимален,

называется оптимальным (u^∗, x^∗). Вектор-функция f(x(t), u(t), t) и скаляр-

ная функция ϕ(x) предполагаются непрерывно дифференцируемыми по всем

аргументам, кроме t. Постановки с интегральными и смешанными функцио-

налами (задачи Больца и Лагранжа) путем введения дополнительных фазо-

вых координат могут редуцироваться к представленной задаче Майера. Для

подобных детерминированных задач, в которых уравнения движения, крите-

рий качества и ограничения известны точно, оптимальное значение критерия

качества (3), реализуемое в классе программных управлений и управлений

по принципу обратной связи, является одним и тем же. ЗОУ в данной фор-

мулировке считается классической [12, 16] и часто встречается в различных

приложениях.

123

3. Традиционные подходы к исследованию

стандартной ЗОУ

В теории оптимального управления принято различать два типа числен-

ных подходов: прямые (direct) и непрямые (indirect). Прямые методы заклю-

чаются в дискретизации состояния и управления и тем самым сводят исход-

ную задачу к задаче нелинейной оптимизации с ограничениями. Непрямые

методы состоят из численного решения краевой задачи, вытекающей из при-

менения принципа максимума Понтрягина, и приводят к методам стрельбы

(или методам пристрелки shooting methods). В связи со значительными

трудностями построения аналитического решения прикладных задач опти-

мального управления ключевое значение приобрели различные приближен-

ные и численные методы их исследования. В зависимости от алгоритмической

основы метода он может быть отнесен к той или иной группе.

3.1. Методы, основанные на использовании

принципа максимума Понтрягина

В непрямых методах вместо предварительной дискретизации, как в пря-

мых методах, сначала применяется принцип максимума Понтрягина (ПМП)

как условие первого порядка к задаче оптимального управления. Согласно

этому принципу оптимальную траекторию следует искать среди соответст-

вующих экстремалей, для которых он выполняется. Подобные подходы могут

опираться на сведение исходной задачи к краевой задаче нахождения экстре-

мального решения сопряженной системы. Решить такую нелинейную систему

из n уравнений с n неизвестными на практике можно, например, с помощью

методов ньютоновского типа. Таким образом, ПМП является универсальным

необходимым условием оптимальности первого порядка в стандартной ЗОУ.

Традиционно он наиболее эффективен в системах управления с максималь-

ным быстродействием и минимальным расходом энергии, где применяются

управления релейного типа, принимающие крайние, а не промежуточные зна-

чения на допустимом интервале управления.

Построение вычислительных схем, основанных на применении ПМП, мо-

жет опираться на следующие этапы: а) формируется и решается систе-

ма уравнений из условия равенства нулю градиента функции Понтрягина;

б) в критических точках исследуется на знакоопределенность матрица вто-

рых производных, в случае ее положительной определенности получается

точка строгого локального минимума, отрицательно определенная матри-

ца характеризует локальный максимум; в) анализируются критические точ-

ки, в которых матрица вторых производных не является знакоопределенной;

г) найденные точки локальных экстремумов исследуются на глобальный экс-

тремум, если это возможно.

Для линейно-выпуклых задач оптимального управления выполнение усло-

вия максимума функции Понтрягина является и достаточным условием оп-

тимальности, и может быть использовано для нахождения глобального ми-

нимума функционала. В общем случае, когда правые части системы и подын-

тегральная функция критерия качества дифференцируемы по управлениям,

может использоваться линеаризованный или дифференциальный принцип

124

максимума [8, 9], часто применяемый в вычислительных схемах для проверки

оптимальности полученного в результате итерационного процесса решения.

Методы последовательных приближений для поиска управлений, удовлетво-

ряющих линеаризованному ПМ, опираются на использование информации

о градиенте функции Понтрягина и применяются, фактически, для реше-

ния конечномерных задач максимизации гамильтониана в заданных точках

временного отрезка. Важно помнить, что принцип максимума как необхо-

димое условие оптимальности, вообще говоря, порождает не оптимальные

траектории, а экстремали, для которых требуется отдельно обосновывать оп-

тимальность. Для этой цели могут быть использованы достаточные условия

оптимальности.

3.2. Методы, опирающиеся на дискретизацию ЗОУ

Для использования многочисленных существующих прямых методов необ-

ходимо выбирать конечномерные представления управления и состояния,

а затем дискретно выражать дифференциальные уравнения, описывающие

динамическую систему, критерий минимизации и присутствующие в зада-

че ограничения. После того, как все статические и динамические ограни-

чения редуцированы к задаче с конечным числом переменных, необходимо

решить полученную задачу оптимизации, используя какой-либо адаптиро-

ванный метод.

В качестве примера можно привести самый простой способ дискретизации,

основанный на равномерном разбиении временного отрезка на подынтервалы.

Управления дискретизированы таким образом, чтобы являться кусочно-по-

стоянными на каждом подынтервале и удовлетворять заданным ограниче-

ниям. Самым простым методом дискретизации обыкновенных дифференци-

альных уравнений для численной реализации (в том числе для организа-

ции параллельных вычислений) является стандартный явный метод Эйлера.

Множество допустимых управлений можно также дискретизировать, напри-

мер, кусочно-постоянными функциями или сплайнами, а обыкновенные диф-

ференциальные уравнения аппроксимировать дискретными соотношениями с

использованием методов типа Рунге-Кутты различных порядков. В результа-

те из непрерывной задачи оптимального управления получаем задачу конеч-

номерной минимизации, в которой переменные подчиняются ограничениям,

вытекающим из дифференциальной системы и ограничений на управления.

В плане соответствия редуцированной задачи исходной можно утверждать

следующее: стандартная задача оптимального управления характеризует-

ся управляющими воздействиями кусочно-непрерывного типа, соответствую-

щая фазовая траектория является кусочно-гладкой и при выполнении усло-

вия роста с учетом ограничений на управления можно с уверенностью счи-

тать, что соответствующая конечномерная задача, полученная путем дискре-

тизации, будет поддаваться численному решению с использованием методов

конечномерной оптимизации при небольших размерностях. Это связано с на-

личием дифференциальной связи фазовых координат и управляющих воз-

действий, которая позволяет получать редуцированные конечномерные за-

дачи с адекватными свойствами. Непрерывная дифференцируемость правых

частей системы дифференциальных уравнений по фазовым переменным и

125

выполнение соответствующего условия Липшица позволяют обеспечить су-

ществование и единственность решения в задаче Коши для любого допусти-

мого управления.

4. Модификация алгоритма доверительного бруса

Предлагаемый алгоритм основан на использовании информации о главной

диагонали матрицы Гессе. Потому как использование полного гессиана при

реализации алгоритмов может оказаться не слишком рентабельной операци-

ей. Помимо большого объема памяти, требуемой для размещения матрицы

Гессе, вычисление информации второго порядка может оказаться достаточно

трудоемкой задачей при недоступных аналитических формулах для вторых

производных. В такой ситуации обычно используются варианты разностных

схем либо второго порядка, опирающихся на алгоритм вычисления функ-

ции, либо первого порядка, основанных на вычислении вектора градиентов.

В отличие от классических методов ньютоновского типа в реализованном

алгоритме используются элементы только главной диагонали матрицы Гессе

и для нахождения направления движения на каждой итерации формулиру-

ется и решается задача квадратичного программирования на брусе. Решение

этой вспомогательной задачи, в данном случае сепарабельной, тривиальное и

получается в замкнутом виде, что позволяет достичь как хорошей скорости,

так и достаточно высокой точности. Заметим, что от классических методов

доверительного интервала (см., например, [6]) реализованный подход отлича-

ется способом ограничения вариации на каждой итерации: вместо эллипсои-

дального ограничения в данном случае применяется брусовое. Это влечет за

собой другую постановку вспомогательной задачи и, очевидно, другие свой-

ства общего алгоритма.

Реализованные варианты алгоритма используют аппроксимацию диагона-

ли с помощью двух градиентов (V ar1, [11]) и классическую аппроксимацию

по разностной схеме второго порядка (V ar2, см., например, [13]). Помимо оп-

тимизации памяти такой подход существенно ускоряет решение внутренней

задачи линейной алгебры, которая в таком случае становится тривиальной.

Для обеспечения способности алгоритма генерировать улучшающие итера-

ции с любой начальной точки, в конструкции используется техника криво-

линейного шага поиска [11]. Алгоритм позволяет быстро находить решение в

классе квазисепарабельных функций, особенно на функциях с диагональным

преобладанием в матрице Гессе [1].

Для вспомогательной процедуры одномерного поиска в зависимости от

трудоемкости обработки матрицы Гессе может использоваться как грубый

алгоритм одномерного поиска, начинающий итерации с единичного шага,

и дробящий шаг до достижения релаксирующего приближения, так и спе-

циализированный высокоточный алгоритм локального одномерного поиска

(в разработанном подходе комбинация методов золотого сечения и обрат-

ной параболической интерполяции (см., например, [2, 10]). В обоих реализо-

ванных вариантах алгоритма вспомогательные поисковые методы опираются

на использование квадратичной вариационной конструкции, приводящей к

аппроксимации ¾ньютоновской¿ точки при единичном шаге и приближаю-

щейся к направлению антиградиента при малых шагах (см. алгоритм 1).

126

Алгоритм 1. Алгоритм доверительного бруса

Require: Задаются алгоритмические параметры, выбираются x⁰, δ^K = δ_start.

for K = 0, . . . , T_out do



∇f(x^K )<= εng then

x^∗ = x^K

brake

end if

if V ar1 then

Вычисляется аппроксимация Z^K диагонали гессиана

с помощью алгоритма, основанного на градиентах

с шагом сдвига α_D

end if

if V ar2 then

10:

Вычисляется аппроксимация Z^K диагонали гессиана

с использованием алгоритма, основанного на разностной схеме

с шагом Stdif

11:

end if

[

12:

B^K =

x^K - δ^K,x^K + δ^K

13:

p^k = arg min pZ^Kp - ∇f(x^K)p, p ∈ B^K

14:

x(α) = x^K + α²p^K - α(1 - α)∇f(x^K ).

15:

α^K = arg min_α∈[0,1] f(x(α)).

16:

x^K+1 = x^K + α^2Kp^K - α^K(1 - α^K)∇f(x^K).

17:

if α^K < 0,5 then

18:

δ^K = 0,9δ^K

19:

if δ^K < δ_min then

20:

δ^K = δ_start

21:

end if

22:

end if

23:

if α^K > 0,5 then

24:

δ^K = 1,1δ^K

25:

if δ^K > δ_max then

26:

δ^K = δ_start

27:

end if

28:

end if

29:

end for

Выход: x^∗ если было достигнуто условие досрочного завершения, иначе

xTout+1.

Влиять на вычислительные свойства программной реализации предло-

женного алгоритма можно путем изменения значений алгоритмических па-

раметров. К общим алгоритмическим параметрам для двух реализован-

ных вариантов [тносятся:] εng

точность критерия остановки по нор-

ме градиента

10^-12, 100

, в качестве стандартного значения выбирает-

ся 10^-5; α₀

начальный шаг одномер[ого пои]ка, принимающий на стар-

те наибольшее значение из интервала

10^-10, 1

; tol_n

точность одномер-

127

[

]

ного поиска выбирается из интервала

10^-12, 0,1

и задается равной 10^-4;

[

]

ε_fi

точность критерия остановки по релаксации ∈

10^-15, 100

и выбира-

ется по умолчанию равной 10[-6; δstart] начальный размер доверительных

брусов

0,1,

из интервала

10^-6, 10

; δ_min минимальный размер довери-

[

]

тельных брусов

10^-4,

10^-12, 1

; δ_max максимальный размер доверитель-

[

]

ных брусов выбирается из интервала

10^-6, 10³

равным 10.

К специализированным алгоритмическим параметрам для первого вари-

ан[та отно]ится шаг сдвига от точки первого градиента до второго αd = 0,1 ∈

∈

10^-6, 1

. Для второго варианта алгоритма - шаг численного дифференци-

[

]

рования Stdif, принимающий значение из интервала

10^-12, 1

, стандартное

значение равно 10^-10. Настройка значений алгоритмических параметров мо-

жет повысить эффективность программной реализации алгоритма для вы-

бранного класса задач.

5. Вычислительные эксперименты

Расчеты проводились на персональном компьютере, тактовая частота про-

цессора 2.8GHz, Intel Core i7. Использован компилятор BCC 5.5 под управле-

нием виртуальной машины MaC OS, Windows XP. Для исследования свойств

реализованного алгоритма сформирована небольшая коллекция тестовых за-

дач, включающая: тестовые примеры cепарабельных и квазисепарабельных

функций, а также функции Розенброка-Скокова [5], ориентированные на

сравнение и исследование свойств программных реализаций предложенного

алгоритма.

5.1. Результаты решения вспомогательной задачи

конечномерной оптимизации

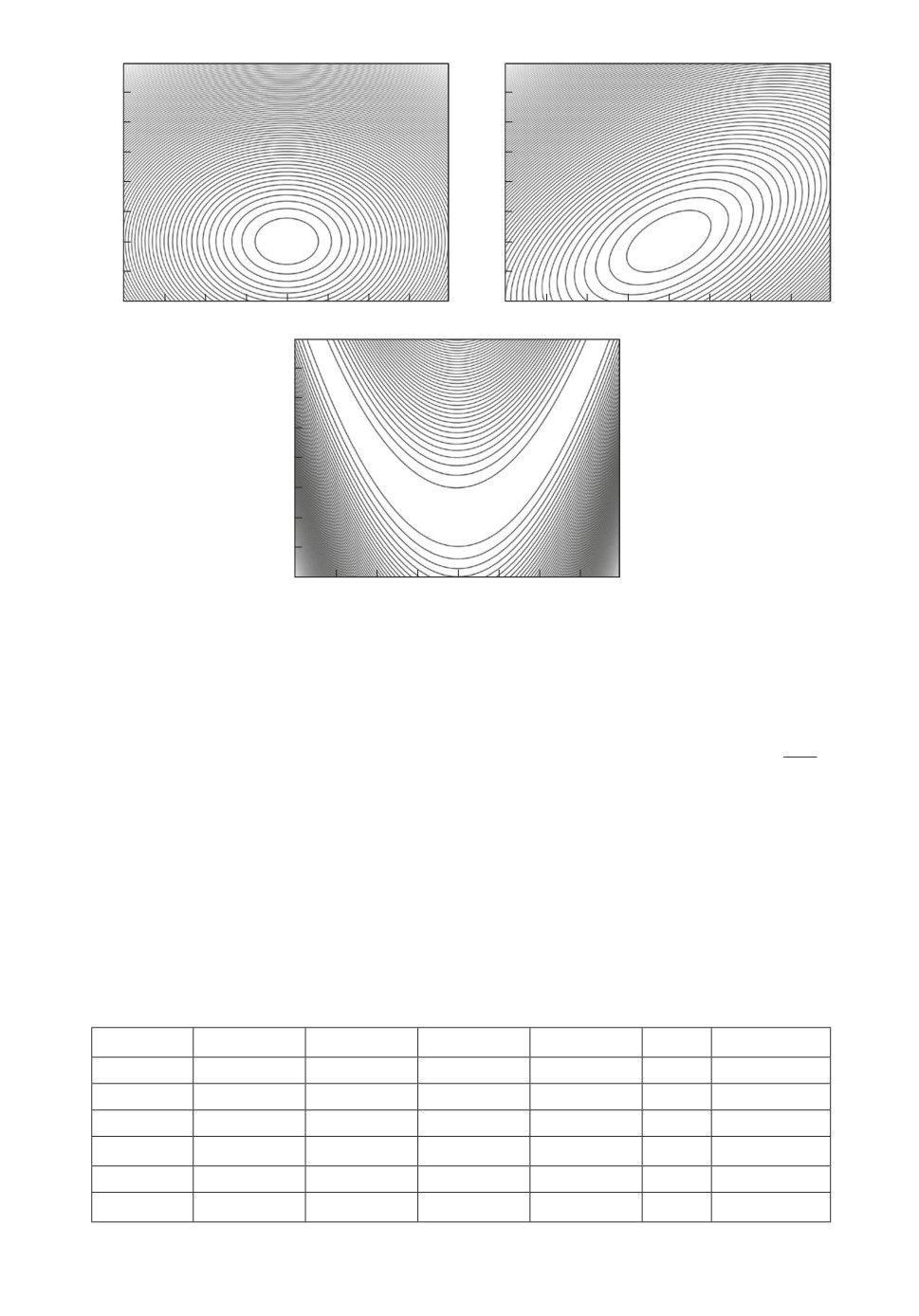
5.1.1. Сепарабельная функция. Наиболее простая по структуре функ-

ция это первая тестовая функция, на которой можно проверить работо-

способность алгоритмов оптимизации и сравнить их свойства (рис. 1). Раз-

мерность данной задачи легко изменяется (вычислительные эксперименты

проводились в том числе для Large-size problem (табл. 1).

∑

f (x) =

x²ⁱ → min, x⁰ⁱ = 0,5 + i · 10^-6, i = 1,n.

i=1

5.1.2. Квазисепарабельная функция. Сложность квазисепарабельных

функций при изменении значения множителя, входящего в состав второго

слагаемого, может возрастать. Функции данного типа также являются попу-

лярными для проведения вычислительных экспериментов по исследованию

алгоритмов оптимизации (см., например, [4]).

∑

f (x) =

x²ⁱ + 0,001

i(x_i - x_i+1)² → min, x⁰ⁱ = 1,0 + i · 10^-7, i = 1, n.

i=1

128

2,5

2,0

1,5

1,0

0,5

-0,5

-1,0

-2,0 -1,5 -1,0 -0,5

0,5

1,0

1,5

-2,0 -1,5 -1,0 -0,5

0,5

1,0

1,5

2,5

2,0

1,5

1,0

0,5

-0,5

-1,0

-2,0 -1,5 -1,0 -0,5

0,5

1,0

1,5

Рис. 1. Линии уровня тестовых сепарабельной, квазисепарабельной функций

и функции Розенброка-Скокова.

5.1.3. Функция Розенброка-Скокова.

∑

f (x) = (1 - x₁)² + 100 (x_i - x^2i-1)² → min, x⁰ⁱ = -2,0 + i · 10^-7, i = 1, n.

i=2

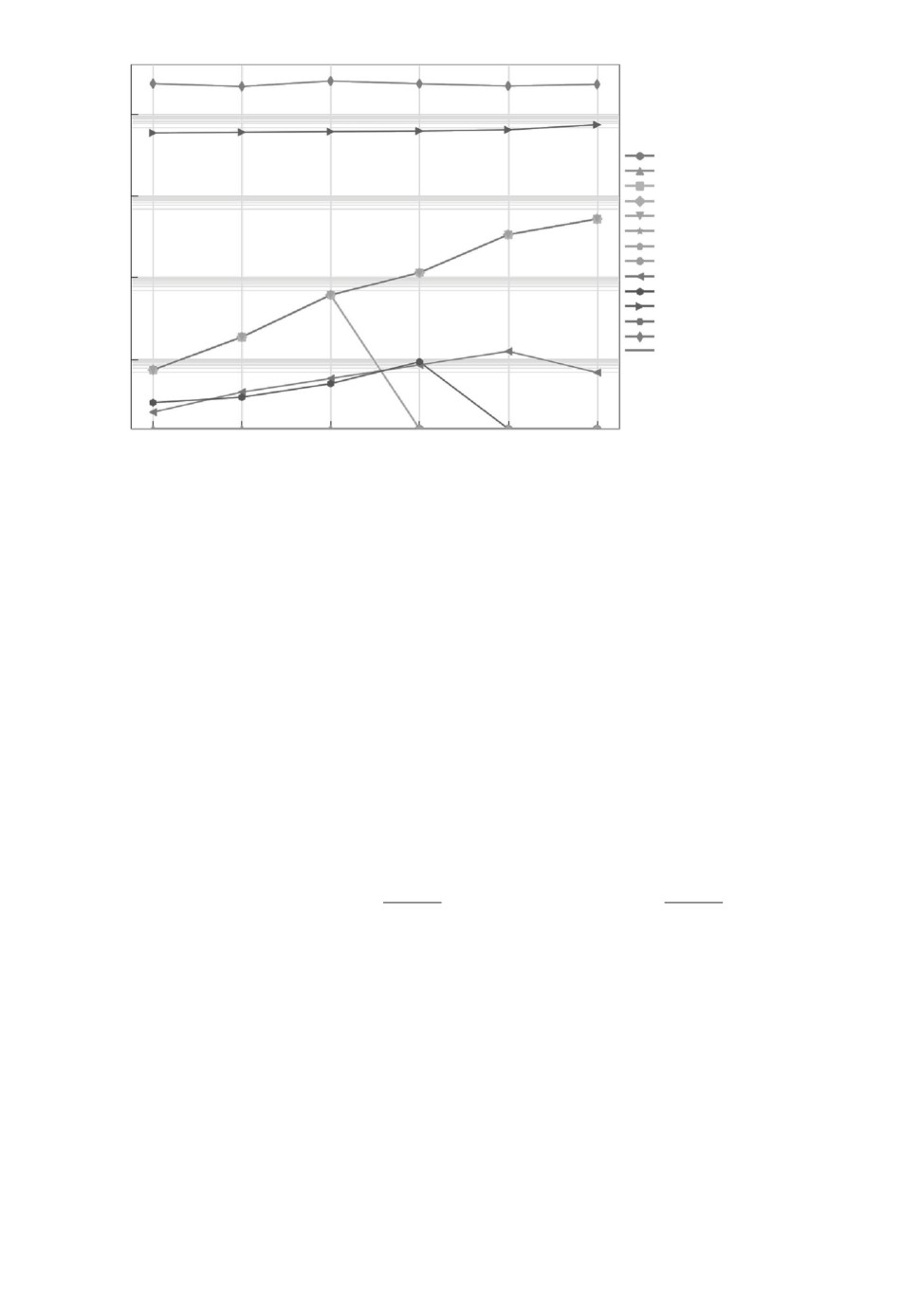
Сравнение работоспособности предложенного алгоритма с авторской биб-

лиотекой алгоритмов оптимизации, включающей программные реализа-

ции методов Ньютона, Барзилаи-Борвейна, Поляка, Бройдена-Флетчера-

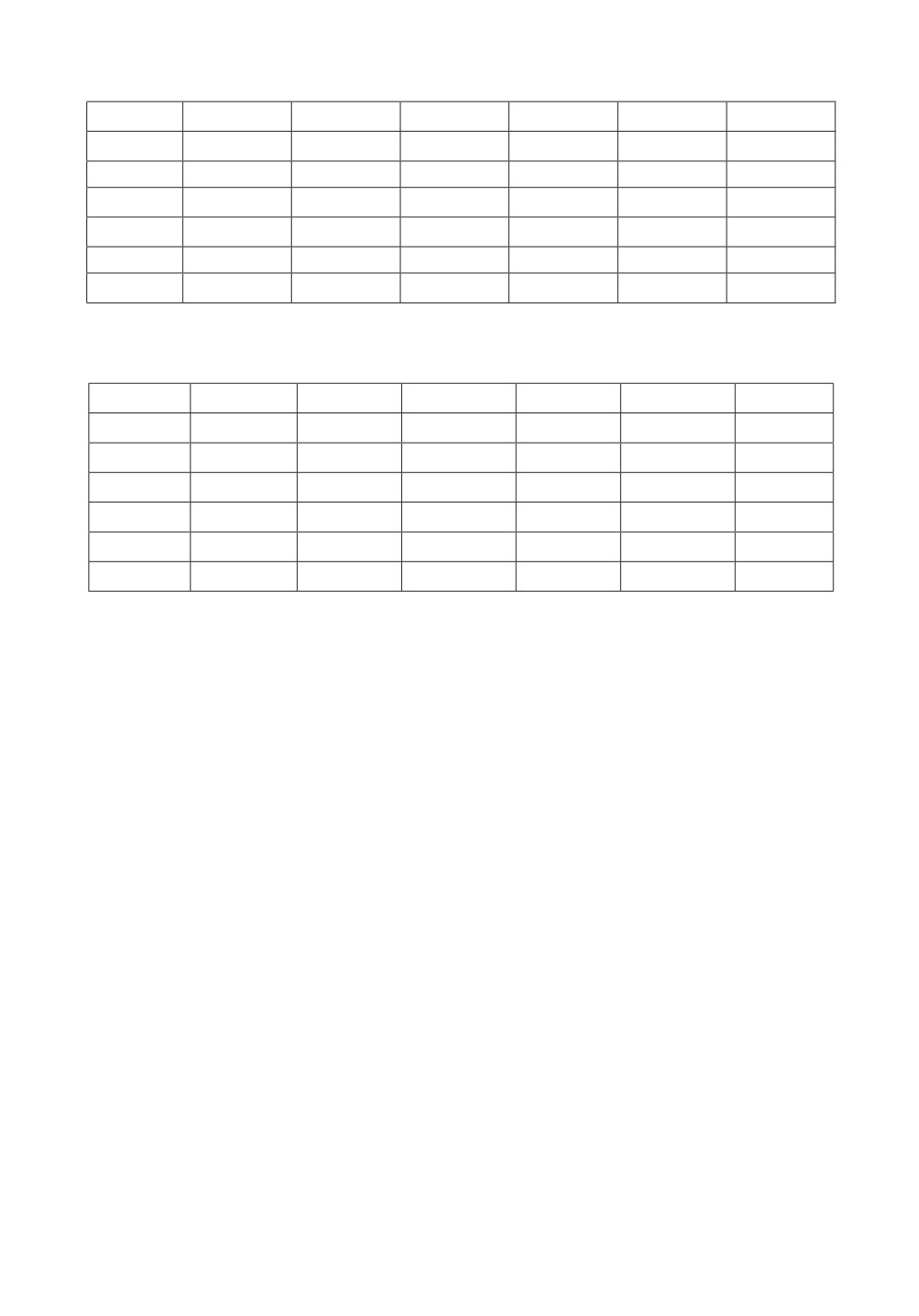
Таблица 1. Результаты вычислительных экспериментов для семейства сепара-

бельных функций. Здесь V ar1 результаты расчетов для первого варианта ал-

горитма, V ar2 для второго варианта алгоритма, f_rec наилучшее достигнутое

значение функции, ng достигнутое значение нормы градиента, iter число

итераций алгоритма

5 · 10²

5 · 10³

5 · 10⁴

5 · 10⁵

V ar1 f_rec

0,00

V ar1 iter

V ar1 ng

0,0

V ar2 f_rec

1,34 · 10^-15

1,33 · 10^-11

9,94 · 10^-31

2,64 · 10^-15

V ar2 iter

V ar2 ng

7,3 · 10^-8

7,0 · 10^-6

3,0 · 10^-15

2,0 · 10^-7

129

f *

1e-10

Method

BFGS (v1)

Barzilai Borwein (v1)

Couchy (v1)

1e-16

Conjugate Gradient (FR, v1)

Conjugate Gradient (HS, v1)

Conjugate Gradient (Nesterov, v1)

DFP (v1)

LBFGS (v1)

1e-22

Newton (v1)

Polyak (v2)

Raider (v1)

Reduced/Conditional Gradient (v1)

Split Gradient (v1)

Trust Region (v2)

1e-28

Рис. 2. Результаты вычислительных экспериментов для библиотеки методов

оптимизации на сепарабельной функции возрастающих размерностей.

Гольдфарба-Шанно и других, отображено на рис. 2. В данном случае тести-

рование проводилось с использованием сепарабельной функции размерности

от 5 до 5 · 10⁵ переменных (табл. 1). Видно, что с использованием предложен-

ной модификации метода доверительных брусов удается решить задачу для

всех рассматриваемых размерностей сепарабельной функции.

5.2. Результаты решения задачи оптимального управления

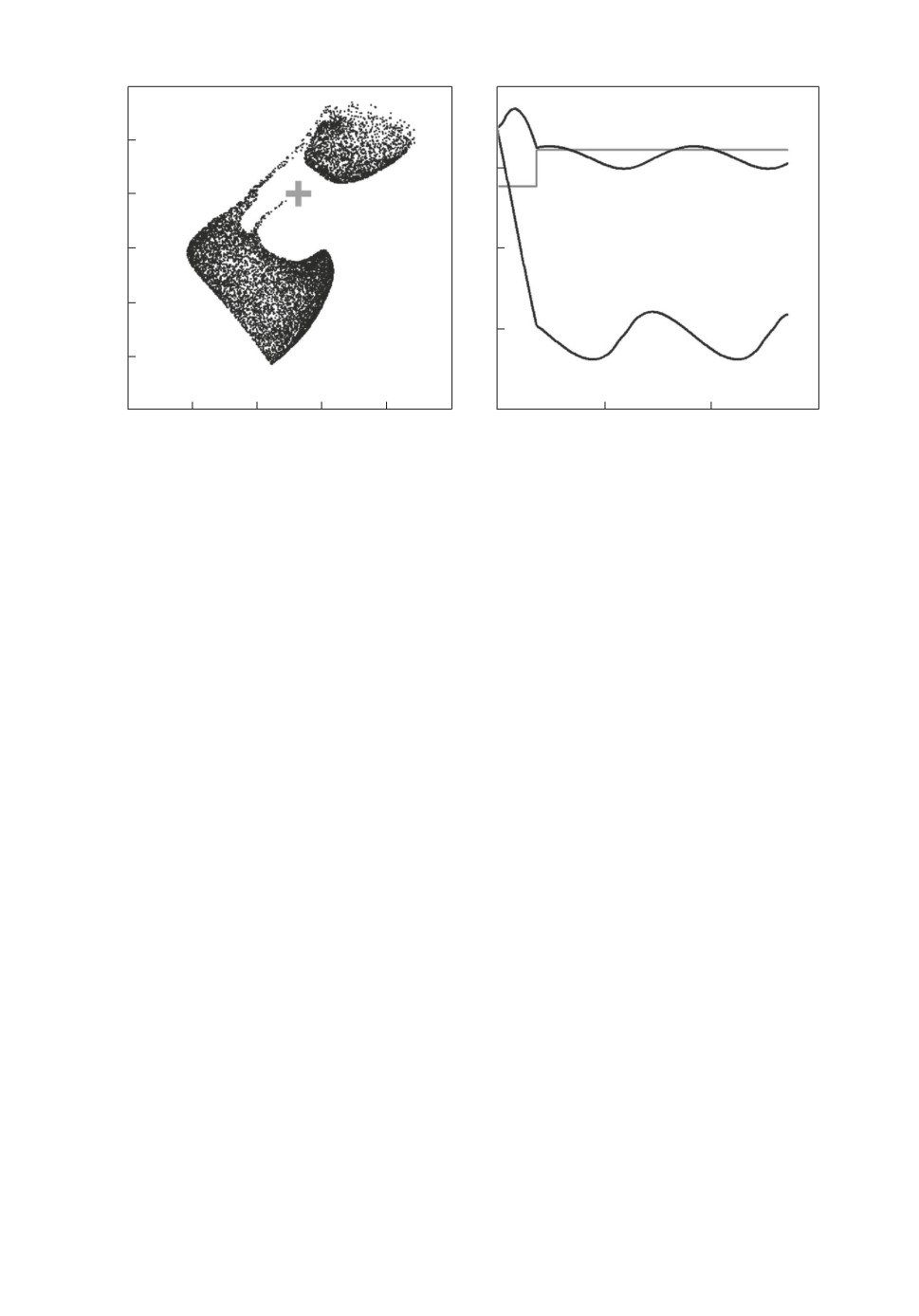
Приведем пример модельной тестовой задачи оптимального управления

с невыпуклым множеством достижимости, характеризующимся малой обла-

стью притяжения глобального экстремума.

√

(4)

x₁(t) = u(t) - sin

|x₁(t)|,

x₂(t) = u(t) + cos

|x₁

(t)|,

(5)

x₁(t₀) = 1, x₂(t₀

) = 1, u(t) ∈ [-0,45,0,45], t ∈ T = [0,27],

(6)

I(u) = (x₁(t₁) + 3)² + (x₂(t₁) + 0,5)²

↓.

Данная тестовая задача позволяет смоделировть вычислительные труд-

ности, характерные для рассматриваемых задач оптимального управления

с нелинейными системами дифференциальных уравнений и невыпуклыми

функционалами. На рис. 3 представлено множество достижимости в при-

веденной тестовой задаче с выделенной экстремальной точкой, в которой до-

стигается наименьшее значение целевого функционала на соответствующих

оптимальных траекториях и управлении (рис. 3).

130

U ', X '

x₂

-10

-2

-20

x₁

-4

-30

-40

-30

-20

-10

-60

Рис. 3. Множество достижимости и экстремальная точка (слева), оптималь-

ные траектории и управление (справа) в представленной модельной задаче.

6. Заключение

Проведенные эксперименты подтвердили теоретический вывод о непри-

емлемости использования разностных схем для решения задач размерности

более 10³. Время, необходимое для получения информации о матрице Гес-

се (точнее, только о ее диагонали), становится совершенно неприемлемым.

Это продемонстрировано в табл. 2 и 3 соотношением производительности

вариантов алгоритма, второй из которых основан на разностной схеме для

аппроксимации диагонали гессиана.

К достоинствам предложенного алгоритма следует отнести его способ-

ность решать задачи существенно больших размерностей, чем любые методы,

требующие полной квадратичной памяти, в том числе, методы ньютоновско-

го типа, квазиньютоновские методы, метод Пауэлла и другие. Наблюдение

графиков сходимости (значений функций с ростом числа итераций) показы-

вает, что, к сожалению, эффект ускорения за счет информации второго по-

рядка в данной конструкции алгоритмов оказывается существенным только

на начальных стадиях расчетов, позволяя очень быстро получить неплохие

результаты. Далее проявляется ¾эффект малых вариаций¿, что объясняется,

очевидно, переходом алгоритма в режим ¾почти градиентного¿ метода.

Данный алгоритм может использоваться для решения стандартной зада-

чи оптимального управления, которая на практике характеризуется наличи-

ем нелинейных систем дифференциальных уравнений и невыпуклых функ-

ционалов, что, как правило, приводит к неединственности решения и необхо-

димости разрабатывать специализированные вычислительные технологии их

исследования. С другой стороны, рост вычислительных мощностей современ-

ных компьютеров позволяет повышать эффективность алгоритмов поиска ре-

шения в задачах оптимизации, в том числе за счет использования технологий

131

Таблица 2. Результаты вычислительных экспериментов для семейства квазисепа-

рабельных функций

5 · 10²

5 · 10³

5 · 10⁴

5 · 10⁵

V ar1 frec 4,29 · 10-21 2,99 · 10-19

1,55 · 10^-7

1,05 · 10-11 1,29 · 10-11 1,36 · 10-11

V ar1 iter

121

1413

17231

V ar1 ng

1,3 · 10^-10

1,1 · 10^-9

8,6 · 10^-9

9,0 · 10^-6

9,9 · 10^-6

1,0 · 10^-5

V ar2 frec 1,07 · 10-12 9,09 · 10-12 1,11 · 10-11 7,69 · 10-12

V ar2 iter

149

V ar2 ng

2,1 · 10^-6

6,0 · 10^-6

6,7 · 10^-6

9,0 · 10^-6

Таблица 3. Результаты вычислительных экспериментов для семейства функций

Розенброка-Скокова

5 · 10²

5 · 10³

5 · 10⁴

5 · 10⁵

V ar1 f_rec

1,03 · 10^-9

2,6 · 10^-13

2,51 · 10^-13

2,5 · 10^-13

1,17 · 10^-12

V ar1 iter

> 6,3 · 10⁶

13587

43997

139219

> 0,2 · 10⁶

V ar1 ng

1,0 · 10^-5

2,2 · 10^-5

V ar2 f_rec

1,06 · 10^-9

2,6 · 10^-13

2,51 · 10^-13

V ar2 iter

> 6,6 · 10⁶

13596

43999

V ar2 ng

1,0 · 10^-5

параллельного запуска однородных процессов. Проведенные вычислительные

эксперименты продемонстрировали возможность использования предложен-

ного алгоритма для решения вспомогательных задач больших размерностей,

возникающих при редукции исходной задачи на мелкой сетке к последова-

тельности конечномерных в рамках стандартной идеологии использования

прямых методов для решения задач оптимального управления.

СПИСОК ЛИТЕРАТУРЫ

1. Andrianov A.N., Anikin A.S., Bychkov I.V., Gornov A.Y. Numerical solution of

huge-scale quasiseparable optimization problems // Lobachevskii Journal of Mathe-

matics. 2017. Vol. 38. No. 5. P. 870-873.

2. Brent R. Algorithms for Minimization without Derivatives. Prentice Hall (reprinted

by Dover, 2013).

3. Bushaw D.W. Differential equations with a discontinuous forcing term. Stevens Inst.

Technol. Experimental Towing Tank Rept. 469, Hoboken, N.J., 1953.

4. Gornov A.Yu., Andrianov A.N., Anikin A.S. Algorithms for the solution of huge qua-

siseparable optimization problems // Proc. of VI International Workshop: “Critical

Infrastructures in the Digital World”. Irkutsk. 2016. P. 76-77.

5. Skokov V.A. Methods and algorithms for unconditional minimization of functions of

many variables (review) // Scientific report. 1974.

6. Ya-Xiang Yuan. Recent advances in trust region algorithms // Math. Program.,

Ser. B. 2015. Vol. 151. P. 249-281.

7. Беллман Р. Динамическое программирование. М.: Изд-во иностр. лит., 1960.

132

8. Васильев О.В. Лекции по методам оптимизации. Иркутск: Изд-во Иркут. ун-та,

1994.

9. Васильев О.В., Аргучинцев А.В. Методы оптимизации в задачах и упражне-

ниях. М.: Физматлит, 1999.

10. Горнов А.Ю. Вычислительные технологии решения задач оптимального управ-

ления. Новосибирск: Наука, 2009.

11. Деннис Дж. мл., Шнабель Р.Б. Численные методы безусловной оптимизации и

решения нелинейных уравнений. М.: Мир, 1988.

12. Дыхта В.А. Оптимизация динамических систем с разрывными траекториями и

импульсными управлениями // Соросовский образоват. журн. 1999. № 8. С. 110-

115.

13. Иванов В.В. Методы вычислений на ЭВМ. Киев: Наукова Думка, 1986.

14. Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф. Матема-

тическая теория оптимальных процессов. М.: Наука, 1961.

15. Фельдбаум А.А. Оптимальные процессы в системах автоматического регулиро-

вания // АиТ. 1953. Т. 14. № 6. С. 712-728.

16. Черноусько Ф.Л., Колмановский В.Б. Вычислительные и приближенные методы

оптимального управления // Итоги науки и техники. Сер. Мат. анализ. Т. 20.

1977. С. 101-166.

Статья представлена к публикации членом редколлегии А.А. Лазаревым.

Поступила в редакцию 01.02.2022

После доработки 19.04.2022

Принята к публикации 29.06.2022

133