Автоматика и телемеханика, № 10, 2022

Е.В. ДЮКОВА, д-р физ.-мат. наук (edjukova@mail.ru)

(Федеральный исследовательский центр

¾Информатика и управление¿

Российской академии наук, Москва)

ОБ ОДНОМ ПОДХОДЕ К РАСШИФРОВКЕ

МОНОТОННОЙ ЛОГИЧЕСКОЙ ФУНКЦИИ

Рассматривается задача расшифровки двузначной монотонной функ-

ции f, определенной на k-значном n-мерном кубе. Традиционным под-

ходом к решению данной задачи является построение оптимального по

Шеннону алгоритма. Оптимальный по Шеннону алгоритм расшифров-

ки имеет минимальную сложность в ¾худшем случае¿ (эффективен для

наиболее трудного варианта задачи). Авторами предложен и исследован

подход к задаче расшифровки, основанный на применении асимптотиче-

ски оптимального алгоритма дуализации над произведением k-значных

цепей. Асимптотически оптимальная расшифровка функции f нацелена

на ¾типичный случай¿ (на типичный вариант задачи). Экспериментально

выявлены условия применимости традиционного и нового подходов.

Ключевые слова: верхний ноль монотонной логической функции, нижняя

единица монотонной логической функции, оптимальный по Шеннону ал-

горитм расшифровки, асимптотически оптимальный алгоритм расшиф-

ровки, максимальный частый элемент, минимальный нечастый элемент,

дуализация над произведением k-значных цепей.

DOI: 10.31857/S0005231022100129, EDN: ALIJYE

1. Введение

Расшифровка двузначной монотонной функции, определенной на k-знач-

ном n-мерном кубе, одна из важнейших задач дискретной математики.

Задача формулируется следующим образом.

Положим

E^nk = {(α₁,... ,α_n)|α_i ∈ {0,1,... ,k - 1} при i = 1,2,... ,n, k ≥ 2}.

Множество E^nk называется k-значным n-мерным кубом. На E^nk устанавлива-

ется частичный порядок, согласно которому элемент β = (β₁, . . . , β_n) из E^nk

следует за элементом α = (α₁, . . . , α_n) из E^nk (α предшествует β), если β_i ≥ α_i

при i = 1, 2, . . . , n. Для обозначения того, что β ∈ E^nk следует за α ∈ E^nk, ис-

пользуется запись α ≼ β или β ≽ α.

Функция f, определенная на E^nk и принимающая два значения 0 и 1, на-

зывается монотонной, если для любых двух элементов α и β из E^nk таких,

что α ≼ β, выполнено f(β) ≥ f(α). Функция f задается при помощи некото-

рого оператора B, который для любого x ∈ E^nk выдает значение f(x). Если

134

f (x) = 0, то элемент x называется нулем функции f, если же f (x) = 1, то

элемент x называется единицей функции f. Требуется путем ¾минимально-

го¿ числа обращений к оператору B найти множество всех нулей функции f

и множество всех ее единиц.

Традиционный подход к решению задачи расшифровки основан на по-

строении оптимального по Шеннону алгоритма (предложен В.К. Коробковым

в 1965 г. в [1]). Согласно данному подходу, сложность алгоритма расшифров-

ки следует оценивать числом обращений к оператору B в худшем случае.

Это означает следующее. Пусть V множество всех двузначных монотон-

ных функций, определенных на E^nk. Пусть A некоторый алгоритм, вы-

полняющий расшифровку функций из V . Под сложностью алгоритма A по-

нимается максимум числа обращений к оператору B, где максимум берется

по всем функциям из V . Алгоритм A называется оптимальным по Шенно-

ну на множестве V , если его сложность минимальна среди всех алгоритмов,

выполняющих расшифровку функций из V .

Оптимальный по Шеннону алгоритм расшифровки монотонной булевой

функции построен Ж. Анселем в 1968 г. [2]. В 1976 г. В.Б. Алексеевым пред-

ложен алгоритм расшифровки функции из V , который является оптималь-

ным в случае k = 2 и близок по сложности к оптимальному в случае k > 2 [3].

Введем понятия верхнего нуля и нижней единицы функции f, f ∈ V . Эти

понятия являются центральными для рассматриваемой задачи расшифров-

ки. Ноль функции f называется верхним, если он не предшествует никакому

другому нулю этой функции. Единица функции f называется нижней, если

она не следует ни за какой другой единицей этой функции. Очевидно, что

для расшифровки f достаточно найти все ее верхние нули и все ее нижние

единицы.

Пусть D произвольная совокупность элементов из E^nk, x ∈ E^nk, s ∈ [0, 1].

Элемент x называется s-частым, если доля элементов в D, следующих за x,

не меньше s, иначе x s-нечастый элемент. Элемент x называется макси-

мальным s-частым, если x s-частый элемент и любой другой следующий

за ним элемент является s-нечастым. Элемент x называется минимальным

s-нечастым, если x s-нечастый элемент и любой другой предшествующий

ему элемент является s-частым.

Пусть X_max и Y_min множества, состоящие соответственно из всех мак-

симальных s-частых и минимальных s-нечастых элементов множества E^nk.

На множестве E^nk определим монотонную функцию f_D,s, которая принимает

значения 0 и 1 соответственно на s-частых элементах и s-нечастых элемен-

тах этого множества. Фактически f_D,s задается при помощи оператора B_D,

который для произвольного x из E^nk выдает значение f_D,s(x) путем вычисле-

ния частоты встречаемости x в D. Таким образом, для расшифровки функ-

ции f_D,s могут применяться методы поиска множеств X_max и Y_min, и наоборот,

для поиска X_max и Y_min применимы методы расшифровки f_D,s.

Следует отметить, что основным приложением методов поиска частых и

нечастых элементов в данных, в том числе частично упорядоченных, явля-

ются вопросы построения ассоциативных правил, впервые возникшие в связи

с задачей анализа потребительской корзины [4]. В машинном обучении логи-

135

ческий анализ признаковых описаний прецедентов фактически основан на

поиске в этих описаниях часто и нечасто встречающихся фрагментов [5].

В [6] анонсирована идея последовательно-совместного перечисления X_max

и Y_min, основанная на решении задачи дуализации над произведением

k-значных цепей, и приведены результаты тестирования последовательно-

совместного поиска X_max и Y_min на случайных модельных данных, показав-

шие его эффективность в случае, когда мощности X_max и Y_min примерно

равны.

В настоящей работе проведено экспериментальное сравнение двух методов

расшифровки функции f_D,s. Первый метод это упомянутый выше алго-

ритм расшифровки В.Б. Алексеева. Второй метод основан на предложенной

в [6] идее последовательно-совместного перечисления X_max и Y_min с приме-

нением асимптотически оптимального алгоритма дуализации над произведе-

нием k-значных цепей RUNC-M+ [7]. Задача дуализации относится к чис-

лу труднорешаемых дискретных задач и асимптотически оптимальные алго-

ритмы дуализации лидируют по скорости счета. На случайных модельных

данных для каждого тестируемого метода расшифровки оценивалось время

работы и число обращений к оператору B_D. Показано, что асимптотически

оптимальная расшифровка функции f_D,s, нацеленная на типичный вариант

задачи, в определенных случаях имеет лучшие результаты по сравнению с

оптимальной по Шеннону расшифровкой, ориентирующейся на самый слож-

ный вариант задачи.

2. Традиционный подход к расшифровке монотонной

логической функции. Алгоритм Алексеева

В настоящем разделе рассматривается алгоритм A_opt расшифровки функ-

ции f из V , описанный в [3]. Как уже было отмечено во введении, этот алго-

ритм является оптимальным по Шеннону в случае k = 2 и близок по слож-

ности к оптимальному в случае k > 2.

Алгоритм A_opt работает в два этапа. На первом этапе куб E^nk разбивается

на непересекающиеся подмножества, каждое из которых является цепью. На

втором этапе выполняется расшифровка f на каждой построенной цепи с

помощью хорошо известного алгоритма двоичного поиска.

Пусть i ∈ {2, . . . , n}, r ∈ {0, 1, . . . , k - 1}. Положим

{

}

S^ir =

(α₁, . . . , α_i-1, r) | (α₁, . . . , α_i-1) ∈ E^i-1k

Процесс разбиения куба E^nk на непересекающиеся цепи происходит путем

последовательного построения разбиений на непересекающиеся цепи кубов

меньшей размерности.

На первом шаге рассматривается куб E^1k, представляющий собой цепь со-

гласно установленному частичному порядку.

Пусть на шаге i

1, 2 ≤ i ≤ n, куб E^i-1k разбит на непересекающиеся це-

пи. Тем самым, очевидным образом на непересекающиеся цепи разбито каж-

дое из множеств S^ir, r ∈ {0, 1, . . . , k - 1}. Далее построенные разбиения мно-

жеств Sⁱ⁰, . . . , S^ik-1 изменяются. Сначала в Sⁱ⁰ добавляются все максимальные

136

элементы цепей из построенных разбиений для множеств Sⁱ¹, . . . , S^ik-1, при

этом все добавленные к Sⁱ⁰ элементы удаляются из множеств Sⁱ¹, . . . , S^ik-1.

Затем аналогичная процедура проводится для измененной последовательно-

⋃_k-1

сти Sⁱ¹, . . . , S^ik-1 и т.д. В результате, учитывая, что E^ik =

S^ir, получается

r=0

требуемое разбиение для куба E^ik.

Построенные на первом этапе работы алгоритма цепи просматриваются

в порядке не убывания их мощности. Пусть C_i очередная цепь. Если для

некоторого элемента x ∈ C_i известно, что x ≼ y, где y ноль, принадлежа-

щий ранее просмотренной цепи C_j (j < i), то x ноль цепи C_i. Аналогично,

если для некоторого элемента x ∈ C_i известно, что y ≼ x, где y единица,

принадлежащая ранее просмотренной цепи C_j (j < i), то x единица цепи C_i.

Таким образом, цепь C_i делится на три отрезка: сначала следуют найденные

нули, затем следуют элементы, на которых значение функции f неизвестно,

после чего следуют найденные единицы. Для расшифровки цепи C_i на втором

отрезке запускается алгоритм двоичного поиска. При этом для определения

значения функции f происходит обращение к оператору B.

Пусть t_A(f) общее число обращений к оператору B алгоритма A, вы-

полняющего расшифровку функции f из V . Сложностью алгоритма A по

Шеннону (сложностью в худшем случае) называется величина max[t_A(f)],

где максимум берется по всем функциям из V . Пусть A₀

любой ал-

горитм расшифровки функций из V с наименьшей сложностью. Тогда

tAopt (f)/tA0 (f) ≤ 0,5(log₂ (k) + 1).

3. Новый подход к расшифровке монотонной логической

функции. Асимптотически оптимальная расшифровка

В данном разделе описывается подход к задаче расшифровки монотонной

логической функции, базирующийся на применении алгоритмов дуализации

над произведением k-значных цепей.

3.1. Дуализация над произведением k-значных цепей

Задача дуализации над произведением k-значных цепей относится к числу

труднорешаемых перечислительных задач дискретной математики и ставит-

ся следующим образом.

Представим множество E^nk в виде декартова произведения n цепей мощ-

ности k, положив E^nk = E₁ × E₂ × . . . × E_n, где каждое E_i = {0, 1, . . . , k - 1}.

Считается, что элемент β = (β₁, . . . , β_n) из E^nk следует за элементом α =

= (α₁, . . . , α_n) из E^nk (α предшествует β), если β_i ≥ α_i при i = 1, 2, . . . , n.

Элемент x ∈ E, E ⊂ E^nk, называется минимальным элементом множе-

ства E, если не существует другого элемента множества E, предшествую-

щего x. Элемент x ∈ E, E ⊂ E^nk называется максимальным элементом мно-

жества E, если не существует другого элемента множества E, следующего

за x.

Пусть E ⊂ E^nk. Введем обозначения: E⁺

множество всех элементов

из E^nk, каждый из которых следует хотя бы за одним элементом из E; E^-

137

множество всех элементов из E^nk, каждый из которых предшествует хотя бы

одному элементу из E; Q(E) множество, состоящее из минимальных эле-

ментов множества E^nk\E^- (здесь и далее обозначение A\B используется для

разности множеств A и B); G(E) множество, состоящее из всех максималь-

ных элементов множества E^nk\E⁺.

Каждая из задач построения множества Q(E) или G(E) называется зада-

чей дуализации над произведением k-значных цепей.

Если k = 2, то к построению Q(E) сводится задача поиска нижних единиц

монотонной булевой функции, заданной множеством нулей E, называемая за-

дачей монотонной дуализации. В матричной формулировке монотонная дуа-

лизация это задача построения неприводимых покрытий булевой матрицы,

строками которой являются элементы из E. Эквивалентной задачей является

перечисление минимальных вершинных покрытий гиперграфа.

Если k ≥ 2 и множество E состоит из попарно несравнимых элементов, то

к построению Q(E) сводится поиск нижних единиц двузначной монотонной

функции k-значной логики, заданной множеством верхних нулей E. Анало-

гично к построению G(E) сводится поиск верхних нулей двузначной моно-

тонной функции k-значной логики, заданной множеством нижних единиц E.

В теории алгоритмической сложности дискретных задач эффективность

алгоритмов для перечислительных задач принято оценивать временем вы-

полнения одного шага, т.е. временем нахождения очередного нового решения.

Наиболее эффективными считаются алгоритмы с полиномиальными вре-

менными оценками. Такие алгоритмы имеют временные оценки вида O(N),

где N полином от размера входа задачи, и называются алгоритмами с

полиномиальными задержками. Причем временные оценки даются для са-

мой сложной индивидуальной задачи. Полиномиальные алгоритмы удалось

построить для немногих частных случаев монотонной дуализации [8]. Наи-

лучший теоретический результат получен в [9]. Предложенный в [9] инкре-

ментальный квазиполиномиальный алгоритм монотонной дуализации имеет

временную оценку вида N^o(logN), где N полином не только от размера вхо-

да задачи, но и от числа решений, найденных на предыдущих шагах, т.е. N

полином от размера входа и выхода задачи.

В [10] предложен подход к построению асимптотически оптимальных алго-

ритмов монотонной дуализации. Эти алгоритмы имеют теоретическое обосно-

вание эффективности и показывают хорошие результаты по скорости счета.

Асимптотически оптимальный алгоритм отличается от алгоритма с полино-

миальной задержкой тем, что имеет лишние полиномиальные шаги. Это ша-

ги, на которых не строятся новые решения. Основное требование: для почти

всех индивидуальных задач число лишних шагов алгоритма должно быть

мало по сравнению с числом всех решений задачи. При этом проверка того,

является ли шаг лишним, должна происходить за полиномиальное от размера

входа время. Данный подход к задаче монотонной дуализации значительно

позже был продемонстрирован в работе [11] на примере задачи построения

минимальных вершинных покрытий гиперграфа.

138

3.2. Последовательно-совместное перечисление верхних нулей

и нижних единиц монотонной логической функции

Алгоритм последовательно-совместного перечисления верхних нулей X_up

и нижних единиц Y_low функции f, f ∈ V , заданной при помощи оператора B,

основан на решении задачи дуализации над произведением k-значных цепей.

Рассматриваемый алгоритм является синтезом последовательного и совмест-

ного подходов к поиску X_up и Y_low, которые подробно описаны в разделе 3.3.

Метод базируется на приведенных ниже утверждениях 1-3.

Утверждение 1. Если X ⊂ X_up, то Q(X) содержит хотя бы один

ноль функции f.

Доказательство. Пусть X ⊂ X_up, x ∈ X_up\X. Из того, что x не срав-

ним ни с одним другим элементом множества X_up, следует, что x ∈ E^nk\X^-.

Таким образом, в Q(X) существует элемент q такой, что q ≼ x и f (q) = 0.

Утверждение 2. Если X ⊂ X_up, а элемент y ∈ Q(X) является едини-

цей функции f, то y нижняя единица функции f.

Доказательство. Пусть y ∈ Q(X_up) = Y_low. Тогда, так как y единица

функции f, то в E^nk\X^-up найдется нижняя единица z такая, что z = y, z ≼ y.

Из (E^nk\X^-up) ⊆ (E^nk\X^-), следует, что z ∈ E^nk\X^-, что противоречит условию

y ∈ Q(X).

Утверждение 3. Пусть X ⊆ X_up, Y ⊆ Y_low. Тогда Q(X) = Y в том и

только в том случае, если X = X_up, Y = Y_low.

Доказательство. Пусть X ⊂ X_up. Из утверждения 1 следует, что Q(X)

содержит хотя бы один ноль f. Однако в множестве Y нет нулей функции f,

следовательно Q(X) = Y_low. Если же X = X_up, то Q(X) = Y_low. Таким обра-

зом, Q(X) = Y тогда и только тогда, когда X = X_up, Y = Y_low.

Последовательно-совместный алгоритм работает следующим образом. По-

ложим X₀ = ∅. Строится последовательность X₁ ⊂ X₂ ⊂ . . . ⊂ X_up.

Шаг 1. Рассматривается множество X₁ = {x}, где x произвольный

верхний ноль f.

Шаг i+1 (i ≥ 1). Решается задача дуализации множества X_i\X_i-1. Пусть

множество Z есть результат дуализации X_i\X_i-1. Согласно утверждению 1,

множество Z содержит хотя бы один ноль функции f. Для каждого нуля

из Z находится один содержащий его верхний ноль. Все найденные верхние

нули, которые не содержатся в множестве X_i, добавляются к X_i, формируя

в результате множество X_i+1. Если же все найденные верхние нули уже со-

держатся в X_i, то происходит дуализация множества X_i, в результате чего

формируется множество Q(X_i). Если в Q(X_i) нет нулей, то, согласно утвер-

ждению 3, следует, что Q(X_i) = Y_low, X_i = X_up, и алгоритм завершает свою

работу. Иначе для каждого нуля из Q(X_i) находится один содержащий его

верхний ноль, который пополняет множество X_i, формируя в результате мно-

жество X_i+1.

139

3.3. Последовательный и совместный поиск X_up и Y_low

Достаточно очевидным является поиск X_up и Y_low функции f, f ∈ V , за-

данной при помощи оператора B, путем последовательного построения этих

множеств. Сначала строится множество X_up, например, алгоритмом Apri-

ori [4, 12], модифицированным на случай произведения k-значных цепей. За-

тем используется свойство двойственности Q (X_up) = Y_low. Аналогично мож-

но сначала строить Y_low модифицированным алгоритмом Apriori, а затем ис-

кать X_up путем дуализации множества Y_low.

В [13] предложена идея совместного перечисления множеств X_max и Y_min,

которая в применении к задаче построения X_up и Y_low заключается в сле-

дующем.

Выбирается произвольный элемент q из E^nk. Если q ноль функции f, то

ищется верхний ноль, следующий за q. Если же q единица функции f, то

ищется нижняя единица, предшествующая q. Пусть на очередной итерации

построены множества X ⊆ X_up и Y ⊆ Y_low. Если X = ∅ и Y = ∅, то выби-

рается любой x ∈ X и ищется элемент q, который не предшествует x. Если

X = ∅ и Y = ∅, то выбирается любой y ∈ Y и ищется элемент q, который

не следует за y. Если же X = ∅ и Y = ∅, то ищется элемент q, который не

предшествует x и не следует за y. Затем аналогичным образом в зависимо-

сти от значения элемента q находится верхний ноль или нижняя единица

функции f.

Алгоритм, основанный на описанной выше идее совместном пере-

числении множеств X_up и Y_low, строит вложенные последовательности:

X₁ ⊂ X₂ ⊂ ... ⊂ X_up и Y₁ ⊂ Y₂ ⊂ ... ⊂ Y_low.

Шаг 1. X₁ = {x}, Y₁ = {y}, где x и y находятся модифицированным ал-

горитмом Apriori.

Шаг i + 1 (i ≥ 1). Строится либо Q(X_i), либо G(Y_i). Пусть построено

множество Q(X_i). Если Q(X_i) не содержит нулей функции f, то, согласно

утверждению 3, оно совпадает с множеством Y_low (в этом случае X_i = X_up

и алгоритм заканчивает работу). Согласно утверждению 2, каждая едини-

ца из множества Q(X_i) является нижней единицей. Эти единицы пополняют

множество Y_i, формируя в результате множество Y_i+1. Для каждого нуля

из Q(X_i) находится один содержащий его верхний ноль элемент путем после-

довательного увеличения текущего нуля согласно заданному порядку, кото-

рый затем пополняет множество X_i, формируя в результате множество X_i+1.

В [6] приведены результаты тестирования последовательного, совместного

и последовательно-совместного поиска X_max и Y_min на случайных модельных

данных. Согласно этим результатам, последовательно-совместное перечисле-

ние наиболее эффективно, когда мощности множеств X_max и Y_min примерно

равны, иначе более эффективным является последовательное перечисление.

Наихудшие показатели у совместного перечисления множеств X_max и Y_min.

4. Эксперименты

Проведено экспериментальное сравнение двух алгоритмов расшифровки

функции f_D,s, описанных в разделах 3.2 и 3.3. Алгоритмы реализованы

140

k = 2, s = 0,3

k = 5, s = 0,3

10¹

Алгоритм Алексеева

10¹

ПС алгоритм

10⁰

10^-1

-1

10^-2

10^-3

10^-2

10^-4

10^-3

2,5

5,0

7,5 10,0 12,5 15,0 17,5 20,0

k = 2, s = 0,1

k = 5, s = 0,1

10¹

Алгоритм Алексеева

10¹

ПС алгоритм

10⁰

10^-1

-1

10^-2

10^-3

10^-4

10^-3

10^-5

2,5

5,0

7,5 10,0 12,5 15,0 17,5 20,0

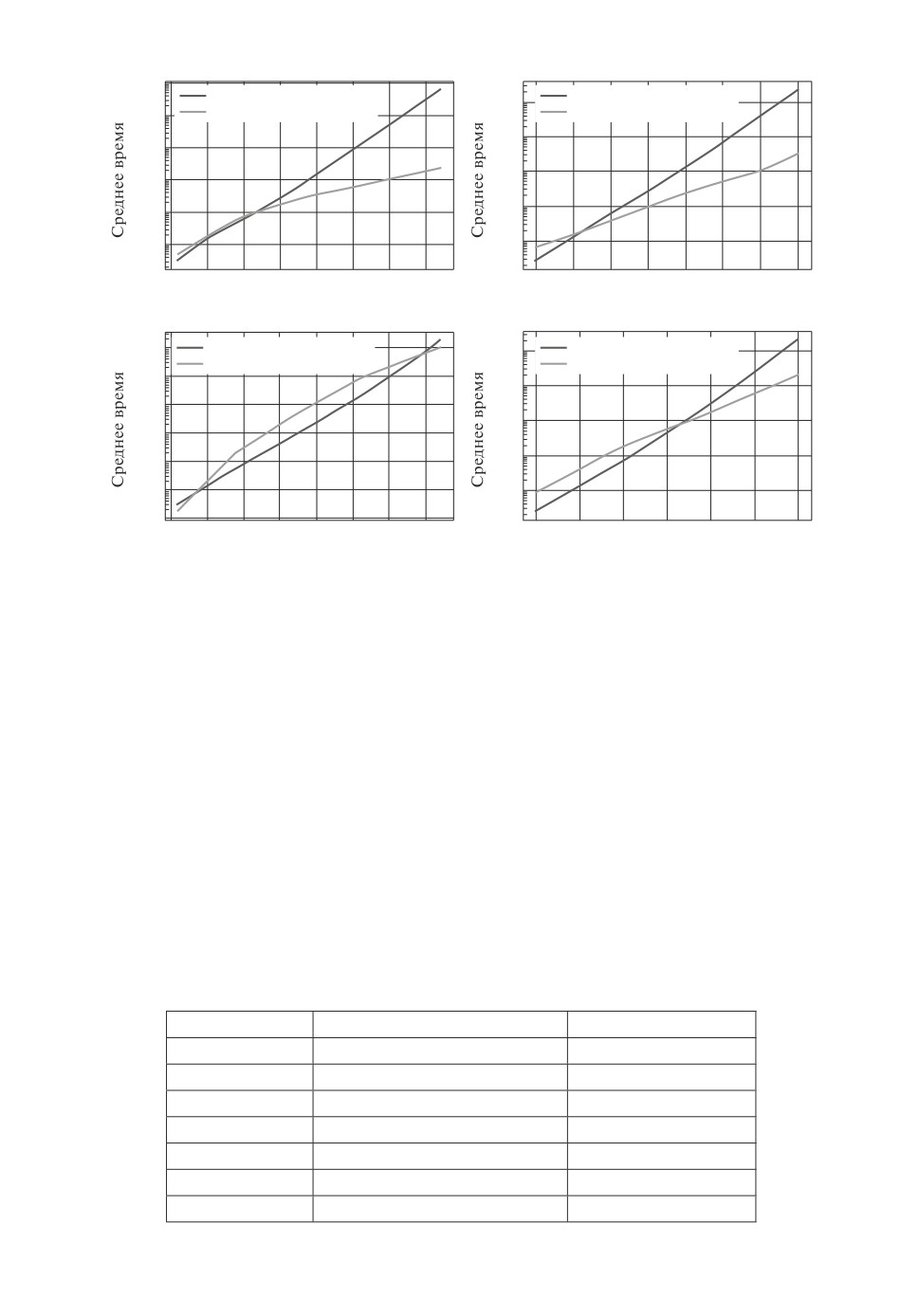
Зависимость времени работы алгоритмов от n в секундах (при различных k и s).

на языке C++. При реализации последовательно-совместного перечисления

верхних нулей и нижних единиц функции f_D,s использовался асимптотически

оптимальный алгоритм над произведением k-значных цепей RUNC-M+ [7].

Эксперименты проведены для случайных множеств D, D ⊂ E^nk, с числом

элементов m = 100. Данные выбирались из равномерного распределения. Ре-

зультаты усреднялись по 20 независимым запускам.

Из представленных на рисунке графиков следует, что при s = 0,3 и n > 5

независимо от значения k последовательно-совместный алгоритм (ПС алго-

ритм) работает быстрее алгоритма Алексеева. Алгоритм Алексеева более эф-

фективен при s = 0,1, k = 2, но при этом время его работы растет быстрее

с ростом n. В случае k = 5, n > 7 последовательно-совместный алгоритм на

порядки быстрее алгоритма Алексеева.

Таблица 1. Среднее число обращений к оператору B_D, m = 100

n; k; s

Алгоритм Алексеева

ПС алгоритм

5; 3; 0,1

111

529

5; 3; 0,3

343

5; 20; 0,3

25484

3039

10; 3; 0,1

2709

10172

10; 3; 0,3

323

3111

10; 5; 0,1

45528

31791

15; 3; 0,3

1142

13940

141

Как видно из табл. 1, в случае небольших значений k, независимо от значе-

ния n, наилучший результат по числу обращений к оператору B_D показыва-

ет алгоритм Алексеева. Заметим, что при небольших значениях k сложность

этого алгоритма почти оптимальна. При значениях k ≥ 5 лучший результат

по числу обращений к оператору B_D показывает последовательно-совместная

расшифровка функции f_D,s.

5. Заключение

Исследованы актуальные вопросы уменьшения временных затрат, возни-

кающие при логическом анализе частично упорядоченных данных. Разра-

ботан и исследован новый подход к задаче расшифровки двузначной моно-

тонной функции, определенной на k-значном n-мерном кубе, основанный на

последовательно-совместном перечислении верхних нулей и нижних единиц

этой функции. Экспериментальное исследование предлагаемого подхода про-

ведено с использованием авторской идеи последовательно-совместного поис-

ка максимальных частых и минимальных нечастых элементов произведения

k-значных цепей, базирующейся на решении задачи дуализации над произве-

дением k-значных цепей. Показана целесообразность применения асимптоти-

чески оптимальных алгоритмов дуализации над произведением k-значных

цепей для рассматриваемой задачи расшифровки монотонной логической

функции.

СПИСОК ЛИТЕРАТУРЫ

1. Коробков В.К. О монотонных функциях алгебры логики // Сб. Проблемы ки-

бернетики. Вып. 13. М.: Наука, 1965. С. 5-28.

2. Ансель Ж. О числе монотонных булевых функций n переменных // Кибернетич.

сб. Нов. сер. Вып. 5. М.: Мир, 1968. С. 53-57.

3. Алексеев В.Б. О расшифровке некоторых классов монотонных многозначных

функций // Журн. вычисл. матем. и матем. физики. 1976. Т. 16. № 1. С. 189-

198.

Alekseev V.B. Deciphering of some classes of monotonic many-valued functions //

Zh. vychisl. Mat. mat. Fiz. 1976. V. 16. No. 1. P. 189-198.

4. Agrawal R., Imielinski T., Swami A. Mining association rules between sets of items in

large databases // Proceedings of the 1993 ACM SIGMOD International Conference

on Management of Data. 1993. P. 207-216.

5. Журавлев Ю.И., Рязанов В.В., Сенько О.В. Распознавание. Математические

методы. Программная система. Практические применения. М.: ФАЗИС, 2006.

Т. 176.

6. Драгунов Н.А., Дюкова Е.В. Поиск минимальных нечастых и максимальных

частых наборов в частично упорядоченных данных // Математические мето-

ды распознавания образов: Тезисы докладов 9-й Всероссийской конференции с

международным участием, 2019. С. 10-12.

7. Дюкова Е.В., Масляков Г.О., Прокофьев П.А. Дуализация над произведени-

ем цепей: асимптотические оценки числа решений // ДАН. 2018. Т. 483. № 2.

С. 130-133.

8. Johnson D.S., Yannakakis M., Papadimitriou C.H. On general all maximal indepen-

dent sets // Inform. Proc. Lett. 1988. V. 27. Iss. 3. P. 119-123.

142

9. Fredman M.L., Khachiyan L. On the complexity of dualization of monotone disjunc-

tive normal forms // J. Algorithms. 1996. No. 21. P. 618-628.

10. Дюкова Е.В. Об асимптотически оптимальном алгоритме построения тупиковых

тестов // ДАН СССР. 1977. Т. 233. № 4. С. 527-530.

Djukova E.V. On an asymptotically optimal algorithm for constructing irredundant

tests // DAN SSSR. 1977. V. 233. No. 4. P. 423-426.

11. Murakami K., Uno T. Efficient algorithms for dualizing large-scale hypergraphs //

Discr. Appl. Math. 2014. V. 170. P. 83-94.

12. Aggarwal C. Frequent Pattern Mining. Springer International Publishing. Switzer-

land, 2014.

13. Elbassioni K. On Finding Minimal Infrequent Elements in Multidimensional Data

Defined Over Partially Ordered Sets. 2014. arXiv:1411.2275.

Статья представлена к публикации членом редколлегии А.А. Лазаревым.

Поступила в редакцию 01.02.2022

После доработки 27.03.2022

Принята к публикации 29.06.2022

143