Автоматика и телемеханика, № 10, 2022

(Уральский федеральный университет, Екатеринбург;

Научно-инженерный центр

¾Надежность и ресурс больших систем и машин¿

УрО РАН, Екатеринбург)

ЭНТРОПИЙНОЕ МОДЕЛИРОВАНИЕ

СЕТЕВЫХ СТРУКТУР¹

В настоящее время довольно часто используется энтропия для описа-

ния сложных систем в различных областях. Рассмотрены вопросы ис-

пользования дифференциальной энтропии для сетевых структур, пред-

ставленных в виде связных графов с корреляционными связями. Извест-

но, что энтропию непрерывного случайного вектора можно разложить

на две составляющие: энтропию случайности и энтропию самоорганиза-

ции. Для сетевых структур наряду с оценкой самой энтропии предложены

другие полезные характеристики энтропийная мера взаимосвязи меж-

ду несколькими подсистемами и энтропия системы в отдельной вершине,

которые расширяют возможности энтропийного моделирования для ис-

следования сетевых структур: позволят оценить взаимосвязанность раз-

ных участков между собой и определить, как изменяется энтропия внутри

таких систем. Рассмотрены примеры на модельных данных.

Ключевые слова: сетевая структура, случайный вектор, дифференциаль-

ная энтропия, граф, система, подсистема, взаимозависимость.

DOI: 10.31857/S0005231022100130, EDN: ALLDVU

1. Введение

Структура

это совокупность устойчивых связей между элементами

системы, обеспечивающих воспроизводимость при изменяющихся услови-

ях [1]. В холистическом понимании структура вместе с элементами образует

систему.

Сетевая структура рассматривается как децентрализованный комплекс

взаимосвязанных элементов, способный расширяться путем включения но-

вых звеньев, что придает сети гибкость и динамичность [2]. В сетевых струк-

турах потенциально могут существовать связи между всеми элементами, при-

чем эти связи могут быть разнонаправленными, т.е. могут быть и двойное

подчинение, и межуровневое взаимодействие [3]. Также в системе могут быть

подсистемы, что тоже должно отражаться в сетевой структуре как взаимо-

связи на уровне подсистем. Поведение реальных систем часто обладает сто-

хастичностью, а связи между их элементами можно адекватно описывать

как корреляционные. Модели таких систем обычно акцентируют внимание

на явном количественном описании вероятностных характеристик тех или

иных ситуаций в жизненном цикле системы [4-7]. Однако такие модели не

¹ Исследование выполнено при финансовой поддержке Российского фонда фундамен-

тальных исследований (проект № 20-51-00001).

144

позволяют учесть системные характеристики сетевых структур, что может

ограничить возможности выработки эффективных управленческих решений.

Энтропия является универсальным параметром, позволяющим объеди-

нять различные проявления физического мира в единое целое, т.е. может

служить системной характеристикой. В настоящее время достаточно распро-

странено использование энтропии для описания поведения открытых стоха-

стических систем в различных областях [8-11]. Общим в этих работах явля-

ется использование введенной К. Шенноном информационной энтропии [12]

∑

(1)

H(D) = - p_i ln p_i,

i=1

где p₁, . . . , , p_L

вероятности того, что система принимает конечное число

соответствующих состояний D_i, т.е. p_i = P (S ∈ D_i).

Согласно (1) модель системы представляется как функция от множества

ее состояний D. Однако использование информационной энтропии в качестве

модели такой системы имеет существенные недостатки:

1. Требуется оценить вероятности p_i. Это требует больших выборок, для

некоторых состояний статистику получить практически невозможно.

2. Некоторые состояния систем заранее могут быть вообще не известны.

3. Затруднено моделирование взаимосвязей между элементами многомер-

ных систем.

4. Не учитывается изменение дисперсии.

5. Основные системные закономерности не учитываются.

6. Адекватные энтропийные модели разработаны только для частных за-

дач.

Поэтому актуальна задача поиска более информативных энтропийных ха-

рактеристик, описывающих поведение сетевых структур.

2. Постановка задачи энтропийного моделирования

сетевых структур

Более адекватным подходом к описанию стохастических систем является

выделение не отдельных состояний, а ее элементов, которые всегда можно за-

дать для конкретной системы. Представим систему в виде непрерывного слу-

чайного вектора Y = (Y₁, . . . , Y_m) с взаимосвязанными компонентами. Плот-

ность вероятности p_Y(x₁, . . . , x_m) полностью описывает распределение веро-

ятностей многомерной случайной величины Y. Поэтому вместо информаци-

онной энтропии будем использовать дифференциальную энтропию [12], яв-

ляющуюся функционалом от плотности вероятности случайного вектора Y,

+∞

∫

(2)

H(Y) = - . . . p_Y(x₁, . . . , x_m) ln p_Y(x₁, . . . , x_m)dx₁ . . . dx_m.

-∞

Формула (2) была предложена К. Шенноном как формальный аналог по-

нятия информационной энтропии (энтропия непрерывного распределения)

145

для m-мерного непрерывного случайного вектора Y. Эта величина впослед-

ствии А.Н. Колмогоровым совместно с И.М. Гельфандом и А.М. Ягломом

была исследована и названа дифференциальной энтропией [13].

В [14] доказано, что если все компоненты Y_i имеют дисперсии σ² , то_Y

дифференциальная энтропия (далее, энтропия) H(Y) случайного вектора Y

равна

∑

∑ (

)

(3)

H(Y) = ln σYi +

κ_i +

1-R²

Y_k|Y₁...Y

k-1

i=1

k=2

⌢

∫_+∞

где κ_i = H(Y_i/σYi ) = H(Yi) = -

дифференциаль-

-∞

p ⌢Yi^(x)lnpYi(x)dx

ные энтропии по плотностям с единичными дисперсиями; R²

Y_k|Y₁...Y_k-1

σ^2Y

k|Y1...Yk-1

индекс детерминации в общем случае нелинейной ре-

σ²

Y_k

грессионной зависимости случайной величины Y_k, от случайных вели-

чин Y₁, . . . , Y_k-1, (доля дисперсии Y_k, объясняемая изменением переменных

Y₁,... ,Y_k-1). При неизвестном виде зависимости для определения R^2Y

k|Y1...Yk-1

можно воспользоваться методами непараметрического регрессионного анали-

за [15].

∑

Первые два слагаемых H_V (Y) =

ln σYi +

κ_i = H(Y_i) равны сумме

i=1

энтропий элементов H(Y_i), что соответствует случаю, когда элементы Y_i си-

стемы Y взаимно независимы. Величина H_V (Y) равна предельной энтропии,

соответствующей взаимной независимости элементов системы, и характери-

зует рассмотрение целостного объекта как состоящего из частей (аддитив-

ность системы). Поэтому H_V (Y) назовем ¾энтропией хаотичности¿.

Возьмем третье слагаемое в (3) со знаком ¾-¿:

∑

(

)

∑ (

)

-G_R(Y) =

1-R^2Y

, т.е. G_R(Y) = -

ln 1-R2

k|Y1...Yk-1

Y_k|Y₁...Y_k-1

k=2

Назовем G_R(Y) энтропийной ¾мерой самоорганизации¿. Она отражает сте-

пень взаимосвязи между элементами системы Y, характеризуя свойства си-

стемы как целого (целостность системы): при полной взаимной независимо-

сти между элементами системы G_R(Y) = 0; при строгой функциональной за-

висимости между хотя бы двумя элементами системы G_R(Y) → +∞. Отме-

тим, что в случае двухкомпонентного вектора Y = (Y₁, Y₂) величина G_R(Y)

определяется средней взаимной информацией между Y₁ и Y₂, которая всегда

неотрицательна [16].

Если Y^◦ гауссов случайный вектор, тогда

∑

√

(4)

H_V (Y^◦) = ln σYi + mln

2πe, G_R(Y^◦) = -

ln |R_Y

i=1

{

}

где R_Y◦ = ρ_Y ◦

Y◦

корреляционная матрица случайного вектора Y^◦.

^j m×m

146

В рамках энтропийного моделирования сетевыми структурами будем на-

зывать системы, каждый из элементов которой связан хотя бы с одним из

других элементов системы. Они могут быть представлены в виде связных

графов, в которых связь между элементами (вершинами) задается в виде

тесноты корреляционной связи.

Физические компоненты инфраструктуры моделируются как связный

граф, где узлы представляют собой такие компоненты, как районы, развяз-

ки автодорог, железнодорожные депо, генераторы, телефонные коммутато-

ры, резервуары воды и т.д. Дуги графа характеризуют взаимосвязи между

элементами. В рамках энтропийного моделирования эти взаимосвязи будем

описывать теснотой корреляционной связи между элементами системы (уз-

лами графа). Для сетевых структур недостаточно ограничиться только моде-

лью (2)-(3), так как наряду с оценкой самой энтропии (2) и ее составляющи-

ми H_V (Y) и G_R(Y) необходимо оценивать энтропийные характеристики как

взаимодействие между собой подсистем, так и для каждого элемента сетевой

структуры.

Цель статьи предложить дополнительный инструментарий, который бы

позволил в рамках энтропийного моделирования учесть системные свойства

сетевых структур для задач принятия решений.

3. Энтропийная мера взаимосвязи между несколькими

подсистемами сетевой структуры

Пусть заданы n подсистем Y^(j) системы Y = (Y₁, . . . , Y_m), таких что

Y^(j) = (Y_j,1,... Yj,mj ) ⊂ Y, j = 1,... ,n, n ∈ {2,3,... ,m}, любая компонента Y_i

входит в состав только одной подсистемы (случайного вектора) Y^(j). Так-

же считаем, что все компоненты Y_i имеют дисперсии. Определим ¾энтро-

пийную меру взаимосвязи¿ между подсистемами (случайными векторами)

Y⁽¹⁾,... ,Y⁽ⁿ⁾ как разность между суммой энтропий подсистем и энтропией

⋃_n

системы (объединения подсистем) Y =

Y^(j) = (Y₁,... ,Y_m)

j=1









⋂

∑ (

)

⋃

(5)

G Y^(j) = H Y^(j)

-H Y^(j).

j=1

Теорема 1. Энтропийная мера взаимосвязи между несколькими подси-

⋃_n

стемами Y⁽¹⁾,... ,Y⁽ⁿ⁾ сетевой структуры Y =

Y^(j) равна

j=1

(

)

⋃





1-d_e

Y^(j)

⋂

j=1

(6)

G Y^(j) = -1

∏

(

)),

j=1

1-d_e

Y^(j)

j=1

(

)

(

)

∏

где d_e(Y) = 1 -

, d_e(Y^(j)) = 1-

1-R²

1-R2Yk|Y₁...Y_k-1

Y_j,k|Y_j,1...Y_j,k-1

k=2

коэффициенты тесноты корреляционной связи между компонентами слу-

чайных векторов Y, Y^(j) соответственно.

147

Доказательство теоремы 1 приведено в Приложении.

Замечание 1. Энтропийная мера взаимосвязи (6), как видно из (5),

не содержит компоненты, характеризующей хаотичность подсистем. Ес-

ли( все эле)енты подсистем между собой взаимно независимы, то

⋂

ⁿ Y^(j)

= 0. В случае, когда хотя бы два элемента разных подсистем

j=1

(⋂

)

между собой строго функционально зависимы, то G

ⁿ Y^(j)

→ +∞.

j=1

Замечание 2. Рассмотрим частные случаи:

(

)

(

)

1-d_e

Y⁽¹⁾ ∪ Y⁽²⁾

1. Для n = 2 G

Y⁽¹⁾ ∩ Y⁽²⁾

(

)(

)

1 - d_e(Y⁽¹⁾)

1 - d_e(Y⁽²⁾)

2. Пусть U и V непрерывные случайные величины, у которых суще-

ствуют дисперсии. Пусть X случайный вектор, у всех компонент которого

существуют дисперсии. Тогда энтропийные меры взаимосвязи между X и U

и между U и V равны

1 - d_e(X ∪ U)

(7)

G(X ∩ U) = 1 -

1 - d_e(X)

(

)

(

)

(8)

G(U ∩ V ) = -

1-R²

V |U

U|V

где R_U|V , R_V|U теоретические корреляционные отношения между U и V.

3. Если Y^◦ гауссов случайный вектор, то







⋃_n

⋂

R

Y^(j)◦



j=1

(9)

G Y^(j)◦ = -1

∏

j=1

|R_Y(j)◦ |

j=1

4. Энтропия в отдельном узле сетевой структуры

Пусть Y = (Y₁, . . . , Y_m) сетевая структура. Определим ¾энтропию сете-

вой структуры в узле Y_l¿ как разницу между энтропией всей Y системы и

энтропией системы без элемента Y_l

(10)

H (Y_l(Y)) = H(Y) - H (Y\Y_l

Поскольку нумерация элементов в системе не влияет на ее энтропию, то

без потери общности считаем, что l = m. Тогда выражение (10) примет вид

∑

∑ (

)

H(Y) - H (Y\Y_m) = ln σYi +

κ_i +

1-R²

k-1

Y_k|Y₁...Y

i=1

k=2

∑

∑ (

)

− ln σYi -

κ_i -

1-R²

k-1

Y_k|Y₁...Y

i=1

^k=2(

)

= ln σYm + κ_m

1-R²

Ym|Y1...Ym-1

}

H(Ym)

148

Поэтому для произвольного номера l элемента в сетевой структуре имеем

(

)

(11)

H (Y_l(Y)) = H (Y_l) +

1-R²

Y_l|Y₁...Y_l-1Y_l+1...Ym

С учетом (11) можно указать на теоретико-информационную интерпре-

тацию формулы (10) как энтропию в узле сети в виде условной энтропии

H(Y) - I (Y_l; Y\Y_l), где I (Y_l; Y\Y_l) неотрицательная средняя взаимная ин-

формация между вершиной Y_l и сетью Y\Y_l, выраженная через коэффици-

енты корреляции.

Таким образом, справедлива следующая

Лемма 1. Энтропия сетевой структуры Y = (Y₁,...,Y_m) в узле Y_l

определяется по формуле (11).

Замечание 3. Энтропию сетевой структуры в узле H (Y_l(Y)) можно раз-

ложить на ¾энтропию хаотичности¿ H (Y_l(Y))_R и ¾энтропийную меру само-

организации¿ H (Y_l(Y))_V в узле Y_l как

(12)

H (Y_l(Y)) = H_V (Y_l(Y)) - G_R (Y_l

(Y)) ,

где H_V (Y_l(Y)) = H(Y_l) = ln σYl + κ_l дифференциальная энтропия элемен-(

)

та (случайной величины) Y_l, G_R (Y_l(Y)) = -¹² ln 1-R2

Y_l|Y₁...Y_l-1Y_l+1...Ym

энтропийная мера взаимосвязи между случайной величиной Y_l и случай-

ным вектором Y\Y_l (при отсутствии корреляционной связи между Y_l и слу-

чайным вектором Y\Y_l G_R (Y_l(Y)) = 0, при строгой функциональной зави-

симости между Y_l и хотя бы двумя элементами случайного вектора Y\Y_l

GR (Yl(Y)) → +∞).

Замечание 4. Если Y^◦ гауссов случайный вектор, то

√

|R_Y◦ |

(13)

H (Y ◦l (Y^◦)) = ln σ_Y ◦

+ ln

2πe +



.



R_Y◦_\Y ◦



5. Примеры реализации. Обсуждение результатов

Выражения (5)-(13) позволят исследовать сетевые структуры: оценивать

взаимосвязанность меду собой различных участков, а также оценивать, как

меняется энтропия внутри таких систем. Рассмотрим примеры. Для упроще-

ния интерпретации результатов рассмотрим гауссовы сетевые структуры.

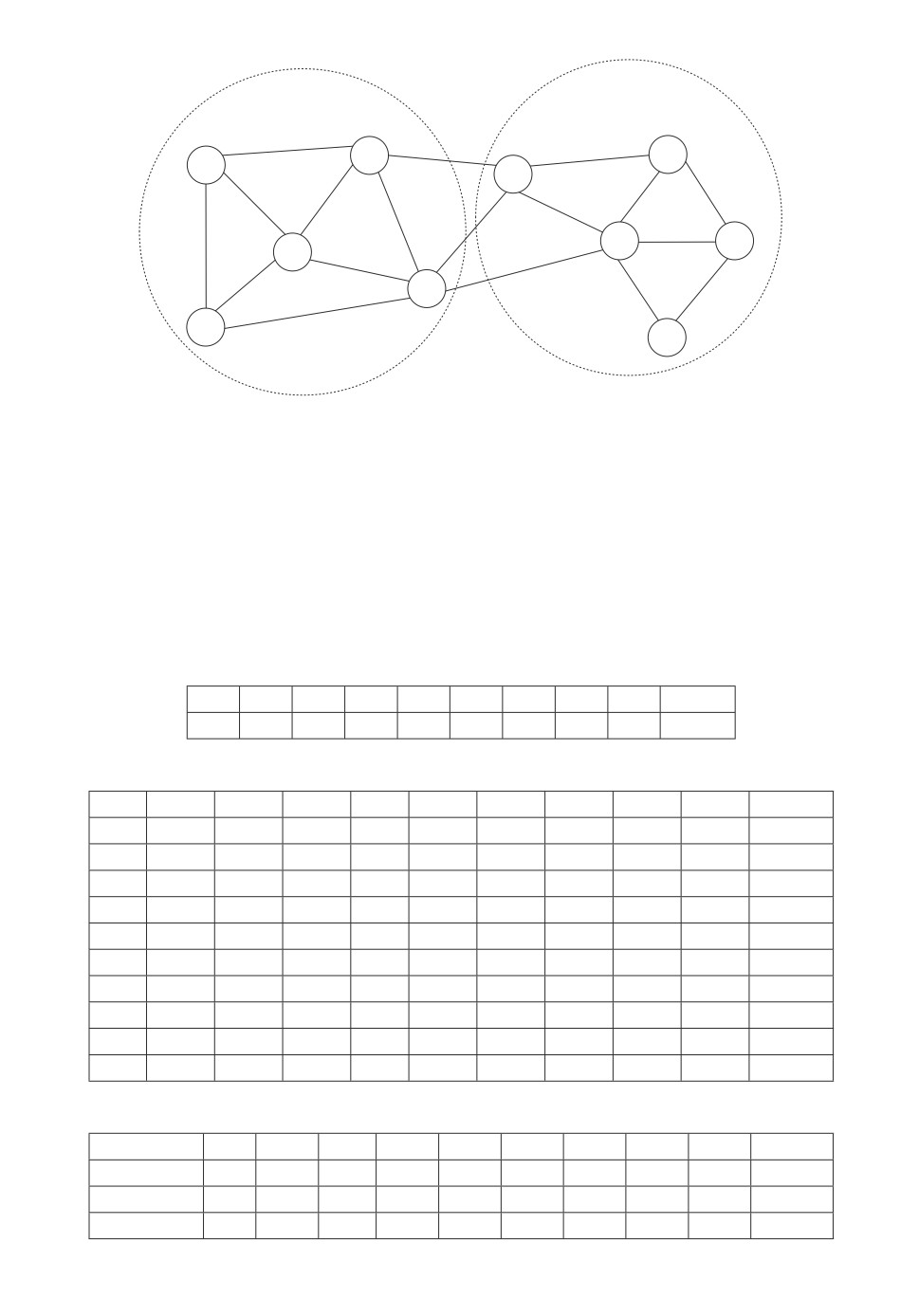
Пример 1. Пусть дана гауссова система X, граф которой приведен на

рис. 1. Она состоит из двух подсистем X⁽¹⁾ = (X₁, X₂, X₃, X₄, X₅) и X⁽²⁾ =

= (X₆, X₇, X₈, X₉, X₁₀).

В табл. 1, 2 приведены значения среднеквадратических отклонений и кор-

реляционной матрицы случайного вектора X.

Выполним вспомогательные расчеты: |R_X(1) | = 0,30920, |R_X(2) | = 0,017723,

|R_X(1)_∪X(2) | = |RX| = 2,6472 · 10^-6. Отсюда энтропийная мера взаимосвязи

(

)

X⁽¹⁾ ∩ X⁽²⁾

= 3,82.

149

Рис. 1. Граф сетевой структуры X, состоящей из двух подсистем.

Выполнив расчеты по формулам (12), (13), получим значения энтропий в

узлах сетевой структуры X, которые приведены в табл. 3. Видим, что наи-

большие значения энтропийной меры самоорганизации находятся в вершинах

X₅, X₆, X₇, которые расположены на границе между подсистемами. Самые

высокие значения энтропии хаотичности наблюдаются в вершинах, имеющих

наибольшие дисперсии.

Таблица 1. Среднеквадратические отклонения элементов

случайного вектора X

X₁

X₂

X₃

X₄

X₅

X₆

X₇

X₈

X₉

X₁₀

1,53

1,08

2,00

1,23

1,21

1,84

1,34

1,78

1,00

1,54

Таблица 2. Корреляционная матрица случайного вектора X

X₁

X₂

X₃

X₄

X₅

X₆

X₇

X₈

X₉

X₁₀

X₁

1,00

0,41

-0,13

0,21

0,04

0,05

-0,01

-0,04

-0,05

0,07

X₂

0,41

1,00

0,08

0,35

0,00

-0,04

-0,01

0,03

0,00

-0,01

X₃

-0,13

0,08

1,00

0,60

0,41

0,23

-0,12

0,04

0,00

-0,01

X₄

0,21

0,35

0,60

1,00

0,46

0,58

0,02

0,05

0,01

0,14

X₅

0,04

0,00

0,41

0,46

1,00

0,40

-0,34

0,01

0,02

-0,02

X₆

0,05

-0,04

0,23

0,58

0,40

1,00

0,59

0,18

0,02

0,63

X₇

-0,01

-0,12

0,02

-0,34

0,59

1,00

0,59

0,33

0,45

X₈

-0,04

0,03

0,04

0,05

0,01

0,18

0,59

1,00

0,74

-0,28

X₉

-0,05

0,00

0,01

0,02

0,33

0,74

1,00

-0,58

X₁₀

0,07

-0,01

0,14

-0,02

0,63

0,45

-0,28

-0,58

1,00

Таблица 3. Значения энтропий в вершинах сетевой структуры X

X_l

X₁

X₂

X₃

X₄

X₅

X₆

X₇

X₈

X₉

X₁₀

H (X_l(X))

1,17

-0,35

0,21

-1,34

-1,72

-1,74

-2,18

-1,02

-0,11

0,08

H_V (X_l(X))

1,84

1,50

2,11

1,63

1,61

2,03

1,71

2,00

1,42

1,85

G_R(X_l(X))

0,67

1,85

1,90

2,97

3,33

3,76

3,89

3,02

1,53

1,77

150

V = X È Y È Z

X₁

X₂

Z₂

Y₁

Z₁

Y₂

Рис. 2. Граф гауссовой системы V, состоящей из трех подсистем.

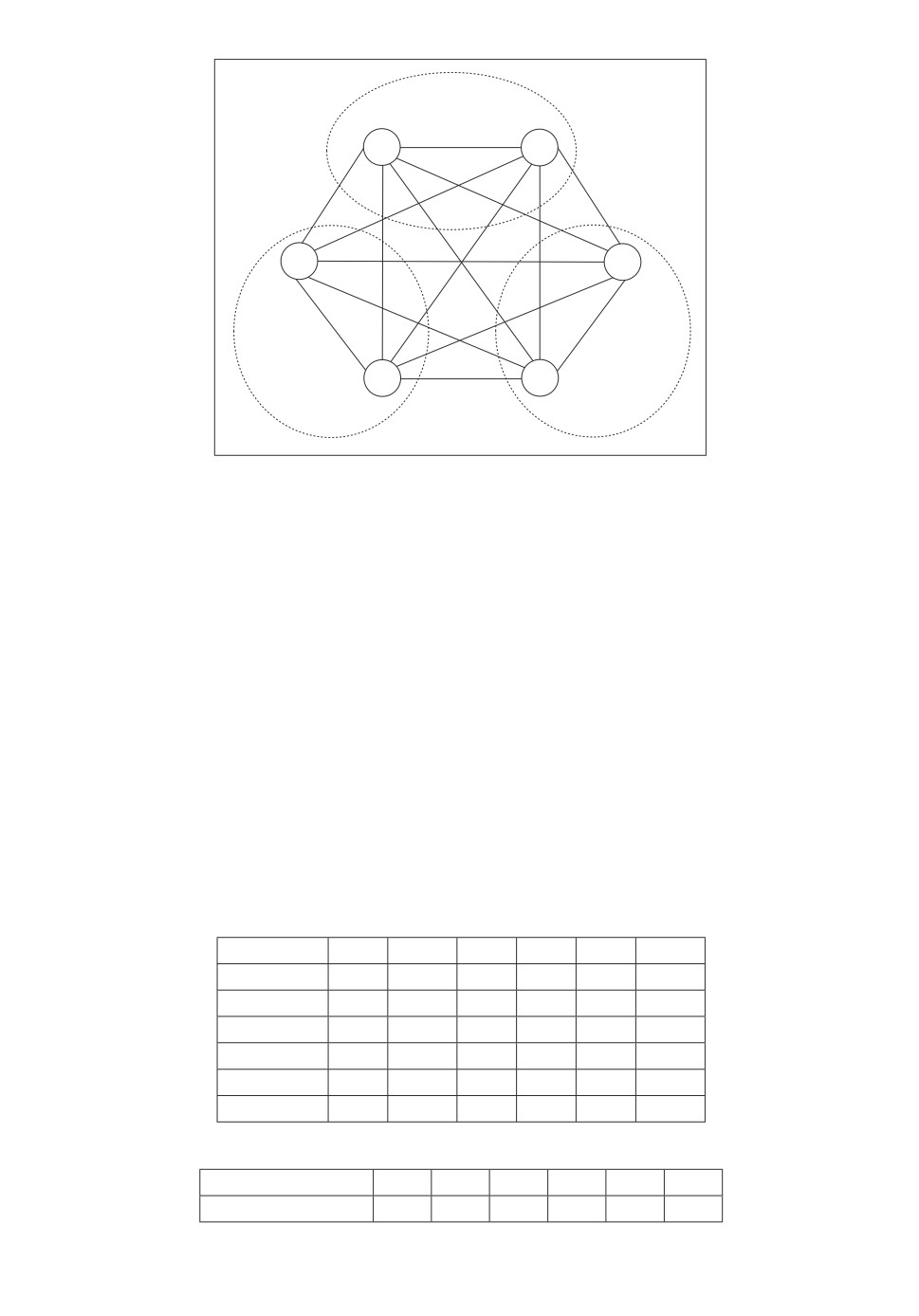
Пример

2. Имеем гауссову систему V, состоящую из подсистем

X = (X₁,X₂), Y = (Y₁,Y₂), Z = (Z₁,Z₂), т.е.

V = X ∪ Y ∪ Z = (X₁,X₂,Y₁,Y₂,Z₁,Z₂).

Граф системы приведен на рис. 2.

Зададим дисперсии всех шести элементов равными 1. Корреляционная

матрица системы V приведена в табл. 4.

Найдем по формулам (12), (13) энтропию во всех шести узлах системы.

Результаты расчетов приведены в табл. 5. Самая высокая энтропия наблю-

дается в узлах Y₁ и Z₁, а самая низкая в вершинах X₂ и Z₂.

Изменим значения парных корреляций.

Случай 1. Коэффициенты парной линейной корреляции приведены в

табл. 4.

Таблица 4. Исходная корреляционная матрица

Элемент X₁

X₂

Y₁

Y₂

Z₁

Z₂

X₁

0,5

0,7

0,3

0,5

X₂

0,5

0,2

-0,3

Y₁

0,5

0,7

0,6

0,3

Y₂

0,7

0,5

0,7

0,5

Z₁

0,3

0,2

0,6

0,5

Z₂

0,5

-0,3

0,3

0,5

Таблица 5. Значения энтропии в вершинах системы V

Вершина

X₁

X₂

Y₁

Y₂

Z₁

Z₂

Энтропия в узле

0,66

0,47

0,95

0,72

0,97

0,40

151

Таблица 6. Значения энтропийной меры взаимосвязи

между подсистемами X, Y, Z

Случаи

Энтропия взаимосвязи

1,52

1,76

1,68

Случай 2. Значение коэффициента парной линейной корреляции между

элементами Y₁ и Z₂ изменим с 0,3 на 0,45.

Случай 3. Значение коэффициента парной линейной корреляции между

элементами Z₁ и Z₂ изменим с 0,5 на 0,1.

Результаты расчета энтропийной меры взаимосвязи между подсистемами

X, Y, Z для трех случаев приведены в табл. 6.

Результаты в табл. 6 говорят о следующем:

1. Увеличение тесноты корреляции между элементами разных подсистем

приводит к росту тесноты взаимосвязи в целом между подсистемами.

2. Уменьшение тесноты корреляции между элементами в отдельной подси-

стеме приводит к росту тесноты взаимосвязи в целом между подсистемами.

6. Заключение

В рамках векторной энтропийной модели введены новые энтропийные ха-

рактеристики энтропийная мера взаимосвязи между несколькими подси-

стемами и энтропия системы в отдельном узле. Эти характеристики рас-

ширяют возможности исследования сетевых структур: позволят оценивать

взаимосвязанность между собой различных участков, а также определять,

как меняется энтропия внутри таких систем.

Предложенный подход рассчитан на сетевые структуры, представимые в

виде корреляционных графов. Например, он может применяться для иссле-

дования городских систем, транспортных систем, систем связи, систем про-

мышленной безопасности и т.д. Представляет интерес связать векторное эн-

тропийное моделирование с методами риск-анализа. Из-за ограниченности

объема статьи был рассмотрен частный случай гауссовой сетевой структу-

ры. Для него определение введенных энтропийных характеристик сводится

к определению средних квадратических отклонений компонент системы и

определителей корреляционных матриц подсистем и всей системы (сетевой

структуры). В дальнейшем планируется рассмотреть применение метода для

практических задач.

ПРИЛОЖЕНИЕ

Доказательство теоремы 1.

Зададим n непрерывных случайных векторов произвольных размерно-

ст

(

)

(

)

(

)

= Y⁽¹⁾¹,... ,Ym1)

,Y⁽²⁾ = Y⁽²⁾¹,...,Ym2)

,...

,Y⁽ⁿ⁾ = Y⁽ⁿ⁾¹,...,Ymn)

. Ком-

поненты в любом из случайных векторов Y^(l) могут быть корреляционно

взаимно зависимыми. Для этого множества случайных векторов введем их

152

объединение в виде вектора

⋃

(Π.1) Y = Y^(j) =

j=1

= (Y₁, . . . , Ym1

}

Y(1)

Y⁽²⁾

Y⁽ⁿ⁾

Поскольку





⋃

H Y^(j) = H(Y),

j=1

то





∑ (

)

⋃

H_V

Y^(j)

=H_V 

Y^(j) = H_V (Y).

j=1

Поэтому формула (5) с учетом (3) примет вид





⋂

∑

(

)

(Π.2)

G Y^(j)=GR(Y) - GR

Y^(j)

j=1

∑

Пусть M_j = m_k, j = 1, . . . , n, M₀ = 0, M_n = m₁ + . . . + m_n = m. В [17]

k=1

показано, что

m_j

(

)

(

)

∑

(Π.3)

Y^(j)

1-R²

Y (j)k|Y ^(j)1...Y ^(j)

k-1

k=2

∑ (

)

(Π.4)

GR(Y) = -

1-R²

Y_k|Y₁...Y_k-1

k=2

(

)

Очевидно, что если m_j = 1, то G_R

Y^(j)

= 0. С учетом (П.1)-(П.4) имеем

(

)

∏

∑_n

1-R²

-2

j=1

G_R(Y^(j))

Y (j)k|Y ^(j)1...Y ^(j)

j=1 k=M_j-1+2

k-1

e^2G(⋂j=1Y(j)) =e

(

)

e^-2GR^(Y)

∏

1-R²

Y_k|Y₁...Y_k-1

k=2





∏

(

∏

1 - R2Yk|Y₁...Y_k-1

1-R2

.

Y_Mj+1|Y₁...Y

1-R²

j=1

k=M_j+2

Y_k|Y_Mj+1Y_Mj+2...Y_k-1

153

Далее умножим слева и справа последнее выражение на

∏ (

)

1-R²

Y_k|Y_Mj+1Y_Mj+2...Y_k-1

j=1 k=M_j+2

M_j

∏

(

)

(

)

и учтем, что ∀j

1-d_e

Y^(j)

1-R²

Y_k|Y_Mj-1+1Y_Mj-1+2...Y_k-1

k=M_j-1+2

∏

(

)

e^2G(⋂j=1Y(j))

1 - d_e(Y ^(j))

j=2

∏

(

∏

(

)

1-R²

Y_Mj+1|Y₁...Y

Y_k|Y_Mj+1Y_Mj+2...Y_k-1

j=1

k=M_j+2

Умножив и разделив последнее выражение справа на

∏(

)

1-R²

Y_k|Y₁...Y_k-1

k=2

∏

(

)

(

)

и учтя, что 1 - d_e

Y⁽¹⁾

1-R²

, получим

Y_k|Y₁...Y_k-1

k=2

∏

(

∏

(

)

e^2G(⋂j=1Y(j) )

1-d_e

Y^(j)

1-R²

Y_k|Y₁...Y_k-1

j=1

k=1





⋃

=1-d_e

 Y^(j).

j=1

Следовательно,





⋃





1-d_e

Y^(j)

⋂

j=1

G Y^(j) = -1

(

∏

j=1

1 - d_e(Y^(j))

j=1

что и требовалось доказать.

СПИСОК ЛИТЕРАТУРЫ

1. Современный философский словарь: 2-е изд. / Под общей ред. проф. В.Е. Ке-

мерова. Лондон, Франкфурт-на-Майне, Париж, Люксембург, Москва, Минск:

ПАНПРИНТ, 1998.

154

Лысак И.В., Косенчук Л.Ф. Современное общество как общество сетевых струк-

тур // Информационное общество. 2015. № 2-3. С. 45-51.

Новиков Д.А. Сетевые структуры и организационные системы. М.: ИПУ РАН,

2003.

Goldstein H. Multilevel Statistical Models: 4th ed. Wiley, 2011.

Pardoe I. Applied Regression Modeling: 2nd ed. Wiley, 2012.

Lanchier N. Stochastic Modeling. Springer, 2017.

Булатов В.В. Введение в математические методы моделирования сложных си-

стем. М.: ОнтоПринт, 2018.

Frank S.A., Smith D.E. Measurement Invariance, Entropy, and Probability // En-

tropy. 2010. V. 12. No. 3. P. 289-303.

Wilson A.G. Entropy in Urban and Regional Modelling: Retrospect and Prospect //

Geographical Analysis. 2010. V. 42. No. 4. P. 364-394.

10.

Czyz T., Hauke J. Entropy in Regional Analysis // Quaestiones Geographicae. 2015.

V. 34. No. 4. P. 69-78.

11.

Попков Ю.С., Дубнов Ю.А., Попков А.Ю. Энтропийная редукция размерно-

сти в задачах рандомизированного машинного обучения // АиТ. 2018. № 11.

С. 106-122.

Popkov Y.S., Dubnov Y.A., Popkov A.Y. Entropy Dimension Reduction Method for

Randomized Machine Learning Problems // Autom. Remote Control. 2018. V. 79.

No. 11. P. 2038-2051.

12.

Shannon C.E. A Mathematical Theory of Communication // The CityplaceBell Sys-

tem Technical Journal. 1948. V. 27. No. 3. P. 379-423; No. 4. P. 623-656.

13.

Гельфанд И.М., Колмогоров А.Н., Яглом А.М. Количество информации и энтро-

пия для непрерывных распределений / Труды III Всесоюзного математического

съезда. М.: АН СССР, 1958. Т. 3. С. 300-320.

14.

Тырсин А.Н. Энтропийное моделирование многомерных стохастических систем.

Воронеж: Научная книга, 2016.

15.

Хардле В. Прикладная непараметрическая регрессия: Пер. с англ. М.: Мир, 1993.

16.

Галлагер Р. Теория информации и надежная связь: Пер. с англ. М.: Советское

радио, 1974.

17.

Тырсин А.Н. Скалярная мера взаимозависимости между случайными вектора-

ми // Зав. лаборатория. Диагностика материалов. 2018. Т. 84. № 7. С. 76-82.

https://doi.org/10.26896/1028-6861-2018-84-7-76-82.

Статья представлена к публикации членом редколлегии А.А. Лазаревым.

Поступила в редакцию 23.01.2022

После доработки 11.06.2022

Принята к публикации 29.06.2022

155