Автоматика и телемеханика, № 10, 2022

(Институт математики и информатики Московского

педагогического государственного университета;

Московский физико-технический институт)

ОБ ОДНОЙ РОБАСТНОЙ СХЕМЕ ГРАДИЕНТНОГО

БУСТИНГА НА ОСНОВЕ АГРЕГИРУЮЩИХ ФУНКЦИЙ,

НЕЧУВСТВИТЕЛЬНЫХ К ВЫБРОСАМ¹

Предложена одна новая робастная схема построения алгоритмов гра-

диентного бустинга. Она основана на применении дифференцируемых

оценок среднего значения, нечувствительных или малочувствительных к

выбросам, при построении робастного функционала эмпирического рис-

ка. Это позволило применить метод итеративного перевозвешивания для

для поиска очередной базовой функции и ее веса. Такая процедура гра-

диентного бустинга позволяет находить искомую зависимость по данным,

которые содержат относительно большую долю выбросов.

Ключевые слова: градиентный бустинг, робастная оценка, регрессия,

классификация.

DOI: 10.31857/S0005231022100142, EDN: ALQEEL

1. Введение

Методы бустинга [1] являются разновидностью методов машинного обу-

чения для построения ансамблей базовых алгоритмов. Модель базовых ал-

горитмов позволяет строить слабые алгоритмы, которые имеют относитель-

но небольшую сложность и заведомо не являются переобученными. Модель

базовых алгоритмов также может позволять строить сложные алгоритмы

с высокими показателями качества, но склонные к переобучению. В таких

случаях в методах бустинга они, как правило, используются с ограничения-

ми на сложность, которые позволяют исключить переобучение базовых ал-

горитмов, но в то же время делают их более слабыми. Целевой алгоритм,

как правило, строится в виде линейной комбинации базовых алгоритмов. Та-

кой подход к построению алгоритмов машинного обучения позволяет строить

сильные алгоритмы машинного обучения из более слабых алгоритмов.

Метод градиентного бустинга направлен на решение задачи построения

линейной композиции некоторого заранее неизвестного количества базовых

алгоритмов, которые минимизируют оценку эмпирического риска на обучаю-

щем множестве примеров. В классической схеме построения алгоритмов ма-

шинного обучения для решения задач регрессии и классификации эмпириче-

¹ Работа выполнена при поддержке научного проекта № АААА-А20-120122190034-9 Мос-

ковского педагогического государственного университета.

156

ский риск оценивается как среднее арифметическое от потерь:

∑

(1)

Q(w) =

ℓ(f(x_k; w), y_k

k=1

где f(x; w) параметризованная зависимость, {x₁, . . . , x_N } ⊂ Rⁿ обучаю-

щие входы, {y₁, . . . , y_N } ожидаемые значения на выходе, ℓ(y, y) - неотри-

цательная дифференцируемая функция потерь. Например:

1) в задаче регрессии ℓ(y, y) = ̺(y - y), где ̺(r) квазивыпуклая функция

с минимумом в нуле, например ̺(r) = r²;

2) в задаче классификации для двух классов ℓ(y, y) = ̺(1 - yy), где ̺(r)

монотонно убывающая функция, строго положительная при r < 0 и стремя-

щаяся к нулю при r → +∞, например, ̺(r) = max(0, 1 - yy) (функция Хин-

жа).

Требуется найти

w^⋆ = arg min Q(w).

Для повышения робастности ранее предлагалось использовать более ро-

бастные функции потерь [2]. Например, в задаче регрессии:

√

1) ̺(r) =

ε² + r² - ε (̺^′(r) ограничена);

2) ̺(r) = ln(a² + r²) - 2 ln a (̺^′(r) → 0 при r → ±∞);

√

3) ̺(r) = |r| /

ε² + r² (̺(r) ограничена),

а в задаче классификации:

1) ̺(r) = ln (1 + max(0, 1 - r)) (̺^′(r) → 0 при r → ±∞);

2) ̺(r) = η (max(0, 1 - r)), где η(s) монотонно возрастающая ограниченная

функция при s > 0.

Для поиска w^⋆, которая минимизирует Q(w) с более “робастными” функ-

циями потерь, применяется метод итеративного перевзвешивания [3, 4]. На-

пример,

1) в случае робастной регрессии решение задачи

∑

w^⋆ = arg min

̺ (f(x_k; w) - y_k)

w N

k=1

сводится к решению цепочки задач:

∑

(2)

w^t+1 = arg min v^tk (f(x_k;w) - y_k)² ,

k=1

где

(

)

v^tk = ϕ

f(x_k;w^t)-y_k

ϕ(r) = ̺^′(r)/r;

157

2) в случае задачи классификации решение задачи

∑

w^⋆ = arg min

̺ (max (0, 1 - y_kf(x_k; w)))

w N

k=1

сводится к решению цепочки задач:

∑

(3)

w^t+1 = arg min v^tk max(0,1 - y_kf(x_k

;w)) ,

k=1

где

(

)

v^tk = ϕ

1-y_kf(x_k;w^t)

, ϕ(r) = ̺^′(r)/r при r < 0 и ϕ(r) = 0 при r ≥ 0.

Здесь на каждом шаге процедуры итерационного перевзвешивания мини-

мизируется взвешенная сумма квадратов ошибки (в задаче регрессии) или

взвешенная сумма отступов с обратным знаком (в задаче классификации).

Подобные схемы хорошо известны. Однако если обучающие данные содер-

жат выбросы, из-за которых распределение значений потерь неизбежно бу-

дет содержать выбросы, то такой подход сталкивается с трудностями из-за

неустойчивости среднего арифметического. Поэтому для преодоления этой

проблемы было предложено использовать оценки среднего значения, кото-

рые нечувствительны или малочувствительны к выбросам [4, 5]. В этом слу-

чае робастная оценка средних потерь имеет вид

Q(w) = M {ℓ(f(x₁; w), y₁), . . . , ℓ(f(x_N ; w), y_N )} ,

где M{z₁, . . . , z_N } усредняющая агрегирующая функция. В [6, 7] было пред-

ложено использовать дифференцируемые оценки среднего, которые являют-

ся сглаженными вариантами известных робастных оценок среднего медиа-

ны, α-квантиля и винзоризированного среднего арифметического. Это поз-

воляет тоже применить метод итеративного перевзвешивания, но с другой

схемой пересчета весов в (2) и (3). В настоящей работе эта робастная схема

распространяется на метод градиентного бустинга. Далее сначала опишем

классическую схему градиентного бустинга, а затем робастную.

2. Классическая схема градиентного бустинга

Классическую схему метода градиентного бустинга [8] можно описать

следующим образом. Рассмотрим класс функций L(H), состоящий из линей-

ных комбинаций базовых функций из некоторого класса функций H

∑

H(x) = α_j h_j (x),

j=1

где α_j ∈ R, h_j ∈ H, x ∈ Rⁿ.

158

В классе L(H) ищется оптимальная функция H^∗, которая доставляет ми-

нимум

H^∗ = arg min Q(H)

H∈L(H)

функционалу Q(H):

∑

(4)

Q_V (H) = v_kℓ(H(x_k), y_k

k=1

где V = {v_k : k = 1, . . . , N}, v_k ≥ 0 веса примеров, такие что v₁+· · ·+v_N = 1.

Например, v_k = 1/N.

Для произвольных α ∈ R и h ∈ H рассматривается функционал

(

)

(

)

∑

(5)

Q_V

h, α

=Q_V

H + αh

= v_kℓ( Hk + αh(x_k), y_k

k=1

где

H_k = H(x_k).

Функция h и параметр α в (5) выбираются в результате решения задачи

минимизации:

(6)

h^⋆,α^⋆ = arg minQV

(h, α).

h,α

Для поиска минимума Q_V (h, α) можно применить процедуру поиска h и α

из известных алгоритмов градиентного бустинга, которые основаны на мини-

мизации взвешенной суммы потерь. Для нахождения экстремума Q_V будем

применять итеративный метод поочередной минимизации (alternating mini-

mization) [9]

h^p+1 = arg minQV (h,αp)

(7)

α^p+1 = arg minQV (hp+1,α).

На каждом шаге итерации сначала решается первая задача для поиска h^p+1,

а затм вторая задача для поиска αp+1. Итерационный процесс завершается,

если

Q(h^p+1, α^p+1) - Q(h^p, α^p)<εдлязаданногоε>0,илиеслиt=tmax,

где t_max максимальное число шагов итерации. Для упрощения вычислений

иногда в алгоритмах градиентного бустинга выполняется только один шаг

метода (7). Практика также показала, что достаточно использовать неболь-

шое число таких шагов. В некоторых случаях α^p+1 можно вычислить явно

(опираясь на необходимое условие экстремума Q_V по α), например

1) для задачи регрессии с ℓ(y, y) =¹² (y - y)² следующим образом:

^N v_k(H_k - y_k)h^p+1(x_k)

α^p+1 =^k=1N

;

∑ vk (hp+1(x_k

))²

k=1

159

2) для задачи классификации с ℓ(y, y) = max(0, 1-yy) следующим образом:

∑ v_k(1 - y_kH_k)y_kh^p+1(x_k)

α^p+1 =k∈Ip ∑

vk (ykh^p+1(xk))²

k∈Ip

где

v_k

v_k =

1-y_kH_k -α^py_kh^p+1(x_k)

{

}

I_p =

k: 1-y_kH_k -α^py_kh^p+1(x_k)>0

В целом алгоритм градиентного бустинга можно выразить при помощи

следующего псевдокода:

def gb_fit(M,V ):

H₀ = 0

for j in [1, . . . , M]:

(

)

h_j,α_j = arg minQV

H_j-1 + αh

h,α

H_j = H_j-1 + α_jh_j(x)

return H_M

3. Робастная схема градиентного бустинга

Эмпирическое распределение значений

{

}

z_k = z_k(h,α) = ℓ(Hk + αh(x_k), y_k): k = 1,... ,N

может содержать выбросы из-за искажений в данных или неадекватности

части данных по отношению к выбранной модели зависимости, особенно на

начальной стадии градиентного бустинга. Так как среднее арифметическое

чувствительно к выбросам, то в результате минимизации (5), как правило,

получаются искаженные h и α.

Проблему выбросов можно было бы решить путем подбора набора ве-

сов v₁, . . . , v_N , так чтобы для индексов k, соответствующих выбросам, зна-

чения v_k были достаточно малы, чтобы невелировать их влияние. Однако за-

дача поиска таких значений весов по сложности сопоставима с задачей иден-

тификации выбросов. Ниже сформулируем подход, который может позволить

преодолеть влияние выбросов, а также найти соответствующие значения ве-

сов v₁, . . . , v_N .

Для этого сформулируем более робастную постановку задачи:

(8)

h^⋆,α^⋆ = arg minQM

(h, α),

h,α

160

где

Q_M(h,α) = M{z₁(h,α),... ,z_N(h,α)},

где M{z₁, . . . , z_N } дифференцируемая усредняющая агрегирующая функ-

ция, более устойчивая к выбросам в данных [10].

Необходимое условие экстремума дает систему уравнений

∑

v_k(h,α)∇_h,αℓ(Hk + αh(x_k), y_k) = 0,

k=1

где

∂M{z₁(h,α),... ,z_N (h,α)}

(9)

ν_k(h,α) =

∂z_k

Дифференцируемые усредняющие агрегирующие функции M{z₁, . . . , z_N }, по

построению, такие что ∂M/∂z_k ≥ 0 для всех k = 1, . . . , N и

∂M/∂z₁ + ··· + ∂M/∂z_N = 1.

Для поиска оптимальных значений h^⋆ и α^⋆ (решения задачи (8)) будем

применять процедуру итеративного перевзвешивания, следуя [11]:

∑

(

)

(10)

h^t,α^t = arg min

ν_k

h^t-1,α^t-1

ℓ(Hk + αh(x_k), y_k

h,α

k=1

Данная схема итеративного перевзвешивания возникает в результате при-

менения общего метода Якоби для решения системы нелинейных уравнений



∂M{z₁(h,α),... ,z_N (h,α)}





v_k =

∂z_k

∑



 v_k∇_h,αℓ( Hk + αh(x_k), y_k) = 0,

k=1

которая возникает из необходимого условия экстремума для (8).

В этой итеративной схеме на шаге t осуществляется минимизация взве-

шенной суммы потерь

∑

Q^tV

(h, α) =

v^tkℓ(Hk + αh(x_k), y_k),

k=1

где

{

}

V_t =

v^tk = ν_k(h^t-1,α^t-1): k = 1,... ,N

161

def gb_fit_step_M(H, t_max):

инициализация h⁰, α⁰

H_k = H(x_k), k = 1,... ,N

for t = 1, . . . , t_max:

h^t,α^t = arg minQt (h,α).V

h,α

if выполнено условие останова:

break

return h^t, α^t

def gb_fit_M(M):

H₀ = 0

for j = 1, . . . , M:

h_j,α_j = gb_fit_step_M(H_j-1, t_max)

H_j = H_j-1 + α_jh_j(x)

return H_M

Для поиска решения задачи минимизации Q^t (h, α) будем применять про-_V

цедуру альтернативной минимизации (alternating minimization) [9]

∑

h^tp = arg min

v^tkℓ(Hk + α^t-1p-1h(x_k), y_k)

k=1

∑

α^tp = arg min

v^tkℓ(Hk + αh^tp(x_k), y_k),

k=1

где h^t-10 = h^t-1, α^t-10 = α^t-1.

Для решения приведенных задач минимизации использовался метод гра-

диентного спуска с применением схемы ADAM [12].

Рассмотрим отдельно некоторые варианты реализации метода робастного

градиентного бустинга для задачи регрессии и задачи классификации, кото-

рые можно получить в рамках предложенной выше схемы.

3.1. Задача регрессии

В задаче регрессии функция потерь, как правило, имеет вид: ℓ(y, y) =

= ̺(y - y), где ̺ неотрицательная дифференцируемая квазивыпуклая уни-

модальная функция, 0 ∈ arg min ̺(r).

Итерационная схема (10) принимает вид:

∑

(

)

h^t,α^t = arg min

ν_k(h^t-1,α^t-1)̺

H_k - y_k + αh(x_k)

h,α

k=1

где

H_k - y_k + αh(x_k) величина ошибки для k-го прецедента.

162

Типичный пример ̺(r) = r². В рамках классической схемы построения ро-

бастной регрессии [13] можно построить следующую процедуру итеративного

перевзвешивания:

∑

(

)₂

h^t = arg min

v_k(h^t-1,α^t-1)

H_k - y_k + α^t-1h(x_k)

h∈H

k=1

∑

(

)₂

α^t = arg min

v_k(h^t-1,α^t-1)

H_k - y_k + αh^t(x_k)

k=1

(

)

где v_k(h, α) = ν_k(h, α)ϕ

H_k-y_k+αh(x_k)

, ϕ(r) = ̺^′(r)/r, ν_k(h, α) вычисляется

по формуле (9).

Величину α^t в данной схеме можно вычислить явно

^N v_k(h^t-1,α^t-1)(y_k - H_k)h^t(x_k)

α^t =^k=1N

∑ v_k(ht-1,αt-1)(ht(x_k

))^t

k=1

3.2. Задача классификации

В задаче классификации для двух классов функция потерь может иметь

вид ℓ(y, y) = ̺(1 - yy), где ̺(r) неотрицательная монотонно возрастающая

функция, lim

̺(r) = +∞, ̺(r) > 0 при r < 0.

r→+∞

Итерационная схема (10) принимает вид:

∑

(

)

h^t,α^t = arg min

ν_k(h^t-1,α^t-1)̺

1 - y_k H_k - αy_kh(x_k)

h,α

k=1

где y_k H_k + αy_kh(x_k) величина отступа для k-го прецедента.

Приведем примеры:

̺(r) = max(0, r);

̺(r) =

ln(1 + e^λr);

(

√

)

̺(r) =

-r +

ε² + r²

В рамках классической схемы построения робастной регрессии [13] постро-

им следующую процедуру итеративного перевзвешивания:

∑

(

)₂

h^t = arg min

v_k(h^t-1,α^t-1)

1 - y Hk - α^t-1y_kh(x_k)

h∈H

k=1

∑

(

)₂

α^t = arg min

v_k(h^t-1,α^t-1)

1-y_k H_k -αy_kh^t(x_k)

k=1

163

где

(

)

v_k(h,α) = ν_k(h,α)ϕ

1-y_k H_k -α^t-1y_kh^t-1(x_k)

ϕ(r) = ̺^′(r)/r при r < 0

ϕ(r) = 0

при r ≥ 0.

Величину α^t можно вычислить явно:

^N v_k(h^t-1,α^t-1)(1 - y_k H_k)y_kh^t-1(x_k)

α^t =^k=1

∑ v_k(ht-1,αt-1)(y_kht-1(x_k

))²

k=1

4. Иллюстративные примеры

В следующих примерах будет использоваться робастная оценка среднего

∑

WM_α{z₁,... ,z_N } =

min(z_k, z_α),

k=1

где

∑

zα = Mα{z1, . . . , zN } = arg min

ρ_α(z_k - u),

k=1

√

{ αρ(r),

если r ≥ 0

ρ_α(r) =

ρ(r) =

ε² + r² - ε.

(1 - α)ρ(r), если r < 0,

Здесь M_α

¾гладкий вариант¿ α-квантиля, ε = 0,001. Робастная оценка

WM_α среднее арифметическое предварительно отцензурированных неот-

рицательных значений при помощи порогового значения z_α. В качестве функ-

ции потерь в задачах регрессии будет выступать ℓ(y, y) =¹² (y - y)² квадрат

ошибки.

Функции h(x, w) выбираются из класса сигмоидальных нейронов

h(x, w) = σ(w₀ + w₁x₁ + · · · + w_nx_n),

где σ(s) = th λs (по умолчанию λ = 1, если не оговорено иное). Таким об-

разом, класс функций L(H) описывает функции преобразования нейронной

сети со скрытым слоем из сигмоидальных нейронов. Количество нейронов в

скрытом слое относительно небольшое во избежание переобучения.

Все вычисления выполнены с помощью языка программирования python и

библиотеки mlgrad (https://bitbucket.org/intellimath/mlgrad).

164

44,4% выбросов (m = 30)

44,4% выбросов (m = 40)

WM(a = 0,56)

-10

-20

-30

-10

-5

-10

-5

Рис. 1. Графики восстановленных функций для примера с линейной регрессией.

1. Наглядный пример с линейной регрессией. В этом примере вы-

бран набор точек на плоскости, расположенных вдоль некоторой прямой ли-

нии. К ним добавлены новые точки выбросы, которые расположены кучно

по разные стороны от прямой линии, так чтобы при восстановлении линей-

ной функции при помощи метода наименьших квадратов найденная прямая

линия сильно поворачивалась, притягиваясь к выбросам. Выбросы состав-

ляют 44% выборки. Параметр λ = 0,5 в σ(s). На рис. 1 приведены графики

восстановленных функций.

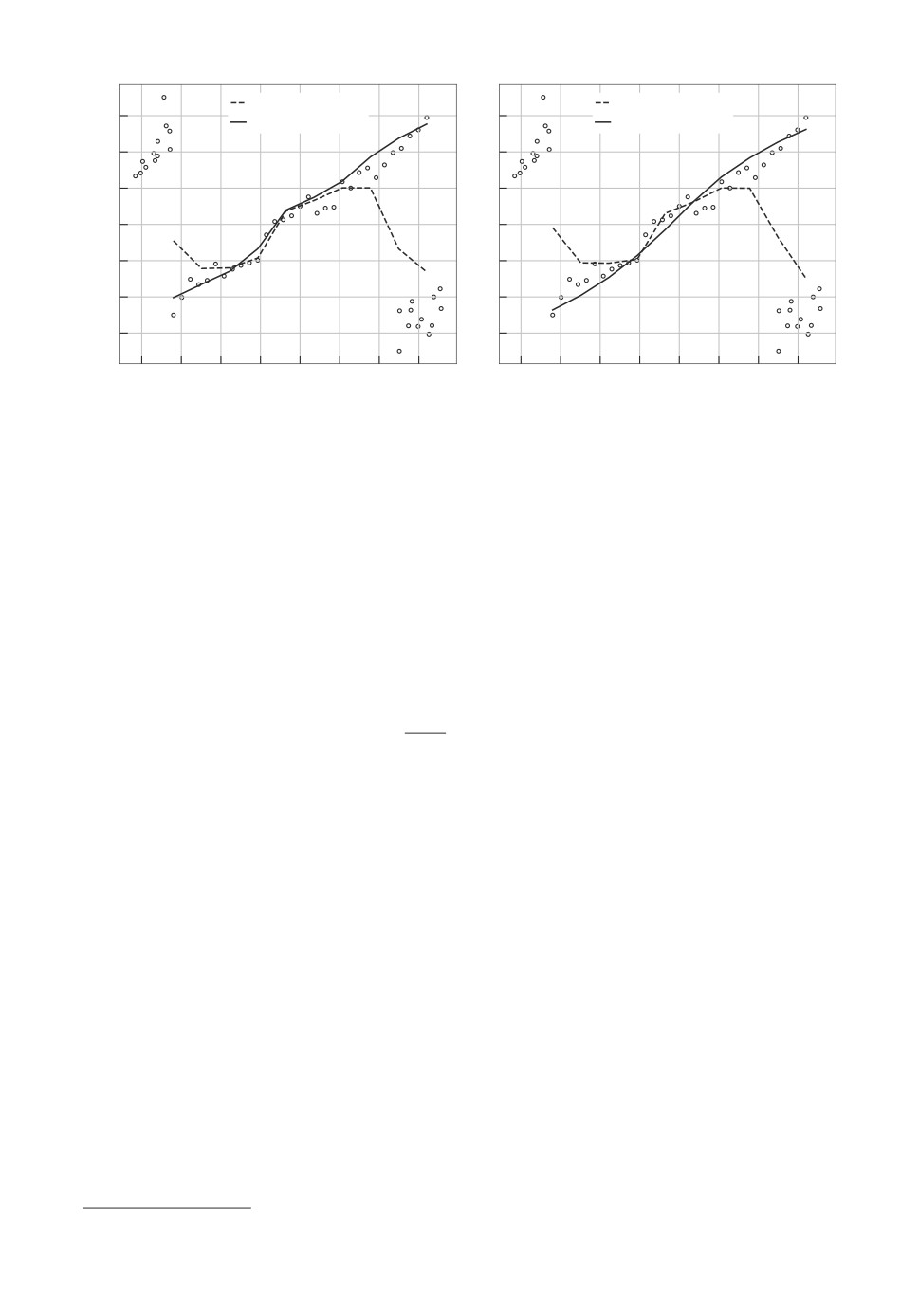
2. Набор данных breast_cancer.² Ко входным векторам предвари-

тельно была применена проце{ра с}андартного масштабирования при по-

x_k-x

мощи преобразования {x_k} →

, где x

среднее арифметическое, а

σ стандартное отклонение, для приведения значений признаков ко взаимно

сопоставимым масштабам значений. Для этого набора строились два вари-

анта функции H(x), которые содержат небольшое число слагаемых (m = 20

и m = 30). В робастном варианте α = 0,95. На рис. 3 построены кривые рас-

пределения абсолютных значений ошибок в логарифмических координатах.

Нетрудно увидеть, что применение более робастной функции оценки средне-

го значения может позволить уменьшить абсолютную величину ошибок для

подавляющего большинства примеров.

3. Сгенерированная однослойная нейронная сеть с одним скры-

тым слоем. Это искусственно сгенерированный набор данных на основе

функции

∑

H(x) = α_j σ(w_j,0 + w_j,1x₁ + w_j,2x₂), m = 40,

k=1

в которой значения весов w_j,0, w_j,1, w_j,2 и коэффициентов α_j для простоты

выбраны случайно из равномерного распределения на [-1, 1] (то, что значе-

ния выбраны из равномерного распределения принципиального значения не

² https://archive.ics.uci.edu/ml/datasets/Breast+Cancer

165

Распределение ошибок (m = 20)

Распределение ошибок (m = 30)

10⁰

WM(a = 0,95)

10^-1

10^-2

10^-3

-4

10^-4

-5

10^-5

10^-6

10^-7

10⁰

10¹

10²

10⁰

10¹

10²

Ранг

Рис. 2. Графики распределения абсолютных значений ошибок в примере 2.

Распределение ошибок

(m = 40, выбросы: 0.30)

(m = 40, выбросы: 0.40)

10⁴

10²

10⁰

10^-2

10^-4

10^-6

10¹

10²

10⁰

10¹

Ранг

Рис. 3. Графики распределения абсолютных значений ошибок в примере 3.

имеет). Аналогично случайно выбирается набор входов {x_k : k = 1, . . . , 100}⊂

⊂ [-3, 3]². Для всех k вычисляются значения y_k = H(x_k). Из этого набора

данных создаются два набора с долями выбросов M = 30% и M = 40%. Зна-

чение y_k в точке выбросов увеличивается в 10 раз. На рис. 3 построены кри-

вые распределения абсолютных значений ошибок в логарифмических коор-

динатах. На рисунках сплошная кривая соответствует робастному вариан-

ту градиентного бустинга. Нетрудно увидеть, что применение более робаст-

ной функции среднего значений может позволить ощутимо уменьшить абсо-

лютную величину ошибок практически для всех выбросов. При применении

стандартной процедуры градиентного бустинга в точках, которые не являют-

ся выбросами, наблюдаются очень большие значения ошибок. В результате

применения робастной процедуры градиентного бустинга ошибки для нор-

мальных точек могут стать достаточно малы.

166

5. Заключение

Предложенный в данной статье подход сравним с известным подходом

к повышению робастности алгоритмов регрессии и классификации, основан-

ным на применении более робастных функций потерь. Существенное отличие

предложенной выше робастной схемы состоит в способе пересчета весов при-

меров в процедуре итеративного перевзвешивания. В случае применения в (5)

с v_k = 1/N более робастных функций потерь веса примеров вычисляются по

формуле вида

v_k = ϕ(z_k),

где ϕ(z) неотрицательная, как правило, убывающая функция от z или |z|.

Эффект снижения влияния выбросов достигается за счет малости весов при-

меров, которые являются выбросами (как правило, с большими значениями z

или |z|). В нашем подходе веса пересчитываются по формуле вида:

v_k = ψ(z_k - z),

где ϕ(z) тоже неотрицательная убывающая функция от z, z величина

робастной оценки среднего значения z₁, . . . , z_N , которая нечувствительна или

малочувствительна к выбросам. Отличие состоит в том, здесь вес примера яв-

ляется функцией отклонения z_k от среднего значения. Так, в задаче регрес-

сии, когда значения z_k соответствуют ошибкам, в ситуации, со значением z

существенно отличающимся от нуля, значения весов примеров в предложен-

ном робастном подходе оказываются существенно меньше. Это получается

потому, что когда все ошибки существенно отделены от нуля, они оказыва-

ются в области значений z, где значение функции ϕ (в (2) и (3)) убывает

медленнее, чем около нуля. В предложенном робастном подходе случае раз-

ность z_k - z оказывается ближе к нулю и поэтому происходит более быстрое

падение значений весов примеров по мере удаления z_k от z. В результате в

рамках предложенного здесь метода примеры, соответствующие выбросам,

получают такие малые значения весов (по сравнению с весами примеров, ко-

торые не являются выбросами), достаточные для того, чтобы преодолеть их

влияние.

СПИСОК ЛИТЕРАТУРЫ

1. Freund Y., Schapire R.E. A decision-theoretic generalization of on-line learning and

an application to boosting // J. of Comput. and Syst. Sci. 1997. V. 55. No. 1.

P. 119-139.

2. Kanamori T., Takenouchi T., Eguchi S., Murata N. Robust loss functions for boost-

ing // Neural Computation. 2007. V. 19. No. 8. P. 2183-2244.

3. Holland P.W., Welsch R.E. Robust regression using iteratively reweighted least

squares // Communications in Statistics Theory and Methods. 1977. V. 6. No. 9.

P. 813-827.

4. Rousseeuw P.J., Leroy A.M. Robust Regression and Outlier Detection. New York:

John Wiley and Sons. 1987.

167

5. Rousseeuw P.J., Hubert M. High-breakdown estimators of multivariate location and

scatter / Becker C., Fried R., Kuhnt S., editors. Robustness and Complex Data

Structures. Springer, 2013. P. 49-66.

6. Шибзухов З.М. О принципе минимизации эмпирического риска на основе усред-

няющих агрегирующих функций // Докл. РАН. 2017. Т. 476. № 5. С. 495-499.

7. Shibzukhov Z.M. Machine learning based on the principle of minimizing robust mean

estimates / Advances in Intelligent Systems and Computing. V. 1310. P. 472-477.

Springer International Publishing. 2020.

8. Friedman J.H. Greedy function approximation: A gradient boosting machine // An-

nals Statist. 2001. V. 29. No. 5.

9. Csiszar I., Tusnady G. Information geometry and alternating minimization proce-

dures // Statistics and Decisions, Supplement Issue. 1984. No. 1. P. 205-237.

10. Calvo T., Beliakov G. Aggregation functions based on penalties // Fuzzy Sets and

Systems. 2010. V. 161. No. 10. P. 1420-1436.

11. Shibzukhov Z.M., Semenov T.A. Machine learning based on minimizing robust mean

estimates. In: Pattern Recognition. ICPR International Workshops and Challenges.

P. 112-119. Springer International Publishing. 2021.

12. Kingma D.P., Ba J. Adam: A method for stochastic optimization. arXiv:1412.6980.

https://doi.org/10.48550/arXiv.1412.6980

13. Huber P.J. Robust Statistics. John Wiley and Sons. 1981.

Статья представлена к публикации членом редколлегии А.А. Лазаревым.

Поступила в редакцию 31.01.2022

После доработки 23.05.2022

Принята к публикации 29.06.2022

168