Автоматика и телемеханика, № 11, 2022

Линейные системы

М.В. ХЛЕБНИКОВ, д-р физ.-мат. наук (khlebnik@ipu.ru)

(Институт проблем управления им. В.А. Трапезникова РАН, Москва;

Национальный исследовательский университет

“Московский физико-технический институт”, Москва)

НОВЫЕ КРИТЕРИИ

НАСТРОЙКИ ПИД-РЕГУЛЯТОРОВ¹

Предлагается новый подход к задаче настройки и оптимизации пара-

метров ПИД-регулятора, основанный на сведении проблемы к задаче оп-

тимизации. При этом качество регулятора оценивается по квадратично-

му критерию от выхода системы: ПИД-регулятор настраивается против

неопределенности в начальных условиях так, чтобы выход системы был

равномерно малым; при этом дополнительно гарантируется заданная сте-

пень устойчивости замкнутой системы. Выписан градиентный метод для

отыскания параметров ПИД-регулятора.

Как показывают многочисленные примеры, предлагаемая рекуррент-

ная процедура является весьма эффективной и приводящей к вполне

удовлетворительным по инженерным критериям качества ПИД-регуля-

торам. Статья продолжает серию работ авторов, посвященную синтезу

обратной связи в задачах управления с позиций оптимизации.

Ключевые слова: линейная система, ПИД-регулятор, оптимизация, урав-

нение Ляпунова, градиентный метод, сходимость.

DOI: 10.31857/S0005231022110022, EDN: KDYNHU

1. Введение

Теория ПИД-регуляторов имеет 80-летнюю историю, восходя к работе [1]

Циглера и Николса 1942 г. С тех пор появилось множество работ, посвящен-

ных теории и практике их настройки, были предложены различные принципы

их настройки (см., например, [2]). Здесь можно упомянуть монографии [3-6]

и многие другие. Однако до настоящего времени есть не так много работ,

где формулируются явные критерии оптимальности ПИД-регуляторов, на-

пример такие, как H_∞-оптимальность [7, 8].

В целом регуляторы низкого порядка настраивают по самым разным кри-

териям, используя при этом, как правило, подбор, прямой поиск, перебор

по сетке и т.п., см., например, [9, 10]. В настоящей работе предлагается но-

вый подход к настройке ПИД-регуляторов, а именно предлагается как новая

¹ Исследование выполнено при частичной поддержке Российского научного фонда (про-

ект № 21-71-30005).

постановка задачи, решение которой определяет ПИД-регулятор, так и ал-

горитм ее решения, явным образом выписывая градиент для квадратичного

функционала и применяя градиентный метод.

В отличие от упомянутых выше критериев, будем рассматривать в неко-

тором смысле близкую к LQR постановку. А именно, неопределенность со-

держится не во входах системы, а в начальных условиях, при этом крите-

рий качества близок по своей структуре к LQR-задаче: качество оценивается

по квадратичному критерию от выхода системы. Таким образом, искомый

ПИД-регулятор настраивается против неопределенности в начальных усло-

виях так, чтобы выход системы был равномерно малым (в квадратичном

смысле).

В связи с этим напомним о новых подходах для классической проблемы

линейно-квадратичного регулирования. Ее можно рассматривать как задачу

оптимизации, где переменной является матрица обратной связи, а миними-

зируется интегральный квадратичный показатель качества переходного про-

цесса. Градиент такой функции (для управления по состоянию) выписан еще

в основополагающей работе Калмана [11], а для обратной связи по выходу

в статье Левина и Атанса [12]. С тех пор неоднократно применялись итера-

тивные методы оптимизации градиентного типа (см., например, обзор [13]),

однако обоснование подобных методов появилось лишь недавно в [14-18].

Помимо малости выхода, естественно стремиться к тому, чтобы синтези-

рованный ПИД-регулятор удовлетворял и инженерным критериям качества.

Так, если замкнутая система окажется близкой к границе устойчивости, это

приведет к ее неудовлетворительной реакции на внешнее возмущение. Поэто-

му вполне естественно требовать, чтобы ПИД-регулятор дополнительно га-

рантировал замкнутой системе некоторую (заданную) степень устойчивости.

Настоящая статья продолжает серию работ [18-20], посвященную синтезу

обратной связи в задачах управления с позиций оптимизации. Предложен-

ный в ней подход позволяет, с одной стороны, конструктивно решать задачи

настройки и оптимизации параметров регулятора, а с другой, он предостав-

ляет “хорошие” по обычным инженерным показателям регуляторы. Как по-

казывают многочисленные примеры, предлагаемая рекуррентная процедура

является весьма эффективной и приводящей к вполне удовлетворительным

ПИД-регуляторам. Вычислительным аспектам предлагаемого подхода посвя-

щена публикация [22].

Статья организована следующим образом. Раздел 2 содержит постановку

задачи; в разделе 3 обсуждается подход к ее решению; в разделе 4 представ-

лен алгоритм решения оптимизационной задачи, а раздел 5 посвящен разно-

образным примерам. Раздел 6 содержит обсуждение и возможные обобщения

полученных результатов.

Всюду далее | · | евклидова норма вектора,^T символ транспонирова-

ния, tr

след матрицы, I единичная матрица соответствующей размер-

ности, а λ_i(A) собственные значения матрицы A.

2. Постановка задачи

Рассмотрим SISO-систему управления

x = Ax + bu, x(0) = x₀,

(1)

y = c^Tx,

с состоянием x(t) ∈ Rⁿ, выходом y(t) ∈ R и управлением u(t) ∈ R в виде

ПИД-регулятора

∫t

(2)

u(t) = -k_P y(t) - k_I y(τ)dτ - k_D

y(t)

с некоторыми числовыми параметрами k_P , k_I и k_D.

(

)

Целью является определение параметров K =

k_P k_I k_D

стабилизирую-

щей обратной связи (2), которая

а) доставляет замкнутой системе степень устойчивости σ > 0 и

б) минимизирует квадратичный функционал

∫∞

(3)

J (K) = E_x(0) y²(t)dt + ρ|K|²

ρ > 0.

Вторая компонента в (3) представляет собой штраф за величину управления

(при этом коэффициент ρ > 0 регулирует его важность). Ее наличие позволя-

ет избежать появления больших значений коэффициентов ПИД-регулятора.

Далее будем предполагать, что начальные условия x(0) распределены с

нулевым средним и ковариационной матрицей Σ.

3. Сведение к параметрической LQR-задаче

Введем в рассмотрение вспомогательную скалярную переменную z сле-

дующим образом:

Ż = y, z(0) = 0.

Тогда, вводя расширенный вектор состояния

(

)

∈Rⁿ⁺¹

системе (1) можно придать эквивалентный вид

)

(A 0

(b)

(x₀)

ġ=

u, g(0) =

c^T

(4)

(

)

c^T

При этом согласно (1), (2) имеем:

∫t

u = -k_Py(t) - k_I y(τ)dτ - kD y(t) =

= -k_P c^Tx - k_Iz - k_Dc^T ˙x = -k_P c^Tx - k_Iz - k_Dc^T(Ax + bu) =

(

)

(

)

(

)

= -k_P

c^T

g-k_I

g-k_D

c^TA 0

g - k_Dc^Tbu,

откуда

(

)

(

)

(

)

(1 + k_Dc^Tb)u = -k_P

c^T

g-k_I

g-k_D

c^TA 0

или

k_P

(

)

k_I

(

)

k_D

(

)

(5)

u=-

c^T

c^TA

1+k_Dc^Tb

Если ввести новые переменные

k_P

k_I

k_D

k₁ =

k₂ =

k₃ =

1+k_Dc^Tb

то (5) примет вид

(

)

(6)

u=-

k₁c^T + k₃c^TA k₂

Замыкая систему (4) обратной связью (6), приходим к замкнутой системе

)

(A - k₁bc^T - k₃bc^TA -k₂b

(x₀)

(7)

ġ=

g, g(0) =

c^T

которой можно придать вид

)

(x₀

(8)

ġ = (A₀ + k₁A₁ + k₂A₂ + k₃A₃)g, g(0) =

где

)

(A 0

(-bc^T

(0 -b)

(-bc^TA 0)

A₀ =

A₁ =

A₂ =

A₃ =

c^T

При этом исходные параметры ПИД-регулятора восстанавливаются един-

ственным образом:

k₁

k₂

k₃

k_P =

k_I =

k_D =

1-k₃c^Tb

Замечание 1. Обратим внимание, что если векторы b и c ортогональны,

то

k₁ = k_P , k₂ = k_I, k₃ = k_D.

Как показывают многочисленные примеры, это вполне типичная ситуация,

так что для упрощения записи все дальнейшие выкладки относятся

именно к этому случаю.

Для удобства введем обозначение:

{A, K} = k₁A₁ + k₂A₂ + k₃A₃.

Для того, чтобы гарантировать желаемую степень устойчивости σ > 0 за-

мкнутой системы, введем в ее матрицу компоненту σI:

(9)

ġ = (A₀

+ {A, K} + σI)g.

В самом деле, для стабилизирующего систему (9) регулятора K матрица A₀ +

+ {A, K} + σI является гурвицевой. Отсюда непосредственно вытекает, что

maxRe λi(A0 + {A,K} + σI) = maxReλi(A0 + {A,K}) + σ < 0,

т.е. степень устойчивости исходной системы не меньше σ:

maxRe λi(A0 + {A,K}) < -σ.

Продолжим и перейдем к преобразованию функционала (3). Поскольку

(

)

(x₀

то начальные условия g(0) =

будут распределены с нулевым средним

и ковариационной матрицей

(Σ 0)

По лемме Беллмана для системы (7) имеем:

∫∞

J (K) = E_x(0) y²(t)dt + ρ|K|² =

∫∞

)

(cc^T

= E_g(0) g^T(t)

g(t)dt + ρ|K|² =

(Σ 0)

= E_g(0)g^T(0)Qg(0) + ρ|K|² = tr Q

+ ρ|K|².

Здесь Q ∈ R^(n+1)×(n+1) решение уравнения Ляпунова

)

(cc^T

(10)

A^TKQ + QA_K = -

где

A_K = A₀ + {A,K} + σI.

Сделаем следующее

(

)

Предположение. Пусть известен регулятор K₀ =

k01 k02 k03

, ста-

билизирующий систему с заданным запасом устойчивости σ, т.е. такой,

что матрица AK0 = A₀ + {A, K₀} + σI гурвицева.

Перейдем к описанию свойств функции J(K).

Лемма 1. Функция J(K) определена и положительна на множестве S

стабилизирующих регуляторов.

Действительно, если матрица A_K гурвицева, то решение Q ≽ 0 уравнения

Ляпунова (10) существует; тем самым, определена функция J(K) > 0. Мно-

жество ее определения S может быть невыпуклым и несвязным, причем его

границы могут быть негладкими.

Перейдем к вычислению градиента функции J(K).

Лемма 2. Функция J(K) определена на множестве стабилизирующих

обратных связей K. На этом допустимом множестве она дифференцируе-

ма, причем градиент дается выражениями

∂J(K)

(11)

= ∇_iJ(K) = 2tr Y QA_i + 2ρk_i

i = 1,2,3,

∂k_i

где матрица Y является решением уравнения Ляпунова

(

)

Σ 0

(12)

A_KY + Y A^TK +

= 0.

Доказательство этого утверждения приведено в Приложении.

4. Алгоритм решения

Авторы предлагают следующий итеративный подход к решению этой за-

дачи; в его основе лежит применение градиентного метода по переменной K.

Приведем принципиальную схему алгоритма.

Алгоритм 1 для минимизации J(K):

1. Задаемся параметрами ε > 0, γ > 0, 0 < τ < 1 и начальным стабилизирую-

щим приближением K₀.

2. На j-й итерации задано K_j . Вычисляем AKJ = A₀ + {A, K_j }, решаем урав-

нения (10), (12) и находим матрицы Q и Y ; вычисляем градиент

H_j = ∇J(K_j)

из уравнения (11). Если ∥H_j ∥ ≤ ε, то K_j принимаем за приближенное ре-

шение.

3. Делаем шаг градиентного метода

K_j+1 = K_j - γ_jH_j.

Длину шага γ_j > 0 подбираем дроблением γ до выполнения условий:

а. K_j+1

стабилизирующий регулятор;

б. J(K_j+1) ≤ J(K_j ) - τγ_j∥H_j ∥².

4. Переходим к п. 2.

Сделаем несколько замечаний. Прежде всего, нетривиальным моментом

является выбор начального стабилизирующего регулятора K₀. Здесь мож-

но прибегнуть к помощи D-разбиения [21] или воспользоваться методами

прямого поиска (см., например, [9]). В некоторых случаях может оказать-

ся полезным следующий прием: для некоторой положительно-определенной

матрицы Q попытаться разрешить неравенство Ляпунова ATK0 Q + QAK0 ≺ 0

относительно K₀. Также часто в практических задачах требуется улучшить

качество уже имеющегося ПИД-регулятора путем настройки его параметров.

Наконец, если исходная система управления является устойчивой (как часто

и бывает на практике), вопрос выбора начального регулятора решается оче-

видным образом.

Еще одним важным моментом является выбор пробного шага градиентно-

го метода. Весьма перспективным является его выбор из следующих сообра-

жений. Найдем для некоторого стабилизирующего регулятора K_j решение Q

уравнения Ляпунова

(A₀ + σI + {A, K_j })^TQ + Q(A₀ + σI + {A, K_j }) = -I.

Рассмотрим приращение по K:

K_j → K_j - γH_j, H_j = ∇J(K_j),

и найдем, для каких γ матрица Q останется матрицей квадратичной функции

Ляпунова для AKj -γH_j = A0 + σI + {A, Kj - γHj }, т.е.

(A₀ + σI + {A, K_j - γH_j})^TQ + Q(A₀ + σI + {A, K_j - γH_j }) ≺ 0.

С учетом исходного уравнения имеем

γ(-{A, H_j }^TQ - Q{A, H_j }) ≺ I,

откуда

γ < λ^-1max(-{A,H_j}^TQ - Q{A,H_j}).

5. Примеры

Рассматриваемые далее примеры взяты из статьи [23]. Всюду в этом раз-

деле будем полагать Σ = I.

Пример 1. Рассмотрим передаточную функцию

G(s) =

α = 0,5.

(1 + s)(1 + αs)(1 + α²s)(1 + α³s)

Matlab-процедура tf2ss доставляет матрицы системы в пространстве со-

стояний:











-15 -70 -120 -64

1























0

,

0,

0

.

Пусть

σ = 0,25, ρ = 10.

При выборе в качестве начального стабилизирующего регулятора

(

)

K₀ =

9,5717

4,8538

8,0028

оптимизационная процедура приводит к регулятору

(

)

K_∗ =

7,6296

3,4331

3,1795

|K_∗| = 8,9502,

доставляющему интегральной части функционала J(K) значение 3,5327·10³.

Возьмем теперь начальное приближение

(

)

K^′0 =

4,3141

9,1065

1,8185

;

в результате получим регулятор

(

)

K^′∗ =

7,6265

3,4327

3,1782

|K_∗| = 8,9469,

и значение функционала, равное J(K^′∗) = 3,5333 · 10³.

Как видно, значения функционала и нормы получившихся регуляторов

отличаются на доли процента.

Передаточная функция ПИД-регулятора с коэффициентами K_∗ имеет вид

3,4331

GPID(s) = 7,6296 +

+ 3,1795s.

Система, замкнутая ПИД-регулятором K_∗, является устойчивой по крите-

рию Найквиста; ее минимальный запас устойчивости по модулю составляет

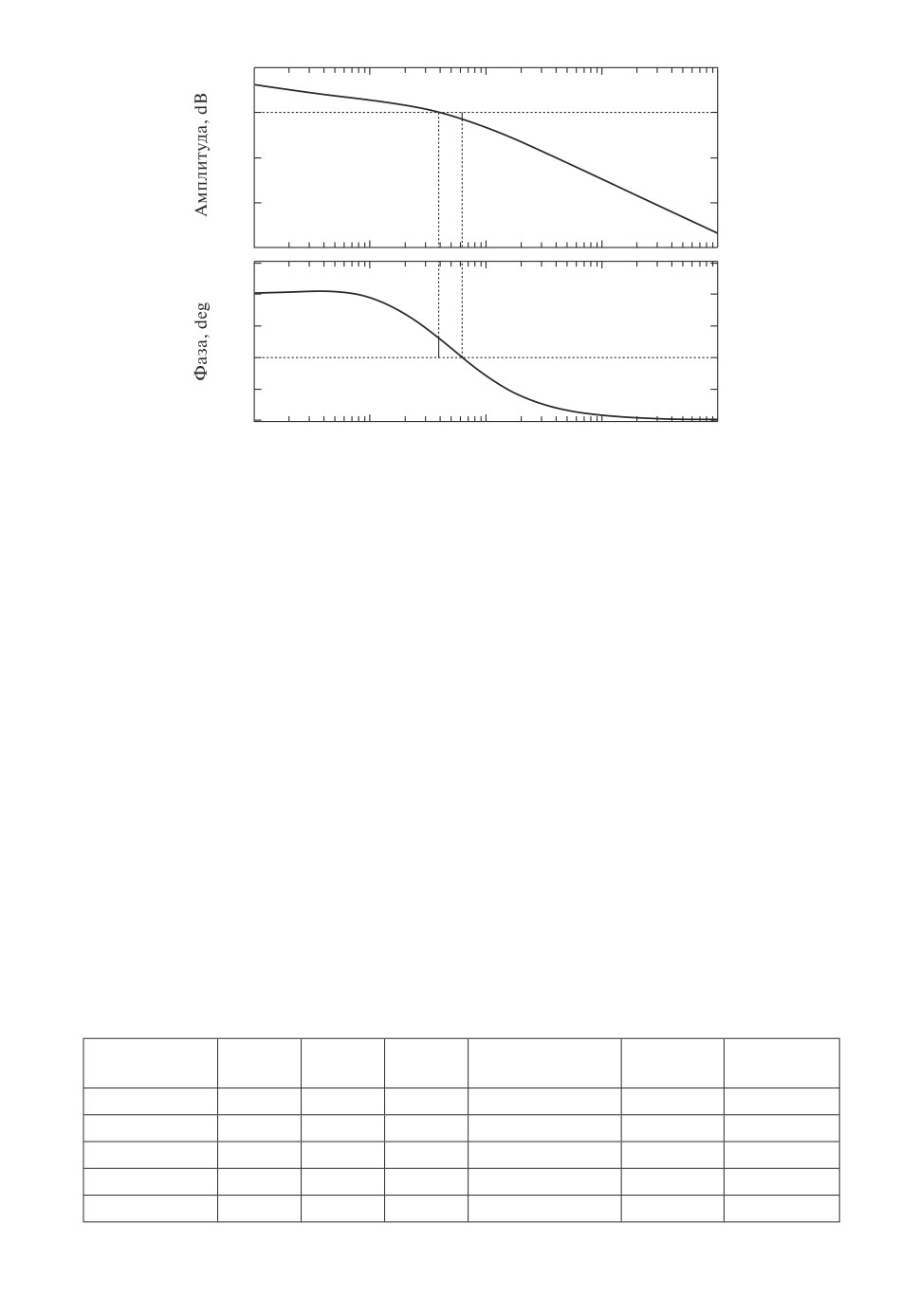
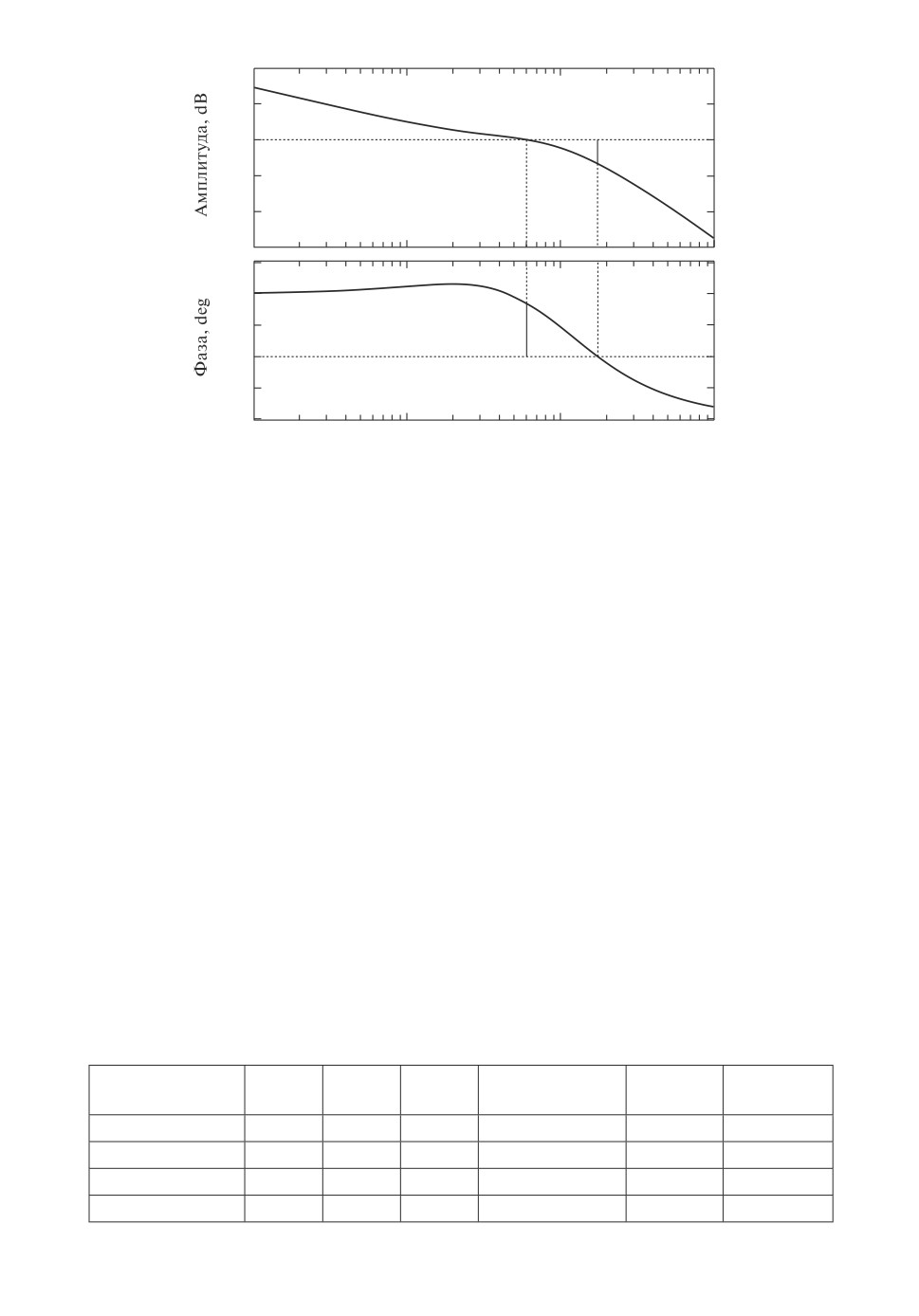
7,41 дБ, а по фазе

27,5^◦, см. рис. 1.

-50

-100

-150

-45

-90

-135

-180

-225

-270

10^-1

10⁰

10¹

10²

10³

Частота, rad/s

Рис. 1. ЛАФЧХ замкнутой системы из примера 1.

Сравним полученный ПИД-регулятор с регуляторами, полученными по

методу Циглера-Николса (ZN) [1], гармонического поиска (Harmony Search,

HS) [24], улучшенной версии алгоритма пчел (Improved Bees’ Algorithm,

IBA) [25] и алгоритма пчелиной колонии (Artificial Bee Сolony, ABC) [26],

подробнее см. [27]. Соответствующие результаты представлены в табл. 1.

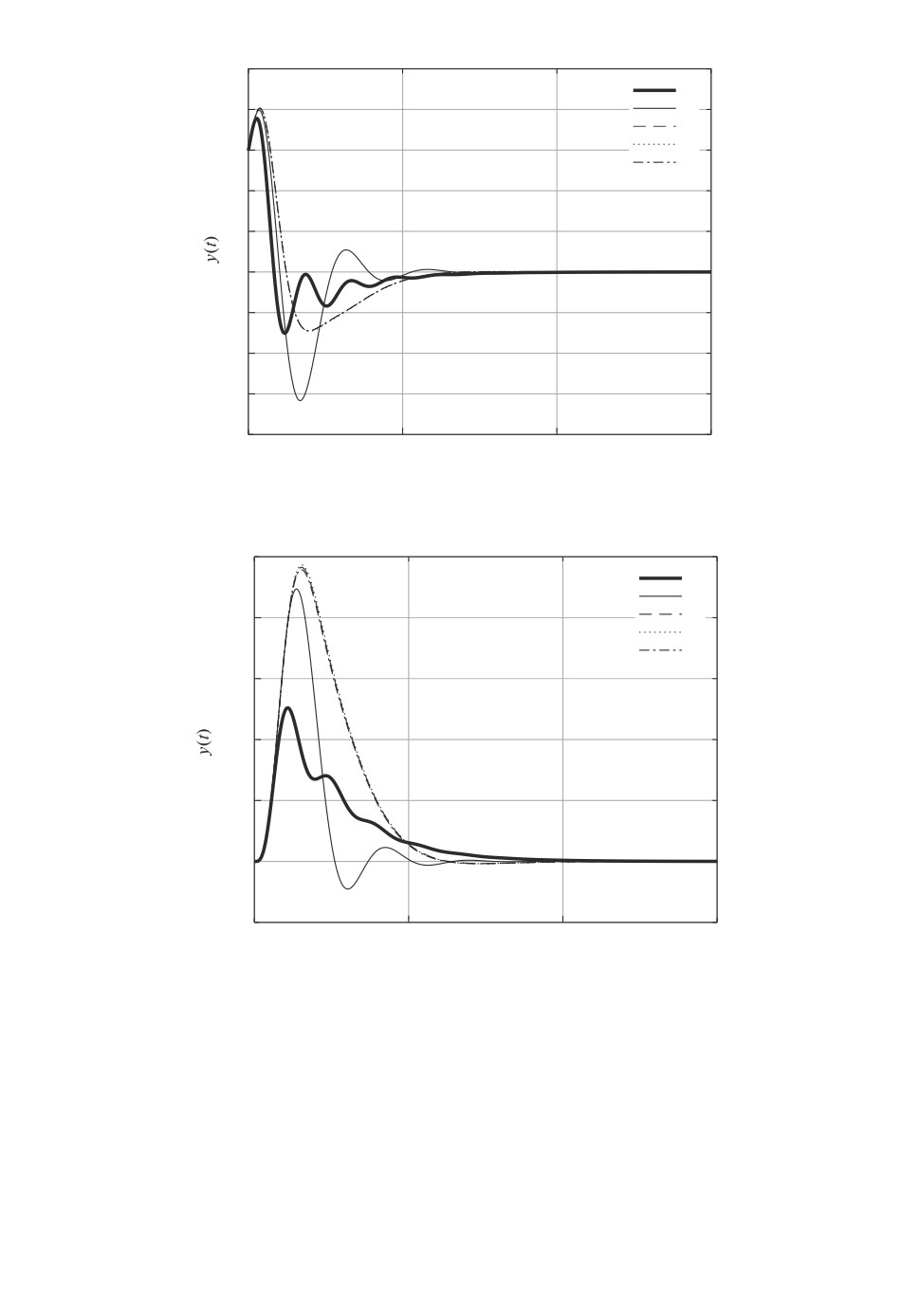
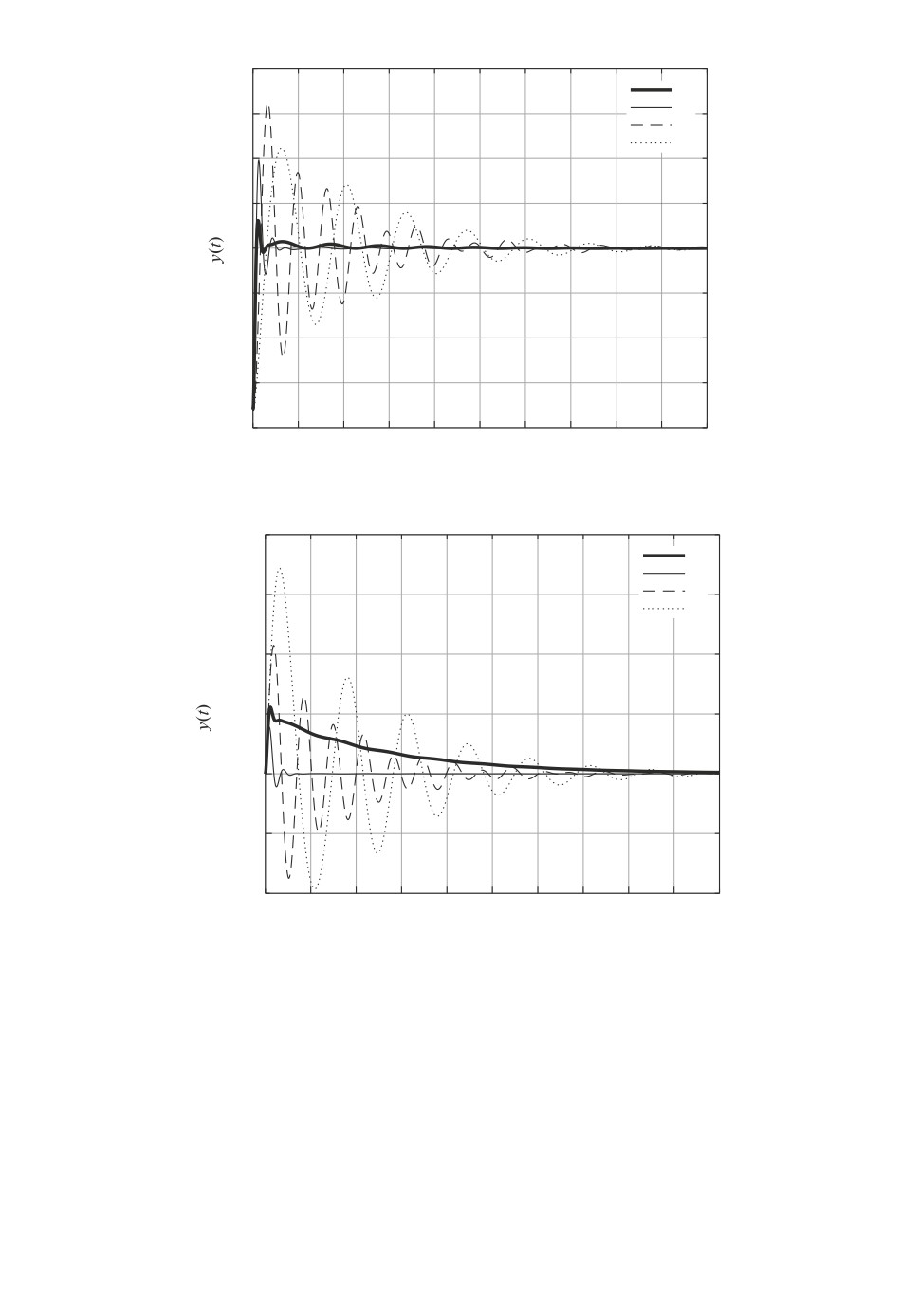
На рис. 2 показана динамика выхода y(t) рассматриваемой системы при

некотором начальном условии





-0,5715

-0,1249





x₀ =



 0,6635

0,4664

из единичного шара: при замыкании найденным ПИД-регулятором K_∗ (жир-

ная линия) и регуляторами из табл. 1.

Таблица 1. Сравнение ПИД-регуляторов по интегральной части функционала

и запасам устойчивости для примера 1

∫

k_P

k_I

k_D

E_x(0) y²(t)dt G_m (дБ) P_m (град)

Алгоритм 1

7,6296

3,4331

3,1795

2,7303 · 10³

7,41

27,5

3,9706

3,5749

1,1026

4,3752 · 10³

12,4

35,0

2,8206

1,8022

1,4330

3,6654 · 10³

15,6

68,0

IBA

2,7852

1,7873

1,4157

3,6872 · 10³

15,7

68,5

ABC

2,8458

1,8278

1,4535

3,6545 · 10³

15,5

67,8

1400

1200

1000

800

600

400

200

100

120

140

N_iter

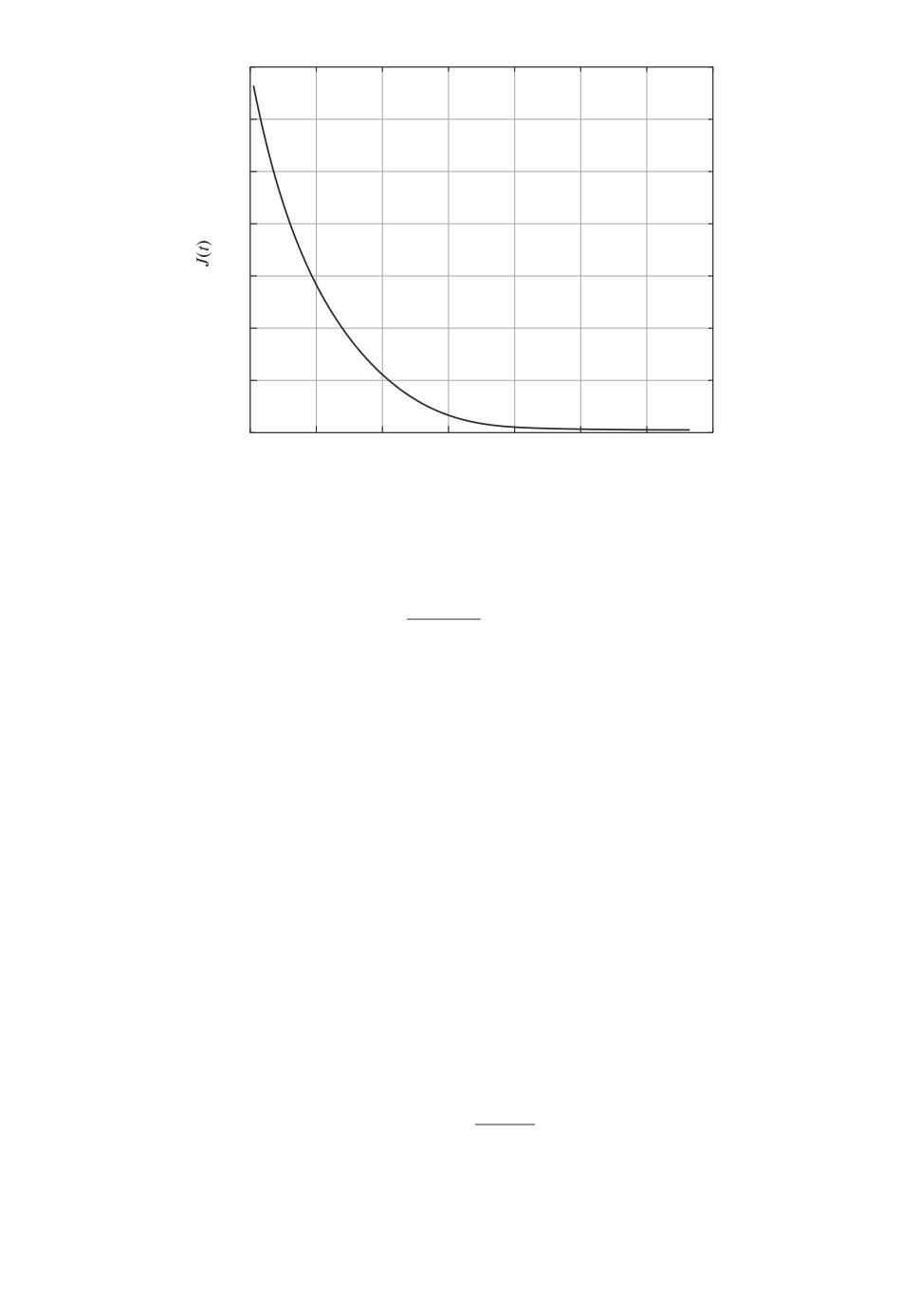
Рис. 4. Оптимизационная процедура в примере 2.

Пример 2. Рассмотрим передаточную функцию

1 - αs

G(s) =

α = 0,1.

(s + 1)²

Matlab-процедура tf2ss доставляет матрицы системы в пространстве со-

стояний:







-3 -3 -1

1

,b= 0,c= -0,1.

A= 1

Полагая ρ = 10, σ = 0,1 и выбрав

(

)

K₀ =

3,8710

6,1308

8,9234

в качестве начального стабилизирующего регулятора, при завершении опти-

мизационной процедуры получаем регулятор

(

)

K_∗ =

0,4010

0,1870

0,0382

доставляющий интегральной части функционала J(K) значение 8,5440, см.

рис. 4.

Передаточная функция ПИД-регулятора с коэффициентами K_∗ имеет вид

0,1870

GPID(s) = 0,4010 +

+ 0,0382s.

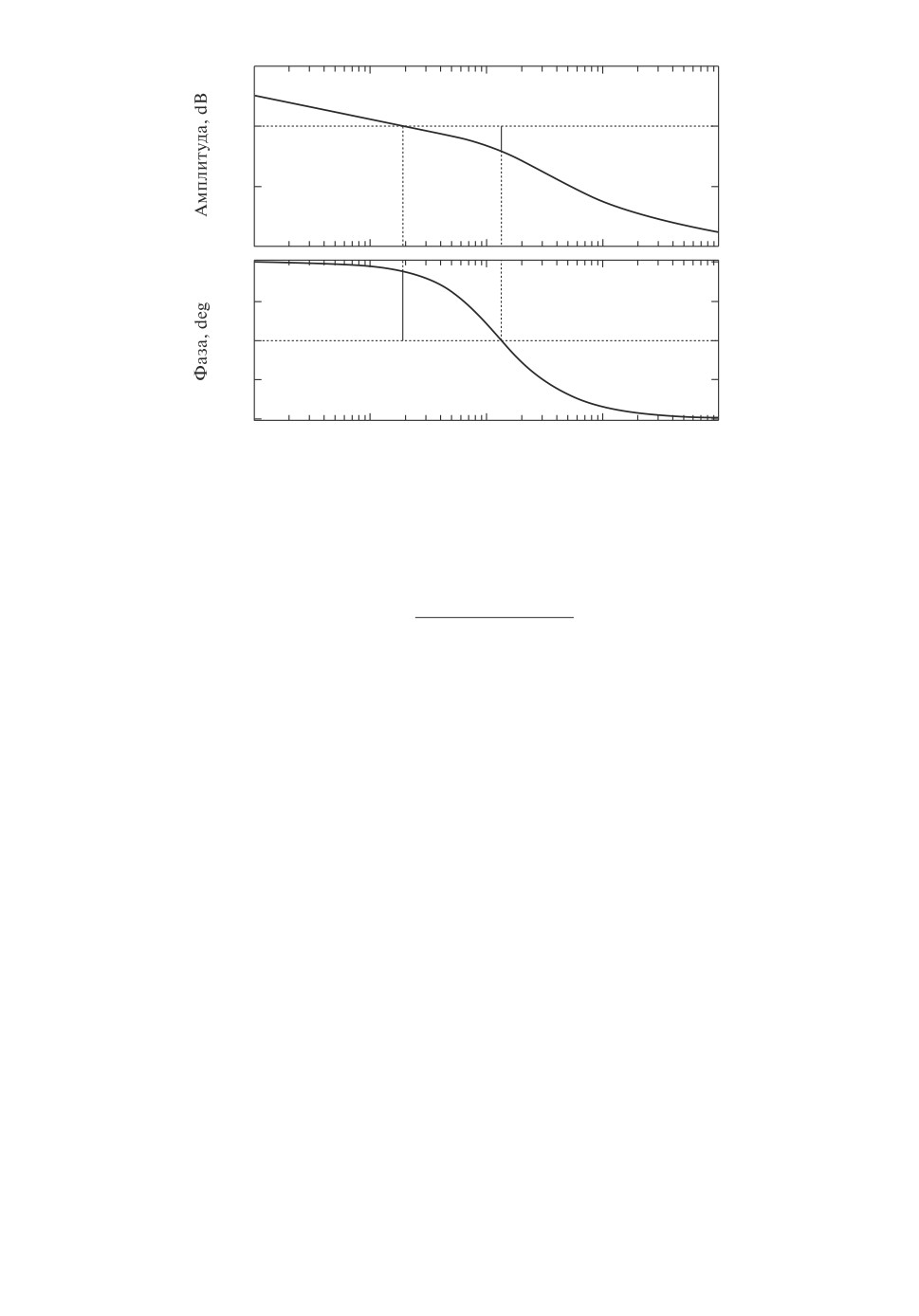
Замкнутая система с ПИД-регулятором K_∗ является устойчивой по крите-

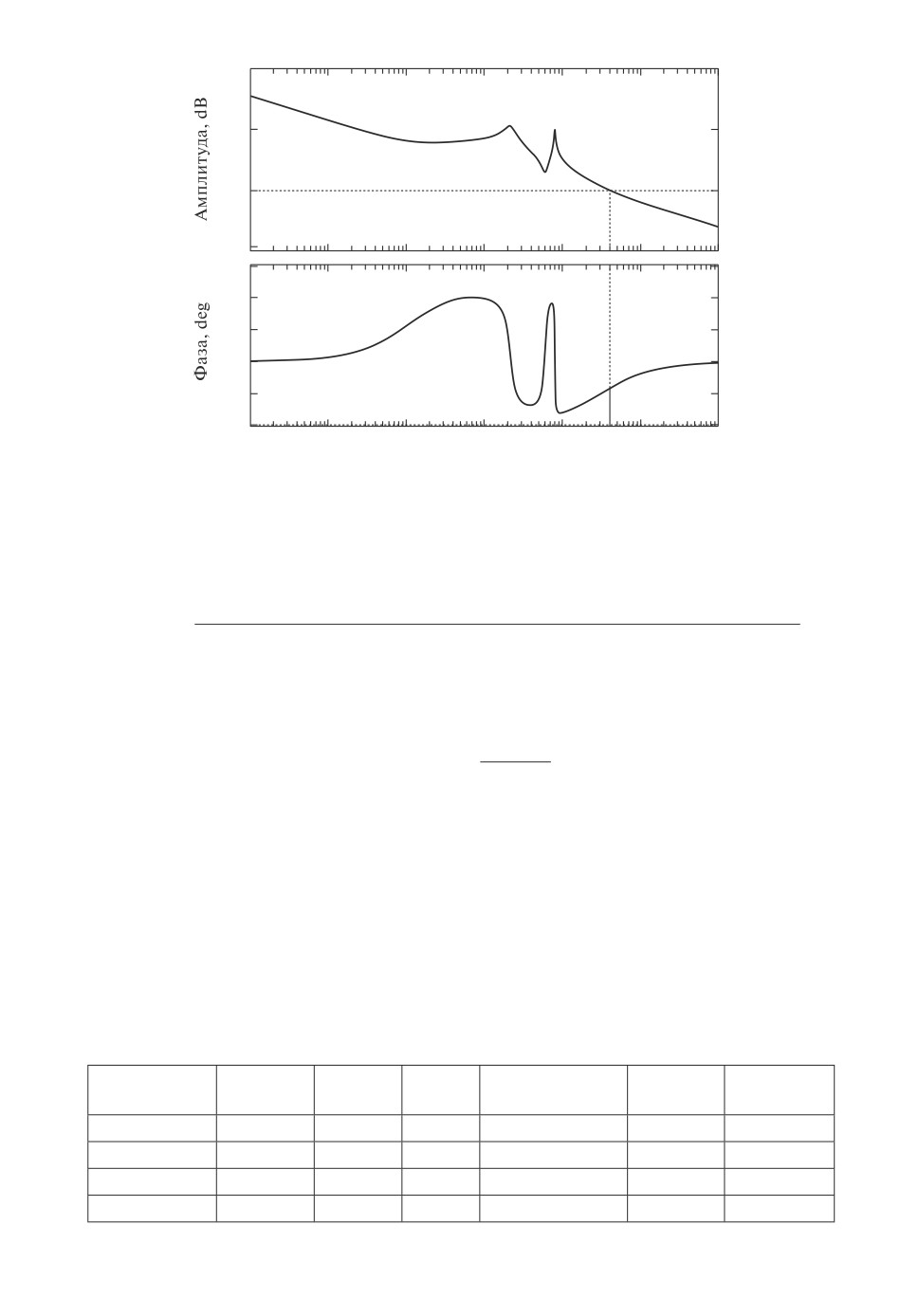
рию Найквиста; ее минимальный запас устойчивости по модулю составляет

21,1 дБ, а по фазе 78,9^◦, см. рис. 5.

-50

-100

270

225

180

135

10^-2

10^-1

10⁰

10¹

10²

Частота, rad/s

Рис. 5. ЛАФЧХ замкнутой системы из примера 2.

Пример 3. Рассмотрим передаточную функцию

(s + 6)

G(s) =

s(s + 1)²(s + 36)

Matlab-процедура tf2ss доставляет матрицы системы в пространстве со-

стояний:











-39 -111 -109 -36

1























0

,

0,

12.

При

ρ = 10, σ = 0,1,

и выборе в качестве начального стабилизирующего регулятора

(

)

K₀ =

10,1955

9,8265

2,4392

оптимизационная процедура приводит к регулятору

(

)

K_∗ =

6,7538

1,2114

2,2965

доставляющему интегральной части минимизируемого функционала значе-

ние 1,4774 · 10³.

Замкнутая система с ПИД-регулятором K_∗ является устойчивой по крите-

рию Найквиста; ее минимальный запас устойчивости по модулю бесконечен,

а по фазе равен 55,2^◦, см. рис. 6.

-20

-40

-60

-45

-90

-135

-180

-225

-270

10^-2

10^-1

10⁰

10¹

Частота, rad/s

Рис. 8. ЛАФЧХ замкнутой системы из примера 4.

Он доставляет интегральной части минимизируемого функционала значе-

ние 8,9878 и обладает минимальным запасом устойчивости по модулю 13,2 дБ,

а по фазе 76,2^◦, см. рис. 8.

Сравнение найденного регулятора с тремя ПИД/ПИ-регуляторами, пред-

ложенными для этого же примера в работах [28-30], представлено в табл. 2.

На рис. 9 показана динамика изменения выхода y(t) рассматриваемой си-

стемы при некотором начальном условии



-0,2456

-0,6435





x₀ =

-0,6921

-0,2161

из единичного шара: при замыкании найденным ПИД-регулятором K_∗ (жир-

ная линия) и регуляторами из табл. 2.

На рис. 10 показана динамика выхода y(t) рассматриваемой системы, за-

мкнутой найденным ПИД-регулятором K_∗ (жирная линия) и регуляторами

Таблица 2. Сравнение ПИД-регуляторов по интегральной части функционала

и запасам устойчивости для примера 4

∫

k_P

k_I

k_D E_x(0) y²(t)dt G_m (дБ) P_m (град)

Алгоритм 1

1,7408

0,2849

1,8615

8,9878

13,2

76,2

Из работы [28]

0,925

0,9

2,86

9,6715

14,87

43,0

Из работы [29]

0,83

0,318

0,3569

10,7752

14,34

62,5

Из работы [30]

1,031

0,3529

12,5559

17,25

96,2

100

-50

-45

-90

-135

-180

10^-3

10^-2

10^-1

10⁰

10¹

10²

10³

Частота, rad/s

Рис. 11. ЛАФЧХ замкнутой системы из примера 5.

Пример 5. Рассмотрим передаточную функцию

10s³ + 9s² + 362,4s + 36,16

G(s) =

2s⁵ + 2,7255s⁴ + 138,4292s³ + 156,471s² + 637,6472s + 360,1779

из статьи [7].

Предложенный алгоритм (при ρ = 0,001, σ = 0,01) дает ПИД-регулятор

75,9364

GPID(s) = 201,1057 +

+ 6,2735s,

доставляющий интегральной части минимизируемого функционала значение

1,0614 · 10³ и обладающий бесконечным запасом устойчивости по модулю и

запасом по фазе 52,2^◦, см. рис. 11.

Его сравнение с тремя ПИД-регуляторами, предложенными для рассмат-

риваемой системы в работе [8], представлено в табл. 3.

Синтезированный ПИД-регулятор обладает весьма удовлетворительными

характеристиками. На рис. 12 показана динамика изменения выхода y(t) рас-

Таблица 3. Сравнение ПИД-регуляторов по интегральной части функционала

и запасам устойчивости для примера 5

∫

k_P

k_I

k_D E_x(0) y²(t)dt G_m (дБ) P_m (град)

Алгоритм 1

201,1057

75,9364

6,2735

1,0614 · 10³

∞

52,2

#1 из [8]

185

2986

1,7338 · 10³

-10,2

60,8

#2 из [8]

800

1,3503 · 10⁴

-7,79

87,5

#3 из [8]

200

1,3769 · 10⁴

-10

78,6

На рис. 13 показана динамика выхода y(t) рассматриваемой системы, за-

мкнутой найденным ПИД-регулятором K_∗ (жирная линия) и регуляторами

из табл. 3 при единичном ступенчатом возмущении (и нулевом начальном

условии).

Таким образом, синтезированный ПИД-регулятор обладает вполне удовле-

творительными характеристиками.

6. Заключение

В статье рассмотрены только SISO-системы, однако предлагаемый под-

ход полностью может быть перенесен и на многомерный случай. При этом

выкладки становятся несколько более громоздкими, в то время как идейная

сторона меняется мало.

ПРИЛОЖЕНИЕ

Лемма П.1. Пусть X и Y решения двойственных уравнений Ляпуно-

ва с гурвицевой матрицей A:

A^TX + XA + W = 0 и AY + Y A^T + V = 0.

Тогда

tr XV = tr Y W.

Доказательство леммы П.1. В самом деле, прямым вычислением

имеем

(

)

tr (XV ) = tr

X(-AY - Y A^T)

= -tr(XAY ) - tr(XY A^T) =

= -tr(XAY )^T - tr(A^TXY )^T = tr(Y (-A^TX - XA)) = tr(Y W).

Лемма П.1 доказана.

Доказательство леммы 2. В уравнении (10) придадим величине K

приращение ΔK и обозначим соответствующее приращение Q через ΔQ:

(

)

cc^T

A^TK+ΔK(Q + ΔQ) + (Q + ΔQ)A_K+ΔK = -

или

)

(cc^T

(A_K + {A, ΔK})^T(Q + ΔQ) + (Q + ΔQ)(A_K + {A, ΔK}) = -

откуда после линеаризации имеем

(Π.1)

A^TKΔQ + ΔQA_K + Q{A,ΔK} + {A,ΔK}^T

Q = 0.

Вычислим приращение функционала f(K), линеаризуя соответствующие

величины:

)

(Σ 0

(Σ 0)

ΔJ(K) = tr (Q + ΔQ)

+ ρ|K + ΔK|² - tr Q

- ρ|K|² =

)

(Σ 0

= tr ΔQ

+ 2ρ(K, ΔK).

Рассмотрим уравнение Ляпунова (12), двойственное к (Π.1). По лемме П.1

из уравнений (Π.1) и (12) имеем

)

(Σ 0

ΔJ(K) = tr ΔQ

+ 2ρ(K, ΔK) = 2 tr Y Q{A, ΔK} + 2ρ(K, ΔK),

так что

∑

dJ(K) = 2 tr Y Q A_idk_i + 2ρ(K, dK),

i=1

откуда имеем (11). Лемма 2 доказана.

СПИСОК ЛИТЕРАТУРЫ

1. Ziegler J.B., Nichols N.B. Optimum Settings for Automatic Controllers // Transact.

ASME. 1942. V. 64. P. 759-768.

2. Visioli A. Practical PID Control. London: Springer-Verlag, 2006.

Åström K.J., Hägglund T. PID Controllers: Theory, Design, and Tuning. Research

Triangle Park: Instrument Society of America, 1995.

Åström K.J., Hägglund T. Advanced PID Control. Research Triangle Park: The

Instrumentation, Systems, and Automation Society, 2006.

5. Bhattacharyya S.P., Keel L.H. Linear Multivariable Control Systems. Cambridge

University Press, 2022.

6. Wang Q.-G., Ye Z., Cai W.-J., Hang C.-C. PID Control for Multivariable Processes.

Berlin: Springer, 2008.

7. Blanchini F., Lepschy A., Miani S., Viaro U. Characterization of PID and Lead/Lag

Compensators Satisfying Given H_∞ Specifications // IEEE Transact. Autom. Con-

trol. 2004. V. 49. No. 5. P. 736-740.

8. Han S., Keel L.H., Bhattacharyya S.P. PID Controller Design with an H^∞ Crite-

rion // IFAC-PapersOnLine. 2018. V. 51. No. 4. P. 400-405.

9. Киселев О.Н., Поляк Б.Т. Cинтез регуляторов низкого порядка по критерию H^∞

и по критерию максимальной робастности // АиТ. 1999. № 3. С. 119-130.

Kiselev O.N., Polyak B.T. Design of Low-Order Controllers by the H^∞-criterion and

Maximum-Robustness Performance Indices // Autom. Remote Control. 1999. V. 60.

No. 3. P. 393-402.

10.

Грязина Е.Н., Поляк Б.Т., Тремба А.А. Синтез регуляторов низкого порядка по

критерию H_∞: параметрический подход // АиТ. 2007. № 3. С. 94-105.

Gryazina E.N., Polyak B.T., Tremba A.A. Design of the Low-Order Controllers by

the H_∞ Criterion: A Parametric Approach // Autom. Remote Control. 2007. V. 68.

No. 3. P. 456-466.

11.

Kalman R.E. Contributions to the Theory of Optimal Control // Boletin de la So-

ciedad Matematica Mexicana. 1960. V. 5. No. 1. P. 102-119.

12.

Levine W., Athans M. On the Determination of the Optimal Constant Output Feed-

back Gains for Linear Multivariable Systems // IEEE Trans. Automat. Control.

1970. V. 15. No. 1. P. 44-48.

13.

Mäkilä P.M., Toivonen H.T. Computational Methods for Parametric LQ Problems -

A Survey // IEEE Trans. Automat. Control. 1987. V. 32. No. 8. P. 658-671.

14.

Fazel M., Ge R., Kakade S., Mesbahi M. Global Convergence of Policy Gradient

Methods for the Linear Quadratic Regulator // Proc. 35th Int. Conf. Machine Learn-

ing. Stockholm, Sweden, July 10-15, 2018. V. 80. P. 1467-1476.

15.

Mohammadi H., Zare A., Soltanolkotabi M., Jovanović M.R. Global Exponential

Convergence of Gradient Methods Over the Nonconvex Landscape of the Linear

Quadratic Regulator // Proc. 2019 IEEE 58th Conf. Decision Control. Nice, France,

December 11-13, 2019. P. 7474-7479.

16.

Zhang K., Hu B., Basar T. Policy Optimization for H₂ Linear Control with H_∞

Robustness Guarantee: Implicit Regularization and Global Convergence // arXiv:

1910.09496, 2020.

17.

Bu J., Mesbahi A., Fazel M., Mesbahi M. LQR through the Lens of First Order

Methods: Discrete-Time Case // arXiv:1907.08921, 2019.

18.

Fatkhullin I., Polyak B. Optimizing Static Linear Feedback: Gradient Method //

SIAM J. Control Optim. 2021. V. 59. No. 5. P. 3887-3911.

19.

Поляк Б.Т., Хлебников М.В. Синтез статического регулятора для подавления

внешних возмущений как задача оптимизации // АиТ. 2021. № 9. С. 86-115.

Polyak B.T., Khlebnikov M.V. Static Controller Synthesis for Peak-to-Peak Gain

Minimization as an Optimization Problem // Autom. Remote Control. 2021. V. 82.

No. 9. P. 1530-1553.

20.

Поляк Б.Т., Хлебников М.В. Синтез обратной связи по выходу при помощи на-

блюдателя как задача оптимизации // АиТ. 2022. № 3. С. 7-32.

Polyak B.T., Khlebnikov M.V. Observer-Aided Output Feedback Synthesis as an

Optimization Problem // Autom. Remote Control. 2022. V. 83. No. 3. P. 303-324.

21.

Грязина Е.Н., Поляк Б.Т., Тремба А.А. Современное состояние метода D-раз-

биения // АиТ. 2008. № 12. С. 3-40.

Gryazina E.N., Polyak B.T., Tremba A.A. D-Decomposition Technique State-of-the-

art // Autom. Remote Control. 2008. V. 69. No. 12. P. 1991-2026.

22.

Шатов Д.В. Синтез параметров пропорционально-интегрирующих и пропор-

ционально-интегрально-дифференцирующих регуляторов для стационарных

линейных объектов с ненулевыми начальными условиями // Известия РАН.

Теория и системы управления. 2023. № 1. (в печати)

23.

Åström K.J., Hägglund T. Benchmark Systems for PID Control // IFAC Proceedings

Volumes. 2000. V. 33. Iss. 4. P. 165-166.

24. Geem Z.W., Kim J.H., Loganathan G.V. A New Heuristic Optimization Algorithm:

Harmony Search // Simulation. 2002. V. 76. No. 2. P. 60-68.

25. Pham D.T., Sholedolu M. The Bees Algorithm with Attraction to Global Best So-

lutions // Proc. 5th I*PROMS International Virtual Conference on Innovative Pro-

duction Machines and Systems (IPROMS 2009). Cardiff, UK, July 6-17, 2009.

26. Karaboga D. An Idea Based on Honey Bee Swarm for Numerical Optimization. Tech-

nical Report TR06. Erciyes University, 2005.

27. Karaboga D., Akay B. Proportional-Integral-Derivative Controller Design by Using

Artificial Bee Colony, Harmony Search, and the Bees Algorithms // Proceedings

of the Institution of Mechanical Engineers. Part I: J. Syst. Control Engineer. 2010.

V. 224. No. 7. P. 869-883.

28. Panagopoulos H.,

Åström K.J., Hägglund T. Design of PID Controllers Based on

Constrained Optimization // Proc. 1999 American Control Conference. San Diego,

USA, June 2-4, 1999. V. 6. P. 3858-3862.

29. Li Y., Ang K.H., Chong G.C.Y. PID Control System Analysis and Design // IEEE

Control Syst. Magaz. 2006. V. 26. No. 1. P. 32-41.

30. Leva A., Papadopoulos A.V. Tuning of Event-Based Industrial Controllers with Sim-

ple Stability Guarantees // J. Process Control. 2013. V. 23. P. 1251-1260.

Статья представлена к публикации членом редколлегии Л.Б. Рапопортом.

Поступила в редакцию 15.05.2022

После доработки 20.07.2022

Принята к публикации 28.07.2022