Автоматика и телемеханика, № 11, 2022

Стохастические системы

(Федеральный исследовательский центр

“Информатика и управление” РАН, Москва)

L₁-ОПТИМАЛЬНАЯ ФИЛЬТРАЦИЯ МАРКОВСКИХ

СКАЧКООБРАЗНЫХ ПРОЦЕССОВ III:

ИДЕНТИФИКАЦИЯ ПАРАМЕТРОВ СИСТЕМЫ¹

Работа является продолжением цикла статей [1, 2] и посвящена реше-

нию задачи оценивания параметров скрытых марковских моделей. В ка-

честве скрытого состояния выступает однородный марковский скачкооб-

разный процесс с конечным множеством состояний. Доступные наблюде-

ния являются косвенными и содержат винеровские процессы, интенсив-

ности которых различны и зависят от скрытого состояния. Оцениванию

подлежат как матрица интенсивностей переходов марковского состояния,

так и параметры сноса и диффузии наблюдений. Для идентификации

предложен итеративный алгоритм, основанный на сглаживании состоя-

ния системы по наблюдениям на фиксированном интервале времени. За-

тем по данным оценкам восстанавливаются параметры. В работе детально

описаны все численные схемы оценивания состояния и идентификации па-

раметров. Приведен комплекс иллюстративных численных примеров, де-

монстрирующих высокое качество предлагаемых оценок идентификации.

Ключевые слова: скрытая марковская модель, мультипликативные шумы

в наблюдениях, сглаживание на фиксированном интервале наблюдения,

L₁-оптимальная оценка, ЕМ-алгоритм.

DOI: 10.31857/S0005231022110058, EDN: KEKCHY

1. Введение

Проблемам идентификации параметров систем наблюдения, состояния ко-

торых описываются марковскими процессами с конечным множеством воз-

можных состояний, скоро исполнится 60 лет [3, 4]. Несмотря на возраст, тео-

ретические решения и алгоритмы их реализации [5-7] не теряют своей акту-

альности из-за своей востребованности для решения широкого спектра при-

кладных задач системного анализа. Другой причиной неослабевающего вни-

мания к проблемам идентификации является постоянное расширение клас-

сов систем наблюдения и моделей доступной измерительной информации.

¹ Работа выполнена с использованием инфраструктуры Центра коллективного пользо-

вания “Высокопроизводительные вычисления и большие данные” (ЦКП “Информатика”)

ФИЦ ИУ РАН, Москва.

121

К настоящему времени существуют оценки параметров марковских цепей по

наблюдениям с аддитивными и мультипликативными шумами [8], а также

марковских скачкообразных процессов (МСП) по непрерывным косвенным

наблюдениям в присутствии аддитивных винеровских процессов [9-11].

Целью данной статьи является разработка нового алгоритма идентифика-

ции параметров скрытых марковских моделей (СММ) с непрерывным време-

нем по наблюдениям, шумы в которых зависят от скрытого состояния. Обыч-

но такие шумы называют мультипликативными. Задачи оценивания состоя-

ний и параметров систем по наблюдениям такого типа исследуются доста-

точно редко из-за известных теоретических сложностей [12, 13]. Корректная

постановка и формальное решение задачи оптимальной фильтрации состоя-

ний МСП по диффузионным наблюдениям с мультипликативными шумами

совместно с реализующим его комплексом численных методов представлены

в [1, 2]. Данная статья является естественным продолжением этих исследо-

ваний.

Работа организована следующим образом. Раздел 2 содержит описание ис-

следуемой системы наблюдения и постановку задачи идентификации ее па-

раметров. Раздел включает сравнение различных СММ, для которых задача

идентификации решалась с помощью ЕМ-алгоритма. В разделе также пред-

ставлены доводы в пользу предлагаемого алгоритма идентификации. Они

основываются на возможности построения для исследуемых СММ высоко-

точных оценок сглаживания на фиксированном интервале для скрытого со-

стояния в случае выполнения некоторых необременительных условий иден-

тифицируемости. В разделе 3 представлен численный алгоритм двухфиль-

трового сглаживания, позволяющий получить искомую сглаженную оценку

в виде некоторой комбинации оценок фильтрации состояния МСП в прямом

и обратном времени.

Раздел 4 посвящен алгоритмам фильтрации состояний МСП в прямом

и обратном времени по диффузионным наблюдениям, предварительно дис-

кретизованным по времени. В контексте работы численные алгоритмы оце-

нивания состояния МСП называются устойчивыми, если они гарантируют

доставляемым оценкам выполнение условий неотрицательности компонент

и нормировки. Например, численный алгоритм фильтрации, основанный на

схеме Эйлера-Маруямы решения стохастической дифференциальной систе-

мы (СДС), описывающей фильтр Вонэма, не обеспечивает выполнения этих

условий: как только они нарушаются, вычисленные по данной схеме оценки

“взрываются”. Именно в контексте этого явления предложенные алгоритмы

названы устойчивыми.

Вычисление сглаженных оценок состояния представляет собой E-шаг в

EM-процедуре. М-шаг и вся процедура идентификации описаны в разделе 5.

В нем представлены формулы пересчета L₂-оптимальных оценок сглажи-

вания в L₁-оптимальные, а также формулы вычисления функционалов от

траекторий наблюдений и оценок МСП, на основании которых собственно и

122

вычисляются оценки параметров СММ. Предложенные в работе алгоритмы

оценивания состояния МСП и идентификации параметров СММ названы эф-

фективными в том смысле, что они не являются сеточными. При решении

задач оценивания состояния МСП это означает, что алгоритмы не требуют

решения стохастических дифференциальных уравнений в частных производ-

ных типа Закаи или Кушнера-Стратоновича. При решении задачи иденти-

фикации это означает, что алгоритм не привлекает аппарат байесовского оце-

нивания и описания оцениваемых параметров с помощью их вероятностного

распределения. С вычислительной точки зрения это означает, что эффек-

тивные алгоритмы используют радикально меньше оперативной памяти и

требуют меньше вычислений для своей реализации.

Раздел 6 содержит результаты комплекса иллюстративных вычислитель-

ных экспериментов. Проведен численный анализ качества оценок фильтра-

ции в прямом и обратном времени состояния МСП в сравнении с оценками

сглаживания на фиксированном интервале наблюдения. Сравнение проведе-

но для случая известных параметров СММ. Представлены результаты оцени-

вания параметров СММ, выполненного с помощью предложенного алгоритма

идентификации. Исследовано качество последующей фильтрации скрытого

состояния МСП с использованием идентифицированных параметров в срав-

нении с “идеальным вариантом”: фильтрацией состояний при точно извест-

ных параметрах системы наблюдения. Раздел 7 содержит заключительные

замечания.

2. Постановка задачи

На триплете с фильтрацией (Ω, F, P, {F}_t∈[0,T]) рассматривается СММ

∫t

(1)

X_t = X₀ + Λ^⊤X_sds + M^Xt

t ∈ [0,T],

∫tr

∫

∑

(2)

Y_r = fX_sds+

n dWs, r ∈ {1, . . . , R}, tr

= rδ, T = Rδ,

n=1

tr-1

где

• X_t = col(X1t ,...,X^Nt) ∈ S^N

ненаблюдаемое состояние, являющееся

однородным МСП с конечным множеством состояний S^N ≜ {e₁, . . . , e_N }

(S^N

множество единичных векторов евклидова пространства R^N ),

матрицей интенсивностей переходов (МИП) Λ и начальным распределе-

нием π = col (π¹, . . . , π^N ); процесс M^Xt является F_t-согласованным мар-

тингалом,

• Y_r = col(Y^1r,...,Y^Mr) ∈ R^M диффузионные наблюдения

∫t

∫

∑

(3)

Y_t = fX_sds +

n dWs,

n=1

123

дискретизованные по времени с шагом δ; W_t = col (W¹

,...,W^Mt)∈R

является F_t-согласованным стандартным винеровским процессом, ха-

рактеризующим шумы в наблюдениях, M × N-мерная матрица f и на-

бор M × M-мерных матриц {g_n}_n=1,N определяют снос и интенсивность

шумов при условии X_t = e_n.

Ниже в изложении неубывающее семейство σ-подалгебр, порожденных

наблюдениями Y, полученными до момента времени t_r, обозначено Y_r ≜

≜ {Y_q : q = 1, r}, Y₀ ≜ {∅, Ω}.

Для системы наблюдения (1)-(2) предполагаются выполненными следую-

щие условия.

1. Триплет с фильтрацией (Ω, F, P, {F}_t∈[0,T]) является пространством

Винера-Пуассона [15].

2. Все параметры СММ Λ, f и {g_n}_n=1,N являются неизвестными неслу-

чайными матрицами подходящей размерности.

3. Матрица Λ удовлетворяет условию min λ^ij > 0, а также обычному тож-

i,j: i=j

∑

деству МИП:_j λ^ij ≡ 0.

4. Шумы в наблюдениях Y равномерно невырождены [16], т.е. min

g_n >

1≤n≤N

> αI > 0 для некоторого α > 0; здесь и далее I единичная матрица подхо-

дящей размерности.

5. Набор матриц интенсивностей шумов {g_n}_n=1,N удовлетворяет условию

идентифицируемости [14], заключающемуся в том, что все g_n различны.

Задача идентификации СММ заключается в построении оценок парамет-

ров Λ, f и {g_n}_n=1,N по имеющимся наблюдениям {Y₁, . . . , Y_R}.

Поставленная задача представляет собой аппроксимацию аналогичной за-

дачи идентификации по исходным диффузионным наблюдениям (1), (3).

В [9, 10] исследовалась схожая проблема. Наблюдения были скалярными с

аддитивными винеровскими процессами (т.е. g_n ≡ g = I). Авторы представи-

ли процедуру совместной фильтрации состояния МСП и идентификации па-

раметров, основанной на применении EM-алгоритма. Собственно процедура

идентификации параметров требовала оценки числа скачков МСП e_i → e_j

(i = j)

∫t

(4)

N^i,jt = X^is-dX^js,

а также суммарного времени пребывания МСП в различных состояниях e_i

∫t

(5)

O^it = X^is

ds, i = 1, N .

В монографии [8] был исследован аналог системы (1), (3) с дискретным

временем. В качестве доступных наблюдений выступал векторный процесс

124

с мультипликативным шумом. Авторы модифицировали ЕМ-алгоритм, ис-

пользуя в нем не оценки фильтрации функционалов {N^i,jt }, {O^it}, а их бо-

лее точные аналоги, полученные сглаживанием на фиксированном интервале

наблюдений, а также оценки дополнительных функционалов т.н. “уровневых

сумм” (level sums):

∫t

(6)

Q^i,qt = X^isq(Y_s)dY_s,

где q = q(y) некоторая детерминированная функция. Статья [11] была по-

священа алгоритмам численной реализации решения задачи идентификации

параметров СММ с дискретным временем по скалярным наблюдениям с ад-

дитивными шумами неизвестной интенсивности (g_n ≡ g неизвестный ска-

ляр). Идентификация в этом случае также проводилась с использованием

оценок функционалов {N^i,jt }, {O^it} и {Q^i,qt}, вычисленных на фиксированном

интервале наблюдений.

В [14] представлено решение задачи оптимальной фильтрации состояния

МСП по векторным диффузионным наблюдениям с мультипликативными

шумами. Предложено некоторое преобразование, разбивающее исходные на-

блюдения на совокупность диффузионных процессов с единичной диффузи-

ей, а также набор считающих процессов и случайных векторов, доступных в

неслучайные моменты времени. Аналитическое решение задачи фильтрации

представлено в виде решения некоторой дискретно-непрерывной нелинейной

СДС с непрерывными и считающими процессами в правой части. В статье

показано, что выполнение условия идентифицируемости 5) достаточно для

точного восстановления состояния МСП по имеющимся зашумленным на-

блюдениям.

К сожалению, решение указанной СДС не удается реализовать численно

с помощью известных классических методов [17] из-за того, что упомянутое

преобразование наблюдений представляет собой результат двойного предель-

ного перехода, примененного к исходным наблюдениям. Чтобы избежать чис-

ленной реализации данной операции в [2] было предложено перейти к филь-

трации по наблюдениям, предварительно дискретизованным по времени. Был

представлен комплекс соответствующих численных алгоритмов, а также ха-

рактеристики точности соответствующих оценок. Следует отметить, что оце-

ниванию в [2] подвергалось только само состояние МСП X_t, а не процессы

{N^i,jt}, {O^it} и {Q^i,qt}, участвующие в процедуре идентификации. Идея пред-

лагаемой статьи заключается в том, чтобы строить оценки этих процессов не

непосредственно путем обработки дискретизованных наблюдений, а на осно-

ве полученных оптимальных оценок сглаживания состояния X_t.

В статье используются следующие обозначения:

• 1

вектор-строка подходящей размерности, состоящая из единиц,

• I_A(x) индикаторная функция множества A,

• ∥α∥^2K ≜ α^⊤Kα,

125

• N^Xr случайное число скачков состояния X_t, произошедших на интер-

вале времени [t_r-1, t_r],

∫ tr

• τ_r = col(τ^1r,...,τ^Nr) ≜

X_sds случайный вектор, компоненты τ^nr

tr-1

которого равны времени пребывания процесса X в каждом из возможных

состояний e_n на интервале [t_r-1, t_r],{

}

∑

• D ≜ u = col(u¹,...,u^N) : uⁿ ≥ 0,

uⁿ = h

(N - 1)-мерный сим-

n=1

плекс в пространстве R^N ; D является носителем распределения векто-

ра τ_r{

}

∑

• Π ≜ π = col(π¹,...,π^N) : πⁿ ≥ 0,

πⁿ = 1

“вероятностный сим-

n=1

плекс”, содержащий возможные значения начального распределения π,

• ρ^r,ℓ(du)

условное распределение вектора Xℓtr τ_r при условии Xtr-1 =

= e_k, т.е. для любого множества G ∈ B(R^N) верно равенство

{

}

∫

E I_G(τ_r)X^ℓ

|Xtr-1 = e_k

= ρ^k,ℓr(du),

• ρ^r,ℓ,q(du)

условное распределение вектора Xℓtr I_{q}(N^Xr )τ_r при условии

Xtr-1 = e_k, т.е. для любого множества G ∈ B(R^N) верно равенство

∫

{

}

E I_G(τ_r)I_{q}(N^Xr)X^ℓ

|Xtr-1 = e_k

= ρ^k,ℓ,qr(du),

• ̺^r,ℓ(du)

условное распределение вектора Xℓtr τ_r+1 при условии

Xtr+1 = e_k, т.е. для любого множества G ∈ B(R^N) верно равенство

{

}

∫

E I_G(τ_r+1)X^ℓ

|Xtr+1 = e_k

̺^k,ℓr(du),

• ̺^r,ℓ,q(du)

условное распределение вектора Xℓtr I_{q}(N^Xr+1)τ_r+1 при усло-

вии Xtr+1 = e_k, т.е. для любого множества G ∈ B(R^N ) верно равенство

{

}

∫

E I_G(τ_r+1)I_{q}(N^Xr+1)X^ℓ

|Xtr+1 = e_k

̺^k,ℓ,qr(du),

{

}

• N (y,m,K) ≜ (2π)^-M/2 det^-1/2 K exp

∥y - m)∥²

M -мерная

K^-1

гауссовская плотность со средним m и невырожденной ковариационной

матрицей K,

(

)

• ξ ≜ vec(Λ,f,{g_n}_1,N)

N (N - 1) + NM + NM²

-мерный вектор оцени-

ваемых параметров СММ,

• Y_t ≜ σ{Y_s, 0 ≤ s ≤ t}

естественный поток σ-алгебр, порожденный

непрерывными наблюдениями Y_s, полученными до момента времени t

включительно.

126

3. Вспомогательная задача: сглаживание

на фиксированном интервале наблюдения

Предлагаемый алгоритм идентификации параметров СММ основан на

итеративном вычислении оценок {Xsr}_r=1,R:

≜ E {Xtr|Y_R} сглаживания

на фиксированном интервале наблюдения [0, T ]. Для эффективной реализа-

ции этой процедуры предлагается использовать двухфильтровую процедуру

сглаживания [18-20].

Во-первых, представим алгоритм вычисления оптимальной оценки филь-

трации в прямом времениXr ≜ E {Xtr |Y_r}.

Для этого введем в рассмотрение следующие положительные случайные

числа и матрицы, составленные из них:





∫

∑

(7)

θ^kjr ≜ N Y_r,fu,

u^pgp ρk,jr(du),

θ_r ≜ ∥θ^kjr∥_k,j=1,N.

p=1

Предложение 1. Условное математическое ожидание (УМО)Xr вы-

числяется по рекуррентной формуле

X₀

(8)

X_r = (1θ^⊤r X_r-1)^-1θ^⊤r X_r-1, r > 0,

= π.

Доказательство предложения 1 вполне аналогично доказательству лем-

мы 2 в [1].

Во-вторых, предложим мартингальное представление МСП X_t в обратном

времени, а также формулы вычисления оптимальной оценки фильтрации со-

стояния МСП в обратном времени.

На исходном вероятностном пространстве (Ω, F, P) рассмотрим

• поток σ-алгебр {F^rt}_t∈[0,T] в обратном времени: F^rt ≜ σ{X_s, Y_T -Y_s : t ≤

≤ s ≤ T};

• набор дискретизованных наблюдений, Y^br ≜ σ{Y_q : r < q ≤ R}; Y^bR ≜

≜ {∅, Ω}, полученных на интервале времени (t_r, T ].

Благодаря условию 3) компоненты распределения МСП π(t) = E {X_t},

являющегося единственным решением системы уравнений Колмогорова

∫t

π(t) = π +

Λ^⊤π(s)ds, строго положительны πⁿ(t) > 0 для любых n = 1,N и

t > 0 [16]. Поэтому можно корректно определить матричнозначную функцию

-1

(9)

Γ(t) ≜

diag π(t)Λ^⊤diag π(t) -

diag π(t)diag (Λ^⊤

π(t)),

являющуюся МИП процесса X_t в обратном времени.

Предложение 2. МСП X_t (1) является единственным сильным реше-

нием следующей стохастической системы в обратном времени





∫T

∫

(10)

X_t = X_T + Γ^⊤(s)X_sds + M^Xt - M^XT - (Γ(s) + Λ)^⊤ X_sds.

127

Процесс

∫T

M^bXt ≜ M^Xt - M^XT - (Γ(s) + Λ)^⊤ X_sds

представляет собой F^rt-согласованный квадратично интегрируемый мар-

тингал:

{

}

E M^bXt|F^r

= M^bXs P - п.н. для любых 0 ≤ t ≤ s ≤ T.

Доказательство предложения 2 приведено в [19, 21].

Для вычисления оценки фильтрации в обратном времени по аналогии с

прямым временем определим следующие положительные случайные величи-

ны и матрицы из них:





∫

∑

(11)

ϑ^kjr ≜ N Y_r+1,fu,

u^pgp ̺k,jr(du),

ϑ_r ≜ ∥ϑ^kjr∥_k,j=1,N.

p=1

{

}

Можно показать, что оценка фильтрации

≜E

Xtr |Y^br

состояния

МСП в обратном времени может быть вычислена с помощью рекуррентного

алгоритма аналога (8)

(12)

= (1ϑ^⊤r X^br+1)^-1ϑ^⊤r X_r+1, r < R,

= π(T).

В-третьих, оптимальная оценка сглаживания на фиксированном интер-

вале наблюдения может быть получена как симметричное преобразование

оценок фильтрации в прямом и обратном времени.

П р е д л о ж е н и е 3. Оптимальная оценка сглаживания

= col ( X1sr, . . . , XNsr) = E {Xtr |Y_R}, r = 0, R поэлементно определяется фор-

мулой

Xns

(13)

n = 1,N,

∑_N

X^js

j=1

где ненормированная оценкаXsr ≜ col ( X^1sr, . . . , X^Nsr) является функцией оце-

нок фильтрации в прямомXr и обратномXbr времени, а также априорного

распределения π(t_r):

Xnb

Xns

(14)

n = 1,N, r = 1,R.

πⁿ(t_r)

Доказательство предложения 3 аналогично доказательству теоремы 4

в [20].

128

4. Численный алгоритм решения задачи фильтрации

Ни условное распределение ρ^k,ℓ в прямом времени, ни его аналог ̺^k,ℓ в

обратном времени не являются абсолютно непрерывными по мере Лебега,

поэтому вычисление интегралов (7) и (11) является нетривиальной задачей.

По формуле полной вероятности









∫

∑

θ^kjr ≜ N Y_r,fu,

u^pgpρk,jr(du) =

NY_r,fu, u^pgpρk,j,qr(du).

p=1

q=0 D

Явный вид отдельных слагаемых ρ^k,ℓ,q представлен в [2] для q = 0, 1, 2, об-

щий же вид может быть выведен также с использованием формулы полной

вероятности. Было показано, что в этом нет необходимости: при достаточно

малом шаге δ бесконечная сумма в последней формуле хорошо аппрокси-

мируется первыми двумя слагаемыми (q = 0 и 1). В этом случае оценкаXr

приближается аналитической аппроксимацией порядка 1 :

(15)

Xr = (1κ^rXr-1)^-1κ^rXr-1, r > 0,

X₀

= π,

где





∫

∑

(16)

κ^kjr ≜

NY_r,fu, u^pgp ρk,j,qr(du),

κ_r ≜ ∥κ^kjr∥_k,j=1,N.

q=0D

p=1

Данное приближение учитывает не более одного скачка МСП на интервале

дискретизации [t_r-1, t_r]. Если λ ≜ max

|λ_nn|, и шаг δ так мал, что λδ < 1, то

1≤n≤N

(см. [2])

∑

(λδ)^k

(17)

C ≜e^-λδ

< 1,

(λδ)²

k=2

и точность аппроксимации характеризуется неравенством

(

)_r

{



}



(λδ)²

X

r -^Xr



≤2-2

1-C

∼ λ²δt_r при δ → 0.

Элементы κ^rj имеют следующий явный вид:

∫

(18)

κ^kjr = δ_kjeλjjδN(Y_r,δf^j,δg_j) + (1 - δ_kj)λ_kjeλjjδ V^kj(Y_r

, u)du,

где δ_kj

символ Кронекера, а

(

)

(19)

V kj(y,u) ≜ e(λkk-λjj)uN y,uf^k + (δ - u)f^j

, ug_k + (δ - u)g_j

129

Интеграл в (18), а вместе с ним и вся аппроксимация X_r не могут быть

вычислены аналитически, поэтому их приходится находить численно, вно-

ся дополнительную ошибку. Для этого предлагается использовать составной

метод средних прямоугольников с малым шагом δ^1+α, α > 0:

(20) κ^kjr ≈ ψ^kjr ≜ δ_kj eλjj δN (Y_r, δf^j , δg_j ) +

[δ^-α]∑

(

))

+ (1 - δ_kj )λ_kjδ1+α

Vkj Y_r,δ1+α i-

i=1

Используя обозначения ψ_r ≜ ∥ψ^rj ∥_k,j=1,N , можно представить численную ап-

проксимацию порядка min(α,1), основанную на составной схеме средних пря-

моугольников

(21)

X_r = (1ψ^⊤r X_r-1)^-1ψ^⊤r X_r-1, r > 0,

X₀

= π.

Суммарная ошибка аппроксимацииXr характеризуется следующим нера-

венством [2]:

{



}



X

r -Xr



≤ C₁(δ + C₂δ^α)t_r

для некоторых положительных констант C₁ и C₂. Из этого неравенства следу-

ет, что рациональным с точки зрения точности выбором параметра α будет 1.

Все рассуждения выше относились к аппроксимации оценки фильтрации

в прямом времени. Данный подход может быть применен и при вычислении

оценки фильтрации в обратном времени. Как и в случае прямого течения

времени предполагается, что на интервале временной дискретизации состоя-

ние МСП может совершить не более одного скачка. При этом приходится

учитывать тот факт, что МСП X_t в обратном времени в общем случае не

обладает свойством однородности. Аналог формулы (18) принимает вид

_t



∫

(22) ζ^kjr = δ_kj exp 

γ_kk(u)du N(Y_r+1,δf^k,δg_k) +

∫δ

+ (1 - δ_kj) U^kjr(Y_r+1, u)du,

где





∫

(23) U^kjr(y, u) ≜ γ_kj(u) exp  γ_kk(s)ds +

γ_jj(s)ds ×

(

)

× N y,uf^k + (δ - u)f^j

, ug_k + (δ - u)g_j

130

Формулы (22) и (23) содержат интегралы, которые вновь приближенно вы-

числяются по составной схеме средних прямоугольников

(

(t_r +t_r+1))

(24) ζ^kjr ≈ φ^kj

= δ_kj exp δγ_kk

[δ^-α]∑

(

))

+ (1 - δ_kj)δ1+α

U^kj Y_r+1,δ1+α i-

i=1

где

(25)

U^kjr(y,u) ≜

(

(u+t_r)

(u+t_r+1))

≜ γ_kj(u)exp (u - t_r)γ_kk

+ (t_r+1 - u)γ_jj

(

)

× N y,uf^k + (δ - u)f^j, ugk + (δ - u)gj

Используя матрицы φ_r ≜ ∥φ^rj ∥_k,j=1,N , можно представить численную ап-

проксимацию порядка min(α, 1), основанную на составной схеме средних пря-

моугольников для фильтра в обратном времени

(26)

= (1φ^⊤r X^br+1)^-1φ^⊤r X^br+1, r < R,

= π(T).

Таким образом, искомая оценкаXsr сглаживания состояния МСП Xtr на фик-

сированном интервале наблюдений вычисляется по формулам (13), (14), в

которых оценки фильтрацииX иXb заменены их аппроксимациямиX (21)

и X^b (26).

5. Алгоритм идентификации параметров

скрытой марковской модели

Перед представлением алгоритма идентификации параметров СММ при-

ведем некоторые наводящие соображения.

Рассмотрим СММ с непрерывным временем (1), (3), в которой оба процес-

са X_t и Y_t являются наблюдаемыми. По усиленному закону больших чисел

для МСП [22] и процессов восстановления [23] имеет место следующая схо-

димость:

N^ijT

(27)

→λ^ij

при T → ∞ P - п.н. для любых i, j = 1, N : i = j,

Oⁱ

(28)

Q^i,1T → fe_i

при T → ∞ P - п.н. для любых i = 1, N .

Oⁱ

131

Помимо этого





(

∫

(

)

(29)

Q^i,1

Q^i,1T

- Q^i,1sd

Q^i,1s

^⊤ - dQ^i,1s(Q^i,1s)⊤=gi

Oⁱ

для любых i = 1, N на множестве {ω ∈ ω : O^iT (ω) > 0}. В (27), (28) и (29)

• процессы N^ijt and O^it определяются формулами (4) и (5),

• уровневая сумма Q^i,1t является частным случаем (6):

∫t

(30)

Q^i,1t = X^isdY_s.

Формулы (27) и (28) могут быть интерпретированы как вариант метода

моментов [24]. Если X_t ненаблюдаемое состояние МСП, но выполняется

условие идентифицируемости 5), то X_t может быть восстановлен точно по

наблюдениям {Y_t}:

(31)

X_t ≜ E {X_t|Y_t+} = X_t

P - п.н. для любого

0≤t<T.

Это означает, что в условиях 5) оценка X_t также позволяет идентифици-

ровать параметры СММ ξ, если использовать ее в формулах (4), (5) и (30)

вместо истинного значения X_t. Однако точное вычисление X_t невозможно:

оценка является решением некоторой дискретно-непрерывной СДС, помимо

этого, ее вычисление требует знания истинных значений параметров ξ иден-

тифицируемой СММ.

Для преодоления этих сложностей и построения субоптимального алго-

ритма идентификации предлагается сделать несколько шагов.

Во-первых, согласно [25], при выполнении необременительных условий

имеет место непрерывная зависимость решений СДС по параметру, т.е. если

последовательность параметров {ξ_u}_u∈N сходится к ξ при u → ∞, то после-

→X(ξ) при u → ∞.

Это означает, что в случае достаточной близости используемых в алгорит-

ме оценивания параметров ξ_u к истинным значениям ξ качество получаемой

оценки X(ξ_u) будет близко к качеству оптимальной оценки условному сред-

нему X(ξ) относительно имеющихся наблюдений.

Во-вторых, в случае известных параметров ξ и вложенной последова-

тельности разбиений {t_r}_r=1,R по теореме Леви имеет место сходимость [16]

X_r → Xtr P- п.н. при R → ∞. Это означает, что при выполнении условия 5),

оценка оптимальной фильтрацииXr, вычисленная по дискретизованным на-

блюдениям Y, будет достаточно близка к истинному состоянию Xtr , и оценка

оптимального сглаживанияXsr тем более будет обладать этим свойством.

В-третьих, траектории состояния МСП X_t и их оценок X_t по диффузи-

онным наблюдениям Y_t (3) являются кусочно-постоянными функциями со

132

значениями в S^N . В отличие от них, значение УМО

X_r, вычисленное по

дискретизованным наблюдениям Y (2), принадлежат “вероятностному сим-

плексу” Π. Эту проблему легко решить, заменяя

X_r на оценки максимума

апостериорной вероятности X_r:

(

)

X_r

(32)

X_r = argmax e^⊤

Заметим при этом, что условное среднееXr является L₂-оптимальной оцен-

кой, в то время как

X_r L₁-оптимальная оценка.

В-четвертых, формулы (27)-(29), в которых истинные значения N^ijR , O^iR

и Q^i,1R заменены их оценками

∑

(33)

N^i,jR = δ

X^isr-1

X^jsr

X^jsr-1

r=1

∑

(34)

=δ

X^isr-1,

r=1

∑

Q^i,1

(35)

X^isr-1Y_r,

r=1

позволяют построить следующие оценки параметров СММ:

i,j

N_R

(36)

λ^ij =

i = j,

^R∑

(37)

λⁱⁱ = -

λ^ij ,

j:j=i

Q^i,1

(38)

fe_i =

Oⁱ

∑

(39)

gi =

X^isr(Y_r -

fe_i)(Y_r -

fe_i)^⊤.

Oⁱ

R r=1

Пересчет параметров СММ может выполняться в цикле: сначала вычисля-

ются оценки состояния МСП, а затем по этим оценкам происходит уточнение

параметров СММ. Выход из этой процедуры может быть выполнен по пре-

вышении некоторого максимального числа итераций N_iter, но возможно и

другое условие. Пусть ξ_u и ξ_u+1 оценки параметров СММ, вычисленные

на u-й и (u + 1)-й итерациях соответственно. Условием остановки итерацион-

ного процесса может быть выбрано выполнение неравенства

∥ξ_u+1 - ξ_u∥

(40)

≤ε^ξ,

∥ξ_u∥

133

т.е. падение относительного изменения вектора параметров ниже некоторого

фиксированного порога ε^ξ.

В процессе идентификации также следует обеспечивать выполнение усло-

вия 3) строгой положительности внедиагональных элементов оценки МИПΛ.

Для этого следует зафиксировать некоторый “барьерный” параметр ε^λ, и вме-

сто оценкиλij(u + 1) (36) на (u + 1)-м шаге использовать его модификацию

(

)

λij

(41)

(u + 1) = max ε^λ|λii(u)|,λij (u + 1)

Относительно ограничительное условие 3) в данной статье было использо-

вано для того, чтобы продемонстрировать возможность использования “ба-

рьеров” для учета различной априорной информации о допустимых обла-

стях оцениваемых параметров. Вообще говоря, 3) может быть заменено ме-

нее ограничительным условием эргодичности МСП X_t, что достаточно для

идентификации МИП Λ.

Суммируя все вышесказанное, алгоритм идентификации параметров

СММ имеет следующий вид.

Шаг 1. Инициализация начальных значений параметров СММξ0 и цикла

идентификации u := 0.

Шаг 2. Начало цикла u := u + 1.

Шаг 3. Вычисление оценок фильтрации в прямом времени {Xr(ξ_u-1)}_r=1,R

по формулам (20) и (21) с использованием оценок параметровξu-1,

вычисленных на предыдущем шаге цикла.

Шаг 4. Вычисление оценок фильтрации в обратном времени {Xbr(ξ_u-1)}_r=1,R

по формулам (24) и (26) с использованием оценок параметровξu-1,

вычисленных на предыдущем шаге цикла.

Шаг 5. Вычисление оценок сглаживания на фиксированном интервале

{Xsr(ξ_u-1)}_r=1,R по формулам (13) и (14).

Шаг 6. Пересчет оценок {Xsr(ξ_u-1)}_r=1,R в оценки максимума апостериорной

вероятности

X_r(ξ_u-1)}_r=1,R по формуле (32).

Q^i,1

Шаг 7. Вычисление оценок

N^i,jR(ξ_u-1),

(ξ_u-1) и

(ξ_u-1) по формулам

(33), (34) и (35).

Шаг 8. Вычисление оценокλuj

f_u и g_u по формулам (36), (37), (38) и (39).

Шаг 9. Если u < N_Iter и∥ξu+1-ξu∥∥ξ

> ε^ξ, то перейти к Шагу 2, в противном

u∥

случае закончить процесс идентификации.

Для одной итерации предложенного алгоритма идентификации можно теоре-

тически оценить зависимость трудоемкости ее выполнения от объема имею-

щихся наблюдений и параметров СММ:

• линейная зависимость от числа обрабатываемых измерений (длины об-

щего отрезка наблюдения [0, T ], частоты дискретизации δ^-1),

• степенная зависимость от размерности N скрытого состояния с показа-

телем, больше 2,

134

• степенная зависимость от размерности M размерности наблюдаемого

процесса с показателем, больше 2.

В настоящий момент времени не существует формальных утверждений,

гарантирующих сходимость предложенного алгоритма идентификации, одна-

ко высокая точность численных алгоритмов фильтрации состояния СММ по

наблюдениям с мультипликативными шумами, а также набросок алгоритма

идентификации параметров СММ с дискретным временем, представленный

в [8], вселяет надежду на возможность доказательства этой сходимости.

Между предложенной процедурой идентификации и ЕМ-алгоритмом име-

ется следующая связь. Известно, что последний представляет собой итера-

ционное повторение двух шагов. На Е-шаге по всей совокупности наблю-

дений {Y_r}_r=1,R вычисляются оценки состояния СММ {Xtr }_r=1,R, исполь-

зуя оценки неизвестных параметров системы ξ_n-1, вычисленные на преды-

дущем шаге. Этому шагу соответствуют формулы (33)-(35). На М-шаге по

вновь рассчитанным оценкам состояния пересчитывается условная функция

правдоподобия, для которой затем находится максимум оценка парамет-

ров ξ_n на текущем шаге. Этому шагу соответствуют формулы (36)-(39). Да-

лее цикл повторяется. Ключевым свойством EM-алгоритма, доказанным для

системы наблюдения (1), (3) в случае аддитивных шумов в наблюдениях,

является его сходимость к локальному максимуму условной функции прав-

доподобия [9, 10]. Так оказалось, что формулы М-шага (36)-(38) совпали с

формулами метода моментов. Однако формула (39) в [9, 10] не использова-

лась: во-первых, задача оценивания интенсивностей шумов наблюдений {g_n}

не ставилась, во-вторых, [9, 10] не содержит решения задачи фильтрации

состояния СММ по наблюдениям с мультипликативными шумами. В предло-

женной статье по аналогии с тем, что (36)-(38) формулы метода моментов

для оценивания Λ и f, предлагается использовать формулу (39) как вари-

ант метода моментов для оценивания {g_n}. Так что пересчет оценок Λ и f

осуществляется в полном соответствии с М-шагом, а оценивание {g_n} осу-

ществляется методом моментов.

6. Численные эксперименты

Для демонстрации качества оценок идентификации был выполнен ком-

плекс численных экспериментов. Для возможности объективного сравнения

все вычисления проводились для СММ с одинаковыми параметрами: N = 3;

M = 1; δ = 0,0002;









-5

0,3571

[

]

Λ= 5

-10

; π =  0,2858

;f=

;

-5

0,3571

g₁ = 0,1; g₂ = 0,2; g₃ = 0,3.

135

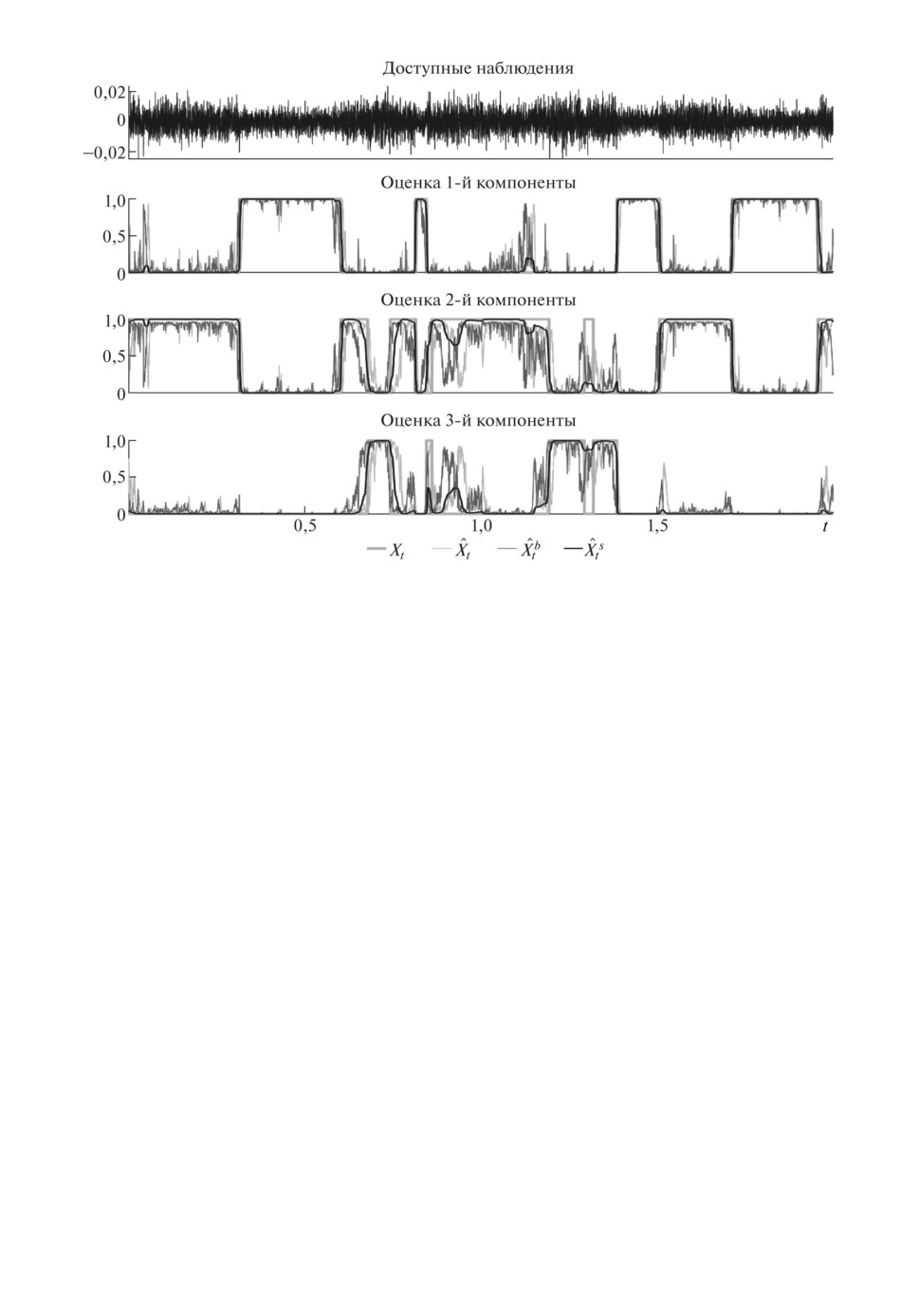
Рис. 1. Доступные наблюдения, компоненты МСП и их оценки.

Начальное распределение было выбрано совпадающим со стационарным, мо-

делирование траекторий выполнялось с шагом 0,00002.

Первая часть экспериментов посвящена сравнению качества оценок филь-

трации и сглаживания на фиксированном интервале при условии, что точные

значения параметров СММ известны.

На рис. 1 представлены результаты решений задач оценивания, выполнен-

ные для исследуемой СММ на отрезке наблюдения [0; 2]:

• наблюдения Y_r, доступные на [0; 2],

• точные значения компонентов МСП X_t,

• оценки фильтрацииXt в прямом времени,

• оценки фильтрацииXbt в обратном времени,

• оценки сглаживанияXst на фиксированном интервале наблюдения [0; 2].

Для сравнительного анализа точности оценивания по пучку траекторий

объемом 1000 вычислены выборочные дисперсии ошибок оценок фильтрации

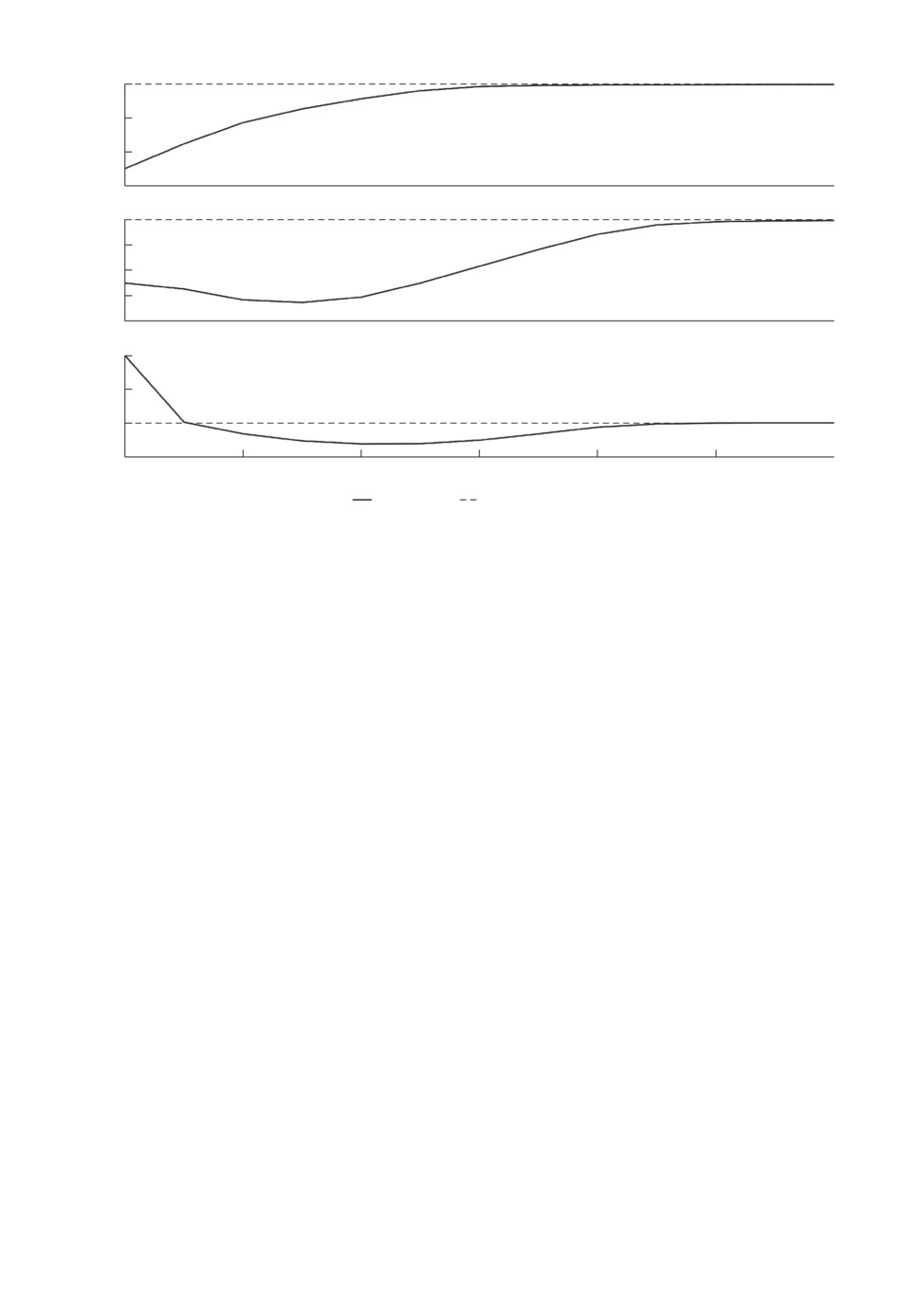
и сглаживания. На рис. 2 представлены:

• выборочная дисперсия D_t ошибок оценок фильтрации в прямом време-

ни,

• выборочная дисперсия D^bt ошибок оценок фильтрации в обратном вре-

мени,

• выборочная дисперсия D^st ошибок оценок сглаживания на фиксирован-

ном интервале наблюдения.

136

Дисперсии ошибок оценок 1-й компоненты

0,10

0,05

Дисперсии ошибок оценок 2-й компоненты

0,10

0,05

Дисперсии ошибок оценок 3-й компоненты

0,10

0,05

0,5

1,0

1,5

D_t

D_tb

D_t

Рис. 2. Выборочные дисперсии ошибок оценок фильтрации и сглаживания.

По результатам первого численного эксперимента можно сделать следующие

выводы.

1. С визуальной точки зрения доступные наблюдения малопригодны для

оценивания состояния МСП.

2. Нулевой снос в наблюдениях затрудняет процессы оценивания. Тем не

менее интенсивности шумов в наблюдениях при разных состояниях МСП

различны, поэтому в исследуемой системе наблюдения выполнены усло-

вия идентифицируемости 5).

3. В проведенном эксперименте оценки сглаживания обеспечивают высокую

точность. К подобному выводу позволяют прийти следующие заключения.

Как само оцениваемое состояние, так и его оценка лежат в “вероятностном

симплексе” Π, поэтому ошибка оценки имеет негауссовское распределение,

а значит и пользоваться “правилом трех сигм” в данном случае бессмыс-

ленно. Дисперсия каждой компоненты оцениваемого состояния является

индексом статистической неопределенности. Действительно, тривиаль-

ной оценкой компонент являются их математические ожидания, а дис-

персии численно характеризуют меру разброса компонент относительно

своих средних величин тривиальных оценок. Следует отметить, что

математические ожидания строятся только на основе априорной инфор-

мации, без привлечения каких-либо наблюдений. Рассмотрим, например,

1-ю компоненту. Она имеет распределение Бернулли с параметром 0,3571,

а значит дисперсию 0,2296. Сравним эту дисперсию с дисперсией ошиб-

ки оптимальной оценки сглаживания: из рис. 2 можно сделать вывод, что

она колеблется в районе 0,01-0,03 (среднее значение 0,0225), т.е. мень-

137

Таблица

Истинное значение Λ Начальное условие Λ₀

Оценка

−5,0

4,0

1,0

-1,0

0,5

-4,5455

3,7613

0,7842

5,0

-10,0

5,0

0,5

-1,0

0,5

4,3470

-8,4221

4,0751

1,0

4,0

-5,0

0,5

-1,0

0,8508

3,3833

-4,2341

Истинное значение f Начальное условие f₀

Оценка

0,0

-1,0

0,0

1,0

-0,02

0,0278

-0,0171

Истинное значение g Начальное условие g₀

Оценка g

0,1

0,2

0,3

0,05

0,15

0,4

0,0997

0,1992

0,3003

ше исходного значения дисперсии в 10 раз. Если использовать дисперсию

в качестве показателя неопределенности, то данный эксперимент демон-

стрирует, что статистическая неопределенность снизилась в 10 раз. Соот-

ношение дисперсий других компонент состояния имеет тот же порядок.

Вообще, отношение дисперсии ошибки оценки к дисперсии оцениваемого

сигнала в линейной регрессии достаточно известный показатель RSS

(Residual Sum of Squares).

4. Выборочные дисперсии ошибок сглаживания вдвое меньше дисперсий

ошибок фильтрации в прямом и обратном времени. Это означает, что

использование в процедуре идентификации оценок сглаживания вместо

оценок фильтрации способно принести существенный выигрыш в точно-

сти.

5. Точность оценивания различных состояний зависит не только от пара-

метров оцениваемого СММ, но и характеристик наблюдений. В рассмат-

риваемом примере состояния 1 и 3 оцениваемого МСП “симметричны”:

вероятности пребывания в них и интенсивности переходов в них и из них

одинаковы. Тем не менее выборочная дисперсия оценки 3-го компонента

МСП в 2 раза больше, чем соответствующее значение для 1-го компо-

нента. Это связано с тем, что интенсивность шумов в наблюдениях при

условии X_t = e₁ равна 0,1, в то время как соответствующее значение при

условии X_t = e₃ равно 0,3.

Вторая часть экспериментов посвящена исследованию качества оценок па-

раметров СММ. Оценивание выполнялось по наблюдениям, полученным на

отрезке времени [0; 1000]. Максимальное число итераций N_Iter = 15, мини-

мальный порог относительного изменения оценок параметров ε^ξ = 0,005. “Ба-

рьерные” значения, отделяющие оценки внедиагональных элементов λ_ij от

нуля ε^λ = 0,1.

Приведенная выше таблица содержит истинные значения оцениваемых па-

раметров ξ СММ, начальные условия ξ₀ для старта итерационной процедуры

идентификации и окончательные оценкиξ.

В данном эксперименте процесс идентификации закончился после 12 ите-

раций. Эволюция оценок параметров в зависимости от номера итерации Iter

138

Оценки внедиагональных коэффициентов 1-й строки матрицы L

Оценки внедиагональных коэффициентов 2-й строки матрицы L

Оценки внедиагональных коэффициентов 3-й строки матрицы L

Iter

Оценка 1-го

Истинное значение

Оценка 2-го

Истинное значение

коэфф.

1-го коэфф.

коэфф.

2-го коэфф.

Рис. 3. Оценки и точные значения внедиагональных элементов МИП Λ.

Оценки 1-го коэффициента строки f

-0,5

-1,0

Оценки 2-го коэффициента строки f

0,06

0,04

0,02

Оценки 3-го коэффициента строки f

1,0

0,5

Iter

Оценка

Истинное значение

Рис. 4. Оценки и точные значения параметров сноса f.

в сравнении с истинными значениями оцениваемых параметров приведены

на рис. 3 для элементов МИП Λ, на рис. 4 для параметров сноса f, на

рис. 5

для параметров диффузии g.

139

Оценка 1-го коэффициента g

0,10

0,08

0,06

Оценка 2-го коэффициента g

0,20

0,18

0,16

0,14

Оценка 3-го коэффициента g

0,40

0,35

0,30

Iter

Оценка

Истинное значение

Рис. 5. Оценки и точные значения параметров диффузии g.

По результатам второго численного эксперимента можно сделать следую-

щие выводы:

1. Итерационный процесс идентификации демонстрирует быструю сходи-

мость.

2. В результате идентификации ни один из внедиагональных элементов оцен-

ки МИПΛ не совпадает с “барьерным” значением, что означает, что ба-

рьерные ограничения в полученной оценке неактивны, и оценка совпадает

с некоторым локальным максимумом условной функции правдоподобия.

3. Качество оценок параметров сноса f и диффузии g выше, чем качество

оценивания МИП Λ.

Идентификация параметров СММ не является самоцелью: обычно в при-

кладных задачах полученные значения используются для последующего ре-

шения задач оценивания и/или стохастического управления по неполной ин-

формации. Третья часть экспериментов посвящена сравнению оценок филь-

трации состояния МСП, вычисленной с использованием идентифицирован-

ных параметров, и “эталонных” оценок фильтрации, вычисленных по точным

значениям параметров СММ.

На рис. 6 представлены графики траекторий оценок фильтрации на от-

резке [0; 1], вычисленных по идентифицированным и точным значениям па-

раметров модели.

На рис. 7 приведены графики выборочных дисперсий ошибок фильтрации,

вычисленных по идентифицированным и точным значениям параметров мо-

дели. Дисперсии вычислялись методом Монте-Карло по пучку траекторий

объемом 100 000.

140

Доступные наблюдения

0,02

-0,02

Оценки 1-й компоненты

1,0

0,5

Оценки 2-й компоненты

1,0

0,5

Оценки 3-й компоненты

1,0

0,5

1,0

1,5

X_t

XEt

Рис. 6. Оценки фильтрации состояний МСП X_t, вычисленные по идентифи-

цированным

X_t и точным параметрам

СММ.

Дисперсии ошибок оценок 1 -й компоненты

0,023

0,022

0,021

Дисперсии ошибок оценок 2-й компоненты

0,062

0,060

0,058

Дисперсии ошибок оценок 3-й компоненты

0,045

0,044

0,043

0,042

0,1

0,2

0,3

0,4

0,5

0,6

0,7

0,8

0,9

D_t

Рис. 7. Выборочные дисперсии ошибок фильтрации состояний МСП, вычис-

ленных по идентифицированным D_t и точным D^Et параметрам СММ.

По результатам третьего численного эксперимента можно сделать следую-

щие выводы:

1. Оценки фильтрации, вычисленные с помощью идентифицированных зна-

чений параметров СММ, визуально не отличаются от оценок, вычислен-

ных со знанием точных значений параметров.

141

2. Даже при большом объеме пучка траекторий, используемых в методе

Монте-Карло, разница выборочных дисперсий ошибок фильтрации, по-

лученных по идентифицированным и точным параметрам, находится на

уровне статистической погрешности.

7. Заключение

Статья представляет субоптимальный алгоритм идентификации парамет-

ров СММ с непрерывным временем. В качестве скрытого состояния высту-

пает однородный МСП с конечным множеством состояний. Имеющиеся на-

блюдения являются косвенными и содержат мультипликативные шумы.

Предложена итерационная процедура оценивания параметров СММ, род-

ственная ЕМ-алгоритму. Она основана на попеременном решении задач сгла-

живания скрытого состояния и вычислении на основе этих результатов и

имеющихся наблюдений оценок параметров СММ методом моментов.

Алгоритм идентификации сходится за малое число итераций. Проведен-

ные численные примеры демонстрируют высокое качество оценивания мат-

риц сноса f и диффузии g, и приемлемое качество оценивания МИП Λ. Тем не

менее продемонстрированной точности достаточно для последующего успеш-

ного решения задач фильтрации скрытого состояния МСП с использованием

идентифицированных значений параметров.

Несмотря на то что в статье показаны положительные качества алгоритма

и его потенциальные возможности, существует целый ряд направлений, по

которым он может быть модифицирован.

Во-первых, алгоритм обладает свойством “жадности”: он сходится к ло-

кальному максимуму условной функции правдоподобия, ближайшей к на-

чальному условию итерационного процесса. При этом у функции правдоподо-

бия могут существовать другие локальные максимумы с большими значения-

ми. Улучшение качества оценивания возможно с помощью выбора начально-

го условия путем некоторой предобработки имеющихся наблюдений. Другим

способом является параллельный запуск нескольких экземпляров итерацион-

ного процесса, стартующих из различных начальных условий. В этом случае

механизм выбора этих условий также играет существенную роль.

Во-вторых, предложенный алгоритм идентификации не обеспечивает опе-

ративную обработку наблюдений нарастающего объема - это связано с “при-

родой” ЕМ-алгоритма. Дело в том, что СММ включает в себя как наблюдае-

мые, так и скрытые компоненты, поэтому возможно построить только услов-

ную функцию правдоподобия, характеризующую распределение скрытого со-

стояния X_[0,T], относительно имеющихся наблюдений Y_R на всем интервале

наблюдения [0, T ]. Данное условное осреднение автоматически означает сгла-

живание на фиксированном интервале наблюдения, и это решение этой зада-

чи не может быть представлено в рекуррентной форме. Каждое следующее

наблюдение, полученное в момент t_r, должно быть обработано для уточне-

ния всей траектории состояния на отрезке [0, t_r-1] и оцениванию состояния в

142

новой точке t_r. Таким образом, с ростом интервала наблюдения растет и дли-

на траектории скрытого состояния, которая должна быть сглажена по всему

имеющемуся массиву наблюдений. Данное свойство ЕМ-алгоритм демонстри-

рует во всех задачах, в которых он может быть применен для идентификации

параметров СММ: начиная от классического алгоритма Баума-Велча [3, 4],

применяемого для идентификации параметров частично наблюдаемых мар-

ковких цепей, и заканчивая алгоритмами идентификации параметров СММ

с непрерывным временем [8-11]. Представляется перспективной разработка

рекуррентных модификаций алгоритма, позволяющих проводить идентифи-

кацию параметров СММ в реальном масштабе времени по наблюдениям на-

растающего объема.

В-третьих, в текущей версии алгоритма учет доступной априорной инфор-

мации о множестве допустимых значений оцениваемых параметров (на при-

мере условия 3) строгой положительности интенсивностей переходов) реали-

зуется с помощью использования некоторых “барьеров”, препятствующих вы-

ходу оценок из этого множества. Алгоритм может быть улучшен путем более

гибкого подбора значений “барьеров”.

Перечисленные направления исследований представляются интересными

не только с точки зрения эмпирического улучшения работы алгоритма и

повышения его точности, но и в плане поиска теоретического обоснования

свойств алгоритма и его модификаций.

СПИСОК ЛИТЕРАТУРЫ

1. Борисов А. L₁-оптимальная фильтрация марковских скачкообразных процес-

сов I // АиТ. 2020. № 11. C. 11-31.

Borisov A. L₁-Optimal Filtering of Markov Jump Processes I // Autom. Remote

Control. 2020. V. 81. No. 11. P. 1945-1962.

2. Борисов А. L₁-оптимальная фильтрация марковских скачкообразных процессов

II // АиТ. 2020. № 12. C. 24-49.

Borisov A. L₁-Optimal Filtering of Markov Jump Processes II // Autom. Remote

Control. 2020. V. 81. No. 12. P. 2160-2180.

3. Baum L., Petrie T. Statistical Inference for Probabilistic Functions of Finite State

Markov Chains // Ann. Math. Statist. 1966. V. 37. No. 6. P. 1554-1563.

4. Baum L., Petrie T., Soules G., Weiss N. Technique Occurring in the Statistical

Analysis of Probabilistic Functions of Markov Chains // Ann. Math. Statist. 1970.

V. 41. No. 1. P. 164-171.

5. Cappé O., Moulines E., Rydén T. Inference In Hidden Markov Models. New

York: Springer, 2005.

6. Rabiner L. A tutorial on hidden Markov models and selected applications in speech

recognition // Proc. IEEE. 1989. V. 77. No. 2. P. 257-286.

7. Ephraim Y., Merhav N. Hidden Markov Processes // IEEE Trans. Inf. Theory.

2002. V. 48. No. 6. P. 1518-1569.

8. Elliott R.J., Moore J.B., Aggoun L. Hidden Markov Models: Estimation and Control.

New York: Springer, 2008.

143

Zeitouni O., Dembo A. Exact filters for the estimation of the number of transitions

of finite-state continuous-time Markov processes // IEEE Trans. Inf. Theory. 1988.

No. 34. P. 890-893.

10.

Dembo A., Zeitouni O. Parameter estimation of partially observed continuous time

stochastic processes via the EM algorithm // Stochast. Proces. Their Appl. 1986.

V. 23. P. 91-113.

11.

James M., Krishnamurthy V., Le Gland F. Time Discretization of Continuous-Time

Filters and Smoothers for HMM Parameter Estimation // IEEE Trans. Autom.

Contr. 1996. V. 42. No. 2. P. 593-605.

12.

Липцер Р., Ширяев А. Теория мартингалов. М.: Физматлит, 1986.

13.

Takeuchi Y., Akashi H. Least-squares state estimation of systems with state-

dependent observation noise // Automatica. 1985. V. 21. No. 3. P. 303-313.

14.

Borisov A., Sokolov I. Optimal Filtering of Markov Jump Processes Given Observa-

tions with State-Dependent Noises: Exact Solution and Stable Numerical Schemes //

Mathematics. 2020. V. 8. No. 4. 506.

15.

Ishikawa Y., Kunita H. Malliavin calculus on the Wiener-Poisson space and its appli-

cation to canonical SDE with jumps // Stochast. Proces. Their Appl. 2006. V. 116.

P. 1743-1769.

16.

Липцер Р.Ш., Ширяев А.Н. Статистика случайных процессов. М.: Наука, 1974.

17.

Platen E., Bruti-Liberati N. Numerical Solution of Stochastic Differential Equations

with Jumps in Finance. Berlin: Springer, 2010.

18.

Badawi F., Lindquist A., Pavon M. A stochastic realization approach to the smooth-

ing problem // IEEE Trans. Autom. Contr. 1979. V. 24. P. 878-888.

19.

Борисов А. Представление марковских скачкообразных процессов в обратном

времени и смежные вопросы. I // АиТ. 2006. № 8. C. 51-76.

Borisov A. Backward representation of Markov jump processes and related problems.

I // Autom. Remote Control. 2006. V. 67. No. 8. P. 1228-1250.

20.

Борисов А. Представление марковских скачкообразных процессов в обратном

времени и смежные вопросы. II // АиТ. 2006. № 9. C. 120-141.

Borisov A. Backward representation of Markov jump processes and related problems.

II // Autom. Remote Control. 2006. V. 67. No. 9. P. 1466-1484.

21.

Elliott R.J. Reverse-Time Markov Processes // IEEE Trans. Inf. Theory. 1986. V. 32.

P. 290-292.

22.

Meyn S., Tweedie R. Markov Chains and Stochastic Stability. Berlin: Springer, 1993.

23.

Боровков А. Теория вероятностей. М.: Физматлит, 1986.

24.

Боровков А. Математическая статистика. М.: Физматлит, 1984.

25.

Крылов Н. Управляемые процессы диффузионного типа. М.: Физматлит, 1977.

Статья представлена к публикации членом редколлегии А.И. Кибзуном.

Поступила в редакцию 04.04.2022

После доработки 10.07.2022

Принята к публикации 28.07.2022

144