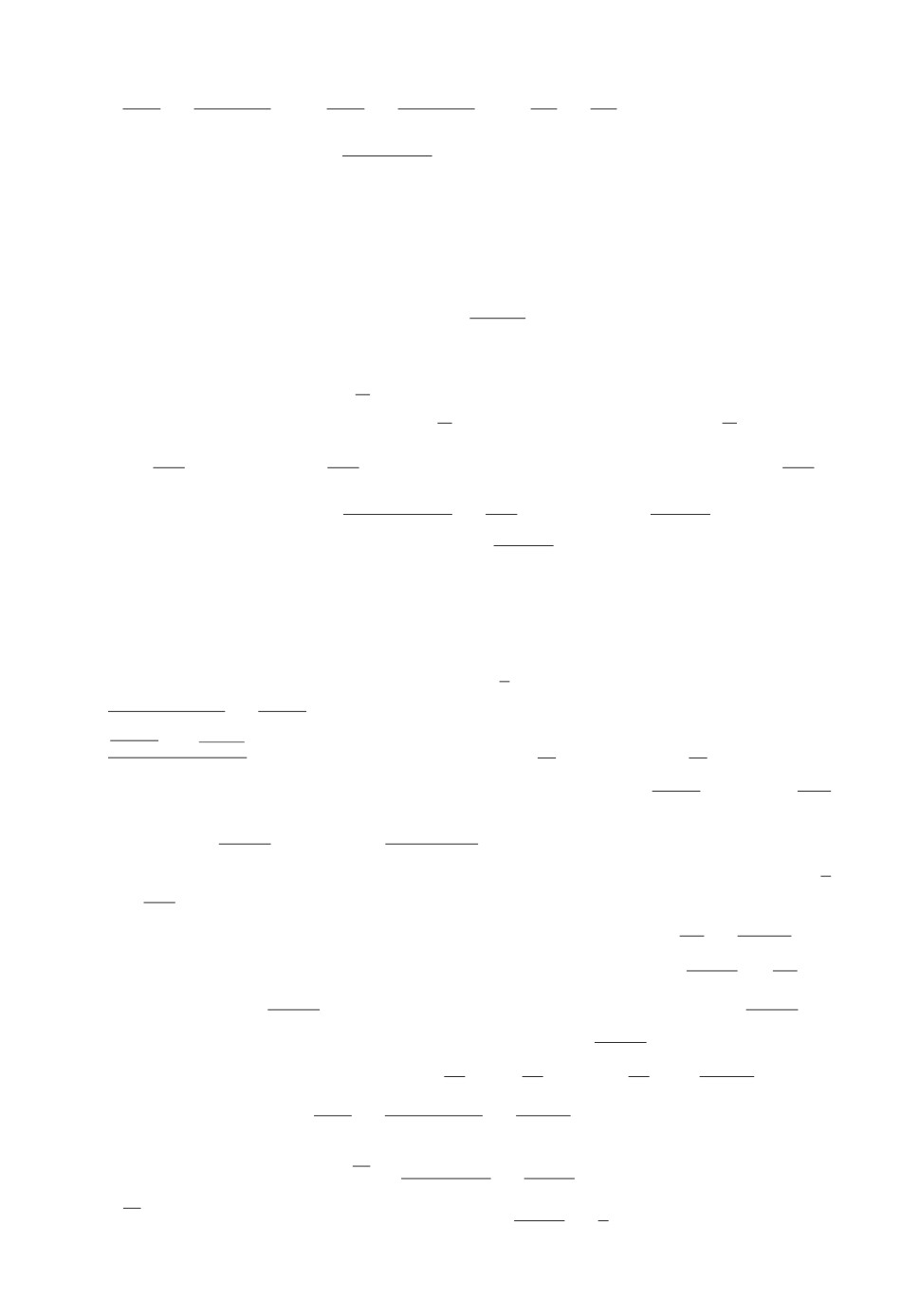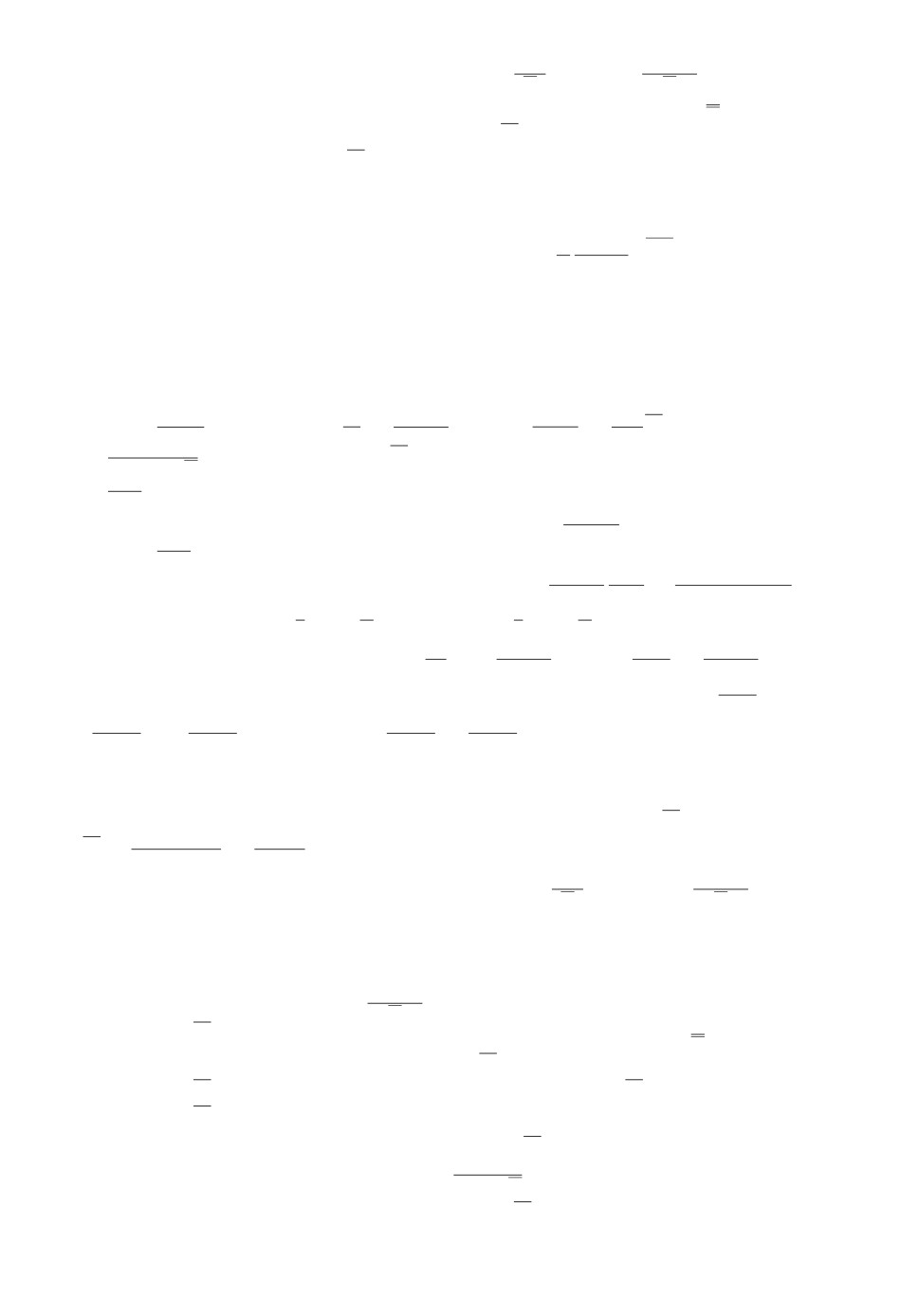Автоматика и телемеханика, № 11, 2022
Управление в социально-экономических
системах
© 2022 г. М.И. ГЕРАСЬКИН, д-р эконом. наук (innovation@ssau.ru)
(Самарский национальный исследовательский
университет им. академика С.П. Королева)
ВЛИЯНИЕ РЕФЛЕКСИИ НА СВОЙСТВА РАВНОВЕСИЙ В
НЕЛИНЕЙНОЙ МОДЕЛИ ОЛИГОПОЛИИ ШТАКЕЛЬБЕРГА
Рассматривается теоретико-игровая проблема выбора оптимальных
стратегий агентов рынка олигополии при линейной функции спроса и
нелинейных функциях издержек агентов. Исследовано влияние рефлек-
сивного поведения на число и свойства равновесий в игре для агентов,
имеющих различные типы функций издержек: вогнутые, соответствую-
щие положительному эффекту расширения масштаба, и выпуклые, соот-
ветствующие отрицательному эффекту. Доказано, что в случае выпуклых
функций издержек существует только одно равновесие, а в случае вогну-
тых функций издержек может существовать два равновесия, одно из ко-
торых меньше равновесия при линейных издержках, а другое больше.
Установлено, что при выпуклых функциях издержек равновесное дей-
ствие увеличивается с ростом рефлексии агента и снижается с ростом
рефлексии окружения, как и в модели с линейными функциями издер-
жек. При вогнутых функциях издержек влияние рефлексии зависит от
знака суммы предположительных вариаций S: с повышением рефлексии
агента большее равновесие растет, а меньшее снижается при S < 0, а при
S >0
наоборот.
Ключевые слова: олигополия, игра Штакельберга, вогнутость и выпук-
лость функции издержек, рефлексия.
DOI: 10.31857/S000523102211006X, EDN: KELPWF
1. Введение
В играх олигополии с нелинейными функциями издержек агентов тра-
диционный подход вычисления равновесия Курно-Нэша [1, 2] требует совер-
шенствования, поскольку включение в модель лидерства по Штакельбергу [3]
приводит к расширению содержания понятия ¾тип агента¿. Если в самой
распространенной модели с линейными издержками [4-6] параметром типа
агента являются предельные издержки агентов, то нелинейная модель с ли-
дерством по Штакельбергу, во-первых, типизирует агента по признаку вы-
пуклости (вогнутости) функции издержек, т.е. по специфике технологии, и,
во-вторых, по типу рефлексивного поведения.
145
В рамках рефлексии исследуется многообразие представлений агента
1) о стратегиях окружения (т.е. других игроков), 2) о представлениях окру-
жения о стратегии агента; 3) о представлениях окружения о представлении
агента о стратегиях окружения и т.д. В этом ряду номер представления на-
зывается рангом [7]. Модель рефлексивной игры является инструментом опи-
сания информированности агентов, с помощью которого экзогенно заданная
информированность сводится к множеству возможных игр с полной инфор-
мированностью. Поэтому решением рефлексивной игры является информа-
ционное равновесие [8]. Рефлексивное поведение агентов исследовалось в по-
становке Курно-Штакельберга в процессах стратегической и информацион-
ной рефлексии [9-13], а также в рамках динамики установления равновесия
Курно [14] и Штакельберга 15].
Таким образом, тип агента представляет собой множество из двух ха-
рактеристик, первая из которых выражает технологию производства аген-
та, а вторая его способ мышления. Поскольку технология предопределяет
вид зависимости производственных издержек от выпуска, то первый элемент
множества параметров типа, т.е. технологический тип агента, характери-
зуется значениями коэффициентов его функции издержек. В соответствии
с видом функции издержек агента могут быть следующие технологические
типы: 1) постоянная отдача от расширения масштаба производства, при ко-
торой издержки возрастают прямо пропорционально выпуску, а технология
оптимальна, так как достигла предела улучшения; 2) отрицательный эффект
расширения масштаба, когда издержки возрастают ускоренным темпом от-
носительно роста выпуска, и технология рецессивная, т.е. тормозит расши-
рение производства; 3) положительный эффект расширения масштаба, ес-
ли издержки возрастают замедленным темпом относительно роста выпуска,
что соответствует прогрессирующей технологии, способствующей расшире-
нию производства. Для реальных фирм выявлена [16] следующая тенденция
перехода от одного технологического типа к другому в процессе развития
фирмы: вначале наблюдается третий тип (положительный эффект), затем
совершенствование технологии приводит к оптимуму, т.е. первому типу (по-
стоянная отдача), после чего технология деградирует и наступает второй тип
(отрицательный эффект). Следовательно, вообще в экономике могут сосуще-
ствовать агенты различных технологических типов. Однако олигополии, как
рынки, возникшие из монополии и, следовательно, предлагающие покупате-
лю идентичный товар, как правило, включают в себя фирмы, пребывающие
на одной и той же стадии развития. Поэтому в статье исследуется игра оли-
гополии, в которой все агенты имеют одинаковые технологические типы.
В свою очередь, ментальное поведение агента в игре при взаимодействии с
окружением характеризуется рангом его рефлексии, которому можно поста-
вить в соответствие предположительную вариацию, т.е. предполагаемое из-
менение выпуска контрагента, вызываемое единичным увеличением выпуска
агента. Поэтому второй элемент множества параметров типа агента, т.е. мен-
тальный тип, количественно измеряется его предположительной вариацией,
146
точнее, в игре более двух агентов, суммой предположительных вариаций ка-
сательно всех агентов окружения. По этому признаку агентов можно разде-
лить на следующие типы: 1) ведомый агент, не выдвигающий предположений
о стратегиях окружении, вследствие чего сумма предположительных вариа-
ций такого агента равна нулю; 2) лидер по Штакельбергу (первого уровня),
предполагающий, что его окружают ведомые агенты, что, как известно [3],
означает отрицательную предположительную вариацию, т.е. предположено
снижение выпуска контрагента в ответ на рост выпуска лидера; 3) лидер
по Штакельбергу второго уровня (или более высоких уровней), предпола-
гающий, что его окружают лидеры первого уровня (или последующих, но
низших уровней). В этой классификации типов с ростом уровня лидерства
сумма предположительных вариаций лидера возрастает по абсолютной ве-
личине, оставаясь отрицательной, если лидера окружают агенты первого и
второго технологических типов. Однако если окружение имеет третий техно-
логический тип (положительный эффект), то углубление рефлексии (т.е. рост
ранга) агента может приводить к атипичному предположению о том, что рост
выпуска агента вызывает увеличение выпуска контрагента; в таком случае
сумма предположительных вариаций атипичного агента положительна [17].
Следовательно, на ментальный тип агента опосредованно, через функции из-
держек агентов как общее знание, влияет технологический тип окружения, и
предположительные вариации в результате могут принимать значения в диа-
пазоне (-∞, ∞). Поэтому дискретный набор ментальных типов моделируется
в статье непрерывной величиной суммы предположительных вариаций.
Поскольку совместное влияние технологического и ментального компонен-
тов типа агентов на равновесие в агрегативной игре олигополистов не иссле-
довано, то эта проблема является предметом данной статьи.
2. Методология
Рассмотрим рынок олигополии, на котором фирмы (агенты) имеют сте-
пенные функции издержек следующего вида:
(1)
∈ (0, 2) , i ∈ N,
Ci (Qi) = CFi + BiQβii, CFi ≥ 0, Bi > 0, βi
где Qi действие (объем выпуска) i-го агента; N = {1, . . . , n} множество
агентов рынка; n количество агентов; CFi, Bi, βi коэффициенты функ-
ций издержек агентов. Степенная функция издержек (1) в диапазоне коэф-
фициентов βi ∈ (0, 2) обобщает три технологических типа: агент с постоян-
ной отдачей от расширения масштаба описывается линейной функцией из-
держек (βi = 1), агент с отрицательным эффектом выпуклой функцией
при 1 < βi < 2, агент с положительным эффектом расширения масштаба
вогнутой функцией издержек при 0 < βi < 1. Следовательно, коэффициенты
Bi, βi представляют собой параметры технологического типа агента.
В агрегативной игре на рынке олигополии с линейной функцией спроса
агенты выбирают оптимальные действия из условия максимума функции по-
147
лезности:
{
}
maxΠi (Q,Qi) = max
(a - bQ) Qi - CFi - BiQβi
,
i
Qi≥0
Qi≥0
(2)
∑
Qi ≥ 0, Q = Qi, i ∈ N,
i∈N
при условии1
(2а)
a>C′iQ
∀β ∈ [1,2) , a > β-1C′
∀β ∈ (0,1) ,
i
iQi
где Πi функция полезности (прибыль) i-го агента; Q суммарный объем
рынка; a, b коэффициенты обратной функции спроса, a > 0, b > 0, a ≫ b.
Равновесие Нэша в модели (2) есть вектор действий агентов при выбран-
ных действиях окружения (т.е. других агентов), который определяется из
уравнений
∂Πi (Qi,ρij)
(3)
= 0, i, j ∈ N,
∂Qi
где ρij = Q′
предположительная вариация i-го агента, т.е. предполагае-
jQi
мое изменение выпуска j-го агента в ответ на единичный прирост выпуска∑
i-го агента. Сумма вариаций i-го агента Si =
ρil выражает ментальный
l∈N\i
параметр типа агента.
Стратегическая игра Г есть кортеж множества агентов, множества стра-
тегий (действий), множества функций полезности и множества уровней ли-
дерства по Штакельбергу:
(4)
Γ = 〈N,{Qi,i ∈ N},{Πi
,i ∈ N},G〉,
где G = (M0, M1, . . . , ML) множество уровней лидерства агентов; L ко-
личество уровней лидерства агентов; Mr (r = 0, . . . , L) множества агентов;
M0
множество ведомых агентов; Mr (r = 1, . . . , L) множество лидеров
r-го уровня. Формально уровни лидерства определяются следующим обра-
зом. Нулевой уровень, соответствующий ведомому η0-му агенту, имеет место,
если в η0-м уравнении системы (3) полагается ρ0η0j=0∀j∈N\η0,гдеверхний
индекс вариации обозначает уровень лидерства r. Первый уровень лидерства
η1-го агента возникает, если в η1-м уравнении системы (3) вариации ρ1η1jвы-
числяются дифференцированием по Qη1 остальных (n - 1) уравнений (3), в
которых полагается ρ0ij = 0 ∀j ∈ N\i. Произвольный r-й уровень лидерства
ηr-го агента возникает, если в ηr-м уравнении системы (3) вариации ρrηrjвы-
числяются дифференцированием по Qηr остальных (n - 1) уравнений (3), в
которых полагается ρij = ρr-1ij ∀j ∈ N\i.
Рефлексией [7] будем называть выполняемую ηr-м агентом мыслитель-
ную операцию вычисления вариации ρrηr jизсистемы(3)впредположении
ρij = ρr-1ij ∀j ∈ N\i; соответственно, индекс r для агента, выполнившего эту
операцию, есть ранг рефлексии.
1 Условие существования стационарной точки функции полезности.
148
Ростом рефлексии будем называть увеличение параметра Sri по абсолют-
ной величине, поскольку в модели с линейными издержками с увеличением r
модуль ρij растет.
Обозначим нормированное действие агента как yi =Qi
∈ (0, 1), где
Qmax
Qmax =ab есть максимальный объем рынка. Введем обозначения:
βi-1
â - Biβi (2 - βi) x
Biβi (βi - 1)
i
αi =
,
δi = 2 +
xβi-2i + Sri,
b
b
â = Qmaxa,
b = Q2maxb,
Bi = QβimaxBi,
где параметры xi удовлетворяют следующим условиям:
yi - xi < εi, xi < yi, Ωi = xi + ξi (yi - xi),
(5)
ξi,xi ∈ (0,1) , εi ∈ (0,Ωi) , i ∈ N.
Переменные xi представляют собой параметры линеаризации системы (3),
поэтому имеют ту же размерность, что и равновесные действия yi, и должны
быть им равны с точностью до малых положительных чисел εi.
Решение системы (3) было получено [18] в виде следующей формулы рав-
новесия:
θi
a0i + a1ix
i
(6а)
yi =
,
b0i + b1ixθi-1
i
где коэффициенты вычисляются по следующим формулам:
1-λi
θi = βi - 1 ∈ (-1,1) , a0i =
,
a1i = θ2i - 1 < 0,
Bi
(6б)
1+Sr
+τi
i
b0i =
,
b1i = θi (θi + 1) ,
Bi
при условии2 [19]
(6в)
Sri ∈ Ξi, i ∈ N, Ξi = {Sri : δi
> 0} ,
где
∑
Bi
1
Bi =
,
λi = τi
αj , τi =
,
i
ωj
∑
bQmax
1
j=i
1+
ωj
(6г)
j=i
{
> 0, θi ∈ (0, 1) ,
ωi = δi - 1, b1i
< 0, θi ∈ (-1, 0) .
Поставим задачу анализа влияния параметров функций издержек агентов
и суммы предположительных вариаций Si на функцию равновесного дей-
ствия агента (6а).
2 Условие максимума функции полезности в стационарной точке.
149
3. Результаты
Опишем свойства равновесий, определяемых формулой (6а), для различ-
ных типов функций издержек и ментальных типов агентов. В дальнейшем
рассмотрим i-го агента, поэтому для упрощения записи опустим индекс ¾i¿, а
если рассуждения касаются окружения, используем индекс ¾-i¿; также опу-
стим индекс ¾r¿, считая, что каждый агент имеет некоторый ранг рефлексии,
приводящий к сумме вариаций Sr.
Для оценки свойств равновесий важную роль играют характеристики па-
раметров (6г), которые представим в виде следующего вспомогательного ре-
зультата.
Лемма 1. Коэффициенты τ и λ при различных параметрах типа окру-
жения в равновесии удовлетворяют следующим условиям:
(0, 1) , если θ-i ∈ [0, 1) ,
[
)
(0, 1) , если θ-i ∈ (-1, 0) пр
S-i ∈
S,∞
,
(7а)
τ ∈
(
)
1
(
)
-
,0
, если θ-i ∈ (-1,0) пр
S-i ∈
S - 1,S
,
n-2
(0, 1) , если θ-i ∈ [0, 1) ,
[
)
(0, 1) , если θ-i ∈ (-1, 0) пр
S-i ∈
S,∞
,
(7б)
λ∈
(
)
(0, 1) , если θ-i ∈ (-1, 0) пр
S-i ∈
S - 1,S
и n ∈ (n2,∞),
(
)
(1, 2) , если θ-i ∈ (-1, 0) пр
S-i ∈
S - 1,S
и n ∈ (n1,n2),
∂τ
∂λ
∂τ
∂λ
(7в)
> 0,
< 0,
=
= 0,
∂S-i
∂S-i
∂S
∂S
где
(
)
2-αmax
S =b-1
B
θ
θ+1
Qθ-1 - 1, n1 =4-αmax,
n2 =
,
2-αmax
1-αmax
(
)
B 1-θ2 Qθmax
∑
1
αmax = 1 -
∈ (0,1),
S-i =
Sj;
a
n-1
j=i
θ,
B подобраны из условий
(
)
∑
(
)
∑
1
1
ω
θ
B =
ωj, α
θ
B =
αj.
n-1
n-1
j=i
j=i
Содержательно коэффициент τ характеризует интенсивность рефлексии
окружения данного агента, так как если S-i < 0, то с увеличением |S-i| па-
раметр ω-i уменьшается и τ стремится к нулю, а если параметр S-i > 0, то
его рост приводит к повышению τ. Коэффициент λ это комплексная оценка
типа окружения, он объединяет коэффициент τ и характеристику нелинейно-
сти функций издержек окружения α: чем больше |θ|, т.е. чем более выпуклы
150
(или вогнуты) функции издержек, тем коэффициент α ближе к единице, а
чем меньше |θ|, тем α ближе к нулю.
Таким образом, коэффициенты τ и λ положительны и не превышают еди-
ницы в случаях линейных или выпуклых функций издержек окружения (по-
стоянного или отрицательного эффектов расширения масштаба), а также в
случае вогнутых функций издержек окружения, если средняя сумма вариа-
ций окружения S-i не меньше S; если эта величина меньше S, то коэффици-
1
ент τ отрицательный и по модулю меньше
, а коэффициент λ либо также
n-2
не превышает единицы при большом числе агентов (больше n2), либо не пре-
вышает двух при меньшем числе агентов (от n1 до n2). Важно, что с ростом
рефлексии окружения, т.е. с увеличением |S-i|, в случае S-i > 0 коэффици-
ент τ растет, а α снижается, а в случае S-i < 0 наоборот. Опосредованно
через функцию y (S, S-i) коэффициенты τ и λ испытывают также влияние
изменения равновесия, но эта зависимость будет исследована в нижеследую-
щих утверждениях.
Равновесие3 (6а) отклоняется от классического равновесия Курно [20]
вследствие двух факторов нелинейности функции издержек агента, ха-
рактеризуемой параметром θ, а также рефлексии агента (параметр S) и его
окружения (параметры λ и τ). Поэтому для факторного анализа устраним
влияние нелинейности, т.е. рассмотрим случай θ = 0 (или β = 1), что позво-
ляет выявить чистое влияние фактора рефлексии.
Утверждение 1. В игре агентов с линейными функциями издержек
(β = 1) равновесное действие yβ=1
i) единственное, конечное, отличное от нуля, вычисляется по формуле
a-B
(8а)
yβ=1 = χβ=1
,
Qmaxb
ii) растет с ростом рефлексии агента и снижается с ростом рефлексии
окружения
∂χβ=1
∂χβ=1
(8б)
< 0,
> 0,
∂S
∂S-i
iii) превышает равновесное действие по Курно yK =a-B(n+1)Q
, т.е.
maxb
χβ=1 > χK, при следующих ограничениях:
(8в)
κ < 0 ∨ (n < κ ∧ κ > 0),
1
где χβ=1 =τ1+S+τ , κ =S+1S
S-i, χK =
, индекс K равновесие Курно.
-i-S
n+1
Содержательно коэффициент χ показывает изменение действия агента
вследствие рефлексии по сравнению с равновесным действием по Курно.
Далее рассмотрим игру агентов, имеющих технологии с отрицательным
эффектом расширения масштаба, т.е. выпуклыми функциями издержек.
3 Здесь и далее термин ¾равновесие¿ используется также как синоним термина ¾равно-
весное действие¿.
151
Утверждение 2. В игре агентов с выпуклыми функциями издержек
(β > 1) равновесие агента yβ>1
i) существует при следующих условиях:
(9а)
S ∈ (max{-1,s2},0], если
{S, τ, λ} ⊂ Ωβ>1,
⌢
причем s2 > -1, если λ + τ < 1 и Qmax < Q
,
max
ii) при β = 2 вычисляется по формуле
(9б)
yβ=2 = χβ=2,
iii) меньше равновесия при линейных функциях издержек
(9в)
yβ=2 < yβ=1 при S < S
⌢,
iiii) растет с ростом рефлексии агента и снижается с ростом рефлексии
окружения
∂χβ=2
∂χβ=2
(9г)
< 0,
> 0,
∂S
∂S-i
iiiii) влияние рефлексии ниже, чем при линейных функциях издержек
∂χβ=2
∂χβ=1
∂χβ=2
∂χβ=1
(9д)
<
,
<
,
∂S
∂S
∂S-i
∂S-i
где
τ
χβ=2 =
,
s2 = -βB - (λ + τ),
1 + S + τ + 2b-1B
) 1
(
)
⌢
(B β
1-β
a
B
Q
max
=
,
S
⌢ =
2
1-
-1-τ,
a 1-λ-τ
b
a
Ωβ>1 = {(S,τ,λ) : a0 > 0 ∧ b0 > 0}.
Наконец, исследуем игру агентов, имеющих технологии с положительным
эффектом расширения масштаба, т.е. вогнутыми функциями издержек.
Утверждение 3. В игре агентов с вогнутыми функциями издержек
(β < 1) равновесие агента yβ<1
i) существует при следующих условиях:
}
(max {s0, s1} , s3) при a0 > |a1| ,
если
{S,τ,λ} ⊂ Ω1β<1,
(max {s0, s1} , s2) при a0 < |a1| ,
(10а)
(max {s0, s2} , s4) , если
{S,τ,λ} ⊂ Ω2β<1,
S∈
(s0, s2) , если
{S,τ,λ} ⊂ Ω3β<1,
(s0, min {s1, s2}) , если
{S,τ,λ} ⊂ Ω4β<1,
152
ii) при β = 0,5 вычисляется по формуле
√
ζ±
d
y+,-β=0,5 =
, если
{S,τ,λ} ⊂ Ω2β<1,
2(1 + S + τ)
(10б)
yβ=0,5 =
(
)2
0,5B
3 , если {S, τ, λ} ⊂ Ω1β<1
⋃Ω3β<1⋃
Ω4β<1,
1+S+τ
iii) соотносится с равновесием при линейных функциях издержек как
y+β=0,5 > yβ=1 ∧ y-β=0,5 < yβ=1 при λ < λ, если
{S,τ,λ} ⊂ Ω2β<1,
(10в)
yβ=1 < yβ=0,5 при Qmax > Qmax, если
{S, τ, λ} ⊂ Ω1β<1,
iiii) зависит от рефлексии агента и рефлексии окружения следующим
образом:
∂y+β=0,5
∂y-β=0,5
< 0,
> 0,
∂S
∂S
если
{S, τ, λ} ⊂ Ω2β<1,
∂y+β=0,5
∂y-β=0,5
(10г)
> 0,
< 0 при λ > λ
⌢,
∂S-i
∂S-i
∂yβ=0,5
∂yβ=0,5
< 0,
< 0, если
{S, τ, λ} ⊂ Ω1β<1
⋃Ω3β<1⋃
Ω4β<1,
∂S
∂S-i
iiiii) влияние рефлексии по сравнению со случаем линейных функций
издержек сказывается следующим образом:
⌢
∂yβ=1
y+β=0,5
⌢
∂
при λ > λ
+,
>
∂S
∂S
⌢
∂yβ=1
y-β=0,5
∂
⌢
при λ > λ
−,
если
{S, τ, λ} ⊂ Ω2β<1,
>
∂S
∂S
∂yβ=1
y+,-β=0,5
(10д)
∂
при λ > λ
⌢ +⌢-i,
>
∂S-i
∂S-i
∂yβ=1
∂yβ=0,5
∂yβ=1
∂yβ=0,5
>
,
>
∂S
∂S
∂S-i
∂S-i
при Qmax > Qmax, если
{S,τ,λ} ⊂ Ω1β<1,
где
Ω1β<1 = {(S,τ,λ) : a0 > 0 ∧ b0 > 0 ∧ b0 < |b1|},
Ω2β<1 = {(S,τ,λ) : a0 > 0 ∧ b0 > 0 ∧ b0 > |b1| ∧ a0 > |a1|} ,
Ω3β<1 = {(S,τ,λ) : a0 < 0 ∧ b0 < 0} ,
Ω4β<1 = {(S,τ,λ) : a0 > 0 ∧ b0 < 0} ,
153
ζ = 1 - λ, d = ζ2 - 2B (1 + S + τ), λ = 1 - τ (1 - B/a),
⌢
⌢
⌢
2τ (1 - B/a)
⌢
2τ (1 - B/a)
λ
+ =1-
,
λ
− =1-
,
Δ1 + 2
Δ1
s0 = β (1 - β) Byβ-2 - 2, s1 = - (1 + τ), s2 = -βB - (λ + τ) ,
s3 = β (1 - β) B - (1 + τ) , s4 = β (1 - β) ψ - (1 + τ) ,
2
⌢
2(1 - B/a)(1 + S) - Δ2
(0,5B/a)
λ
-i =
,
Qmax =
,
λ
⌢ =
1-(1+S +τ)α,
2+Δ1
τ3(1-B/a)3
0,5
Qm,ax (1 - τα (n - 1))
(B/a)0,5 (1 + τ)
Δ1 =
- 1, Δ2 =
,
ϕ0,5
ϕ0,5
ϕ = Q0,5max (1 - τα(n - 1))2 - 2B
(1 + τ) ,
a
y-, y+ меньшее и большее равновесия.
Таким образом, исследована полная совокупность возможных игровых си-
туаций, возникающих при различных технологических и ментальных типах
агентов олигополии.
4. Численный эксперимент и обсуждение результатов
Игра агентов с линейными функциями издержек, свойства равновесия в
которой описаны в утверждении 1, является референтным случаем. В этом
случае равновесные действия агентов выше, чем в классическом случае Кур-
но, если рефлексия агента выше рефлексии окружения (т.е. |S| > |S-i|) при
любых n > 1, а если окружение рефлексирует сильнее (т.е. |S| < |S-i|), то при
некотором ограниченном числе агентов, т.е. n < κ. Кроме того, поскольку в
случае линейных издержек S < 0 и S-i < 0, то рост рефлексии агента все-
гда ведет к росту его равновесия, а рост рефлексии окружения способствует
снижению равновесия агента.
В игре агентов, имеющих технологии с отрицательным эффектом масшта-
ба, т.е. выпуклые функции издержек, описанной в утверждении 2, область
значений S, при которых равновесие в игре существует, может сужаться по
сравнению с линейным случаем, когда S ∈ (-1, 0]. Это проявляется при ма-
лых значениях λ и τ, т.е. когда S-i → -1 (окружение интенсивно рефлекси-
рует) и |θ| → 0 (функции издержек окружения близки к линейным). Выпук-
лость функций издержек приводит к уменьшению равновесного действия по
сравнению с моделью линейных издержек при условии S < S
⌢, что является
типичным случаем, поскольку S
⌢ ≫ 1, так как ab ≫ 1. Кроме того, при выпук-
лых функциях издержек снижается влияние рефлексии по сравнению с ли-
нейным случаем, а тип влияния рефлексии на равновесие остается прежним:
рост рефлексии агента повышает его равновесное действие, а рост рефлексии
окружения снижает.
154
Коэффициенты функций издержек телекоммуникационных компаний РФ
i
Агент
Bi
βi
1
ПАО ¾МТС¿
2,41
0,76
2
ПАО ¾МегаФон¿
1,36
0,85
3
ПАО ¾ВымпелКом¿
2,46
0,81
Игра агентов, технологии которых характеризуются положительным эф-
фектом расширения масштаба, когда у всех агентов вогнутые функции из-
держек, описана в утверждении 3. При этом равновесие существует в менее
широком диапазоне, чем S ∈ (-∞, ∞) [19]. Следовательно, в этом случае S
может быть как положительным, так и отрицательным, поэтому понятие ро-
ста рефлексии можно трактовать двояко: при S < 0, как и ранее, ростом
рефлексии будем считать увеличение параметра S по абсолютной величине,
т.е. уменьшение S; при S > 0 будем называть ростом рефлексии увеличение
параметра S.
Возможны две ситуации: существование двух равновесий в случае
{S, τ, λ} ⊂ Ω2β<1 или одного равновесия в случае {S, τ, λ} ⊂ Ω1β<1 ∪Ω3β<1 ∪Ω4β<1.
В ситуации двух равновесий одно из них больше равновесия в линейном
случае, а другое меньше, если λ < λ, а поскольку λ близко к единице при
достаточно большом n, то эта закономерность типична. Кроме того, в этой
ситуации рост рефлексии агента при S < 0 влечет за собой увеличение боль-
шего равновесия и уменьшение меньшего, а при S > 0, наоборот, приводит
к снижению большего равновесия и повышению меньшего. В свою очередь,
рост рефлексии окружения вызывает противоположный эффект при условии
λ>λ
⌢.
В ситуации единственного равновесия его значение больше равновесия в
линейном случае при условии Qmax > Qmax, которое выполняется при малых
значениях Qmax, т.е. когда B ≪ a. Кроме того, в данной ситуации при S < 0
рост рефлексии агента и окружения способствует уменьшению равновесия, а
при S > 0 ведет к увеличению равновесия.
При вогнутых функциях издержек влияние рефлексии на равновесие отли-
чается от случая линейных издержек следующим образом: 1) в ситуации двух
равновесий рефлексия агента в линейном случае влияет сильнее, чем в нели-
⌢
⌢
нейном, при условии λ > λ
+ для большего равновесия и λ > λ⌢⌢- для мень-
шего равновесия, а рефлексия окружения при условии λ > λ
⌢ + ⌢-i; 2) в си-
туации одного равновесия рефлексия агента и окружения влияет сильнее в
линейном случае при условии Qmax > Qmax.
Проведем моделирование равновесий на основе параметров функций спро-
са a = 1,77, b = 0,0009 и издержек (таблица), полученных для телекоммуни-
кационных компаний РФ [19], причем CFi = 0, i = 1, 2, 3. Поскольку βi < 1,
i = 1,2,3, то для всех агентов имеет место наиболее интересный случай по-
ложительного эффекта масштаба, описанный в утверждении 3, в котором
могут наблюдаться два равновесия.
155
0,8
0,6
0,4
0,2
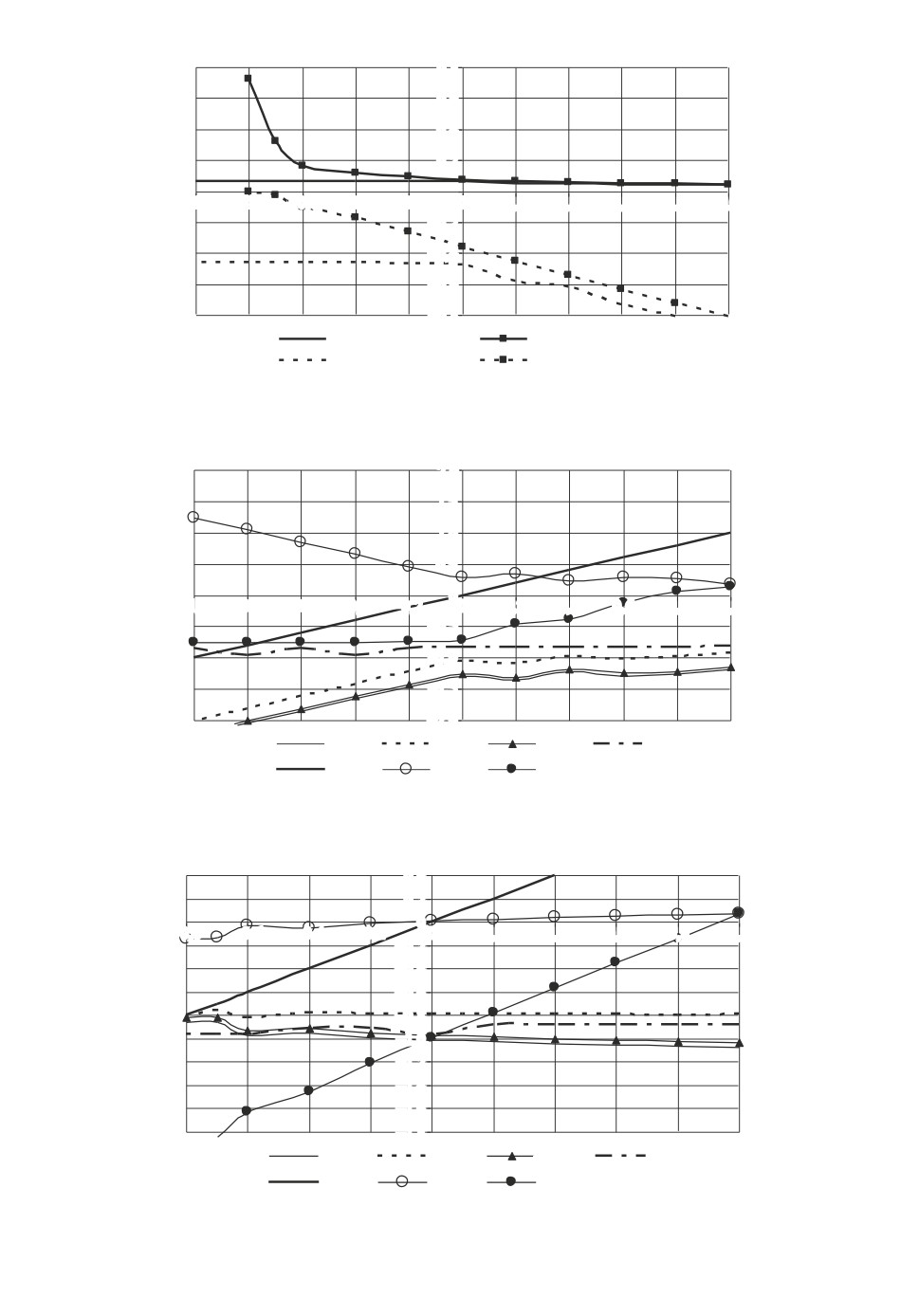
0
-1,0
-0,8
-0,6
-0,4
-0,2
0
0,2
0,4
0,6
0,8
1,0
-0,2
-0,4
-0,6
-0,8
S
y-
y+
(a0 - b0 - b)-/10
(a0 - b0 - b)+/10
Рис. 1. Влияние рефлексии агента 1 на точки и условия равновесия.
2,0
1,5
1,0
0,5
0
-1,0
-0,8
-0,6
-0,4
-0,2
0
0,2
0,4
0,6
0,8
1,0
-0,5
-1,0
-1,5
-2,0
-
-
S
s1-
s2-
s3
S -
-
s0
S
t-
Рис. 2. Ограничения на рефлексию агента 1 в первой точке равновесия.
0,4
0,2
0
-0,8
-0,6
-0,4
-0,2
0
0,2
0,4
0,6
0,8
1,0
-0,2
-0,4
-0,6
-0,8
-1,0
-1,2
-1,4
-1,6
-1,8
-
S
s+
s+
s+
S +
+
S
t+
s0
Рис. 3. Ограничения на рефлексию агента 1 во второй точке равновесия.
156
1,0
0,8
0,6
0,4
0,2
0
-1,0
-0,8
-0,6
-0,4
-0,2
0
0,2
0,4
0,6
0,8
1,0
-0,2
-0,4
ё
-0,6
-0,8
-1,0
-1,2
-1,4
S-i
(y-)´10
(y+)´10
(a0 - b0 - b)-/10
(a0 - b0 - b)+/10
(y+)´10
Рис. 4. Влияние рефлексии окружения агента 1 на точки и условия
равновесия.
1,5
1,0
0,5
0
-1,0
-0,8
-0,6
-0,4
-0,2
0
0,2
0,4
0,6
0,8
1,0
-0,5
-1,0
-1,5
-2,0
-2,5
-3,0
-3,5
-
-
S-i
s1-
s2-
s3
S -
l͡-
l-
s0-
Рис. 5. Ограничения на рефлексию окружения агента 1 в первой точке
равновесия.
0,6
0,4
0,2
0
-1,0
-0,8
-0,6
-0,4
-0,2
0
0,2
0,4
0,6
0,8
1,0
-0,2
-0,4
-0,6
-0,8
-1,0
-1,2
-1,4
-
S-i
s+
s+
s+
S +
+
l͡+
l+
s0
Рис. 6. Ограничения на рефлексию окружения агента 1 во второй точке
равновесия.
157
Поскольку для таких исходных данных не выполняются условия приме-
нимости приближенных формул (10) [18], то равновесия рассчитаны путем
численного решения уравнения (9а) [18], т.е. f (y) =b0a0 y+b1aa1 yβ-1 =1.Для0
всех агентов выполняются условия a0 > 0, b0 > 0, b0 > |b1|, a0 > |a1| [18], при
которых может быть два равновесия, а условия существования двойного рав-
новесия a0 - b0 - β < 0 и u∞ > 0 соблюдаются в определенных диапазонах S
и S-i. Во всех точках равновесия выполняется условие S = s4, т.е. u∞ = 0
(или f(y) = 1). Кроме того, моделирование показало, что при равновесии со-
блюдается соотношение ωi = -τi ∀i ∈ N; это свойство не было установлено
аналитически.
Рассмотрим влияние на равновесия рефлексии агента (рис. 1-3), считая
S-i = 0. Для равновесия y+ при S < -0,8 нарушается условие a0 - b0 - β < 0
(рис. 1), т.е. условие S > s2 (рис. 3). Для равновесия y- при S < -0,8 наруша-
ется условие (6в), т.е. S > s0, в результате становится τ > 1 (рис. 2). Поэтому
равновесия рассчитаны в указанных диапазонах. Характер изменения рав-
новесий с ростом S подтверждает условия (10г): с ростом S равновесие y+
уменьшается, а равновесие y- возрастает.
Рассмотрим влияние на равновесия рефлексии окружения (рис. 4-6), по-
лагая S = 0. Изменение S-i не ведет к нарушению условий a0 - b0 - β < 0 и
u∞ > 0 в данных диапазонах (рис. 4), однако условие (6в), т.е. S > s0, для
равновесия y- выполняется только в диапазоне S-i ∈ (-0,6; 0), поэтому y-
представлено в указанном диапазоне. В соответствии с условиями (10г) с ро-
стом S-i равновесие y- уменьшается, а равновесие y+ возрастает, если λ > λ⌢
(рис. 6).
5. Заключение
Исследование совместного влияния технологического и ментального порт-
ретов агентов на равновесие в игре олигополии продемонстрировало зави-
симость количества равновесий и величины равновесных действий как от
выпуклости (вогнутости) функций издержек агентов, так и от их рефлек-
сивного поведения. Если в случае линейных функций издержек существует
единственное равновесие и рост рефлексии агента всегда ведет к увеличению
его равновесия, а рост рефлексии окружения способствует снижению равно-
весия агента, то нелинейный характер издержек приводит к существенным
особенностям.
Первая особенность игры агентов с нелинейными функциями издержек
состоит в сужении допустимого диапазона суммы предположительных ва-
риаций агента, в котором существует игровое равновесие, по сравнению с
возможным значением этой суммы с точки зрения менталитета агента.
Вторая особенность присуща игре агентов с вогнутыми издержками, в ко-
торой может существовать два равновесия, одно из которых меньше равнове-
сия в линейном случае, а другое больше; если же равновесие единственно, то
оно, как правило, больше равновесного действия в линейном случае. В случае
158
с выпуклыми издержками равновесие, как правило, меньше, чем в линейном
случае.
Третье свойство касается степени влияния рефлексии на равновесие при
выпуклых или вогнутых издержках. Выпуклость функций издержек приво-
дит к ослаблению влияния рефлексии по сравнению с линейным случаем,
но характер влияния совпадает с линейным случаем. В случае вогнутых из-
держек рефлексия агента и рефлексия окружения, как правило, слабее, чем
в линейном случае, влияют на изменение единственного равновесия, а если
равновесия два, то рефлексия окружения может влиять как сильнее, так и
слабее.
ПРИЛОЖЕНИЕ
Доказательство леммы 1. Поскольку условия (5) определяют непо-
движную точку, т.е. x = y, то преобразуем выражения α, δ и ω:
(
)
a-B
1-θ2
Qθ
α=
,
δ = 2 + S + b-1Bθ(θ + 1)Qθ-1,
Qmaxb
ω = 1 + S + b-1Bθ(θ + 1)Qθ-1.
Введем следующее упрощение: так как параметры τ и λ зависят от сумм
α-i
1
и
по множеству -i = {N\i}, то без ограничения общности положим
ω-i
ω-i
параметры α и ω равными средним в этом множестве, т.е. α-i = α, ω-i = ω
∑n
1
(символом ¾∼¿ обозначим такжеθ
B
S-i, при которых ω =
ωj,
n-1
j=i
∑n
1
α=
αj). Тогда
n-1
j=i
1
ω
α
(n - 1) α
τ =
=
,
λ = τ (n - 1)
=
1 + (n - 1) 1
ω+n-1
ω
ω+n-1
ω
Из этих формул следует:
∂τ
ω′S (ω + n - 1) - ωω′S
ω′S (n - 1)
=
=
,
∂S
(ω + n - 1)2
(ω + n - 1)2
∂λ
-ω′S (n - 1) α
∂λ
∂τ
=
,
α
=
∂S
(ω + n - 1)2
∂S
∂S
Производные
ω′S = 1 + b-1Bθ(θ + 1)(θ - 1)Qθ-2Q′S,
ω′S
= b-1Bθ(θ + 1)(θ - 1)Qθ-2Q′S
-i
-i
учитывают неявную зависимость Q (S, S-i), но поскольку оцениваются зна-
ки производных∂τ∂S ,∂λ∂S с целью последующего вывода о знаках Q′S
, Q′
,
i
S-i
которые связаны со знаками τ′Si , τ′
, то эта зависимость не учитывается и
S-i
159
считается, что в равновесии Q (S, S-i) = const. Поэтому ω′S = 1, ω′
= 0. То-
S-i
∂τ
∂λ
гда
= (n-1)
> 0,
= -(n-1)α
< 0,∂τ∂S
= ∂λ = 0. Заметим, что так∂S
∂S-i
(ω+n-1)2
∂S-i
(ω+n-1)2
i
i
θ
B(1-θ2)Q
как Qmaxb = a, то α = 1 -
< 1 ∀Q > 0. Кроме того, из условия (2а)
a
следует, что α > 0, так как a
B(1 -θ2)Qθ > 0 при θ-i ∈ (0, 1), если a > C′
,
iQi
т.е. a
B(1 +θ)Qθ, и a -
B(1 -θ2)Qθ > 0 при θ-i ∈ (-1, 0), если a > β-1C′
,
iQi
т.е. a
BQθ. Поэтому α ∈ (0, 1).
В случае θ-i ∈ [0, 1) доказано, что S-i ∈ (-1, 0] [19], поэтому ω-i > 0, значит,
τ ∈(0,1); при этом λ∈(0,1), так как(n-1)α
> 0 ∀n > 1 и (n - 1)(α - 1) <
ω+n-1
< ω ∀n > 1. В случае θ-i ∈ (-1,0) по [19] S-i ∈ (-∞,∞), но с учетом (6в), из
которого следует ω > -1, возможны два варианта: i) ω ≥ 0 при услови
S≥
≥b-1
B|θ|(θ+ 1)Qθ-1 - 1 = S; в этом случае, как и в предыдущем, τ ∈ (0, 1),
λ∈(0,1);ii) ω<0приуслови
S<S и ω>-1приуслови
S > S - 1; тогда
(
)
(
)
τ ∈
-1n-2,0 , а λ ∈
0,n-1n-2 α при n > 2, причем λ ∈ (0, 1), если α <n-2n-1 =
θ
B(1-θ2)Qm
ax
= n2, т.е. если αmax = 1 -
< n-2n-1, откуда n > 2-αmax; а при λ > 11-̃α
a
max
условие λ - 1 ≤ 1 выполняется, если n ≥4−αmax2m=n1,тогдаλ∈(1,2).
Доказательство утверждения 1. В случае β = 1 (или θ = 0) по-
казано [19], что S < 0, |S| ∈ [0, 1), поэтому δ = 2 + S > 1, значит, ω = δ - 1 =
= S + 1 ∈ (0,1). Если все агенты окружения интенсивно рефлексируют, т.е.
|S-i| → 1, то ω-i → 0, поэтому по (6г) τ → 0; если окружение не рефлексиру-
ет, т.е. |S-i| = 0, то ω-i = 1, поэтому τ =1n . Поскольку a1 = -1, b1 = 0, α =
= aQmax-BQmax
= a-BQ
при θ = 0, то, во-первых, из
(6а) следует y =
Q2maxb
maxb
a
∑n
∑n
Qmaxb
1
= Qmaxb-λ
,
во-вторых, λ = ατ
= ατ
1 = ατ (τ - 1).
1+S+τ
j=i ωj
j=1\i ωj
Причем из (2а) следует, что a > B. Следовательно, y = χa-BQ
, где χ =τω+τ .
maxb
Сравним данное решение с равновесным действием при условии гипотезы
Курно QKi =a-B(n+1)b или yK =a-B(n+1)Q
[20], т.е. когда предположительные
maxb
вариации всех агентов равны нулю (S = 0, S-i = 0), поэтому ω = 1, τ =1n ,
1
χK =
. Покажем, как рефлексивное поведение агентов влияет на увели-
n+1
чение действия, т.е. при каких n выполняется неравенствоχ
= τ(n+1)ω+τ > 1:
χK
пусть S-i одинаковы для всех агентов окружения, тогда τ =S-i+1S,иχ
>1
-i+n
χK
при условиях n >S+1S
S-i, если S-i - S > 0 (т.е. κ < 0) или n <S+1S
S-i,
-i-S
-i-S
если S-i - S < 0 (т.е. κ > 0), где обозначено κ =S+1S
S-i; очевидно, что
-i-S
n > κ ∀n > 1 при κ < 0. Поскольку ∂ω∂S > 0, ∂τ∂S = 0, то ∂χ∂S = -τ
ω′ < 0, а
(ω+τ)2
∂χ
с учетом (7в) получим
= τ′(ω+τ)-ττ′
= τ′ω
> 0.
∂S-i
(ω+τ)2
(ω+τ)2
Доказательство утверждения 2. В случае β > 1 (или θ > 0) пока-
B
зано, что S ∈ (-1, 0] [19], и B =
= B
; из условия (2а) вытекает,
bQmaxQm
ax
aQmax
что B < 1, так как из a > βBQβ-1 следуетB
<1β < 1.
aQ1-β
160
1+S+τ
Рассмотрим случай t = 1 [18], когда a0 =1-λ
> 0, b0 =
> 0, т.е. λ < 1,
B
B
1+S+τ >0. Условие равновесия a0-b0-β <0 имеет вид - 1
(λ + S + τ)-
B
−β < 0, откуда следует λ + S + τ > -βB. Поэтому получаем систему:
S > -(1 + τ) = s1, S > -βB - (λ + τ) = s2. С учетом S ∈(-1,0] и (7а) огра-
ничение S > s1 не играет роли, так как s1 < -1. Поэтому будет следующее
решение: если s2 ≤ -1, то S ∈ (-1, 0], а если s2 > -1, то S ∈ (s2, 0]. Вариант
(
)
1
B β
s2 > -1 имеет место, если λ + τ < 1 и Qmax <
1-β .
a 1-λ-τ
В случае t = 2 [18], когда a0 < 0, b0 > 0, равновесие отсутствует, поскольку
λ > 1 противоречит (7б). Случаи t = 3,4 [18], когда b0 < 0, т.е. 1 + S + τ < 0,
невозможны при S ∈ (-1, 0] и (7а).
Получим аналитическое решение в случае t = 1 для наиболее характерно-
го варианта нелинейности β = 2 (или θ = 1), используя формулу (10а) [18]:
1
yβ=2 =
,
,
k1+k2
где k1 =b0a0 =1
1-λ
k2 =b1-a1a0 =1−λB.Тогдаyβ=2=
1-λ
=
, причем при θ = 1: B = b-1B, ω = 1 + S + 2b-1B, поэтому yβ=2 =
1+S+τ+2B
=1-λω+τ . Если θ = 1 для всех агентов, то α-i = 1. Аналогично лемме 1 рас-
смотрим средние значени
S-i,θ,
B, тогда λ =(n-1)̃ω+n-1, и 1 - λ = τ, поэтому
yβ=2 =τω+τ = χβ=2.
τ
Сравним yβ=1 и yβ=2, пусть yβ=1 > yβ=2, т.е.τa-B1+S+τa ÷
> 1,
1+S+2b-1B+τ
(
)
(
)
откуда 1+S+τ <2ab
1-Ba
, или S < 2ab
1-Ba
-1-τ =S
⌢. Как и в
τ′
ω
∂χ
S-i
утверждении 1, доказывается, что∂χ∂S = -τ
ω′S < 0,
=
> 0. Но
(ω+τ)2
∂S-i
(ω+τ)2
∂τ
поскольку ω′β=1S = ω′β=2S = 1, ωβ=2 > ωβ=1, τβ=2 > τβ=1 (так как
> 0), то
∂ω-i
χβ=2
χβ=1
χβ=2
∂
<
∂
, аналогично,∂
, так как τ′β=2S
>τ′
∂S
∂S
∂S-i
S-i
β=1S-i
-i
Доказательство утверждения 3. В случае β < 1 (или θ < 0) по-
казано S ∈ (-∞, ∞) [19], но из условия (6в) ω = 1 + S + b-1Bθ (θ + 1) Qθ-1 =
= δ - 1 > -1, т.е. S > b-1B |θ|(θ + 1)Qθ-1 - 2 = β (1 - β)Byβ-2 - 2 = s0, и
B=B
= B
< 1 из условия (2а).
bQmaxQm
ax
aQmax
Рассмотрим случай t = 5 [18], когда a0 =1-λ
> 0, b0 = 1+S+τ
> 0, т.е.
B
B
λ < 1, 1 + S + τ > 0.
Случай t = 5.1: введем множество параметров (S, τ, λ), соответствую-
щих этому случаю, в виде Ω1β<1 = {(S, τ, λ) : a0 > 0 ∧ b0 > 0 ∧ b0 < |b1|}; усло-
1+S+τ
вие b0 < |b1| равносильно
< |θ| (θ + 1) = β (1 - β), т.е.
1+S+τ <
B
< β (1 - β)B; условие равновесия a0 - b0 - β > 0 имеет вид - 1
(λ + S + τ) -
B
−β > 0, откуда следует λ + S + τ < -βB. Поэтому получаем систему: S >
> β (1 - β)Byβ-2 - 2 = s0, S > -(1 + τ) = s1, S < -βB - (λ + τ) = s2, S <
< β (1 - β)B - (1 + τ) = s3.
В этой системе s2 < s3, т.е. 1 - λ < β (2 - β) B при условии a0 < |a1|, и s3 < s2
1-τ
при a0 > |a1|; неравенство s1 < s0, т.е.
< yβ-2 может выполняться при
β(1-β)B
y→0,так как yβ-2 имеет порядок Qmax, а B-1 имеет порядок Qmax. Поэто-
161
{(max {s0, s1} , s3) при a0 > |a1| ,
му решением системы будет диапазон S ∈
(max{s0,s1},s2) при a0 < |a1|.
Этот диапазон не пуст в частных случаях, например, s1 < s3 (так как
β (1 - β) B > 0); s1 < s2, если βB < 1 - λ.
В случае t = 5.1 аналитическое решение для варианта нелинейности
β = 0,5 (или θ = -0,5) следует из формулы (10) [18]:
(√
√
)2
√
√
3
yβ=0,5
=
-q +
D +3 -q -
D
,
0,5
где k1 =1+S+τ1-λ =γζ , k2 =
B = 0,5ζ B, γ = 1 + S + τ, ζ = 1 - λ, q =k2 =2k
1-λ
1
= 0,25Bγ , D = 27k2k1-4
. Поскольку λ < 1, то ζ3 ≪ 1, поэтому
108k31
08γ3
2
√
√
D ≈ 0,25B4γ2 , значит, -q +
D = 0, -q -
D = - B2γ, следовательно, yβ=0,5 =
(
)
2
0,5B
=
3.
1+S+τ
Сравним yβ=1 и yβ=0,5, учитывая, что из формулы
(8а) следует
yβ=1 =τ(1-ϑ)1+S+τ , где ϑ = Bβ=1 =Ba < 1 при a > B (но иное невозможно, так как
yβ=1 < 0 при a < B), а в формуле (9б) Bβ=0,5 =B
. Пусть yβ=0,5 > yβ=1,
aQma
x
(
)
2
(
)
3
0,5Bβ=0,5
τ(1-ϑ)
т.е.
3 ÷
> 1, откуда следуетτ3(1-ϑ)
> 1 + S + τ; по-
1+S+τ
1+S+τ
(0,5Bβ=0,5)2
скольку 0 < 1 + S + τ < β (1 - β) B < 1 по свойствам случая t = 5.1, то за-
3
меним это неравенство на более жесткоеτ3(1-ϑ)
Qmax > 1, откуда Qmax >
(0,5ϑ)2
2
> (0,5ϑ)
=Qmax.
τ3(1-ϑ)3
(
)
2
∂yβ=0,5
Оценим влияние S и S-i:
=-23
0,5Bβ=0,5
3 (1 + S + τ)-3
< 0,
∂S
(
)2
∂yβ=0,5
=-23
0,5Bβ=0,5
3 (1 + S + τ)-3 τ′
< 0, так как
1+S+τ >0
и
∂S-i
S-i
yβ=1
yβ=0,5
τ′S-i > 0 согласно
(7в). Неравенство
∂
>
∂
, учитывая, что
∂S
∂S
(3)3
∂yβ=1
τ3(1-ϑ)3
=-τ(1-ϑ)
, приводит к
> (1 + S + τ)5, которое также
∂S
(1+S+τ)2
2
(0,5Bβ=0,5)2
2
(0,5ϑ)
yβ=1
yβ=0,5
выполняется при Qmax >
= Qmax. Неравенство
∂
>
∂
вер-
τ3(1-ϑ)3
∂S-i
∂S-i
но по аналогии.
Случай t = 5.2: условие b0 > |b1| равносильно 1 + S + τ > β (1 - β) B, усло-
вие a0 < |a1| ⇒1-λ
< 1 - θ2 ⇒ λ > 1 - β (2 - β)B. Если суммировать эти
B
два неравенства, то λ + S + τ > -βB, поэтому a0 - b0 - β < 0, т.е. производ-
ная функции (6а) не меняет знака при y ∈ (0, 1), значит, равновесие не суще-
ствует.
{
Случай t = 5.3: обозначим Ω2β<1 = (S, τ, λ) : a0 > 0 ∧ b0 > 0 ∧ b0 > |b1| ∧
}
∧a0 > |a1|
; условие b0 > |b1| равносильно 1 + S + τ > β (1 - β) B, условие
a0 > |a1| ⇒ 1 - λ > β (2 - β) B. Условие равновесия a0 - b0 - β < 0 имеет
162
вид
-1
(λ + S + τ) - β < 0, откуда следует λ + S + τ > -βB. Дополни-
B
θ
тельное условие
b0θ-1
равносильно
1 + S + τ < β (1 - β)Bψ, где
-a0a1 >
b1
(
)
β-2
(
)β-2
a0
1-λ
ψ=
β-1 =
β-1 > 1 (в силу λ < 1 - β (2 - β) B). Поэтому по-
|a1|
Bβ(2-β)
лучаем систему: S > β (1 - β) Byβ-2 - 2 = s0, S > - (1 + τ) = s1, S > -βB-
- (λ + τ) = s2, S > β (1 - β) B - (1 + τ) = s3, S < β (1 - β) ψ - (1 + τ) = s4.
В этой системе s3 < s2 (из условия a0 > |a1|), s1 < s3 (так как β(1 - β)B > 0),
т.е. s1 < s3 < s2; а s0 < s2 в случае βB((1 - β)yβ-2 + 1) < 2 - (λ + τ). Поэтому
решением системы будет диапазон S ∈ (max{s0, s2}, s4), который может быть
не пустым в частных случаях: например, s0 < s4, если β(1 - β)B(ψ - yβ-2) >
(
)
1
a0
> τ - 1, т.е. когда ψ > yβ-2 (так как τ < 1) или y <
β-1 , что выпол-
|a1|
няется для меньшего из двух равновесий [18]; кроме того, s2 < s4, если
βB ((1 - β)ψ + 1) > 1 - λ; отметим, что более слабое неравенство s3 < s4 вер-
но, так как соответствует ψ > 1.
В случае t = 5.3 найдем решение для варианта β = 0,5 (или θ = -0,5),
из формулы (10) [18] для β = 0, поскольку она отражает два равнове-
сия, yβ=0,5 =1±√1-4k1k2 , подставив параметры, соответствующие t = 5.1:2k
1
√
d
1 - 4k1k2 = 1 - 2Bγ
= ζ2-2Bγ
. Тогда получим: y+,-β=0,5 =ζ±
, d = ζ2 - 2Bγ,
ζ2
ζ2
2γ
γ=1+S+τ.
√
d
Сравним yβ=1 и y+,-β=0,5, пусть y+β=0,5 > yβ=1, т.е.ζ+
÷ τ(1-ϑ)γ > 1, что при-
2γ
водит к неравенству 2τζ (1 - ϑ) - 2τ2 (1 - ϑ)2 - Bγ > 0, в котором последним
членом можно пренебречь, заменив неравенство на более жесткое, в результа-
те получим ζ - τ (1 - ϑ) > 0, откуда следует λ < 1 - τ (1 - B/a). Аналогично,
y-β=0,5 < yβ=1 при том же условии λ < 1 - τ (1 - B/a) = λ.
+
√
∂yβ
d)
=0,5
Оценим влияние S на равновесие:
=0,5d-0,5dS2γ-2(ζ+
=
∂S
4γ2
√
√
√
2
d+d)
d+d)
(ζ+
d)
∂y-β=0,5
= -2Bγ-√(ζ
= -ζ2-d+√(ζ
=-
√
< 0, по аналогии,
=
4
dγ2
4
dγ2
4
dγ2
∂S
√
2
(ζ-
d)
=
√
> 0.
4
dγ2
Оценим влияние S-i на равновесие, учитывая, что d′S-i = 2ζλ′S-i - 2Bτ′
,
S-i
(
)
√
+
ζ′S
+0,5d-0,5d′S
∂yβ
2γ-2τ′ (ζ+
d)
=0,5
-i
-i
S-i
ζ′S-i = -λ′S-i, λ′S-i = -ατ′S-i:
=
=
∂S-i
4γ2
√
√
√
-
d+αζ-B)γ-ζ
d-d
(
d+ζ)(γα-ζ)+Bγ
∂yβ
=0,5
=τ′ (α
√
=τ′
√
;
аналогично,
=
S-i
2γ2
d
S-i
2γ2
d
∂S-i
√
+
(
d-ζ)(γα-ζ)-Bγ
∂yβ
=0,5
=τ′
√
. Поскольку τ′S-i > 0 по
(7в), то
> 0 будет,
S-i
2γ2
d
∂S-i
)
(√
если верно неравенство
d + ζ (γα - ζ) + Bγ > 0, которое заменим (учи-
(√
)
тывая, что Bγ мало) на более жесткое
d + ζ (γα - ζ) > 0, верное при
-
∂yβ
=0,5
γα - ζ > 0, откуда следует λ > 1 - γα = λ
⌢. Аналогично,
< 0 будет
∂S-i
163
)
(√
√
при
d - ζ (γα - ζ) > 0, а поскольку ζ >
d, то также при γα - ζ > 0 или
λ>λ
⌢.
+,-
yβ=1
∂yβ
=0,5
yβ=1
∂y+β=0,5
Сравним
∂
и
Пусть
∂
>
т.е.τ(1-ϑ)÷
∂S
∂S
.
∂S
∂S
,
γ2
√
2
√
(ζ+
d)
(ζ+
d)2
÷
√
> 1; отсюда следует 2τ (1 - ϑ) > ζ2√Bγ
+ ζ, поскольку
√
=
4
dγ2
d
d
(
)
ζ2-Bγ√
=2
+ζ
; заменим это неравенство на более жесткое
d
(
)
2
ζ
ζ
(Π.1)
2τ (1 - ϑ) >
√
+ζ =ζ
√ +1
d
d
(так как Bγ ≪ζ22изусловияd>0);численныеэкспериментыпоказывают,
1
чт
√
≈ 1, поэтому сделаем замен
√
≤ 1 + Δ1, откуда (1 + Δ1)2 ≥
;
d
d
2Bγ
1-
ζ2
правая часть этого неравенства наибольшая при наибольшемγζ2 , или ко-
гда γ = 1 + τ (т.е. S = 0) и λ = τα (n - 1) (т.е. при ω = 1, когда S-i = 0),
1+τ
1
поэтомуγ
<
; тогда (1 + Δ1)2 ≥
, откуда Δ1 ≥
ζ2
(1-τα(n-1))2
2ϑ
1+τ
1-
2
Qma
(1-τ α(n-1))
x
≥ Qm,ax(1-τα(n-1))ϕ0,5 - 1, где ϕ = Qm,ax (1 - τα (n - 1))2 - 2ϑ (1 + τ); следова-
тельно, из неравенства (П.1) вытекает
2τ (1 - ϑ) > ζ (Δ1 + 2), откуда
⌢
⌢
yβ=1
λ>1-2τ(1-ϑ)Δ
=λ
+. При аналогичных рассуждениях условие
∂
>
1+2
∂S
−
∂yβ
=0,5
>
риводит к виду 2τ (1 - ϑ) > ζΔ1, или λ > 1 -2τ(1-ϑ) = λ⌢⌢-.Δ
∂S
п
1
∂yβ=1
(1-ϑ)(1+S)
Поскольку
=τ′
, то определим условие, при котором
∂-i
S-i
γ2
(
yβ=1
∂y+β=0,5
∂y+β=0,5
∂y-β=0,5
yβ=1
∂
>
тметим, что поскольку
то
∂
>
∂S-i
∂S-i
о
∂S-i
>
∂S-i
,
∂S-i
−
)
√
∂yβ
=0,5
2(1-ϑ)(1+S)
d
>
удет также выполнено при таком условии , т.е.
√
>
∂S-i
б
(
d+ζ)(γα-ζ)+Bγ
> 1; запишем это в виде
(
)
ζ
Bγ
(Π.2)
2(1 - ϑ)(1 + S) >
1+
√
(γα - ζ) +
√ ;
d
d
как было показано при анализе (П.1)
√
≤ 1 + Δ1; численные эксперименты
d
1
показывают, что√γ
≈ 0, поэтому √γ
≤ Δ2, откуда Δ22 ≥
и наибольшее
d
d
ζ2
-2
Bγ
значение правая часть неравенства принимает при наименьшемζ2
(как и
Bγ
1
для (П.1)), поэтому сделаем замену Δ22 ≥
, откуда Δ2 ≥
Qma
x (1-τ α(n-1))2
-2
ϑ
1+τ
0,5
≥ ϑ0,5(1+τ)ϕ0,5
; значит, (П.2) можно записать в виде
2(1 - ϑ)(1 + S) >
> (2 + Δ1) (γα - ζ) + Δ2, откуда следует λ > 1 - γα + 2(1-ϑ)(1+S)-Δ2 =2+Δ
1
=λ
⌢ + ⌢ -i, где ⌢ -i = 2(1-ϑ)(1+S)-Δ2.2+Δ
1
164
В случае t = 6 [18] обозначим Ω3β<1 = {(S, τ, λ) : a0 < 0 ∧ b0 < 0}, a0 =
=1-λ
< 0, b0 = 1+S+τ
< 0, т.е. λ > 1, 1 + S + τ < 0. Условие равновесия
B
B
a0 - b0 - β > 0 имеет вид -1
(λ + S + τ) - β > 0, откуда следует λ + S + τ <
B
< -βB. Поэтому получаем систему: S > β (1 - β) Byβ-2 - 2 = s0, S <
< -(1 + τ) = s1, S < -βB - (λ + τ) = s2. Поскольку s2 < s1 (в силу λ - 1 >
> -βB), то решение будет S ∈ (s0,s2); этот диапазон не пуст при условии
(
)
s0 < s2, т.е. βB
(1 - β) yβ-2 + 1
< 2 - (λ + τ). Решение вычисляется как при
t = 5.1, но хотя λ > 1, тем не менее ζ3 ≪ 1, так как при условии (7б) λ < 2.
В случае t = 7 [18] обозначим Ω4β<1 = {(S, τ, λ) : a0 > 0 ∧ b0 < 0}, a0 =
=1-λ
> 0, b0 = 1+S+τ
< 0, т.е. λ < 1, 1 + S + τ < 0. Условие равновесия
B
B
−1
(λ + S + τ) - β > 0 дает λ + S + τ < -βB. Поэтому получаем систе-
B
му: S > β (1 - β) Byβ-2 - 2 = s0, S < - (1 + τ) = s1, S < -βB - (λ + τ) = s2.
В этом случае s2 < s1 не всегда, а только при условии 1 - λ > βB, поэтому ре-
шением является область S ∈ (s0, min {s1, s2}), которая не пуста при условиях
(
)
1-τ
s0 < s1, т.е.
> yβ-2, и s0 < s2, т.е. βB
(1 - β) yβ-2 + 1
< 2 - (λ + τ).
β(1-β)B
Отметим, что в этом случае, как и при t = 6, сравнение yβ=1 и yβ=0,5, а также
их производных по S и S-i, невозможно, так как yβ=1 > 0 не существует при
1 + S + τ < 0.
В случае t = 8 [18] a0 < 0, b0 > 0, и условие a0 - b0 - β > 0 не может быть
выполнено, поэтому равновесие отсутствует.
СПИСОК ЛИТЕРАТУРЫ
1. Nash J. Non-cooperative Games // Ann. Math. 1951. No. 54. P. 286-295.
2. Cournot A.A. Researches into the Mathematical Principles of the Theory of Wealth.
London: Hafner, 1960. (Original 1838).
3. Stackelberg H. Market Structure and Equilibrium: 1st Edition. Translation into En-
glish, Bazin, Urch & Hill: Springer, 2011. (Original 1934).
4. Sarkar S., Tarafdar S. Investment Choice with Managerial Incentive Schemes. Int.
Game Theory Rev. 2021. No. 23(2). Р. 2050016.
5. Cao B.-B., Gong Z.-J., You T.-H. Stackelberg Pricing Policy in Dyadic Capital-
Constrained Supply Chain Considering bank’s Deposit and Loan Based on Delay
Payment Scheme // J. Industr. Manag. Optimiz. 2021. No. 17(5). Р. 2855-2887.
6. Li M., Zhang J., Xu Y., Wang W. Effect of disruption risk on a supply chain with
price-dependent demand // J. Industr. Manag. Optimiz. 2020. No. 16(6). Р. 3083-
3103.
7. Novikov D.A., Chkhartishvili A.G. Reflexion and Control: Mathematical Models.
London: CRC Press, 2014.
8. Novikov D., Korepanov V., Chkhartishvili A. Reflexion in mathematical models
of decision-making // Int. J. Parall., Emergent Distribut. Syst. 2018. No. 33(3).
P. 319-335.
9. Novikov D.A., Chkhartishvili A.G. Mathematical Models of Informational and
Strategic Reflexion: a Survey // Advan. Syst. Sci. Appl. 2014. No. 3. P. 254-277.
165
10.
Chkhartishvili A.G., Korepanov V.O. Adding Informational Beliefs to the Players
Strategic Thinking Model // IFAC-PapersOnLine. 2016. No. 49(32). P. 19-23.
11.
Алгазин Г.И., Алгазина Д.Г. Коллективное поведение в модели Штакельберга
в условиях неполной информации // АиТ. 2017. № 9. С. 91-105.
Algazin G.I., Algazina D.G. Collective behavior in the Stackelberg model under
incomplete information // Autom. Remote Control. 2017. No. 78(9). P. 1619-1630.
12.
Filatov A.Yu., Makolskaya Ya.S. The equilibrium and socially effective number
of firms in oligopoly: theory and empirics // VIII Moscow Int. Conf. Oper. Res.
(ORM2016). 2016. P. 207-208.
13.
Korepanov V. Strategic Thinking Models for Team Building // Proc. 2019 1st Int.
Conf. Control Syst. Mathem. Modell., Autom. Energy Eff., SUMMA 2019. 2019.
No. 8947593. P. 185-187.
14.
Алгазин Г.И., Алгазина Д.Г. Рефлексивная динамика в условиях неопределен-
ности олигополии Курно // АиТ. 2020. № 2. С. 115-133.
Algazin G.I., Algazina D.G. Reflexive Dynamics in the Cournot Oligopoly under
Uncertainty // Autom. Remote Control. 2020. No. 81(2). P. 287-301.
15.
Алгазин Г.И., Алгазина Д.Г. Процессы рефлексии и равновесие в модели оли-
гополии с лидером // АиТ. 2020. № 7. С. 113-128.
Algazin G.I., Algazina D.G. Reflexion Processes and Equilibrium in an Oligopoly
Model with a Leader // Autom. Remote Control. 2020. No. 81(7). P. 1258-1270.
16.
Уолтерс А.А. Производственные функции и функции затрат: эконометрический
обзор // Теория фирмы. Т. 2. СПб: Экономич. школа. 2000. С. 160-204.
Walters A.A. Production and cost functions: and econometric survey // Econometr.
1963. No. 31(1). Р. 1-66.
17.
Гераськин М.И. Свойства предположительных вариаций в нелинейной модели
олигополии Штакельберга // АиТ. 2020. № 6. С. 105-130.
Geraskin M. The Properties of Conjectural Variations in the Nonlinear Stackelberg
Oligopoly Model // Autom. Remote Control. 2020. No. 81(6). P. 1051-1072.
18.
Гераськин М.И. Анализ равновесий в нелинейной модели олигополии // АиТ.
2022. № 8. С. 140-158.
19.
Гераськин М.И. Приближенное вычисление равновесий в нелинейной модели
олигополии Штакельберга на основе линеаризации // АиТ. 2020. № 9. С. 120-143.
Geraskin M. Approximate Calculation of Equilibria in the Nonlinear Stackelberg
Oligopoly Model: A Linearization Based Approach // Autom. Remote Control. 2020.
No. 81(9). P. 1659-1678.
20.
Intriligator M.D. Mathematical Optimization and Economic Theory. New Jersey:
Prentice-Hall. Englewood Cliffs. 1971.
Статья представлена к публикации членом редколлегии Д.А. Новиковым.
Поступила в редакцию 28.01.2022
После доработки 15.04.2022
Принята к публикации 10.06.2022
166